Planar hexacoordinate chlorine

Abstract

Cl©Zn₆O₆⁻ is identified as a genuine global minimum, which contains a planar hexacoordinate chlorine atom, extending the coordination limit of halogens from five to six. An exhaustive potential energy surface exploration, combined with high-level CCSD(T)/aug-cc-pVTZ calculations, confirms its thermodynamic stability, while Born–Oppenheimer molecular dynamics shows that the planar framework retains its structural integrity up to 900 K. Bonding analyses indicate that Cl©Zn₆O₆⁻ is stabilized predominantly by multicenter ionic interactions between Cl⁻ and the Zn₆O₆ ring. The electronic structure features four Cl lone pairs, Zn–O σ bonds, Zn–O–Zn π bonds, and electrostatic Cl–Zn interactions. With a HOMO–LUMO gap of 5.31 eV and a vertical detachment energy of 7.40 eV, Cl©Zn₆O₆⁻ qualifies as a superhalogen anion. These results show the coexistence of planar hypercoordination and superhalogen character, establishing structural and electronic principles for designing planar hypercoordinate superhalogens.

---

Introduction

Exploring planar hypercoordination and its unconventional bonding patterns has challenged classical views of chemical bonding for more than half a century. The idea traces back to 1968, when Monkhorst proposed planar tetracoordinate carbon (ptC) as a hypothetical transition state.¹ Two years later, Hoffmann, Alder, and Wilcox formalized the ptC concept and suggested stabilizing strategies that became foundational for planar hypercoordinate chemistry.² Shortly after, the identification of the 1,1-dilithiumcyclopropane (C₃H₄Li₂) local minimum initiated the theoretical exploration of viable planar hypercoordinate carbon species.³ Later, photoelectron spectroscopy on clusters such as CAl₄²⁻, CAl₄⁻, CAl₃Si⁻, CAl₃Ge⁻, CAl₄H⁻, C₅Al₅⁻, and CAl₁₁⁻ provided experimental support and guided the expansion of planar carbon chemistry.^4–9 Encouraged by the success in stabilizing ptCs, chemists soon explored whether even higher coordination numbers could be achieved while maintaining planarity. In 2008, Schleyer and Zeng predicted the first planar pentacoordinate carbon (ppC) cluster, CAl₅⁺.¹⁰ Since then, numerous ppC species have been reported.¹¹

According to Hoffmann's electronic strategy, ligands that act as good σ donors and π acceptors can stabilize a ptC atom. Meeting the geometric and electronic requirements simultaneously, however, makes planar hexacoordinate carbon (phC) particularly difficult to realize. More recently, in 2021, Merino and Tiznado designed a series of phC clusters, CE₃M₃⁺ (E = S–Te and M = Li–Cs), using a half-and-half ionic–covalent approach.¹² These phC species are isoelectronic with the previously reported CB₆²⁻ local minimum.^13,14

Planar hypercoordination has since extended beyond carbon. Schleyer and Boldyrev explored planar tetracoordination for second-period elements (B, C, N, O) in 1991.¹⁵ Later, Wang, Boldyrev, and co-workers combined photoelectron spectroscopy experiments with quantum-chemical calculations to determine the global minima of boron cluster anions featuring planar tetra- to octacoordinate boron centers,^16,17 and reported transition-metal-centered boron “molecular wheels” with planar hypercoordinate transition metals.^18–20 These pioneering studies broadened the concept of planarity beyond carbon and inspired further exploration of even higher coordination numbers across the periodic table. For instance, planar hexacoordinate silicon and germanium species, such as Cu₂Si and M₂Ge (M = Cu, Ni),^21–23 were later identified as global minima in two-dimensional potential energy surfaces, showing that coordination numbers beyond four can also be achieved for heavier Group-14 elements. The groups of Cui and Merino extended the concept to alkaline-earth metals (honorary transition metals).²⁴ Current maxima for planar coordination numbers are 10 for transition metals, 15 for alkaline-earth metals, and 8 for nonmetals. Although s-block elements lack p orbitals for π delocalization, they can form clusters featuring planar hypercoordinate atoms. Examples include planar pentacoordinate alkali-metal atoms stabilized purely by σ aromaticity,²⁵ ptBe M₄Be (M = Li, Na), ppBe BeAu₅⁺, phBe Be©Be₆Cl₆, and phM MC₆Al₃⁻ (M = Be, Mg).^26–29 Even hydrogen has recently joined the family of planar hypercoordinate elements.^30–37

Halogens, the most electronegative main-group elements, pose special challenges. Their high electronegativity and localized p orbitals hinder effective delocalization with ligands, so halogens typically appear as terminal (µ¹), bridging (µ²), or face-capping (µ³) atoms. In 2021, the group of Merino predicted the first series of planar tetracoordinate fluorine (ptF) species (FIn₄⁺, FTl₄⁺, FGaIn₃⁺, FIn₂Tl₂⁺, FIn₃Tl⁺, and FInTl₃⁺) as global minima.³⁸ However, subsequent analyses showed that these structures correspond to transition states at the CCSD(T) level with a quadruple-ζ basis set.³⁹ Nevertheless, the small energy differences between planar and nonplanar forms, together with a low imaginary frequency, suggest that these systems exhibit vibrationally average planarity. Later studies reported several ptF global minima, including FLi₄H₃⁻, FK₄H₄⁻, FLi₄X₄⁻ (X = Cl, Br, I).^40–42 Most recently, Cui, Merino, and coworkers predicted planar pentacoordinate halogens Li₅X₆⁻ (X = F, Cl, Br) stabilized mainly by multicenter ionic interactions rather than electron delocalization.⁴³

To date, the highest planar coordination number for halogens is five. Could this limit be extended to six? Here, we target planar hexacoordinate halogen atoms (phX) by systematically examining three series of D_6h X©M₆X₆′⁻ clusters (Scheme 1). The first series (X = F–I; M = Li–Cs; X′ = H, F–I), inspired by known planar pentacoordinate halogens,⁴³ yielded six local minima: X©Li₆X₆′⁻ (X = Cl, Br; X′ = H, F) and I©Na₆X₆′⁻ (X′ = H, F) (Table S1). Highly ionic M–X′ bonding weakens ring rigidity, while the larger in-plane ligand count increases electrostatic repulsion, both unfavorable for planarity. Seeking greater rigidity, we next explored X©M₆X₆′⁻ with alkaline-earth metals (M = Be–Ba), and chalcogenide ligands (X′ = O–Po), motivated by the ppO O©Be₅O₅²⁻ dianion.⁴⁴ Finally, we examined Zn-group analogs (M = Zn–Hg). Among 160 structures, two minima were identified, namely Br©Mg₆O₆⁻ and Cl©Zn₆O₆⁻, with the latter corresponding to the global minimum (Tables S2 and S3).

Scheme 1 The workflow chart for exploring the global minimum (GM) of D_6h phX clusters.

Stabilizing a planar hexacoordinate halogen atom requires multiple chemical design principles rather than a single controlling parameter. First, the ligand ring must be sufficiently rigid to preserve planarity, yet flexible enough to accommodate the central atom. Second, the bonding between the ligands and the metal framework must maintain the integrity of the ring while allowing effective interaction with the central halogen. Finally, a favorable electrostatic coordination environment is essential, such that the central atom is stabilized predominantly by ionic confinement rather than by localized covalent bonding. The systematic screening of alkali-metal, alkaline-earth, and group-12 metal frameworks was therefore used to progressively tune these factors.

So, we report Cl©Zn₆O₆⁻ (1) as the first viable planar hexacoordinate chlorine cluster with high dynamical stability. Its stability arises primarily from multicenter ionic bonding. Localized Zn–O two-center–two-electron (2c–2e) σ bonds and delocalized Zn–O–Zn 3c–2e π bonds confer substantial ring rigidity. Notably, 1 has a large vertical detachment energy (VDE) at the OVGF/aug-cc-pVTZ level,^45–47 classifying it as a superhalogen anion and linking planar hypercoordination with superhalogen chemistry.

Results and discussion

Structure and stability

Structure 1 adopts a symmetric star-like structure with a central Cl atom surrounded by six Zn atoms bridged by six O atoms. The lowest vibrational frequencies (15–33 cm⁻¹, Table S4) confirm that the D_6h structure is a true minimum at all eight tested theoretical levels. Bond distances, Wiberg bond indices (WBIs), and natural population analysis (NPA) charges at the PBE0-D3(BJ)/aug-cc-pVTZ level are summarized in Fig. 1.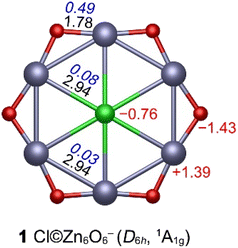

Fig. 1 PBE0-D3(BJ)/aug-cc-pVTZ geometry of Cl©Zn₆O₆⁻. Bond distances (Å, black), WBIs (blue), and NPA charges (|e|, red) are shown.

The Cl–Zn bond distance (2.94 Å) is far longer than a covalent single bond (2.17 Å from Pyykkö's self-consistent covalent radii),⁴⁸ and the small WBI_Cl–Zn (0.08) indicates mainly ionic interactions. Zn–O distances (1.78 Å) are slightly shorter than the standard Zn–O single bond (1.81 Å), with a moderate WBI_Zn–O of 0.49 that is consistent with single-bond character in a highly polar environment. By contrast, Zn–Zn separations (2.94 Å) exceed the sum of covalent radii (2.36 Å), and WBI_Zn–Zn is very low (0.03), consistent with negligible Zn–Zn bonding.

Pauling electronegativities for Cl, Zn, and O are 3.16, 1.65, and 3.44, respectively. Consequently, Zn is expected to donate electron density, whereas Cl and O act as acceptors. The NPA charges (Cl, −0.76; Zn, +1.39; O, −1.43|e|) define an inward-to-outward negative–positive–negative distribution that favors electrostatic stabilization of the planar structure. So, structurally, the system corresponds to a planar core–shell assembly, approximated as [Cl⁻]©[Zn₆O₆].

The global minimum 1 and the seven lowest isomers at the PBE0-D3(BJ)/aug-cc-pVTZ level are shown in Fig. S1 with single-point CCSD(T) relative energies. While isomer 1B, where Cl binds terminally to a tubular Zn₆O₆ framework, is 4.0 kcal mol⁻¹ less stable than 1, the most stable triplet isomer lies 57.7 kcal mol⁻¹ above 1. We also evaluated both the stability and the reference quality of the electronic wavefunction. SCF stability analyses performed for 1 confirm that the reference wavefunction corresponds to a true minimum with no symmetry-breaking instabilities. In addition, the T₁ diagnostic value for 1 is 0.021, which lies well within the accepted range for reliable single-reference treatments. These results indicate that multireference effects are not significant for Cl©Zn₆O₆⁻ and support the robustness of the reported CCSD(T) energetics.

Interestingly, the hollow Zn₆O₆ ring is a local minimum,^49,50 but reoptimization at the PBE0-D3(BJ)/aug-cc-pVTZ level places it 1.9 kcal mol⁻¹ above its own global minimum, consistent with repulsion between adjacent positively charged Zn atoms. The incorporation of a Cl⁻ ion into the central cavity alleviates this repulsion and stabilizes the system, to such an extent that the insertion reaction (Zn₆O₆ + Cl⁻ → Cl©Zn₆O₆⁻) becomes thermodynamically favorable, with a calculated reaction energy of −70.5 kcal mol⁻¹ (including zero-point corrections).

The ability of chlorine to sustain a planar hexacoordinate arrangement within the Zn₆O₆ framework reflects a balance between geometric compatibility and electronic response. Although F, Cl, and Br all form highly polar Zn–X interactions, their different sizes and polarizabilities lead to qualitatively distinct behaviors in the same rigid ligand environment. Natural population analysis (Fig. S2) shows that the central X atoms in D_6h X©Zn₆O₆⁻ (X = F, Cl, Br) carry substantial negative charges (−0.88, −0.76, and −0.64|e|, respectively), consistent with an anion confined by an electrostatic coordination environment. However, size matching between the central atom and the rigid Zn–O ring is critical. D_6h F©Zn₆O₆⁻ and Br©Zn₆O₆⁻ correspond to higher-order saddle points or transition states at the PBE0-D3(BJ)/aug-cc-pVTZ level. In the fluorine case, the imaginary mode (115i cm⁻¹) corresponds to an in-plane displacement of the undersized F atom, whereas for bromine the imaginary mode (29i cm⁻¹) involves an out-of-plane motion along the principal axis, reflecting its excessive size. Chlorine lies between these extremes, providing the optimal size and polarizability required to fit within the rigid Zn–O ring without inducing structural distortion, thereby stabilizing a genuine planar hexacoordinate minimum.

Dynamic stability was evaluated by Born–Oppenheimer molecular dynamics (BOMD) simulations at 300, 600, and 900 K for 50 ps starting from 1. As shown in Fig. S3, the average root-mean-square deviation (RMSD) values are small (0.05, 0.06, and 0.08 Å), with only minor out-of-plane fluctuations of the central Cl atom and negligible Zn or O migration. No isomerization or fragmentation was noted, indicating substantial dynamic robustness. To evaluate the relative roles of geometric constraint and electronic stabilization in enforcing planarity, we examined the energetic response of the central chlorine atom to out-of-plane displacements. The resulting potential energy profile, evaluated at the single-point CCSD(T)/aug-cc-pVTZ level and shown in Fig. S4, reveals that small distortions are relatively soft. Displacing Cl by 0.4 Å along the perpendicular axis costs only 0.4 kcal mol⁻¹, while a larger displacement of 1.0 Å requires 3.7 kcal mol⁻¹. These results indicate that, although the Zn₆O₆ ligand ring provides a geometrically rigid platform, the planar configuration is not imposed purely by mechanical constraint. Instead, electronic interactions play the dominant stabilizing role, with the rigid Zn–O framework enabling (but not solely enforcing) the planar hexacoordinate arrangement.

Chemical bonding

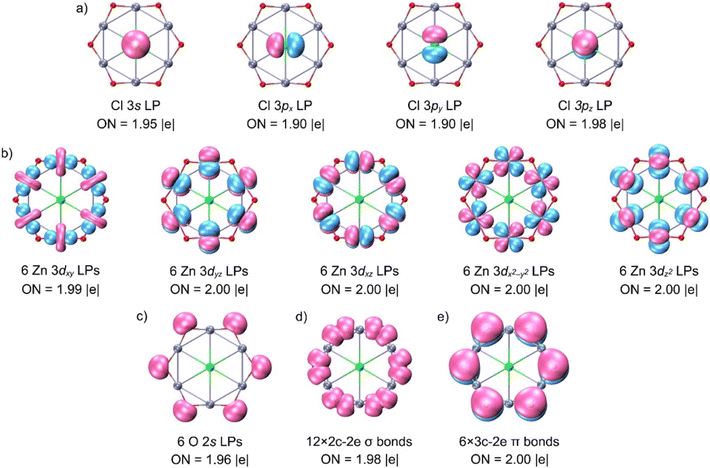
To rationalize the origin of this stability, we next analyzed the bonding using adaptive natural density partitioning (AdNDP), which is well suited to n-center–two-electron (nc–2e) interactions (Fig. 2). The 116 valence electrons in 1 partition into five subsets. First, four 1c–2e lone pairs reside on Cl (derived from 3s, 3p_x, 3p_y, and 3p_z atomic orbitals; ON = 1.90–1.98|e|). When these electrons are alternatively distributed in four delocalized 7c–2e bonds over the ClZn₆ hexagon, the ONs increase slightly to 2.00|e|. This small difference between the two descriptions indicates limited overlap between Cl and the ring, consistent with a predominantly ionic Cl–ring interaction and only a minor covalent component. Second, each Zn contributes five nearly ideal 3d lone pairs (ON = 1.99–2.00|e|). Third, each O carries one s-type lone pair, giving six in total. Finally, the periphery features twelve 2c–2e Zn–O σ bonds (ON = 1.98|e|) and six 3c–2e Zn–O–Zn π bonds (ON = 2.00|e|). These multicenter σ and π interactions provide the mechanical rigidity within the ring. Table S5 lists occupied canonical molecular orbitals (CMOs), which are fully consistent with the AdNDP bonding scheme. Additionally, the electron-density analysis in Fig. S5 further supports the connectivity.

Fig. 2 AdNDP analysis for Cl©Zn₆O₆⁻. Occupation numbers (ONs) are in |e|. (a) Four lone pairs (LPs) of Cl atom; (b) thirty LPs of Zn atoms; (c) six LPs of O atoms; (d) twelve 2c–2e Zn–O σ bonds; (e) six 3c–2e Zn–O–Zn π bonds.

We further examined the interaction of the phCl center with the Zn₆O₆ ring using the energy decomposition analysis (EDA) with natural orbitals for chemical valence (NOCV) at the PBE0/TZ2P-ZORA level. Because the choice of molecular fragments strongly influences the interpretation of EDA-NOCV results, several combinations with different charges and spin states were systematically tested (Table S6). The lowest orbital interaction energy (ΔE_oi) is obtained for the singlet Cl⁻ and singlet Zn₆O₆ fragments, indicating the most suitable bonding model. Quantitatively, the interaction comprises approximately 75.9% electrostatic and 24.1% covalent contributions, so bonding is predominantly ionic, with a smaller but meaningful covalent component. Decomposition of ΔE_oi into individual contributions (Table 1) and the corresponding deformation densities (Fig. 3) shows that relevant interactions correspond to two degenerate Cl⁻ (3p_x, 3p_y) → Zn₆O₆ donations and one weaker Cl⁻ (3s) → Zn₆O₆ donation. Together, they account for 73.8% of ΔE_oi, confirming their dominant stabilizing role. In other words, while an ionic model provides the correct qualitative description, inclusion of covalent effects is required for a physically complete and quantitatively accurate account of the planar hexacoordinate structure.

Table 1 EDA-NOCV results for 1 using Cl⁻ and Zn₆O₆ as interacting fragments at the PBE0/TZ2P-ZORA level. All energy values are given in kcal mol⁻¹

Energy terms	Interaction	Cl^− (singlet, 3s^23px^23py^23pz^2) Zn6O6 (singlet)
a The percentage contribution with respect to the total attraction is given in parentheses.b The percentage contribution with respect to the total orbital interaction is given in parentheses.
ΔEint		−76.9
ΔEPauli		76.9
ΔEelstat^a		−116.8 (75.9%)
ΔEoi^a		−37.0 (24.1%)
ΔEoi(1)^b	Cl^− (3px) → Zn6O6 donation	−11.4 (30.8%)
ΔEoi(2)^b	Cl^− (3py) → Zn6O6 donation	−11.4 (30.8%)
ΔEoi(3)^b	Cl^− (3s) → Zn6O6 donation	−4.5 (12.2%)
ΔEoi(rest)^b		−9.7 (26.2%)

---

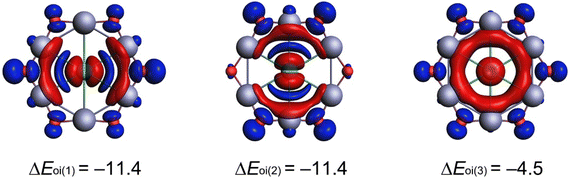Fig. 3 Deformation densities (Δρ) plots from EDA-NOCV analysis. The isovalue of the surfaces is 0.0003 a.u. Charge flows from red (donor) to blue (acceptor). Energy values are given in kcal mol⁻¹.

To quantify ionic and covalent contributions, we applied interacting quantum atoms (IQA) analysis within the Bader framework. The total interatomic interaction energy (V^IQA) separates into electrostatic (V_C) and exchange-correlation (V_XC) terms. Table S7 shows V_C(Cl–Zn) = −106.9 kcal mol⁻¹, substantially larger in magnitude than V_XC(Cl–Zn) = −14.8 kcal mol⁻¹, confirming predominantly ionic Cl–Zn interactions with a non-negligible covalent component. By the IUPAC definition of coordination number (atoms directly linked to a specified atom), Cl in Cl©Zn₆O₆⁻ is genuinely hexacoordinate in the plane. For Zn–O, the covalent component is about half the electrostatic term, lending cohesion and rigidity to the ring, whereas adjacent Zn–Zn interactions are dominated by electrostatic repulsion, consistent with the very small WBIs.

Magnetic response and (lack of) delocalization

The magnetic response of 1 was analyzed to probe possible electronic delocalization (Fig. 4). Examination of the z-component of the induced magnetic field (B^ind_z)^51,52 shows that an external field applied perpendicular to the molecular plane produces a pronounced shielding cone centered on the chlorine atom, arising from its localized lone-pair electrons. However, no extended shielding pattern is found, and the computed ring-current strength (0.31 nA T⁻¹) is very small. So, the analysis of both the induced magnetic field (B^ind) and the induced current density (J^ind)⁵³ confirms this behavior. Instead of a continuous diatropic circulation typical of aromatic systems, only local currents around the Zn and O nuclei and the central Cl are found. This pattern shows that the magnetic response is dominated by local interactions, with no evidence of electron delocalization.

Fig. 4 (a) Magnetically induced current density J^ind maps for Cl©Zn₆O₆⁻. Arrows indicate the direction of the current density. (b) B^ind_z isolines plotted in the molecular plane (bottom) and a transverse plane (top) of the Cl©Zn₆O₆⁻. The external magnetic field is oriented perpendicular to the molecular plane.

Vertical detachment energy

As shown in Fig. S6, 1 has a large HOMO–LUMO gap of 5.31 eV, indicating electronic robustness. The HOMO (b_1g), predominantly O-based (93.64%), has a strongly negative energy (−3.90 eV), while the Zn-based LUMO (a_1g, 82.07%) lies at 1.41 eV. Removing an electron from the HOMO or adding one to the LUMO is therefore energetically disfavored, consistent with the electronic robustness inferred from the wide gap. Indeed, D_6h Cl©Zn₆O₆²⁻ and the neutral D_6h Cl©Zn₆O₆ correspond to saddle points with three or two imaginary frequencies at the PBE0-D3(BJ)/aug-cc-pVTZ level, respectively, confirming that the anion 1 represents an electronically optimal configuration.

For anions, a wide HOMO–LUMO gap often correlates with a large first VDE. The ground-state VDE for 1 is 7.40 eV at the OVGF/aug-cc-pVTZ level, which classifies it as a superhalogen anion. Since Boldyrev introduced superhalogens in 1981, many species have been predicted and experimentally characterized,⁵⁴ though most known superhalogens are three-dimensional. The question then arises whether planar hypercoordinate halogens can display superhalogen behavior. The two areas, long developed in parallel, began to intersect in 2024, when some of us predicted the planar pentacoordinate chlorine superhalogen ppCl Cl©Li₅Cl₅⁻ (D_5h, ),⁵⁵ followed by planar tetracoordinate fluorine superhalogens FLi₄X₄⁻ (X = Cl, Br, I).⁴² As the first planar hexacoordinate chlorine superhalogen, 1 extends this connection, broadening planar hypercoordination and introducing a class of planar hypercoordinate superhalogens that enriches the understanding of electronic stability and structural diversity in main-group chemistry.

From an experimental perspective, cluster-beam techniques combined with photoelectron spectroscopy provide a well-established framework for probing the electronic structure and relative stability of gas-phase cluster anions. In this context, Cl©Zn₆O₆⁻ could in principle be generated by laser ablation of ZnO-based targets doped with chloride salts, followed by mass selection and photodetachment measurements. To facilitate future experimental identification, we simulated the photoelectron spectra of the global minimum and the low-lying isomer (1B) at the TD-PBE0/aug-cc-pVTZ level (Fig. S7), providing distinct spectroscopic fingerprints. At the same time, it should be noted that the very large electron affinity of Cl©Zn₆O₆⁻ (>6 eV) poses a practical challenge, as conventional photoelectron spectroscopy setups may not provide sufficiently high photon energies. This limitation places the present prediction within a realistic experimental context without overstating immediate feasibility.

Conclusions

We have identified and characterized Cl©Zn₆O₆⁻ as the first planar hexacoordinate chlorine superhalogen. The cluster represents a true D_6h global minimum, as confirmed by vibrational analysis, large insertion energy (−70.5 kcal mol⁻¹), and BOMD showing full structural integrity up to 900 K. The planar structure is maintained through a combination of electrostatic and multicenter bonding interactions within a Zn₆O₆ ligand ring.

Bonding analyses reveal a coherent picture of stability. AdNDP identifies four lone pairs on chlorine, twelve Zn–O σ bonds, and six delocalized Zn–O–Zn π bonds that reinforce the mechanical rigidity of the ring. EDA-NOCV partitions the interaction between Cl⁻ and the Zn₆O₆ framework into ∼75.9% electrostatic and ∼24.1% covalent contributions, dominated by Cl (3p_x, 3p_y) and Cl (3s) → Zn₆O₆ dative interactions. The central Cl therefore interacts mainly through ionic attraction complemented by modest covalent coupling.

Electronic-structure calculations yield a wide HOMO–LUMO gap (5.31 eV) and a large vertical detachment energy of 7.40 eV, classifying 1 unambiguously as a superhalogen anion. These findings extend the coordination limit of halogens from five to six and show that planar hypercoordination and superhalogen chemistry can coexist within a single species. The results establish design principles for planar hypercoordinate superhalogens: a geometrically rigid, π-delocalized ligand ring; strong multicenter ionic binding; and targeted covalent donation. The prediction of 1 thus opens a new domain connecting planar hypercoordination with superhalogen behavior, offering a framework for designing future main-group clusters with extreme electronic stability and high electron affinity.

Computational details

The potential energy surface of Cl©Zn₆O₆⁻ was explored using the Coalescence Kick (CK) algorithm at the PBE0/LANL2DZ level, generating approximately 6000 initial geometries (3000 singlets and 3000 triplets).^56,57 In addition to the automated global search, a limited number of candidates were manually constructed to improve coverage of chemically reasonable bonding motifs.⁵⁸ This complementary step was guided by established chemical considerations, including preservation of D_6h symmetry, maintenance of a rigid Zn–O framework, and the presence of an electrostatic coordination environment involving the central halogen and multiple metal centers. Practically, additional isomers were generated through small structural modifications of the lowest-lying candidates obtained from the CK searches, as well as by introducing a Cl atom into low-energy Zn₆O₆ frameworks using common coordination modes, namely terminal, bridging, and face-capping arrangements. This procedure was intended to complement the stochastic search by ensuring that relevant planar hypercoordinate bonding patterns were adequately sampled, rather than to bias the exploration of the potential energy surface. All low-energy candidates were reoptimized at the PBE0-D3(BJ)/aug-cc-pVTZ level,^59,60 followed by harmonic vibrational frequency analyses to confirm their nature as minima or transition states. Final single-point energies were refined at the CCSD(T)/aug-cc-pVTZ level, including zero-point energy (ZPE) corrections from the PBE0-D3(BJ)/aug-cc-pVTZ calculations.⁶¹ Unless otherwise specified, energetic discussion refers to CCSD(T)/aug-cc-pVTZ//PBE0-D3(BJ)/aug-cc-pVTZ results.

Natural bond orbital (NBO) analysis was performed to obtain WBIs and natural population NPA charges.⁶² Bonding was further analyzed using AdNDP, CMO inspection, and Bader analyses.^63,64 Orbital compositions and Bader analysis were examined with Multiwfn.⁶⁵ All electronic-structure calculations were performed using Gaussian16.⁶⁶ The CCSD(T) calculations were carried out using the Molpro 2012.1 package.⁶⁷ IQA and energy decomposition analysis with natural orbitals for chemical valence (EDA-NOCV) were carried out with ADF 2023.^68,69

The induced magnetic field (B^ind) and current density (J^ind) were computed at the DFT level using the BHandHLYP⁷⁰ functional and the def2-TZVP basis set with the GIAO formalism. B^ind was obtained with Aromagnetic,⁷¹ which automatically generated the three-dimensional grid and exploited the D_6h symmetry of the molecule to reduce computational cost. The induced currents were calculated with GIMIC⁷² from the same electron densities. The external magnetic field was applied along the z axis (0, 0, 1), corresponding to the principal symmetry axis.

Dynamic stability of the phCl cluster was evaluated through Born–Oppenheimer molecular dynamics (BOMD) simulations at 300, 600, and 900 K for 50 ps using the CP2K program with GTH-PBE pseudopotentials and the DZVP-MOLOPT-SR-GTH basis set.^73,74

Conflicts of interest

The authors declare no conflict of interest.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5sc09167e.

Acknowledgements

This work was funded by the National Natural Science Foundation of China (No. 22173053).

References

1. H. J. Monkhorst, Chem. Commun., 1968, 1111–1112.
2. R. Hoffmann, R. W. Alder and C. F. Wilcox, J. Am. Chem. Soc., 1970, 92, 4992–4993.
3. J. B. Collins, J. D. Dill, E. D. Jemmis, Y. Apeloig, P. v. R. Schleyer, R. Seeger and J. A. Pople, J. Am. Chem. Soc., 1976, 98, 5419–5427.
4. X. Li, L. S. Wang, A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1999, 121, 6033–6038.
5. X. Li, H. F. Zhang, L. S. Wang, G. D. Geske and A. I. Boldyrev, Angew. Chem., Int. Ed., 2000, 39, 3630–3632.
6. L. S. Wang, A. I. Boldyrev, X. Li and J. Simons, J. Am. Chem. Soc., 2000, 122, 7681–7687.
7. J. Xu, X. X. Zhang, S. Yu, Y. H. Ding and K. H. Bowen, J. Phys. Chem. Lett., 2017, 8, 2263–2267.
8. C. J. Zhang, P. Wang, X. L. Xu, H. G. Xu and W. J. Zheng, Phys. Chem. Chem. Phys., 2021, 23, 1967–1975.
9. C. J. Zhang, W. S. Dai, H. G. Xu, X. L. Xu and W. J. Zheng, J. Phys. Chem. A, 2022, 126, 5621–5631.
10. Y. Pei, W. An, K. Ito, P. v. R. Schleyer and X. C. Zeng, J. Am. Chem. Soc., 2008, 130, 10394–10400.
11. V. Vassilev-Galindo, S. Pan, K. J. Donald and G. Merino, Nat. Rev. Chem., 2018, 2, 0114.
12. L. Leyva-Parra, L. Diego, O. Yañez, D. Inostroza, J. Barroso, A. Vásquez-Espinal, G. Merino and W. Tiznado, Angew. Chem., Int. Ed., 2021, 60, 8700–8704.
13. K. Exner and P. v. R. Schleyer, Science, 2000, 290, 1937–1940.
14. B. B. Averkiev, D. Y. Zubarev, L. M. Wang, W. Huang, L. S. Wang and A. I. Boldyrev, J. Am. Chem. Soc., 2008, 130, 9248–9250.
15. P. v. R. Schleyer and A. I. Boldyrev, J. Chem. Soc., Chem. Commun., 1991, 1536–1538.
16. A. P. Sergeeva, I. A. Popov, Z. A. Piazza, W. L. Li, C. Romanescu, L. S. Wang and A. I. Boldyrev, Acc. Chem. Res., 2014, 47, 1349–1358.
17. T. Jian, X. N. Chen, S. D. Li, A. I. Boldyrev, J. Li and L. S. Wang, Chem. Soc. Rev., 2019, 48, 3550–3591.
18. T. R. Galeev, C. Romanescu, W. L. Li, L. S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed., 2012, 51, 2101–2105.
19. T. Heine and G. Merino, Angew. Chem., Int. Ed., 2012, 51, 4275–4276.
20. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Acc. Chem. Res., 2013, 46, 350–358.
21. L. M. Yang, V. Bačić, I. A. Popov, A. I. Boldyrev, T. Heine, T. Frauenheim and E. Ganz, J. Am. Chem. Soc., 2015, 137, 2757–2762.
22. L. M. Yang, I. A. Popov, T. Frauenheim, A. I. Boldyrev, T. Heine, V. Bačić and E. Ganz, Phys. Chem. Chem. Phys., 2015, 17, 26043–26048.
23. L. M. Yang, I. A. Popov, A. I. Boldyrev, T. Heine, T. Frauenheim and E. Ganz, Phys. Chem. Chem. Phys., 2015, 17, 17545–17551.
24. X. B. Liu, W. Tiznado, L. J. Cui, J. Barroso, L. Leyva-Parra, L. H. Miao, H. Y. Zhang, S. Pan, G. Merino and Z. H. Cui, J. Am. Chem. Soc., 2024, 146, 16689–16697.
25. M. H. Wang, A. J. Kalita, M. Orozco-Ic, G. R. Yan, C. Chen, B. Yan, G. Castillo-Toraya, W. Tiznado, A. K. Guha, S. Pan, G. Merino and Z. H. Cui, Chem. Sci., 2023, 14, 8785–8791.
26. L. H. Miao, L. J. Cui, H. Y. Zhang, M. Orozco-Ic, Y. F. Yang, S. Pan and Z. H. Cui, J. Chem. Phys., 2024, 161, 244303.
27. C. Chen, Y. Q. Liu and Z. H. Cui, Inorg. Chem., 2021, 60, 16053–16058.
28. B. Jin, X. L. Guan, M. Yan, Y. J. Wang and Y. B. Wu, Chem.–Eur. J., 2023, 29, e202302672.
29. G. R. Yan, Y. Q. Liu, X. B. Liu, M. H. Wang, Z. H. Cui and S. Pan, J. Chem. Phys., 2023, 159, 054301.
30. K. Sarmah, A. J. Kalita and A. K. Guha, Inorg. Chem., 2023, 62, 20919–20922.
31. A. J. Kalita, S. S. Rohman, P. P. Sahu and A. K. Guha, Angew. Chem., Int. Ed., 2024, 63, e202403214.
32. L. X. Bai, Y. X. Jin and J. C. Guo, Chem. Commun., 2024, 60, 6300–6303.
33. K. Sarmah, A. J. Kalita, S. K. Purkayastha and A. K. Guha, Angew. Chem., Int. Ed., 2024, 63, e202318741.
34. L. J. Cui, X. B. Liu, H. Y. Zhang, B. Yan, M. Orozco-Ic, S. Pan and Z. H. Cui, Inorg. Chem., 2024, 63, 13938–13947.
35. H. F. Yan and J. C. Guo, Phys. Chem. Chem. Phys., 2025, 27, 7383–7388.
36. L. X. Bai, Y. X. Jin, M. Orozco-Ic, G. Merino and J. C. Guo, Chem. Commun., 2024, 60, 14996–14999.
37. B. Jin and Y. J. Wang, Chem.–Eur. J., 2025, 31, e202403790.
38. G. Castillo-Toraya, M. Orozco-Ic, E. Dzib, X. Zarate, F. Ortíz-Chi, Z. H. Cui, J. Barroso and G. Merino, Chem. Sci., 2021, 12, 6699–6704.
39. J. Kim, E. Park, J. Park, J. Kim, W. Seo, D. Oh, J. Lee and T. K. Kim, J. Phys. Chem. A, 2023, 127, 5815–5822.
40. K. Sarmah, A. J. Kalita and A. K. Guha, Phys. Chem. Chem. Phys., 2024, 26, 6678–6682.
41. Y. X. Jin, L. X. Bai and J. C. Guo, Inorg. Chem., 2024, 63, 19949–19955.
42. Y. X. Li, L. X. Bai and J. C. Guo, Molecules, 2024, 29, 5810.
43. L. J. Cui, L. H. Miao, M. Orozco-Ic, L. Li, S. Pan, G. Merino and Z. H. Cui, Angew. Chem., Int. Ed., 2025, 64, e202416057.
44. R. Sun, Y. Yang, X. Wu, H. J. Zhai, C. X. Yuan and Y. B. Wu, Chem. Sci., 2025, 16, 12873–12878.
45. L. S. Cederbaum, J. Phys. B: At., Mol. Opt. Phys., 1975, 8, 290–303.
46. J. V. Ortiz, J. Chem. Phys., 1988, 89, 6348–6352.
47. J. V. Ortiz, Adv. Quantum Chem., 1999, 35, 33–52.
48. P. Pyykkö, J. Phys. Chem. A, 2015, 119, 2326–2337.
49. A. A. Al-Sunaidi, A. A. Sokol, C. R. A. Catlow and S. M. Woodley, J. Phys. Chem. C, 2008, 112, 18860–18875.
50. I.-P. Zaragoza, L.-A. Soriano-Agueda, R. Hernández-Esparza, R. Vargas and J. Garza, J. Mol. Model., 2018, 24, 164.
51. G. Merino, T. Heine and G. Seifert, Chem.–Eur. J., 2004, 10, 4367–4371.
52. R. Islas, T. Heine and G. Merino, Acc. Chem. Res., 2012, 45, 215–228.
53. D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678.
54. G. L. Gutsev and A. I. Boldyrev, Chem. Phys., 1981, 56, 277–283.
55. L. X. Bai, C. Y. Gao, J. C. Guo and S. D. Li, Molecules, 2024, 29, 3831.
56. M. Saunders, J. Comput. Chem., 2004, 25, 621–626.
57. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
58. V. S. Thimmakondu, A. Sinjari, D. Inostroza, P. Vairaprakash, K. Thirumoorthy, S. Roy, A. Anoop and W. Tiznado, Phys. Chem. Chem. Phys., 2022, 24, 11680–11686.
59. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
60. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
61. G. D. Purvis III and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918.
62. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
63. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
64. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
65. T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592.
66. M. J. Frisch, et al., in Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, U.S.A., 2016.
67. H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
68. M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975.
69. ADF2023, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands.
70. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
71. F. Martínez-Villarino, M. Orozco-Ic, G. Merino, Aromagnetic 2.0, Cinvestav Mérida, Mérida, Mexico, 2025.
72. J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963.
73. J. M. Millam, V. Bakken, W. Chen, W. L. Hase and H. B. Schlegel, J. Chem. Phys., 1999, 111, 3800–3805.
74. T. D. Kühne, et al., J. Chem. Phys., 2020, 152, 194103.

---