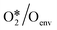Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Comprehensive understanding of ethylene epoxidation on copper catalysts: a microkinetic study with coverage effects†
Zhuozheng
Wang
abc,
Wenbo
Xie
bc,
Yarong
Xu
d,
Yulan
Han
c,
Jiayan
Xu
c and
P.
Hu
 *bc
*bc
aPetroChina Petrochemical Research Institute, Beijing 102206, China
bSchool of Physical Science and Technology, ShanghaiTech University, 393 Middle Huaxia Road, Shanghai 201210, China
cSchool of Chemistry and Chemical Engineering, The Queen's University of Belfast, Belfast BT9 5AG, UK. E-mail: p.hu@qub.ac.uk
dResearch Institute of Urumqi Petrochemical Company, PetroChina Company Limited, Urumqi 830019, China
First published on 7th August 2024
Abstract
Ethylene epoxidation is one of the fundamental industrial reactions, garnering extensive theoretical and experimental studies. While silver has traditionally been the catalyst of choice for this reaction, copper has received comparatively little attention. In this study, we apply a coverage-dependent microkinetic modeling to quantitatively investigate ethylene epoxidation on Cu(111), serving as a model system to study the intrinsic activity and selectivity of Cu catalysts. The coverage-dependent simulation takes into account both self and cross-interactions of adsorbates, as well as the coverage effects on the transition states of each elementary step. In contrast, the coverage-independent modeling is conducted without considering coverage effects. We observe that the coverage-dependent modelling reveals the Cu(111) surface with coverage exceeding 30% oxygen atoms with a high turnover frequency (log(TOF) = 2.65) at 500 K. In contrast, the coverage-independent results indicate the Cu(111) surface being completely covered by oxygen atoms, leading to detrimental poisoning effects (log(TOF) = −2.47). We show that the EO selectivity on Cu(111) can be at a high level of 80% under all studied conditions in contrast to only ∼40% EO selectivity on Ag(111). Detailed structural analyses unveil the fundamental reasons why Cu catalysts are more selective for ethylene epoxidation. Furthermore, we suggest that reducing temperature and increasing oxygen pressure can effectively improve EO selectivity for industrial ethylene epoxidation.
1. Introduction
Ethylene epoxidation plays a crucial role in the industry due to the wide range of applications of ethylene epoxide. One notable example is the increased demand for medical equipment disinfectants in recent years, representing a primary ethylene epoxide utilization. Furthermore, ethylene epoxide serves as a precursor for various complex chemical products, including ethylene glycol and ethanolamine. Over the past century, numerous studies on epoxidation have been reported, contributing to the continuous advancement of the ethylene industry.1–5 The industrial relevance of EO has driven extensive research into the development of efficient and selective catalysts, with transition metal catalysts being the most prominent for this transformation.The main oxidation involves the interaction of ethylene with adsorbed oxygen atoms on the metal surface, leading to the formation of ethylene epoxide or acetaldehyde through the oxametallocycle (OME) intermediate, as depicted in Scheme 1. Significant research has been conducted to comprehend the mechanism of ethylene epoxidation on metal catalyst surfaces.6–10 In this regard, a study was conducted by Liu and co-workers on the process of ethylene epoxidation on silver surfaces, which employed machine learning for global pathway sampling. The study identified three reaction pathways and emphasized the often-neglected dehydrogenation pathway via the OME intermediate. This insightful study provides meaningful and valuable information regarding the ethylene epoxidation process on silver-based catalysts.
The selectivity of ethylene epoxide (EO) is a critical parameter for evaluating the performance of an ethylene catalyst. In traditional industrial ethylene production, silver catalysts supported on alumina are widely employed to enhance EO selectivity.11–14 Currently, various industrial catalysts have demonstrated the ability to achieve high EO selectivity. For instance, Ag/Al2O3 catalysts doped with alkali metals14,15 and Re/Cs/Ag/Al2O3 catalysts doped with sulfur and molybdenum oxide16,17 have shown promising results. Another approach involves the utilization of chlorine as a dopant to improve EO selectivity.11,14,18 However, the complexity of dopants and the high cost of precious metal materials pose significant challenges to the development of industrial ethylene epoxidation catalysts. Therefore, achieving high EO selectivity at a lower cost has emerged as a pivotal concern in the ethylene oxidation industry. Copper, belonging to the same group as silver and gold but less expensive, has long been considered a primary candidate for replacing silver catalysts due to its commercial value and similar chemical properties.19–22 Previous studies have demonstrated that utilizing copper exhibits significantly higher selectivity in the epoxidation of olefins such as ethylene,23,24 styrene,25,26 methyl styrene,27 and propylene28 compared to silver catalysts. However, there is still ongoing debate regarding the intermediates, reaction networks, and reaction kinetics involved in ethylene epoxidation on Cu(111). The details of ethylene epoxidation on Cu(111) are still shrouded in mist. Given the exceptional performance of copper in olefin epoxidation, there is a clear need for a comprehensive investigation into the mechanism and intrinsic activity of ethylene epoxidation on Cu(111). In addition, comparing the activity and selectivity of the Cu(111) model system to those of Ag(111) may provide some insights into ethylene epoxidation.
In recent years, there has been a notable application of first-principles-based microkinetic modeling in various heterogeneous catalytic systems, yielding promising outcomes.29–32 This approach enables the determination of the rates of all given elementary steps, thereby facilitating quantitative studies on the activity and selectivity of different products.33–35 Moreover, the utilization of coverage-dependent microkinetic models has proven valuable in quantifying conflicting findings and reconciling oversimplified theoretical frameworks.36–39 This highlights the significance of considering the coverage effect to obtain precise kinetic results. Previous studies on ethylene epoxidation on silver surfaces have demonstrated that considering the coverage effect is crucial for obtaining consistent kinetic results that align with experimental values. Conversely, neglecting the coverage effect leads to significant distortions in the obtained results.40 While there have been brief investigations into ethylene epoxidation on Cu(111), these studies have primarily focused on fundamental aspects, and more comprehensive quantitative simulation models are desirable. Furthermore, the detailed structures of various intermediates, transition states, and surface-adsorbed species still require to be determined. Therefore, there is a pressing need for a systematic investigation of ethylene epoxidation on Cu(111) to establish a robust theoretical foundation for the design and development of novel copper-based catalysts.
In this work, the ethylene epoxidation on Cu(111) was systematically studied utilizing DFT calculations and first-principles-based microkinetic modeling. We are addressing the following issues: (i) what are the reaction networks of ethylene epoxidation on Cu(111)? Is EO the main product? (ii) Is Cu(111) more suitable as a catalyst for ethylene epoxidation than Ag(111)? (iii) Does oxygen coverage affect ethylene epoxidation on Cu(111)? If so, what quantitative insights could be obtained through the coverage-dependent microkinetic analysis? In the subsequent sections, we will provide detailed findings and explanations attacking the abovementioned questions. Primarily, the self-consistent coverage-dependent microkinetic model was established to clarify the mechanism of ethylene epoxidation on Cu(111). Comprehensive inclusion of the interactions of all surface adsorption species and transition states (TSs) involved in the catalytic cycle was ensured. The ethylene epoxidation activity and selectivity on Cu(111) were determined utilizing the coverage-dependent microkinetic model, yielding results consistent with experimental values. Based on the findings from the coverage-dependent microkinetic model, several suggestions for optimizing the operational conditions of ethylene epoxidation were proposed. Moreover, it has been demonstrated that the conventional model used in heterogeneous catalysis fails to yield appropriate results for ethylene epoxidation and may not be applicable to other reaction systems.
2. Computational method
2.1 Energy calculation
The ethylene epoxidation was studied using calculations of density functional theory (DFT). All the DFT calculations were performed utilizing the Vienna ab initio Simulation Package (VASP).41,42 The generalized gradient approximation (GGA) Perdew–Burke–Ernzerhof (PBE) functional was adopted for all ground state calculations.43 The projector-augmented-wave (PAW) pseudopotentials were utilized with 400 eV cutoff energy.42,44 The constrained minimization method was utilized for the transition state search.45–48 The Cu(111) surface was modeled by a p(3 × 3) supercell, which was sampled with a 2 × 2 × 1 Monkhorst–Pack k-point mesh.49 The DFT-D3 approximation method was utilized to include van der Waals (vdW) interactions.50 In all the simulations, the vacuum layer was built at a thickness of 12 Å. The desired level of structural optimization accuracy was achieved when the forces on the relaxed atoms were below 0.05 eV Å−1. All the free energies were obtained based on calculated potential energies with thermodynamic corrections. All the gas-phase molecules were optimized in a (10 × 10 × 10) Å3 box with the thermodynamic correction calculated by Gaussian 09.512.2 Microkinetic models
The ethylene epoxidation on Cu(111) was thoroughly investigated using coverage-dependent microkinetic models. Table 1 presents the nine elementary steps that are widely acknowledged for ethylene epoxidation on metal surfaces. Among them, ki and k−i denote the forward and reverse reaction rate constants, respectively, while ri represents the reaction rate of the i-th step. The rate constant calculation incorporates the transition state theory, as follows, | (1) |
In the equation, T is temperature, ΔG‡i is the standard Gibbs free energy of activation barrier between transition state and initial state for step i, kB is the Boltzmann constant, and h is the Planck's constant.
Considering the coverage effect, the adsorption energies under different coverages could be defined as,
| Gads(θn) = Gn − Gn−1 − Ggas | (2) |
There are nine active site on the Cu(111) surface, which are defined as 100% coverage when all of them are occupied, namely, one monolayer (1 ML). Each surface species occupies only one active site. Consequently, if there is an adsorbed oxygen atom on the surface, the coverage is 0.11 ML, which is the coverage employed in the coverage-independent modeling. The two-line model was utilized to simulate the adsorption energy and activation barrier of all surface adsorbates affected by coverage effects.33,34,39 The two-line model elaborated the linear relationship between the energy and the coverage, serving as an approach to describe reaction kinetics.52,53 The adsorption energy, considering the interaction between target adsorbates and environmental adsorbates under different coverages, can be expressed as follows,
 | (3) |
The turnover frequency (TOF) is a vital parameter used to characterize the intrinsic activity of catalytic materials. A self-consistent iterative method, as depicted in Fig. S1,† was employed to calculate the TOF value.54,55 The well-established software CATKINAS was utilized for microkinetic modeling and data analysis.56–59 To obtain reliable results, the coverage of species and kinetic values at the steady state were collected once the convergence value X reached a sufficiently small value (X < 0.001).
To investigate the detailed impact of reaction kinetics on selectivity and activity, the degree of rate control (DRC) analysis is incorporated herein. The DRC concept, as defined by Campbell, quantifies the influence of individual elementary steps on the overall reaction rate.60,61 Mathematically, it can be expressed as follows:
 | (4) |
3. Results and discussion
3.1 Conventional ethylene epoxidation on Cu(111)
The ethylene epoxidation reaction adheres to the well-established OME intermediate mechanism.6,7Fig. 1 illustrates the ethylene epoxidation reaction network, which comprises nine elementary steps derived from the mechanism as mentioned above. Fig. 2 depicts the surface adsorbates, intermediates, and transition state structures involved in the reaction. The reaction mechanism of ethylene epoxidation can be divided into three main stages. Firstly, oxygen molecules adsorb (1) and dissociate (3) on the surface, while ethylene molecules adsorb on the surface (2). Subsequently, ethylene undergoes a partial oxidation reaction, leading to the formation of the OME intermediate. Given the ongoing controversy surrounding the Langmuir–Hinshelwood (4) and Eley–Rideal mechanisms (5),62–65 both were considered in order to construct a comprehensive and rigorous reaction network. Finally, the simultaneous formation (6 and 7) and desorption (8 and 9) of ethylene epoxide and acetaldehyde occur. All the transition states during ethylene epoxidation were taken into account, including oxygen dissociation (TSOO), OME intermediate formation (TS1), EO formation (TSEO), and AA formation (TSAA). The corresponding structures are illustrated in Fig. 2. It is noteworthy that the formations of ethylene epoxide and acetaldehyde, referred to as OME* → EO* and OME* → AA*, respectively, are defined as the selective competition steps.On the Cu(111) surface, the hollow sites are occupied by oxygen atoms, whereas ethylene undergoes adsorption in a parallel π-configuration. Both carbon atoms in the ethylene molecule are located at the bridge site with the molecular center positioned at the top site. Subsequently, one carbon atom of the ethylene molecule remains at the top site, occupying the hexagonal hollow site on the Cu(111) surface, while another carbon atom approaches the oxygen atom, leading to OME formation. Subsequently, the carbon occupying the top site leaves the surface while cyclization and H-transfer occur in parallel, generating ethylene epoxide and acetaldehyde. EO and AA produced from the OME intermediate exhibit relatively weak adsorption mainly due to the van der Waals interaction on the surface, making them prone to desorption. It is clear that the selective competition steps should be the most crucial steps affecting epoxidation selectivity.
3.2 Establishment of the coverage-dependent microkinetic model
To quantitatively investigate the influence of oxygen coverage, we developed a coverage-dependent model that includes the presence of pre-adsorbed oxygen atoms, the so-called environmental species. We then optimized the structures of all the adsorbed species based on pre-adsorbed oxygen atoms on Cu(111) with varying coverages. It is important to note that every possible surface structure was thoroughly optimized under each coverage. The structure with the lowest energy was then chosen to define the surface structure and determine the chemisorption energy for that particular coverage. As an illustration, in the study of O*/Oenv self-interaction at 0.33 ML, the adsorbed oxygen atom (O*) occupies a single site on the surface, whilst two environmental oxygen species (Oenv) occupy two sites on the surface. The structure with the lowest energy was chosen to calculate the adsorption free energy, shown in Fig. 3. (ESI†) S2 contains other surface species at various coverages.The linear relationship between coverage and energy is established based on the adsorption free energy obtained from the coverage-dependent model. Fig. 4 depicts the linear relationship observed between the self-interaction of adsorbed oxygen atoms (O*/Oenv) and the cross-interaction between OME and oxygen atoms (OME*/Oenv) at 490 K on Cu(111). Additional information regarding the linear relationships of other surface adsorbed species can be found in ESI† S3. The determination of adsorption energies was carried out with reference to the formation energies to minimize simulation errors,34,66 and further details can be found in ESI† S4. Fig. 4 shows that the adsorption weakens as the number of environmental species increases. The bonding competition theory and surface repulsion effect aid in explaining the observed phenomenon of change.67–70 As more adsorbates accumulate on the surface, the surface becomes crowded by adsorbates and is thus less active. This implies that the greater the number of adsorbates present on the surface, the more challenging it is for new adsorption to occur.
In the two-line model, the intercept at low coverages represents the adsorption free energy with the coverage approaching to the zero. It is a measure of adsorption strength without any interactions. In the realm of linear regression, the slope serves as a quantification of the degree of change. The slope in the two-line model holds significant chemical implications, as it represents a measure of interaction between adsorbates. O* is the only main species on the catalyst under the reaction steady state, and thus the slopes are largely determined by oxygen coverage. Within the context of the linear relationships between O*/Oenv and OME*/Oenv (Fig. 4), the slopes for low and high coverage are found to be 0.818, 0.545, and 4.957, 7.818, respectively. For instance, in the O*/Oenv system, as the O coverage increases from 0.11 ML to 0.33 ML (a low coverage region), the adsorption free energy rises by 0.68 eV. When the coverage further increases from 0.44 ML to 0.67 ML (a high coverage region), the adsorption free energy increases by 1.14 eV, indicating a stronger interaction between adsorbed O species at the higher coverages. These observations suggest that under low coverage, the adsorption free energy changes at a slow rate. Conversely, the changes occur more rapidly under high coverage due to the stronger interactions between environmental species and target species. Table 2 further demonstrates that the significant difference between high and low coverage exists in all temperature and adsorbed species, indicating that the two-line model is both necessary and efficient.
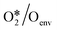 and OME*/Oenv at different temperatures from 480 K and 600 K on Cu(111)
and OME*/Oenv at different temperatures from 480 K and 600 K on Cu(111)
We conducted an in-depth analysis on the structural changes of the transition states and the impact of coverage on the reaction barrier. In ESI† S2 and S3, we present the TS-adsorbate cross-interaction structures and linear relationships, while Table 3 outlines the slopes of cross-interactions of all the transition state-environmental species at high coverage on Cu(111). Our microkinetic modeling has taken into account all the coverage effects on the transition states involved in ethylene epoxidation, including TSOO, TS1, TSEO, and TSAA. Among these transition states, the impact of the coverage effects on TSOO is the most significant, with a slope of 7.304 at high coverage and 490 K, indicating that oxygen dissociation plays a crucial role. This is attributed to the fact that only the oxygen atoms among all the surface adsorbates are closest to the surface (1.12 Å) and the adsorption is strongest. The adsorption energies of other adsorbates are relatively weaker and positioned farther from the surface, and the requirements on the geometrical space of adsorption are relatively smaller. The bonding between the surface and the adsorbed carbon atom of ethylene in TSAA necessitates the presence of at least one vacant hexagonal cavity on the surface. Moreover, the ethylene structures at TSAA and TS1 are positioned further away from the Cu(111) surface, thereby rendering them less susceptible to the coverage compared to TSOO. TSEO is the least coverage affected as the ethylene structure is enclosed by oxygen atoms and is distanced from the surface by a significant margin (3.06 Å), thereby providing insulation from environmental species.
| Slope (eV ML−1) | 480 K | 490 K | 500 K | 520 K | 540 K | 600 K |
|---|---|---|---|---|---|---|
| TSOO/Oenv | 7.297 | 7.304 | 7.320 | 7.277 | 7.277 | 7.244 |
| TS1/Oenv | 4.470 | 4.480 | 4.475 | 4.457 | 4.465 | 4.430 |
| TSEO/Oenv | 2.840 | 2.849 | 2.858 | 2.822 | 2.849 | 2.849 |
| TSAA/Oenv | 5.520 | 5.519 | 5.520 | 5.520 | 5.476 | 5.432 |
Some typical structures of the transition state-adsorbate cross-interaction are illustrated in Fig. 5. The O–O bond length on the copper surface changes from 1.69 Å to 1.96 Å, as the coverage is increased from 0.11 ML to 0.89 ML. Similarly, the C1–O bond length changes from 1.87 Å to 2.04 Å with the coverage increases from 0.11 ML to 0.78 ML. It signifies that the transition state structure approaches the dissociation state as the coverage increases. Although the trend of structural changes is the same, the resulting energy barrier changes are the opposite. Specifically, environmental oxygen atoms hinder the adsorption of more oxygen atoms on the surface, thereby impeding oxygen dissociation at high coverage and leading to a rapid increase in the energy barrier. Conversely, in the TSEO structure, an increase in the coverage of environmental oxygen atoms tends to repel the TSEO structure fragments due to the ethylene fragments being held aloft by oxygen atoms. Thus, the TSEO structure is more prone to forming the final state, i.e., the adsorbed ethylene epoxide, which leads to a decrease in the TSEO energy barrier. These changes in structure and energy barrier are consistent with slope changes of adsorbates, and the specific energy barrier changes will be further elaborated on in the subsequent section.
3.3 Comparison of coverage distributions and reaction kinetics between coverage-independent and coverage-dependent modellings on Cu(111)
This section presents the microkinetic modeling results to understand the connection between the coverage effect and reaction kinetics. Here we focus on the coverage-dependent microkinetic of ethylene epoxidation on the Cu(111) surface. The coverage-independent model was also included herein to highlight their limitations. All adsorption and desorption steps were treated as quasi-equilibrium steps in the modeling. In the kinetic analysis, pO2 = 20 kPa and pEt = 2.66 kPa were used as they are common experimental conditions for ethylene epoxidation.In Fig. 6(a), the log(TOF) results of ethylene epoxidation are presented for conditions of 500 K, pEt = 2.66 kPa and pO2 = 20 kPa. Our findings reveal that when considering the coverage effect on Cu(111), the log(TOF) results closely matched both the experimental values71 and the simulation results on Ag(111),40 with values of 2.65, 1.77, and 2.34, respectively. Conversely, the coverage-independent log(TOF) on Cu(111) is significantly lower than the values mentioned before, with a value of −2.47, implying that neglecting the coverage effect leads to distorted results. Incorporating the self-interaction and cross-interaction of adsorbates significantly improves the modeling accuracy. The distortion observed in the coverage-independent microkinetic modeling is primarily due to its neglect of the substantial changes in the oxygen dissociation barrier. Surface reactions are hindered by many adsorbed oxygen atoms, and numerous surface oxygen atoms cause surface poisoning (99.9%), as depicted in Fig. 6(b). Nonetheless, the coverage-dependent microkinetic modeling indicates a total surface coverage of 36.1% at the steady-state, including 34.5% adsorbed oxygen atoms and 1.6% OME intermediates, which appears to be a more reasonable outcome. As mentioned in the introduction, OME may undergo decomposition. In this work, we have also taken the OME decomposition into account. Our results show that the OME decomposition process has a negligible effect on the kinetic outcomes, as evidenced in ESI† S5.
The free energy profiles obtained from the coverage-independent and coverage-dependent modeling are compared in Fig. 6(c). It is observed that the hindrance of surface environmental oxygen atoms causes a significant increase in the oxygen dissociation energy barrier, from 0.05 eV to 0.63 eV, reducing the dissociation of oxygen molecules under high coverage. On the other hand, the energy barriers of the selective competition steps decrease when considering the coverage effect, leading to increased activity. Fig. 6(c) displays only the free energy profiles from the L–H mechanism (step 4) and the results from E–R mechanism (step 5) have not been included in the diagram. Nevertheless, the microkinetic modelling has considered both mechanisms, and the energy profiles of the E–R mechanism can be found in Fig. S8.† The trend of energy barrier TSEO and TSAA with temperature in the selective competition steps considering the coverage effect is shown in Fig. 7(a). As the persistence of TSEO is lower than that of TSAA, the energy barrier of TSEO decreases faster as the temperature drops, indicating that low temperature helps to improve the EO selectivity. Finally, Fig. 7(b) suggests that the results of coverage-independent log(TOF) consistently displays a lower value than coverage-dependent log(TOF) as temperature changes, suggesting that temperature variations do not contribute to the improvement of coverage-independent modeling results. Furthermore, it should be noted that ESI† S7 comprises a set of the DRC analysis, aimed at quantitatively examining the rate-determining steps in the ethylene epoxidation.
3.4 Kinetic analysis and comparison of activity and selectivity between Cu(111) and Ag(111)
In this section, we present a comprehensive kinetic analysis. Our previous model on Ag(111) for the kinetics of ethylene epoxidation has demonstrated a good agreement with the experimental results.40 Thus, it would be useful to compare the microkinetic outcomes on Ag(111) with those from Cu(111). Acetaldehyde is the primary byproduct that emerges in ethylene epoxidation. However, given its low commercial value in the chemical industry compared to ethylene epoxide, improving the selectivity of ethylene epoxide is a critical concern in the ethylene industry. In this regard, we systematically investigated the selectivity of EO on the Cu(111) surface using the coverage-dependent microkinetic modeling. The definition of selectivity can be expressed as follows: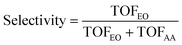 | (5) |
In the preceding discussion, a significant difference in activity and coverage between coverage-dependent and coverage-independent models was compared. It is pertinent to note that the two models have differences in selectivity evaluation. For instance, at 500 K, pEt = 2.66 kPa, and pO2 = 20 kPa, the EO selectivity of the coverage-independent model is 99%, which aligns with the earlier DFT calculation.24 Conversely, the EO selectivity of the coverage-dependent model under the same conditions is 92%. It is believed that the variation in selective competition steps (step 6 and step 7) is the primary factor affecting selectivity, and the low selectivity of the coverage-dependent model is consistent with corresponding activation barriers. As noted earlier, TSAA is more significantly impacted by the coverage effect than TSEO. Considering the coverage effect, the energy decline of TSAA is more remarkable than TSEO, leading to a diminution in EO selectivity. Linic et al. proposed a preliminary evaluation of selectivity utilizing the difference in transition state energy barriers, expressed as ΔE = EAA − EEO where EAA and EEO represent the AA and EO formation energy barriers, respectively.72,73 A larger ΔE indicates greater EO selectivity. The coverage-independent model yielded ΔE = 0.2, while the coverage-dependent model yielded ΔE = 0.11, signifying a decrease in selectivity. These findings highlight the critical role of coverage effects in kinetic analysis and emphasize the need for thorough consideration in quantitative calculations.
Fig. 8(a) displays the coverage-dependent log(TOF) of Cu(111) and Ag(111) as a function of temperature. The trends on both Cu(111) and Ag(111) are similar with the log(TOF) increasing as the temperature rises. Moreover, the log(TOF) results of both Cu(111) and Ag(111) fall within the range of 2 to 3. However, there are significant differences between the results from Cu(111) and Ag(111). As shown in Fig. 8(b), within the oxygen partial pressure range of 0–20 kPa, the trends of Cu(111) and Ag(111) are consistent; the log(TOF) increases as the oxygen pressure rises. But, the results obtained from Cu(111) remain superior to those of Ag(111). The differences in log(TOF) are more noticeable in Fig. 8(c). Under high oxygen pressure conditions, the log(TOF) on Cu(111) elevates significantly faster than that on Ag(111) with the increase of ethylene pressure. The surface activity is significantly influenced by surface-covered oxygen species when the oxygen partial pressure is high. It is clear that the coverage effect of the copper surface is more prominent than that of the silver surface, thus resulting in superior performance of copper activity.
It is worth noting that the selectivity of EO on Cu(111) is considerably superior to that on Ag(111), as illustrated in Fig. 8(d)–(f). As Fig. 8(d) displays, the range of EO selectivity on Ag(111) is between 30% and 50%, whereas on Cu(111), the EO selectivity remains high at over 90%. Fig. 8(e) exhibits the most notable change in EO selectivity, where the pressure of oxygen increases, and the EO selectivity rises from 84% to 96%. Regardless of various temperatures, oxygen pressure, and ethylene pressure conditions, the EO selectivity on the Cu(111) surface consistently remains above 80%. Compared to ethylene epoxidation on the silver surface, ethylene epoxidation on the Cu(111) surface shows higher EO selectivity and activity.
Experimental results by Jankowiak and Barteau indicate that the EO selectivity in ethylene epoxidation of the copper–silver alloy catalyst was higher than the silver catalyst under all detected conditions, as demonstrated in Fig. 9(a),13 indicating that Cu may be superior to the Ag catalyst. This is indirectly consistent with our results. This high selectivity can also be attributed to the transition state structures. The figure presented in Fig. 9(b) displays the four transition state structures – TSEO-Cu, TSAA-Cu, TSEO-Ag, and TSAA-Ag – on Cu(111) and Ag(111). The hydrogen transfer transition states, TSAA-Cu and TSAA-Ag, for the acetaldehyde formation on Cu(111) and Ag(111), respectively, share the same characteristics. However, the ethylene epoxide formation TSEO-Cu on Cu(111) has a lower energy barrier than the acetaldehyde formation TSAA-Cu compared to Ag(111), which is closer to the OME intermediate structure. The suspended carbon atoms are found to be only 2.94 Å away from the surface on Cu(111), while they are 4.1 Å away from the surface on Ag(111). This indicates that the dynamic pathway for producing ethylene epoxide from OME intermediate via TSEO is closer on Cu(111) than Ag(111), leading to higher EO selectivity on the copper surface.
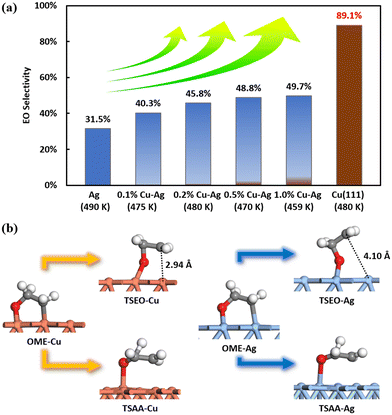 | ||
| Fig. 9 (a) The illustration of the calculated EO selectivity utilizing the coverage-dependent microkinetic modelling on Cu(111) and the experimental EO selectivity of silver and copper–silver alloys from Jankowiak and Barteau.13 It is important to note that the calculated results on the Cu surface cannot be quantitatively compared directly with the experimental data on the Cu–Ag alloy. (b) Comparison of transition state structures of selective competition steps on Cu(111) and Ag(111). Brown represents the copper surface, while blue represents the silver surface. | ||
3.5 Activity and selectivity of ethylene epoxidation on Cu(111) under industrial conditions
Based on the comprehensive kinetic analysis conducted earlier, it can be inferred that Cu(111) is highly effective for ethylene epoxidation. As a result, we have performed a range of kinetic simulations for optimizing operational conditions. These models can aid in enhancing catalyst efficiency and boosting overall production effectiveness. In the kinetic analysis, the reaction temperature range was set to 480 K to 540 K, and the pressure range was pEt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pO2 = 588 kPa
pO2 = 588 kPa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 kPa to 588 kPa
47 kPa to 588 kPa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 447 kPa. Such a temperature and pressure range are sufficient to accurately describe ethylene epoxidation under industrial conditions.
447 kPa. Such a temperature and pressure range are sufficient to accurately describe ethylene epoxidation under industrial conditions.
The coverage-dependent microkinetic modeling was employed to investigate the activity of the catalyst systematically. Fig. 10(a) shows the log(TOF) variation with temperature and pressure. The log(TOF) value gradually increases from 3.34 to 3.97 as the temperature rises, with pEt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pO2 = 588 kPa
pO2 = 588 kPa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 kPa. At 480 K, log(TOF) rises from 3.34 to 3.74 with an increase in oxygen partial pressure. The activity increases sharply from 3.74 to 4.35 with an increase in temperature when the partial pressure of oxygen reaches its maximum value. The correlation between temperature and pressure exhibits a significant degree of synergy. However, the rate of change in TOF at low temperatures and pressures is moderate.
47 kPa. At 480 K, log(TOF) rises from 3.34 to 3.74 with an increase in oxygen partial pressure. The activity increases sharply from 3.74 to 4.35 with an increase in temperature when the partial pressure of oxygen reaches its maximum value. The correlation between temperature and pressure exhibits a significant degree of synergy. However, the rate of change in TOF at low temperatures and pressures is moderate.
 | ||
Fig. 10 (a) Turnover frequency values (TOF) and (b) EO selectivity from 480 K to 540 K with pEt/pO2 ranging from 588![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 kPa to 588 47 kPa to 588![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 447 kPa. 447 kPa. | ||
An interesting result about EO selectivity was observed, shown in Fig. 10(b). At 480 K, the EO selectivity rises from 90.36% to 93.88% with an increase in oxygen partial pressure. As the temperature increases, the EO selectivity across the entire pressure range exhibits a declining trend. For instance, when pEt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pO2 = 588 kPa
pO2 = 588 kPa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 kPa, the EO selectivity decreases rapidly from 90.36% to 85.16%. As discussed in the previous section (section 3.3), the energy barrier variations in selective competition steps with temperature can cause changes in selectivity. Fig. 7(a) justifies this outcome by demonstrating that, as the temperature increases, TSEO rises at a faster rate as compared to TSAA, causing a reduction in EO selectivity. While an increase in oxygen pressure may enhance EO selectivity, an increase in temperature can lead to a decline in EO selectivity. Generally, increasing the temperature and oxygen partial pressure results in an enhancement of activity. Furthermore, it was reported that the increase of O2 pressure on Cu–Ag alloy catalysts leads to an increase in EO selectivity. These findings align with the experimental trend observed by Jankowiak and Barteau on Cu–Ag alloys.13
47 kPa, the EO selectivity decreases rapidly from 90.36% to 85.16%. As discussed in the previous section (section 3.3), the energy barrier variations in selective competition steps with temperature can cause changes in selectivity. Fig. 7(a) justifies this outcome by demonstrating that, as the temperature increases, TSEO rises at a faster rate as compared to TSAA, causing a reduction in EO selectivity. While an increase in oxygen pressure may enhance EO selectivity, an increase in temperature can lead to a decline in EO selectivity. Generally, increasing the temperature and oxygen partial pressure results in an enhancement of activity. Furthermore, it was reported that the increase of O2 pressure on Cu–Ag alloy catalysts leads to an increase in EO selectivity. These findings align with the experimental trend observed by Jankowiak and Barteau on Cu–Ag alloys.13
After conducting the thorough analysis, we have observed that there is an inverse relationship between high activity and EO selectivity; lower activity results in higher EO selectivity. To optimize reaction conditions and enhance EO selectivity, we recommend a strategy of gradually increasing oxygen pressure at low temperatures. This approach offers several advantages, such as reducing energy costs by lowering the reaction temperature and minimizing catalyst deactivation. Additionally, the extended service life of the catalyst obtained through this method reduces maintenance and replacement expenses. Furthermore, the risk of potential accidents associated with high-temperature reactions can be mitigated by reducing the reaction temperature, thereby improving production process safety. It is worth noting that Cu(111) may be oxidized under experimental conditions. Our study aims to investigate the intrinsic activity and selectivity of EO on metallic copper catalysts and compare these results with those obtained on metallic silver catalysts, providing a deeper understanding of EO activity and selectivity.
4. Conclusions
In this work, we present a quantitative microkinetic study based on DFT calculations for ethylene epoxidation on Cu(111). We conducted a comprehensive analysis of the coverage effect, taking into account both self-interaction and cross-interaction between adsorbates by optimizing all the structures of surface adsorbates and transition states at different coverages and obtaining their respective energies. Additionally, we established a coverage-dependent microkinetic model based on DFT calculations to explore more realistic reaction kinetics. Based on our findings, we draw the following conclusions:i. Through a comprehensive coverage-dependent modeling, we have determined that TSOO is most impacted by the coverage effect. This effect was further observed in both coverage-dependent and coverage-independent modeling, where the difference of the TSOO energy barrier was found to be as high as 0.58 eV. Moreover, we have observed that TSAA is more susceptible to the coverage effect in the selective competition steps, resulting in variations in EO selectivity between coverage-dependent and coverage-independent modelling.
ii. The copper surface is poisoned by oxygen atoms when the coverage effect is not considered. We were able to obtain a steady-state copper surface composition that includes 34.5% oxygen atoms, 1.6% OME intermediates, and 63.9% free sites through coverage-dependent modelling. Our analysis revealed that the coverage-dependent log(TOF) on Cu(111) is 2.65, while the coverage-independent log(TOF) is −2.47.
iii. We found that Cu(111) exhibits higher activity and EO selectivity compared to silver catalysts, provided the Cu(111) surface remain in its metallic state. Namely, Cu(111) can maintain over 80% EO selectivity under all studied conditions.
iv. Our kinetic simulations showed that the process of ethylene epoxidation can be optimized by reducing the reaction temperature and increasing oxygen pressure. This strategy can yield substantial benefits, including cost reduction and improved production efficiency.
Our findings provide valuable insights for optimizing ethylene epoxidation catalysts, offering a reasonable theoretical foundation and practical guidance for improving catalyst performance in the ethylene epoxidation process.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We are grateful to the NSFC (92045303) and NKRDPC (2021YFA1500700). We are grateful for computational support from the UK national high-performance computing service ARCHER funded by EPSRC grant ref EP/P022561/1 and QUB Kelvin HPC service funded by ESPRC (EP/T022175/1). We are grateful to the UK Materials and Molecular Modeling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1).References
- J. Deng, J. Yang, S. Zhang and X. Yuan, J. Catal., 1992, 138, 395–399 CrossRef CAS.
- P. Christopher and S. Linic, J. Am. Chem. Soc., 2008, 130, 11264–11265 CrossRef CAS PubMed.
- C. T. Campbell and M. T. Paffett, Surf. Sci., 1984, 139, 396–416 CrossRef CAS.
- M. Huš, M. Grilc, J. Teržan, S. Gyergyek, B. Likozar and A. Hellman, Angew. Chem., Int. Ed., 2023, e202305804 Search PubMed , 1–10.
- J.-X. Liu, S. Lu, S.-B. Ann and S. Linic, ACS Catal., 2023, 13, 8955–8962 CrossRef CAS.
- S. Linic and M. A. Barteau, J. Am. Chem. Soc., 2002, 124, 310–317 CrossRef CAS PubMed.
- S. Linic, H. Piao, K. Adib and M. A. Barteau, Angew. Chem., Int. Ed., 2004, 43, 2918–2921 CrossRef CAS PubMed.
- S. Linic and M. A. Barteau, J. Am. Chem. Soc., 2003, 125, 4034–4035 CrossRef CAS PubMed.
- G. S. Jones, M. Mavrikakis, M. A. Barteau and J. M. Vohs, J. Am. Chem. Soc., 1998, 120, 3196–3204 CrossRef CAS.
- D. Chen, P. L. Kang and Z. P. Liu, ACS Catal., 2021, 11, 8317–8326 CrossRef CAS.
- C. J. Chen, J. W. Harris and A. Bhan, Chem. – Eur. J., 2018, 24, 12405–12415 CrossRef CAS PubMed.
- T. Pu, H. Tian, M. E. Ford, S. Rangarajan and I. E. Wachs, ACS Catal., 2019, 9, 10727–10750 CrossRef CAS.
- J. T. Jankowiak and M. A. Barteau, J. Catal., 2005, 236, 366–378 CrossRef CAS.
- J. T. Jankowiak and M. A. Barteau, J. Catal., 2005, 236, 379–386 CrossRef CAS.
- A. Ayame, T. Yoshida, M. Yamaguchi, H. Miura, Y. Sakai and N. Nojiri, J. Catal., 1986, 100, 401–413 CrossRef CAS.
- W. Diao, C. D. Digiulio, M. T. Schaal, S. Ma and J. R. Monnier, J. Catal., 2015, 322, 14–23 CrossRef CAS.
- T. E. Jones, R. Wyrwich, S. Böcklein, E. A. Carbonio, M. T. Greiner, A. Y. Klyushin, W. Moritz, A. Locatelli, T. O. Menteş, M. A. Niño, A. Knop-Gericke, R. Schlögl, S. Günther, J. Wintterlin and S. Piccinin, ACS Catal., 2018, 8, 3844–3852 CrossRef CAS.
- T. C. R. Rocha, M. Hävecker, A. Knop-Gericke and R. Schlögl, J. Catal., 2014, 312, 12–16 CrossRef CAS.
- B. Yang, R. Burch, C. Hardacre, G. Headdock and P. Hu, Catal. Sci. Technol., 2017, 7, 1508–1514 RSC.
- B. Yang, R. Burch, C. Hardacre, G. Headdock and P. Hu, ACS Catal., 2012, 2, 1027–1032 CrossRef CAS.
- D. Xu, P. Wu and B. Yang, J. Phys. Chem. C, 2019, 123, 8959–8966 CrossRef CAS.
- H. Li, A. Cao and J. K. Nørskov, ACS Catal., 2021, 11, 12052–12057 CrossRef CAS.
- D. Torres, N. Lopez and F. Illas, J. Catal., 2006, 243, 404–409 CrossRef CAS.
- D. Torres, N. Lopez, F. Illas and R. M. Lambert, J. Am. Chem. Soc., 2005, 127, 10774–10775 CrossRef CAS PubMed.
- A. K. Santra, J. J. Cowell and R. M. Lambert, Catal. Lett., 2000, 67, 87–91 CrossRef CAS.
- V. R. Choudhary, R. Jha, N. K. Chaudhari and P. Jana, Catal. Commun., 2007, 8, 1556–1560 CrossRef CAS.
- R. L. Cropley, F. J. Williams, A. J. Urquhart, O. P. H. Vaughan, M. S. Tikhov and R. M. Lambert, J. Am. Chem. Soc., 2005, 127, 6069–6076 CrossRef CAS PubMed.
- J. Teržan, M. Huš, B. Likozar and P. Djinović, ACS Catal., 2020, 10, 13415–13436 CrossRef.
- F. Studt, F. Abild-Pedersen, T. Bligaard, R. Z. Sørensen, C. H. Christensen and J. K. Nørskov, Science, 2008, 320, 1320–1322 CrossRef CAS PubMed.
- Z. Yao, J. Zhao, R. J. Bunting, C. Zhao, P. Hu and J. Wang, ACS Catal., 2021, 11, 1202–1221 CrossRef CAS.
- Z. Wang, H. F. Wang and P. Hu, Chem. Sci., 2015, 6, 5703–5711 RSC.
- Y. Mao and P. Hu, Sci. China: Chem., 2020, 63, 850–859 CrossRef CAS.
- Y. Ding, Y. Xu, Y. Song, C. Guo and P. Hu, J. Phys. Chem. C, 2019, 123, 27594–27602 CrossRef CAS.
- W. Xie, J. Xu, Y. Ding and P. Hu, ACS Catal., 2021, 11, 4094–4106 CrossRef CAS.
- W. Xie and P. Hu, Catal. Sci. Technol., 2021, 11, 5212–5222 RSC.
- W. Xie, J. Xu, J. Chen, H. Wang and P. Hu, Acc. Chem. Res., 2022, 55, 1237–1248 CrossRef CAS PubMed.
- P. Chen, Y. Liu, Y. Xu, C. Guo and P. Hu, JACS Au, 2023, 3, 165–175 CrossRef CAS PubMed.
- Z. Yao, C. Guo, Y. Mao and P. Hu, ACS Catal., 2019, 9, 5957–5973 CrossRef CAS.
- C. Guo, Y. Mao, Z. Yao, J. Chen and P. Hu, J. Catal., 2019, 379, 52–59 CrossRef CAS.
- Z. Wang, W. Xie, Y. Xu, M. Jia, J. Xu and P. Hu, Catal. Sci. Technol., 2023, 13, 3689–3700 RSC.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- Z. P. Liu and P. Hu, J. Am. Chem. Soc., 2003, 125, 1958–1967 CrossRef CAS PubMed.
- A. Michaelides, Z. P. Liu, C. J. Zhang, A. Alavi, D. A. King and P. Hu, J. Am. Chem. Soc., 2003, 125, 3704–3705 CrossRef CAS PubMed.
- A. Alavi, P. Hu, T. Deutsch, P. L. Silvestrelli and J. Hutter, Phys. Rev. Lett., 1998, 80, 3650–3653 CrossRef CAS.
- H. F. Wang and Z. P. Liu, J. Am. Chem. Soc., 2008, 130, 10996–11004 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 1–19 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- N. Yang, A. J. Medford, X. Liu, F. Studt, T. Bligaard, S. F. Bent and J. K. Nørskov, J. Am. Chem. Soc., 2016, 138, 3705–3714 CrossRef CAS PubMed.
- L. C. Grabow, B. Hvolbæk and J. K. Nørskov, Top. Catal., 2010, 53, 298–310 CrossRef CAS.
- D. Mei, P. A. Sheth, M. Neurock and C. M. Smith, J. Catal., 2006, 242, 1–15 CrossRef CAS.
- H. Molero, B. F. Bartlett and W. T. Tysoe, J. Catal., 1999, 181, 49–56 CrossRef CAS.
- X. Sun, P. Wang, Z. Shao, X. Cao and P. Hu, Sci. China: Chem., 2019, 62, 1686–1697 CrossRef CAS.
- J. Chen, M. Jia, Z. Lai, P. Hu and H. Wang, J. Chem. Phys., 2021, 154, 1–8 Search PubMed.
- J. F. Chen, Y. Mao, H. F. Wang and P. Hu, ACS Catal., 2016, 6, 7078–7087 CrossRef CAS.
- J. Chen, M. Jia, P. Hu and H. Wang, J. Comput. Chem., 2021, 42, 379–391 CrossRef CAS PubMed.
- C. T. Campbell, ACS Catal., 2017, 7, 2770–2779 CrossRef CAS.
- C. T. Campbell, Top. Catal., 1994, 1, 353–366 CrossRef CAS.
- J. R. H. Carucci, V. Halonen, K. Eränen, J. Wärnå, S. Ojala, M. Huuhtanen, R. Keiski and T. Salmi, Ind. Eng. Chem. Res., 2010, 49, 10897–10907 CrossRef CAS.
- L. Petrov, A. Eliyas and D. Shopov, Appl. Catal., 1985, 18, 87–103 CrossRef CAS.
- P. C. Borman and K. R. Westerterp, Ind. Eng. Chem. Res., 1995, 34, 49–58 CrossRef CAS.
- T. Salmi, J. Hernández Carucci, M. Roche, K. Eränen, J. Wärnå and D. Murzin, Chem. Eng. Sci., 2013, 87, 306–314 CrossRef CAS.
- A. J. Medford, C. Shi, M. J. Hoffmann, A. C. Lausche, S. R. Fitzgibbon, T. Bligaard and J. K. Nørskov, Catal. Lett., 2015, 145, 794–807 CrossRef CAS.
- Z. P. Liu, P. Hu and M. H. Lee, J. Chem. Phys., 2003, 119, 6282–6289 CrossRef CAS.
- J. Feibelman, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 12133–12138 CrossRef PubMed.
- K. Bleakley and P. Hu, J. Am. Chem. Soc., 1999, 121, 7644–7652 CrossRef CAS.
- Z. P. Liu and P. Hu, J. Am. Chem. Soc., 2003, 125, 1958–1967 CrossRef CAS PubMed.
- C. T. Campbell, J. Catal., 1985, 94, 436–444 CrossRef CAS.
- S. Linic, J. Jankowiak and M. A. Barteau, J. Catal., 2004, 224, 489–493 CrossRef CAS.
- H. Li, A. Cao and J. K. Nørskov, ACS Catal., 2021, 11, 12052–12057 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cy00617h |
| This journal is © The Royal Society of Chemistry 2024 |