Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Polariton condensation in a microcavity using a highly-stable molecular dye†
Kirsty E.
McGhee
 a,
Rahul
Jayaprakash
a,
Rahul
Jayaprakash
 a,
Kyriacos
Georgiou
a,
Kyriacos
Georgiou
 ab,
Stephanie L.
Burg
ab,
Stephanie L.
Burg
 a and
David G.
Lidzey
a and
David G.
Lidzey
 *a
*a
aDepartment of Physics and Astronomy, University of Sheffield, Hicks Building, Hounsfield Road, Sheffield, S3 7RH, UK. E-mail: d.g.lidzey@sheffield.ac.uk
bDepartment of Physics, University of Cyprus, P.O. Box 20537, Nicosia 1678, Cyprus
First published on 28th February 2022
Abstract
We have fabricated dielectric microcavities containing the molecular dye 1,4-bis[2-[4-[N,N-di(p-tolyl)amino]phenyl]vinyl]benzene (DPAVB) dispersed in a transparent polymer matrix. We show that despite the relatively broad absorption linewidth of the DPAVB, the cavities enter the strong coupling regime. We use <330 ps pulses at 355 nm from a Nd:YAG laser to generate amplified spontaneous emission from control films and polariton condensation from the strongly-coupled microcavity in air and at room temperature. Here, polariton condensation is observed at an excitation threshold of 215 μJ cm−2. Significantly, we show that the DPAVB dye has a very high degree of photostability, with polariton condensation still observed from the cavity after 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 excitation pulses, showing promise for its use in practical polaritonic devices.
000 excitation pulses, showing promise for its use in practical polaritonic devices.
1. Introduction
Organic exciton-polaritons are of great interest due to their ability to undergo room temperature polariton lasing.1 Exciton-polaritons arise from the strong coupling between Frenkel excitons (bound electron–hole pairs) and a confined photon mode within an optical cavity. Such quasiparticles are a mixture of light and matter, and for convenience are referred to as cavity-polaritons or simply polaritons. Unlike polaritons in most inorganic based microcavities (which mainly exist at cryogenic temperatures due to their low exciton binding energies), organic polaritons exist at room temperature due to the high binding energy of Frenkel excitons (100's of meV). Such a high degree of thermal stability makes organic polaritons of significant interest for practical room temperature applications.2Polaritons can be described using Bose-Einstein statistics and – at high occupation density – can undergo condensation. Such polariton condensates are usually formed at the bottom of the lower polariton branch, which acts as an energetic trap in momentum space. This results from a stimulated scattering process by which uncoupled excitons located in a reservoir populate the ground polariton state. The condensates formed can have macroscopic dimensions (10's of microns diameter) and have long-range spatial and temporal coherence (100's of ps).3,4 Such condensates are non-equilibrium in nature as they undergo spontaneous emission as their photonic component escapes the cavity.1,5 The emitted photons have the same energy and phase, with such emission considered a form of lasing (often referred to as polariton lasing).5,6 Significantly, this lasing process does not require the formation of a population inversion and thus it can occur at a lower excitation threshold than conventional photon lasing. Polariton condensates are of interest as new types of high-efficiency light sources and as ‘polariton simulators’; here, complex problems can be mapped onto the pseudo-spins of a lattice of interacting condensates, with the ground state of the lattice corresponding to the solution of the Hamiltonian of interest.7–9
A number of different molecular materials have been shown to undergo polariton condensation in suitably-designed structures. These include the conjugated polymers MeLPPP10 and PFO;4 the molecular dyes BODIPY-Br,11 BODIPY-G1,12 and TDAF;13 the fluorescent proteins eGFP14 and m-Cherry;15 and PDI-O microcrystals.16 For a recent review on polariton condensation in organic microcavities, see ref. 17. For practical applications, it is desirable that such molecules have a high degree of photostability. The BODIPY family of molecular dyes that we have previously studied have relatively low stability, a feature that required a single-pulse imaging technique for lasing studies.11,12,18
In this paper, we demonstrate polariton condensation in a cavity containing an organic laser dye with a much higher degree of photostability. We confirm this enhanced stability by performing measurements in both the linear and non-linear regimes and demonstrate that the cavity can exhibit non-linear emission over more than 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 excitation pulses. We believe that such a material will be of interest for studies that wish to explore the interactions between organic exciton-polariton condensates.
000 excitation pulses. We believe that such a material will be of interest for studies that wish to explore the interactions between organic exciton-polariton condensates.
2. Results and discussion
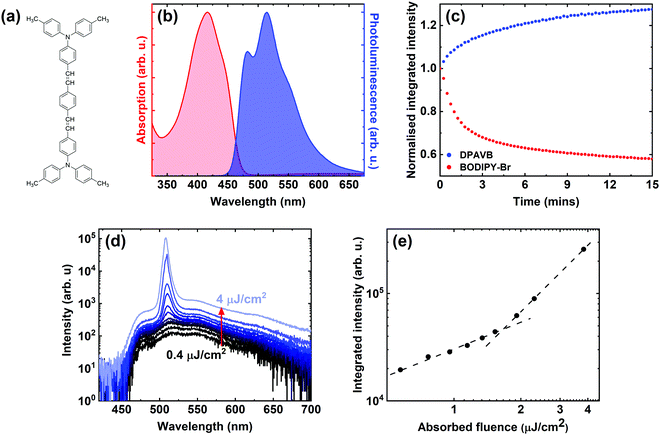
We have used the fluorescent dye 1,4-bis[2-[4-[N,N-di(p-tolyl)amino]phenyl]vinyl]benzene (DPAVB) as the active material in our microcavities. The molecular structure of DPAVB is shown in Fig. 1(a). This styrylbenzene derivative has been investigated as a laser dye,19,20 as a dopant for other laser dyes,21 and as a dopant for sky-blue organic light emitting diodes (OLEDs).22–24 It has a high optical gain (19.8 cm−1 for a 2% DPAVB/polystyrene film25) and a low lasing threshold of 2.3 μJ cm−2 in a distributed feedback structure.19 Such low thresholds have been previously attributed to the symmetrical structure of the dye, which results in reduced intermolecular interactions.20 Used as a dopant, DPAVB (at 4% weight) has also been shown to reduce the threshold of distributed feedback lasers based on the conjugated polymer BN-PFO from 3 μJ cm−2 to 0.75 μJ cm−2 using an ultraviolet diode laser with a pulse width of 50 ns.21,26 However, it was also found that a build-up of long-lived triplet states on the DPAVB molecules resulted in a large increase in the lasing threshold when longer excitation pulses were used. This effect was not observed in undoped BN-PFO structures, which are able to undergo quasi-CW lasing.272.1 Characterisation of DPAVB films
To investigate the properties of DPAVB, we explored it when doped at a range of concentrations into a polystyrene (PS) matrix. Here, we focus our discussion on DPAVB/PS films where the DPAVB is present at high concentration (50% by mass). This is because to achieve strong coupling, it is necessary that the Rabi splitting energy, Ω, is greater than the absorption linewidth according to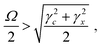 | (1) |
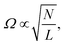 | (2) |
To prepare DPAVB/PS films, the materials were first dissolved in dichloromethane. This solution was then spin-coated onto a glass substrate to form a thin film, with the DPAVB molecules dispersed in the PS. Here, the role of the PS is to spatially separate the individual DPAVB molecules in order to supress aggregation and crystallisation. The PS also provides additional control over the thickness of the films (by varying its concentration in the solvent), allowing the fabrication of films several hundred nm thick. In this way, they can support waveguide modes for amplified spontaneous emission (ASE) and optical modes within a microcavity.
The normalised absorption and photoluminescence of a DPAVB/PS film are shown in Fig. 1(b) where the DPAVB has a relative mass fraction of 50%. It can be seen that the absorption of the DPAVB peaks around 420 nm (2.95 eV) and has a total linewidth of 140 nm (0.5 eV). The DPAVB emission is characterised by a number of poorly-resolved peaks at 479 nm, 512 nm and 551 nm that we associate with the 0–0, 0–1 and 0–2 transitions (see peak fit in ESI† Fig. S1). We have found that the 50% DPAVB/PS films explored have a photoluminescence quantum yield between 5 and 10% dependent on measurement protocols.
We have explored the relative photostability of DPAVB. This measurement was benchmarked against a thin film of BODIPY-Br (10% by mass in PS). This molecule was chosen as it has been widely explored in both strong coupling and polariton lasing experiments.8,11,30–32 In our measurements, 200 nm thick films of DPAVB/PS and BODIPY-Br/PS coated by a thin film of PVA were exposed to light from a 405 nm continuous wavelength diode laser in air, with the laser flux adjusted such that both films absorbed an optical power of 34 μW. Experiments were carried out over 15 minutes with the PL emission recorded every 15 seconds. This experiment was designed to explore the relative photostability of the two dyes when exposed in a linear excitation regime. The relative emission intensity of the two films are shown in Fig. 1(c). Here it can be seen that at the end of the 15 minutes, the emission from the DPAVB film has actually increased by nearly 30%, with the emission from the BODIPY-Br dropping by more than 40% over the same time period. The exact origin of the increase in the emission intensity from DPAVB is not understood; however, it is consistent with a relative decrease in the number of non-radiative decay channels open to exciton decay. This rise in intensity extends for around half an hour, at which point the emission intensity saturates, with no changes observed in spectral emission shape (see Fig. S2 of the ESI†). We suspect therefore that this effect results from an inactivation of molecules that have some type of structural defect associated with non-radiative emission. Indeed, our measurements indicate that this ‘inactivation’ of non-radiative defects appears to be essentially non-recoverable. Significantly, this result suggests that DPAVB is a highly-photostable material and should be of interest for polariton lasing applications.
To characterise the non-linear emission properties of DPAVB, we have measured its amplified spontaneous emission (ASE). Here, we focused a 355 nm pulsed (<330 ps) laser with a cylindrical lens into a stripe that was positioned close to the edge of a 200 nm thick DPAVB/PS film. Here, the stripe essentially acts as a waveguide, with the resultant emission from the edge of the sample collected by an optical fibre coupled to a spectrometer. Measurements were made as a function of laser fluence as shown in Fig. 1(d). Here it can be seen that a peak emerges at 508 nm having a linewidth of 4.4 nm (21 meV), indicating the action of ASE. This peak coincides with the 0–1 peak observed in the PL emission, indicating the action of a 4-level laser. Fig. 1(e) plots the integrated intensity under each spectrum on a log–log scale as a function of absorbed laser fluence, where the fluence is defined as the energy per pulse divided by the excitation area. Here, two straight-line fits have been used to identify the ASE threshold, which in this film is around 1.7 μJ cm−2.
2.2 DPAVB cavity design, fabrication and linear characterisation
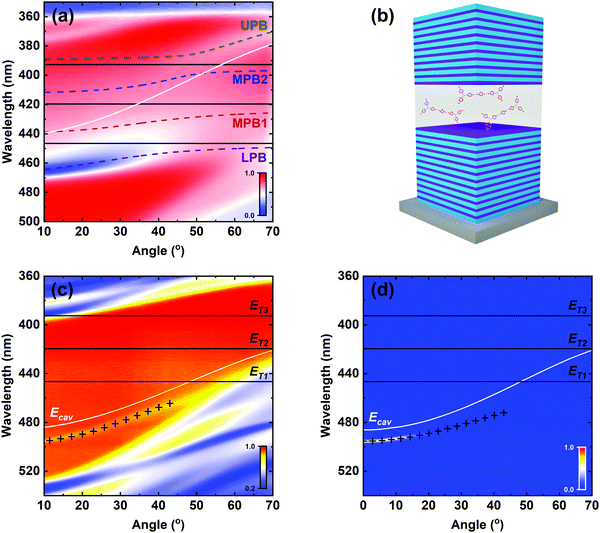
DPAVB cavities were designed using a transfer matrix reflectivity (TMR) model. The refractive index (n) and extinction coefficient (k) of DPAVB were first determined using spectroscopic ellipsometry. Here, a pure solution of DPAVB in dichloromethane was spin-coated onto a silicon wafer. Literature values (from ref. 33) for the optical properties of the silicon and its native oxide were used as included in the Woollam analysis software, which resulted in an excellent fit to the substrates based on a 1.8 nm thick layer of native oxide. Ellipsometry data for the DPAVB films was then fit with a transparent b-spline wavelength expansion to obtain the n and k values (see Fig. S1 in the ESI†). These values were used with known n and k values for PS (from ref. 34) to calculate the values for the 50% DPAVB/PS film. Three Lorentzian functions were fit to the DPAVB/PS k data and these were used in the TMR model to describe three transitions (see Fig. S1, ESI†).To explore strong coupling using DPAVB, initial experiments focused on lower-finesse cavities that were designed to allow the observation of an anti-crossing between the polariton branches. Additionally, the exciton-photon detuning was chosen to ensure that resonance occurred at relatively low angles (∼35°). Microcavities were fabricated by depositing a distributed Bragg reflector (DBR) made of alternating λ/4 thick layers of SiO2 and TiO2 onto a quartz-coated glass substrate using electron-beam evaporation. DPAVB/PS solutions at different relative DPAVB concentrations (10%, 20%, 30%, 40% and 50% by mass) were spin-coated onto the DBRs to form 265 nm thick films. A second DBR was then deposited on top of this using the electron beam.
To characterise the cavities, we performed angle-dependent white light reflectivity measurements. Fig. 2(a) shows reflectivity data for a cavity containing 50% DPAVB/PS with both DBRs consisting of 6 SiO2/TiO2 pairs. The data for the lower concentration cavities is shown in Fig. S3 in the ESI.† Here, we find that no Rabi splitting is evident in the cavity containing 10% DPAVB. As the DPAVB concentration is increased, a splitting begins to appear and the cavities enter the strong coupling regime around 30–40%. It can be seen that the cavity containing 50% DPAVB (see Fig. 2(a)) shows a distinct splitting between the lower (LPB) and upper (UPB) polariton branches. To quantify this, we have used a coupled oscillator model to determine the magnitude of the Rabi splitting. We again use three Lorentzians centred at 447 nm, 420 nm and 393 nm, which we henceforth label as T1, T2 and T3 (see the fit to the imaginary part of the refractive index determined from ellipsometry in Fig. S1, ESI†). The coupling of these transitions to the cavity mode is described using the following Hamiltonian
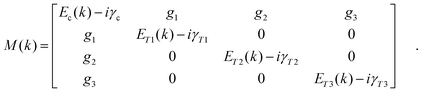 | (3) |
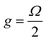 .
.
This model is then fit to the LPB and UPB dispersions as shown in Fig. 2(a). To do this, we used the relative height of each of the transitions from our Lorentzian fits and scaled their coupling strength according to these ratios. We find that the model describes the data very well, and we determine Rabi splittings of Ω1 = 168 meV, Ω2 = 260 meV and Ω3 = 227 meV. Here, two middle polariton branches (MPB1 and MPB2) are predicted; however, these are not resolvable in the experimental data due to strong absorption by the DPAVB molecules at these wavelengths. Applying eqn (1) to the three transitions, we find that the Rabi splittings for T1 and T2 exceed the condition required for strong coupling. When we apply the same analysis to T3, we find that it does not meet the condition and is therefore weakly-coupled. The parameters used in these calculations are shown in Table S1 in the ESI.†
As the Q-factor of these cavities was relatively low (∼400 according to TMR modelling), they were less suitable for condensation measurements and higher Q-factor structures were fabricated. Here, a 12-pair DBR was used for the bottom mirror with a 10-pair top DBR. To ensure the cavities operated in the strong coupling regime, 50% DPAVB/PS was used. Preliminary measurements (data not shown) indicated that to achieve polariton condensation, it was necessary to position the LPB around 495–500 nm (see discussion on scattering mechanisms in Section 2.3). A schematic of the microcavities constructed is shown in Fig. 2(b).
The angle-dependent white light reflectivity and PL emission from one of these higher Q-factor cavities are shown in Fig. 2(c and d), respectively. To generate PL, the cavity was excited non-resonantly using a CW laser at 405 nm, with a 450 nm long-pass filter used in the collection arm. In both PL and reflectivity measurements, we detect a dispersive branch located around normal incidence at 496 nm, which (using results from a TMR model) we identify as the lower polariton branch. We note that the UPB is not visible in these cavities and indeed it is also not visible in our TMR model. We believe this is caused by a combination of large negative cavity detuning and the high reflectivity of the DBRs. We note that studies on strong coupling in inorganic microcavities based on GaN and ZnO similarly do not report the observation of an UPB35–37 where it is masked by absorption from exciton continuum states. Other studies on organic polariton condensation in strongly-coupled microcavities also indicate that the upper polariton branch can be difficult to detect.4,13,38 Nevertheless, despite the absence of an UPB, we have used a combination of TMR modelling together with a coupled oscillator model (fit shown together with discussion in Fig. S4 of the ESI†) to estimate Rabi splittings between the photon and the different excitonic transitions in this cavity of Ω1 = 168 meV, Ω2 = 260 meV and Ω3 = 227 meV.
2.3 Polariton condensation
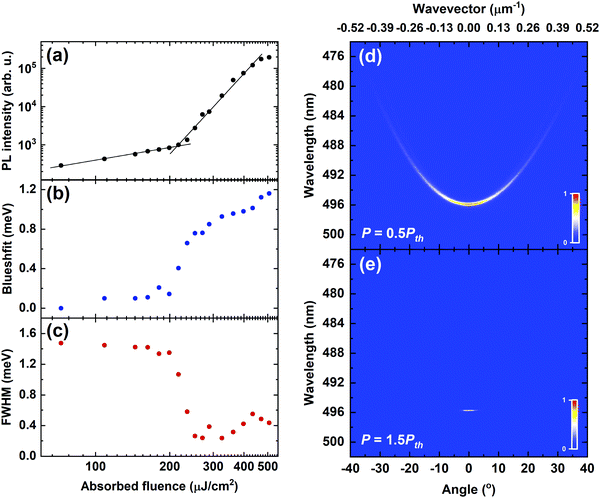
To generate polariton condensation, the 10-/12-pair DBR microcavity was pumped non-resonantly at normal incidence in a transmission configuration, with emission detected using a k-space imaging technique. The cavity was excited through the quartz substrate by a pulsed Nd:YAG laser at 355 nm focused into a 30 μm diameter spot. The pulse width and repetition frequency were <330 ps and 100 Hz, respectively. The microcavity emission was then collected through the top 10-pair DBR using a 10 mm objective (NA = 0.6) and focused into a CCD spectrometer with a spectral resolution of 0.39 meV (0.09 nm).Fig. 3(a) shows a plot of the power-dependent PL intensity determined over a solid angle of ±1.56° around the bottom of the lower polariton branch (k = 0) for the cavity shown in Fig. 2(c and d). Fig. 3(b and c) show the blueshift of the LPB and its linewidth at full-width half maximum (FWHM), respectively, as a function of excitation power. Here, the blueshift and FWHM data were extracted from Lorentzian fits to the emission spectra recorded at k = 0. From this data, we identify a condensation threshold fluence (Pth) of 215 μJ cm−2. This threshold is accompanied by a reduction in the emission linewidth from 1.5 meV to ∼0.2 meV. We note that the condensation threshold is significantly higher than the ASE threshold (∼130 times), which we attribute to the different excitation geometries, resonator structure and nature of the emitting state in the two measurements. The methods used to calculate the two thresholds are outlined in Section 3 of the ESI.† In Fig. 3(d and e), we show the normalised PL dispersion recorded at P = 0.5 Pth and P = 1.5 Pth, respectively. In (e), the collapse of all emission to the bottom of the LPB is clearly evident.
We now discuss the origin of the emission blueshift in more detail. This spectral blueshift occurs around threshold and then continues to increase (albeit at a slower rate) as the pump power is further increased, with the total blueshift observed being around 1.2 meV. We suspect that this is mostly attributable to a reversible photobleaching of the DPAVB molecular ground-state as the excitation is increased, resulting in a change in the effective refractive index of the active layer and a reduction in the Rabi splitting.39 Indeed, we show (by recording cavity emission below, above and then below the condensation threshold) that a fully reversible blueshift of as much as 1.6 meV can occur following excitation at 1.7 Pth (see Fig. S5(a), ESI†). We believe, however, that some part of the maximum blueshift observed in Fig. 3(b) results from a degree of irreversible photodegradation of the sample caused by extended exposure to the excitation laser (see Fig. S5(b) and Section 4 of the ESI†). Indeed, photodegradation most likely explains the slow blueshift observed at the highest pump powers, with our findings highlighting the need to consider the effect of even limited amounts of photodegradation when interpreting spectral blueshifts.
The non-linear properties of our microcavity are consistent with previous reports on polariton condensation. Indeed, we note that the condensation threshold is similar to that observed in microcavities containing BODIPY-Br and BODIPY-G1 (also suspended in PS matrices)11,12 and also the polymer MeLPPP.10 Similarly, the reduction in linewidth (∼7 times) is consistent with that observed in BODIPY containing cavities.
The condensate formed is created by a stimulated scattering mechanism that is determined by the occupation of the final state.40 It has previously been shown that polariton condensates can be populated through vibron-mediated energy relaxation, with this process being efficient when the energy separation between a “hot-exciton” and the bottom of the LPB is equal to the energy of a molecular vibrational mode.41,42 We have considered this mechanism as the origin of the stimulated scattering process in these cavities. To do this, we have performed Raman spectroscopy on a DPAVB solution, the results of which are shown in Fig. S6 of the ESI.† This identifies a strong Raman-active peak at 1593 cm−1, corresponding to an energy shift of 198 meV. Interestingly, this energy corresponds to the difference in energy between the edge of the DPAVB absorption (around 460 nm) and the condensate energy, indicating that a fully-thermalised DPAVB exciton in the reservoir could scatter into the LPB following the emission of a vibrational quantum. Indeed, we note that polariton condensation was only observed in cavities whose LPB was positioned around 496 nm at k = 0. We do not, however, rule out a radiative pumping mechanism in which photon emission from weakly-coupled excitons in the DPAVB reservoir “pumps” the photon component of the lower branch polaritons. We have previously shown that this mechanism dominates the population of the LPB at low pumping densities in strongly-coupled microcavities containing BODIPY-Br.30 Indeed, this process is expected to be highly efficient in the cavities studied here as states at the bottom of the LPB are highly photon-like (∼90%) due to the relatively large cavity detuning used. We believe, therefore, that further studies are required to determine the relative importance of these two mechanisms in the observed stimulated scattering processes.
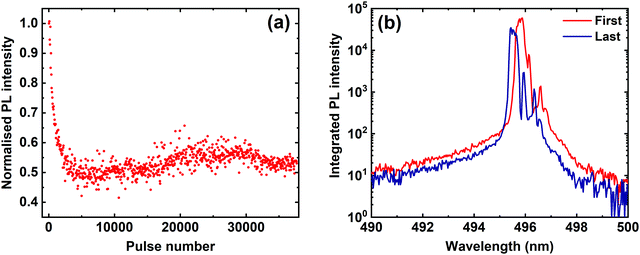
Finally, we have explored the stability of the condensate emission from our cavities. Here, the laser excitation power was adjusted to P = 2 Pth and PL spectra were recorded by integrating the cavity emission over 0.5 seconds. The excitation laser had a repetition frequency of 100 Hz, and thus each spectrum was generated using 50 pulses. The experiment was performed 755 times sequentially, with the cavity being exposed to a total of 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 pulses.
750 pulses.
In Fig. 4(a), we plot the normalised integrated PL intensity against pulse number. From the data plotted in Fig. 3(a), we determine that the integrated PL intensity at P = 2 Pth is ∼150 times that at P = Pth, and thus we expect the cavity to remain in the non-linear emission regime until the emission intensity drops to a factor of ∼0.007 of its initial normalised value. It can be clearly seen in Fig. 4(a) that although there is a fast initial decay in the cavity emission (occurring over the first ∼4000 pulses), it then stabilises and remains at an intensity of ∼50% of its initial value for the remaining duration of the experiment. This indicates a very promising level of condensate emission stability and is consistent with the high degree of stability evidenced in the linear emission measurements presented in Fig. 1(c). In Fig. 4(b), we plot the first and last spectra recorded, where it can be seen that the emission is very similar in both, indicating that the cavity is still in a non-linear regime at the end of the measurement.
3. Conclusions
We have fabricated polariton microcavities containing a green-emitting molecular dye (DPAVB) dispersed into a polystyrene (PS) matrix despite the fact that the DPAVB has a relatively broad absorption linewidth. Using angular-dependent white light reflectivity measurements, we demonstrate that cavities constructed from two low reflectivity (6-pair) DBRs that contain 50% DPAVB in PS by mass operate within the strong coupling regime, with the observation of a lower (LPB) and an upper (UPB) polariton branch. At lower DPAVB concentrations, no clear splitting is observed and we conclude that such structures were weakly-coupled. Higher Q-factor microcavities were then constructed from higher reflectivity DBR mirrors (10 and 12 pairs) containing 50% DPAVB/PS by mass that had a larger exciton-photon detuning. Here, an LPB was observed in reflectivity and non-resonant photoluminescence measurements; however, the UPB was not evident due to the high reflectivity of the DBRs and the large angle at which the exciton-photon crossing occurs. Nevertheless, we are certain these cavities operate in the strong coupling regime and we have explored non-linear emission from them, demonstrating that they undergo polariton condensation at a threshold of 215 μJ cm−2 following excitation using sub-ns (<330 ps) pulses. This process is accompanied by a spectral blueshift of the LPB by 1.2 meV, which likely occurs from a combination of reversible ground-state bleaching together with a limited degree of irreversible photodegradation, and a linewidth reduction of the LPB around k = 0 from 1.5 meV to 0.2 meV. We have explored the photostability of control DPAVB/PS thin films, and find an unexpected slow, photo-brightening effect that we ascribe to a gradual reduction in the relative density of non-radiative channels. We have also studied polariton condensate emission at double the threshold fluence and have shown that it displays remarkable photostability, with the cavity remaining in the non-linear regime for more than 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 pulses. This result is especially promising as all measurements were performed in air. We expect that this material will be of interest in experiments looking to explore condensate-condensate interactions and condensation in polariton lattices.7,9
000 pulses. This result is especially promising as all measurements were performed in air. We expect that this material will be of interest in experiments looking to explore condensate-condensate interactions and condensation in polariton lattices.7,9
Methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) in dichloromethane. Thin films were made by spin coating the solution onto quartz-coated glass substrates, with a Bruker DektakXT profilometer then used to measure film thickness.
000) in dichloromethane. Thin films were made by spin coating the solution onto quartz-coated glass substrates, with a Bruker DektakXT profilometer then used to measure film thickness.
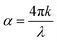 closely matches the absorption spectrum shown in Fig. 1(b). These values along with the n and k values of the SiO2 and TiO2 layers (determined using ellipsometry) were used in the TMR model. DBRs were fabricated using an Ångstrom Engineering electron beam to deposit λ/4-thick alternating layers of SiO2 and TiO2. The bottom and top mirrors consisted various numbers of DBR pairs and were centred around 460 nm. The bottom mirror was deposited onto a piece of quartz-coated glass. This was followed by the deposition of a film of DPAVB/PS by spin-coating, followed by the top DBR.
closely matches the absorption spectrum shown in Fig. 1(b). These values along with the n and k values of the SiO2 and TiO2 layers (determined using ellipsometry) were used in the TMR model. DBRs were fabricated using an Ångstrom Engineering electron beam to deposit λ/4-thick alternating layers of SiO2 and TiO2. The bottom and top mirrors consisted various numbers of DBR pairs and were centred around 460 nm. The bottom mirror was deposited onto a piece of quartz-coated glass. This was followed by the deposition of a film of DPAVB/PS by spin-coating, followed by the top DBR.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the UK EPSRC for funding this research via the Programme Grant ‘Hybrid Polaritonics’ (EP/M025330/1). K. E. M. also thanks the EPSRC for the award of a Doctoral Training Account PhD studentship.References
- J. Keeling and S. Kéna-Cohen, Bose–Einstein Condensation of Exciton-Polaritons in Organic Microcavities, Annu. Rev. Phys. Chem., 2020, 71, 435–459 CrossRef CAS PubMed.
- D. Sanvitto and S. Kéna-Cohen, The road towards polaritonic devices, Nat. Mater., 2016, 15, 1061–1073 CrossRef CAS PubMed.
- K. S. Daskalakis, S. A. Maier and S. Kéna-Cohen, Spatial Coherence and Stability in a Disordered Organic Polariton Condensate, Phys. Rev. Lett., 2015, 115, 035301 CrossRef CAS PubMed.
- M. Wei, et al., Low-threshold polariton lasing in a highly disordered conjugated polymer, Optica, 2019, 6, 1124 CrossRef CAS.
- T. Byrnes, N. Y. Kim and Y. Yamamoto, Exciton-polariton condensates, Nat. Phys., 2014, 10, 803–813 Search PubMed.
- D. Bajoni, Polariton lasers. Hybrid light–matter lasers without inversion, J. Phys. D: Appl. Phys., 2012, 45, 313001 CrossRef.
- M. Dusel, et al., Room temperature organic exciton–polariton condensate in a lattice, Nat. Commun., 2020, 11, 1–7 Search PubMed.
- R. Jayaprakash, et al., Two-Dimensional Organic-Exciton Polariton Lattice Fabricated Using Laser Patterning, ACS Photonics, 2020, 7, 2273–2281 CrossRef CAS.
- F. Scafirimuto, et al., Tunable exciton–polariton condensation in a two-dimensional Lieb lattice at room temperature, Commun. Phys., 2021, 4, 39 CrossRef.
- J. D. Plumhof, T. Stöferle, L. Mai, U. Scherf and R. F. Mahrt, Room-temperature Bose-Einstein condensation of cavity exciton-polaritons in a polymer, Nat. Mater., 2014, 13, 247–252 CrossRef CAS PubMed.
- T. Cookson, et al., A Yellow Polariton Condensate in a Dye Filled Microcavity, Adv. Opt. Mater., 2017, 5, 1700203 CrossRef.
- D. Sannikov, et al., Room Temperature Broadband Polariton Lasing from a Dye-Filled Microcavity, Adv. Opt. Mater., 2019, 7, 1–5 Search PubMed.
- K. S. Daskalakis, S. A. Maier, R. Murray and S. Kéna-Cohen, Nonlinear interactions in an organic polariton condensate, Nat. Mater., 2014, 13, 271–278 CrossRef CAS PubMed.
- C. P. Dietrich, et al., An exciton-polariton laser based on biologically produced fluorescent protein, Sci. Adv., 2016, 2, 1–8 Search PubMed.
- S. Betzold, et al., Coherence and Interaction in Confined Room-Temperature Polariton Condensates with Frenkel Excitons, ACS Photonics, 2020, 7, 384–392 CrossRef CAS.
- J. Tang, et al., Room temperature exciton–polariton Bose–Einstein condensation in organic single-crystal microribbon cavities, Nat. Commun., 2021, 12, 1–8 CrossRef PubMed.
- Z. Jiang, A. Ren, Y. Yan, J. Yao and Y. S. Zhao, Exciton-Polaritons and Their Bose–Einstein Condensates in Organic Semiconductor Microcavities, Adv. Mater., 2022, 34, 2106095 CrossRef CAS PubMed.
- K. E. McGhee, et al., Polariton condensation in an organic microcavity utilising a hybrid metal-DBR mirror, Sci. Rep., 2021, 11, 20879 CrossRef CAS PubMed.
- K. P. Kretsch, et al., Distributed feedback laser action from polymeric waveguides doped with oligo phenylene vinylene model compounds, Appl. Phys. Lett., 2000, 76, 2149–2151 CrossRef CAS.
- M. Ichikawa, et al., Gain-narrowing characteristics of fluorescent organic molecules with symmetrical or asymmetrical structures in a neat thin-film optical waveguide, J. Photochem. Photobiol., A, 2003, 158, 219–221 CrossRef CAS.
- T. Riedl, et al., Tunable organic thin-film laser pumped by an inorganic violet diode laser, Appl. Phys. Lett., 2006, 88, 2–4 CrossRef.
- M. T. Lee, H. H. Chen, C. H. Liao, C. H. Tsai and C. H. Chen, Stable styrylamine-doped blue organic electroluminescent device based on 2-methyl-9, 10-d/(2-naphthyl)anthracene, Appl. Phys. Lett., 2004, 85, 3301–3303 CrossRef CAS.
- C.-H. Liao, M.-T. Lee, C.-H. Tsai and C. H. Chen, Highly efficient blue organic light-emitting devices incorporating a composite hole transport layer, Appl. Phys. Lett., 2005, 86, 203507 CrossRef.
- X. R. Wang, J. S. Chen, H. You, D. G. Ma and R. G. Sun, Efficiency and color coordinate improvement using codopants in blue organic light-emitting diode, Jpn. J. Appl. Phys., Part 1, 2005, 44, 8480–8483 CrossRef CAS.
- K. P. Kretsch, et al., Amplified spontaneous emission and optical gain spectra from stilbenoid and phenylene vinylene derivative model compounds, J. Appl. Phys., 1999, 86, 6155–6159 CrossRef CAS.
- T. Rabe, et al., Threshold reduction in polymer lasers based on poly(9,9-dioctylfluorene) with statistical binaphthyl units, Adv. Funct. Mater., 2005, 15, 1188–1192 CrossRef CAS.
- M. Lehnhardt, T. Riedl, U. Scherf, T. Rabe and W. Kowalsky, Spectrally separated optical gain and triplet absorption: Towards continuous wave lasing in organic thin film lasers, Org. Electron., 2011, 12, 1346–1351 CrossRef CAS.
- V. Savona, L. C. Andreani, P. Schwendimann and A. Quattropani, Quantum well excitons in semiconductor microcavities: Unified treatment of weak and strong coupling regimes, Solid State Commun., 1995, 93, 733–739 CrossRef CAS.
- D. Ballarini and S. De Liberato, Polaritonics: From microcavities to sub-wavelength confinement, Nanophotonics, 2019, 8, 641–654 CAS.
- R. T. Grant, et al., Efficient Radiative Pumping of Polaritons in a Strongly Coupled Microcavity by a Fluorescent Molecular Dye, Adv. Opt. Mater., 2016, 4, 1615–1623 CrossRef CAS.
- K. Georgiou, et al., Generation of Anti-Stokes Fluorescence in a Strongly Coupled Organic Semiconductor Microcavity, ACS Photonics, 2018, 5, 4343–4351 CrossRef CAS.
- A. Putintsev, et al., Nano-second exciton-polariton lasing in organic microcavities, Appl. Phys. Lett., 2020, 117, 123302 CrossRef CAS.
- C. M. Herzinger, B. Johs, W. A. McGahan, J. A. Woollam and W. Paulson, Ellipsometric determination of optical constants for silicon and thermally grown silicon dioxide via a multi-sample, multi-wavelength, multi-angle investigation, J. Appl. Phys., 1998, 83, 3323–3336 CrossRef CAS.
- N. Sultanova, S. Kasarova and I. Nikolov, Dispersion properties of optical polymers, Acta Phys. Pol., A, 2009, 116, 585–587 CrossRef CAS.
- S. Christopoulos, et al., Room-Temperature Polariton Lasing in Semiconductor Microcavities, Phys. Rev. Lett., 2007, 98, 126405 CrossRef CAS PubMed.
- L. Orosz, et al., LO-phonon-assisted polariton lasing in a ZnO-based microcavity, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 1–5 CrossRef.
- R. Jayaprakash, et al., Ultra-low threshold polariton lasing at room temperature in a GaN membrane microcavity with a zero-dimensional trap, Sci. Rep., 2017, 7, 1–9 CrossRef CAS PubMed.
- M. Wei, et al., Room Temperature Polariton Lasing in Ladder-Type Oligo(p-Phenylene)s with Different π-Conjugation Lengths, Adv. Photonics Res., 2021, 2, 2000044 CrossRef.
- T. Yagafarov, et al., Mechanisms of blueshifts in organic polariton condensates, Commun. Phys., 2020, 3, 1–10 CrossRef.
- J. Kasprzak, et al., Bose–Einstein condensation of exciton polaritons, Nature, 2006, 443, 409–414 CrossRef CAS PubMed.
- C. Gadermaier, et al., Dynamics of higher photoexcited states in m-LPPP probed with sub-20 fs time resolution, Chem. Phys. Lett., 2004, 384, 251–255 CrossRef CAS.
- A. V. Zasedatelev, et al., A room-temperature organic polariton transistor, Nat. Photonics, 2019, 13, 378–383 CrossRef CAS.
- H. Fujiwara, Spectroscopic Ellipsometry: Principles and Applications, John Wiley & Sons Ltd, 2007 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc05554b |
| This journal is © The Royal Society of Chemistry 2022 |