Intramolecular micellization and nanopatterning in pH- and thermo-responsive molecular brushes†
Varvara M.
Prokacheva
 a,
Oleg V.
Rud
a,
Oleg V.
Rud
 *ab,
Filip
Uhlík
*ab,
Filip
Uhlík
 a and
Oleg V.
Borisov
a and
Oleg V.
Borisov
 bc
bc
aDepartment of Physical and Macromolecularz Chemistry, Faculty of Science, Charles University, Hlavova 8, 128 00 Praha 2, Czech Republic. E-mail: varvara.prokacheva@natur.cuni.cz; oleg.rud@natur.cuni.cz
bInstitute of Macromolecular Compounds of the Russian Academy of Sciences, 199004 St. Petersburg, Russia
cInstitut des Sciences Analytiques et de Physico-Chimie pour l'Environnement et les Matériaux, CNRS, Université de Pau et des Pays de l'Adour UMR 5254, Pau, France. E-mail: oleg.borisov@univ-pau.fr
First published on 18th November 2019
Abstract
Conformational transitions and nanoscale self-organization triggered in double pH- and thermo-responsive molecular brushes by varying environmental conditions are studied by means of analytical mean-field theory and numerical Scheutjens–Fleer self-consistent field modelling. Such molecular brushes are composed of multiple thermo-responsive side chains end-grafted onto the main chain (backbone) and are capable of acquiring ionic charges via reversible (de)protonation of the monomer units. Competition of long-range Coulomb repulsion with short-range solvophobic interactions leads to complex patterns in the intramolecular self-organization of molecular brushes. In particular, we observed formation of pearl necklace-like structures with multiple dense nanodomains formed by weakly ionized collapsed side chains and stabilized by a fraction protruding into the solution and strongly ionized ones. Such structures are thermodynamically stable in a certain parameter range and can be termed as intramolecular micelles. The stimuli-induced intramolecular nanopatterning occurs via a sequence of quasi-first order phase transitions corresponding to splitting/fusion of collapsed domains accompanied by jumps in the average degree of ionization and macromolecular dimensions. A re-entrant sequence of transitions is observed when the salt concentration is used as a control parameter. These theoretical predictions provide guidelines for design of smart unimolecular devices, for example multicompartment nanocarriers of active substances or nanosensors.
1 Introduction
Regularly branched ionizable macromolecules exemplify soft nanoparticles that are capable of changing their size, shape and intra-molecular structural organization upon the influence of external stimuli. Among them comb-shaped polyelectrolytes and molecular brushes, in which charged side chains are tethered at regular intervals onto a long linear main chain (backbone), have recently attracted considerable attention.1–6The possibility to manipulate the size and shape of such single responsive nanoobjects by external stimuli, e.g., the temperature, pH and ionic strength of the solution, as well as their capacity for interaction and complex formation with other molecules and oppositely charged macro-ionic species, opens fascinating perspectives for their use as nanosensors, molecular templates, smart nanocarriers for drug delivery applications,7–10 and non-viral vectors for genetic material.11–13 In particular, the combination of pH- and thermo-sensitive properties enables synthesizing smart multi-responsive molecular brushes capable of reacting in a programmed way to such biologically relevant stimuli as temperature and pH.
Molecular brushes with weak anionic poly(acrylic acid)14 and poly(methacrylic acid)7,8 and cationic (poly(N,N-dimethylaminoethyl methacrylate) (PDMAEMA))15–17 side chains were recently synthesized and their solution properties, responsive behavior with respect to the pH and ionic strength of the solution and performance in drug delivery were experimentally studied. PDMAEMA brushes are of particular interest since they exhibit both pH- (weak polybase) and thermo- (lower critical solution temperature) responsiveness. The cationic charge of PDMAEMA makes these brushes most promising for gene delivery (through polyplex formation with DNA/RNA) and fabrication of materials with antibacterial properties.
The interplay of long-range Coulomb repulsion and short-range hydrophobic attraction results in intra-molecular nanostructuration. For example, in the seminal work of Dobrynin, Rubinstein, and Obukhov18 it was predicted that the balance of long-range Coulomb repulsion with short-range attraction in a single linear chain hydrophobic polyelectrolyte molecule gives rise to a longitudinally periodical pearl-necklace structure. This theoretical prediction has found convincing support from numerical methods19,20 as well as from experimental evidence.21
The inherent spherical symmetry of a star-like polyelectrolyte molecule results in different patterns in the partially-collapsed conformation. In the case of strong polyelectrolytes a formation of bundles of arms isotropically distributed in the azimuthal direction was observed in Monte Carlo (MC) simulations.22 On the contrary, due to the possibility to adjust the local degree of ionization of the arms, partially collapsed in poor solvent weak polyelectrolyte stars exhibit a spherically symmetrical core–corona structure: the central core is composed of weakly ionized collapsed arms fully embedded into the core whereas the corona is constituted of more ionized extended arms. Such core–corona structures have been predicted on the basis of numerical Scheutjens–Fleer Self-Consistent Field (SF-SCF) modelling23 and later confirmed by MC simulations.22
Intuitively, one could expect that partially collapsed weak polyelectrolyte molecular brushes exhibit similar core–corona structure with a cylindrical central core domain surrounded by a corona, resembling a cylindrical polyelectrolyte brush. However, a uniformly collapsed single cylindrical core might exhibit longitudinal instability, similar to that found in a linear polyelectrolyte chain in poor solvent.18–20
The goal of this work is to explore pathways of nanostructuration occurring in a polyelectrolyte molecular brush with double pH- and thermo-sensitive side chains upon variation of the ionic strength and pH of the solution and tuned by the temperature solubility of (uncharged) monomer units. Our major interest is to predict how the size and shape of the intramolecular structures emerging in a partially-collapsed molecular brush evolve as a function of these controlling parameters.
The rest of the paper is organized as follows. We start by presenting an analytical mean-field theory of conformational transitions in weak polyelectrolyte brushes (Section 2). In Section 3 we describe our model and the SF-SCF computational method. In Section 4 we present results of the analytical mean-field theory and SF-SCF calculations showing the effect of salt concentration and pH on the ionization, overall dimensions and internal structure of a molecular brush.
2 Analytical theory: the box-like model
The swelling-to-collapse transition in double pH- and thermo-responsive molecular brushes can be first qualitatively analyzed on the basis of a simplified mean-field analytical theory. Such a model assumes (i) local electroneutrality of the intra-molecular volume, i.e., vanishing of the net local charge density due to neutralization of the charge immobilized on the polyion by an excess concentration of mobile counterions, (ii) equal and uniform extension of the chains and (iii) neglecting the radial gradients in the concentrations of monomer units and small ions and in the degree of ionization. This kind of approach was introduced by Borisov et al.24 and Pincus and Ross25 for the study of collapse-to-swelling transitions in polyelectrolyte brushes of different morphologies and later applied by Polotsky et al.26 and Rud et al.23 to pH-responsive amphiphilic star-like macromolecules.The box-like model allows for analytical solutions for integral properties of the brush (e.g., overall dimensions or average concentration of monomer units) as a function of the set of relevant control parameters. It can be generalized in a straightforward way for brushes of any arbitrary generic morphology. We will discuss here one particular case, namely a cylindrical brush. Details for other types of geometry, such as planar and spherical, are shown in the ESI.†
The average polymer concentration (volume fraction) in the brush is equal to
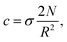 | (1) |
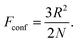 | (2) |
| F(c) = Fconf(c) + Fint(c) + Fionic(c) | (3) |
| Fint(c) = N(vc + wc2) | (4) |
The last term, Fionic(c), in eqn (3) describes the contribution of ionic interactions in the brush28
 | (5) |
 | (6) |
| αb = (1 + 10pK−pH)−1 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K.
K.
The minimization of free energy leads to the following equation for the equilibrium polymer concentration in the brush:
 | (8) |
 | (9) |
Eqn (8) together with eqn (6) and (7) allows obtaining the equilibrium dimensions (or intramolecular polymer concentration) and ionization degree of the brush-forming chains as a function of external parameters cs, v(χ(T)) and pH.
Analysis of the system of eqn (8), eqn (6) and eqn (7) shows that the intramolecular concentration c is a single-valued function of cs and pH at v(χ(T)) ≥ 0, i.e., at χ ≤ 0.5. On the contrary, under poor solvent conditions, χ > 0.5, eqn (8) may have multiple solutions for c, which implies jump-wise variation of the brush dimensions (and consequently the degree of ionization) upon a smooth variation in cs and pH.
3 Numerical approach
3.1 Model
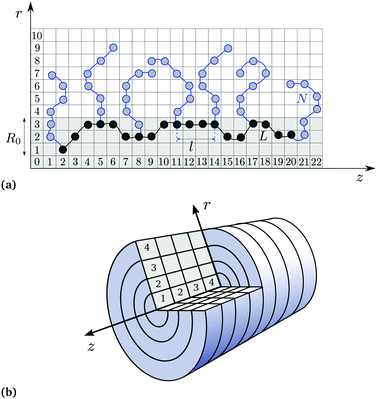
We study a molecular brush consisting of a semi-rigid polyelectrolyte backbone of length L = 61 segments and flexible side chains with length N = 30 segments grafted on every third segment of the backbone (the number of side chains n = 21). The model is schematically illustrated in Fig. 1a. The segments of the backbone are able to freely move in cylindrical disks of radius R0 = 3 and of thickness one z-layer.All monomer units of the brush-forming chains can be either neutral or ionized according to the reaction
 | (10) |
 | (11) |
For the description of interactions between polymer and solvent particles we use the Flory–Huggins parameter χ (which characterizes the solvent quality).29 We use the same χ value for contacts of both charged and neutral monomers with positive (Na+, H3O+) and negative (Cl−, OH−) ions. We consider a hydrophobic molecular brush, so the Flory–Huggins parameter χ > 0.5.
3.2 Scheutjens–Fleer self-consistent field method (SF-SCF)
The SF-SCF30–34 method employs the main idea of mean-field theory, namely to replace direct particle–particle interactions by an interaction of each particle with an effective mean-field from other particles. Although this approximation neglects fluctuations, it brings enormous savings in computational costs. Basically, it reduces the 3N-dimensional problem (of N particles) to a three-dimensional problem of component density distributions in the field. Further computational savings can be achieved using the symmetry of the studied system. Namely, the three-dimensional problem is reduced to a one- or two-dimensional one by averaging over the remaining coordinates. In the present work, we use the two-dimensional cylindrical lattice schematically illustrated in Fig. 1b, where a gradient in the density is present in the two r- and z-directions, but inside of each rz-ring the density is constant.The task of solving the mean-field problem comes down to the minimization of the free energy functional with respect to the spatial density profiles ci(r) of all species i. The minimization yields the probability of finding species i at a certain location r, which obeys the Boltzmann equation
 | (12) |
| ui({c(r)}) = u′ + ushorti + ueli, | (13) |
 . The term ushorti is the part of the field associated with short range interactions
. The term ushorti is the part of the field associated with short range interactions | (14) |
 | (15) |
In the Scheutjens–Fleer SCF method the polymer chains are modeled as trajectories of random walks.30–32 In other words, the method considers a polymer as an ensemble of random walks in a mean-field created by the surrounding solution and by the chain itself. In order to calculate the density distribution of all the possible random walk trajectories which polymer chains may be forming, the Edwards diffusion equation is used. This equation was originally derived to describe the diffusion of Brownian particles in an external field.35,36 The statistical weights of the walks of a chain are therefore given by
 | (16) |
The equilibrium density profiles which minimize the free energy functional need to be found numerically in an iterative procedure. Starting with an initial guess for the density distributions, one calculates the mean-field potentials from these densities then updates the densities based on the calculated potentials. The iterations proceed until self-consistency is reached, i.e., until the density profiles and potentials are mutually consistent within a specified accuracy threshold.
The SF-SCF theory implements a discretized version of the Edwards diffusion equation for a random walk on a lattice. The space discretization is schematically illustrated in Fig. 1b for the two-gradient cylindrical symmetry approximation. In this case, both r and s become discrete variables, called the layer number and the segment ranking number. In the discretized version, it is possible to explicitly count the statistical weights of all possible random walks on the lattice. Such an implementation includes the excluded volume of the polymer monomer units as well as other monomeric species via the incompressibility constraint. It assumes that each polymer segment or small solute occupies exactly one lattice site, and this lattice site cannot be occupied by any other species. Additional constraints can be imposed as boundary conditions, e.g., pinning of the side chain starting segments at the origin axis of the lattice, or setting the bulk concentration of H+ ions as a boundary condition. Each monomer unit of the backbone has a certain z-position, whereas its r-coordinate may assume values from 1 to 3 (see Fig. 1a).
The SF-SCF method has been extended by Israëls et al.38 and Klein Wolterink et al.39 to treat ionization equilibria in weak polyelectrolytes by introducing different states for each segment (ionized and non-ionized), and obtaining coupled equations analogous to eqn (16) for individual states. This theory has been already applied to weak polyelectrolyte stars and brushes, and also to weak polyelectrolyte hydrogels.23,39–42
4 Results
4.1 Effect of pH on the ionization and dimensions of the molecular brush
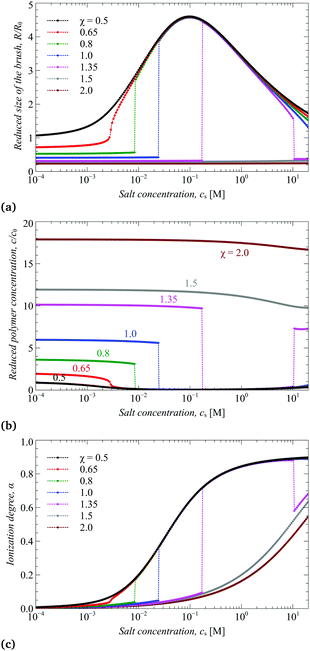
In Fig. 2 we present the calculated (according to eqn (8)) reduced transversal dimension R/Rθ, volume fraction of monomer units c/cθ, and ionization degree α as a function of pH at a constant value of χ = 1 and a series of values of salt concentrations cs ranging from 2 × 10−3 to 2 × 101 M. Here, Rθ is the thickness of a non-charged brush at the theta-temperature. Although Fig. 2a and b contain the same information about the variation of the brush transversal dimensions, we present them both for the purpose of better resolution of the collapsed state.In order to describe the cross-sectional dimensions of the molecular brush obtained by the SF-SCF approach, we use the z component of the gyration tensor of the molecule, which represents its reduced moment of inertia during rotation around the z-axis of the cylindrical lattice (see Fig. 1b). It is calculated as
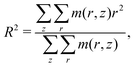 | (17) |
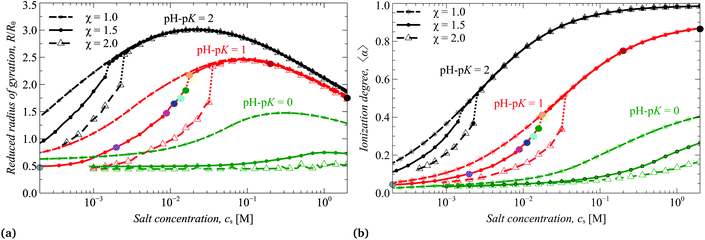
In Fig. 3a and b we present the reduced thickness of the brush R/Rθ calculated using eqn (17) and the ionization degree 〈α〉 averaged over all monomer units in the brush calculated by means of SF-SCF.
As one can see from Fig. 2c and 3b, both the box-like model and SF-SCF demonstrate that the (average) degree of ionization of the brush monotonously increases as a function of pH − pK. The α vs. pH − pK curves are systematically shifted to smaller pH − pK values as the salt concentration increases and in the limit of high salt concentration approach the “ideal titration” curve
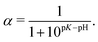 | (18) |
An increase in α upon an increase in pH leads to an increase in the brush thickness R, as demonstrated by Fig. 2a and 3a, which is explained by increasing osmotic pressure inside the brush. The box-like model, Fig. 2a and c, predicts that the increase in both R and α as a function of pH exhibits a jump from the collapsed and weakly ionized (α ≈ 0) to the swollen and moderately ionized (α ≈ 0.4) state of the brush at low salt concentration and the size of the jump decreases and shifts to higher ionization degree at high salt concentration. Remarkably, these discontinuities in the average R and α are also observed but are much less pronounced in the results of the SF-SCF calculations, Fig. 3a and b. While at high salt concentration, the transversal dimensions and ionization degree change continuously.
4.2 Effect of salt concentration on the ionization and conformation of the molecular brush
The main trend demonstrated by both the analytical model and numerical SF-SCF calculation (see Fig. 7) is non-monotonous (re-entrant) variation of the brush thickness as a function of salt concentration. The increase in the brush thickness versus cs at low salt concentration is directly related to a concomitant steep increase in the degree of ionization α, which leads to an increase in the osmotic pressure inside the brush.
On the contrary, at high salt concentration, the degree of ionization approaches its maximal value close to αb, whereas the osmotic pressure decreases due to an increase in the bulk salt concentration, which leads to shrinkage of the brush. A similar trend has been predicted for planar weak polyelectrolyte brushes in ref. 43 and for weak polyelectrolyte stars under good44 and also under poor26 solvent conditions.
As demonstrated by the analytical model in Fig. 5, under theta- or moderately poor solvent conditions and pH − pK = 1 (corresponding to αb ≈ 0.91) the brush thickness varies non-monotonically but smoothly as a function of cs, which is accompanied by a monotonous smooth increase in α. A decrease in the solvent strength (an increase in χ) leads to the appearance of a jump in the R(cs) curves, indicating a quasi-first order phase transition from the collapsed to the swollen conformation (we use quasi- to distinguish from the true (bulk) counterparts that are only defined in the thermodynamic limit). This jump-wise swelling of the brush is accompanied by a jump-wise increase in ionization. This coupling between the polymer concentration and degree of ionization in the brush is described by eqn (6). Upon a further increase in salt concentration, the brush thickness either passes through a maximum or monotonously decreases. Most interesting, under sufficiently poor solvent (χ ≥ 1.0) conditions a jump-wise collapse of the brush may occur at high salt concentration: this collapse of the brush is accompanied by a drop in the ionization degree and occurs due to insufficient (at high salt) osmotic pressure inside the brush and a substantial gain in the free energy upon formation of a dense (collapsed) state. If the solvent is very poor χ ≥ 1.5 the brush remains in the collapsed state in the whole range of salt concentration, though it exhibits a weak decrease in density in the intermediate salt concentration range. The degree of ionization is much smaller than αb except for the very high salt concentration range.
When the solvent is moderately poor (χ = 1) the shape of the R(cs) curves is affected by the pH − pK value (see Fig. 4). At extreme pH − pK ≥ 6 the brush is fully ionized at any salt concentration and behaves as a quenched polyelectrolyte brush with α = const. Therefore, the brush remains swollen and virtually unaffected by the salt in a wide range of salt concentrations (the so-called “osmotic regime”). Only when the salt concentration in the bulk of the solution becomes comparable with or exceeds the concentration of the entrapped in the brush counter-ions does the brush start to shrink. As long as the polymer concentration in the brush remains low and the contribution of non-electrostatic binary interactions is negligible, the approximate dependence R ∼ cs−1/4 holds. However, at pH − pK ≤ 5 the R versus cs curves acquire a characteristic non-monotonic shape (corresponding to a salt-induced re-entrant collapse-to-swelling-to-collapse transition) and at pH − pK ≤ 4 a weak initial increase in the thickness of the virtually uncharged brush is followed by jump-wise swelling and a concomitant jump-up in the degree of ionization. Upon a further increase in salt concentration a smooth re-entrant swelling-to-collapse transition is observed. The position c(max)s of the maximum in the brush thickness is systematically shifted to higher salt concentration, whereas the magnitude of the jump and the maximum thickness of the brush systematically decrease as pH − pK decreases. A further decrease in pH − pK below unity results first in the appearance of the jump-wise collapse transition with a concomitant drop in the ionization degree. At pH − pK ≤ 0 the brush remains in a collapsed and fairly uncharged state in the whole range of salt concentration.
In the three-dimensional plot Fig. 6 we combine results from Fig. 2a and 4a for the dependence of the brush reduced size on the salinity and pH − pK in poor solvent conditions χ = 1. The color of the surface in the plot refers to the degree of ionization of the brush. The figure indicates a smooth change of the brush size when it is almost fully ionized (the red part of the surface), the collapsed conformation when the brush is almost uncharged (the violet part) and the sharp boundary between these two regions separating the swollen and charged brush from the collapsed and uncharged one. Moreover, the presence and the size of the jump can be tuned by the solution salinity and pH as well as by the solvent quality (the dependence on χ was shown before, Fig. 5).
The predicted by the theory complex patterns in the dependence of the brush thickness on salt concentration in poor solvent appear because of the delicate interplay between short-range monomer–monomer attraction (contracting force) and osmotic pressure created by mobile ions (expanding force) and different power law dependencies of these two competing forces. Moreover, the ionization state of the brush forming chains itself depends on the conformation viaeqn (6). We remark that jump-wise salt-induced collapse was predicted within the box-like model also for quenched polyelectrolyte stars in poor solvent.26 In the case of a weak polyelectrolyte brush, such a jump-wise collapse transition occurs at sufficiently large salt concentration when the ionization degree approaches its maximal value αb.
However, the magnitudes of these jumps are significantly smaller than those predicted by the analytical theory. The decrease in the brush size at high salt concentration according to the SF-SCF results is always continuous; the ionization degree monotonously increases approaching the plateau value of αb. In both limits of high and low salt the brush is less collapsed (the polymer volume fraction is larger) than predicted by the analytical theory. This can be explained by underestimation of short-range repulsive interactions in the collapsed brush within the analytical approach, which accounts only for three-body repulsive interactions. However, when the volume fraction of the polymer in the brush reaches a few tens of percent, higher order repulsive interactions fully accounted for by the SF-SCF scheme become important. As a result, the polymer volume fraction in the collapsed (at low ionic charge) brush only weakly increases when χ increases beyond 1–1.5, as seen from the SF-SCF results. Also, the analytical theory considers all mobile ions as infinitely small, whereas in the SF-SCF scheme each of them occupies a lattice site, which also prevents the brush from undergoing deep collapse.
The most important advantage of the SF-SCF approach is that it enables us to obtain detailed information about structural changes in the brush that occur in the course of the re-entrant collapse-to-swelling transition. Indeed, in contrast to the box-like model that pre-assumes that the polymer volume fraction and degree of ionization of the chains are fairly uniform across the brush and the brush swells or collapses as a whole, the SF-SCF approach enables us to follow the evolution of a two-dimensional distribution of the polymer density and local degree of ionization upon the conformational transition.
This information is collected in Fig. 8 where the local polymer volume fraction c(r,z) (left), volume fraction of end segments cend(r,z) (middle) and local degree of ionization α(r,z) (right) are presented for a set of increasing (from the bottom to the top) values of salt concentration. This set of “snapshots” corresponds to the presented in Fig. 7 dependence of the mean-square brush thickness and average ionization degree on salt concentration at pH − pK = 1 and χ = 1.5 (the red curve with circle symbols).
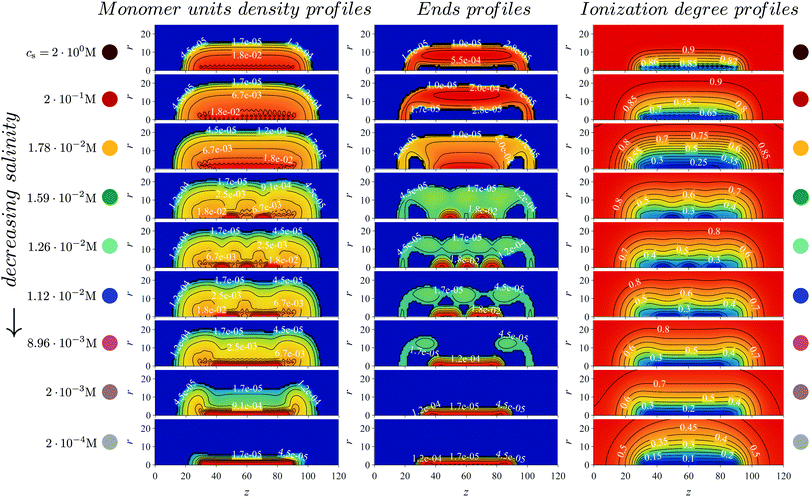 | ||
| Fig. 8 The distribution of the polymer, terminal groups and ionization degree are the first, second and third column, respectively. The profiles correspond to the systems at different salt concentrations marked by circle symbols on the red curve with pH − pK = 1 in Fig. 7a and b at χ = 1.5. The distributions show changes in the density from denser (red color) to less dense (blue color). | ||
Comparison of the lower and upper panels, both corresponding to the collapsed state of the brush with either a vanishing (at low salt) or maximal (at high salt) degree of ionization, indicates that in both cases the brush exhibits a longitudinally uniform structure: the polymer density is the largest close to the axis and decays in the radial direction but is independent (apart from the end effects) of the z-coordinate. The weak oscillation in c(r,z) visible close to the z axis at high salt concentration corresponds to grafting points of the side chains to the main chain. A decrease in salt concentration down to ≈100 M leads to noticeable swelling of the brush in the radial direction without significant changes in the shape of the polymer distribution. An essentially new structural motif appears when the salt concentration drops below ≈10−1 M. In Fig. 7a this corresponds approximately to the range of steep (quasi jump-wise) variation in the transversal dimensions of the brush. One can clearly distinguish formation of two domains with large polymer density localized close to the axis. At even lower salt concentration these two dense domains first re-arrange into three smaller domains that upon a further decrease in salt concentration again re-arrange into two domains that eventually fuse into the longitudinally uniform collapsed core. The appearance and subsequent fusion of the dense domains is clearly seen also in the 2-dimensional profiles of local ionization, which is strongly suppressed within the domains with high local polymer concentration.
Most interestingly, this re-entrant longitudinal “nanopatterning” of the brush is manifested in the evolution of the distribution of the end segments of the chains. As one can see from the middle panel of Fig. 8, the dense domains are enriched in the end segments of the collapsed and virtually deionized chains that form these domains. At the same time there is a significant fraction of the end segments distributed across the brush that correspond to the population of extended and moderately ionized chains.
Finally, in Fig. 9 we plot a phase diagram in solvent quality χ–salt concentration cs coordinates illustrating the transition of the molecular brush from the swollen state to the collapsed one. In this diagram the color corresponds to the value of the collapsed polymer fraction λ. As the collapsed polymer we consider lattice sites where the volume fraction of polymer is above 0.5 and its gradient is above 0.2. The dark blue color represents the swollen brush when all side chains are stretched while the dark red color corresponds to the brush when almost all side chains are collapsed on a backbone. We can achieve the fully collapsed state of the brush by decreasing the solvent quality and salinity of the solution with intermediate states of partially collapsed side chains forming domains of different shapes. The details of the calculation of the collapsed polymer fraction λ are given in the ESI.†
5 Conclusions
We have employed a combination of analytical mean-field theory and numerical self-consistent field modeling with the aim (i) to study conformational transitions occurring in double (pH- and thermo-) responsive polyelectrolyte molecular brushes upon variation in pH, salt concentration or temperature and (ii) to analyze the morphology of the intramolecular nanoscale structures emerging as an outcome of such transitions.The combination of analytical and numerical approaches was most beneficial because the ability to react to multiple independent stimuli and the presence of internal degrees of freedom (i.e., ionized and non-ionized states of monomer units) leads to complex patterns in the response functions of the system.
While the analytical theory operates with a simplified box-like model, which enables us to predict the dependence of the integral properties of the macromolecule (i.e., average intramolecular concentration and degree of ionization of monomer units) on a combination of multiple independently varied control parameters, the numerical SF-SCF approach in its 2-gradient version allows for monitoring the variation of the size and shape of emerging complex nanoscale structures. Moreover, the resolution power of the SF-SCF method enabled detecting segregation of side chains into populations of strongly and weakly ionized (collapsed) ones, which leads to formation of micelle-like intra-molecular structures in a relevant parameter range.
The most interesting finding of our work is a prediction that a partially collapsed (e.g., at pH ≈ pK and moderate salt concentration) molecular brush acquires a conformation of multi-compartment intramolecular micelles of a pearl-necklace shape. Such micelles comprise multiple dense core domains with a hydrophobic local microenvironment formed by a population of weakly ionized collapsed side chains. These dense domains are stabilized by a corona formed by another population of side chains that are ionized and extended. Such coronas are strongly solvated and assure aggregative stability of the intramolecular micelles.
Remarkably, such a core–corona micellar structure in a homopolymer molecular brush and intra-molecular segregation into hydrophobic and hydrophilic domains are possible due to the presence of internal degrees of freedom – the possibility of monomer units to acquire or to lose charge depending on the local micro-environmental conditions (in the cores or in the corona). In turn, the specific topology of the molecular brush makes possible formation of multiple hydrophobic domains (multi-compartment structure) organized in a pearl-necklace morphology. The formation of multi-compartment micellar structure occurs via a sequence (cascade) of intramolecular quasi-first order phase transitions accompanied by splitting/fusion of hydrophobic domains and concomitant jump-wise variation in the integral properties (dimensions and average ionization degree) of the molecular brush.
Finally, the most peculiar prediction concerns the re-entrant sequence of conformational transitions occurring in a pH-sensitive molecular brush upon a monotonous increase in salt concentration: at low salt concentration the brush as a whole is fairly non-ionized and collapsed into one hydrophobic domain. An initial increase in salt concentration promotes ionization of (a fraction of) side chains and enhancement of intra-molecular Coulomb repulsions. As a result, a hydrophobic domain successively splits into an increasing number of smaller ones. However, a further increase in salt concentration leads to screening and weakening of the Coulomb repulsions and, as a result, re-entrant fusion of small hydrophobic domains into larger ones is observed.
We anticipate that our theoretical predictions can be beneficial for molecular design of smart multi-compartment unimolecular nanocontainers for delivery of drugs and biologically active molecules with controlled size, loading capacity and built-in response functions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Ministry of Research and Education of the Russian Federation (state contract 14.W03.31.0022) and by the Grant Agency of Charles University (project 676218). We would like to thank Prof. Frans Leermakers for providing the SFbox software package. The access to computing facilities of National Grid Infrastructure MetaCentrum (LM2015042) and CERIT Scientific Cloud (LM2015085) is appreciated.References
- J. Yuan, A. H. E. Müller, K. Matyjaszewski and S. Sheiko, Polymer Science: A Comprehensive Reference, Elsevier, Amsterdam, 2012, pp. 199–264 Search PubMed.
- M. Müllner, Macromol. Chem. Phys., 2016, 217, 2209–2222 CrossRef.
- M. Müllner and A. H. E. Müller, Polymer, 2016, 98, 389–401 CrossRef.
- T. Pelras, C. S. Mahon and M. Müllner, Angew. Chem., Int. Ed., 2018, 57, 6982–6994 CrossRef CAS.
- S. Tu, C. K. Choudhury, I. Luzinov and O. Kuksenok, Curr. Opin. Solid State Mater. Sci., 2019, 23, 50–61 CrossRef CAS.
- G. Xie, M. R. Martinez, M. Olszewski, S. S. Sheiko and K. Matyjaszewski, Biomacromolecules, 2019, 20, 27–54 CrossRef CAS.
- N. Y. Shilyagina, N. N. Peskova, S. A. Lermontova, A. A. Brilkina, V. A. Vodeneev, A. V. Yakimansky, L. G. Klapshina and I. V. Balalaeva, J. Biophoton., 2017, 10, 1189–1197 CrossRef CAS.
- A. V. Yakimansky, T. K. Meleshko, D. M. Ilgach, M. A. Bauman, T. D. Anan'eva, L. G. Klapshina, S. A. Lermontova, I. V. Balalaeva and W. E. Douglas, J. Polym. Sci., Part A: Polym. Chem., 2013, 51, 4267–4281 CrossRef CAS.
- H. Li, H. Liu, T. Nie, Y. Chen, Z. Wang, H. Huang, L. Liu and Y. Chen, Biomaterials, 2018, 178, 620–629 CrossRef CAS PubMed.
- H. Tang, W. Zhao, J. Yu, Y. Li and C. Zhao, Molecules, 2018, 24, 4 CrossRef.
- M. A. Mintzer and E. E. Simanek, Chem. Rev., 2009, 109, 259–302 CrossRef CAS.
- A. Schallon, C. V. Synatschke, V. Jérôme, R. Müller and R. Freitag, Biomacromolecules, 2012, 13, 3463–3474 CrossRef CAS.
- A. P. Majewski, U. Stahlschmidt, V. Jerome, R. Freitag, A. H. E. Mueller and H. Schmalz, Biomacromolecules, 2013, 14, 3081–3090 CrossRef CAS.
- H. Lee, J. R. Boyce, A. Nese, S. S. Sheiko and K. Matyjaszewski, Polymer, 2008, 49, 5490–5496 CrossRef CAS.
- Y. Xu, S. Bolisetty, M. Drechsler, B. Fang, J. Yuan, M. Ballauff and A. H. E. Müller, Polymer, 2008, 49, 3957–3964 CrossRef CAS.
- M. Wang, S. Zou, G. Guerin, L. Shen, K. Deng, M. Jones, G. C. Walker, G. D. Scholes and M. A. Winnik, Macromolecules, 2008, 41, 6993–7002 CrossRef CAS.
- A. P. Filippov, E. V. Belyaeva, N. V. Zakharova, A. S. Sasina, D. M. Ilgach, T. K. Meleshko and A. V. Yakimansky, Colloid Polym. Sci., 2015, 293, 555–565 CrossRef CAS.
- A. V. Dobrynin, M. Rubinstein and S. P. Obukhov, Macromolecules, 1996, 29, 2974–2979 CrossRef CAS.
- H. J. Limbach, C. Holm and K. Kremer, Europhys. Lett., 2002, 60, 566–572 CrossRef CAS.
- H. J. Limbach and C. Holm, J. Phys. Chem. B, 2003, 107, 8041–8055 CrossRef CAS.
- V. Aseyev, H. Tenhu and S. Klenin, Macromolecules, 1999, 32, 1838–1846 CrossRef CAS.
- F. Uhlík, P. Košovan, E. B. Zhulina and O. V. Borisov, Soft Matter, 2016, 12, 4846–4852 RSC.
- O. V. Rud, A. A. Mercurieva, F. A. M. Leermakers and T. M. Birshtein, Macromolecules, 2012, 45, 2145–2160 CrossRef CAS.
- O. Borisov, T. Birshtein and E. Zhulina, J. Phys. II, 1991, 1, 521–526 CrossRef CAS.
- R. S. Ross and P. Pincus, Macromolecules, 1992, 25, 2177–2183 CrossRef CAS.
- A. A. Polotsky, E. B. Zhulina, T. M. Birshtein and O. V. Borisov, Soft Matter, 2012, 8, 9446–9459 RSC.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, Oxford, UK, 2003, pp. 137–165 Search PubMed.
- E. Zhulina and O. Borisov, Macromolecules, 2002, 35, 9191–9203 CrossRef CAS.
- P. Flory, Principles of Polymer Chemistry, Cornell University Press, 1953 Search PubMed.
- J. Scheutjens and G. Fleer, J. Phys. Chem., 1979, 83, 1619–1635 CrossRef CAS.
- J. Scheutjens and G. Fleer, J. Phys. Chem., 1980, 84, 178–190 CrossRef CAS.
- J. Scheutjens and G. Fleer, Macromolecules, 1985, 18, 1882–1900 CrossRef CAS.
- G. J. Fleer, M. A. Cohen Stuart, T. Cosgrove and B. Vincent, Polymers at interfaces, Chapman and Hall, London, 1993 Search PubMed.
- G. Fleer and F. Leermakers, Curr. Opin. Colloid Interface Sci., 1997, 2, 308–314 CrossRef CAS.
- S. Edwards, Proc. Phys. Soc., London, 1965, 85, 613–624 CrossRef CAS.
- M. Doi and S. F. Edwards, The theory of polymer dynamics, Oxford Science Publications, 1986 Search PubMed.
- P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, 1979 Search PubMed.
- R. Israëls, F. A. M. Leermakers, G. J. Fleer and E. B. Zhulina, Macromolecules, 1994, 27, 3249–3261 CrossRef.
- J. Klein Wolterink, J. van Male, M. A. Cohen Stuart, L. K. Koopal, E. B. Zhulina and O. V. Borisov, Macromolecules, 2002, 35, 9176–9190 CrossRef.
- O. V. Rud and T. M. Birshtein, Polym. Sci., 2013, 55, 757–771 CAS.
- O. V. Rud, F. a. M. Leermakers and T. M. Birshtein, Langmuir, 2014, 30, 48–54 CrossRef CAS.
- O. Rud, T. Richter, O. Borisov, C. Holm and P. Košovan, Soft Matter, 2017, 13, 3264–3274 RSC.
- E. B. Zhulina, T. M. Birshtein and O. V. Borisov, Macromolecules, 1995, 28, 1491–1499 CrossRef CAS.
- O. Borisov and E. Zhulina, Eur. Phys. J. B, 1998, 4, 205–217 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01961h |
| This journal is © The Royal Society of Chemistry 2020 |