Structure and dynamics of titania – poly(N-vinyl caprolactam) composite hydrogels†
O. I.
Timaeva
 *a,
G. M.
Kuz'micheva
*a,
G. M.
Kuz'micheva
 a,
I. I.
Pashkin
a,
I. I.
Pashkin
 a,
O.
Czakkel
a,
O.
Czakkel
 b and
S.
Prevost
b and
S.
Prevost
 b
b
aFederal State Budget Educational Institution of Higher Education “MIREA – Russian Technological University”, pr. Vernadskogo 86, Moscow, 119571, Russia. E-mail: gertrudejames@mail.ru
bInstitut Laue-Langevin, CS 20156, F-38042 Grenoble Cedex 9, France
First published on 19th November 2019
Abstract
The morphologies and dynamics of poly(N-vinyl caprolactam) (PVCL) based hydrogels with titania nanoparticles in different states (native, air-dried to a constant weight and swollen in H2O or D2O) are studied by a combination of complementary techniques: wide angle X-ray scattering, small angle neutron scattering, neutron spin echo spectroscopy, differential scanning calorimetry. The results suggest the presence of different structural types of water leading to different properties of the hydrogels. We propose a hierarchical structure of hydrogels spanning from the molecular to the microscopic scale consistent with both the static structure (polymer mesh size, association of the nodes of crosslinks and microchains of PVCL) and the dynamics (rate of relaxation of polymer chains, hydrodynamic polymer-polymer correlation length). The presence of nanoscale titania does not change the molecular structure and nanostructure due to its aggregation into meso-domains, but does affect the microstructure, changing the response rate to a temperature jump from 20 to 50 °C. Titania nanoparticles do not change the equilibrium swelling degree of hydrogels.
Introduction
Hydrogels are water-based polymeric networks physically (molecular weaves, hydrophobic interactions, ionic or hydrogen bonds) or chemically (covalent bonds) crosslinked. Smart hydrogels, that respond to stimuli such as pH, temperature, electric field, etc. are the most interesting. Poly(N-vinyl caprolactam) (PVCL) is a temperature sensitive water-soluble polymer with a lower critical solution temperature (32–34 °C) near that of the human body,1 which has better biocompatibility compared to the well-studied thermo-sensitive poly(N-isopropyl acrylamide) (pNIPAM) polymer, as it does not decompose into a large number of low molecular weight amines during hydrolysis.2The design of stimuli-responsive hydrogels with specific properties can be achieved chemically, via the synthesis of new polymers, or much simpler by forming hybrid composites, enhancing existing hydrogels via additives. Composite PVCL-based hydrogels with different functional groups are used for medical purposes:3,4 antibacterial microgels (PVCL/Ag),5 antitumor drug delivery by (PVCL/N-(2-hydroxypropyl)methacrylamide nanogels loaded with doxorubicin),6 cartilage tissue engineering (PVCL hydrogel loaded with stem cells),7 immobilization of enzymes and cells (PVCL/calcium alginate hydrogels).8 Solid inorganic nanoparticles are a typical example of such additive, and in particular titania nanoparticles (TiO2, named NT in the following) have been often studied for their photocatalytic9,10 and antimicrobial activities.11 Thus, we are interested in studying how the temperature-sensitive PVCL will be affected by the presence of titania.
Such properties of hydrogels as elasticity, transparency, and response to external influences are determined by their composition, morphology and dynamics. But there are only few works on the study of the elements of the static structure of PVCL-based hydrogels by microscopy, differential scanning calorimetry, small-angle X-ray and neutron scattering, IR spectroscopy, two-dimensional correlation spectroscopy, dynamic light scattering.12–18 In addition, among the literature sources, there is no information about the dynamics of PVCL hydrogels and their response to temperature effects, which is the subject of this work. There are some works on other thermosensitive polymer pNIPAM based hydrogels with titania nanoparticles.19,20 But, dynamics of polymer matrix was not studied. The aim is to prepare physical hydrogels by mixing titania nanoparticles to poly(N-vinyl caprolactam) and tetraethoxysilane as nominally pure and identify their structure and dynamics. The prepared pure gels and their titania nanoparticles containing derivates (NT/PVCL) are investigated by X-ray diffraction, differential scanning calorimetry, scanning electron microscopy, small-angle neutron scattering, and neutron spin-echo spectroscopy.
Materials and methods
Hydrogel synthesis
PVCL-based hydrogels were synthesized by sol–gel technology using 10 wt% PVCL ((C8H13NO)n with molecular weight Mw = 1 × 106 Da,21 overlap concentration – where η is the intrinsic viscosity22 of 10 wt% PVCL aqueous solution at 25 °C) tetraethoxysilane (TEOS, SiC8H20O4, reagent grade, Sigma Aldrich, USA), dimethylaminoethanol catalyst (DMAE, C4H11NO, ≥99.5%, Sigma Aldrich, USA) and macadamia oil Glycereth-8 Esters (Glycereth-8, ResPharma, Italy) with the weight ration of TEOS
– where η is the intrinsic viscosity22 of 10 wt% PVCL aqueous solution at 25 °C) tetraethoxysilane (TEOS, SiC8H20O4, reagent grade, Sigma Aldrich, USA), dimethylaminoethanol catalyst (DMAE, C4H11NO, ≥99.5%, Sigma Aldrich, USA) and macadamia oil Glycereth-8 Esters (Glycereth-8, ResPharma, Italy) with the weight ration of TEOS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Glycereth-8
Glycereth-8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMAE = 140
DMAE = 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The mixture was stirred at room temperature (22 ± 1 °C) for 30 minutes and poured into a mold. For the preparation of composite hydrogels TiO2 (commercial sample Hombifine N, Sachtleben Chemie GmbH, in anatase form) was added in amounts of 0.25, 0.50 and 1.00 wt% before the introduction of TEOS (Table 1). These hybrid samples are respectively referred to as 0.25, 0.50 or 1.0NT/PVCL. The TiO2 nanoparticles have been previously characterized by scanning electron microscopy, which revealed that the primary particle size is about 100–150 Å (86%), while approximately 14% of the particles are aggregated in larger structure with ∼200–800 Å or larger diameter.22
1. The mixture was stirred at room temperature (22 ± 1 °C) for 30 minutes and poured into a mold. For the preparation of composite hydrogels TiO2 (commercial sample Hombifine N, Sachtleben Chemie GmbH, in anatase form) was added in amounts of 0.25, 0.50 and 1.00 wt% before the introduction of TEOS (Table 1). These hybrid samples are respectively referred to as 0.25, 0.50 or 1.0NT/PVCL. The TiO2 nanoparticles have been previously characterized by scanning electron microscopy, which revealed that the primary particle size is about 100–150 Å (86%), while approximately 14% of the particles are aggregated in larger structure with ∼200–800 Å or larger diameter.22
| Name | NT content (wt%) | PVCL content (wt%) | TEOS (wt%) | DMAE (wt%) | Macadamia oil Glycereth-8 esters (wt%) |
|---|---|---|---|---|---|
| PVCL | — | 92.85 | 7.00 | 0.05 | 0.1 |
| 0.25NT/PVCL | 0.25 | 92.60 | |||
| 0.50NT/PVCL | 0.50 | 92.35 | |||
| 1.0NT/PVCL | 1.00 | 91.85 |
The synthesis conditions of hydrogels PVCL and NT/PVCL are the same (there is a slight change in TEOS/PVCL ration (<1%), see Table 1 and Fig. S1, ESI†). Pure PVCL hydrogel is transparent, in contrast to the composite hydrogels NT/PVCL, which have a white opaque appearance due to multiple light scattering by titania nanoparticles.
There are several studies on the synthesis of PVCL-based hydrogels using the sol–gel method,16,18 where tetramethoxysilane (TMOS, Si(CH3OH)4) is used as a crosslinking agent. Hydrolysis of TMOS followed by condensation of hydrolysis products occurs under mild conditions in the absence of a catalyst. As a result of such reactions, methanol is formed as a byproduct, which is unacceptable for the use of such hydrogels in medicine and cosmetology. In this regard, the synthesis of organo-inorganic hydrogels using tetraethoxysilane (TEOS, Si(C2H5OH)4) is preferable, because the byproduct is ethanol, which gives the hydrogel antiseptic and protective properties.
Acid hydrolysis of TEOS is used to obtain stable sols, and inorganic acids (HCl, HNO3, etc.) are used as acid catalysts. There are two different ways to perform sol–gel synthesis: one-stage (acid) or two-stage (acid/acid) hydrolysis of TEOS.23 In both cases, the first stage is often carried out with a lack of water. TEOS is a crosslinking agent for the formation of hydrogels, hydrolyzed in the presence of an acid catalyst. Silanol reactive groups (Si–OH) of hydrolyzed alkoxide silicon are subjected to reactions of condensation, which depend on the pH and temperature of the solution, with the formation of siloxane (Si–O–Si) linkages, forming a 3D porous structure of the gel.
Wide angle X-ray scattering
X-ray measurements were carried out on PVCL and NT/PVCL air-dried gel disks of 1 mm thickness and taken in a rotation mode on an HZG-4 diffractometer (graphite monochromator) using CuKα radiation in 0.02 Å steps with counting times of 10 s per step over the angle range 2θ = 2–50°. We used the “Program for processing diffractograms with the possibility of adjusting the original data”.24 The average crystallite sizes of NT were calculated by the formulaD = Kλ/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, θ, | (1) |
Differential scanning calorimetry
Differential scanning calorimetry (DSC) of native (as-prepared) PVCL and 0.50NT/PVCL hydrogels was performed on Netzsch DSC 204 (Phoenix, Germany). A sample with a weight of 22.5 mg for PVCL or 13 mg for 0.50NT/PVCL was placed in a standard aluminum sample pan with a vented cover. The scanning was performed at a rate of 10° min−1 under an argon atmosphere (99.99%) at a flow rate of 100 mL min−1 in the temperature range from −80 to 600 °C. The results (peak area, extreme temperatures) were processed with the Netzsch Proteus software. The temperature was determined with an accuracy of 0.1 °C.Small angle neutron scattering (SANS)
SANS was applied to investigate structure of the gels on the nanometric lengthscale. SANS data25 were acquired on the small angle diffractometer D11 at the Institut Laue-Langevin, Grenoble, France (DOI: http://10.5291/ILL-DATA.9-12-510). For these experiments, air-dried gel disks were swollen in D2O in order to enhance the scattering contrast between the polymer and the matrix. The scattering length densities (SLD) of the main components of the systems are listed in Table 2.| Component | SLD, Å2 |
|---|---|
| PVCL (C8H13NO)n | 0.939 × 10−6 |
| SiO2 | 4.18 × 10−6 |
| SiOOH | 3.14 × 10−6 |
| NT (TiO2) | 2.628 × 10−6 |
| D2O | 6.335 × 10−6 |
Samples of ∼1.5 mm nominal thickness and 10 mm diameters were placed in sandwich cells of 1.5 mm pathway. Three configurations were used with sample-to-detector distances of 1.4, 8 and 39 m, with collimations at 5.5, 8 and 40.5 m respectively, at a constant wavelength λ = 5.0 Å (fwhm 9%) leading to a q-range of 0.0016–0.53 Å−1, where q is the magnitude of the wavevector
 | (2) |
Neutron spin-echo (NSE) measurements
The microscopic dynamics of the PVCL matrix in the pure PVCL and NT/PVCL composite hydrogels were explored by NSE spectroscopy. NSE measurements were done on the IN11 spectrometer at the Institut Laue-Langevin (Grenoble, France) in the IN11A high-resolution set-up. For these experiments, gel films of 4 mm nominal thickness and 3 × 4 cm cross-section were used. Prior to the measurements, the gel samples were air-dried and then reswollen in excess D2O for at least 3 days at 22.0 ± 0.1 °C. The swollen samples were placed in 4 mm thick sandwich-type cells with quartz windows. The remaining space in the sample holder was filled with D2O to exclude air and avoid deswelling. Measurements were performed at 22.0 ± 0.1 °C, in the transfer vector q-range 0.042 Å−1 ≤ q ≤ 0.219 Å−1. The incident neutron wavelength was 8 Å. The resolution functions of the instrument were determined for the different experimental conditions using the elastic scattering of graphite. The NSE method measures directly the intermediate scattering function I(q,τ) as a function of q and the Fourier time τ, i.e., it yields directly the time dependence of the density–density autocorrelation function.28 The resulting intermediate scattering functions were corrected for the D2O background dynamics.Equilibrium swelling degree
Equilibrium swelling degree (ESD) of the samples was measured on air-dried gel disks with a diameter of 9 mm and thicknesses of 1 and 2 mm. A known weight of the hydrogels was taken and immersed in an excess of water for fixed time intervals at 25.0 ± 0.2 °C and then the polymers were removed after a certain point in time, wiped with tissue paper to remove excess water, and weighed immediately during ∼11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 min for 2 mm thickness and ∼6500 min for 1 mm thickness hydrogels. After reaching swelling equilibrium in distilled water at 25.0 ± 0.2 °C, the ESD was determined as
000 min for 2 mm thickness and ∼6500 min for 1 mm thickness hydrogels. After reaching swelling equilibrium in distilled water at 25.0 ± 0.2 °C, the ESD was determined as  , where m and m0 are the mass of the swollen and dry samples, respectively. The measurements were performed three times leading to a typical standard-deviation of ca. 5%.
, where m and m0 are the mass of the swollen and dry samples, respectively. The measurements were performed three times leading to a typical standard-deviation of ca. 5%.
The kinetics of the temperature shrinkage 25 → 50 °C
To examine the response of hydrogels to temperature influence hydrogel disks in an equilibrium swelling state (after the ESD experiment) were plunged into a water bath at 50.0 ± 0.1 °C. The thermally induced shrinkage was tracked by regularly measuring the mass of the disks until they reached equilibrium. Three parallel samples were measured in each case. The measured data were fitted to a bi-exponential function: | (3) |
Fig. 1 shows the sample preparation scheme of PVCL and NT/PVCL samples for the research methods used in this work.
Results and discussions
Swelling degree
The swelling process of air-dried PVCL and NT/PVCL hydrogels in H2O obeys the second-order kinetics: | (4) |
 | (5) |
| Sample | 2 mm thickness | 1 mm thickness | ||||
|---|---|---|---|---|---|---|
| K, min−1 | ESD, % | K, min−1 | ESD, % | Syneresis ratio, % | The duration of syneresis, h | |
| a Syneresis was not established. b The sample has not been studied. | ||||||
| PVCL | 2.1 × 10−7 | 1135 | 1.98 × 10−5 | 1144 | —a | |
| 0.25NT/PVCL | 2.3 × 10−7 | 1160 | 3.09 × 10−5 | 1052 | 135 | 6 |
| 0.50NT/PVCL | 3.7 × 10−7 | 1074 | 7.52 × 10−5 | 1088 | 120 | 6 |
| 1.0NT/PVCL | 2.2 × 10−7 | 1094 | —b | |||
All studied hydrogels are characterized by a high swelling degree (Fig. 2). The presence of NT in NT/PVCL composite hydrogels slightly changes their swelling degree compared to pure PVCL hydrogel. Titania nanoparticles was not released from NT/PVCL composite hydrogel during the swelling process (as controlled spectrophotometrically (Akvilon SF 103, Russia) and visually (absence of NT sediment)). The analysis of water content after hydrogel swelling showed that less than 1 wt% of PVCL is washed out from the hydrogels (probably fractions of polymer with the lowest molecular weights). It indicates that almost all TEOS and PVCL are incorporated into the hydrogel structure.
 | ||
| Fig. 2 Swelling curves for air-dried pure PVCL and NT/PVCL composite gels with (a) 2 mm and (b) 1 mm thicknesses. The inset shows an enlarged view of the time range of 10–40 hours. | ||
The thickness of the initial air-dried hydrogels influences their swelling rate, but not the swelling degree. For hydrogels with a thickness of 1 mm, the rate of swelling is larger than for ones with a thickness of 2 mm (Table 3). For the achievement of a full equilibrium state, hydrogels with a thickness of 2 mm need 6000 min, while hydrogels with a smaller thickness of 1 mm only needs 600 min (Fig. 2).
For composite hydrogel samples with a thickness of 1 mm, syneresis is characteristic during the swelling process (Fig. 2(b), inset). Syneresis is an instability phenomenon described as a “spontaneous contraction of a gel accompanied by the expulsion of liquid from the pores”.29 The syneresis ratio was calculated using the following equation:
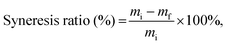 | (6) |
In composite hydrogels of 1 mm thickness, while the initial equilibrium swelling in water took place in about 10 h, a fluctuation in mass was observed 10 h later, lasting for 3 h (Table 1). We hypothesize that an increase in NT content in PVCL hydrogels reduces the syneresis ratio during swelling. The syneresis may depend on a form and thickness of samples. It should be noted that in the work30 syneresis was not observed.
As SANS and NSE experiments were performed in D2O, the kinetics of swelling process in D2O of air-dried PVCL and NT/PVCL hydrogels with a thickness of 1 mm was checked (Fig. S2, ESI†). The equilibrium swelling degree of PVCL and NT/PVCL hydrogels in D2O was found to be marginally higher than in H2O.
The synthesized hydrogels have a higher swelling degree in water compared to samples in the literature: 750% (PVCL hydrogel synthesized by free radical cross-linking polymerization),31 550% (chitosan-graft-poly(N-vinylcaprolactam) hydrogel, 25 °C, pH = 7.4).32 Makhaeva et al. Synthesized the PVCL-based hydrogels, for which swelling in water is accompanied by a 2500% increase in the initial mass.33
The kinetics of the temperature shrinkage 25 → 50 °C
After placing the pure PVCL hydrogel in a water bath at 50 °C, it changed its color from transparent to white. It indicates the phase separation of the hydrogel. Observation of such a phenomenon for composite hydrogels was not possible as all hydrogels with NT initially have a white color; the photographs of dried/swollen samples are shown in Fig. S3 (ESI†). Phase separation happens at first at the local level, and two phases exist at the same time: polymer-rich and solvent-rich.34 When observed with pNIPAM hydrogels, it was suggested that the rapid shrinking may accompany a characteristic change in morphology, such as bubble formation.35 The bubble formation is evidence of inhomogeneous network structure characterized by a large population of loops and dangling chains. It allows the solvent to find many paths outgoing from the gel. Some of the fluxes may be captured by the outmost layer of the network, resulting in bubble formation.The deswelling kinetics of polymer hydrogels depends sensitively on the number of structural inhomogeneities present in the network. The inhomogeneities can also be generated by drying these gels and allowing them to reswell.36
All PVCL and NT/PVCL hydrogels have a multi-exponential dependence of loss of weight on time at temperature jump of 25 → 50 °C and reach the final state  at 2000 min (Fig. 3). It should be noted that in the work37 PVCL-based hydrogels with clay nanosheets as a crosslinker reach their deswelling equilibrium state after ∼12 min of rapidly increasing temperature (25 → 45 °C). The difference in data can be due to the different methods for producing hydrogels.
at 2000 min (Fig. 3). It should be noted that in the work37 PVCL-based hydrogels with clay nanosheets as a crosslinker reach their deswelling equilibrium state after ∼12 min of rapidly increasing temperature (25 → 45 °C). The difference in data can be due to the different methods for producing hydrogels.
 | ||
| Fig. 3 Plot of the temperature jump 20 → 50 °C of PVCL, 0.25NT/PVCL, 0.50NT/PVCL and 1.0NTPVCL hydrogels. Lines are fits to eqn (3). | ||
The obtained data in this work were described by eqn (3). A bi-exponential function approximate the experimental data and reveals uneven release of solvent from hydrogels.
The kinetic curve for 1.0NT/PVCL hydrogel has a more complex shape in comparison with other samples (Fig. 3 and Table 4). Table 4 also lists the goodness-of-fit χ2 and R2 ( where dof – degrees of freedom, Oi – data value, Ci – function value;
where dof – degrees of freedom, Oi – data value, Ci – function value;  where R – the coefficient of determination, n – the number of points in the data sample, k – is the number of independent regressors). For 1.0NT/PVCL hydrogel χ2 = 8.04, which shows the limit of a 2-rate process for this particular sample.
where R – the coefficient of determination, n – the number of points in the data sample, k – is the number of independent regressors). For 1.0NT/PVCL hydrogel χ2 = 8.04, which shows the limit of a 2-rate process for this particular sample.
All these findings show that adding titania nanoparticles in PVCL hydrogels leads to a significant change in the relaxation of the system, composite hydrogels exhibiting a much faster response to the temperature.
Wide angle X-ray scattering
In swollen state, the diffraction pattern of NT/PVCL, similarly to other hydrogels (PVP,38 pNIPAM39) corresponds essentially to the signal from water, presenting two shallow peaks. The diffraction pattern of the fully swollen (ESD = 1160%) 0.25NT/PVCL hydrogel is shown on Fig. 4(a) (the sample underwent the following preparation: native → air-drying → swelling in water).Based on the literature,38–40 water in PVCL hydrogels can be classified in 4 categories: free water (fills the pores of all sizes and the space between the polymer chains and can be easily removed from the hydrogels under mild conditions) (I), bound water (water attached by hydrogen bonds –N–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–O–H with hydrophilic functional group –N–C
O⋯H–O–H with hydrophilic functional group –N–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O of the PVCL side chain is an integral part of the hydrogel structure and can be removed at elevated temperatures) (II), intermediate water (water not connected to the hydrogel network, but physically trapped between polymer chains: cluster water) (III), semi-bound water (a type of water with intermediate bound and free water properties) (IV).
O of the PVCL side chain is an integral part of the hydrogel structure and can be removed at elevated temperatures) (II), intermediate water (water not connected to the hydrogel network, but physically trapped between polymer chains: cluster water) (III), semi-bound water (a type of water with intermediate bound and free water properties) (IV).
The 2nd diffraction peak of PVCL comes from correlations between side chains, similar to PVP41 For the swollen hydrogel 0.25NT/PVCL, it is strongly shifted towards large angles (Fig. 4(a); 2θ = 27.32° with d2 = 3.153 Å) compared to air-dried samples (Fig. 4(b); 2θ ∼ 20° with d2 ∼ 4.5 Å), which indicates the presence of water I and water II.
The high content of water I in the swollen 0.25NT/PVCL leads to a strong increase in the average distance between the backbone C–C chains (Fig. 5),38,42i.e., significantly increases the interplanar distance d1 beyond the diffractogram (Fig. 4(a) and 6(a)). In the hydrogels, crosslinking points are clusters of variable composition [SixOy(OH)z(H2O)vRw] (R – C2H5) (Fig. 6(b)), formed by the products of hydrolytic polycondensation of TEOS (Fig. S1, ESI†). The diffuse peak at 2θ = 40.39° (d = 2.231 Å) for 0.25NT/PVCL (Fig. 4(a)), absent on the diffractograms of the dried samples (Fig. 4(b)), is responsible for water clusters (water III) in the PVCL – water system, which are trapped between polymer chains, similar to PVP41 (Fig. 5).
It should be noted that no other diffraction peaks were recorded either due to the small number of phases outside the sensitivity of the WAXS technique or because of their X-ray amorphous state.
The 1st diffraction peak of PVCL is split for PVCL hydrogel (solid red line in Fig. 4(b) and Table 5) and asymmetric for 0.50NT/PVCL (dashed red line in Fig. 4(b) and Table 5), which can also be associated with the action of water. This type of water can be interpreted based on the cluster model of polymers.43 The chain entanglement (physical crosslink) of the polymer network44 are clusters with different content of bound water molecules (Fig. 5), and therefore different interplanar distances lead to the splitting of the 1st peak of PVCL and asymmetry for 0.50NT/PVCL (Fig. 4(b)). Since this bound water is structurally not the same as water II (Fig. 5), and the structural meaning of water IV is not clear, bound water in ordered regions is caused by water IV, otherwise, a new type of water should be introduced.
| PVCL | 0.25NT/PVCL | 0.50NT/PVCL | Assignment of peaks in Fig. 4 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 2θ, ° | d,a Å | I, % | 2θ, ° | d,a Å | I, % | 2θ, ° | d,a Å | I, % | |
a
d, Å = λ/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ – interplanar distance.
b The peak is asymmetric, the angle shown corresponds to Imax. θ – interplanar distance.
b The peak is asymmetric, the angle shown corresponds to Imax.
|
|||||||||
| 9.9 | 8.9 | 70 | 11.68 | 7.8 | 55 | 8.6 | 10.3 | 50 | 1 (splitting) |
| 11.32 | 7.8 | 65 | 12.00 | 7.3 | 70 | ||||
| 19.88b | 4.46 | 100 | 20.94 | 4.24 | 100 | 21.14 | 4.20 | 90 | 2 |
| 25.04 | 3.55 | 90 | 25.08 | 3.55 | 100 | ||||
| 37.52 | 2.395 | 5 | 37.48 | 2.398 | 5 | ||||
| 48.44 | 1.878 | 2 | 47.72 | 1.904 | 3 | ||||
The PVCL and NT bind to each other via hydrogen bonds between amide –N–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group, which can bind no more than two water molecules1 (bound water) and water molecules and OH-groups on the NT surface.
O group, which can bind no more than two water molecules1 (bound water) and water molecules and OH-groups on the NT surface.
The introduction of NT has a different effect on the diffraction behavior of the 2nd peak of PVCL depending on the concentration (dashed black line in Fig. 4(b)): the peak is shifted towards large angles for air-dried 0.25NT/PVCL (green line in Fig. 4(b)), indicating a higher content of water II in this sample compared to 0.50NT/PVCL (solid black line in Fig. 4(b)).
The average crystallite size of nanosized anatase in the composite hydrogel is substantially smaller (D = 42 ± 2 Å for 0.25NT/PVCL and D = 54 ± 3 Å for 0.50NT/PVCL) than for the original Hombifine N (D = 82 ± 4 Å) (Table 5), indicating an amorphization of the nanoparticles (greater for 0.25NT/PVCL) caused by hydration of their shell.
Differential scanning calorimetry (DSC)
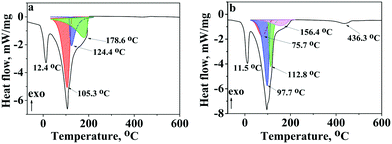
Fig. 7 shows thermograms of native PVCL and 0.50NT/PVCL hydrogels.To describe the effects on thermograms (Fig. 7), it is necessary to refer to the properties of structural water:45water I – free water (does not form hydrogen bonds with the polymer, NT and TEOS derivatives and behaves similarly to pure water with respect to freezing and melting), water II – non-freezing water (strongly associated with polymer chains hydrogen bonds; will not freeze but will evaporate at the highest temperature), water III – freezing water (weakly interacts with polymer chains; the reduced hydrogen bonding with the solvent implies a higher freezing temperature and a lower boiling temperature than pure water). We expect water IV,46 as intermediate between I and III, to be indistinguishable from water I and/or III.
Based on this systematization and the data of X-ray diffraction and DSC, Table 6 presents the endothermic peaks assigned with possible water types in PVCL and 0.50NT/PVCL hydrogels.
| PVCL | 0.50NT/PVCL | Assignment of peaks | ||
|---|---|---|---|---|
| T, °C | ΔH, J g−1 | T, °C | ΔH, J g−1 | |
| 12.4 | 242.0 | 11.5 | 270.5 | Water III (freezing) |
| 75.7 | 386.7 | The removal of physically adsorbed water from the surface of titania nanoparticles | ||
| 105.3 | 1088.9 | 97.7 | 977.4 | Water I |
| 124.4 | 397.9 | 112.8 | 421.0 | Water III (evaporation) |
| 178.6 | 765.4 | 156.4 | 251.4 | Water II |
| 434.9 | 436.3 | Decomposition of PVCL | ||
It is possible that the endothermic peak at 75.7 °C is caused by the removal of water due to the presence of NT in the system. We do not consider water related to Si–O formations due to their small amounts.
Small angle neutron scattering
Small angle neutron scattering reveals that the structure of the hydrogels is practically not modified by the presence of the TiO2 nanoparticles (Fig. 8). The intensity upturn at low q-values in the cases of NT/PVCL samples follows a q−3 trend and indicates the presence of large fractal aggregates, most probably of poorly dispersed TiO2, larger than the window of observation (2π/qmin = 3700 Å). The region 0.015 Å−1 ≤ q ≤ 0.4 Å−1 has been fitted to the 1-level Beaucage model47–49 (eqn (7)) which models the Guinier and Porod regions with a smooth transition between them and yields a radius of gyration and a Porod exponent (Table 7): | (7) |
 | ||
| Fig. 8 SANS response curves of PVCL (red), 0.25NT/PVCL (blue) and 0.50NT/PVCL (green) hydrogels. Broken lines are fits to Beaucage unified model (eqn (7)). Inset shows the Kratky plots. Data with NT were shifted in intensity to match those of pure PVCL where the polymer scatters, i.e., at mid and high q (factors 1.12 and 0.79 for 0.25NT/PVCL and 0.50NT/PVCL respectively). | ||
| R g, Å | P | B, cm−1 | G, cm−1 | G/B | |
|---|---|---|---|---|---|
| PVCL | 70 | 2.20 | 2.3 × 10−3 | 34.0 | 15 × 104 |
| 0.25NT/PVCL | 70 | 2.20 | 2.0 × 10−3 | 30.4 | 15 × 104 |
| 0.50NT/PVCL | 74 | 2.23 | 2.7 × 10−3 | 46.6 | 17 × 104 |
The fitting results confirm that the presence of TiO2 hardly affects the structure of the gels (Fig. 6(c)): the value of Rg is unchanged at low NT concentration, and increases only marginally at higher NT content. The Porod exponents (P) do not differ significantly. This non-effect of the NT is likely due to the fact that NT is present in the form of very large aggregates. The position of the maxima at q ∼0.023 Å−1 visible on the Kratky plots (Fig. 8 inset) is unaffected by the NT as well. The differences in G and B values are caused by small differences in swelling degree (variation of the concentration of PVCL), as shown by the rather constant ratio G/B.
Neutron spin echo measurements (NSE)
The NSE method measures the energy transfer of neutrons at an extremely high-energy resolution as a phase shift in the Larmor precession of the neutron spins in a magnetic field.28 The I(q,t) curves obtained for the pure PVCL and NT/PVCL composite hydrogels normalized by the signal I(q,0) of a fully elastic scatterer (graphite), are shown in Fig. 9 at q = 0.042, 0.110, 0.137 and 0.192 Å−1. | ||
| Fig. 9 Experimental intermediate scattering functions from NSE with the corresponding single exponential fits for (a) the pure PVCL hydrogel and (b) 0.50NT/PVCL composite hydrogel, measured at 22 °C. | ||
The curves I(q,τ)/I(q,0) can be fitted by an exponential function
 | (8) |
It is obvious that at low q-values (q = 0.042–0.137 Å−1) the measurable Fourier time is too small to obtain the complete decay of I(q,τ)/I(q,0). But at q-value 0.192 Å−1, the scattering functions decay to zero (Fig. 9). For the investigated gels, pure PVCL and composite 0.50NT/PVCL, the intermediate scattering functions appear to decay to zero at infinite time, indicative of practically or pseudo-ergodic behavior, i.e., there is no frozen-in component.50,51
The measured relaxation rates (Γ = 1/τ) are proportional to q2 (Fig. 10), characteristic of the diffusive motion of polymer chains. The diffusion coefficient (Ddiff) is obtained directly from the linear fit.
| Γ = Ddiffq2 | (9) |
 | ||
| Fig. 10 Relaxation rates (Γ) vs. q2 for the PVCL and 0.50NT/PVCL hydrogels. Solid lines are linear fits. | ||
The hydrodynamic correlation length (ξH) is determined from the Stokes–Einstein relation
 | (10) |
According to SEM data for the 0.25NT/PVCL hydrogel,37 NT nanoparticles are covered and settled in pores of the PVCL hydrogel and form aggregates of 200–600 Å sizes, reducing the PVCL pore sizes from ∼14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Å for PVCL to ∼3000 Å for 0.25NT/PVCL (Fig. 6(d) and Fig. S5, ESI†).
000 Å for PVCL to ∼3000 Å for 0.25NT/PVCL (Fig. 6(d) and Fig. S5, ESI†).
Thus, titania nanoparticles does not affect the atomic structure (Fig. 6(a)) and nanostructure (Fig. 6(b) and (c)) of hydrogels.
Conclusions
Poly(N-vinyl caprolactam) (PVCL) based hydrogels with titania nanoparticles were synthesized by admixing TiO2 nanoparticles with PVCL and tetraethoxysilane (TEOS), then characterized by wide angle X-ray scattering, differential scanning calorimetry, small angle neutron scattering, and neutron spin echo spectroscopy. The hydrogels structure consists of hydrophobic PVCL backbone chains with side chains with hydrophilic groups –N–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O binding no more than two water molecules.1 Titania nanoparticles and PVCL are bonded via hydrogen bonding between –N–C
O binding no more than two water molecules.1 Titania nanoparticles and PVCL are bonded via hydrogen bonding between –N–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group and water molecules and OH-groups on the surface of NT.
O group and water molecules and OH-groups on the surface of NT.
The primary nanostructure is a spatial molecular PVCL network of PVCL crosslinking points consisting of clusters of variable composition [SixOy(OH)z(H2O)vRw] (R – C2H5), formed by the products of hydrolytic polycondensation of TEOS. Free and semi-bound types of water are located in a hydrogel 3D-network. The presence of cluster (freezing) water is likely due to hydrophobic interactions.
However, neutron scattering measurements revealed that the structure of the PVCL hydrogels is not affected by the presence of NTs in the investigated lengthscale, possibly due to the fact that NTs form very large aggregates. The microscopic dynamics of the gel is marginally affected, as revealed by neutron spin-echo spectroscopy.
Titania nanoparticles do not change the equilibrium swelling degree of PVCL-based hydrogels but affect their response rate to the temperature jump 20 → 50 °C. Moreover, the NT concentration changes the form of the response curve.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was financially supported by the Russian Foundation for Basic Research (Project No. 18-03-00330). We also acknowledge ILL for the beamtime allocation and the staff of IN11 and D11 for the support on data analysis. This work benefited from the use of the SasView application, originally developed under NSF award DMR-0520547. SasView contains code developed with funding from the European Union's Horizon 2020 Research and Innovation Programme under the SINE2020 project, grant agreement no. 654000.References
- Yu. E. Kirsh, Water soluble poly-N-vinylamides. Synthesis and physicochemical properties, John Wiley and Sons, Chichester, 1998 Search PubMed.
- L. K. Kostanski, R. Huang, R. Ghosh and C. D. M. Filipe, J. Biomater. Sci., Polym. Ed., 2008, 19, 275 CrossRef CAS.
- A. Imaz and J. Forcada, J. Polym. Sci., Part A: Polym. Chem., 2010, 48, 1173 CrossRef CAS.
- A. K. Gaharwar, N. A. Peppas and A. Khademhosseini, Biotechnol. Bioeng., 2014, 111, 441 CrossRef CAS.
- N. Hantzschel, R. D. Hund, H. Hund, M. Schrinner, C. Luck and A. Pich, Macromol. Biosci., 2009, 9, 444 CrossRef.
- Y. Tian, Y. Wang, S. Shen, X. Jiang, Y. Wang and W. Yang, Part. Part. Syst. Charact., 2015, 32, 1092 CrossRef CAS.
- R. L. Sala, M. Y. Kwon, M. Kim, S. E. Gullbrand, E. A. Henning, R. L. Mauk, E. R. Camargo and J. A. Burdick, Tissue Eng., 2017, 23, 935 CrossRef CAS.
- S. V. Kuptsova, T. Y. Mareeva, A. A. Vikhrov, T. N. Dugina, S. M. Strukova, Y. N. Belokon, K. A. Kochetkov, E. N. Baranova, V. P. Zubov, D. Poncelet, V. S. Parmar, R. Kumar and L. D. Rumsh, Appl. Biochem. Biotechnol., 2000, 88, 145 CrossRef.
- Sh. M. Gupta and M. Tripathi, Chin. Sci. Bull., 2011, 56, 1639 CrossRef CAS.
- A. Mills and S. L. Hunte, J. Photochem. Photobiol., A, 1997, 108, 1 CrossRef CAS.
- H. Mahipati, Ya. Jung-Sik Kim and Sh. H. Pawar, Korean J. Chem. Eng., 2016, 33, 1989 CrossRef.
- G. J. Schneider, A. Pich, F. Schneider, Y. B. Melnichenko, A. Balaceanu, J. Allgaier, D. Richter and Z. Di, Soft Matter, 2017, 13, 2738 RSC.
- G. Su, T. Zhou, X. Liu and Y. Zhang, Phys. Chem. Chem. Phys., 2017, 19, 27221 RSC.
- B. Xue, V. Kozlovskaya and E. Kharlampieva, J. Mater. Chem. B, 2017, 5, 9 RSC.
- E. Gau, F. Flecken, A. N. Ksiazkiewicz and A. Pich, Green Chem., 2018, 20, 43 RSC.
- I. V. Bakeeva, L. A. Ozerina, A. N. Ozerin and V. P. Zubov, Polym. Sci., Ser. A, 2010, 52, 496 CrossRef.
- K. M. Rao, K. S. V. K. Rao and C. Ha, Gels, 2016, 2, 19 CrossRef.
- W. Loos, S. Verbrugghe, E. J. Goethals, F. E. D. Prez, I. V. Bakeeva and V. P. Zubov, Macromol. Chem. Phys., 2003, 204, 98 CrossRef CAS.
- G. Huerta-Angeles, K. Hishchak, A. Strachota, B. Strachota, M. Slouf and L. Matejka, Eur. Polym. J., 2014, 59, 341 CrossRef CAS.
- L. Zhang, S. Zhang, B. He, Zh. Wu and Zh. Zhang, Z. Naturforsch., B: J. Chem. Sci., 2008, 63, 973 CAS.
- Yu. E. Kirsh, T. M. Karaputadze and V. I. Shumskii, USSR Inventor's Certificate no. 1613446 A1, Byull. Izobret., 1990, no. 46.
- O. Timaeva, I. Chihacheva, G. Kuzmicheva, N. Ivanovskaya and A. Dorohov, J. Mater. Res., 2018, 33, 1475 CrossRef CAS.
- P. Kakkar and B. Madhan, Mater. Sci. Eng., 2016, 66, 178 CrossRef CAS.
- Russia ‘Program for processing of diffraction patterns of nanosized and amorphous substances and calculation of the substructure’, 2017610699, 2017.
- https://dx.doi.org/10.5291/ILL-DATA.9-12-510 .
- D. Richard, M. Ferrand and G. J. Kearley, J. Neutron Res., 1996, 4, 33 CrossRef.
- I. Brebler, J. Kohlbrecher and A. F. Thunemann, J. Appl. Crystallogr., 2015, 48, 1587 CrossRef.
- Neutron Spin Echo Spectroscopy – Basics, Trends and Applications, ed. F. Mezei, C. Pappas and T. Gutberlet, Springer, Heidelberg, 2003 Search PubMed.
- G. W. Scherer, J. Non-Cryst. Solids, 1989, 108, 18 CrossRef CAS.
- O. I. Timaeva, I. I. Pashkin, G. M. Kuz’micheva and N. V. Sadovskaya, Mendeleev Commun., 2019, 29, 647 CrossRef.
- S. Cavus, E. Cakal and L. M. Sevgili, Chem. Pap., 2015, 69, 1367 CAS.
- M. Prabaharan, J. J. Grailer, D. A. Steeber and S. Gong, Macromol. Biosci., 2008, 8, 843 CrossRef CAS.
- E. M. Makhaeva, L. T. M. Thanh, S. G. Starodoubtsev and A. R. Khokhlov, Macromol. Chem. Phys., 1996, 197, 1973 CrossRef CAS.
- T. Takigawa, T. Yamawaki, K. Takahashi and T. Masuda, Polym. J., 1999, 31, 595 CrossRef CAS.
- M. Shibayama and K. Nagai, Macromolecules, 1999, 32, 7461 CrossRef CAS.
- K. Laszlo, A. Fluerasu, A. Moussaid and E. Geissler, Soft Mater., 2010, 6, 4335 RSC.
- K. Shi, Z. Liu, C. Yang, X. Y. Li, Y. M. Sun, Y. Deng, W. Wang, X. J. Ju, R. Xie and L. Y. Chu, ACS Appl. Mater. Interfaces, 2017, 9, 21979 CrossRef CAS.
- J. Teng, S. Bates, D. Engers, K. Leach, P. Schields and Y. Jang, J. Pharm. Sci., 2010, 99, 3815 CrossRef CAS.
- R. Naohara, K. Narita and T. Ikeda-Fukazawa, Chem. Phys. Lett., 2017, 670, 84 CrossRef CAS.
- Introduction to Hydrogels. In Biomedical Applications of Hydrogels Handbook, ed. R. M. Ottenbrite, Springer, London, 2010 Search PubMed.
- T. Matsunaga, T. Sakai, Y. Akagi, U. Chung and M. Shibayama, Macromolecules, 2014, 47, 763 CrossRef.
- R. Busselez, A. Arbe, S. Cerveny, S. Capponi, J. Colmenero and B. Frick, J. Chem. Phys., 2012, 137, 084902 CrossRef.
- M. Arzhakov, Relaxation in Physical and Mechanical Behavior of Polymers, CRC Press, Taylor & Francis Group Boca Raton, London, New York, 2019 Search PubMed.
- J. M. Uruena, A. A. Pitenis, R. M. Nixon, K. D. Schulze, T. E. Angelini and W. G. Sawyer, Biotribology, 2015, 1-2, 24 CrossRef.
- B. Cursaru, P. O. Stanescu and M. Teodorescu, Sci. Bull. - Univ. “Politeh.” Bucharest, Ser. B, 2010, 72, 99 CAS.
- B. Hammouda, D. L. Ho and S. Kline, Macromolecules, 2004, 37, 6932 CrossRef CAS.
- G. Beaucage and D. Schaefer, J. Non-Cryst. Solids, 1994, 797, 172 Search PubMed.
- G. Beaucage, J. Appl. Crystallogr., 1995, 28, 717 CrossRef CAS.
- G. Beaucage, J. Appl. Crystallogr., 1996, 29, 134 CrossRef CAS.
- B. Berke, O. Czakkel, L. Porcar, E. Geissler and K. Laszlo, Soft Matter, 2016, 12, 7166 RSC.
- T. Hellweg, K. Kratz, S. Pouget and W. Eimer, Colloids Surf., A, 2002, 202, 223 CrossRef CAS.
- Water in biology, chemistry, and physics: Experimental overviews and computational methodologies, ed. G. W. Robinson, S. B. Zhu, S. Singh and M. W. Evans, World Scientific, Singapore, 1996 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01619h |
| This journal is © The Royal Society of Chemistry 2020 |