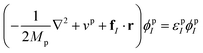Electronic insights into the role of nuclear quantum effects in proton transfer reactions of nucleobase pairs†
Received
21st February 2025
, Accepted 31st March 2025
First published on 31st March 2025
Abstract
Double proton transfer in nucleobase pairs leads to point mutations in nucleic acids. A series of constrained nuclear-electronic orbital calculations combined with natural bond orbital and non-covalent interaction analyses, and kinetic studies have quantitatively revealed the importance of nuclear quantum effects (NQEs) in the reaction. Compared with the classical treatment of the nuclei, the probability of forming the tautomeric isomers of Cytosine–Guanine, when explicitly accounting for NQEs, increased by a factor of 8.0. This outcome can be attributed to enhancing the interaction between the orbitals at the reactive site due to NQEs, which increased the number of electrons occupying the antibonding orbitals.
1. Introduction
The double proton transfer (DPT) reaction in DNA produces “biologically undesirable” tautomeric isomers that can lead to cancer and other diseases, as proposed in Löwdin's point mutation model.1 Elucidating the reaction mechanism is therefore a biochemically critical issue. Previous biological experimental research has examined the mutation probability in various organisms.2–6 Some studies have shown a bias towards the Cytosine–Guanine (C…G) base pair being more prone to mutation than the Thymine–Adenine (T…A) base pair.7–10 In contrast, theoretical studies using QM calculations under the Born–Oppenheimer (BO) approximation, QM/MM calculations, and molecular dynamics simulations have revealed that the T…A base pair tautomer (T*…A*) is unstable, with a low reverse reaction barrier, leading to a rare occurrence of tautomerization. On the other hand, the C…G base pair tautomer (C*…G*) can remain relatively stable, providing valuable insights into mutation probabilities in base pairs (Fig. 1).
 |
| | Fig. 1 Structures of the cytosine–guanine base pair (C…G) and its tautomer (C*…G*). | |
To quantitatively evaluate the DPT and hydrogen bonding interactions, it is crucial to consider nuclear quantum effects (NQEs), which arise from the quantum wave nature of protons and coupled proton–electron motions.11–13 Recently, Angiolari et al. demonstrated that NQEs lower the DPT reaction Gibbs free energy in C…G by 2 to 3 kcal mol−1, accelerating the reaction rate by approximately 30 times at 300 K using density functional tight binding-ring polymer molecular dynamics (DFTB-RPMD) simulations.14 Applying the Wigner–Moyal–Caldeira–Leggett equation under the same temperature conditions, Slocombe et al. also showed that the probability of tautomer formation increases to 1.73 × 10−4 due to NQEs.15 These results indicate that quantum mechanical acceleration in the tautomeric isomerization of C…G is much more significant than previously thought. This highlights the importance of proton–electron coupling in the electronic structure and underscores the need for treatments beyond the BO theory for biomolecular reactions.
This study aims to elucidate how NQEs affect the electronic structure of C…G. Additionally, we investigate the underlying reasons for promoting the DPT reaction. The influence of the surrounding environment on the DPT reaction is well-established.14–19 To assess the impact of NQEs on the reaction, we have conducted both BO and beyond-BO calculations.
2. Methods
2.1. Constrained nuclear-electronic orbital
We focused on the constrained nuclear-electronic orbital (cNEO) method,20–22 which has been developed in recent years, to take NQEs into account in quantum chemical calculations. The cNEO is a theory that has been developed by Yang et al.23 and is an extended theory of the NEO method developed by Hammes-Schiffer et al.24 In the NEO method, to account for the quantum nature of the nucleus (in particular, the hydrogen nucleus), the total wave function of the system is expressed as the product of the electron wave function and the nucleus wave function.In this context, e and p represent electrons and protons, respectively. In NEO-DFT, which combines the NEO method and DFT, the total energy is expressed as a functional that depends on the density of electrons and protons.| |  | (2) |
Ts[ρe] and Ts[ρp] are kinetic energies. Jee[ρe], Jpp[ρp] and Jep[ρe,ρp] are mean-field Coulomb interaction energies. Eexc[ρe] and Epxc[ρp] are exchange–correlation energies. Eepc[ρe,ρp] are electron–proton correlation energies. Eeext[ρe] and Epext[ρp] are external potential energies. The electron and proton densities are, respectively, derived from the orbitals:| |  | (3) |
| |  | (4) |
where i and I represent electrons and quantum nuclei, and ϕei and ϕpI are 1-particle orbitals. In the NEO-DFT method, the Kohn–Sham equations for electrons and protons are expressed as follows:| | 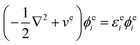 | (5) |
| |  | (6) |
where εei![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and εpI
and εpI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) are 1-particle orbital energies, and ve and vp are the effective potentials for the particles given as follows:
are 1-particle orbital energies, and ve and vp are the effective potentials for the particles given as follows:| | | ve = veeJ + vpeJ + vexc + veepc + veext | (7) |
| | | vp = vppJ + vepJ + vpxc + vpepc + vpext | (8) |
The NEO-DFT method has been employed in several studies, yet a discrepancy exists between the coordinates yielded through structural optimization and the expected values. This discrepancy can be attributed to the fact that the potential energy surface of NEO-DFT is contingent upon the coordinates of the classical nucleus alone. The cNEO method offers a solution to this issue. Consequently, the Kohn–Sham equations for electrons and protons in the cNEO-DFT method are expressed as follows:| |  | (9) |
| | 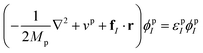 | (10) |
where fI·r is the positional constraint of each proton. As εe depends on the Coulomb potential of the proton, the potential is affected by the constraint indirectly. The coordinate expectation of each quantum proton can be defined as follows:With the constraint, the electronic/protonic orbitals must be normalized. The Lagrangian is defined by| |  | (12) |
2.2. Non-covalent interaction analysis
Non-covalent interaction (NCI) analysis is a tool used to visualize non-covalent interactions,25–27 including hydrogen bonding, van der Waals, and steric repulsion interaction, through the use of electron density (ρ) and its derivatives. NCI is based on a two-dimensional representation of the reduced density gradient (s) and electron density.| |  | (13) |
The reduced density gradient is close to zero in the case of non-covalent interactions between atoms or molecules. The specific nature of the interaction is determined by the sign of the second eigenvalue of ∇2ρ (= λ1 + λ2 + λ3 [λ1 < λ2 < λ3]), which can be classified as follows: (λ2 < 0 corresponds to an attractive interaction, λ2 ≈ 0 indicates a van der Waals-type weak interaction, and λ2 > 0 signifies a repulsive interaction).
2.3. Computational details
Focusing on the DPT reaction of C…G as a case study, electronic structures in the BO approximation (CAM-B3LYP/aug-cc-pVDZ) and the beyond-BO constrained nuclear-electronic orbital method (cNEO-CAM-B3LYP/aug-cc-pVDZ;PB4-F1) were evaluated.20–22,28
First, structural optimization and frequency analysis of C…G and C*…G* were performed in PySCF (version 2.4.0),29–32 which implements the cNEO as reported by Yang et al.23 The effective potential energy surface obtained using the cNEO includes NQEs such as zero-point vibrational energy. Structural optimizations were performed using the geomeTRIC (version 1.0.2) optimizer.33 No imaginary vibrational mode was found for the optimized structures for both BO and cNEO. The chemical reaction paths at the BO and cNEO levels were also traced using the climbing image nudged elastic band (CI-NEB) method34 by linking PySCF and ASE (version 3.22.1).35,36 In the CI-NEB calculations, the number of intermediate images, the spring constant (k), and the force threshold (fmax) for convergence were set to 18,37 0.1 eV Å−1, and 0.05 eV Å−1, respectively, following previous research. Then, the differences in the characteristics and reactivity of each chemical bond were evaluated using natural bond orbital (NBO)38–40 and NCI analyses.25–27
The DFT grid was set to (99, 974) in all the calculations. The SCF convergence was set to 10−11 a.u. In the cNEO calculation, all hydrogen atoms were treated as quantized particles. Electronic structure analyses by NBO and NCI were carried out using NBO7 (version 7.0.10),41 and NCIPLOT (version 4.2).42
3. Results and discussion
It has been reported that double counting of zero-point energy (ZPE) must be avoided when calculating activation barriers using the cNEO method and applying transition state theory.43 Therefore, we carried out a reaction analysis based on total energy. BO and cNEO differ in whether the total energy includes ZPE. Thus, comparing the results of BO and cNEO corresponds to examining the NQEs on hydrogen, the most critical element in DPT, in the reaction.
The DPT path from the cNEO calculation is shorter than that of BO (Fig. 2). This is because NQEs strengthen the hydrogen bonding interactions of the reactants. The reaction path of cNEO is more linear than that of BO, which means the two proton transfers become synchronous due to the tunneling effect caused by NQEs. This result is consistent with a previous DFTB-RPMD study.14 For NQEs, the activation barrier decreases by 5.7 kcal mol−1.
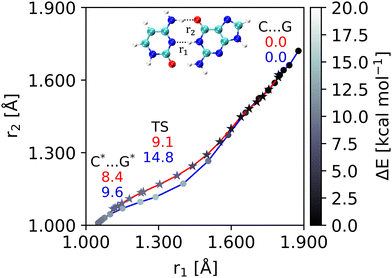 |
| | Fig. 2 DPT reaction profiles. The color density of each point represents the relative energy. The energy values of the BO/cNEO theory are depicted in blue/red for the representative structures. | |
Assuming that the DPT of C…G is a first-order reversible reaction and that there are no products at t = 0, then from the Eyring equation (eqn (14)), the reaction rate constant and the probability of formation of tautomeric isomers (eqn (15)) are as follows:44
| |  | (14) |
| |  | (15) |
Here,
i (= f,r),
kB,
h,
R,
T, Δ
Ei,
t, and [X]
t represent the reaction direction (forward or reverse), Boltzmann constant, Planck constant, gas constant, absolute temperature, activation barrier, reaction time, and the concentration of
X at time
t, respectively. The time to reach equilibrium was approximately 6.00 × 10
3 ps and 5.75 ps under the BO approximation and with NQEs, respectively (Fig. S1, ESI
†).
At physiological temperature (300 K), NQEs accelerated the forward/reverse reaction rate by a factor of 103 to 104 and increased the probability of isomer formation by 8.0 times (Table 1). A study on the mutation rate across the entire genome of 78 trios of Icelandic parents and children by Kong et al. showed that the average de novo mutation rate per nucleotide per generation was 1.20 × 10−8 in the samples.6 Our results theoretically explain this probability. The results also align with previous studies showing that NQEs increase the probability of tautomeric isomer formation.15 Of course, the generation of tautomerism is not limited to those derived from DPT, and the probability varies depending on the species. However, the overall probability of this order is 8.0 times the probability increase due to NQEs, which is not negligible.
Table 1 Rate constants [s−1] of the DPT forward/reverse reactions and tautomerization probability [× 10−5 %] at equilibrium (300 K)
|
|
BO |
cNEO |
|
k
f
|
1.12 × 102 |
1.48 × 106 |
|
k
r
|
1.09 × 109 |
1.80 × 1012 |
| Tautomerization probability |
1.03 |
8.24 |
BO and cNEO electron topological analyses help explain why NQEs lower the activation barrier and increase the probability of tautomer formation (Fig. 3 and Table 2). The interaction between the lone pair NBO (LP) and the N–H antibonding NBO (BD*), which drives DPT, is enhanced by 5 to 15 kcal mol−1 by NQEs, with the most significant enhancement occurring at the DPT reaction site (Table 2: LP/BD* interaction).
 |
| | Fig. 3 Antibonding (BD*) and lone pair (LP) NBOs. | |
Table 2 Donor (LP)–acceptor (BD*) NBO interaction [kcal mol−1] and electron occupancy of BD* in C…G
| Sitea |
LP–BD* interaction |
BD* occupancy |
| BO |
cNEO |
Δ
NQEs
|
BO |
cNEO |
Δ
NQEs
|
|
See Fig. 3.
|
| N–H…O |
33.5 |
48.7 |
+15.2 |
0.06 |
0.09 |
+0.03 |
| N…H–N |
26.4 |
35.5 |
+9.1 |
0.07 |
0.09 |
+0.02 |
| O…H–N |
19.0 |
24.7 |
+5.7 |
0.04 |
0.05 |
+0.01 |
The electron occupancy of BD* indicates that the two remaining N–H bonds are made more reactive by NQEs compared to the unreactive N–H bond. The absolute value of the BD* electron occupancy increases due to NQEs, and the difference between N–H…O and N…H–N becomes smaller (Table 2: BD* occupancy). This is consistent with the fact that the reactivity of the N–H bond is enhanced when NQEs are considered, and the transfer reaction of the two protons becomes synchronous (Fig. 2).14
The results of the NCI analysis also support this. According to the NCI analysis results (Fig. 4), the van der Waals repulsion caused by the formation of a pseudo-ring structure at the hydrogen bonding site and the steric repulsion of the nucleobase's ring structure remain primarily unchanged when NQEs are considered.
 |
| | Fig. 4 NCI 2D and 3D plots (isovalue = 0.50). The blue, green, and red surfaces in the 3D plots represent hydrogen bonding (λ2 < 0), van der Waals (λ2 ≅ 0), and steric repulsion interactions (λ2 > 0). | |
Conversely, it can be observed that NQEs reinforce hydrogen bonding interactions. Upon examining the 3D plot, it becomes evident that the hydrogen bonding site that does not undergo a reaction, O…H–N (Fig. 3), exhibits the lightest blue coloration and minimal alteration even when NQEs are incorporated. In contrast, the hydrogen bonding sites (N–H…O and N…H–N in Fig. 3), where the reaction progresses, exhibit a darker blue hue, indicating that NQEs strengthen the hydrogen bonding interaction. This result is consistent with the NBO findings. The comparison of BO and cNEO theories explains why NQEs accelerate the reaction from the electronic structure perspective.
4. Conclusion
This study performed a series of reaction analyses of DPT involved in C…G point mutations through multicomponent quantum chemical calculations, NBO, NCI, and kinetic analyses. The activation barrier for the C…G DPT reaction is lowered by 5.7 kcal mol−1 due to NQEs, and the probability of tautomeric isomer formation increases by 8.0. In other words, although NQEs have a relatively weak effect, they significantly impact the physical properties of nucleobase pairs. According to NBO analysis, the decrease in the activation barrier due to NQEs is explained by the increased electron occupancy of the N–H antibonding orbital at the reaction site and the enhancement of the interaction between the LP/BD* orbitals. The results have significant practical implications for understanding point mutations in nucleobase pairs. For example, they may inform the development of new mutation prevention and treatment strategies. The next stage of the investigation will focus on elucidating the impact of the explicit environment on electron–proton coupling.
Author contributions
H. M. conceived the project. K. M. performed multicomponent quantum chemical calculations and analysis. K. M. wrote the first version of the manuscript. H. M. revised the manuscript and contributed to its finalization. The manuscript was written with contributions from all authors. All authors approved the final version of the manuscript.
Data availability
The data supporting this study's findings are available in this article's ESI.†
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The calculations were performed using resources provided by the Research Center for Computational Science (RCCS) at the Okazaki Research Facilities of the National Institutes of Natural Sciences (NINS), Japan (Project no. 24-IMS-C013).
Notes and references
- P.-O. Löwdin, Rev. Mod. Phys., 1963, 35, 724–732 CrossRef.
- H. Lee, E. Popodi, H. Tang and P. L. Foster, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E2774–E2783 Search PubMed.
- K. C. Cheng, D. S. Cahill, H. Kasai, S. Nishimura and L. A. Loeb, J. Biol. Chem., 1992, 267, 166–172 CrossRef PubMed.
- J. W. Drake, B. Charlesworth, D. Charlesworth and J. F. Crow, Genetics, 1998, 148, 1667–1686 CrossRef PubMed.
- M. W. Nachman and S. L. Crowell, Genetics, 2000, 156, 297–304 CrossRef PubMed.
- A. Kong, M. L. Frigge, G. Masson, S. Besenbacher, P. Sulem, G. Magnusson, S. A. Gudjonsson, A. Sigurdsson, A. Jonasdottir, A. Jonasdottir, W. S. W. Wong, G. Sigurdsson, G. B. Walters, S. Steinberg, H. Helgason, G. Thorleifsson, D. F. Gudbjartsson, A. Helgason, O. T. Magnusson, U. Thorsteinsdottir and K. Stefansson, Nature, 2012, 488, 471–475 CrossRef PubMed.
- P. A. Lind and D. I. Andersson, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17878–17883 CrossRef PubMed.
- D. R. Denver, P. C. Dolan, L. J. Wilhelm, W. Sung, J. I. Lucas-Lledó, D. K. Howe, S. C. Lewis, K. Okamoto, W. K. Thomas, M. Lynch and C. F. Baer, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 16310–16314 CrossRef CAS PubMed.
- S. Ossowski, K. Schneeberger, J. I. Lucas-Lledó, N. Warthmann, R. M. Clark, R. G. Shaw, D. Weigel and M. Lynch, Science, 2010, 327, 92–94 CrossRef CAS PubMed.
- F. Hildebrand, A. Meyer and A. Eyre-Walker, PLoS Genet., 2010, 6, 1–9 Search PubMed.
- A. Pérez, M. E. Tuckerman, H. P. Hjalmarson and O. A. von Lilienfeld, J. Am. Chem. Soc., 2010, 132, 11510–11515 CrossRef.
- Y. Tao, T. J. Giese and D. M. York, Molecules, 2024, 29, 2703 CrossRef CAS.
- W. Fang, J. Chen, M. Rossi, Y. Feng, X.-Z. Li and A. Michaelides, J. Phys. Chem. Lett., 2016, 7, 2125–2131 CrossRef CAS PubMed.
- F. Angiolari, S. Huppert, F. Pietrucci and R. Spezia, J. Phys. Chem. Lett., 2023, 14, 5102–5108 CrossRef CAS PubMed.
- L. Slocombe, M. Sacchi and J. Al-Khalili, Commun. Phys., 2022, 5, 1–9 CrossRef.
- J. P. Cerón-Carrasco and D. Jacquemin, Phys. Chem. Chem. Phys., 2015, 17, 7754–7760 RSC.
- A. Gheorghiu, P. V. Coveney and A. A. Arabi, Interface Focus, 2020, 10, 20190120 CrossRef CAS PubMed.
- L. Slocombe, M. Winokan, J. Al-Khalili and M. Sacchi, Commun. Chem., 2022, 5, 1–9 CrossRef PubMed.
- M. Winokan, L. Slocombe, J. Al-Khalili and M. Sacchi, Sci. Rep., 2023, 13, 1–12 CrossRef.
- X. Xu and Y. Yang, J. Chem. Phys., 2020, 152, 084107 CrossRef CAS PubMed.
- X. Xu and Y. Yang, J. Chem. Phys., 2020, 153, 074106 CrossRef CAS.
- X. Xu and Y. Yang, J. Chem. Phys., 2021, 154, 244110 CrossRef CAS PubMed.
-
https://github.com/theorychemyang/pyscf
.
- F. Pavošević, T. Culpitt and S. Hammes-Schiffer, Chem. Rev., 2020, 120, 4222–4253 CrossRef PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- R. A. Boto, F. Peccati, R. Laplaza, C. Quan, A. Carbone, J.-P. Piquemal, Y. Maday and J. Contreras-García, J. Chem. Theory Comput., 2020, 16, 4150–4158 CrossRef CAS.
- Q. Yu, F. Pavošević and S. Hammes-Schiffer, J. Chem. Phys., 2020, 152, 244123 CrossRef PubMed.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, WIREs Comput. Mol. Sci., 2018, 8, e1340 CrossRef.
- Q. Sun, X. Zhang, S. Banerjee, P. Bao, M. Barbry, N. S. Blunt, N. A. Bogdanov, G. H. Booth, J. Chen, Z.-H. Cui, J. J. Eriksen, Y. Gao, S. Guo, J. Hermann, M. R. Hermes, K. Koh, P. Koval, S. Lehtola, Z. Li, J. Liu, N. Mardirossian, J. D. McClain, M. Motta, B. Mussard, H. Q. Pham, A. Pulkin, W. Purwanto, P. J. Robinson, E. Ronca, E. R. Sayfutyarova, M. Scheurer, H. F. Schurkus, J. E. T. Smith, C. Sun, S.-N. Sun, S. Upadhyay, L. K. Wagner, X. Wang, A. White, J. D. Whitfield, M. J. Williamson, S. Wouters, J. Yang, J. M. Yu, T. Zhu, T. C. Berkelbach, S. Sharma, A. Y. Sokolov and G. K.-L. Chan, J. Chem. Phys., 2020, 153, 024109 CrossRef CAS PubMed.
- Q. Sun, J. Comput. Chem., 2015, 36, 1664–1671 CrossRef CAS PubMed.
- S. Lehtola, C. Steigemann, M. J. Oliveira and M. A. Marques, SoftwareX, 2018, 7, 1–5 CrossRef.
- L.-P. Wang and C. Song, J. Chem. Phys., 2016, 144, 214108 CrossRef PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys. Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
-
https://gitlab.com/ase/ase
.
- L. Slocombe, J. S. Al-Khalili and M. Sacchi, Phys. Chem. Chem. Phys., 2021, 23, 4141–4150 RSC.
- E. D. Glendening, C. R. Landis and F. Weinhold, WIREs Comput. Mol. Sci., 2012, 2, 1–42 CrossRef CAS.
- F. Weinhold, J. Comput. Chem., 2012, 33, 2363–2379 CrossRef CAS PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241 Search PubMed.
-
E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7.0., Theoretical Chemistry Institute, University of Wisconsin, Madison, 2018 Search PubMed.
-
https://github.com/juliacontrerasgarcia/NCIPLOT-4.2
.
- Z. Chen, J. Zheng, D. G. Truhlar and Y. Yang, J. Chem. Theory Comput., 2025, 21, 590–604 CrossRef CAS.
- K. Umesaki and K. Odai, J. Phys. Chem. B, 2020, 124, 1715–1722 CAS.
|
| This journal is © the Owner Societies 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*



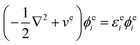

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and εpI
and εpI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) are 1-particle orbital energies, and ve and vp are the effective potentials for the particles given as follows:
are 1-particle orbital energies, and ve and vp are the effective potentials for the particles given as follows: