Conformational effects in the identification and quantification of ketohydroperoxides in the oxidation of n-pentane

Abstract

Stereochemistry plays a key role in both fundamental chemical processes and the dynamics of a large set of molecular systems of importance in chemistry, medicine and biology. Predicting the chemical transformations of organic precursors in such environments requires detailed kinetic models based on laboratory data. Reactive intermediates play a critical role in constraining the models but their identification and especially their quantification remain challenging. This work demonstrates, via the study of the gas-phase autoxidation of n-pentane, a typical fuel surrogate, that accounting for spatial orientation is essential for accurate characterization of such intermediates and for their further evolution. Using synchrotron-based photoelectron photoion coincidence spectroscopy and high-level quantum calculations to investigate the electronic structure and ionization dynamics of the main ketohydroperoxide isomer formed during the oxidation of n-pentane, we reveal the multiple thermally accessible conformers of the chain-branching agent, highlighting how their distinct ionization energies and fragmentation pathways can significantly affect intermediate quantification via photoionization-based probes, a universal in situ method of choice. This research underscores the importance of stereochemistry not only in combustion systems but in any chemical system where a molecular-level understanding is crucial for developing accurate predictive models for both scientific and industrial applications.

---

For decades, the critical influence of molecular conformation large-scale observables through mechanisms like reaction kinetics, enzyme specificity, sensory perception, and environmental interactions has been recognized across a wide range of chemical processes, including combustion, gas-phase reactions, surface adsorption, enzymatic catalysis, pharmacology, and atmospheric, organic and inorganic chemistries.^1–9 For instance in atmospheric processes, studies have shown that the stereochemical configurations of precursor molecules, helped by the chiral nature of many biogenic volatile organic compounds,^10,11 can be transferred to particle-phase organic material during oxidation processes.¹² This stereochemical transfer can influence the physical and chemical properties of aerosols, potentially affecting their hygroscopicity and other characteristics.¹³ Research also demonstrated that heterogeneous ozonolysis rates can differ between diastereomers based on their molecular orientation,¹⁴ and that stereoselectivity also occurs in atmospheric autoxidation reactions.¹⁵ Stereochemical effects significantly influence combustion modeling, reaction networks, and kinetics. Deviations between diastereomers can alter dominant reaction pathways, thereby impacting ignition delay times in internal combustion engines.¹⁶ The extent of these effects depends on the fuel's molecular structure, the type of stereoisomerism, and the combustion stage. These factors can either enhance or suppress the overall reactivity of the system,^17,18 affecting not only the energy barriers of reactions but also the interconversion barriers between chemical species and transition states.^19,20 A notable example, highlighted by Danilack et al.,²¹ demonstrates how two diastereomeric chiral species and their respective transition states in diethyl ether oxidation calculations increase both rate coefficients and the concentration of chain-branching ketohydroperoxide (KHP, HOOP=O) intermediates. The decomposition of KHP into hydroxy and oxy radicals is a key step in initiating the first stage of autoignition in thermal engines.²² Despite the significance of these effects, many gas-phase chemical models still neglect the distinction between stereoisomers. However, recent efforts to incorporate stereoisomeric and diastereomeric resolution into these models are improving the accuracy of simulation predictions.²³

Developing kinetic models that accurately depict the balance between the various reaction pathways at play under operando conditions in gas-phase autoxidation systems is a major scientific challenge where stereochemical effects influence the outcomes of such processes. As in atmospheric sciences and combustion chemistry, these chemical systems are primarily driven by radical-growth reactions involving peroxy (ROO) intermediates. Those intermediates are key to the ignition behavior observed in internal combustion engines and play a critical role in the formation and evolution of highly oxygenated organic molecules (HOMs), which can later condense to form particulate matter in the troposphere.^7,22,24–26

Accurate experimental data relying on the identification and quantification of such intermediates are fundamental to confront kinetic models’ predictions and assess their performance.²⁷ However, this represents a real challenge due to the large number of constitutional isomers,²⁸ in particular when the size of the such compounds increases (more than 104 conformers for an organic molecule containing 10 C atoms). For hydroperoxides, this issue is worsened by their tendency to fragment easily during photoionization,²⁹ even when in their ground cationic state,³⁰ leading to large and undesirable uncertainties in quantification.

Over the past two decades, significant advancements have been achieved in hydroperoxide analysis thanks to the use of synchrotron-based vacuum ultraviolet photoionization mass spectrometry (SVUV-PIMS) technique,^31–38 and more recently by adding photoelectron spectroscopy, via a photoelectron photoion coincidence (SVUV-PEPICO) scheme, offering both the sensitivity for the detection of elusive intermediates and an enhanced resolution required for isomeric-discrimination.^39–45 The analysis of the recorded threshold mass-selected photoelectron spectra (ms-TPES), containing the specific vibronic transitions of molecular species to their respective cations, already helped addressing significant discrepancies between experimental results and kinetic models.^46,47

The SVUV-PEPICO experiments are based on molecular-beam sampling to maximize the detection of intermediate species, using a free-jet expansion from a reactor in which collisions with the carrier gas tend to quench the vibrational and rotational states of molecules cooling them down to their lowest-energy conformation. This rotational interconversion depends on the height of the energy barriers. If these barriers are high enough, the molecules may preserve the conformer distribution resulting from the high temperature of the reactor, as the higher energy conformers are “trapped” and not fully converted to the lowest-energy state.^1,48,49 For flexible molecular systems like hydroperoxide intermediates in the troposphere or in a thermal engine, the number of thermally accessible conformational arrangements can be large, facilitated by large-amplitude motions. Although these conformations may have closely lying energy levels, they can feature relatively high barriers to interconversion.

The present work demonstrates through a concrete case from the literature, how accounting for conformer populations when attempting to accurately quantify elusive intermediates in gas-phase autoxidation reactions can significantly impact their identification and quantification, leading to important considerations for future studies. We choose the low-temperature oxidation of n-pentane, a typical fuel surrogate in gasoline engines,^50–52 as such case study. In 2021, Battin-Leclerc et al.⁴⁶ investigated the formation of KHPs after oxidation of n-pentane using a PEPICO spectrometer to probe the gas mixture in a heated jet-stirred reactor (JSR). The analysis of the recorded TPES of m/z 118 was attributed mainly to 4-hydroperoxy-2-pentanone (referred to as 2,4-KHP, m/z 118), other possible KHP isomers being ruled out due to higher calculated ionization energies. However, despite considering all possible KHP isomers, not all features observed in the TPES of m/z 118 could be explained. Besides, Battin-Leclerc et al.⁴⁶ observed that 2,4-KHP underwent dissociative photoionization, resulting in the formation of three main fragment ions (m/z 43, 57, and 85), based on similar thermal profiles as KHP (m/z 118), energy threshold correlation, and time-of-flight peak broadening due to fragment kinetic energy release. This result addressed the large and unusual gap between experimental measurements and kinetic model predictions that had remained for the low-temperature oxidation of n-pentane in the literature until now.⁵³ To explain the formation of the three fragments, Battin-Leclerc et al.⁴⁶ proposed, but without the support of theoretical calculations, a new dissociative photoionization mechanism involving an intermediate dione cation through a H₂O-loss from 2,4-KHP that would almost immediately dissociate into the three fragments. More recently, Hu et al.⁴⁷ confirmed 2,4-KHP as the main KHP via SVUV-PIMS experiments coupled with off-line gas chromatography-mass spectrometry (GC-MS) analysis and also confirmed m/z 85 as a KHP fragment. However they did not detect the additional fragments m/z 43 and 57 reported by Battin-Leclerc et al.⁴⁶ Supported by theoretical quantum calculations, they explained the formation of the m/z 85 fragment from 2,4-KHP through the loss of an –OOH group, the conventional dissociative photoionization mechanism assumed for KHP in literature.^54,55 However, with this mechanism starting with the H-abstraction from the C–OOH function by the oxygen of the carbonyl group, no intramolecular rearrangements can explain the formation of the two other fragments (m/z 43 and m/z 57).

The experimental data used in the present study are taken from the same experimental campaign as the works of Bourgalais et al.⁴⁴ and Battin-Leclerc et al.⁴⁶ The latter contain all the necessary experimental details, and the reader is referred to these publications for more comprehensive information. Here, only the most critical aspects, essential for understanding the analysis, are recalled. The experimental conditions in this work were chosen to optimize the formation of KHPs, based on existing literature data on the oxidation of n-pentane. A lean reactive gas mixture (n-pentane + O₂ + He) where “lean” indicates a fuel-air mixture with less fuel than required for stoichiometric combustion, was prepared with an equivalence ratio of ϕ = 0.5. The equivalence ratio, defined as the ratio of the actual fuel-to-air ratio to the stoichiometric fuel-to-air ratio, signifies that the mixture contains twice as much air as required for stoichiometric combustion. This mixture was continuously flowed into a near-atmospheric pressure JSR maintained at a constant temperature of T = 585 K. The residence time, defined as the average time the gas mixture remains inside the JSR, was 3 s. Note that the JSR is heated using Thermocoax resistances and the temperature inside the JSR is measured with a K-type thermocouple placed in a glass finger near the center of the JSR, with an uncertainty of 1%.⁵⁶ The SAPHIRS molecular beam end-station,⁵⁷ located at one of the monochromatized branches of the VUV DESIRS beamline at the SOLEIL synchrotron, housed the JSR. The gas mixture from the oxidation of n-pentane within the JSR was analyzed using a double-imaging i²PEPICO spectrometer, which allowed recording mass-selected TPES (see ESI† for more information regarding the analysis of the JSR gas mixture and the acquisition of the TPES).⁵⁸

Complementary off-line measurements were achieved in this work using a liquid sample collected at the outlet of the JSR at synchrotron SOLEIL, with additional details provided in the ESI.† The identification of KHPs was achieved using gas chromatography with mass spectrometry (GC/MS) detection (see chromatogram in Fig. S1, ESI†) by comparing its expected MS fragmentation pattern (Fig. S2, ESI†) with the pattern previously recorded by Hu et al.,⁴⁷ demonstrating a strong similarity. Furthermore, the MS of another KHP, 2-hexanone-4-hydroperoxide, reported by Jorand et al.,⁵⁹ showed identical fragmentation pattern (Fig. S3, ESI†), further reinforcing the confidence in the detection of 2,4-KHP.

In addition, despite the higher energy (70 eV) of the electron impact source used in GC/MS compared to the typical photon energy (9–11.5 eV) employed in SVUV-PEPICO experiments, major peaks observed in GC/MS (m/z 43, 57, 71, 85, 100, and 118, see Fig. S2, ESI†) were also detected in PEPICO experiments, as reported in Bourgalais et al.⁴⁴ and Battin-Leclerc et al.⁴⁶ However, all the detected masses are not necessarily coming from the dissociative photoionization of 2,4-KHP. In Fig. S4 (ESI†), the evolutions of m/z 71 and 100 with the JSR temperature recorded during SOLEIL campaigns are compared with those of m/z 43, 57, and 85 that were previously identified as KHP cation fragments. The thermal profile of m/z 71 exhibits a distinct pattern, indicating that it is not a fragment of KHP, while the thermal profile of m/z 100 shows a similar rise as m/z 43, 57, and 85 but the decrease is different. As a conclusion, the present additional GC/MS measurements reinforce the state-selected fragmentation pattern for 2,4-KHP found in Battin-Leclerc et al.⁴⁶

In Battin-Leclerc et al.,⁴⁶ not all the structures of the TPES of m/z 118 could be explained, especially the first transition, and the authors suggested neutral vibrational excitations since the simulations were performed at 0 K. However, conformers was only done for the cationic structures that most closely mirrored their corresponding neutral. In the present study, a rigorous and thorough conformational analysis following the procedure outlined in Huang et al.⁶⁰ was conducted at the M06-2X-D3/cc-pVTZ level of theory for the electronic structure calculations. As weak interactions in many systems, particularly involving H-bonds can impact the accuracy of energy calculations, (R)CCSD(T)/aug-cc-pVTZ calculations were performed to get the respective adiabatic ionization energies (AIEs) of the main six 2,4-KHP conformers that have been considered in this work based on their Boltzmann distribution (see the Theoretical method section in the ESI†).

The respective structures of the conformers are displayed in Fig. 1 along with the relative energies of both the neutral and cation forms, AIE, VIE, and Boltzmann distribution calculated using the Gibbs free energy at T = 585 K, i.e., the reactor temperature. This value implicitly assumes that the subsequent sampling of the reactor contents through an adiabatic expansion effectively freezes the conformer population, i.e., that interconversion barriers are relatively high, above thermal energies. Despite the fact that the temperature beam is not here accurately known, this assumption is supported by previous studies reporting efficient cooling in molecular beams, around 50 to 150 K in this setup,^61,62 even for reactors operating at higher temperatures (up to 700 K).⁶³

Fig. 1 Geometries and electronic energies (relative to Conf-1, Black) of the main 2,4-KHP conformers considered in this work, as well as their adiabatic ionized energy (AIE) values (Red), calculated at the (R)CCSD(T)/aug-cc-pVTZ//M06-2X-D3/cc-pVTZ level of theory. Detailed energies and Boltzmann distribution at 585 K of the main 2,4-KHP conformers are provided in Table S1 (ESI†), while optimized coordinates and frequencies of the conformers are given in Table S2 (ESI†). Conformational search and identification were performed by xtb⁶⁴ and Molclus,⁶⁵ with the following parameters used to distinguish two conformers, ΔG ≥ 0.5 kcal mol⁻¹ and RMSD ≥ 0.5 Å. All energies are in eV.

The four lowest-energy conformers have less than 70 meV of difference in energy (see Fig. 1). Interestingly, the lowest-energy conformer changes when considering the Boltzmann distribution calculated using the Gibbs free energy, which is a more suitable indicator for relative populations, especially at high temperatures where the thermal factor can significantly influence the distribution of conformers.^16,66–68 However, the uncertainty in calculating Gibbs free energy, which includes thermal and entropic corrections, can also be higher, particularly due to the challenges in accurately calculating entropic contributions.^69,70 Therefore, the ranking based on either electronic energy or Gibbs free energy here is provided for informational purposes only and should be taken with caution when the calculated energies lie too close from one another.

In contrast to the closely lying neutral electronic energies of those conformers, the AIEs are markedly different, with ∼0.5 eV of variability. For instance, while the first two conformers (Conf-1 and Conf-3) are basically isoenergetic, with only 19 meV of difference (see Fig. 1), their AIEs differ significantly; Conf-1 has the higher AIE, of 9.508 eV, while Conf-3 has an AIE of 9.062 eV, which is in agreement with the value reported by Hu et al.⁴⁷ The overall conformer spread regarding vertical ionization energies (VIEs), are even larger, reaching more than 0.7 eV (see Fig. 1).

The lowest AIE is below 9.1 eV, (see Conf-2 and Conf-3), which is qualitatively consistent with the starting of the experimental signal of KHP observed in the TPES of m/z 118 shown in Fig. 2. Weak signal is detected ∼8.9 eV but computational analysis of the conformational distribution and AIE revealed that conformers with AIE within the 8.8–9.0 eV range represent a negligible part of the Boltzmann distribution at 585 K (see Fig. 1) therefore this signal is more likely related to hot bands as demonstrated hereafter. Indeed, the vibrational modes below 400 cm⁻¹ of the neutral ground electronic state of the molecules can be populated due to the relatively high temperature of the JSR. Conversely, a significant portion of conformers exhibit AIE around 9.2–9.4 eV which is also qualitatively consistent with the maximum of the TPES of m/z 118 (at ∼9.4 eV) displayed in Fig. 2.

Fig. 2 TPES of m/z 118 (open dots) compared to the simulated total PES of 2,4-KHP at 585 K (blue line) resulting from the sum of the individual 2,4-KHP conformers weighted by the Boltzmann distribution calculated using the Gibbs free energy. The shaded blue and red areas indicate a fragmentation region based on experiment and theory respectively. See text for details.

The simulated spectra, based on Franck–Condon factors (FCF) calculations including rigorous hot band contributions, of the five main 2,4-KHP conformers, which account for 99% of the Boltzmann distribution, were calculated independently and then weighted according to their Boltzmann distribution using the Gibbs free energy to reproduce the total simulated PES of 2,4-KHP (see more information regarding the simulation of vibronic envelopes in ESI† along with Fig. S5–S11, ESI†). The total simulated PES of 2,4-KHP is compared to the TPES of m/z 118 in Fig. 2. The first part of the experimental spectrum is very well matched by the simulated PES, including the ionization threshold below 9.0 eV.

Beyond 9.4 eV, the experimental TPES decreases while the simulated PES continues to rise. This discrepancy, highlighted in blue in Fig. 2, is attributed to the unimolecular decomposition of KHP cations and the loss of parent signals, as the theoretical model used to simulate the PES only considers direct ionizing transition and not the subsequent relaxation dynamics in the parent ion potential energy surfaces. The peak of the simulated PES should then be compared to the signal of the corresponding KHP cation fragments (m/z 43, 57, and 85) provided in Fig. S12 (ESI†). The maximum of the simulated TPES occurs around 9.5–9.6 eV, aligning well with the plateau reached by the fragment signals.

Theoretical calculations on the further evolution of those conformers were then conducted based on the dehydration mechanism hypothesized in Battin-Leclerc et al.⁴⁶Fig. 3 demonstrates the conformational transformation and dehydration pathways for 2,4-KHP⁺ conformers calculated in this work. The dehydration process starts with hydrogen abstraction from the CH group by the oxygen atom of the ketocarbonyl group. The hydrogen atom is then transferred to the hydroxyl group of the OOH function, releasing H₂O and forming a 2,4-pentanedione cation intermediate at m/z 100.

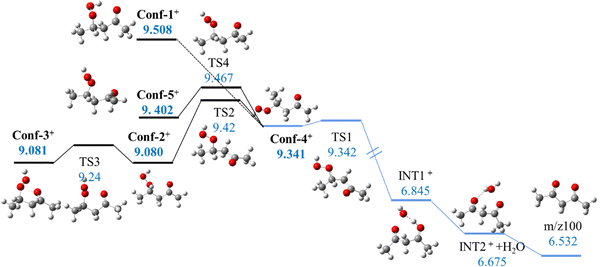Fig. 3 Conformational transformation (dark line) and representative dehydration pathways (bule line) of 2,4-KHP cationic conformers. (unit: eV). Energies are given with respect to neutral Conf-1.

Stereochemistry plays a crucial role in this dehydration mechanism, since the orientation of functional groups significantly affects their reactivity. For example, Conf-4⁺ can directly undergo a two-step dehydration process via a barrierless reaction because of the alignment between the H atom in the CH group and the O atom from the C=O group. In contrast, other conformers must overcome an additional re-orientation barrier before dehydration. As a result, Conf-2⁺ has a lower AIE than Conf-4⁺ but a higher barrier to dehydration, of 0.4 eV. Note that the potential energy surface scan on Conf-1⁺ shows a very low barrier for the rotation around the C–C bond, making difficult the determination of the structure of the transition state.

Fig. 4 shows how the three fragments m/z 43, 57, and 85 are then formed via the unimolecular decomposition of 2,4-pentanedione cations as most available internal energy is deposited into it due to its larger number of modes compared to those of the H₂O fragment. The formation of m/z 85 without a barrier should cause this fragment to be the dominant compared to m/z 43 and m/z 57, which is consistent with experimental observations. As observed in Fig. S12 (ESI†), the ms-TPES of the three fragments share the same 9.3–9.4 eV onset, which is consistent with the calculated pathways displayed in Fig. 3 that predict a narrow onset between 9.34 eV and 9.508 eV to isomerization and 2,4-KHP cation dehydration, followed by dissociation of the 2,4-pentadione cation (Fig. 4).⁴⁶ This theoretical range, highlighted in red in Fig. 2, is also in good agreement with the fragmentation region deduced from the experimental TPES.

Fig. 4 Decomposition pathways of the dehydration product (m/z = 100) (unit: eV). Energies are given with respect to neutral Conf-1.

Hu et al.⁴⁷ explained the formation of the m/z 85 fragment from 2,4-KHP⁺via a two-step intramolecular rearrangement, starting with a H-migration from the –OOH function to the carbonyl group and then from the –CH₂ group before a β–C–O bond dissociation. The loss of an –OOH group is the conventional dissociative photoionization mechanism assumed for KHPs in the literature^54,55 and it would lead in this case to the formation of a C₅H₉O⁺ fragment at m/z 85 with an appearance energy of 9.48 eV, corresponding to the first transition state calculated at the G4 level of theory. However, this is in disagreement with their reported 9.72 eV value calculated at the (R)CCSD(T)/CBS level, suggesting that the barrier is likely higher than 9.5 eV. To compare directly with the dehydration mechanism, calculations were performed in this work for the –HOO dissociation pathways of the cationic conformers at the same level of theory. As shown in Fig. 5, three consecutive transition states were found as in Hu et al.⁴⁷ but lying about 0.5 eV above 2,4-KHP cation, leading to an appearance energy for the m/z 85 fragment of 9.638 eV for all conformers. These results are consistent with the higher barrier from the (R)CCSD(T)/CBS calculations of Hu et al.⁴⁷ but not compatible with the ionization threshold of m/z 85 observed experimentally in Fig. S12 (ESI†). Indeed, we find that the barrier is higher when the carbonyl function is close to H of OOH (HOO-dissociation mechanism) rather than when in phase with the H of the CH group (dehydration mechanism), and that the lower barrier (9.3–9.4 eV) of dehydration is in better agreement with the experimental onset of m/z 85 than the HO₂ dissociation (9.5–9.6 eV) pathway.

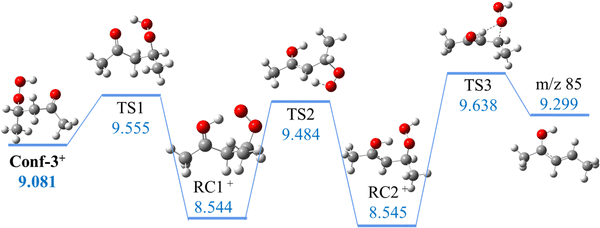Fig. 5 Representative HOO dissociative pathway of 2,4-KHP (unit: eV). Energies are given with respect to neutral Conf-1.

As an additional result, this study supports the quantification of 2,4-KHP made by Battin-Leclerc et al.⁴⁶via the total KHP signal, including the signal of the KHP⁺ parent (m/z 118) and the signal of the three fragments (m/z 43, 57, and 85). Importantly, it is not necessary to know all the fragment ions of a parent molecule to achieve accurate quantification, provided that partial PICS are known (see ESI† for the quantification method). In practice, total PICS are typically used due to the lack of data on partial PICS and for which it is essential to know all the major fragments to achieve accurate quantification of the parent ion. However, it is important to note that total PICS are usually estimated using theoretical calculations or the group additivity method of Bobeldijk et al.,⁷¹ which introduce significant uncertainties in the results.

In the latter approach, the molecule is made of groups defined as bonded atom pairs, for which cross-section contribution values have been estimated in the literature at only a few photon energy. The total PICS is then obtained by summing these contributions (see ESI†). However, the values for each group vary significantly between studies (see ESI† in Rodriguez et al.⁷²). Consequently, we adopted the values for each group as calculated by Rodriguez et al.,⁷² which represent the average of the literature data, and used the standard deviation as the uncertainty for each group. The uncertainty for the total PICS was then estimated using a common variance formula to calculate error propagation (see ESI†).

Thanks to the experimental measurements of the partial PICS of m/z 85 and 118 in Hu et al.,⁴⁷ a comparison of the quantification of 2,4-KHP is accomplished using three approaches (see Fig. 6):

Fig. 6 Predictions of the mole fraction of 2,4-KHP (black line) as a function of temperature compared to the experimental mole fraction calculated at 585 K for a photon energy of 10.5 eV from the signal of the m/z 118 KHP parent (red dot), the m/z 85 KHP fragment (green dot), and the total KHP including parent: m/z 118 + fragments: m/z 43, 57, and 85 (blue dot).

(1) The parent signal of KHP⁺ at m/z 118,

(2) The fragment signal of m/z 85,

(3) And the total signal of KHP cation (parent m/z 118 + fragments m/z 43, 57, and 85).

The fragment signals were obtained by integrating the peak area in the mass spectrum presented in the Fig. 3 in Bourgalais et al.⁴⁴ To assess the reliability of the experimental mole fraction values for KHP, they were compared with the predictions of the NUIGMech1.1 mechanism,⁷³ which simulates n-pentane oxidation under the experimental conditions of the SOLEIL experiments. The simulations were conducted using the openSMOKE++ software package,^74,75 employing a perfectly stirred reactor scheme to model the JSR. The experimental KHP mole fractions derived using the partial PICS of m/z 85 and m/z 118 from Hu et al.⁴⁷ are in good agreement with the predictions from the kinetic model. Among the approaches tested, the mole fraction of KHP calculated using only the m/z 85 signal provides the closest agreement with the kinetic model predictions, suggesting that m/z 85 is the most reliable signal for quantifying KHP under the conditions studied. This result aligns with the observation that the partial PICS of m/z 118 is significantly smaller than that of m/z 85, which may introduce greater uncertainties when relying solely on m/z 118. Furthermore, we note that using the total KHP signal—incorporating both the parent signal and its main fragments—can achieve similar accuracy when the total PICS is estimated via the group additivity method. However, it should be noted that this method based on mass signals is subject to more uncertainties as the photon energy increases due to potential contributions from other molecules that can fragment upon photoionization within the same mass channels. In this case, fragments at m/z 43 are quite common, such as with decomposition of acetone,⁷⁶ therefore explaining the increase above 10 eV in the TPES of m/z 43 (see Fig. S12, ESI†) and its contribution is significant as it is a dominant product in the oxidation of n-pentane.⁷³

Due to the good agreement and the similarity of the TIY of the m/z 85 and 118 fragments with those reported by Hu et al.⁴⁷ (see Fig. S13, ESI†), these curves were compared in Fig. S14 (ESI†) with the total PICS calculated using the method by Moshammer et al.⁷⁷ Despite an overall agreement within a factor of 2 as claimed in the literature, the theory overestimates the PICS at low photon energy and underestimates it above 10 eV. The underestimation at high photon energy could be due to the fact that the current theoretical method only considers the direct photoionization process of the outermost molecular orbital (HOMO) and does not account for the photoionization from deeper occupied molecular orbitals or the contributions of autoionizing processes. Conversely, the overestimation at low photon energy can be due to the missing contribution from the other fragments m/z 43 and 57 for which the partial PICS remains unknown.

Conclusions

This study investigates the electronic structure and ionization dynamics of the predominant isomer of KHP in a representative combustion system, the low-temperature oxidation of n-pentane. With the help of high level calculations, the analysis of existing data from literature and the analysis of additional experimental data from this work, we clearly confirm the identification of 2,4-KHP as the main isomer and m/z 43, 57, and 85 as its three main fragments. The TPES analysis showed multiple thermally accessible conformers of KHP, which are very similar in energy but differ significantly in their adiabatic and vertical ionization energies, making TPES analysis challenging. This variation underlies a significant change in spatial orientations upon photoionization, therefore affecting the initial steps of their fragmentation with significant differences in barrier heights and intramolecular rearrangements that need to be considered for a proper quantification by mass spectrometry, a universal method of choice. The orientation of the functional groups significantly influences the decomposition mechanism, and we have shown that a dehydration mechanism after isomerization into Conf-4⁺ is, for all initial neutral conformers, more efficient, presenting a lower barrier than the previously considered loss of an –HOO group.

The conformational effects observed here are not limited to combustion chemistry nor to small, volatile molecules. In atmospheric chemistry, for instance, conformers are critical in the behavior of reactive intermediates like peroxy radicals. The variability in conformer populations can strongly influence the rates of key reactions, such as ozonolysis, impacting air quality models and climate predictions. Similarly, in biological systems, conformational diversity affects host–guest interactions such as enzyme activity and drug action, as higher-energy conformers can enable crucial reaction steps such as substrate binding or product release while second order nucleophilic substitutions outcomes are dominated by stereodynamical effects. One could also mention chiral recognition, a very basic process in metabolism which is greatly favored by conformational flexibility. As the size and complexity of chemical systems increase—whether in polymerization processes, material science, or pharmaceuticals—the number of possible conformations grows, affecting properties like stability, reactivity, and even solubility. The insights gained from this work can thus inform the development of more accurate models in both scientific and industrial applications, including combustion engines, environmental monitoring, and even pharmaceutical drug design.

Author contributions

OH, PA, LST, GV, FBL, and JB collected the experimental data. GAG, MH, HHC, and LN provided support for the analysis. DL, DL, and JH performed the theoretical calculations. JB, FZ, and JB analyzed the data and wrote the original draft. All the authors contributed to review the final manuscript.

Data availability

The datasets supporting this article have been uploaded as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to the whole SOLEIL staff for smoothly running the facility under project 20180021. High performance computing resources were provided by the EXPLOR centre hosted by the University of Lorraine. HHC acknowledges funding by the Aragón Government (ref. T22_23R), cofounded by EFRD 2014-2020 “Construyendo Europa desde Aragón”. FZ acknowledges financial support from the Innovation Program for Quantum Science and Technology (2021ZD0303303). JB acknowledges financial support from the Italian Ministry of University and Research (MUR) through the PRIN program (PRIN 2020 prot. 2020HTSXMA) and computed resources from the High Performance Computing center of Scuola Normale Superiore.

References

1. S. T. Park, S. K. Kim and M. S. Kim, Nature, 2002, 415, 306–308.
2. Y.-P. Chang, K. Długołęcki, J. Küpper, D. Rösch, D. Wild and S. Willitsch, Science, 2013, 342, 98–101.
3. N. Singhal, A. L. Koner, P. Mal, P. Venugopalan, W. M. Nau and J. N. Moorthy, J. Am. Chem. Soc., 2005, 127, 14375–14382.
4. M. H. Kim, L. Shen, H. Tao, T. J. Martinez and A. G. Suits, Science, 2007, 315, 1561–1565.
5. M. Olivucci and F. Santoro, Angew. Chem., Int. Ed., 2008, 47, 6322–6325.
6. D. D. Boehr, D. McElheny, H. J. Dyson and P. E. Wright, Science, 2006, 313, 1638–1642.
7. E. Praske, R. V. Otkjær, J. D. Crounse, J. C. Hethcox, B. M. Stoltz, H. G. Kjaergaard and P. O. Wennberg, Proc. Natl. Acad. Sci. U.S.A., 2018, 115, 64–69.
8. S. M. Morrow, A. J. Bissette and S. P. Fletcher, Nat. Nanotech., 2017, 12, 410–419.
9. Y. Zhang, R. M. Malamakal and D. M. Chenoweth, Angew. Chem., Int. Ed., 2015, 54, 10826–10832.
10. E. G. Stephanou, Nature, 2007, 446, 991.
11. J. Byron, J. Kreuzwieser, G. Purser, J. Van Haren, S. N. Ladd, L. K. Meredith, C. Werner and J. Williams, Nature, 2022, 609, 307–312.
12. C. J. Ebben, S. R. Zorn, S.-B. Lee, P. Artaxo, S. T. Martin and F. M. Geiger, Geophys. Res. Lett., 2011, 38, L16807.
13. J. M. Cash, M. R. Heal, B. Langford and J. Drewer, Environ. Sci.: Processes Impacts, 2016, 18, 1369–1380.
14. G. Y. Stokes, E. H. Chen, A. M. Buchbinder, W. F. Paxton, A. Keeley and F. M. Geiger, J. Am. Chem. Soc., 2009, 131, 13733–13737.
15. K. H. Møller, E. Praske, L. Xu, J. D. Crounse, P. O. Wennberg and H. G. Kjaergaard, J. Phys. Chem. Lett., 2019, 10, 6260–6266.
16. S. N. Elliott, K. B. Moore III, C. R. Mulvihill, A. V. Copan, L. Pratali Maffei and S. J. Klippenstein, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2024, 14, e1710.
17. A. C. Doner, M. M. Davis, A. L. Koritzke, M. G. Christianson, J. M. Turney, H. F. Schaefer, L. Sheps, D. L. Osborn, C. A. Taatjes and B. Rotavera, Int. J. Chem. Kinet., 2021, 53, 127–145.
18. A. C. Doner, J. Zádor and B. Rotavera, Faraday Discuss., 2022, 238, 295–319.
19. Y. Duan, M. Monge-Palacios, E. Grajales-Gonzalez, D. Han and S. M. Sarathy, Fuel, 2022, 326, 125046.
20. S. Y. Mohamed, A. C. Davis, M. J. Al Rashidi and S. M. Sarathy, J. Phys. Chem. A, 2018, 122, 3626–3639.
21. A. D. Danilack, C. R. Mulvihill, S. J. Klippenstein and C. F. Goldsmith, J. Phys. Chem. A, 2021, 125, 8064–8073.
22. Z. Wang, O. Herbinet, N. Hansen and F. Battin-Leclerc, Prog. Energy Combust. Sci., 2019, 73, 132–181.
23. A. V. Copan, K. B. Moore III, S. N. Elliott, C. R. Mulvihill, L. Pratali Maffei and S. J. Klippenstein, J. Phys. Chem. A, 2024, 128, 3711–3725.
24. A. S. Hansen, T. Bhagde, K. B. Moore, D. R. Moberg, A. W. Jasper, Y. Georgievskii, M. F. Vansco, S. J. Klippenstein and M. I. Lester, Science, 2021, 373, 679–682.
25. S. Wang, Y. Zhao, A. W. H. Chan, M. Yao, Z. Chen and J. P. D. Abbatt, Chem. Rev., 2023, 123, 1635–1679.
26. R. L. Caravan, T. J. Bannan, F. A. F. Winiberg, M. A. H. Khan, A. C. Rousso, A. W. Jasper, S. D. Worrall, A. Bacak, P. Artaxo, J. Brito, M. Priestley, J. D. Allan, H. Coe, Y. Ju, D. L. Osborn, N. Hansen, S. J. Klippenstein, D. E. Shallcross, C. A. Taatjes and C. J. Percival, Nat. Geosci., 2024, 17, 219–226.
27. H. J. Curran, Proc. Combust. Inst., 2019, 37, 57–81.
28. J. Zádor, C. A. Taatjes and R. X. Fernandes, Prog. Energy Combust. Sci., 2011, 37, 371–421.
29. K. Moshammer, A. W. Jasper, D. M. Popolan-Vaida, A. Lucassen, P. Diévart, H. Selim, A. J. Eskola, C. A. Taatjes, S. R. Leone and S. M. Sarathy, J. Phys. Chem. A, 2015, 119, 7361–7374.
30. M. Jarraya, A. Bellili, L. Barreau, D. Cubaynes, G. A. Garcia, L. Poisson and M. Hochlaf, Faraday Discuss., 2022, 238, 266–294.
31. Y. Li and F. Qi, Acc. Chem. Res., 2010, 43, 68–78.
32. C. A. Taatjes, N. Hansen, A. McIlroy, J. A. Miller, J. P. Senosiain, S. J. Klippenstein, F. Qi, L. Sheng, Y. Zhang and T. A. Cool, Science, 2005, 308, 1887–1889.
33. B. Yang, C. Huang, L. Wei, J. Wang, L. Sheng, Y. Zhang, F. Qi, W. Zheng and W.-K. Li, Chem. Phys. Lett., 2006, 423, 321–326.
34. D. L. Osborn, P. Zou, H. Johnsen, C. C. Hayden, C. A. Taatjes, V. D. Knyazev, S. W. North, D. S. Peterka, M. Ahmed and S. R. Leone, Rev. Sci. Instrum., 2008, 79, 104103.
35. N. Hansen, T. A. Cool, P. R. Westmoreland and K. Kohse-Höinghaus, Prog. Energy Combust. Sci., 2009, 35, 168–191.
36. F. Battin-Leclerc, O. Herbinet, P.-A. Glaude, R. Fournet, Z. Zhou, L. Deng, H. Guo, M. Xie and F. Qi, Angew. Chem., 2010, 122, 3237–3240.
37. O. Kostko, B. Bandyopadhyay and M. Ahmed, Annu. Rev. Phys. Chem., 2016, 67, 19–40.
38. S. R. Leone, M. Ahmed and K. R. Wilson, Phys. Chem. Chem. Phys., 2010, 12, 6564–6578.
39. I. Fischer and S. T. Pratt, Phys. Chem. Chem. Phys., 2022, 24, 1944–1959.
40. P. Hemberger, A. Bodi, T. Bierkandt, M. Köhler, D. Kaczmarek and T. Kasper, Energy Fuels, 2021, 35, 16265–16302.
41. T. Baer and R. P. Tuckett, Phys. Chem. Chem. Phys., 2017, 19, 9698–9723.
42. J. Pieper, S. Schmitt, C. Hemken, E. Davies, J. Wullenkord, A. Brockhinke, J. Krüger, G. A. Garcia, L. Nahon, A. Lucassen, W. Eisfeld and K. Kohse-Höinghaus, Z. Phys. Chem., 2018, 232, 153–187.
43. X. Mercier, A. Faccinetto, S. Batut, G. Vanhove, D. K. Božanić, H. R. Hróðmarsson, G. A. Garcia and L. Nahon, Phys. Chem. Chem. Phys., 2020, 22, 15926–15944.
44. J. Bourgalais, Z. Gouid, O. Herbinet, G. A. Garcia, P. Arnoux, Z. Wang, L.-S. Tran, G. Vanhove, M. Hochlaf and L. Nahon, Phys. Chem. Chem. Phys., 2020, 22, 1222–1241.
45. B. Sztáray, K. Voronova, K. G. Torma, K. J. Covert, A. Bodi, P. Hemberger, T. Gerber and D. L. Osborn, J. Chem. Phys., 2017, 147, 013944.
46. F. Battin-Leclerc, J. Bourgalais, Z. Gouid, O. Herbinet, G. Garcia, P. Arnoux, Z. Wang, L.-S. Tran, G. Vanhove and L. Nahon, Proc. Combust. Inst., 2021, 38, 309–319.
47. Z. Hu, Q. Di, B. Liu, Y. Li, Y. He, Q. Zhu, Q. Xu, P. Dagaut, N. Hansen, S. M. Sarathy, L. Xing, D. G. Truhlar and Z. Wang, Proc. Natl. Acad. Sci. U.S.A., 2023, 120, e2220131120.
48. V. Yatsyna, R. Mallat, T. Gorn, M. Schmitt, R. Feifel, A. M. Rijs and V. Zhaunerchyk, Phys. Chem. Chem. Phys., 2019, 21, 14126–14132.
49. T. F. Miller, D. C. Clary and A. J. H. M. Meijer, J. Chem. Phys., 2005, 122, 244323.
50. H. Jin, J. Pieper, C. Hemken, E. Bräuer, L. Ruwe and K. Kohse-Höinghaus, Combust. Flame, 2018, 193, 36–53.
51. M. Elkelawy, H. Alm-Eldin Bastawissi, E. A. El Shenawy, M. Taha, H. Panchal and K. K. Sadasivuni, Energy Convers. Manage.: X, 2021, 10, 100058.
52. A. T. Navinprasad, R. Prakash, J. Yoganandh, B. Meenakshipriya and K. Ramakrishnan, IOP Conf. Ser.: Mater. Sci. Eng., 2021, 1070, 012126.
53. A. Rodriguez, O. Herbinet, Z. Wang, F. Qi, C. Fittschen, P. R. Westmoreland and F. Battin-Leclerc, Proc. Combust. Inst., 2017, 36, 333–342.
54. J. Bourgalais, C. Smith Lewin, O. Herbinet, G. A. Garcia, P. Arnoux, L.-S. Tran, G. Vanhove, L. Nahon and F. Battin-Leclerc, Combust. Flame, 2023, 258, 113065.
55. M. Demireva, K. Au and L. Sheps, Phys. Chem. Chem. Phys., 2020, 22, 24649–24661.
56. O. Herbinet and G. Dayma, in Cleaner Combustion, ed. F. Battin-Leclerc, J. M. Simmie and E. Blurock, Springer London, London, 2013, pp. 183–210.
57. X. Tang, G. A. Garcia, J.-F. Gil and L. Nahon, Rev. Sci. Instrum., 2015, 86, 123108.
58. J. C. Poully, J. P. Schermann, N. Nieuwjaer, F. Lecomte, G. Grégoire, C. Desfrançois, G. A. Garcia, L. Nahon, D. Nandi, L. Poisson and M. Hochlaf, Phys. Chem. Chem. Phys., 2010, 12, 3566.
59. F. Jorand, A. Heiss, O. Perrin, K. Sahetchian, L. Kerhoas and J. Einhorn, Int. J. Chem. Kinet., 2003, 35, 354–366.
60. J. Huang, C. Huang, Q. Hou, M. Wu, X. Wu, Y. Zhang, G. Tian and F. Zhang, Combust. Flame, 2022, 112490.
61. S. Hartweg, G. A. Garcia and L. Nahon, J. Phys. Chem. A, 2021, 125, 4882–4887.
62. J. Bourgalais, Z. Jiang, J. Bloino, O. Herbinet, H.-H. Carstensen, G. A. Garcia, P. Arnoux, L.-S. Tran, G. Vanhove, L. Nahon, F. Battin-Leclerc and M. Hochlaf, Phys. Chem. Chem. Phys., 2022, 24, 10826.
63. P. Hemberger, X. Wu, Z. Pan and A. Bodi, J. Phys. Chem. A, 2022, 126, 2196–2210.
64. C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493.
65. T. Lu, Molclus program, version 1.12, https://www.keinsci.com/research/molclus.html.
66. S. J. Klippenstein, Faraday Discuss., 2022, 238, 11–67.
67. S. N. Elliott, C. R. Mulvihill, M. K. Ghosh, H. J. Curran and S. J. Klippenstein, Proc. Combust. Inst., 2024, 40, 105618.
68. L. Zhu, S. Panigrahy, S. N. Elliott, S. J. Klippenstein, M. Baigmohammadi, A. A. E.-S. Mohamed, J. W. Hargis, S. Alturaifi, O. Mathieu, E. L. Petersen, K. A. Heufer, A. Ramalingam, Z. Wang and H. J. Curran, Combust. Flame, 2023, 248, 112562.
69. O. Isayev, L. Gorb and J. Leszczynski, J. Comput. Chem., 2007, 28, 1598–1609.
70. J. C. Faver, W. Yang and K. M. Merz, J. Chem. Theory Comput., 2012, 8, 3769–3776.
71. M. Bobeldijk, W. J. van der Zande and P. G. Kistemaker, Chem. Phys., 1994, 179, 125–130.
72. A. Rodriguez, O. Herbinet, X. Meng, C. Fittschen, Z. Wang, L. Xing, L. Zhang and F. Battin-Leclerc, J. Phys. Chem. A, 2017, 121, 1861–1876.
73. J. Bugler, A. Rodriguez, O. Herbinet, F. Battin-Leclerc, C. Togbé, G. Dayma, P. Dagaut and H. J. Curran, Proc. Combust. Inst., 2017, 36, 441–448.
74. A. Cuoci, A. Frassoldati, T. Faravelli and E. Ranzi, Energy Fuels, 2013, 27, 7730–7753.
75. A. Cuoci, A. Frassoldati, T. Faravelli and E. Ranzi, Comput. Phys. Commun., 2015, 192, 237–264.
76. E. E. Rennie, A.-M. Boulanger, P. M. Mayer, D. M. P. Holland, D. A. Shaw, L. Cooper and L. G. Shpinkova, J. Phys. Chem. A, 2006, 110, 8663–8675.
77. K. Moshammer, A. W. Jasper, D. M. Popolan-Vaida, Z. Wang, V. S. Bhavani Shankar, L. Ruwe, C. A. Taatjes, P. Dagaut and N. Hansen, J. Phys. Chem. A, 2016, 120, 7890–7901.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04184d

---