Calculating and analyzing the relationship between thermal conductivity and microstructure in rare-earth doped fluoride crystals

Abstract

Rare earth (RE) ion-doped fluoride crystals have shown great application potential in various fields, attracting the attention of many researchers. The abnormal thermal transformation behavior of RE ion-doped fluoride crystals leads to the singularity and weakness in their application fields. Here, the influence of different structural characteristics of RE ion-doped fluoride crystals on the variation of thermal conductivity is further analyzed using phonon scattering calculation. Firstly, based on the effect of the phonon scattering mechanism on the thermal conductivity of RE ion-doped fluoride, a comprehensive analysis examines the diverse factors that affect the abnormal thermal behavior of different doping types and fluoride crystals. The actual thermal conductivity characteristics are predicted to optimize the crystal performance in various application fields of RE ion-doped fluoride crystals. Next, the influence mechanism of the mass and radius difference caused by RE ion doping structure on the thermal conductivity of RE ion-doped fluorides is thoroughly investigated. Ultimately, a theoretical foundation for the behavior and influence of disorder crystals' thermal conductivity is established.

---

1 Introduction

RE ion-doped fluoride crystals have garnered significant interest owing to their remarkable capabilities in lasers, TBCs, thermoelectric materials, and other domains.^1–7 Among these, thermal behavior is a crucial property that restricts the application of RE ion-doped fluoride crystals. Thermal conductivity requires additional optimization based on the application fields.^8,9 The thermal conductivity of RE ion-doped fluoride shows abnormal behavior. When RE ions are inserted in fluoride crystals, the thermal conductivity exhibits significant abnormal characteristics. For instance, when Yb³⁺ ions are doped at 0.1 at%, the thermal conductivity drops by 50% compared to pure CaF₂ crystals. At this stage, the thermal conductivity of the 0.1 at% Yb:CaF₂ crystal remains in line with the traditional trend, where thermal conductivity decreases with increasing temperature. When the doping concentration of Yb:CaF₂ in the crystal exceeds 1 at%, its thermal conductivity no longer follows the traditional crystalline material behavior, instead exhibiting glass-like thermal conductivity. In other words, as the doping concentration increases, the thermal conductivity of RE ion-doped fluoride single crystals transitions from a crystalline to an amorphous (glass) state, exhibiting glass-like thermal conductivity.^10,11 In previous works,^12–15 rare earth ions (RE³⁺) were substituted for the intrinsic cationic ions (Ca²⁺/Sr²⁺/Ba²⁺) in the RE-doped fluoride crystal structure. This heterovalent substitution leads to charge imbalance, introducing interstitial fluoride ions and resulting in a single substitutional point defect. As the doping concentration increases, the number of rare earth ion clusters increases, attributed to the aggregation of single substitutional point defects through dipole interactions. The evolution of clusters under varying doping concentrations has been calculated.^16–19 Single substitutional point defects dominate in crystals with doping concentrations below 0.1 at%, whereas crystals with doping concentrations exceeding 1 at% predominantly contain clusters. Therefore, the structural evolution is closely linked to the changes in the thermal conductivity behavior of RE ion-doped fluoride crystals.^20,21 Among them, the primary reason for the continuous change in thermal conductivity between crystalline and amorphous states with concentration is that in RE ion-doped fluorides, disordered structures like point defects and clusters coexist with the original fluoride lattice order structure, which leads to the competition between defect phonon scattering and phonon–phonon scattering with concentration.

Therefore, based on the point defects and cluster structure transformation, the effects of various cluster structures generated by RE ion-doped fluoride crystals at different doping concentrations on the thermal conductivity are explored by phonon scattering coefficient calculation. The influences of different doping ions and fluoride matrices in RE ion-doped fluoride crystals on thermal conductivity are provided.^22,23 In different RE ion-doped fluoride systems, the calculated results of the phonon scattering coefficient have a favorable correlation with the variation of thermal conductivity of RE ion-doped fluoride crystals, providing a qualitative explanation for the abnormal thermal behavior of RE ion-doped fluoride crystals.²⁴ In addition, the differences between RE ions and lattice ions in RE ion-doped fluoride are analyzed by using the intrinsic characteristics of various cluster structures. The impact of variations in mass and radius on thermal conductivity is thoroughly discussed. The refinement and classification of the mass field and strain field on the glass state transition of thermal conductivity are explored, and the factors influencing the transition from a crystalline state to an amorphous state of RE ion-doped fluoride crystals are provided with a detailed explanation.

The above research has important guiding significance for analyzing the cause of abnormal thermal conductivity of rare earth ion doped fluoride and other disordered crystals and estimating the trend of thermal conductivity change.

2 The microstructure influences the thermal conductivity of RE ion-doped fluoride crystals

The insertion of RE ions into fluoride crystals significantly alters the system's microstructure, leading to an abnormal variation in thermal conductivity. According to the variation trend of thermal conductivity with doping concentration, it can be divided into two stages. With lower doping concentrations (<1 at%), the RE ion-doped fluoride systems mainly generate point defects and exhibit a transition in thermal conductivity between a crystalline state and a crystalline-like state. At high doping concentrations (>1 at%), the complex cluster structure predominantly influences the thermal conductivity of RE ion-doped fluorides, displaying thermal behavior comparable to that of glass. The influences of point defects and clusters on the thermal conductivity of RE ion-doped fluoride crystals are discussed.

A parameter called the phonon scattering coefficient is introduced to describe the thermal behavior of RE ion-doped fluorides.²⁴ The decisive factor of phonon scattering is the structure modification of RE ion-doped fluorides, which shows the variation trends of the mass and radius with doping. The phonon scattering coefficient is calculated by eqn (1). The thermal conductivity of the fluoride crystals is related to the scattering of phonons, as shown in eqn (2).²⁴ Hence, the phonon scattering coefficient reveals the relationship between the microstructure and the thermal conductivity variation in RE ion-doped fluorides.

κ ∝ Γ^−0.5 (2)

where i represents the element species of RE ion-doped fluorides; x stands for the proportion of elements; M represents the atomic mass of RE ion-doped fluorides; δ stands for the ion radius of RE ion-doped fluorides.

2.1 Point defects influence RE ion-doped fluorides' thermal conductivity with low doping concentration

When doping a modest amount of RE ions, the doped fluoride systems produce point defects, which cause progressive disorder, intense phonon scattering, and diminished thermal conductivity. The relationship between the point defect phonon scattering coefficients of doped CaF₂, SrF₂, and BaF₂, with different kinds of RE dopants, with concentration is calculated according to eqn (1), as shown in Fig. 1, to investigate the variation of the point defect phonon scattering coefficients in fluoride crystals with doping RE ions. Fig. 1a shows that the point defect phonon scattering coefficients change approximately as a linear function relation with the concentration when the doping concentration is less than 0.1 at%. Next, the increasing trends of point defect phonon scattering coefficients steadily slow down as the doping concentration increases. When reaching a certain doping concentration, the point defect phonon scattering coefficients are close to a maximum value. In other words, the point defects significantly impact the RE:CaF₂ systems' thermal conductivity at this concentration. The point defects caused by the doping of RE ions start to transform into clusters under the influence of dipole interaction, and the factors of clusters on the thermal conductivity then start to dominate.¹⁷

Fig. 1 (a) Point defect phonon scattering coefficients of RE:CaF₂ crystals with doping concentration; (b) point defect phonon scattering coefficients of RE:SrF₂ crystals with doping concentration; (c) point defect phonon scattering coefficients of RE:BaF₂ crystals with doping concentration.

Furthermore, the point defect phonon scattering coefficients increase with the number of doped RE atoms rising, as indicated by the curve variation rule in Fig. 1a. This phenomenon may be due to the gradual increase in the difference between the mass and radius of RE ions and the lattice calcium ions. As a result, the system's mass field and strain field fluctuations enhance, lattice distortion and disorder degree surrounding RE ions increase, and the phonon scattering becomes intense.^25–27 By comparing the point defect phonon scattering coefficients with the atomic number of different fluoride crystals doped with RE ions, similar conclusions can also be obtained in RE ion-doped SrF₂ crystal systems (Fig. 1b). Whereas, the scattering coefficients of point defect phonons of RE ion-doped BaF₂ crystals are slightly opposite to that of CaF₂ and SrF₂ systems (Fig. 1c). Among them, the point defect phonon scattering coefficient of the Y:BaF₂ system is significantly larger than that of the BaF₂ crystals doped with lanthanide RE ions.²⁸ The main reason is that the mass and radius difference between Y³⁺ and Ba²⁺ is greater than tho of the lanthanide RE ions and Ba²⁺, while the mass and radius difference between Y and Ca/Sr ions is smaller than that between lanthanide RE ions and Ca/Sr ions.

The variation trends and maximum values of the point defect phonon scattering coefficient differ for various fluoride systems. According to Fig. 2, the point defect phonon scattering coefficient in RE ion-doped CaF₂ crystals changes sharply with doping concentration. Compared with the SrF₂ and BaF₂ systems, the RE ion-doped CaF₂ systems have higher peak values of the point defect phonon scattering coefficients. Moreover, the doping concentration of CaF₂ crystals is the lowest when it reaches the peak of the point-defect phonon scattering coefficient (Fig. 1). In other terms, CaF₂ crystals embedded with RE ions are more likely to produce point defects to cluster transformation, resulting in more severe phonon scattering.

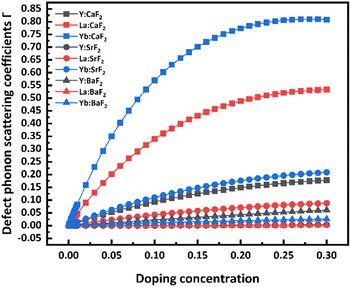Fig. 2 Point defect phonon scattering coefficients of Y/La/Yb:Ca/Sr/BaF₂ crystals with doping concentration.

The relationship between the point defect phonon scattering coefficient and thermal conductivity of RE ion-doped fluorides can be semi-quantitatively analyzed²¹ by a functional relationship (eqn (2)).²⁹Fig. 3 illustrates the variation rule of thermal conductivity that can be derived by the point defect phonon scattering coefficient of RE ion-doped Ca/Sr/BaF₂ (Fig. 1). At the doping concentration of ≤1 at%, the thermal conductivity rapidly decreases, and then is stable with the doping concentration rising.^26,30

Fig. 3 (a) Variation law of thermal conductivity of RE:CaF₂ crystals with doping concentration; (b) variation law of thermal conductivity of RE:SrF₂ crystals with doping concentration; (c) variation law of thermal conductivity of RE:BaF₂ crystals with doping concentration.

The increasing doping atomic number leads to an obvious changing trend of thermal conductivity and inferior thermal conductivity values. At low concentrations, the thermal conductivity of RE ion-doped fluorides varies dramatically due to the change in atomic types. However, as the doping concentration increases, the difference in fluoride systems' thermal conductivity with different atomic types becomes less noticeable. For different fluoride systems, the changing trend of thermal conductivity of CaF₂ crystals is more significant and the thermal conductivity value reduces drastically. Additionally, the glass-like thermal conductivity transition of RE ion-doped fluorides is qualitatively explored by contrasting the calculated and measured thermal conductivity values.

Firstly, by comparing the doping of different kinds of RE ions, the 0.5 at% Yb:CaF₂ has been transformed into having glass-like thermal conductivity, while the glass-like thermal conductivity of 1 at% Ce:CaF₂ is not distinct. Therefore, RE ion-doped fluoride systems with large atomic numbers are prone to glass-like thermal conductivity behavior. This is consistent with the previous conclusion that fluoride crystals with large atomic numbers have low thermal conductivity and considerable phonon scattering.

The CaF₂ crystal system has strong point defect phonon scattering, the thermal conductivity value decreases rapidly, and the transition from crystalline to amorphous thermal conductivity is more likely to occur under the same doping concentrations and types of doping atoms when only evaluating the doping concentration without taking the influence of the fluoride matrix on thermal conductivity. The variation of thermal conductivity is shown in Fig. 4 (red dotted lines). The thermal conductivity drops substantially with the large point defect phonon scattering coefficient in the RE ion-doped CaF₂ systems, which also has a similar relationship with the above-mentioned.^10,31–34

Fig. 4 (a) Thermal conductivity of Ce:Ca/BaF₂ crystals with temperature (low doping concentration); (b) thermal conductivity of Yb:Ca/Sr/BaF₂ crystals with temperature (low doping concentration).

2.2 Clusters influence RE ion-doped fluorides' thermal conductivity with high doping concentration

It is assumed that the configurations of clusters change to the highest order under extremely high doping concentrations. According to eqn (1), the variation laws of the cluster phonon scattering coefficient with concentration are calculated, as shown in Fig. 5. The cluster phonon scattering coefficient in RE ion-doped fluoride crystals grows progressively and shows a great increasing trend as the concentration increases.

Fig. 5 (a) Cluster phonon scattering coefficients of RE:CaF₂ crystals with doping concentration; (b) cluster phonon scattering coefficients of RE:SrF₂ crystals with doping concentration.

This phenomenon indicates that cluster phonon scattering has an additive effect as the number of clusters increases, which causes extreme changes in thermal conductivity and the transition from a crystalline to an amorphous state. In addition, the cluster scattering coefficient increases with the atomic number of doped RE ions, which exerts enormous influences on the thermal conductivity of crystals (according to eqn (2)).^35,36 Depending on the difference in doping atomic types, the thermal conductivity is connected to the phonon scattering coefficients of highest-order cluster configurations. For the lanthanide RE elements with small atomic numbers, the highest-order clusters of the RE ion-doped fluoride systems have relatively small order and simple configurations. As shown in Fig. 5a, the highest-order clusters are a tetramer, and the cluster phonon scattering coefficients are low when the doped RE ions are La, Ce, Pr, and other low atomic number elements, which has little influence on the change trend and value of thermal conductivity. However, the highest-order cluster is a hexamer when the doped RE ions are Ho, Er, Yb, and Lu. The increase of cluster phonon scattering coefficients causes the thermal conductivity to transition into an amorphous state.^24,36

As illustrated in Fig. 6, the influences of various cluster structure types on the cluster phonon scattering and thermal conductivity are examined. In the La/Nd/Gd:Ca/SrF₂ crystal systems, the cluster phonon scattering coefficients of all kinds of cluster configurations are gradually enhanced with doping concentration, and the growth rate accelerates dramatically at high concentrations. It is demonstrated that the increase of doping concentration has a beneficial effect on the cluster phonon scattering coefficient, the aggregation degree increases rapidly, the thermal conductivity exhibits a significant amorphous change, and thermal conductivity values fall abruptly.

Fig. 6 (a) Cluster phonon scattering coefficients of La:Ca/SrF₂ crystals with doping concentration; (b) cluster phonon scattering coefficients of Nd:Ca/SrF₂ crystals with doping concentration; (c) cluster phonon scattering coefficients of Gd:Ca/SrF₂ crystals with doping concentration.

Furthermore, under the same concentration of RE ion doping, the cluster configuration progressively becomes more complex, indicating that the cluster phonon scattering coefficient increases. The cluster configuration gradually transforms from a monomer to a higher-order configuration, such as a dimer, trimer, tetramer, or pentamer, and the cluster phonon scattering steadily enhances. In a word, the doping concentration of RE ions and intricate cluster configuration result in phonon scattering, which leads to the enhancement of thermal resistance and the decrease of thermal conductivity. To further study the influence mechanism of different kinds of fluoride matrices on the thermal conductivity in RE ion-doped fluorides, Y:CaF₂, Y:SrF₂, and Y:BaF₂ are taken as examples, as illustrated in Fig. 7. This further proves the impact of doping concentrations and cluster types on thermal conductivity. The thermal conductivity declines abruptly in complex clusters and high doping concentrations. For various fluoride matrices, the cluster phonon scattering coefficient of the Y:CaF₂ system changes strongly with doping concentration and doping has an obvious negative effect on heat transfer behavior. The relationship between the scattering coefficient of cluster phonons and thermal conductivity will not be demonstrated again, since the relationship between phonon scattering and thermal conductivity is already provided in eqn (2) and explained in 2.1 above. Next, the heat transfer of glass-like thermal conductivity in fluoride systems is analyzed by comparing the calculated thermal conductivity values with the measured thermal conductivity data.^26,30

Fig. 7 Cluster phonon scattering coefficients of Y:Ca/Sr/BaF₂ crystals with doping concentration.

Initially, the system's thermal conductivity transitions into a glass-like thermal behavior when the doping concentration is ≤1 at%. The 1 at% Ce:BaF₂ and 1 at% Yb:BaF₂ both show crystalline thermal conductivity behavior, however the thermal conductivity of 1 at% Ce:CaF₂ and 1 at% Yb:CaF₂ has started to change to a glass-like state. Among them, 1 at% Yb:CaF₂ has a more apparent glass-like thermal conductivity than 1 at% Ce:CaF₂, as demonstrated in Fig. 8a and b (purple dotted lines). The thermal conductivity behavior is negatively impacted by atomic number and it is relatively easy to obtain a thermal conductivity behavior similar to that of glass. It is deduced that the thermal conductivity of RE ion-doped fluoride systems can transition from a crystalline state to a non-crystalline state within a critical value, which is approximately 1 at%. It is also confirmed that the cluster phonon scattering coefficients of RE ion-doped CaF₂ systems are higher in each cluster configuration than those of the SrF₂ systems. RE ion doping on CaF₂ crystals are more likely to produce a transition from crystalline thermal conductivity to amorphous thermal conductivity.

Fig. 8 (a) Thermal conductivity of Ce:Ca/BaF₂ crystals with temperature (high doping concentration); (b) thermal conductivity of Yb:Ca/Sr/BaF₂ crystals with temperature (high doping concentration); (c) thermal conductivity of Ca/Sr/BaF₂ crystals with temperature.

As illustrated in Fig. 8a and b (yellow dotted lines), the thermal conductivity of Ce/Yb:CaF₂ in the high-temperature region is greater than that of Ce/Yb:BaF₂, despite the system's thermal conductivity changing to a glass-like thermal conductivity with high doping concentration. The impact mechanism of the fluoride matrix on thermal conductivity is necessary and the effect of RE ion doping on thermal conductivity cannot be the only one considered. The BaF₂ pure crystals have a lower thermal conductivity than CaF₂, as Fig. 8c illustrates. The direct effect of the fluoride matrix on the thermal conductivity trend cannot be entirely reversed by doping RE ions, even though the thermal conductivity declines through doping RE ions. As a result, the thermal conductivity of La/Yb:BaF₂ is lower.^10,31–34

Therefore, the effect of phonon scattering on the thermal conductivity of RE ion-doped fluoride crystals is shown in Fig. 9. The structure of the dominant phonon scattering ranges from single-point defects to clusters, leading to a reduction in crystalline thermal conductivity while amorphous thermal conductivity increases. Consequently, the overall thermal conductivity evolves into a glass-like state.

Fig. 9 Phonon scattering and thermal conductivity of RE-ion doped fluoride crystals.

3 Influence of different concentration mass and radius phonon scattering on thermal conductivity of RE ion-doped fluoride crystals

The phonon scattering coefficient primarily includes radius scattering and mass scattering in the system structure, as shown in eqn (1), which states that the thermal conductivity values of RE ion-doped fluoride crystals are closely related to the difference of mass and radius in the microstructure, such as point defects and clusters. The mechanism of mass scattering and radius scattering in different structures (point defect and cluster) of RE ion-doped fluoride crystals are researched, and the relationship between the variation of thermal conductivity of RE ion-doped fluoride and the microstructure of mass and radius is described.^37–42

3.1 Influence of low-concentration mass and radius phonon scattering on thermal conductivity

The RE ion replacement and interstitial fluoride ion compensation appear in the doped calcium fluoride system at low doping concentrations, resulting in a high concentration of point defects. The formation of point defects causes the shortwave phonon scattering of RE ion-doped fluoride to increase, and the thermal conductivity values reduce. The impact of radius and mass scattering on the thermal conductivity of RE ion-doped fluoride is concretely studied based on the point defect phonon scattering in 2.1 above.

As illustrated in Fig. 10 and 1a, the mass scattering and total scattering of RE ion-doped CaF₂ exhibit comparable variation tendencies and approximately equal values. The mass scattering values of RE ion-doped CaF₂ are significantly greater than the radius scattering values. Therefore, the mass difference between RE ions and lattice Ca ions is dominant. The mass phonon scattering of RE ion-doped CaF₂ influences the heat conduction behavior, the system's thermal conductivity changes from a crystalline state to a crystal-like state, and the thermal conductivity value reduces but the changing trend does not significantly alter. Furthermore, when the doping concentration of RE ions increases, the mass scattering of the doped CaF₂ growth trend gradually slows down, and the radius scattering growth trend steadily increases. The radius scattering of RE ion-doped CaF₂ could have a significant impact on the thermal conductivity from a crystal-like state to a glass-like state with high doping concentration.^40,43,44 For different RE ion doping, both mass and radius scattering increase with the increase of atomic number, which is consistent with the variation rule of the total phonon scattering coefficient. As demonstrated in the ESI,† comparable results have also been reached for SrF₂ and BaF₂ systems doped with RE ions (Fig. S1 and S2†).

Fig. 10 (a) Mass phonon scattering coefficients of RE:CaF₂ crystals with low doping concentration; (b) radius phonon scattering coefficients of RE:CaF₂ crystals with low doping concentration.

The mass and radius phonon scattering coefficients of low doping Y/La/Yb:Ca/Sr/BaF₂ systems are extracted, and the thermal conductivity of various fluoride matrices is proved, as shown in Fig. 11. For the different fluoride matrices, the CaF₂ inset with RE ions has the highest mass phonon scattering coefficients (Fig. 11a). However, the largest radius scattering coefficient is seen in the RE ion-doped BaF₂, as shown in Fig. 11b. The radius and mass scattering coefficients are opposite influences on the fluoride matrices with low doping concentrations. Compared to the radius scattering coefficient, the mass scattering coefficient is substantially greater.

Fig. 11 (a) Mass phonon scattering coefficients of Y/La/Yb:Ca/Sr/BaF₂ crystals with low doping concentration; (b) radius phonon scattering coefficients of Y/La/Yb:Ca/Sr/BaF₂ crystals with low doping concentration.

Hence, the mass scattering coefficient displays a profound impact on thermal conductivity. In the low doping concentration, the calcium fluoride systems' thermal conductivity diminishes, resulting in heat transfer behavior that is similar to that of the crystal.

The contribution of mass scattering and radius scattering of RE ion-doped fluoride to the thermal conductivity at low doping concentration is investigated, as shown in Fig. 12, as the thermal conductivity can be calculated using eqn (2).²⁹ When the doping concentration is less than 1 at%, the impact of mass and radius phonon scattering on thermal conductivity is noticeable. The variation trend of thermal conductivity is steadily stable with doping concentration when the doping concentration is more than 1 at%. Similar to the total defect phonon scattering, mass phonon scattering has a considerable influence on thermal conductivity, leading to the decline of thermal conductivity. The thermal conductivity is barely impacted by radius phonon scattering.^45,46 In addition, the thermal conductivity estimated by mass and radius scattering coefficients is low when various RE ion species have large RE atomic numbers. For RE ion-doped SrF₂ and BaF₂ systems, there is a comparable variation tendency (see Fig. S3 and S4†).

Fig. 12 (a) Variation law of thermal conductivity of RE:CaF₂ crystals in mass phonon scattering coefficients with low doping concentration; (b) variation law of thermal conductivity of RE:CaF₂ crystals in radius phonon scattering coefficients with low doping concentration.

3.2 Influence of high-concentration mass and radius phonon scattering on thermal conductivity

Under high-concentration doping, the point defects of RE ions gradually gather to form clusters, leading to the scattering of long-wavelength phonons, which reduce the thermal conductivity and further transform into an amorphous state. Based on the cluster phonon scattering coefficients in 2.2 above, the specific influence factors and value ranges of cluster mass scattering and radius scattering on the thermal conductivity of RE ion-doped fluoride are investigated, for example, the CaF₂ systems. Due to the high doping concentrations, the crystal systems form several different kinds of clusters. The mass and radius scattering coefficients are calculated by taking the highest-order cluster as an example. Fig. 13 illustrates that mass and radius phonon scattering steadily enhance with high doping concentration and atomic number, which exerts the opposite influence on the doped fluoride systems' thermal conductivity. Moreover, the changing trend of both the mass and radius scattering coefficients with doping concentration are comparable to total defect phonon scattering (Fig. 5a). The cluster radius phonon scattering coefficients are larger than the cluster mass phonon scattering coefficients. Then, the cluster radius phonon scattering coefficients vary considerably more than that of point defects. Consequently, the radius scattering is sensitive to cluster generation behavior. The impact of radius scattering on the trend change in the thermal conductivity of RE ion-doped fluoride (from crystalline to amorphous thermal conductivity) is necessary, and it plays a major role.^47–49 The mass and radius scattering of the highest-order clusters grows with the increasing atomic number for various RE ion doping. The system of SrF₂ doped with RE ions exhibits the same conclusions (Fig. S5†).

Fig. 13 (a) Mass phonon scattering coefficients of RE:CaF₂ crystals with high doping concentration; (b) radius phonon scattering coefficients of RE:CaF₂ crystals with high doping concentration.

Next, fluoride systems that generate various types of clusters are analyzed to further demonstrate the effects of mass phonon scattering and radius phonon scattering of clusters on the thermal conductivity of different crystal systems (Fig. 14). The mass and radius phonon scattering increase and the heat transfer reaction decreases as cluster complexity (from monomer to highest-order cluster) increases. Conversely, with SrF₂ and BaF₂ crystals, CaF₂ crystals possess larger cluster mass and radius scattering values. The RE ion-doped CaF₂ crystal is easier to alter to the glass-like state, further demonstrating the critical role that cluster phonon scattering plays in reducing thermal conductivity and achieving glass-like thermal behavior.

Fig. 14 (a) Mass phonon scattering coefficients of Y:Ca/Sr/BaF₂ crystals with high doping concentration; (b) radius phonon scattering coefficients of Y:Ca/Sr/BaF₂ crystals with high doping concentration.

Using eqn (1), the effect of cluster mass and radius differences on thermal conductivity is further evaluated. Fig. 15 shows the trend of Y:Ca/Sr/BaF₂ thermal conductivity with doping concentration. The considerable changes in thermal conductivity induced by the radius phonon scattering coefficient with doping concentration shows that the radius difference positively affects the thermal conductivity of RE ion-doped fluoride at high doping concentrations. Among them, the radius scattering of various cluster types has a regular influence on the thermal conductivity of RE ion-doped fluoride. The highest-order cluster has a more substantial impact on thermal conductivity. The difference in radius scattering of various fluoride matrices on thermal conductivity is not easily observed. It is further demonstrated that radius phonon scattering makes the thermal conductivity transition to an amorphous state during the generation of clusters. Moreover, the mass and radius phonon scattering increase as the cluster combination degree increases. Under mass scattering and radius scattering, RE ion-doped fluoride's thermal conductivity exhibits abnormal thermal behavior. For different fluoride matrices, the thermal conductivity results due to mass and radius scattering of calcium fluoride are at the lowest value.^45,48–53

Fig. 15 (a) Variation law of thermal conductivity of Y:Ca/Sr/BaF₂ crystals in mass phonon scattering coefficients with high doping concentration; (b) variation law of thermal conductivity of Y:Ca/Sr/BaF₂ crystals in radius phonon scattering coefficients with high doping concentration.

Therefore, the effects of mass scattering and radius scattering on the thermal conductivity of RE ion-doped fluoride crystals are shown in Fig. 16. The radius phonon scattering affects the amorphous thermal conductivity transition of fluoride crystals, while the mass phonon scattering only results in the decrease of the thermal conductivity.

Fig. 16 Mass phonon scattering and radius phonon scattering and RE ion-doped fluoride crystal thermal conductivity.

4 Conclusions

In conclusion, the investigation of RE ion-doped fluoride's abnormal thermal conductivity has been conducted, accompanying a thorough examination of the interaction between phonon scattering and thermal conductivity. Firstly, under different RE ions and fluoride matrices, the impact of diverse point defects and cluster structures at varying concentrations on thermal conductivity is explored. The relationship between the calculated thermal conductivity of phonon scattering and the actual measured thermal conductivity data has been analyzed. Furthermore, the influence of phonon scattering caused by the difference in mass and radius on the abnormal thermal properties of RE-doped fluoride has been systematically explored.

The phonon scattering coefficient calculation has demonstrated that the thermal conductivity of fluoride crystals diminishes with increasing doping concentration and atomic number, which can rapidly transition into a glass-like state. The complexity and superposition of the clusters also lead to a decline in the thermal conductivity of RE ion-doped fluoride at high concentrations. Next, for various fluoride crystals, it has been discovered that CaF₂ crystals doped with RE ions are more susceptible to the formation concentration of clusters, leading to a transition of the glass-like thermal conductivity. Due to the large mass of Ba atoms in the BaF₂ crystal, the thermal conductivity of RE ion-doped BaF₂ is not easy to transition to a glass-like state, but the thermal conductivity value is always at a lower value. Moreover, the calculated thermal conductivity of phonon scattering matches well with the actual measured thermal conductivity data.

Additionally, it has been discovered that the thermal characteristics of RE ion-doped fluoride crystals are influenced by the mass and radius discrepancies between RE-doped ions and lattice ions in a variety of point defects and cluster structures. Among them, under the different concentrations, the variation in mass and radius causes the RE ion-doped fluoride's thermal conductivity to decrease. However, after the generation of clusters in high doping concentration, the radius scattering coefficient's variation degree is more than the mass scattering coefficient compared to the point defect with low concentration. This is mainly because of the radius disorder caused by the alteration in ionic radius, and this distortion of the lattice exhibits an association with the amorphous transformation of thermal conductivity. For various fluoride systems, the CaF₂ crystal has the highest mass scattering coefficient. Whereas CaF₂ has the biggest radius scattering coefficient at high concentrations, BaF₂ has the largest at low concentrations. These factors cause the system structure to become disordered, which finally causes the thermal conductivity of RE ion-doped fluorides to change to an amorphous state.

Thus, the thermal behavior of RE ion-doped fluoride can be universality calculated and analyzed using the phonon scattering coefficient, which also offers theoretical support for other research fields on RE ion-doped fluoride systems. Consequently, further research on the heat conduction of RE ion-doped fluoride will better integrate theoretical simulations with experimental tests, creating the way for thorough thermal analyses of the RE ion-doped fluoride crystals and extending the range of applications.

Next, there are two specific suggestions for studying the thermal behavior of RE ion-doped fluoride crystals. Firstly, the influence of different cluster structures, doping concentration, and thermal conductivity is still in the preliminary stage, and it is difficult to directly reveal the specific evolution law of cluster structure and the changing trend of thermal conductivity under different concentrations. Mainly, additional investigation and validation are necessary due to the lack of intuitive structural characterization. In addition, the accuracy of the cross-scale study between the calculated thermal conductivity using the microstructure and the measured thermal conductivity needs to be further improved, in the relationship between the temperature and concentration needs to be explored.

Data availability

Data for this article, including thermal conductivity data are available at the following DOIs. The details are listed in the references.

https://doi.org/10.1134/s102833580804006x.

https://doi.org/10.1134/s1028335814050036.

https://doi.org/10.1134/s1063774515050107.

https://doi.org/10.1134/s1063774517020225.

https://doi.org/10.1134/s1028335808080016.

https://doi.org/10.1134/s1028335808070045.

Author contributions

Investigation, data curation, validation, formal analysis, and writing – original draft (Kexin Liu); resources, supervision, funding acquisition, project administration, and writing – review & editing (Dapeng Jiang, Gang Bian and Liangbi Su). All authors participated in discussing and editing the manuscripts.

Conflicts of interest

There is no conflict of interest in this manuscript.

Acknowledgements

This work has been financially supported by the National Key Technologies R&D Program (2023YFB3507403), the National Natural Science Foundation of China (61925508), the Science and Technology Commission of Shanghai Municipality (23511102700), and the CAS Project for Young Scientists in Basic Research (YSBR-024).

Notes and references

1. J. Zhou, G. Chen, E. Wu, G. Bi, B. Wu, Y. Teng, S. Zhou and J. Qiu, Nano Lett., 2013, 13, 2241–2246.
2. Q. Y. Zhang and X. Y. Huang, Prog. Mater. Sci., 2010, 55, 353–427.
3. M. Runowski, N. Stopikowska, D. Szeremeta, S. Goderski, M. Skwierczynska and S. Lis, ACS Appl. Mater. Interfaces, 2019, 11, 13389–13396.
4. L. Zhu, Z. Zhang, Y. Wang, H. Ding, D. Jiang, Y. Zhao, G. Xie, J. Xu and L. Su, Opt. Lett., 2024, 49, 4286–4289.
5. Y. Kenzhebayeva, I. Gorbunova, A. Dolgopolov, M. V. Dmitriev, T. S. Atabaev, E. A. Stepanidenko, A. S. Efimova, A. S. Novikov, S. Shipilovskikh and V. A. Milichko, Adv. Photonics Res., 2024, 5, 2300173.
6. N. A. Zhestkij, A. S. Efimova, Y. Kenzhebayeva, M. V. Dmitriev, A. S. Novikov, I. D. Yushina, A. Krylov, M. V. Timofeeva, A. N. Kulakova, N. V. Glebova, A. A. Krasilin, S. A. Shipilovskih and V. A. Milichko, Adv. Opt. Mater., 2023, 11, 2300881.
7. Y. A. Mezenov, S. Bruyere, A. Krasilin, E. Khrapova, S. V. Bachinin, P. V. Alekseevskiy, S. Shipiloskikh, P. Boulet, S. Hupont, A. Nomine, B. Vigolo, A. S. Novikov, T. Belmonte and V. A. Milichko, Inorg. Chem., 2022, 61, 13992–14003.
8. N. Kulachenkov, M. Barsukova, P. Alekseevskiy, A. A. Sapianik, M. Sergeev, A. Yankin, A. A. Krasilin, S. Bachinin, S. Shipilovskikh, P. Poturaev, N. Medvedeva, E. Denislamova, P. S. Zelenovskiy, V. V. Shilovskikh, Y. Kenzhebayeva, A. Efimova, A. S. Novikov, A. Lunev, V. P. Fedin and V. A. Milichko, Nano Lett., 2022, 22, 6972–6981.
9. A. N. Usoltsev, T. S. Sukhikh, A. S. Novikov, V. R. Shayapov, D. P. Pishchur, I. V. Korolkov, I. F. Sakhapov, V. P. Fedin, M. N. Sokolov and S. A. Adonin, Inorg. Chem., 2021, 60, 2797–2804.
10. P. A. Popov, P. P. Fedorov, S. V. Kuznetsov, V. A. Konyushkin, V. V. Osiko and T. T. Basiev, Dokl. Phys., 2008, 53, 198–200.
11. P. A. Popov, P. P. Fedorov and V. V. Osiko, Dokl. Phys., 2014, 59, 199–202.
12. C. Andeen, D. Link and J. Fontanella, Phys. Rev. B: Solid State, 1977, 16, 3762–3767.
13. R. J. Booth and B. R. McGarvey, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 1627–1635.
14. C. R. A. Catlow, J. Phys. C: Solid State Phys., 1973, 6, L64–L70.
15. F. Ma, F. Su, R. Zhou, Y. Ou, L. Xie, C. Liu, D. Jiang, Z. Zhang, Q. Wu, L. Su and H. Liang, Mater. Res. Bull., 2020, 125, 110788.
16. F. Ma, D. Jiang, Z. Zhang, X. Tian, Q. Wu, J. Wang, X. Qian, Y. Liu and L. Su, Opt. Mater. Express, 2019, 9, 4256–4272.
17. F. Ma, Z. Zhang, D. Jiang, Z. Zhang, H. Kou, A. Strzep, Q. Tang, H. Zhou, M. Zhang, P. Zhang, S. Zhu, H. Yin, Q. Lv, Z. Li, Z. Chen and L. Su, Cryst. Growth Des., 2022, 22, 4480–4493.
18. F. Ma, H. Zhou, Q. Tang, L. Su, M. Zhang, P. Zhang, H. Yin, Z. Li, Q. Lv and Z. Chen, J. Alloys Compd., 2022, 899, 162913.
19. B. Lacroix, C. Genevois, J. L. Doualan, G. Brasse, A. Braud, P. Ruterana, P. Camy, E. Talbot, R. Moncorge and J. Margerie, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 125124.
20. K. Liu, G. Bian, Z. Zhang, F. Ma and L. Su, CrystEngComm, 2022, 24, 6468–6476.
21. K. Liu, G. Bian, Z. Zhang, F. Ma and L. Su, Chin. J. Phys., 2024, 88, 584–593.
22. R. D. Shi, M. Y. Liu, X. L. Zhu and X. M. Chen, J. Materiomics, 2022, 8, 815–822.
23. X. Yang, C. Xie, J. Sun, W. Xu, S. Li, X. Tang and G. Tan, Mater. Today Phys., 2023, 33, 101047.
24. M. Zhao and W. Pan, Acta Mater., 2013, 61, 5496–5503.
25. N. S. Chauhan, D. Bhattacharjee, T. Maiti, Y. V. Kolen'ko, Y. Miyazaki and A. Bhattacharya, ACS Appl. Mater. Interfaces, 2022, 14, 54736–54747.
26. K. Papadopoulos, E. Myrovali, D. Karfaridis, M. Farle, U. Wiedwald and M. Angelakeris, J. Alloys Compd., 2023, 969, 172337.
27. Z. Shi, J. Zhang, J. Wei, X. Hou, S. Cao, S. Tong, S. Liu, X. Li and Y. Zhang, J. Mater. Chem. C, 2022, 10, 15582–15592.
28. Y. Zhang, K. Ren, W. Y. Wang, X. Gao, R. Yuan, J. Wang, Y. Wang, H. Song, X. Liang and J. Li, J. Mater. Sci. Technol., 2024, 168, 131–142.
29. Y. Shen, R. M. Leckie, C. G. Levi and D. R. Clarke, Acta Mater., 2010, 58, 4424–4431.
30. P. Gougeon, P. Gall, S. Misra, A. Leon, C. Gendarme, S. Migot, J. Ghanbaja, S. El Oualid, B. Lenoir and C. Candolfi, J. Mater. Chem. C, 2023, 11, 7575–7587.
31. P. A. Popov, P. P. Fedorov and V. A. Konyushkin, Crystallogr. Rep., 2015, 60, 744–748.
32. P. A. Popov, P. P. Fedorov and V. A. Konyushkin, Crystallogr. Rep., 2017, 62, 283–287.
33. P. A. Popov, P. P. Fedorov, V. A. Konyushkin, A. N. Nakladov, S. V. Kuznetsov, V. V. Osiko and T. T. Basiev, Dokl. Phys., 2008, 53, 413–415.
34. P. A. Popov, P. P. Fedorov, S. V. Kuznetsov, V. A. Konyushkin, V. V. Osiko and T. T. Basiev, Dokl. Phys., 2008, 53, 353–355.
35. R. Chen, Q. Jiang, L. Jiang, R. Min, H. Kang, Z. Chen, E. Guo, X. Yang and T. Wang, Chem. Eng. J., 2023, 455, 140676.
36. R. Yang, J. Xu, M. Wei, J. Zhu, X. Meng, P. Zhang, J. Yang and F. Gao, Ceram. Int., 2022, 48, 28586–28594.
37. Y. Liu, H. Xie, Z. Li, Y. Zhang, C. D. Malliakas, M. Al Malki, S. Ribet, S. Hao, T. Pham, Y. Wang, X. Hu, R. dos Reis, G. J. Snyder, C. Uher, C. Wolverton, M. G. Kanatzidis and V. P. Dravid, J. Am. Chem. Soc., 2023, 145, 8677–8688.
38. M. Wei, J. Xu, J. Zhu, R. Yang, X. Meng, P. Zhang, J. Yang and F. Gao, J. Am. Ceram. Soc., 2023, 106, 2037–2048.
39. W. Xiong, H. Zhang, Z. Hu, M. J. Reece and H. Yan, Appl. Phys. Lett., 2022, 121, 112901.
40. J. Zhu, M. Wei, J. Xu, R. Yang, X. Meng, P. Zhang, J. Yang, G. Li and F. Gao, J. Adv. Ceram., 2022, 11, 1222–1234.
41. A. J. Wright, Q. Wang, Y.-T. Yeh, D. Zhang, M. Everett, J. Neuefeind, R. Chen and J. Luo, Acta Mater., 2022, 235, 118056.
42. G. Sun, W. Wang and X. Sun, Ceram. Int., 2022, 48, 8589–8595.
43. K. S. Bayikadi, S. Imam, M. Ubaid, A. Aziz, K.-H. Chen and R. Sankar, J. Alloys Compd., 2022, 922, 166221.
44. K.-J. Liu, Z.-W. Zhang, C. Chen, L.-H. Wei, H.-L. He, J. Mao and Q. Zhang, Rare Met., 2022, 41, 2998–3004.
45. L. Lai, M. Gan, J. Wang, L. Chen, X. Liang, J. Feng and X. Chong, J. Am. Ceram. Soc., 2023, 106, 4343–4357.
46. O. Cherniushok, R. Cardoso-Gil, T. Parashchuk, R. Knura, Y. Grin and K. T. Wojciechowski, Chem. Mater., 2022, 34, 6389–6401.
47. L. Chen, M. Hu, X. Zheng and J. Feng, Acta Mater., 2023, 251, 118870.
48. K. Ma, X. Shi, G. He, J. Li, J. Xu, J. Zuo and M. Li, Ceram. Int., 2023, 49, 21206–21212.
49. F. Li Lin, B. Liu, Q. W. Zhou, Y. H. Cheng and K. X. Song, J. Eur. Ceram. Soc., 2023, 43, 6909–6915.
50. G. Chen, C. Li, H. Jia, H. Li, S. Li, B. Gong, L. An and K. Chen, J. Eur. Ceram. Soc., 2023, 43, 2586–2592.
51. M. Tihtih, J. E. F. M. Ibrahim, M. A. Basyooni, E. Kurovics, W. Belaid, I. Hussainova and I. Kocserha, Ceram. Int., 2023, 49, 1947–1959.
52. A. J. Wright, Q. Wang, S.-T. Ko, K. M. Chung, R. Chen and J. Luo, Scr. Mater., 2020, 181, 76–81.
53. Y. Wang, Y.-J. Jin, T. Wei, Z.-G. Wang, G. Cao, Z.-Y. Ding, Z.-G. Liu, J.-H. Ouyang, Y.-J. Wang and Y.-M. Wang, J. Alloys Compd., 2022, 918, 165636.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ce01308e

---