Organic fluorine mediated intermolecular interactions: insights from experimental and theoretical charge density analyses†
Sakshi‡
 a,
Yogita
Gupta‡
b,
Craig M.
Robertson
*c,
Parthapratim
Munshi
a,
Yogita
Gupta‡
b,
Craig M.
Robertson
*c,
Parthapratim
Munshi
 *b and
Angshuman
Roy Choudhury
*b and
Angshuman
Roy Choudhury
 *a
*a
aDepartment of Chemical Sciences, Indian Institute of Science Education and Research, Mohali, Knowledge City, Sector 81, S. A. S. Nagar, Manauli PO, Mohali, Punjab 140306, India. E-mail: angshurc@iisermohali.ac.in
bMultifunctional Molecular Materials Laboratory, Department of Chemistry, School of Natural Sciences, Shiv Nadar Institution of Eminence Deemed to be University, Delhi NCR, Uttar Pradesh 201314, India. E-mail: parthapratim.munshi@snu.edu.in
cDepartment of Chemistry, University of Liverpool, Crown Street, Liverpool, L69 7ZD, UK. E-mail: craig.robertson@liverpool.ac.uk
First published on 14th October 2024
Abstract
The significance of fluorine-mediated weak intermolecular interactions in crystal lattices has been debated over the past few decades. Structural, computational, and theoretical insights on such interactions have resulted in controversies on them. Therefore, to demonstrate the pivotal role of “organic fluorine” in guiding crystal structures, multipole modelling based experimental and theoretical charge density analyses were performed in 1-(2,3-difluorophenyl)-2-(2,5-difluorophenyl)-6-methoxy-1,2,3,4-tetrahydroisoquinoline. Further, a search on C–F⋯F–C interactions using the Cambridge structural database revealed that type I interactions are generally preferred, followed by type II and quasi-type I/II. The search highlighted the significance of C–F⋯F–C interactions in the presence and absence of strong hydrogen bonds. However, the major intermolecular interactions involving the F atoms in the title compound are found to be C–F⋯H–C and type II C–F⋯F–C. The directional nature and the sigma hole on the F atoms were depicted in terms of the deformation of the electron density maps. The topological analyses of electron densities illustrated that “organic fluorine” mediated intermolecular interactions have a closed shell type. The analysis of electrostatic potentials brought out the attractive nature of the C–F⋯F–C interaction. Thus, the salient features of weak but significant type II C–F⋯F–C interaction and C–H⋯F–C hydrogen bonds were characterized based on the quantitative and qualitative analyses of electron densities.
1 Introduction
The understanding and applications of various interatomic and intermolecular interactions have received significant importance in the literature over the last century. While interactions involving ionic species were characterized and effectively utilized in building various materials for targeted applications,1 non-ionic and non-covalent interactions remained an area of active research over the last few decades.2–4 Strong and weak hydrogen bonds were extensively studied for building the basis of crystal engineering.5–7 Several structural analyses of small organic molecules illustrated the importance of strong hydrogen bonds (15–40 kcal mol−1), intermolecular interactions (4–15 kcal mol−1), very weak contacts (<4 kcal mol−1), and interactions involving π systems.8–14 However, interactions involving halogens, especially fluorine, have been recognized as highly important as their contribution to crystal packing is small yet significant.15–17 Due to their high electronegativity, halogens have high potency to form short intermolecular contacts. However, halogens bonded to carbon atoms (C–X group, X = F, Cl, Br, and I) behave differently than their corresponding anions (X−). Among the halogens, the F atom has gained huge importance in medicinal chemistry as nearly 70% of drugs contain this atom.18 Moreover, substituting H with F in organic compounds leads to significant changes in their physical properties and chemical reactivity.19 Early studies on intermolecular interactions offered by C–F groups initiated several controversies. While a few researchers highlighted20–22 the importance of fluorine-mediated intermolecular interactions, many groups refuted23–25 their role in building crystalline architecture. Fluorine bound to carbon was termed as ‘organic fluorine’ by Dunitz and Taylor in 1997.26 The importance of the C–H⋯F–C hydrogen bond was first systematically studied by Thalladi et al., in 1998 using in situ crystallization of a series of fluorinated benzenes.27 Organic fluorine offers weak C–H⋯F–C hydrogen bonds and C–F⋯π and C–F⋯F–C interactions in both small organic compounds and macromolecules.28–31 We have been involved in the systematic structural analysis of crystal structures of small organic molecules containing one or more F atoms.32–37 To the best of our knowledge, Ramasubbu et al. performed the first study on halogen⋯halogen (X⋯X) interactions using the Cambridge structural database (CSD) in 1986.38 Subsequently, the X⋯X interactions were categorized as type I and type II by Desiraju and Parthasarathy in 1989.39 Further, based on CSD analysis, in 2013, Tothadi et al.40 classified C–X⋯X–C interactions into three categories, namely type I, type II, and quasi type I/type II. The classification criterion is based on the difference between angles θ1 and θ2, as described below.• 0° ≤ |θ1 − θ2| ≤ 15° – contacts will be classified as type I,
• 30° ≤ |θ1 − θ2| – contacts will be classified as type II, and
• 15° ≤ |θ1 − θ2| ≤ 30° – contacts will be classified as quasi type I/type II interactions.
Although these database analyses were performed irrespective of the identity of the halogens, the studies highlighted that the F atoms behave differently than the other halogens.41 However, to our knowledge, such a study has not been performed exclusively on C–F⋯F–C interactions using the latest entries in the CSD.
With modern diffractometers, high-intensity X-ray sources, and highly sensitive area detectors, experimental electron density analysis has gained momentum in the last couple of decades.42–44 Further, recent developments in quantum crystallographic tools allow for efficiently generating electron densities and deriving topological properties.45–47 In this context, Hibbs et al. highlighted the differences in topological properties associated with the polar C–F bond from experimental and theoretical analyses.48 Their studies emphasized the importance of electrostatic potential (ESP) in establishing long-range interactions in drug design. Further, the topological analysis of electron densities was also performed to characterize type II Cl⋯F and type I F⋯F interactions.49 Furthermore, Pavan et al. illustrated type II C–F⋯F–C and C–F⋯S–C interactions in pentafluorophenyl 2,2-bithiazole based on charge density analysis and identified the “sigma-hole” on the F atom and designated the C–F⋯S–C interaction as a halogen bond instead of a chalcogen bond.50 Recently, some of us performed charge density analysis to investigate type I and quasi-type I/type II C–F⋯F–C interactions in N-(2,5-difluorophenyl)-3,5-difluoro-N-(3-methoxyphenethyl)benzamide.37
In our continued efforts to understand the role of ‘organic fluorine’ mediated interactions in guiding and stabilizing the crystal lattice, here, we have carried out a comprehensive analysis of C–F⋯F–C interactions (Fig. 1) using the CSD to elucidate their salient features. We have also analyzed the Hirshfeld surfaces51 for quantitative understanding of the interaction energies for the dimeric units formed via C–H⋯F–C hydrogen bonds and C–F⋯F–C interactions using CrystalExplorer 21.52,53 The molecular packing energies for those dimeric units were also computed using the UNI force field54,55 through Mercury.56
Fluorine mediated interactions play a crucial role in pharmaceuticals. The significance of “organic fluorine” mediated interactions is best studied in molecules with no other stronger interactions. Over the past decades, some of us have analysed the structural features of a series of fluorinated phenylacetanilides and the corresponding isoquinolines synthesized by a ring closure reaction.30,31,57 Some of these fluorinated isoquinolines were found to have useful biological properties.58
Herein, we have performed charge density analyses on 1-(2,3-difluorophenyl)-2-(2,5-difluorophenyl)-6-methoxy-1,2,3,4-tetrahydroisoquinoline (1, Fig. 2) using Hansen and Coppens multipolar formalism59 to derive electron densities using high-resolution X-ray diffraction data and structure factors generated using periodic calculations. We employed Bader's quantum theory of atoms in molecules (QTAIM)60 approach to evaluate the topological properties of the electron densities based on experimental and theoretical multipolar atom models. Thus, we assessed the accurate features and attractive nature of the C–F⋯F–C and C–H⋯F–C interactions via qualitative and quantitative analyses of electron densities.
 | ||
| Fig. 2 (a) Chemical structure and (b) ORTEP drawn based on multipole refinement after SHADE at 50% ellipsoid probability for all the atoms of 1. | ||
2 Experimental and theoretical sections
2.1 Data collection and refinement strategy
An excellent quality single crystal was selected for data collection under an optical polarizable microscope and mounted on a Hampton Research CryoLoop using Paratone-N oil. The crystal was cooled to 100 K, and high-resolution X-ray diffraction data (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ = 1.11 Å−1) was collected using a Rigaku 007HF four-circle diffractometer equipped with a Mo rotating anode X-ray tube and hybrid pixel array detector (HyPix 6000HE). The crystal-to-detector distance was set to 40 mm. The data was collected for about 40 hours with variable exposure time for low and high-angle regions, and the scan width was 0.5° per frame. Data reduction and integration were performed using CrysAlisPro.61 The data sets were scaled, averaged, and merged using the program SORTAV62 embedded in the WINGX63 package suite. The crystal structure of the compound was solved by direct methods using SHELXT,64 and structure refinement was done based on the independent atom model (IAM) using SHELXL,65 which is included in the OLEX2 suite.66 The non-H atoms were located in the successive difference Fourier maps and refined with anisotropic thermal parameters. All H atoms were placed at the calculated positions and refined using a riding model with appropriate HFIX commands. The corresponding crystal data parameters are listed in Table 1.
θ/λ = 1.11 Å−1) was collected using a Rigaku 007HF four-circle diffractometer equipped with a Mo rotating anode X-ray tube and hybrid pixel array detector (HyPix 6000HE). The crystal-to-detector distance was set to 40 mm. The data was collected for about 40 hours with variable exposure time for low and high-angle regions, and the scan width was 0.5° per frame. Data reduction and integration were performed using CrysAlisPro.61 The data sets were scaled, averaged, and merged using the program SORTAV62 embedded in the WINGX63 package suite. The crystal structure of the compound was solved by direct methods using SHELXT,64 and structure refinement was done based on the independent atom model (IAM) using SHELXL,65 which is included in the OLEX2 suite.66 The non-H atoms were located in the successive difference Fourier maps and refined with anisotropic thermal parameters. All H atoms were placed at the calculated positions and refined using a riding model with appropriate HFIX commands. The corresponding crystal data parameters are listed in Table 1.
| Chemical formula | C22H17F4NO |
|---|---|
| Formula weight | 387.36 |
| Space group | I2/a |
| a (Å), b (Å), c (Å) | 16.07317(10), 6.24689(4), 35.5828(2) |
| β (°) | 101.2015(6) |
| Volume (Å3) | 3504.72(4) |
| Z, Z′ | 8, 1 |
| Resolution (Å) | 0.45 |
| 2θ range | 4.668° to 105.068° |
| (hkl) ranges | −35, 35; −13, 12; −79, 79 |
| T min, Tmax | 0.792, 1.000 |
| μ (mm−1) | 0.119 |
| R int, Rmerge | 0.0303, 0.030 |
| Measured reflections | 213![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 234 234 |
| Unique reflections | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 075 075 |
| Completeness (%), redundancy | 99.8, 10.3 |
| Independent atom model (IAM) | |
|---|---|
| Reflections used [I > 2σ(I)] | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 075 075 |
| R obs, wR2 (F2) | 0.0368, 0.109 |
| GooF | 1.081 |
| Δρmax, Δρmin (e Å−3) | 0.616, −0.244 |
| Multipole model (experimental) | |
|---|---|
| Reflections used [I > 3σ(I)] | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 242 242 |
| R(F), wR2(F2) | 0.0164, 0.0242 |
| N ref/Nv | 20.7986 |
| GooF | 1.526 |
| Δρmax, Δρmin (e Å−3) | 0.156, −0.174 |
2.2 Computational details
Hirshfeld surfaces for the dimers were analysed using CrystalExplorer 21.52,53 The analysis was carried out based on crystal geometries. Further, the ESPs mapped on the electron density surfaces for the dimers were investigated using the B3LYP/6-31G(d,p) level of theory. For quantitative understanding, the interaction energies (IEs) for the molecular pairs present in the dimers were calculated by normalizing the C–H distances to 1.083 Å using the B3LYP/6-31G(d,p) level of theory. Further, the molecular packing energies were also estimated via Mercury56 using the UNI force field for the three dimeric units.54,552.3 Multipole modelling
To describe the aspherical electron density of the atoms, multipole refinement (based on F2) against high-resolution X-ray diffraction data was performed based on Hansen–Coppens formalism59 using XD2016 (Table 1).67 The structural information from IAM was imported to the XD package using the XDINI module. Multipole refinement based on the least square method was done using the XDLSM module. In the first step, the scale factor was refined against the whole resolution range of diffraction data. The positions and anisotropic displacement parameters for all the non-hydrogen atoms were refined using high-angle reflection data (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ > 0.8 Å−1). The C–H bond lengths were restrained to average neutron bond distance values (C(Ar)–H = 1.083 Å, C3–Csp3–H = 1.099 Å, C2–Csp3–H2 = 1.092 Å, and C–Csp3–H3 = 1.077 Å).68 The isotropic thermal parameters of the H atoms were refined using low-angle reflections (sin
θ/λ > 0.8 Å−1). The C–H bond lengths were restrained to average neutron bond distance values (C(Ar)–H = 1.083 Å, C3–Csp3–H = 1.099 Å, C2–Csp3–H2 = 1.092 Å, and C–Csp3–H3 = 1.077 Å).68 The isotropic thermal parameters of the H atoms were refined using low-angle reflections (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ ≤ 0.8 Å−1). Subsequently, the multipoles were refined stepwise for all the atoms. The multipole refinement for all the non-H atoms (except F) was performed up to the octupole (lmax = 3) level, while for the F atoms, the refinements were performed up to the hexadecapole (lmax = 4) level. For H atoms, all multipoles were refined up to the dipole level (lmax = 1). A total of 19 sets of kappa (κ) and kappa prime (κ′) were assigned to different atoms based on their chemical environments. For the H atoms, both parameters were fixed at 1.2. The model thus obtained was used to estimate the anisotropic displacement parameters (ADPs) of H atoms using SHADE2.1.69 The ADPs of the H atoms in subsequent refinements were constrained to the values obtained from SHADE. The refinements were repeated with the fixed ADPs of H atoms until convergence. Up to the fourth order, Gram–Charlier70 coefficients using high-angle reflections (sin
θ/λ ≤ 0.8 Å−1). Subsequently, the multipoles were refined stepwise for all the atoms. The multipole refinement for all the non-H atoms (except F) was performed up to the octupole (lmax = 3) level, while for the F atoms, the refinements were performed up to the hexadecapole (lmax = 4) level. For H atoms, all multipoles were refined up to the dipole level (lmax = 1). A total of 19 sets of kappa (κ) and kappa prime (κ′) were assigned to different atoms based on their chemical environments. For the H atoms, both parameters were fixed at 1.2. The model thus obtained was used to estimate the anisotropic displacement parameters (ADPs) of H atoms using SHADE2.1.69 The ADPs of the H atoms in subsequent refinements were constrained to the values obtained from SHADE. The refinements were repeated with the fixed ADPs of H atoms until convergence. Up to the fourth order, Gram–Charlier70 coefficients using high-angle reflections (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ ≥ 0.8 Å−1) were refined to treat the anharmonic thermal motions of F atoms. Multipole refinements of all the atoms described above were repeated until convergence. Further, the κ parameters (set equal to κ′) of the H atoms and κ′ values of the F atoms were transferred from the values obtained from the multipole refinement based on the theoretical structure factors as discussed below.
θ/λ ≥ 0.8 Å−1) were refined to treat the anharmonic thermal motions of F atoms. Multipole refinements of all the atoms described above were repeated until convergence. Further, the κ parameters (set equal to κ′) of the H atoms and κ′ values of the F atoms were transferred from the values obtained from the multipole refinement based on the theoretical structure factors as discussed below.
2.4 Calculation of theoretical structure factors
The experimental atomic coordinates were used as an input to perform periodic calculations for generating theoretical structure factors using CRYSTAL17.71 The periodic wave function was obtained using the B3LYP/6-31G** level of theory.49 Upon convergence, the wave function was calculated to generate theoretical structure factors against the reflections observed from the high-resolution X-ray diffraction experiment using the XFAC module. The same level of multipoles used for the experimental model was also used for multipole modelling using the theoretical structure factors.3 Results and discussion
3.1 Cambridge structure database search for C–F⋯F–C interactions
The search of C–F⋯F–C interactions (Fig. 1) with the distance (d) between the interacting organic fluorine atoms in the range of 1.60–2.94 Å and the angles (θ1, θ2) in the range of 90–180° was performed using the CSD (Conquest Version 2024.1.0), including the latest update.Depending on the presence of other intermolecular interactions among the molecules containing C–F⋯F–C interactions, the searches were divided into four sets. The first set (search 1) contained molecules with C–F⋯F–C interactions as well as the other possible intermolecular interactions including strong (O–H⋯O, O–H⋯N, N–H⋯N, and N–H⋯O) and weak (C–H⋯O, C–H⋯N, O–H⋯F, N–H⋯F, and C–H⋯π) hydrogen bonds and any other interactions [X–H⋯π (X = C, N, O etc.), π⋯π etc.]. The second set (search 2) excluded the molecules with strong intermolecular hydrogen bonds but included those with weaker ones and other interactions. The third set (search 3) excluded the molecules having strong and weak hydrogen bonds but included those comprising of C–H⋯F–C hydrogen bonds and other possible weaker interactions. In the fourth set (search 4), the molecules with strong and weak hydrogen bonds, including C–H⋯F–C hydrogen bonds, were excluded to select only C–F⋯F–C and other weaker interactions. The outcome of the searches without any restriction on the data collection temperature is summarised in Table 2. However, searches with a filter of 80–120 K on the data collection temperature showed a similar statistical trend to those without any such filter (Table S1, ESI†). Among these sets, the shortest distance of 1.774 Å for the C–F⋯F–C interaction was noticed for the structure with refcode FFMXZP. The ratio of the number of hits of type I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) type II
type II![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) quasi type I/type II remained almost the same across the four sets, indicating that the occurrence and influence of the C–F⋯F–C interaction is essential in the absence and presence of other intermolecular interactions and type I interactions are preferred in general. The crystal structure of the title compound belongs to the category of search 3.
quasi type I/type II remained almost the same across the four sets, indicating that the occurrence and influence of the C–F⋯F–C interaction is essential in the absence and presence of other intermolecular interactions and type I interactions are preferred in general. The crystal structure of the title compound belongs to the category of search 3.
| Statistical parameters | Search 1 | Search 2 | Search 3 | Search 4 |
|---|---|---|---|---|
| No. of hits | 7912 | 6415 | 4495 | 1154 |
| No. of interactions | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 952 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 221 221 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 910 910 |
3400 |
| Maximum range for θ1 (°) | 120–135 | 120–135 | 120–135 | 120–160 |
| Maximum range for θ2 (°) | 120–135 | 120–135 | 120–135 | 120–160 |
| Maximum range for distance (Å) | 2.90–2.94 | 2.90–2.94 | 2.90–2.94 | 2.90–2.94 |
| No. of type I interactions [0° ≤ |θ1 − θ2| ≤ 15°] | 8383 | 6923 | 5109 | 1640 |
| No. of type II interactions [30° ≤ |θ1 − θ2|] | 5080 | 4312 | 3439 | 1013 |
| No. of quasi type I/type II interactions [15° ≤ |θ1 − θ2| ≤ 30°] | 3489 | 2986 | 2362 | 747 |
Ratio of the number of hits of type I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) type II type II![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) quasi type I/type II quasi type I/type II |
2.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.45 1.45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
2.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.44 1.44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
2.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.45 1.45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
2.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.36 1.36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Most of the C–F⋯F–C interactions were populated in the range of longer distances, close to 2.90 Å (Fig. S1–S3†). The histograms of the angles indicate that both θ1 and θ2 prefer the range between 120–135°. However, in the absence of stronger interactions (Fig. S4, ESI†), the molecules prefer 120–130° for θ1 and a more linear angular range of 140–160° for θ2. The heat plots for θ1 and θ2 indicate a preference for type I geometry over others with a larger population around 90° ≤ θ1 ≅ θ2 ≤ 95° and 125° ≤ θ1 ≅ θ2 ≤ 130°. In the case of search 4, a higher population was observed for θ1 ≅ θ2 ranges of 90–95°, 125–130°, 140–≤145° and 150–≤155° (Fig. S4d†), indicating the versatile nature of type I C–F⋯F–C interactions.
3.2 Synthesis and crystallization
Recently, some of us have reported the synthesis, structure, and computational analysis of compound 1 (Fig. 2).57 Compound 1 was freshly recrystallized from a mixture of acetonitrile![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hexane (1
hexane (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to obtain colorless single crystals via the slow evaporation method at room temperature.
1) to obtain colorless single crystals via the slow evaporation method at room temperature.
3.3 Molecular packing analysis
The crystal structure and the atom labels are shown in Fig. 2b. The crystal structure analysis of 1 reveals that the molecules pack (Fig. S5a, ESI†) in their crystal lattice via one C–F⋯F–C (highlighted in blue) interaction and three distinct C–H⋯F–C (highlighted in orange) hydrogen bonds (Table 3). The C–F⋯F–C interactions form a dimer and are of type II (Fig. S5b, ESI†). While the molecules along the c-axis arrange via dimeric C–F⋯F–C interactions and C–H⋯F–C hydrogen bonds, those along the a-axis pack via two C–H⋯F–C interactions of different lengths (Fig. S5c and d, ESI†). In the subsequent sections, we highlight our discussions on the interactions involved in the dimeric units.| D–X⋯Y | D⋯Y/(Å) | X⋯Y/(Å) | ∠D–X⋯Y/(°) | Symmetry codes |
|---|---|---|---|---|
| C12–F2⋯F4–C20 | 3.1558(9) | 2.9015(7) | 129.53(3) | 1 − x, 1 − y, 1 − z |
| C18–H18⋯F2–C12 | 3.146(2) | 2.48 | 126.86 | 1 − x, 2 − y, 1 − z |
| C21–H21⋯F1–C11 | 3.289(2) | 2.36 | 163.49 | x, y + 1, z |
| C2–H2A⋯F3–C17 | 3.408(1) | 2.51 | 150.86 |
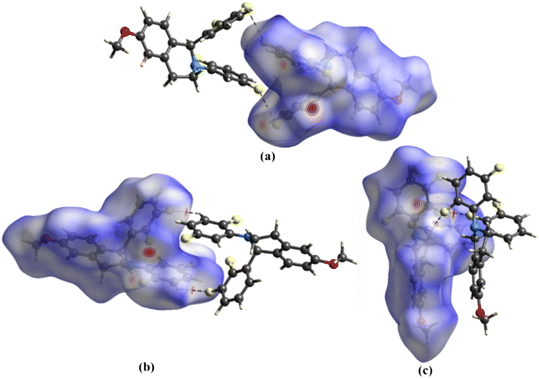
3.4 Hirshfeld surface analysis and interaction energies for the dimers
The Hirshfeld surface analysis on 1 provided further insights into the intermolecular interactions (Fig. 3). The white and red surfaces highlight the lighter and deeper interpenetration of the surfaces for the C12–F2⋯F4–C20 interactions (Fig. 3a) and the C–H⋯F hydrogen bonds (Fig. 3b and c), respectively. The intensity of the red surfaces around the C–H⋯F–C hydrogen bonds correlates well with the distance of these interactions. Further, the ESP map of the dimeric units reveals the directional nature and complementarity of the C12–F2⋯F4–C20 interactions (Fig. 4a) and C–H⋯F–C hydrogen bonds (Fig. 4b and c). For the quantitative analysis, the components of pairwise IEs for the dimers, namely electrostatic, polarization, dispersion, and repulsion, are calculated and tabulated in Table 4. The results indicate that dispersion energies are the major contributors to the total IEs of the three dimers. For the C12–F2⋯F4–C20 interaction, although the electrostatic component averages out almost to zero, the total IE of −10.8 kJ mol−1 suggests its stabilizing nature. The total IE of the C18–H18⋯F2–C12 hydrogen bond is −7.95 kJ mol−1, and for C21–H21⋯F1–C11 and C2–H2A⋯F3–C17 hydrogen bonds, the average total IE is −16.65 kJ mol−1. Further, the packing energies for the dimeric units computed using the UNI force field follow a similar trend to those obtained from CrystalExplorer 21 (Table 4).| Dimeric interactions | Interaction length (Å) | CrystalExplorer based energies | UNI force field-based energies | ||||
|---|---|---|---|---|---|---|---|
| (Symmetry code) | E elec | E pol | E dis | E rep | E tot | E tot | |
| C12–F2⋯F4–C20 | 2.902 | 0.8 | −1.1 | −36.4 | 16.5 | −21.6 | −26.4 |
| (1 − x, 1 − y, 1 − z) | |||||||
| C18–H18⋯F2–C12 | 2.401 | −7.2 | −1.2 | −18.1 | 13.5 | −15.9 | −6.0 |
| (1 − x, 2 − y, 1 − z) | |||||||
| C21–H21⋯F1–C11 | 2.240 | −8.8 | −1.9 | −42.1 | 22.7 | −33.3 | −28.0 |
| (x, y + 1, z) | |||||||
| C2–H2A⋯F3–C17 | 2.430 | ||||||
| (x, y + 1, z) | |||||||
3.5 Analysis of multipole model
Various statistical methods were employed to scrutinize the accuracy of the multipole model constructed using the X-ray diffraction data. The quality of the data and the multipole model were inspected via DRK plots72,73 (Fig. S6, ESI†). Throughout the resolution range, the deviations of the scale factor from unity up to 5% indicate an excellent model. The Gaussian distribution of pixel population plotted against residual electron density (Fig. S7a, ESI†) and the parabolic nature of the fractal dimension plot (Fig. S7b, ESI†) indicate the accuracy of the multipole model. Further, Hirshfeld's rigid bond test74 was performed for all the non-H atoms, and the differences in the Uij components were found to be within the limit, i.e. <1 × 10−4 Å2. The featureless residuals in the different molecular planes indicate the reliability of the multipole model (Fig. S8, ESI†). For both experimental and theoretical models, after the final refinements, the atomic charges were found to be appropriate (Table S2, ESI†).3.6 Deformation electron density
The accurate features of the covalent bonds of molecule 1 and the atomic lone pair of electrons are depicted via 2D deformation electron density maps (Fig. S9, ESI†). The directionality and orientation of the lone pair of electrons of fluorine, nitrogen, and oxygen atoms are highlighted by plotting 3D-deformation electron density maps (Fig. S10, ESI†). The intermolecular interactions involving F atoms are displayed via 3D-deformation density maps (Fig. 5 and S11, ESI†). In the case of the C12–F2⋯F4–C10 interaction (Fig. 5a), the sigma hole on the F4 atom is directed towards the charge concentration region of the F2 atom of the following molecule confirms the attractive nature of the type II F⋯F interaction. The deformation density maps obtained from the experimental and theoretical analyses represent similar features and are in good accordance.3.7 Topological analyses of electron densities
The module XDPROP, implemented in the XD package, was used to derive the topological properties. The bond critical points (BCPs), the corresponding bond paths (BPs) for the covalent bonds, the ring critical points (RCPs), and the Laplacian maps confirm the accuracy of the electron density features in 1 (Fig. S12 and S13, ESI†). The topological parameters at the BCPs for the covalent bonds (Table S3, ESI†) and those of the C–F⋯F–C interaction and C–H⋯F–C hydrogen bonds (Table 5) derived from the experimental and theoretical analyses agree well. For the F⋯F interaction, at the BCP, the experimental/theoretical values of electron density, ρCP(r) (0.040/0.038 e Å−3), its second derivative, ∇2ρCP(r), the Laplacian (0.760/0.741 e Å−5), and the bond path length, Rij (2.916/2.921 Å) compare well with those of type II F⋯F interactions reported in the literature.50 The positive values of the Laplacian and the ratio (|VCP(r)|/|GCP(r)| < 1)75,76 of the potential energy density (Vcp(r)) to the kinetic energy density (GCP(r)) for the F⋯F (0.64) interaction, C18–H18⋯F2–C12 (0.66/0.68), C2–H2A⋯F3–C17 (0.62/0.64), and C21–H21⋯F1–C11 (0.64) hydrogen bonds indicate their closed shell nature. The corresponding total energy density (HCP(r)) values, the sum of GCP(r) and VCP(r) at the BCP, compare well with those reported in the literature.50| Intermolecular interactions | ρ CP(r) (e Å−3) | ∇2ρCP(r) (e Å−5) | R ij (Å) | G CP(r) (kJ mol−1 Bohr−3) | V CP(r) (kJ mol−1 Bohr−3) | H CP(r) (kJ mol−1 Bohr−3) | |
|---|---|---|---|---|---|---|---|
| (Symmetry code) | |||||||
| C12–F2⋯F4–C20 | 0.040 (1) | 0.760 (1) | 2.916 | 15.35 | −09.87 | 5.48 | 0.64 |
| (1 − x, 1 − y, 1 − z) | 0.038 (1) | 0.741 (1) | 2.921 | 14.80 | −09.41 | 5.38 | 0.64 |
| C18–H18⋯F2–C12 | 0.047 (4) | 0.882 (2) | 2.447 | 17.93 | −11.84 | 6.09 | 0.66 |
| (1 − x, 2 − y, 1 − z) | 0.052 (1) | 0.944 (1) | 2.422 | 19.41 | −13.10 | 6.30 | 0.68 |
| C2–H2A⋯F3–C17 | 0.036 (4) | 0.809 (1) | 2.435 | 15.92 | −09.80 | 6.12 | 0.62 |
| (x, y + 1, z) | 0.041 (1) | 0.821 (1) | 2.434 | 16.43 | −10.50 | 5.93 | 0.64 |
| C21–H21⋯F1–C11 | 0.053 (7) | 1.209 (1) | 2.250 | 24.29 | −15.65 | 8.64 | 0.64 |
| (x, y + 1, z) | 0.054 (1) | 1.245 (1) | 2.240 | 25.02 | −16.13 | 8.89 | 0.64 |
As expected, the BCPs for the F⋯F interactions are exactly in the middle of the BP (Fig. 6), and those of the C–H⋯F–C interactions (Fig. S14, ESI†) are slightly towards the H atoms. The corresponding results from the theoretical multipole model (Fig. S15, ESI†) display similar features.
The Laplacian maps for the F⋯F interaction show a polar flattening effect on the F atoms (Fig. 7a), and the asymmetric valence shell charge concentration of F atoms is evident, especially on the theoretical map. The Laplacian maps of C18–H18⋯F2–C12 (Fig. 7b) and the other two C–H⋯F–C hydrogen bonds (Fig. S16, ESI†) indicate a directional preference of the lone pair of electrons of the F atom towards the H atom. The Laplacian maps from the theoretical multipole model agree well with those obtained from the experimental model.
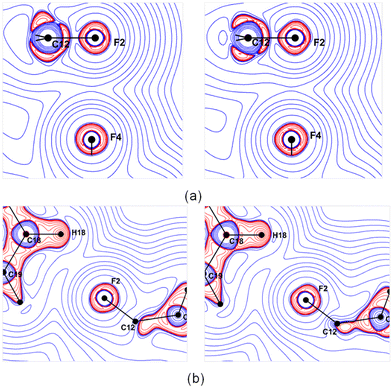 | ||
| Fig. 7 Experimental (left) and theoretical (right) Laplacian maps for (a) C12–F2⋯F4–C10 interaction and (b) C18–H18⋯F2–C12 hydrogen bond drawn at the logarithmic interval of −∇2ρ e Å−5. | ||
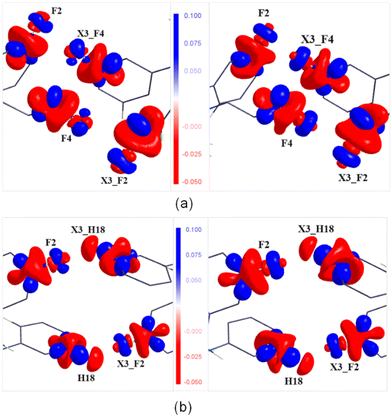
3.8 Analysis of electrostatic potential maps
A qualitative agreement has been noticed between the experimental and theoretical ESP maps (Fig. S17, ESI†) plotted using the program MoleCoolQT.77 However, the F atoms in the theoretical map display a slightly higher electronegative characteristic than the experimental map. In the intermolecular interaction region, the electrostatic complementarity of the F⋯F interaction and the C–H⋯F–C hydrogen bond are highlighted in Fig. 8. In the case of F2⋯F4, the negative region of the F4 atom points towards the electropositive region of the F2 atom, suggesting an attractive nature of these interactions. Similarly, the attractive nature of the C18–H18⋯F2–C12 interaction is also highlighted, where the electropositive region of the C18–H18 group is facing the electronegative region of the F2 atom. The same feature is also observed in the cases of the other two hydrogen bonds (Fig. S18, ESI†). | ||
| Fig. 8 Experimental (left) and theoretical (right) 3D ESP maps for (a) the C12–F2⋯F4–C20 interaction and (b) C18–H18⋯F2–C12 hydrogen bond plotted at an interval of ±0.1 e Å−3. | ||
4 Conclusions
In this study, we employed high-resolution X-ray diffraction data and theoretical structure factors to perform experimental and theoretical charge density analyses and highlighted the nature of intermolecular interactions mediated via “organic fluorine”. Additionally, we conducted a database search using the CSD to pinpoint the frequent occurrence of C–F⋯F–C interactions and their importance in stabilizing the crystal structure in the presence of other strong interactions. The major intermolecular interactions involving the F atom in the title compound, 1-(2,3-difluorophenyl)-2-(2, 5-difluorophenyl)-6-methoxy-1,2,3,4-tetrahydroisoquinoline, are C–F⋯H–C and type II C–F⋯F–C and they have stable energies. The qualitative analysis of electron densities via deformation density maps highlighted the directional nature and the sigma hole on the F atoms. The topological analyses of electron densities based on experimental and theoretical multipole models illustrated that the “organic fluorine” mediated intermolecular interactions are closed shell type. The ESP maps indicated the polar nature of the C–F bond. Further, the electrostatic complementarity highlighted via ESP maps brought out the attractive nature of the C–F⋯F–C interaction. The qualitative and quantitative analyses demonstrated the stabilizing nature of the type II C–F⋯F–C interaction in the presence of weak C–H⋯F–C hydrogen bonds. Our study suggested that the intermolecular interactions involving “organic fluorine” are directional and actively contribute to stabilizing the crystal structure, and the type II C–F⋯F–C interactions are attractive in nature. Finally, our findings will provide valuable insights, particularly for understanding intermolecular interactions in pharmaceutical compounds containing F atoms.Data availability
The data supporting this article have been included in the ESI,† and the crystallographic data for compound 1 has been deposited at the CCDC under CCDC code 2357897.Author contributions
ARC performed the crystal growth experiment. CMR collected the X-ray diffraction data. Sakshi and YG performed the diffraction data analysis, multipole modeling, and subsequent electron density analyses under the supervision of PM. ARC and PM supervised the project. PM and ARC wrote the manuscript with the help of Sakshi and YG.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Sakshi and Y. G. thank IISER Mohali and SNIoE, respectively, for the research fellowship. PM and ARC thank SNIoE and IISER Mohali, respectively, for the financial support and the research facilities. We thank Dr. Hare Ram Yadav for synthesizing the title compound.References
- M. Giese, M. Albrecht and K. Rissanen, Chem. Rev., 2015, 115, 8867–8895 CrossRef CAS PubMed.
- F. H. Allen, J. P. M. Lommerse, V. J. Hoy, J. A. K. Howard and G. R. Desiraju, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 1006–1016 CrossRef.
- Y. Umezawa, S. Tsuboyama, K. Honda, J. Uzawa and M. Nishio, Bull. Chem. Soc. Jpn., 1998, 71, 1207–1213 CrossRef CAS.
- J. D. Dunitz and A. Gavezzotti, Chem. Soc. Rev., 2009, 38, 2622–2633 RSC.
- K. Biradha, CrystEngComm, 2003, 5, 374–384 RSC.
- B. K. Saha, A. Nangia and M. Jaskólski, CrystEngComm, 2005, 7, 355–358 RSC.
- G. R. Desiraju, Cryst. Growth Des., 2011, 11, 896–898 CrossRef CAS.
- G. R. Desiraju, S. Kashino, M. M. Coombs and J. Glusker, Acta Crystallogr., Sect. B: Struct. Sci., 1993, 49, 880–892 CrossRef PubMed.
- M. Nishio, CrystEngComm, 2004, 6, 130–158 RSC.
- G. R. Desiraju, J. Chem. Soc., Dalton Trans., 2000, 3745–3751 RSC.
- J. A. R. P. Sarma and G. R. Desiraju, Acc. Chem. Res., 1986, 19, 222–228 CrossRef CAS.
- G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond in Structural Chemistry and Biology, Oxford University Press, Oxford, 1999 Search PubMed.
- K. C. K. Swamy, S. Kumaraswamy and P. Kommana, J. Am. Chem. Soc., 2001, 123, 12642–12649 CrossRef CAS PubMed.
- S. J. Grabowski, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2006, 102, 131–165 RSC.
- S. L. Price, A. J. Stone, J. Lucas, R. S. Rowland and A. E. Thornley, J. Am. Chem. Soc., 1994, 116, 4910–4918 CrossRef CAS.
- S. K. Nayak, M. K. Reddy, T. N. G. Row and D. Chopra, Cryst. Growth Des., 2011, 11, 1578–1596 CrossRef CAS.
- A. Takemura, L. J. McAllister, P. B. Karadakov, N. E. Pridmore, A. C. Whitwood and D. W. Bruce, CrystEngComm, 2014, 16, 4254–4264 RSC.
- W. K. Hagmann, J. Med. Chem., 2008, 51, 4359–4369 CrossRef CAS PubMed.
- H. J. Böhm, D. Banner, S. Bendels, M. Kansy, B. Kuhn, K. Müller, U. Obst-Sander and M. Stahl, ChemBioChem, 2004, 5, 637–643 CrossRef PubMed.
- V. R. Thalladi, H. C. Weise, R. Boese, A. Nangia and G. R. Desiraju, Acta Crystallogr., Sect. B: Struct. Sci., 1999, 55, 1005–1013 CrossRef PubMed.
- M. D. Prasanna and T. N. G. Row, CrystEngComm, 2000, 2, 134–140 RSC.
- A. R. Choudhury, U. K. Urs, T. N. G. Row and K. Nagarajan, J. Mol. Struct., 2002, 605, 71–77 CrossRef CAS.
- G. R. Desiraju and R. Parthasarathy, J. Am. Chem. Soc., 1989, 111, 8725–8726 CrossRef CAS.
- L. Shimoni and J. P. Glusker, Struct. Chem., 1994, 5, 383–397 CrossRef CAS.
- J. A. K. Howard, V. J. Hoy, D. O'Hagan and G. T. Smith, Tetrahedron, 1996, 52, 12613–12622 CrossRef CAS.
- J. D. Dunitz and R. Taylor, Chem. – Eur. J., 1997, 3, 89–98 CrossRef CAS.
- V. R. Thalladi, H. C. Weiss, D. Bläser, R. Boese, A. Nangia and G. R. Desiraju, J. Am. Chem. Soc., 1998, 120, 8702–8710 CrossRef CAS.
- A. R. Choudhury, U. K. Urs, P. S. Smith, R. Goddard, J. A. K. Howard and T. N. G. Row, J. Mol. Struct., 2002, 641, 225–232 CrossRef CAS.
- I. Saraogi, V. G. Vijay, S. Das, K. Sekar and T. N. G. Row, Cryst. Eng., 2003, 6, 69–77 CrossRef CAS.
- A. R. Choudhury and T. N. G. Row, Cryst. Growth Des., 2004, 4, 47–52 CrossRef CAS.
- A. R. Choudhury and T. N. G. Row, CrystEngComm, 2006, 8, 265–274 RSC.
- G. Kaur, P. Panini, D. Chopra and A. R. Choudhury, Cryst. Growth Des., 2012, 12, 5096–5110 CrossRef CAS.
- G. Kaur and A. R. Choudhury, CrystEngComm, 2015, 17, 2949–2963 RSC.
- G. Kaur, S. Singh, A. Sreekumar and A. R. Choudhury, J. Mol. Struct., 2016, 1106, 154–169 CrossRef CAS.
- H. R. Yadav and A. R. Choudhury, J. Mol. Struct., 2017, 1150, 469–480 CrossRef CAS.
- S. Dhingra, D. J. Barman, H. R. Yadav, J. Eyyathiyil, P. Bhowmik, P. Kaur, D. Adhikari and A. R. Choudhury, CrystEngComm, 2018, 20, 716–727 RSC.
- L. Singla, A. Kumar, C. M. Robertson, P. Munshi and A. R. Choudhury, Cryst. Growth Des., 2023, 23, 853–861 CrossRef CAS.
- N. Ramasubbu, R. Parthasarathy and P. Murray-Rust, J. Am. Chem. Soc., 1986, 108, 4308–4314 CrossRef CAS.
- G. R. Desiraju and R. Parthasarathy, J. Am. Chem. Soc., 1989, 111, 8725–8726 CrossRef CAS.
- S. Tothadi, S. Joseph and G. R. Desiraju, Cryst. Growth Des., 2013, 13, 3242–3254 CrossRef CAS.
- T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296 CrossRef CAS PubMed.
- P. Coppens, Acta Crystallogr., Sect. A: Found. Crystallogr., 1998, 54, 779–788 CrossRef.
- T. S. Koritsanszky and P. Coppens, Chem. Rev., 2001, 101, 1583–1628 CrossRef CAS PubMed.
- P. Munshi and T. N. G. Row, Crystallogr. Rev., 2005, 11, 199–241 CrossRef CAS.
- A. Genoni, L. Bucinsky, N. Claiser, J. Contreras-Gracia, B. Dittrich, P. M. Dominiak, E. Espinosa, C. Gatti, P. Giannozzi, J.-M. Gillet, D. Jayatilaka, P. Macchi, A. O. Madsen, L. Massa, C. F. Matta, K. M. Merz Jr., P. N. H. Nakashima, H. Ott, U. Ryde, K. Schwarz, M. Sierka and S. Grabowsky, Chem. – Eur. J., 2018, 24, 10881–10905 CrossRef CAS PubMed.
- A. Kumar, B. Mohanty and P. Munshi, Cryst. Growth Des., 2023, 23(1), 580–591 CrossRef CAS.
- S. K. Mandal, G. Benoit and P. Munshi, CrystEngComm, 2020, 22, 4363–4373 RSC.
- D. E. Hibbs, J. Overgaard, J. A. Platts, M. P. Waller and M. B. Hursthouse, J. Phys. Chem. B, 2004, 108, 3663–3672 CrossRef CAS.
- V. R. Hathwar and T. N. G. Row, Cryst. Growth Des., 2011, 11, 1338–1346 CrossRef CAS.
- M. S. Pavan, K. D. Prasad and T. N. G. Row, Chem. Commun., 2013, 49, 7558 RSC.
- M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32 RSC.
- P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, CrystalExplorer, J. Appl. Crystallogr., 2021, 54, 1006–1011 CrossRef CAS PubMed.
- C. F. Mackenzie, P. R. Spackman, D. Jayatilaka and M. A. Spackman, CrystalExplorer, IUCrJ, 2017, 4, 575–587 CrossRef CAS PubMed.
- A. Gavezzotti, Acc. Chem. Res., 1994, 27, 309–314 CrossRef CAS.
- A. Gavezzotti, J. Phys. Chem., 1994, 98, 4831–4837 CrossRef CAS.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS PubMed.
- L. Singla, H. R. Yadav and A. R. Choudhury, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76, 604–617 CrossRef CAS PubMed.
- K. Nagarajan, P. K. Talwalker and C. L. Kulkarni, Indian J. Chem., Sect. B: Org. Chem. Incl. Med. Chem., 1985, 24, 83–97 Search PubMed.
- N. K. Hansen and P. Coppens, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1978, 34, 909–921 CrossRef.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, International Series of Monographs on Chemistry 22, Oxford Univ. Press, 1990 Search PubMed.
- CrysAlisPro 1.171.39.35c, Rigaku Oxford Diffraction, Rigaku Corporation, Tokyo, Japan, 2017 Search PubMed.
- R. H. Blessing, Acta Crystallogr., Sect. A: Found. Crystallogr., 1995, 51, 33–38 CrossRef PubMed.
- L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849–854 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- A. Volkov, P. Macchi, L. J. Farrugia, C. Gatti, P. Mallinson, T. Richter and T. Koritsanszky, XD2016 - A computer program for multipole refinement, topological analysis of charge densities and evaluation of intermolecular energies from experimental or theoretical structure factors, 2016 Search PubMed.
- F. H. Allen and I. J. Bruno, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 380–386 CrossRef CAS PubMed.
- A. Ø. Madsen, J. Appl. Crystallogr., 2006, 39, 757–758 CrossRef CAS.
- P. R. Mallinson, T. Koritsanszky, E. Elkaim, N. Li and P. Coppens, Acta Crystallogr., Sect. A: Found. Crystallogr., 1988, 44, 336–343 CrossRef PubMed.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, WIREs Comput. Mol. Sci., 2018, 8, e1360 CrossRef.
- V. V. Zhurov, E. A. Zhurova and A. A. Pinkerton, J. Appl. Crystallogr., 2008, 41, 340–349 CrossRef CAS.
- V. Zavodnik, A. Stash, V. Tsirelson, R. De Vries and D. Feil, Acta Crystallogr., Sect. B: Struct. Sci., 1999, 55, 45–54 CrossRef CAS PubMed.
- F. L. Hirshfeld, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 239–244 CrossRef.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS.
- E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542 CrossRef CAS.
- C. B. Hubschle and B. Dittrich, J. Appl. Crystallogr., 2011, 44, 238 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Statistical analysis based on CSD search, molecular packing diagrams, DRK plots, atomic charges, residual density maps, 2D and 3D static deformation electron density maps, BCPs and associated bond paths, Laplacian maps, topological parameters, and electrostatic potential maps. CCDC 2357897. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4ce00829d |
| ‡ Equal contributions. |
| This journal is © The Royal Society of Chemistry 2025 |