Energetics of charges in organic semiconductors and at organic donor–acceptor interfaces

Abstract

We calculated the energy landscape of charged molecules that is determined by electrostatic and induction interaction using the fully polarizable force field DRF90 in the bulk and at interfaces of the electron accepting material C₆₀, and two exemplary electron donating materials pentacene and phthalocyanine. In particular, we compared the energy of a non-interacting electron–hole pair (NI-EH) without mutual electrostatic interactions to the energy of a Coulomb-bound interfacial charge-transfer state (CT). Our calculations show that due to electrostatic interactions with the environment a NI-EH state is destabilized on the phthalocyanine–C₆₀ interface, whereas it is stabilized on the interface between pentacene and C₆₀, even without the interaction with the counter charge. Upon adding the mutual electrostatic interaction between the opposite charges the electrostatic term overall stabilizes the CT state in both systems. This stabilization is not compensated by the reduced induction term. The resulting binding energy of the CT state amounts to several tenths of an eV, which contradicts the evidence of working solar cells based on these systems. The overestimated CT state binding energy for charges localized on a single molecule suggests that charge delocalization over multiple molecules might play an important role. Nevertheless, our results indicate clear opportunities to engineer electrostatic interactions at the interface that might lead to destabilization of NI-EH and hence to a lower binding energy of CT.

---

Introduction

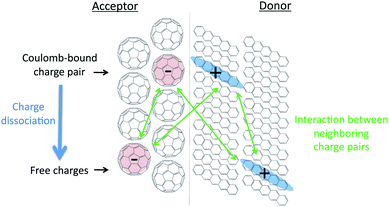
Conjugated organic molecules and polymers constitute a class of materials that is of considerable interest for application in electronic devices such as field effect transistors,¹ light-emitting diodes² and organic solar cells.³ For a detailed understanding of the performance of these materials in such devices it is of key importance to understand the relationship between the structure on the molecular scale and the electronic properties. The energetics of charged species in conjugated materials play a prominent role in the efficiency of devices.⁴ For instance, in field effect transistors the energy of a charged species in the solid state determines the voltage at which charges can be injected in the materials, which is not necessarily the same for the surface of the material and the bulk. Another example is the separation of electron–hole pairs on interfaces between electron donor and acceptor materials in organic solar cells; see Fig. 1.^5–8 This is a subject of intense scientific debate and there is currently no consensus whether a Coulomb-bound charge-transfer (CT) state on the interface has a lower energy than two free charges in the bulk.^9–14 Therefore, it is of considerable interest to perform reliable calculations of the energetics of charges in organic semiconductors and at organic donor–acceptor interfaces. It is relatively straightforward to determine the ionization potential and electron affinity of conjugated molecules in a vacuum, either experimentally or through electronic structure calculations. The opposite is true for the energy that is required to generate a charge on the surface or in the bulk of solid-state materials. The complication is partially related to intermolecular interactions but there are also other aspects such as the delocalization of a charge, which is directly determined by the electronic coupling between neighbouring molecules.¹⁵ The interaction between a charged molecule and the surrounding molecules in the solid is usually very different from that of a neutral molecule. The difference between the ionization potential or electron affinity in the gas phase and in the solid state due to these interactions is known as the polarization energy, P, and consists of several contributions as summarized in eqn (1).

P = E_nuc + E_el + E_ind (1)

Fig. 1 Overview of the interactions that play a role in organic solar cells.

The first contribution, E_nuc, is the nuclear relaxation of the molecule and the lattice due to the presence of the charge. This term has been argued to be small compared to the other two. The two main interactions between the charged molecules and the environment are electrostatic (E_el) and induction (E_ind, dipole-induced dipole) interactions. E_ind is the only true electronic polarization term and therefore the term polarization energy that is used historically is somewhat misleading. A charged molecule inside a solid matrix of neutral molecules will induce dipole moments around itself. These dipoles always have an attractive interaction with the charge that induces them and hence these induction interactions lead to stabilization of the charged molecule compared to the vacuum state. The electrostatic interactions with the surrounding molecules, for instance with permanent dipoles or quadrupoles, can either be repulsive or attractive, depending on the solid state structure of the material and the orientation of these dipoles/quadrupoles with respect to the charged molecule. The calculation of the electrostatic interactions is standard in all force fields for classical molecular dynamics calculations since it is a pairwise additive interaction. A full calculation of the induction interaction is more rare in such force fields since it requires a self-consistent calculation of all induced dipoles, including many body interactions.

In this work we used the fully polarizable Direct Reaction Field (DRF) force field¹⁶ to study the energy of charges and electron–hole pairs in crystalline organic semiconductors in terms of electrostatic and induction interactions. We have investigated the energetics of charges in the bulk and at the surface of several materials that are of importance in organic field effect transistors and organic solar cells. Additionally, we made estimates of the energy required to separate a Coulomb-bound electron–hole pair at a donor–acceptor interface (the CT state) into separate charges. The data presented extend on previous theoretical work that was mostly focused on pentacene–C₆₀ interfaces and the two individual materials.¹⁷ We present data for more materials and explicitly discuss differences between bulk energetics, energetics on the surface and at interfaces. The results show considerable differences in the stabilization energies for charged species in different materials that are primarily dictated by the electrostatic term. It is also shown that for interfacial CT states consisting of charges localized on a single molecule, the binding energy between the electron and the hole is typically an order of magnitude higher than the thermal energy at room temperature. This suggests that for efficient operation of organic solar cells, the delocalization of a charge over multiple molecules is a key requisite.

Computational methodology

In the calculations presented here we have used the classical DRF force field.¹⁶ As noted above, this fully polarizable force field includes a self-consistent calculation of all induced dipoles in the material. The charge distribution over a single molecule was simulated by atomic point charges that were fitted to the electrostatic potential derived from density functional theory calculation in the vacuum using the B3LYP hybrid functional with a cc-pVDZ basis set in the Gaussian 09 program package.¹⁸ The description of the polarisabilities is according to Thole's method for interaction polarizabilities.^19,20

We have used a standard set of polarisabilities that has been parameterized on the basis of a large set of experimental molecular polarisabilities. It has been shown that this yields a transferable method that reproduces experimental polarisabilities of a large range of organic molecules with reasonable accuracy (typically of the order of 5% or less). The quality of the description of the induction interactions by this combination of polarisabilities and point charges has been demonstrated for the calculation of many-body interactions where excellent agreement with ab initio calculations was obtained.²¹ In the DRF approach the polarisability of the molecules can be represented in two ways. In the molecular model each molecule is described by a single anisotropic polarisability at the centre of the molecule. This may lead to over-polarisation in cases where the electric fields inside the material are large, as is the case in this work. A more accurate approach is the atomic model where the polarisability is distributed over all atoms that together constitute the molecular polarisability. A drawback of this approach is the much higher computation cost associated with it. As a compromise we have also examined a mixed model, where the first few layers of molecules are described using the atomic model. At larger distances from the central charged molecules the over polarisation is less problematic and a molecular model is used. A comparison of these models is given in the calculations below. The calculations were performed on spherical clusters of molecules that were generated using the crystal structures of C₆₀, pentacene and phthalocyanine that are known from the literature. For the calculations of charges at the surface of the respective material, the spherical clusters were cut along the most densely packed plane. In order to simulate the interface of the donor and acceptor materials, two of such hemispheres were put together at the distance of the van der Waals radii.

Results and discussion

Charges in organic semiconductors

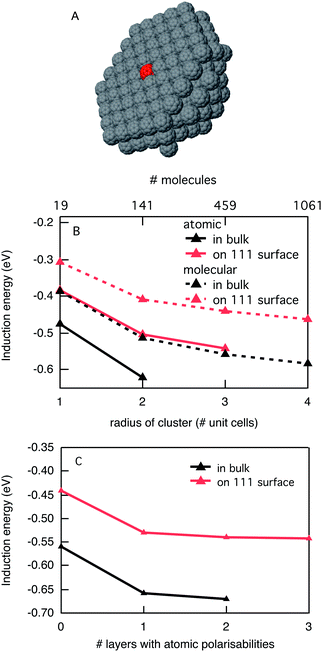
The energy of a charged species in a crystalline organic semiconductor depends strongly on the electronic and geometrical structure of the individual molecules, but also on their packing in the solid state. As discussed above, the main interactions that determine the energy of a charged molecule in the solid are the induction interaction and the electrostatic interaction. The induction interaction is always present, while the electrostatic interaction is only important when the neutral molecules of the material have an appreciable dipole or quadrupole moment. We start our discussion by considering crystalline C₆₀ where electrostatic interactions can be neglected since C₆₀ has no dipole or quadrupole moment. Since C₆₀ is generally considered as an electron acceptor, we have placed a single negatively charged C₆₀ at the center of a spherical cluster of neutral C₆₀ molecules, see Fig. 2A. We calculated the total induction energy for this charged C₆₀ as a function of the size of the cluster of polarizable neutral C₆₀ molecules around it, both using molecular polarisabilities and using a distributed model with 60 atomic polarisabilities per molecule. The results in Fig. 2B show that there is a considerable difference in the calculated induction energy in the molecular polarisability model and the atomic model. The molecular model leads to an underestimation of the induction energy by about 25% for all cluster sizes. This is unfortunate since the computational cost of having 60 times as many polarisabilities in the distributed model limits the size of the clusters that can be treated, especially since the computational cost does not scale linearly with the number of polarisabilities. An interesting intermediate solution for this would be a mixed model in which the first layer(s) of neutral molecules around the charged C₆₀ are treated in terms of atomic polarisabilities while the outer layers are described by molecular polarisabilities. This can be justified by the fact that the largest dipoles are induced in the closest neighbours. In Fig. 2C we show a calculation for a C₆₀ cluster with the fixed radius of three unit cells (459 molecules) with an increasing number of layers of atomic polarisabilities. As noted above, for zero layers of atomic polarisabilities, i.e. only molecular polarisabilities, the induction interaction is considerably underestimated. Addition of a single layer with atomic polarisabilities overcomes this discrepancy for the most part. Using more layers of molecules described with atomic polarisabilities only leads to minor improvements. Therefore, in the case of C₆₀, a mixed description with a single layer of polarisabilities described in atomic detail is a good compromise.

Fig. 2 (A) Schematic representation of a hemispherical C₆₀ cluster with a central negatively charged molecule (in red); (B) induction energy as a function of cluster size for the C₆₀ surface and bulk in the atomic and molecular polarisability description; and (C) effect of combining the atomic and molecular polarisability descriptions.

Using this description, the computational costs are lowered so that the induction energy can be calculated for bigger clusters. The induction energy of a negatively charged C₆₀ inside a C₆₀ crystal converges to −0.66 eV for the largest cluster considered. This means that the electron affinity of C₆₀ increases from 2.65 eV in the gas phase to 3.31 eV in the solid state. When the charged C₆₀ is placed at the surface of a crystal the total induction energy amounts to −0.55 eV, which is about 15% lower than in the bulk. This reduction in the induction energy is relatively small when we consider that only polarisabilities on one side of the central molecule are taken into account. This is a direct consequence of the many-body nature of the induction interactions. The central charge induces dipoles in the surroundings that have an overall attractive interaction with that charged molecule. However, the induced dipoles also have a mutual interaction, and for instance two induced dipoles on opposite (symmetric) sides of the charged C₆₀ will repel each other. Therefore it is impossible to directly extrapolate the induction interactions based on the number of surrounding molecules. For crystalline C₆₀ it means that a negative charge that is injected will prefer to reside in the bulk of the material and not at the surface. This is generally true for all materials if only the induction interaction plays a role. We are not aware of any direct experimental estimate of the difference between the electron affinity in the vacuum and in the solid state. In a UV photo emission spectroscopy study of C₆₀ in the solid state by Sato et al., it was reported that the difference between vacuum and solid state ionization potentials is 0.76 eV.²² It can be expected that the stabilization by the surroundings is similar for a positive and negative charge in C₆₀ since electrostatic interactions do not play a role here. Thus, we find our estimate of the stabilization energy of 0.66 eV in solid C₆₀ in good agreement with the experimental results.

It is of interest to consider how the stabilization of a charge by induction interactions changes when it is delocalized over multiple molecules. Delocalization of a charge will decrease its energy by an amount that is related to the electronic coupling between neighbouring molecules. For two neighbouring C₆₀ molecules in the crystal geometry we have calculated an electronic coupling between the LUMO orbitals of 0.025 eV using the fragment orbital approach. This is a very small value, even compared to the reorganization energy for C₆₀ calculated by density functional theory of 0.2 eV. This is low compared to most other electron accepting materials. Therefore, negative charges are likely to be rather localized in C₆₀. This tendency to localise is strengthened in the solid state since the distribution of a charge over a large number of atoms generally decreases the induction interaction with the surroundings. For C₆₀, when a negative charge is equally distributed over two neighbouring molecules the induction energy reduces by 0.2 eV to −0.46 eV. This shows that a localised charge is likely to be considerably more stable in C₆₀ than a strongly delocalised charge, contrary to what is often assumed.²³

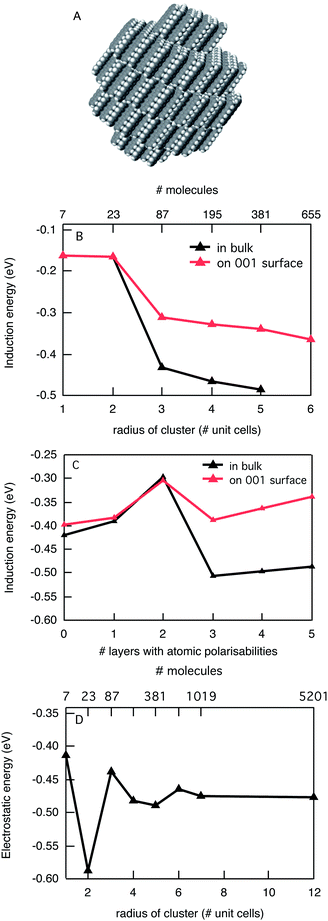
While crystalline C₆₀ is an attractive model material, it is also rather ideal in terms of estimates of the stabilization energy of charges inside the crystal due to the absence of electrostatic interactions and a perfectly isotropic polarisability. This is generally not the case for conjugated organic molecules. Therefore we consider a prototype p-type organic semiconductor, pentacene. Pentacene has an elongated planar structure resulting in an appreciable quadrupole moment and a very anisotropic polarisability. The solid-state structure of pentacene is a layered conformation as shown in Fig. 3A. In Fig. 3B the calculated induction energy is shown as a function of the cluster size for the description in terms of atomic polarisabilities. For the largest cluster that could be considered, the induction energy is −0.49 eV for the bulk, while it is −0.34 eV on the surface. The difficulties related to the large anisotropy in the polarisability of pentacene are illustrated in Fig. 3C where we explore the possibility to limit the description in terms of atomic polarisabilities only to the first few layers. It is clear from this figure that the combination of atomic and molecular descriptions leads to large oscillations in the induction interactions as a function of the number of layers of atomic polarisabilities that is included. For up to two layers of atomic polarisabilities only an increasing number of molecules in the (001) plane of the charged pentacene are described in terms of atomic polarisabilities. Due to the elongated shape of the molecules the large point polarizability located at the centre of mass of the molecule is relatively close to the neighbouring pentacene in the same layer, leading to substantial over-polarization when only molecular polarisabilities are considered. This overpolarisation is reduced upon increasing the number of atomic polarisabilities in the same layer (0–2 layers and 3–5 layers). However, at the same time the induction term is underestimated because of the large distance between the charged pentacene and the group polarisability of molecules in the adjacent (001) plane. This explains the strong increase in induction stabilization at 3 layers with atomic polarisabilities.

Fig. 3 (A) Space-filling model of a spherical cluster of pentacene molecules. (B) Induction interaction as a function of size for a positive charge at the center of a spherical pentacene and on the surface. (C) Effect of adding multiple layers of atomic polarizabilities in a molecular polarizability model. (D) Electrostatic interaction of a positive charge in a spherical pentacene cluster as a function of the size of the cluster.

The presence of a large quadrupole moment in pentacene means that appreciable electrostatic interactions of the charged molecules with the surrounding are expected. In Fig. 3D we show the electrostatic interaction as a function of the size of the cluster considered. The electrostatic interactions show peculiar oscillatory behaviour that can be understood when considering the shape of the cluster of molecules in each case. For cluster sizes with radii up to the dimensions of two unit cells all molecules are oriented parallel in the same layer of molecules. This leads to strongly attractive electrostatic interactions of up to 0.6 eV. When the size of the cluster is increased further, additional layers of molecules are added and the interaction of the charge with these layers is repulsive and the total electrostatic interaction decreases. For the limit of large cluster sizes the electrostatic interaction converges to −0.48 eV in the bulk, and −0.63 eV on the surface. The larger electrostatic interactions for a charge on the surface are due to the repulsive interaction of the positively charged pentacene molecule with the positive point charges on the H atoms of neutral pentacene molecules in neighbouring layers. While the electrostatic interactions make it favourable for a charge to reside on the surface of the crystal, the induction interactions are larger in the bulk of the material and in the case of the (001) surface in pentacene the differences exactly cancel. This leads to an overall stabilization of a positive charge in pentacene of −0.97 eV for both the surface and the bulk as compared to the gas phase. This value is in agreement with recent theoretical estimates by Ryno et al. who derived a value for what they call a polarization energy of −1.02 eV using a very similar polarizable force field.¹⁷ Both theoretical estimations are substantially smaller than the experimental estimate derived from UV photoelectron spectroscopy in the gas phase and for solid-state pentacene.²⁴ From these measurements a value of −1.63 eV was obtained. One source for this discrepancy is the absence of lattice relaxation and surface reorganisation in our model.

Allowing the surrounding pentacene molecules to adapt their position and orientation to the presence of the charge would lead to an increase of the interaction energy, however, it has been argued that such lattice relaxation is relatively small (∼10 meV).^24–26 Additionally, delocalization of the charge over multiple molecules can lead to stabilization.²⁷

It is interesting to note that the calculation for a negative charge in pentacene gives a very different result. While the induction interactions are very similar to the positive charge, the electrostatic interactions are repulsive. Consequently, the calculated electron affinity of pentacene in the solid state is approximately the same as in the vacuum since the stabilization by induction is cancelled by the repulsive electrostatic interactions. This explains the lower polarization energy found experimentally (−1.17 eV) for excess negative charges in pentacene, as compared to those for the holes.²⁴

The total difference between the vacuum and solid-state ionization potential is still substantial, suggesting that there is another source of stabilization, apart from induction and electrostatics that is not included in our calculations.

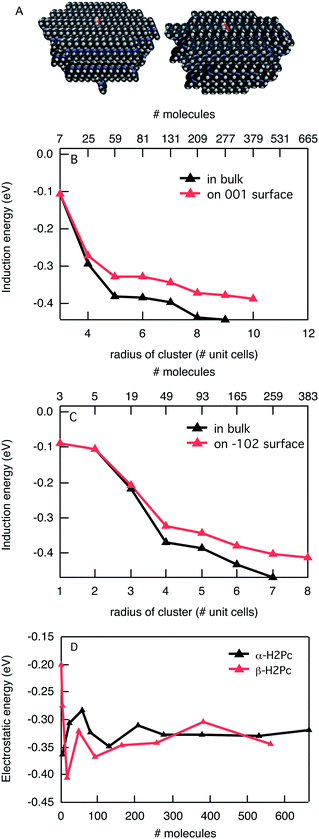
The size and shape of molecules and the way they are organized in the crystal structure can influence the energetics strongly. An additional illustration of this is presented by the energy of positive charges in phthalocyanine in two different crystal structures as presented in Fig. 4. In Fig. 4B and C the induction interaction is shown as a function of the size of the spherical cluster and on the surface of a semi sphere for the α- and β-crystal phases of phthalocyanine, respectively. The calculations were performed in the distributed atomic polarisability description. Again, the total induction interaction slowly converges for larger cluster sizes but for the largest size it is not fully saturated. As was the case for C₆₀ and pentacene, the induction is larger in the bulk than it is on the surface, but only by about 20%. The electrostatic interaction shows similar oscillatory behavior as for pentacene but with a smaller overall value. The latter is due to a more delocalized charge over the larger phthalocyanine molecule compared to a pentacene molecule. The oscillatory behaviour is again caused by differences in the interactions of the charged molecule with those surrounding it. These interactions can either be attractive of repulsive. The total stabilization of the charge in α-phthalocyanine is −0.76 eV in the bulk and −0.70 eV on the surface, while for β-phthalocyanine the corresponding values of −0.82 eV and −0.68 eV are found. The results show that in this case the difference between the two crystal forms of phthalocyanine is small. This can be understood when considering the structure of the crystal. On a small scale, the stacking of neighbouring molecules in the solid is very similar, while there are substantial differences in the mutual orientation of the neighbouring stacks. Since the nearest molecules have the largest effect, both on the electrostatic and induction interaction, the differences are small here. The overall stabilization of the charge in phthalocyanine by roughly 0.8 eV leads to a lowering of the gas phase ionization potential of 6.41 eV (ref. 28) to 5.6 eV in the bulk. This is in reasonable agreement with experimental estimates of the solid state ionization potential of 5.0–5.2 eV.^29,30 In both crystal structures a charge is stabilized more in the bulk than on the surface, which is a result of both electrostatic and induction effects. Yoshida et al. have recently estimated the differences in stabilization energy for the surface and the bulk for several organic semiconductors using angle-resolved photoemission spectroscopy.³¹ The difference in stabilization found for Cu-phthalocyanine was 0.2 eV, which is reasonably close to the value of 0.14 eV that we find for β-phthalocyanine.

Fig. 4 (A) Space-filling model of α (left) and β (right) phthalocyanine clusters. (B) Induction interaction of a positive charge in α-phthalocyanine in the bulk and on the surface. (C) Induction interaction of a positive charge in β-phthalocyanine in the bulk and on the surface. (D) Electrostatic interaction of a charged molecule in a spherical cluster of α- and β-phthalocyanine.

Charge separation at organic donor–acceptor interfaces

For organic solar cells it is of particular interest to consider the energetics of charges at the interface between an electron donating and an electron accepting material. We have chosen two donor–acceptor combinations that have been widely studied experimentally; pentacene–C₆₀ and β-phthalocyanine–C₆₀. The energetics of the individual electron and hole at the donor–acceptor interface were studied in spherical clusters consisting of two hemispheres of the respective materials as shown in Fig. 5. These calculations indicate whether the individual electron or hole is more stable at the interface than in the bulk material. In the terminology used in the field of inorganic semiconductors this information indicates the type of band bending on an interface between different materials.

Fig. 5 Interfaces between a (111) surface in C₆₀ and a (001) surface of pentacene and a (1̄02) surface in β-phthalocyanine.

The combined energetics of such a non-interacting electron–hole pair (NI-EH) was compared to that of a Coulomb-bound electron–hole pair forming an interfacial CT state. The results of the calculations are summarized in Table 1.

Table 1 Energetics of charges and interfacial charge transfer states on the interface of organic donor and acceptor materials. All energies are given in eV

		Negative			Positive
		E ind	E elst	E tot	E ind	E elst	E tot
C60–pentacene	Bulk	−0.66	0.0	−0.66	−0.49	−0.48	−0.97
	Int.	−0.52	−0.16	−0.68	−0.49	−0.63	−1.12
C60–β-phthalocyanine	Bulk	−0.66	0.0	−0.66	−0.47	−0.35	−0.82
	Int.	−0.63	+0.07	−0.56	−0.46	−0.28	−0.74
		NI-EH			CT state
C60–pentacene	Bulk	−1.15	−0.48	−1.63	−1.15	−0.48	−1.63
	Int.	−1.01	−0.79	−1.80	−0.48	−2.00	−2.48
C60–β-phthalocyanine	Bulk	−1.13	−0.35	−1.48	−1.13	−0.35	−1.48
	Int.	−1.09	−0.21	−1.30	−0.54	−1.44	−1.98

---

For a single negative charge in C₆₀ at the interface with pentacene the total induction interaction is −0.52 eV, which is less than in the bulk of C₆₀. Although it is tempting to attribute this to a difference in the dielectric constant of the two materials, it is important to realize that the dielectric constant is not a valid quantity on a molecular scale.³² Not only can the dielectric response be different on this small scale, there can also be anisotropy effects especially when considering elongated molecules with a specific orientation in the crystal. The electrostatic interaction of a negatively charged C₆₀ at the interface with pentacene is −0.16 eV, showing a clear attractive interaction with the quadrupolar pentacene. Note that upon choosing a different crystal orientation of pentacene, the electrostatic interaction might be repulsive. Overall, a negative charge in C₆₀ is slightly more stabilized on the interface (by ∼0.02 eV) than in the bulk. For a positive charge in pentacene the induction interactions are of equal magnitude on the interface with C₆₀ as they are in the bulk of pentacene. This is a result of the specific interaction on a small scale and clarifies the argument stated above that the difference in induction interaction cannot be related to the macroscopic dielectric constant in a straightforward manner. The electrostatic interaction of a positive charge in pentacene at the interface with C₆₀ is equally stabilizing as at the pentacene surface in the calculations presented above since all electric multipole moments of C₆₀ are zero. Therefore, also the positive charge in pentacene is overall stabilized at the interface. Most importantly, the results show that both positive and negative charges prefer to reside at the pentacene–C₆₀ interface, even though no counter charge is present at the other side of the interface. For pentacene–C₆₀ the total energy of the NI-EH state at the interface is 0.17 eV lower than that of two charges in the respective bulk materials.

An opposite trend is observed for the interface between β-phthalocyanine and C₆₀. For a negative charge the induction interaction on the interface and in the bulk of C₆₀ are very similar, −0.63 eV and −0.66 eV, respectively. The electrostatics however give rise to stabilization by 0.07 eV of the charge in the bulk, indicating a repulsive interaction between the charge and the quadrupole of phthalocyanine in this particular orientation. In total, the negative charge is stabilized by 0.10 eV in the bulk of C₆₀, as compared to the interface. Similarly, the induction interaction of the positive charge in β-phthalocyanine is virtually the same in the bulk and at the interface but the electrostatic stabilization is larger in the bulk by 0.08 eV.

Consequently, in contrast to the observations for the pentacene–C₆₀ interface, both charges will move away from the interface when disregarding the attractive interaction with the counter charge. The energy of the interfacial NI-EH state is 0.18 eV higher in energy than the energy of free charges in the bulk materials. These results are in qualitative agreement with experimental work by Akaike et al. who studied the electronic structure of phthalocyanine–C₆₀ interfaces.³³ From a combination of UV photoelectron, X-ray photoelectron and inverse photoemission spectroscopies they concluded that the polarization energy (the energy difference between the ionization potential in the vacuum and in the solid) is smaller at the interface than in the bulk material for both the electron and the hole.³³

The calculations above do not take any mutual interaction between the positive and negative charge on the interface into account, neither induction nor electrostatic. However, these interactions do play a key role in the transition from a Coulomb-bound electron–hole pair at the interface to free charges in the respective bulk materials. While the attractive Coulomb interaction can simply be added on top of the so far calculated interactions of NI-EH, the induction interaction between the two charges is not additive. This is due to a different induction interaction of the interfacial charge-transfer state with the environment as compared to the induction interaction of two individual isolated charges on the interface. Therefore, the induction energy has to be calculated in a separate calculation with the opposite charges at the interface. In Table 1 we list the energetics for these interfacial CT states on pentacene–C₆₀ and β-phthalocyanine–C₆₀ interfaces and compare them to the total stabilization of the two separated charges in the respective bulk materials. In both materials the total induction interaction for the CT state is lower by more than a factor of two, compared to the free charges in the bulk. This can easily be understood since the dipoles that are induced by positive and negative charges have opposite directions. Hence, a dipole induced by a negatively charged C₆₀ will have a repulsive interaction with the positive charge on the pentacene nearby. Therefore, if only the induction interaction is considered, the separation of the CT state into separate charges is energetically favourable. However, the total electrostatic interaction is much larger for the interfacial charge transfer state compared to the two charges in the bulk. Overall, this leads to stabilization of the CT state at the interface for both combinations studied here. For pentacene–C₆₀ the CT state is more stable by 0.85 eV, while for β-phthalocyanine–C₆₀ the energy difference is 0.50 eV. Both these values are very large compared to the thermal energy at room temperature and it is very unlikely that charges should escape from recombination when they are formed close together on these interfaces. This is in disagreement with the experimental observations that highly efficient solar cells can be constructed of both of these material combinations, with internal quantum efficiencies close to 100%. One of the reasons for this discrepancy can be the absence of geometry relaxation in our model (and in most other classical evaluations of CT energetics); we have used static geometries for these calculations. While intramolecular and intermolecular geometry relaxation can give stabilization energies up to a few tenths of an eV, it is not likely that there are large differences for charged molecules in the bulk and on the interface, especially for intramolecular relaxation. A more plausible explanation is the restrictions in the delocalization of the charge imposed by our static classical model. The charge distribution is fixed on a single molecule. This means that possible delocalization of the charge over multiple molecules is not accounted for. Such delocalization would lead to significantly reduced electrostatic interactions in the CT state since the average distance is larger. At the same time, the stabilization of a delocalized charge by induction interaction in the bulk state is also reduced compared to a localized charge, as shown above for C₆₀. It is not clear a priori which of these two effects will dominate. An accurate theoretical prediction of the degree of charge delocalization is certainly not straightforward. For instance in density functional theory, there are severe problems in describing charge delocalization, already inside a single molecule.³⁴ An additional shortcoming in our present approach is the static charge distribution of the charged molecules, which were calculated for isolated molecules. The presence of a neighbouring charge in an interfacial CT state could lead to substantial redistribution of the charges in the molecules. The attraction by a counter charge may lead to localization of the charge because of an increased electrostatic interaction. Whether this is important depends on the relative magnitude of the increased electrostatic interaction and the energetic cost of polarization.

Conclusions

In this paper we have discussed the energetics of charges in organic semiconductors and on organic donor–acceptor interfaces using a fully polarizable classical force field. It is shown that both the induction and electrostatic interactions converge only for large clusters of molecules and that it is in general necessary to use an atomic description of the polarisabilities rather than molecular polarisabilities. Induction interactions of a charged molecule with the surroundings are always larger in the bulk material than on the surface by approximately 25%. Electrostatic interactions are strongly dependent on the organization on the molecular scale and may either be repulsive or attractive. Therefore, a charge may either be stabilized more in the bulk or on the surface. The same is true for the interface between an electron-donating and an electron-accepting material. For a pentacene–C₆₀ interface both the positive and negative charges have a lower energy on the interface than in the bulk. In phthalocyanine–C₆₀ this trend is reversed; charges are stabilized more in the bulk than on the surface, resulting in an energy landscape that is favourable for efficient charge separation in organic solar cells. For an interfacial charge-transfer state it was found that the induction interaction is larger for the free charges in the bulk than for a CT state at the interface by roughly a factor of two. This is not sufficient to overcome the strong stabilization of the CT state by the mutual electrostatic attraction between the positive and negative charge. This strongly attractive term, together with the stabilization of the individual charges at the pentacene–C₆₀ interface, results in a high binding energy for the CT state of 0.85 eV. But also in phthalocyanine–C₆₀ the mutual attraction outweighs the destabilization of both the induction and the (in this case favourable) energy landscape for formation of free charges, resulting in a CT state that is stabilized by 0.5 eV. However, the significantly lower binding energy suggests that by finding an optimal combination of donor and acceptor combination in terms of materials, crystal structures, and crystal orientation, an energy landscape of free charges might be achieved that compensates the mutual attraction and diminishes the binding energy. Additionally, we have to point out that the large stabilization of the CT state at the interface, obtained in our calculation, would exclude efficient charge separation, contrary to experimental observations. We believe that the delocalization of charge over multiple molecules is a likely explanation for this discrepancy.¹³ To allow charge delocalization it is necessary to describe a sufficiently large part of the system quantum mechanically while keeping a fully polarizable surrounding.³⁵ Such a QM/MM approach has been implemented for the DRF force field that is used here however, the use of such models for accurate predictions is not straightforward, especially since the description of charge delocalization in a fully quantum mechanical calculation already suffers from artefacts.

Acknowledgements

This work was supported by the Netherlands Organization for Scientific Research (NWO) through an VIDI grant to FCG and by the European Research Council (ERC) in the form of ERC Starting Grant to FCG. The following organizations are thanked for financial support: the Ministerio de Ciencia e Innovación (MICINN, project number CTQ2011-25086/BQU) and the DIUE of the Generalitat de Catalunya (project number 2009SGR528, and Xarxa de Referència en Química Teòrica i Computacional). Financial support from MICINN (Ministry of Science and Innovation, Spain) and the FEDER fund (European Fund for Regional Development) was provided by grant UNGI08-4E-003.

Notes and references

1. H. Sirringhaus, P. J. Brown, R. H. Friend, M. M. Nielsen, K. Bechgaard, B. M. W. Langeveld-Voss, A. J. H. Spiering, R. A. J. Janssen, E. W. Meijer, P. Herwig and D. M. de Leeuw, Nature, 1999, 401, 685–688.
2. J. H. Burroughes, D. D. C. Bradley, A. R. Brown, R. N. Marks, K. MacKay, R. H. Friend, P. L. Burns and A. B. Holmes, Nature, 1990, 347, 539–541.
3. C. W. Tang, Appl. Phys. Lett., 1986, 48, 183–185.
4. L. E. Lyons, J. Chem. Soc., 1957, 5001–5007.
5. D. Beljonne, J. Cornil, L. Muccioli, C. Zannoni, J. L. Bredas and F. Castet, Chem. Mater., 2011, 23, 591–609.
6. S. R. Yost and T. Van Voorhis, J. Phys. Chem. C, 2013, 117, 5617–5625.
7. S. R. Yost, L.-P. Wang and T. Van Voorhis, J. Phys. Chem. C, 2011, 115, 14431–14436.
8. G. D'Avino, S. Mothy, L. Muccioli, C. Zannoni, L. Wang, J. Cornil, D. Beljonne and F. Castet, J. Phys. Chem. C, 2013, 117, 12981–12990.
9. R. D. Pensack and J. B. Asbury, J. Am. Chem. Soc., 2009, 131, 15986–15987.
10. C. Deibel, T. Strobel and V. Dyakonov, Phys. Rev. Lett., 2009, 103, 036402.
11. T. M. Clarke and J. R. Durrant, Chem. Rev., 2010, 110, 6736–6767.
12. J. R. Durrant, Philos. Trans. R. Soc. London, Ser. A, 2013, 371, 20120195.
13. D. H. K. Murthy, M. Gao, M. J. W. Vermeulen, L. D. A. Siebbeles and T. J. Savenije, J. Phys. Chem. C, 2012, 116, 9214–9220.
14. K. S. Jeong, R. D. Pensack and J. B. Asbury, Acc. Chem. Res., 2013, 46, 1538–1547.
15. M. Pope and C. E. Swenberg, Electronic processes in organic crystals and polymers, Oxford University Press, Oxford, 1999.
16. M. Swart and P. T. van Duijnen, Mol. Simul., 2006, 32, 471–484.
17. S. M. Ryno, S. R. Lee, J. S. Sears, C. Risko and J. L. Bredas, J. Phys. Chem. C, 2013, 117, 13853–13860.
18. M. J. Frisch, G. W. Trucks, S. H. B., G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford, CT, 2009.
19. B. T. Thole, Chem. Phys., 1981, 59, 341–350.
20. P. T. van Duijnen and M. Swart, J. Phys. Chem. A, 1998, 102, 2399–2407.
21. F. C. Grozema, R. W. J. Zijlstra and P. T. van Duijnen, Chem. Phys., 1999, 246, 217–227.
22. N. Sato, Y. Saito and H. Shinohara, Chem. Phys., 1992, 162, 433–438.
23. B. Bernardo, D. Cheyns, D. Verreet, R. D. Schaller, B. P. Rand and N. C. Giebink, Nat. Commun., 2014, 5, 3245.
24. N. Sato, H. Inokuchi and E. A. Silinsh, Chem. Phys., 1987, 115, 269–277.
25. E. A. Silinsh and V. Capek, Organic molecular crystals: Interaction, localization and transport phenomena, AIP, New York, 1994.
26. F. Amy, C. Chan and A. Kahn, Org. Electron., 2005, 6, 85–91.
27. Z. G. Soos, M. H. Hennessy and G. Wen, Chem. Phys., 1998, 227, 19–32.
28. J. Berkowitz, J. Chem. Phys., 1979, 70, 2819–2828.
29. F. Piersimoni, D. Cheyns, K. Vandewal, J. V. Manca and B. P. Rand, J. Phys. Chem. Lett., 2012, 3, 2064–2068.
30. D. R. T. Zahn, G. N. Gavrila and M. Gorgoi, Chem. Phys., 2006, 325, 99–112.
31. H. Yoshida and N. Sato, J. Phys. Chem. C, 2012, 116, 10033–10038.
32. P. T. Van Duijnen and M. Swart, J. Phys. Chem. C, 2010, 114, 20547–20555.
33. K. Akaike, K. Kanai, Y. Ouchi and K. Seki, Adv. Funct. Mater., 2010, 20, 715–721.
34. F. C. Grozema, L. P. Candeias, M. Swart, P. T. van Duijnen, J. Wildeman, G. Hadziioannou, L. D. A. Siebbeles and J. M. Warman, J. Chem. Phys., 2002, 117, 11366–11378.
35. F. C. Grozema, M. Swart, R. W. J. Zijlstra, J. J. Piet, L. D. A. Siebbeles and P. T. Van Duijnen, J. Am. Chem. Soc., 2005, 127, 11019–11028.

---