 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Pattern formation of lipid domains in bilayer membranes†
Qiwei
Yu
 a and
Andrej
Košmrlj
a and
Andrej
Košmrlj
 *bc
*bc
aLewis-Sigler Institute for Integrative Genomics, Princeton University, Princeton, NJ 08544, USA
bDepartment of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA. E-mail: andrej@princeton.edu
cPrinceton Materials Institute, Princeton University, Princeton, NJ 08544, USA
First published on 5th May 2025
Abstract
Phase separation plays an important role in spatial organization and material distribution of biological membranes, which are essential for crucial biological functions ranging from signaling and stress response to vesicle trafficking. Domains arising from demixing of molecules coarsen indefinitely unless growth is arrested at a finite size by additional mechanisms (e.g., membrane elasticity). The resulting finite-size domains self-organize into regular patterns such as stripes and dots, which are called modulated phases. Here, we examine the size and morphology of lipid domains with a minimal theoretical model that considers both the elastic deformation of the membrane and the chemical interactions between lipids, which are coupled by a preferred membrane curvature that depends on the local lipid composition. Microscopically, the coupling is caused by an asymmetry between leaflets which emerges after extra lipids (e.g., DPPC) are introduced to the outer leaflet. The additional lipid partitions preferentially to domains where it is enriched, creating a preferred curvature that depends on local composition. We use an amplitude expansion to determine the domain size and morphology of patterns that minimize the total free energy, which is validated by numerical simulations and compared against experiments in synthetic model membranes and cell-derived membranes. The morphology of patterns varies with membrane lipid composition following a complex morphological diagram, which is in good agreement with experiments. The domain size decreases monotonically with a membrane bending modulus but can be non-monotonic with surface tension. Our results offer testable predictions, such as pattern hysteresis upon cycling external stimuli, diverse pattern morphology near critical points, and non-monotonic dependence of the domain size on osmotic pressure, which motivate future experiments. The presented theoretical framework is generally applicable to pattern formation on deformable surfaces.
1 Introduction
The heterogeneous spatial organization of lipids, proteins, and other components of biological membranes plays a crucial role in essential physiological functions.1,2 To understand the mechanism underpinning the formation of these spatial structures, several model systems have been established, including cell-derived membranes3 and artificial membrane systems such as giant unilamellar vesicles (GUVs).4,5 One important mechanism is liquid–liquid phase separation, which organizes the membrane into domains with distinct compositions. These phase-separated domains participate in the regulation of various physiological processes, such as signaling, immune response, and vesicle trafficking.6–10 Notably, phase separation in yeast vacuoles can promote survival under stress by organizing proteins for a nutrient-sensing pathway or by facilitating lipophagy.11–13 One possible mechanism for lipid domains to achieve regulatory functions is by facilitating condensation of proteins on the membrane through a prewetting transition.14One important aspect of membrane organization is how domain size and morphology are regulated. In artificial membranes, phase separation has been observed in membranes consisting of as few as three components.4,15,16 When the membrane is quenched into the 2-phase region, phase separation commences with the nucleation of many small droplets, which subsequently grow in size until reaching the dimension of the system.17 Eventually, only a few macroscopic domains persist. Under certain conditions (such as bilayer asymmetry), however, the domains can remain at a small size and form stable periodic patterns such as stripes or dots. These extensive periodic structures are also referred to as “modulated phases”.18–21 These domains do not strictly result from equilibrium phase separation, where only one domain of each phase should remain; however, we use the term “phase separation” to reflect that lipid demixing arises from the same interactions as macroscopic phase separation, in line with terminology in the field.22,23 A recent experiment18 studied in detail domains in both synthetic membranes (GUVs) and cell-derived membranes by measuring their length scale and spatial organization under different experimental conditions, including temperature, membrane composition, and tension (see Fig. 1E for micrographs of patterns). The domain size was found to increase with surface tension but decrease with temperature, and the morphology could switch between stripes and dots as the average lipid composition was varied (see Fig. 1D and E). These quantitative measurements enabled close comparisons with multiple existing theories.20–38 In particular, two of the approaches considered spontaneous curvature at the level of monolayer25,26 and bilayer.22 Both captured many aspects of the experiments, but neither appeared consistent with all the observations:18 the monolayer theory incorrectly predicts anti-registration between leaflets; the bilayer theory does not capture the morphology near the critical points, possibly because it employed a simplified depiction of the free energy of chemical interactions of lipids, which only contained a line tension between different domains. Other mechanisms were also considered but ruled out, including correlated critical fluctuations30 or lipid cycling.34 Electric dipole interaction can drive pattern formation in lipid monolayers,39–41 but it does not appear to be the dominant mechanism for domain formation in a bilayer.18,27–29 Lineactants effects are also unlikely since the system lacks hybrid lipids,18,31 and the additional DPPC would likely partition to one of the domains instead of at the interface.42,43 Thus, finding a theory consistent with the existing measurements will be crucial for understanding the mechanism underlying lipid domain formation.
 | ||
Fig. 1 The theoretical model captures pattern formation on the membrane. (A) Schematics of the model. The membrane consists of three molecules: the two phospholipids (pink and gray) and cholesterol (green). They demix into phase A (yellow) and phase B (gray). Phase A is rich in lipid species 1 and therefore more curved. h describes the deformation of the membrane. (B) Pattern morphology as a function of the average volume fractions ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 1,2,3. The colored regions indicate analytical predictions of the morphology, and the colored dots are numerical simulations. The black dashed line indicates a typical tie line, with the white line indicating its perpendicular direction. The two critical points are marked by red ★. (C) Examples of the steady-state solution ϕ1(x,y) with different pattern morphologies, including stripes [upper left, ( 1,2,3. The colored regions indicate analytical predictions of the morphology, and the colored dots are numerical simulations. The black dashed line indicates a typical tie line, with the white line indicating its perpendicular direction. The two critical points are marked by red ★. (C) Examples of the steady-state solution ϕ1(x,y) with different pattern morphologies, including stripes [upper left, (![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 1, 1,![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 2) = (0.45,0.40)], mixed [upper right, ( 2) = (0.45,0.40)], mixed [upper right, (![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 1, 1,![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 2) = (0.45,0.34)], dots [lower left, ( 2) = (0.45,0.34)], dots [lower left, (![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 1, 1,![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 2) = (0.43,0.29)], and localized [lower right, ( 2) = (0.43,0.29)], and localized [lower right, (![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 1, 1,![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 2) = (0.21,0.25)] patterns. (D) and (E) Experimental phase diagram and micrographs for DiPhyPC/DPPC/cholesterol vesicles, reproduced from Fig. 10 of Cornell et al.18 with permission. The black line connecting the circles denotes a tie line. Parameters for (B) and (C): χ12 = 1.8, χ13 = 1.4, χ23 = 1.65, ξ = 4.8, κ = 20, σ = 0.1, 2) = (0.21,0.25)] patterns. (D) and (E) Experimental phase diagram and micrographs for DiPhyPC/DPPC/cholesterol vesicles, reproduced from Fig. 10 of Cornell et al.18 with permission. The black line connecting the circles denotes a tie line. Parameters for (B) and (C): χ12 = 1.8, χ13 = 1.4, χ23 = 1.65, ξ = 4.8, κ = 20, σ = 0.1,  . . | ||
In this work, we present a minimal theoretical model to demonstrate that local curvature-composition coupling is sufficient for explaining existing experiments. Specifically, the model incorporates both the elastic deformation of the membrane and the chemical interactions of lipids, which are coupled by a preferred membrane curvature. The preferred curvature depends on the composition of lipids and emerges from a leaflet asymmetry resulting from introducing extra lipids to the outer leaflet, which was indeed an essential procedure for stabilizing small domains in the experiments.18 Our model demonstrates that the coupling between curvature and composition arrests the coarsening of lipid domains, leading to patterns at a finite length scale. This model shares ingredients of previous works on curvature-composition coupling,22,24–26,35 but we aim to identify the minimal model to explain the experimentally observed patterns.
Our model generates useful insights into pattern size and morphology. First, we use an amplitude expansion to obtain analytical solutions for all possible patterns, which are confirmed by numerical simulations of the full model. In particular, we construct a phase diagram of all possible morphologies in a ternary membrane, providing important intuitions for systematically probing them in experiments. Second, the theory also predicts that domain size decreases with temperature and increases with membrane tension when the tension is sufficiently large, consistent with experiments. Third, amplitude expansion identifies bistability between morphologies and predicts that the morphology will undergo hysteresis when parameters such as osmotic pressure or temperature are cycled. The hysteresis is demonstrated in the simulations and can be tested in experiments in order to further constrain model parameters. It will also be interesting to study the dynamics of defects during morphological transitions. Overall, these results uncover new directions for probing the mechanism underlying small domains in biological membranes and provide valuable insights for understanding pattern formation on curved and deformable surfaces.
2 Model and methods
The theory considers three interacting lipid species that can move on a deformable bilayer membrane (Fig. 1A). They include two phospholipids (red and gray) (such as DPPC and DiPhyPC used in ref. 18) and cholesterol (green). The shape of the membrane is described by the height field h(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), defined as the distance from a flat reference plane. The composition of the membrane is defined by the (local) volume fractions occupied by different molecules ϕi(
), defined as the distance from a flat reference plane. The composition of the membrane is defined by the (local) volume fractions occupied by different molecules ϕi(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), with i = 1, 2, 3 labeling the three lipid species, respectively. They are constrained by an incompressibility condition
), with i = 1, 2, 3 labeling the three lipid species, respectively. They are constrained by an incompressibility condition  . Motivated by experimental evidence,18 the two leaflets of the bilayer are assumed to be in registration, i.e. with the same volume fractions. Therefore, only a single set of fields ϕi(
. Motivated by experimental evidence,18 the two leaflets of the bilayer are assumed to be in registration, i.e. with the same volume fractions. Therefore, only a single set of fields ϕi(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is considered for both leaflets. The membrane composition and shape undergo dynamics governed by the following free energy:
) is considered for both leaflets. The membrane composition and shape undergo dynamics governed by the following free energy: | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) = (x,y)]. The free energy due to membrane deformation is given by
= (x,y)]. The free energy due to membrane deformation is given by | (2) |
 .
.
The second part of the free energy comes from the interaction and mixing of lipids:
 | (3) |
The free energy governs the time evolution of the fields, with h undergoing unconserved (model A) dynamics and ϕ1,2 undergoing conserved (model B) dynamics:48
 | (4) |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) c = fc/(nkBT) as well as the nondimensionalized material properties
c = fc/(nkBT) as well as the nondimensionalized material properties ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) = κ/(nkBT),
= κ/(nkBT), ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = σλ2/(nkBT). Space is rescaled as
= σλ2/(nkBT). Space is rescaled as ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = x/λ, and the preferred curvature is rescaled as
= x/λ, and the preferred curvature is rescaled as ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) 1 = λc1. For the sake of simplicity, we assume equal mobilities M1 = M2 = M and rescale time as
1 = λc1. For the sake of simplicity, we assume equal mobilities M1 = M2 = M and rescale time as ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = t/t0 = tnkBTM/λ2 so that the rescaled mobilities are 1. h is nondimensionalized so that the rescaled Mh is also 1. From now on, we will omit− and refer to nondimensionalized quantities unless explicitly stated.
= t/t0 = tnkBTM/λ2 so that the rescaled mobilities are 1. h is nondimensionalized so that the rescaled Mh is also 1. From now on, we will omit− and refer to nondimensionalized quantities unless explicitly stated.
In this theory, the preferred curvature plays the key role of coupling deformation h and concentrations ϕi. In the absence of preferred curvature (c1 = 0), the membrane is flat (h = 0) and the concentrations behave like a typical ternary liquid mixture, which is either uniform or demixed into different domains. When demixed, the domains coarsen perpetually until they reach the system size. These large domains have been observed in many membrane systems.16,17,49 By coupling the concentrations to membrane deformation, the preferred curvature introduces an effective free energy cost against coarsening, which, when significant enough, arrests domain coarsening at a finite length scale. Hence, as will be shown analytically in the following sections, the steady-state domain size is selected by a competition between the chemical interactions of lipids and membrane deformation. This mechanism should be distinguished from that of domain formation in block copolymers, where the energetic repulsion between constituent monomers is balanced by the entropic forces of polymer chain configurations.50–55 The latter is usually referred to as microphase separation, which is fundamentally different from the mechanism described here.
Numerical simulation of the model reveals patterns with a variety of morphologies (Fig. 1C), including stripes, dots (arranged in a hexagonal lattice), mixed states (a combination of stripes and dots), and localized states (isolated and stationary droplets). These patterns are similar to those observed in experiments18 and are reminiscent of those found in phase field crystal models.56–62 The stable morphology of the pattern depends on the average composition of the membrane ϕi, which is illustrated by a phase diagram (Fig. 1B). The parameters were chosen such that the phase diagram qualitatively resembles that measured experimentally (Fig. 1D and E).18 The same set of parameters is used throughout unless varied explicitly. Note that each of the morphologies is a modulated phase of macroscopic extent, each of which occupies a distinct region in the phase diagram (Fig. 1B). Here, we refer to them as “states” to avoid confusion with individual lipid domains that arise from demixing, which may experience coarsening arrest to form finite domains. In the following, we characterize these patterns combining analytical and numerical methods and discuss implications for both existing and future experiments.
3 Results
3.1 Membrane deformation arrests domain coarsening
We start by analyzing the size of the small domains. The characteristic domain size is defined as , where
, where  is the Fourier transform of the concentration field. Fig. 2A and B shows the time evolution of domain size Lc(t) for different bending modulus κ and membrane tension σ. In the limit of small κ and large σ, the system behaves like a typical ternary mixture, with domain coarsening following the standard Lc(t) ∝ t1/3 scaling (black triangles). This scaling is consistent with coarsening by either (Brownian-motion induced) coalescence or Ostwald ripening,63,64 and has been reported in taut membranes.17 For large κ and small σ, however, domain coarsening is arrested at a finite length scale, which sets the size of the patterns.
is the Fourier transform of the concentration field. Fig. 2A and B shows the time evolution of domain size Lc(t) for different bending modulus κ and membrane tension σ. In the limit of small κ and large σ, the system behaves like a typical ternary mixture, with domain coarsening following the standard Lc(t) ∝ t1/3 scaling (black triangles). This scaling is consistent with coarsening by either (Brownian-motion induced) coalescence or Ostwald ripening,63,64 and has been reported in taut membranes.17 For large κ and small σ, however, domain coarsening is arrested at a finite length scale, which sets the size of the patterns.
 | ||
Fig. 2 (A) and (B) The time evolution of the characteristic domain size Lc for different (A) bending modulus κ and (B) membrane tension σ. The black triangles indicate t1/3 scaling. Mean composition: (![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 1, 1,![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 2) = (0.38,0.36). (C) The characteristic domain size Lc as a function of the bending modulus κ. The solid lines indicate theory [eqn (9)] with the fitted value of the line tension μ between phases. The horizontal dashed lines are the limit of infinite bending modulus κ → ∞, and the vertical dashed lines show the critical value 2) = (0.38,0.36). (C) The characteristic domain size Lc as a function of the bending modulus κ. The solid lines indicate theory [eqn (9)] with the fitted value of the line tension μ between phases. The horizontal dashed lines are the limit of infinite bending modulus κ → ∞, and the vertical dashed lines show the critical value  below which the characteristic domain size becomes unbounded. (D) The characteristic domain size Lc as a function of the membrane tension σ. The vertical dashed line shows σc = κ2c12/μ beyond which the characteristic domain size becomes unbounded. For the blue curve, σc is outside the range of the plot. Parameters are the same as in Fig. 1 unless otherwise stated. All quantities are nondimensionalized as discussed in the text. below which the characteristic domain size becomes unbounded. (D) The characteristic domain size Lc as a function of the membrane tension σ. The vertical dashed line shows σc = κ2c12/μ beyond which the characteristic domain size becomes unbounded. For the blue curve, σc is outside the range of the plot. Parameters are the same as in Fig. 1 unless otherwise stated. All quantities are nondimensionalized as discussed in the text. | ||
The finite droplet size is selected by a competition between the energy costs of membrane deformation and phase separation, with the former preferring small-scale variations and the latter large domains. The deformation energy depends on the height field h(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), whose steady-state solution can be given in the Fourier space:
), whose steady-state solution can be given in the Fourier space:
 | (5) |
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) | and δϕ1(
| and δϕ1(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) is the Fourier transform of δϕ1(
) is the Fourier transform of δϕ1(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = ϕ1(
) = ϕ1(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) −
) − ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 1 with
1 with ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 1 being the mean concentration of lipid species 1. Therefore, the deformation field follows the concentration profile. It stays flat for the uniform state and gets modulated once patterns form (Fig. 1C). Using h from eqn (5) simplifies the steady-state free energy due to membrane deformation:
1 being the mean concentration of lipid species 1. Therefore, the deformation field follows the concentration profile. It stays flat for the uniform state and gets modulated once patterns form (Fig. 1C). Using h from eqn (5) simplifies the steady-state free energy due to membrane deformation: | (6) |
The coefficient 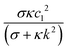 decreases monotonically with k, thereby favoring small length scales. However, it has to compete with the Flory–Huggins free energy
decreases monotonically with k, thereby favoring small length scales. However, it has to compete with the Flory–Huggins free energy  , which always favors large domains in order to reduce the interface length between domains. Since
, which always favors large domains in order to reduce the interface length between domains. Since ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) e increases monotonically with κ, it dominates over
e increases monotonically with κ, it dominates over ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) c when κ is large enough, resulting in finite domains. Conversely,
c when κ is large enough, resulting in finite domains. Conversely, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) c dominates in the small κ limit, leading to t1/3 scaling as shown in Fig. 2A.
c dominates in the small κ limit, leading to t1/3 scaling as shown in Fig. 2A.
In the absence of membrane deformation energy (fe), phase separation occurs along tie lines of the ternary mixture phase diagram (determined by fc), which can be located by constructing the convex hull of the free energy landscape.65 Motivated by numerical evidence, we assume that the full system (h ≠ 0) also demixes along the same tie lines, whose slope gives the ratio of the concentration change δϕ2/δϕ1, where δϕi = ϕi − ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) i with
i with ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) i being the average composition of component i. The assumption fixes the ratios of δϕi but not their magnitudes. Consequently,
i being the average composition of component i. The assumption fixes the ratios of δϕi but not their magnitudes. Consequently, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) c can be simplified by expanding along the tie line. Combining it with
c can be simplified by expanding along the tie line. Combining it with ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) e leads to an effective total free energy (see ESI,† Section IB for derivation):
e leads to an effective total free energy (see ESI,† Section IB for derivation):
 | (7) |
 | (8) |
The selection of the preferred length scale is dictated by the second term in the free energy eqn (7), which involves both a membrane deformation term that favors large k and a lipid interaction term that favors small k. Minimizing free energy with respect to k leads to the characteristic length scale (domain size)
 | (9) |
The predicted Lc is confirmed by numerical solution of the dynamical equations. Fig. 2C presents Lc as a function of the bending modulus κ. While small κ always leads to perpetual coarsening (Lc → ∞), coarsening is arrested beyond a critical value  (vertical dashed lines). The domain size Lc decreases monotonically with κ and converges to Lc = 2π(σc12/μ)−1/4 in the infinite κ limit (horizontal dashed lines). The theory (solid lines) agrees well with numerical simulations (circles), with a single fitting parameter μ to account for a modified line tension between the two phases since the chemical composition at the interface deviates slightly from the tie lines (Fig. S1, ESI†). μ can also be estimated by expanding the free energy along the tie lines (see ESI,† Section IB), which leads to a slightly worse agreement (Fig. S2, ESI†).
(vertical dashed lines). The domain size Lc decreases monotonically with κ and converges to Lc = 2π(σc12/μ)−1/4 in the infinite κ limit (horizontal dashed lines). The theory (solid lines) agrees well with numerical simulations (circles), with a single fitting parameter μ to account for a modified line tension between the two phases since the chemical composition at the interface deviates slightly from the tie lines (Fig. S1, ESI†). μ can also be estimated by expanding the free energy along the tie lines (see ESI,† Section IB), which leads to a slightly worse agreement (Fig. S2, ESI†).
The domain size Lc has a different functional dependence on the membrane tension σ (Fig. 2D). Finite domains only emerge when σ < σc = κ2c12/μ. Lc reaches minimum at an intermediate value σm = κ2c12/(4μ) = σc/4 and diverges in limits σ → 0 and σ → σc. In the σ → 0 limit, the energy cost for stretching is absent, so the preferred curvature condition can be satisfied everywhere on the membrane, allowing for indefinite coarsening. In addition to the divergence of domain size, another possibility in the large σ limit (taut membrane) is that the membrane remains flat inside each of the domains, and the system behaves like a ternary mixture with either a uniform concentration or coarsening droplets. The transition to the large σ regime is discussed below in a later section. As shown in Fig. 2D, the predicted Lc agrees well with numerical simulations. The membrane tension can be varied by tuning the exterior osmotic pressure, which was found to monotonically increase domain size with tension for synthetic and cell-derived membranes.18 These experiments are likely performed at relatively high membrane tension since the vesicles appeared taut before introducing DPPC to the outer leaflet. Moreover, large domains (in the sense that coarsening was not arrested) were observed toward the end of the experiment, indicating that σ eventually exceeds σc. Hence, they are consistent with the right branch (σ > σm) of the predicted Lc(σ) (Fig. 2D). It will be interesting to measure the domain size at low membrane tension (which can be achieved by high exterior osmotic pressure) and look for potential non-monotonicity with tension.
Finally, we consider the effect of temperature T. While all the material properties and interaction parameters can depend on temperature, we assume that none of them varies drastically in the experimental range. Specifically, since energy is measured in units of nkBT, the rescaled parameters ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ,
, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) , χ, and ξ all have a 1/(kBT) dependence on temperature, while the entropy term does not. Since the two-phase region in the phase diagram shrinks with increasing temperature,47 we expect the composition difference between the two domains and thus the line tension to decrease with temperature. Thus, the rescaled line tension μ will likely decrease more rapidly than T−1. Under this assumption, eqn (9) predicts that the characteristic domain size Lc decreases with temperature T, which is confirmed by numerical simulations (see Fig. S3, ESI†) and is consistent with experiments.18
, χ, and ξ all have a 1/(kBT) dependence on temperature, while the entropy term does not. Since the two-phase region in the phase diagram shrinks with increasing temperature,47 we expect the composition difference between the two domains and thus the line tension to decrease with temperature. Thus, the rescaled line tension μ will likely decrease more rapidly than T−1. Under this assumption, eqn (9) predicts that the characteristic domain size Lc decreases with temperature T, which is confirmed by numerical simulations (see Fig. S3, ESI†) and is consistent with experiments.18
3.2 Pattern morphology predicted by amplitude expansion
Next, we determine the steady-state pattern morphologies with an amplitude expansion around the uniform state:66 | (10) |
 and keeping only the leading order terms in the amplitudes. This results in a dynamical system for Ȧn(t) = F[{An(t)}], whose fixed points correspond to different pattern morphologies. The stability of these fixed points determines possible steady-state patterns (see ESI,† Section I). Since the theory is an expansion in amplitudes, it is the most accurate near the critical points as the higher order terms in An become less important.
and keeping only the leading order terms in the amplitudes. This results in a dynamical system for Ȧn(t) = F[{An(t)}], whose fixed points correspond to different pattern morphologies. The stability of these fixed points determines possible steady-state patterns (see ESI,† Section I). Since the theory is an expansion in amplitudes, it is the most accurate near the critical points as the higher order terms in An become less important.
We find three fixed points representing uniform, dot (Fig. 1C, lower left), and stripe (Fig. 1C, upper left) morphologies, respectively. Their stability is governed by the following control parameter:
 | (11) |
 , and
, and  , respectively. Stripes and dots are bistable in the overlap region
, respectively. Stripes and dots are bistable in the overlap region  ; their coexistence is referred to as the mixed state (Fig. 1C, upper right). In the coexistence region, the observed pattern is history-dependent. With random initialization, we find that dots and stripes form individual patches. The size of each dot or stripe domain is given by the characteristic length scale eqn (9), but the size of dot/stripe patches stabilizes at a finite value. The latter is likely due to kinetic trapping since rearranging dots and stripes requires going over a large free energy barrier. Another bistable region is
; their coexistence is referred to as the mixed state (Fig. 1C, upper right). In the coexistence region, the observed pattern is history-dependent. With random initialization, we find that dots and stripes form individual patches. The size of each dot or stripe domain is given by the characteristic length scale eqn (9), but the size of dot/stripe patches stabilizes at a finite value. The latter is likely due to kinetic trapping since rearranging dots and stripes requires going over a large free energy barrier. Another bistable region is 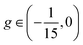 , where individual dots are stable in a uniform background, which leads to localized states (Fig. 1C, lower right) similar to the localized states found in the Swift–Hohenberg equation.56,57 The history dependence of morphologies in the bistable regions will be further illustrated by hysteresis (Fig. 4).
, where individual dots are stable in a uniform background, which leads to localized states (Fig. 1C, lower right) similar to the localized states found in the Swift–Hohenberg equation.56,57 The history dependence of morphologies in the bistable regions will be further illustrated by hysteresis (Fig. 4).
The predicted phase morphologies are summarized in a phase diagram (Fig. 1B), which are confirmed by numerical simulation (represented by filled circles). No fitting parameters are involved when constructing the phase diagram as (a,b,c,μ) are evaluated by expanding the free energy along the tie lines. The agreement between theory and simulation is especially good near the two critical points (indicated by red stars), where the amplitude expansion is the most accurate. Moving away from the critical points, the expansion becomes less precise, but most of the morphologies are still correctly captured. The structure of the phase diagram is robust to the form of the interaction free energy of lipids fc, as long as it exhibits generic phase separation behaviors.
The phase diagram is qualitatively consistent with experiments in GUVs.18 In particular, when the mean composition is varied along any of the tie lines (a typical tie line is indicated by the black dashed line in Fig. 1B), the system always morphs from dots to stripes and eventually back to dots, which is the same as the sequence of morphologies observed in experiments18 (Fig. 1D and E). When varied in the normal (perpendicular) direction (indicated by the white dashed line in Fig. 1B), the patterns can switch between dots and stripes, as observed in experiments.18 The exact sequence of patterns is not unique: it depends on where the normal line crosses the tie line. Hence, further experimental characterization of the phase diagram of patterns formed after introducing extra lipids will be informative for determining the model parameters and understanding the underlying interactions.
The morphology near the critical points has been suggested as an important criterion for distinguishing different mechanisms for the small domains.18 In particular, the observation of stripe domains near the critical point was used to rule out a previous model involving bilayer curvature.18,22 In our model, however, the system can exhibit any of the morphologies near the two critical points (indicated by red stars), depending on the direction in which the critical point is approached. An analogous effect was reported in a diblock copolymer model,53 although the physical mechanism for pattern formation is different. Since all the phase boundaries become tangent to the miscibility boundary at the critical points, the stripe phase becomes dominant in its vicinity. In other words, if we draw a circle near the critical point (ϕ1c, ϕ2c) with radius ε, both the stripe phase and the uniform phase will occupy half the area in the circle as ε → 0, with all the other morphologies occupying infinitesimal area. This may explain the experimental observation of stripes near the critical point. It will be interesting to test experimentally whether departing the critical point in different directions eventually leads to different morphologies.
3.3 Droplets coarsen in taut membranes
The small domains discussed so far only emerge at relatively low surface tension. As the membrane becomes more taut, its behavior approaches a ternary mixture with either a uniform state or large domains (in the sense that coarsening is not arrested). The transition into these two states are driven by different dynamical processes: the transition to the uniform state can be described by a saddle-node bifurcation in the amplitude space, while the transition to the large, coarsening domain phase is best understood as a crossover of free energy. Fig. 3 illustrates these two types of transitions. For transition to the uniform state, the morphology parameter g decreases with σ (in the regime where Lc stays finite) and eventually crosses the threshold g = −1/15 (Fig. 3A), below which only the uniform state is stable. Throughout the transition, the deformation field h(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) can be well described by the sum of a few Fourier modes (eqn (10) and Fig. 3B), but its amplitude vanishes at large σ due to a saddle-node bifurcation. On the other hand, the transition to coarsening lipid domains can be understood by a free energy crossover. For these domains, the membrane remains flat (h = const.) within bulk phases, which can no longer be described by the sum of Fourier modes (Fig. 3D). The composition of the bulk phases can be determined by a convex hull construction with an extra free energy penalty
) can be well described by the sum of a few Fourier modes (eqn (10) and Fig. 3B), but its amplitude vanishes at large σ due to a saddle-node bifurcation. On the other hand, the transition to coarsening lipid domains can be understood by a free energy crossover. For these domains, the membrane remains flat (h = const.) within bulk phases, which can no longer be described by the sum of Fourier modes (Fig. 3D). The composition of the bulk phases can be determined by a convex hull construction with an extra free energy penalty  [see eqn (2)]. These flat droplets always coarsen to reach the system size. As shown in Fig. 3C, the free energy density of the patterns (blue line) increases with σ and eventually exceeds that of the flat droplet phase (red line). The crossover of free energy density defines a transition point beyond which patterns of finite-sized domains are no longer observed. This crossover is also observed in simulations (orange dots).
[see eqn (2)]. These flat droplets always coarsen to reach the system size. As shown in Fig. 3C, the free energy density of the patterns (blue line) increases with σ and eventually exceeds that of the flat droplet phase (red line). The crossover of free energy density defines a transition point beyond which patterns of finite-sized domains are no longer observed. This crossover is also observed in simulations (orange dots).
 | ||
Fig. 3 Domain coarsening in taut membranes. (A) The morphology control parameter g as a function of σ. The black dashed line is g = −1/15 below which only the uniform solution is stable. (B) The deformation field h(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) across a droplet (blue line in the bottom panel, corresponding to the black dashed line in the top panel) can be well described by fitting h = h0 + h1 ) across a droplet (blue line in the bottom panel, corresponding to the black dashed line in the top panel) can be well described by fitting h = h0 + h1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(kr + ψ) (red dashed line). (C) The free energy density as a function of σ. Orange dots are simulation results; the blue line is calculated from amplitude expansion. The black and red lines are the free energy densities of the uniform state and flat droplet domains, respectively. (D) h( sin(kr + ψ) (red dashed line). (C) The free energy density as a function of σ. Orange dots are simulation results; the blue line is calculated from amplitude expansion. The black and red lines are the free energy densities of the uniform state and flat droplet domains, respectively. (D) h(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) across a droplet. The deformation is flat except near the interface, which cannot be captured by fitting a shifted sin function (red dashed line). Mean composition: (A) and (B) ( ) across a droplet. The deformation is flat except near the interface, which cannot be captured by fitting a shifted sin function (red dashed line). Mean composition: (A) and (B) (![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 1, 1,![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 2) = (0.34,0.19); (C) and (D) ( 2) = (0.34,0.19); (C) and (D) (![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 1, 1,![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 2) = (0.15,0.34). Parameters are the same as Fig. 1 unless otherwise stated. 2) = (0.15,0.34). Parameters are the same as Fig. 1 unless otherwise stated. | ||
3.4 Hysteresis of pattern morphologies
The bistability of stripes and dots in the mixed state suggests the possibility for the hysteresis of pattern morphology due to cycling control parameters. Namely, it is possible to observe either or a mixture of these two morphologies depending on the history of the control parameter. One of the most accessible parameters is membrane tension, which can be tuned by exterior osmotic pressure. Fig. 4 shows a hypothetical experiment where the external salt concentration is first increased and then decreased. Increasing salt concentration decreases the surface tension, which leads to a transition from dots to stripes; decreasing concentration leads to the opposite transition. Indeed, the backward transition takes place around σ = 0.185, which is much larger than the threshold for the forward transition σ = 0.135. Hysteresis is also observed when cycling temperature (see Fig. S4, ESI†), although we had to again assume that temperature dependence predominantly enters through the mixing entropy. Since the morphology control parameter g [eqn (11)] is non-monotonic in σ, it may also be possible to observe hysteresis in stripe-dot-stripe transitions by tuning the exterior salt concentration. These hysteresis experiments will help elucidate the validity of the bistable solutions found here, and the transition thresholds may be used to quantitatively determine parameters in our model. | ||
Fig. 4 Pattern hysteresis due to tuning the (non-dimensionalized) surface tension σ, which is first decreased and then increased (as indicated by the arrow), with a fixed composition (![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 1, 1,![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 2) = (0.45,0.40). All the other parameters are the same as in Fig. 1. 2) = (0.45,0.40). All the other parameters are the same as in Fig. 1. | ||
One interesting aspect of the pattern morphologies is the persistence of defects: places where the parallel stripes order or the hexagonal dots order are locally violated. These defects were also seen in experiments.18 Since patterns are mesoscopic, thermal noise at this scale is not strong enough to effectively remove defects during experimentally relevant timescales. Indeed, these defects are common in mesoscopic patterns.67,68 However, cycling parameters appear effective in reducing defects (e.g., compare the initial and final state at σ = 0.21 in Fig. 4). It will be interesting to study these defects in more detail both experimentally and theoretically.
4 Discussion
In this paper, we have proposed a theoretical model to describe the patterns formed by small domains in biological membranes. The model is minimal in the sense that it successfully captures existing measurements of the pattern morphology and length scales by only requiring local coupling between the bilayer curvature and the local lipid composition. Several future experimental directions are proposed to reveal more information on the underlying mechanism. One possibility is to tune the membrane tension in a larger dynamical range and in cycles to search for a non-monotonic change in the domain size as well as hysteresis of pattern morphologies. Another direction is to examine the rich structures of the morphological phase diagram (Fig. 1B) by carefully exploring the composition space. In particular, the theory predicts that different patterns can be observed when approaching the critical point (Fig. 1B, red stars) from different directions, which has not been explored experimentally.The microscopic picture for curvature-composition coupling is that the extra lipids (DPPC) introduced to the outer leaflet partitions preferentially to lipid domains, inducing different local curvature. Hence, it will be interesting to test this hypothesis by exploring how the patterns depend on the amount of DPPC introduced to the outer leaflet, which affects the c1 parameter in the model. It should also be noted that while this particular mechanism should be tested, our results are valid for generic mechanisms for curvature-composition coupling, which will produce the same term to the first order in ϕ1 but with a different interpretation of c1 that depends on the mechanism.
New experimental information will also enable further theoretical work, such as accurately fitting the phase boundaries and inverse design of pattern morphologies.69 Another direction to extend the theory is to consider the hydrodynamics of the bulk solvent exhibiting either passive70 or active flows71 or by exploring the interactions between membrane proteins (especially ones that sense curvature72) and lipid domains in giant plasma membrane vesicles (GPMVs) and membranes of living cells.73,74
While we have mostly focused on lipid interactions, many important biological functions involve protein–membrane interactions.11–13,75–77 For example, lipid domains could organize proteins in stress response.11–13 They can also serve as substrates for proteins to phosphorylate/dephosphorylate.75 Domains may form due to the phase separation of membrane proteins, such as cell adhesion receptors,76 which form clustering patterns due to coupling with membrane deformation. Dot and stripe domains can also arise when phase-separating proteins bind to membranes and induce deformation.78 The present formalism can be extended to include additional fields for membrane-associated proteins to describe these important biological processes. It will also be interesting to see if the model can be extended to include electric dipole interactions in order to study complex patterns observed in a monolayer at the air–water interface.39–41
The patterns discussed here arise from equilibrium interactions governed by an overall free energy. Nonetheless, biological membranes under physiological conditions are highly nonequilibrium, influenced by various active processes that physically deform79 or chemically modify75,80 the membrane. These nonequilibrium interactions enable rich spatiotemporal behaviors such as traveling waves of lipids,75 proteins,81 and membrane shape changes.82 The clustering of lipids and proteins are important for biological functions such as cell shape regulation81,82 and signaling.83–85 By explicitly modeling the kinetics of nonequilibrium processes (e.g. phosphorylation/dephosphorylation cycles), the theoretical framework developed here can be extended to offer more insights into the morphology and dynamics of these nonequilibrium patterns.
Author contributions
Q. Y. and A. K. designed research, performed research, and wrote the manuscript.Data availability
Details of the analytical derivations and numerical simulations have been included as part of the ESI.†Conflicts of interest
The authors declare no competing interests.Note added after first publication
This article replaces the version published on 5th May 2025, which contained an error in the radius notation in Section 3.2.Acknowledgements
We thank S. L. Keller and I. Levin for introducing us to this experimental system and for many stimulating discussions at various stages of this work. We thank E. Frey, J. Dunkel, and M. Haataja for useful discussions. This work is supported by the National Science Foundation, through the Princeton Center for Complex Materials (DMR-2011750) and the Center for the Physics of Biological Function (PHY-1734030), and by the Princeton Catalysis Initiative. The work by Q. Y. is supported in part by a Harold W. Dodds Fellowship from Princeton University.References
- S. Semrau and T. Schmidt, Soft Matter, 2009, 5, 3174 RSC.
- T. Sych, C. O. Gurdap, L. Wedemann and E. Sezgin, Membranes, 2021, 11, 323 CrossRef CAS PubMed.
- T. Baumgart, A. T. Hammond, P. Sengupta, S. T. Hess, D. A. Holowka, B. A. Baird and W. W. Webb, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 3165–3170 CrossRef CAS PubMed.
- C. Dietrich, L. Bagatolli, Z. Volovyk, N. Thompson, M. Levi, K. Jacobson and E. Gratton, Biophys. J., 2001, 80, 1417–1428 CrossRef CAS PubMed.
- R. Dimova, S. Aranda, N. Bezlyepkina, V. Nikolov, K. A. Riske and R. Lipowsky, J. Phys.: Condens. Matter, 2006, 18, S1151–S1176 CrossRef CAS PubMed.
- P. Sengupta, B. Baird and D. Holowka, Semin. Cell Dev. Biol., 2007, 18, 583–590 CrossRef CAS.
- P. S. Kabouridis, Mol. Membr. Biol., 2006, 23, 49–57 CrossRef CAS PubMed.
- S. Mañes and A. Viola, Mol. Membr. Biol., 2006, 23, 59–69 CrossRef PubMed.
- R. G. Parton and A. A. Richards, Traffic, 2003, 4, 724–738 CrossRef CAS.
- C. Salaün, D. J. James and L. H. Chamberlain, Traffic, 2004, 5, 255–264 CrossRef.
- A. Murley, J. Yamada, B. J. Niles, A. Toulmay, W. A. Prinz, T. Powers and J. Nunnari, J. Cell Biol., 2017, 216, 2679–2689 CrossRef CAS.
- A. Y. Seo, P.-W. Lau, D. Feliciano, P. Sengupta, M. A. L. Gros, B. Cinquin, C. A. Larabell and J. Lippincott-Schwartz, eLife, 2017, 6, e21690 CrossRef PubMed.
- C. L. Leveille, C. E. Cornell, A. J. Merz and S. L. Keller, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2116007119 CrossRef CAS.
- M. Rouches, S. L. Veatch and B. B. Machta, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2103401118 CrossRef CAS.
- S. L. Veatch and S. L. Keller, Phys. Rev. Lett., 2002, 89, 268101 CrossRef PubMed.
- S. L. Veatch and S. L. Keller, Biophys. J., 2003, 85, 3074–3083 CrossRef CAS PubMed.
- C. Stanich, A. Honerkamp-Smith, G. Putzel, C. Warth, A. Lamprecht, P. Mandal, E. Mann, T.-A. Hua and S. Keller, Biophys. J., 2013, 105, 444–454 CrossRef CAS.
- C. E. Cornell, A. D. Skinkle, S. He, I. Levental, K. R. Levental and S. L. Keller, Biophys. J., 2018, 115, 690–701 CrossRef CAS.
- M. Seul and D. Andelman, Science, 1995, 267, 476–483 CrossRef CAS PubMed.
- P. B. Sunil Kumar, G. Gompper and R. Lipowsky, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 4610–4618 CrossRef CAS PubMed.
- R. Shlomovitz, L. Maibaum and M. Schick, Biophys. J., 2014, 106, 1979–1985 CrossRef CAS PubMed.
- J. Harden, F. MacKintosh and P. Olmsted, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011903 CrossRef CAS.
- T. R. Shaw, S. Ghosh and S. L. Veatch, Annu. Rev. Phys. Chem., 2021, 72, 51–72 CrossRef CAS PubMed.
- F. Schmid, Biochim. Biophys. Acta, Biomembr., 2017, 1859, 509–528 CrossRef CAS PubMed.
- M. Schick, J. Phys. Chem. B, 2018, 122, 3251–3258 CrossRef CAS PubMed.
- D. W. Allender and M. Schick, J. Membr. Biol., 2022, 255, 451–460 CrossRef CAS PubMed.
- J. Liu, S. Qi, J. T. Groves and A. K. Chakraborty, J. Phys. Chem. B, 2005, 109, 19960–19969 CrossRef CAS.
- J. Liu, J. T. Groves and A. K. Chakraborty, J. Phys. Chem. B, 2006, 110, 8416–8421 CrossRef CAS PubMed.
- R. D. Usery, T. A. Enoki, S. P. Wickramasinghe, M. D. Weiner, W.-C. Tsai, M. B. Kim, S. Wang, T. L. Torng, D. G. Ackerman, F. A. Heberle, J. Katsaras and G. W. Feigenson, Biophys. J., 2017, 112, 1431–1443 CrossRef CAS.
- A. R. Honerkamp-Smith, B. B. Machta and S. L. Keller, Phys. Rev. Lett., 2012, 108, 265702 CrossRef PubMed.
- Y. Hirose, S. Komura and D. Andelman, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2012, 86, 021916 CrossRef PubMed.
- S. Meinhardt, R. L. C. Vink and F. Schmid, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4476–4481 CrossRef CAS.
- J. J. Amazon, S. L. Goh and G. W. Feigenson, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2013, 87, 022708 CrossRef PubMed.
- J. Fan, M. Sammalkorpi and M. Haataja, Phys. Rev. Lett., 2010, 104, 118101 CrossRef.
- S. Sadeghi, M. Müller and R. Vink, Biophys. J., 2014, 107, 1591–1600 CrossRef CAS PubMed.
- F. C. MacKintosh, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 2891–2897 CrossRef CAS PubMed.
- R. Shlomovitz and M. Schick, Biophys. J., 2013, 105, 1406–1413 CrossRef CAS PubMed.
- M. Schick, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2012, 85, 031902 CrossRef CAS.
- H. M. McConnell, Annu. Rev. Phys. Chem., 1991, 42, 171–195 CrossRef CAS.
- S. L. Keller and H. M. McConnell, Phys. Rev. Lett., 1999, 82, 1602–1605 CrossRef CAS.
- D. J. Keller, H. M. McConnell and V. T. Moy, J. Phys. Chem., 1986, 90, 2311–2315 CrossRef CAS.
- B. Palmieri and S. A. Safran, Langmuir, 2013, 29, 5246–5261 CrossRef CAS PubMed.
- C. J. Garvey, S. J. Bryant, A. Elbourne, T. Hunt, B. Kent, M. Kreuzer, M. Strobl, R. Steitz and G. Bryant, J. Colloid Interface Sci., 2023, 638, 719–732 Search PubMed.
- P. J. Flory, J. Chem. Phys., 1942, 10, 51–61 CrossRef CAS.
- M. L. Huggins, J. Chem. Phys., 1941, 9, 440 CrossRef CAS.
- T. Idema, J. M. J. van Leeuwen and C. Storm, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2009, 80, 041924 CrossRef CAS.
- S. L. Veatch, K. Gawrisch and S. L. Keller, Biophys. J., 2006, 90, 4428–4436 CrossRef CAS PubMed.
- P. C. Hohenberg and B. I. Halperin, Rev. Mod. Phys., 1977, 49, 435–479 CrossRef CAS.
- M. Yanagisawa, M. Imai, T. Masui, S. Komura and T. Ohta, Biophys. J., 2007, 92, 115–125 CrossRef CAS.
- F. S. Bates and G. H. Fredrickson, Annu. Rev. Phys. Chem., 1990, 41, 525–557 CrossRef CAS.
- G. Fredrickson and F. Bates, Annu. Rev. Mater. Sci., 1996, 26, 501–550 CrossRef CAS.
- F. S. Bates and G. H. Fredrickson, Phys. Today, 1999, 52, 32–38 CrossRef CAS.
- M. W. Matsen and M. Schick, Phys. Rev. Lett., 1994, 72, 2660–2663 CrossRef CAS.
- M. W. Matsen and F. S. Bates, Macromolecules, 1996, 29, 1091–1098 CrossRef CAS.
- F. Liu and N. Goldenfeld, Phys. Rev. A:At., Mol., Opt. Phys., 1989, 39, 4805–4810 CrossRef CAS.
- U. Thiele, A. J. Archer, M. J. Robbins, H. Gomez and E. Knobloch, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2013, 87, 042915 CrossRef PubMed.
- E. Knobloch, IMA J. Appl. Math., 2016, 81, 457–487 Search PubMed.
- H. Emmerich, H. Löwen, R. Wittkowski, T. Gruhn, G. I. Tóth, G. Tegze and L. Gránásy, Adv. Phys., 2012, 61, 665–743 Search PubMed.
- K. R. Elder, Z.-F. Huang and N. Provatas, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2010, 81, 011602 CrossRef CAS.
- P. Stefanovic, M. Haataja and N. Provatas, Phys. Rev. Lett., 2006, 96, 225504 CrossRef.
- P. C. Matthews and S. M. Cox, Nonlinearity, 2000, 13, 1293–1320 CrossRef.
- S. M. Cox, Phys. Lett. A, 2004, 333, 91–101 CrossRef CAS.
- I. Lifshitz and V. Slyozov, J. Phys. Chem. Solids, 1961, 19, 35–50 CrossRef.
- B. A. Camley and F. L. H. Brown, J. Chem. Phys., 2011, 135, 225106 CrossRef PubMed.
- S. Mao, D. Kuldinow, M. P. Haataja and A. Košmrlj, Soft Matter, 2019, 15, 1297–1311 RSC.
- M. C. Cross and P. C. Hohenberg, Rev. Mod. Phys., 1993, 65, 851–1112 CrossRef CAS.
- N. Stoop and J. Dunkel, Soft Matter, 2018, 14, 2329–2338 RSC.
- D. Boyer and J. Viñals, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2002, 65, 046119 CrossRef.
- C. P. Goodrich, E. M. King, S. S. Schoenholz, E. D. Cubuk and M. P. Brenner, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2024083118 CrossRef CAS.
- B. A. Camley and F. L. H. Brown, Phys. Rev. Lett., 2010, 105, 148102 CrossRef PubMed.
- D. P. Arnold, A. Gubbala and S. C. Takatori, Phys. Rev. Lett., 2023, 131, 128402 CrossRef CAS.
- S. Yang, X. Miao, S. Arnold, B. Li, A. T. Ly, H. Wang, M. Wang, X. Guo, M. M. Pathak, W. Zhao, C. D. Cox and Z. Shi, Nat. Commun., 2022, 13, 7467 CrossRef CAS.
- B. A. Camley and F. L. H. Brown, Soft Matter, 2013, 9, 4767 RSC.
- B. A. Camley and F. L. H. Brown, J. Chem. Phys., 2014, 141, 075103 CrossRef.
- T.-S. Hsieh, V. A. Lopez, M. H. Black, A. Osinski, K. Pawłowski, D. R. Tomchick, J. Liou and V. S. Tagliabracci, Science, 2021, 372, 935–941 CrossRef CAS PubMed.
- S.-Z. Lin, R. Changede, A. J. Farrugia, A. D. Bershadsky, M. P. Sheetz, J. Prost and J.-F. Rupprecht, Phys. Rev. Lett., 2024, 132, 188402 CrossRef CAS.
- N. Ramakrishnan, P. B. Sunil Kumar and R. Radhakrishnan, Phys. Rep., 2014, 543, 1–60 CrossRef CAS.
- A. Winter, Y. Liu, A. Ziepke, G. Dadunashvili and E. Frey, Phys. Rev. E, 2025, 111, 044405 CrossRef CAS.
- J. C. Stachowiak, F. M. Brodsky and E. A. Miller, Nat. Cell Biol., 2013, 15, 1019–1027 CrossRef CAS PubMed.
- B. H. Falkenburger, J. B. Jensen, E. J. Dickson, B.-C. Suh and B. Hille, J. Physiol., 2010, 588, 3179–3185 CrossRef CAS.
- T. H. Tan, J. Liu, P. W. Miller, M. Tekant, J. Dunkel and N. Fakhri, Nat. Phys., 2020, 16, 657–662 Search PubMed.
- M. C. Wigbers, T. H. Tan, F. Brauns, J. Liu, S. Z. Swartz, E. Frey and N. Fakhri, Nat. Phys., 2021, 17, 578–584 Search PubMed.
- L. B. Case, J. A. Ditlev and M. K. Rosen, Annu. Rev. Biophys., 2019, 48, 465–494 Search PubMed.
- J. M. Keegstra, F. Avgidis, Y. Mullah, J. S. Parkinson and T. S. Shimizu, bioRxiv, 2022, preprint DOI:10.1101/2022.12.04.518992.
- D. Hathcock, Q. Yu and Y. Tu, Nat. Commun., 2024, 15, 8892 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00276a |
| This journal is © The Royal Society of Chemistry 2025 |
