 Open Access Article
Open Access ArticleMeasurement of fluid viscosity based on pressure-driven flow digital-printed microfluidics†
Yan
Ge
 ab,
Xingxing
Huang
ab,
Xingxing
Huang
 ab,
Baojian
Zhang
c,
Zhixiong
Song
d,
Xusheng
Tang
ab,
Shuai
Shao
ab,
Lujiale
Guo
ab,
Baojian
Zhang
c,
Zhixiong
Song
d,
Xusheng
Tang
ab,
Shuai
Shao
ab,
Lujiale
Guo
 e,
Peng
Liang
*abd and
Bei
Li
*abd
e,
Peng
Liang
*abd and
Bei
Li
*abd
aChangchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, P. R. China. E-mail: liangpeng1@ciomp.ac.cn; beili@ciomp.ac.cn
bUniversity of Chinese Academy of Sciences, Beijing 100049, P. R. China
cSchool of Ophthalmology & Optometry, Eye Hospital, Wenzhou Medical University, Wenzhou 325027, P.R. China
dHooke Instruments Ltd, Changchun 130031, P. R. China
eZhongshan Hospital of Fudan University, Shanghai 200032, P.R. China
First published on 27th February 2025
Abstract
Viscosity is an important characteristic of fluids. Microfluidics has shown significant advantages in the viscosity measurement of biopharmaceuticals, especially in meeting the needs of low sample volumes and accurately controlling microscale fluids. However, the viscosity chip of the traditional straight channel structure has limitations, and the processing technology is also facing challenges. In this study, a variable cross-section microfluidic chip structure was designed and successfully manufactured by photocuring 3D printing technology. A digital-printed (DP) microfluidic viscometer was realized by a pressure-driven flow combined with optical imaging. The device measures the change in sample viscosity with shear rate by recording the change in pressure and flow velocity with time. The whole experiment requires only 25 μl of reagents per time, and the single experiment time is less than 2 minutes, which not only reduces the consumption of samples dramatically, but also improves the efficiency of the experiment significantly. Compared with commercial viscometers, our measurements are accurate and capable of supporting non-Newtonian fluids. The proposed platform provides good cost-effectiveness and operational simplicity and lays the methodological foundation for viscosity measurements of more complex properties of fluids.
1. Introduction
Viscosity, as a core indicator of fluid properties, plays a crucial role in the biomedical field.1 In clinical diagnosis and health monitoring, the viscosity of blood and plasma is an important physiological indicator, which can effectively reflect the health status of the human body.2 For some biological drugs, viscosity tends to increase;3–5 however, excessively high viscosity levels can complicate drug formulation6,7 and amplify patient discomfort during administration.8,9 Therefore, viscosity needs to be precisely controlled in biological drug development,10 biomedical research,11 drug delivery systems,11 and other related fields.12However, traditional viscosity measurement methods, such as the capillary method13,14 and the rotational viscometer method, usually require a large sample volume and direct contact with the sample, which can easily lead to contamination and sample waste. In recent years, some new viscometers have been based on MEMS sensors,15etc. Although these technologies offer the possibility of non-contact measurement, some devices still require the cantilever to be immersed in the sample being tested,16 posing a risk of contamination. As the development of highly concentrated formulations continues to advance, the amount of sample to be measured is often small, placing greater technical demands on the viscosity measurement of micro samples. Given the precious nature of biopharmaceuticals and the increasing need for non-contact measurements, it is critical to develop techniques that can accurately measure the viscosity of micro samples without contact.
Microfluidic chip technology, an emerging technology, provides a means of viscosity measurement with high sensitivity and resolution17 by controlling the flow of fluids in micrometer-scale channels.18 This technique not only drastically reduces the consumption of reagents and samples, but also improves the accuracy and reproducibility of the measurements by precisely controlling the experimental conditions. Combined with optical imaging technologies, such as CCD and CMOS cameras, it can achieve non-contact detection of samples, which is very suitable for accurate viscosity measurement of micro-volume samples and has a broad application prospect.19
Microfluidic technology combined with optical imaging for viscosity measurement has been extensively studied.19 Currently, common viscosity chips primarily include two types: the Y-shaped structure with a constant cross-section20 and the serpentine structure.20 The measurement method of the Y-shaped structure requires a reference fluid,21 and the measurement result of the liquid to be measured relies on the relationship between it and the reference fluid in the flow length22 or the flow width,23etc.24 Although it can be observed by portable devices such as mobile phones, it has limitations in the detection of non-Newtonian fluids due to the reliance on the reference fluid for relative viscosity measurement. Chips with a serpentine structure rely on the larger transverse-to-longitudinal ratio of the flow channel and shear for direct viscosity measurements;25 however, this structure usually needs to be observed under a microscope,18,26–28 and due to the limited field of view, serpentine structures are often used in the design to increase the flow length.29 There is a study that has adopted a design where a microfluidic chip is connected to a glass capillary tube, abandoning traditional serpentine structures and bulky microscopic equipment, thereby achieving high-throughput measurements of both Newtonian and non-Newtonian fluids.30 However, this method also has some limitations. For instance, under high pressure, the PDMS microchannels may undergo elastic deformation,31 and the required sample volume is constrained by the fabrication process of the glass capillary tube, leading to a relatively large sample volume requirement. In this study, a variable cross-section digital-printed (DP) microfluidic viscosity chip was designed to support the measurement of true viscosity over a wide range of shear rates by combining different sizes of cross-section channels, as compared to the traditional constant cross-section chip. The chip can realize the visualization of liquid in the channel by using an ordinary industrial camera or smartphone. The operation is simple and portable, making it suitable for micro-volume and precise viscosity measurements.
The complex structure of variable cross-section microfluidic viscosity chips and the need to maintain smooth flow channel surfaces between channels of different cross-sections place higher demands on fabrication techniques. Early microfluidic viscosity chips mainly relied on microelectromechanical systems to fabricate microstructures on silicon or glass.26 However, the complexity and high cost of these fabrication techniques limited their application in mass production. Currently, the mainstream chip fabrication processes can be divided into three main categories. First, the compound mould method. It is necessary to make chip moulds and then produce them by overmoulding, in which soft lithography, mainly PDMS, is widely used.20,28,32,33 There are also chips that use moulds for hot embossing,34 and the main problem with these methods is the high initial cost of mould making, which usually needs to be spread through mass production, and the long turnaround time for mould fabrication. Second, material reduction manufacturing. It includes CNC milling and laser cutting. However, these methods lead to large chip surface roughness and obvious burrs and are not conducive to processing complex runner structures. Third, additive manufacturing. This technology has been rapidly developed in recent years, supporting a wide range of printing materials from polymers, metals, and ceramics35 to biomaterials.36 Whether it is extrusion37,38 or photopolymerization39 printing technology, additive manufacturing is gradually becoming a promising approach in microfluidic chip fabrication40 due to its flexibility and innovation. Compared with other chip manufacturing processes, additive manufacturing, a digital technology as a chip rapid prototyping technology, supports the manufacturing of complex structures41 and significantly reduces the production cycle and costs of chip making. It is portable and ready to use, showing a wide range of application potential. Although additive manufacturing technology provides a new way to fabricate variable cross-section microfluidic viscosity chips, its requirement for fineness and smoothness of the embedded flow paths poses a challenge to equipment performance, and in addition, the dependence of microfluidic systems on peripheral equipment limits their wide application. Meanwhile, the light transmittance problem may lead to the collapse and blockage of the interlayer. To address these issues, this study used a layered printed open-channel microfluidic chip design,42 successfully realized the production of this DP microfluidic viscosity chip, and applied it to the viscosity measurement system.
In this paper, a simple and effective method of fluid viscosity measurement is proposed, which is achieved indirectly by recording only the changes in external pressure and the flow velocity at the leading edge of the liquid surface over time. This technology provides researchers with an important reference for low-cost, rapid and accurate measurement of reagent viscosity, and has high practical value. Based on the microfluidic principle of pressure-driven flow, the DP microfluidic viscometer designed in this study is paired with a microfluidic chip of variable cross-section manufactured by light-curing 3D printing technology, which effectively gets rid of the bulky limitations of traditional microscopy peripherals, and allows visual observation of liquids using an ordinary industrial camera or a smartphone, without relying on strict light conditions, which brings great convenience to experimental operation.
This microfluidic viscometer supports viscosity measurements of non-Newtonian fluids without the need for a reference fluid. It is easy to operate, wherein researchers only need to place the chip under the appropriate field of view and fixed in the chip holder, apply the ramp pressure signal, and record the flow sequence at the leading edge of the liquid surface through an industrial camera or mobile phone, and then combine it with the algorithm to obtain the viscosity measurement value.
This article is structured as follows: Part 2 describes the specific structure of the DP chip, the theoretical background, and the fabrication and characterization of the chip. Part 3 reports on the experimental setup and the calibration of the experimental system. Part 3 reports on the comparisons between the data from different liquids measured using a digital microfluidic viscometer and a commercial viscometer, verifying its excellent performance. Finally, Part 4 and Part 5 discuss and summarize the whole study.
2. Experimental section
2.1 The variable cross-section chip design
The digital printing (DP) microfluidic viscometer chip consists of three main structures: the connector (for connecting to the pressure controller), the variable cross-section microfluidic channel (divided into two parts, with the depth of the fluid flow area being 30 μm and 1 mm in flow channel I and II, respectively), and the waste liquid storage area. As shown in Fig. 1(a), the fluid enters flow channel I through the connector, then flows into channel II, and finally moves to the waste area. The aspect ratio of flow channel I should be less than 0.1 to effectively shear the fluid and serve as the primary region for pressure dissipation.25 In contrast, flow channel II features a significantly larger cross-sectional area compared to flow channel I, with an aspect ratio close to 1. The size of flow channel II should not be excessively large, ensuring the fluid maintains laminar flow throughout the channel. Additionally, the length of flow channel I should exceed 10 mm. A longer flow channel II allows the camera to capture a greater number of flow sequences, thereby providing a wider range of shear rates. Flow channel I has an aspect ratio of 0.06, which primarily determines the fluid's flow velocity and pressure distribution, with a total length of 10 mm. Flow channel II has an aspect ratio close to 1, with both its width and height measuring 1 mm, and its length can be adjusted according to the field of view of the lens. The entire structure is roughly divided into four layers: a bottom pressure-sensitive membrane l1 and three printed structural layers l2–l4.2.2 Theoretical modeling
The experiment is essentially a study of the two-phase displacement law, through the pressure-driven liquid to be measured to replace the original air present in the flow channel, the formation of solid–liquid two-phase contact with the liquid surface, the purpose of the experiment is to record the trajectory of the leading edge of the liquid and indirectly through the fluid dynamics of the relevant principles of the viscosity value. For a steady flow in a rectangular channel, p is the pressure, W is the rectangular cross-section width, H is the rectangular cross-section length, and τw is the wall shear rate. The force on the fluid microelement is shown in Fig. 1(b).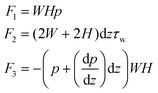 | (1) |
When the fluid reaches a stable laminar flow within the pipe, there is a force balance in the flow channel.25 For incompressible viscous fluids in steady laminar motion within a rectangular pipe of constant cross-section, the projection of the external forces acting on the rectangular fluid element in the direction of fluid motion sums to 0. Therefore, the expression for shear stress can be derived as follows:
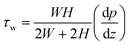 | (2) |
For a rectangular channel of length L with a pressure drop Δp, as shown in Fig. 1(b), the pressure gradient driving the liquid column is directly proportional to the pressures at both ends and inversely proportional to the length of the liquid.
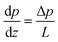 | (3) |
Considering the channels within the chip as rigid pipes, for a Newtonian fluid with constant dynamic shear viscosity η0, the relationship can be expressed as follows:
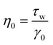 | (4) |
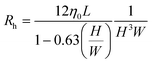 | (5) |
According to the fundamental laws of fluid mechanics, for a slit-type flow channel (a pipe with a high aspect ratio), with the help of the microfluidic circuit model in Fig. 1(c), the pressure difference Δp required to maintain a stable volumetric flow rate Q through the channel is given by pressure drop = fluid resistance × flow rate:
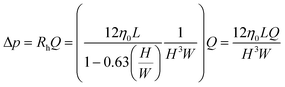 | (6) |
By combining with the Hagen–Poiseuille relation, the apparent shear rate γa can be expressed as:
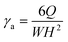 | (7) |
The velocity profile of a Newtonian fluid in a rectangular channel follows Poiseuille flow, exhibiting a parabolic shape that is symmetric about the centerline, where the apparent shear rate equals the true shear rate. In contrast, for non-Newtonian fluids, the velocity profile does not exhibit a parabolic distribution. Using the power-law fluid model, the flow characteristics of non-Newtonian fluids can be described using the following equation:
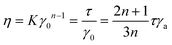 | (8) |
Here, n and K represent the power-law index and consistency coefficient, respectively. η is the true viscosity of the liquid. γ0 is the real shear rate, which can be expressed by the apparent shear rate. Theoretically, the relationship between Δp and the flow velocity v(t) can be expressed as follows:
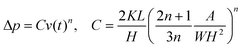 | (9) |
When the liquid is a Newtonian fluid, n = 1, indicating a linear relationship. As the leading edge of the liquid continuously advances over time, the wall viscosity can be expressed as follows:
 | (10) |
In the process of continuous advancement of the liquid, L(t) represents the displacement of the fluid's leading edge. The equation involves three variables: v(t), L(t) and Δp, where the average flow velocity can be derived from the centerline flow velocity using the following equation (the theoretical derivation is shown in ESI A†).
 | (11) |
This means that the central line flow velocity umax can be obtained through external equipment, and the average flow velocity umax can be obtained indirectly, which is convenient for subsequent related calculations. Then the moving distance can be expressed as the following, which is a function of time.
 | (12) |
Because the flow velocity changes with time, the liquid movement distance may have a certain error due to the uncertainty of the flow velocity. However, by designing the cross-section of the flow channel into a variable cross-section structure, it can not only simplify the calculation formula, but also effectively eliminate the distance error caused by the change of flow velocity, thereby improving the accuracy of the measurement. As shown in Fig. 1(c), starting from the liquid entering the flow channel II, L1 is the displacement of the liquid surface flowing through the flow channel I, which is constant, according to the continuity theorem, the flow velocity of the small cross-section channel can be expressed by the flow rate and cross-sectional area of the large cross-section channel.
 | (13) |
Due to the surface tension of the liquid, capillary forces will be present in smaller sized pipes and can be expressed as:
 | (14) |
Since the viscosity of the liquid needs to be taken into account, tangential forces are generated and mechanical energy is consumed during the movement. The liquid in the pipeline mainly comes from the frictional head loss and local head loss. Frictional head loss is due to the viscous effect of the liquid on the pipe wall and the fluid molecules between the shear stress caused by the continuous energy loss, usually proportional to the flow length.
 | (15) |
The above equation is also called the Darcy–Weisbach equation. λ is the Darcy friction factor, and is also a function of the Reynolds number (Re) and the relative roughness of the pipe (ε/D). However, in the laminar region, the Darcy friction factor of the slit-type cross-section can be expressed as λ = 96/Re (the theoretical derivation is shown in ESI B†), where the Reynolds number Re = ρuavgDe/μ, L is the pipe length, g is the gravitational acceleration, uavg is the average flow velocity, μ is the liquid viscosity, and De is the hydraulic diameter.
Local head loss occurs in the pipeline when the fluid flows through the local obstacles, due to the direction of the flow velocity and other rapid changes in the direction of the fluid micro-cluster collision leads to the loss of energy.
 | (16) |
 | (17) |
Among them, Asmall is the cross-sectional area of the small cross-section pipe, and Alarge is the cross-sectional area of the large cross-section pipe. If the small rectangular cross section (width ws, height Hs) is expanded to the large rectangular cross section (width wl, height Hl), the local head loss is
 | (18) |
The total head loss is
| hw = ∑hf + ∑hj | (19) |
The liquid will be accompanied by the resistance loss along the small cross-section channel and the large cross-section channel, and the resistance loss along the variable cross-section microfluidic chip is
 | (20) |
The viscosity solution formula can be simplified as
 | (21) |
There are only two variables in the formula, and only the instantaneous external pressure p and instantaneous flow velocity need to be recorded, which brings convenience to the solution of Newtonian fluid and non-Newtonian fluid.
2.3 Chip fabrication and characterization
In a yellow light room, the DP microfluidic viscosity chip was printed using a light-curing 3D printer (MP-100-6L, Prismlab, China). The flow channel surface was then observed using a white light interferometer (ZYGO). The results are presented in Fig. 3(a) and (b), where the point cloud data obtained from the white light interferometer indicates that the surface height fluctuations between the two channels are minimal. The arithmetic mean height of the flow channel surface I is 0.103 μm that of the flow channel surface II is 4.681 μm, indicating good surface flatness. A UV-curable polymer material, photosensitive resin (RP-405-NM02T), with a wavelength of 405 nm was used in the printing process. As light curing 3D printing is challenging to fabricate embedded channels due to light transmission issues and it is difficult to ensure the precise shape of flow channels, his study chose to print open flow channels in layers. The photosensitive resin was cured layer by layer from bottom up according to the design drawing (as shown in Fig. 1(a)). The aspect ratio of the channels is critical for achieving accurate viscosity measurements. The depth of flow channel I was characterized using a white light interferometer (ZYGO), as shown in Fig. 2(c), where the surface heights at different x-positions of the chip were measured along slice 1. The results indicate that the light-curing 3D printing technique can generally achieve a printing precision of approximately 30 μm. In the experiments, the interlayer waiting time and exposure time were adjusted according to the depth of the flow channel, and the model was compensated appropriately.44 After printing, the DP microfluidic viscometer chip was cleaned in an ethanol-filled ultrasonic cleaner for three minutes to remove excess photosensitive resin. The channels were flushed repeatedly using an ethanol-filled syringe until they were fully cleared, followed by nitrogen drying. The processed chip was then further cured in a UV curing oven and placed in a drying chamber to relieve thermal stress. The contact angle is about 70° (as shown in ESI C. Fig. S1†) indicating that the material is hydrophilic, which is conducive to the loading operation of the aqueous solution. At the same time, the capillary force is much smaller than the external pressure, so the influence of the capillary force can be ignored during the experiment.3. Materials and methods
3.1 Sample preparation
Since some injectable reagents and biofluids are aqueous solutions, in order to verify the applicability of the DP microfluidic viscometer, a series of aqueous solutions with different characteristics were prepared in this study at room temperature with varying concentrations. Glycerol and Tween 20 were diluted in the experiments and glycerol–water solutions (10%, 25%, 40% 50%, and 80%, respectively) as well as Tween 20–water solutions (2%, 5%and 10%) with the same concentrations were prepared. In addition, different mass concentrations of sucrose solutions (10%, 30%, 40%, 50%, and 60%, respectively) were prepared in the experiment by dissolving sucrose in 1 ml of water. To prepare polyethylene oxide (PEO) solutions, 150 mg and 200 mg of PEO powder were added layer by layer to 10 ml of water, respectively, with thorough stirring during the addition process to avoid the formation of large aggregates. In this way, 1.5% and 2% PEO solutions were obtained. After preparation, these solutions were wrapped in aluminium foil and stored under light protected conditions to prevent their decomposition. Similarly, different concentrations of bovine serum albumin (BSA) solutions were prepared. By dissolving different masses of BSA layer by layer into 1 ml of phosphate buffer solution (PBS), BSA solutions with concentrations of 50 mg ml−1, 100 mg ml−1, 150 mg ml−1, 200 mg ml−1, 250 mg ml−1, 300 mg ml−1, and 500 mg ml−1 were obtained. All the prepared solutions were allowed to stand for a period of time to ensure that the air bubbles were completely dissipated before the measurements were carried out.3.2 Experimental setup
Due to the design of the variable cross-section flow channel, there is no need to record the liquid level condition inside the flow channel I, so there is no need to equip a microscope. The schematic diagram of the experimental setup is shown in Fig. 3. A black-and-white industrial camera (MER2-230-168U3M, Daheng Imaging, China) with an acquisition frame rate of 168 fps, paired with a lens (SH-200-03, Daheng Imaging, China) was used to observe the liquid movement inside the microfluidic system under the illumination of a surface light source, with a spatial resolution of about 0.0192 μm per pixel. For specific details of the liquid flow sequence captured by the camera, please refer to D. Fig. S2 in the ESI.† No additional light-blocking treatment was required. During the experiment, a microfluidic pressure controller (OB1 MK4, Elveflow, France) was used to apply a ramp pressure signal, pumping the test liquid into the microfluidic system. Each experiment required 25 μL of the test liquid, and all experiments were conducted at room temperature (25 °C). For comparison, a commercial viscometer (Honeybun, USA) was used to measure the viscosity at 25 °C.3.3 Liquid movement process acquisition
The analysis of the liquid movement process is carried out using an automated Python script. Initially, the captured motion sequence is cropped to a resolution of 1450 × 170 pixels and output as .bmp files at a rate of 20 fps s−1. In related research, the researchers used the Otsu threshold method to convert the image into a binary image,45 and located the liquid edge by analyzing the pixel intensity of the region of interest (ROI), showing good performance.41 A Gaussian blur filter is applied to remove noise, and a threshold is set on the image, followed by an automatic matching algorithm that identifies the position of the leading edge of the liquid surface in each frame (as shown in Fig. 3). By calculating the pixel displacement between neighboring frames separated by i frames, the actual displacement is determined using the known spatial resolution. The value of i is adjusted based on the measured viscosity of the liquid, with higher viscosity corresponding to a larger i value. The algorithmic processing of the flow sequence records the flow velocity on the centerline.3.4 Calibration
Due to the geometric errors of the flow channel and the systematic errors of the instrument, the actual viscosity is | (22) |
4. Results and discussion
4.1 Verification of system accuracy using glycerol–water and tween 20–water solutions
To validate the measurement performance of the pressure-driven DP microfluidic viscometer chip in microchannels, this study selected Newtonian fluids with different volume concentrations as test samples, including glycerol–water and Tween 20–water solutions. Glycerol–water solutions are biocompatible and can be used as green lubricants,46 making them a common choice for verifying the accuracy of viscosity measurement systems.22,47–49 Tween 20, a widely used non-ionic surfactant, finds applications in cosmetics, pharmaceuticals, and the food industry,50 as it enhances the solubility of drugs in water and is often used in formulations to improve the solubility of active ingredients.In the experiments, as shown in Fig. 4, glycerol–water mixtures of 10%, 25%, 40%, 50%, and 80% vol% were measured using both the commercial viscometer Honeybun and the DP microfluidic viscosity chip. The results showed an excellent correlation between the viscosity values measured using two methods. The glycerol–water and Tween 20–water solutions exhibited Newtonian behavior across a wide range of shear rates. The average experimental values and their statistical standard deviations are presented in the figures, confirming the accuracy and stability of the device in measuring high-viscosity solutions. When measuring the 80% glycerol solution with the commercial viscometer Honeybun, the standard deviation (SD) was found to be 2.9 cP, with a coefficient of variation (CV) of 4.8%. In contrast, the experimental values obtained with the DP microfluidic viscometer chip had an SD of 1.575 cP and a CV of 2.567%, indicating less variability in the experimental results compared to the commercial viscometer. Additionally, the measurement process with the DP microfluidic viscosity chip was very rapid; even for the highest viscosity solution (80% glycerol), the entire experiment took no more than 2 minutes, while the measurement time for lower viscosity liquids was only a few seconds.
4.2 Response of the DP microfluidic viscosity chip to sucrose and BSA solutions
In order to evaluate the responsiveness of the DP microfluidic viscosity chip to different concentrations of reagents, viscosity measurements of Newtonian fluid sucrose solutions48,51 and BSA51 solutions were carried out in this study, and Fig. 4 illustrates the experimental results. In Fig. 4(e), measurements of sucrose and BSA solutions at different concentrations were performed using a DP microfluidic viscosity chip and compared with measurements from a commercial viscometer, Honeybun. The experimental data demonstrated a significant agreement between the viscosity measurement system developed in this study and the commercial viscometer with a correlation coefficient R2 = 0.9989. In addition, Fig. 4(f) and (g) show that the viscosity of the reagents increased exponentially with respect to the concentration of the reagents, which could be fitted by the exponential growth equation, and the results of the fit were in good agreement with the correlation coefficients of R2 = 0.9954 and R2 = 0.9981 for sucrose solution and BSA solution, respectively. The fitting of the exponential growth equation shows that the viscosity measurement system is able to respond sensitively to changes in different concentrations of reagents. This property is essential for applications where precise control of reagent concentration is required (e.g., pharmaceutical formulation, biochemical research). In addition, with the fitted curves, the DP microfluidic viscosity chip can accurately predict the viscosity values corresponding to other concentrations of reagents.4.3 Validate the applicability of the DP microfluidic viscosity chip for non-Newtonian fluids
PEO (Polyethylene Oxide) solution, as a non-Newtonian fluid, exhibits shear-thinning behavior and is a standard polymer type used in microfluidic applications, with widespread use in various fields.18 In this study, the power law index n of the PEO solution was calculated based on model eqn (9), and its viscosity values were computed using eqn (22). Fig. 5(a) presents the nonlinear power law fitting curves for 1.5% and 2% PEO solutions. The power law index n for the 1.5% PEO solution is 0.8994 with a coefficient of determination of 0.8698; for the 2% PEO solution, n is 0.8698 with a coefficient of determination of 0.9988, indicating a strong correlation. These results further confirm the non-Newtonian characteristics of the PEO solution. Additionally, pressure directly affects flow velocity, which indirectly determines the shear rate, suggesting that controllable viscosity detection within a shear rate range can be achieved by adjusting the pressure input. Furthermore, Fig. 5(b) compares the viscosity values of different concentrations of PEO solutions measured at various shear rates using the DP microfluidic viscosity chip and the commercial viscometer Honeybun. The data show that the viscosity of the PEO solution significantly decreases with increasing shear rate, reflecting the typical shear-thinning behavior of non-Newtonian fluids. The high consistency between the viscosity data obtained from both measurement methods validates the accuracy and reliability of the DP microfluidic viscometer chip in measuring the viscosity of non-Newtonian fluids.4.4 Discussion
In this study, a wide range of solutions of varying concentrations and properties, comparing the results with those obtained from commercial viscometers. The experimental data clearly demonstrate the excellent precision of the viscosity measurement system developed using the DP microfluidic viscosity chip. This system achieves viscosity measurements within a range of 0–60 cP across various shear rates 0–5 × 104 s−1 using 25 μl of the experimental sample with the entire experimental process taking no more than 2 minutes. The DP microfluidic viscometer chip allows for small-volume viscosity measurements, which is significant for the development and research of valuable reagents and biofluids. The pressure flow microfluidic technology combined with the image provides an effective way for high-throughput measurement of viscosity. By exposing the DP chip as much as possible to the imaging field of view, parallel measurement of multiple liquid viscosities can be achieved.52 In addition, this method based on visual imaging can also be combined with intelligent algorithms to further realize the prediction of complex liquid viscosity and the measurement of other liquid properties,18 thus promoting the development of viscosity research to a more microscopic level.Additionally, the application of UV-curable 3D printing technology in the field of viscosity detection marks an innovative beginning. The rapid response and cost-effectiveness of 3D printers, combined with the ready-to-use features of DP chips, demonstrate the potential of additive manufacturing technologies to create more functional devices for processing.40 For example, with 3D printing technology, it is possible to design and manufacture microfluidic chips that integrate multifunctional components such as mixers, reactors, and sensors.53 This integration would enable microfluidic systems to perform more complex biochemical analyses and diagnostic tasks.54 The rapidity of 3D printing can also allow researchers to carry out more confirmatory experiments and improve the theory of microfluidic systems.
In this study, we only measured the viscosity of liquids within the range of 0–60 cP and did not conduct experimental measurements for liquids with higher viscosity. Therefore, the highest viscosity value that the system can measure has not been clearly defined. Additionally, the time required to measure high-viscosity liquids is relatively long. To achieve rapid measurement, it may be necessary to design microfluidic chip structures with different dimensions. It is worth noting that the hydrophilic and hydrophobic properties of 3D printing materials are limited by the characteristics of the light-curing resin. To meet the needs of different viscosity measurements, future work could consider using resins of different materials or surface coatings to improve the precision of the microfluidic system. At the same time, the use of optical imaging technology to observe the flow of fluids within the microchannels depends on the optical transparency of the microfluidic chips, which sets higher requirements for the light-curing resin. Currently, we have only established a power-law fluid model for non-Newtonian fluids. For other non-Newtonian fluids with different characteristics (such as blood and polymer solutions), more complex constitutive models need to be developed to accurately describe their rheological behavior.
In the current design, the system temperature is typically maintained at 22–25 °C to ensure the characterization of sample viscosity under ambient conditions. However, liquid viscosity varies with temperature, so temperature fluctuations can affect the test results and are one of the main sources of viscosity measurement errors. To enhance the precision of the system and the comprehensiveness of the research, future studies should consider introducing a temperature control system to further explore the impact of temperature on viscosity55 and to establish a temperature-viscosity coupling database. In addition, using a microfluidic viscometer, the impact of different excipients on drug viscosity can also be studied. During the drug formulation process, the type and concentration of excipients have significant effects on viscosity, stability, and rheological properties. Through the microfluidic viscometer, the influence of different excipients on drug viscosity can be precisely analyzed, providing a scientific basis for new drug development and optimization of formulation processes. It is important to note that the application of the microfluidic viscometer is not limited to drug viscosity measurement. Future research can expand its application areas to include the detection of advanced lubricants, cosmetics, edible oils, and more. With the increasing demands for product quality and performance in industrial and consumer markets, the microfluidic viscometer holds great potential for application in these fields, offering important technical support for optimizing formulations and enhancing product performance.
5. Conclusions
This study shows that a variable cross-section microfluidic viscosity chip structure based on pressure-driven microfluidics and optical imaging technology is proposed and a digital-printed microfluidic viscometer is designed. By testing liquids with different concentrations and characteristics and comparing them with a commercial viscometer, the results show that the device has excellent testing performance. This viscosity measurement method is a low-cost, convenient and accurate way with low sample volumes. In particular, the high aspect ratio structure of the small cross-section pipe, the precision machining process, and the design of a large cross-section size which is much larger than a small cross-section size play a crucial role in viscosity measurement. Meanwhile, the use of light-curing 3D printing technology to fabricate microfluidic channels not only improves the fabrication accuracy of variable cross-section microfluidic chips, but also significantly enhances the machining convenience of variable cross-section chip structures with different sizes.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work was financially supported by the Jilin Province Science and Technology Development Program (No. 20230402046GH).References
- F. Yang, Z. Chen and D. Xing, IEEE Trans. Med. Imaging, 2020, 39, 1791–1800 Search PubMed.
- M. Brust, C. Schaefer, R. Doerr, L. Pan, M. Garcia, P. E. Arratia and C. Wagner, Phys. Rev. Lett., 2013, 110, 078305 CrossRef CAS PubMed.
- M. Desai, A. Kundu, M. Hageman, H. Lou and D. Boisvert, mAbs, 2023, 15, 2285277 CrossRef CAS PubMed.
- N. Whitaker, J. Xiong, S. E. Pace, V. Kumar, C. R. Middaugh, S. B. Joshi and D. B. Volkin, J. Pharm. Sci., 2017, 106, 3230–3241 CrossRef CAS PubMed.
- W. Jiskoot, A. Hawe, T. Menzen, D. B. Volkin and D. J. A. Crommelin, J. Pharm. Sci., 2022, 111, 861–867 CrossRef CAS PubMed.
- C. Jin, F. Wu, Y. Hong, L. Shen, X. Lin, L. Zhao and Y. Feng, Carbohydr. Polym., 2023, 311, 120731 CrossRef CAS PubMed.
- S. von Bülow, M. Siggel, M. Linke and G. Hummer, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 9843–9852 CrossRef PubMed.
- S. J. Shire, Curr. Opin. Biotechnol, 2009, 20, 708–714 CrossRef CAS PubMed.
- T. Heise, L. Nosek, S. Dellweg, E. Zijlstra, K. A. Præstmark, J. Kildegaard, G. Nielsen and T. Sparre, Diabetes Obes. Metab., 2014, 16, 971–976 CrossRef CAS PubMed.
- M. Zidar, P. Rozman, K. Belko-Parkel and M. Ravnik, J. Colloid Interface Sci., 2020, 580, 308–317 CrossRef CAS PubMed.
- Y. Q. Chen, M. C. Wu, M. T. Wei, J. C. Kuo, H. W. Yu and A. Chiou, Mater. Today Bio, 2024, 26, 101058 CrossRef CAS PubMed.
- H. Fabek, S. Messerschmidt, V. Brulport and H. D. Goff, Food Hydrocolloids, 2014, 35, 718–726 CrossRef CAS.
- Á. de la Rosa, E. Poveda, G. Ruiz, R. Moreno, H. Cifuentes and L. Garijo, Constr. Build. Mater., 2020, 260, 119715 CrossRef.
- S. Oh, B. Kim, J. K. Lee and S. Choi, Sens. Actuators, B, 2018, 259, 106–113 CrossRef CAS.
- L. Theuer, M. Lehmann, S. Junne, P. Neubauer and M. Birkholz, Int. J. Mol. Sci., 2017, 18(6), 1235 CrossRef PubMed.
- L. Huang, W. Li, G. Luo, D. Lu, L. Zhao, P. Yang, X. Wang, J. Wang, Q. Lin and Z. Jiang, Microsyst. Nanoeng., 2022, 8, 38 CrossRef CAS PubMed.
- E. K. Sackmann, A. L. Fulton and D. J. Beebe, Nature, 2014, 507, 181–189 CrossRef CAS PubMed.
- F. Del Giudice and C. Barnes, Anal. Chem., 2022, 94, 3617–3628 CrossRef CAS PubMed.
- Y. Ge, X. Huang, X. Tang, Y. Wang, F. Chen, D. Xiao, P. Liang and B. Li, Opt. Lasers Eng., 2024, 181, 108413 CrossRef.
- Y. J. Kang and S.-J. Lee, Analyst, 2018, 143, 2723–2749 RSC.
- P. S. Venkateswaran, A. Sharma, S. Dubey, A. Agarwal and S. Goel, IEEE Sens. J., 2016, 16, 3000–3007 CAS.
- P. S. Lenzen, F. Dingfelder, M. Muller and P. Arosio, Anal. Chem., 2024, 96, 13185–13190 CrossRef CAS PubMed.
- S. Kim, K. C. Kim and E. Yeom, Opt. Lasers Eng., 2018, 104, 237–243 CrossRef.
- Y. Li, K. R. Ward and M. A. Burns, Anal. Chem., 2017, 89, 3996–4006 CrossRef CAS PubMed.
- Y. Son, Polymer, 2007, 48, 632–637 CrossRef CAS.
- N. Srivastava and M. A. Burns, Anal. Chem., 2006, 78, 1690–1696 CrossRef CAS PubMed.
- J. Lee, T. C. Chou, D. Kang, H. Kang, J. Chen, K. I. Baek, W. Wang, Y. Ding, D. D. Carlo, Y. C. Tai and T. K. Hsiai, Sci. Rep., 2017, 7, 1980 CrossRef PubMed.
- R. Khnouf, D. Karasneh, E. Abdulhay, A. Abdelhay, W. Sheng and Z. H. Fan, Biomed. Microdevices, 2019, 21, 80 CrossRef CAS PubMed.
- J. Lee, T.-C. Chou, D. Kang, H. Kang, J. Chen, K. I. Baek, W. Wang, Y. Ding, D. D. Carlo, Y.-C. Tai and T. K. Hsiai, Sci. Rep., 2017, 7, 1980 CrossRef PubMed.
- D. Solomon, A. Abdel-Raziq and S. Vanapalli, Rheol. Acta, 2016, 55, 727–738 CrossRef CAS.
- S. Pal and A. Bhattacharyya, Polym. Test., 2025, 143, 108687 CrossRef CAS.
- M. Bianco, A. Zizzari, L. Gazzera, P. Metrangolo, G. Gigli, I. Viola and V. Arima, Sens. Actuators, B, 2018, 265, 91–97 CrossRef CAS.
- Y. J. Kang, E. Yeom and S. J. Lee, Anal. Chem., 2013, 85, 10503–10511 CrossRef CAS PubMed.
- L. J. Kricka, P. Fortina, N. J. Panaro, P. Wilding, G. Alonso-Amigo and H. Becker, Lab Chip, 2002, 2, 1–4 RSC.
- C. Zhang, Z. Luo, C. Liu, J. Zhu, J. Cao, J. Yuan, P. Wang, C. Liu, C. Lao and Z. Chen, Ceram. Int., 2021, 47, 11097–11108 CrossRef CAS.
- H. Ravanbakhsh, V. Karamzadeh, G. Bao, L. Mongeau, D. Juncker and Y. S. Zhang, Adv. Mater., 2021, 33, e2104730 CrossRef PubMed.
- A. C. Daly, M. E. Prendergast, A. J. Hughes and J. A. Burdick, Cell, 2021, 184, 18–32 CrossRef CAS PubMed.
- G. I. Salentijn, P. E. Oomen, M. Grajewski and E. Verpoorte, Anal. Chem., 2017, 89, 7053–7061 CrossRef CAS PubMed.
- F. P. Melchels, J. Feijen and D. W. Grijpma, Biomaterials, 2010, 31, 6121–6130 CrossRef CAS PubMed.
- V. Karamzadeh, A. Sohrabi-Kashani, M. Shen and D. Juncker, Adv. Mater., 2023, 35, e2303867 CrossRef PubMed.
- H. Hong, I. Doh, J. Jeong and E. Yeom, Results Eng., 2024, 24, 103362 CrossRef.
- H. Hong, J. M. Song and E. Yeom, Biomicrofluidics, 2019, 13, 014104 CrossRef PubMed.
- I. C. Christov, J. Phys.: Condens. Matter., 2021, 34(6), 063001 CrossRef PubMed.
- B. Ping, J. Huang and F. Meng, J. Manuf. Process., 2023, 101, 807–819 CrossRef.
- H. Hong, J. M. Song and E. Yeom, Sci. Rep., 2022, 12, 8986 CrossRef CAS PubMed.
- V. Fadaei Naeini, M. Björling, J. A. Larsson and R. Larsson, J. Mol. Liq., 2023, 390, 122990 CrossRef CAS.
- M. F. DeLaMarre, A. Keyzer and S. A. Shippy, Anal. Chem., 2015, 87, 4649–4657 CrossRef CAS PubMed.
- A. Grupi and A. P. Minton, Anal. Chem., 2012, 84, 10732–10736 CrossRef CAS PubMed.
- T. A. Lee, W. H. Liao, Y. F. Wu, Y. L. Chen and Y. C. Tung, Anal. Chem., 2018, 90, 2317–2325 CrossRef CAS PubMed.
- N. MohdMaidin, M. J. Oruna-Concha and P. Jauregi, Food Chem., 2019, 271, 224–231 CrossRef CAS PubMed.
- I. C. Esfahani, N. A. Tehrani, S. Ji and H. Sun, J. Pharm. Sci., 2024, 113, 2715–2722 CrossRef CAS PubMed.
- D. E. Solomon, A. Abdel-Raziq and S. A. Vanapalli, Rheol. Acta, 2016, 55, 727–738 CrossRef CAS.
- R. D. Sochol, E. Sweet, C. C. Glick, S. Venkatesh, A. Avetisyan, K. F. Ekman, A. Raulinaitis, A. Tsai, A. Wienkers, K. Korner, K. Hanson, A. Long, B. J. Hightower, G. Slatton, D. C. Burnett, T. L. Massey, K. Iwai, L. P. Lee, K. S. Pister and L. Lin, Lab Chip, 2016, 16, 668–678 RSC.
- J. Wang, C. Shao, Y. Wang, L. Sun and Y. Zhao, Engineering, 2020, 6, 1244–1257 CrossRef CAS.
- M. Peleg, Crit. Rev. Food Sci. Nutr., 2018, 58, 2663–2672 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: A. The relationship between the average flow velocity and the central linear flow velocity. B. Darcy friction factor. C. Measurement results of contact angle. D. Liquid flow sequence. ) E. The viscosity of water. See DOI: https://doi.org/10.1039/d4an01550a |
| This journal is © The Royal Society of Chemistry 2025 |





