Effect of different morphologies on the creep behavior of high-density polyethylene

Abstract

With the wide use of polymer materials as pressure parts, people have started paying more attention to the safety and longevity of polymeric materials. Creep is one of the most important factors to evaluate materials. In this study, a self-designed oscillatory shearing injection molding (OSIM) device was utilized to prepare pure HDPE specimens with special morphologies. According to a comparison of the creep behavior of the OSIM specimens with conventional injection molding (CIM) specimens, the distinction between the resistivity to creep due to the special morphologies was observed. Two initial external stress levels (10 MPa and 15 MPa) and three temperatures (ambient temperature 25 °C, 40 °C and 60 °C) were employed in this experiment. Different morphologies resulted in different responses to creep. The deformation and compliance of the CIM specimens were triple or more than those found for the OSIM specimens under the same conditions. The instantaneous deformation of the OSIM specimens was 0.2% compared with 0.6% found for the CIM specimens under 10 MPa at 25 °C. The deformation of the OSIM specimens was 4% after creep for an hour, but the CIM specimens were already necked at less than 50 min under 15 MPa at 40 °C. At 60 °C, too much plastic deformation appears in the creep behavior of the CIM specimens and the creep behavior was nearly not observed under these conditions. In addition, the creep behavior of the OSIM specimens can be observed at 60 °C. According to our tests and analysis, the property of creep resistivity for the OSIM specimens was better than that found for the CIM samples, in both the amorphous phase and crystalline region. In addition, the creep behavior of the OSIM and CIM specimens was satisfactorily described using the generalized Kelvin–Voigt model with one retardation time.

---

Introduction

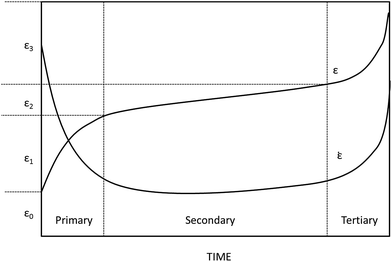
Over the past 100 years, in increasing number of fields, metal materials have been replaced with polymeric materials under certain critical working pressures because of their useful properties such as lightness, low density, corrosion resistance, and good longevity; moreover, they are easy to transport.¹ Creep—the development of deformations over time under a constant stress—is known as one of the features of polymeric materials.² Many studies have tried to theoretically explain the non-linear viscoelasticity behavior of polymers.^3–5 A schematic curve obtained from the strain and time of creep is shown in Fig. 1.

Fig. 1 Schematic of the creep stage by strain.

According to the curve, the entire processes in creep of polymers can be considered as four stages, namely, (I) instantaneous deformation with ε₀, (II) primary creep with ε₁, (III) secondary creep with ε₂, and (IV) tertiary creep with ε₃.^6,7 The instantaneous deformation is independent of time and is caused by the elastic and plastic deformation of polymer once the initial external stress is applied. At the start of the primary creep stage, the creep rate is relatively high and then decreases rapidly with time, which may be due to the orientation of the polymer chains under persistent stress. Viscoelastic flow in the polymer occurs and the duration is relatively long if it is under a low stress level in the secondary creep stage; the creep rate reaches a steady-state value after a certain period of time. In addition, strain hardening may appear at this stage. Finally, the material falls into the tertiary creep stage, where the creep rate increases rapidly with the occurrence of final creep rupture or advanced necking,⁶ as illustrated in Fig. 1.

Creep is a complex phenomenon, which depends on the properties of material and the external environment. Creep occurs under a stress far lower than ultimate stress at ambient temperature.⁸

Because of the combination of elastic and plastic deformation in creep behavior, the strain of creep increases non-linearly with time. Thus, the behavior of creep depends on the material properties, temperature and the applied stress. Oriented polymers have a good creep resistivity because the highly orientated fibers increase the number of load-bearing fibers.²⁹ Amorphous phases also play an important part in long-term properties such as creep and slow crack growth.¹⁹ Indeed, the structure of the polymer plays the most important role, especially its crystal structure.

In this study, we have utilized the oscillatory shear injection molding (OSIM), the technology exploited by Prof. Shen Kaizhi. The key of the technology is that two vibratory plungers driven by a hydraulic cylinder is installed into the hot runner manifold of the mold. We can control the temperature of the melt accurately and give the melt better plastication using this technology. Test experiments on the mechanical properties indicate that the tensile strength and the modulus of the OSIM HDPE specimens show a great improvement (from 23 MPa to 93 MPa and 1 GPa to 5 GPa, respectively). Analysis experiments indicate that a shish-kebab structure appeared in the samples prepared using this technology, with more perfect crystallization and an obvious molecular orientation along the direction of flow.⁹ No other study has previously carried out the same creep investigation on the OSIM specimens studied in this article.

The time–temperature superposition principle is often used to extend the time domain of creep behavior. For thermo-rheologically simple polymers, the method involves registering the creep compliance at different temperatures over short durations. Then, a more complete curve, named as the master curve, can be built on a larger time scale by the horizontal shift in the experimental series along the time axis. The shift factor obeys the William–Landel–Ferry (or WLF) equation.^10,11 In fact, this method is relevant for many amorphous polymers but is not appropriate for semi-crystalline thermoplastics for which the time–temperature superposition principle is not valid.¹² In this study, we have used the combination of the Maxwell model and generalized the Kelvin–Voigt model to fit the actual creep curve approximately.

In this study, we hope to improve the creep property of a polymer with a special morphology structure prepared using OSIM, extend the longevity of polymers and find an appropriate model to fit the creep behavior.

Experimental section

Materials

High-density polyethylene (HDPE), 5000 s of density 0.951 g cm⁻³ with an MFR (GB3682-89) of 0.8–1.2/10 min was obtained from the Chinese Lanzhou petrochemical company.

Facilities

A plastic injection-molding machine was obtained from Haitian Rubber Ltd., Ningbo. A differential scanning calorimeter (DSC), Q20, was obtained from TA, America. A scanning electron microscope (SEM), S-450, was obtained from Hitachi, Japan. An X'Pert Pro diffractometer was obtained from Philips, Netherlands, to study X-ray diffraction (XRD). An online displacement recorder was obtained from Qili Sensing system engineering Co., Ltd., Bangbu. A dynamic mechanical analysis (DMA) apparatus, Q800, was obtained from TA, America. The self-designed creep device and oscillatory shear injection molding apparatus are shown in Fig. 2 and 3. The minimum weight applied to the specimens was 12 kg due to the limit of the weight of the connecting rod and scale.

Fig. 2 Sketch illustrating the molding process during oscillatory shear injection.

Fig. 3 Sketch of the structure of the creep device.

Preparation of the specimens

Pure HDPE was dried in an oven for 6 hours, and then the dried HDPE granules were injected into the plastic injection-molding machine. We divided the sample into conventional injection molding (CIM) samples and oscillatory shear injection molding (OSIM) samples. The difference between the two types of samples is that the OSIM samples experienced a reciprocating shearing action in the hot runner during the cooling and packing of the samples. This makes the samples permanently sheared, and then the morphology in the interior of the OSIM samples can be changed. For the CIM samples, there was no oscillatory shear during the cooling or packing stage. Both the OSIM and CIM specimens were dumbbell-shaped. The other parameters used in the process are uniform. All the parameters are shown in Table 1.

Table 1 Parameters for the sample preparation process

Injection pressure (MPa)	Temperature of the melt (°C)	Temperature of the mold (°C)	Vibration interval (s)	Packing pressure (MPa)	Packing time (s)	Vibration pressure (bar)
60	200	45	0	Section 1: 10	60	0
60	200	45	2.0			85
				Section 2: 20	60
				Section 3: 30	60

---

Experimental

We cut the specimens as the shape of the collet. The temperature was maintained from ambient temperature (25 °C) to 60 °C in the calorstat and the environment was air. The initial external stress F of the CIM and OSIM specimens in the experiment was the same under all the temperatures studied. The specimens were clamped using a collet at different temperatures and the stress was loaded after the temperature of the calorstat reached the desired temperature for more than one hour to reach a thermal equilibrium. The displacement of the specimens was recorded by an online displacement recorder connected to a computer. In the beginning of the creep, the interval for recording the data was 0.1 s and after the primary state, the interval for recording the data was changed to 1 s. For the accuracy of the experiment, three specimens were tested to study the creep process for each condition studied. If the experimental data was inconsistent, two specimens were tested to obtain more accurate experimental results.

Results and analysis

Analysis of the creep behavior

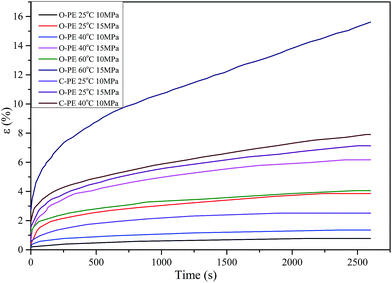
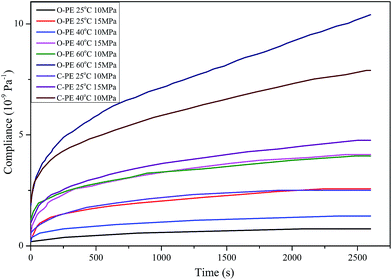
The experiment used to study the uniaxial tensile creep was carried out at two applied stress levels (10 MPa and 15 MPa) and three temperature levels (ambient temperature 25 °C, 40 °C, and 60 °C). The curves for deformation and compliance versus time are shown in Fig. 4 and 5, respectively. Fig. 6 shows the curve for deformation and compliance for the CIM specimens under 15 MPa at 40 °C. The creep behavior was nearly not found in the curve due to the plastic deformation at 40 °C, which took hold of the whole curve, and the creep behavior was hidden under the plastic deformation. On the other hand, the stress could not be lower than 10 MPa due to the limit of the weight of the connecting rod and scale. Thus, the curves for the CIM specimens under 60 °C are not shown in the paper.

Fig. 4 Curves for deformation versus time (O-OSIM and C-CIM).

Fig. 5 Curves for compliance versus time (O-OSIM and C-CIM).

Fig. 6 Curves for deformation and compliance of the CIM specimens at 40 °C and under 15 MPa.

Creep as a function of temperature. The deformation and compliance of the OSIM and CIM specimens as a function of temperature are shown in Fig. 4 and 5, respectively. An increase in temperature led to higher macromolecular mobility and high deformation during creep.⁸ The instantaneous deformation increases with an increase in temperature for both the OSIM and CIM specimens. The chains are straightened and some unsubstantial regions slip with the stress upon loading. Obviously, a higher temperature indicates large slippage and more plastic deformation. Creep rate also increases with an increase in temperature because of the active polymer chains.

Creep as a function of applied stress. The deformation and compliance of the OSIM and CIM specimens as a function of the initial applied stress are shown in Fig. 4 and 5, respectively. An increase in the initial applied stress results in an increase in deformation and compliance. The deformation after the transient response, however, was insensitive to the creep rate dependence,¹³ which was a result of the rapid orientational hardening that occurred in the amorphous regions once the specimen was persistently loaded, in which the stress was not high enough to produce further deformation of the polymer. At the same time, the strength perpendicular to the direction of stress becomes weaker, which resulted in de-bonding and slippage of the orientated polymer chains. Of course, the time of the progress should be shorter with a higher stress.

Creep as a function of different morphology. The deformation and compliance of the OSIM and CIM specimens as a function of different morphology are shown in Fig. 4 and 5, respectively. At the same temperature, irrespective of the instantaneous deformation, the creep rate and final deformation of the CIM specimens was considerably larger than those found for the OSIM specimens.

The instantaneous deformation is shown in Fig. 7. The instantaneous deformation of the OSIM specimens was 0.2% compared with 0.6% found for the CIM specimens under 10 MPa at 25 °C. The resistivity to slippage of the OSIM specimens was much better than that found for the CIM specimens and was proved by the abovementioned results. Upon increasing the temperature, the difference became larger. High temperature was accompanied by a large instantaneous deformation, except in the OSIM specimens at 25 °C and 40 °C tested under 10 MPa. The reason why the transient response just after loading was the same although the temperature increased may due to the special morphology that appears in the OSIM specimens. After oscillatory shearing, the morphology of the specimens changes to an interlocked shish-kebab morphology including ridge fibers, overgrown lamellas and tie molecules that cross through the lamellas. It was supposed that when the weight was loaded, the random coil becomes straight and ordered but the tie molecules and ridge fibers, which are interlocked with the lamellas, make the slippage harder. Although the temperature increases, 10 MPa was also not sufficiently large to damage the interlocked morphology. In addition, the instantaneous deformation of the CIM specimens at 25 °C under 10 MPa was the same as that found for the OSIM specimens at 40 °C under 15 MPa. This indicates that the interlocked shish-kebab morphology has a more perfect resistance to time-independent deformation.

Fig. 7 Curves for the instantaneous deformation of the OSIM and CIM specimens.

The slippage of polymer chains and damage to the oriented fibers in the CIM specimens results in a high creep rate during the primary stage. After stress loading, the chains in the CIM specimens become straight and disentangle quickly. The links between the different crystalline regions decrease at the same time. Then, long slippage appears in both the crystalline regions and amorphous regions. The creep rate of the CIM specimens may be twice or more than that found for the OSIM specimens under the same conditions. The shish-kebab structure combines more chains to support the load and the chains interlocked with each other to resist the slippage of the chains.

The plastic deformation in the CIM specimens is obvious as shown in Fig. 5. As time increases, the slippage and fiber damage observed in the CIM specimens becomes partial failure. Large deformation in crystallized polymer such as the pulling out of chain folds by a crystal slip process and an irreversible transition in an amorphous polymer such as the pulling out of chain entanglement and orientation crystallization under external stress^14,15 results in macroscopical creep. Microvoids appear in the specimens and the progress accelerates. Plastic deformation was nearly not found in the OSIM specimens under low temperature and applied stress. Only slippage and dislocation appear in the OSIM specimens while the temperature rises until the conditions reach 60 °C and 15 MPa. The pulling out of the crystalline region becomes difficult due to the interactions of tie molecules, overgrown lamella and the orientated chain bundles.

Discussion

To understand the differences in the morphologies of the OSIM and CIM specimens, the DSC, SEM, XRD and DMA are carried out. We analyzed the shear layer (0.5 mm to the surface) and core (3 mm to the surface) of the specimens to find the relationship between the different morphologies and creep behavior. The curves for creep were also analyzed.

X-Ray diffraction

XRD experiments were conducted using a Philips 3 kW X-diffractometer (Netherlands) to characterize the crystalline structure. A graphite curved crystal monochromator and Co K_α1 radiation were used. The tube voltage and current were 45 kV and 40 mA, respectively, with a scanning rate of 0.03° min⁻¹. The scattered intensities were registered in the range of scattering angles 2θ from 15° to 30°. To further investigate the relationship between the inner structure (crystal size and orientation degree of the specimens) inside the specimens under different processing conditions and the creep process, we used XRD to test the shear layer and the core of the CIM and OSIM specimens, respectively.

Fig. 8 shows the XRD curves for the CIM and OSIM HDPE specimens and Table 2 shows the XRD results of the specimens obtained using the XRD analysis software (X'Pert Highscore Plus). Generally, HDPE has four crystal faces, namely, (110), (200), (210), and (020), and the angles of the crystal diffraction peaks are 21.55°, 23.89°, 30.01°, and 36.20°,^16,17 respectively. We only analyzed the strong diffraction peaks of crystal face, namely, (110) and (200), in the discussion because the diffracted intensity of the (210) and (020) crystal faces are very weak compared with that found for the (110) and (220) crystal faces. The diffracted intensity depends on the microcrystal size in the three directions of the crystal and on the number of the microcrystals¹⁸ based on the theory of XRD intensity. We discovered that the diffracted intensity of the (110) direction was considerably stronger than that of (200). This indicated that the formation of the microcrystal in the (110) direction was easiest. The orientation and direction of the crystal can be preliminary judged through the ratio of the diffracted intensity of the crystal faces.¹⁹ Compared with the CIM specimens, for the shear layer of the OSIM specimens, the diffracted intensity and the ratio of peak height (the ratio of peak height of the (200) and the (110) planes) of the crystal face are higher. This indicates that the degree of orientation in the (110) and (200) crystal faces of the OSIM HDPE specimens changes and the degree of orientation was bigger than that found for the CIM specimens. For the (110) crystal face, the diffracted intensity of the shear layer was bigger than that of the core because the shear action was maintained with quick cooling on the surface layer during the injection molding process. In addition, for the shear layer, the peak width at half height for the OSIM specimens decreased for both the (110) and (200) crystal face compared with those found for the CIM samples. According to the Scherrer equation,²⁰ it can be concluded that crystallite size at the shear layer of the OSIM specimens becomes greater than that found for the CIM samples due to the perfect crystallinity caused by oscillatory shear.

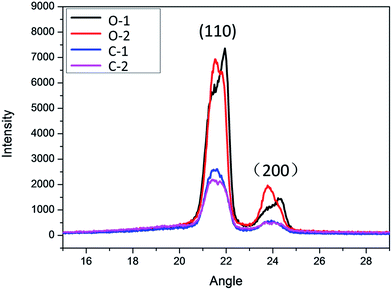Fig. 8 XRD curves for different specimens (C – CIM specimen, O – OSIM specimen; 1 – shear layer, 2 – core).

Table 2 XRD results for different specimens^a

Specimen	Crystal face (110)			Crystal face (200)			Peak height ratio
	2θ	dhkl	B	2θ	dhkl	B
a 2θ – scattering angle; dhkl – interplanar spacing; B – peak width at half height.
C-Shear layer	21.5	4.1281	0.88	23.9	3.7257	0.94	0.18
C-Core	21.5	4.1261	0.95	23.9	3.7211	1.18	0.17
O-Shear layer	21.6	4.1132	0.88	24.0	3.7090	0.99	0.18
O-Core	21.5	4.1218	0.76	23.8	3.7327	0.82	0.24

---

Differential scanning calorimetry

The morphology of the injected specimens can be investigated using thermal analysis. Specific information such as the behavior of crystallization, crystalline liquation and the changes in micromorphology can be acquired by subjecting the HDPE specimens to different injection conditions. We tested the different surfaces in the injection specimens using DSC from 25 to 160 °C at a heating rate of 10 °C min⁻¹, and the degree of crystallinity was estimated using eqn (1).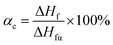α_c degree of crystallinity, ΔH_f enthalpy of fusion, ΔH_fα (PE is 293 J g⁻¹) enthalpy of fusion of a perfect crystal of the same polymer.

Both surfaces of the CIM specimens have single melting peaks, as shown in Fig. 9, and the melting point displayed a little increase from shear layer to core. The reason for this may be that the melt temperature during the injection molding process was very high and the cooling rate was slow, allowing the crystals to grow perfectly. The increase in melting point for the OSIM specimens indicates that the lamella thickness increases or the crystal was more perfect after oscillatory shear. Furthermore, the melting curve shows that the OSIM specimens present two melting peaks in both surfaces, and a different melting peak indicates different structure in the crystal. The melting peaks at about 133 °C and at about 136 °C represent the melting of the PE lamellas and the melting of some of the oriented structures such as ridge fibers or the shish-kebab structure, respectively. Thus, we can draw the conclusion that the oriented structures or shish-kebab structure were formed in some parts of the specimens under the conditions used in the oscillatory shear process and the shish-kebab structure has a better heat stability compared with the homologous lamellae. The results correspond to the results reported in the previous literatures.

Fig. 9 DSC curves for different surfaces (C – CIM specimen, O – OSIM specimen; 1 – shear layer, 2 – core).

The degree of crystallinity in the specimens injected under different shearing conditions can be further determined. The degree of crystallinity in the OSIM specimens possesses different values in the different surfaces; however, it was much higher than the degree of crystallinity in the CIM specimens. The level of compliance increased with an increasing degree of crystallinity.²¹ Fig. 10 shows the schematic of the internal morphology of the CIM and OSIM specimens. After stress loading, the ridge fibers in the OSIM specimens become straight and the distance between the overgrown lamellas becomes larger. Because of the high orientation of ridge fibers, the craze among the fibers barely occurred, and the high-density tie molecules limit the movement of the overgrown lamellas. Under the same conditions, the CIM specimens with spherocrystals develop craze and microvoid quickly; subsequently, local fractures and slippage occur in the network between the crystalline regions.

Fig. 10 Schematic of the internal morphology of the CIM and OSIM specimens.

Scanning electron microscope

Fig. 11 shows the SEM images of the CIM and OSIM specimens. The images of the CIM specimen shows that the crystal formed in the shear layer, middle layer and core are all spherocrystal. However, in the images of the OSIM specimen, a mass of orderly ridge fibers and overgrown lamella can be observed. In addition, the spherocrystals cannot be found in this layer. In the middle layer, the shish-kebab structure is not obvious as that found in the shear layer. The spherocrystals become the major crystal form in the core of the OSIM specimen.

Fig. 11 SEM images of the CIM (line A) and OSIM (line B) specimens (×16 000).

The phenomenon shown in the SEM images appears because of the method of injection. For the CIM specimens, the processing of packing without shear contributes to the formation of spherocrystals. Therefore, the spherocrystal was the major crystal form in the CIM specimens. For the OSIM specimens, the infliction of shear makes the polymer chains orient along the direction of flow. The cooling of the shear layer was very fast because it was close to the surface of the specimen, which is contiguous with the wall of the model. Thus, the shish-kebab structure was retained. In the core of the specimen, the cooling was very slow, which makes the crystal form become spherocrystal. In addition, in the middle of the specimen, the cooling was not very slow and the shear was not violent because of freezing in the surface and shear layers. Thus, the shish-kebab structure was not as perfect as that found in the shear layer.

The structure without orientation in the CIM specimens leads to a weak resistivity against creep because of the defects that appear just after loading. However, the oriented ridge fibers, which are shown in the SEM images of the OSIM specimens, hinder the local failure, and the high-density tie modulus through the lamellas control the movement of the lamellas. This is the reason for the considerably different phenomenon observed for the creep behavior between the OSIM and CIM specimens. The non-linear viscoelastic behavior was considered to be the plastic deformation and/or failure process accompanied with crazes and voids caused by the external load applied. The stacked lamellar clusters initially separate at low strain,²² and intercluster tie-links or bundled tie molecules between adjacent lamellar clusters support the external force, leading to a portion of the lamellar cluster to be bent around each intercluster link. During the creep behavior, the fragmentation of the lamellar clusters into cluster units occurs when the elastic energy stored in the bending clusters reaches a critical value, and is considered to be accompanied by the dislocation and cleavage processes in the crystalline phases, as demonstrated by Young.²³ The OSIM specimens have a better resistivity on the movement above than that found for the CIM specimens because the ridge fibers strengthen the link and hinder the bending clusters. A detailed explanation for such creep behavior requires a more intensive investigation of the structural changes that occur during creep deformation.

Dynamic mechanical analysis

The crystalline region is the major factor in the resistivity against creep, but the crystalline region was less than 60% according to the DSC results (Table 3). This indicates that the effect of the amorphous region cannot be ignored. After stress loading on the specimens, the random coil in the amorphous region was stretched and then craze occurs because of the localized stress concentration. It is known that PE is locally rubbery in the amorphous region and it is rigid due to the network made between the crystalline region and the entanglement of amorphous phases.^24,25 OSIM makes the network between the crystalline regions stronger and the craze made by the stress occurrence more difficult. The slippage in the polymers was caused by craze, thus the OSIM specimens have a better resistivity in their crystalline phases. On the other hand, the resistivity to creep in the amorphous region was determined by the mobility of the amorphous phase.²⁶ When the amorphous phase was mobile, more material can be sucked into the craze and then they become orientated locally. This was beneficial to make the amorphous regions difficult to undergo slippage and damage. This process competes with the process of disentanglement. To monitor this mobility, dynamic mechanical analysis (DMA) is a suitable method because DMA is very sensitive to relaxation in different phases.

Table 3 Results of DSC tests

Specimen (thickness)	Melting peak temperature (°C)	Enthalpy of fusion (J g^−1)	Degree of crystallinity (%)
C-1/(shear layer)	132.39	155.9	53.21%
O-1/(shear layer)	132.49, 134.5	170.9	58.33%
C-2/(core)	132.93	160.3	54.71%
O-2/(core)	133.73, 136	172.6	58.91%

---

Fig. 12 shows the measurement of DMA. (, where G′ is the storage module and G′′ is the loss module.) A broad peak in the high-temperature range of the curve was α-relaxation because of the characteristic drop behavior in the high-temperature range of G′. An upward curvature in the low-temperature range is called the γ-process.²⁷ In the intermediate-temperature range, the curves indicate an additional relaxation process, generally termed as β-relaxation (from −50 to 25 °C). The β-process was related to relaxation phenomena in the amorphous phase and is called the dynamic glass transition.²⁷ The absolute value for the β-relaxation in the tan δ curve is a measure of the mobility in the amorphous phase.²⁶ According to the DMA curves, it was found that the mobility in the amorphous phase of the OSIM specimens was stronger than that found for the CIM specimens. This indicates that the resistivity of the amorphous phase in the OSIM specimens was better than that found in the CIM specimens. In other words, both in the crystalline region and the amorphous phases, the resistivity of the OSIM specimens to creep was better than those found for the CIM samples.

Fig. 12 Loss tangent tan δ as a function of temperature measures at 1 Hz using DMA. β-Relaxation lies in a temperature range of −50 to 25 °C.

Generalized Kelvin–Voigt model

It is well established that the rheological behavior of a polymer can be described using the analytical models based on the series and parallel association of elastic and viscous elements.^11,28 The generalized Kelvin–Voigt model, which is the association of springs and dashpots shown in Fig. 13, was found to obtain reliable results in this study.

Fig. 13 Representation of the generalized Kelvin–Voigt model.

Each unique E_i characterizes a spring and η_i characterizes a dashpot. The applied stress is constant and the creep rate depends on time, thus the equation defined compliance of the model¹⁰ is

where C₀ is the compliance at t = 0 and η₀ is the polymer viscosity. As the polymer under the test temperature is solid (η₀ → ∞), thus the dashpot in series is ignored. θ_i is the retardation time of the ith parallel element . The equation changes towhen n = 1, it is the simplest condition of this model. Then, the equation can be written as

The parameters of C₀, C₁ and θ calculated from the results of the tests can be found in Table 4. The OSIM specimens always have a long retardation time under the same conditions. This indicates that the movement of the chain is more difficult in the OSIM specimens than that found in the CIM specimens.

Table 4 Parameters of the generalized Kelvin–Voigt model with one retardation time at 10 MPa

	C0	C1	θ
O-PE 25 °C	0.1928 × 10^−9/Pa	0.4938 × 10^−9/Pa	605.9 s
O-PE 40 °C	0.1928 × 10^−9/Pa	0.7713 × 10^−9/Pa	216.4 s
C-PE 25 °C	1.543 × 10^−9/Pa	0.5785 × 10^−9/Pa	434.8 s
C-PE 40 °C	1.928 × 10^−9/Pa	2.314 × 10^−9/Pa	86.56 s

---

The curves for the experiment and the fitted curves are shown in Fig. 14. The fitting curve for the OSIM specimens at 25 °C under 10 MPa is close to the real experiment because there is little plastic deformation during the creep. Although the fitting curve for the CIM specimens under the same conditions has a little deviation, it can be found that the two curves are nearly parallel. In fact, the two curves are nearly coincidental if the plastic deformation of the test was removed from the curve of the real test. This indicates that the generalized Kelvin–Voigt model can fit the creep behavior appropriately. The more parallel elements added to the fitting, the more contact ratio in the fitted curve and the real test curve was observed.

Fig. 14 Curves for the real creep behavior and fitting using Kelvin–Voigt model with one parallel element.

Conclusions

At all the applied stress levels and temperature levels, the deformation and compliance of the OSIM specimens were much less than those found for the CIM specimens. Upon increasing the temperature to 60 °C, the creep behavior of the CIM specimens cannot be observed.

Active mobility caused by high temperature results in slippage and easier local fracture. Extending the applied stress has the same effect. The large difference in the creep behavior between the OSIM and CIM specimens is mainly attributed to the different morphologies in the specimens. The slippage and the pulling of the chains out of the crystalline region become difficult due to the shish-kebab structure and the interlocked morphology. The movement of lamellas clusters and the dislocation and cleavage processes of the crystalline phases become difficult because of the existence of ridge fibers and tie molecules in the OSIM specimens. The DMA results indicate that the amorphous phase in the OSIM specimens has better resistivity to creep than that found in the CIM specimens due to the oriented fibers produced by the good mobility. This indicates that in both the crystalline regions and amorphous phases, the special morphology made by OSIM has a good resistivity to creep behavior compared with the CIM samples.

The generalized Kelvin–Voigt model with one parallel element efficiently fits the real creep. However, the model cannot describe the creep behavior with an obvious plastic deformation very accurately. It can only fit the trend observed for creep development.

Acknowledgements

We would like to express our great thanks to the National Natural Science Foundation of China (51033004 and 51121001) for financial support.

References

1. X. L. Dong, The mechanical fracture of plastics pressure pipe from the perspective of application, New Building Materials, 1999, 10, 11–13.
2. J. Jansons, A. Aniskevich and L. Pazhe, Analysis of reversible and irreversible strains in the creep of a nonlinear viscoelastic polymer, Mech. Compos. Mater., 2012, 48(2), 209–216.
3. I. I. Bugakov, Creep of polymer materials [in Russian], Nauka, Moscow, 1973.
4. R. A. Schapery, Nonlinear viscoelastic and viscoplastic constitutive equations based on thermodynamics, Mech. Time-Depend. Mater., 1997, 1(2), 209–240.
5. H. F. Brinson and L. C. Brinson, Polymer engineering science and viscoelasticity, Berlin, Springer, 2008, pp. 403–414.
6. J. L. Yang, Z. Zhang, A. K. Schlarb and K. Friedrich, On the characterization of tensile creep resistance of polyamide 66 nanocomposites. Part I. Experimental results and general discussions, Polymer, 2006, 47(8), 2791–2801.
7. ASTM D 2990–01. Standard test methods for tensile, compressive, and flexural creep and creep-rupture of plastics, ASTM International, West Conshohocken, 2001.
8. S. Houshyar, R. A. Shanks and A. Hodzic, Tensile creep behaviour of polypropylene fibre reinforced polypropylene composites, Polym. Test., 2005, 24(2), 257–264.
9. Y. Pan, X. Gao, Z. Wang, J. Lei, Z. Li and K. Shen, Effect of different morphologies on slow crack growth of high-density polyethylene, RSC Adv., 2015, 5(36), 28191–28202.
10. A. Habas-Ulloa, J. R. M. D'Almeida and J. P. Habas, Creep behavior of high density polyethylene after aging in contact with different oil derivates, Polym. Eng. Sci., 2010, 50(11), 2122–2130.
11. J. D. Ferry, Viscoelastic properties of polymers, John Wiley & Sons, 1980, p. 37.
12. C. F. Popelar, C. H. Popelar and V. H. Kenner, Viscoelastic material characterization and modeling for polyethylene, Polym. Eng. Sci., 1990, 30(10), 577–586.
13. J. Sweeney and I. M. Ward, A constitutive law for large deformations of polymers at high temperatures, J. Mech. Phys. Solids, 1996, 44(7), 1033–1049.
14. H. Zhang, Z. Zhang, J. L. Yang and K. Friedrich, Temperature dependence of crack initiation fracture toughness of various nanoparticles filled polyamide 66, Polymer, 2006, 47(2), 679–689.
15. M. A. Wilding and I. M. Ward, Creep and recovery of ultra-high modulus polyethylene, Polymer, 1981, 22(7), 870–876.
16. M. Yasuniwa, R. Enoshita and T. Takemura, X-ray studies of polyethylene under high pressure, Jpn. J. Appl. Phys., 1976, 15(8), 1421.
17. Y. Maeda, H. Kanetsuna, K. Nagata, K. Matsushige and T. Takemura, Direct observation of phase transitions of polyethylene under high pressure by a PSPC X-ray system, J. Polym. Sci., Polym. Phys. Ed., 1981, 19(9), 1313–1324.
18. M. Kakudo and N. Kasai, X-Ray Diffraction by Polymers, Ko-dansha, Tokyo, 1972, p. 46.
19. Y. F. Men, J. Rieger, H. F. Enderle and D. Lilge, The mobility of the amorphous phase in polyethylene as a determining factor for slow crack growth, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 15(4), 421–425.
20. L. L. Bohm, H. F. Enderle and M. Fleifßner, High-density polyethylene pipe resins, Adv. Mater., 1992, 4(3), 234–238.
21. K. H. Nitta and H. Maeda, Creep behavior of high density polyethylene under a constant true stress, Polym. Test., 2010, 29(1), 60–65.
22. K. H. Nitta and M. Takayanagi, Novel proposal of lamellar clustering process for elucidation of tensile yield behavior of linear polyethylenes, J. Macromol. Sci., Part B: Phys., 2003, 42(1), 107–126.
23. R. J. Young, Screw dislocation model for yield in polyethylene, in Materials forum, Institute of Metals and Materials Australasia, 1988, vol. 11, pp. 210–216.
24. Y. Men and G. Strobl, Critical strains determining the yield behavior of s-pp*, J. Macromol. Sci., Part B: Phys., 2001, 40(5), 775–796.
25. Y. Men and G. Strobl, Evidence for a mechanically active high temperature relaxation process in syndiotactic polypropylene, Polymer, 2002, 43(9), 2761–2768.
26. Y. F. Men, J. Rieger, H. F. Enderle and D. Lilge, The mobility of the amorphous phase in polyethylene as a determining factor for slow crack growth, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 15(4), 421–425.
27. G. R. Strobl, The physics of polymers, Vol. 2, Springer, Berlin, 1997.
28. I. M. Ward and D. W. Hadley, An introduction to the mechanical properties of solid polymers, John Wiley & Sons Ltd.; John Wiley & Sons, Inc., 1993.
29. G. K. El'yashevich, Structure and long-term mechanical properties of oriented polyethylene, Phys. Solid State, 2005, 47(6), 1020–1027.

---