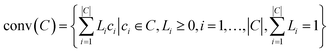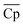Open Access Article
Open Access ArticleScreening and property targeting of thermochemical energy storage materials in concentrated solar power using thermodynamics-based insights and mathematical optimization†
Ishan
Bajaj
ab,
Xinyue
Peng
 c and
Christos T.
Maravelias
c and
Christos T.
Maravelias
 *bd
*bd
aDepartment of Chemical Engineering, Indian Institute of Technology Kanpur, Kanpur, Uttar Pradesh, India
bAndlinger Center for Energy and the Environment, Princeton University, Princeton, New Jersey, USA. E-mail: maravelias@princeton.edu
cDepartment of Chemical and Biological Engineering, University of Wisconsin–Madison, Wisconsin, USA
dDepartment of Chemical and Biological Engineering, Princeton University, Princeton, New Jersey, USA
First published on 15th February 2024
Abstract
We propose a computational framework to systematically identify promising solid–gas reaction candidates for thermochemical energy storage (TCES) in concentrating solar power (CSP) plants. The framework is based on four steps that include the generation of reaction candidates, screening based on thermodynamic criteria, solving a process model to estimate the levelized cost of electricity (LCOE) and thermal energy storage (TES) costs, and selection of the promising reactions. Our approach identifies twelve reactions from a pool of three hundred and sixty-four possible reactions. Furthermore, we develop an optimization model to simultaneously optimize the material properties, design, and operating conditions while considering the limitations on thermodynamic properties and the correlation between different material properties. The solution of the model yields a target (best possible) LCOE for a range of material prices. By comparing the LCOE of the systems employing the top-performing materials with the target LCOE, we discover that the LCOE of the systems is 9.7% to 15.9% higher than the target LCOE. Finally, we provide insights into the desired material properties to attain the target LCOE.
Sustainability spotlightConcentrating solar power (CSP) with integrated thermal energy storage has the potential to generate cost-effective and dispatchable renewable power. Among different types of storage technologies, thermochemical energy storage (TCES) has many desirable features (e.g., high storage density and operating temperature) but is still in its infancy due to, among other reasons, the system complexity. It remains unclear which reaction should be selected and what are the desired material properties. Towards this goal, we develop computational frameworks to identify existing cost-effective reaction candidates and the target properties for new reactions to further reduce the levelized cost of electricity (LCOE). Importantly, our analysis can serve as guidelines for further developing TCES materials with tailored properties. Our work aligns with the following UN sustainable development goals: affordable and clean energy (SDG 7), industry, innovation, and infrastructure (SDG 9), and climate action (SDG 13). |
1. Introduction
To keep the global temperature rise below 2 °C in accordance with the Paris Agreement, it is necessary that an increasing fraction of world's energy demand is satisfied by renewable energy.1 Many U.S. states and territories, including California, Maine, New Mexico, Washington, and Hawaii, have mandated that electricity must be generated by renewable resources by 2040–2050.2–6 However, generating electricity reliably using intermittent resources such as solar and wind requires storing excess energy. While using a combination of photovoltaic or wind power with battery can provide reliable electricity, another promising strategy to deliver cost-effective, reliable, and dispatchable renewable power is integrating concentrated solar power (CSP) with thermal energy storage (TES).Due to technological innovation, CSP costs were reduced by 68% during the previous decade. It is estimated that CSP could provide 11% of global electricity by 2050.7 Furthermore, CSP can also be used to convert CO2 and H2O into solar fuels.8–10 Today, more than 21 GWh of TES, based mainly on molten salts, are operational, and most new CSP plants are incorporating TES.11 Interestingly, while the global installed capacity of solar photovoltaics is 100 times greater than CSP, TES installed worldwide is twice that of utility-scale batteries. Moreover, recent studies compared the economics of CSP with TES to PV with battery storage and concluded that the LCOE of the former is lower than the latter when the storage duration is greater than 4–6 hours.12
Although molten salts are used for TES in existing plants, they have two major drawbacks. First, heat is delivered to the power cycle at a lower temperature (∼565 °C), resulting in low solar-to-electricity efficiency. Second, due to the low energy density of molten salt, a large quantity of material is needed, which can become too costly for large-scale systems. Thermochemical energy storage (TCES) systems, on the other hand, are a promising alternative for the next generation CSP plants because of their high energy density, ability to deliver heat at a higher temperature, and low heat loss over long storage times.
TCES is based on a reversible reaction, wherein heat is required for the forward reaction, and thus, the reaction enthalpy is stored in the products. In addition to chemically stored heat, sensible heat stored in the reaction products can also be utilized. Fluid-phase and solid–gas reactions are the two classes of TCES systems that have been studied. Peng et al.13 analyzed gas-phase reactions, including ammonia dissociation and methane reforming. They reported that systems that employ reactions that require storage of reacting gases have low energy efficiency and high cost. Solid–gas reactions encompass various possible chemistries, including redox, hydroxide, and carbonate. They can be promising because the products can be easily separated and may require less energy-intensive and expensive storage. Therefore, the primary focus of this work is on analyzing solid–gas TCES systems.
A solid–gas reaction is expressed as νAA (s) + ΔHr ↔ νBB (s) + νCC (g), where ΔHr denotes the reaction enthalpy and νA, νB, and νC are the stoichiometric coefficients. For simplicity, we refer to the above reaction as A/B. Most of the literature on TCES has focused on carbonate,14–19 hydroxide,20–23 and redox24–29 reaction systems and studied various characteristics, including thermodynamics, kinetics, and reversibility. Among various carbonate reaction systems, calcium carbonate/calcium oxide (CaCO3/CaO) is the most extensively studied due to its high equilibrium temperature (895 °C at 1 bar CO2 partial pressure), high energy density (692 kW h per m3 CaCO3), and abundance of cheap limestone feedstock.30 The strontium carbonate/strontium oxide (SrCO3/SrO) system has also been found to be promising because of its higher equilibrium temperature (∼1200 °C).31 Among hydroxide reaction systems, calcium hydroxide/calcium oxide (Ca(OH)2/CaO),barium hydroxide/barium oxide (Ba(OH)2/BaO), and strontium hydroxide/strontium oxide (Sr(OH)2/SrO) are found to be promising.32 Cobalt tetraoxide/cobalt oxide(Co3O4/CoO), manganese(III) oxide/trimanganese tetraoxide (Mn2O3/Mn3O4), barium peroxide/barium oxide (BaO2/BaO), and iron (II, IIIIII) oxide/ferrous oxide (Fe3O4/FeO) are proposed to be the promising candidates33,34 for CSP integrated with solid–gas TCES systems (hereinafter referred as CSP-TCES).
Several studies have presented system-level analysis for the CSP-TCES systems, including thermodynamic analysis, process design, and techno-economic analysis (TEA). Energy/exergy analysis studies have been conducted for CSP employing carbonate,35–38 hydroxide,39 and redox40 TCES systems. Schmidt et al.21 and Criado et al.41 performed conceptual process design for the Ca(OH)2/CaO TCES system. Bravo et al.42 and Salas et al.43 performed TEA for CSP integrated with CaCO3/CaO and Ca(OH)2/CaO TCES systems, respectively. Bayon et al.33 estimated the energy storage costs for 17 solid–gas TCES systems.
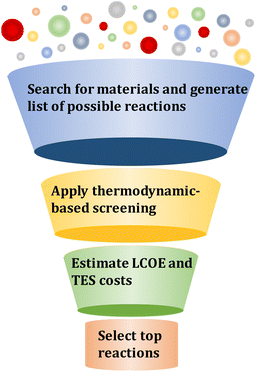
Deploying CSP-TCES systems at an industrial scale would require both material- and process-level considerations. Previous studies have considered these aspects in isolation. As indicated in the previous paragraph, most system-level studies were performed on a few reaction systems while most previous reaction screening studies selected promising reaction candidates based on equilibrium temperature, gravimetric, and volumetric energy densities.44–46 However, not much attention has been given to issues such as plant design and operations under different solar conditions. The cost-effectiveness of a TCES system depends on, among others, material price, densities, heat capacities, kinetics, reaction type, and enthalpy. Thus, to consider different trade-offs, the material performance must be evaluated in the context of an optimized process. Accordingly, in this work, we develop a computational framework that enables the screening of large reaction databases to identify promising candidates leading to the most cost-effective CSP-TCES systems.
Recent studies indicate that the thermodynamic properties of a class of TCES materials can be tuned.47–50 For instance, Babiniec et al.51 investigated materials in the LaxSr1−xCoyMn1−yO3−δ and LaxSr1−xCoyFe1−yO3−δ families and showed that energy density of 250 kJ kg−1 could be obtained by manipulating x and y. Since the above class of materials is not cost-effective, in their follow-up article, Babiniec et al.52 proposed CaAl0.2Mn0.8O3−δ and CaTi0.2Mn0.8O3−δ for thermal energy storage and estimated their energy densities to be 390 kJ kg−1 and 370 kJ kg−1, respectively. Imponenti et al.53,54 evaluated the performance of Ca1−xSrxMnO3−δ and CaCryMn1−yO3−δ, and estimated their energy density to be 555 kJ kg−1 and 392 kJ kg−1, respectively for x = y = 0.05.
Most of these studies focused on tuning materials to enhance the energy density of the material. While higher energy density is critical to improving the storage costs, lower storage costs do not necessarily result in a lower levelized cost of electricity (LCOE).55,56 Although computational material science techniques (e.g., quantum-mechanical calculations) has made it possible to construct novel crystal structures and accurately predict their properties, the number of possible materials is considerable, and an exhaustive screening of such a search space is impractical. Accordingly, in the latter part of our article, we develop a systematic material property targeting strategy. To accomplish this goal, we develop an optimization model to simultaneously optimize the material properties, design, and operating conditions while considering limitations in material thermodynamic properties. The analysis provides insights into the desirable material properties to minimize LCOE.
The contributions of the article include the following:
(1) Development of an in silico reaction screening framework to identify promising reaction candidates for CSP-TCES plants based on thermodynamic criteria and system-level analysis.
(2) Derivation of insights into the energetic and economic performance of the top-performing reactions; identification of key factors contributing to the efficiency and economics of the CSP-TCES plants for those reactions.
(3) Development of a material targeting strategy to identify promising material properties. Two approaches are proposed and compared to bound and correlate material properties.
(4) Comparison of desirable material properties to the properties of existing materials.
The rest of the article is organized as follows. Section 2 provides the description of CSP-TCES system and Section 3 describes the material screening and optimization methodology. Section 4 presents the results and finally, conclusions are given in Section 5.
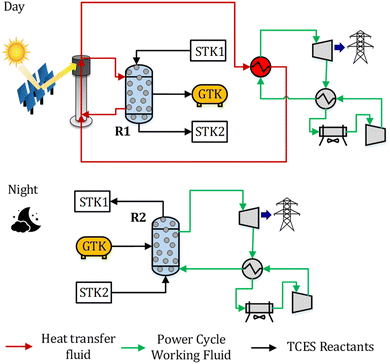
2. System description
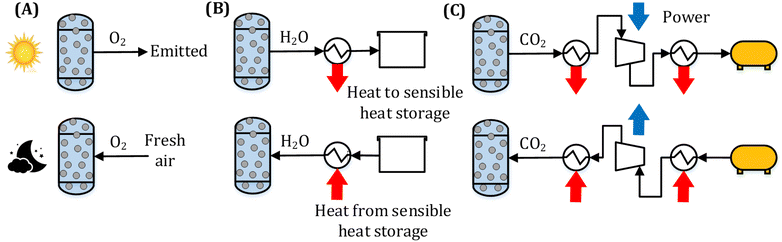
A CSP-TCES plant is shown in Fig. 1. It has four components: collector, receiver, TCES system, and power cycle. The collector uses reflector facets to concentrate sunlight and directs the concentrated flux to a smaller receiver. The receiver converts sunlight to heat and uses a heat transfer fluid (HTF). The key units of the TCES system are two reactors: R1 and R2. In reactor R1, the forward endothermic reaction (νAA (s) → νBB (s) + C (g)) occurs, and in R2, the reverse exothermic reaction occurs. In a previous work, Peng et al.56 analyzed several configurations and found that the configuration with indirect heat transfer to R1 employing fluidized-bed reactors was the most efficient. Therefore, this configuration is selected in this work. The power cycle converts the collected solar heat to electricity via a thermodynamic cycle. Molten salt is used as HTF in a commercial CSP plant, with a maximum attainable temperature of 565 °C. To attain higher turbine efficiency, supercritical CO2 (s-CO2) is proposed as a promising candidate for both HTF and working fluid (WF) for the next-generation CSP plants. Emerging receiver technologies57 based on gas,58,59 liquid,60,61 and solid particles62,63 are being actively researched for CSP. In this study, we employ a s-CO2 based tubular receiver to enable easier heat transfer to the reactor and the power cycle. Previous studies have described the design of direct s-CO2 receivers capable of operating at high pressure and temperature.64,65 Furthermore, recent studies suggest that s-CO2 Brayton cycles are more efficient and economical.66,67 Therefore, s-CO2 is used as both the HTF and WF, and the Brayton cycle is used for power generation.The plant shown in Fig. 1 operates as follows. The collector reflects the sunlight to the receiver during the “sun hours”, where HTF is heated. The flow of HTF is split such that a part of it flows through R1 to drive the forward endothermic reaction, and the remaining flows through the power cycle to provide heat. Solids are transferred from a tank to R1, where A is converted to B and C. Solid mixture containing B and unconverted A is stored in a tank, and based on the properties of gas C, different storage options are chosen (Fig. 2). We study three types of solid–gas reactions: redox, hydroxide, and carbonate. Redox reactions utilize an open-loop configuration, where the generated O2 is directly emitted, and the air is used as a source of O2 during discharging. Hydroxide and carbonate reactions operate in a closed-loop configuration, where the generated CO2 and H2O are stored in liquid CO2 (75 bar and 25 °C) and water (1 bar and 25 °C) vessels, respectively. During the night, the solids and gas stored in STK2 and GTK are transferred to R2, where the exothermic reaction occurs. The solid mixture containing A and unconverted B is sent to a tank.
Typically, the reactions occur at high temperatures; however, gas C needs to be stored at low temperatures to reduce the volume of the storage tank. Furthermore, during discharging, C needs to be reheated. Thus, to achieve high system efficiency, a sensible heat storage unit is employed to store the heat associated with cooling gas C. This heat is then reused to preheat C entering R2 during discharging. During charging, a compressor is used to store CO2 into the storage vessels for the carbonate reaction (Fig. 2 (C)). During discharging, CO2 expands through a turbine and generates power.
3. Material screening and property targeting: methodology
In this section, the methods for material screening and property targeting are discussed.3.1 Material screening
The computational screening framework to identify promising TCES systems is based on generating reaction candidates, eliminating reactions based on thermodynamic criteria, developing an optimization model to obtain design and operating conditions that result in minimizing LCOE for a specific reaction, and selecting the top-performing reaction candidates (Fig. 3).| MOx ↔ MOy + (x − y)/2O2 | (1) |
| M(OH)x ↔ MOx/2 + x/2H2O | (2) |
| M(CO3)x ↔ MOx + xCO2 | (3) |
Based on the materials considered, we identify 364 reactions comprising of 328 redox, 19 hydroxide, and 17 carbonate systems that are stoichiometrically possible. While perovskites and spinels69–72 have attractive properties, including reaction rate and reversibility, we consider pure metal oxides to limit the scope of the study. However, the developed computational framework can be applied to screen promising perovskites and spinels. The list of the reactions and corresponding equilibrium temperature (Teq) and reaction enthalpy (ΔHr) are given in ESI Table S1.† The equilibrium temperature is estimated using the following equation:
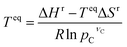 | (4) |
| ΔHr = νCHC(Teq) + νBHB(Teq) − νAHA(Teq) | (5) |
We also validate the estimated properties by comparing them with those obtained by Pardo et al.,32 who used HSC Chemistry. The results of the comparison are shown in ESI Fig. S1.† The mean squared error (MSE) of reaction enthalpy estimated using Aspen Plus and HSC Chemistry for redox, hydroxide, and carbonate reactions are 0.25%, 0.15%, and 1.18%, respectively. The MSE of equilibrium temperature estimated by the two software tools for redox, hydroxide, and carbonate reactions are 0.33%, 0.46%, and 0.04%, respectively, suggesting that the estimated properties are rather accurate. Furthermore, our reported equilibrium temperatures of Co3O4/CoO (888 °C), CuO/Cu2O (1031.8 °C), Fe2O3/Fe3O4 (1340 °C), and Mn2O3/Mn3O4 (901 °C) systems lie within the oxidation and reduction temperatures reported in experimental works.73,74 We also note that we used theoretical ΔHr values, which are typically lower than the experimental values. For instance, theoretical ΔHr for Co3O4/CoO and CuO/Cu2O are 821.3 J g−1 and 816 J g−1, and experimental values are 576 J g−1 and 652 J g−1, respectively.73
(1) the material remains stable with cycles, and no side products are formed.
(2) The solid reactants are available in appropriate size so that the reactors operate optimally.
(3) For fluidized-bed reactors, the temperature of the solids is assumed to be spatially uniform. For other types, the assumption can be adapted appropriately.
(4) The reactors operate at atmospheric pressure to avoid the additional cost of compressors.
(5) Since the kinetics data for all the considered reactions are unavailable, reactors are designed considering only heat transfer limitations. However, we discuss the impact of the conversion on LCOE for different reaction systems.
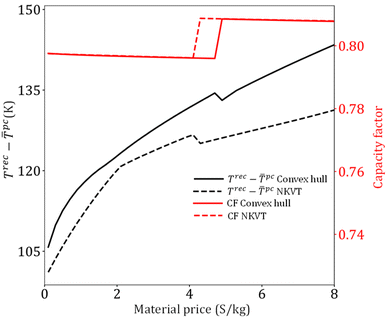
Based on previous works,13,55,56,75 we develop a process model for the design and operation of CSP plants with solid–gas TCES systems employing fluidized-bed reactors. The input required by the model is (1) TCES reaction, (2) reaction properties (enthalpy, equilibrium temperature), (3) material price and properties (Cp, ρ), (4) equipment cost parameters, (5) weather data, and (6) plant capacity. It is assumed that the CSP plant employs a solar tower configuration, and its capacity is 100 MW. The plant location is Daggett, California, and its weather data (direct normal irradiation and sun hours) is obtained from National Solar Radiation Data Base.75 A stochastic programming approach is adopted to account for variability in direct normal irradiation (DNI) and sun hours. This approach is frequently used to model optimization problems involving uncertainty.76,77 Six representative scenarios are chosen from the annual data using the centroid clustering algorithm. The DNI, sun hours, and occurrence frequency of each representative scenario can be found in Peng et al.55
The objective function of the model is to minimize LCOE. The constraints account for the performance and efficiency of plant components, mass and energy balances, and equipment sizing and costing calculations. The major plant components include collector, receiver, TCES, and power cycle. The collector is characterized by concentration ratio (ϕcol) and efficiency (ηcol), where ϕcol is the ratio of the collector area to the receiver area, ηcol is defined as the ratio of sunlight that reaches the receiver divided by the sunlight incident on the collector and it is less than one because of imperfect reflection and varying solar elevation. The receiver consists of an absorber that converts sunlight to heat and piping that carries HTF. The receiver efficiency (ηrec) is defined as:
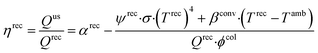 | (6) |
The TCES system comprises of six units, including reactors, compressor/turbine, heat exchanger, sensible heat storage, and gas and solid storage tanks. We employ fluidized-bed reactors of shell-and-tube-type with HTF/WF flowing on the tube side and the solids on the shell side. The reactor is modeled as a mixed-flow reactor, and the optimal heat exchange area and volume that achieves the desired heat transfer for all scenarios is determined. Carbonate TCES requires a compressor during charging and a turbine for power generation when CO2 expands during discharging. The compressor is designed based on the electricity consumption required to compress CO2 from 1 bar to 75 bar. A heat exchanger is used to preheat gas C using the solids at a higher temperature exiting R1 during charging. The area of the heat exchanger is estimated based on the temperature difference between the two streams, the rate of heat transfer, and the average heat transfer coefficient (βhx). A sensible heat storage unit is utilized to store the heat associated with the cooling of gas C and reusing the heat to increase its temperature while discharging. Its size is estimated based on the amount of heat stored. The storage tanks are designed based on the flow rates and charging/discharging time. Each unit is designed at the maximum required size to guarantee operational feasibility in different modes and scenarios.
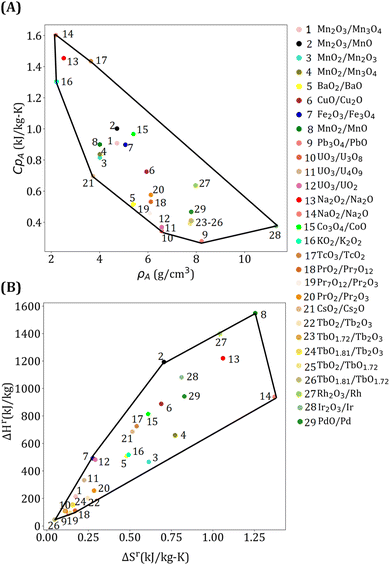
To generate power, s-CO2 Brayton cycle with a simple recuperative configuration (ESI Fig. S2†) is used because of its higher efficiency, lower cost, and smaller equipment.78 A mathematical model is developed for the power cycle by assuming that (i) HTF and turbine inlet pressure are 25 MPa, (ii) turbine pressure ratio is 3, (iii) compressor and turbine efficiencies are 0.9, (iv) compressor inlet temperature is 40 °C, and (v) the minimum approach temperature of the recuperator is 10 °C. A surrogate model is developed to obtain the power cycle efficiency (ηpc) as a function of turbine inlet temperature (Tpc) by using simulation data:
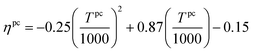 | (7) |
The cost parameters for various equipment and model parameters are given in ESI Table S3.† The material price is taken from the USGS database79 and listed in ESI Table S2.† Since the price of all the materials is not available, it is chosen based on the following rules:
(1) if the prices of both A and B are available in the database, then the lower of the two prices is chosen.
(2) If the price of either of A or B is available, then the available material price is chosen.
(3) If the price of neither A nor B is known, but the prices of other compounds related to the metal in A and B are known, then the average price of these compounds is used. For instance, the prices of KO2 and K2O2 are unavailable in the USGS database, but the prices of KCl, K2SO4, and KNO3 are, so the material price is chosen to be the average of the prices of the three compounds.
The resulting optimization model is a nonlinear programming model and it is formulated in GAMS. The model equations are given in ESI Section S4.† A solution strategy is developed to solve the model to global optimality. The details of the strategy are given in ESI Section S5.† The solution of the model gives the optimal design (collector area, reactor volume, heat exchange area, etc.) and scenario-specific operational variables (unit temperature, flow rates of streams, storage hours, fraction of chemical and sensible heat storage, etc.) from which the LCOE is calculated.
3.2 Material property targeting strategy
To exploit recent advances in synthesizing materials with tailored properties, it is critical to understand the impact of material properties on LCOE. Thus, this section develops a material property targeting strategy that can serve as a guideline for developing new materials. Importantly, an optimization model is developed such that material properties, design, and operating conditions are simultaneously optimized while considering seasonal solar variability. Specifically, the properties that are of interest are ΔHr, ΔSr, Cp, ρ, and ω, denoted by P, and stoichiometry coefficient of gas C (νC). For brevity, we assume that gas C is O2.There are two major challenges that need to be addressed. First, practical bounds on various properties need to be enforced. Second, the correlation between different material properties should be evaluated. One approach to bound the values of the properties is to use the minimum and maximum values of the properties of the existing materials. However, this approach does not consider the correlation between material properties. Thus, it is likely that extreme values of all the properties are obtained on solving the optimization problem. We propose two methods to overcome these challenges. The first one is based on approximating the feasible property space by a convex hull. The second method is based on developing empirical relationships (ER). These are derived by combining the Neumann–Kopp rule80 and volume-based thermodynamic equations of Glasser and Jenkins.81,82 We denote the latter approach by NKVT for brevity. We note that the two methods provide similar insights. Therefore, we only discuss the former method here, whereas the latter is discussed in ESI Section S6.†
Before providing details of the approach, we define a convex hull. The convex hull of a set of points is defined as the smallest convex polytope containing the points. Mathematically, the convex hull of a set of points, ci ∈ C, denoted as conv(C) is:
The ability of this approach to provide practical bounds on material properties and consider correlations between different properties is illustrated using Fig. 4. The figure is generated by independently considering two pairs of properties for better visualization. From Fig. 4(A), it is apparent that materials with high Cp have low ρ. In fact, Glasser and Jenkins81,82 state that Cp is inversely proportional to ρ (Cp ∝ 1/ρ). The convex hull captures this correlation and ensures that the regions corresponding to both high Cp and ρ and low Cp and ρ are not selected. Similarly, the regions with high ΔHr and low ΔSr and low ΔHr and high ΔSr are also not chosen as shown in Fig. 4(B).
 | ||
| Fig. 4 Data and convex hull of (A) heat capacity and density of A, and (B) reaction enthalpy and entropy for reaction set N. | ||
The following set of equations are added to the optimization model given in ESI Section S4:†
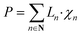 | (8) |
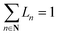 | (9) |
The following set of equations are also added:
 | (10) |
| TR1 ≥ Teq + 10 | (11) |
| TR2 ≤ Teq − 10 | (12) |
 | (13) |
| ωA = ωB + νC·ωC | (14) |
4. Results
In this section, we first present material screening results followed by insights into the optimal material properties.4.1 Material screening analysis
Based on the three thermodynamic criteria (Section 3.1.2), 325 reactions are eliminated. Among the remaining 39 reactions, 29 are redox, 4 are hydroxide, and 6 are carbonate reactions. The reactions obtained after screening, and their properties, including Cp, ρ, material price, ΔHr, and Teq, are given in ESI Table S2.† The key properties of the selected reactions are shown in Fig. 5.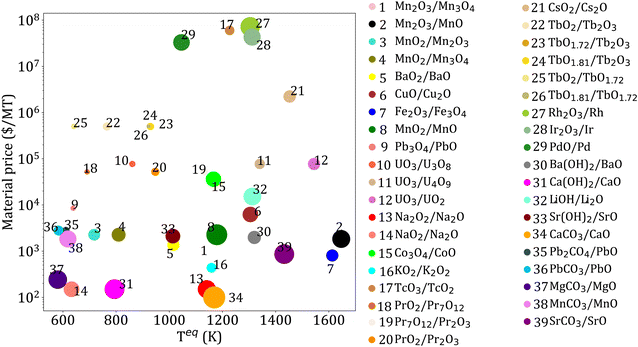 | ||
| Fig. 5 Key parameters for reactions obtained after applying thermodynamic criteria. Each bubble represents a candidate reaction, and its size represents reaction enthalpy. | ||
The optimization model discussed in Section 3.1.3 is solved to global optimality for each of the reactions in set N. The results are summarized in Table 1, where we show reactions for which LCOE ≤ 40 ₵ per kW h. The table lists the overall system efficiency (ηs−e), defined as the ratio of net electricity output to solar energy input, TES costs, and LCOE. As expected, the reactions with high efficiency and low TES costs have low LCOE. The optimal design and operation variables for a representative Fe2O3/Fe3O4 system is shown in ESI Section S7.†
| No. | Reactions | η s−e | TES cost ($ per kW h-heat) | LCOE (₵ per kW h) |
|---|---|---|---|---|
| 1 | Mn2O3/Mn3O4 | 0.205 | 32.92 | 11.18 |
| 2 | Mn2O3/MnO | 0.178 | 18.53 | 11.28 |
| 3 | MnO2/Mn2O3 | 0.189 | 28.21 | 11.87 |
| 4 | MnO2/Mn3O4 | 0.196 | 25.28 | 11.38 |
| 5 | BaO2/BaO | 0.204 | 31.21 | 11.01 |
| 6 | CuO/Cu2O | 0.21 | 48.28 | 11.58 |
| 7 | Fe2O3/Fe3O4 | 0.185 | 16.62 | 10.98 |
| 8 | MnO2/MnO | 0.218 | 21.12 | 10.29 |
| 9 | Pb3O4/PbO | 0.162 | 287.22 | 27.34 |
| 10 | UO3/U4O9 | 0.145 | 692.86 | 38.21 |
| 11 | UO3/UO2 | 0.147 | 599.72 | 33.90 |
| 12 | Na2O2/Na2O | 0.218 | 19.92 | 10.24 |
| 13 | NaO2/Na2O | 0.171 | 18.14 | 12.04 |
| 14 | Co3O4/CoO | 0.183 | 161.92 | 17.24 |
| 15 | KO2/K2O2 | 0.203 | 41.39 | 11.72 |
| 16 | Pr7O12/Pr2O3 | 0.147 | 532.29 | 33.29 |
| 17 | PrO2/Pr2O3 | 0.164 | 532.09 | 34.00 |
| 18 | Ba(OH)2/BaO | 0.21 | 49.83 | 11.7 |
| 19 | Ca(OH)2/CaO | 0.195 | 31.28 | 11.78 |
| 20 | LiOH/Li2O | 0.198 | 67.11 | 12.88 |
| 21 | Sr(OH)2/SrO | 0.208 | 50.99 | 11.89 |
| 22 | CaCO3/CaO | 0.218 | 46.03 | 11.29 |
| 23 | Pb2CO4/PbO | 0.168 | 109.57 | 17.99 |
| 24 | PbCO3/PbO | 0.165 | 86.81 | 17.51 |
| 25 | MgCO3/MgO | 0.169 | 43.13 | 14.54 |
| 26 | MnCO3/MnO | 0.175 | 46.22 | 14.32 |
| 27 | SrCO3/SrO | 0.206 | 40.58 | 11.32 |
Due to our assumption that no side products are formed, we obtain an equilibrium temperature of 1179 K for the MnO2/MnO system. However, considering the other oxides (Mn2O3, Mn3O4), MnO formation occurs at a high temperature (∼1900 K).83 First, MnO2 reduces to Mn2O3 at 700 K, which further reduces to Mn3O4 at 1200 K. Therefore, we discard the MnO2/MnO system. We found Na2O2/Na2O and KO2/K2O2 to be promising because of their attractive thermodynamic properties and low price. While sodium and potassium air batteries have been explored, to the authors' knowledge, no experimental work has studied the systems for TCES application. Thus, there is high uncertainty in their thermodynamic properties. Therefore, we exclude the two systems from the list of top-performing reaction systems.
The overall system efficiency depends on the efficiency of the four plant components. The collector efficiency is constant, whereas the receiver and power cycle efficiencies are functions of temperature, as shown in eqn (6) and (7). While the receiver efficiency decreases with Trec, the power cycle efficiency increases with Tpc. For high ηs−e, Trec should be low, Tpc should be high, and the difference between Trec and Tpc (Trec − Tpc) should be as small as possible to minimize exergy losses. The temperature-enthalpy diagram of the heat transfer process for day and night operation is shown in ESI Fig. S6.† It is impossible to have both low Trec and high Tpc because the second law of thermodynamics needs to be satisfied for heat transfer. While the difference between Trec and Tpc is low during the day operation because HTF transfers heat to WF, it is high during the night operation because heat is transferred to WF by reactor R2. Thus, Tpc lies between TR1 and TR2, moving towards TR2 as the fraction of sensible heat storage decreases.
Note that TR1 needs to be higher than Teq for forward reaction and TR2 should be lower for the reverse reaction (TR1 > Teq > TR2). Furthermore, high Trec − Tpc indicates more sensible heat storage, which becomes more important for expensive materials. The optimization balances these tradeoffs and chooses design and operation variables that result in minimum LCOE. The top twelve reactions based on LCOE are selected, and the results corresponding to complete conversion are shown in Fig. 6. The overall efficiency of the selected reactions lies between 0.18 and 0.22 (Table 2). Except for Fe2O3/Fe3O4, Mn2O3/MnO, MnO2/Mn3O4, Ca(OH)2/CaO, and MnO2/Mn2O3 reaction systems, the remaining systems have an efficiency of more than 0.2. The critical operating temperatures that affect ηs−e are listed in Table 2. The equilibrium temperature of reactions with high ηs−e lies in the range 1000–1400 K. Note that Teq and Trec are high for Fe2O3/Fe3O4 and Mn2O3/MnO systems, resulting in lower ηrec. On the other hand, MnO2/Mn3O4, Ca(OH)2/CaO, and MnO2/Mn2O3 reaction systems have lower Teq and Tpc, leading to low ηpc.
| Reactions | Operating temperature | Properties | Efficiency | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T rec (K) |
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) pc (K)
pc (K) |
T eq (K) | ΔHr (kJ kg−1) | (kJ (kg−1 K) |
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (kg m−3) (kg m−3) |
Price ($ per kg) | η rec | η pc | η s−e | |
| Fe2O3/Fe3O4 | 1673 | 1383 | 1613 | 487 | 0.88 | 5010 | 0.80 | 0.64 | 0.57 | 0.18 |
| BaO2/BaO | 1345 | 1150 | 1015 | 475 | 0.44 | 5570 | 1.36 | 0.81 | 0.51 | 0.20 |
| Mn2O3/Mn3O4 | 1454 | 1220 | 1174 | 204 | 0.89 | 4655 | 1.84 | 0.77 | 0.53 | 0.21 |
| Mn2O3/MnO | 1727 | 1447 | 1647 | 1102 | 0.91 | 4955 | 1.84 | 0.59 | 0.58 | 0.18 |
| CaCO3/CaO | 1349 | 1211 | 1169 | 1665 | 1.13 | 2950 | 0.10 | 0.81 | 0.53 | 0.22 |
| SrCO3/SrO | 1512 | 1308 | 1432 | 1349 | 0.75 | 4180 | 0.86 | 0.74 | 0.55 | 0.21 |
| MnO2/Mn3O4 | 1329 | 1057 | 809 | 646 | 0.81 | 4300 | 2.27 | 0.82 | 0.46 | 0.19 |
| CuO/Cu2O | 1435 | 1243 | 1305 | 816 | 0.68 | 5985 | 6.22 | 0.78 | 0.54 | 0.21 |
| Ba(OH)2/BaO | 1400 | 1207 | 1320 | 588 | 0.61 | 5105 | 1.98 | 0.79 | 0.53 | 0.21 |
| Ca(OH)2/CaO | 1264 | 1012 | 794 | 1342 | 1.22 | 2745 | 0.15 | 0.84 | 0.45 | 0.19 |
| MnO2/Mn2O3 | 1298 | 1010 | 718 | 458 | 0.80 | 4365 | 2.27 | 0.83 | 0.44 | 0.19 |
| Sr(OH)2/SrO | 1374 | 1167 | 1014 | 736 | 0.88 | 4115 | 2.11 | 0.80 | 0.51 | 0.21 |
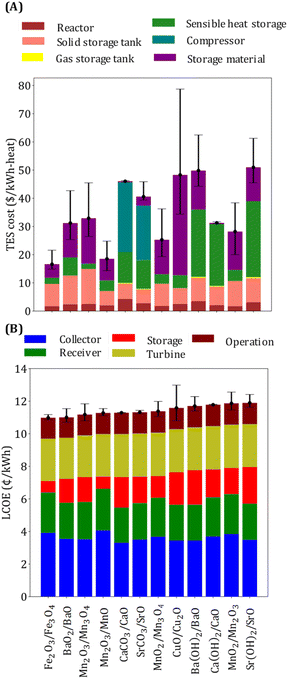
Thermal energy storage requires six equipment types: reactors, solid and fluid storage tanks, heat exchangers, a sensible heat storage unit, and a compressor. Since reactors are designed considering heat transfer limitations, their costs depend on the heat exchange area, which in turn depends on the overall heat transfer coefficient, the average temperature difference between the hot and the cold streams, and the heat exchange rate. The contribution of reactor costs is similar for all the selected reactions (Fig. 6(A)) because a comparable heat exchange area is needed. Solid tank cost depends on the amount of material required, which is, in turn, dependent on ΔHr, Cp, and ρ. The sensible heat storage cost depends on the amount of type of gas C and TR1. The cost of storage material is affected by ΔHr, Cp, and its price. Sensible heat storage cost is the main cost driver for the three hydroxide systems (Ba(OH)2/BaO, Ca(OH)2/CaO, and Sr(OH)2/SrO) because of the need to store large amounts of heat in the form of heat of vaporization. Compressor cost is the main cost contributor for the carbonate systems because CO2 needs to be compressed before it can be stored. Among oxides, BaO2/BaO, Mn2O3/Mn3O4, and CuO/Cu2O have TES cost greater than 30 $ per kW h-heat. Solid storage tanks and storage material are the main cost driver for BaO2/BaO system because of its low ΔHr and Cp. The main limiting property of Mn2O3/Mn3O4 system is its low ΔHr compared to other manganese oxide systems, whereas the major cost contributor for CuO/Cu2O system is its high price.
The operating and turbine costs are assumed to be proportional to the plant capacity, which is the same for all the reaction systems (Fig. 6(B)). The overall efficiency impacts the collector and receiver costs. Note that the systems with ηs−e < 0.2 (e.g., Fe2O3/Fe3O4, Mn2O3/MnO, etc.) have lower TES costs (<$30 per kW h-heat), and those with high TES costs (e.g., CaCO3/CaO, CuO/Cu2O) have higher ηs−e. The lower and the upper caps of the error bars represent the LCOE and the TES costs when the material price is reduced by half and doubled, respectively. The error bars are larger for systems with higher material price.
While most experimental studies on the s-CO2 Brayton cycle have working temperatures below 1050 K, we observe that the optimal power cycle temperature for all listed systems exceeds this temperature suggesting that more research is needed to enable operation at higher temperatures. We illustrate the effect of temperature constraints on the performance of the MnO2/Mn3O4 system by limiting the maximum cycle temperature to 1050 K. The optimal LCOE increases to ₵12.4 per kW h from ₵11.38 per kW h, ηs−e remains the same, and the TES costs increase to $39.83 per kW h-heat from $25.82 per kW h-heat. The primary reason for the increase in the TES costs is due to the lower fraction of sensible heat storage, resulting in higher material costs.
The results presented above are based on the assumption that the reaction kinetics is fast and that 100% conversion for the forward and reverse reaction is achieved. Note that low conversion implies less chemical energy stored per unit mass, resulting in more material requirement. At the same time, less chemical energy storage also leads to higher Trec − Tpc, resulting in lower ηs−e.
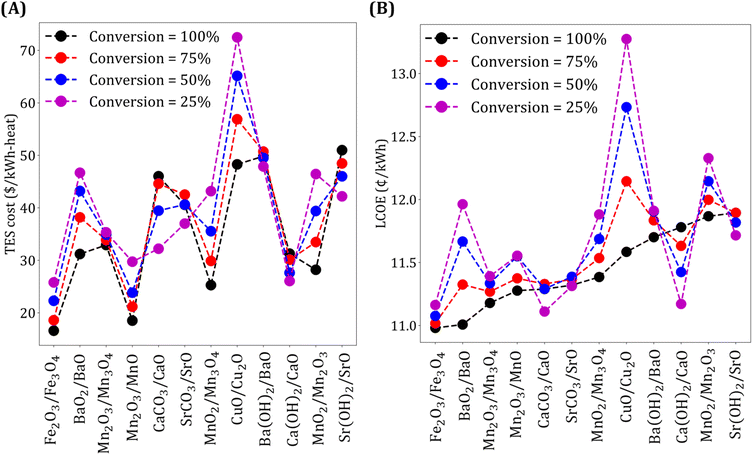
We study the effect of conversion on TES cost and LCOE, and the results are shown in Fig. 7. We make five key observations. First, for the oxide systems, lower conversion leads to higher TES cost and LCOE. Second, as expected, the impact of the conversion on the two metrics is more significant for expensive materials (e.g., CuO/Cu2O). Third, TES cost and LCOE increase with an increase in conversion for the two carbonate systems. This may seem non-intuitive initially because, as mentioned earlier, higher fraction of chemical energy storage results in higher ηs−e and more material requirements. However, an increase in TES cost with conversion can be explained by noting that higher conversion leads to a higher CO2 yield, which means more gas needs to be compressed, thereby, increasing the compression cost. The increase in compression cost is higher than the decrease in material cost obtained with an increase in conversion. To explain the increase in LCOE, we note that while higher conversion results in higher ηs−e, the increase in TES cost is more significant than the reduction in collector and receiver costs obtained due to higher ηs−e. Fourth, for Ca(OH)2/CaO and Sr(OH)2/SrO systems, TES cost and LCOE increase with an increase in conversion because of the higher cost contribution of sensible heat storage unit compared to the material cost. In summary, for the two carbonate and hydroxide systems, a reduction in TES cost dominates the increase in collector and receiver costs that follow due to a decrease in ηs−e. Fifth, for Ba(OH)2/BaO system, due to comparable material and sensible heat storage costs, the reduction in TES cost is not significant with a decrease in conversion, and thus LCOE is lower when conversion is high.
4.2 Practical application of selected systems
While MnO2-based TCES systems (MnO2/MnO, MnO2/Mn3O4, and MnO2/Mn2O3) have attractive properties, and their thermodynamic data suggest that they should undergo reversible reactions, experimental works suggest that MnO2-based systems are not fully reversible.84 Thus, more work is needed to identify appropriate conditions to improve reversibility as carried out for other TCES materials.85,86 Though the Fe2O3/Fe3O4 system has not been substantially explored in the TCES literature, it has been widely studied for thermochemical hydrogen production.87,88 This is primarily due to its high reduction temperature, making the TCES system challenging to implement in solar tower plants with s-CO2 power cycles. However, our analysis suggests that Fe2O3/Fe3O4 can be promising for next-generation CSP plants capable of efficiently operating at high temperatures. Furthermore, ongoing work on cationic doping to reduce the reduction temperature can enable extensive application of Fe2O3/Fe3O4 in CSP plants.89”The BaO2/BaO system is an attractive TCES candidate due to its high energy storage density, material availability, and moderate working temperature making it suitable for CSP plants with a central receiver and s-CO2 Brayton cycle. Nevertheless, there are disadvantages related to the reactivity of BaO with H2O and CO2 and material cyclability90 that need to be addressed. The Mn2O3/Mn3O4 is one of the most studied TCES systems. While it has moderate working temperature, its disadvantages include low energy density, slow oxidation kinetics of Mn3O4, and material degradation. Several works have developed strategies based on morphological and chemical modification to overcome these challenges.91,92 Previous works have explored the application of the Mn2O3/MnO system for thermochemical hydrogen production.93 However, limited work has been done to explore its applicability for TCES.94
The CaCO3/CaO system has the advantage that the materials are abundant, inexpensive, and less toxic. The SrCO3/SrO system has also been reported recently as promising for storing solar thermal heat.95 However, both carbonate systems have drawbacks related to particle deactivation, which are being addressed by morphological and chemical modifications.95,96 The CuO/Cu2O system is also promising due to its high energy density. A previous study performed a kinetic analysis of the system and found that thermal reduction of CuO is much faster than oxidation of Cu2O. The high price of CuO makes it important for the material to remain stable over cycles. Stability assessment studies show that decreasing the reduction temperature by lowering the partial pressure of O2 improves stability.97 However, lowering the pressure requires sweeping inert gas or vacuum, increasing costs.
Among the hydroxide systems, Ca(OH)2/CaO has been studied the most. It has the advantage of high energy density and a low price, but one of its main drawbacks is the poor mechanical stability of CaO due to volume change during hydration/dehydration cycles. Several approaches have been proposed to improve the mechanical properties of the system, including adding SiO2,98 Al oxides,99 and material encapsulation.100
In summary, TCES materials are at an early stage of development and several challenges need to be addressed before they can be applied on an industrial scale. While we do not rank the TCES materials, we provide critical insights into the desirable materials' properties and study their impact on the process economics.
4.3 Material property targeting results
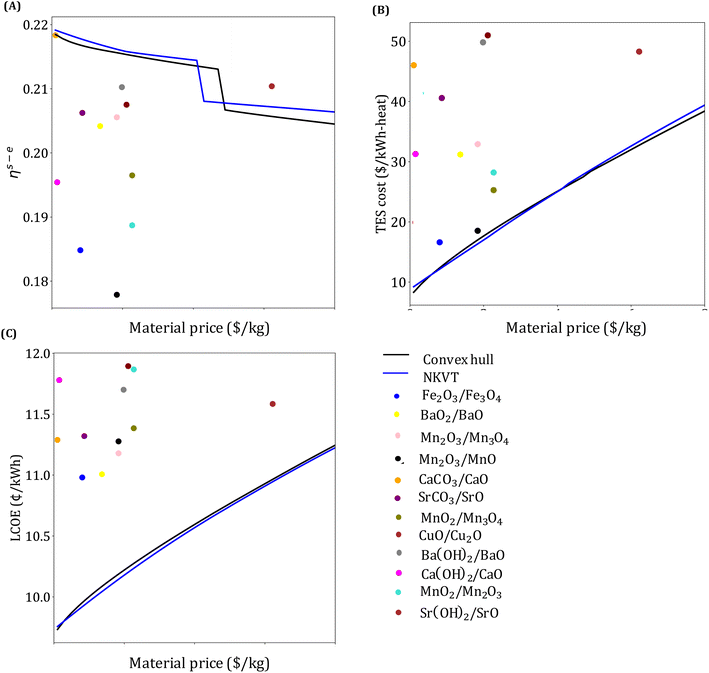
Our analysis in this section has three goals. First, we compare the LCOE of the top-performing materials identified in Section 4.1 with the target LCOE. Second, we provide insights into the target material properties as a function of material price. Finally, we compare the results obtained from the convex hull and the NKVT approach. Since we don't know the material a priori, we solve the optimization model discussed in Section 3.2 for a range of material prices.The variation of ηs−e, TES cost, and LCOE with material price are given in Fig. 8. The convex hull and NKVT approach results are shown in solid black and blue lines, respectively. Circles denote the metrics for the top materials obtained after the material screening. The curves corresponding to ηs−e (Fig. 8(A)) and TES cost (Fig. 8(B)) can be interpreted as the target efficiency and energy storage costs to achieve the target LCOE (Fig. 8(C)). Although some existing reactions have higher ηs−e than the target efficiency curve, there are none that has lower TES cost and LCOE. The LCOE of the top-performing reaction systems is 9.7% to 15.9% higher than the target LCOE.
The overall efficiency of the Fe2O3/Fe3O4system is 0.186, whereas the target efficiency corresponding to the material price of the Fe2O3/Fe3O4 system obtained by the convex hull and NKVT approach are 0.217 and 0.218, respectively. The TES cost of the Fe2O3/Fe3O4 system is $17.14 per kW h-heat, and the target TES cost obtained by the convex hull and the NKVT approach is $12.4 per kW h-heat and $12.19 per kW h-heat, respectively. A comparison of various factors contributing to TES cost is shown in Fig. 9, and key material properties affecting TES cost are given in Table 3.
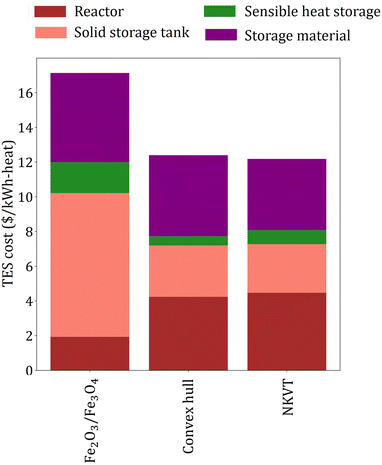 | ||
| Fig. 9 A comparison of TES cost of Fe2O3/Fe3O4 system with the target TES cost obtained by convex hull and NKVT approach. | ||
We make three key observations from Fig. 9. First, the solid tank cost is the lowest for the NKVT approach because of the highest material density and lowest material requirement. Second, the cost of sensible heat storage unit is the highest for Fe2O3/Fe3O4 system. Recall that the cost of sensible heat storage depends on the mass of O2 released, which in turn is directly proportional to νC and inversely proportional to ωA or ωB. The ratio νC/ωB is fixed for the Fe2O3/Fe3O4 system, whereas νC, ωA, and ωB are variables obtained by solving the optimization model corresponding to the convex hull and the NKVT approach. Optimization identifies that lower νC/ωB results in lower sensible heat storage costs. Third, the reactor cost is the lowest for Fe2O3/Fe3O4 because of lower heat exchanged and higher heat transfer coefficient because of higher gas velocity.
As expected, an increase in material price results in an increase in TES cost and LCOE. The target efficiency curve lies within 0.2–0.22, decreasing monotonically with an increase in material price because it becomes economical to increase the sensible heat storage fraction, which leads to higher Trec − Tpc (Fig. 10). However, note that the decrease is non-smooth. This can be explained by noting a sudden increase in the optimal capacity factor (CF). Recall that CF is defined as the ratio of the amount of electricity produced over a specified period, to the electricity that could have been generated if the power plant was operating continuously at full capacity. Increasing CF requires more energy storage during low DNI scenarios, which leads to oversizing the collector and discarding excess solar energy during high DNI scenarios.
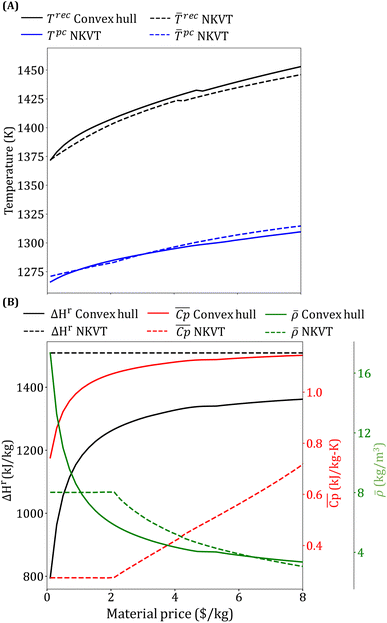
The optimal receiver and the average power cycle temperature increase monotonically with an increase in material price and range between 1372–1459 K and 1266–1315 K, respectively (Fig. 11(A)). An increase in Trec leads to a reduction in the receiver efficiency. In contrast, an increase in ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) pc increases power cycle efficiency. Although both Trec and
pc increases power cycle efficiency. Although both Trec and ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) pc increase, Trec increases more significantly so that overall Trec −
pc increase, Trec increases more significantly so that overall Trec − ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) pc increases with material price.
pc increases with material price.
 | ||
| Fig. 11 Variation of optimal (A) receiver and power-cycle temperature, and (B) reaction enthalpy, average heat capacity, and average density of solid materials with price. | ||
Although with an increase in material price, TES cost will inevitably increase, the material properties, including ΔHr, average heat capacity of A and B (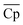 ), and average density of A and B (
), and average density of A and B (![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) ), vary to reduce the amount of required material. The results obtained using the convex hull approach suggest that the optimal ΔHr and
), vary to reduce the amount of required material. The results obtained using the convex hull approach suggest that the optimal ΔHr and 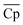 should increase with an increase in material price. However, the optimal
should increase with an increase in material price. However, the optimal ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) decreases with an increase in material price, which may appear counterintuitive at first, as high density is critical for reducing the volume of solid storage tanks. This occurs because, as illustrated in Fig. 4(A), Cp is inversely correlated with ρ. Second, the reactor volume is directly proportional to the amount of heat transferred (eqn (25)–(27) ESI†), which remains constant for material prices less than $4.7/kg (Fig. 10). The weight of solid material required in the reactor is directly proportional to its density (eqn (34) and (35) ESI†). Thus, increasing density reduces the volume of storage tanks and increases the amount of material needed in the reactors. Heat transfer increases once the material price exceeds $4.7/kg. Accordingly, a small decrease and an increase are observed in
decreases with an increase in material price, which may appear counterintuitive at first, as high density is critical for reducing the volume of solid storage tanks. This occurs because, as illustrated in Fig. 4(A), Cp is inversely correlated with ρ. Second, the reactor volume is directly proportional to the amount of heat transferred (eqn (25)–(27) ESI†), which remains constant for material prices less than $4.7/kg (Fig. 10). The weight of solid material required in the reactor is directly proportional to its density (eqn (34) and (35) ESI†). Thus, increasing density reduces the volume of storage tanks and increases the amount of material needed in the reactors. Heat transfer increases once the material price exceeds $4.7/kg. Accordingly, a small decrease and an increase are observed in 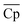 and
and ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) , respectively.
, respectively.
The optimal LCOE, target efficiency, and TES cost curves obtained by the NKVT approach are remarkably close to those obtained by the convex hull approach. The optimal receiver and power cycle temperature curves are also quite close. However, we observe differences in ΔHr, 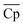 , and
, and ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) obtained by the two methods. Notably, except for ΔHr, the properties curves obtained by the two methods follow the same trend. It can be observed that ΔHr obtained by the NKVT approach corresponds to its upper bound because the approach does not correlate ΔHr with the other properties. Thus, there is a need to extend the NKVT approach to accurately correlate ΔHr with other material properties.
obtained by the two methods. Notably, except for ΔHr, the properties curves obtained by the two methods follow the same trend. It can be observed that ΔHr obtained by the NKVT approach corresponds to its upper bound because the approach does not correlate ΔHr with the other properties. Thus, there is a need to extend the NKVT approach to accurately correlate ΔHr with other material properties.
5. Conclusions
We developed a large-scale in silico reaction screening framework to identify economical CSP-TCES systems. Twelve reactions with the lowest LCOE are identified from a pool of 364 candidate reactions. The material properties and optimal operating conditions of the twelve CSP-TCES systems are analyzed to see how various plant components are affected. We also study the effect of conversion on plant economics and illustrate that TES costs and the LCOE decrease with an increase in conversion for the oxide systems. In contrast, for the hydroxide and carbonate systems, TES costs and the LCOE increase. We also developed an optimization model for the simultaneous optimization of material properties, system design, and operating conditions. Two approaches are developed to consider the limitations and correlations between material properties. The first approach is based on a convex hull of properties of known materials, and the second is based on empirical relationships. Our results suggest that the target LCOE ranges between 9.7–11.5 ₵ per kW h for material prices between $0.1 and 8/kg. We also obtain the corresponding target overall efficiency and TES cost. We show how the target efficiency TES cost decreases with an increase in material price. Furthermore, our system-level approach considers various trade-offs and provides insights into the target material properties and operating conditions. We elucidate that while energy density is critical for low TES cost and LCOE, other material properties also critically impact the system performance. We hope our analysis will facilitate the development of novel TCES materials and help accelerate the commercial deployment of CSP-TCES plants.Nomenclature
Abbreviations
| CSP | Concentrating solar power |
| LCOE | Levelized cost of electricity |
| HTF | Heat transfer fluid |
| TES | Thermal energy storage |
| s-CO2 | Supercritical carbon dioxide |
| TCES | Thermochemical energy storage |
| WF | Working fluid in power cycle |
| MSE | Mean squared error |
| CF | Capacity factor |
Parameters and variables
| T eq | Reaction equilibrium temperature |
| ν A, νB, νC | Stoichiometry coefficients |
| ΔGr | Gibb's energy of reaction |
| R | Universal gas constant |
| p C | Partial pressure of gas C |
| T mA, TmB | Melting points of A and B, respectively |
| ϕ col | Ratio of the collector area to the receiver area |
| η col | Collector efficiency |
| η rec | Receiver efficiency |
| Q us | Net heat absorbed by the receiver |
| Q rec | Solar energy incident upon the receiver |
| α rec | Receiver solar absorptance |
| ψ rec | Receiver thermal emittance |
| σ | Stefan–Boltzmann constant |
| T rec | Receiver temperature |
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) pc
pc
| Average power cycle temperature |
| T amb | Ambient temperature |
| β conv | Convective heat transfer coefficient |
| η pc | Power cycle efficiency |
| T pc | Turbine inlet temperature |
| T R1, TR2 | Temperature of endothermic and exothermic reactors |
Author contributions
Ishan Bajaj: conceptualization, methodology, software, investigation, writing – original draft, writing – review and editing. Xinyue Peng: conceptualization, software. Christos T. Maravelias: conceptualization, methodology, investigation, writing – original draft, writing – review and editing, supervision, funding acquisition.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in the paper.References
- M. Z. Jacobson, M. A. Delucchi, Z. A. F. Bauer, S. C. Goodman, W. E. Chapman, M. A. Cameron, C. Bozonnat, L. Chobadi, H. A. Clonts, P. Enevoldsen, J. R. Erwin, S. N. Fobi, O. K. Goldstrom, E. M. Hennessy, J. Liu, J. Lo, C. B. Meyer, S. B. Morris, K. R. Moy, P. L. O'Neill, I. Petkov, S. Redfern, R. Schucker, M. A. Sontag, J. Wang, E. Weiner and A. S. Yachanin, 100% Clean and Renewable Wind, Water, and Sunlight All-Sector Energy Roadmaps for 139 Countries of the World, Joule, 2017, 1, 108–121, DOI:10.1016/j.joule.2017.07.005.
- California Legislative Information, Senate Bill 100 California Renewables Portfolio Standard Program: emissions of greenhouse gases, Legislation, 2018, https://leginfo.legislature.ca.gov/faces/billNavClient.xhtml?bill_id=201720180SB100, accessed February 14, 2022 Search PubMed.
- Maine Legislature, An Act To Reform Maine's Renewable Portfolio Standard, Legislation, 2019, https://legislature.maine.gov/legis/bills/bills_129th/billtexts/SP045701.asp, accessed February 14, 2022) Search PubMed.
- New Mexico Legislature, Senate Bill 489 Energy Transition Act, Legislation, 2019 Search PubMed.
- Washington State Legislature, Supporting Washington's clean energy economy and transitioning to a clean, affordable, and reliable energy future, Legislation, 2019, https://app.leg.wa.gov/billsummary?BillNumber=5116%26Initiative=false%26Year=2019, accessed February 14, 2022 Search PubMed.
- Hawaii State Legislature, Renewable Portfolio Standards , Legislation, 2015, https://www.capitol.hawaii.gov/Archives/measure_indiv_Archives.aspx?billtype=HB%26billnumber=623%26year=2015, accessed February 14, 2022 Search PubMed.
- IEA publications, Energy Technology Perspectives, 2017, http://www.iea.org/t%26c/, accessed February 14, 2022 Search PubMed.
- R. Schäppi, D. Rutz, F. Dähler, A. Muroyama, P. Haueter, J. Lilliestam, A. Patt, P. Furler and A. Steinfeld, Drop-in fuels from sunlight and air, Nature, 2022, 601, 63–68, DOI:10.1038/s41586-021-04174-y.
- S. Zoller, E. Koepf, D. Nizamian, M. Stephan, A. Patané, P. Haueter, M. Romero, J. González-Aguilar, D. Lieftink, E. de Wit, S. Brendelberger, A. Sizmann and A. Steinfeld, A solar tower fuel plant for the thermochemical production of kerosene from H2O and CO2, Joule, 2022, 6, 1606–1616, DOI:10.1016/J.JOULE.2022.06.012.
- Z. Zhang, C. Mao, D. Motta Meira, P. N. Duchesne, A. A. Tountas, Z. Li, C. Qiu, S. Tang, R. Song, X. Ding, J. Sun, J. Yu, J. Y. Howe, W. Tu, L. Wang and G. A. Ozin, New black indium oxide-tandem photothermal CO 2-H 2 methanol selective catalyst, Nat. Commun., 2022, 13, 1512, DOI:10.1038/s41467-022-29222-7.
- REN21, Renewables 2021 Global Status Report, 2021 Search PubMed.
- D. Feldman, R. Margolis, P. Denholm and J. Stekli, Exploring the Potential Competitiveness of Utility-Scale Photovoltaics Plus Batteries with Concentrating Solar Power, 2015-2030, National Renewable Energy Laboratory (NREL), Golden, CO, 2016 Search PubMed.
- X. Peng, T. W. Root and C. T. Maravelias, Storing solar energy with chemistry: The role of thermochemical storage in concentrating solar power, Green Chem., 2017, 19, 2427–2438, 10.1039/c7gc00023e.
- Y. Kato, M. Yamada, T. Kanie and Y. Yoshizawa, Calcium oxide/carbon dioxide reactivity in a packed bed reactor of a chemical heat pump for high-temperature gas reactors, Nucl. Eng. Des., 2001, 210, 1–8, DOI:10.1016/S0029-5493(01)00421-6.
- A. Meier, E. Bonaldi, G. M. Cella, W. Lipinski, D. Wuillemin and R. Palumbo, Design and experimental investigation of a horizontal rotary reactor for the solar thermal production of lime, Energy, 2004, 29, 811–821, DOI:10.1016/S0360-5442(03)00187-7.
- A. Meier, E. Bonaldi, G. M. Cella, W. Lipinski and D. Wuillemin, Solar chemical reactor technology for industrial production of lime, Sol. Energy, 2006, 80, 1355–1362, DOI:10.1016/j.solener.2005.05.017.
- V. Nikulshina, C. Gebald and A. Steinfeld, CO2 capture from atmospheric air via consecutive CaO-carbonation and CaCO3-calcination cycles in a fluidized-bed solar reactor, Chem. Eng. J., 2009, 146, 244–248, DOI:10.1016/J.CEJ.2008.06.005.
- A. Steinfeld, A. Imhof and D. Mischler, Experimental Investigation of an Atmospheric-Open Cyclone Solar Reactor for Solid-Gas Thermochemical Reactions, J. Sol. Energy Eng., 1992, 114, 171, DOI:10.1115/1.2930001.
- E. Bagherisereshki, J. Tran, F. Lei and N. AuYeung, Investigation into SrO/SrCO3 for high temperature thermochemical energy storage, Sol. Energy, 2018, 160, 85–93, DOI:10.1016/J.SOLENER.2017.11.073.
- F. Schaube, I. Utz, A. Wörner and H. Müller-Steinhagen, De- and rehydration of Ca(OH)2 in a reactor with direct heat transfer for thermo-chemical heat storage. Part B: Validation of model, Chem. Eng. Res. Des., 2013, 91, 865–873, DOI:10.1016/j.cherd.2013.02.019.
- M. Schmidt, A. Gutierrez and M. Linder, Thermochemical energy storage with CaO/Ca(OH)2– Experimental investigation of the thermal capability at low vapor pressures in a lab scale reactor, Appl. Energy, 2017, 188, 672–681, DOI:10.1016/j.apenergy.2016.11.023.
- M. Schmidt, M. Gollsch, F. Giger, M. Grün and M. Linder, Development of a moving bed pilot plant for thermochemical energy storage with CaO/Ca(OH)2, in SolarPACES 2015, 2016, p. 050041, DOI:10.1063/1.4949139.
- P. Pardo, Z. Anxionnaz-Minvielle, S. Rougé, P. Cognet and M. Cabassud, Ca(OH)2/CaO reversible reaction in a fluidized bed reactor for thermochemical heat storage, Sol. Energy, 2014, 107, 605–616, DOI:10.1016/j.solener.2014.06.010.
- M. Neises, S. Tescari, L. de Oliveira, M. Roeb, C. Sattler and B. Wong, Solar-heated rotary kiln for thermochemical energy storage, Sol. Energy, 2012, 86, 3040–3048, DOI:10.1016/j.solener.2012.07.012.
- C. Agrafiotis, M. Roeb, M. Schmücker and C. Sattler, Exploitation of thermochemical cycles based on solid oxide redox systems for thermochemical storage of solar heat. Part 2: Redox oxide-coated porous ceramic structures as integrated thermochemical reactors/heat exchangers, Sol. Energy, 2015, 114, 440–458, DOI:10.1016/j.solener.2014.12.036.
- S. M. Babiniec, J. E. Miller, A. Ambrosini, E. Stechel, E. N. Coker, P. G. Loutzenhiser and C. K. Ho, Considerations for the Design of a High-Temperature Particle Reoxidation Reactor for Extraction of Heat in Thermochemical Energy Storage Systems, in Volume 1: Biofuels, Hydrogen, Syngas, and Alternate Fuels; CHP and Hybrid Power and Energy Systems; Concentrating Solar Power; Energy Storage; Environmental, Economic, and Policy Considerations of Advanced Energy Systems; Geothermal, Ocean, and Emerging E, ASME, 2016, p. V001T04A021, DOI:10.1115/ES2016-59646.
- M. Gigantino, S. Sas Brunser and A. Steinfeld, High-Temperature Thermochemical Heat Storage via the CuO/Cu 2 O Redox Cycle: From Material Synthesis to Packed-Bed Reactor Engineering and Cyclic Operation, Energy Fuels, 2020, 34, 16772–16782, DOI:10.1021/acs.energyfuels.0c02572.
- M. Gigantino, D. Kiwic and A. Steinfeld, Thermochemical energy storage via isothermal carbonation-calcination cycles of MgO-stabilized SrO in the range of 1000–1100 °C, Sol. Energy, 2019, 188, 720–729, DOI:10.1016/J.SOLENER.2019.06.046.
- K. Randhir, K. King, N. Rhodes, L. Li, D. Hahn, R. Mei, N. AuYeung and J. Klausner, Magnesium-manganese oxides for high temperature thermochemical energy storage, J. Energy Storage, 2019, 21, 599–610, DOI:10.1016/J.EST.2018.11.024.
- C. Ortiz, M. C. Romano, J. M. Valverde, M. Binotti and R. Chacartegui, Process integration of Calcium-Looping thermochemical energy storage system in concentrating solar power plants, Energy, 2018, 155, 535–551, DOI:10.1016/j.energy.2018.04.180.
- N. R. Rhodes, A. Barde, K. Randhir, L. Li, D. W. Hahn, R. Mei, J. F. Klausner and N. Auyeung, Solar Thermochemical Energy Storage Through Carbonation Cycles of SrCO3/SrO Supported on SrZrO3, ChemSusChem, 2015, 8, 3793–3798, DOI:10.1002/cssc.201501023.
- P. Pardo, a. Deydier, Z. Anxionnaz-Minvielle, S. Rougé, M. Cabassud and P. Cognet, A review on high temperature thermochemical heat energy storage, Renewable Sustainable Energy Rev., 2014, 32, 591–610, DOI:10.1016/j.rser.2013.12.014.
- A. Bayon, R. Bader, M. Jafarian, L. Fedunik-Hofman, Y. Sun, J. Hinkley, S. Miller and W. Lipiński, Techno-economic assessment of solid–gas thermochemical energy storage systems for solar thermal power applications, Energy, 2018, 149, 473–484, DOI:10.1016/j.energy.2017.11.084.
- F. Lei, A. Dyall and N. AuYeung, An in-depth investigation of BaO2/BaO redox oxides for reversible solar thermochemical energy storage, Sol. Energy Mater. Sol. Cells, 2021, 223, 110957, DOI:10.1016/J.SOLMAT.2021.110957.
- C. Ortiz, J. M. Valverde, R. Chacartegui and L. A. Perez-Maqueda, Carbonation of Limestone Derived CaO for Thermochemical Energy Storage: From Kinetics to Process Integration in Concentrating Solar Plants, ACS Sustain. Chem. Eng., 2018, 6, 6404–6417, DOI:10.1021/acssuschemeng.8b00199.
- X. Chen, X. Jin, X. Ling and Y. Wang, Exergy Analysis of Concentrated Solar Power Plants with Thermochemical Energy Storage Based on Calcium Looping, ACS Sustain. Chem. Eng., 2020, 8, 7928–7941, DOI:10.1021/acssuschemeng.0c01586.
- E. Karasavvas, K. D. Panopoulos, S. Papadopoulou and S. Voutetakis, Energy and exergy analysis of the integration of concentrated solar power with calcium looping for power production and thermochemical energy storage, Renewable Energy, 2020, 154, 743–753, DOI:10.1016/j.renene.2020.03.018.
- S. E. B. Edwards and V. Materić, Calcium looping in solar power generation plants, Sol. Energy, 2012, 86, 2494–2503, DOI:10.1016/j.solener.2012.05.019.
- U. Pelay, L. Luo, Y. Fan, D. Stitou and C. Castelain, Integration of a thermochemical energy storage system in a Rankine cycle driven by concentrating solar power: Energy and exergy analyses, Energy, 2019, 167, 498–510, DOI:10.1016/j.energy.2018.10.163.
- K. J. Albrecht, G. S. Jackson and R. J. Braun, Evaluating thermodynamic performance limits of thermochemical energy storage subsystems using reactive perovskite oxide particles for concentrating solar power, Sol. Energy, 2018, 167, 179–193, DOI:10.1016/j.solener.2018.03.078.
- Y. A. Criado, M. Alonso, J. C. Abanades and Z. Anxionnaz-Minvielle, Conceptual process design of a CaO/Ca(OH) 2 thermochemical energy storage system using fluidized bed reactors, Appl. Therm. Eng., 2014, 73, 1087–1094, DOI:10.1016/j.applthermaleng.2014.08.065.
- R. Bravo, C. Ortiz, R. Chacartegui and D. Friedrich, Hybrid solar power plant with thermochemical energy storage: A multi-objective operational optimisation, Energy Convers. Manage., 2020, 205, 112421, DOI:10.1016/j.enconman.2019.112421.
- D. Salas, E. Tapachès, N. Mazet and D. Aussel, Economical optimization of thermochemical storage in concentrated solar power plants via pre-scenarios, Energy Convers. Manage., 2018, 174, 932–954, DOI:10.1016/j.enconman.2018.08.079.
- S. Kiyabu, J. S. Lowe, A. Ahmed and D. J. Siegel, Computational Screening of Hydration Reactions for Thermal Energy Storage: New Materials and Design Rules, Chem. Mater., 2018, 30, 2006–2017, DOI:10.1021/acs.chemmater.7b05230.
- L. André, S. Abanades and G. Flamant, Screening of thermochemical systems based on solid-gas reversible reactions for high temperature solar thermal energy storage, Renewable Sustainable Energy Rev., 2016, 64, 703–715, DOI:10.1016/j.rser.2016.06.043.
- M. Deutsch, D. Müller, C. Aumeyr, C. Jordan, C. Gierl-Mayer, P. Weinberger, F. Winter and A. Werner, Systematic search algorithm for potential thermochemical energy storage systems, Appl. Energy, 2016, 183, 113–120, DOI:10.1016/j.apenergy.2016.08.142.
- S. Wu, C. Zhou, E. Doroodchi, R. Nellore and B. Moghtaderi, A review on high-temperature thermochemical energy storage based on metal oxides redox cycle, Energy Convers. Manage., 2018, 168, 421–453, DOI:10.1016/j.enconman.2018.05.017.
- R. Jacobs, T. Mayeshiba, J. Booske and D. Morgan, Material Discovery and Design Principles for Stable, High Activity Perovskite Cathodes for Solid Oxide Fuel Cells, Adv. Energy Mater., 2018, 8, 1702708, DOI:10.1002/AENM.201702708.
- J. Vieten, B. Bulfin, P. Huck, M. Horton, D. Guban, L. Zhu, Y. Lu, K. A. Persson, M. Roeb and C. Sattler, Materials design of perovskite solid solutions for thermochemical applications, Energy Environ. Sci., 2019, 12, 1369, 10.1039/c9ee00085b.
- A. Zaki, J. Carrasco, D. Bielsa and A. Faik, Tunable Redox Temperature of a Co 3−x Mn x O 4 (0 ≤ x ≤ 3) Continuous Solid Solution for Thermochemical Energy Storage, ACS Appl. Mater. Interfaces, 2020, 12, 28, DOI:10.1021/acsami.9b14369.
- S. M. Babiniec, E. N. Coker, J. E. Miller and A. Ambrosini, Investigation of LaxSr1-xCoyM1-yO3-δ (M=Mn, Fe) perovskite materials as thermochemical energy storage media, Sol. Energy, 2015, 118, 451–459, DOI:10.1016/j.solener.2015.05.040.
- S. M. Babiniec, E. N. Coker, J. E. Miller and A. Ambrosini, Doped calcium manganites for advanced high-temperature thermochemical energy storage, Int. J. Energy Res., 2016, 40, 280–284, DOI:10.1002/ER.3467.
- L. Imponenti, K. J. Albrecht, R. J. Braun and G. S. Jackson, Measuring Thermochemical Energy Storage Capacity with Redox Cycles of Doped-CaMnO3, ECS Trans., 2016, 72, 11–22, DOI:10.1149/07207.0011ecst.
- L. Imponenti, K. J. Albrecht, J. W. Wands, M. D. Sanders and G. S. Jackson, Thermochemical energy storage in strontium-doped calcium manganites for concentrating solar power applications, Sol. Energy, 2017, 151, 1–13, DOI:10.1016/j.solener.2017.05.010.
- X. Peng, M. Yao, T. W. Root and C. T. Maravelias, Design and Analysis of Concentrating Solar Power Plants with Fixed-bed Reactors for Thermochemical Energy Storage, Appl. Energy, 2020, 262, 114543, DOI:10.1016/j.apenergy.2020.114543.
- X. Peng, I. Bajaj, M. Yao and C. T. Maravelias, Solid-gas thermochemical energy storage strategies for concentrating solar power: Optimization and system analysis, Energy Convers. Manage., 2021, 245, 114636, DOI:10.1016/j.enconman.2021.114636.
- C. K. Ho, Advances in central receivers for concentrating solar applications, Sol. Energy, 2017, 152, 38–56, DOI:10.1016/j.solener.2017.03.048.
- J. Ortega, S. Khivsara, J. Christian, C. Ho and P. Dutta, Coupled modeling of a directly heated tubular solar receiver for supercritical carbon dioxide Brayton cycle: Structural and creep-fatigue evaluation, Appl. Therm. Eng., 2016, 109, 979–987, DOI:10.1016/j.applthermaleng.2016.06.031.
- A. L. Ávila-Marín, Volumetric receivers in Solar Thermal Power Plants with Central Receiver System technology: A review, Sol. Energy, 2011, 85, 891–910, DOI:10.1016/j.solener.2011.02.002.
- J. C. Gomez-Vidal and R. Tirawat, Corrosion of alloys in a chloride molten salt (NaCl-LiCl) for solar thermal technologies, Sol. Energy Mater. Sol. Cells, 2016, 157, 234–244, DOI:10.1016/j.solmat.2016.05.052.
- H. Benoit, L. Spreafico, D. Gauthier and G. Flamant, Review of heat transfer fluids in tube-receivers used in concentrating solar thermal systems: Properties and heat transfer coefficients, Renewable Sustainable Energy Rev., 2016, 55, 298–315, DOI:10.1016/j.rser.2015.10.059.
- W. Wu, D. Trebing, L. Amsbeck, R. Buck and R. Pitz-Paal, Prototype testing of a centrifugal particle receiver for high-temperature concentrating solar applications, Journal of Solar Energy Engineering, Trans. ASME, 2015, 137, 041011, DOI:10.1115/1.4030657.
- N. P. Siegel, C. K. Ho, S. S. Khalsa and G. J. Kolb, Development and evaluation of a prototype solid particle receiver: On-sun testing and model validation, J. Sol. Energy Eng. Trans. ASME, 2010, 132, 0210081–0210088, DOI:10.1115/1.4001146.
- S. M. Besarati, D. Y. Goswami and E. K. Stefanakos, Development of a solar receiver based on compact heat exchanger technology for supercritical carbon dioxide power cycles, J. Sol. Energy Eng. Trans. ASME, 2015, 137, 031018, DOI:10.1115/1.4029861.
- B. Liao, L. Guo, Y. Lu and X. Zhang, Solar receiver/reactor for hydrogen production with biomass gasification in supercritical water, Int. J. Hydrogen Energy, 2013, 13038–13044, DOI:10.1016/j.ijhydene.2013.03.113.
- T. Neises and C. Turchi, Supercritical carbon dioxide power cycle design and configuration optimization to minimize levelized cost of energy of molten salt power towers operating at 650 °C, Sol. Energy, 2019, 181, 27–36, DOI:10.1016/j.solener.2019.01.078.
- M. Binotti, M. Astolfi, S. Campanari, G. Manzolini and P. Silva, Preliminary assessment of sCO2 cycles for power generation in CSP solar tower plants, Appl. Energy, 2017, 204, 1007–1017, DOI:10.1016/j.apenergy.2017.05.121.
- I. Barin, O. Knacke and O. Kubaschewski, Thermochemical Properties of Inorganic Substances, Springer Berlin Heidelberg, 1977, DOI:10.1007/978-3-662-02293-1.
- N. W. Hlongwa, D. Sastre, E. Iwuoha, A. J. Carrillo, C. Ikpo, D. P. Serrano, P. Pizarro and J. M. Coronado, Exploring the thermochemical heat storage capacity of AMn2O4 (A = Li or Cu) spinels, Solid State Ionics, 2018, 320, 316–324, DOI:10.1016/j.ssi.2018.03.019.
- X. Chen, M. Kubota, S. Yamashita and H. Kita, Exploring Cu-Based Spinel/Delafossite Couples for Thermochemical Energy Storage at Medium-High Temperature, ACS Appl. Energy Mater., 2021, 4, 7242–7249, DOI:10.1021/acsaem.1c01352.
- A. Zaki, J. Carrasco, D. Bielsa and A. Faik, Tunable Redox Temperature of a Co3-xMn xO4 (0 ≤ x ≤ 3) Continuous Solid Solution for Thermochemical Energy Storage, ACS Appl. Mater. Interfaces, 2020, 12, 7010–7020, DOI:10.1021/acsami.9b14369.
- S. Wu, C. Zhou, E. Doroodchi, R. Nellore and B. Moghtaderi, A review on high-temperature thermochemical energy storage based on metal oxides redox cycle, Energy Convers. Manage., 2018, 168, 421–453, DOI:10.1016/j.enconman.2018.05.017.
- S. Tescari, C. Agrafiotis, S. Breuer, L. De Oliveira, M. Neises-Von Puttkamer, M. Roeb and C. Sattler, Thermochemical solar energy storage via redox oxides: Materials and reactor/heat exchanger concepts, Energy Procedia, 2014, 1034–1043, DOI:10.1016/j.egypro.2014.03.111.
- T. Block and M. Schmücker, Metal oxides for thermochemical energy storage: A comparison of several metal oxide systems, Sol. Energy, 2016, 126, 195–207, DOI:10.1016/j.solener.2015.12.032.
- X. Peng, T. W. Root and C. T. Maravelias, Optimization-based process synthesis under seasonal and daily variability: Application to concentrating solar power, AIChE J., 2019, 65, e16458, DOI:10.1002/aic.16458.
- N. Nolzen, A. Ganter, N. Baumgärtner, L. Leenders and A. Bardow, Where to Market Flexibility? Optimal Participation of Industrial Energy Systems in Balancing-Power, Day-Ahead, and Continuous Intraday Electricity Markets, arXiv, 2022, preprint, arXiv:2212.12507, DOI:10.48550/arXiv.2212.12507.
- M. Langiu, D. Y. Shu, F. J. Baader, D. Hering, U. Bau, A. Xhonneux, D. Müller, A. Bardow, A. Mitsos and M. Dahmen, COMANDO: A Next-Generation Open-Source Framework for Energy Systems Optimization, Comput. Chem. Eng., 2021, 152, 107366, DOI:10.1016/j.compchemeng.2021.107366.
- C. K. Ho, M. Carlson, P. Garg and P. Kumar, Technoeconomic Analysis of Alternative Solarized s-CO2 Brayton Cycle Configurations, J. Sol. Energy Eng. Trans. ASME, 2016, 138, 051008, DOI:10.1115/1.4033573.
- United States Geological Survey, Mineral Commodity Summaries, 2022 Search PubMed.
- H. Kopp, Investigations of the specific heat of solid bodies, Philos. Trans. R. Soc. London, 1865, 155, 71–292 CrossRef.
- L. Glasser, H. Donald and B. Jenkins, Predictive thermodynamics for ionic solids and liquids, Phys. Chem. Chem. Phys., 2016, 18, 21226, 10.1039/c6cp00235h.
- L. Glasser and H. D. B. Jenkins, Volume-based thermodynamics: A prescription for its application and usage in approximation and prediction of thermodynamic data, J. Chem. Eng. Data, 2011, 56, 874–880, DOI:10.1021/JE100683U.
- E. Alonso, C. Hutter, M. Romero, A. Steinfeld and J. Gonzalez-Aguilar, Kinetics of Mn2O3-Mn3O4 and Mn3O4-MnO redox reactions performed under concentrated thermal radiative flux, Energy Fuels, 2013, 4884–4890, DOI:10.1021/ef400892j.
- D. Müller, C. Knoll, W. Artner, M. Harasek, C. Gierl-Mayer, J. M. Welch, A. Werner and P. Weinberger, Combining in-situ X-ray diffraction with thermogravimetry and differential scanning calorimetry – An investigation of Co3O4, MnO2 and PbO2 for thermochemical energy storage, Sol. Energy, 2017, 153, 11–24, DOI:10.1016/j.solener.2017.05.037.
- J. Zhou, D. Xiang, P. Zhu, J. Deng, C. Gu, H. Xu, J. Zhou and G. Xiao, ZrO2-Doped Copper Oxide Long-Life Redox Material for Thermochemical Energy Storage, ACS Sustain. Chem. Eng., 2023, 11, 47–57, DOI:10.1021/acssuschemeng.2c03632.
- D. Yilmaz, E. Darwish and H. Leion, Investigation of the combined Mn-Si oxide system for thermochemical energy storage applications, J. Energy Storage, 2020, 28, 101180, DOI:10.1016/j.est.2019.101180.
- F. Fresno, T. Yoshida, N. Gokon, R. Fernández-Saavedra and T. Kodama, Comparative study of the activity of nickel ferrites for solar hydrogen production by two-step thermochemical cycles, Int. J. Hydrogen Energy, 2010, 35, 8503–8510, DOI:10.1016/j.ijhydene.2010.05.032.
- J. R. Scheffe, J. Li and A. W. Weimer, A spinel ferrite/hercynite water-splitting redox cycle, Int. J. Hydrogen Energy, 2010, 35, 3333–3340, DOI:10.1016/j.ijhydene.2010.01.140.
- T. Block and M. Schmücker, Metal oxides for thermochemical energy storage: A comparison of several metal oxide systems, Sol. Energy, 2016, 126, 195–207, DOI:10.1016/j.solener.2015.12.032.
- A. J. Carrillo, D. Sastre, D. P. Serrano, P. Pizarro and J. M. Coronado, Revisiting the BaO2/BaO redox cycle for solar thermochemical energy storage, Phys. Chem. Chem. Phys., 2016, 18, 8039–8048, 10.1039/c5cp07777j.
- A. J. Carrillo, D. P. Serrano, P. Pizarro and J. M. Coronado, Thermochemical heat storage based on the Mn2O3/Mn3O4 redox couple: Influence of the initial particle size on the morphological evolution and cyclability, J. Mater. Chem. A, 2014, 2, 19435–19443, 10.1039/c4ta03409k.
- M. Wokon, T. Block, S. Nicolai, M. Linder and M. Schmücker, Thermodynamic and kinetic investigation of a technical grade manganese-iron binary oxide for thermochemical energy storage, Sol. Energy, 2017, 153, 471–485, DOI:10.1016/j.solener.2017.05.045.
- J. Marugán, J. A. Botas, M. Martín, R. Molina and C. Herradón, Study of the first step of the Mn 2O 3/MnO thermochemical cycle for solar hydrogen production, Int. J. Hydrogen Energy, 2012, 7017–7025, DOI:10.1016/j.ijhydene.2011.10.124.
- Q. Lei, R. Bader, P. Kreider, K. Lovegrove and W. Lipiński, Thermodynamic analysis of a combined-cycle solar thermal power plant with manganese oxide-based thermochemical energy storage, in E3S Web of Conferences, EDP Sciences, 2017, DOI:10.1051/e3sconf/20172200102.
- N. R. Rhodes, A. Barde, K. Randhir, L. Li, D. W. Hahn, R. Mei, J. F. Klausner and N. Auyeung, Solar Thermochemical Energy Storage Through Carbonation Cycles of SrCO3/SrO Supported on SrZrO3, ChemSusChem, 2015, 8, 3793–3798, DOI:10.1002/cssc.201501023.
- M. Benitez-Guerrero, J. M. Valverde, A. Perejon, P. E. Sanchez-Jimenez and L. A. Perez-Maqueda, Low-cost Ca-based composites synthesized by biotemplate method for thermochemical energy storage of concentrated solar power, Appl. Energy, 2018, 210, 108–116, DOI:10.1016/j.apenergy.2017.10.109.
- M. Deutsch, F. Horvath, C. Knoll, D. Lager, C. Gierl-Mayer, P. Weinberger and F. Winter, High-Temperature Energy Storage: Kinetic Investigations of the CuO/Cu2O Reaction Cycle, Energy Fuels, 2017, 31, 2324–2334, DOI:10.1021/acs.energyfuels.6b02343.
- M. Xu, X. Huai and J. Cai, Agglomeration Behavior of Calcium Hydroxide/Calcium Oxide as Thermochemical Heat Storage Material: A Reactive Molecular Dynamics Study, J. Phys. Chem. C, 2017, 121, 3025–3033, DOI:10.1021/acs.jpcc.6b08615.
- K. G. Sakellariou, G. Karagiannakis, Y. A. Criado and A. G. Konstandopoulos, Calcium oxide based materials for thermochemical heat storage in concentrated solar power plants, Sol. Energy, 2015, 122, 215–230, DOI:10.1016/j.solener.2015.08.011.
- S. Afflerbach, M. Kappes, A. Gipperich, R. Trettin and W. Krumm, Semipermeable encapsulation of calcium hydroxide for thermochemical heat storage solutions, Sol. Energy, 2017, 148, 1–11, DOI:10.1016/j.solener.2017.03.074.
Footnote |
| † Electronic supplementary information (ESI) available: Reaction list and comparison of properties, reactions obtained after thermodynamic screening, power cycle, model equations, solution strategy, derivation of empirical relationships for material property targeting, optimization results for Fe2O3/Fe3O4 system, heat transfer process. See DOI: https://doi.org/10.1039/d3su00244f |
| This journal is © The Royal Society of Chemistry 2024 |