Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The electrocatalytic activity for the hydrogen evolution reaction on alloys is determined by element-specific adsorption sites rather than d-band properties†
Maximilian
Schalenbach
 *a,
Rebekka
Tesch
*bc,
Piotr M.
Kowalski
*a,
Rebekka
Tesch
*bc,
Piotr M.
Kowalski
 bc and
Rüdiger-A.
Eichel
ad
bc and
Rüdiger-A.
Eichel
ad
aFundamental Electrochemistry (IEK-9), Institute of Energy and Climate Research, Forschungszentrum Jülich, Wilhelm-Johnen-Straße, 52425 Jülich, Germany. E-mail: m.schalenbach@fz-juelich.de; r.tesch@fz-juelich.de
bTheory and Computation of Energy Materials (IEK-13), Institute of Energy and Climate Research, Forschungszentrum Jülich, Wilhelm-Johnen-Straße, 52425 Jülich, Germany
cJülich Aachen Research Alliance JARA Energy & Center for Simulation and Data Science (CSD), 52425 Jülich, Germany
dInstitute of Physical Chemistry, RWTH Aachen University, 52062 Aachen, Germany
First published on 30th April 2024
Abstract
Trends of the electrocatalytic activities for the hydrogen evolution reaction (HER) across transition metals are typically explained by d-band properties such as center or upper edge positions in relation to Fermi levels. Here, the universality of this relation is questioned for alloys, exemplified for the AuPt system which is examined with electrocatalytic measurements and density functional theory (DFT) calculations. At small overpotentials, linear combinations of the pure-metals’ Tafel kinetics normalized to the alloy compositions are found to precisely resemble the measured HER activities. DFT calculations show almost neighbor-independent adsorption energies on Au and Pt surface-sites, respectively, as the adsorbed hydrogen influences the electron density mostly locally at the adsorption site itself. In contrast, the density of states of the d-band describe the delocalized conduction electrons in the alloys, which are unable to portray the local electronic environments at adsorption sites and related bonding strengths. The adsorption energies at element-specific surface sites are related to overpotential-dependent reaction mechanisms in a multidimensional reinterpretation of the volcano plot for alloys, which bridges the found inconsistencies between activity and bonding strength descriptors of the common electrocatalytic theory for alloys.
Introduction
The hydrogen evolution reaction (HER) in acidic media is one of the most studied electrochemical reactions in the literature,1–3 representing a simple electrocatalytic model system with adsorbed hydrogen as the only reaction intermediate. With regard to application, the HER is an essential part of water electrolysis,4 displaying a cornerstone chemical reaction for a transition towards sustainability.5 Although the HER has been excessively studied over more than a century, the detailed physicochemical mechanisms of the reaction and its relation to the material properties are still a matter of controversial debate in the literature.6,7 The electronic interactions of different elements in alloys are discussed to improve HER electrocatalysts,8,9 while the detailed physicochemical interactions that may cause such increase in electrocatalytic activities are not fully understood yet.Sabatier's principle of heterogeneous catalysis generally states that the bonding strength of an intermediate to a catalyst is responsible for the activity towards the catalytic conversion.10,11 A stronger or weaker adsorption than the optimum adsorption strength kinetically slows down the reaction, as typically visualized by the so-termed “volcano plot” of the catalytic activity as a function of the bonding strength. In the case of the HER, the exchange current density typically serves as an activity descriptor, which is obtained from the Tafel analysis of the electrochemical potential–current characteristic.12 The first volcano plots for the activities of transition metals towards the HER contained hydrogen bonding strength descriptors that were derived from metal-electronegativities or measured heats of adsorptions.13–15 Computationally derived descriptors for the bonding strength led to the modern state of the art volcano plots.16,17 Reported volcano plots for the HER of pure metals across the periodic table typically neglected the oxides formed on non-noble metals, displaying an error source for the calculated adsorption strength and measured activities.18 With the reliable data of the noble metals only, the volcano plot loses one flank, resulting in a linear relation of activity and adsorption energy.18
Approaches to derive hydrogen bonding strengths via density functional theory (DFT) were introduced in the mid-1990s.19 Hammer and Nørskov20,21 found that besides the chemically active electronic states near the Fermi level also the position of the entire d-band relative to the Fermi level is decisive for the hydrogen bonding strength. Their comparison of the density of states of Ni, Cu, Pt, and Au revealed the trend that lower-lying d-bands decrease the adsorption energy by filling of repulsive anti-bonding metal-adsorbate states.20 These states explain Pt's higher electrocatalytic activity for the HER and lower nobleness despite of a higher work function in comparison to Au,15 displaying an impressive success of computational electrochemistry. Nowadays – almost 30 years later – the relation of adsorption strength and d-band position (commonly known as d-band model) proposed by Hammer and Nørskov represents a cornerstone in the computational modeling of electro-catalysts.19
Driven by the scope to tune the hydrogen adsorption energy towards the volcano's peak via alloying, a manifold of experimental and theoretical works (such as8,22,23) reported superior alloy activities than those of its pure constituents. However, such increases of the electrocatalytic activities often can be traced back to morphology effects.24 For instance, over several decades NiMo alloys were considered as effective catalysts for the alkaline HER, which had later been ascribed to high surface areas resulting from the manufacturing procedure rather than electronic properties.25 At the atomic level, the well-known increase in HER activity with small fractions of metal dopant atoms (e.g. Pd or Pt nano-islands, clusters or single atoms at an Au support)26,27 is most commonly explained by electronic structure changes of catalyst particles due to the support28–31 with Nørskov's d-band model. Moreover, the d-band properties are often used as a computational-derived tool to screen alloy-electrocatalysts.32–34 Only few studies stressed the importance of local effects on the activity, by considering individual metal states28,31 and the importance of defect sites in the activity of Au alloys.35,36
The aim of this study is to critically access the current understanding of electrocatalysis by reevaluating d-band properties of alloys as measures for hydrogen bonding strengths and electrocatalytic activities. Hereto, polished AuPt alloys provide an ideal experimental model system by simultaneously ruling out contributions of surface morphology (i.e. porosity)24 and surface oxides18 due to the nobleness of both metals.20,37 Pt dissolves up to a content of 15% in the Au fcc-type lattice,38 so that Pt dopings in the Au matrix are tunable over a broad range of compositions. In the alloys, Au and Pt surface sites are found to show similar electrocatalytic activities and hydrogen adsorption energies as those in the pure metal systems, respectively. This finding is shown to contradict the d-band model. Moreover, DFT calculations show that the hydrogen adsorption changes the electronic states mostly locally in the direct vicinity of the adsorption site. Hence, delocalized electrons in the d-band seem inadequate measures for the localized bonding of hydrogen on surface atoms. Overpotential-dependent changes of the reaction pathways are found to complicate a classical Tafel analysis and the determination of the commonly used current exchange density as activity descriptor. Hence, drawbacks of the classical activity and bonding strength descriptors in electrocatalysis are pointed out. To overcome these inconsistencies, interacting descriptors are introduced by coupling overpotential-dependent and site-specific turnover frequencies with the combination of adsorption energies involved in the hydrogen formation. Hereto, a multidimensional reinterpretation of the volcano plot for alloy electrocatalysts is proposed.
Methods
Experimental
An induction furnace (iew Induktive Erwärmungsanlagen GmbH) was used to metallurgically fabricate the pure metal and alloy specimens from powders (Junker Edelmetalle GmbH and Alfa Aesar) with graphite crucibles in Ar atmosphere. A detailed description of the fabrication procedure is given in the ESI.† The thus produced metal specimens have a diameter of 6 mm and a height of approximately 5 mm. The metal specimens were grinded with 4000 grid sandpaper to achieve a smooth and polished surface. To avoid surface contamination of the specimen with organic lubricants further polishing with diamond dispersions was omitted. The structures of the polycrystalline specimens were examined with powder X-ray diffractometry (see ESI†). For the alloys, lattice distortions of combined phases show that Pt dissolves in the Au matrix, as expected from the metallurgical phase diagram.38 The surface composition of the polished alloys is examined with energy-dispersive X-ray spectroscopy and chemical composition analysis (see ESI†).The metal specimens were mounted in an in-house manufactured “V”-shaped flow cell made of polypropylene. Blueprints of the cell are provided in the ESI.† A stamped fluoroelastomer flat sealing with a thickness of 500 μm and an open diameter of 0.4 cm connected the plastic body of the cell with the metal specimens, exposing 0.126 cm2 of their polished surfaces to the electrolyte. A peristaltic pump pumped a 1 M HClO4 electrolyte with a flow rate of 220 ml min−1 through the cell. The electrolyte entered the cell horizontally and exited vertically to the top, so that the ascending bubbles were additionally carried by the convective electrolyte flow to a gas separator. In the cell, the electrolyte first passed a Nafion membrane, behind which an Ag/AgCl reference electrode (Metrohm) was placed. In the direction of flow, the electrolyte next came to the polished metal surface that acted as the working electrode, where the flow direction is changed by 90°. Last, the electrolyte passed a Pt wire counter electrode.
Before entering the cell, the electrolyte was pumped through a cylindrically shaped polyethylene container that contained a column of 10 cm of the electrolyte. Using a fine glass frit, the electrolyte was purged either with Ar or carbon monoxide (CO). This container also served as the gas separator at the cell outlet. The electrolyte was replaced after every measurement, to avoid any contamination from previous measurements. Prior to electrochemical characterization, the purged electrolyte was pumped through the cell and the gas separator for 15 min to reduce the amount of dissolved oxygen.
A Zahner Zennium XC potentiostat was used for the electrochemical measurements and controlled with a Python script. This script started at an electrode potential of 0.1 V vs. RHE, which was reduced stepwise by 0.01 mV with a waiting time of 0.3 s to reduce the effect of capacitive currents. After reaching a current density of 0.1 A cm−2 of the HER, a stepwise potential increase by the same increment led back to the initial potential. This procedure was repeated three times. Larger HER current densities than 0.1 A cm−2 were not applicable to the polished specimens as these resulted in severe bubble blockage of the electrode as noticeable by noisy currents,39 as below discussed in more detail.
Evaluation of kinetic data
To extract the overpotential for the HER from the measured electrochemical potential–current relation, the offset of the Ag/AgCl reference electrode is added to the measured potential and the Ohmic drop is subtracted. The Ohmic resistance R of the cell is extracted from the high frequency resistance as determined by impedance spectroscopy. Using Ohms's law, the overpotential η is determined as a function of the measured potential E and current I:| η = E − RI | (1) |
The overpotential for the HER is here defined as negative. The current density is determined by dividing the negative measured current I by the metal specimens area A of 0.126 cm2 that is exposed to the electrolyte:
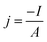 | (2) |
The sign of the HER current density is defined positive to ease logarithmic depictions of the data. In electrocatalysis, the potential–current relation is typically described by the Butler–Volmer relation. In the limit of significant overpotentials, the Butler–Volmer relation simplifies to the Tafel equation,12 which describes an exponential dependence of the current density j as a function of the overpotential
| j = j0e−aη, | (3) |
To characterize the hydrogen evolution in Ar purged electrolyte, the above-described electrochemical measuring procedure was applied to each specimen at least three times. For every repetition measurement the surface of the specimen was freshly prepared by the grinding procedure introduced above. All the data obtained for a specimen were merged, providing statistical measurement errors and ensuring reproducibility. The commonly used method of surface area estimations by double layer capacitances was not used here, as a recent study41 showed their drawbacks (which here arise from the pseudocapacitance of the Pt component). To average the experimental data and to determine the statistic measurement error, the merged potential–current curves of different scans and repetition measurements were sliced with an increment of 30 mV into individual data frames. Based on such a data frame, the mean current density and its standard variation were extracted and related to the mean overpotential. Thus, step by step a value for the overpotential was related to a value of the current density, while all repetition measurements contributed to the statistical measurement error. Based on this stepwise overpotential–current density relation, the Tafel slope was extracted by the derivative of the overpotentials in the logarithmic density. All source codes for the calculations, data treatment, and data evaluation are supplied in the ESI.†
DFT calculations
The Au(111) facet is the most stable Au facet42,43 and was selected as a model system for the conducted DFT calculations. Different concentrations and positions of Pt dopant atoms (surface and subsurface) were modeled (see Table 1). The surfaces were computed as periodic slabs of 6 × 6 surface unit cells with four atomic layers thickness. The two bottom layers were fixed to the bulk atom positions. The computed bulk lattice parameter of Au (4.17 Å) was used for all slab models, except for the Pt(111) and the Au monolayer (ML) coated Pt(111) slabs, which used the computed Pt bulk lattice parameter (3.98 Å). The Effective Screening Medium44 was used as dipole correction scheme.Hydrogen atoms were placed at top or fcc hollow sites, which are the most stable ones on the considered Au and Pt (111) surfaces.31,45 The adsorption energies Eads per hydrogen atom were computed by
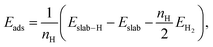 | (4) |
All calculations were performed with the QuantumESPRESSO plane-wave code,48 using the PBE exchange–correlation functional.49 Core electrons were described by ultrasoft pseudopotentials, with the Au 6s15d10, Pt 6s15d9, H 1s1, C 2s22p2 and O 2s22p4 electrons computed explicitly. All calculations were spin unpolarized. A Monkhorst–Pack k-point mesh of 4 × 4 × 1 was used for the surface slabs, whereas the isolated H2 and CO molecules were computed at the Gamma point. Kinetic energy cutoffs for wave functions and electronic densities were 60 and 360 Ry, respectively. Orbital occupations were Gaussian broadened by 0.015 Ry. Geometries were optimized with convergence thresholds of 10−4 Ry for energies and 10−3 Ry a0−1 (where a0 is the Bohr radius) for forces. 5d-projected electronic densities of states (d-DOS) were computed with a Gaussian broadening of 0.2 eV and d-band centers were computed as the centroids of the 5d-bands. Images of the slabs were created with VESTA.50
Results and discussion
A structural analysis of the metal specimens examined in this study is provided in the ESI,† including X-ray diffraction (XRD), energy-dispersive X-ray spectroscopy (EDS), and a chemical analysis of the alloy composition via inductively coupled plasma optical emission spectroscopy (ICP-OES). For the chemical analysis, abrasive probes of the measured surfaces were extracted aiming to estimate the surfaces’ compositions. With the XRD data, uniform mixing of the elements in the alloys is shown. The alloy-compositions that will be stated in following all refer to the chemical analysis via the ICP-OES data. Besides pure Au and Pt specimens, six alloy specimens with Pt contents of 0.02, 0.33, 0.88, 3.1, 6.7, 11.2 atomic percent (%Pt) will be examined in the following. With DFT, five model systems will be analyzed regarding their hydrogen adsorption energies and density of states. The measured and DFT-modeled data and thereon based descriptors for electrocatalytic activities and bonding strengths will be linked in a multidimensional reinterpretation of the volcano plot.Characterization of the electrocatalytic activity
Fig. 1(A) shows the experimentally obtained Tafel plots12 of the manufactured polycrystalline pure Au and Pt specimens, in which the overpotential η for the HER is depicted as a function of the logarithm of the current density j (plots with higher resolutions are shown in the ESI†). Between overpotentials of −0.1 and 0 V, current densities in the range of a few μA cm−2 are measured for the Au specimen, which include significant contributions of the reduction of oxygen impurities and capacitive currents. Between overpotentials of −0.5 and −0.1 V, the three repetition measurements conducted show a point cloud that indicates a linear trend. A Tafel fit was conducted to that point cloud, showing a Tafel slope of approximately 110 mV dec−1. The scattering of the measured data results from different responses of the forward and backward scan of the applied potential steps, which is attributable to a hysteresis of the bubble coverage. The three repetition measurements with newly polished surfaces, respectively, also led to differences of the response, leading to a statistical error and a measure for the reproducibility of the prepared surfaces.Fig. 1(B) shows the Tafel slopes39 in Volts per decade of the current density (V dec−1), which is extracted from the data of Fig. 1(A) by the procedure discussed in the ‘Methods section’. Up to a current density of 50 mA cm−2, the Au specimen shows an approximately constant Tafel slope (like ref. 51) of approximately 110 mV dec−1. Above 50 mA cm−2, a diverging Tafel slope can be observed, which is attributed to transport mechanisms that are related excessive bubble coverage of the specimen's surface. Koper et al.39 discussed these transport effects and their effect on electrochemical measurements in detail.
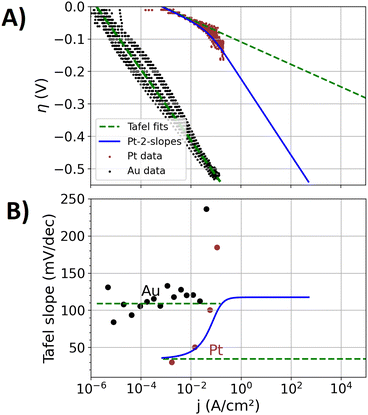 | ||
| Fig. 1 Kinetic analysis on the experimental data of the pure Au and Pt specimens (scatter) with Tafel fits (dashed green lines). The activity of the Pt component is in addition described by an empirical function that leads to two Tafel slopes (blue line, denoted as Pt-2-slopes), which shall represent a change of reaction mechanisms on the Pt surface-sites towards larger overpotentials. (A) Tafel plot. Higher resolution plots for the data on the Au and Pt specimen are supplied in the ESI,† respectively. (B) Tafel slopes as a function of the current density. | ||
In the case of the Pt specimen, the Tafel fit to the electrocatalytic data was conducted between overpotentials of −0.02 and −0.05 V. The Tafel slope of this fit is 36 mV dec−1. Tafel slopes of the HER on Pt are reported to depend on the surface orientation52 and accordingly also on preparation methods.53,54 Between −0.02 and 0 V, the small values of the overpotential are more prone to the measurement uncertainty of the reference electrode of approximately 3 mV. Moreover, in this overpotential-regime, the pseudo-capacitance of the H adsorption on Pt55 contributes to the measured current. At more negative overpotentials than −0.05 V, the electrochemical data deviates from the fit and the Tafel slope increases, similar to previously reported kinetics on Pt electrodes.52
Tafel slopes of 30, 40 and 120 mV dec−1 are commonly associated with the Tafel, Heyrovsky, and Volmer rate determining steps,56 respectively. The Tafel step represents the formation of a hydrogen molecule from two adsorbed hydrogen atoms, the Heyrovsky step describes the hydrogen molecule formation by one adsorped hydrogen atom and a proton from the solution, and the Volmer step represents the initial hydrogen adsorption at the catalyst. Between overpotentials of −0.05 and −0.02 V, the Tafel slope of approximately 36 mV dec−1 of the Pt specimen indicates Tafel and Heyrovsky rate determining steps. Towards more negative overpotentials, a growing contribution of the Volmer step to the rate determining step may explain the increase of the Tafel slope. However, also transport effects are expected to increase the Tafel slope. Different hydrophilicities on Au and Pt are expected to affect the bubble attachment and transport in different ways. In the case of the Au specimen, the bubble transport effects may be overshadowed by sluggish kinetics for which a more ideal Tafel relation results.
Two different approaches to describe the overpotential dependence of the current density jPt(η) at the Pt component are graphed in Fig. 1: (i) the classic Tafel equation in terms of eqn (3), denoted as “Pt-1-slope”. (ii) Two slopes in the Tafel plot that account for a mechanistic change of the HER as a function of the overpotential, denoted as “Pt-2-slopes”. This approach consists of an empirical function that aims to track the varying rate limiting steps on the Pt surface sites in the alloys as a function of the overpotential (detailed equation and parameterization given in the ESI†). Between overpotentials of −0.05 and −0.02 V, the values of both approaches for jPt(η) are similar (see detailed plot in ESI†) while more negative overpotentials lead to significant differences.
At more negative overpotentials than −0.05 V, the calculated data of the Pt-2-slopes approach does not exactly represent the average of the measured data on the Pt specimen in Fig. 1(A). The Pt-2-slopes approach is explicitly designed for the AuPt alloys, where the electrocatalytic mechanisms at high current densities are different from those of the pure Pt specimen. Moreover, isolated Pt atoms surrounded by Au atoms may also lead to a different bubble formation behavior than that at the pure Pt specimens. The most negative overpotential applied to an alloy specimen (discussed below) is −0.45 V, causing high local current densities on the Pt surface sites. Fig. 1(A) and (B) display this overpotential range and the related high local current density on Pt surface sites of the Pt-2-slopes approach.
Based on the measured activities of the pure metals, the activity of the alloys is described an interpolation procedure (IPP). Hereto, the activity of Au and Pt sites in the alloys are assumed to equal that in the pure metals. Hence, the alloy activity results from a linear combination of the current densities of the pure Au and Pt specimen multiplied by their mole fractions xPt and xAu = 1 − xpt, respectively. Thus, the mole fractions normalize the element-specific currents to their share of the surface area. The overall current density jalloy at the alloy is estimated by:
| jalloy(η) = xAujAu(η) + xPtjPt(η) | (5) |
The current density of the Au component jAu(η) in the alloys is calculated via the Tafel equation (see eqn (3)). To describe the Pt component, the above introduced two approaches to describe jPt(η) are incorporated into the IPP, in the following denoted as “IPP-Pt-1-slope” and “IPP-Pt-2-slopes”, respectively. The current densities jAu(η) and jPt(η) itself are independent of the alloy composition.
Fig. 2(A) shows the measured data on the alloy and pure metal specimens in a Tafel plot. The electrocatalytically activity of the alloys increases towards higher the Pt contents of the alloys. Above current densities of 40 mA cm−2, the bubble transport affects the measurements and lead to abrupt non-linear contributions in the Tafel plot. Fig. 2(B) shows the Tafel plots calculated via the IPPs. With the IPP-Pt-2-slopes approach the same trends and similar values as the measured data in Fig. 2(A) are calculated. In contrast, with the IPP-Pt-1-slope approach the electrocatalytic activities of the alloys are significantly overestimated. For example, at an overpotential of −0.35 V, a current density of approximately 27 mA cm−2 is measured for the alloy specimen with a Pt content of 0.33 at%. At this overpotential, the Tafel fit of Au leads to a current of 2.7 mA cm−2. With the Pt-1-slope description, the current density at pure Pt is calculated to jPt(−0.35 V) = 9.4 MA cm−2. Relating these currents to the surface composition viaeqn (5), a current density of jalloy(−0.35 V) = 31 kA cm−2 results with the IPP-Pt-1-slope approach. This value is apparently orders of magnitude higher than any applicable current density on polished electrodes. Using IPP-Pt-2-slopes approach, jPt(−0.35 V) = 12 A cm−2 results for pure Pt. In combination with the surface composition (eqn (5)) the current density carried by the Pt surface sites is calculated to 40 mA cm−2. Added to that of Au, a total current density of jalloy(−0.35 V) ≈ 43 mA cm−2 results, representing a reasonable estimation of the measured 27 mA cm−2. More detailed comparisons of the IPPs and the measured data follow below.
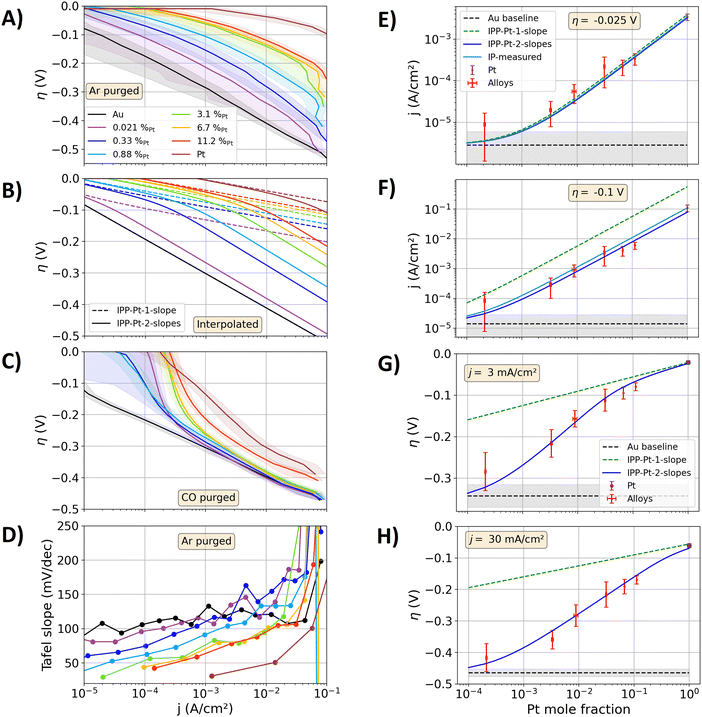 | ||
| Fig. 2 Measured and interpolated kinetics of the AuPt alloys. (A)–(C) Tafel plots for the HER on the polished metal specimens in 1 M HClO4. (A) Measurements, electrolyte purged with Ar. The solid lines represent the mean of three forward and backward scans, while the shaded areas represent the standard variation between these measurements. (B) Calculated alloy activities with the interpolation procedure based on the IPP-Pt-1-slope (dashed lines, one Tafel slope) and IPP-Pt-2-slope description (solid lines, two Tafel sloped) of jPt(η) from Fig. 1. (C) Same as A, but with CO purged electrolyte. (D) Tafel slopes extracted from the measurements graphed in (A). (E)–(H) Comparison of measured activities and the results of the interpolation procedures as a function of the Pt mole fraction. Black dashed line: mean of the Au measurements serving as a guide to the eye. Grey shadings: standard variation of the measurements on Au. Red scatters with error bars: measured data on the alloy samples. Brown scatters with error bars: data of the Pt specimen. Green dashed line: data of the IPP-Pt-1-slope approach. Solid blue lines: data of the IPP-Pt-2-slope approach. (E) and (F) Current densities at overpotentials of −0.025 and −0.1 V. Solid light blue line: interpolation between the measured Pt data and the Au Tafel fit at these overpotentials (denoted as IP-measured). (G) and (H) Overpotentials at current densities of 3 and 30 mA cm−2. | ||
Fig. 2(D) shows the measured Tafel slopes of all metal specimen as a function of the current density, where only the Au specimen shows a constant value. At low current densities, the lowest reliable Tafel slopes of the alloys show values of approximately 40 to 80 mV dec−1, which increase to values between 90 and 170 mV dec−1 at 20 mA cm−2. These variations of the Tafel slope result in non-linearities of the Tafel plots (compare to Fig. 2(A) and (B)). Hence, reliable Tafel fits to the kinetic data of the alloys are not possible. Consequently, the values of exchange current densities j0 (typically extracted from linear fits in the Tafel plot) cannot be reliably determined for the alloys.
In Fig. 2(E)–(H), the interpolated data of Fig. 2(B) are directly compared to the measured data from Fig. 2(A) as a function of the alloy composition. In Fig. 2(E), the interpolated and measured current densities are compared for an overpotential of −0.025 V. In addition to the above introduced IPP-Pt-1-slope and IPP-Pt-2-slopes approaches, the current densities for the alloys at −0.025 V were directly interpolated based on the graphed current densities on the pure Au and Pt specimens, respectively (for detailed calculation procedure see source code in the ESI†). This direct interpolation (light blue line in Fig. 2(E)) is denoted as “IP-measured”. Its outcome agrees with the values determined by the IPP-Pt-1slope and IPP-Pt-2-slopes approach. Hence, at the overpotential of −0.025 V, the activities of the alloys resemble a direct linear combination of those of its pure metal constituents.
In the highly diluted alloys neighboring Pt surface sites are unlikely, which hinders the hydrogen molecule formation at two neighboring Pt–Hads sites by the Tafel step. However, hydrogen atoms adsorped on Pt surface sites can diffuse to the Au surface sites, a phenomenon commonly known as spillover.57–59 Hence, the Tafel step may proceed via neighboring Pt–Hads and Au–Hads sites. However, such spillover from Pt to Au surface-sites is energetically uphill (see adsorption energies below), limiting the rates for such an active-site transfer. Alternatively, the hydrogen can be formed via the Heyrovsky step on Pt–Hads at an isolated Pt surface site with the same reaction step as that in the pure Pt specimen. With the small overpotential of −0.025 V, the impact of the different Tafel slopes of the reaction pathways negligibly contribute to the current densities. Moreover, Gasteiger et al.40 discussed that the kinetics of the HER on Pt catalysts are overshadowed by diffusion processes, which complicates an analysis of the reaction mechanisms with a Tafel slope analysis.
Fig. 2(F) shows the same comparison as that in Fig. 2(E) but for an overpotential of −0.1 V. At this overpotential, Fig. 1 showed significant differences between the Pt-1-slope and Pt-2-slope description for jPt(η). The IPP-Pt-1-slope approach significantly overestimates the measured current densities, while the current densities obtained with IP-measured approach match better to the alloy data. Using the IPP Pt 2-slopes approach, the best match to the experimental data is achieved. In Fig. 1(A), the results of the IPP-Pt-2-slope approach show slight deviations from the overpotential–current characteristic of the pure Pt specimen, as the empirical function for jPt(η) for the Pt-2-slopes approach was explicitly designed to describe the alloy data. In Fig. 2(F), the overpotential of −0.1 V is large enough to show these differences and their effect on the results of the IP-measured and IPP-Pt-2-slope approach. As discussed above, the reaction pathways may be not the same for the alloys and the pure Pt specimen. The more negative overpotential now amplifies the effect of the different Tafel slopes on the overpotential–current characteristic. Moreover, the discussed differences of the bubble detachment may significantly come into play at such large overpotentials, which are expected to affect the Pt surface in the alloys (described by IPP-Pt-2-slopes) differently than that at pure Pt (described by the IP-measured approach).
To compare the alloy activities at equal hydrogen production rates, Fig. 2(G) and (H) show measured and interpolated overpotentials for current densities of 3 mA cm−2 and 30 mA cm−2, respectively. The results of the IPP-Pt-1-slope approach show significantly smaller overpotentials for the alloys than those measured. In contrast, using IPP-Pt-2-slopes approach, the measured data is precisely described. In summary, the Fig. 2(E)–(H) show that the IPP-Pt-2-slopes approach can describe the measured alloy kinetics in a broad overpotential and current density window. Above, the example of the 0.33%Pt specimen at an overpotential of −0.35 V was discussed, in which the IPP-Pt-2-slope approach leads to jPt(−0.35 V) = 12 A cm−2. At this current density, Fig. 1(B) shows a Tafel slope close to 120 mV dec−1 for the IPP-Pt-2-slope, which may indicate that the Volmer step becomes the rate determining step for the HER at isolated Pt surface sites under high local current densities. By spillover of hydrogen initially adsorped on Pt surface sites to Au surface sites, the hydrogen molecule formation on Au surface sites may reduce the load on Pt surface sites regarding local transport limitations of the gas transport.
Fig. 2(C) shows the Tafel plots of the alloys that were obtained with CO purged electrolytes. The current at the Au specimen is negligibly affected by CO as it does not bond to the Au surface. In contrast, CO blocks Pt surface sites and thereby reduces their HER activity, so that in the range of the current density from 1 to 10 mA cm−2 (where the experimental shows the highest reliability) the specimens with a Pt content of 3.3% or less show similar activities to that of the Au specimen. Hence, the electrocatalytic activity of the Au surface sites are negligibly affected by the Pt doping and its effect on the bulk band structure.
The following main findings and conclusions can be drawn from the evaluation of the experimental data: (1) at overpotentials between −0.02 and −0.05 V, the measured alloy activities can be precisely described by a linear combination of those of the pure Au and Pt specimens normalized to the mole fractions (described by the IPP viaeqn (5)), respectively. (2) Towards more negative overpotentials, an increase of the Tafel slope at Pt surface sites is required to describe the measured data with the IPP. This change of the Tafel slope is attributed to altered reaction pathways and limitations of the bubble transport. (3) The exchange current density cannot be used as activity descriptor for the alloys, as it is not unambiguously defined due to continuously changing Tafel slopes (see Fig. 2(D)). Alternatively, overpotentials and current densities are suggested as two-dimensional activity descriptors, which directly represent the alloy kinetics based on the measurements. Hence, per definition, all physicochemical effects that contributed to the alloy activities are incorporated into the activity descriptor. (4) Blocking of Pt surface sites by CO drastically reduces the activities of the alloys (see Fig. 2(C)), leading to similar values of the overpotential–current relation between 1 and 10 mA cm−2 as that of the Au specimen. Hence, the influence of subsurface Pt-doping on the activity of Au surface sites is negligible.
DFT derived bonding strength descriptors
In the following, DFT-derived measures for the bonding strength on the AuPt alloys will be discussed. In Table 1, five unit cells with different concentrations and arrangements of Au and Pt atoms are defined, which serve as model systems for the DFT calculations. These model systems all show a (111) surface orientation. In the case of the face-centered cubic (fcc) crystal structure of Au, Pt, and their alloys, the (111) surface is typically considered as the most stable facet60 with the lowest surface energy.61 Hence, for the above experimentally examined polycrystalline alloys, the (111) facet is expected as the most prominent appearing surface-orientation. Other surface facets show different adsorption strengths.62,63 Moreover, the hydrogen adsorption at edges of the grains or steps is different than that on regular surface-sites.64 However, the different facets have less impact (typically <0.2 eV62,63) on the hydrogen adsorption energies than that of the different metal sites (>0.5 eV, see below). In addition, the trends for the hydrogen adsorption energies at the (111) surfaces across transition metals are partly transferable to other facets.63 Hence, the trends for the individual adsorption energies on the modeled (111) systems display rough estimations for those at the different facets of the measured polycrystalline alloys.Typically, four hydrogen adsorption sites are considered in the literature at the (111) surfaces,65 of which the top (hydrogen is placed on top of a surface atom) and the fcc (hydrogen located in a hollow formed by three surface atoms) sites are energetically favorable.31,66,67Table 2 shows computed hydrogen adsorption energies for two different cases of the hydrogen coverage: (i) the adsorption of one hydrogen atom on a top or fcc site and (ii) the mean adsorption of a full monolayer coverage at the fcc sites. The lower the value of the adsorption energy, the more exothermic is the hydrogen bond and the higher is the bonding strength. The computed hydrogen adsorption energies for the pure Au(111) and Pt(111) surfaces agree well with previously reported values.31,67,68 The bonding strength at Au surface sites neighboring a Pt surface site weakens from 0.35 eV for pure Au(111) to 0.39 eV. The adsorption energies on the more distant Au surface sites are not influenced by the Pt dopant. If Pt surface sites are accessible, the lowest hydrogen adsorption energy is found on top of them. The bonding strength of hydrogen at the Pt top sites is weakened from −0.43 eV for pure Pt to −0.35 eV for the 1Pt:Au(111) model system. This minor difference of the adsorption energies has probably a negligible effect on the electrocatalytic activities of Pt surface sites in the pure and alloyed systems. Hence, the DFT results on the hydrogen adsorption energies support the experimental findings of mostly composition independent electrocatalytic activities of Au and Pt surface sites at small overpotentials, respectively.
| Surface | Surface Pt [%] | Adsorption position | E ads at top site [eV] | E ads at fcc site [eV] | Mean Eads of 1 ML coverage at fcc [eV] |
|---|---|---|---|---|---|
| Au(111) | 0 | Au | 0.35 (0.30a) | 0.12 (0.13a, 0.14b) | 0.26 |
| 1Pt:Au(111) | 2.78 | Pt | −0.35 | −0.20 | 0.22 |
| Au (Pt-neighbor) | 0.39 | 0.16 | |||
| Au (more distant) | 0.35 | 0.11 | |||
| Pt(111) | 100 | Pt | −0.43 (−0.48c) | −0.49 (−0.54c, −0.46b) | −0.40 (−0.46c) |
| 1Pt:Au(111) subsurface | 0 | Au (above Pt) | 0.31 | 0.24 | 0.26 |
| 1Pt:Au(111)–COtop(Pt) | 2.78 | Au (Pt-neighbor) | 0.39 | 0.17 | 0.26 |
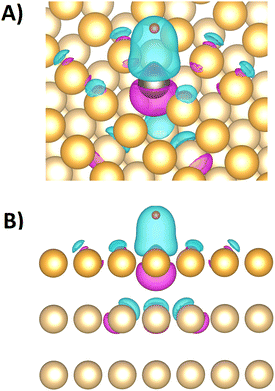
Sub-surface Pt doping slightly increases the bonding strength on the overlaying Au top site to 0.31 eV in comparison to the 0.35 eV of the pure Au model system, showing again a minor impact of adjacent atoms on the bonding strength at a specific surface site. When the Pt top sites are blocked with CO, hydrogen must adsorb at an Pt fcc site (if this is spatially accessible) or a neighboring Au site, both associated with lower bonding strengths. Hence, CO-blocked Pt surface-sites lose most of their catalytic activity, agreeing with the trends of the measured data in Fig. 2(C). Fig. 3 shows the electron density difference between the 1Pt:Au(111) surface models with and without an adsorbed hydrogen atom at the Pt top site. The electron density locally increases between the Pt site and the adsorped hydrogen, while it thins out at the Pt site towards the crystal lattice. Significant changes in electron density extend only up to the neighboring and next neighboring atoms in the crystal lattice, showing that the hydrogen adsorption influences the electronic states in the alloys mainly locally.
Total bonding strength vs. site-specific bonding strength
In Table 2, the mean adsorption energies of a full monolayer coverage of hydrogen are more positive than those of the single atom adsorption, as lateral repulsive adsorbate interactions reduce the bonding strength. As expected from negative adsorption energies at Pt sites vs. positive adsorption energies at Au sites, the adsorption strength for a full monolayer hydrogen coverage increases when Pt dopants are introduced. However, from a kinetic point of view, the principle of the least resistance is decisive for the catalytic activity, which states that the reaction will follow the lowest energy path.69 For instance, the mean hydrogen adsorption energy of the 1Pt:Au(111) model system is with 0.22 eV slightly lower than that of the Au(111) surface with 0.26 eV. However, the experimental data on the alloy specimen with a Pt content of 3.1 at% (similar Pt to Au surface atom ratio as the 1Pt:Au(111) model system) in Fig. 2(A) shows more than hundred times higher current densities than the Au specimen with respect to the same overpotential. This example shows that small amounts of Pt dopants have a small effect on the mean surface properties, whereas locally they make a substantial difference for the electrocatalytic properties. Thus, a proper bonding strength descriptor must include site-specific properties of the alloys instead of mean surface properties.d-Band density of states
With reference to the linear relation between d-band centers (DBCs) and adsorption energies described by the d-band model,20,21 DBCs are often used as easily accessible activity descriptors.70,71 The d-band model has been frequently applied to metal alloys and often a single DBC is reported for each alloy compound and related to activity descriptors.29,72–74 Rarely, contributions of single alloying metals are explicitly resolved in the framework of the d-band model.20,28,31,75 Nørskov et al.76 discussed that the DBC alone is a non-reliable measure for the activities of alloy catalysts as the states in the electronic structure closest to the Fermi level are most important for the catalytic activity. Hence, these authors introduced the upper d-band edge as another bonding strength descriptor that is derived from the band structure.76Fig. 4 shows the densities of states (DOS) projections to Au and Pt orbitals computed for the d-bands of the model unit cells in Table 1. The contributions of all layers and surface layers are considered separately while the d-band centers (DBCs) are marked. The projections are calculated with an atomic orbitals basis set, so that the individual contributions of both elements to the DOSs can be seen. The d-band centers are computed for Au and Pt states separately, or for the whole d-band, respectively. All atoms in the alloys contribute to the electronic band structure so that the total density of states of the 1Pt:Au(111) model systems with surface or subsurface Pt atoms are almost identical in Fig. 4. Yet, both cases show a drastically different lowest DFT-derived adsorption energies in Table 2. To avoid this obvious inconsistency, the d-band model is typically used with the surface atoms only to extract bonding strength measures.20,72,77 However, it is questionable whether local projections are a physically meaningful approach to describe the delocalized d-electrons in conductive metal alloys that can be approximated by the “free electron” model.
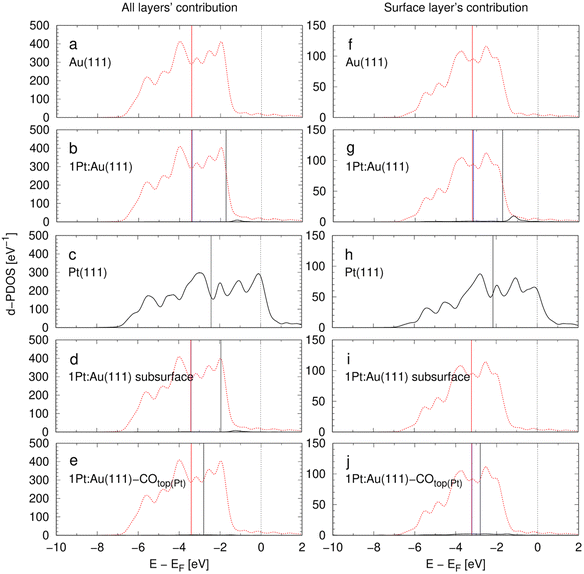 | ||
| Fig. 4 d-Projected DOS (d-DOS) of the 5d-states for the eight model systems introduced in Table 1. The Fermi level is at 0 eV. Left: d-DOS of all four layers of the surface slab. Right: Contributions of the surface layer to the d-DOS. Au 5d states and Pt 5d states are shown by red dashed and black full lines, respectively. Vertical black lines: d-band centers (DBCs) of the Pt components. Vertical red lines: DBCs of the Au components. Vertical blue lines (if not covered by the red or black lines): DBCs of all components in the alloys. | ||
Table 3 shows the d-band centers (DBCs) extracted from the DOS data of Fig. 4. The total DBC of Au(111) and 1Pt:Au(111) are almost equal as the low amount of Pt negligibly affects the overall d-band. However, the Pt site introduces a new state near the Fermi edge in Fig. 4, that is expected to drastically affect the catalytic activity, as described by Nørskovs upper d-band edge model.76 When the projection on the Pt component in the 1Pt:Au(111) system is considered, the DBC is with −1.73 eV significantly higher than the −3.16 eV of the total system. However, it is also 0.43 eV higher than that of the pure Pt(111) that has a value of −2.16 eV. In the framework of the d-band theory, this difference means that the Pt surface site in 1Pt:Au(111) has a higher hydrogen bonding strength than that in the pure Pt(111) system, which is contrary the adsorption energies calculated in Table 2. The Pt doping negligibly influences the Fermi level of the Au matrix, so that the DBC of the Pt component in this alloy shifts to higher values than that of pure Pt. This biasing of the relative energy level displays a systematic error that hinders precise bonding strength description for alloys from DOS data.
| Surface | Total DBC (eV) | Au DBC (eV) | Pt DBC (eV) | |
|---|---|---|---|---|
| Surface layer contributions only | Au(111) | −3.21 (−3.56) | −3.21 (−3.56) | — |
| 1Pt:Au(111) | −3.16 | −3.20 | −1.73 | |
| Pt(111) | −2.16 (−2.25) | — | −2.16 (−2.25) | |
| 1Pt:Au(111) subsurface | −3.21 | −3.21 | — | |
| 1Pt:Au(111)–COtop | −3.21 | −3.22 | −2.80 | |
| All layers contributions | Au(111) | −3.41 | −3.41 | — |
| 1Pt:Au(111) | −3.39 | −3.41 | −1.73 | |
| Pt(111) | −2.42 | — | −2.42 | |
| 1Pt:Au(111) subsurface | −3.40 | −3.41 | −1.94 | |
| 1Pt:Au(111)–COtop | −3.41 | −3.41 | −2.80 | |
Projections of the electronic band structure to specific sites or elements20,28,31,75 may correlate in one or the other way to the adsorption strength if new metrics such as the upper d-band edge are introduced76 and localized projections of delocalized electronic states are employed. However, as the adsorption shows a mostly local impact on the electron density (see Fig. 3) and the Pt dopant shows little effect on adsorption energies on distant Au sites (see Table 2), properties derived from the electronic band structure that describe delocalized conduction electrons in metals are not expected to meaningfully portray the localized nature of the adsorption. Moreover, the discussed offset of the Fermi level displays an intrinsic error of the d-band-derived metrics. Hence, the site-specific adsorption energies displayed in Table 2 are here preferred over the d-band-derived metrics as bonding strength descriptors.
The d-band model correlates the amount of bonding and anti-bonding orbitals with the position of the d-band center.15,19–21 The discussed results with the almost neighbor-independent adsorption energies indicate that the elemental properties in terms of the electronic orbitals of the surface atom itself are mostly responsible for the amount of bonding and anti-bonding states. Adjacent atoms have a minor impact on the properties of the adsorption site. For the pure metals, band structure and surface site adsorption are both significantly determined by the intrinsic orbital structure of the metal atoms. Thus, in pure metals, d-band properties directly correlate with the ability of surface sites to form bonding and anti-bonding orbitals. However, in the case of alloys, this correlation is distorted, so that the d-band properties do not correlate with adsorption properties any more. The atomic orbital interactions between surface sites and adsorbates (included in the DFT-derived adsorption energies) seem more precise and straightforward descriptors of bonding and anti-bonding states.
Volcano plots reinterpreted for alloy electrocatalysts
Volcano-type plots of the catalytic activity as a function of the bonding strength display an intuitive outcome of Sabatier's principle. In the case of the HER, the exchange current density is typically used as a descriptor for the kinetic activity in volcano plots.13–18 Above, the non-linear Tafel plots of the examined alloys (Fig. 2(A), (B), and (D)) were discussed to hinder a precise determination of the exchange current density. The bonding strength descriptors typically derived from electronic band structure properties and mean adsorption energies were unable to resolve the site-specific adsorption in alloys and their individual adsorption energies. Hence, standard volcano plots are obviously unable to portray the site-specific turnover-frequencies, site-specific adsorption energies, overpotential-dependent reaction mechanisms, and their respective interactions. To overcome these drawbacks, a novel multidimensional volcano plot will be introduced in the following, in which the measured overpotential–current relation will be used as a two-dimensional activity descriptor. The weighted adsorption energy will be introduced as a new bonding strength descriptor, accounting for the adsorption energies at the different surface sites as a function of their electrocatalytic utilization.Fig. 5A illustrates the current contributions of Pt surface sites to the overall current in the alloys, extracted from the previously presented results of the IPP-Pt-2-slopes approach. In the current density range between 1 and 100 mA cm−2 and for Pt contents above 0.88%, at least 97% of the produced hydrogen is formed on Pt surface sites. Towards lower Pt contents, the contributions of the Au surface-sites become more prominent.
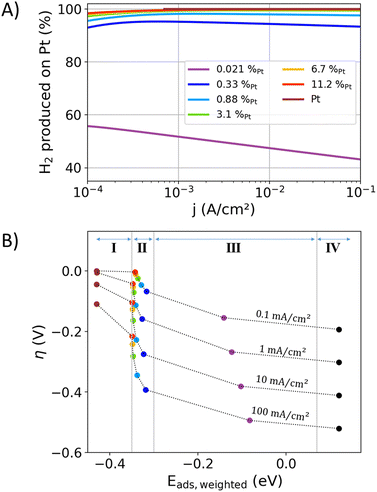 | ||
| Fig. 5 (A) The contributions of the Pt surface atoms to the overall current of the HER extracted from the “IPP-Pt-2-slopes” data from Fig. 1(C). (B) A four-dimensional volcano plot, in which the kinetics are represented by the overpotential (y-axis) and current density (dashed profile lines). The weighted adsorption energy Eads,weighted from eqn (6) is used as a bonding strength descriptor (x-axis), which averages the adsorption energies of hydrogen atoms that eventually react to hydrogen molecules. The fourth dimension is represented by the alloy composition (colored scatter). | ||
The current composition affects the combination of bonding strengths involved in the hydrogen evolution. The weighted adsorption energy Eads,weighted is here introduced as a bonding strength descriptor, aiming to relate the current composition with the site-specific adsorption energies EAuads and EPtads at the strongest bonding sites of the Au and Pt component (see Table 2), respectively. It is calculated as the arithmetic mean of the adsorption energies normalized to the current composition that is described by eqn (5):
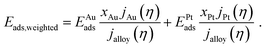 | (6) |
In the case of the AuPt alloys, the mechanistic change of the reaction at the Pt component (described by two Tafel slopes) influences Eads,weighted as a function of the mole fraction and the overpotential–current relation. A four-dimensional interplay of the weighted adsorption energy, mole fraction, current density, and overpotential results. Hence, the bonding strength descriptor interacts with the actual kinetic process, accounting for the dynamics of the surface site utilization by changing reaction pathways as a function of the overpotential. If hydrogen is adsorped on a Pt surface site and diffuses by spillover to an Au surface site, it is here counted as a contribution of the Pt surface site due to its higher bonding strength that initiated the reaction. Yet, with an approximately 0.7 eV lower adsorption strength of the hydrogen atom on Au than Pt sites (see Table 2), negligible rates for the spillover of an active-site transfer from Pt to Au are expected.
Fig. 5(B) shows the proposed reinterpretation of the volcano plot, using overpotential and current density as two-dimensional activity descriptors and Eads,weighted as descriptor for the bonding strength. For the discussed AuPt alloys only one flank in the four-dimensional volcano plot results (like ref. 18). Both flanks can occur when the interaction between the alloy-constituents significantly affect the electrocatalytic activity or bonding strength. The data in Fig. 5(B) is separated into four categories, which aim to show the interaction of the descriptors for the kinetics and bonding strengths: (I) the adsorption energies on Pt top sites are slightly impacted by alloying, from −0.43 eV for Pt and −0.35 eV for highly diluted Pt in Au matrix. Au surface-sites have a minor contribution to the produced hydrogen. Thus, Eads,weighted is dominated by the Pt sites. (II) The values of Eads,weighted increase towards higher current densities and lower Pt surface contents as more Au surface-sites are involved in the hydrogen production. The Pt component carries most of the current and is decisive for the most of the electrocatalytic activity. (III) In this region a significant proportion of the current is carried by the Au sites. The hydrogen formation on Au significantly increases Eads,weighted. In the case of the AuPt alloys, this region is only accessible with highly diluted alloys, in which the turnover frequency at Pt sites becomes comparable to the less active but more abundant Au sites. (IV) The average adsorption energy of pure Au with a negligible amount of Pt impurities.
When the model systems were previously introduced, the different adsorption energies on polycrystalline alloy facets and the (111) model surface were elucidated. With reference to this discussion, the adsorption energies derived from the model surfaces represent estimations for the bonding strength distributions on the many facets of the experimentally examined alloys. Hence, Fig. 5(B) shows rather qualitative data that aim to understand the interaction of surface-site occupation, alloy composition, mean adsorption energy, and the resulting electrocatalytic activity. A recent analysis of temperature-dependent electrocatalytic HER data revealed that the relation between adsorption energies and Butler–Volmer-kinetics is not yet fully resolved.78 In detail, the common assumptions to describe the impact of the bonding strength on j0 could not be aligned with activation energies derived from temperature-dependent electrocatalytic data.78 This discrepancy shows todays lack of understanding electrocatalytic interactions, however, the fundamental relation of bonding strength to activity described by Sabatier's principle is not doubted here. To summarize, the predictive strength of electrocatalytic alloy-properties with the proposed “volcano-plot” is limited due to the inability to model complex polycrystalline surfaces and unknown interactions that connect bonding strengths with catalytic properties.
An outlook for alloy electrocatalysts
Adsorbed hydrogen is the only reaction intermediate during the acidic HER. Hence, for this reaction, alloy catalysts are advantageous if electronic interactions between the alloy-constituents can significantly alter the hydrogen adsorption strengths at individual surface sites. For instance, electronic interactions of Fe dopings in a NiOOH matrix lead to a change of the spin state of the Fe ions79 that significantly affects bonding strengths at the Fe-sites and the activity for the alkaline oxygen evolution reaction.80 In contrast, if the adsorption strengths on the surface sites are mostly independent of the alloy composition (as in the case of the discussed AuPt alloys), the design of electrocatalysts can be improved in terms of the catalytic utilization of surface sites. With an abundant and cheap base metal, alloys with diluted Pt dopings can lead to highly utilized catalytic surface sites that resemble the concept of single atom electro-catalysts.81 For reactions with multiple reaction intermediates, site changes of adsorbates on alloy surfaces can lower the energy path of the reaction. In this case, the interaction of site-transfer rate and site-specific bonding strength of reaction intermediates can be included as additional dimensions in the proposed volcano plot to portray the electrocatalytic process of more complex electrocatalytic reactions on alloys.Conclusions
In this study, the role of d-band properties for the electrocatalytic activity of the HER was discussed for AuPt-alloys. These alloys display physicochemical model systems by providing oxide-free surfaces and profoundly different electrocatalytic activities of their constituents. For overpotentials between −0.02 and −0.05 V, the measured electrocatalytic data of the alloys were precisely described by linear combinations of the pure metals’ HER activities with respect to the alloy-composition. DFT calculations showed that the single hydrogen atom adsorption energies on Au and Pt surface sites are almost independent of neighboring metal atoms, respectively, reflecting the experimental findings of element-determined electrocatalytic activities. The DFT calculations also showed that the hydrogen adsorption affects the electron density only locally at the adsorption site. In contrast, the d-band describes delocalized electronic states. Consequently, the experimental findings of interpolate-able electrocatalytic activities of Au and Pt in the alloys could not be reasonably explained by their d-band properties. More negative overpotentials than −0.05 V caused non-linearity in the Tafel plots of the alloy specimens and the Pt specimen, which were ascribed to a utilization-dependent reaction mechanism at Pt surface site. Hence, the exchange current densities could not be determined for the alloys. Alternatively, the measured overpotential–current relations were used as two-dimensional activity descriptors. The weighted adsorption energy of hydrogen atoms was suggested as a bonding strength descriptor, which pays tribute to the site-specific adsorption energies and their share to current composition. Standard volcano plots are unable to portray the site-specific turnover-frequencies, site-specific adsorption energies, overpotential-dependent reaction mechanisms, and their interactions. Hence, a new type of multidimensional volcano plot was introduced, which relates the proposed novel kinetic and bonding strength descriptors with respect to their interaction and site-specificities.Author's contributions
MS designed and led the study, conducted the experiments, and provided analysis of the experimental data. MS and RE formulated the main conclusions. RT and PMK provided the DFT data and helped with their interpretation. MS and RT drafted the manuscript. All authors contributed to editing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the German Federal Ministry of Education and Research (BMBF) through the project DERIEL (03HY122C). Computational resources provided by the Jülich Aachen Research Alliance-Center for Simulation and Data Science (JARA-CSD, project JIEK61) are gratefully acknowledged. We thank Xinwei Zhu and Michael Eikerling of IEK-13 (Forschungszentrum Jülich) for the discussions on the interpretation of the measured potential–current relations.References
- E. Santos, P. Quaino and W. Schmickler, Theory of electrocatalysis: hydrogen evolution and more, Phys. Chem. Chem. Phys., 2012, 14, 11224–11233 RSC.
- J. O. Bockris and E. C. Potter, The Mechanism of the Cathodic Hydrogen Evolution Reaction, J. Electrochem. Soc., 1952, 99, 169 CrossRef CAS.
- Y. Zheng, Y. Jiao, M. Jaroniec and S. Z. Qiao, Advancing the electrochemistry of the hydrogen- Evolution reaction through combining experiment, Angew. Chem., Int. Ed., 2015, 54, 52–65 CrossRef CAS PubMed.
- M. Schalenbach, G. Tjarks, M. Carmo, W. Lueke, M. Mueller and D. Stolten, Acidic or alkaline? Towards a new perspective on the efficiency of water electrolysis, J. Electrochem. Soc., 2016, 163, F3197–F3208 CrossRef CAS.
- S. H. Jensen, P. H. Larsen and M. Mogensen, Hydrogen and synthetic fuel production from renewable energy sources, Int. J. Hydrogen Energy, 2007, 32, 3253–3257 CrossRef CAS.
- A. R. Zeradjanin, J. P. Grote, G. Polymeros and K. J. J. Mayrhofer, A Critical Review on Hydrogen Evolution Electrocatalysis: Re-exploring the Volcano-relationship, Electroanalysis, 2016, 28, 2256–2269 CrossRef CAS.
- N. Dubouis and A. Grimaud, The hydrogen evolution reaction: From material to interfacial descriptors, Chem. Sci., 2019, 10, 9165–9181 RSC.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. B. Chorkendorff and J. K. Nørskov, Computational high-throughput screening of electrocatalytic materials for hydrogen evolution, Nat. Mater., 2006, 5, 909–913 CrossRef CAS PubMed.
- C. C. L. McCrory, S. Jung, I. M. Ferrer, S. M. Chatman, J. C. Peters and T. F. Jaramillo, Benchmarking HER and OER Electrocatalysts for Solar Water Splitting Devices, J. Am. Chem. Soc., 2015, 137, 4347–4357 CrossRef CAS PubMed.
- A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, From the Sabatier principle to a predictive theory of transition-metal heterogeneous catalysis, J. Catal., 2015, 328, 36–42 CrossRef CAS.
- H. Ooka, J. Huang and K. S. Exner, The Sabatier Principle in Electrocatalysis: Basics, Limitations, and Extensions, Front. Energy Res., 2021, 9, 1–20 Search PubMed.
- Y. H. Fang and Z. P. Liu, Tafel kinetics of electrocatalytic reactions: From experiment to first-principles, ACS Catal., 2014, 4, 4364–4376 CrossRef CAS.
- R. Parsons, The Rate of Electrolytic Hydrogen Evolution and the Heat of Adsorption of Hydrogen, Trans. Faraday Soc., 1958, 54, 1053–1063 RSC.
- B. E. Conway and J. O. Bockris, The d-Band Character of Metals and the Rate and Mechanism of the Electrolytic Hydrogen Evolution Reaction, Nature, 1956, 178, 448–489 Search PubMed.
- S. Trasatti, Work function, electronegativity, and electrochemical behaviour of metals III. Electrolytic hydrogen evolution in acid solutions, J. Electroanal. Chem. Interfacial Electrochem., 1972, 39, 163–184 CrossRef CAS.
- J. Norskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, Trends in the Exchange Current for Hydrogen Evolution, J. Electrochem. Soc., 2005, 152, J23–J26 CrossRef CAS.
- W. Schmickler and S. Trasatti, Comment on ‘Trends in the Exchange Current for Hydrogen Evolution’ [J. Electrochem. Soc., 152, J23 (2005)], J. Electrochem. Soc., 2006, 153, L31–L32 CrossRef CAS.
- P. Quaino, F. Juarez, E. Santos and W. Schmickler, Volcano plots in hydrogen electrocatalysis – uses and abuses, Beilstein J. Nanotechnol., 2014, 5, 846–854 CrossRef PubMed.
- M. Andersen, Revelations of the d band, Nat. Catal., 2023, 6, 460–461 CrossRef.
- B. Hammer and J. K. Norskov, Why gold is the noblest of all the metals, Nature, 1995, 376, 238–240 CrossRef CAS.
- B. Hammer and J. K. Nørskov, Electronic factors determining the reactivity of metal surfaces, Surf. Sci., 1995, 343, 211–220 CrossRef CAS.
- A. B. Laursen, R. B. Wexler, M. J. Whitaker, E. J. Izett, K. U. D. Calvinho, S. Hwang, R. Rucker, H. Wang, J. Li, E. Garfunkel, M. Greenblatt, A. M. Rappe and G. C. Dismukes, Climbing the Volcano of Electrocatalytic Activity while Avoiding Catalyst Corrosion: Ni3P, a Hydrogen Evolution Electrocatalyst Stable in Both Acid and Alkali, ACS Catal., 2018, 8, 4408–4419 CrossRef CAS.
- F. Safizadeh, E. Ghali and G. Houlachi, Electrocatalysis developments for hydrogen evolution reaction in alkaline solutions – A Review, Int. J. Hydrogen Energy, 2015, 40, 256–274 CrossRef CAS.
- A. R. Akbashev, Electrocatalysis Goes Nuts, ACS Catal., 2022, 12, 4296–4301 CrossRef CAS.
- M. Schalenbach, F. D. Speck, M. Ledendecker, O. Kasian, D. Goehl, A. M. Mingers, B. Breitbach, H. Springer, S. Cherevko and K. J. J. Mayrhofer, Nickel-Molybdenum alloy catalysts for the hydrogen evolution reaction: Activity and stability revised, Electrochim. Acta, 2017, 259, 1154–1161 CrossRef.
- H. Wolfschmidt, D. Weingarth and U. Stimming, Enhanced reactivity for hydrogen reactions at pt nanoislands on Au(111), ChemPhysChem, 2010, 11, 1533–1541 CrossRef CAS PubMed.
- P. J. Schäfer and L. A. Kibler, Incorporation of Pd into Au(111): Enhanced electrocatalytic activity for the hydrogen evolution reaction, Phys. Chem. Chem. Phys., 2010, 12, 15225–15230 RSC.
- P. Quaino, E. Santos, H. Wolfschmidt, M. A. Montero and U. Stimming, Theory meets experiment: Electrocatalysis of hydrogen oxidation/evolution at Pd-Au nanostructures, Catal. Today, 2011, 177, 55–63 CrossRef CAS.
- J. Greeley and M. Mavrikakis, Alloy catalysts designed from first principles, Nat. Mater., 2004, 3, 810–815 CrossRef CAS PubMed.
- X. B. Li, T. Cao, F. Zheng and X. Chen, Computational Screening of Electrocatalytic Materials for Hydrogen Evolution: Platinum Monolayer on Transitional Metals, J. Phys. Chem. C, 2019, 123, 495–503 CrossRef CAS.
- S. Venkatachalam and T. Jacob, Hydrogen adsorption on Pd-containing Au(111) bimetallic surfaces, Phys. Chem. Chem. Phys., 2009, 11, 3263–3270 RSC.
- J. Greeley and J. K. Nørskov, Combinatorial Density Functional Theory-Based Screening of Surface Alloys for the Oxygen Reduction Reaction, J. Phys. Chem. C, 2009, 4932–4939 CrossRef CAS.
- J. Wang, S. Xin, Y. Xiao, Z. Zhang, Z. Li, W. Zhang, C. Li, R. Bao, J. Peng, J. Yi and S. Chou, Manipulating the Water Dissociation Electrocatalytic Sites of Bimetallic Nickel-Based Alloys for Highly Efficient Alkaline Hydrogen Evolution, Angew. Chem., Int. Ed., 2022, 61, e202202518 CrossRef CAS PubMed.
- P. Kuang, Z. Ni, B. Zhu, Y. Lin and J. Yu, Modulating the d-Band Center Enables Ultrafine Pt3Fe Alloy Nanoparticles for pH-Universal Hydrogen Evolution Reaction, Adv. Mater., 2023, 35, 1–11 CrossRef PubMed.
- M. E. Björketun, G. S. Karlberg, J. Rossmeisl, I. Chorkendorff, H. Wolfschmidt, U. Stimming and J. K. Nørskov, Hydrogen evolution on Au(111) covered with submonolayers of Pd, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 1–9 CrossRef.
- J. A. Santana and J. Meléndez-Rivera, Hydrogen adsorption on au-supported pt and pd nanoislands: A computational study of hydrogen coverage effects, J. Phys. Chem. C, 2021, 125, 5110–5115 CrossRef CAS PubMed.
- K. P. Kepp, Chemical Causes of Metal Nobleness, ChemPhysChem, 2020, 21, 360–369 CrossRef CAS PubMed.
- H. Okamoto and T. B. Massalski, The Au–Pt (Gold-Platinum) system, Bull. Alloy Phase Diagrams, 1985, 6, 46–56 CrossRef CAS.
- O. van der Heijden, S. Park, J. J. J. Eggebeen and M. T. M. Koper, Non-Kinetic Effects Convolute Activity and Tafel Analysis for the Alkaline Oxygen Evolution Reaction on NiFeOOH Electrocatalysts, Angew. Chem., Int. Ed., 2023, 135, 1–9 CrossRef.
- W. Sheng, H. A. Gasteiger and Y. Shao-Horn, Hydrogen Oxidation and Evolution Reaction Kinetics on Platinum: Acid vs Alkaline Electrolytes, J. Electrochem. Soc., 2010, 157, B1529 CrossRef CAS.
- M. Schalenbach, L. Raijmakers, V. Selmert, A. Kretzschmar, Y. E. Durmus, H. Tempel and R.-A. Eichel, How Microstructures, Oxide Layers, and Charge Transfer Reactions influence Double Layer Capacitances. Part 1: Impedance Spectroscopy and Cyclic Voltammetry to estimate Electrochemically Active Surface Areas (ECSAs), Phys. Chem. Chem. Phys., 2024, 20, 1 Search PubMed.
- H. L. Skriver and N. M. Rosengaard, Surface energy and work function of elemental metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 7157–7168 CrossRef CAS PubMed.
- L. Vitos, A. V. Ruban, H. L. Skriver and J. Kollár, The surface energy of metals, Surf. Sci., 1998, 411, 186–202 CrossRef CAS.
- M. Otani and O. Sugino, First-principles calculations of charged surfaces and interfaces: A plane-wave nonrepeated slab approach, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 1–11 CrossRef.
- T. T. T. Hanh, Y. Takimoto and O. Sugino, First-principles thermodynamic description of hydrogen electroadsorption on the Pt(111) surface, Surf. Sci., 2014, 625, 104–111 CrossRef CAS.
- H. Steininger, S. Lehwald and H. Ibachi, On the adsorption of CO on Pt(111), Surf. Sci. Lett., 1982, 123, A453 CrossRef.
- G. S. Blackman, M.-L. Xu, D. F. Ogletree, M. A. Van Hove and G. A. Somorjai, Mix of Molecular Adsorption Sites Detected for Disordered CO on Pt(111) by Diffuse Low-Energy Electron Diffraction, Phys. Rev. Lett., 1988, 61, 2352–2355 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 1–19 CrossRef PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, Rationale for mixing exact exchange with density functional approximations, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- J. Ferez, E. R. Gonzalez and H. M. Villuiias, Hydrogen evolution reaction on gold single-crystal electrodes in acid solutions, J. Phys. Chem. B, 1998, 102, 10931–10935 CrossRef.
- N. M. Marković, B. N. Grgur and P. N. Ross, Temperature-dependent hydrogen electrochemistry on platinum low-index single-crystal surfaces in acid solutions, J. Phys. Chem. B, 1997, 101, 5405–5413 CrossRef.
- V. Climent and J. M. Feliu, Thirty years of platinum single crystal electrochemistry, J. Solid State Electrochem., 2011, 15, 1297–1315 CrossRef CAS.
- J. O’M Bockris, The mechanism of the hydrogen evolution reaction on platinum, silver, and tungsten surfaces in acid solutions, J. Phys. Chem., 1957, 61, 976 Search PubMed.
- M. Schalenbach, Y. E. Durmus, H. Tempel, H. Kungl and R. A. Eichel, The role of the double layer for the pseudocapacitance of the hydrogen adsorption on platinum, Sci. Rep., 2022, 12, 1–10 CrossRef PubMed.
- T. Shinagawa, A. T. Garcia-Esparza and K. Takanabe, Insight on Tafel slopes from a microkinetic analysis of aqueous electrocatalysis for energy conversion, Sci. Rep., 2015, 5, 1–21 Search PubMed.
- M. Eikerling, J. Meier and U. Stimming, Hydrogen evolution at a single supported nanoparticle: A kinetic model, Z. Phys. Chem., 2003, 217, 395–414 CrossRef CAS.
- S. J. Gutić, A. S. Dobrota, E. Fako, N. V. Skorodumova, N. López and I. A. Pašti, Hydrogen evolution reaction-from single crystal to single atom catalysts, Catalysts, 2020, 10, 1–38 CrossRef.
- R. Guo, X. Xu, Y. Xia, W. Huang, Z. Li and B. Teng, Insights into electrocatalytic hydrogen evolution reaction in acidic medium at in-situ dispersed Pt atoms on nanoporous gold films, J. Catal., 2018, 368, 379–388 CrossRef CAS.
- D. J. S. Sandbeck, O. Brummel, K. J. J. Mayrhofer, J. Libuda, I. Katsounaros and S. Cherevko, Dissolution of Platinum Single Crystals in Acidic Medium, ChemPhysChem, 2019, 20, 2997–3003 CrossRef CAS PubMed.
- D. Opalka, C. Scheurer and K. Reuter, Ab Initio Thermodynamics Insight into the Structural Evolution of Working IrO2 Catalysts in Proton-Exchange Membrane Electrolyzers, ACS Catal., 2019, 9, 4944–4950 CrossRef CAS.
- M. J. Kolb, F. Calle-Vallejo, L. B. F. Juurlink and M. T. M. Koper, Density functional theory study of adsorption of H2O, H, O, and OH on stepped platinum surfaces, J. Chem. Phys., 2014, 140(13), 134708 CrossRef PubMed.
- P. Ferrin, S. Kandoi, A. U. Nilekar and M. Mavrikakis, Hydrogen adsorption, absorption and diffusion on and in transition metal surfaces: A DFT study, Surf. Sci., 2012, 606, 679–689 CrossRef CAS.
- D. Nelli, V. Mastronardi, R. Brescia, P. P. Pompa, M. Moglianetti and R. Ferrando, Hydrogen Promotes the Growth of Platinum Pyramidal Nanocrystals by Size-Dependent Symmetry Breaking, Nano Lett., 2023, 23, 2644–2650 CrossRef CAS PubMed.
- Z. H. Zeng, J. L. F. Da Silva, H. Q. Deng and W. X. Li, Density functional theory study of the energetics, electronic structure, and core-level shifts of NO adsorption on the Pt(111) surface, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 1–13 Search PubMed.
- A. M. Pessoa, J. L. C. Fajín, J. R. B. Gomes and M. N. D. S. Cordeiro, Ionic and radical adsorption on the Au(hkl) surfaces: A DFT study, Surf. Sci., 2012, 606, 69–77 CrossRef CAS.
- I. Hamada and Y. Morikawa, Density-functional analysis of hydrogen on Pt(111): Electric field, solvent, and coverage effects (Journal of Physical Chemistry C (2008) 112C (10897)), J. Phys. Chem. C, 2008, 112, 17486 CrossRef CAS.
- W. Sheng, M. Myint, J. G. Chen and Y. Yan, Correlating the hydrogen evolution reaction activity in alkaline electrolytes with the hydrogen binding energy on monometallic surfaces, Energy Environ. Sci., 2013, 6, 1509–1512 RSC.
- M. Jørgensen and H. Grönbeck, Perspectives on Computational Catalysis for Metal Nanoparticles, ACS Catal., 2019, 9, 8872–8881 CrossRef.
- J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Density functional theory in surface chemistry and catalysis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943 CrossRef PubMed.
- L. Kristinsdóttir and E. Skúlason, A systematic DFT study of hydrogen diffusion on transition metal surfaces, Surf. Sci., 2012, 606, 1400–1404 CrossRef.
- A. Ruban, B. Hammer, P. Stoltze, H. L. Skriver and J. K. Nørskov, Surface electronic structure and reactivity of transition and noble metals, J. Mol. Catal. A, 1997, 115, 421–429 CrossRef CAS.
- V. R. Stamenkovic, B. S. Mun, M. Arenz, K. J. J. Mayrhofer, C. A. Lucas, G. Wang, P. N. Ross and N. M. Markovic, Trends in electrocatalysis on extended and nanoscale Pt-bimetallic alloy surfaces, Nat. Mater., 2007, 6, 241–247 CrossRef CAS PubMed.
- M. Paßens, V. Caciuc, N. Atodiresei, M. Moors, S. Blügel, R. Waser and S. Karthäuser, Tuning the surface electronic structure of a Pt3Ti(111) electro catalyst, Nanoscale, 2016, 8, 13924–13933 RSC.
- H. Thirumalai and J. R. Kitchin, Investigating the Reactivity of Single Atom Alloys Using Density Functional Theory, Top. Catal., 2018, 61, 462–474 CrossRef CAS.
- H. Xin, A. Vojvodic, J. Voss, J. K. Nørskov and F. Abild-Pedersen, Effects of d-band shape on the surface reactivity of transition-metal alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 1–5 CrossRef.
- T. Jiang, D. J. Mowbray, S. Dobrin, H. Falsig, B. Hvolbœk, T. Bligaard and J. K. Nørskov, Trends in CO oxidation rates for metal nanoparticles and close-packed, stepped, and kinked surfaces, J. Phys. Chem. C, 2009, 113, 10548–10553 CrossRef CAS.
- A. R. Zeradjanin, P. Narangoda, J. Masa and R. Schlögl, What Controls Activity Trends of Electrocatalytic Hydrogen Evolution Reaction? Activation Energy Versus Frequency Factor, ACS Catal., 2022, 12, 11597–11605 CrossRef CAS.
- Z. Da He, R. Tesch, M. J. Eslamibidgoli, M. H. Eikerling and P. M. Kowalski, Low-spin state of Fe in Fe-doped NiOOH electrocatalysts, Nat. Commun., 2023, 14, 1–9 Search PubMed.
- L. Trotochaud, S. L. Young, J. K. Ranney and S. W. Boettcher, Nickel-Iron Oxyhydroxide Oxygen-Evolution Electrocatalysts: The Role of Intentional and Incidental Iron Incorporation, J. Am. Chem. Soc., 2014, 136, 6744–6753 CrossRef CAS PubMed.
- N. Cheng, S. Stambula, D. Wang, M. N. Banis, J. Liu, A. Riese, B. Xiao, R. Li, T. K. Sham, L. M. Liu, G. A. Botton and X. Sun, Platinum single-atom and cluster catalysis of the hydrogen evolution reaction, Nat. Commun., 2016, 7, 1–9 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Blueprint of the electrochemical flow cell; manufacturing of the alloys; composition analysis of the alloys via ICP-OES and EDS; XRD characterization of the alloys; detailed Tafel analysis of the Au and Pt specimen; codes for the presented interpolation procedure (IPP) and data treatment. See DOI: https://doi.org/10.1039/d4cp01084a |
| This journal is © the Owner Societies 2024 |