Open Access Article
Open Access ArticleSurface phase diagrams from nested sampling†
Mingrui
Yang
 a,
Livia B.
Pártay
a,
Livia B.
Pártay
 b and
Robert B.
Wexler
b and
Robert B.
Wexler
 *a
*a
aDepartment of Chemistry and Institute of Materials Science and Engineering, Washington University in St. Louis, St. Louis, MO 63130, USA. E-mail: wexler@wustl.edu
bDepartment of Chemistry, University of Warwick, Coventry, CV4 7AL, UK
First published on 17th April 2024
Abstract
Studies in atomic-scale modeling of surface phase equilibria often focus on temperatures near zero Kelvin due to the challenges in calculating the free energy of surfaces at finite temperatures. The Bayesian-inference-based nested sampling (NS) algorithm allows for modeling phase equilibria at arbitrary temperatures by directly and efficiently calculating the partition function, whose relationship with free energy is well known. This work extends NS to calculate adsorbate phase diagrams, incorporating all relevant configurational contributions to the free energy. We apply NS to the adsorption of Lennard-Jones (LJ) gas particles on low-index and vicinal LJ solid surfaces and construct the canonical partition function from these recorded energies to calculate ensemble averages of thermodynamic properties, such as the constant-volume heat capacity and order parameters that characterize the structure of adsorbate phases. Key results include determining the nature of phase transitions of adsorbed LJ particles on flat and stepped LJ surfaces, which typically feature an enthalpy-driven condensation at higher temperatures and an entropy-driven reordering process at lower temperatures, and the effect of surface geometry on the presence of triple points in the phase diagrams. Overall, we demonstrate the ability and potential of NS for surface modeling.
1 Introduction
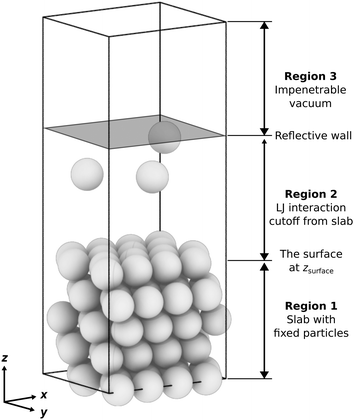
The structure and composition of solid surfaces play an essential role in determining their properties for various high-stakes applications, including gas sensing1 and optoelectronics,2 in addition to those central to mitigating the effects of climate change, such as photovoltaics3 and catalysis. For the latter, studies show that operando surface reconstruction, i.e., changes in the structure and composition of the topmost layers of a solid, can govern the activity and selectivity of heterogeneous catalysts for the CO2 reduction,4,5 H2 evolution,6–8 O2 evolution,9–11 and O2 reduction reactions,12 to name a few examples. Therefore, designing catalysts for these reactions and functional materials for other surface-specific processes requires an atomic-scale understanding of surface reconstruction and its dependence on operating conditions. However, the experiments that can measure these properties are typically done under conditions that differ from operating conditions,13 with only a few exceptions.14To fulfill the need for atomic-scale information about operando surface phases, the field has often turned to computer simulations, which typically fall under one of three categories: thermodynamic, optimization-based, and statistical thermodynamic approaches. The most notable example of the former is ab initio surface thermodynamics, pioneered by Scheffler and coworkers.15–17 In this approach, one uses quantum-mechanics-based simulation techniques to calculate the grand potentials per unit surface area for a set of slabs, the structures and compositions of which are typically guided by chemical and physical intuition (see Fig. 1 for an example of a surface slab model). The resulting surface grand potentials are usually approximate because only those finite-temperature effects associated with the enthalpy and entropy of harmonic vibrations are included, if at all. The contributions due to anharmonic vibrations and, more generally, configurational degrees of freedom are commonly ignored18 (except for gas phases, where reference measurements or the ideal gas equation of state have been used) to make surface calculations computationally tractable, especially when employing an ab initio-based description of the chemical bonds, such as density functional theory.
While ab initio thermodynamics can be insightful, in the absence of input from careful measurements, the variety of possible surface structures one must intuit is unclear. Optimization-based approaches have shown promise in more comprehensively navigating the ambiguity of surface phase space. These include enumerating mean-field configurations,19 random structure searching,20 simulated annealing,21 basin hopping,22 global activity search,23 stochastic surface walking,24 evolutionary/genetic algorithms,25–28 particle swarm optimization,29 active learning,30 and reinforcement learning.31 The methods above guide the search for structures that minimize the zero-Kelvin surface energy as a function of composition, which are used as inputs for ab initio thermodynamics in the grand canonical ensemble. Recent studies have increasingly employed (Markov chain) Monte Carlo (MC) simulations in various ensembles, such as canonical,32 grand canonical,33–36 and semi-grand canonical,37 to facilitate the discovery of operando surface phases. These simulations leverage the Metropolis–Hastings algorithm, allowing efficient sampling from specific probability distributions within defined thermodynamic constraints. This approach is particularly effective for potential energy surfaces (PESs) characterized by shallow wells. However, it encounters limitations in systems with deep potential wells, where ergodicity can be broken. This results in simulations that heavily depend on initial conditions and may not comprehensively explore configuration space. Consequently, accurately calculating the free energy in such systems remains a complex task. In these scenarios, generating accurate surface phase diagrams is challenging unless it is established that entropic contributions are minimal.
Recently, Zhou, Scheffler, and Ghiringhelli introduced an approach to efficiently estimate the free energy of surfaces from replica-exchange (RE) grand-canonical sampling and the multi-state Bennett acceptance ratio method.18 Their algorithm marks a notable advancement in computational surface science, especially with the inclusion of anharmonic contributions to free energy. It is interesting to consider that calculating free energy involves an integral over the phase space volume. Therefore, employing a sampling grid based on phase space volume, in contrast to the temperature-based approach used in RE and the energy-based approach used in Wang–Landau sampling,38,39 could provide a more accurate and efficient approach to sampling near and away from surface phase transitions. This method offers the advantage of not requiring prior knowledge of the stable phases,40 further enhancing the already significant capabilities of the RE approach. We propose an alternative approach based on nested sampling (NS), which constructs a set of slabs equidistant in the natural logarithm of surface phase space volume. NS was first introduced in Bayesian statistics,41,42 and was later adopted by various research fields43 and adapted to sample the PES of atomic-scale systems.40,44,45 The power of NS has been demonstrated in studying various systems, including the formation of clusters,46,47 calculation of the quantum partition function,48 sampling transition paths,49 as well as computing the pressure–temperature phase diagram for various metals, alloys, and model potentials,50–54 which often identified previously unknown stable solid phases.
This study uses NS to calculate coverage-temperature adsorbate phase diagrams, a subset of surface phase diagrams, as a proof of concept for future investigations of more complex material interfaces and interfacial conditions. Here, “coverage” follows the standard definition as the ratio between the number of adsorbed particles on a surface and the number of particles in a filled monolayer (ML) on that surface. We carry out NS for surfaces of the Lennard-Jones (LJ) solid, constructing the canonical partition function from potential energy values recorded while compressing the natural logarithm of the adsorbate phase space volume by a constant factor at each iteration. While a considerable body of research exists on the LJ system, much of this work has concentrated on its bulk solid (for example, see ref. 55–57) and fluid phases (for example, see ref. 58–60), as well as the physical properties of its bulk-terminated surfaces (for example, see ref. 61–63). Significant progress has been made in understanding these aspects.
Nonetheless, the comprehensive examination of coverage-temperature adsorbate phase diagrams for LJ solids, especially beyond two-dimensional models and simpler lattice frameworks, presents an opportunity for further exploration. This aspect has not been as extensively covered as other areas, as seen in the more focused research that primarily addressed two-dimensional cases (for example, see ref. 64–68). Our approach differs by sampling a continuum of particle positions within the canonical ensemble rather than discretized particle positions (i.e., a lattice gas model) in the grand canonical ensemble.69–71 While the grand canonical ensemble offers insights more directly pertinent to catalyst design, employing the canonical ensemble is more computationally efficient. This efficiency is particularly beneficial in reducing the computational demands associated with benchmarking surface NS. Our work thus contributes to a more nuanced understanding of the LJ system, complementing existing research while exploring new and potentially fruitful areas.
Utilizing the constructed canonical partition function, we compute ensemble averages of thermodynamic properties such as the constant-volume heat capacity and order parameters that describe the structure of adsorbate phases. For simplicity, the particles in the solid are not allowed to move; thus, the surface is not allowed to relax or reconstruct under the influence of the adsorbed particles. Such simplification ensures that only the direct interplay between adsorbed particles and the surface is captured, providing a clearer picture of the adsorption processes. More details are included in Section 2. Notably, we identify phase transitions of the adsorbed particles on both flat and stepped surfaces. Most flat surfaces exhibit an enthalpy-driven condensation at higher temperatures, an entropy-driven reordering process within the condensed layer at lower temperatures, and a coverage above which a disordered adsorbate phase is unstable. Ultimately, we showcase the capabilities and potential of NS for surface modeling.
2 Computational methods
2.1 Nested sampling
Previous studies have detailed NS, outlining its use in studying clusters at constant volume40,72 and bulk materials at constant pressure;44,45 here, we will concentrate on adsorbates at constant volume. In our study, we differentiate between particles that make up the surface and those that adsorb or condense onto it. The adsorbing particles, which we term free particles, can move and change position, even when condensed on the surface. In contrast, fixed particles refer to those in the fixed structure of the surface, which do not change position during sampling. This distinction helps to simplify our model system, focusing on the key interactions between mobile free particles and the static surface. With the primary objective of establishing proof of concept, we have prioritized simplicity to eliminate potential complexities that could obscure the phenomena of interest.
Once the initial walkers are generated, the iterative part of the sampling proceeds as follows:
1. Identify and record the walker with the highest potential energy, denoted as Emaxi = max{E}. The phase space volume, Γ, of the PES below Emaxi is given by Γi = [K/(K + 1)]i.40
2. Replace the highest-potential-energy walker with a new walker, where the particle positions of the new configuration are chosen randomly, but such that Enew < Emaxi. As configurations with lower potential energy are sampled, the available phase space volume shrinks. Consequently, the probability of generating an acceptable random walker diminishes. Hence, we generate a new walker by cloning a randomly selected existing walker. We then employ rejection sampling to conduct a random walk in configuration space, ensuring the walker's potential energy remains below Emaxi. This process effectively decorrelates the new configuration, making it statistically independent of its starting point.
3. Let i ← i + 1 and return to Step 1.
Once sufficiently low-potential-energy regions of configuration space are explored, NS can stop, and using the set of recorded potential energy values from the replaced walkers, we can calculate the canonical partition function, Z, as
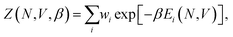 | (1) |
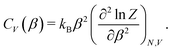 | (2) |
To determine the peak positions on the CV(β) curve – and hence the adsorbate phase transition temperatures – for different coverages, we used the scipy.signal.find_peaks() function with prominence = 0.02 to automatically find peaks for each CV curve. We then manually connected adjacent peaks for neighboring coverages to construct a coverage-temperature phase diagram.
With access to the canonical partition function, we can also calculate the ensemble average of any configuration-dependent property, A(ri), at a given temperature, β, as
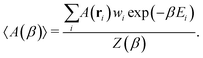 | (3) |
We calculate surface order parameters to gain insight into the structural phase transitions of LJ surfaces. These include the average vertical position of the free particles relative to that of the fixed surface particles, 〈Δz〉 = 〈zfree〉 − zsurface, and the average coordination number of the free particles, 〈CN〉, including free-free and free-fixed particle–particle bonds.
The probability Pi of sampling configuration i from the canonical ensemble is used to identify representative equilibrium structures of the system at a specific temperature. The calculation is performed using the following equation:
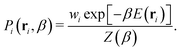 | (4) |
In this equation, E(ri) is used to emphasize that the potential energy E is determined by the particle positions r of configuration i. The structure that maximizes Pi at a given temperature β is thus the most likely to occur at that temperature. However, it is important to note that there can be numerous structures with probabilities close to the maximum, especially in stable high-entropy phases and at phase boundaries. Leveraging the recorded potential energy values for the replaced walkers in the NS method could also allow for constructing an optimal ensemble representation of fluxional catalytic interfaces32,73,74 in the thermodynamic limit.
2.2 Simulation details
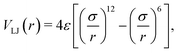 | (5) |
• Region 1: a slab with fixed particles and a thickness of approximately 4σ, depending on the surface features, e.g., flat or stepped. The slab comprises several layers, each containing an identical count of particles. These layers are characterized by a fixed interlayer spacing, which varies based on the surface features. For a more detailed and quantitative description of different slab geometries, refer to Table S1 in the ESI.†
• Region 2: a space that extends 4σ above the fixed slab, where the free particles can interact with the fixed slab and each other. The initial walkers are randomly and uniformly drawn from configurations in this region. We limit the space to a thickness of ≤4σ (i.e., the value of the LJ cutoff radius) to exclude any space where the free particles do not interact with the slab (we call these “voids”, see Section S2, ESI†). For systems having only one or two free particles or a disproportionately large gas phase region where the particles fall outside the interaction range of the surface, the sampling can struggle to find configurations with lower energies. In this case, additional measures could be necessary to ensure that NS proceeds to subsequent iterations by avoiding regions of configuration space where neighboring configurations have the same potential energy due to being outside the range of interaction with the surface. We describe such scenarios and solutions in Section S2 of the ESI.†
• Region 3: the topmost region is an impenetrable vacuum created by a reflective boundary located 4σ below the cell's top. This boundary prevents the free particles from interacting with the slab's bottom due to periodic boundary conditions. Alternative boundary conditions, such as fluctuating boundaries, will be explored in future studies. These aim to eliminate the constraints imposed by the simulation cell's size, thus preventing artificial commensurability. They achieve this by introducing a phase shift at the boundary (also an MC simulation variable).76
We constructed slabs with a 4 × 4 surface unit cell and the following numbers of layers along the surface normal: five for LJ(111), eight for LJ(110), six for LJ(100), and eight for LJ(311). Different facets require different numbers of layers due to their different interlayer spacing (see Table S1 in the ESI†). We used these numbers of layers to ensure that the bottom surface is the deepest possible layer within the LJ cutoff radius from free particles adsorbed on the surface, representing a semi-infinite bulk crystal beneath the top surface. Fig. 2 displays each facet's top and side views with the surface features highlighted. All four facets explored in this work have unique surface characteristics: LJ(111), a flat surface featuring a triangular lattice-like arrangement with three-fold binding sites; LJ(100), a flat surface featuring a square lattice-like arrangement with four-fold binding sites; LJ(311), a stepped surface characterized by shallow troughs (depth = 0.48σ, opening angle = 125.3°) with elongated triangular binding sites, where an adsorbate can bind three fixed particles on the surface and two additional ones underneath the surface; and LJ(110), another stepped surface, distinguished by its deeper troughs (depth = 0.56σ, opening angle = 109.5°) with stretched square binding sites, where an adsorbate can bind four fixed particles on the surface and an extra one underneath the surface. For each facet, the number of free particles included in the NS calculations ranges from one to 16. With 16 free particles, an ML can be formed on the fixed slab. We analyzed the finite-size effects of our system. Our calculations, which are based on a 4 × 4 surface, effectively capture the fundamental physics of the system. Selecting a 4 × 4 surface guarantees qualitative accuracy while remaining computationally feasible, as Section S1 of the ESI† explains.
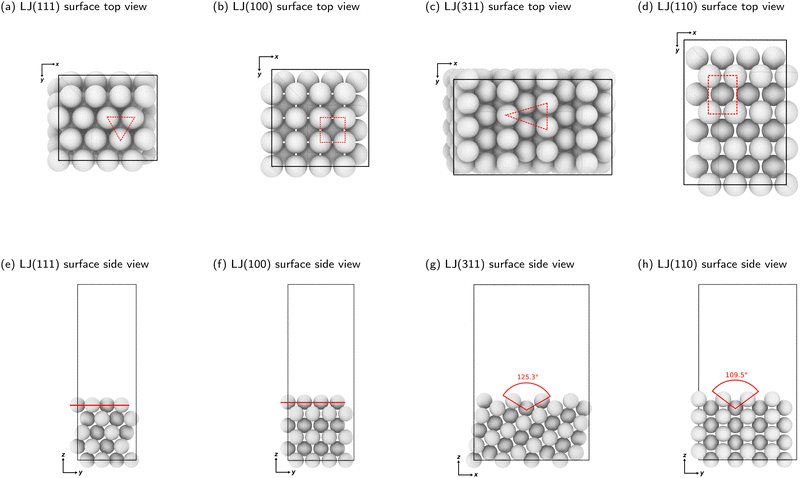 | ||
| Fig. 2 Top and side views of clean LJ(111), LJ(100), LJ(311), and LJ(110) surfaces. The dashed lines in panels (a)–(d) show a binding site on each surface. The red lines in panels (e) and (f) show the LJ(111) and LJ(100) surfaces, which are considered flat. The angles indicated in red in panels (g) and (h) display the decrease in planarity of the LJ(311) and LJ(110) surfaces, respectively. Note that the angles shown are not the bond angles but the opening of the troughs, viewed from the side. Detailed surface specifications are included in the ESI† Table S1. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 NS iterations (calculated as 80 × 250 × 16).
000 NS iterations (calculated as 80 × 250 × 16).
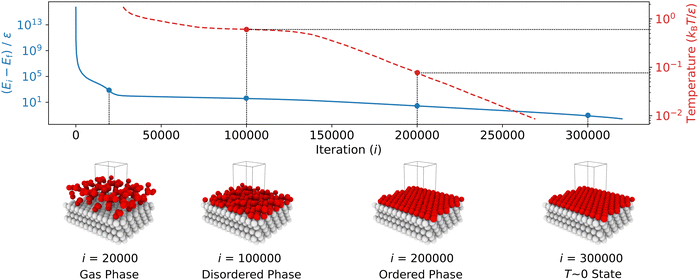
The typical variation of potential energy during an NS run is illustrated in Fig. 3. Initially, the algorithm identifies and replaces configurations with high potential energy, which have minimal impact on the partition function due to their small Boltzmann factors. High potential energies result from the proximity between particles, causing increased potential energy due to LJ repulsion. As the NS progresses, the sampled potential energies tend to decrease, eventually converging to the system's lowest potential energy state.
As described in Step 2, the new walkers were generated by cloning an existing walker and then decorrelating it via a 1600-step random walk while ensuring the energy remained below the current maximum Emaxi. We controlled the acceptance rate of new configurations by incrementally reducing the translational move step size during sampling. We kept the simulation cell's shape and volume constant throughout this process. Every 100 NS iterations, we recorded the configurations being replaced. These recorded structures were later used to calculate surface order parameters and to investigate metastable states.
We performed three independent NS calculations for each system, all with the same NS parameters but starting from different initial walkers. These initial configurations were created by randomly placing particles in Region 2 of Fig. 1. Our implementation of surface NS is available in the open-source pymatnest software, accessible at https://github.com/libAtoms/pymatnest. The input files used to perform the NS calculations with pymatnest and all output data are publicly available at DOI: 10.7936/6RXS-103650.
3 Results
We used surface NS to predict the adsorbate phase diagrams for four facets of the face-centered-cubic (fcc) LJ solid. We considered two flat facets, (111) and (100), and two stepped facets, (311) and (110), to analyze the effect of planarity on adsorbate phase equilibria. Additionally, we chose these four specific facets because they are some of the lowest index, lowest surface energy, and highest surface area fraction facets on the Wulff shape of fcc elemental solids.77 Our study employs a 4 × 4 surface unit cell for modeling the phase diagrams, which, while computationally efficient, may introduce non-trivial finite-size effects. Given these potential limitations, it is important to exercise caution when extrapolating our findings to real surfaces. However, this research aims to demonstrate surface NS's capabilities within the well-understood LJ system, setting a foundation for more comprehensive and realistic simulations in future studies. Section 3.1 concentrates on the flat LJ(111) surface. We present its phase diagram and examine thermodynamic properties computed from the partition function calculated via NS. A comprehensive analysis of phase transitions on the LJ(111) surface is provided. Section 3.2 elucidates the relationship between phase transitions and surface planarity by comparing the phase diagrams of the LJ(100), LJ(311), and LJ(110) surfaces with that of LJ(111).3.1 LJ(111) phase diagram
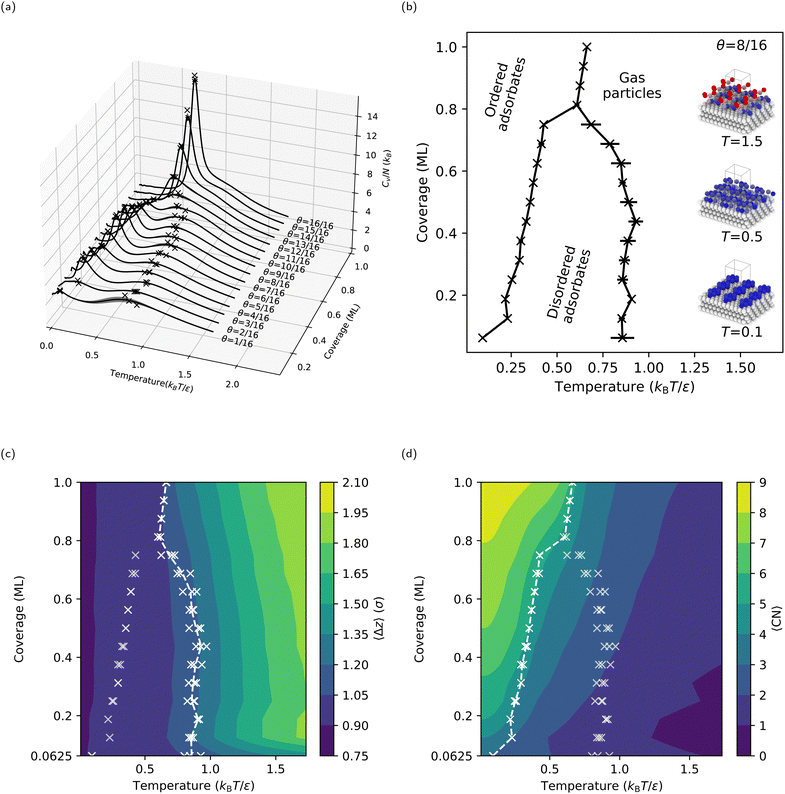
Following the procedures described in Section 2, we first compute CV(T* = kBT/ε) for the flat LJ(111) surface with coverages ranging from θ = 1/16 ML to one ML (i.e., θ = 16/16 ML). The CV curves for the LJ(111) surface (see Fig. 4a) display different behaviors in the lower coverage (θ < 12/16 ML) and higher coverage (θ ≥ 12/16 ML) regimes. In the case of the lower coverage surfaces, two peaks in the CV curve can be observed. A broad and shallow peak in CV is noticeable in the lower temperature range between 0.7 and 1.0 kBT/ε. In contrast, at temperatures between 0.2 and 0.5 kBT/ε, a sharper and more distinct peak in CV emerges. At coverages above θ ≥ 12/16 ML, the two CV peaks merge, rising sharply as the coverage increases toward one ML. The resulting coverage-temperature phase diagram for the LJ(111) surface (see Fig. 4b, where each “×” marks a peak found by the automatic peak finder) shows two distinct adsorbate phase boundaries for coverages lower than 13/16 ML, as expected. The two boundaries move towards each other as the coverage increases and eventually meet at a triple-point, at θ = 13/16 ML and approximately 0.6 kBT/ε.To characterize the adsorbate phases and their transitions, we calculated two order parameters, 〈Δz〉 (see Fig. 4c) and 〈CN〉 (see Fig. 4d), as described in Section 2.1.2. As expected, 〈Δz〉 decreases as the temperature decreases because the free particles start adsorbing on the surface; we refer to this process as surface condensation. The 1.2σ contour coincides with the higher temperature coexistence curve, suggesting that the adsorbed free particles form a quasi-two-dimensional layer with a thickness approximately equal to 1.2σ upon cooling. Note that 0.92σ is the interlayer spacing in an LJ(111) bulk, meaning the free particles are now, on average, near the positions where an additional ML should form. Since the higher-temperature adsorbate phase transition corresponds to a vertical ordering of the free particles, the lower-temperature adsorbate phase transition must correspond to the approximately two-dimensional ordering of the free particles (or adsorbates, after condensation) within the surface layer. To quantify this surface-layer ordering, we calculated 〈CN〉, which increases with decreasing temperature (see Fig. 4d). At high temperatures and low coverages, the free particles rarely interact with one another, resulting in a 〈CN〉 ≈ 0. However, once the temperature is less than that of the condensation, 〈CN〉 quickly reaches its maximum possible value: for example, three for one free particle (because the free particle occupies a hollow site between three fixed surface particles), and four for two free particles (because the two free particles occupy neighboring hollow sites). The maximum 〈CN〉 is nine, where an adsorbed free particle is close-packed by six adsorbed free particles at neighboring hollow sites. Overall, the lower temperature coexistence curve coincides with a contour in 〈CN〉, separating a lower coordination adsorbate phase with disordered adsorbates above the transition temperature from a higher coordination adsorbate phase with ordered adsorbates below the transition temperature.
Interestingly, the 4 × 4 (and 6 × 6, see Section S1, ESI†) LJ(111) surface has a triple point near a coverage of three-quarters (θ = 13/16 ML) and at a temperature between the two adsorbate phase transitions observed for lower coverages. For coverages θ ≥ 13/16, the CV curves in Fig. 4a show only one sharp peak. Given the lack of a lower coordination adsorbate phase with disordered adsorbates at intermediate temperatures for coverages θ ≥ 13/16 ML, we will refer to this process as surface deposition, where gas-phase free particles form an adsorbate phase with ordered adsorbates below the deposition temperature. One can see from Fig. 4c that the phase boundary now coincides with the 〈Δz〉 = 1.05σ contour versus the 〈Δz〉 = 1.20σ contour for the lower-coverage, higher-temperature transition, showing that the phase transition processes happen closer to the fixed slab compared to the surface condensation. We can rationalize the origin of these two different behaviors for lower and higher coverages – i.e., condensation and deposition, respectively – by comparing the stable surface structures below the condensation and deposition temperatures, respectively (see Section S6 in the ESI†). For lower coverages, the free particles form islands and stripes (see the inset in Fig. 4b for an example structure at θ = 8/16 ML and T = 0.1 kBT/ε) on the surface, with many isoenergetic options for reconfiguration. However, for higher coverages, the free particles form a continuous ML with vacancies, which have limited options for reconfiguration.
Another observation from our NS results is that, on the LJ(111) surface, the adsorbed free particles form a hexagonal-close-packed (hcp) ML on top of the fcc LJ solid at absolute zero. As shown in ref. 78, the LJ solid's lowest potential energy state stacking structure depends on how the potential around the truncation distance is treated. In our specific setup, the potential energy of the hcp ML is less than that of the fcc ML by 2 × 10−7ε per adsorbed free particle. Thus, NS finds the hcp ML the lowest potential energy structure. On the other hand, molecular dynamics simulations show that crystal growth on an LJ(111) surface consistently forms a mix of fcc and hcp structures, with the fcc LJ(111) surface being slightly kinetically favored.63,79 However, Somasi et al. used an LJ cutoff radius of 2.5σ; therefore, based on ref. 78, we cannot simply compare their system to ours.
3.2 Effect of surface geometry on adsorbate phase diagrams
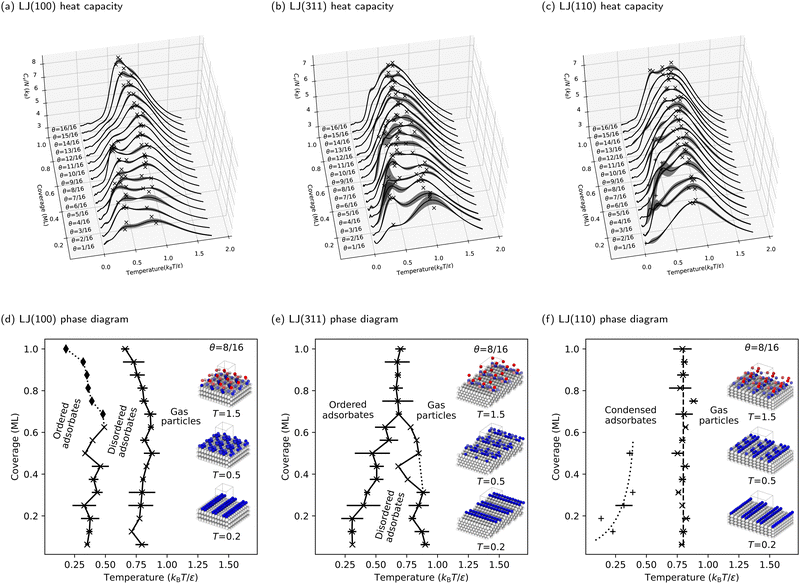
The preceding section deepened our understanding of phase transitions on the LJ(111) surface. This section expands our investigation to three additional facets of the LJ solid, demonstrating the versatility of our NS approach in studying adsorbate phase diagrams. The heat capacities for the LJ(100), LJ(311), and LJ(110) surfaces are detailed in Fig. 5a–c, respectively. Correspondingly, the phase diagrams for these surfaces are presented in Fig. 5d–f.Moreover, redefining what constitutes an ML on these stepped surfaces is important. In this context, an ML consists of all particles at the same height, differing from flat surfaces where all exposed particles are typically considered part of an ML. This approach effectively redefines the ML, preventing the misleading impression of double particle counting per ML. To facilitate a direct comparison of phase diagrams, we maintained the same number of free particles (and, consequently, degrees of freedom) as used for the LJ(111) and LJ(100) surfaces. This consistency is key to understanding the nuanced behaviors of these complex surfaces.
In our examination of the LJ(311) surface, the phase diagram, shown in Fig. 5e, bears a resemblance to that of LJ(111), featuring two adsorbate phase transitions at low coverages and a triple point around three-quarters coverage. However, a key distinction is the lack of a pronounced increase in heat capacity at higher coverages above the triple point. Additionally, on LJ(311), high-temperature phase transitions linked to the condensation process become more dominant, overshadowing the lower-temperature ordering transition and complicating phase boundary delineation. This effect is further amplified on the LJ(110) surface, as Fig. 5f shows. Here, the low-temperature peaks in the CV curves are overshadowed by broad, high-temperature peaks, making the phase boundary between the ordered and disordered phases challenging to identify. Consequently, we focus only on delineating the phase boundary between the gas and condensed phases for LJ(110), where the condensation process is markedly more complex and distinct from flat surfaces. Interestingly, condensation on LJ(110) appears to be coverage-independent, as indicated by the vertical dashed line in Fig. 5f, representing a consistent phase transition temperature ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) θ = 0.8 kBT/ε across all coverages.
θ = 0.8 kBT/ε across all coverages.
The stepped nature of LJ(311) and LJ(110) surfaces, which have deeper and more directional binding sites in the troughs, drives phase transitions primarily through enthalpy changes, contrasting with the entropy-driven ordering transitions on flat surfaces. The reduction in surface symmetry on these stepped surfaces significantly diminishes entropy contributions, as free particles are more constrained by the stronger binding and the reduced number of energetically equivalent adsorption sites.
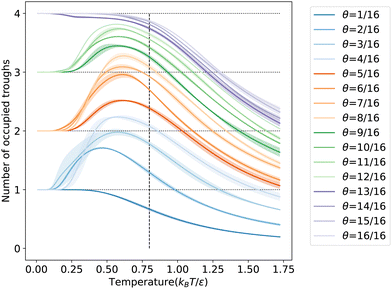
To further understand the microscopic aspects of phase transitions, we computed the ensemble average number of occupied troughs on the LJ(110) surface at various temperatures and coverages, as depicted in Fig. 6. Observing the temperature range from high to low in Fig. 6, we notice an increasing trend in trough occupancy as free particles begin to populate the troughs, continuing until the temperature reaches ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) θ for all coverages. Below
θ for all coverages. Below ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) θ, for coverages greater than 12/16 ML, the number of occupied troughs monotonically approaches four, the total count in the unit cell. For lower coverages (≤12/16 ML), the occupied trough count trends towards ⌈N/4⌉, reflecting the ability of each trough to house up to four particles in an ML configuration. This behavior is further evidenced by the rapid rearrangement of free particles into the same troughs to maximize coordination, as shown in Fig. S7b in the ESI.† Such rearrangements, typically accompanied by a reduction in entropy, result in a more ordered state within the same trough, particularly noticeable at lower coverages with numerous unoccupied binding sites. The observed ordering process is linked to the shoulder peaks on the CV curves in Fig. 5c at specific coverages. Our order parameter analysis indicates that these peaks signify an ordering phase transition occurring near the temperatures of the condensation transition.
θ, for coverages greater than 12/16 ML, the number of occupied troughs monotonically approaches four, the total count in the unit cell. For lower coverages (≤12/16 ML), the occupied trough count trends towards ⌈N/4⌉, reflecting the ability of each trough to house up to four particles in an ML configuration. This behavior is further evidenced by the rapid rearrangement of free particles into the same troughs to maximize coordination, as shown in Fig. S7b in the ESI.† Such rearrangements, typically accompanied by a reduction in entropy, result in a more ordered state within the same trough, particularly noticeable at lower coverages with numerous unoccupied binding sites. The observed ordering process is linked to the shoulder peaks on the CV curves in Fig. 5c at specific coverages. Our order parameter analysis indicates that these peaks signify an ordering phase transition occurring near the temperatures of the condensation transition.
4 Discussion
4.1 Surface planarity and adsorbate disorder
We first address the disappearance of the disordered adsorbate phase when transitioning from flat to stepped surfaces. Disordered adsorbate phases are observed at intermediate temperatures on the flat LJ(111) and LJ(100) surfaces. However, this is not true for the stepped LJ(110) surface. As Section 3.2 outlines, the LJ(110) surface transitions directly from gas to ordered adsorbates during condensation. This directness suggests a close link between the ordering process and condensation, influenced by the surface geometry. On the LJ(110) surface, adsorbates settle deeply into troughs post-condensation for maximum coordination, merging the condensation and ordering processes. This overlap is evident from concurrent peaks in heat capacities, indicating a need for refined analytical approaches to separate these overlapping peaks. Such challenges are common in numerical simulations and experimental studies (e.g., ref. 82 and 83), emphasizing the crucial role of surface topology in adsorption and ordering behaviors.Furthermore, the LJ(311) surface, with its shallower and wider troughs (depth = 0.48σ, opening angle = 125.3°), compared to LJ(110) (depth = 0.56σ, opening angle = 109.5°), exhibits a rougher topology than flat surfaces. This is reflected in the LJ(311) phase diagram, which shows a narrower range of temperatures and coverages where the disordered adsorbate phase is stable (see Fig. 5e). This phase diagram is a transitional point between flat and stepped surfaces, highlighting the critical role of planarity in determining the equilibrium structures of adsorbates on LJ solids.
The troughs of stepped surfaces reduce the number of isoenergetic adsorption sites, decreasing the configurational entropy of adsorbed particles compared to flat surfaces. As a result, the boundary of the entropy-stabilized disordered adsorbate phase is less distinct on LJ(110) and at high coverages on LJ(311). One key observation is the correlation between the presence of a triple point on the phase diagram and surface geometry. Despite their different topologies, the triple point is evident on LJ(111) and LJ(311) surfaces, which feature triangular binding sites. In contrast, the LJ(100) and LJ(110) surfaces, with their square and rectangular binding sites, show no clear triple point. Instead, they display pronounced coverage-independent phase transitions.
4.2 Transferability of surface NS
This work demonstrates that NS can compute the coverage-temperature phase diagrams of solid surfaces. However, other state variables, such as pressure and chemical potential, can also be considered. For instance, NS could be performed with particle addition and removal steps and translational moves to construct composition–temperature phase diagrams in the case of semi-grand canonical NS84 and chemical potential-temperature phase diagrams in the case of grand canonical NS. Developing the latter will be essential to predict surface reconstructions under operating conditions, i.e., operando chemical potentials, robustly. Our NS implementation is also not limited to studying surface-adsorbate phase equilibria. We define a general interfacial system with two interacting subsystems: (1) a fixed host phase, which in our case is a surface slab model (see Fig. 1) and (2) a free guest phase, which in our case are particles that start as a randomly and uniformly distributed gas and end as an adsorbed monolayer. The generalization of this setup to other interfacial systems involves substituting the host and guest with subsystems of interest. For example, consider the solid surface-liquid solvent interface in heterogeneous catalysis and typical rechargeable batteries. Here, the host would be the solid catalyst or electrode surface, and the guest would be the liquid phase. The liquid phase could be treated using explicit solvent particles coupled with implicit solvation in a continuous dielectric medium to improve computational efficiency. Alternatively, our approach could be extended to study interfaces between two solids, such as those at grain boundaries (where reconstructions called complexions can form) and electrical junctions. In these cases, the host and guest would be solids, but care would have to be taken in selecting or designing sampling moves to increase the acceptance ratio, as it can be low in condensed phases.4.3 Opportunities for improving surface NS
Finally, we have adopted a simplified view of the surface, i.e., as a host whose constituent particles can interact with other particles but cannot move for computational convenience and model simplicity. While this simplification allows us to focus exclusively on the free particle–surface interplay, it precludes the surface from contributing to the free energy via its vibrational and configurational degrees of freedom, and it neglects effects such as adsorbate-induced surface reconstructions. Such processes can be critical for modeling specific systems realistically, for example, CO adsorption on Pt(100),85,86 or hydrogen adsorption on W(110).87,88 To include at least some of these surface contributions, we propose the introduction of “flexible” surface particles that are neither fixed nor free but confined harmonically to their lattice sites. Such an approach, which we intend to develop in future work, would allow NS to capture the effect of harmonic surface vibrations in the system partition function. In future work, we also aim to benchmark the accuracy and efficiency of NS against methods such as numerical integration, replica exchange,89–92 and the Wang–Landau algorithm.38,93 This comparison will provide valuable insights into the strengths and limitations of each approach.5 Conclusions
In this study, we developed the nested sampling (NS) algorithm for surfaces, extending its use to predict coverage-temperature adsorbate phase diagrams and compute surface thermodynamic properties at finite temperatures. We employed surface NS to construct partition functions for Lennard-Jones (LJ) solid surfaces with fixed and free particles. We calculated the constant-volume heat capacity from these partition functions, using its peaks to delineate coverage-temperature adsorbate phase diagrams.Our analysis revealed that free particles on these surfaces typically undergo two phase transitions: a higher-temperature, enthalpy-driven condensation followed by a lower-temperature, entropy-driven reordering. This NS-based approach effectively resolved phase diagrams for both flat and stepped surfaces. Order parameters were crucial for stepped surfaces, where phase boundaries are less clear. These parameters, calculated as ensemble averages of observables from the partition function, provide statistical insights into complex surface behaviors.
This work enhances our understanding of surface processes and paves the way for future implementations of NS on open thermodynamic systems and multi-species surfaces. Such advancements are critical for identifying interfacial phases that are key in material performance for commercial, industrial, and climate change mitigation applications.
Data availability
The data supporting this study's findings are publicly available at WashU Research Data DOI: 10.7936/6RXS-103650. The open-source package pymatnest is freely available on GitHub at https://github.com/libAtoms/pymatnest.Conflicts of interest
There are no conflicts to declare.Acknowledgements
RBW acknowledges support from the National Science Foundation under Grant No. 2305155. LBP acknowledges support from the EPSRC through an individual Early Career Fellowship (EP/T000163/1). MY used resources from the Argonne Leadership Computing Facility, a US Department of Energy Office of Science user facility at Argonne National Laboratory. LBP used computing facilities provided by the Scientific Computing Research Technology Platform of the University of Warwick.Notes and references
- A. Wander, F. Schedin, P. Steadman, A. Norris, R. McGrath, T. S. Turner, G. Thornton and N. M. Harrison, Phys. Rev. Lett., 2001, 86, 3811–3814 CrossRef CAS PubMed.
- V. K. Ravi, P. K. Santra, N. Joshi, J. Chugh, S. K. Singh, H. Rensmo, P. Ghosh and A. Nag, J. Phys. Chem. Lett., 2017, 8, 4988–4994 CrossRef CAS PubMed.
- R. Ohmann, L. K. Ono, H.-S. Kim, H. Lin, M. V. Lee, Y. Li, N.-G. Park and Y. Qi, J. Am. Chem. Soc., 2015, 137, 16049–16054 CrossRef CAS PubMed.
- Z. Chen, J. M. P. Martirez, P. Zahl, E. A. Carter and B. E. Koel, J. Chem. Phys., 2019, 150, 041720 CrossRef PubMed.
- T. H. Phan, K. Banjac, F. P. Cometto, F. Dattila, R. García-Muelas, S. J. Raaijman, C. Ye, M. T. M. Koper, N. López and M. Lingenfelder, Nano Lett., 2021, 21, 2059–2065 CrossRef CAS PubMed.
- D. Cheng, Z. Wei, Z. Zhang, P. Broekmann, A. N. Alexandrova and P. Sautet, Angew. Chem., 2023, 135, e202218575 CrossRef.
- C. Wan, Z. Zhang, J. Dong, M. Xu, H. Pu, D. Baumann, Z. Lin, S. Wang, J. Huang, A. H. Shah, X. Pan, T. Hu, A. N. Alexandrova, Y. Huang and X. Duan, Nat. Mater., 2023, 22(8), 1022–1029 CrossRef CAS PubMed.
- Z. Zhang, Z. Wei, P. Sautet and A. N. Alexandrova, J. Am. Chem. Soc., 2022, 144, 19284–19293 CrossRef CAS PubMed.
- J. M. P. Martirez, S. Kim, E. H. Morales, B. T. Diroll, M. Cargnello, T. R. Gordon, C. B. Murray, D. A. Bonnell and A. M. Rappe, J. Am. Chem. Soc., 2015, 137, 2939–2947 CrossRef CAS PubMed.
- M. L. Weber, G. Lole, A. Kormanyos, A. Schwiers, L. Heymann, F. D. Speck, T. Meyer, R. Dittmann, S. Cherevko, C. Jooss, C. Baeumer and F. Gunkel, J. Am. Chem. Soc., 2022, 144, 17966–17979 CrossRef CAS PubMed.
- A. R. Akbashev, V. Roddatis, C. Baeumer, T. Liu, J. T. Mefford and W. C. Chueh, Energy Environ. Sci., 2023, 16, 513–522 RSC.
- J. Schröder, J. A. Zamora Zeledón, G. A. Kamat, M. E. Kreider, L. Wei, A. S. Mule, A. Torres, K. Yap, D. Sokaras, A. Gallo, M. B. Stevens and T. F. Jaramillo, ACS Energy Lett., 2023, 2962–2969 CrossRef.
- A. R. Akbashev, Curr. Opin. Electrochem., 2022, 35, 101095 CrossRef CAS.
- D. Grumelli, T. Wiegmann, S. Barja, F. Reikowski, F. Maroun, P. Allongue, J. Balajka, G. S. Parkinson, U. Diebold, K. Kern and O. M. Magnussen, Angew. Chem., Int. Ed., 2020, 59, 21904–21908 CrossRef CAS PubMed.
- X.-G. Wang, W. Weiss, S. K. Shaikhutdinov, M. Ritter, M. Petersen, F. Wagner, R. Schlögl and M. Scheffler, Phys. Rev. Lett., 1998, 81, 1038–1041 CrossRef CAS.
- X.-G. Wang, A. Chaka and M. Scheffler, Phys. Rev. Lett., 2000, 84, 3650–3653 CrossRef CAS PubMed.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035406 CrossRef.
- Y. Zhou, M. Scheffler and L. M. Ghiringhelli, Phys. Rev. B, 2019, 100, 174106 CrossRef CAS.
- Z. W. Ulissi, A. R. Singh, C. Tsai and J. K. Nørskov, J. Phys. Chem. Lett., 2016, 7, 3931–3935 CrossRef CAS PubMed.
- G. Schusteritsch and C. J. Pickard, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 035424 CrossRef CAS.
- J. Timmermann, F. Kraushofer, N. Resch, P. Li, Y. Wang, Z. Mao, M. Riva, Y. Lee, C. Staacke, M. Schmid, C. Scheurer, G. S. Parkinson, U. Diebold and K. Reuter, Phys. Rev. Lett., 2020, 125, 206101 CrossRef CAS PubMed.
- N. Rønne, M.-P. V. Christiansen, A. M. Slavensky, Z. Tang, F. Brix, M. E. Pedersen, M. K. Bisbo and B. Hammer, J. Chem. Phys., 2022, 157, 174115 CrossRef PubMed.
- G. Sun, J. T. Fuller, A. N. Alexandrova and P. Sautet, ACS Catal., 2021, 11, 1877–1885 CrossRef CAS.
- D. Chen, C. Shang and Z.-P. Liu, J. Chem. Phys., 2022, 156, 094104 CrossRef CAS PubMed.
- Q. Zhu, L. Li, A. R. Oganov and P. B. Allen, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195317 CrossRef.
- S. Chiriki, M.-P. V. Christiansen and B. Hammer, Phys. Rev. B, 2019, 100, 235436 CrossRef CAS.
- Y. Wang, Y.-Q. Su, E. J. M. Hensen and D. G. Vlachos, ACS Nano, 2020, 14, 13995–14007 CrossRef CAS PubMed.
- R. Wanzenböck, M. Arrigoni, S. Bichelmaier, F. Buchner, J. Carrete and G. K. H. Madsen, Digital Discovery, 2022, 1, 703–710 RSC.
- S. Lu, Y. Wang, H. Liu, M.-S. Miao and Y. Ma, Nat. Commun., 2014, 5, 3666 CrossRef CAS PubMed.
- M. K. Bisbo and B. Hammer, Phys. Rev. Lett., 2020, 124, 086102 CrossRef CAS PubMed.
- M. S. Jørgensen, H. L. Mortensen, S. A. Meldgaard, E. L. Kolsbjerg, T. L. Jacobsen, K. H. Sørensen and B. Hammer, J. Chem. Phys., 2019, 151, 054111 CrossRef.
- Z. Zhang, B. Zandkarimi and A. N. Alexandrova, Acc. Chem. Res., 2020, 53, 447–458 CrossRef CAS PubMed.
- D. Fantauzzi, S. Krick Calderón, J. E. Mueller, M. Grabau, C. Papp, H.-P. Steinrück, T. P. Senftle, A. C. T. van Duin and T. Jacob, Angew. Chem., Int. Ed., 2017, 56, 2594–2598 CrossRef CAS PubMed.
- R. B. Wexler, T. Qiu and A. M. Rappe, J. Phys. Chem. C, 2019, 123, 2321–2328 CrossRef CAS.
- V. Somjit and B. Yildiz, ACS Appl. Mater. Interfaces, 2022, 14, 42613–42627 CrossRef CAS PubMed.
- J. Xu, W. Xie, Y. Han and P. Hu, ACS Catal., 2022, 12, 14812–14824 CrossRef CAS.
- X. Du, J. K. Damewood, J. R. Lunger, R. Millan, B. Yildiz, L. Li and R. Gómez-Bombarelli, Nat. Comput. Sci., 2023, 3(12), 1034–1044 CrossRef PubMed.
- F. Wang and D. P. Landau, Phys. Rev. Lett., 2001, 86, 2050–2053 CrossRef CAS PubMed.
- F. Wang and D. P. Landau, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 056101 CrossRef CAS PubMed.
- L. B. Pártay, A. P. Bartók and G. Csányi, J. Phys. Chem. B, 2010, 114, 10502–10512 CrossRef PubMed.
- J. Skilling, Bayesian Inference and Maximum Entropy Methods in Science and Engineering: 24th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, 2004, pp. 395–405.
- J. Skilling, Bayesian Anal., 2006, 1, 833–859 Search PubMed.
- G. Ashton, N. Bernstein, J. Buchner, X. Chen, G. Csányi, A. Fowlie, F. Feroz, M. Griffiths, W. Handley, M. Habeck, E. Higson, M. Hobson, A. Lasenby, D. Parkinson, L. B. Pártay, M. Pitkin, D. Schneider, J. S. Speagle, L. South, J. Veitch, P. Wacker, D. J. Wales and D. Yallup, Nat. Rev. Methods Primers, 2022, 2, 39 CrossRef CAS.
- R. J. N. Baldock, L. B. Pártay, A. P. Bartók, M. C. Payne and G. Csányi, Phys. Rev. B, 2016, 93, 174108 CrossRef.
- L. B. Pártay, G. Csányi and N. Bernstein, Eur. Phys. J. B, 2021, 94, 159 CrossRef.
- K. Rossi, L. B. Pártay, G. Csányi and F. Baletto, Sci. Rep., 2018, 8, 9150 CrossRef CAS PubMed.
- J. Dorrell and L. B. Pártay, Phys. Chem. Chem. Phys., 2019, 21, 7305–7312 RSC.
- B. Szekeres, L. B. Pártay and E. Mátyus, J. Chem. Theory Comput., 2018, 14, 4353–4359 CrossRef CAS PubMed.
- P. G. Bolhuis and G. Csányi, Phys. Rev. Lett., 2018, 120, 250601 CrossRef CAS PubMed.
- R. J. N. Baldock, N. Bernstein, K. M. Salerno, L. B. Pártay and G. Csányi, Phys. Rev. E, 2017, 96, 043311 CrossRef PubMed.
- A. Gola and L. Pastewka, Modelling Simul. Mater. Sci. Eng., 2018, 26, 055006 CrossRef.
- J. Dorrell and L. B. Pártay, J. Phys. Chem. B, 2020, 124, 6015–6023 CrossRef CAS PubMed.
- A. P. Bartók, G. Hantal and L. B. Pártay, Phys. Rev. Lett., 2021, 127, 015701 CrossRef PubMed.
- G. A. Marchant, M. A. Caro, B. Karasulu and L. B. Pártay, npj Comput. Mater., 2023, 9, 131 CrossRef.
- M. Sprik, R. W. Impey and M. L. Klein, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 4368 CrossRef CAS.
- B. W. Van De Waal, Phys. Rev. Lett., 1991, 67, 3263–3266 CrossRef PubMed.
- M. A. van der Hoef, J. Chem. Phys., 2000, 113, 8142–8148 CrossRef CAS.
- J. Nicolas, K. Gubbins, W. Streett and D. Tildesley, Mol. Phys., 1979, 37, 1429–1454 CrossRef CAS.
- B. Smit, J. Chem. Phys., 1992, 96, 8639–8640 CrossRef CAS.
- M. Mecke, J. Winkelmann and J. Fischer, J. Chem. Phys., 1997, 107, 9264–9270 CrossRef CAS.
- J. Broughton and G. Gilmer, Acta Metall., 1983, 31, 845–851 CrossRef CAS.
- S. Valkealahti and R. M. Nieminen, Phys. Scr., 1987, 36, 646–650 CrossRef CAS.
- S. Somasi, B. Khomami and R. Lovett, J. Chem. Phys., 2001, 114, 6315–6326 CrossRef CAS.
- A. N. Berker, S. Ostlund and F. A. Putnam, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17, 3650–3665 CrossRef CAS.
- S. Ostlund and A. N. Berker, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 5410–5423 CrossRef CAS.
- A. Patrykiejew, Thin Solid Films, 1986, 139, 209–219 CrossRef CAS.
- P. Borowski, A. Patrykiejew and S. Sokolowski, Thin Solid Films, 1989, 177, 333–346 CrossRef.
- A. Patrykiejew and P. Borowski, Thin Solid Films, 1991, 195, 367–380 CrossRef CAS.
- T. D. Lee and C. N. Yang, Phys. Rev., 1952, 87, 410–419 CrossRef CAS.
- G. Doyen, G. Ertl and M. Plancher, J. Chem. Phys., 1975, 62, 2957–2966 CrossRef CAS.
- K. Binder and D. Landau, Surf. Sci., 1976, 61, 577–602 CrossRef CAS.
- S. Martiniani, J. D. Stevenson, D. J. Wales and D. Frenkel, Phys. Rev. X, 2014, 4, 031034 Search PubMed.
- P. Poths and A. N. Alexandrova, J. Phys. Chem. Lett., 2022, 13, 4321–4334 CrossRef CAS PubMed.
- R. H. Lavroff, H. T. Morgan, Z. Zhang, P. Poths and A. N. Alexandrova, Chem. Sci., 2022, 13, 8003–8016 RSC.
- S. Stephan, M. Thol, J. Vrabec and H. Hasse, J. Chem. Inf. Model., 2019, 59, 4248–4265 CrossRef CAS PubMed.
- P. Olsson, Phys. Rev. Lett., 1994, 73, 3339–3342 CrossRef CAS PubMed.
- R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson and S. P. Ong, Sci. Data, 2016, 3, 160080 CrossRef CAS PubMed.
- L. B. Pártay, C. Ortner, A. P. Bartók, C. J. Pickard and G. Csányi, Phys. Chem. Chem. Phys., 2017, 19, 19369–19376 RSC.
- L. A. Báez and P. Clancy, J. Chem. Phys., 1995, 102, 8138–8148 CrossRef.
- C. Stampfl, H. J. Kreuzer, S. H. Payne, H. Pfnür and M. Scheffler, Phys. Rev. Lett., 1999, 83, 2993–2996 CrossRef CAS.
- C. J. Mize, L. D. Crosby, S. B. Isbill and S. Roy, J. Phys. Chem. C, 2022, 126, 5343–5353 CrossRef CAS.
- A. D. Migone, Z. R. Li and M. H. W. Chan, Phys. Rev. Lett., 1984, 53, 810–813 CrossRef CAS.
- D. M. Butler, J. A. Litzinger and G. A. Stewart, Phys. Rev. Lett., 1980, 44, 466–468 CrossRef CAS.
- C. W. Rosenbrock, K. Gubaev, A. V. Shapeev, L. B. Pártay, N. Bernstein, G. Csányi and G. L. W. Hart, npj Comput. Mater., 2021, 7, 24 CrossRef CAS.
- Y. Kinomoto, S. Watanabe, M. Takahashi and M. Ito, Surf. Sci., 1991, 242, 538–543 CrossRef CAS.
- J. Raskó, J. Catal., 2003, 217, 478–486 CrossRef.
- E. Hulpke and J. Lüdecke, Phys. Rev. Lett., 1992, 68, 2846–2849 CrossRef CAS PubMed.
- E. S. Altshuler, D. L. Mills and R. B. Gerber, Surf. Sci., 1997, 374, 229–242 CrossRef CAS.
- R. H. Swendsen and J.-S. Wang, Phys. Rev. Lett., 1986, 57, 2607–2609 CrossRef PubMed.
- E. Marinari and G. Parisi, EPL, 1992, 19, 451 CrossRef CAS.
- Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151 CrossRef CAS.
- M. R. Shirts and J. D. Chodera, J. Chem. Phys., 2008, 129, 124105 CrossRef PubMed.
- A. N. Morozov and S. H. Lin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 026701 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: finite-size analysis, system setup procedures, specifications of surface structure, calculations of order parameters, and illustrations of maximum-probability surface structures. See DOI: https://doi.org/10.1039/d4cp00050a |
| This journal is © the Owner Societies 2024 |