A coarse-grained simulation model for colloidal self-assembly via explicit mobile binders†
Gaurav
Mitra
 a,
Chuan
Chang
b,
Angus
McMullen
c,
Daniela
Puchall
a,
Jasna
Brujic
ce and
Glen M.
Hocky
a,
Chuan
Chang
b,
Angus
McMullen
c,
Daniela
Puchall
a,
Jasna
Brujic
ce and
Glen M.
Hocky
 *ad
*ad
aDepartment of Chemistry, New York University, New York, New York 10003, USA
bDepartment of Physics, Cornell University, Ithaca, New York 14853, USA
cCenter for Soft Matter Research and Department of Physics, New York University, New York, New York 10003, USA
dSimons Center for Computational Physical Chemistry, New York University, New York, New York 10003, USA. E-mail: hockyg@nyu.edu
eLaboratoire de Physique et Mécanique des Milieux Hétérogènes, UMR 7636, CNRS, ESPCI Paris-PSL, Sorbonne Université, Université Paris Cité, 75005 Paris, France
First published on 5th May 2023
Abstract
Colloidal particles with mobile binding molecules constitute a powerful platform for probing the physics of self-assembly. Binding molecules are free to diffuse and rearrange on the surface, giving rise to spontaneous control over the number of droplet–droplet bonds, i.e., valence, as a function of the concentration of binders. This type of valence control has been realized experimentally by tuning the interaction strength between DNA-coated emulsion droplets. Optimizing for valence two yields droplet polymer chains, termed ‘colloidomers’, which have recently been used to probe the physics of folding. To understand the underlying self-assembly mechanisms, here we present a coarse-grained molecular dynamics (CGMD) model to study the self-assembly of this class of systems using explicit representations of mobile binding sites. We explore how valence of assembled structures can be tuned through kinetic control in the strong binding limit. More specifically, we optimize experimental control parameters to obtain the highest yield of long linear colloidomer chains. Subsequently tuning the dynamics of binding and unbinding via a temperature-dependent model allows us to observe a heptamer chain collapse into all possible rigid structures, in good agreement with recent folding experiments. Our CGMD platform and dynamic bonding model (implemented as an open-source custom plugin to HOOMD-Blue) reveal the molecular features governing the binding patch size and valence control, and opens the study of pathways in colloidomer folding. This model can therefore guide programmable design in experiments.
1 Introduction
Self-assembly of colloidal materials can create non-trivial and programmable structures with wide-ranging and tunable material properties. The spatio-temporal visualization of colloids renders them as useful model systems for probing the underlying physics behind assembly processes of molecular systems.1–4 The synthesis of colloidal particles with chemically or physically patterned solid surfaces—“patches”—has been an active area of research due to the desire to control the bond valence and orientation, going beyond what can be achieved through isotropic interactions.4–7 For example, a long-desired target is a diamond lattice, with an open structure that is difficult to achieve without an imposed tetrahedral symmetry.8The most common approach to engineering specific interactions between patches is to use complementary strands of DNA, whose interaction strength can be tuned by the length and specific sequence of nucleotides.2,9–13 Each DNA duplex has an associated melting temperature (Tmelt) and it is possible to employ multiple sets of complementary strands exhibiting different Tmelt to control the types of bonds present during an annealing protocol.14
Self-assembly of patchy particles can be studied in simulations using short-range directional non-bonded interactions15 or using only pairwise interactions in combination with specific geometric constraints that prevent multiple bonding to the same patch.6,16–18 Interactions due to many DNAs on a colloidal surface can also be computed using more detailed MD simulations,19 or through a mean-field approach.20 An alternative strategy to modeling explicit patches is to develop pair-potentials from inverse design principles, which have been successfully leveraged to produce systems that assemble with low valence, such as dimers or chains.21,22
An intriguing alternative to patchy particles of fixed valence is a system of particles coated with mobile adhesion molecules. In this case, it is possible for particles to “choose” their valence based on the number of available neighbors with complementary binding molecules, minimizing the total free energy of the system. Experimentally, using oil droplets in water provides a mobile interface on which the DNA linkers segregate into patches by diffusion to give rise to e.g., dimers when all the DNA is recruited into a single patch or droplet chains at higher concentrations of DNA where two patches per droplet are favored.23 Colloids with mobile binders can also be formed by coating solid particles with fluid lipid bilayers,24,25 or by directly functionalizing liposomes or giant unilamellar vesicles.26–29 The mobility of the linkers broadens the melting temperature window of the DNA, facilitating equilibrium self-assembly.2,30 Particles with mobile binders can also serve as a physical mimic for biological adhesion, where cells use a variety of dynamic binding molecules to stick to each other and to surfaces.31 To this end, biomimetic emulsion droplets have been successfully functionalized with adhesive mobile proteins, such as biotin–streptavidin complexes,32,33 cadherin ectodomains,34 or other ligand-binder pairs relevant for immunotherapy.35 Early theoretical work expanding on the model of ref. 20 predicts that such particles could have an equilibrium valence that depends on the number of available neighboring particles in the system.36
Our previous work shows that monodisperse PDMS oil droplets functionalized with different flavors of single-stranded DNA on the surface can self-assemble into structures of tunable valence.23,25,37–40 Under conditions where DNA bonds are reversible at room temperature, these systems achieve their equilibrium valence configuration. These results are predicted by a free-energy functional that takes into account the molecular properties of the system, including DNA binding strength, flexibility, steric repulsion, and concentration.41 Optimizing for valence two, the self-assembly of complementary DNA-coated droplets yields linear colloidomer chains.23 Further programming the secondary interactions along the chains offers a physical model system to probe the energy landscape of biopolymer folding, and for building small ‘foldamer’ structures that can serve as the basis for larger scale assemblies.42–44 A complementary work demonstrated the formation of reconfigurable colloidal molecules using polydisperse droplets surrounded by ligands.45 It has also been shown previously through both experiments and simulation studies that anisotropic interactions between polymer-grafted nanoparticles (NPs)46–49 can result in self-assembly of sheets and string-like structures. The graft density of the polymers and the relative size of the graft to the NP can play a crucial role in determining the kind of structures observed during self-assembly, quite analogous to how the density of the mobile DNA binders on the surface of oil droplets can be used to tune the droplet valence.
Motivated by these experimental studies, our work develops a coarse-grained molecular dynamics (CGMD) simulation model and framework to study the self-assembly of these colloidal chains with mobile binders, and their subsequent folding. The crucial feature of our model is the use of explicit mobile linkers with bonds between complementary binding partners. Prior work on these types of systems used implicit models of binding between neighboring droplets via the formation of adhesion patches, and some models included approximations to account for the dynamics of adhesion.26,36,50–53 The use of explicit mobile binders allows us to test the underlying assumptions in a more realistic model, albeit at the cost of additional complexity. For example, our model explicitly shows how steric repulsion between binders (designed to mimic electrostatic repulsion between DNA strands) affects the adhesion patch size and the concentration of binders therein. These results in turn explain the overall valence distribution that results from the assembly process. To demonstrate the capabilities of our model, we describe the parameters that optimize the formation of colloidal chains under kinetic control, and show that it exhibits the folding behavior of two-dimensional colloidal chains commensurate with what has been recently demonstrated experimentally.44 Our scheme lays the groundwork for studying the mechano-sensitive effects of mobile binders at interfaces, including the role of catch bonds, lateral interactions, or cooperativity in strengthening adhesions.34,54
2 Description of the model
2.1 Coarse-grained model for colloidal particles with explicit mobile binders
The central unit of our simulation model is a droplet, as shown in Fig. 1a. Each droplet consists of a central spherical particle of radius R (type A) with Nb binders distributed on the surface. Each binder is composed of two particles – the outer particle (type C or D) is responsible for binding complementary partners, while the inner one (type B) is used to modulate excluded volume between binders. The positions of the binders are initialized in a “Fibonacci” arrangement to prevent overlap between any adjacent binders in the initial configurations.55 This pair of particles mimics the combination of the double-stranded tether and the single-stranded sticky-end DNA used in experiments23 (Fig. 1a). This configuration also allows us to apply an angular term to tune the propensity of the binder to stand vertically from the surface. The binders diffuse on the surface25 due to a harmonic bond between the center of the droplet and that of the inner binder particle with a spring constant kAB and rest length l0AB.The inner and outer particles in the binder are similarly held together by a harmonic bond with spring constant kBC and lBC = rB + rC, the sum of their radii. To have the binder stick outward from the droplet, the two binder particles are forced to align along the radial vector from the center of the droplet, by introducing a harmonic angular potential between the triplet of particles with parameters kABC and rest angle θ0ABC = 180°. In each case, the spring constants are chosen such that the thermal standard deviation  (where kB is the Boltzmann's constant) is a small fraction of the rest length or angle (see Table S5, ESI†). As a trade-off between enforcing rigid bonds and using an infinitesimal MD time step, we chose to use spring constants where the standard deviation is 1–2%.
(where kB is the Boltzmann's constant) is a small fraction of the rest length or angle (see Table S5, ESI†). As a trade-off between enforcing rigid bonds and using an infinitesimal MD time step, we chose to use spring constants where the standard deviation is 1–2%.
2.2 Non-bonded interactions
To prevent overlap between particles, we use a soft repulsion given by | (1) |
Our CGMD model can be used to study droplet interactions in three dimensions, but we add an optional confining potential for comparison with recent experiments where droplets are found in a plane due to the effect of gravity. To replicate a quasi two-dimensional arrangement in our system, we use a force-shifted Lennard-Jones wall potential56 on each droplet, between a fixed z-position and the center of the droplet A particle. The origins of the walls are given by (0,0,2.5R) and (0,0, −2.5R).
2.3 Dynamic bonding model
We model interactions between binders through covalent bonds. To do so, we develop a plugin to HOOMD-Blue57,58 that builds upon a model for epoxy binding developed in ref. 59. Adhesive bonds form only between complementary outer binder particles of respective droplets, as shown in Fig. 1b. In the simplest case, we have a mixture of droplets containing outer binder particles that are 100% of types C and D, respectively. The model allows for individual droplets to contain mixtures of binder types, and there may be many more than two types, as designated by the user. In this study, harmonic bonds are added with spring constant kdyn and length ldyn = rC + rD, the sum of the radii of particles forming a bond. Here, we choose harmonic bonds, but any form of bond implemented in HOOMD-Blue could be used, since our algorithm only changes the bond table within the MD simulation, and does not compute or apply forces.‡In our approach, we enforce that each binder can only participate in one possible binding reaction at a time, such that all binding events are independent. In this case, each reaction can be characterized as a two-state reaction, where the effective free energy difference between a bound and an unbound state is given by
 | (2) |
In Section A2 we describe details of the algorithm for binding and unbinding, satisfying detailed balance. Additionally, in Section A3 we describe how the binding and unbinding rates are made temperature dependent in such a way that the fraction of bound pairs at the equilibrium distance tends smoothly to zero at high T, with 50% bound pairs at a specified melting temperature Tmelt (Fig. 9).
2.4 Comparison of model and experiment geometry
While this CGMD model is generic, Fig. 10 shows how the geometry can be compared to the experimental setup in ref. 23. The radius of one binder sphere corresponds to the sticky end of length ∼5.1 nm, which is our reduced unit of length. Therefore, a droplet radius of R = 300 corresponds to the droplet size of ∼1530 nm used in ref. 23. Smaller particle sizes studied in Section 4 are also used in experiments.Practically, our simulations are computationally limited to hundreds of binders per droplet. Therefore, we equate the scale of the simulations to experiments by matching the excluded volume of all binders to that of DNA surface coverage in the experiment. More specifically, the surface coverage, p is defined as
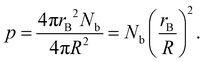 | (3) |
In the experiment, for droplets of radius R = 1530 nm, an effective repulsive radius of DNA of 1.5 nm,41,60,61 and an estimated 1×103–2×104 DNA strands,23,41p ranges from ∼0.001–0.02 or 0.1–2% coverage. For many simulations below, we use rB = 1, R = 50, and Nb = 100, in which case p = 0.04. From this perspective, each binder plays the collective role of hundreds of DNA.
3 Simulation methods
MD simulations62 of droplets coated with mobile binders were performed using HOOMD-blue version 2.9.6.57,58,63 The Langevin integrator64 was used to integrate all particles forward in time. Two different values of the drag coefficient γ were used: one for the droplets (γA) and the other for the binders (γbinder).The equation of motion for each particle i in Langevin dynamics65 is given by:
 | (4) |
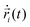 is the velocity of the particle,
is the velocity of the particle, 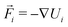 is the force on particle i derived from the total potential energy function of the system, and η(t) is the delta-correlated random white noise, with zero mean and unit variance. We use the tree neighbor list66,67 to accelerate non-bonded calculations, and in the construction of our list of possible pairs to bond as described above.
is the force on particle i derived from the total potential energy function of the system, and η(t) is the delta-correlated random white noise, with zero mean and unit variance. We use the tree neighbor list66,67 to accelerate non-bonded calculations, and in the construction of our list of possible pairs to bond as described above.
4 Results and discussion
4.1 Main objectives
In this section, we optimize simulation conditions to robustly self-assemble long colloidomers, suppressing branched structures. We explore both the molecular properties of the system (droplet radius, binder concentration, and binder interaction strength), and the experimental conditions for assembly (particle concentration and solution viscosity). The detailed parameters used for our MD simulations are listed in Tables S5–S8 (ESI†). Our results indicate that kinetic factors can be rationally employed to target the desired outcome with high yield and fidelity for fixed-time experiments. We subsequently show that our model allows us to study the folding process for colloidomer chains.4.2 Adhesion patch formation is a two-stage process for high bond strengths
The formation of chains requires that each droplet has two contacting neighbors. Monomers first form dimers, after which they either combine with monomers to make trimers, or with other dimers to make tetramers. We therefore first probe the physical processes involved in forming a patch in a dimer or trimer configuration, and then consider de novo assembly in Section 4.5.Simulations of patch formation begin with dimers and trimers in an initial configuration with a single bond already formed between the droplets. Subsequently, the patches progressively grow until they reach steady-state. We find that patch formation (at intermediate and high binding affinities, around ε > 13) happens in two stages, as illustrated in Fig. 2 (see Fig. S1, ESI†). Fitting the fraction of unbound binders versus time with a double exponential function reveals two time scales, as shown in Section S1.1 (ESI†). Initially, the fast time scale of recruitment of binders describes the formation of a stable adhesion patch (τ1), while the saturation of the patch is captured by a 1–2 orders of magnitude slower timescale (τ2). Table S1 (ESI†) reports values of τ1 and τ2 for some of these conditions. Slowing binder motion by increasing γbinder or slowing binding by decreasing kon at fixed bond strength ε increase the recruitment time τ1, as shown in Fig. S2 (ESI†); these changes should increase the yield of higher valences, discussed in Section 4.5. Modulation of kon could perhaps be realized in experiment by modifying the length of the spacer molecule, which would change the probability of finding a binding partner. The two-step patch recruitment has important consequences for the kinetically controlled assembly mechanism of colloidal chains at high ε.
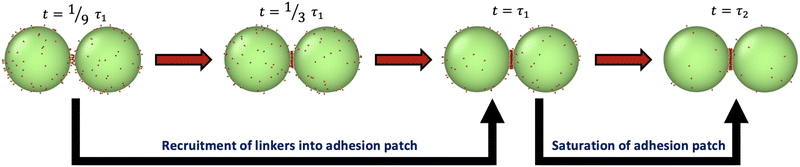 | ||
| Fig. 2 Illustration of adhesion patch formation for a dimer of droplets. Patch formation under conditions with high binding affinity occurs via a process with two time scales (τ1 and τ2), one for recruitment of most linkers into a patch, and a second proceeding to saturation. The conditions for this particular simulation are R = 50, Nb = 100 and ε = 20.7. See Section S1.1 and Table S1 (ESI†) for more details. | ||
4.3 Optimizing bond strength, droplet size, and binder concentration for colloidomerization
Optimal conditions for colloidomerization require considering both the dimer and the trimer assembly, since we must find a condition where not all binders are exhausted in the dimer, where ∼50% of binders are available on a terminal droplet of a trimer, and where very few are left on the trimer middle droplet, preventing branching. Fig. 3a shows a systematic study of the self-assembly of droplets of varying R and ε, for a fixed total number of binders Nb = 100. The heat maps show the fraction of unbound binders in three configurations: a droplet–droplet dimer, a terminal droplet in a trimer, and a central droplet in a trimer. Conditions for colloidomerization are satisfied in the region where the dashed ovals overlap. Later, we choose R = 50, ε = 20.7 and Nb = 100 to demonstrate that this condition results in the robust assembly of colloidomers.The number of binders in a patch at equilibrium is dictated by the free energy of patch formation, which can be considered as the difference in the chemical potential inside and outside the patch.41 The driving force for a binder to enter the adhesion patch is determined by the energy of forming individual bonds, ε, and opposed by steric repulsion between binders, the stretching of binders at the interface, as well as the loss of entropy as the binder motion is constrained in a patch. As ε increases, the fraction of free binders decreases monotonically in the case of both dimers and trimers until it reaches an asymptotic value that is limited by the steric repulsion between binders.
Similarly, increasing droplet size in the strong binding limit recruits progressively more binders into the patch, since there is more space at the interface between larger droplets (Fig. 3a). For large R in both dimers and trimers, we observe that the transition from no binding to all binders in the patch is very sharp as energy gain overtakes entropic losses without a penalty from steric repulsion. In contrast, for small radii, the recruitment of binders into the patch is more gradual with ε due to crowding.
Changing the droplet size not only changes the cost of packing binders into a patch, but also the entropic cost of patch formation, which increases with droplet size. Therefore, at intermediate values of ε we observe a non-monotonic recruitment of binders into the patch as a function of droplet size. While crowding dominates in small droplets, entropic costs dominate in large droplets, giving rise to an optimal size for binder recruitment, e.g. R = 120 for ε = 15 in the dimer configuration. We thus show that competition between the energy of binding, steric repulsion between binders, and the entropy of free binders can collectively result in non-monotonic patch density when tuning e.g. the droplet radius.
We can now consider the transition from dimer to trimer, where two adhesion patches are formed. Competition between the two adhesion patches results in an approximately equal split of binders on the middle droplet; therefore, even in cases where more than half of binders can pack into a patch, only half of the binders on each terminal droplet are exhausted. This situation occurs for higher ε, whereas for weaker binding, entropy dominates and many binders remain outside of the two adhesion patches on both the central and terminal droplets. We note that for high ε, rearrangement of binders between patches is expected to be slow. In Fig. S3 (ESI†) we show that there is some asymmetry between patches except at weak binding, and therefore conclude that the onset of effectively irreversible patch formation occurs roughly at ε ∼ 10.
In Fig. 3b we fix ε = 20.7 at the goldilocks value from Fig. 3a, and explore the effect of varying binder surface coverage. In this strong binding regime, we eventually saturate the geometric limit set by the droplet size and binder repulsion (see also Fig. S4, ESI†). If Nb is increased above this limit, it simply results in additional free binders. For small droplets, we quickly reach the situation where not all binders on the middle droplet of a trimer can fit into two patches, but we see that for larger droplets there is a very wide tolerance for binder concentration which might be useful for colloidomerization.
 | ||
| Fig. 3 Heat maps showing the percentage of binders remaining on the surface of a droplet in a dimer geometry, and on the terminal or central droplets in a trimer geometry. Conditions predicted to be “good” for colloidomer assembly are indicated by dashed ovals, and selected conditions marked by red open circles are illustrated in Fig. 4. (a) Fraction of remaining binders at fixed number of binders, varying droplet radius and bond strength. (b) Fraction of remaining binders at fixed high bond strength, varying number of binders and droplet radius. | ||
In summary, for certain parameters (including ε = 20.7, R = 50, Nb = 100) we find that <100% of the binders are recruited for dimers, while in trimers patches contain exactly half of the binders due to the competition between neighbors. This is an optimal situation for the self-assembly of colloidomers, and we proceed to study assembly of these droplets in Section 4.5.
4.4 Illustrating a molecular recipe for colloidomers
Fig. 4 illustrates scenarios that are predicted to be good or bad for colloidomer assembly, as described above; full trajectories for these conditions are also shown in Supplementary movies M1 and M2.† Considering the dimer, we see that large droplets and high ε allow almost all the binders to fit into a patch, which is detrimental for colloidomer assembly because it terminates the polymerization reaction. Decreasing droplet size to R = 50 limits binders due to their steric repulsion in the patch, leaving just enough binders to seed a trimer with no remaining binders on the middle droplet, thus imposing the self-assembly of linear chains. Lowering the droplet size further or decreasing the binding strength leaves too many binders free on the trimer middle droplet at equilibrium, which would eventually lead to the self-assembly of branched colloidomers. Fig. 4b illustrates that for a fixed droplet size and bond strength, the number of binders must be chosen such that dimers have free binders to grow the chain, while trimers have no free binders for branching via the middle droplet, as is the case for Nb = 100. On the other hand, Nb = 50 has almost all the binders (97%) recruited in the case of the dimer, terminating colloidomer assembly. For Nb = 300, the central droplet of a trimer has 21% binders remaining on the surface, which would result in the branching of colloidomers. | ||
| Fig. 4 Illustrations showing the dimer and trimer geometries simulated in Fig. 3, and the “molecular” features of our droplet model that can be tuned to optimize for linear chains. Both results for dimers and trimers must be considered to predict the resulting polymerization reaction. (a) Varying R and ε at fixed number of binders Nb = 100, with dimer on left and trimer on right. (b) Varying the number of binders Nb at fixed R = 50 and ε = 20.7. In (a) and (b), the % of free binders available (averaged over 10 independent runs) is indicated in parentheses beside each of these conditions for a droplet in a dimer as well as the terminal and central droplet(s) of a trimer. Based on the values of the percentage of free binders available, the conditions which are not suitable for colloidomer assembly (almost all used up in dimer, too many remaining on central droplet in a trimer) are indicated by a red X. | ||
4.5 Kinetic optimization of colloidomerization
Beyond dimers and trimers, the self-assembly of chains requires further optimization of competing experimental timescales. Combining a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of droplets containing complementary binders of particles type ‘C’ and ‘D’ mimics the experiments in ref. 23. Tuning the density ϕ (area fraction) of droplets modulates the thermodynamic driving force for assembly, but also controls the collision time between droplets and allows us to optimize the formation of long colloidomers out of equilibrium for fixed time of assembly. Given that the droplets are undergoing simple diffusion, the collision time τcollision ∼ 〈l2〉/D, where l is the distance between droplets and D is the diffusion constant. In two dimensions, l2 ∼ ϕ−1, such that the collision time is inversely proportional to the droplet density. The Einstein relation gives D = kBT/γ, therefore τcollision ∼ γ, the drag on a particle.
1 mixture of droplets containing complementary binders of particles type ‘C’ and ‘D’ mimics the experiments in ref. 23. Tuning the density ϕ (area fraction) of droplets modulates the thermodynamic driving force for assembly, but also controls the collision time between droplets and allows us to optimize the formation of long colloidomers out of equilibrium for fixed time of assembly. Given that the droplets are undergoing simple diffusion, the collision time τcollision ∼ 〈l2〉/D, where l is the distance between droplets and D is the diffusion constant. In two dimensions, l2 ∼ ϕ−1, such that the collision time is inversely proportional to the droplet density. The Einstein relation gives D = kBT/γ, therefore τcollision ∼ γ, the drag on a particle.
In Fig. 5, we show that by fixing the previously optimized R, Nb, ε parameters and varying ϕ and γA, we can maximize the yield of colloidomers (with results from two lower values of ε shown in Fig. S8–S10, ESI†). Previous arguments suggest that higher valences would be preferred at equilibrium,50–52 but in this case our goal is to maximize the yield of linear chains. We therefore adopt the strategy of kinetic control, where we predict that chains can be formed whenever adhesion patches form and exhaust approximately half of available binders before subsequent droplet collisions and patch formation, based on the strategies in the previous section. To achieve this control, we first vary the droplet density ϕ. Since droplet collisions are fast in dense suspensions, we observe many droplets with valence three or four at the highest initial density. At lower densities, valence two predominates as predicted based on our dimer or trimer experiments; whenever that does not occur “defects” result, producing branched structures.
 | ||
Fig. 5 Effect of area fraction ϕ and the droplet drag coefficient γA on self-assembly in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of 81 R = 50 droplets containing Nb = 100 complementary binders of type C and D (with one surplus droplet of C/D). ε = 20.7. Here, ϕ = 0.1, 0.2, 0.3, 0.4 (increasing from left to right) and γA = 0.01, 1.0 (bottom and top). Every system is the same size, but each snapshot has identically sized field of view by area, meaning droplets are cropped at ϕ < 0.4. Droplets are colored according to structure as shown in the key. Each condition is accompanied with bar charts representing quantities computed over 10 independent runs that can quantitatively help in collectively deciding the ‘winning condition’ for colloidomer formation. These quantities are labeled in the second key, and described in detail in the main text, and for each quantity, optimal would be a larger bar. The few droplets that have valence 3 or higher are also marked with a ‘cross’ in the representative configurations to reinforce that even the branched structures which are considered part of ‘errors’ have long segments of droplets with valence = 2. The condition we consider optimal, ϕ = 0.3, γA = 1.0 is highlighted with a red box. Snapshots at ϕ = 0.4 show periodic images to emphasize that structures are extended across the periodic boundaries. The distributions of structures obtained, particle valences, and of colloidomer chain lengths for each of these 8 conditions are provided in Fig. S5–S7 (ESI†) respectively. Timing data for these simulations as well as larger systems are given in Tables S2 and S3 (ESI†). 1 mixture of 81 R = 50 droplets containing Nb = 100 complementary binders of type C and D (with one surplus droplet of C/D). ε = 20.7. Here, ϕ = 0.1, 0.2, 0.3, 0.4 (increasing from left to right) and γA = 0.01, 1.0 (bottom and top). Every system is the same size, but each snapshot has identically sized field of view by area, meaning droplets are cropped at ϕ < 0.4. Droplets are colored according to structure as shown in the key. Each condition is accompanied with bar charts representing quantities computed over 10 independent runs that can quantitatively help in collectively deciding the ‘winning condition’ for colloidomer formation. These quantities are labeled in the second key, and described in detail in the main text, and for each quantity, optimal would be a larger bar. The few droplets that have valence 3 or higher are also marked with a ‘cross’ in the representative configurations to reinforce that even the branched structures which are considered part of ‘errors’ have long segments of droplets with valence = 2. The condition we consider optimal, ϕ = 0.3, γA = 1.0 is highlighted with a red box. Snapshots at ϕ = 0.4 show periodic images to emphasize that structures are extended across the periodic boundaries. The distributions of structures obtained, particle valences, and of colloidomer chain lengths for each of these 8 conditions are provided in Fig. S5–S7 (ESI†) respectively. Timing data for these simulations as well as larger systems are given in Tables S2 and S3 (ESI†). | ||
A second way to modulate our kinetic yield of chains can be achieved is by increasing γA for the droplet, which slows down the collision rates without changing the thermodynamic driving force for assembly and increases the yield of linear chains, while also avoiding loop formation (Fig. 5-upper row); full trajectories for the upper row are also provided in Supplementary movie M3.† As described in the simulation methods (Section 3), it is important to note that we control drag on the central droplet and binders separately; here we only varied the drag on the droplet particle ‘A’ (γA) and kept γbinder at a very small constant value, because increasing γ for each of the binder particles can also slow down the diffusion of the droplet as a whole. We also predict that decreasing the binding rate kon at fixed bond strength ε would be detrimental to our goal of assembling chains, since as described earlier it would take longer to assemble a patch as compared to the collision time of droplets (see Fig. S2, ESI†). The relative speeds of the two competing processes of patch recruitment and droplet–droplet collision can thus be tuned to dictate the kind of structures observed in self-assembly and provide more insights on kinetic control.
More quantitatively, we compute the distribution of structures produced at the end of 108 steps, averaging over 10 independent simulations. We partition every interconnected assembly using an algorithm described in Section S2.1 (ESI†), and then classify these structures as monomers, dimers, linear chains (N ≥ 3), loops, and ‘other’ (at least one droplet has valence ≥3). To define the best conditions for chain assembly, we sought to maximize three quantities that are shown in bar charts next to each condition in Fig. 5: (1) fraction of droplets present in structures that are not monomers or branched—which we call “success” (purple bar), (2) fraction of droplets with valence 2 (green bar), and (3) the average maximum chain length (blue bar, which we scale by the highest value 〈Nmax〉highest = 20 observed for the condition ϕ = 0.4, γA = 1.0).
While conditions at ϕ = 0.4 have the longest chains and a high fraction of particles with valence 2, there are also many ‘errors’ due to chain branching, and so we eliminate high density. Conditions at lower ϕ have fewer errors but also shorter chains. Based on maximizing these three metrics, we choose the condition (ϕ = 0.3, γA = 1.0) as our best, and we provide more details about the structures observed at this condition in Fig. 6.
 | ||
| Fig. 6 Best choice of parameters for obtaining maximum quality of colloidomer chains: Nb = 100, R = 50, ϕ = 0.3, ε = 20.7, γA = 1.0. (a) Fraction of droplets in each possible valence versus time. (b) Final valence distribution obtained across the 10 simulations. Open squares show optimal valence distribution from Fig. 2g in ref. 23. (c) A combined histogram showing the fraction of the total number of droplets present as a particular kind of structure from 10 different final configurations for this condition. (d) Distribution of linear chain lengths P(N) obtained for this condition, with the errorbars computed using a bootstrapping procedure described in Section S2.3 (ESI†).68,69 Open squares show experimental length distribution from Fig. 3a in ref. 23. | ||
In Fig. 6a, we show the evolution of bond valence versus time, which reflects on average, colloidomers are formed by conversion of monomers to dimers, followed by the conversion of dimers to trimers. Fig. 6b shows the distribution of valence, and for this condition, we observe that only ≈5% of droplets had valence higher than 2, which is indicative of a small number of branching points in chains. This result actually has a higher yield of linear chains than the best condition found experimentally in ref. 23. However, even a small fraction of droplets with valence 3 can prevent extremely high quality assembly of only chains, as shown in Fig. 6c, where we observe that ≈30% of droplets are present in structures that contain at least one particle of valence 3 (cyan bar), and hence are considered as errors. Finally, Fig. 6d shows that the distribution of chain lengths seems to follow an exponential distribution, with an average length longer than in the optimal conditions in ref. 23. An exponential distribution implies that it will be challenging to obtain a large median chain length via a simple self-assembly strategy. This comports with experimental findings, where for efficiency, a new methodology was developed to engineer longer chains using magnetic fields applied to a dispersion in a ferrofluid.44
4.6 Application of the model to colloidomer folding
Folding of colloidomer chains and the study of their pathways towards stable structures is an area of active research.44 Here, we demonstrate that our CG model can capture experimentally relevant folding behavior of colloidomer chains and use this to highlight additional features of our CG framework.Our CG framework allows the user to generate an initial linear colloidomer chain of any length and an arbitrary sequence of binder types. Moreover, there can be multiple types of binders on the same droplet. To study colloidomer folding, we mimic the experimental setup of having two types of binders on the same droplet, C and D, each of which is self-complementary. Here, C–C bonds are intended to make up the backbone of the chain, while D–D bonds are the ones driving folding. As described earlier, our dynamic bonding model can also have temperature dependent binding/unbinding (see Section A3 for full details). We therefore choose different melting temperatures such that D–D bonds melt at a lower temperature, while C–C bonds stay in place.
Here, we generate folded structures using a square wave heating and cooling cycle. During the first segment at higher temperature, the backbone adhesion patches form and the chain explores unfolded configurations. After that, repeated cooling and heating are used to generate low energy structures.
In contrast to our work in Section 4.3 on optimizing colloidomer assembly, here we do want to produce higher valences. This is achieved through the use of smaller R = 20 and lower εDD = 4.6, where reversible bonding allows for rearrangements such that equilibrated structures form. Low R has the additional benefit of faster folding times, allowing us to generate many structures in relatively little computational time.
As a benchmark case to confirm that our model would be applicable in future studies of colloidomer chain folding, we investigate the heptamer case consisting of N = 7 droplets that has been experimentally realized in ref. 44. There are four possible rigid structures which are the low energy states of the heptamer. Scanning a small range of R and εDD over 15 heating–cooling cycles we uncover the aforementioned condition (R = 20, εDD = 4.6) where all four possible structures are observed in a single simulation, as shown in Fig. 7a, and Supplementary movie M4.†
 | ||
| Fig. 7 (a) Folding and unfolding cycles shown for a heptamer of droplets with 100 ‘C’ binders and 100 ‘D’ binders on each droplet, R = 20, εDD = 4.6, εCC = ∞, and γA = 0.1. Tmelt = 1.2 for D–D bonds and temperature is cycled between 1.0 and 1.3. The variation of the average bond valence 〈Bn〉 (red) with simulation time is shown, as the temperature (navy blue) is alternately raised and lowered. An expected 〈Bn〉 = 1.7 is obtained when the structures unfold back to chains. (b) Histogram showing the yield of each of the four possible folded rigid structures (ladder, chevron, rocket and flower)44 from a total of 1500 folded structures obtained from 300 independent simulations each consisting of 5 folding and unfolding cycles. (only 5/1500 did not reach one of these structures, and are not shown in this histogram). | ||
Having obtained all structures in a single long simulation, we wished to quantify the population of each stable folded state. We ran 300 independent simulations each consisting of 5 folding/unfolding cycles and show in Fig. 7b the yields of each structure; the ladder and the chevron structures are kinetically accessible and have a higher yield than the rocket and flower geometries, in good agreement with ref. 44.
From these preliminary studies of folding within our model, we have learned several key principles. Firstly, we only observe the flower structure—which has the highest bond count—when εDD is very low; this is because folding to this structure is not fully downhill, and requires the breaking of a droplet–droplet bond (dissolving an entire adhesion patch) to reach the final state. Second, every droplet contains both C and D binders, and so it could be a concern that the D's become exhausted in forming backbone bonds, which would tend to form faster than bonds farther away in sequence space. In our simulation, this is prevented by choosing R and Nb where the patch is fully saturated by C's (see Fig. S4 and S11, ESI†), meaning that there is no opportunity for D's to enter the backbone.
Moreover, the exclusion of D's from the adhesion patches means there is a smaller area for them to occupy, which results in faster formation of bonds during the folding process. The factors which contribute to the speed of folding are also important to our results, since both in simulations and in experiments we do not want to wait arbitrarily long times in the cooling phase when generating low energy structures.
5 Conclusions
In this work, we report a CG model and simulation framework for colloidal liquid droplets with explicit mobile binders. The core of this model is a dynamic bonding protocol that satisfies detailed balance, that is very flexible in allowing one to control separately binding and unbinding rate constants, as well as implementing a tunable temperature dependence. Both the dynamic bonding code and the pyColloidomer framework are easy to use and freely available with examples from https://github.com/hocky-research-group/pyColloidomer_2023.Previous modeling works have studied colloidal liquid droplets with implicit mobile linkers, such that bonds are formed or removed based on a statistical mechanical model that predicts the strength of a patch and which can include timescales for bonding. Our model with explicit binders complements these studies—while having many explicit binders makes the model higher resolution, and hence slower, it also allows us to build insight into the adhesion patch formation process. For example, the use of explicit binders allowed us to see the effects of excluding particles from patches once they are formed, which had major consequences for ensuring valence = 2 structures in optimizing colloidomer assembly, and in preventing binders from being used up in colloidomer backbones in our folding studies. We also observe that above a certain binding strength (around ε > 13), the growth of a patch can follow a process characterized by two timescales, where saturation can take much longer than initial formation and recruitment. This could have an important effect at higher densities and lower viscosities, where droplet collisions can take place before patches are fully recruited; this effect could be incorporated into simulation models that use a parameterized equation for the recruitment process, such as recently done in ref. 53. The separation of the timescales for the motion of the droplet and for the binders in our CGMD model can also be applied in the case of systems such as polymer-grafted nanoparticles (NPs)46–49 which can help in kinetically controlling the interactions and hence the formation of non-equilibrium structures such as sheets and strings.
In ongoing work, we are now using these explicit binders to test the contributions to the free energy of patch formation and patch shape predicted experimentally in ref. 41. We are also expanding our dynamic bonding model to include the effect of force on unbinding rates54,70,71 to probe its effect on adhesion patch formation,23,41 a dependence which is known to play an important role in the behavior of biomimetic assemblies of cellular adhesion proteins.33 Preliminary data shows that our model captures observed behavior for folding of two dimensional colloidomer homopolymer chains; in future work we can use our model to compare the structures and pathways generated through the use of explicit binders with those using very reduced models.44,72 We can also trivially expand our folding studies to three dimensions by removing confinement, which will allow us to detail folding pathways in ways that are difficult to quantify in experiment.
Our CG model is quite versatile and can also be adapted to represent the behavior of analogous systems of lipid bilayers mentioned earlier;24–29 it can also be used to explore the assembly of colloidal nanoparticles coated with ligands that bond via formation of reversible dynamic bonds with secondary linker molecules.73,74 Linker-mediated colloidal assembly is a ripe area for exploration because the mobility of the secondary linkers and the reversibility in bonding can lead to formation of kinetically controlled structures such as string-like gels. Tuning the ratio of the linker to the colloid concentration73,74 can appropriately control the phase behavior. It would be fascinating to explore the consequences of assembling our particles with mobile binders using explicit free linkers with complementary binding sites rather than using direct binding.
Although our model captures what we believe to be the most crucial features of systems with mobile binding sites, there are simplifications whose effects we would like to investigate in the future. For example, the presence of a spring between the center of the droplet and binders allows the binders' vertical position to vary, and by tuning this parameter we can explore the tendency to form a planar adhesion patch—however, we are missing the lateral coupling between binders that could be important in the case of deformable droplets. Our work also currently employs harmonic springs, and we plan to investigate the differences where more complex stretching behavior is taken into account.41 Our powerful and flexible framework is freely available and simple to use, and so we hope others will build upon our work and take these studies in new directions.
Conflicts of interest
There are no conflicts to declare.Appendices
A1 Non-bonded interaction details

| (A1) |
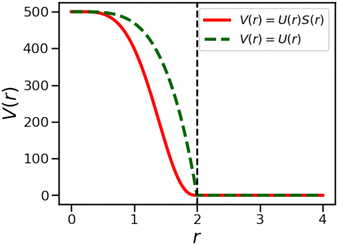
Here, εsoft is the strength of the interaction potential (in units of kBT) and rcut is the cut-off distance, as shown by the dotted green curve in Fig. 8. A smoothing function was applied to this potential Usoft(r) that results in both the potential energy and the force going smoothly to 0 at r = rcut, in this case the XLPOR smoothing75 function S(r), given by
 | (A2) |
Here, ron is chosen as the point at which the smoothing starts. We set ron = 0.1 rcut for our simulations. The modified potential is shown in Fig. 8 and is given by
 | (A3) |
The soft potential was implemented by using HOOMD-Blue's tabulated potential option (with 1000 interpolation points between rmin = 0 and rmax = 1.05 rcut).
The wall potential is given by a shifted LJ potential with rcut = 21/6(2R).
| Vwall(r) = VFLJ(r) − VFLJ(rcut) | (A4) |
 | (A5) |
 | (A6) |
A2 Algorithm for binding and unbinding
Every n steps of the MD simulation (run using HOOMD-Blue), a Dynamic Bond Updater is called. The Dynamic Bond Updater is an open source C++ plugin (based on previous work on epoxy curing59) that stochastically adds or removes dynamic bonds during the course of the MD simulation. If there is more than one dynamic bond type present in the system, the Bond Updater has to be configured for each independently.Each time the bond updater is called, it first iterates over all the existing dynamic bonds to attempt unbinding. The probability of unbinding is calculated, given by
| P0off = nkoff dt | (A7) |
After performing unbinding, we create a list of proposed bonds to add. We iterate over particles which were unbound at the start of the binding update (but not those freed by unbinding), and find the closest available complementary particle which is also unbound and whose distance from the particle under consideration is between lmin and lmax (by iterating over HOOMD-Blue's neighbor list). If an eligible neighbor exists, and neither particle is already in the proposed bonds list, then this pair is appended. Our binding algorithm is inspired by (but not identical) to the implementations in ref. 76–78.
We then iterate over the proposed bond list, generating new uniform random numbers and creating a bond if r < Pon. By default, P0on = nkon dt. Here we choose kon such that kon(ndt) = 1, i.e. the fastest possible reaction rate for a specific time discretization because we want to form as many bonds as possible without rejecting too many Monte Carlo79 moves. We note that as a consequence, this scheme does not intend to match detailed chemical kinetics of the underlying processes, which would require schemes that would be more computationally demanding such as the Gillespie algorithm80 used in ref. 51. To ensure detailed balance for individual binding reactions, the probability of binding is modified71,81 such that Pon = P0one−ΔU(d)/kBT, where ΔU is the additional energy added by creating a bond of length d, possibly away from its rest length. Since we are only using harmonic bonds in this work,
 | (A8) |
As in ref. 81, we are putting all of the energetic dependence into the binding step and none in the unbinding step, although other choices are possible.71 The stretch dependent binding rates prevents formation of bonds which are very unlikely, so this helps in preventing non-equilibrium heating of the system. This choice of stretch-dependent on rate and constant off rate does not correspond to our belief about the detailed molecular kinetics of DNA unbinding, but rather is an algorithmic choice that is valid because we are not currently interested in including the detailed effect of stretching on the rates, although we are planning to pursue this direction in the future.54,70,71
Detailed balance for the overall binding/unbinding reaction is satisfied to the best of our ability when performing a large set of binding/unbinding reactions at once (as compared to only doing one single binding/unbinding per trial) by ensuring that every event is independent such that the probability of the total change in bonded pairs factorizes, and each individually satisfies a Metropolis criterion.62,79 We ensure independence by generating a list of possible reactions in a deterministic order and only allowing a particle to possibly bind with one other particle. The only possibly weak breaking of detailed balance comes in the rare situation where upon unbinding, one or both of the particles was assigned a different binding partner since it was not bound to the neighbor from whom its distance is most close to the equilibrium bond length. In practice, because we use a stiff spring this is very unlikely, and moreover, the configuration evolves n steps between binding/unbinding trials, we do not expect this to cause any substantial non-equilibrium effects.
A3 Temperature dependence of binding/unbinding
Our dynamic bonding model allows us to use non-constant values of koff, kon. As one example, for this work we have incorporated an optional dependence of the rate constants on temperature. Since our binders here might represent double stranded DNA, which dissociates in a cooperative manner, we implemented an optional tunable sigmoidal dependence on temperature for the rate constants. Without trying to match the behavior of any specific module, we implemented a two parameter sigmoidal dependence on temperature to represent cooperative melting, | (A9) |
| kon/off(T) = kiniton/off(1 − g(T)) + kmelton/offg(T) | (A10) |
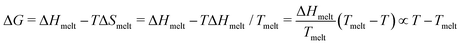 ; ΔS = ΔH/Tmelt because ΔG(T = Tmelt) = 0.
; ΔS = ΔH/Tmelt because ΔG(T = Tmelt) = 0.
Combining these results in for either off or on rates and ΔT = T − Tmelt,
 | (A11) |
For a two-state model, the bound fraction is given by
 | (A12) |
| kiniton + kmelton = kinitoff + kmeltoff | (A13) |
 | ||
| Fig. 9 (a) g(T) vs. T (b) Fraction fbound(T) of DNA that is bound for a single DNA pair vs. T for two different binding strengths ε = 3.0 and 16.0 (the temperature is in units of T*). | ||
Combining all of these facts together, we get
 | (A14) |
 | (A15) |
We note that the on rate expression is the commonly used Glauber rule83 from Monte Carlo simulations62,79,84 assuming a difference in (free) energy between two states proportional to ΔT as explained above, but here the off rate is a modification of this Glauber rule that switches between two finite rates rather than zero and infinity.
 | ||
| Fig. 10 Complementary binders in our CG model mapped onto the dsDNA and ssDNA configuration of ref. 23 for scale. Complementary outer binder particles (red and blue) form a dynamic bond representing the interaction between complementary DNA strands (figure created with https://biorender.com/). | ||
A4 Comparison of our droplet model with experimental geometry
Acknowledgements
We thank Joshua A. Anderson for helping us with technical issues pertaining to our HOOMD-Blue plugin development. We also thank Stephen Thomas and Eric Jankowski for discussions on the details of their dynamic bonding plugin. G. M. and G. M. H. were primarily supported by the National Institutes of Health (NIH) via Award No. R35-GM138312. G. M. and D. P. received additional support through the Department of Energy via Award No. DE-SC0019695. A. M. and J. B. were supported by the National Science Foundation under grants, NSF DMR-1710163 and NSF DMR-2105255. J. B.'s work was also supported by the Paris Region (Région Île-de-France) under the Blaise Pascal International Chairs of Excellence. This work was supported in part through the NYU IT High Performance Computing resources, services, and staff expertise, and simulations were partially executed on resources supported by the Simons Center for Computational Physical Chemistry at NYU (SF Grant No 839534).References
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed
.
- W. B. Rogers, W. M. Shih and V. N. Manoharan, Nat. Rev. Mater., 2016, 1, 1–14 Search PubMed
.
- L. Cademartiri and K. J. Bishop, Nat. Mater., 2015, 14, 2–9 CrossRef CAS PubMed
.
- T. Hueckel, G. M. Hocky and S. Sacanna, Nat. Rev. Mater., 2021, 6, 1053–1069 CrossRef CAS
.
- Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Nature, 2012, 491, 51–55 CrossRef CAS PubMed
.
- Z. Zhang and S. C. Glotzer, Nano Lett., 2004, 4, 1407–1413 CrossRef CAS PubMed
.
- Y.-J. Kim, J.-B. Moon, H. Hwang, Y. S. Kim and G.-R. Yi, Adv. Mater., 2022, 2203045 Search PubMed
.
- M. He, J. P. Gales, É. Ducrot, Z. Gong, G.-R. Yi, S. Sacanna and D. J. Pine, Nature, 2020, 585, 524–529 CrossRef CAS PubMed
.
- C. A. Mirkin, R. L. Letsinger, R. C. Mucic and J. J. Storhoff, Nature, 1996, 382, 607–609 CrossRef CAS PubMed
.
- A. P. Alivisatos, K. P. Johnsson, X. Peng, T. E. Wilson, C. J. Loweth, M. P. Bruchez and P. G. Schultz, Nature, 1996, 382, 609–611 CrossRef CAS PubMed
.
- P. L. Biancaniello, A. J. Kim and J. C. Crocker, Phys. Rev. Lett., 2005, 94, 058302 CrossRef PubMed
.
- D. Nykypanchuk, M. M. Maye, D. Van Der Lelie and O. Gang, Nature, 2008, 451, 549–552 CrossRef CAS PubMed
.
- M. R. Jones, N. C. Seeman and C. A. Mirkin, Science, 2015, 347, 1260901 Search PubMed
.
- M.-P. Valignat, O. Theodoly, J. C. Crocker, W. B. Russel and P. M. Chaikin, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 4225–4229 CrossRef CAS PubMed
.
- N. Kern and D. Frenkel, J. Chem. Phys., 2003, 118, 9882–9889 CrossRef CAS
.
- F. Sciortino, E. Bianchi, J. F. Douglas and P. Tartaglia, J. Chem. Phys., 2007, 126, 194903 CrossRef PubMed
.
- J. Russo, P. Tartaglia and F. Sciortino, J. Chem. Phys., 2009, 131, 014504 CrossRef PubMed
.
- Z. Zhang and K. H. DuBay, J. Phys. Chem. B, 2021, 125, 3426–3437 CrossRef CAS PubMed
.
- M. N. OBrien, H.-X. Lin, M. Girard, M. Olvera de la Cruz and C. A. Mirkin, J. Am. Chem. Soc., 2016, 138, 14562–14565 CrossRef CAS PubMed
.
- P. Varilly, S. Angioletti-Uberti, B. M. Mognetti and D. Frenkel, J. Chem. Phys., 2012, 137, 094108 CrossRef PubMed
.
- D. Banerjee, B. A. Lindquist, R. B. Jadrich and T. M. Truskett, J. Chem. Phys., 2019, 150, 124903 CrossRef CAS PubMed
.
- M. Dijkstra and E. Luijten, Nat. Mater., 2021, 20, 762–773 CrossRef CAS PubMed
.
- A. McMullen, M. Holmes-Cerfon, F. Sciortino, A. Y. Grosberg and J. Brujic, Phys. Rev. Lett., 2018, 121, 138002 CrossRef CAS PubMed
.
- S. A. van der Meulen and M. E. Leunissen, J. Am. Chem. Soc., 2013, 135, 15129–15134 CrossRef CAS PubMed
.
- L. Feng, L.-L. Pontani, R. Dreyfus, P. Chaikin and J. Brujic, Soft Matter, 2013, 9, 9816–9823 Search PubMed
.
- S. J. Bachmann, J. Kotar, L. Parolini, A. Šarić, P. Cicuta, L. Di Michele and B. M. Mognetti, Soft Matter, 2016, 12, 7804–7817 RSC
.
- Y.-H. M. Chan, P. Lenz and S. G. Boxer, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18913–18918 CrossRef CAS PubMed
.
- R. J. Rawle, B. van Lengerich, M. Chung, P. M. Bendix and S. G. Boxer, Biophys. J., 2011, 101, L37–L39 CrossRef CAS PubMed
.
- M. Chung, B. J. Koo and S. G. Boxer, Faraday Discuss., 2013, 161, 333–345 RSC
.
- X. Xia, H. Hu, M. P. Ciamarra and R. Ni, Sci. Adv., 2020, 6, eaaz6921 CrossRef CAS PubMed
.
- G. I. Bell, M. Dembo and P. Bongrand, Biophys. J., 1984, 45, 1051 CrossRef CAS PubMed
.
- M. Hadorn, E. Boenzli, K. T. Sørensen, H. Fellermann, P. Eggenberger Hotz and M. M. Hanczyc, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 20320–20325 CrossRef CAS PubMed
.
- L.-L. Pontani, I. Jorjadze, V. Viasnoff and J. Brujic, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9839–9844 CrossRef CAS PubMed
.
- L.-L. Pontani, I. Jorjadze and J. Brujic, Biophys. J., 2016, 110, 391–399 CrossRef CAS PubMed
.
- K. B. M'Barek, D. Molino, S. Quignard, M.-A. Plamont, Y. Chen, P. Chavrier and J. Fattaccioli, Biomaterials, 2015, 51, 270–277 CrossRef PubMed
.
- S. Angioletti-Uberti, P. Varilly, B. M. Mognetti and D. Frenkel, Phys. Rev. Lett., 2014, 113, 128303 CrossRef PubMed
.
- L.-L. Pontani, M. F. Haase, I. Raczkowska and J. Brujic, Soft Matter, 2013, 9, 7150–7157 RSC
.
- N. A. Elbers, J. Jose, A. Imhof and A. van Blaaderen, Chem. Mater., 2015, 27, 1709–1719 CrossRef CAS
.
- Y. Zhang, A. McMullen, L.-L. Pontani, X. He, R. Sha, N. C. Seeman, J. Brujic and P. M. Chaikin, Nat. Commun., 2017, 8, 1–7 CrossRef PubMed
.
- Y. Zhang, X. He, R. Zhuo, R. Sha, J. Brujic, N. C. Seeman and P. M. Chaikin, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9086–9091 CrossRef CAS PubMed
.
- A. McMullen, S. Hilgenfeldt and J. Brujic, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2112604118 CrossRef CAS PubMed
.
- I. Coluzza, P. D. van Oostrum, B. Capone, E. Reimhult and C. Dellago, Soft Matter, 2013, 9, 938–944 RSC
.
- I. Coluzza, P. D. van Oostrum, B. Capone, E. Reimhult and C. Dellago, Phys. Rev. Lett., 2013, 110, 075501 CrossRef PubMed
.
- A. McMullen, M. Muñoz Basagoiti, Z. Zeravcic and J. Brujic, Nature, 2022, 610, 502–506 CrossRef CAS PubMed
.
- I. Chakraborty, D. J. Pearce, R. W. Verweij, S. C. Matysik, L. Giomi and D. J. Kraft, ACS Nano, 2022, 16, 2471–2480 CrossRef CAS PubMed
.
- P. Akcora, H. Liu, S. K. Kumar, J. Moll, Y. Li, B. C. Benicewicz, L. S. Schadler, D. Acehan, A. Z. Panagiotopoulos and V. Pryamitsyn,
et al.
, Nat. Mater., 2009, 8, 354–359 CrossRef CAS PubMed
.
- V. Pryamtisyn, V. Ganesan, A. Z. Panagiotopoulos, H. Liu and S. K. Kumar, J. Chem. Phys., 2009, 131, 221102 CrossRef PubMed
.
- T.-Y. Tang and G. Arya, Macromolecules, 2017, 50, 1167–1183 CrossRef CAS
.
- N. A. Mahynski and A. Z. Panagiotopoulos, J. Chem. Phys., 2015, 142, 074901 CrossRef PubMed
.
- S. Angioletti-Uberti, B. M. Mognetti and D. Frenkel, Phys. Chem. Chem. Phys., 2016, 18, 6373–6393 RSC
.
- S. J. Bachmann, M. Petitzon and B. M. Mognetti, Soft Matter, 2016, 12, 9585–9592 RSC
.
- B. M. Mognetti, P. Cicuta and L. Di Michele, Rep. Prog. Phys., 2019, 82, 116601 CrossRef CAS PubMed
.
- P. A. Sánchez, A. Caciagli, S. S. Kantorovich and E. Eiser, J. Mol. Liq., 2023, 382, 121895 CrossRef
.
- D. Gomez, W. J. Peña Ccoa, Y. Singh, E. Rojas and G. M. Hocky, J. Phys. Chem. B, 2021, 125, 12115–12124 CrossRef CAS PubMed
.
- R. Swinbank and R. James Purser, Q. J. R. Meteorol. Soc., 2006, 132, 1769–1793 CrossRef
.
-
S. Toxvaerd and J. C. Dyre, Communication: Shifted forces in molecular dynamics, 2011 Search PubMed
.
- J. A. Anderson, C. D. Lorenz and A. Travesset, J. Comput. Phys., 2008, 227, 5342–5359 CrossRef
.
- J. A. Anderson, J. Glaser and S. C. Glotzer, Comput. Mater. Sci., 2020, 173, 109363 Search PubMed
.
- S. Thomas, M. Alberts, M. M. Henry, C. E. Estridge and E. Jankowski, J. Chem. Theor. Comput., 2018, 17, 1840005 CrossRef CAS
.
- M. E. Ferrari and V. A. Bloomfield, Macromolecules, 1992, 25, 5266–5276 CrossRef CAS
.
- I. Koltover, K. Wagner and C. R. Safinya, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 14046–14051 CrossRef CAS PubMed
.
-
D. Frenkel, B. Smit and M. A. Ratner, Understanding molecular simulation: from algorithms to applications, Academic press, San Diego, 1996, vol. 2 Search PubMed
.
- J. Glaser, T. D. Nguyen, J. A. Anderson, P. Lui, F. Spiga, J. A. Millan, D. C. Morse and S. C. Glotzer, Comput. Phys. Commun., 2015, 192, 97–107 CrossRef CAS
.
- C. L. Phillips, J. A. Anderson and S. C. Glotzer, J. Comput. Phys., 2011, 230, 7191–7201 CrossRef CAS
.
-
B. Leimkuhler and C. Matthews, Molecular dynamics, Springer, 2015, vol. 36 Search PubMed
.
- M. P. Howard, J. A. Anderson, A. Nikoubashman, S. C. Glotzer and A. Z. Panagiotopoulos, Comput. Phys. Commun., 2016, 203, 45–52 CrossRef CAS
.
- M. P. Howard, A. Statt, F. Madutsa, T. M. Truskett and A. Z. Panagiotopoulos, Comput. Mater. Sci., 2019, 164, 139–146 CrossRef CAS
.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed
.
-
B. Efron and R. J. Tibshirani, An introduction to the bootstrap, CRC press, 1994 Search PubMed
.
- W. J. Peña Ccoa and G. M. Hocky, J. Chem. Phys., 2022, 156, 125102 CrossRef PubMed
.
- S. Marbach and C. E. Miles, arXiv, 2022, preprint, arXiv:2212.08777 DOI:10.48550/arXiv.2212.08777.
- A. Trubiano and M. Holmes-Cerfon, Soft Matter, 2021, 17, 6797–6807 RSC
.
- M. N. Dominguez, M. P. Howard, J. M. Maier, S. A. Valenzuela, Z. M. Sherman, J. F. Reuther, L. C. Reimnitz, J. Kang, S. H. Cho and S. L. Gibbs,
et al.
, Chem. Mater., 2020, 32, 10235–10245 CrossRef CAS
.
- J. Kang, S. A. Valenzuela, E. Y. Lin, M. N. Dominguez, Z. M. Sherman, T. M. Truskett, E. V. Anslyn and D. J. Milliron, Sci. Adv., 2022, 8, eabm7364 Search PubMed
.
- J. A. Anderson and S. C. Glotzer, arXiv, 2013, preprint, arXiv:1308.5587, 26 DOI:10.48550/arXiv.1308.5587.
- S. L. Freedman, S. Banerjee, G. M. Hocky and A. R. Dinner, Biophys. J., 2017, 113, 448–460 Search PubMed
.
- S. L. Freedman, G. M. Hocky, S. Banerjee and A. R. Dinner, Soft Matter, 2018, 14, 7740–7747 RSC
.
- S. L. Freedman, C. Suarez, J. D. Winkelman, D. R. Kovar, G. A. Voth, A. R. Dinner and G. M. Hocky, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 16192–16197 CrossRef CAS PubMed
.
- N. Metropolis and S. Ulam, J. Am. Stat. Assoc., 1949, 44, 335–341 CrossRef CAS PubMed
.
- D. T. Gillespie, Annu. Rev. Phys. Chem., 2007, 58, 35–55 CrossRef CAS PubMed
.
- O. Maxian, A. Donev and A. Mogilner, Biophys. J., 2022, 121, 1230–1245 CrossRef CAS PubMed
.
-
D. Barrick, Biomolecular thermodynamics: From theory to application, CRC Press, 2017 Search PubMed
.
- R. J. Glauber, J. Math. Phys., 1963, 4, 294–307 CrossRef
.
-
M. E. Newman and G. T. Barkema, Monte Carlo methods in statistical physics, Clarendon Press, 1999 Search PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Electronic supporting information contains additional figures and tables as described in the main text. Additionally, four movies are available: M1. Movies showing the growth and saturation of the adhesion patch in a dimer for the exact same conditions as illustrated in Fig. 4. M2. Movies showing the growth and saturation of the two adhesion patches in a trimer for the exact same conditions as illustrated in Fig. 4. M3. Movies showing self-assembly of 50/50 mixtures of C and D droplets with R = 50, Nb = 100, ε = 20.7, γA = 1.0 for 4 area fractions ϕ = 0.1, 0.2, 0.3, 0.4 (see Fig. 5). M4. A movie showing 15 heating–cooling cycles for a 7-mer of droplets with R = 20, Nb = 200, γA = 0.1, εDD = 4.6, εCC = ∞ and Tmelt,DD = 1.2 (see Fig. 7a). See DOI: https://doi.org/10.1039/d3sm00196b |
| ‡ The Metropolis criterion employed for binding/unbinding described later requires knowing the energy of adding or removing a bond. At this time only a harmonic interaction is supported, but this can be trivially extended. |
| This journal is © The Royal Society of Chemistry 2023 |