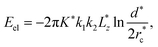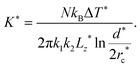Structures, thermodynamics and dynamics of topological defects in Gay–Berne nematic liquid crystals†
Yulu
Huang
 a,
Weiqiang
Wang
a,
Jonathan K.
Whitmer
a,
Weiqiang
Wang
a,
Jonathan K.
Whitmer
 b and
Rui
Zhang
b and
Rui
Zhang
 *a
*a
aDepartment of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, P. R. China. E-mail: ruizhang@ust.hk
bDepartment of Chemical and Biomolecular Engineering, University of Notre Dame, Notre Dame, IN 46556, USA
First published on 30th November 2022
Abstract
Topological defects are a ubiquitous phenomenon across different physical systems. A better understanding of defects can be helpful in elucidating the physical behaviors of many real materials systems. In nematic liquid crystals, defects exhibit unique optical signatures and can segregate impurities, showing their promise as molecular carriers and nano-reactors. Continuum theory and simulations have been successfully applied to link static and dynamical behaviors of topological defects to the material constants of the underlying nematic. However, further evidence and molecular details are still lacking. Here we perform molecular dynamics simulations of Gay–Berne particles, a model nematic, to examine the molecular structures and dynamics of +1/2 defects in a thin-film nematic. Specifically, we measure the bend-to-splay ratio K3/K1 using two independent, indirect measurements, showing good agreement. Next, we study the annihilation event of a pair of ±1/2 defects, of which the trajectories are consistent with experiments and hydrodynamic simulations. We further examine the thermodynamics of defect annihilation in an NVE ensemble, leading us to correctly estimate the elastic modulus by using the energy conservation law. Finally, we explore effects of defect annihilation in regions of nonuniform temperature within these coarse-grained molecular models which cannot be analysed by existing continuum level simulations. We find that +1/2 defects tend to move toward hotter areas and their change of speed in a temperature gradient can be quantitatively understood through a term derived from the temperature dependence of the elastic modulus. As such, our work has provided molecular insights into structures and dynamics of topological defects, presented unique and accessible methods to measure elastic constants by inspecting defects, and proposed an alternative control parameter of defects using temperature gradient.
1 Introduction
Liquid crystals (LCs) represent a range of condensed matter phases that exhibit features of both simple liquids and crystalline solids.1,2 The nematic phase, in which LC molecules display orientational ordering without positional ordering, is most studied thanks to its wide spectrum of applications, including display technology,3 sensors,4,5 directed self-assembly,6,7 and autonomous materials.8 The direction-dependent material properties of an LC are rooted in the anisotropic shape of its constituent molecules. Molecular dynamics (MD) simulations can therefore provide molecular-level insights into a variety of unique phenomena in LCs.9–12 Examples include revealing molecular self-assembly structure on the interface of an LC nanodroplet,13 elucidating surface anchoring conditions for LC-liquid14,15 and LC-solid boundaries,16 and resolving the molecular structure of topological defects.17,18 Despite the above-mentioned advances of molecular models in understanding the equilibrium properties of LCs, dynamical behaviors of LCs are much less studied by molecular simulations.9,19–21A widely used coarse-grained model of low molecular weight LCs is the Gay–Berne (GB) model.22–24 GB particles interact through a modified Lennard–Jones (LJ) potential accounting for particle shape anisotropy and interaction anisotropy.22–24 The GB model can capture isotropic, nematic, smectic, and columnar phases in LCs.25–31 Moreover, by carefully picking its parameters, the GB model can well simulate certain common LC molecules, e.g., 4-cyano-4′-pentylbiphenyl (5CB)32 and p-terphenyl.33 The advantages of the GB model against other atomistic models are its affordable computational costs and its convenience in studying the genuine physics of LCs.34 Previous works have been devoted to measuring material constants of GB particles by different methods. For example, orientational elastic moduli of GB particles have been measured using the direct correlation function method,35 density of states,36 free energy calculations,34,37 and equilibrium orientational fluctuations.38,39 Viscous coefficients of nematic GB systems were measured using equilibrium MD40–46 and non-equilibrium MD simulations.47–53 These fundamental studies have revealed microscopic structures and properties of LCs, and have paved the way toward more quantitative study of LC materials using molecular models.
Indeed, the GB model has been used to quantitatively elucidate a range of LC-related phenomena, such as anchoring effects,54 wetting,55 droplet shape,56 nanofilm,57–59 nanoconfinement effect,60–72 nanoparticle effect,73–77 boundary absorption of LC molecules,16,78 and the phase behavior of GB–GB mixtures79–83 and GB–LJ mixtures.84,85 Other physics, such as the effect of external field86,87 and the addition of charges88,89 or dipoles90–92 are also introduced in the GB model, showing interesting phenomena such as reorientation91 and the tilted phase.92 Recent GB particle simulation works have been extended to discotic,93 biaxial,94–101 deformable,102 or even active103 LCs. These efforts have shed light on the structures of LCs at the microscopic scale, which is difficult to observe in experiments and inaccessible by continuum simulations.
In spite of the above research progress, the study of topological defects using the GB model is scarce. Topological defects are a consequence of broken symmetry in ordered systems. Because of its ubiquity, topological defects are important for understanding a wide variety of phenomena in various physical systems.104 Topological defects in nematic LCs are regions where the orientational ordering of the molecules is frustrated. Point defects in two-dimensional (2D) nematics and wedge disclinations in three-dimensional nematics can be characterized by their winding number or topological charge, defined as k = α/2π, where α is the angle by which the director rotated (positive for counterclockwise rotation and negative for clockwise rotation) after a counterclockwise traversal of the Burgers circuit surrounding the defect.105 Because of the nematic symmetry, the topological charge of a 2D point defect can be multiples of half integer. The self energy of such defect is proportional to the square of its topological charge.105 Therefore, defects carrying the lowest topological charge ±1/2 are the stable ones in 2D nematics, which will be heavily studied here.
There is a recent interest in studying the structures and dynamics of topological defects in nematic LCs,8,106–108 thanks to its emerging applications in defect-directed self-assembly,109 material transport,110 and micro reactors. Interestingly, recent studies also showed that topological defects can reveal material properties of the LC. For instance, the morphology of a +1/2 defect is recently used to infer the elasticity of a lyotropic nematic LC;111,112 it is believed that during the annihilation event of a pair of ±1/2 defects, the +1/2 defect moves faster than the −1/2 defect due to hydrodynamic effects.111,113 Despite the success of continuum models that can reproduce the above-mentioned phenomena, molecular insights into these mechanisms are still lacking.
Here, we use MD simulations to investigate morphological and dynamical properties of topological defects in a nematic represented by GB particles. We first measure the shape of equilibrated +1/2 defects constructed by GB models with varying parameters and infer their bend-to-splay ratio K3/K1. Subsequently, we use the distance between two +1/2 defects in a quasi 2D nematic confined to a disk to infer K3/K1. The two independent, indirect measurements of the elasticity ratio agree well with previously published results. We next study the annihilation event of a pair of ±1/2 defects and find qualitative agreement with experiments and hydrodynamic simulations in terms of defect speed disparity and defect orientation dependence. We further extend our model to elucidate the thermodynamics of defects. Specifically, our micro-canonical ensemble (NVE) simulation gives a simple way of measuring the LC's elastic modulus using the energy conservation law. We also show that higher temperature leads to a longer time of defect annihilation. Finally, we demonstrate one special feature of MD simulation by considering the dynamics of a +1/2 defect under a spatial gradient of temperature. We find that its moving speed is accelerated along the positive gradient direction but decelerated in the opposite direction. This can be understood by considering the negative coupling between the temperature and the elastic modulus. Taken together, our MD simulations confirm that dynamical phenomena observed in macroscopic systems are also present at the nanoscale, which also agree with the continuum theory. Our simulations provide simple methods to infer elastic moduli of a nematic by inspecting defect structures and thermodynamics. Further, the prediction of temperature gradient effect on defect dynamics shows its promise in controlling defects for applications in, for example, defect-directed self-assembly, molecular transport, and nano-reactors.
2 Model and simulation details
2.1 Gay–Berne potential
The Gay–Berne (GB) potential is an anisotropic version of the LJ potential to mimick prolate and oblate spheroid molecules.22–24 The interaction potential between two uniaxial GB particles can be written as follows:22–24 | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_char_0072_20d1.gif) ij = rij
ij = rij![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij is the center-to-center vector pointing from particle j to i. σ0 is the diameter of the cross-section of the particle normal to its orientation (Fig. S1 in ESI,† Section S1). The ‘softness’ of the potential dw allows for appropriate scaling of oblate spheroid particles, set to 0.345 for the κ = 0.345 oblate spheroid GB particles and 1 for all prolate spheroid particles. R approximates the surface-to-surface distance by
ij is the center-to-center vector pointing from particle j to i. σ0 is the diameter of the cross-section of the particle normal to its orientation (Fig. S1 in ESI,† Section S1). The ‘softness’ of the potential dw allows for appropriate scaling of oblate spheroid particles, set to 0.345 for the κ = 0.345 oblate spheroid GB particles and 1 for all prolate spheroid particles. R approximates the surface-to-surface distance byR = rij − σ(ûi,ûj,![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij) + dwσ0. ij) + dwσ0. |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij) takes the following form
ij) takes the following formwhere the ratio χ = (κ2 − 1)/(κ2 + 1) characterizes the asphericity of the liquid crystal molecules, and κ represents the aspect ratio of the GB particle (Fig. S1 in ESI,† Section S1). The molecular anisotropy potential ε(ûi,ûj,
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij) in eqn (1) is given by
ij) in eqn (1) is given byε(ûi,ûj,![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij) = ε0εν1(ûi,ûj)εμ2(ûi,ûj, ij) = ε0εν1(ûi,ûj)εμ2(ûi,ûj,![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij), ij), |
and
Parameters ν and μ are dimensionless. Parameter
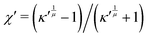 , where κ′ = εss/εee is the ratio of the potential well depths corresponding to the side-to-side (ss) and end-to-end (ee) configuration, respectively (Fig. S1 in ESI,† Section S1). A cut-off distance rcut is introduced to eqn (1) such that the potential U* = 0 when rij ≥ rcut. A GB model can be fully determined by four parameters, denoted by GB(κ, κ′, μ, ν). In this paper, we use three kinds of GB particles, i.e., GB(4.4, 20, 1, 1), GB(3, 5, 1, 3) and GB(0.345, 0.2, 1, 2). Elementary units, i.e., energy scale ε0, length scale σ0, mass scale m0, and the Boltzmann constant kB, are set to 1. All units are multiples of these fundamental values, with distance x scaled as x* = x/σ0, volume V as V* = V/σ03, energy U as U* = U/ε0, temperature T as T* = kBT/ε0, density ρ as ρ* = Nσ03/V (N is the number of particles), pressure P as P* = Pσ03/ε0, time t as t* = t(kBT/m0σ02)1/2, elastic modulus Ki as
, where κ′ = εss/εee is the ratio of the potential well depths corresponding to the side-to-side (ss) and end-to-end (ee) configuration, respectively (Fig. S1 in ESI,† Section S1). A cut-off distance rcut is introduced to eqn (1) such that the potential U* = 0 when rij ≥ rcut. A GB model can be fully determined by four parameters, denoted by GB(κ, κ′, μ, ν). In this paper, we use three kinds of GB particles, i.e., GB(4.4, 20, 1, 1), GB(3, 5, 1, 3) and GB(0.345, 0.2, 1, 2). Elementary units, i.e., energy scale ε0, length scale σ0, mass scale m0, and the Boltzmann constant kB, are set to 1. All units are multiples of these fundamental values, with distance x scaled as x* = x/σ0, volume V as V* = V/σ03, energy U as U* = U/ε0, temperature T as T* = kBT/ε0, density ρ as ρ* = Nσ03/V (N is the number of particles), pressure P as P* = Pσ03/ε0, time t as t* = t(kBT/m0σ02)1/2, elastic modulus Ki as 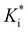 = Kiσ0/ε0, and viscosity η as η* = ησ03/ε0τ0. In what follows, units are omitted if simulation units are used.
= Kiσ0/ε0, and viscosity η as η* = ησ03/ε0τ0. In what follows, units are omitted if simulation units are used.
2.2 Simulation details
MD simulations were carried out using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS).114 Periodic boundary conditions are applied in all three directions, and the Nosé–Hoover thermostat is adopted to control the temperature in the isobaric-isothermal ensemble (NPT) and canonical ensemble (NVT). The time step is dt = 0.001 for GB(4.4, 20, 1, 1), GB(3, 5, 1, 3) and dt = 0.0001 for GB(0.345, 0.2, 1, 2) in simulation units for all investigations unless otherwise specified. The cut-off distance for GB(4.4, 20, 1, 1), GB(3, 5, 1, 3) and GB(0.345, 0.2, 1, 2) is rcut = 6σ0, 5σ0 and 1.6σ0, respectively. The NPT ensemble is set up using pressures extracted from NVT ensemble simulations, which is variable depending on the model and temperature used. The densities of GB(4.4, 20, 1, 1), GB(3, 5, 1, 3) and GB(0.345, 0.2, 1, 2) are ρ* = 0.1932, 0.3, and 2.36, respectively. To characterize nematic–isotropic phase transition, we use a cube as the simulation box (Fig. 1(a)). For the rest of the prolate GB systems, the z-dimension is much smaller than the other two dimensions and we treat them as quasi 2D systems. The simulation details of the parameter setting are summarized in Table 1.
is much smaller than the other two dimensions and we treat them as quasi 2D systems. The simulation details of the parameter setting are summarized in Table 1.
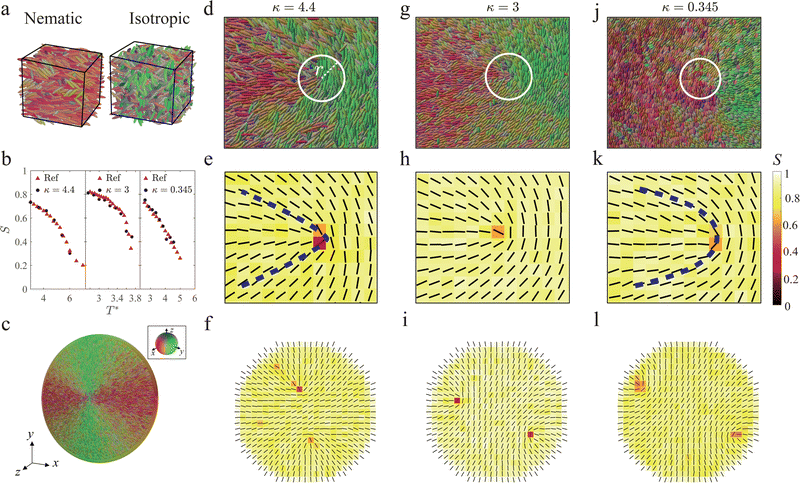 | ||
| Fig. 1 Morphology and structure of +1/2 defects in Gay–Berne nematics. (a) Phase behavior of a bulk nematic of GB(4.4, 20, 1, 1). (b) Scalar order parameter S as a function of temperature for three types of GB particles with comparison to the ref. 36. (c) GB(4.4, 20, 1, 1) particles confined to a disk with a homeotropic anchoring boundary condition. Defects morphology displayed by particle for GB(4.4, 20, 1, 1) (d), GB(3, 5, 1, 3) (g) and GB(0.345, 0.2, 1, 2) (i). r in (d) indicates the radial distance used to measure the morphology of +1/2 defects. Defects morphology displayed director field for GB(4.4, 20, 1, 1) (e), GB(3, 5, 1, 3) (h) and GB(0.345, 0.2, 1, 2) (k). The color bar indicates the order parameter S and dashed blue lines highlight the shape of the +1/2 defects. Two +1/2 defects observed in a disk region for GB(4.4, 20, 1, 1) (f), GB(3, 5, 1, 3) (i) and GB(0.345, 0.2, 1, 2) (l). Inset in (c): Colormap indicates the particle orientation for (a), (c), (d), (g) and (j). | ||
We use the Q-tensor formalism to calculate the scalar order parameter S and the director field in the nematic. The tensor representation is based on a spatial average of the dyadic product of individual molecular orientations. It is defined as115,116
 | (2) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) of the region is the eigenvector of Q associated with its largest eigenvalue S, which corresponds to the scalar order parameter in the local region quantifying its degree of nematic ordering. The size effect study of the sampling region shows that the scalar order parameter S is only marginally dependent on Nr (ESI,† Section S2). To measure the hydrodynamic velocity field in our GB system, we divide the simulation box into 15 × 15 regions in the xy plane, and use individual particle's time-dependent position vector to calculate a local region's average velocity
of the region is the eigenvector of Q associated with its largest eigenvalue S, which corresponds to the scalar order parameter in the local region quantifying its degree of nematic ordering. The size effect study of the sampling region shows that the scalar order parameter S is only marginally dependent on Nr (ESI,† Section S2). To measure the hydrodynamic velocity field in our GB system, we divide the simulation box into 15 × 15 regions in the xy plane, and use individual particle's time-dependent position vector to calculate a local region's average velocity ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_char_0076_20d1.gif) . For the k-th region, the velocity vector
. For the k-th region, the velocity vector ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_char_0076_20d1.gif) k is computed from
k is computed from | (3) |
 denotes the i-th particle in the region, and
denotes the i-th particle in the region, and ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_char_0078_20d1.gif) i(t*) represents the i-th particle's position vector at time t*. The time interval for the measurement is chosen to be Δt* = 200. Note that this hydrodynamic velocity vector
i(t*) represents the i-th particle's position vector at time t*. The time interval for the measurement is chosen to be Δt* = 200. Note that this hydrodynamic velocity vector ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_char_0076_20d1.gif) is different from the instantaneous velocity
is different from the instantaneous velocity ![[V with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_char_0056_20d1.gif) of individual GB particles.
of individual GB particles.
3 Results
We first study the nematic ordering of a bulk GB particle system at different temperatures using an NVT ensemble. For the temperature range we considered, nematic and isotropic phases are respectively detected below and above a critical temperature TNI (Fig. 1(b)). Our measured scalar order parameter S as a function of temperature T* quantitatively agrees with the benchmark results reported in literature36 for all three GB parameters, serving as a validation of our calculations (Fig. 1(b)).Topological defects in a nematic LC are associated with high elastic energy region.105 In continuum theory, the Frank–Oseen elastic energy density of a nematic LC is expressed in the following:117
To simulate the defect annihilation process in a GB system, we prepare a thin-film nematic containing a pair of ±1/2 defects separated by a distance d* = 16–70 and equilibrate these defects under an NPT ensemble (pressure obtained from NVT ensemble simulations) to reach the desired density for a short duration of t* = 5. Hereafter, we perform simulations in the NVT ensemble during which the two defects approach each other and eventually annihilate driven by the elastic force. We further measured the scalar order parameter S and the director ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) around the core of the +1/2 defect based on eqn (2) well before the pair of defects are annihilated (Fig. 1(e), (h) and (k)), and the equilibrium S is different across the three types of GB particles. The low scalar order parameter areas (dark color) defined by S < 0.5 correspond to the defect cores and their sizes are
around the core of the +1/2 defect based on eqn (2) well before the pair of defects are annihilated (Fig. 1(e), (h) and (k)), and the equilibrium S is different across the three types of GB particles. The low scalar order parameter areas (dark color) defined by S < 0.5 correspond to the defect cores and their sizes are 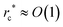 (Fig. 1(e), (f), (h), (i), (k), (l) and ESI,† Section S3). The comet-like shape of the director field around the defect core is also slightly different among the three types of GB systems (Fig. 1(e), (h) and (k)). The defect associated with κ = 4.4 and 0.345 exhibits a V-like and a U-like shape, respectively. Whereas the defect associated with the intermediate aspect ratio κ = 3 shows an intermediate shape. To quantitatively characterize the shape of the +1/2 defect and to avoid boundary effect, we measure the azimuth dependence of the director orientation angle θ around the defect core at a fixed radial distance r* from the defect core before two defects are too close. This radial distance r* = 8, 8, 4 for κ = 4.4, 3, 0.345, respectively, which are chosen much shorter than the box dimension to minimize the influence of the other defect or the far field (Fig. 1(d), (g) and (j)). Note that the local Frank elastic constants close to defect core regions could deviate from their equilibrium values due to the lowering of the scalar order parameter S caused by the diverging elastic distortions. Therefore, r* is chosen to be considerably larger than
(Fig. 1(e), (f), (h), (i), (k), (l) and ESI,† Section S3). The comet-like shape of the director field around the defect core is also slightly different among the three types of GB systems (Fig. 1(e), (h) and (k)). The defect associated with κ = 4.4 and 0.345 exhibits a V-like and a U-like shape, respectively. Whereas the defect associated with the intermediate aspect ratio κ = 3 shows an intermediate shape. To quantitatively characterize the shape of the +1/2 defect and to avoid boundary effect, we measure the azimuth dependence of the director orientation angle θ around the defect core at a fixed radial distance r* from the defect core before two defects are too close. This radial distance r* = 8, 8, 4 for κ = 4.4, 3, 0.345, respectively, which are chosen much shorter than the box dimension to minimize the influence of the other defect or the far field (Fig. 1(d), (g) and (j)). Note that the local Frank elastic constants close to defect core regions could deviate from their equilibrium values due to the lowering of the scalar order parameter S caused by the diverging elastic distortions. Therefore, r* is chosen to be considerably larger than 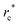 .
.
To quantify the shape of +1/2 defect, we set a polar coordinate system represented by (r,ϕ) centered at the defect core and measure the orientation angle θ, defined as the angle between the y-axis and the director orientation ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) , as a function of the azimuth angle ϕ at the fixed radial distance r* (Fig. 2(a) inset). Our measurements indeed reveal the quantitative difference among the three GB systems we study here (Fig. 2(a)). By fitting our data with Frank elasticity theory,111 we can further extract the elasticity ratio K3/K1. We find that the higher the aspect ratio κ is, the larger K3/K1 is. Moreover, κ > 1 and <1 lead to K3/K1 > 1 and <1, implying that the bend constant K3 is larger (smaller) than the splay constant K1 in a rod-(disk-)like system. These observations are consistent with our expectations; as past results have suggested that shape (rather than enthalpy or molecular identity) comprises most of the information necessary to capture liquid crystal ordering and elasticity.36,119,120
, as a function of the azimuth angle ϕ at the fixed radial distance r* (Fig. 2(a) inset). Our measurements indeed reveal the quantitative difference among the three GB systems we study here (Fig. 2(a)). By fitting our data with Frank elasticity theory,111 we can further extract the elasticity ratio K3/K1. We find that the higher the aspect ratio κ is, the larger K3/K1 is. Moreover, κ > 1 and <1 lead to K3/K1 > 1 and <1, implying that the bend constant K3 is larger (smaller) than the splay constant K1 in a rod-(disk-)like system. These observations are consistent with our expectations; as past results have suggested that shape (rather than enthalpy or molecular identity) comprises most of the information necessary to capture liquid crystal ordering and elasticity.36,119,120
We can also measure the elasticity ratio from an alternative system, namely a disk region consisting of two +1/2 defects. Specifically, we equilibrate a disk region of diameter D of GB particles with homeotropic anchoring by fixing the GB particles (one layer near the boundary) along the radial direction with time step dt = 0.0001. The separation distance between the two defects d is an outcome of the competition between splay and bend energy cost. Our MD simulations show that the average separation distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) of the two defects is different among the three types of GB systems (Fig. 1(f), (i) and (l)). The higher κ is, the closer the two defects are. By minimizing the free energy of a nematic confined to a disk region using Ginzburg–Landau equation121 (ESI,† Section S4), we can theoretically find the equilibrium separation distance d of the two +1/2 defects with a known elastic constant ratio K3/K1 (Fig. 2(b)). The higher K3/K1 is, the more costly bend distortion is in the system, which will bring the two defects closer; otherwise, the two defects will move away from each other to suppress splay deformation. In the special case when K3/K1 = 1, our calculation shows d/D ∼ 0.667, consistent with what is reported in literature.122,123
of the two defects is different among the three types of GB systems (Fig. 1(f), (i) and (l)). The higher κ is, the closer the two defects are. By minimizing the free energy of a nematic confined to a disk region using Ginzburg–Landau equation121 (ESI,† Section S4), we can theoretically find the equilibrium separation distance d of the two +1/2 defects with a known elastic constant ratio K3/K1 (Fig. 2(b)). The higher K3/K1 is, the more costly bend distortion is in the system, which will bring the two defects closer; otherwise, the two defects will move away from each other to suppress splay deformation. In the special case when K3/K1 = 1, our calculation shows d/D ∼ 0.667, consistent with what is reported in literature.122,123
By pairing the elasticity ratio K3/K1 from the defect shape measurement and the defect separation distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) /D from the disk simulation, the different size data points (K3/K1,
/D from the disk simulation, the different size data points (K3/K1,![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) /D) corresponding to the three different GB particle types collapse onto the theoretical curve (Fig. 2(b)). The slight deviation between data points and theoretical curve can be understood by considering effects of finite anchoring and unevenly distributed scalar order parameter (ESI,† Section S5). This remarkable result demonstrates that Frank elasticity theory still works in the nanoscale.
/D) corresponding to the three different GB particle types collapse onto the theoretical curve (Fig. 2(b)). The slight deviation between data points and theoretical curve can be understood by considering effects of finite anchoring and unevenly distributed scalar order parameter (ESI,† Section S5). This remarkable result demonstrates that Frank elasticity theory still works in the nanoscale.
The elastic constant ratio reported from the density of state method36 and our measurements are summarized in the following table:
For both prolate and oblate (discotic) particles, three different measurements of K3/K1 differ by less than 12% (Table 2). The two methods provide a simple visual way to measure the elastic constant ratio in nematic LCs.
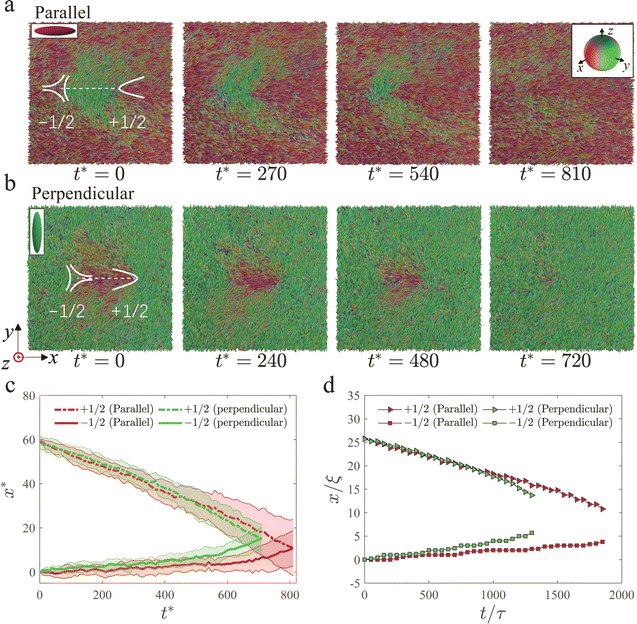
After studying the static properties of topological defects using the GB model, we turn to studying their dynamical behaviors. In what follows, we focus on GB(4.4, 20, 1, 1) system. A pair of ±1/2 defects in an otherwise uniform thin-film nematic is prepared to study their annihilation process. We consider two scenarios of defects configurations, namely a parallel scenario and a perpendicular scenario111 (Fig. 3(a) and (b)). In a parallel (perpendicular) scenario, the auxiliary line connecting (dashed white line in Fig. 3(a) and (b)) the two defect cores is parallel (perpendicular) to the nematic far-field, the orientation of which is represented by the zoomed red and green particles in Fig. 3(a) and (b). In both scenarios, the two defects will approach each other to reduce the elastic energy of the system. The comet-like +1/2 defect will therefore move forward (backward) with respect to its head in the parallel (perpendicular) scenario (Fig. 3(a) and (b)). After the annihilation, the system returns to a uniform state.
We have run 10 independent simulations starting from the same defect separation distance for each scenario, and measured the averaged defect trajectories shown in Fig. 3(c). For comparison, we have also performed hybrid lattice Boltzmann method (LBM) simulation using the same elastic constant ratio (K3/K1 = 2.50).124 Our calculations show that the speed of the −1/2 defect is lower than that of the +1/2 defect (Fig. 3(c)), in line with the literature111 and the hydrodynamic simulations (Fig. 3(d)), indicating that a hydrodynamic effect that causes defect speed disparity also exists in our nanoscale system.111,113 We also notice that the two scenarios show different annihilation times. Specifically, the perpendicular scenario has faster annihilation dynamics than the parallel scenario (Fig. 3(c)), again consistent with the actin-based experiment111 and the hydrodynamic simulations (Fig. 3(d)). Moreover, both MD and LBM simulations agree on the relative position of the annihilation point: the annihilation point of the two defects for the parallel scenario is closer to the original position of the −1/2 defect; whereas the annihilation point of the perpendicular scenario is slightly closer to the center point between the original positions of the two defects. Therefore, there is a semi-quantitative agreement between the two simulations in terms of the defect trajectories. No significant size effect on defect annihilation event is observed in our simulation (ESI,† Section S6). We further measure the velocity and the scalar order parameter field in the MD simulation (Fig. 4(a) and (c)) and contrast them to the hydrodynamic simulation results (Fig. 4(b) and (d)). The velocity vector field measured from the GB system based on eqn (3) is similar to that calculated from the hydrodynamic simulations (Fig. 4) and the literature.108 During the annihilation, the prolate spheroid GB particles rotate and translate collectively to accommodate the re-arrangement of the director field, leading to a hydrodynamic flow (Fig. 4(a) and (c)). For both scenarios, two vortices of flow are seen distributed on the two sides of the auxiliary line connecting the two defects, which push the +1/2 defect to move towards the −1/2 defect (Supplementary Movie, ESI†). Whereas there is no significant large-scale flow near the −1/2 defect. This backflow effect explains the observation that the +1/2 defect moves faster than the −1/2 defect in GB systems (Fig. 3(c)). The annihilation time difference between the two scenarios can be understood by considering the viscous coefficients associated with the backflow. In the parallel scenario, the director field between the two defects is perpendicular to the flow. For the perpendicular case, however, the director field between the two defects is aligned with the flow. Therefore, the relevant Miesowicz viscosity125 in parallel and perpendicular scenarios is η2 and η1, respectively. Because η2 > η1 in GB(4.4, 20, 1, 1),46 the hydrodynamic flow is stronger in perpendicular scenario than in parallel scenario, therefore explaining the annihilation time difference between the two scenarios.
Although we averaged the velocity in each region, the velocity fluctuations in MD simulations are more significant than that in LBM simulations. The color in Fig. 4 of two methods look differently. That is because thermal fluctuations of the order parameter are absent in an LBM simulation, which is based on a continuum model. In MD simulations, thermal fluctuations are naturally included and are reflected by the non-uniform color in the images. For equilibrium simulations, this noise can be reduced by doing longer time average. For dynamic simulation in which defects move and annihilate, the instantaneous scalar order parameter will be noisy. In MD simulations, the displacement of the defects in the y-direction fluctuates, making the vortex center and vertex shapes change during the annihilation (Fig. 4(a) and (c)). Moreover, there is a diverging flow at the final stage of the annihilation process in the LBM simulation, which is not observed in the MD simulation. Nevertheless, an acceleration of the −1/2 defect speeds is found in MD simulation, consistent with the fact that the elastic force diverges as their separation distance approaches zero, driving a strong flow in the final stage of the annihilation process (Fig. 3(c)).
To estimate the Ericksen number of the GB model in the defect annihilation event, we have measured the rotational viscosity 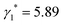 using rotating field method (ESI,† Section S7.1). The characteristic velocity of the two defects
using rotating field method (ESI,† Section S7.1). The characteristic velocity of the two defects ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = 0.036σ0/τ0 (Fig. 3(c)), the core size of defects during annihilation ξ = 2
= 0.036σ0/τ0 (Fig. 3(c)), the core size of defects during annihilation ξ = 2 , and choose the mean elastic constant K* = 4.25.36 This gives rise to
, and choose the mean elastic constant K* = 4.25.36 This gives rise to 
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ξ/K* = 0.224, comparing to Er = 0.219 in the LBM simulation. Therefore, the viscous effect is considerable but less important than the elastic force for this range of the Ericksen number. This is also consistent with the fact that the hydrodynamic effect is present in our GB systems. Note that, similar to the concept that one can estimate orientational elastic moduli by inspecting defect shapes, one can also estimate viscous coefficients by inspecting defect velocities. Indeed, this method yields
ξ/K* = 0.224, comparing to Er = 0.219 in the LBM simulation. Therefore, the viscous effect is considerable but less important than the elastic force for this range of the Ericksen number. This is also consistent with the fact that the hydrodynamic effect is present in our GB systems. Note that, similar to the concept that one can estimate orientational elastic moduli by inspecting defect shapes, one can also estimate viscous coefficients by inspecting defect velocities. Indeed, this method yields  , which is in the same order of magnitude of the rotating field measurement (ESI,† Section S7.2).
, which is in the same order of magnitude of the rotating field measurement (ESI,† Section S7.2).
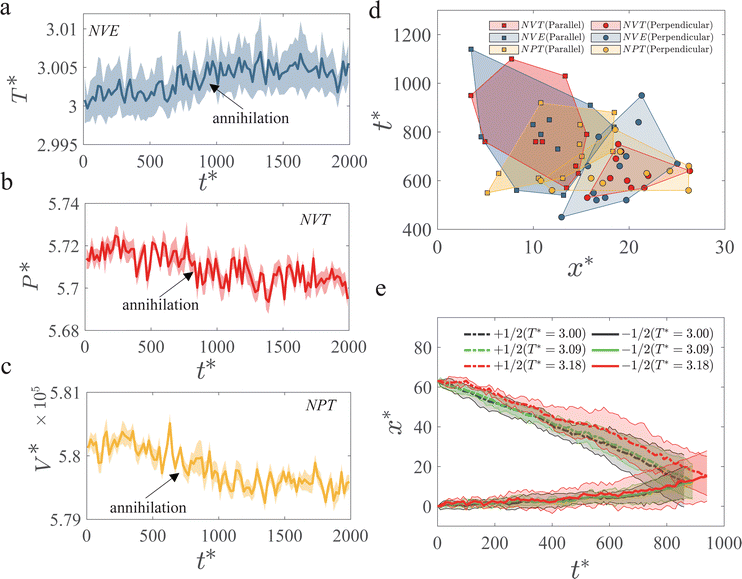
We next study the thermodynamics of defect annihilations using different ensembles. We first consider an NVE ensemble and set the initial temperature to T* = 3. During annihilation, we detect a steady increase of the temperature despite strong fluctuations in the measurements (Fig. 5(a)). After annihilation, temperature fluctuates with respect to a higher mean value with T* ≈ 3.005 (Fig. 5(a)). The increase of the thermal energy associated with the temperature rise allows us to estimate the elastic modulus of the nematic. Specifically, the elastic energy corresponding to the initial state of the two defects separated by a distance d* = 70 can be approximated by a elastic energy formula under one-constant approximation:105
 is the characteristic size of the defect core. After annihilation, this elastic energy is dissipated into heat in the NVE ensemble. The thermal energy change in the simulation is:
is the characteristic size of the defect core. After annihilation, this elastic energy is dissipated into heat in the NVE ensemble. The thermal energy change in the simulation is:| Ethermal = NkBΔT*. |
The estimation of elastic constant is K* = 4.61, agreeing well with (K1 + K3)/2 = 4.25 reported in literature.36 We also find that when the distance d* is comparable to the defect core size, the elastic constant measurement using the energy conservation law will become inaccurate (ESI,† Section S8). This provides a convenient method to estimate the order of magnitude of the elastic modulus of the nematic in MD simulations. This estimate, if combined with the visual measurement of the elasticity ratio, can be used to determine the absolute values of both K1 and K3. This idea of applying thermodynamic frameworks to study defect annihilation dynamics is a fertile area for future works.
To ensure that our calculations are independent of the choice of the ensemble, we simulate defect annihilations in otherwise equivalent NPT, NVT and NVE ensembles using GB(4.4, 20, 1, 1). A change in thermodynamic variables during defect annihilation is also observed. In the NVT ensemble, the measured pressure P has dropped by ∼0.35%; whereas, in the NPT ensemble, the measured volume has shrunk by ∼0.17%. Note that the presence of defects can distort the nematic and lead to less efficient packing of the GB particles, resulting in higher pressure for the fixed volume system and larger volume for the fixed pressure system. In all the three ensembles we consider here, the fluctuations of thermodynamic variables, 〈Δx〉/〈x〉 (x = T, P, or V) is in the order of 10−3, comparing to 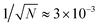 . This shows that our nanoscale system is within the thermodynamic limit (ESI,† Section S9). To compare defect annihilation dynamics between different ensembles, we conduct NVT, NVE, and NPT ensemble simulations with the same initial temperature and density, and compare their annihilation dynamics in terms of annihilation time t* and the location of annihilation point x* (Fig. 5(d)). There is no significant difference between different ensembles within statistical uncertainty, confirming that the GB system is indeed in the thermodynamic limit and different ensembles are indifferent.
. This shows that our nanoscale system is within the thermodynamic limit (ESI,† Section S9). To compare defect annihilation dynamics between different ensembles, we conduct NVT, NVE, and NPT ensemble simulations with the same initial temperature and density, and compare their annihilation dynamics in terms of annihilation time t* and the location of annihilation point x* (Fig. 5(d)). There is no significant difference between different ensembles within statistical uncertainty, confirming that the GB system is indeed in the thermodynamic limit and different ensembles are indifferent.
We further investigate the temperature dependence of defect annihilation processes using the NVT ensemble. The effect of temperature has two folds. On the one hand, viscous coefficients are usually lower at higher temperature,46 which can facilitate hydrodynamic flows and help accelerate defect annihilation. On the other hand, elastic moduli are lower at higher temperature,36 which will reduce the driving force of the defects, slowing down the annihilation process. Our MD simulations can be used to ascertain the relative importance of these two competing effects. Our measured defect trajectories at three different temperatures show that higher temperature leads to a longer time of annihilation (Fig. 5(e)), implying that elasticity is more important than the viscous effect in terms of annihilation dynamics in the GB system considered here. This is again consistent with the estimated Ericksen number Er = 0.224 < 1 of the system at which elastic effect wins over viscous effect.
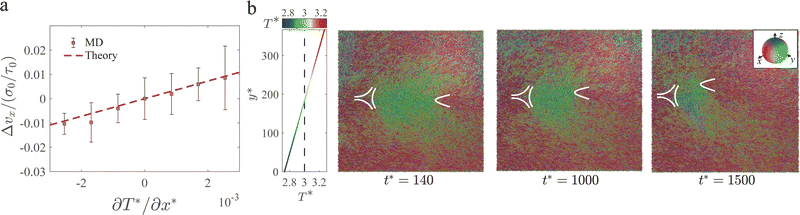
Finally, we study the effect of temperature gradient on defect dynamics. It is advantageous to use MD simulations against continuum simulations to study non-uniform temperature systems. The temperature dependence of material constants such as elastic moduli and viscous coefficients has to be implemented ad hoc in continuum simulations. In molecular models, however, they emerge naturally. In what follows, we use the GB model to investigate how a +1/2 defect moves under a temperature gradient. To this end, we consider a pair of ±1/2 defects separated in the x-direction along which the local temperature varies linearly from 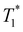 at the center to
at the center to 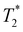 at the two edges of the box, where the periodic boundary condition requires that their temperatures are equal (Fig. 6(a) and (b)). If
at the two edges of the box, where the periodic boundary condition requires that their temperatures are equal (Fig. 6(a) and (b)). If  , the +1/2 defect facing towards the center is under a positive temperature gradient (Fig. 6(a)); if otherwise, the +1/2 defect is under a negative temperature gradient (Fig. 6(b)). The temperature range of the system bounded by
, the +1/2 defect facing towards the center is under a positive temperature gradient (Fig. 6(a)); if otherwise, the +1/2 defect is under a negative temperature gradient (Fig. 6(b)). The temperature range of the system bounded by 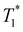 and
and 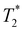 are within the nematic phase. Our simulations show that the +1/2 defect under a positive temperature gradient spends less time to move to the center of the box than under a negative temperature gradient (Fig. 6(c) and (d)). We also notice that GB particles tend to rotate out of the plane near the center of the box, a similar behavior found in uniform temperature systems (Fig. 3). This phenomenon is more severe for the positive temperature gradient scenario in which the box center is hotter, where stronger thermal fluctuations may promote the out-of-plane rotations of the GB particles.
are within the nematic phase. Our simulations show that the +1/2 defect under a positive temperature gradient spends less time to move to the center of the box than under a negative temperature gradient (Fig. 6(c) and (d)). We also notice that GB particles tend to rotate out of the plane near the center of the box, a similar behavior found in uniform temperature systems (Fig. 3). This phenomenon is more severe for the positive temperature gradient scenario in which the box center is hotter, where stronger thermal fluctuations may promote the out-of-plane rotations of the GB particles.
We further quantify the change of moving speed of +1/2 defects under different temperature gradients. We subtract the defect velocity vx by vx0 measured from a simulation of a uniform temperature  and plot Δvx = vx − vx0 against
and plot Δvx = vx − vx0 against  in Fig. 7(a). The results show that the more positive (negative) the temperature gradient is, the higher (lower) the defect speed will be.
in Fig. 7(a). The results show that the more positive (negative) the temperature gradient is, the higher (lower) the defect speed will be.
We can understand the above behavior using a continuum theory. The elastic energy of the system is 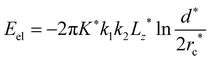 under one-constant approximation,105 where K* is a function of temperature T*.36 The force acting on the +1/2 defect can be derived by differentiating the elastic energy
under one-constant approximation,105 where K* is a function of temperature T*.36 The force acting on the +1/2 defect can be derived by differentiating the elastic energy 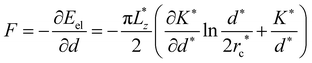 , where the first term contributes to the change of defect speed Δvx and the second term corresponds to vx0 for a uniform temperature system. Therefore, the theory shows that there is a linear relation between Δvx and ∂T*/∂x* and the proportionality is
, where the first term contributes to the change of defect speed Δvx and the second term corresponds to vx0 for a uniform temperature system. Therefore, the theory shows that there is a linear relation between Δvx and ∂T*/∂x* and the proportionality is 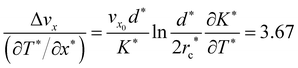 , comparing to 3.95 measured from a linear fit to the simulation data (Fig. 7(a)). This quantitative agreement again demonstrates that the molecular system can be understood from a continuum point of view. The above predictions can be further tested in future experiments. Note that a recent experiment of a colloid dispersed in nematic 5CB has reported a similar phenomenon that the colloid tends to move toward the hotter region.126 This is due to a similar physical reason that the elastic modulus of the hotter regions is lower, which provides a force to push the colloid to the hot zone to reduce the elastic distortion costs incurred by the presence of the colloid, an opposite direction when dispersed in an isotropic medium under the same temperature gradient.126 To further support our proposed mechanism, we perform a separate simulation in which a temperature gradient is along the transverse direction (y-direction), where the periodic boundary condition is turned off to suppress any global flow (Fig. 7(b)). The results also show that the +1/2 defect tends to move towards the hotter region, which provides an additional support of these theoretical arguments.
, comparing to 3.95 measured from a linear fit to the simulation data (Fig. 7(a)). This quantitative agreement again demonstrates that the molecular system can be understood from a continuum point of view. The above predictions can be further tested in future experiments. Note that a recent experiment of a colloid dispersed in nematic 5CB has reported a similar phenomenon that the colloid tends to move toward the hotter region.126 This is due to a similar physical reason that the elastic modulus of the hotter regions is lower, which provides a force to push the colloid to the hot zone to reduce the elastic distortion costs incurred by the presence of the colloid, an opposite direction when dispersed in an isotropic medium under the same temperature gradient.126 To further support our proposed mechanism, we perform a separate simulation in which a temperature gradient is along the transverse direction (y-direction), where the periodic boundary condition is turned off to suppress any global flow (Fig. 7(b)). The results also show that the +1/2 defect tends to move towards the hotter region, which provides an additional support of these theoretical arguments.
4 Discussion and conclusion
In this work, we have performed molecular dynamics simulations of topological defects in a thin-film Gay–Berne nematic. We first use two independent, indirect methods to measure the bend-to-splay ratio K3/K1 for three types of GB particles, including two different prolate particles and one discotic particle. In the first method, we inspect the shape of the +1/2 defect and fit it with a continuum theory. In the second method, we measure the distance of two +1/2 defects of a nematic confined to a disk region with homeotropic anchoring. By comparing to the continuum theory, K3/K1 measured by the two methods agree with each other and are within ∼10% difference with the literature.36 This provides a direct molecular evidence of the Frank elasticity theory. We next study the spontaneous annihilation process of a pair of ±1/2 defects in an otherwise uniform nematic of GB(4.4, 20, 1, 1). The defect trajectories indicate that the +1/2 defect moves faster than the −1/2 defect, and the configuration of the director field can also dictate the annihilation speed. Both features are thought to originate from hydrodynamic effects of the nematic. This agreement with experiments and continuum simulations confirms the hydrodynamic theory of nematics. We can also extract the flow field of the GB system during defect annihilation and compare favorably with that calculated from hydrodynamic simulations. We further examine the thermodynamics of the system before and after defect annihilation. The NVE ensemble simulation allows us to correctly estimate the elastic modulus by equating the elastic energy stored in the defect-bearing state and the thermal energy acquired after defect annihilation. Combined with the visual methods of measuring the elasticity ratio, it is possible to use the information of defect structures and dissipated energy during defect annihilation to determine the absolute values of K1 and K3. By varying temperature, simulations show that defect annihilation is faster for lower temperature, underscoring the importance of the elastic effect, which becomes stronger at lower temperature. This is consistent with our estimated Ericksen number of the system Er = O(0.1) at which elastic force wins over viscous force.Temperature gradients can lead to spatial gradients of elastic constants, viscous coefficients, and diffusion constants. Landau–de Gennes theory can be used in the quasi-static limit and when thermal noise is not considered. In general, a hydrodynamic model accounting for elastic constant gradients, back-flow effects, and thermal diffusion effects has to be developed to fully describe the thermophoresis phenomenon of defects. In addition to the complexity of this model, the temperature dependence of these material constants is unknown, with limited measurements available from which to estimate their magnitude, therefore requiring they be set ad hoc in the model as well. In the molecular model, however, the temperature dependency of these constants naturally arises and no ad hoc assumption is required, and all the physics are included. Therefore, the molecular model provides a convenient platform onto which to theoretically study the temperature gradient effect. Finally, we simulate defect motion in a region of nonuniform temperature. Our calculations show that +1/2 defects tend to move to hotter area. Using a simple theory based on the temperature dependence of the elastic modulus, we are able to quantitatively explain the change of defect speed due to local temperature gradient. There is a recent interest in studying the transport phenomena of topological defects in nematic liquid crystals. For example, certain types of defects can self propel in active nematics.123 Because defects tend to segregate foreign molecules and particles in nematic liquid crystals,6,109,127 controlled motion of defects motion can lead to applications in, for example, defect-carried material transport and micro reactors. In active nematics, internal stresses have to be maintained to mobilize these defects. Therefore, temperature gradient provides an alternative method to mobilize defects locally and in demand.
Put together, our work presents a compendium of new investigations into the physics of topological defects in nematic liquid crystals; we have systematically compared MD and continuum simulations in terms of defects structures, thermodynamics, and annihilation dynamics. The study shows that there is a quantitative agreement between the two physical models of distinct length scales, including the measured elastic constant ratio, annihilation dynamics, and temperature gradient effect on defect motion. Moreover, the measurement of viscoelastic constants of a material is often-times cumbersome and inevitably involves the application of external fields. In this work, we propose passive methods to measure these constants, namely through inspecting defect structure, defect separation distance, or measuring temperature change during an annihilation event. The temperature gradient effect provides an alternative way to control defect dynamics using heat, and presents a novel prediction which should stimulate future experimental interest, particularly as thermophoretic effects are likely to be present in the burgeoning field of active liquid crystals.
Author contributions
Y. H. performed MD simulations and analyzed the data. W. W. performed LBM simulations and analyzed the data. R. Z. designed, supervised the study, and performed continuum calculations. Y. H. and R. Z. interpreted the data and wrote the first draft. All authors contributed to the revision of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support from the Research Grants Council of Hong Kong SAR through grant no. 16300221 and the HKUST Central High Performance Computing Cluster (HPC3). JKW acknowledges support from the US National Science Foundation, Award No. DMR-1751988. The authors also thank Tiezheng Qian, Xinyu Wang and Shengzhu Yi for fruitful discussions. The authors also thank the Referees for their inspiring and helpful suggestions.Notes and references
- P.-G. De Gennes and J. Prost, The physics of liquid crystals, Oxford University Press, 1993 Search PubMed.
- P. Oswald and P. Pieranski, Nematic and cholesteric liquid crystals: concepts and physical properties illustrated by experiments, CRC Press, 2005 Search PubMed.
- R. H. Chen, Liquid crystal displays: fundamental physics and technology, John Wiley & Sons, 2011 Search PubMed.
- I.-H. Lin, D. S. Miller, P. J. Bertics, C. J. Murphy, J. J. de Pablo and N. L. Abbott, Science, 2011, 332, 1297–1300 CrossRef CAS PubMed.
- M. Sadati, A. I. Apik, J. C. Armas-Perez, J. Martinez-Gonzalez, J. P. Hernandez-Ortiz, N. L. Abbott and J. J. de Pablo, Adv. Funct. Mater., 2015, 25, 6050–6060 CrossRef CAS.
- J. K. Whitmer, X. Wang, F. Mondiot, D. S. Miller, N. L. Abbott and J. J. de Pablo, Phys. Rev. Lett., 2013, 111, 1–5 CrossRef PubMed.
- M. Rahimi, T. F. Roberts, J. C. Armas-Pérez, X. Wang, E. Bukusoglu, N. L. Abbott and J. J. de Pablo, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5297–5302 CrossRef CAS PubMed.
- R. Zhang, A. Mozaffari and J. J. de Pablo, Nat. Rev. Mater., 2021, 6, 437–453 CrossRef CAS.
- C. Care and D. Cleaver, Rep. Prog. Phys., 2005, 68, 2665 CrossRef CAS.
- R. Berardi, L. Muccioli, S. Orlandi, M. Ricci and C. Zannoni, J. Phys.: Condens. Matter, 2008, 20, 463101 CrossRef PubMed.
- C. Zannoni, Liq. Cryst., 2018, 45, 1880–1893 CrossRef CAS.
- M. P. Allen, Mol. Phys., 2019, 117, 2391–2417 CrossRef CAS.
- J. A. Moreno-Razo, E. J. Sambriski, N. L. Abbott, J. P. Hernández-Ortiz and J. J. de Pablo, Nature, 2012, 485, 86–89 CrossRef CAS PubMed.
- M. Sadati, H. Ramezani-Dakhel, W. Bu, E. Sevgen, Z. Liang, C. Erol, M. Rahimi, N. Taheri Qazvini, B. Lin and N. L. Abbott, et al. , J. Am. Chem. Soc., 2017, 139, 3841–3850 CrossRef CAS PubMed.
- H. Ramezani-Dakhel, M. Sadati, M. Rahimi, A. Ramirez-Hernandez, B. Roux and J. J. de Pablo, J. Chem. Theory Comput., 2017, 13, 237–244 CrossRef CAS PubMed.
- V. Palermo, F. Biscarini and C. Zannoni, Phys. Rev. E, 1998, 57, 2519–2522 CrossRef.
- M. Rahimi, H. Ramezani-Dakhel, R. Zhang, A. Ramirez-Hernandez, N. L. Abbott and J. J. de Pablo, Nat. Commun., 2017, 8, 1–8 CrossRef PubMed.
- O. D. Lavrentovich, P. Pasini, C. Zannoni and S. Zumer, Defects in liquid crystals: Computer simulations, theory and experiments, Springer Science & Business Media, 2001, vol. 43 Search PubMed.
- P. Pasini and C. Zannoni, Advances in the computer simulations of liquid crystals, Springer Science & Business Media, 1999, vol. 545 Search PubMed.
- D. Cheung, S. Clark and M. R. Wilson, Chem. Phys. Lett., 2002, 356, 140–146 CrossRef CAS.
- Z. Ran, P. Zeng-Hui, L. Yong-Gang, Z. Zhi-Gang and X. Li, Chin. Phys. B, 2009, 18, 4380 CrossRef.
- B. J. Berne and P. Pechukas, J. Chem. Phys., 1972, 56, 4213–4216 CrossRef CAS.
- J. Gay and B. Berne, J. Chem. Phys., 1981, 74, 3316–3319 CrossRef CAS.
- P. Prybytak, W. Frith and D. Cleaver, Interface Focus, 2012, 2, 651–657 CrossRef CAS PubMed.
- E. de Miguel, L. F. Rull, M. K. Chalam and K. E. Gubbins, Mol. Phys., 1991, 74, 405–424 CrossRef CAS.
- E. de Miguel, E. M. Del Rio, J. T. Brown and M. P. Allen, J. Chem. Phys., 1996, 105, 4234–4249 CrossRef CAS.
- M. A. Bates and G. R. Luckhurst, J. Chem. Phys., 1999, 110, 7087–7108 CrossRef CAS.
- V. V. Ginzburg, M. A. Glaser and N. A. Clark, Liq. Cryst., 1997, 23, 227–234 CrossRef CAS.
- E. de Miguel and C. Vega, J. Chem. Phys., 2002, 117, 6313–6322 CrossRef CAS.
- D. Caprion, L. Bellier-Castella and J.-P. Ryckaert, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 041703 CrossRef CAS PubMed.
- J. A. Moreno-Razo, O. Cienegas-Caceres, E. Díaz-Herrera and J. Quintana, AIP Conf. Proc., 2008, 979, 120–129 CrossRef CAS.
- H. Fukunaga, J.-I. Takimoto, T. Aoyagi, T. Shoji, F. Sawa and M. Doi, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 2001, 365, 739–746 CrossRef CAS.
- G. Luckhurst and P. Simmonds, Mol. Phys., 1993, 80, 233–252 CrossRef CAS.
- A. A. Joshi, J. K. Whitmer, O. Guzmán, N. L. Abbott and J. J. de Pablo, Soft Matter, 2014, 10, 882–893 RSC.
- A. Avazpour, Liq. Cryst., 2012, 39, 1491–1497 CrossRef CAS.
- H. Sidky and J. K. Whitmer, Liq. Cryst., 2016, 43, 2285–2299 CrossRef CAS.
- J. Stelzer, L. Longa and H.-R. Trebin, J. Chem. Phys., 1995, 103, 3098–3107 CrossRef CAS.
- M. P. Allen, M. A. Warren, M. R. Wilson, A. Sauron and W. Smith, J. Chem. Phys., 1996, 105, 2850–2858 CrossRef CAS.
- A. Humpert and M. P. Allen, Mol. Phys., 2015, 113, 2680–2692 CrossRef CAS.
- A. Smondyrev, G. B. Loriot and R. A. Pelcovits, Phys. Rev. Lett., 1995, 75, 2340 CrossRef CAS PubMed.
- S. Sarman, J. Chem. Phys., 1998, 108, 7909–7916 CrossRef CAS.
- A. Cuetos, J. M. Ilnytskyi and M. R. Wilson, Mol. Phys., 2002, 100, 3839–3845 CrossRef CAS.
- S. Sarman and A. Laaksonen, Chem. Phys. Lett., 2009, 479, 47–51 CrossRef CAS.
- S. Sarman and A. Laaksonen, J. Chem. Phys., 2009, 131, 144904 CrossRef PubMed.
- G. R. Luckhurst and K. Satoh, J. Chem. Phys., 2010, 132, 184903 CrossRef.
- K. Satoh, Mol. Cryst. Liq. Cryst., 2015, 615, 78–88 CrossRef CAS.
- N. Mori, J. Morimoto and K. Nakamura, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1997, 307, 1–15 CrossRef CAS.
- L. Bennett and S. Hess, Proceedings of the 26th Freiburger Arbeitstagung Flussigkristalle, 1997.
- L. Bennett, S. Hess, C. Pereira Borgmeyer and T. Weider, Int. J. Thermophys., 1998, 19, 1143–1153 CrossRef CAS.
- L. Bennett and S. Hess, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 5561 CrossRef CAS PubMed.
- N. Mori, R. Semura and K. Nakamura, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 2001, 367, 445–453 CrossRef CAS.
- C. Wu, T. Qian and P. Zhang, Liq. Cryst., 2007, 34, 1175–1184 CrossRef CAS.
- S. Sarman, Y.-L. Wang and A. Laaksonen, Phys. Chem. Chem. Phys., 2015, 17, 16615–16623 RSC.
- J. A. Moreno-Razo, E. J. Sambriski, G. M. Koenig, E. Díaz-Herrera, N. L. Abbott and J. J. de Pablo, Soft Matter, 2011, 7, 6828–6835 RSC.
- D. Vanzo, M. Ricci, R. Berardi and C. Zannoni, Soft Matter, 2016, 12, 1610–1620 RSC.
- D. Vanzo, M. Ricci, R. Berardi and C. Zannoni, Soft Matter, 2012, 8, 11790–11800 RSC.
- A. P. Emerson, S. Faetti and C. Zannoni, Chem. Phys. Lett., 1997, 271, 241–246 CrossRef CAS.
- S. J. Mills, C. M. Care, M. P. Neal and D. J. Cleaver, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 3284 CrossRef CAS.
- S. J. Mills, C. M. Care, M. P. Neal, M. R. Wilson, M. P. Allen and D. J. Cleaver, J. Mol. Liq., 2000, 85, 185–195 CrossRef CAS.
- G. D. Wall and D. J. Cleaver, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 4306 CrossRef CAS.
- R. E. Webster, N. J. Mottram and D. J. Cleaver, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 021706 CrossRef PubMed.
- R. Latham and D. J. Cleaver, Chem. Phys. Lett., 2000, 330, 7–14 CrossRef CAS.
- E. Cañeda-Guzmán, J. A. Moreno-Razo, E. Díaz-Herrera and E. J. Sambriski, Mol. Phys., 2014, 112, 1149–1159 CrossRef.
- D. Salgado-Blanco, C. I. Mendoza, M. A. Chávez-Rojo, J. A. Moreno-Razo and E. Díaz-Herrera, Soft Matter, 2018, 14, 2846–2859 RSC.
- D. Salgado-Blanco, E. Daz-Herrera and C. I. Mendoza, J. Phys.: Condens. Matter, 2019, 31, 105101 CrossRef PubMed.
- D. Caprion, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 28, 305–313 CrossRef CAS PubMed.
- Q. Ji, R. Lefort and D. Morineau, Chem. Phys. Lett., 2009, 478, 161–165 CrossRef CAS.
- Q. Ji, R. Lefort, R. Busselez and D. Morineau, J. Chem. Phys., 2009, 130, 234501 CrossRef PubMed.
- Q. Ji, R. Lefort, A. Ghoufi and D. Morineau, Chem. Phys. Lett., 2009, 482, 234–238 CrossRef CAS.
- R. Busselez, C. V. Cerclier, M. Ndao, A. Ghoufi, R. Lefort and D. Morineau, J. Chem. Phys., 2014, 141, 134902 CrossRef PubMed.
- J. Karjalainen, J. Lintuvuori, V.-V. Telkki, P. Lantto and J. Vaara, Phys. Chem. Chem. Phys., 2013, 15, 14047–14057 RSC.
- S. I. Hernández, J. A. Moreno-Razo, A. Ramírez-Hernández, E. Díaz-Herrera, J. P. Hernández-Ortiz and J. J. de Pablo, Soft Matter, 2012, 8, 1443–1450 RSC.
- B. T. Gettelfinger, J. A. Moreno-Razo, G. M. Koenig, J. P. Hernández-Ortiz, N. L. Abbott and J. J. de Pablo, Soft Matter, 2010, 6, 896–901 RSC.
- T. Stieger, M. Schoen and M. G. Mazza, J. Chem. Phys., 2014, 140, 1–10 CrossRef PubMed.
- T. Stieger, S. Püschel-Schlotthauer, M. Schoen and M. G. Mazza, Mol. Phys., 2016, 114, 259–275 CrossRef CAS.
- O. Guzmán, E. B. Kim, S. Grollau, N. L. Abbott and J. J. de Pablo, Phys. Rev. Lett., 2003, 91, 1–4 CrossRef PubMed.
- A. D. González-Martínez, M. A. Chávez-Rojo, E. J. Sambriski and J. A. Moreno-Razo, RSC Adv., 2019, 9, 33413–33427 RSC.
- G. D. Wall and D. J. Cleaver, Mol. Phys., 2003, 101, 1105–1112 CrossRef CAS.
- O. Cienega-Cacerez, C. García-Alcántara, J. A. Moreno-Razo, E. Díaz-Herrera and E. J. Sambriski, Soft Matter, 2016, 12, 1295–1312 RSC.
- R. A. Bemrose and C. M. Care, Mol. Phys., 1997, 90, 625–636 CAS.
- S. J. Mills, C. M. Care, M. P. Neal and D. J. Cleaver, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1999, 330, 1667–1674 CAS.
- J. A. Moreno-Razo, E. Díaz-Herrera and S. H. Klapp, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 19–21 CrossRef PubMed.
- R. Berardi and C. Zannoni, Soft Matter, 2012, 8, 2017–2025 RSC.
- D. Antypov and D. J. Cleaver, J. Phys.: Condens. Matter, 2004, 16, S1887 CrossRef CAS.
- R. Berardi, A. Costantini, L. Muccioli, S. Orlandi and C. Zannoni, J. Chem. Phys., 2007, 126, 044905 CrossRef PubMed.
- R. Berardi, S. Orlandi and C. Zannoni, Phys. Chem. Chem. Phys., 2000, 2, 2933–2942 RSC.
- E. E. Burnell, R. Berardi, R. T. Syvitski and C. Zannoni, Chem. Phys. Lett., 2000, 331, 455–464 CrossRef CAS.
- S. Orlandi, L. Muccioli, M. Ricci, R. Berardi and C. Zannoni, Chem. Cent. J., 2007, 1, 1–13 CrossRef PubMed.
- M. Lamarra, L. Muccioli, S. Orlandi and C. Zannoni, Phys. Chem. Chem. Phys., 2012, 14, 5368–5375 RSC.
- R. Berardi, S. Orlandi and C. Zannoni, J. Chem. Soc., Faraday Trans., 1997, 93, 1493–1496 RSC.
- R. Berardi, S. Orlandi and C. Zannoni, Int. J. Mod. Phys. C, 1999, 10, 477–484 CrossRef.
- R. Berardi, S. Orlandi and C. Zannoni, Mol. Cryst. Liq. Cryst., 2003, 394, 141–151 CrossRef CAS.
- O. Cienega-Cacerez, J. A. Moreno-Razo, E. Díaz-Herrera and E. J. Sambriski, Soft Matter, 2014, 10, 3171–3182 RSC.
- R. Berardi, C. Fava and C. Zannoni, Chem. Phys. Lett., 1995, 236, 462–468 CrossRef CAS.
- D. J. Cleaver, C. M. Care, M. P. Allen and M. P. Neal, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 559 CrossRef CAS PubMed.
- R. Berardi, C. Fava and C. Zannoni, Chem. Phys. Lett., 1998, 297, 8–14 CrossRef CAS.
- R. Berardi and C. Zannoni, J. Chem. Phys., 2000, 113, 5971–5979 CrossRef CAS.
- R. Berardi, M. Cecchini and C. Zannoni, J. Chem. Phys., 2003, 119, 9933–9946 CrossRef CAS.
- R. Berardi, J. S. Lintuvuori, M. R. Wilson and C. Zannoni, J. Chem. Phys., 2011, 135, 134119 CrossRef PubMed.
- S. Orlandi, L. Muccioli and R. Berardi, Liq. Cryst., 2018, 45, 2400–2415 CrossRef CAS.
- L. Querciagrossa, M. Ricci, R. Berardi and C. Zannoni, Phys. Chem. Chem. Phys., 2017, 19, 2383–2391 RSC.
- L. Muccioli and C. Zannoni, Chem. Phys. Lett., 2006, 423, 1–6 CrossRef CAS.
- R. F. de Souza, S. Zaccheroni, M. Ricci and C. Zannoni, J. Mol. Liq., 2022, 352, 118692 CrossRef CAS.
- J. J. Sandford O’Neill, P. S. Salter, M. J. Booth, S. J. Elston and S. M. Morris, Nat. Commun., 2020, 11, 1–8 CrossRef PubMed.
- M. Kleman and O. D. Lavrentovich, Soft matter physics: an introduction, Springer, 2003 Search PubMed.
- J. Brugués, J. Ignés-Mullol, J. Casademunt and F. Sagués, Phys. Rev. Lett., 2008, 100, 037801 CrossRef PubMed.
- J. Galanis, R. Nossal, W. Losert and D. Harries, Phys. Rev. Lett., 2010, 105, 168001 CrossRef PubMed.
- X. Tang and J. V. Selinger, Soft Matter, 2019, 15, 587–601 RSC.
- X. Wang, D. S. Miller, E. Bukusoglu, J. J. De Pablo and N. L. Abbott, Nat. Mater., 2016, 15, 106–112 CrossRef CAS PubMed.
- R. Zhang, S. A. Redford, P. V. Ruijgrok, N. Kumar, A. Mozaffari, S. Zemsky, A. R. Dinner, V. Vitelli, Z. Bryant and M. L. Gardel, et al. , Nat. Mater., 2021, 20, 875–882 CrossRef CAS PubMed.
- R. Zhang, N. Kumar, J. L. Ross, M. L. Gardel and J. J. de Pablo, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E124–E133 CAS.
- S. Zhou, S. V. Shiyanovskii, H.-S. Park and O. D. Lavrentovich, Nat. Commun., 2017, 8, 1–7 CrossRef CAS PubMed.
- G. Tóth, C. Denniston and J. Yeomans, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 051705 CrossRef PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- K. Schiele and S. Trimper, Phys. Status Solidi B, 1983, 118, 267–274 CrossRef CAS.
- I. W. Stewart, The static and dynamic continuum theory of liquid crystals: a mathematical introduction, CRC Press, 2019 Search PubMed.
- F. C. Frank, Discuss. Faraday Soc., 1958, 25, 19–28 RSC.
- S. D. Hudson and E. L. Thomas, Phys. Rev. Lett., 1989, 62, 1993 CrossRef CAS PubMed.
- H. Sidky, J. J. de Pablo and J. K. Whitmer, Phys. Rev. Lett., 2018, 120, 107801 CrossRef CAS PubMed.
- J. Shi, H. Sidky and J. K. Whitmer, Mol. Syst. Des. Eng., 2020, 5, 1131–1136 RSC.
- M. Ravnik and S. Žumer, Liq. Cryst., 2009, 36, 1201–1214 CrossRef CAS.
- V. Vitelli and D. R. Nelson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 051105 CrossRef PubMed.
- A. Mozaffari, R. Zhang, N. Atzin and J. de Pablo, Phys. Rev. Lett., 2021, 126, 227801 CrossRef CAS PubMed.
- R. Zhang, T. Roberts, I. S. Aranson and J. J. de Pablo, J. Chem. Phys., 2016, 144, 084905 CrossRef PubMed.
- M. Miesowicz, Nature, 1946, 158, 27 CrossRef CAS PubMed.
- J. Kołacz, A. Konya, R. L. Selinger and Q.-H. Wei, Soft Matter, 2020, 16, 1989–1995 RSC.
- X. Wang, Y.-K. Kim, E. Bukusoglu, B. Zhang, D. S. Miller and N. L. Abbott, Phys. Rev. Lett., 2016, 116, 147801 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01178f |
| This journal is © The Royal Society of Chemistry 2023 |

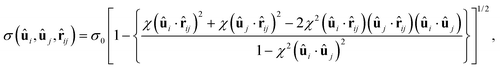
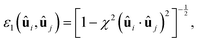


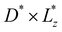
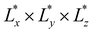

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 540–59
540–59