Open Access Article
Open Access ArticleCritical assessment of selenourea as an efficient small molecule fluorescence quenching probe to monitor protein dynamics†
Subhrakant
Jena
 ab,
Kiran Devi
Tulsiyan‡
ab,
Rudhi Ranjan
Sahoo‡
ab,
Saiprakash
Rout
ab,
Kiran Devi
Tulsiyan‡
ab,
Rudhi Ranjan
Sahoo‡
ab,
Saiprakash
Rout
 ab,
Akshay Kumar
Sahu
ab and
Himansu S.
Biswal
ab,
Akshay Kumar
Sahu
ab and
Himansu S.
Biswal
 *ab
*ab
aSchool of Chemical Sciences, National Institute of Science Education and Research (NISER), PO-Bhimpur-Padanpur, Via-Jatni, District-Khurda, PIN-752050, Bhubaneswar, India. E-mail: himansu@niser.ac.in; himansubiswal@gmail.com
bHomi Bhabha National Institute, Training School Complex, Anushakti Nagar, Mumbai 400094, India
First published on 26th September 2023
Abstract
Organoselenium compounds have recently been the experimentalists’ delight due to their broad applications in organic synthesis, medicinal chemistry, and materials science. Selenium atom replacement of the carbonyl oxygen of the urea moiety dramatically reduces the HOMO–LUMO gap and oxidation potential, which completely changes the physicochemical properties of selenocarbonyl compounds. To our surprise, the photophysics and utility of a simple molecule such as selenourea (SeU) have not been explored in detail, which persuaded us to investigate its role in excited state processes. The steady-state emission, temperature-dependent time-correlated single photon counting, and femtosecond fluorescence upconversion experimental results confirmed that SeU significantly enhances the fluorescence quenching through a photoinduced electron transfer (PET) mechanism with an ∼10 ps ultrafast intrinsic PET lifetime component which is mostly absent in thiourea (TU). A wide range of fluorophores, based on their different redox abilities and fluorescence lifetimes covering a broad spectral window (λex: 390–590 nm and λem: 490–690 nm), were chosen to validate the proof of the concept. It was extended to tetramethylrhodamine (TMR)-5-maleimide labeled lysozyme protein, where we observed significant fluorescence quenching in the presence of SeU. The present work emphasizes that the high quenching efficiency with an ultrafast PET process, reduced orbital energy gap, and higher negative free energy change of the electron transfer reaction are the representative characteristics of selenourea or selenoamides to enable them as potential surrogates of thioamides or oxoamides quenching probes to monitor protein conformational changes and dynamics.
Introduction
Organoselenium compounds have promising applications in antineoplastic activities, catalysis, and functional materials.1–5 In addition, selenium is usually incorporated into proteins and nucleic acids for photosensitizing activity,6 inhibitory properties,7 solving phase correction problems,8 and many more. The fundamental causes for these interesting phenomena are due to the unusual atomic properties of selenium, which include higher polarizability and nucleophilicity, low basicity, and better-leaving group ability.9–11 Selenium analogs of cysteine (selenocysteine) and methionine (selenomethionine) are present in proteins and peptides. Selenomethionine is the only selenium-containing natural amino acid with several interesting properties, including non-conventional hydrogen bonds, as shown in Fig. 1A.9 As the occurrence of selenium derivatives is rare in nature, they are obtained through synthesis and one of the widely adopted approaches of selenium derivatization is the single-atom replacement of carbonyl oxygen with selenium. Selenourea (obtained by selenium substitution of oxygen in urea, SeU) belongs to an important class of organoselenium compounds that exhibits several exciting features. SeU-based organic molecules are helpful in ion sensing,12 PbSe nanocrystal synthesis,5 chiral molecule recognition,13etc. The main reasons for SeU exhibiting interesting properties are diffused molecular electrostatic potential distribution, the elongated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Se bond, and lone pair orbitals showing labile electrons, as shown in Fig. 1B and C. A comparison of the important molecular properties of SeU with its oxygen (urea, U) and sulfur (thiourea, TU) analogs is shown in Fig. 1D. The discussed applications of SeU derivatives are based on the ground state properties. In contrast, the involvement of SeU derivatives in excited state reactions and their photophysics is almost unexplored. The weaker C
Se bond, and lone pair orbitals showing labile electrons, as shown in Fig. 1B and C. A comparison of the important molecular properties of SeU with its oxygen (urea, U) and sulfur (thiourea, TU) analogs is shown in Fig. 1D. The discussed applications of SeU derivatives are based on the ground state properties. In contrast, the involvement of SeU derivatives in excited state reactions and their photophysics is almost unexplored. The weaker C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Se bond and loosely bound non-bonding electrons result in a lower HOMO–LUMO gap and reduced oxidation potentials. These properties of SeU could be advantageous in excited state electron transfer reactions.
Se bond and loosely bound non-bonding electrons result in a lower HOMO–LUMO gap and reduced oxidation potentials. These properties of SeU could be advantageous in excited state electron transfer reactions.
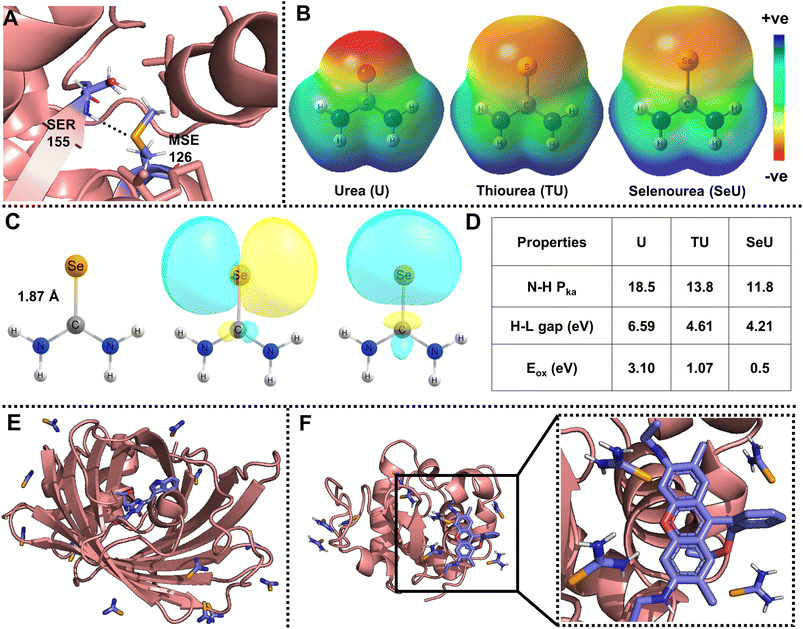 | ||
| Fig. 1 (A) Representative example of an amide N–H⋯Se hydrogen bond observed in phosphoethanolamine N-methyltransferase (PDB ID: 4KRG, resolution: 1.8 Å);9; (B) visualization of molecular electrostatic potential (MESP) isosurfaces for urea (U), thiourea (TU), and selenourea (SeU), (isovalue = 0.005 au); (C) molecular structure displaying an elongated selenocarbonyl bond, and Natural Bond Orbital (NBO) analysis showing the availability of diffused lone pairs of electrons of SeU. The isovalue for the NBO plot is 0.02 au; the MESP and NBO calculations were performed at the MP2/aug-cc-pVDZ level of theory. Comparison for the structure and visualization of MESP and lone pair orbitals is given for U, TU, and SeU in Fig. S1.† (D) Comparison of important properties such as amide proton acidity, HOMO–LUMO (H–L) gaps, and oxidation potentials vs. SCE of U, TU, SeU;13,52,53; (E) SeU binding sites in cyan fluorescence protein with twelve sites (PDB ID: 5T3I); (F) Rh6G docked lysozyme protein with nine SeU binding sites (PDB ID: 5T3F). | ||
Electron transfer (ET) plays many crucial roles in chemical and biological processes.14–16 Photoinduced electron transfer (PET) is one type of ET process driven by light energy. PET occurs naturally in biological systems in sunlight, i.e., photosynthesis.17,18 Over the past decades, tremendous efforts have been made to improve and refine the PET process and implement it in various applications. Many studies and thorough investigations elucidated that PET can be artificially constructed between the fluorophore and a quencher for application in solar cells,19–21 biosensors,22 organic synthesis,23 and models for monitoring biomolecule structural dynamics. Among these applications, developing biocompatible small organic molecules as fluorescence quenching probes for probing biomolecule dynamics has attracted increased attention from the scientific community.24–26 The biomolecular structural dynamics can be monitored through several spectroscopic methods; among them, fluorescence spectroscopy is the most adopted as it is very sensitive to minimal structural perturbations.27–30 This technique is not limited to the size of biomolecules and provides real-time information from several microseconds to hundreds of femtoseconds. It also helps to study biomolecules at a single molecular level, imaging their interactions in vivo and in vitro. Among several photophysical processes, fluorescence quenching is a widely studied phenomenon as it gives valuable information on biomolecular association, structure, and functions of biomolecules. The fluorescence quenching can happen through several processes, such as fluorescence resonance energy transfer,31 the Dexter energy transfer mechanism,32 inter-system crossing,33 molecular aggregation,34 and PET.35 One of the general approaches to design quenching probes is to use thiocarbonyls instead of oxocarbonyls.35–39 The thiocarbonyl modification, in fact, gives rise to intriguing physicochemical and photophysical properties.40–45 A single O-to-S atom change does not affect the probe size but can provide better structural and dynamics information without perturbing biomolecules. Thioamides have already been developed as efficient fluorescence quenching probes, which can be used as an alternative to conventional quenchers for monitoring protein structure and dynamics in a distance-dependent manner.35,37 It has also been reported that thioamides quench the fluorescence of intrinsic chromophores and several fluorophores through FRET and PET processes.35–37,46–48 The reduced HOMO–LUMO gap and oxidation potential are the major players in designing FRET and PET donor–acceptor pairs. However, monitoring PET has several advantages over FRET as it does not require spectral overlap and is not restricted to certain spectral windows. PET is mostly governed by redox mechanisms.49
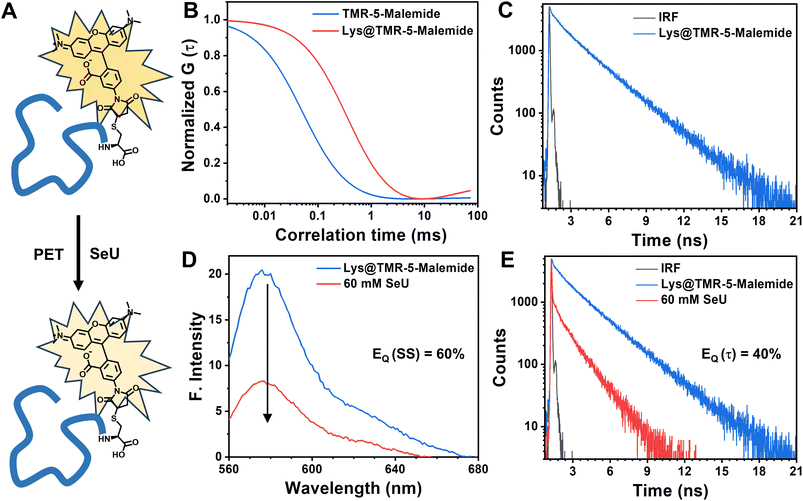
Even though thioamides have been proven to be efficient quenching probes for PET, not much work has been devoted to exploring selenoamide and telluoroamides as alternative probes. It is well explored that down the chalcogen group, heavier analogs such as selenoamide and telluoroamides are useful in synthetic transformation, preparation of relevant peptides, and heterocyclic drugs.50 The oxidation potentials and HOMO–LUMO gap further decrease with selenium substitution and the obtained selenoamide can be used as a better fluorescence quenching probe without affecting the molecular size of the probe.51,52 Selenium is also introduced into crystals of proteins and nucleic acids by soaking with SeU and can be a convenient vehicle for solving phase correction problems.54,55Fig. 1E shows the binding sites of SeU in a cyan-fluorescent protein where the tryptophan-based chromophore serves as the intrinsic fluorophore. Fig. 1F displays the SeU-bound lysozyme protein docked with rhodamine 6G (Rh6G) and used as an extrinsic fluorophore. The priorly existence of SeU in biological systems may construct fluorophore quencher pairs and be involved in fluorescence quenching processes, which necessitates a deeper understanding of the mechanism. In the present study, SeU has been chosen as the model SeU-based compound as it is structurally simple, moderately stable, and can be considered a selenoamide analog. SeU can participate in FRET and PET, but this work focuses on fluorescence quenching through the PET mechanism; the reasons are mentioned above. To the best of our knowledge, there are no reports of using SeU or any selenoamides as PET quenching probes, which persuaded us to explore their fluorescence quenching efficiency. We have chosen Rh6G as the representative fluorophore to investigate the PET reaction with SeU. In addition, the quenching efficiency of SeU was further explored with other biologically important fluorophores and a covalently bound protein–dye conjugate. We also investigated the respective oxygen and sulfur analogs, i.e., U and TU, as quenchers for comparison purposes. The free energy change (ΔGET) and HUMO–LUMO gap (ΔE) were used as the descriptors of PET to quantify the ET feasibility. With the help of steady-state and time-resolved fluorescence spectroscopy, we ascertain the binding nature and mechanism of electron transfer.
Results and discussion
Energetic feasibility of a PET process
The Marcus model is one of the finest models used to understand the underlying principles of electron transfer reactions in solutions.56 For a weakly coupled donor–acceptor (D–A) system, the rate of a biomolecular ET (KET) reaction depends on (i) the free energy change of the reaction (ΔG°); (ii) the reorganization energy (λ); (iii) the electronic coupling between D–A (Hel). According to the Marcus theory,56 the KET has a quadratic dependency on ΔG° and can be expressed as following eqn (1):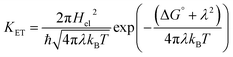 | (1) |
Further, the ΔG° of an ET reaction can be obtained experimentally using the Rehm–Weller model57 as following eqn (2):
| ΔGET = F{Eox(D) − Ered(A)} − E0–0 + Cw | (2) |
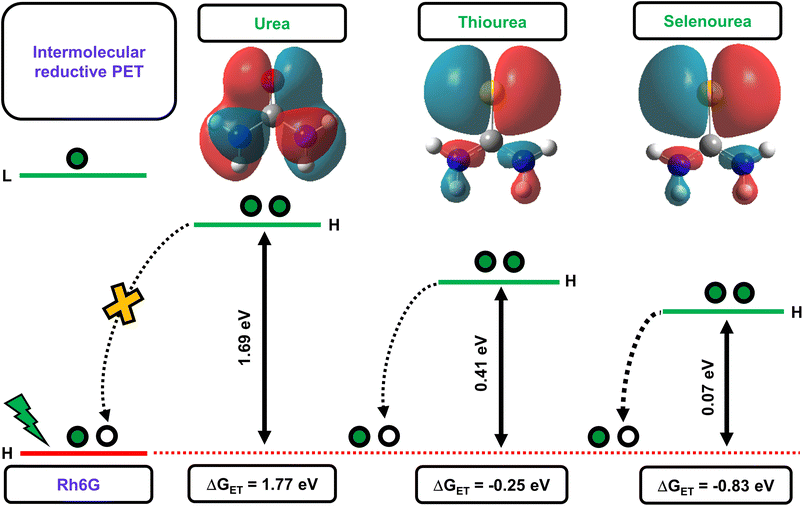
The above-discussed factors affecting the PET process guided us in interpreting the feasibility of the electron transfer reaction. Initially, we determined the energy gaps (ΔE) between the HOMO energy levels of Rh6G and the studied quenchers. The computed results showed that the ΔE between the HOMO energy level of the Rh6G–quencher pair decreases with sulfur and selenium substitution (Fig. 2). The decrease in the HOMO energy level in the case of thiourea (TU) and selenourea (SeU) can be attributed to the lower energy π–π* transition from the weaker thio and seleno-carbonyl groups. The HOMOs of urea, thiourea, and selenourea are displayed in Fig. 2. It shows more diffused and labile lone pair of electrons of sulfur and selenium which are more localized at the respective atomic site. The situation is different in the case of the oxygen atom due to its higher electronegativity. Furthermore, we calculated the change in Gibb’s free energy (ΔGET) for the electron transfer from a donor to an acceptor molecule (Fig. 2). To calculate ΔGET, previously reported electrochemical properties, i.e., the reduction potential of Rh6G (Ered = −0.95 eV vs. SCE), the oxidation potential of quenchers (Eox (urea) = 3.1 eV vs. SCE,53Eox (thiourea) = 1.07 eV vs. SCE,53Eox (selenourea) = 0.5 eV vs. SCE),52 and the zero–zero electronic excitation energy of Rh6G (E0–0 = 2.28 eV), were considered. The analysis of eqn (2) provides a large positive ΔGET = 1.77 eV along with a high energy gap (ΔE = 1.69 eV) for the Rh6G–U pair, ruling out the possibility of the PET process. In sharp contrast, ΔGET = −0.25 eV with reduced ΔE = 0.41 eV for the Rh6G–TU pair raises the possibility of PET. It is in line with several previous studies that demonstrated thioamides as efficient fluorescent quenchers for a wide range of fluorophores.35 Interestingly, a significant reduction in the ΔGET = −0.83 eV and ΔE = 0.07 eV for the Rh6G–SeU pair provides clear evidence of the pronounced PET from the SeU to Rh6G molecule. The obtained theoretical and experimental results predict that the presence of SeU in the biological system could quench the intrinsic and extrinsic fluorophores. Preliminary analyses were further carefully performed using steady-state and time-resolved fluorescence spectroscopy.
Fluorescence spectroscopic investigations
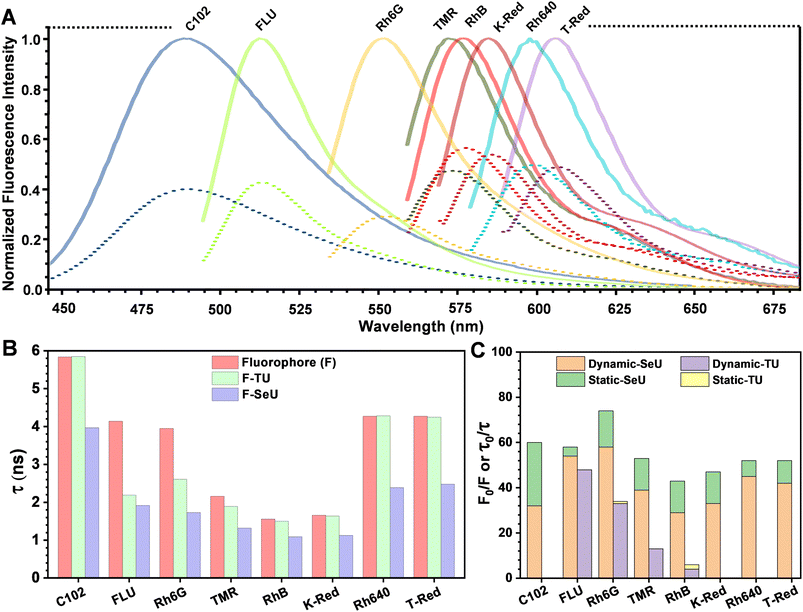
The fluorescence quenching of Rh6G in the presence of SeU in phosphate buffer solution (pH 7.4, 100 mM) was investigated. A significant quenching in the Rh6G fluorescence was observed upon subsequent addition of SeU up to 60 mM concentration (Fig. 3D). We also performed the fluorescence titration experiments of the equimolar solution of the fluorophore in the presence of 60 mM urea and thiourea as control. In the case of thiourea, moderate quenching was observed, while no quenching was noticed upon the addition of urea (Fig. 3A and S2†). This observation supported the earlier reports on thioamide quenching of fluorescent probes through photoinduced electron transfer (PET).35 We further estimated the quenching efficiency (EQ) for TU and SeU at the emission maximum of Rh6G from the recorded steady-state (SS) fluorescence data (eqn (S1)†). A comparison of EQ(SS) for TU and SeU shows that TU quenches the fluorescence of Rh6G by 34%, whereas SeU quenches with an efficiency of 74%. The experimental findings corroborate our earlier prediction based on the reduced ΔE value and more negative ΔGET value for the studied fluorophore quencher pairs. The drastic decrease in the Rh6G fluorescence in the presence of SeU compared to its thio analog needs a detailed analysis to unravel the quenching mechanism.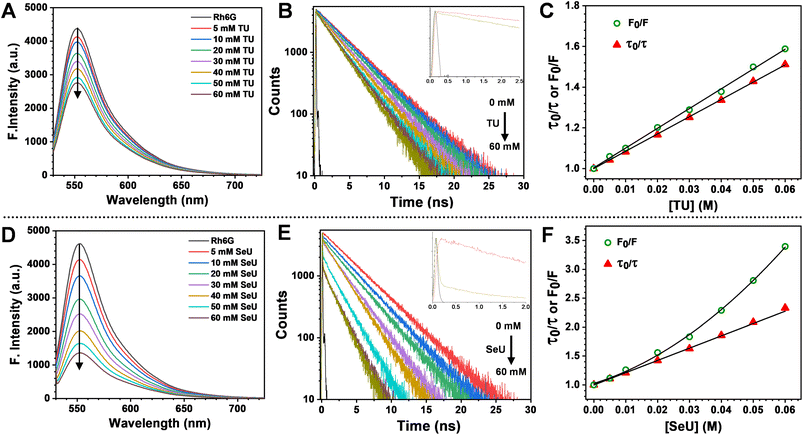 | ||
| Fig. 3 Top panel: steady-state emission spectra, time-resolved fluorescence decay curves (405 nm excitation) and comparison of steady-state and time-resolved S–V plots (the steady-state data fit to eqn (S3) and lifetime data fit to eqn (S4)†) of Rh6G from left to right (A–C) with incremental addition from 5 mM to 60 mM of TU and bottom panel: (D–F) with incremental addition from 5 mM to 60 mM of SeU. Error estimates: ±1% for TU and ±3% for SeU. | ||
We performed time-correlated single photon counting (TCSPC) experiments to decipher the exact nature of quenching and whether the observed phenomenon is due to static or dynamic processes. Fig. 3B and E represent the fluorescence lifetime decay curves for Rh6G in the absence and presence of quenchers (TU and SeU respectively). To our surprise, we noticed the presence of an ultrafast decay component during the time-resolved fluorescence quenching experiments. The contribution of this short component to the fluorescence quenching of Rh6G is much less for TU and quite significant in the case of SeU. The contribution of this fast component becomes more prominent as the quencher concentration increases. The occurrence of such a feature may arise from the interference by the lamp profile of the diode laser during titration experiments. Another possibility for the appearance of a fast component could be PET, which takes place in the ultrafast timescale. The observed ultrafast component falls within the instrument response function temporal profile, and its assignment to a true PET process is inconclusive. Thus the observed decay profiles were fitted single exponentially. However, the significance of the presence of an ultrafast component in PET reactions has been discussed in the later part.
The fluorescence lifetime of Rh6G was found to be 3.93 ns. Upon the addition of 60 mM TU, the lifetime decreased to 2.6 ns, corresponding to an EQ(τ) of 33% (Fig. 3B and eqn (S2)†). The concentration-dependent lifetime measurement helped us to generate a linear Stern–Volmer (S–V) plot with a Stern–Volmer constant (KSV) of 8.49 M−1 (Fig. 3C and eqn (S3)†). We also calculated a near-identical KSV of 9.7 M−1 from the steady-state measurements. The KSV value obtained from the steady-state measurements was greater than that obtained under identical conditions from time-resolved measurements. Therefore, we used eqn (S4)† to fit the steady-state Stern–Volmer data accounting for both static (KS) and dynamic (KD) quenching contributions. The fitting gave rise to KD = 8.62 M−1 and KS = 0.81 M−1. The comparable KD values explain the purely dynamic nature of the observed quenching for the Rh6G–TU pair. On the other hand, the constructed Stern–Volmer curve from steady-state measurements for the Rh6G–SeU fluorophore quencher pair showed an upward behavior. Interestingly, the dynamics seemed different when we performed the lifetime measurements for the Rh6G–SeU pair. Upon the addition of SeU gradually up to 60 mM concentration, the lifetime of Rh6G decreased from 3.93 ns to 1.69 ns (Fig. 3E). The calculated EQ(τ) is 58%, which is different from the steady-state observation.
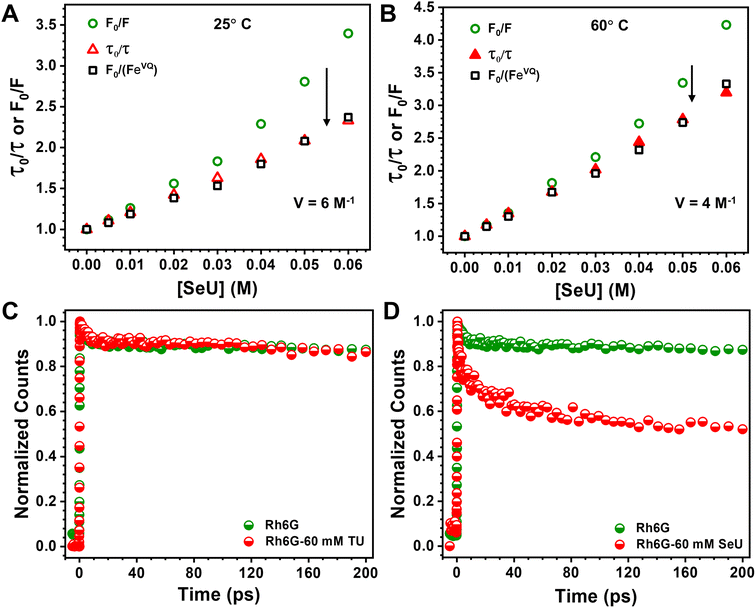
At a sphere volume of 6 M−1, a linear S–V curve (Fig. 4A) for F0/F vs. [Q] was obtained. It matches pretty well with the τ0/τ vs. [Q] curve. The calculated volume in which the Rh6G and SeU are present at the moment of excitation can be treated as the contribution from the static process. Considering a sphere of volume 6 M−1, the radius of the sphere was determined to be 13.4 Å. The calculated molecular van der Waals radius for Rh6G and SeU is 7.78 Å and 3.42 Å, confirming that the fluorophore–quencher pair can present and diffuse inside the sphere. Close association within the sphere may result in apparent static quenching and lead to a positive deviation from the linearity. We also calculated the collisional quenching constant KSV, which is 21.7 M−1. The higher collisional quenching constant (KSV = 21.7 M−1) value compared to the static quenching constant of 6 M−1 indicates the predominantly dynamic nature of the quenching.
To achieve this, we used a femtosecond FUC technique with a time resolution better than ∼300 fs. The fluorescence upconversion experiments were performed at 25 °C for Rh6G–TU and Rh6G–SeU fluorophore–quencher pairs. The decay traces at emission maximum ∼550 nm of Rh6G for the 400 nm excitation wavelength was first recorded. Although Rh6G has low absorbance at 400 nm, the pre-aligned laser setup gave us an appreciable signal-to-noise ratio. For Rh6G, a single exponential fitting gave a lifetime value of 3.98 ns, nearly identical to the lifetime value obtained from TCSPC measurement. Fig. 4C and D depict the normalized femtosecond transients of Rh6G in the absence and presence of 60 mM TU and SeU. Interestingly, we observed a drastic reduction in the initial part of the normalized femtosecond transients for the Rh6G in the presence of 60 mM SeU (Fig. 4D). The decay curve was fitted to a bi-exponential, which gave rise to two components, suggesting two lifetimes. An ultrafast component of 10 ps, which further decays radiatively with a lifetime of 1.55 ns, was noticed. The slow component is very similar to the lifetime observed from TCSPC measurements. We did not observe any significant changes in the decay curve up to 200 ps in the presence of TU. However, the contribution of the 10 ps lifetime component is very negligible. We observed changes in the later part of the decay curve (Fig. S7†). The fitting gave a lifetime of 2.7 ns, which matches quite well with our TCSPC data.
The diffusion-controlled PET process with near unity quenching generally occurs in a few tens of ps.21 The presence of an ultrafast component of 10 ps can be assigned to the intrinsic PET process. Such a situation arises when the fluorophore and quencher are nearby during the excitation time. Our sphere of action model suggests apparent static quenching where there is a higher probability of the presence of Rh6G and SeU within the sphere. Such conditions may result in less diffusion and instantaneous electron transfer upon electronic excitation. The proposed quenching model supports this finding, whereas the absence of any such scenario in the case of TU could be the reason for the absence of any ultrafast processes. The femtosecond FUC experiment helped to detect the ultrafast component responsible for intrinsic PET.
Conclusions
In summary, we proposed selenourea (SeU) as an efficient fluorescence quenching probe for the first time. The fluorescence quenching of the model Rh6G–SeU pair was explained through a photoinduced electron transfer mechanism. We found that SeU significantly enhances the quenching efficiency compared to its sulfur analog i.e. thiourea (TU). It was also observed that the quenching mechanism in the case of Rh6G–TU could be explained using the modified Stern–Volmer model. In sharp contrast, the quenching sphere of action model was needed to explain the quenching mechanism of the Rh6G–SeU pair. Temperature-dependent studies confirmed the predominantly dynamic nature of the PET process for the studied complexes. As per the sphere of action model, the close association between SeU and Rh6G leads to an ultrafast intrinsic electron transfer process of 10 ps, which was further confirmed using femtosecond fluorescence upconversion experiments. The utility of SeU as an efficient fluorescence probe was examined by considering several important fluorophores with different photophysical properties that are regularly used for imaging and single molecule fluorescence correlation spectroscopy of biomolecules. The lysozyme labeling experiments showed the potentiality of SeU as a fluorescent quencher, even for the covalently bound fluorophore. The site-specific incorporation of SeU inside the protein or selenium substitution of oxo-amides could further be exploited to monitor protein dynamics in a distance-dependent manner. Recent reports suggest that the use of selenium in proteins and biomedical applications is gaining importance.71,72 This fundamental finding will also be useful for researchers while interpreting the fluorescence properties of biomolecules containing selenoamides. The present work elucidates that SeU can be used as an efficient minimalistic quenching probe to monitor protein structure and dynamics, an avenue that needs to be explored in detail.Data availability
The data supporting this work are uploaded as a part of the ESI.†Author contributions
S. J., and H. S. B. conceptualised the research idea. S. J., K. D. T., R. R. S., S. R., A. K. S. performed the experiments. S. J., and H. S. B. analysed the results and wrote the manuscript. H. S. B. supervised the project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This manuscript is dedicated to the birth centenary of Prof. Rudolph A. Marcus, who revolutionized research on electron transfer processes. S. J., K. D. T., R. R. S., S. R. A. K. S. and H. S. B. acknowledge financial support from the Department of Atomic Energy, Science and Engineering Research Board, Department of Science and Technology (project file no. CRG/2022/001096), Govt. of India.Notes and references
- G. Spengler, M. Gajdács, M. A. Marć, E. Domínguez-Álvarez and C. Sanmartín, Molecules, 2019, 24, 336 CrossRef PubMed.
- F. V. Singh and T. Wirth, in Organoselenium Compounds in Biology and Medicine: Synthesis, Biological and Therapeutic Treatments, The Royal Society of Chemistry, 2018, pp. 77–121, 10.1039/9781788011907-00077.
- V. Gandin, P. Khalkar, J. Braude and A. P. Fernandes, Free Radical Biol. Med., 2018, 127, 80–97 CrossRef CAS PubMed.
- S. Park, A. K. Dutta, C. Allacher, A. Abramov, P. Dullinger, K. Kuzmanoska, D. Fritsch, P. Hitzfeld, D. Horinek, J. Rehbein, P. Nuernberger, R. M. Gschwind and A. Breder, Angew. Chem., Int. Ed., 2022, 61, e202208611 CrossRef CAS PubMed.
- M. P. Campos, M. P. Hendricks, A. N. Beecher, W. Walravens, R. A. Swain, G. T. Cleveland, Z. Hens, M. Y. Sfeir and J. S. Owen, J. Am. Chem. Soc., 2017, 139, 2296–2305 CrossRef CAS PubMed.
- M. Jiang, J. Wu, W. Liu, H. Ren, S. Wang and P. Wang, J. Photochem. Photobiol., B, 2022, 233, 112488 CrossRef CAS PubMed.
- R. Gowda, S. V. Madhunapantula, D. Desai, S. Amin and G. P. Robertson, Cancer Biol. Ther., 2012, 13, 756–765 CrossRef CAS PubMed.
- J. Sheng and Z. Huang, Int. J. Mol. Sci., 2008, 9, 258–271 CrossRef PubMed.
- V. R. Mundlapati, D. K. Sahoo, S. Ghosh, U. K. Purame, S. Pandey, R. Acharya, N. Pal, P. Tiwari and H. S. Biswal, J. Phys. Chem. Lett., 2017, 8, 794–800 CrossRef CAS PubMed.
- A. Chand, D. K. Sahoo, A. Rana, S. Jena and H. S. Biswal, Acc. Chem. Res., 2020, 53, 1580–1592 CrossRef CAS PubMed.
- S. Jena, J. Dutta, K. D. Tulsiyan, A. K. Sahu, S. S. Choudhury and H. S. Biswal, Chem. Soc. Rev., 2022, 51, 4261–4286 RSC.
- A. Casula, P. Begines, A. Bettoschi, J. G. Fernandez-Bolaños, F. Isaia, V. Lippolis, Ó. López, G. Picci, M. Andrea Scorciapino and C. Caltagirone, Chem. Commun., 2017, 53, 11869–11872 RSC.
- G. Bian, S. Yang, H. Huang, H. Zong, L. Song, H. Fan and X. Sun, Chem. Sci., 2016, 7, 932–938 RSC.
- Z. Zhang, L. Huang, V. M. Shulmeister, Y.-I. Chi, K. K. Kim, L.-W. Hung, A. R. Crofts, E. A. Berry and S.-H. Kim, Nature, 1998, 392, 677–684 CrossRef CAS PubMed.
- B. Bagchi and N. Gayathri, in Advances in Chemical Physics, 1999, pp. 1–80, DOI:10.1002/9780470141663.ch1.
- H. Fu, H. Lam, M. A. Emmanuel, J. H. Kim, B. A. Sandoval and T. K. Hyster, J. Am. Chem. Soc., 2021, 143, 9622–9629 CrossRef CAS PubMed.
- G. Cornic and N. R. Baker, in Photosynthesis: Plastid Biology, Energy Conversion and Carbon Assimilation, eds. J. J. Eaton-Rye, B. C. Tripathy and T. D. Sharkey, Springer Netherlands, Dordrecht, 2012, pp. 591–605, DOI:10.1007/978-94-007-1579-0_23.
- J. P. Menzel, H. J. M. de Groot and F. Buda, J. Phys. Chem. Lett., 2019, 10, 6504–6511 CrossRef CAS PubMed.
- P. Song, Y. Li, F. Ma, T. Pullerits and M. Sun, Chem. Rec., 2016, 16, 734–753 CrossRef CAS PubMed.
- Z. Chen and H. Zhu, J. Phys. Chem. Lett., 2022, 13, 1123–1130 CrossRef CAS PubMed.
- K. Mishra, A. Das and S. Ghosh, J. Phys. Chem. C, 2021, 125, 9638–9645 CrossRef CAS.
- Q. Liu, J. Lian, M. Liu, Y. Jin and B. Li, Anal. Methods, 2018, 10, 2257–2262 RSC.
- S. Dadashi-Silab, S. Doran and Y. Yagci, Chem. Rev., 2016, 116, 10212–10275 CrossRef CAS PubMed.
- X. Tian, L. C. Murfin, L. Wu, S. E. Lewis and T. D. James, Chem. Sci., 2021, 12, 3406–3426 RSC.
- A. P. de Silva, H. Q. N. Gunaratne, T. Gunnlaugsson, A. J. M. Huxley, C. P. McCoy, J. T. Rademacher and T. E. Rice, Chem. Rev., 1997, 97, 1515–1566 CrossRef CAS PubMed.
- H.-W. Liu, L. Chen, C. Xu, Z. Li, H. Zhang, X.-B. Zhang and W. Tan, Chem. Soc. Rev., 2018, 47, 7140–7180 RSC.
- R. Brahma, A. Das and H. Raghuraman, STAR Protoc., 2022, 3, 101200 CrossRef CAS PubMed.
- S. G. Harroun, D. Lauzon, M. C. C. J. C. Ebert, A. Desrosiers, X. Wang and A. Vallée-Bélisle, Nat. Methods, 2022, 19, 71–80 CrossRef CAS PubMed.
- Y. Liu, C. H. Wolstenholme, G. C. Carter, H. Liu, H. Hu, L. S. Grainger, K. Miao, M. Fares, C. A. Hoelzel, H. P. Yennawar, G. Ning, M. Du, L. Bai, X. Li and X. Zhang, J. Am. Chem. Soc., 2018, 140, 7381–7384 CrossRef CAS PubMed.
- C. A. Royer, Chem. Rev., 2006, 106, 1769–1784 CrossRef CAS PubMed.
- E. R. H. Walter, Y. Ge, J. C. Mason, J. J. Boyle and N. J. Long, J. Am. Chem. Soc., 2021, 143, 6460–6469 CrossRef CAS PubMed.
- N. Haase, A. Danos, C. Pflumm, P. Stachelek, W. Brütting and A. P. Monkman, Mater. Horiz., 2021, 8, 1805–1815 RSC.
- K. Nagarajan, A. R. Mallia, K. Muraleedharan and M. Hariharan, Chem. Sci., 2017, 8, 1776–1782 RSC.
- W.-K. Tsai, C.-I. Wang, C.-H. Liao, C.-N. Yao, T.-J. Kuo, M.-H. Liu, C.-P. Hsu, S.-Y. Lin, C.-Y. Wu, J. R. Pyle, J. Chen and Y.-H. Chan, Chem. Sci., 2019, 10, 198–207 RSC.
- J. M. Goldberg, S. Batjargal, B. S. Chen and E. J. Petersson, J. Am. Chem. Soc., 2013, 135, 18651–18658 CrossRef CAS PubMed.
- J. M. Goldberg, R. F. Wissner, A. M. Klein and E. J. Petersson, Chem. Commun., 2012, 48, 1550–1552 RSC.
- J. M. Goldberg, S. Batjargal and E. J. Petersson, J. Am. Chem. Soc., 2010, 132, 14718–14720 CrossRef CAS PubMed.
- E. J. Petersson, J. M. Goldberg and R. F. Wissner, Phys. Chem. Chem. Phys., 2014, 16, 6827–6837 RSC.
- D. M. Robkis, E. M. Hoang, P. Po, C. J. Deutsch and E. J. Petersson, Biopolymers, 2021, 112, e23384 CrossRef CAS PubMed.
- S. Jena, K. D. Tulsiyan, A. Rana, S. S. Choudhury and H. S. Biswal, ChemPhysChem, 2020, 21, 1826–1835 CrossRef CAS PubMed.
- N. Mahanta, D. M. Szantai-Kis, E. J. Petersson and D. A. Mitchell, ACS Chem. Biol., 2019, 14, 142–163 CrossRef CAS PubMed.
- S. Jena, C. Routray, J. Dutta and H. S. Biswal, Angew. Chem., Int. Ed., 2022, 61, e202207521 CrossRef CAS PubMed.
- S. Jena, K. D. Tulsiyan, A. Kumari, R. Das and H. S. Biswal, J. Phys. Chem. B, 2022, 126, 6083–6094 CrossRef CAS PubMed.
- L. A. Ortiz-Rodríguez and C. E. Crespo-Hernández, Chem. Sci., 2020, 11, 11113–11123 RSC.
- J. Tang, M. A. Robichaux, K.-L. Wu, J. Pei, N. T. Nguyen, Y. Zhou, T. G. Wensel and H. Xiao, J. Am. Chem. Soc., 2019, 141, 14699–14706 CrossRef CAS PubMed.
- J. M. Goldberg, L. C. Speight, M. W. Fegley and E. J. Petersson, J. Am. Chem. Soc., 2012, 134, 6088–6091 CrossRef CAS PubMed.
- R. F. Wissner, S. Batjargal, C. M. Fadzen and E. J. Petersson, J. Am. Chem. Soc., 2013, 135, 6529–6540 CrossRef CAS PubMed.
- S. Jena, K. D. Tulsiyan, R. K. Kar, H. K. Kisan and H. S. Biswal, Chem.–Eur. J., 2021, 27, 4373–4383 CrossRef CAS PubMed.
- T. Ueno, Y. Urano, K.-i. Setsukinai, H. Takakusa, H. Kojima, K. Kikuchi, K. Ohkubo, S. Fukuzumi and T. Nagano, J. Am. Chem. Soc., 2004, 126, 14079–14085 CrossRef CAS PubMed.
- M. Koketsu and H. Ishihara, Curr. Org. Chem., 2007, 4, 15–29 CAS.
- K. M. Farrell, M. M. Brister, M. Pittelkow, T. I. Sølling and C. E. Crespo-Hernández, J. Am. Chem. Soc., 2018, 140, 11214–11218 CrossRef CAS PubMed.
- B. Mishra, D. K. Maity, K. I. Priyadarsini, H. Mohan and J. P. Mittal, J. Phys. Chem. A, 2004, 108, 1552–1559 CrossRef CAS.
- F. G. Bordwell, D. J. Algrim and J. A. Harrelson, J. Am. Chem. Soc., 1988, 110, 5903–5904 CrossRef CAS.
- Z. Luo, Sci. Rep., 2016, 6, 37123 CrossRef CAS PubMed.
- Z. Luo, W. Gu, Y. Wang, Y. Tang and D. Li, Crystals, 2022, 12, 976 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- D. Rehm and A. Weller, Isr. J. Chem., 1970, 8, 259–271 CrossRef CAS.
- A. Rosspeintner, M. Koch, G. Angulo and E. Vauthey, J. Am. Chem. Soc., 2012, 134, 11396–11399 CrossRef CAS PubMed.
- S. Ghosh, S. K. Mondal, K. Sahu and K. Bhattacharyya, J. Chem. Phys., 2007, 126, 204708 CrossRef PubMed.
- S. Ghosh, K. Sahu, S. K. Mondal, P. Sen and K. Bhattacharyya, J. Chem. Phys., 2006, 125, 054509 CrossRef PubMed.
- S. Ghosh, S. K. Mondal, K. Sahu and K. Bhattacharyya, J. Phys. Chem. A, 2006, 110, 13139–13144 CrossRef CAS PubMed.
- G. A. Parada, Z. K. Goldsmith, S. Kolmar, B. Pettersson Rimgard, B. Q. Mercado, L. Hammarström, S. Hammes-Schiffer and J. M. Mayer, Science, 2019, 364, 471–475 CrossRef CAS PubMed.
- A. P. de Silva, T. S. Moody and G. D. Wright, Analyst, 2009, 134, 2385–2393 RSC.
- W. Chi, J. Chen, W. Liu, C. Wang, Q. Qi, Q. Qiao, T. M. Tan, K. Xiong, X. Liu, K. Kang, Y.-T. Chang, Z. Xu and X. Liu, J. Am. Chem. Soc., 2020, 142, 6777–6785 CrossRef CAS PubMed.
- M. R. Eftink and C. A. Ghiron, J. Phys. Chem., 1976, 80, 486–493 CrossRef CAS.
- K. M. Watson and J. B. Asbury, J. Phys. Chem. C, 2022, 126, 4995–5003 CrossRef CAS.
- K. Mishra, A. Das and S. Ghosh, J. Phys. Chem. C, 2020, 124, 24115–24125 CrossRef CAS.
- A. Rosspeintner, G. Angulo and E. Vauthey, J. Am. Chem. Soc., 2014, 136, 2026–2032 CrossRef CAS PubMed.
- M. M. Islam, S. Barik, N. Preeyanka and M. Sarkar, J. Phys. Chem. B, 2020, 124, 961–973 CrossRef CAS PubMed.
- B. C. Swain, S. K. Mukherjee, J. Rout, Sakshi, P. P. Mishra, M. Mukherjee and U. Tripathy, Anal. Bioanal. Chem., 2020, 412, 2565–2577 CrossRef CAS PubMed.
- J. Wang, M. Chen, Z. Zhang, L. Ma and T. Chen, Coord. Chem. Rev., 2023, 493, 215278 CrossRef CAS.
- G. Goldsztejn, V. R. Mundlapati, V. Brenner, E. Gloaguen and M. Mons, Molecules, 2022, 27, 3163 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc04287a |
| ‡ Kiran Devi Tulsiyan and Rudhi Ranjan Sahoo contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |