A Predictive machine-learning model for propagation rate coefficients in radical polymerization†
Emma
Van de Reydt
a,
Noam
Marom
b,
James
Saunderson
 b,
Mario
Boley
c and
Tanja
Junkers
b,
Mario
Boley
c and
Tanja
Junkers
 *a
*a
aPolymer Reaction Design Group, School of Chemistry, Monash University 19 Rainforest Walk, Building 23, Clayton, Vic 3800, Australia. E-mail: tanja.junkers@monash.edu
bElectrical and Computer Systems Engineering, Monash University, 14 Alliance Lane, Building 72, Clayton, Vic 3800, Australia
cFaculty for Information Technology, Monash University, 20 Exhibition Walk, Clayton, Vic 3800, Australia
First published on 10th March 2023
Abstract
Using a ridge regression, the propagation rate coefficients for radical polymerization are correlated with basic molecular properties. These are either available from literature, or from simple and non-time-consuming calculations. Parameters under consideration are molecular weights, boiling points, and dipole moments. The model is applicable to both acrylates and methacrylates with linear and branched structures, as well as monomers that are known to be influenced strongly by H-bonding, allowing to fit all data in a single approach. The model also successfully correlates monomers such as styrene and acrylonitrile. Absolute rate coefficients, as well as Arrhenius activation parameters can be described with good accuracy. With the presented model it is thus possible to describe practically all monomers for which kinetic data is available simultaneously and to carry out predictions for monomers for which no experimental data exist.
Introduction
The correct assessment of reaction kinetics, and the determination of reliable rate coefficients for reactions is often tedious and requires sophisticated methods.1 This is especially true for kinetic rate coefficients in radical polymerization. In polymerizations, to make it more complicated, rate parameters do not merely predict the rate of a polymerization. They also play a crucial role in the design and synthesis of novel materials since individual reaction rates influence the structure of a polymer. A meaningful prediction of monomer conversions, molecular weights, and polymer dispersities is only achievable if reactivity information of the monomers can be correlated with the rate coefficient of chain propagation and termination at minimum.2 The invention of the pulsed laser polymerization - size exclusion chromatography (PLP-SEC) method 35 years ago marked a turning point in investigations in polymerization kinetics by providing highly reliable measurements of propagation rate coefficients in a comparatively simple fashion.3 Over the years, a number of monomers has been investigated by this technique, and IUPAC working groups have benchmarked data for a number of important monomers.4 PLP-SEC allows for determinations with relatively high precision – typically an error of 10 to 20% is estimated. Yet, no unifying approach exists to date that correlates the structure of a monomer with its rate of propagation, and therefore no meaningful prediction of kinetic data can be made. Within specific families of monomers, most notably the (meth)acrylates, some trends are known.5 For example, the – on first glance counterintuitive to most chemists – increase of the propagation rate coefficient (kp) with the length of the ester side chain. Yet, already smaller differences in structure such as branching vs. linear ester chains are not captured in the literature.6 The traditional way to predict kp is to use high level ab initio quantum chemical calculation.7,8 While by themselves highly interesting, these calculations have for some monomers confirmed experimental values, but they struggle to make absolute predictions.It is largely known that the propagation rate coefficients of monomers depend on a series of factors. Molecular weight is certainly important. Similarly, resonance stability of the propagating radical plays a major role. Also, H-bonding has been identified to cause significant rate effects and polarity is speculated to impact kp.9 These effects have, however, always only been investigated as insular effects, and no general theory could so far be formed that would unify all different aspects in one approach. Part of this issue might be that in the classical approach, physical chemists look for scientific understanding rather than for a correlation or pure association.10 In complex interdependent systems, this can be a difficult endeavour since accurate data is often difficult to find, and actual causations might not be obvious. Association is much simpler to establish though via purely statistical approaches. Machine-learning (ML) harnesses this relative simplicity to predict complex behaviour of systems.9,11,12 Hence, the question could be raised if it is possible to correlate complex propagation rate coefficients with fundamental and readily available information of monomers without the attempt to establish exact equations reflecting the underpinning processes. If such an approach was successful the resulting correlation can ideally be used to reach a better theoretical understanding. More importantly though, if statistical association is successful (without necessarily identifying the underlying causal mechanism), then rate coefficients would in principle become predictable. Propagation rate coefficients provide an ideal scenario for testing this hypothesis since relatively accurate coefficients are available for a series of molecules. In the following, we discuss if these kinetic rate coefficients can indeed be predicted on a purely statistical basis rather than using high level ab initio calculations using transition state theory. It should be mentioned that very recently, work has been published that follows a in principle similar approach using DFT calculations of features, which underpins the validity of our methodology.13 In that work, the biggest difference to our approach is, next to using only computational data rather than including physical properties as features, that experimental kp from different temperatures is directly fitted, while we use the evaluated Arrhenius parameters per monomer, hence averaged values. This reduces the size of the available dataset in comparison, which has the effect that while we work from a statistically more robust databasis, larger errors are received in the regression models, since relative errors of the regressions are correlated with the number of datapoints processed. This is a particularly important difference since an IUPAC working party recently demonstrated that not the amount of available data per monomer is determining its accuracy, but rather the number of different labs providing data.12
Results and discussion
Scientific discovery vs. scientific understanding
Ab initio methods, as much as all other chemical approaches to understand the structure property relationships of propagation rate coefficients have to date been based on an accurate calculation of specific influences, based on quantum chemical methods, or based on equations that directly relate properties based on physical laws. In our current approach we have turned this approach upside down. Rather than understanding relationships and correlations on the basis of physical understanding, we aimed to identify correlations purely based on statistical methods. As such, the tool we describe address pure scientific discovery, as outlined in a recent perspective.9 In this approach, a deeper understanding for the reason of correlation of parameters is per se not required. However, once correlations are established, this information can be used to infer new scaling laws, eventually leading to a better physical understanding. As for the basis of correlation, we have chosen physical properties of monomers that can be easily measured14 or calculated by simple means. The aim is hereby to provide a framework that is as simple and accessible as possible.Training data and initial feature selection
Any statistical model approach requires a dataset that can be used to train a model. As mentioned above, kp is ideal since the IUPAC has benchmarked rate coefficients for a series of monomers.4kp data for these monomers can be assumed to be fairly accurate.15 In fact, recently an online database was established that allows to retrieve these coefficients directly.16 In order to benchmark a monomer, IUPAC typically requires more than one laboratory to provide data. In addition, several laboratories have provided sole PLP-SEC data that can still be regarded as fairly reliable. We collated data for close to 40 monomers that we deemed reliable (it should be noted that the IUPAC also defined reliability criteria that make such selection possible). We omitted acidic monomers, since it is known that they are governed largely by pH, and hence are outliers in the complete set of available data.17 Most data is available for the monomer families of acrylates and methacrylates. It is known that these monomers can be correlated within their respective families, allowing for some inference from one family to the other. All other monomers have no known quantitative correlation, even though it is common knowledge that radical stability plays a major role in predicting their reactivity. A full list of monomers and their respective values in Arrhenius form are given in the ESI.† For the sake of this work in this study, four distinct groups of monomers have been identified, these being as described above (i) acrylates, (ii) methacrylates (iii) monomers exhibiting strong H-bonding effects and (iv) ‘others’, such as the important monomer styrene. When considering monomers in radical polymerization, several molecular properties, in the following referred to as ‘features’ in line with data science terminology, are obvious to consider. It is known from literature that polarity is an important quantity that has direct influence on propagation kinetics. Thus, the dipole moment of the monomer is of general interest. Note that experimental data is mostly available for bulk polymerization, hence where the polarity of the monomer concomitantly influences radical reactivity and the solvent environment. Further, the length of ester side chains in (meth)acrylates are known to at least indirectly correlate with kp.5 Thus, molecular weight was added as a further feature. Already when collating experimental data on dipole moments, it is unfortunately evident that gathering such data is by far not trivial, and generally leads to scattered datasets. To solve this issue, we decided to include calculated data as features in our analysis. To this end, we used the General Atomic and Molecular Electronic Structure System software package (GAMESS, version: 2018, R1). interfaced with the software ChemDraw 3D, and used also data provided by ChemSpider, and the ACD/Labs Percepta Platform - PhysChem Module predictions listed therein. Via GAMESS, we accessed dipole moments, boiling points, melting points and Gibbs free energies for each monomer under investigation (relative to ethylene as the simplest radically polymerizable monomer possible), using a low-level HF calculation method. ChemSpider provided some experimental data on boiling points and refractive index, and predictions for the same, plus predictions for surface tension and polarizability. Comparison of calculations with available experimental values showed that the theoretical values are certainly not perfect when examining absolute values, but are reasonable when comparing series of monomers with each other.An important point is that we used literature data on Arrhenius relations rather than absolute measured kp's. Hence, for each monomer, we use an overall averaged parameter stemming from a series of experiments, partially from experiments across several research groups. This makes the kp data for each monomer statistically very robust and minimizes the experimental error. For the sake of practicality, we did all initial correlations on kp values calculated for 25 °C from the Arrhenius parameters. Later we then demonstrate how also the Arrhenius parameters themselves can be correlated and predicted.
Methodology
Various machine-learning algorithms were initially tested to treat the available data, such for example a random forest. Yet, not enough datapoints are available to make use of such more advanced methods. Thus, data was fitted via multivariate linear regression, which is a combination of multiple linear regressions on independent variables for one dependant variable. Specifically, fitting was performed by regularised least squares, i.e., by minimising the sum of squared errors plus a positive regularisation term that penalises large regression coefficients and, thus, avoids overfitting. This term is either the sum of squared regression coefficients (ridge regression) or the sum of magnitudes of the regression coefficients (LASSO regression), in both cases multiplied by a tuneable hyper-parameter λ (see ESI†). This parameter is used to calibrate the degree of flexibility of the model to fit a set of training data. When λ increases, the model bias increases and the model variance decreases. In this context, bias describes how well a model tends to match a data set, whereas variance describes how much a model tends to change when it is trained with a different training set. The sum of the squared bias and the variance determines the expected squared error of a model (averaged over all possible training sets and independent test points). To choose an optimal λ and to perform overall model evaluation with limited data, unbiased model error estimates where obtained using leave-one-out cross validation (LOOCV). In an outer LOOCV, the model was fitted n times, each time using n-1 monomers as training data and the remaining monomer as test point. An overall scaled squared error estimate (r2) was obtained through the average squared error across these n model fits. Similarly, an inner LOOCV was performed to determine an optimal λ for each training set. The resulting nested cross validation scheme (Scheme 1) uses n times n-1 model fits to obtain an overall unbiased performance estimate for the model when refitting it with all available data (and again using a LOOCV for choosing λ). Fitting and performance estimation were performed for a number of increasingly complex models (sets of dependent variables) as outlined below. It should be noted that this procedure yields in principle a prediction for each monomer under consideration, hence predicted values can be compared to experiments. All following figures use this comparison to demonstrate the quality of regressions. It is noteworthy to add that some monomers will be better represented by certain models. This can occur because the regression model tends to predict certain types of monomers better than others – or be a simple coincidence. It is thus important to evaluate the total r2 of a fit rather than single values in order to avoid overinterpretation of the results.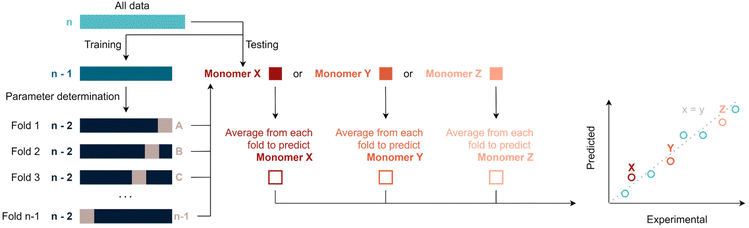 | ||
| Scheme 1 Overview of the nested leave one out cross validation (LOOCV) approach for hyper-parameter selection and overall evaluation of the regression model. | ||
Visualizing the state of the art
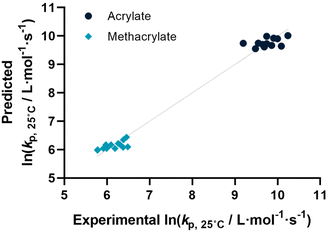
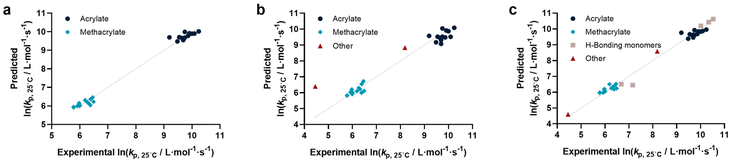
Before describing the regressions on the complete feature set, it is worthwhile to examine the state-of-the-art in predicting propagation rate coefficients. Two influences are known with fairly high accuracy, that is that the propagation rate coefficient increases with the length of the ester side chain in (meth)acrylates; and acrylates propagate up to a factor 100 faster than methacrylates. For all other monomers, no clear correlation has to date been quantified. Thus, in principle, for acrylates and methacrylates individually linear regressions with molecular weight can be carried out. Based on literature assumptions, this should yield some predictivity. Indeed, when plotting experimental kp as a function of molecular weight, a slight tendency towards increasing molecular weight can be observed. The overall correlation is, however, less than satisfactory. This is due to the list of monomers containing examples that have branched side chains, or that are associated with H-bonding. Nonetheless, this simplistic model can be used to derive a more general visualization of data. Using the LOOCV method, individual kp was predicted for each linear acrylate and methacrylate. For this, we fitted each group of monomers individually as would classically be done. This results in a predicted value for each of the monomers. This residual, predicted value is then plotted against its measured value. Ideally, if the experiment was error free and if the prediction was 100% accurate, a linear plot with the slope of 1 should be observed. The sum of squares of this line can hence be used to quantify the predictivity of the underlying model used. The outcome of this data procedure is shown in Fig. 1. It should be noted that for all predictions, the logarithm of kp was used rather than its actual value; this prevents the model from predicting non-physical negative values. As can be seen from the figure, the linear regression representing the state of the art basically predicts two plateaus, one for methacrylates and one for acrylates. Rather than predicting an increasing kp with molecular weight, it thus results in not more than a rough average per monomer group. This shows that the perceived correlation between ester side chain length and kp of each monomer is not statistically robust (while not necessarily wrong). It cannot be used to predict any unknown propagation rate coefficient from a statistical point of view. This is, taking the large scatter of data into account, not really surprising.Coming from this rather sobering result, we then extended the feature set of the regressions, taking all available physical properties into account, hence molecular weight, dipole moment, melting and boiling point and Gibbs free energy values. The outcome of such prediction is given in Fig. 2. As can be seen, no correlation is obvious and the plot seems almost random. Hence, we moved forward by adding further information to the feature set. To achieve this aim, we first broke the number of datapoints down, and isolated the (meth)acrylates from the list. Then, we introduced a binary differentiation for acrylates (one) and methacrylates (zero), see Fig. 3a. This alone lead to a reasonable representation of data, showing that the calculated physical properties of monomers have a positive effect, and are aiding in the prediction of rate coefficients. However, several difficulties remained. For example, hydroxy ethyl acrylate was not appropriately predicted. Also branched monomers, while improved compared to the state-of-the-art representation in Fig. 1, still showed significant deviations. To solve these issues, the feature set was extended by two parameters. One parameter described the inductive effect of the side chain, the other quantifies H-bonding between monomers (see ESI for details†). For both effects, literature was screened, and property tables provided by quantum mechanical calculation were used.18,19 It should be hereby noted that H-bonding is not easy to quantify, and only the presence of major functional groups was accounted for. Despite the shortcomings of this process, a very good prediction is obtained in this way. Fig. 3a depicts the case fitting of acrylates and methacrylates without inclusion of strongly H-bonding monomers. It should be noted that both LASSO and Ridge regressions yield similarly reasonable results, while conventional linear regressions perform significantly less well. Nonetheless, the r2 value of the plot shown in Fig. 3a is 0.991, underpinning its overall high quality. Statistical analysis of the LASSO regression shows that either the melting point or the boiling point can be used, both information is not required since they display high collinearity. The same was true for surface tension data and refractive index data. Both features were practically redundant when polarizability was used. All other features do contribute to the results.
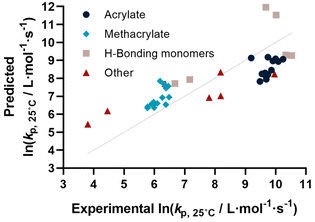
Yet, when including all monomers back into the fit, also this procedure still yielded an unsatisfactory result. The obvious reason for this is that none of the features sufficiently describes resonance effects, which play a major role in reactivity of monomers.20 Surprisingly, while qualitative orders of reactivity are obviously known for practically all polymerizable vinyl monomers, no quantitative data on the resonance stability, or radical stability could be found in the literature. The closest information that we identified were dissociation constants of macroalkoxyamines, that were determined for nitroxide-mediated polymerization from EPR spectroscopy on the alkoxyamine dissociation. At least for styrene, acrylonitrile, as well for an average of methacrylates and acrylates, numeric values could be assigned. We normalized these dissociation constants, and provide our best prediction, shown in Fig. 3b. Finally. Since this plot yielded a very reasonable fit, we then directly also included the H-bonding monomers, as depicted in Fig. 3c. Fig. 3c displays the final result of our correlation work, and all used features for the given fit are highlighted in colour in Table S3.† Again, it is an interesting observation, that correlation of H-bonding has also a positive predictive effect for example for styrene (the datapoint with the lowest overall kp). As can be seen, both acrylonitrile and styrene (orange triangles) fall very well on the line with the (meth)acrylates. r2 in this case is 0.986, which is a very good result considering that both added monomers have nothing in common with the other monomers in question regarding all other used features. It can be assumed that if actual data for resonance stability of propagating radicals become available for other monomers (such as vinyl acetate for example), that also these monomers can then be adequately correlated. Overall, the ridge regression analysis for weighting of the various features shows that resonance stability by far is the most important feature, overshadowing the importance of dipole moments and substituent effects. Yet, this is at the moment only a qualitative observation that needs further study. Table 1 below gives an overview on the fit parameter and relative contributions to the final model. However, as stated earlier, we believe such quantitative data should be read with care at this stage (fit coefficients for the other plots see ESI†).
| Parameters | Coefficients | Importance |
|---|---|---|
| Dissociation constant A2 | −0.00676 | 2.203144 |
| Molecular weight MW | 0.01508 | 1.308853 |
| Polarizability | −0.10046 | 1.120701 |
| Dissociation constant A1 | 1.09465 | 1.038845 |
| Inductive effect A | −0.57508 | 0.596737 |
| Inductive effect of ester R | −0.13211 | 0.255578 |
| Effect of H-donor H_don | −0.06727 | 0.096749 |
| Effect of H-acceptor H_acc | −0.00045 | 0.001883 |
A further consideration is that data for some features may be more accurate than others. This can in principle be accounted for by introducing a weighting for each individual feature to force the regression to put more emphasis on these features. We found though that doing this reduced the quality of regressions overall, and indeed in machine learning this is usually discouraged in order to not introduce biases.
With this method at hand, we tested if not only individual kp can be predicted, but also activation parameters. To this end, we calculated kp for 25, 50, 75 and 100 °C based on reported activation energies and frequency factors. As for the 25 °C data in Fig. 3, similarly reasonable fits were obtained. For each individual monomer the predicted kp values at the four temperatures were fitted to the Arrhenius equation, yielding a predicted Arrhenius factor A and a predicted activation energy EA. Using the same representation as for kp, it can be shown (Fig. 4a and b) that also the activation parameters are well predicted by our model. Specifically, Ea is represented very well, while ln(A) shows some more scatter. This scatter is a result of the sensitivity of A on small variations in Ea and correlates with the typically also higher scatter of experimental data for this value. This approach may appear somewhat indirect. In principle one can also directly correlate EA and A with our methodology. However, this would require a simultaneous regression of both parameters, since A and Ea are highly interdependent. If fitted individually for Ea, a reasonable direct correlation is found, yet not for A. The approach to determine both values via individual kp‘s’ is hence more successful and reliable. Fig. 4a and b depict the activation parameter correlation.
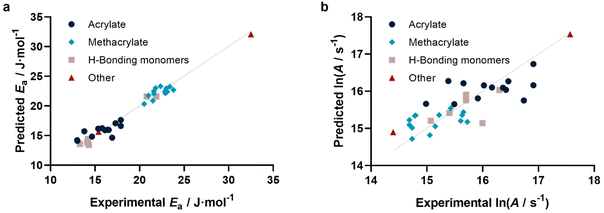 | ||
| Fig. 4 (a) Activation energies (r2 = 0.963, RMSE = 0.823) and (b) Arrhenius factors (r2 = 0.666, RMSE = 0.427) determined from prediction of individual kp at four different temperatures. | ||
From correlation to prediction
Until this point we only demonstrated that the data can be successfully correlated. Of course, the aim of any such investigation is to predict rate coefficients for monomers for which no experimental kp data is available. With the good correlation demonstrated in Fig. 3c, predictions of rate coefficients should be possible as long as the unknown monomer largely falls into a similar category as the training data, i.e. doesn't feature exotic functional groups or represents a monomer with very different radical stability. Since practically all features in our model are based on calculated features, it is fairly straight forward to include further monomers into the list. As monomers in question we chose ethyl acrylate, propyl acrylate, cyclohexyl acrylate and propyl methacrylate. Arguably, the rate coefficients of these monomers are fairly simple to predict with ballpark figures even without advanced regression models. It is known that propagation rate coefficients increase generally with the size of the ester side chain for both acrylates and methacrylates, and reference data are available for the corresponding methyl and butyl (meth)acrylates. While the predictions made thus seem to be not too ambitious, they provide a reasonable test in order to see if the regression model can produce numbers within expectations. All ML-predicted kp values are given in Table 2 alongside errors derived from the overall r2 of the fit in Fig. 3c.| Monomer | k p(25 °C)/L mol−1 s−1 |
|---|---|
| Ethyl acrylate | 9300 < 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 210 < 18 210 < 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 770 770 |
| Propyl acrylate | 9540 < 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 560 < 19 560 < 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 260 |
| Cyclohexyl acrylate | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 < 14 260 < 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 < 20 570 < 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
| Propyl methacrylate | 270 < 390 < 550 |
As a first observation of the data in Table 1, one can see that qualitatively the order of predicted propagation rates in the acrylates is correct, based on what is generally known about the behaviour of kp with increasing side chain lengths.5 A slight increase in rate for the ethyl to the propyl acrylate is seen, while the cyclohexyl acrylate monomer exhibits the highest rate coefficient. For both the acrylate and methacrylate the correct order of magnitude is predicted (which is, given the large number of monomers used in the correlation from these two families not surprising). Starting from the experimental propagation rate coefficients for methyl and butyl methacrylate, a kp between 323 and 370 would be expected. The value for propyl methacrylate is very close in the range of expectations. Given that size-exclusion chromatography, which is key to experimental kp determinations is commonly associated with an error of up to 20%, this match is exceptionally good, and outperforms any prediction based on ab initio calculations provided so far. For the acrylates, using the same comparison, a kp between 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 (methyl acrylate) and 16
130 (methyl acrylate) and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 380 (butyl acrylate) would be expected. Again, the predictions made by our regressions meet this range. For cyclohexyl acrylate, the produced value seems also to be a reasonable estimate when compared to early PLP data provided by Tanaka et al., who found that cyclohexyl kp is similar to that of butyl acrylate.21 It will be interesting to see in the future if these values will be confirmed by experiments. The error limits given in Table 1 are rather large, and disparate towards higher and lower values. This is due to predictions being made on a log scale. The overall error estimate is probably rather conservative, and reflects also the error in all used training data, which of course is not absolute at all. Regardless, we have made our Python script for the prediction available via the github platform, so that other researchers can make their own predictions based on need.
380 (butyl acrylate) would be expected. Again, the predictions made by our regressions meet this range. For cyclohexyl acrylate, the produced value seems also to be a reasonable estimate when compared to early PLP data provided by Tanaka et al., who found that cyclohexyl kp is similar to that of butyl acrylate.21 It will be interesting to see in the future if these values will be confirmed by experiments. The error limits given in Table 1 are rather large, and disparate towards higher and lower values. This is due to predictions being made on a log scale. The overall error estimate is probably rather conservative, and reflects also the error in all used training data, which of course is not absolute at all. Regardless, we have made our Python script for the prediction available via the github platform, so that other researchers can make their own predictions based on need.
Conclusions
The predictions made based on the model presented herein may not be able give a 100% accurate representation of small effects such as ester side chain length, yet they provide very reasonable data that can be used for future work. Accuracies are within standard error limits of experimental determinations, and relative effects are accurately predicted. With the exception of the predictions presented by Shi et al.,10 no prediction of kp values with the same accuracy by any other theoretical method has to date been provided. With increasing data coming available from experiments, and potentially with further refinement of feature calculations, we hope the accuracy of our method can be further refined in future work. The match of data currently seen for monomers with available experimental data on boiling points should be extendable to the full dataset. Generally, it is remarkable that only very little experimental data input is required in all predictions. We suggest that radical stability should be probed experimentally and theoretically in order to provide more valuable data that can refine the machine learning approach in this work. We envisage that in future a full predictivity with even higher accuracy will become available, allowing researchers to simply dial in a monomer and to obtain an accurate estimate of kp. We also believe that with further data it will become possible to predict kp in a broader monomer space, and not only (meth)acrylates as done in here. Further the presented methodology also allows to refine data for monomers with existing experimental data, since the LOOCV method allows for averaging over the entire monomer space compared to ‘only’ fitting data for each single monomer by itself.Regardless of the predictivity of the regressions, this work marks an important point for full correlation of complex kinetic rate coefficients with chemical structures and their basic physical properties. Machine-learning, even in its simple form of sets of regressions as used in here, has tremendous potential for simple, and readily available predictions of kinetic data. It should be noted hereby that the performed predictions occur within seconds, and can be easily implemented in kinetic modelling codes in the future.
The code used in this work is made available via: https://github.com/PRDMonash/kp_predictor.
Author contributions
EvdR performed most of the research, developed the used software, took care of data curation, revision of the manuscript and methodology development. NM contributed significantly to earlier software versions and data curation. JS gave guidance, aided in methodology and edited the manuscript. MB was involved in supervision, methodology development and editing the manuscript. TJ came up with the initial concept, provided project administration and supervision, wrote the original draft and edited the final version.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Support by Monash University is kindly acknowledged. We also wish to thank Dr Yohan Guillaneuf for the hint to look for NMP dissociation constants to assess propagating radical stability.References
- M. Buback, R. G. Gilbert, R. A. Hutchinson, B. Klumperman, F.-D. Kuchta, B. G. Manders, K. F. O'Driscoll, G. T. Russell and J. Schweer, Macromol. Chem. Phys., 1995, 196, 3267–3280 CrossRef CAS.
- S. Beuermann and M. Buback, Prog. Polym. Sci., 2002, 27, 191–254 CrossRef CAS.
- O. F. Olaj, I. Bitai and F. Hinkelmann, Makromol. Chem., 1987, 188, 1689–1702 CrossRef CAS.
- (a) S. Beuermann, M. Buback, T. P. Davis, R. G. Gilbert, R. A. Hutchinson, O. F. Olaj, G. T. Russell, J. Schweer and A. M. van Herk, Macromol. Chem. Phys., 1997, 198, 1545–1560 CrossRef CAS; (b) S. Beuermann, M. Buback, T. P. Davis, R. G. Gilbert, R. A. Hutchinson, A. Kajiwara, B. Klumperman and G. T. Russell, Macromol. Chem. Phys., 2000, 201, 1355–1364 CrossRef CAS; (c) S. Beuermann, M. Buback, T. P. Davis, N. García, R. G. Gilbert, R. A. Hutchinson, A. Kajiwara, M. Kamachi, I. Lacík and G. T. Russell, Macromol. Chem. Phys., 2003, 204, 1338–1350 CrossRef CAS; (d) J. M. Asua, S. Beuermann, M. Buback, P. Castignolles, B. Charleux, R. G. Gilbert, R. A. Hutchinson, J. R. Leiza, A. N. Nikitin, J.-P. Vairon and A. M. van Herk, Macromol. Chem. Phys., 2004, 205, 2151–2160 CrossRef CAS; (e) S. Beuermann, M. Buback, P. Hesse, F.-D. Kuchta, I. Lacík and A. M. van Herk, Pure Appl. Chem., 2007, 79, 1463–1469 CrossRef CAS; (f) C. Barner-Kowollik, S. Beuermann, M. Buback, P. Castignolles, B. Charleux, M. L. Coote, R. A. Hutchinson, T. Junkers, I. Lacík, G. T. Russell, M. Stach and A. M. van Herk, Polym. Chem., 2014, 5, 204–212 RSC; (g) C. Barner-Kowollik, S. Beuermann, M. Buback, R. A. Hutchinson, T. Junkers, H. Kattner, B. Manders, A. N. Nikitin, G. T. Russell and A. M. van Herk, Macromol. Chem. Phys., 2017, 218, 1600357 CrossRef.
- K. B. Kockler, A. P. Haehnel, T. Junkers and C. Barner-Kowollik, Macromol. Rapid Commun., 2016, 37, 123–134 CrossRef CAS PubMed.
- (a) A. P. Haehnel, M. Schneider-Baumann, L. Arens, A. M. Misske, F. Fleischhaker and C. Barner-Kowollik, Macromolecules, 2014, 47(10), 3483–3496 CrossRef CAS; A. P. Haehnel, M. Schneider-Baumann, K. U. Hiltebrandt, A. M. Misske and C. Barner-Kowollik, Macromolecules, 2013, 46(1), 15–28 Search PubMed.
- See for example: E. I. Izgorodina and M. L. Coote, Chem. Phys., 2006, 324, 96–110 CrossRef CAS.
- J. P. A. Heuts, R. G. Gilbert and L. Radom, Macromolecules, 1995, 28, 8771 CrossRef CAS.
- S. Beuermann and D. Nelke, Macromol. Chem. Phys., 2003, 204, 460–470 CrossRef CAS.
- M. Krenn, R. Pollice, S. Y. Guo, M. Aldeghi, A. Cervera-Lierta, P. Friederich, G. d. P. Gomes, F. Häse, A. Jinich, A. K. Nigam, Z. Yao and A. Aspuru-Guzik, Nat. Rev. Phys., 2022, 4, 761–769 CrossRef PubMed.
- S. Wu, Y. Kondo, M. Kakimoto, B. Yang, H. Yamada, I. Kuwajima, G. Lambard, K. Hongo, Y. Xu, J. Shiomi, C. Schick, J. Morikawa and R. Yoshida, npj Comput. Mater., 2019, 5, 66 CrossRef.
- Y. Gu, P. Lin, C. Zhou and M. Chen, Sci. China: Chem., 2021, 64, 1039–1046 CrossRef CAS.
- Y. Shi, M. Yu, F. Yan, Z. H. Luo and Y. N. Zhou, Macromolecules, 2022, 55, 9397–9410 CrossRef CAS.
- L. M. Ghiringhelli, J. Vybiral, S. V. Levchenko, C. Draxl and M. Scheffler, Phys. Rev. Lett., 2015, 114, 105503 CrossRef PubMed.
- S. Beuermann, S. Harrisson, R. A. Hutchinson, T. Junkers and G. Russell, Polym. Chem., 2022, 13, 1891–1900 RSC.
- J. Van Herck, S. Harrisson, R. A. Hutchinson, G. T. Russell and T. Junkers, Polym. Chem., 2021, 12, 3688–3692 RSC.
- I. Lacík, S. Beuermann and M. Buback, Macromol. Chem. Phys., 2004, 205, 1080–1087 CrossRef.
- D. Santos-Martins and S. Forli, J. Chem. Theory Comput., 2020, 16, 2846–2856 CrossRef CAS PubMed.
- C. Hansch and T. Fujita, J. Am. Chem. Soc., 1964, 86, 1616–1626 CrossRef CAS.
- G. Moad and D. H. Solomon, The Chemistry of Radical Polymerization, Elsevier Science Ltd, second edition, 2005 Search PubMed.
- K. Tanaka, B. Yamada, R. Willemse and A. M. van Herk, Polym. J., 2002, 34, 692–699 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Complete dataset used, information regression procedures and collated plots for various selections of feature sets. See DOI: https://doi.org/10.1039/d2py01531e |
| This journal is © The Royal Society of Chemistry 2023 |