Tuning nanoscale plasmon–exciton coupling via chemical interface damping†
Jyotirban
Dey
 ,
Alisha
Virdi
,
Alisha
Virdi
 and
Manabendra
Chandra
and
Manabendra
Chandra
 *
*
Department of Chemistry, Indian Institute of Technology Kanpur, Kanpur, Uttar Pradesh-208016, India. E-mail: mchandra@iitk.ac.in
First published on 10th October 2023
Abstract
Understanding the exact role of each plasmon decay channel in the plasmon–exciton interaction is essential for realizing the translational potential of nanoscale plexciton hybrids. Here, using single-particle spectroscopy, we demonstrate how a particular decay channel, chemical interface damping (CID), influences the nanoscale plasmon–exciton coupling. We investigate the interaction between cyanine dye J-aggregates and gold nanorods in the presence and absence of CID. The CID effect is introduced via surface modification of the nanorods with 4-nitrothiophenol. The relative contribution of CID is systematically tuned by varying the diameter of the nanorods, while maintaining the aspect ratio constant. We show that the incorporation of the CID channel, in addition to other plasmon decay channels, reduces the plasmon–exciton coupling strength. Nanorods’ diameter-dependency measurements reveal that in the absence of CID contribution, the plasmon mode-volume factor gradually dominates over the plasmon decoherence effects as the diameter of the nanorods decreases, resulting in an increase in the plasmon–exciton coupling strength. However, the situation is entirely different when the CID channel is active: plasmon dephasing determines the plasmon–exciton coupling strength by outweighing the influence of even a very small plasmon mode-volume. Most importantly, our findings indicate that CID can be used to controllably tune the plasmon–exciton coupling strength for a given plexciton system by modifying the nanoparticle's surface with suitable adsorbates without the need for altering either the plasmonic or excitonic systems. Thus, judicious exploitation of CID can be tremendously beneficial in tailoring the optical characteristics of plexciton hybrid systems to suit any targeted application.
Introduction
The interaction of localized surface plasmons (LSP) in metal nanostructures with excitons in organic dye molecules,1–4 semiconductor quantum dots5,6 and transition metal dichalcogenides7–9 has gained tremendous interest due to its potential applications in various fields such as ultrafast reversible switching,10–12 light harvesting,13 quantum computing14,15etc. The development of a predictive understanding of the factors controlling the plasmon–exciton coupling strength is very important and a prerequisite to expand the utility of plexcitonic systems for real-life applications. The strong spatiotemporal field confinement capability of plasmonic metal nanostructures (which are essentially open cavities) in a sub-diffraction-limit length scale, accompanied by high dipole moments2,16,17 of the excitonic systems, can even drive the plasmon–exciton interaction to the so called “strong coupling” regime.17–20 Such plasmon–exciton couplings are found to be stronger than the coupling between excitons and the cavity modes of a conventional microcavity (i.e., closed cavity) although metal nanoparticles have much poor quality factor (Q < 100).21 The metal nanostructure acts as an open cavity and interacts with the exciton to produce two completely new polaritonic modes, upper plexciton branch (UPB) and lower plexciton branch (LPB), and they show avoided crossing behavior as a function of LSPR detuning.3,16,22 The energy difference between UPB and LPB at zero detuning gives the Rabi splitting (ħΩRabi), which is a measure of the extent of coupling between plasmons and excitons.The plasmon–exciton interaction is generally described classically using the coupled oscillator model,23–27 which says that the plasmon–exciton coupling strength depends on the plasmon–exciton energy exchange rate and the decay rate of the plasmon excitation. Strong coupling is achieved when the rate of energy exchange between them is faster than their dissipation (dephasing) rate. Hence, a thorough comprehension of the impact of plasmon dephasing on the plasmon–exciton coupling is extremely important. Plasmon dephasing can take place through four damping (or decay) channels, which individually contribute to the total plasmon homogeneous linewidth (Γhomo) and they are (i) bulk damping (Γbulk), (ii) radiation damping (Γrad), (iii) electron-surface scattering damping (Γsurf) and (iv) chemical interface damping (ΓCID).28–31
| Γhomo = Γbulk + Γrad + Γsurf + ΓCID | (1) |
Bulk damping is the scattering of electrons with thermal phonons and impurities, which finally transforms the absorbed energy into heat. Usually, these scattering efficiencies are the same as bulk metals and free from any kind of size and shape dependencies.32 Radiation damping arises due to far-field light scattering, and electron-surface scattering damping describes the scattering of excited electrons at the surface of the nanaopartcles.29,33 CID describes the direct transfer of the interfacial hot-electron from a metal to a molecule present on the nanoparticle's surface.28,34–36 Although plasmon decay channels greatly influence the plasmon–exciton interaction at the nanoscale, proper study about them is still unavailable other than a very few theoretical and experimental investigations.19,22,37–39 Although the investigations into the role of other decay channels in influencing various properties of metal nanoparticles, including plasmon–exciton coupling, have been initiated in recent years,19,22,37–39 CID is probably the least explored and understood one.31 Unlike the contribution of other plasmon decay channels (Γbulk, Γrad, and Γsurf) to the overall homogenous linewidth, the contribution of CID is not fixed for a nanoparticle of a given size and shape; the contribution of CID to the overall homogenous linewidth can be systematically tailored for a given nanoparticle simply by changing the chemical interface.36,40–42 Developing a predictive comprehension of the role of CID in influencing plasmon–exciton coupling is therefore crucial from both a fundamental and translational standpoint. Here in this paper, using single-particle dark-field microspectroscopy, we investigate the impact of CID on plasmon–exciton coupling. Here, CID is introduced by nanoparticle's surface modification using 4-nitrothiophenol (4-NTP). We synthesized three nanorod samples of different average lengths and diameters but identical aspect ratios (ensures identical LSPR positions) and measured homogeneous linewidths of each nanorod having different chemical interfaces. This allows us to estimate the contribution of CID to the overall linewidth of each of the nanorod samples. In line with previous results, we find that the larger the diameter of the nanorod, the lower is the contribution of CID.31 To explore the effect of the CID channel on the strength of plasmon–exciton coupling, plexciton hybrids comprising of J-aggregates of the cyanine dye Cy78 and gold nanorods, both surface modified and unmodified, were prepared and studied. Both ensemble-level extinction and single-particle level dark-field scattering experiments show a consistent decrease in the plasmon–exciton coupling extent (Rabi splitting values) after incorporation of the CID channel. The decrease in plasmon–exciton coupling strength is found to go hand in hand with the observed trend in the contribution of CID to the overall homogenous linewidth. Most importantly, our findings indicate that this additional damping channel can be used to tune the plasmon–exciton coupling strength for a given plexciton system by modifying the nanoparticle's surface with suitable adsorbates, without the need for altering either the plasmonic or excitonic systems.
Results and discussion
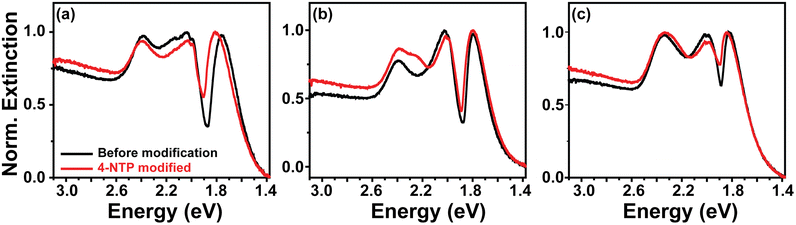
We synthesized three gold nanorod samples (NR1, NR2, and NR3) having different diameters (d) but identical aspect ratios (AR) shown in Fig. 1a–c. The reason for keeping the AR constant is to ensure that all three nanorods show an identical LSPR position.43 Maintaining identical LSPR positions for all the different nanorods is essential to exclude any indirect effect of particle size and shape through LSPR maxima in the plasmon–exciton coupling. The detailed procedure for nanorod synthesis is provided in section S1 of the ESI.† The dimensional parameters of the nanorod samples have been measured using a transmission electron microscope (TEM) and are listed in Table S1 in section S2 of the ESI.† The diameters (d) of the Au NRs follow the order dNR1 < dNR2 < dNR3 and they fall in different plasmon dephasing regimes. Usually, the effect of CID on plasmonic nanoparticles’ optical properties is best observed using substituted aromatic thiols because of the strong affinity of the thiol (–SH) group toward gold and their capability of substantially altering the electron density of the metal nanoparticle surface via a judicious choice of substituents on the aromatic ring.36,41 This soft–soft binding between the gold surface and sulfur is essential for the formation of the required hybridized surface states between the adsorbate and gold nanoparticle surface that facilitates the direct transfer of hot charge carriers.36 In this study, we used 4-nitrothiophenol (4-NTP) to realize the CID effect. The LSPR maxima of all three Au NRs were chosen to be ∼650 nm because the exciton used (J-aggregates of Cy78) shows a plexciton transparency dip at ∼650 nm when coupled to a plasmonic system.44 Choosing the LSPR of all the nanorods identical and coinciding the plexcitonic dip wavelength allows us to measure the Rabi splitting directly from the extinction spectra.Before going into the detail about the effect of CID on plasmon–exciton coupling, let us first discuss the LSPR properties of the Au NRs and how CID influences their LSPR spectra. Fig. S2 (in section S3 of the ESI†) shows the ensemble-level extinction spectra of three nanorods, before and after the addition of 4-NTP. The linewidths (Γext; for longitudinal mode) of CTAB-capped NR1, NR2, and NR3 (centrifuged and redispersed in water) were extracted through multipeak fitting (see section S4 of the ESI†) and were found to be 358 meV, 355 meV, and 368 meV, respectively (Table 1). Next, we added 1 μmol of 4-NTP to each of the three NR solutions and incubated them at room temperature for 8 hours. This led to the attachment of 4-NTP onto the gold nanorod surface. Attachment of 4-NTP onto the Au nanorod surface was confirmed via surface enhanced Raman scattering (SERS) spectroscopy (see section S5 of the ESI† for details). The surface modification by 4-NTP results in a broadening of the LSPR linewidth, accompanied by a slight redshift of 2–3 nm. The amount of line broadening was found to be nanorod's diameter dependent. The linewidths (ΓCIDext; for longitudinal mode) of 4-NTP modified NR1, NR2, and NR3 are found to be 400 meV, 384 meV, and 380 meV, respectively (Table 1). From Table 1, it is obvious that the LSPR linewidth concomitantly increases with a decrease in nanorods’ diameter upon surface modification of Au NR with 4-NTP. Since, in our experiment, we are changing only the adsorbate, the observation of such a size-dependent increase in the nanorod's LSPR linewidths on exchanging CTAB with 4-NTP is a clear indication of chemical interface damping of plasmon excitation.31,36,40 The largest ΔΓCIDext (= ΓNR-NTPext − ΓNRext) is obtained for NR1, which has the lowest diameter (∼12 nm), while the smallest ΔΓCIDext is obtained for the nanorod having the largest diameter i.e., NR3 (∼40 nm) (Table 1).
| Samples | LSPR linewidth determined from ensemble-level extinction spectra (meV) | Homogeneous LSPR linewidth obtained from single-particle scattering spectra (meV) | ||||
|---|---|---|---|---|---|---|
| Without CID (Γext) | With CID (ΓCIDext) | Difference (ΔΓCIDext) | Without CID (Γscat) | With CID (ΓCIDscat) | Difference (ΔΓCIDscat) | |
| NR1 | 358 | 400 | 42 | 110.8 ± 8.9 | 129.4 ± 7.3 | 17.8 ± 3.9 |
| NR2 | 355 | 384 | 29 | 95.8 ± 10.3 | 105.8 ± 6.3 | 8.8 ± 3.7 |
| NR3 | 368 | 380 | 12 | 141.4 ± 7.0 | 146.0 ± 6.4 | 3.3 ± 2.1 |
These results suggest that CID is substantial in NR1 but insignificant in the case of NR3 and is in line with previous studies.31 At this point, we note that the 2–3 nm redshift in LSPR positions on addition of 4-NTP can be attributed to an increased local refractive index (RI) of the medium surrounding the nanorod surface and the electron withdrawing ability of 4-NTP.31
Next, we prepared the plexciton hybrids of each Au nanorod (CTAB-capped as well as 4-NTP modified) sample using a J-aggregate forming cyanine dye, (5-chloro-2-[2-[5-chloro-3-(4-sulfobutyl)-3H-benzothiazol-2-ylidenemethyl]-but-1-enyl]-3-(4-sulfobutyl)-benzothiazol-3-ium hydroxide, triethylammonium salt) or Cy78, following our previously developed protocol (please see section S6 of the ESI† for a brief description).3,19,22,44,45 The concentration of Cy78 was chosen such that a saturated coverage of dye J-aggregates on the nanorod surface is ensured. The saturated coverage of the nanorod surface with excitons allows us to rationally compare the coupling strengths of different plexciton hybrids.22 All the plexciton hybrids show peak splitting (i.e., formation of UPB and LPB with a transparency dip) of their longitudinal LSPR mode in their ensemble extinction spectra (Fig. 2a–c and Table 2). The energy difference (Rabi splitting) between UPB and LPB values for the plexciton hybrids of CTAB-capped NR1, NR2, and NR3 is measured to be 264 meV, 231 meV, and 177 meV, respectively. We would like to note here that our numerical simulations reveal that incident light polarization has no effect on the Rabi splitting (see the ESI†). This observation of the monotonous increase in Rabi splitting from NR3-plexciton to NR1-plexciton can be very well explained by considering the gradual decrease in plasmon mode-volume from NR3 to NR1.1,2,5,19 Here, the decreasing plasmon mode-volume (from NR3 to NR1) allows the plasmon–exciton energy exchange rate to surpass the plasmon decay rates, be it radiation damping or electron-surface scattering. However, when we look at the extinction spectra of the plexciton hybrids of 4-NTP modified nanorods, the monotonous increase in Rabi splitting from NR3 to NR1 is no longer observed. In this case, the Rabi splitting increases from NR3- (163 meV) to NR2-plexciton (204 meV) and then suddenly drops for NR1-plexciton (194 meV) (Fig. 2a–c and Table 2). We reiterate here that we repeated these measurements multiple times and obtained the same trend every time. It is interesting to see that while a prior surface modification with 4-NTP reduces (compared to the plexciton hybrids of CTAB-capped Au NRs) the ensemble-level Rabi splitting of NR3- and NR2-plexciton by 14 meV and 27 meV, respectively, it reduces the Rabi splitting of NR1-plexciton by a massive 70 meV (i.e., by ∼27%). These results are extremely interesting and indicative of the pivotal role of CID in not only controlling the plasmon decay, but also in dictating the plasmon–exciton energy exchange.
| Samples | Rabi splitting (meV) | |||||
|---|---|---|---|---|---|---|
| Ensemble-level | Single-particle level | |||||
| Without CID | With CID | Change (%) | Without CID | With CID | Change (%) | |
| NR1 | 264 | 194 | 27 | 196 ± 5 | 150 ± 5 | 23 ± 3 |
| NR2 | 231 | 204 | 12 | 181 ± 5 | 156 ± 4 | 14 ± 4 |
| NR3 | 177 | 163 | 8 | 147 ± 4 | 140 ± 3 | 5 ± 4 |
However, it is important to note here that the linewidths of LSPR in ensemble-level extinction spectra are severely affected by the heterogeneity in the sample, which is almost inevitable in nanoparticles prepared via the wet-chemical route. As a result, we merely get an average picture in ensemble-level extinction spectra.31,36,46 To gain a better understanding, we resorted to single-particle level optical dark-field scattering microspectroscopy, which is an ideal tool for extracting unequivocal information regarding the plasmon dephasing dependency of the plasmon–exciton interaction, since it not only mitigates out the effect of sample heterogeneity on linewidth, but also gets rid of other sources of heterogeneous line broadening.46 We first immobilized the CTAB-capped Au nanorods on glass slides, pre-coated with (3-mercaptopropyl)trimethoxysilane or MPTMS,47 and recorded single-particle dark-field scattering spectra using an inverted microscope (NIKON Ti-2E) coupled to a spectrometer (Kymera, Andor) and a monochrome sCMOS (Zyla, Andor) camera. A separate color camera (Nikon) was used to record the scattering images of the Au nanorods (and their plexciton hybrids). The surface of the Au nanorods was modified as per the need by flowing the required solutions (see section S7 in the ESI† for dark-field scattering sample preparation and data acquisition).
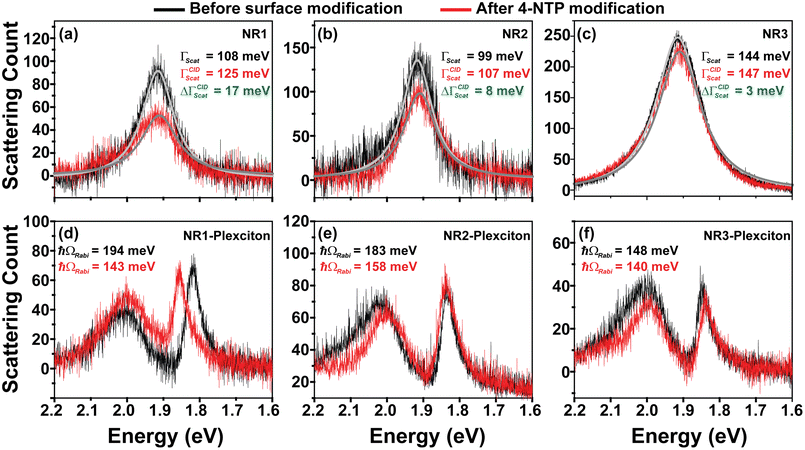
First, the glass slides containing MPTMS-bound Au NRs were washed multiple times with methanol to remove the capping agent (CTAB) from the nanorods’ surface to the maximum extent. Note that in complete agreement with previous studies, the change in LSPR linewidth due to removal of CTAB is very less as compared to the 4-NTP modification, indicating that the CID effect of CTAB is negligible compared to 4-NTP (see the ESI† for detailed discussion).31,36,48 After completely drying the slide, we recorded the single-particle scattering spectra of these nearly surfactant-free “clean” nanorods attached onto the MPTMS coated glass slides. Please note here that ensemble-level measurements did not have this most desired “surface-cleaning” part, as that would lead to immediate aggregation of the nanorods. Each of the acquired scattering spectra was fitted with the Lorentzian function to determine the homogenous linewidth. Note that we collected the individual scattering spectra of a large number of nanorods for each of the three nanorod samples, viz., NR1, NR2, and NR3. The corresponding results are depicted in Fig. 3a–c and described in Table 1. The fitting of the recorded scattering spectra using a single Lorentzian function gave us the homogeneous linewidths (ΓNRscat) of the “surface-cleaned” nanorods as 110.8 ± 8.9 meV, 95.8 ± 10.3 meV, and 141.4 ± 7.0 meV for NR1, NR2, and NR3, respectively (Table 1). This trend is expectedly very similar to what we got for ensemble-level extinction studies but more striking. The LSPR linewidth increases from NR2 to NR3 due to the increase in radiation damping contribution owing to an increase in nanorod diameter. On the other hand, the LSPR linewidth increases from NR2 to NR1 due to an increase in electron-surface scattering owing to a significant decrease in the nanorod diameter. After acquiring the dark-field scattering spectra of a sufficiently large number of surface-cleaned Au nanorods (separately for NR1, NR2, and NR3), a 1 mM methanolic solution of 4-NTP was flowed over them (i.e., the surface-cleaned Au nanorods attached to the MPTMS coated glass slides) for 20 minutes, washed with water and methanol successively, and finally dried. In this case too, the attachment of 4-NTP onto the nanorod surface was confirmed via SERS measurements. Next, the 4-NTP-coated nanorods were subjected to single-particle dark-field scattering experiments. Note that we recorded the scattering spectra of the same nanorods before and after 4-NTP coating (see section S7 of the ESI† for details). Fig. 3a–c show the representative single-particle scattering spectra of NR1, NR2, and NR3 before and after 4-NTP coating. It is apparent from Fig. 3a–c that upon surface modification with 4-NTP, (i) the LSPR linewidth increased for all three nanorods (also see Fig. 4a) (ii) LSPR maxima slightly red-shifted, and (iii) the scattering intensities decreased, indicating an increase in overall damping rate for all three NR samples. The linewidths (ΓNR-NTPscat) for 4-NTP coated NR1, NR2, and NR3 were extracted by fitting the scattering spectra with the Lorentzian function. ΓNR-NTPscat values for 4-NTP coated NR1, NR2, and NR3 are found to be 129.4 ± 7.3 meV, 105.8 ± 6.3 meV and 146.0 ± 6.4 meV, respectively. The changes in LSPR linewidths for each of the nanorod samples upon surface modification with 4-NTP are provided in Table 1. A massive 16% increase in the LSPR linewidth is observed for NR1. Note that neither the modification of the nanorod's electron density nor the change of local RI due to surface modification can account for such a large change in the linewidth.31,36 Therefore, the possible role of CID behind the alteration of the LSPR linewidth must be carefully investigated. In fact, since we are only changing the molecule on the surface, while keeping all other conditions identical, the change in the linewidths of Au NRs have to be due to a change in CID contribution. In other words, the change in linewidths due to CID is ΓCIDscat = ΓNR-NTPscat − ΓNRscat. From Table 1, we can see that ΔΓCIDscat monotonically increases from NR3 to NR1. In order to estimate the contribution of CID (or any other decay channel) to the overall plasmon linewidths of three nanorods, we need to correlate the homogenous linewidths with the dimensional parameters of the nanorods. Persson's theory is a well-accepted tool for explaining the change in homogenous linewidth due to CID.49 According to this theory, ΓCIDscat = ACIDνF/leff. Here, νF is the Fermi velocity and leff is the average distance an electron travels to reach the surface of the nanorods.49ACID is the probability that an electron scattered at the nanorod's surface transfers its energy to the LUMO of the molecule adsorbed at the nanorod surface. Note that leff includes the dimensional parameters as leff = 4V/S50,51 where V is the volume and S is the surface area of a nanorod which can be extracted from the TEM analyses. Fig. 4c clearly shows a linear dependency of ΔΓCIDscat with 1/leff and this explains the observed variation in the contribution of CID to the overall plasmon linewidths of three nanorods. Now, as discussed in detail in section S8 of the ESI,† if the explicit expressions of linewidths corresponding to all the decay channels are considered, then eqn (1) can be written as,
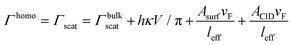 | (2) |
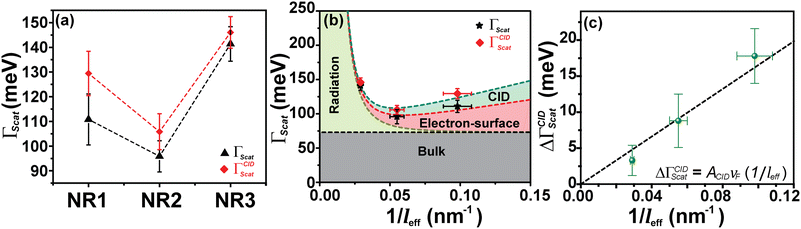 | ||
Fig. 4 (a) Average homogeneous LSPR linewidth obtained from dark-field scattering measurements for three different nanorods. The black tringles (▲) represent the average homogeneous linewidth (Γscat) of NR samples before surface modification, and the red diamonds ( ) represent the average homogeneous linewidth (ΓCIDscat) of NR samples after surface modification with 4-NTP. (b) Effective path length (leff) dependent contributions of different plasmon dephasing channels to the overall homogenous LSPR linewidth (Γhomo = Γscat) of gold nanorods before (black) and after (red) modification with 4-NTP. The variation of bulk damping (Γbulk), radiation damping (Γrad), electron-surface scattering damping (Γsurf) and CID (ΓCID) with 1/leff is shown by black, dark yellow, red, and dark cyan lines, respectively. Individual contributions are as follows, Γbulk = 72 meV (nearly constant for the range 1–2 eV), Γrad = hκV/π. From experimental data and linear regression using the equations, Γsurf = AsurfvF/leff and ΓCID = ACIDvF/leff, the values of Asurf and ACID are calculated. Details regarding this analysis can be found in section S8 of the ESI.† (c) Change in linewidth (ΔΓCIDscat) due to the CID channel in different Au NR samples as a function of 1/leff. Clearly, ΔΓCIDscat shows a linear dependency on 1/leff and is in agreement with Persson's theory. ) represent the average homogeneous linewidth (ΓCIDscat) of NR samples after surface modification with 4-NTP. (b) Effective path length (leff) dependent contributions of different plasmon dephasing channels to the overall homogenous LSPR linewidth (Γhomo = Γscat) of gold nanorods before (black) and after (red) modification with 4-NTP. The variation of bulk damping (Γbulk), radiation damping (Γrad), electron-surface scattering damping (Γsurf) and CID (ΓCID) with 1/leff is shown by black, dark yellow, red, and dark cyan lines, respectively. Individual contributions are as follows, Γbulk = 72 meV (nearly constant for the range 1–2 eV), Γrad = hκV/π. From experimental data and linear regression using the equations, Γsurf = AsurfvF/leff and ΓCID = ACIDvF/leff, the values of Asurf and ACID are calculated. Details regarding this analysis can be found in section S8 of the ESI.† (c) Change in linewidth (ΔΓCIDscat) due to the CID channel in different Au NR samples as a function of 1/leff. Clearly, ΔΓCIDscat shows a linear dependency on 1/leff and is in agreement with Persson's theory. | ||
Using eqn (2) and the homogeneous linewidths obtained from single-particle dark-field scattering measurements, we extract the contribution of each plasmon decay channel to the overall plasmon linewidths for each nanorod studied here (Fig. 4b). The relative contributions of different damping channels to the overall linewidth are summarized in Table 3 and it was found that both electron-surface scattering and CID contributions are higher for NR1 as compared to NR2, where the plasmon dephasing of NR3 is dominated by radiation damping. From Fig. 4b and c, it is evident that the contribution of electron-surface scattering increases inversely with leff which justifies the higher LSPR linewidth of NR1 as compared to NR2. On the other hand, the linewidth changes very rapidly with respect to leff in the radiation damping regime, which makes the linewidth of NR3 go very high. We calculated the energy transfer probability constants for electron-surface scattering (Asurf) and CID (ACID) from Fig. 4b using linear regression. We found Asurf = 0.21, which is slightly higher than the value Link et al. reported.31 Similarly, ACID is found to be 0.17, which means the probability of a scattered electron on the surface transferring its energy to the attached 4-NTP molecule is 17%. For nanorods of different sizes, this probability is the same as long as the same chemical interface is concerned. However, for smaller nanorods, the contribution of CID increases because of the higher efficiency of the electrons reaching the interface due to smaller leff. This is the reason why we found a larger increase in linewidth due to CID for NR1 than for NR2. On the other hand, NR3, being in the radiation damping regime, shows negligible sensitivity toward CID and, as a result, shows a very small amount of increase in linewidth upon surface modification with 4-NTP.
| Samples | % of Γbulkscat | % of Γradscat | % of Γsurfscat | % of ΓCIDscat |
|---|---|---|---|---|
| 4-NTP modified NR1 | 51.6 | 0.9 | 25.0 | 12.0 |
| 4-NTP modified NR2 | 76.2 | 8.4 | 20.7 | 9.9 |
| 4-NTP modified NR3 | 65.9 | 49.5 | 9.5 | 3.6 |
After determining the contribution of CID to the overall homogeneous linewidth for all three nanorods, we investigated the influence of CID on plasmon–exciton coupling using single-particle dark-field scattering microspectroscopy. For that, we prepared plasmon–exciton composites of the nanorods, with and without prior surface modification with 4-NTP. The same Cy78 dye J-aggregates served the role of excitonic components in all the plexciton hybrids. Single-particle dark-field scattering spectra of plexcitonic hybrids of surface unmodified and 4-NTP modified NR1, NR2, and NR3 were recorded. The UPB and LPB energy values of the recorded spectra were fitted to the coupled oscillator model as a function of plasmon detuning (see section S9 in the ESI† for details), and thereby the Rabi splitting energies (ħΩRabi) were determined. The plasmon–exciton coupling constants (g) were extracted using the equation 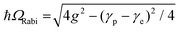 at zero detuning. The anti-crossing behavior of the plexciton modes was observed in all six cases. All the Rabi splitting values determined from the single-particle scattering measurements are shown in Table 2. It is obvious from Table 2 that, like the LSPR linewidth, the Rabi splitting values of the plexciton hybrids obtained from single-particle scattering measurements are consistently lower than the ensemble-level values.19 This is not surprising, and the reasons are explained in section S10 of the ESI.† Nevertheless, the trend in Rabi splitting (with and without CID) obtained via single-particle scattering qualitatively matches well with that obtained from ensemble-level extinction measurements. The Rabi splitting energies (ħΩRabi) for the plexciton hybrids of nanorods before 4-NTP modification are found to be ħΩRabi(NR1) = 196 ± 5 meV, ħΩRabi(NR2) = 181 ± 5 meV and ħΩRabi(NR3) = 147 ± 4 meV, (Fig. 5a), while the coupling constant (g) values for the nanorods before 4-NTP modification are determined to be 99 meV, 91 meV, and 77 meV for NR1, NR2, and NR3, respectively. Note that the coupling strengths of all these plexcitonic hybrids are found to reside within the strong coupling regime as they satisfy the condition,
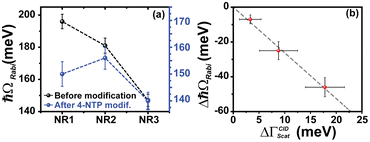
at zero detuning. The anti-crossing behavior of the plexciton modes was observed in all six cases. All the Rabi splitting values determined from the single-particle scattering measurements are shown in Table 2. It is obvious from Table 2 that, like the LSPR linewidth, the Rabi splitting values of the plexciton hybrids obtained from single-particle scattering measurements are consistently lower than the ensemble-level values.19 This is not surprising, and the reasons are explained in section S10 of the ESI.† Nevertheless, the trend in Rabi splitting (with and without CID) obtained via single-particle scattering qualitatively matches well with that obtained from ensemble-level extinction measurements. The Rabi splitting energies (ħΩRabi) for the plexciton hybrids of nanorods before 4-NTP modification are found to be ħΩRabi(NR1) = 196 ± 5 meV, ħΩRabi(NR2) = 181 ± 5 meV and ħΩRabi(NR3) = 147 ± 4 meV, (Fig. 5a), while the coupling constant (g) values for the nanorods before 4-NTP modification are determined to be 99 meV, 91 meV, and 77 meV for NR1, NR2, and NR3, respectively. Note that the coupling strengths of all these plexcitonic hybrids are found to reside within the strong coupling regime as they satisfy the condition, 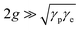 .1,5,52–54 Let us first discuss the plasmon–exciton interaction strengths of the surface unmodified nanorods. The Rabi splitting energies obtained from the nanorods before 4-NTP modification showed a monotonic trend (Fig. 5a), where NR1 shows the highest value and NR3 has the lowest value. This trend is quite understandable. Out of the three nanorods, NR3 has the largest size (and therefore the largest plasmon mode-volume, as per the Purcell's definition55) and an extremely large homogenous LSPR linewidth (i.e., the fastest plasmon dephasing rate owing to very efficient radiation damping). Now, both NR2 and NR1 have lower homogenous LSPR linewidths than NR3, but NR1 has a larger linewidth as compared to NR2 because of the strong contribution coming from electron-surface damping. NR2 falls in the borderline of radiation damping and the electron-surface scattering regime, hence one would expect NR2-plexciton to show larger Rabi splitting compared to NR1-plexciton if the effect of only plasmon dephasing in plasmon–exciton coupling is considered. On the other hand, the mode-volume of NR1 is much smaller than that of NR2, suggesting that NR1-plexciton should show larger Rabi splitting compared to NR2-plexciton.19,22 The smaller the plasmon mode-volume, the greater is the extent of energy exchange between plasmons and excitons. Now, our finding that NR1-plexcition exhibits larger Rabi splitting compared to NR2-plexciton unequivocally suggests that the plasmon mode-volume effect overwhelms the damping effect of electron-surface scattering in NR1, when no CID is involved. In other words, when there is no involvement of the CID channel for plasmon decay, the rate of energy exchange between plasmons and excitons overpowers the plasmon dephasing rate when the plasmon mode volume is sufficiently small and drives the plasmon–exciton interaction to a strong coupling regime.
.1,5,52–54 Let us first discuss the plasmon–exciton interaction strengths of the surface unmodified nanorods. The Rabi splitting energies obtained from the nanorods before 4-NTP modification showed a monotonic trend (Fig. 5a), where NR1 shows the highest value and NR3 has the lowest value. This trend is quite understandable. Out of the three nanorods, NR3 has the largest size (and therefore the largest plasmon mode-volume, as per the Purcell's definition55) and an extremely large homogenous LSPR linewidth (i.e., the fastest plasmon dephasing rate owing to very efficient radiation damping). Now, both NR2 and NR1 have lower homogenous LSPR linewidths than NR3, but NR1 has a larger linewidth as compared to NR2 because of the strong contribution coming from electron-surface damping. NR2 falls in the borderline of radiation damping and the electron-surface scattering regime, hence one would expect NR2-plexciton to show larger Rabi splitting compared to NR1-plexciton if the effect of only plasmon dephasing in plasmon–exciton coupling is considered. On the other hand, the mode-volume of NR1 is much smaller than that of NR2, suggesting that NR1-plexciton should show larger Rabi splitting compared to NR2-plexciton.19,22 The smaller the plasmon mode-volume, the greater is the extent of energy exchange between plasmons and excitons. Now, our finding that NR1-plexcition exhibits larger Rabi splitting compared to NR2-plexciton unequivocally suggests that the plasmon mode-volume effect overwhelms the damping effect of electron-surface scattering in NR1, when no CID is involved. In other words, when there is no involvement of the CID channel for plasmon decay, the rate of energy exchange between plasmons and excitons overpowers the plasmon dephasing rate when the plasmon mode volume is sufficiently small and drives the plasmon–exciton interaction to a strong coupling regime.
Now, if we look at the Rabi splitting energies and the coupling constants of the plexciton hybrids of the 4-NTP-modified nanorods, we found the Rabi splitting values to be 150 ± 5 meV, 156 ± 4 meV and 140 ± 3 meV, for NR1-, NR2-, and NR3-plexciton, respectively. These values are 23 ± 3%, 14 ± 4%, and 5 ± 4% lower as compared to the plexciton hybrids of unmodified Au NRs (see Table 2 for summarized data). More importantly, the Rabi splitting energies obtained from the NR-plexcitons after 4-NTP modification of the nanorods showed a nonmonotonic trend (Fig. 5a), where NR2-plexciton shows the highest and NR3-plexciton shows the lowest Rabi splitting value. The observation of such a drastic change in the plasmon–exciton coupling strength due to surface modification of nanorods by 4-NTP is quite interesting and thought provoking.
When we plot the decrease in Rabi splitting energy (due to 4-NTP modification of the NR surface) as a function of ΔΓCIDscat for different nanorod–plexciton samples (Fig. 5b), a linear dependency between the two is observed. Fig. 5b clearly shows that the Rabi splitting energy decreases purely because of CID. A comparative analysis of Fig. 4 and 5 clearly reveals that the CID-mediated change in Rabi splitting energies for NR-plexciton and the change in the nanorod's homogenous linewidth (ΔΓCIDscat), due to the incorporation of the CID channel, go hand in hand. It is obvious from Table 2 and Fig. 5b that NR1 shows the largest reduction in plasmon–exciton coupling strength. This is due to the largest increase in the plasmon dephasing rate in NR1 due to CID (Fig. 4a and b). On the other hand, 4-NTP modification of NR3 manifests the minimum change in plasmon–exciton coupling strength as the LSPR linewidth of NR3 is the least affected by the CID effect (see Tables 1, 2 and Fig. 4c, 5b). Now the pertinent question here is, unlike the case of surface-unmodified nanorods, why does NR2-plexciton exhibits larger Rabi splitting than NR1-plexciton when their surfaces are pre-modified with 4-NTP? As explained in the earlier section for surface-unmodified NR1 and NR2 (i.e., in the absence of the CID effect), smaller plasmon mode-volume of NR1 overpowers the plasmon decoherence effects to display stronger plexciton coupling than NR2.19 The completely contrasting behavior of plexciton coupling between NR1 and NR2 when their surfaces are pre-modified with 4-NTP clearly suggests that due to the larger CID in NR1 (than NR2), plasmon dephasing comprehensively overpowers the effect of the smaller plasmon mode-volume of NR1 and reduces the plasmon–exciton coupling strength of NR1-plexciton even lower than NR2-plexciton. This result suggests that the presence of the significant contribution of CID to overall plasmon dephasing can become the controlling factor in determining the plasmon–exciton coupling strength even when the plasmon mode-volume is quite small (please see section S11 of the ESI† for a detailed discussion). We would like to mention here about a possibility that the reduction in Rabi splitting might have arisen due to the fact that the attached 4-NTP molecules on the nanorod surface could hinder the formation of J-aggregates of Cy78 (exciton in our case) on the surface of nanorods. In such a scenario, due to the lower number (N) of excitons on the surfaces coherently interacting with the longitudinal surface plasmon mode of the nanorods, the Rabi splitting (ħΩRabi) would decrease since the coupling constant 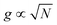 .37 However, if the reduction of Rabi splitting would occur because of a smaller number of interacting excitons, then a dependence of the change in Rabi splitting on the surface area of gold nanorods must have been observed, i.e. NR3 would show the maximum drop in Rabi splitting, while the change would be the least for NR1. But our results categorically disprove such a possibility. Also, we calculated the amount of unabsorbed Cy78 monomer in the solution after the plexciton hybrid formation with and without 4-NTP modified nanorods (see section S12 in the ESI† for details). We found the values to be very similar in both the cases. Thus, the decrease in Rabi splitting after surface modification with 4-NTP cannot be attributed to a reduced number of excitons, but rather to the effect of the enhanced plasmon dephasing rate via the CID channel.
.37 However, if the reduction of Rabi splitting would occur because of a smaller number of interacting excitons, then a dependence of the change in Rabi splitting on the surface area of gold nanorods must have been observed, i.e. NR3 would show the maximum drop in Rabi splitting, while the change would be the least for NR1. But our results categorically disprove such a possibility. Also, we calculated the amount of unabsorbed Cy78 monomer in the solution after the plexciton hybrid formation with and without 4-NTP modified nanorods (see section S12 in the ESI† for details). We found the values to be very similar in both the cases. Thus, the decrease in Rabi splitting after surface modification with 4-NTP cannot be attributed to a reduced number of excitons, but rather to the effect of the enhanced plasmon dephasing rate via the CID channel.
Before concluding, we would like to draw the attention of the reader to one very interesting outcome of this study. A plasmonic system with a given size and shape has a pre-defined plasmon dephasing (bulk, radiation damping, and electron-surface scattering) rate and mode-volume. Thus, for a given set of plasmonic nanostructure and excitonic systems, the “saturated” Rabi splitting is pretty much fixed. In other words, it is not possible to tune the strength of the “saturated” plexciton coupling without changing either the excitonic system altogether, or the dimensional parameters of the plasmonic nanostructure. Interestingly, the results of this work suggest that it is possible to tune the plexciton coupling strength by tuning the CID contribution to the overall plasmon decay rate via suitable selection of adsorbate, without the need to change the plasmonic or excitonic systems.
Conclusions
In conclusion, we have demonstrated how chemical interface damping impacts the coupling between two quasiparticles, plasmons and excitons, at the nanoscale. Three different gold nanorods having different diameters but identical aspect ratios have been used as plasmonic systems, while J-aggregate of a cyanine dye, Cy78, has been used as the excitonic system. The CID channel is introduced within the plasmonic system by surface modification of the Au nanorods with 4-nitrothiophenol. The single-particle dark-field scattering microspectroscopy measurements revealed that upon 4-NTP modification, different Au nanorods exhibit different extents of CID contribution in their homogenous linewidth depending on the effective path length (leff) of the nanorods. The thinnest nanorod (NR1) is found to be the most responsive to the change in the chemical interface, as electrons can reach the surface faster in this case compared to other nanorods. The interaction between the exciton resonance of the cyanine dye J-aggregates with the gold nanorods’ LSPR has been probed both in the presence and absence of CID. Both ensemble-level extinction and single-particle level dark-field scattering experiments clearly show that the incorporation of the CID channel, in addition to other plasmon decay channels, lowers the plasmon–exciton coupling strength, and the extent of the decrease is found to be in sync with the decrease in the relative contribution of CID to the overall homogenous linewidth. In the absence of the CID contribution, we find that when the diameter of nanorods decreases, the plasmon mode-volume factor gradually overwhelms the plasmon decoherence effects, resulting in an increase in plasmon–exciton coupling strength. However, the picture changes dramatically when the CID channel is active: plasmon dephasing controls the plasmon–exciton coupling strength by convincingly outweighing the effect of even a very small plasmon mode-volume. Most importantly, our results suggest that CID can be utilized to controllably tweak the plasmon–exciton coupling strength for a given plexciton system simply by modifying the nanoparticle's surface with a suitable adsorbate, without the need for changing the plasmonic or excitonic systems. Thus, judicious exploitation of CID can be extremely useful in tailoring the optical properties of plexciton hybrid systems to suit specific applications.Author contributions
M. C. conceived the idea and supervised the research. J. D. and A. V. performed experiments including nanorod synthesis, spectroscopic measurements etc. M. C. and J. D. analyzed data and interpreted results. J. D. wrote the first draft of the manuscript. M. C. revised the manuscript. All authors have read and given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. C. gratefully acknowledges the Science and Engineering Research Board, Government of India, for financial support (grant no. CRG/2020/004475). M. C. also thanks the Ministry of Human Resource Development, Government of India, for financial support under the IMPRINT-I initiative. J. D. acknowledges the support from CSIR, Government of India, for the senior research fellowship. A. V. thanks the Indian Institute of Technology Kanpur for the senior research fellowship.References
- G. Zengin, G. Johansson, P. Johansson, T. J. Antosiewicz, M. Käll and T. Shegai, Sci. Rep., 2013, 3, 3074 CrossRef CAS PubMed.
- G. Zengin, M. Wersäll, S. Nilsson, T. J. Antosiewicz, M. Käll and T. Shegai, Phys. Rev. Lett., 2015, 114, 157401 CrossRef PubMed.
- K. Das, B. Hazra and M. Chandra, Phys. Chem. Chem. Phys., 2017, 19, 27997–28005 RSC.
- F. M. Balci, S. Sarisozen, N. Polat and S. Balci, J. Phys. Chem. C, 2019, 123, 26571–26576 CrossRef CAS.
- T. Yoshie, A. Scherer, J. Hendrickson, G. Khitrova, H. M. Gibbs, G. Rupper, C. Ell, O. B. Shchekin and D. G. Deppe, Nature, 2004, 432, 200–203 CrossRef CAS PubMed.
- K.-D. Park, M. A. May, H. Leng, J. Wang, J. A. Kropp, T. Gougousi, M. Pelton and M. B. Raschke, Sci. Adv., 2019, 5, eaav5931 CrossRef CAS PubMed.
- S. Wang, S. Li, T. Chervy, A. Shalabney, S. Azzini, E. Orgiu, J. A. Hutchison, C. Genet, P. Samorì and T. W. Ebbesen, Nano Lett., 2016, 16, 4368–4374 CrossRef CAS PubMed.
- D. Zheng, S. Zhang, Q. Deng, M. Kang, P. Nordlander and H. Xu, Nano Lett., 2017, 17, 3809–3814 CrossRef CAS PubMed.
- J. Sun, H. Hu, D. Zheng, D. Zhang, Q. Deng, S. Zhang and H. Xu, ACS Nano, 2018, 12, 10393–10402 CrossRef CAS PubMed.
- T. Schwartz, J. A. Hutchison, C. Genet and T. W. Ebbesen, Phys. Rev. Lett., 2011, 106, 196405 CrossRef CAS PubMed.
- A.-L. Baudrion, A. Perron, A. Veltri, A. Bouhelier, P.-M. Adam and R. Bachelot, Nano Lett., 2013, 13, 282–286 CrossRef CAS PubMed.
- L. Lin, M. Wang, X. Wei, X. Peng, C. Xie and Y. Zheng, Nano Lett., 2016, 16, 7655–7663 CrossRef CAS PubMed.
- A. Tsargorodska, M. L. Cartron, C. Vasilev, G. Kodali, O. A. Mass, J. J. Baumberg, P. L. Dutton, C. N. Hunter, P. Törmä and G. J. Leggett, Nano Lett., 2016, 16, 6850–6856 CrossRef CAS PubMed.
- S. Sun, H. Kim, G. S. Solomon and E. Waks, Nat. Nanotechnol., 2016, 11, 539–544 CrossRef CAS PubMed.
- L. De Santis, C. Antón, B. Reznychenko, N. Somaschi, G. Coppola, J. Senellart, C. Gómez, A. Lemaître, I. Sagnes, A. G. White, L. Lanco, A. Auffèves and P. Senellart, Nat. Nanotechnol., 2017, 12, 663–667 CrossRef CAS PubMed.
- A. E. Schlather, N. Large, A. S. Urban, P. Nordlander and N. J. Halas, Nano Lett., 2013, 13, 3281–3286 CrossRef CAS PubMed.
- M. Wersäll, J. Cuadra, T. J. Antosiewicz, S. Balci and T. Shegai, Nano Lett., 2017, 17, 551–558 CrossRef PubMed.
- E. S. H. Kang, S. Chen, S. Sardar, D. Tordera, N. Armakavicius, V. Darakchieva, T. Shegai and M. P. Jonsson, ACS Photonics, 2018, 5, 4046–4055 CrossRef CAS.
- M. Kumar, J. Dey, M. S. Verma and M. Chandra, Nanoscale, 2020, 12, 11612–11618 RSC.
- M. S. Tame, K. R. McEnery, Ş. K. Özdemir, J. Lee, S. A. Maier and M. S. Kim, Nat. Phys., 2013, 9, 329–340 Search PubMed.
- A. F. Koenderink, Opt. Lett., 2010, 35, 4208 CrossRef CAS PubMed.
- M. Kumar, J. Dey, S. Swaminathan and M. Chandra, J. Phys. Chem. C, 2022, 126, 7941–7948 CrossRef CAS.
- E.-M. Roller, C. Argyropoulos, A. Högele, T. Liedl and M. Pilo-Pais, Nano Lett., 2016, 16, 5962–5966 CrossRef CAS PubMed.
- P. Törmä and W. L. Barnes, Rep. Prog. Phys., 2015, 78, 013901 CrossRef PubMed.
- L. Yang, X. Xie, J. Yang, M. Xue, S. Wu, S. Xiao, F. Song, J. Dang, S. Sun, Z. Zuo, J. Chen, Y. Huang, X. Zhou, K. Jin, C. Wang and X. Xu, Nano Lett., 2022, 22, 2177–2186 CrossRef CAS PubMed.
- J. Qin, Y.-H. Chen, Z. Zhang, Y. Zhang, R. J. Blaikie, B. Ding and M. Qiu, Phys. Rev. Lett., 2020, 124, 063902 CrossRef CAS PubMed.
- C. Qian, S. Wu, F. Song, K. Peng, X. Xie, J. Yang, S. Xiao, M. J. Steer, I. G. Thayne, C. Tang, Z. Zuo, K. Jin, C. Gu and X. Xu, Phys. Rev. Lett., 2018, 120, 213901 CrossRef CAS PubMed.
- J. Olson, S. Dominguez-Medina, A. Hoggard, L.-Y. Wang, W.-S. Chang and S. Link, Chem. Soc. Rev., 2015, 44, 40–57 RSC.
- C. Novo, D. Gomez, J. Perez-Juste, Z. Zhang, H. Petrova, M. Reismann, P. Mulvaney and G. V. Hartland, Phys. Chem. Chem. Phys., 2006, 8, 3540 RSC.
- C. Dahmen and G. von Plessen, Aust. J. Chem., 2007, 60, 447 CrossRef CAS.
- B. Foerster, A. Joplin, K. Kaefer, S. Celiksoy, S. Link and C. Sönnichsen, ACS Nano, 2017, 11, 2886–2893 CrossRef CAS PubMed.
- M. Liu, M. Pelton and P. Guyot-Sionnest, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 035418 CrossRef.
- C. Dahmen, B. Schmidt and G. von Plessen, Nano Lett., 2007, 7, 318–322 CrossRef CAS PubMed.
- H. Hövel, S. Fritz, A. Hilger, U. Kreibig and M. Vollmer, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 18178–18188 CrossRef PubMed.
- U. Kreibig and M. Vollmer, Optical properties of metal clusters, Springer, Berlin, 1995 Search PubMed.
- S. Y. Lee, P. V. Tsalu, G. W. Kim, M. J. Seo, J. W. Hong and J. W. Ha, Nano Lett., 2019, 19, 2568–2574 CrossRef CAS PubMed.
- T. V. Shahbazyan, Nano Lett., 2019, 19, 3273–3279 CrossRef CAS PubMed.
- J. A. Faucheaux, J. Fu and P. K. Jain, J. Phys. Chem. C, 2014, 118, 2710–2717 CrossRef CAS.
- T. P. Rossi, T. Shegai, P. Erhart and T. J. Antosiewicz, Nat. Commun., 2019, 10, 3336 CrossRef PubMed.
- D. P. Szekrényes, D. Kovács, Z. Zolnai and A. Deák, J. Phys. Chem. C, 2020, 124, 19736–19742 CrossRef.
- M. J. Seo, G. W. Kim, P. V. Tsalu, S. W. Moon and J. W. Ha, Nanoscale Horiz., 2020, 5, 345–349 RSC.
- S. W. Moon and J. W. Ha, Phys. Chem. Chem. Phys., 2019, 21, 7061–7066 RSC.
- S. Link and M. A. El-Sayed, Int. Rev. Phys. Chem., 2000, 19, 409–453 Search PubMed.
- M. Kumar, R. Arjariya, J. Dey, T. G. Gopakumar and M. Chandra, ACS Appl. Nano Mater., 2023, 6(15), 13894–13901 Search PubMed.
- K. Das, J. Dey, M. S. Verma, M. Kumar and M. Chandra, Phys. Chem. Chem. Phys., 2020, 22, 20499–20506 RSC.
- M. Hu, C. Novo, A. Funston, H. Wang, H. Staleva, S. Zou, P. Mulvaney, Y. Xia and G. V. Hartland, J. Mater. Chem., 2008, 18, 1949 RSC.
- N. S. Abadeer, G. Fülöp, S. Chen, M. Käll and C. J. Murphy, ACS Appl. Mater. Interfaces, 2015, 7, 24915–24925 CrossRef CAS PubMed.
- P. Zijlstra, P. M. R. Paulo, K. Yu, Q.-H. Xu and M. Orrit, Angew. Chem., Int. Ed., 2012, 51, 8352–8355 CrossRef CAS PubMed.
- B. N. J. Persson, Surf. Sci., 1993, 281, 153–162 CrossRef CAS.
- M. Liu and P. Guyot-Sionnest, J. Phys. Chem. B, 2004, 108, 5882–5888 CrossRef CAS.
- E. A. Coronado and G. C. Schatz, J. Chem. Phys., 2003, 119, 3926–3934 CrossRef CAS.
- S. A. Maier, Opt. Express, 2006, 14, 1957 CrossRef PubMed.
- Z.-J. Yang, T. J. Antosiewicz and T. Shegai, Opt. Express, 2016, 24, 20373 CrossRef PubMed.
- G. Khitrova, H. M. Gibbs, M. Kira, S. W. Koch and A. Scherer, Nat. Phys., 2006, 2, 81–90 Search PubMed.
- E. M. Purcell, Phys. Rev., 1946, 69, 681 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis and characterization of gold nanorods, ensemble-level extinction spectra of NR samples before and after surface modification, determination of the linewidth in ensemble-level extinction spectra using multi-peak fitting, sample preparation for SERS measurements and results, preparation of plexciton hybrids, sample preparation for single-particle dark-field scattering and data acquisition, the effective path length of electrons (leff) deciding the contribution of different damping channels to total plasmon decay, fitting of UPB and LPB energies according to the coupled oscillator model and estimation of Rabi splitting, explanation of higher Rabi splitting in ensemble-level extinction spectra as compared to single-particle dark-field scattering measurement, competing roles of the plasmon mode volume (Vmode) and plasmon dephasing in controlling plasmon–exciton coupling, determination of the number of J-aggregates interacting with nanorods prior to and after the surface modification with 4-NTP, a comparative CID effect of CTAB and 4-NTP, investigation of the role of near-field enhancement in plasmon–exciton coupling, and incident light polarization dependence of Rabi splitting. See DOI: https://doi.org/10.1039/d3nr04013e |
| This journal is © The Royal Society of Chemistry 2023 |