Quantitative, precise and multi-wavelength evaluation of the light-to-heat conversion efficiency for nanoparticular photothermal agents with calibrated photoacoustic spectroscopy†
Théotim
Lucas‡
ab,
Clément
Linger‡
 ac,
Thomas
Naillon
ac,
Thomas
Naillon
 df,
Mahshid
Hashemkhani
b,
Lise
Abiven
b,
Bruno
Viana
f,
Corinne
Chaneac
df,
Mahshid
Hashemkhani
b,
Lise
Abiven
b,
Bruno
Viana
f,
Corinne
Chaneac
 d,
Gautier
Laurent
d,
Gautier
Laurent
 e,
Rana
Bazzi
e,
Rana
Bazzi
 e,
Stéphane
Roux
e,
Stéphane
Roux
 e,
Sonia
Becharef
b,
Giulio
Avveduto
b,
Florence
Gazeau
e,
Sonia
Becharef
b,
Giulio
Avveduto
b,
Florence
Gazeau
 b and
Jérôme
Gateau
b and
Jérôme
Gateau
 *a
*a
aSorbonne Université, CNRS, INSERM, Laboratoire d'Imagerie Biomédicale, LIB, F-75006, Paris, France. E-mail: jerome.gateau@sorbonne-universite.fr
bUniversité Paris Cité, CNRS UMR 7057, Matière et Systèmes Complexes, MSC, F-75006 Paris, France
cUniversité Paris-Saclay, CNRS, Institut Galien Paris-Saclay, IGPS, F-91400 Orsay, France
dSorbonne Université, CNRS UMR 7574, Laboratoire Chimie de la Matière Condensée de Paris, F-75005 Paris, France
eUniversité de Franche-Comté, CNRS, Institut UTINAM, F-25000 Besançon, France
fChimie ParisTech, CNRS, PSLResearch University, Institut de Recherche de Chimie Paris, F-75231 Paris, France
First published on 10th October 2023
Abstract
Biomedical photothermal therapy with optical nanoparticles is based on the conversion of optical energy into heat through three steps: optical absorption, thermal conversion of the absorbed energy and heat transfer to the surrounding medium. The light-to-heat conversion efficiency (LHCE) has become one of the main metrics to quantitatively characterize the last two steps and evaluate the merit of nanoparticules for photothermal therapy. The estimation of the LHCE is mostly performed by monitoring the temperature evolution of a solution under laser irradiation. However, this estimation strongly depends on the experimental set-up and the heat balance model used. We demonstrate here, theoretically and experimentally, that the LHCE at multiple wavelengths can be efficiently and directly determined, without the use of models, by calibrated photoacoustic spectroscopy. The method was validated using already characterized colloidal suspensions of silver sulfide nanoparticles and maghemite nanoflowers and an uncertainty of 3 to 7% was estimated for the LHCE determination. Photoacoustic spectroscopy provides a new, precise and robust method of analysis of the photothermal capabilities of aqueous solutions of nanoagents.
1. Introduction
The conversion of optical energy into heat using optically absorbing nanoparticles is the fundamental basis of biomedical photothermal therapy. In addition to the biocompatibility and the ability to target the tissue of interest, specifications of nanoparticles developed as photothermal agents include a strong molar absorption coefficient in the near infrared range (first optical window of biological tissue), a large conversion of the absorbed energy into heat and an efficient transfer of the heat to the surrounding environment. The last two specifications are combined in a metric named the light-to-heat conversion efficiency (LHCE), which is one of the main quantitative figures-of-merit for agents dedicated to photothermal therapy.1,2 Therefore, a reliable methodology to determine the LHCE of photothermal nanoagents is of interest to compare quantitatively different types of nanoparticles. Of note, the LHCE may vary with the wavelength of the optical excitation and multi-wavelength determination of the LHCE can guide the choice of the laser used for therapeutic applications.The LHCE is defined in the seminal paper of Roper et al.3 as the fraction of the attenuated light power that is converted into heat flow by the optically absorbing nanoparticles in a solution illuminated with continuous light. The experimental determination of the LHCE by monitoring the temperature evolution of the solution under light irradiation is widespread, but highly challenging. Indeed, the determination of the LHCE value requires an equation modelling the heat balance in the experimental configuration, and a considerable variability is observed between the different models proposed previously.4 Based on a critical analysis of the different pre-existing models, Paściak et al.4 proposed a standardized method that can be considered as the state-of-the-art for the LHCE evaluation relying on the monitoring of the temperature evolution of a solution under light irradiation. However, this LHCE determination method suffers from a large uncertainty (∼39%) and tedious and long experimental procedures when the evaluation is required at several excitation wavelengths. Various particles were characterized by this method and at different wavelengths,2 which provide a reference dataset for the present study.
Alternatively, other physical principles have been investigated to determine the LHCE. For graphene nanoparticles, Savchuk et al.5 computed the LHCE using only measurements of the optical absorption. The light power absorbed by the laser-irradiated solution was measured using a power meter and an integrating sphere. However, the method assumes that all the absorbed energy is transformed into heat, which may be true for graphene but is not valid for luminescent particles for instance. Recently, Gu and Zhong1 reported LHCE evaluation based on a photothermal and electrothermal equivalence (PEE) method consisting in the measurement of the heat dissipation coefficient of a sample under electric heating. They demonstrate that the LHCE value deduced from electrothermal method is equal to that obtained with laser heating for the same temperature rise. However, the method can only be applied with dry solid materials and not solutions, which can cause sample modification during the drying process. Moreover, the heat transfer from the agent to the surrounding medium may be different for dry materials and not applicable to photothermal therapy in biological tissue.
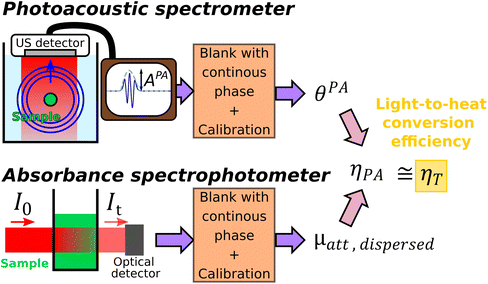
We propose here a new LHCE determination method based on the fact that particles considered as photothermal nanoagents are also contrast agents for photoacoustic imaging.6,7 Indeed, the photoacoustic effect combines the conversion of optical energy into heat (a process that is common with photothermal therapy) with the conversion of heat into pressure and subsequently ultrasound waves. The optical excitation in photoacoustic imaging is performed with nanosecond pulses. As the thermal relaxation time of the solution compartment (>17 ms for an aqueous solution in a compartment with linear dimension >0.1 mm) is much larger than the temporal duration of the optical pulse, the heat transport outside the solution compartment can be ignored during the ultrasound generation. This condition is called thermal confinement. Due to thermal confinement, no model of heat balance is needed for the illuminated solution. Moreover, for gold nanospheres, Prost et al.8 demonstrated that, on a nanometric scale and in the nanosecond regime, the ultrasound generation is almost entirely due to the water layer surrounding the particle (layer thickness ∼50 nm for 8 ns pulses). Therefore, the photoacoustic generation is sensitive to the heat transfer from the particle to the solvent, but it is not sensitive to the macroscopic heat transfer from the heated solution to its environment. Recently, we have developed a calibrated photoacoustic spectrometer9 that enables to convert the amplitude of the photoacoustic signals generated by a aqueous suspension of nanoparticles into spectroscopic units. The evaluated photoacoustic coefficient corresponds to the optical absorption coefficient restricted to the absorption effectively transferred into heat to the surroundings of the nanoagent and corrected for the potentially modified conversion of the heat into pressure compared to water (Grüneisen coefficient).9
In this paper, we develop the theoretical framework supporting that the LCHE can be obtained by computing the ratio of the photoacoustic coefficient of a solution measured with quantitative photoacoustic spectroscopy and the attenuation coefficient obtained by standard transmission spectrophotometry of the same solution. We validate experimentally our innovative method by measuring the LHCE over a broad range of optical wavelengths (680 nm–920 nm) for two classes of colloidal nanoparticles: semiconductor (silver sulfide nanoparticles) and metal oxide (maghemite nanoflowers). The LHCE values of these nanoagents were already measured by Paściak et al.2 by another method allowing to compare and discuss our results.
2. Results and discussion
2.1. Theoretical framework for the determination of the LHCE with quantitative photoacoustic spectroscopy
Photothermal therapy and photoacoustic ultrasound generation both rely on the conversion of the absorbed optical energy into heat. First, we mathematically link the equations of the two modalities to compute the LHCE and give the experimental limits underlying the applicability of these equations and of our approach. The equations are valid for molecular solutions and colloidal suspensions. For the sake of clarity, we will consider that the mixture is a colloid and the terms dispersed phase and continuous phase are used to refer to the solid nanoparticles and the liquid medium in which they are dispersed, respectively.![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) I and the optical attenuation Aλ induced by the dispersed phase for a solution illuminated by a laser at the optical wavelength λ.
I and the optical attenuation Aλ induced by the dispersed phase for a solution illuminated by a laser at the optical wavelength λ.![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) I = I0·(1–10−Aλ)·ηT I = I0·(1–10−Aλ)·ηT | (1) |
To link the photothermal and photoacoustic equations, we derive again the energy balance at mesoscopic scale and perform an integration to the macroscopic scale (see ESI†). For the sake of simplicity, a single kind of absorber is considered given that the generalization to multiple kinds of absorbers can be performed by applying the Beer–Lambert–Bouguer law. We introduce the photothermal conversion efficiency Ept(λ), which is the ratio of the energy effectively converted into a thermal increase of the solution to the total absorbed optical energy. Ept may be inferior to 1, due to various competitive deexcitation pathways such as fluorescence or photochemical reactions, for instance. We demonstrate that the LHCE is actually the product of the photothermal conversion efficiency Ept(λ) of the dispersed phase (unit less) and the ratio between the absorption coefficient of the dispersed phase μa(λ) (in m−1) and the attenuation coefficient of the solution μatt, solution(λ) (in m−1):
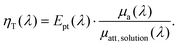 | (2) |
As the attenuation coefficient combines the absorption coefficient and the scattering coefficient, eqn (2) shows that the scattering properties of the solution influence the LHCE. In contrast, Ept(λ) exclusively refers to the absorbed optical energy transformed into heat.
For a non-scattering solution, μatt, solution(λ) = μa(λ) + μa, continuous(λ) with μa, continuous the absorption coefficient of the continuous phase (in m−1). Therefore, ηT equals Ept and the LHCE can effectively be considered has an intrinsic property of the absorber, if the absorption coefficient of the continuous phase can be neglected compared to the dispersed phase. Since μa(λ) is proportional to the concentration of the dispersed phase according to the Beer–Lambert–Bouguer law, a sufficient concentration needs to be reached to neglect the absorption of the continuous phase. For molecular absorbers usually used in biomedical application,10 micromolar to millimolar concentration would be sufficient since the molar absorption coefficient is on the order of 104 to 105 cm−1 M−1, while the decadic absorption coefficient of water11 in the near infrared (NIR) μa, water(λ)/ln(10) varies from 2 × 10−3 cm−1 at λ = 690 nm to 5 × 10−2 cm−1 at 920 nm.
For scattering agents like nanoparticles, the Beer–Lambert–Bouguer law assumes a linear dependence of the absorption and attenuation coefficients with the concentration of agents, and can be considered valid for samples with a small volume fraction of absorbers and a limited slab thickness.12 For nanoparticular agents (order of 100 nm diameter), the volume fraction of the dispersed phase can be considered negligible with regards to the continuous phase at concentrations from tens or hundreds nanomolar. Given that the molar absorption coefficient of nanoagents is a few orders of magnitude higher than for molecular agents, the absorption coefficient of the continuous phase can be neglected compared to the dispersed phase at this particle concentration, and the ratio μa(λ)/μatt, solution can be considered independent from the concentration.
In sum, the light-to-heat conversion efficiency defined by eqn (1) and (2) can be considered to be an intrinsic property of non-scattering and scattering agents for concentrations ensuring an absorption much higher than the continuous phase and a negligible volume fraction of the dispersed phase.
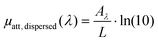 | (3) |
For a tube filled with a solution and illuminated with a laser pulse at the optical wavelength λ, the contribution of the optically absorbing dispersed phase to the ultrasound signal detected at the relative position ri is equal to (see ESI†):
| sdispersedi(t,λ) = Ept(λ)·μa(λ)·Γsolution·χin tube(ri, t, λ) | (4) |
To extract sdispersedi(t, λ) from the recorded ultrasound signal, we subtract the ultrasound signal measured by the detector for the tube filled with the continuous phase from the signal measured for the tested solution. This is equivalent to the blank acquisition in spectrophotometry. The ultrasound detector has a linear response. Therefore, this subtraction removes the contribution of the bath water outside the tube and the tube itself. It also removes the contribution of the continuous phase inside the tube to obtain sdispersedi(t,λ) if two conditions are satisfied: (1) the illumination inside the tube can be considered constant regardless of the solution inside the tube, and (2) the Grüneisen coefficient of the solution is equal to the Grüneisen coefficient of the continuous phase. For a tube diameter of Dtube = 0.2 mm, the first condition implies that the attenuation coefficient of the solution μatt, solution has to be small compared to: 1/Dtube = 50 cm−1. In the current study, we limited the attenuation coefficient to 7 cm−1. For the second condition, it has been shown that, for gold nanospheres illuminated in the nanosecond pulsed regime, the photoacoustic pressure arises from the layer of continuous phase surrounding the heated nanoparticles.8,13 This is true in particular when the thermal volume expansion coefficient of the particles can be considered much lower than that of the continuous phase, and that the mass fraction of the dispersed phase can be considered small. For molecular absorbers and for solid nanoparticles, we assume here that ultrasound emission arises dominantly from the continuous phase and therefore the thermodynamic properties of the continuous phase should be considered for the Grüneisen coefficient. Consequently, Γsolution ≈ Γcontinuous.
From sdispersedi(t,λ) measured over an array of ultrasound detectors, the photoacoustic coefficient θPA(λ) for the solution of absorbers9 is then assessed.
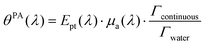 | (5) |
In brief, signals sdispersedi(t,λ) measured with the detector array are projected in an image space to increase the signal-to-noise ratio and the amplitude of the signal is extracted to obtain APA(λ), which is proportional to θPA(λ). Then, two reference solutions are used to calibrate the photoacoustic spectrometer. Both solutions are non-scattering, implying that μa(λ) can be measured by spectrophotometry. Additionally, the reference solutions are assumed to have a photothermal coefficient Ept equal to one. Indeed, the reference optical absorbers have no other deexcitation pathway since they do not have any fluorescence properties nor induce photochemical reaction. The first reference solution, cupric sulfate CuSO4·5H2O (0.25 M or 62.4 g L−1), has a strong absorption all over the investigated wavelength range (680 nm–920 nm), but it has a higher Grüneisen coefficient than water. This solution is used to obtain the per-wavelength calibration. The second reference solution is obtained by mixing nigrosine powder with water (173 mg L−1) and can be considered to have the Grüneisen coefficient of water. However, its absorption coefficient is decaying over the investigated wavelength range. This second solution is used to obtain a global calibration to the Grüneisen coefficient of water Γwater. With the photoacoustic coefficient, we can compute a Light-to-Photoacoustic Conversion Efficiency (LPCE):
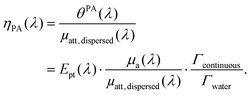 | (6) |
The LPCE is different from the photoacoustic generation efficiency defined elsewhere.9 Indeed, the LPCE is the ratio of the photoacoustic coefficient to the attenuation coefficient of the dispersed phase μatt, dispersed(λ), while the photoacoustic generation efficiency is the ratio of the photoacoustic coefficient to the absorption coefficient μa(λ). Therefore, the LCPE is sensitive to the scattering coefficient of the dispersed phase.
When the attenuation of the solution is dominated by the dispersed phase, the LPCE can be linked to the LHCE according to:
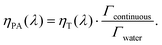 | (7) |
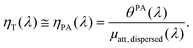 | (8) |
The method of determination of the LHCE with calibrated photoacoustic spectroscopy is schematically illustrated and summarized in Fig. 1.
2.2. Multiwavelength experimental determination of the LHCE for colloidal suspensions of nanoparticles
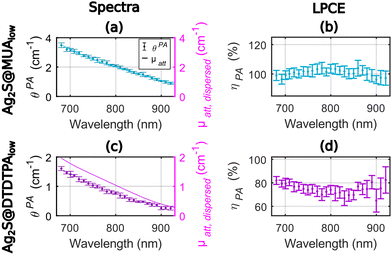
We considered here solutions of solid nanoparticles dispersed in purified water. The thermal volumetric expansion coefficients of the particles are neglected, and we assume that the photoacoustic generation arises from the layer of water surrounding the particles. Therefore, the LHCE can be considered equal to the LPCE. For a straight comparison with the results of Paściak et al.,2 we used nanoparticles synthesized by the same research teams and with the same protocols, but new batches were prepared.Fig. 2 presents the photoacoustic spectra and the attenuation spectra of the two compounds as well as their ratio ηPA in the range 680–920 nm with an evaluation every 10 nm. Experiments were performed on the same 1 mL volume of colloidal suspension. The precision of determination of the LPCE was found on the order of ±4% for Ag2S@MUAlow and for Ag2S@DTDTPAlow.
The LPCE can be considered constant with no dependence on the wavelength for Ag2S@MUAlow (Fig. 2(b)) with an average value of 100%. This result is confirmed by the match between the photoacoustic spectra and the attenuation spectra in Fig. 2(a). Identifying the LPCE and the LHCE, this result indicates that all the absorbed optical energy is converted into heat and that the scattering of the solution can be neglected. Such total conversion of optical energy into heat is in line with the low quantum yield of this agent, which is measured to be equal to 1.9%. For Ag2S@DTDTPAlow, the photoacoustic coefficients were found lower than the attenuation coefficients (Fig. 2(c)) in the range of 680–920 nm. More quantitatively, the determined LPCE values are between 65% and 82% with a mean value of 74% in the range of 680–920 nm, continuously decreasing by 10% between 680 nm and 780 nm (Fig. 2(d)). The quantum yield could not be determined on this sample but a low quantum yield (<1%) was reported in ref. 2 and a low fluorescence signal was measured here. Thus, the photothermal conversion efficiency Ept(λ) is expected to be equal to 1 and the fluorescence properties cannot explain the lower LPCE compare to Ag2S@MUAlow. On the other hand, the small size (∼2.3 nm on the TEM images (Fig. S2.b†), the hydrodynamic size could not be determined properly) of Ag2S@DTDTPAlow particles does not call for a large scattering. However, the large DTDTPA ligand combined with the low absorption of the particles could result in a larger relative contribution of the scattering to μatt, dispersed(λ) for Ag2S@DTDTPAlow compared to Ag2S@MUAlow and could account for the difference in the LPCE. The scattering is expected to be larger at shorter wavelengths which agrees with the decreasing difference μatt, dispersed(λ) − θPA(λ) with the increasing wavelength (Fig. 2(c)).
The difference in the LHCE values for the two Ag2S agents are larger at 790 nm (∼30%) than in the study of Paściak et al.2 (4%). However, the variation of the LHCE with the optical wavelength is smoother for Ag2S@DTDTPAlow and the LHCE uncertainty of our method is only of 4% here compare to 39% in the photothermal evaluation of Paściak et al.2 A LHCE of 100% ± 4% for Ag2S@MUAlow is also consistent with LHCE of 93% ± 8% at 808 nm reported by Shen et al.14 by monitoring of the temperature of a laser illuminated solution of PEG-coated silver sulfide nanoparticles with a quantum yield below 1%.
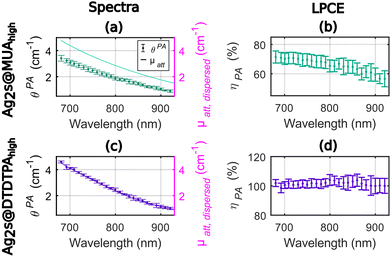
As shown in Fig. 3, the photoacoustic coefficients were found lower than the attenuation coefficients for Ag2S@MUAhigh (Fig. 3(a)) and the LPCE of Ag2S@MUAhigh was determined to be almost constant (Fig. 3(b)) in the range of 680–850 nm (68% ± 2% average ± std). For this sample, the quantum yield was measured to be 28%, which implies that Ept ≤ 72% and can explain the difference of LPCE value compare to Ag2S@MUAlow. The LPCE of Ag2S@DTDTPAhigh was found equal to 100% (Fig. 3(d)), while the quantum yield was found equal to 1.6%. The intensity based hydrodynamic size of Ag2S@DTDTPAhigh was 421 nm whilst it was measured equal to 168 nm for Ag2S@MUAhigh. These data clearly showed that the higher scattering of light due to the presence of large Ag2S@DTDTPAhigh nanoparticles was counterbalanced by the large contribution of the absorption to the attenuation and did not lead to a LPCE below 100%. One can note that the much higher absorbance of Ag2S@DTDTPAhigh compare to Ag2S@DTDTPAlow could explain that the scattering is negligible in the attenuation coefficient of this sample, besides the larger size of the particles. The precision of determination of the LPCE was found on the order of ±4% for Ag2S@MUAhigh and for Ag2S@DTDTPAhigh.
In sum for the silver sulfide nanoparticles, the LPCE could determine a LHCE compatible with the quantum yield of the samples. A LHCE of 100% ± 4% was determined for the samples with a quantum yield lower than 2% and a large optical absorption. Additionally, the LPCE of 68% ± 4% for Ag2S@MUAhigh is consistent with the 28% quantum yield. We could also determine that, for particles with a significant absorption, the influence of the scattering can be neglected while it results in a lower LPCE for Ag2S@DTDTPAlow. The LHCE values determined with our photoacoustic method are consistent with the values determined by Paściak et al. if we consider the large uncertainty of their method and the batch-to-batch variability. Importantly, our photoacoustic method gives access to physical explanations for the LHCE comparison for different materials, particularly the role of fluorescence and scattering properties of the solution, that were not accessible with Paściak et al.'s photothermal method. In addition, the photoacoustic evaluation allows for a spectral and monotonous determination of the LHCE over a large wavelength range providing unprecedented information on the spectral dependence of the LHCE.
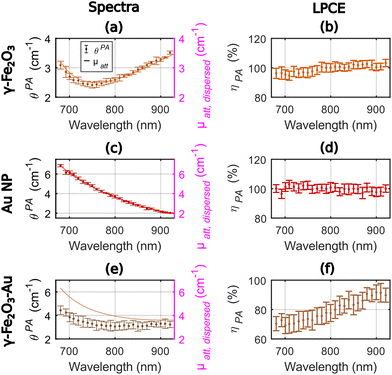
Fig. 4 displays the photoacoustic spectra and the attenuation spectra of the three compounds and ηPA in the range 680–920 nm. For γ-Fe2O3, the LPCE was determined to be around 100% with a slight increase (+4%) in the range 680–780 nm that may be due to a weak scattering of the solution at shorter wavelength (Fig. 4(b)). For Au NP, the photoacoustic and attenuation spectra were superimposed, leading to a constant LPCE equal to 100% (Fig. 4(c) and (d)). The precision of determination of the LPCE was found on the order of ±3% (mean value) for γ-Fe2O3 and Au NP. The LHCE of 100% for γ-Fe2O3, obtained with our photoacoustic method, is consistent with the fact that the particles are not luminescent and only weakly scattering.
For γ-Fe2O3–Au, the attenuation and photoacoustic spectra have different shapes (Fig. 4(e)) with a much larger difference μatt, solute(λ) − θPA(λ) at shorter wavelengths. Interestingly the photoacoustic spectrum of the γ-Fe2O3–Au sample could be decomposed in a linear sum of the photoacoustic spectra of γ-Fe2O3 and Au NP samples with weights 0.79 and 0.29, respectively (see Fig. S4†). However, the attenuation spectrum could be decomposed in a linear sum of the attenuation spectra of the γ-Fe2O3 and Au NP samples with weights 0.71 and 0.52, respectively. The weights for γ-Fe2O3 are close for both the attenuation and the photoacoustic spectra. The weight for the Au NP sample corresponds to the difference in the gold concentration between the colloidal suspensions of Au NP and γ-Fe2O3–Au for the photoacoustic spectrum. The much larger weight of Au NP for the attenuation spectrum could be attributed to the enhanced scattering at the shorter wavelengths of the bimetallic hybrid nanostructures γ-Fe2O3–Au in comparison to their individual constituents γ-Fe2O3 and Au NP. Indeed, the larger hydrodynamic diameter of the γ-Fe2O3–Au particles implies a larger scattering and the exponentially decaying shape of the attenuation spectrum of Au NP in the range 680–920 nm is also typical from what would be expected for scattering. This differences between PA and attenuation spectra results in a continuously increasing LPCE with the increasing wavelength, from 70% to about 90%, with an uncertainty of ±6% on average.
The LHCE determined at 790 nm by the photoacoustic method were equal to 100% ± 3% and 78% ± 7% for γ-Fe2O3 and γ-Fe2O3–Au, respectively. We found a −22% difference compared to the +4% difference in Paściak et al. For our measurements, the difference could be explained by the enhanced scattering properties for γ-Fe2O3–Au compare to γ-Fe2O3. Interestingly for the photoacoustic coefficient that is mostly unsensitive to scattering, the concentration of Au NP in γ-Fe2O3–Au could be retrieved by spectral decomposition. The variation of the LHCE over the investigated wavelength range were found to be monotonous.
2.3. Advantage and limits for the determination of the LHCE with photoacoustic spectrometry
The main advantages of photoacoustic spectrometry for the determination of the LHCE are its ability to obtain multi-wavelength evaluation of LHCE on the same sample and within one experiment, its small uncertainty and the limited volume of solution required for the measurement. The multi-wavelength evaluation is made possible with the use of a tunable nanosecond pulsed laser and the photoacoustic spectra was acquired in four tubes in parallel in less than 30 seconds per acquisition. For methods based on the monitoring of the temperature for an illuminated solution, multiple continuous lasers are required to perform multi-wavelength acquisitions. Moreover, each acquisition last a few minutes to tens of minutes.4 The uncertainty of our determination of the LHCE is on the order of 3% to 7%. This uncertainty is low because of the reproducibility of the measurements and the ability to perform 12 measurements on the same sample to compute median values. The volume of solution required for the 12 measurements is on the order of 500 μL. Each tube as a volume of 15 μL but the injection process is not fully optimized. The same volume can be used for the evaluation of the attenuation coefficient with a spectrophotometer. For comparison, a volume of a few mL is required for temperature monitoring in a cuvette and a few tens of μL can be used for methods with a hanging droplet. We previously determined that solutions with an absorption coefficient as low as 0.3 cm−1 can be measured with the photoacoustic spectrometer.9 Here a photoacoustic coefficient of 0.24 cm−1 was measured at 920 nm for Ag2S@DTDTPA, although we targeted solution with optical attenuation around 2 cm−1 to 4 cm−1 (absorbance of 1 to 2 for a 1 cm length cuvette). The optical absorption coefficient of water11μa, water(λ) varies from 5 × 10−3 cm−1 at λ = 690 nm to 0.1 cm−1 at 920 nm, therefore in addition to being subtracted by the blank acquisition, the absorption of the continuous phase could be neglected here for most of the measured solutions.Compare to the macroscopic evaluations of the LHCE performed by considering the heat balance for a homogenized temperature in the sample compartment, photoacoustic spectrometry senses the heat transfer in the immediate vicinity of the particles, in particular for hard nanoparticles with a negligible thermal volume expansion. Probing the heating capabilities on a local scale before heat diffusion occurs and homogenize the temperature increase can be of interest to detect the capabilities to generate hot spots instead of a global hyperthermia. Local temperature increase has shown to enable photothermal effects inside biological cells specifically on lysosome membrane leading to enhanced cell necrosis of cancerous cells.16 Thermo-responsive drug delivery systems incorporating photothermal agents could also benefit from a local heating.17 At nanometric scale, numerical frameworks were proposed to simulate both the photothermal response and the photoacoustic signals for single nanoparticles illuminated by nanosecond pulses.8,18,19 With a transition from single particles generating photoacoustic signals in the hundreds of MHz to solutions in tubes emitting in the MHz range, comparison between simulated photothermal properties and experimental measurements performed with the photoacoustic spectrometer would be of great interest and will be considered in a future study.
The photoacoustic evaluation of the photothermal properties of nanoparticles has a few limits. First, the Grüneisen coefficient of the solution may be different from that of the continuous phase. In the case of soft nanoparticles such as polymer nanoparticles for instance, the effective Grüneisen coefficient may combine the thermal volume expansion of both the nanoparticle and the continuous phase. A significant contribution of polymer nanoparticles to the effective Grüneisen coefficient has been observed when the constituting material had a thermal volumetric expansion coefficient larger than water and when a thermal confinement occurred at the length scale of the nanoparticles during the optical excitation.20 Indeed, for short optical excitation (pulse width of 800 ps) which induce a heat confinement in polymer nanoparticles with a diameter larger than 100 nm, Aoki et al.20 found that the effective Grüneisen coefficients of colloidal suspensions were larger than the Grüneisen coefficient of the continuous phase. In this case, the LPCE is no longer equivalent to the LHCE. For our photoacoustic spectrometer which operates with longer optical pulses (6–7 ns pulse width), the thermal confinement during the optical excitation is ensured for the spatial scale of the tube (solution compartment), but it is expected to be limited at the spatial scale of the nanoparticle; i.e. the characteristic length of the nanoparticle should be small compared to the thermal diffusion length in its constituting material. Consequently, the photoacoustic method presented here could be applicable for organic nanoparticles if the thermal expansion coefficient of their constituting material is low with respect to water and the thermal diffusivity is high. For continuous phases other than water, the current calibration procedure of the photoacoustic spectrometer should be adapted with the need to find new reference solutions in that solvent. Other than the Grüneisen coefficient, the pulsed optical excitation used in the photoacoustic spectrometer can have an influence compare to the continuous excitation of photothermal therapy when Ept(λ) depends on the illumination duration. This is true in particular when the optically absorbed energy can be stored by intermediate species or excited states living longer than the pulse but shorter than the thermal relaxation time. In this case, the LHCE will be underestimated with photoacoustic spectroscopy.
2.4. Discussion on the relevance of the LHCE
As shown by eqn (2), the LHCE as defined by Roper et al.3 is sensitive to the scattering properties of the solution. The scattering properties of the photothermal nanoagents will impact the penetration of light in a suspension. However, when the nanoparticles are embedded in biological tissues for photothermal therapy, the scattering strength of the nanoagents may be considered negligible compared to the overall scattering induced by the tissue structures. Therefore, the photothermal conversion efficiency Ept(λ) is probably a better quantifier of the amount of optical energy that is converted into heat by the agents. The evaluation of Ept(λ) however requires the evaluation of the absorption coefficient from the attenuation coefficient, which can be challenging for scattering particles even with a spectrophotometer equipped with an integrating sphere.Neither the LHCE nor the photothermal conversion efficiency include the absorption cross section of each particle. To really rank agents in terms of their capability to convert optical energy into heat, a more relevant metric could be the equivalent of the molar absorptivity coefficient. This quantity could be named molar or mass photothermal coefficient:
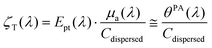 | (9) |
This molar or mass photothermal coefficient could be determined directly with photoacoustic spectrometry if the volume expansion of the nanoparticle can be neglected as for solid nanoparticles used as photothermal agents.
3. Conclusions
Calibrated photoacoustic spectroscopy was shown, both theoretically and experimentally, to provide a novel method for the determination of the Light-to-Heat Conversion Efficiency (LHCE) adapted to colloidal suspensions of solid nanoparticles. The method overcomes the limitations of the heat balance modelling, facilitates multi-wavelength determination of the LHCE and exhibits a low uncertainty.The LHCE was determined to be equal to 100% for particles with weak luminescence and weak scattering properties, which is in line with a full transfer of the optically energy absorbed by the dispersed phase to the continuous phase in the form of heat. The lower LHCE values could be related to photothermal conversion efficiency reduced by the fluorescence quantum yield of the particles or to significant relative contribution of the scattering to the attenuation coefficient of the solution. The influence of the scattering on the LHCE value questions the relevance of this metric to characterize and compare photothermal nanoagents.
Calibrated photoacoustic spectroscopy could be used directly to obtain robust and accurate estimation of the photothermal properties of nanoagents with a mass photothermal coefficient that quantifies the three steps of photothermal therapy all together: optical absorption, thermal conversion of the absorbed energy and heat transfer to the surrounding medium.
4. Methods
4.1. Synthesis of the nanoparticles
For a typical preparation of gold nanoparticles, HAuCl4·3H2O (200 mg, 51 × 10−5 mol) was placed in a 250 mL round-bottom flask and was dissolved with methanol (60 mL). In another flask, DTDTPA (256 mg, 50 × 10−5 mol), water (40 mL) and acetic acid (2 mL) were mixed. This solution containing DTDTPA was added to the gold salt solution under stirring. The mixture turned from yellow to orange. NaBH4 (195 mg, 515 × 10−5 mol) dissolved in water (13.2 mL) was added to the gold–DTDTPA solution under stirring at room temperature. At the beginning of the NaBH4 addition, the solution first became dark brown then a black flocculate appeared. The vigorous stirring was maintained for 1 h before adding aqueous hydrochloric acid solution (2 mL, 1 M). After the partial removal of the solvent under reduced pressure, the precipitate was retained on the polymer membrane and washed thoroughly and successively with 0.1 M hydrochloric acid, water and acetone. The resulting black powder was dried (up to 200 mg of dry powder of Au@DTDTPA) and dispersed in aqueous solution of sodium hydroxide (NaOH 0.01 M) to have a final concentration of 50 mM in gold.
The immobilization of Au@DTDTPA nanoparticles onto the maghemite nanoflowers requires the modification of the gold nanoparticles by dopamine. To obtain chelator-coated gold nanoparticles functionalized with dopamine (Au@DTDTPAd), an aqueous solution (3 mL) containing N-ethyl-N′-(3-dimethylaminopropyl) carbodiimide hydrochloride (EDC, 0.207 g; 1.08 × 10−3 mol) and N-hydroxysuccinimide (NHS, 0.247 g; 2.150 × 10−3 mol) was added to a suspension of Au@DTDTPA gold nanoparticles (6 mL, 50 mM). The suspension was stirred at pH 6 for 90 minutes. Afterwards, an aqueous solution (4 mL) containing dopamine (9.45 × 10−3 g; 2.25 × 10−5 mol) was added to the suspension under stirring at pH 7.5. The mixture is stirred overnight. The purification of the suspension of gold nanoparticles was performed by dialysis against water (MWCO: 6–8 kDa) for 12 h. Water bath was changed three times every 3 h.
The measured suspension had a concentration of 1 g Au L−1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v) for several times to eliminate organic and inorganic impurities. Possible iron hydroxides were removed by treatment with 10% nitric acid. Iron(III) nitrate (Fe(NO3)3·9H2O) (2 g, 4.951 × 10−3 mol) is then dissolved in water (20 mL) and added to the nanoparticles. The resulting mixture is heated to 80 °C for 45 min to achieve a complete oxidation of the nanoparticles. After another treatment with 10% nitric acid, the particles were washed twice with acetone and diethyl ether and redispersed in water. At this stage, an aqueous dispersion of IONF is obtained that is stable in acid or basic conditions with a point of zero charge near pH 7.3.
1, v/v) for several times to eliminate organic and inorganic impurities. Possible iron hydroxides were removed by treatment with 10% nitric acid. Iron(III) nitrate (Fe(NO3)3·9H2O) (2 g, 4.951 × 10−3 mol) is then dissolved in water (20 mL) and added to the nanoparticles. The resulting mixture is heated to 80 °C for 45 min to achieve a complete oxidation of the nanoparticles. After another treatment with 10% nitric acid, the particles were washed twice with acetone and diethyl ether and redispersed in water. At this stage, an aqueous dispersion of IONF is obtained that is stable in acid or basic conditions with a point of zero charge near pH 7.3.
The measured suspension had a concentration of 1.67 g Fe L−1.
4.2. Spectrometers
The concentration of gold and/or iron was determined with Inductively Coupled Plasma-Optical Emission Spectrometry (ICP-OES). The samples were mineralized in ultrapure aqua regia. An ICP-OES (710 ES Varian/Agilent) with axial torch with a concentric nebulizer and cyclonic spray chamber was used. The parameters fixed during measurement were: power of 1.2 kW with argon auxiliary of 1.5 L min−1 and nebulizer pressure of 200 kPa. An ionizing buffer was employed for the measurements. The limit of detection of this technique is 20 μg L−1.
The calibration was performed with the reference solution of pentahydrate copper(II) sulfate (CuSO4·5H2O, ACS reagent, ≥98.0%, Sigma-Aldrich, St Louis, MO, USA) at 250 mM to convert APA in the PA coefficient θPA(λ). This solution is called the calibration solution.
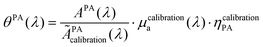 | (10) |
The photoacoustic coefficient of the nanoparticles was measured in four tubes injected with the same solution simultaneously. The calibration was performed per tube. Typically, in a series of experiments, we performed two acquisitions with the calibration solution and one acquisition with the solution of nigrosin, between each sample. The calibration sequence was repeated at least 6 times for a robust estimation. For each sample, three acquisitions in four tubes were performed, leading to a total of 12 measurements per sample. The median of θPA(λ) was used as an estimate to avoid outliers due to possible injection errors. For the evaluation of the measurement error, we used the median absolute deviation with a scale factor 1.4826. The absorption of water increases above 920 nm and results in a degraded performance of our instrument, therefore, measurements performed for optical wavelengths above 920 nm were discarded.
The uncertainty of the estimation of the LPCE was developed in the ESI.†
Author contributions
J. G., T. L. and F. G. are responsible for the conceptualization of the project and experiments. T. L. and J. G. developed the methodology. T. L. and C. L. performed the photoacoustic and spectrophotometric measurements. T. L., C. L. and J. G. analysed and evaluated the data. L. A., T. N. and C. C. prepared and characterized the silver sulfide nanoparticles. M. H. characterized the suspension of silver sulfide nanoparticles. G. L., R. B. and S. R. prepared and characterized the maghemite nanoflowers and gold nanoparticles. All authors discussed and contributed to the preparation of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by Sorbonne University under the program Emergence Sorbonne Université 2019–2020. This project has received financial support from the CNRS through the MITI interdisciplinary programs (Defi Imag'IN, 80 Prime) and from Gefluc Paris, Ile de France. This work was partly funded by France Life Imaging under Grant ANR-11-INBS-0006 and by the ANR Nanothermometry project (ANR-21-CE09-0030-01). This work received financial support from ITMO Cancer of Aviesan within the framework of the 2021-2030 Cancer Control Strategy, on funds administered by Inserm (no. 21CP074-00). L.A. acknowledges support from the European Union Horizon 2020 FETOpen project NanoTBTech (801305). This work was supported by the IdEx Université Paris Cité, ANR-18-IDEX-0001 (IVETh plateform), by the Region Ile de France under the convention SESAME 2019 - IVETh (EX047011) (IVETh plateform), by the Region Ile de France and Banque pour l’Investissement (BPI) under the convention Accompagnement et transformation des filières projet de recherche et développement N° DOS0154423/00 & DOS0154424/00, and Agence Nationale de la Recherche through the program France 2030 (ANR-22-AIBB-0002) and CycLys project (ANR-18-CE09-0015-01).References
- K. Gu and H. Zhong, Light: Sci. Appl., 2023, 12, 120 CrossRef CAS PubMed.
- A. Paściak, R. Marin, L. Abiven, A. Pilch-Wróbel, M. Misiak, W. Xu, K. Prorok, O. Bezkrovnyi, L. Marciniak, C. Chanéac, F. Gazeau, R. Bazzi, S. Roux, B. Viana, V. P. Lehto, D. Jaque and A. Bednarkiewicz, ACS Appl. Mater. Interfaces, 2022, 14(29), 33555–33566 CrossRef PubMed.
- D. K. Roper, W. Ahn and M. Hoepfner, J. Phys. Chem. C, 2007, 111, 3636–3641 CrossRef CAS PubMed.
- A. Paściak, A. Pilch-Wróbel, Ł. Marciniak, P. J. Schuck and A. Bednarkiewicz, ACS Appl. Mater. Interfaces, 2021, 13, 44556–44567 CrossRef PubMed.
- O. A. Savchuk, J. J. Carvajal, J. Massons, M. Aguiló and F. Díaz, Carbon, 2016, 103, 134–141 CrossRef CAS.
- Y. Liu, P. Bhattarai, Z. Dai and X. Chen, Chem. Soc. Rev., 2019, 48, 2053–2108 RSC.
- H. Zhu, B. Li, C. Yu Chan, B. Low Qian Ling, J. Tor, X. Yi Oh, W. Jiang, E. Ye, Z. Li and X. Jun Loh, Adv. Drug Delivery Rev., 2023, 192, 114644 CrossRef CAS PubMed.
- A. Prost, F. Poisson and E. Bossy, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 1–16 CrossRef.
- T. Lucas, M. Sarkar, Y. Atlas, C. Linger, G. Renault, F. Gazeau and J. Gateau, Sensors, 2022, 22, 6543 CrossRef CAS PubMed.
- J. Weber, P. C. Beard and S. E. Bohndiek, Nat. Methods, 2016, 13, 639–650 CrossRef CAS PubMed.
- K. F. Palmer and D. Williams, J. Opt. Soc. Am., 1974, 64, 1107–1110 CrossRef CAS.
- N. M. Anderson and P. Sekelj, Phys. Med. Biol., 1967, 12, 173–184 CrossRef CAS PubMed.
- Y. S. Chen, W. Frey, S. Aglyamov and S. Emelianov, Small, 2012, 8, 47–52 CrossRef CAS PubMed.
- Y. Shen, H. D. A. Santos, E. C. Ximendes, J. Lifante, A. Sanz-Portilla, L. Monge, N. Fernández, I. Chaves-Coira, C. Jacinto, C. D. S. Brites, L. D. Carlos, A. Benayas, M. C. Iglesias-de la Cruz and D. Jaque, Adv. Funct. Mater., 2020, 30, 1–13 Search PubMed.
- A. Nicolás-Boluda, J. Vaquero, G. Laurent, G. Renault, R. Bazzi, E. Donnadieu, S. Roux, L. Fouassier and F. Gazeau, ACS Nano, 2020, 14, 5738–5753 CrossRef PubMed.
- A. Nicolas-Boluda, Z. Yang, T. Guilbert, L. Fouassier, F. Carn, F. Gazeau and M. P. Pileni, Adv. Funct. Mater., 2021, 31, 2006824 CrossRef CAS.
- D. Ghosh Dastidar and G. Chakrabarti, in Applications of Targeted Nano Drugs and Delivery Systems, Elsevier, 2019, pp. 133–155 Search PubMed.
- A. Hatef, B. Darvish, A. Dagallier, Y. R. Davletshin, W. Johnston, J. C. Kumaradas, D. Rioux and M. Meunier, J. Phys. Chem. C, 2015, 119, 24075–24080 CrossRef CAS.
- N. Amjadi, A. Hatef and R. Malekfar, J. Phys. Chem. C, 2022, 126, 20584–20593 CrossRef CAS.
- H. Aoki, M. Nojiri, R. Mukai and S. Ito, Nanoscale, 2015, 7, 337–343 RSC.
- M. Brust, J. Fink, D. Bethell, D. J. Schiffrin and C. Kiely, J. Chem. Soc., Chem. Commun., 1995, 1655 RSC.
- C. Alric, J. Taleb, G. Le Duc, C. Mandon, C. Billotey, A. Le Meur-Herland, T. Brochard, F. Vocanson, M. Janier, P. Perriat, S. Roux and O. Tillement, J. Am. Chem. Soc., 2008, 130, 5908–5915 CrossRef CAS PubMed.
- P.-J. Debouttière, S. Roux, F. Vocanson, C. Billotey, O. Beuf, A. Favre-Réguillon, Y. Lin, S. Pellet-Rostaing, R. Lamartine, P. Perriat and O. Tillement, Adv. Funct. Mater., 2006, 16, 2330–2339 CrossRef.
- P. Hugounenq, M. Levy, D. Alloyeau, L. Lartigue, E. Dubois, V. Cabuil, C. Ricolleau, S. Roux, C. Wilhelm, F. Gazeau and R. Bazzi, J. Phys. Chem. C, 2012, 116, 15702–15712 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr03727d |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2023 |