 Open Access Article
Open Access ArticleImpact of the organic cation on the band-edge emission of two-dimensional lead–bromide perovskites†
Seda
Kutkan
a,
Balaji
Dhanabalan‡
 a,
Miao-Ling
Lin
a,
Miao-Ling
Lin
 b,
Ping-Heng
Tan
b,
Ping-Heng
Tan
 b,
Alexander
Schleusener
b,
Alexander
Schleusener
 a,
Milena P.
Arciniegas
a,
Milena P.
Arciniegas
 a and
Roman
Krahne
a and
Roman
Krahne
 *a
*a
aItalian Institute of Technology (IIT), Via Morego 30, 16163 Genoa, Italy. E-mail: roman.krahne@iit.it
bState Key Laboratory of Superlattices and Microstructures, Institute of Semiconductors, Chinese Academy of Sciences, 100083 Beijing, China
First published on 13th July 2023
Abstract
Organic–inorganic low-dimensional layered metal–halide perovskites are semiconductors in which the optoelectronic properties can be tuned by the material composition and the design of the layered architecture. While the electronic band structure is mainly determined by the inorganic octahedra lattice, the binding and conformation of the organic cations induces related lattice distortions that can break the symmetry and lead to the splitting of the exciton energy levels, and influence the dielectric confinement. Furthermore, organic-induced lattice deformations lead to offsets in k-space (where k is the wavevector) that go along with the exciton energy level splitting. Hence, the electronic transitions between these levels require the momentum contribution of phonons, and contributions of phonons in the exciton recombination dynamics result in thermal broadening of the emission linewidth. In this work, we investigate the band-edge emission of two-dimensional Ruddlesden-Popper lead–bromide perovskites synthesized with different organic cations that vary in their binding head group and their alkyl chain length. We find several peaks in the low-temperature photoluminescence spectra, and the number of peaks in the band-edge emission and their decay dynamics depend strongly on the type of organic cation in the material, which we relate to the difference in the inorganic lattice distortions that the cations induce. For two-dimensional layered perovskites with mainly in-plane distortions, induced by short primary ammonium molecules, we find a two-fold splitting of the band edge emission at low temperatures. If also out-of-plane distortions are present, as for the long-chain primary ammoniums, a three-fold splitting is observed. Interestingly, the low-energy peaks of the split series merge into the highest energy peak with increasing temperature. Thermal broadening analysis of the temperature-dependent photoluminescence linewidth in the structures with out-of-plane distortions yields energies that are larger than those reported for the inorganic lattice phonons. This indicates the involvement of either high-frequency oscillations involving the organic cations, or the broadening might be related to higher order phonon scattering processes in the excitonic recombination process. The strong directionality of the phonon modes in the octahedral lattice could promote the involvement of multiple electron–phonon scattering processes in the exciton relaxation dynamics, for example involving modes with orthogonal directionality.
Introduction
Low-dimensional metal halide perovskites are a highly attractive platform for fundamental research on hybrid organic–inorganic materials1–3 and quantum-confined electronic systems,4–7 as well as for applications in light emission.8,9 Their complex architecture that alternates inorganic octahedra lattices and organic layers allows for a wide variety in material composition by the choice of different metallic and organic cations, in combination with the flexibility in the selection of halides (typically chloride, iodide, and bromide).10 The optical band gap depends strongly on the metal–halide composition, the exciton binding energy, and the dielectric confinement.11,12 The electronic level structure at the band gap is governed by the atomic orbitals of the metal cations and the halides that form the inorganic octahedra.13 For lead–halide structures, the valence band is dominated by hybridized Pb s-orbitals and halide p-orbitals, while the conduction band is determined by the Pb p-orbitals. The band-edge states are formed from a hole with angular momentum Jh = 1/2 and an electron with angular momentum Je = 1/2, resulting in four exciton (electron–hole pair) states that consist of a singlet with total angular momentum J = 0, and a triplet with J = 1 and z-components of 0 and ±1.14,15 The degeneracy of the singlet and triplet is lifted by the exchange interaction, which splits it into a dark singlet and bright triplet state. Further degeneracy can be lifted by the lattice symmetry and the anisotropy in quantum confinement, such that up to four different exciton levels can be observed in the experiments.Recently some works on photoluminescence (PL) spectroscopy in high magnetic fields reported that the lowest exciton state is the dark state in metal halide nanocrystals14,16–18 as well as in two-dimensional layered perovskites (2DLPs).19 However, it is surprising that the band-edge emission intensity increases towards the lowest temperatures (10 K), if the lowest exciton state is dark. Such behavior points to a bottleneck in exciton-phonon coupling between the bright and dark state20,21 that could stem from their difference in angular momentum, or in the layered architecture of two-dimensional perovskites from orthogonal orientation of the oscillating dipoles. However, the discussion on the origin of multiple emission peaks at the band edge is still controversial, since apart from excitonic level splitting these could be due to shallow donors22 or phonon scattering.23 In this context, the occurrence of multiple peaks with regular spacing in the order of several tens of meV in the low-temperature absorption and emission spectra of two-dimensional lead–iodide layered perovskites was related to electron–phonon coupling with high-energy phonons that reside on the organic cations.24
The hybrid organic–inorganic architecture of 2DLPs allows for large freedom in the selection of the organic cations, opening fascinating pathways to modify their structural, electrical and optical properties.10,25–27 The dielectric confinement can be tailored by the thickness and composition of the organic layers,12,28–30 conductive organic cations can be integrated to improve the cross-plane electrical properties,31 and the distortions of the inorganic metal–halide lattice can be tuned by using ammonium molecules with different head groups.32,33 Towards the freedom of choice in the organic cations, the Ruddlesden-Popper configuration that is based on molecules with only one binding group (monocations) to the perovskite lattice is advantageous, since the van der Waals gap formed by the tails of the molecules can be explored for the incorporation of additional structures.34 Although these organic molecules do not directly contribute to the optical band gap of the perovskite materials, the possible structural and dielectric changes that they induce can have a significant impact on the optical properties.12,27,35,36 One very appealing feature of 2DLPs with strongly distorted lattices is white light emission that results from recombination of free excitons at the band edge together with the broadband emission of self-trapped excitons or defects.8,9,37–40 In the view of investigating the band-edge exciton fine structure in low-dimensional layered perovskites it is therefore interesting to study the impact of different organic cations that will lead to differences in the dielectric confinement and in the lattice distortions.
To explore the effect of dielectric confinement and lattice distortions on the exciton fine structure, we chose 2DLPs synthesized with different ammonium molecules as organic cations, as described in Fig. S1.† We selected two primary ammonium molecules (NH3 binding group) with different alkyl chain length, namely butylammonium (BA) and undecylammonium (UDA), that lead to different dielectric confinement and minimal differences in lattice distortions. The third sample is based on the secondary ammonium molecule (NH2 binding group) N-methyldodecylammonium (N-MDDA), that has a similar alkyl chain length as UDA, which results in a marked difference in the inorganic lattice distortions. We focus our investigation on the PL at low temperatures to resolve the excitonic levels and study the temperature dependence of the PL in the cryogenic range to get insight into the thermal effects related to phonons. We resolve several emission peaks in the spectral range of the band edge emission that feature complex temperature dependence and recombination dynamics. We observe a series of PL peaks at temperatures below 80 K, with a spectral separation of the peaks that would translate to a splitting of 20–40 meV of the exciton levels. Since in lead–bromide perovskites the lowest exciton state is a dark state,16,19,24,41,42 the observation of several bright emissive states at the lowest temperature of 10 K confirms the bottleneck in the thermal relaxation from the bright to the dark exciton states. With increasing temperature in the range from 10–80 K, the low energy peaks decrease in intensity and eventually vanish, such that around 80–100 K only the peak at the highest energy of the series remains and dominates the emission. We attribute this exciton peak to the cross-plane confined excitonic state, which then dominates the emission at temperatures above 100 K. Analysis of the thermal linewidth broadening of this emission peak in the low-temperature range yields very different optical phonon energies and coupling strengths for the samples with different organic cations. For the BA sample we obtain a phonon energy of around 8 meV, which falls in the range of the phonons of the inorganic octahedra lattice. However, for the UDA and N-MDDA samples the PL linewidth fitting gives much larger values of 26 meV and 18 meV for the LO phonon energy, respectively, thus at much higher energies compared to the range where the inorganic lattice phonon modes were observed by Raman spectroscopy.
Results and discussion
Fig. S1† shows the configuration of the amine molecules and different views of the crystallographic structure of the samples in which the lattice distortions induced by the organic cations can be appreciated: the BA sample is characterized by a strong in-plane distortion of 152.8° and octahedra that are well-aligned in the vertical direction.43 For the crystallographic views of the primary ammonium with a longer aliphatic chain, we consider 10 carbons in the alkyl chain length, which should lead to a similar in-plane distortion as for BA, along with a small out-of-plane tilting of the octahedra.44 The secondary ammonium sample with N-MDDA cations features significantly tilted octahedra in the vertical direction, and much smaller in-plane distortions (165.5°) than those induced by primary ammonium molecules.32 Since these distortions induced by the different organic cations affect the electronic and excitonic energy levels, we observe very different spectral behavior in the PL spectra, as reported in Fig. 1a.32,33 For simplicity, we refer in the following to the three 2DLP samples with the abbreviation of their organic cation, thus (BA)2PbBr4 = BA, (UDA)2PbBr4 = UDA, and (N-MDDA)2PbBr4 = N-MDDA. The low-temperature PL spectra of the three 2DLP samples with different head groups and different alkyl chain lengths are shown in Fig. 1a.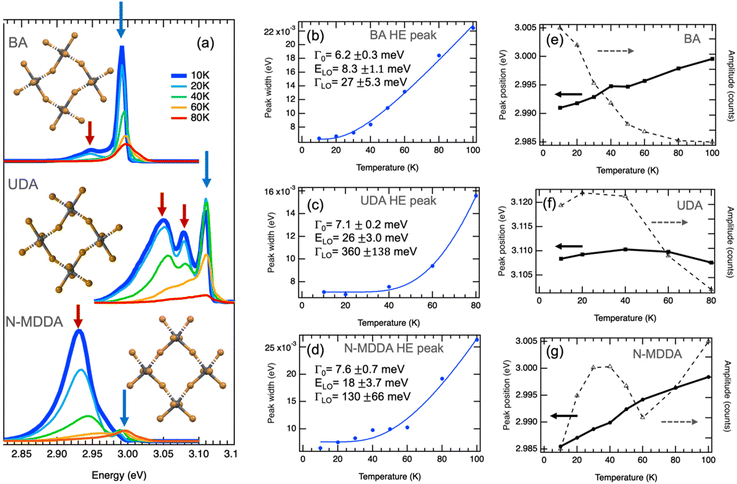 | ||
| Fig. 1 Band-edge photoluminescence at low temperatures. (a) PL spectra of 2D layered lead bromide perovskites with BA, UDA and N-MDDA as organic cations. Spectra at 10 K are highlighted by the thick, dark blue lines. The insets show top views of the inorganic lattice structure that illustrate the in-plane distortions and out-of-plane tilting of the Pb–Br octahedra in the three different materials (see Fig. S1† for details). (b–d) Temperature dependence of the width obtained by Gaussian fitting of the high-energy (HE) emission peaks marked by blue arrows in (a), where the thermal broadening is fitted with eqn (2). (e–g) Temperature dependence of the central position and amplitude of the HE peaks marked by blue arrows in (a). | ||
In all three cases, we observe multiple peaks at the lowest temperature (10 K): we identify a double-peak structure for BA with high intensity in the high-energy (HE) peak, three marked peaks for UDA with approximately similar intensity, and for N-MDDA one broad and intense peak at low energy and two much smaller and narrower peaks at high energy (see also Fig. S2†). The largest optical band gap, derived from the PL spectra, (Fig. 1a) is observed for UDA,32 which we relate to the increased dielectric confinement that results from the thicker organic layer with respect to BA (thicknesses of the organic layers for BA, UDA, and N-MDDA are 7.8 Å, 19.7 Å, 17.8 Å, respectively).28–30,32 The fact that the large molecular length of N-MDDA does not result in a large optical band gap as for UDA should be related to the close position of the methyl group with respect to the octahedra layer, and to the stronger out-of-plane distortions that affect the electronic band gap states and the exciton binding energy (see Fig. S1†). For all three samples, and therefore independent of the impact of the organic cations, the emission intensity decreases with increasing temperature up to 80 K. Here the intensity of the peaks that are lower in energy decreases more strongly than that of the peaks at higher energy, and this decrease in intensity is, in some cases, accompanied by a spectral blueshift of the peak center. At around 80–100 K, we observe only the peak at the highest energy, the lower energy peaks transformed to a shoulder at the low energy side of the main peaks. Fig. S3† shows PL spectra in the temperature range from 100 K–200 K, where the maximum emission intensity occurs.
Fig. 1b and c report the width, central peak energy, and amplitude obtained by Gaussian fitting versus temperature for the HE band-edge emission peaks, where we observe a temperature-dependent width of the PL peak. The thermal broadening of the PL can be described by:45
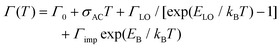 | (1) |
| Γ(T) = Γ0 + ΓLO/[exp(ELO/kBT) − 1] | (2) |
For UDA, we obtain the strongest coupling coefficient ΓLO that goes along with a strong decrease in peak intensity with increasing temperature. Here the average LO phonon energy ELO is much larger (26 meV) than for BA, and also larger than what we observed for the inorganic lattice phonon bands by Raman spectroscopy, see Fig. S5† and ref. 33. However, we observe a weak phonon band at a corresponding frequency (220 cm−1) and other bands at higher frequencies (around 320 cm−1) in the Raman spectrum of UDA (see Fig. S5†) that could be related to vibrational modes of the organic cations, which would be in agreement with what was recently reported for lead–iodide 2DLPs.24,27 In these works, a series of peaks observed in the low-temperature emission of 2DLPs has been attributed to electron–phonon coupling involving the phonon modes of the organic cations, in particular the bending and twisting vibrations of these organic molecules. This interpretation was motivated by the good correspondence of the peak separation in emission to the energy of the observed phonon modes, and supported by testing organic cation molecules with different stiffness in their backbone in the 2DLPs. In Fig. 1, the energy difference of the HE peak (at 3.11 eV) of UDA with the next lower energy peak (at 3.07 eV) is 40 meV (corresponding to 330 cm−1), which agrees reasonably well with the energy range of the three peaks around 320 cm−1, and furthermore the energy obtained by the fitting for the optical phonons agrees well with the phonon band at 220 cm−1 (see inset of Fig. S5†).
However, the large number and strong directionality of the phonon modes of the octahedra lattice in these 2DLPs could also lead to the involvement of multiple low-frequency phonon scattering processes in the recombination dynamic of the excitons. Two-phonon scattering as has been recently reported for bilayer WSe2.47 In our system, the long life time of the band-edge excitons could favor such scattering processes that then would also contribute to the PL linewidth broadening, as illustrated in Fig. 2a. In materials with strong in-plane distortions like UDA, such process could also involve a combination of phonons, for example, those along the major in-plane axes of the octahedra lattice. With respect to eqn (2), such two-phonon scattering could be seen as a new quasiparticle with an energy that would correspond to the sum of the individual phonon mode energies, and this sum would correspond to the fitting parameter that we obtain for the energy of the phonons.
 | ||
| Fig. 2 (a) Illustration of the one-phonon and two-phonon scattering of excitons that leads to the emission linewidth broadening. One-phonon scattering is illustrated by the bend arrows, two-phonon scattering by the rectangular arrows, and emissive recombination is sketched by the waveform arrows. (b) Illustration of the phonon coupling between the bright emitting states and non-radiative defect states. The distortions induced by the organic cations lead to small offsets of the minima of the dispersions in k-space. The stronger quantum confinement in z-direction results in a stronger curvature of the dispersion. The dark exciton level is sketched by a dashed line and the radiative recombination by waveform blue arrows. The thicker line width of the dark blue arrow indicates the brighter emission of the HE band edge peak with respect to the low-energy (x;y) transitions. Phonon-assisted thermal transitions are sketched by the curved red arrows. The inset illustrates the two-phonon coupling between the dark state and the bright z-state.16 | ||
For the HE peak of N-MDDA, the fit yields an intermediate coupling strength to optical phonons (ΓLO = 130 meV) with respect to BA and UDA, and the obtained average LO phonon energy (ELO) is 18 meV, again much larger than that of the octahedra lattice phonon modes in Fig. S5.† Also in this case we observe weak Raman bands at a corresponding frequencies (150–170 cm−1) and highly directional octahedra lattice phonons, thus the same reasoning as presented for UDA can be applied.
The temperature dependence of the PL of the 2DLPs with different organic cations in Fig. 1 suggests that different charge carrier recombination mechanisms are at work, possibly involving the coupling of different excitonic states and multiple phonon scattering. To get more information on the recombination dynamics, we measured the time-resolved PL decay traces related to the peaks marked by the blue and red arrows in Fig. 1a, which are shown in Fig. 3. The life time of the HE peak for BA continuously decreases with increasing temperature (Fig. 3a), which goes along with a decrease in emission intensity. This points to thermal coupling to non-radiative states that typically have a fast decay rate.48,49 The decay traces are dominated by a bi-exponential decay, in agreement with radiative (long life time) and non-radiative (short life time) recombination channels. The decay traces of the low-energy peak of BA show an even more marked bi-exponential behavior, with a much longer life time for the slow recombination channel. For UDA (Fig. 3b), the decay first becomes slower with increasing temperature (from 10–40 K), as was observed by Tamarat and co-workers50 for the two-phonon coupling to the dark state, and then the shape of the decay trace changes significantly, obtaining two distinct linear slopes (in the semi-log plot) that correspond to marked fast and slow components. Interestingly, the intensity of the HE peak remains almost constant in the range from 10–40 K, see Fig. 1c, and then drastically decreases when the strongly bi-exponential decay sets in. The latter points to coupling to a non-radiative state with a short life time. For UDA, the peak at 3.07 eV shows qualitatively a similar behavior as the HE peak at 3.11 eV, and at 80 K all three marked peaks show roughly the same decay traces, which indicates efficient thermal coupling. The low energy peak at 3.05 eV manifests a life time decrease with increasing temperature, with a strong decrease in peak intensity, which indicates coupling to a non-radiative defect.
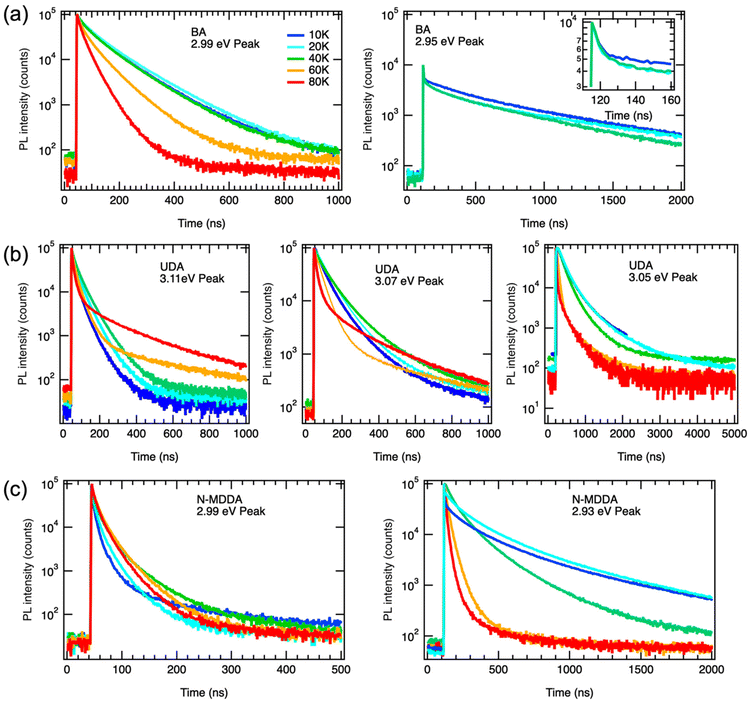 | ||
| Fig. 3 PL decay traces of the samples collected at the emission peaks marked by the blue and red arrows in Fig. 1a: (a) BA HE peak (2.99 eV) and lower peak (2.95 eV). The inset shows the early fast PL decay on an enlarged time scale; (b) UDA HE peak (3.11 eV) and two lower energy peaks (3.07 and 3.05 eV); and (c) N-MDDA HE peak (2.99 eV) and one lower energy peak (2.93 eV). | ||
The decay traces of the HE peak of N-MDDA (Fig. 3c) follow a complex multi-exponential behavior that has the slowest decay at intermediate temperatures of 40–60 K, which coincides with the minimum in emission intensity. Furthermore, the difference in lifetime between the fast and slow recombination channels is more marked at 10 K than at 80 K, and the decay traces of the low energy peak at 2.93 eV show a marked slow component at 10–20 K that vanishes with increasing temperature.
The data in Fig. 1 and 3 show that we observe very different PL spectra and recombination dynamics for the three lead–bromide 2DLPs, evidencing the strong impact that the different organic cations have on the band edge emission. In this discussion on the temperature-dependent bahavior we exclude phase transitions in our materials, since we do not observe any frequency shifts of the phonons with increasing temperature (Fig. S6†). BA features one main band-edge emission peak over most of the temperature range that has an intensity minimum at around 80–100 K, and develops additional low-energy peaks below 80 K. The linewidth of the main band-edge peak can be well fitted with eqn (2), in agreement with thermal broadening due to optical phonons, and yields a phonon energy that falls into the range where the inorganic vibrational bands are observed. Time-resolved PL shows that the fastest decay coincides with the smallest emission intensity, pointing to thermal coupling with non-radiative recombination channels. BA has only negligible out-of-plane distortion of the inorganic lattice and the emission over the full temperature range is dominated by states near the band edge, i.e., there is no significant broadband emission from (self) trapped excitons. Furthermore, the similar behavior of the HE and low-energy peaks with increasing excitation power indicates that both peaks can be related to band edge emission (Fig. S7†).
UDA and N-MDDA show much more complex behavior, which can be attributed to the out-of-plane distortions that also favor the self-trapping of excitons.51 In these systems, a much larger range of phonon modes is present,33 and therefore efficient exciton-phonon coupling in an extended energy range can be expected. This is supported by a factor of 10 (5) larger values for ΓLO for UDA (N-MDDA) with respect to BA, which we obtained in the fitting of the temperature behavior of the FWHM of the band-edge PL. ELO exceeds that of the observed phonons of the octahedra lattice in Raman spectroscopy33 by at least a factor of 2, which indicates that scattering involving vibrations of the organic cations or multi-phonon processes as sketched in Fig. 2a are at work. Interestingly, efficient multi-phonon scattering can enable thermal coupling to several electronic states, including defects and dark excitons. In this respect, the marked increase of the slow recombination channel in the PL decay of the HE peak of UDA with increasing temperature agrees well with the model that Tamarat et al.50 proposed for two-phonon coupling of the bright and dark exciton states in perovskite nanocrystals (as sketched in the inset of Fig. 2b). Moreover, the peak splitting of around 40 meV that we observe roughly agrees with their prediction of the scaling of the exciton fine structure splitting with the quantum confinement.52 Then, the decay trace of the HE peak of UDA manifests two well-separated slopes, thus in addition to the slow channel discussed above, there is a fast channel that is most likely non-radiative, and accounts for the decrease in peak intensity with increasing temperature from 10–80 K. The appearance of three well-defined peaks at 10 K for UDA correlates with the lattice distortions that are present both in-plane and out-of-plane, leading to a splitting of the exciton levels with respect to all spatial dimensions. Furthermore, in addition to the band-edge PL, a broad emission band centered at 2.1 eV is observed for UDA in the range from 20–100 K that can be attributed to self-trapped excitons.33 Such occurrence of self-trapped exciton emission supports the strong exciton–phonon coupling that we derived from our fitting in Fig. 1b. For temperatures above 100 K, only the band-edge emission is observed, which red-shifts, broadens and has the maximum intensity at around 150 K (Fig. S3†).
For N-MDDA we cannot derive clear trends with respect to the temperature dependence of the PL emission and decay dynamics. Most likely, too many competing processes are involved that include the formation of self-trapped excitons, multi-phonon coupling to the dark exciton, and defect-assisted (non-radiative) recombination. We note that in addition to the band-edge PL, weak broadband emission at 2.0 eV and 2.21 eV is observed in the range from 10–80 K, which could be related to trapped excitons. We do not observe a marked increase of a slow recombination component in the PL decay traces as was the case for UDA. Therefore, for N-MDDA we have no indication for two-phonon coupling between bright and dark exciton states.
Fig. 2b illustrates the band dispersions and the thermal coupling processes that we derive from our data in the recombination dynamics in Fig. 3. The distortions of the inorganic lattice induced by the organic cations lead to shifts in the dispersions of the excitonic states in momentum (k) space. Exciton–phonon coupling can provide both the necessary energy for the transitions from the x-, and y-states to the z-state and the required momentum.53 The similar decay traces measured for the UDA peaks at 80 K (Fig. 3) evidence the good thermal coupling of the x, y, and z states. To explain the decrease in emission from the bright states with increasing temperature from 10 to 80 K, we hypothesize coupling to a shallow, non-radiative defect state that requires momentum, and therefore the contribution of phonons. The contribution of such defect to the emission linewidth is negligible if the binding energy of such defect is much smaller than the exciton binding energy, which for exciton binding energies of several hundred meV, as reported for 2DLPs,11 is reasonable. We assume two-phonon coupling of the bright z-state to the dark state for UDA as illustrated in the inset of Fig. 2b. In the above discussion, we neglect the self-trapping of excitons that also takes place in these 2DLP materials. Such self-trapping is strongest for N-MDDA, but at cryogenic temperatures occurs also in UDA (and very weakly in BA).32,33 Thus, for N-MDDA several processes such as thermal coupling between the bright states themselves, the bright states and defects, possibly two-phonon coupling with the dark state, and self-trapping of excitons are at work. This explains why the PL decay traces do not exhibit clear trends for the N-MDDA sample.
To summarize the PL dynamics below 100 K, our results show that for BA these can be rationalized by thermal coupling between the bright states with low coupling strength, and thermal coupling to a non-radiative defect. For UDA, the marked slow component that emerges towards 80 K indicates two-phonon coupling of the bright to the dark state as proposed in ref. 50, and the occurrence of multi-phonon scattering is supported by the large phonon frequency obtained in the line width fitting (roughly corresponding to twice the energy of the observed inorganic phonon bands), and the large number of observed phonon bands by Raman spectroscopy (Fig. S5†).33 For N-MDDA, we find roughly similar spectral behavior of the bright states as for BA and UDA, however, the recombination dynamics are different and highly complex, most likely involving multiple phonon scattering processes, self-trapped excitons, and coupling to defects.
In conclusion, we observe multiple peaks in the low-temperature band-edge emission of 2DLPs that can be correlated to splitting of the bright exciton levels with respect to the spatial (x, y, z) directions in the octahedra lattice. Due to the anisotropy of the layered architecture (strong confinement in z-direction), the exciton z-state can be expected to have the strongest oscillator strength and the highest energy. Therefore, thermal coupling of the bright (x,y,z) states funnels the radiative transitions into the recombination channel of the z-state, which leads to the gradual disappearance of the low-energy (x,y) emission peaks at the band edge with increasing temperature. Furthermore, we find that distortions of the octahedra lattice in the cross-plane directions can lead to the involvement of several phonon modes in the exciton recombination. This is reasonable, since in 2D lattices with tilted octahedra the in-plane vibrations obtain cross-plane components, which can facilitate their coupling to the dominant exciton z-state. Our work demonstrates that in 2DLPs the choice of the organic cations plays a crucial role for the electron–phonon coupling and the exciton recombination dynamics. Therefore, the variety of available organic cations provides a versatile toolbox for designing the emission properties of two-dimensional layered perovskites.
Experimental section
Synthesis
The samples were prepared by following protocols reported in literature.30,32 Briefly, PbBr2 powder was dissolved in hydrobromic acid and acetone in 4 mL glass vials. The mixture was vigorously shaken until it became a transparent solution. To the mixture, the corresponding amine was injected drop by drop and kept under strong magnetic stirring for a few minutes while the crystals nucleated in the solution. The vial left untouched overnight under ambient conditions which allows the crystals to grow larger. Next, the as-grown crystals were collected and washed with acetone multiple times using a Buchner funnel and vacuum pump to remove the excess of precursors and dried on filter paper.Photoluminescence spectroscopy
Steady-state and time-resolved PL were recorded with an Edinburgh FL920 spectrometer with a spectral resolution of 0.5 nm. The samples were illuminated with a pulsed laser diode at 375 nm wavelength through optical fibers, and the light was focused by optical lenses to a spot with diameter of 3 mm. Powders of the 2DLPs were placed between two TED Pella glass slides and compressed gently. The samples were mounted in a closed-cycle cryostat (ARS) and cooled to 10 K. For the temperature-dependent measurements, the temperature was increased from 10 K to 300 K.Raman spectroscopy
Raman experiments were performed in an optical cryostat under non-resonant conditions with 632.8 nm excitation wavelength from a He–Ne laser. The spectra were collected in a backscattering geometry using a home-modified Jobin–Yvon HR800 Raman system equipped with an electron multiplying charged-coupled detector (CCD) and a 50× objective (numerical aperture of 0.45) with long working distance. 2400 lines per mm gratings were used yielding a spectral resolution was 0.19 cm−1 per CCD pixel under 632.8 nm excitation. The laser plasma lines were removed by Bragg-volume-grating-based bandpass filters (BPF) from OptiGrate Corp.Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has received support from the AI4QD project funded by the Italian Ministry of Foreign and International Affairs (MAECI). A. S. acknowledges the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Funding Program (Project TOGETHER, Grant Agreement No. 101067869). P. H. T. and M. L. L. acknowledge support from the National Natural Science Foundation of China (Grant No. 12004377). R. K. thanks Prof. Sergey Artyukhin and Dr Giulia Biffi for valuable discussions.References
- J. C. Blancon, A. V. Stier, H. Tsai, W. Nie, C. C. Stoumpos, B. Traoré, L. Pedesseau, M. Kepenekian, F. Katsutani, G. T. Noe, J. Kono, S. Tretiak, S. A. Crooker, C. Katan, M. G. Kanatzidis, J. J. Crochet, J. Even and A. D. Mohite, Nat. Commun., 2018, 9, 2254 CrossRef PubMed.
- S. B. Todd, D. B. Riley, A. Binai-Motlagh, C. Clegg, A. Ramachandran, S. A. March, J. M. Hoffman, I. G. Hill, C. C. Stoumpos, M. G. Kanatzidis, Z. G. Yu and K. C. Hall, APL Mater., 2019, 7, 081116 CrossRef.
- Q. Tu, I. Spanopoulos, E. S. Vasileiadou, X. Li, M. G. Kanatzidis, G. S. Shekhawat and V. P. Dravid, ACS Appl. Mater. Interfaces, 2020, 12, 20440–20447 CrossRef CAS PubMed.
- D. H. Cao, C. C. Stoumpos, O. K. Farha, J. T. Hupp and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 7843–7850 CrossRef CAS PubMed.
- C. M. M. Soe, C. C. Stoumpos, M. Kepenekian, B. Traoré, H. Tsai, W. Nie, B. Wang, C. Katan, R. Seshadri, A. D. Mohite, J. Even, T. J. Marks and M. G. Kanatzidis, J. Am. Chem. Soc., 2017, 139, 16297–16309 CrossRef CAS PubMed.
- H. Tsai, W. Nie, J.-C. Blancon, C. C. Stoumpos, R. Asadpour, B. Harutyunyan, A. J. Neukirch, R. Verduzco, J. J. Crochet, S. Tretiak, L. Pedesseau, J. Even, M. A. Alam, G. Gupta, J. Lou, P. M. Ajayan, M. J. Bedzyk, M. G. Kanatzidis and A. D. Mohite, Nature, 2016, 536, 312 CrossRef CAS PubMed.
- M. K. Jana, R. Song, Y. Xie, R. Zhao, P. C. Sercel, V. Blum and D. B. Mitzi, Nat. Commun., 2021, 12, 4982 CrossRef CAS PubMed.
- M. D. Smith and H. I. Karunadasa, Acc. Chem. Res., 2018, 51, 619–627 CrossRef CAS PubMed.
- M. D. Smith, B. A. Connor and H. I. Karunadasa, Chem. Rev., 2019, 119, 3104–3139 CrossRef CAS PubMed.
- X. Li, J. M. Hoffman and M. G. Kanatzidis, Chem. Rev., 2021, 121, 2230–2291 CrossRef CAS PubMed.
- Y. Cho and T. C. Berkelbach, J. Phys. Chem. Lett., 2019, 10, 6189–6196 CrossRef CAS PubMed.
- J. V. Passarelli, C. M. Mauck, S. W. Winslow, C. F. Perkinson, J. C. Bard, H. Sai, K. W. Williams, A. Narayanan, D. J. Fairfield, M. P. Hendricks, W. A. Tisdale and S. I. Stupp, Nat. Chem., 2020, 12, 672–682 CrossRef CAS PubMed.
- K. Tanaka, T. Takahashi, T. Kondo, K. Umeda, K. Ema, T. Umebayashi, K. Asai, K. Uchida and N. Miura, Jpn. J. Appl. Phys., 2005, 44, 5923 CrossRef CAS.
- M. Fu, P. Tamarat, H. Huang, J. Even, A. L. Rogach and B. Lounis, Nano Lett., 2017, 17, 2895–2901 CrossRef CAS PubMed.
- J. Ramade, L. M. Andriambariarijaona, V. Steinmetz, N. Goubet, L. Legrand, T. Barisien, F. Bernardot, C. Testelin, E. Lhuillier, A. Bramati and M. Chamarro, Nanoscale, 2018, 10, 6393–6401 RSC.
- P. Tamarat, M. I. Bodnarchuk, J.-B. Trebbia, R. Erni, M. V. Kovalenko, J. Even and B. Lounis, Nat. Mater., 2019, 18, 717–724 CrossRef CAS PubMed.
- L. Chen, B. Li, C. Zhang, X. Huang, X. Wang and M. Xiao, Nano Lett., 2018, 18, 2074–2080 CrossRef CAS PubMed.
- G. Biffi, Y. Cho, R. Krahne and T. C. Berkelbach, J. Phys. Chem. C, 2023, 127, 1891–1898 CrossRef CAS.
- K. Posmyk, N. Zawadzka, M. Dyksik, A. Surrente, D. K. Maude, T. Kazimierczuk, A. Babiński, M. R. Molas, W. Paritmongkol, M. Mączka, W. A. Tisdale, P. Płochocka and M. Baranowski, J. Phys. Chem. Lett., 2022, 13, 4463–4469 CrossRef CAS PubMed.
- F. Thouin, A. R. Srimath Kandada, D. A. Valverde-Chávez, D. Cortecchia, I. Bargigia, A. Petrozza, X. Yang, E. R. Bittner and C. Silva, Chem. Mater., 2019, 31, 7085–7091 CrossRef CAS.
- G. Folpini, D. Cortecchia, A. Petrozza and A. R. Srimath Kandada, J. Mater. Chem. C, 2020, 8, 10889–10896 RSC.
- B. A. Magill, K. Wang, S. McGill, C. J. Stanton, S. Priya and G. A. Khodaparast, AIP Adv., 2022, 12, 015114 CrossRef CAS.
- A. R. Srimath Kandada and C. Silva, J. Phys. Chem. Lett., 2020, 11, 3173–3184 CrossRef CAS PubMed.
- D. B. Straus, S. Hurtado Parra, N. Iotov, J. Gebhardt, A. M. Rappe, J. E. Subotnik, J. M. Kikkawa and C. R. Kagan, J. Am. Chem. Soc., 2016, 138, 13798–13801 CrossRef CAS PubMed.
- D. B. Straus and C. R. Kagan, J. Phys. Chem. Lett., 2018, 9, 1434–1447 CrossRef CAS PubMed.
- M. P. Arciniegas and L. Manna, ACS Energy Lett., 2022, 7, 2944–2953 CrossRef CAS.
- D. B. Straus and C. R. Kagan, Ann. Rev. Phys. Chem., 2022, 73, 403–428 CrossRef PubMed.
- L. Gan, J. Li, Z. Fang, H. He and Z. Ye, J. Phys. Chem. Lett., 2017, 8, 5177–5183 CrossRef CAS PubMed.
- D. B. Straus, N. Iotov, M. R. Gau, Q. Zhao, P. J. Carroll and C. R. Kagan, J. Phys. Chem. Lett., 2019, 10, 1198–1205 CrossRef CAS PubMed.
- B. Dhanabalan, A. Castelli, M. Palei, D. Spirito, L. Manna, R. Krahne and M. Arciniegas, Nanoscale, 2019, 11, 8334–8342 RSC.
- J. V. Passarelli, D. J. Fairfield, N. A. Sather, M. P. Hendricks, H. Sai, C. L. Stern and S. I. Stupp, J. Am. Chem. Soc., 2018, 140, 7313–7323 CrossRef CAS PubMed.
- B. Dhanabalan, G. Biffi, A. Moliterni, V. Olieric, C. Giannini, G. Saleh, L. Ponet, M. Prato, M. Imran, L. Manna, R. Krahne, S. Artyukhin and M. P. Arciniegas, Adv. Mater., 2021, 33, 2008004 CrossRef CAS PubMed.
- M.-L. Lin, B. Dhanabalan, G. Biffi, Y.-C. Leng, S. Kutkan, M. P. Arciniegas, P.-H. Tan and R. Krahne, Small, 2022, 18, 2106759 CrossRef CAS PubMed.
- M. L. Aubrey, A. Saldivar Valdes, M. R. Filip, B. A. Connor, K. P. Lindquist, J. B. Neaton and H. I. Karunadasa, Nature, 2021, 597, 355–359 CrossRef CAS PubMed.
- F. Thouin, D. A. Valverde-Chávez, C. Quarti, D. Cortecchia, I. Bargigia, D. Beljonne, A. Petrozza, C. Silva and A. R. Srimath Kandada, Nat. Mater., 2019, 18, 349–356 CrossRef CAS PubMed.
- D. B. Straus, S. Hurtado Parra, N. Iotov, Q. Zhao, M. R. Gau, P. J. Carroll, J. M. Kikkawa and C. R. Kagan, ACS Nano, 2020, 14, 3621–3629 CrossRef CAS PubMed.
- M. D. Smith, A. Jaffe, E. R. Dohner, A. M. Lindenberg and H. I. Karunadasa, Chem. Sci., 2017, 8, 4497–4504 RSC.
- L. Mao, P. Guo, M. Kepenekian, I. Hadar, C. Katan, J. Even, R. D. Schaller, C. C. Stoumpos and M. G. Kanatzidis, J. Am. Chem. Soc., 2018, 140, 13078–13088 CrossRef CAS PubMed.
- L. Mao, Y. Wu, C. C. Stoumpos, M. R. Wasielewski and M. G. Kanatzidis, J. Am. Chem. Soc., 2017, 139, 5210–5215 CrossRef CAS PubMed.
- J. Yin, R. Naphade, L. Gutiérrez Arzaluz, J.-L. Brédas, O. M. Bakr and O. F. Mohammed, ACS Energy Lett., 2020, 5, 2149–2155 CrossRef CAS.
- P. C. Sercel, J. L. Lyons, D. Wickramaratne, R. Vaxenburg, N. Bernstein and A. L. Efros, Nano Lett., 2019, 19, 4068–4077 CrossRef CAS PubMed.
- H.-H. Fang, J. Yang, S. Adjokatse, E. Tekelenburg, M. E. Kamminga, H. Duim, J. Ye, G. R. Blake, J. Even and M. A. Loi, Adv. Funct. Mater., 2020, 30, 1907979 CrossRef CAS.
- X. Gong, O. Voznyy, A. Jain, W. Liu, R. Sabatini, Z. Piontkowski, G. Walters, G. Bappi, S. Nokhrin, O. Bushuyev, M. Yuan, R. Comin, D. McCamant, S. O. Kelley and E. H. Sargent, Nat. Mater., 2018, 17, 550–556 CrossRef CAS PubMed.
- A. Lemmerer and D. G. Billing, Dalton Trans., 2012, 41, 1146–1157 RSC.
- A. D. Wright, C. Verdi, R. L. Milot, G. E. Eperon, M. A. Pérez-Osorio, H. J. Snaith, F. Giustino, M. B. Johnston and L. M. Herz, Nat. Commun., 2016, 7, 1–9 Search PubMed.
- J. Wang, J. Zhu, Y. Jiang, M. Li, K. Yu and G. P. Wang, Nanophotonics, 2021, 10, 4009–4017 CrossRef CAS.
- M. M. Altaiary, E. Liu, C.-T. Liang, F.-C. Hsiao, J. van Baren, T. Taniguchi, K. Watanabe, N. M. Gabor, Y.-C. Chang and C. H. Lui, Nano Lett., 2022, 22, 1829–1835 CrossRef CAS PubMed.
- Y. Jiang, M. Cui, S. Li, C. Sun, Y. Huang, J. Wei, L. Zhang, M. Lv, C. Qin, Y. Liu and M. Yuan, Nat. Commun., 2021, 12, 336 CrossRef CAS PubMed.
- M. Gerhard, B. Louis, R. Camacho, A. Merdasa, J. Li, A. Kiligaridis, A. Dobrovolsky, J. Hofkens and I. G. Scheblykin, Nat. Commun., 2019, 10, 1698 CrossRef PubMed.
- P. Tamarat, L. Hou, J.-B. Trebbia, A. Swarnkar, L. Biadala, Y. Louyer, M. I. Bodnarchuk, M. V. Kovalenko, J. Even and B. Lounis, Nat. Commun., 2020, 11, 6001 CrossRef CAS PubMed.
- X. Wang, W. Meng, W. Liao, J. Wang, R.-G. Xiong and Y. Yan, J. Phys. Chem. Lett., 2019, 10, 501–506 CrossRef CAS PubMed.
- P. Tamarat, E. Prin, Y. Berezovska, A. Moskalenko, T. P. T. Nguyen, C. Xia, L. Hou, J.-B. Trebbia, M. Zacharias, L. Pedesseau, C. Katan, M. I. Bodnarchuk, M. V. Kovalenko, J. Even and B. Lounis, Nat. Commun., 2023, 14, 229 CrossRef CAS PubMed.
- M. Gramlich, C. Lampe, J. Drewniok and A. S. Urban, J. Phys. Chem. Lett., 2021, 12, 11371–11377 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr02172f |
| ‡ Present address: QustomDot. Technologiepark 66, 9052 Ghent – Zwijnaarde, Belgium. |
| This journal is © The Royal Society of Chemistry 2023 |
