Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploring the intra-4f and the bright white light upconversion emissions of Gd2O3:Yb3+,Er3+-based materials for thermometry†
Talita J. S.
Ramos
 ab,
Ricardo L.
Longo
ab,
Ricardo L.
Longo
 *a,
Carlos D. S.
Brites
*a,
Carlos D. S.
Brites
 b,
Rute A. S.
Ferreira
b,
Rute A. S.
Ferreira
 b,
Oscar L.
Malta
a and
Luís D.
Carlos
b,
Oscar L.
Malta
a and
Luís D.
Carlos
 *b
*b
aDepartamento de Química Fundamental, Universidade Federal de Pernambuco, Cidade Universitária, 50740-560 Recife, PE, Brazil. E-mail: ricardo.longo@ufpe.br
bPhantom-g, CICECO – Aveiro Institute of Materials, Department of Physics, University of Aveiro, 3810-193 Aveiro, Portugal. E-mail: lcarlos@ua.pt
First published on 30th May 2023
Abstract
Upconversion broadband white light emission driven by low-power near-infrared (NIR) lasers has been reported for many materials, but the mechanisms and effects related to this phenomenon remain unclear. Herein, we investigate the origin of laser-induced continuous white light emission in synthesized nanoparticles (Gd0.89Yb0.10Er0.01)2O3 and a mechanical mixture of commercial oxides with the same composition 89% Gd2O3, 10% Yb2O3, and 1% Er2O3. We report their photophysical features with respect to sample compactness, laser irradiation (wavelength, power density, excitation cycles), pressure, temperature, and temporal dynamics. Despite the sensitizer (Yb3+) and activator (Er3+) being in different particles for the mechanical mixture, efficient discrete and continuous upconversion emissions were observed. Furthermore, the synthesized nanoparticles were developed as primary luminescent thermometers (upon excitation at NIR) in the 299–363 K range, using the Er3+ upconversion 2H11/2 → 4I15/2/4S3/2 → 4I15/2 intensity ratio. They were also operating as secondary ones in the 1949–3086 K, based on the blackbody distribution of the observed white light emission. Our findings provide important insights into the mechanisms and effects related to the transition from discrete to continuous upconversion emissions with potential applications in remote temperature sensing.
Introduction
Over the past decades, an unusual type of anti-Stokes (or upconversion, UC) broadband white light emission under near-infrared (NIR) laser excitation has been reported for organometallic complexes,1 organic–inorganic hybrid nanostructures,2 carbon nanotubes,3 graphene,4 and oxides, with5,6 or without7,8 activator ions (trivalent lanthanides, Ln3+, and transition metals). A common and distinguishing feature of this unusual type of UC is the continuous emission from the visible to the IR spectral regions, in contrast to the usual discrete UC emissions observed particularly in Ln3+-based materials.9 Although the continuous white light emission was reported in vacuum in many of these examples, there are several works showing results at ambient pressure.8,10–18 This emission has attracted much attention due to intriguing and exciting applications in luminescence thermometry,19 pressure detection,19,20 high-performance and low-energy solid-state lighting,1,21 increased efficiency of solar panels,22 and optoelectronic devices.4,7 It depends on several factors related either to the materials (e.g., chemical composition, dopant/co-dopant ion concentration, particle size, phonon energy, absorption coefficient, thermal conductivity, bandgap) or to the excitation process (e.g., energy, power density, on/off cycles, exposure time, pressure).4,18,23–26 However, as far as we know, there are no systematic studies describing the impact of these effects on the anti-Stokes continuous white light emission, as well as on the transition from discrete to continuous UC emissions. Moreover, the origin of this continuous emission is still under debate and different processes have been invoked to describe it such as photon avalanche,27 blackbody radiation/incandescence,12,28 thermal avalanche,10 structural defects,11,29 or charge transfer.30,31Here, we investigated the transition of discrete (Er3+ transitions in the red and green spectral regions) to continuous white light UC emissions to gain insights into their nature in a Yb3+/Er3+ co-doped nanopowder, (Gd0.89Yb0.10Er0.01)2O3 (1), and a simple mechanical mixture of Gd2O3, Yb2O3, and Er2O3 oxides (2). For that, the impact on both white light emissions of the compactness of the materials, excitation power density, wavelength and exposure time (808 or 980 nm), pressure, temperature, on–off cycles of irradiation, humidity, as well as their risetime and halftime decays, was analysed in detail. Gd2O3 was selected as a host material because it is the only example reported thus far where both discrete and continuous UC white light emission under NIR laser excitation have been discussed.12,32 Moreover, oxide materials offer advantages such as low thermal conductivity and physical and chemical resistance to high temperatures (>1500 K) being also readily available for use as a “mixed powder sample”. Sample 2 mimics the composition of 1 but with the Yb3+ and Er3+ ions separated in individual particles permitting, thus, understanding the spatial dependence of both UC emissions, particularly the range-dependent nonradiative energy transfer processes. We reported a colour modulation of the discrete UC emission with an increase in the excitation source intensity and under reduced pressure. To comprehend and quantify this colour modulation, we developed a luminescence primary thermometer based on the 2H11/2 → 4I15/2 and 4S3/2 → 4I15/2Er3+ transitions33,34 for 1. For the first time, we established a relationship between the local temperature and the excitation power density. Additionally, we developed a thermometer based on the blackbody radiation distribution of the observed white light emission for high-temperature sensing. We anticipate that the results reported here will provide a deeper understanding of the transition from discrete to continuous white light UC emissions, as well as the nature and underlying nanoscale features of the latter.
Experimental
Materials
Er(NO3)3·5H2O (99.9%), Yb(NO3)3·5H2O (99.9%), Gd(NO3)3 6H2O (99.9%) were purchased from Sigma-Aldrich and NH2CH2COOH (glycine) (>99%) from Alfa Aesar and used as received. A modified co-precipitation procedure reported by Bilir et al.32 was used to prepare the (Gd0.89Yb0.10Er0.01)2O3 nanoparticles, denoted as 1. The starting reagents were dissolved in 1 mL of deionized water under vigorous stirring for 15 min. The solution was heated at 500 °C for 1 hour at 10 °C·min−1. After cooling to room temperature, the precursor was calcined at 1000 °C for 24 hours with heating and cooling rates at 1.6 °C·min−1. The particles were obtained as a white powder and pellets were prepared with 150 mg compressed at 8 × 106 kg for 1 min. A simple mechanical mixture of commercial oxides purchased from Sigma-Aldrich (>99.9%) Gd2O3 (89%), Yb2O3 (10%), and Er2O3 (1%), denoted as 2, was also prepared.Methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ range 5°–89° with a 0.01° step size and 40 s acquisition time per step, in the reflection scanning mode. The samples were placed inside a thermal chamber (Anton Paar HTK 16N) with a Platinum heater. The data were treated considering the instrumental broadening factor measured with a LaB6 (NIST 660a) standard. The reference data were taken from the International Centre for Diffraction Data (ICDD) database. The structural features like lattice parameters have been investigated using Rietveld refinement with High Score Plus software. The crystallite size was estimated by applying the Scherrer equation to the main peak of the diffractograms. The observed full width at half maximum (FWHM) of the peak was corrected from the instrumental and strain broadening factors using the NIST 660a standard. A shape factor characteristic of spherical particles was used (0.94), although the observed agglomerated nanostructures have irregular shapes, as shown by scanning transmission electron microscopy (STEM) images acquired on a Jeol JEM-2200FS (200 kV). Energy-dispersive X-ray spectroscopy (EDS, Oxford) was performed in a Hitachi H-9000 (300 kV) microscope.
θ range 5°–89° with a 0.01° step size and 40 s acquisition time per step, in the reflection scanning mode. The samples were placed inside a thermal chamber (Anton Paar HTK 16N) with a Platinum heater. The data were treated considering the instrumental broadening factor measured with a LaB6 (NIST 660a) standard. The reference data were taken from the International Centre for Diffraction Data (ICDD) database. The structural features like lattice parameters have been investigated using Rietveld refinement with High Score Plus software. The crystallite size was estimated by applying the Scherrer equation to the main peak of the diffractograms. The observed full width at half maximum (FWHM) of the peak was corrected from the instrumental and strain broadening factors using the NIST 660a standard. A shape factor characteristic of spherical particles was used (0.94), although the observed agglomerated nanostructures have irregular shapes, as shown by scanning transmission electron microscopy (STEM) images acquired on a Jeol JEM-2200FS (200 kV). Energy-dispersive X-ray spectroscopy (EDS, Oxford) was performed in a Hitachi H-9000 (300 kV) microscope.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500–19
500–19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 spectral region was fitted using a multiparametric Gaussian function by peak analyser routine of the OriginLab© software. Good fits to the experimental data (R2 > 0.99) were obtained with six and four Gaussian functions describing the 2H11/2 → 4I15/2 and 4S3/2 → 4I15/2 and transitions, respectively. The intensities of the transitions were estimated by the sum of the fitted areas of the respective Gaussian functions. For the calculus of Δ, the 2H11/2 → 4I15/2 and 4S3/2 → 4I15/2 transitions were integrated between 510–542 nm (IH) and 543–573 nm (IS), respectively.
500 cm−1 spectral region was fitted using a multiparametric Gaussian function by peak analyser routine of the OriginLab© software. Good fits to the experimental data (R2 > 0.99) were obtained with six and four Gaussian functions describing the 2H11/2 → 4I15/2 and 4S3/2 → 4I15/2 and transitions, respectively. The intensities of the transitions were estimated by the sum of the fitted areas of the respective Gaussian functions. For the calculus of Δ, the 2H11/2 → 4I15/2 and 4S3/2 → 4I15/2 transitions were integrated between 510–542 nm (IH) and 543–573 nm (IS), respectively.
Results and discussion
Synthesis and morphological characterization
The XRD patterns of 1 and 2 shown in Fig. 1 reveal the presence of the Gd2O3 and Yb2O3 cubic phases.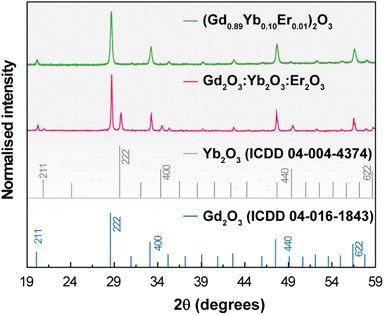 | ||
| Fig. 1 X-ray diffraction patterns of 1 (green line) and 2 (red line) (powders). The reflections of cubic Gd2O3 and Yb2O3 are also depicted. | ||
No diffraction peaks associated with the Er2O3 phase could be discerned in the pattern of 2 because the concentration lies below the experimental detection limit of the technique. Under different conditions of pressure and temperature (ambient conditions, 1273 K, and 10−5 bar), the patterns remain nearly identical indicating that no phase transitions occur in the samples in the tested temperature and pressure cycles (Fig. S1† for the illustrative example of 1). The average crystallite size was estimated as 63 ± 3 nm and 157 ± 3 nm for 1 and 2, respectively, applying the Scherrer equation to the main diffraction peak. STEM images show that both samples exhibit similar agglomerated nanostructures with irregular shapes and EDS reveals the majority presence of Gd atoms and concentration values of Er and Yb one order of magnitude smaller (Fig. S2†), in accord with the proposed stoichiometry of 1 and the relative proportion used in 2. The elemental distributions of the two samples show, despite aggregation, microstructural uniformity, supporting chemical homogeneity (Fig. S2(e)† for 2). This is also supported by identical emission spectra acquired at different spots and under different cycles of laser irradiation in both samples (see below).
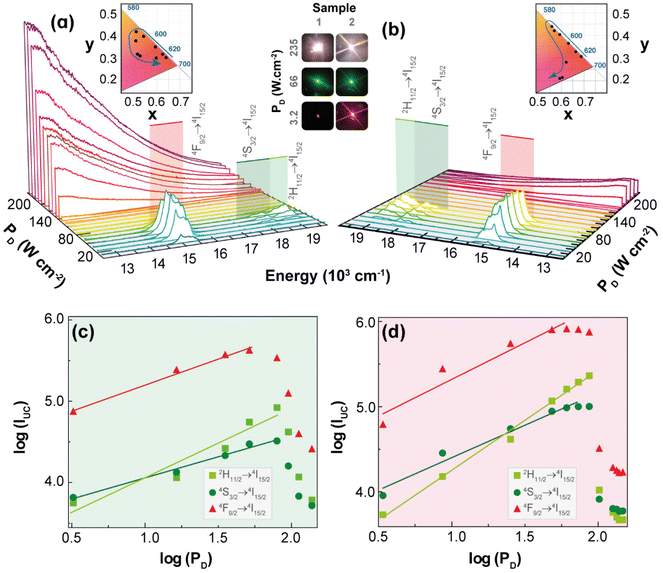
Intra-4f upconversion emission and primary thermometry
Fig. 2 shows the UC emission spectra of 1 and 2 (980 nm excitation) as a function of PD. Given that the absorption cross-section of Yb3+ (ca. 10−20 cm2) is approximately one order of magnitude larger than that of Er3+ (ca. 10−21 cm2) under NIR excitation,37,38 the energy transfer upconversion (ETU) sensitization of Er3+ ions by Yb3+ is the likely mechanism for the discrete UC emissions. Accordingly, the well-known relationship between the integrated UC emission, IUC, and PD: IUC ∝ PnD, where the exponent n can be interpreted as the number of photons involved in the upconversion process,39,40 should be observed. However, the values of n obtained as the slope of the linear fit of the plot of the logarithm of the integrated intensities of the 2H11/2 → 4I15/2 (IH, 510–542 nm), 4S3/2 → 4I15/2 (IS, 543–573 nm), and 4F9/2 → 4I15/2 (IF, 626–714 nm) Er3+ transitions versus the logarithm of PD are smaller than 2.0 and most are near to 1.0 (Table S1†). This unusual behaviour is most likely due to the heating of the excitation region as indicated by the increase in the ratio IH/IS (the so-called thermometric parameter Δ) with PD (see discussion in the next section). Because the transition rates, namely the nonradiative ones and the back-ET rates, are temperature dependent, the increase of PD affects unevenly these rates and the populations of thermally coupled levels, so the interpretation of the exponent n as being the number of photons involved in the UC process is no longer valid. This reasoning is more likely than invoking the competition of different processes (e.g., cross-relaxation between excited states, avalanche process, energy transfer between three ions, and energy transfer to other impurity ions) or possible oscillations of the excitation source.39The differences in the slopes obtained for powders of 1 and 2 are probably due to the dynamics of ETU pathways involving ions within the same particle, for 1, contrasted to ions in different particles, for 2. Because the ETU pathways become less efficient as the distances between ions increase, it is expected that ETU in 1 would be more efficient than in 2, thus causing a lesser dependence of the integrated intensity on PD. Notice that for 1 the slopes n, of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IUCvs. log
IUCvs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PD plots, in the pellets are larger than in powder (Table S1†), which suggests that the higher thermal conductivities of pellets hinder the temperature increase, so the transition rates become almost constant with PD and the slopes n tend to be the number of photons involved in the UC process. On the other hand, when the 1 pellet is placed at low-pressure atmospheres, the thermal conductivity decreases, and the temperature drastically increases with PD, so the slopes n are no longer related to the number of photons, and they become smaller than those at ambient pressure (Table S1†).
PD plots, in the pellets are larger than in powder (Table S1†), which suggests that the higher thermal conductivities of pellets hinder the temperature increase, so the transition rates become almost constant with PD and the slopes n tend to be the number of photons involved in the UC process. On the other hand, when the 1 pellet is placed at low-pressure atmospheres, the thermal conductivity decreases, and the temperature drastically increases with PD, so the slopes n are no longer related to the number of photons, and they become smaller than those at ambient pressure (Table S1†).
The temperature increase within the excitation region with PD,32 can also explain the decrease of the integrated UC emission intensities above a given value of PD (see Fig. 2(c and d)), the so-called absorption saturation regime. The threshold of PD for which the saturation regime of the integrated intensities IH, IS, and IF is observed in 2 (140, 112, and 65.0 W·cm−2, respectively) is higher compared with those of 1 (79.1, 79.1, and 51.4 W·cm−2, respectively). Indeed, this is consistent with the ETU pathways in 2 (sensitizer-activator ions in different particles) being less efficient than in 1 (ions within the same particle), so the former would require a higher PD to reach the saturation regime. The energy transfer rates between Yb3+–Er3+ pairs located in the same particle can be calculated by quantitative models;41,42 however, for ions located in different particles are still a challenging problem, so the UC emissions results reported here for 2 (mechanical mixture) are quite relevant for developing quantitative models.
The insets in Fig. 2(a and b) display the 1931 CIE chromaticity diagram of the UC emission for increasing PD, where the x,y coordinates were calculated based on the emission spectra. The modulation of the UC emission colour by the excitation intensity is an intriguing feature because of its simplicity compared to other strategies of modulation (e.g., co-doping).43–46 Previous example of colour modulation by PD has been achieved in the UC emissions of Ho3+, Tm3+, and Yb3+ tri-doped Gd2(MoO4)3 phosphors,47 which was ascribed to the different dependence of the blue, green, and red UC emissions upon PD. However, explanations and details of these distinct dependencies were not provided.
UC emission colour modulation by PD was also observed in upconverting Y2O3:Yb3+/Er3+ microrods coated by silver nanoparticles (Ag-NPs).48 In this case, the Ag-NPs absorb energy from the excitation beam causing a local increase in temperature that leads to changes in UC emission from red to green upon increasing the excitation intensity. Employing luminescence thermometry, it was shown that local temperature varied from 418 to 1458 K upon increasing PD, which was responsible for the colour modulation.48 Based on this example, and the increase in the thermometric parameter Δ with PD, the colour modulation of the UC emissions observed for 1 and 2 was ascribed to the increase of the temperature within the excitation region, which affected mainly the nonradiative transition rates within each Ln3+ ion and between two ions.
A possible explanation could be the increase of the phonon-assisted ET transfer rate Yb3+ → Er3+ with the increase in temperature, which rises the population of the green emitting levels (2H11/2 and 4S3/2), thus modulating the colour change from red to green. However, a detailed and definite explanation for this colour change requires a model based on the rate equations that employs temperature dependent transition rates, which is still unavailable. To obtain information regarding the dependence of the local temperature increase with PD, it is relevant to determine reliable temperature values that can be achieved with Δ involving the thermally-coupled 2H11/2 and 4S3/2 levels, whose populations are described by the Boltzmann distribution.49,50
The thermometric performance of 1 as a primary thermometer is then based on these two thermally coupled levels with temperature, T, being determined as:33
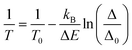 | (1) |
The thermometric parameter increases with the laser power density (Fig. S3(b)†), indicating that the laser-induced local temperature increase causes a rise in the population of the thermally governed 2H11/2 level, at the expense of the 4S3/2 lower energy level, according to the Boltzmann distribution. These levels are thermally coupled with an energy difference of 795 ± 25 cm−1, which is in very good agreement with the values reported in the literature for Gd2O3:Yb3+,Er3+ samples (700 cm−1 ≤ ΔE ≤ 856 cm−1).12,43,51–53 The value of Δ0 is determined by extrapolating the value of Δ to the low-power limit at T0.52 This consists of recording emission spectra at the temperature T0 upon different excitation laser power densities. In the limit of null power density (usually extrapolated using a linear function), the heating due to the irradiation is zero and so the temperature on the luminescent material is T0 (Fig. S3(b)†). Fig. 3(a) presents the temperature dependence in the 297–364 K range of the emission spectra of 1. The temperature dependence of the integrated areas of the IH and IS transitions and the corresponding thermometric parameter, Δ, are presented in Fig. 3(b and c). The experimental values of the reference temperatures were obtained directly through a thermocouple in contact with the sample. Replacing the values of T0, ΔE, Δ, and Δ0 in eqn (1), the predicted temperature, the solid line in c, is in excellent agreement with the reference, indicating that 1 can work as a luminescent primary thermometer (Fig. 3(d)).
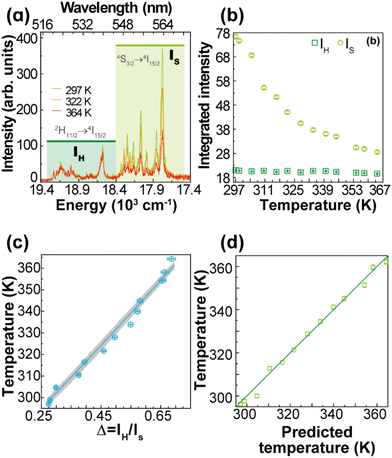 | ||
| Fig. 3 (a) Upconversion emission spectra of 1 (pellet) under 980 nm excitation at selected temperatures (PD = 16.4 W·cm−2). Temperature dependence of (b) IH and IS integrated emission intensities and (c) Δ = IH/IS. The temperature uncertainty (shadowed in grey) is given by eqn (S6),† whereas the line represents the predicted temperature using eqn (1). (d) The reference temperature (y) versus the predicted temperature (eqn (1), x). The line is a guide for the eyes corresponding to y = x. | ||
The performance of the thermometer is estimated by the relative thermal sensitivity, Sr, (eqn (S4) and (S5)†) and temperature uncertainty, δT, (eqn (S6)†), Fig. 4. These parameters (figures-of-merit) allow the comparison between thermometers of different natures and applied in different chemical environments. The calculated Sr and δT are 1.3–0.9% K−1 and 0.03–0.08 K, respectively, for the 299–363 K range. As it can be verified in Fig. S4 and Table S2,† the maximum value of Sr reported in this work is higher than most of the other reports on Gd2O3:Yb3+,Er3+ discussed in the literature, especially in the physiological range. The calculated temperature uncertainty for 1 (Fig. 4(b)) corresponds to the lowest values reported up to now for Gd2O3:Yb3+,Er3+ samples (Table S2†). The temperatures measured by the luminescent thermometer present a linear dependence with the excitation power density, T = αPD + β, with α = 4.1 ± 0.2 K (W·cm−2)−1 and β = 299 ± 10 K (Fig. 4(c)). This is consistent, for instance, with the linear behaviour of the temperature with PD inferred from the increase of the thermometric parameter for NaYF4:20%Yb,2%Er nanocrystals (NCs).54 For the unmodified NaYF4:20%Yb,2%Er NCs, and modified NCs with thioglycollic acid, the slopes are 0.116 and 0.175 K (W·cm−2)−1, respectively,54 which are much smaller than that found for 1, most likely due to the differences in the thermal conductivities and absorption coefficients.
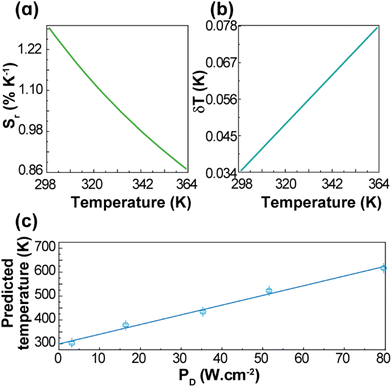 | ||
| Fig. 4 Temperature dependence of (a) Sr and (b) δT of 1 (pellet). (c) Dependence of the predicted temperatures on PD for 1 (pellet). The line is the best linear fit to the data (r2 > 0.985). | ||
Bright white light upconversion emission
Although several works reported the white light emission, characterized as discrete spectra, by Gd2O3:Yb3+/Er3+,55–57 only two works12,32 discussed the white light UC emission as a continuous broadband under NIR excitation. Based on the results of the UC emission colour modulation and the temperature increase measured by the luminescent thermometer, it is proposed that the absorbed excitation radiation is converted into heat that causes a significant temperature increase within the excitation region that leads to thermal or blackbody radiation emission.The excitation intensity has to be high enough to balance the heat dissipation, so the internal energy can rise, causing the temperature to increase. When the heat cannot be dissipated fast enough, especially at the interface of the sample with the atmosphere, the temperature within the excitation region continues to rise until it reaches the Draper point (ca. 800 K), where the thermal emission of typical solids becomes visible (reddish) to the human eye. As PD increases, so does the local temperature, which causes a significant intensification of the UC emission as well as an increase in the fraction of emitted light in the visible region. This process culminates into a highly bright white light emission, with a continuous spectrum, under excitation at the NIR region (photographs in the insets of Fig. 2(a)). This description relies on several properties of the materials such as the absorption coefficient at the excitation wavelength interval, energy transfer, and thermal conductivity. Thus, because of the higher concentration of Yb3+(10%) and their larger absorption cross section at 980 nm, compared to the lower concentration of Er3+ (1%) and smaller cross section at 808 nm, the white light UC emission under 980 nm should be much more pronounced according to the description just proposed. Indeed, the observed emissions at these excitation wavelengths corroborate this assertion. For comparison, to obtain similar white light UC emission, PD needs to be larger than 310 W·cm−2 at 808 nm compared to 240 W·cm−2 at 980 nm, Fig. S5.†
The dependence of the integrated intensity of the white light emission, IWL, with PD (980 nm) is also investigated via log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (IWL) versus log
(IWL) versus log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (PD). The slopes of these plots are usually larger than 4, so they should also have a different interpretation from that of discrete UC emissions. For 1 and 2, these slopes are within 4 to 7 (Fig. 5(a) and Table S3†), which agree with the behaviour of rare-earth oxides.5,7,12,24,27
(PD). The slopes of these plots are usually larger than 4, so they should also have a different interpretation from that of discrete UC emissions. For 1 and 2, these slopes are within 4 to 7 (Fig. 5(a) and Table S3†), which agree with the behaviour of rare-earth oxides.5,7,12,24,27
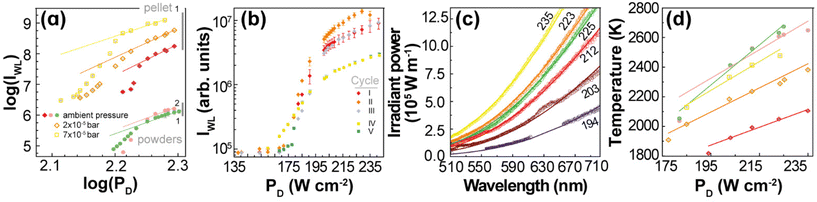 | ||
| Fig. 5 (a) Log–log plot of the PD dependence of IWL for 1 and 2 in powder and at ambient pressure (green and pink dots, respectively), and for 1 in pellet at ambient pressure (red), 2 × 10–5 bar (orange), and 7 × 10–5 bar (yellow). The lines are the best linear fits to the saturation regime data (Table S3†). (b) PD dependence of IWL for 1 (pellet) recorded in different cycles of irradiation before (I, II, and III) and after (IV and V) exposing the sample to a water saturated atmosphere (see the Experimental section for details). (c) Emission spectra of 1 (pellet at ambient pressure) acquired between 194 and 235 W· cm−2. The lines represent the fits to the blackbody radiation distribution with a proportionality constant of 4.2 × 10−21 (Table S4†). (d) PD dependence of the fitted temperatures for 1 and 2 in powder and pellet at different pressure values (Tables S5–S8†). The colour code is the one used in (a). The lines are the best linear fits to the data (Table S9†). | ||
The continuous white light emission was analysed for repeated cycles of laser irradiation with both 1 (Fig. 5(b)) and 2 (Fig. S6†) showing remarkable stability under repeated excitation cycles. Notice that the excitation cycles were performed at different spots on the sample and their similarities indicate the homogeneity of the materials for white light UC emission. The effect of the humidity was also analysed exposing the samples to a water-saturated atmosphere (details in the Experimental section). The humidity significantly decreased the intensity of the white light UC emissions (indeed, 2 showed no white light emission), which is consistent with the increase of the thermal conductivity of the samples upon exposure to air saturated with water as well as the presence of high energy O–H oscillators that affect the nonradiative transitions. The effects of the thermal conductivity can be ascertained by the compactness of the sample,28 which can explain the lower PD threshold (to observe white light emission) for 1 powder (140 W·cm−2, Fig. 2(a)) compared to 1 pellet (200 W·cm−2, Fig. S7†).
As the thermal conductivity of the sample decreases when it becomes more porous28 (e.g., from pellet to nanopowder), the volume able to sustain high temperatures enlarges, so the number of emitters increases. As a result, the white light emission becomes brighter for the powder compared to the pellet or the powder emits the same white light intensity as the pellet, but at a lower excitation power density. Indeed, for Gd2O3, the effective thermal conductivity decreases ca. 3-fold when the effective porosity increases from 0.4 to 0.8 for consolidated and unconsolidated nanopowders of similar materials28 (see ESI†). Another relevant aspect is the large difference in the thermal conductivity of the (solid) sample and the atmosphere surrounding it. In fact, due to this difference, the UC thermal emission is likely a surface phenomenon, constrained to the excitation region and a few particle layers determined by the effective thermal conductivity of the solid. Hence, the thermal conductivity of the atmosphere plays a determining role in establishing the steady-state temperature that can be achieved during the white light UC emission. It is expected that the efficiency of this process depends on the nature of the atmosphere and its pressure, because together with the temperature they determine the thermal conductivity. This explains the significant increase of bright white emission at low pressures.11,12,25,58–60 Indeed, Fig. 5(a) shows that the integrated intensity of the UC emission increases ca. 100 times when the pressure is reduced from 1 bar to 2 × 10−2 mbar, which can be explained simply by the decrease of the thermal conductivity of the environment and there is no need to invoke structural changes with the pressure as previously proposed.59,60 It is noteworthy that the thermal conductivity of gases at very low pressures (for Knudsen number larger than 1) becomes dependent on the pressure. For white light UC processes, the thermal conductivity of air can decrease ca. 50-fold at pressures of 2 × 10−5 bar compared to that at atmospheric pressure (see ESI†), which could explain the significant enhancement of the integrated emission.
The effects of the pressure, hence the thermal conductivity, are significant on the power density of the excitation source, for instance, PD decreases from ca. 190 to 165 to 150 W·cm−2 upon vacuum (1 bar to 7 × 10−5 bar to 2 × 10−5 bar) to produce the same bright white light UC emission (Fig. S7–S9†).
The broadband emission extends from the visible to the infrared spectral range and is well described by the Planck distribution of blackbody radiation,22,24,28
| Lbb(λ,T) = Aλ−5(eB(T)/λ − 1)−1 | (2) |
The temperatures of 1 (Fig. 5(c) and Fig. S10(b)†) and 2 (Fig. S10(a)†) at different PD values were estimated by fitting the emission spectrum to eqn (2). However, the emission intensity was measured, Iobs, as photon counting per second onto an unspecified area of the detector, so Lbb ∝ Iobs. Because the proportionality constant of this relationship is unknown, the quantities A and B(T) in eqn (2) were initially treated as adjustable parameters for each PD. Then, an average of the fitted values of A was employed in a final fitting, keeping A constant (at 4.2 × 10−21), and considering B(T) the only adjustable parameter from which the temperature was determined. Notice that once the proportionality constant in Lbb ∝ Iobs is known, the thermometric parameter Δ = Iobs becomes a primary thermometer. For the emission spectra of 1 (Fig. 5(c)), the estimated temperatures increased systematically from 1818 to 2106 K as PD raised from 194 to 235 W·cm−2 (Fig. 5(d) and Table S4†). Indeed, this temperature dependence on PD is approximately linear (r2 = 0.940) with a slope of 6 ± 1 K· (W·cm−2)−1. This dependence was also observed for 1 at different conditions (vacuum and powder) as well as for 2 (powder at ambient pressure), however, with different slopes (Fig. 5(d) and Table S9†), which is a relevant result for testing and validating new models for describing the bright white light UC emissions. In addition, this observed behaviour is consistent with the observations in the literature for (Gd0.89Yb0.10Er0.01)2O3-Au nanorods.12 The estimated temperatures at the steady-state regime of the white light emission are consistent with those available in the literature22,24 (e.g., 1910 K for Y2O3:Yb3+,Er3+)28 and are below the melting point of Yb2O3 (ca. 3000 K)10 or Gd2O3 (2698 K).61 It is noteworthy that the temperature within the excitation region has the same linear dependence with PD for both discrete Er3+ UC and the continuous white light emission regimes, although with different slopes, ca. 4 and 6 K·(W·cm−2)−1, respectively. This similar behaviour suggests that the heating process by the excitation source is the same in both regimes; however, different heat losses at these regimes are indicated by the distinct slopes. This is another relevant result for developing quantitative models to describe laser heating white light emission.
Temporal dynamics of bright white light emission
For Yb3+/Er3+-codoped materials, the UC emissions were characterized either as a discrete spectrum or as a continuous structureless spectrum described as thermal emission. In addition to these distinct spectra, these UC processes have different dependences on the integrated emission intensity with respect to the excitation power. Because of the distinct nature of these UC processes, it is expected that other behaviours would also be different, particularly, the temporal dependence of the UC emission such as risetime and decay lifetime. The dynamics and kinetics of the discrete UC emissions have already been investigated in different systems and conditions. For instance, Er3+-typical lifetime values associated with a photon avalanche process range from 51 to 231 μs,62 whereas the risetimes of the Er3+ 4S3/2 and 4F9/2 levels in Gd2O3:10%Yb3+,1%Er3+ nanocrystals are 99 and 104 μs, respectively.45 On the other hand, the lifetimes of the red (656 nm) and green (540 nm) UC emissions for NaYF4 doped with 20%Yb3+ and 2%Er3+ are 443 and 194 μs, respectively, which increase to 495 and 210 μs upon doping with 30%Gd3+.63 Other upconverting systems Gd2O3:Yb3+,Er3+ have been investigated, under laser excitation at ca. 980 nm, showing typical emission lifetimes within 10–425 μs,64,65 for the 4S3/2 → 4I15/2 transition, and from 30 to 180 μs65,66 for the 4F9/2 → 4I15/2 one. However, studies regarding the temporal behaviour of the continuous UC emissions are scarce, so it is presented here the temporal behaviour of the white light UC emission for 1 (pellet) under 980 nm excitation, Fig. 6.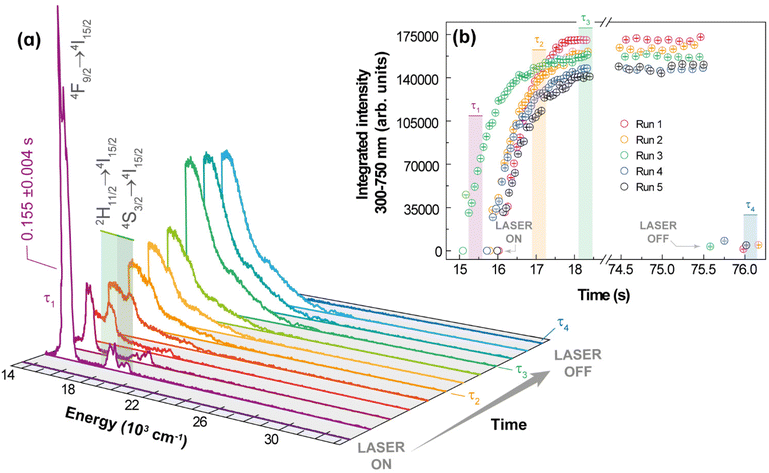 | ||
| Fig. 6 Emission spectra of 1 acquired at 102 W·cm−2 under ambient conditions. (b) Transient integrated intensity over 300 at 750 nm (see text for the meaning of τ1, τ2, τ3, and τ4). | ||
The experimental procedure used to study the dynamics of the white light generation process is described in the ESI.† However, two aspects should be emphasized: there is a shutter between the laser source and the sample, so the source is initially stabilized, and the excitation is started when the shutter is open, thus unambiguously characterizing the initial time, and the spectra were acquired during a minimum time interval (integration time) of 0.1 ms. The temporal behaviour of the white light emission can be characterized by four relevant events: (i) the period for heating the sample up to the white light emission τ1, which is defined as the time interval between the opening of the shutter and the transition between the discrete UC spectrum to the continuum spectrum; (ii) the time related to the sudden increase of the UC emission intensity, denoted as risetime of white light emission τ2, defined as the time interval between τ1 and the time at which the integrated intensity is half of the steady-state intensity; (iii) the interval for which the UC emission remains constant, denoted as the steady-state regime, τ3, which is controlled by the operator and quantifies the stability of the emission; and (iv) the decaying of the UC emission after the shutter is closed (or excitation source is switched off), characterized by a decaying emission τ4, defined as the time required for the intensity to decrease half of its steady-state value. It was noticed in the initial heating of the sample by the excitation source a short-lived (τ1 = 0.155 ± 0.004 s) green emission due to the discrete UC emission, while the risetime was longer (τ2 = 0.47 ± 0.01 s), as can be observed in Fig. 6. The average value over 5 runs of the risetime τ2 is 0.5 s, which is a hundred to a thousand times longer than the typical risetime of the discrete ETU emissions and photon avalanche UC emissions. This result corroborates the assumption of the different nature of the continuous white light UC emission (thermal or blackbody-type emission), which involves non-quantized heat transfer processes, compared to the discrete UC emissions that are based on transitions between discrete (quantized) energy levels obeying specific selections rules. The risetime of white light UC emissions represents a balance between the energy absorbed from the radiation beam and the energy losses such as heat conduction, increase of internal energy, and thermal irradiation. Thus, high excitation intensities are required to achieve bright white light emissions, which because of the several effective pathways for energy losses would require longer times than those involved in transitions (non-radiative, radiative, energy transfer) between discrete quantum states. There are reports in the literature of much longer risetimes related to the white light UC emission,11,13,67 which should be interpreted with care because the time required for stabilization and focusing of the excitation source must be removed from the determination of the risetime.
Regarding the temporal behaviour of the intensity decay of the white light emission, τ4, it was shorter than the spectral acquisition time, which yields a lower limit to τ4 of a fraction of μs, τ4 ≲ 1 μs. This can be rationalized by considering that after the excitation source is switched off, the heated spot rapidly cools down due to efficient energy loss pathways (heat conduction, release of internal energy due to temperature decrease, and thermal irradiation), which are not bounded by selection rules and transition probabilities, as are the usual decays from excited quantum levels to lower discrete states.
Conclusions
The upconversion (UC) features of a mechanical mixture of commercial oxides (89% Gd2O3, 10% Yb2O3, and 1% Er2O3), 2, in comparison to a synthesized sample with the same stoichiometry (Gd0.89Yb0.10Er0.01)2O3, 1, were investigated and reported. Both materials 1 and 2 presented colour modulation of the UC emission simply by varying the excitation source power density, which was ascribed to the effects of the laser on the population dynamics of the 2H11/2 and 4S3/2 Er3+ excited levels. We expect that this colour modulation is unaffected by small changes in environmental conditions. At ambient pressure, the thermal conductivity of air is relatively constant with respect to humidity. Different initial temperatures should be compensated by different temperature gradients, which could compensate for changes in heat losses by conduction.It is noteworthy that efficient energy transfer between ions (Yb3+ to Er3+) in different particles was observed in 2. This study provides a step forward in the understanding of the mechanism behind the white light emission characterized by continuous broadband, under NIR excitation, and describes the relationship between this emission and several factors (e.g., sample compactness, wavelength excitation, power density, temperature, pressure, humidity, and time). The results reported indicate the thermal nature of this emission that shows repeatability, homogeneity, and stability over cycles of excitation. Cooling down to cryogenic temperatures could decrease its brightness, which might be compensated by increasing the excitation power density. Furthermore, the brightness is affected by humidity that, however, does not completely suppress the continuous white light emission. Thus, depending on the application, it would only require recalibration for significant changes in humidity.
As an added benefit, it was demonstrated that 1 is a luminescent thermometer upon 980 nm CW laser excitation over a very broad range (ca. 300–3100 K). Within 299 to 363 K, 1 is a luminescent primary thermometer with a relative thermal sensitivity within 1.28–0.87% K−1 and temperature uncertainty of 0.03–0.08 K.
The emission modulation observed for 1 and 2 under pump power could provide a great opportunity to develop efficient, cheap, and environment-friendly solid-state lighting. We foresee the application of 1, and possibly the simpler material 2, as a temperature sensor with unprecedented range coupled with vacuum detection.
Author contributions
L. C., O. M., and R. L. conceived the project. T. R. synthesized the samples, performed the structural, morphological, and photoluminescence characterization and analysed the data under the supervision of L. C. and R. F. C. B. checked the thermometric performance of the materials and design the final figures. The manuscript was written through contributions of all authors. All authors have approved the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was developed within the scope of the project CICECO-Aveiro Institute of Materials, UIDB/50011/2020, UIDP/50011/2020 & LA/P/0006/2020, financed by national funds through the FCT/MEC (PIDDAC). The Brazilian Agencies FACEPE, CNPq, CAPES, and FINEP are acknowledged for providing partial financial support under grants (FACEPE: BFD 0020-1.05/22, PRONEX APQ-0675-1.06/14, APQ-1007-1.06/15), (CNPq: GD 870024/2001-9, PQ 309177/2018-9), (CAPES PDSE: 88881.623514/2021-01).References
- N. W. Rosemann, J. P. Eussner, A. Beyer, S. W. Koch, K. Volz, S. Dehnen and S. Chatterjee, Science, 2016, 352, 1301–1304 CrossRef CAS PubMed.
- H. Q. Ye, V. Bogdanov, S. Liu, S. Vajandar, T. Osipowicz, I. Hernandez and Q. H. Xiong, J. Phys. Chem. Lett., 2017, 8, 5695–5699 CrossRef CAS PubMed.
- K. Mizuno, J. Ishii, H. Kishida, Y. Hayamizu, S. Yasuda, D. N. Futaba, M. Yumura and K. Hata, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 6044–6047 CrossRef CAS PubMed.
- W. Strek, B. Cichy, L. Radosinski, P. Gluchowski, L. Marciniak, M. Lukaszewicz and D. Hreniak, Light: Sci. Appl., 2015, 4, e237 CrossRef CAS.
- A. K. Soni, S. Mathur and B. P. Singh, ChemistrySelect, 2019, 4, 3408–3415 CrossRef CAS.
- L. Li, Y. Pan, W. X. Chang, Z. S. Feng, P. Chen, C. Li, Z. Y. Zeng and X. J. Zhou, Mater. Res. Bull., 2017, 93, 144–149 CrossRef CAS.
- S. Xu, Y. S. Zhu, W. Xu, B. Dong, X. Bai, L. Xu, C. Miao and H. W. Song, Appl. Phys. Express, 2012, 5, 102701 CrossRef.
- M. Cesaria, J. Collins and B. Di Bartolo, J. Lumin., 2016, 169, 574–580 CrossRef CAS.
- F. Auzel, J. Lumin., 2020, 223, 116900 CrossRef CAS.
- J. Wang and P. A. Tanner, J. Am. Chem. Soc., 2010, 132, 947–949 CrossRef CAS PubMed.
- S. Tabanli, G. Eryurek and B. Di Bartolo, Opt. Mater., 2017, 69, 207–213 CrossRef CAS.
- M. L. Debasu, D. Ananias, I. Pastoriza-Santos, L. M. Liz-Marzán, J. Rocha and L. D. Carlos, Adv. Mater., 2013, 25, 4868–4874 CrossRef CAS PubMed.
- J. H. Wu, C. Xu, J. R. Qiu and X. F. Liu, J. Mater. Chem. C, 2018, 6, 7520–7526 RSC.
- M. Erdem and B. Sitt, Opt. Mater., 2015, 46, 260–264 CrossRef CAS.
- S. A. Khrushchalina, P. A. Ryabochkina, V. M. Kyashkin, A. S. Vanetsev, O. M. Gaitko and N. Y. Tabachkova, JETP Lett., 2016, 103, 302–308 CrossRef CAS.
- G. Bilir, G. Ozen, J. Collins, M. Cesaria and B. Di Bartolo, IEEE Photonics J., 2014, 6, 8200518 Search PubMed.
- G. Bilir, G. Ozen, M. Bettinelli, F. Piccinelli, M. Cesaria and B. Di Bartolo, IEEE Photonics J., 2014, 6, 2201211 Search PubMed.
- S. Tabanli, H. C. Yilmaz, G. Bilir, M. Erdem, G. Eryurek, B. Di Bartolo and J. Collins, ECS J. Solid State Sci. Technol., 2018, 7, R3199–R3210 CrossRef CAS.
- M. Runowski, P. Wozny, S. Lis, V. Lavin and I. R. Martin, Adv. Mater. Technol., 2020, 5, 1901091 CrossRef CAS.
- M. Runowski, P. Wozny and I. R. Martin, J. Mater. Chem. C, 2021, 9, 4643–4651 RSC.
- W. Strek, R. Tomala and M. Lukaszewicz, Opt. Mater., 2018, 78, 335–338 CrossRef CAS.
- J. Wang, T. Ming, Z. Jin, J. Wang, L. D. Sun and C. H. Yan, Nat. Commun., 2014, 5, 5669 CrossRef CAS PubMed.
- Y. J. Zheng, Q. Lu, J. L. Wang, G. H. Zhang, Y. Gao and Z. B. Liu, Opt. Laser Technol., 2014, 63, 39–44 CrossRef CAS.
- C. I. Silva, A. L. Oliveira, S. C. F. Pereira, G. F. de Sa, L. L. da Luz and S. Alves, Dalton Trans., 2019, 48, 2574–2581 RSC.
- W. Strek, R. Tomala, M. Lukaszewicz, B. Cichy, Y. Gerasymchuk, P. Gluchowski, L. Marciniak, A. Bednarkiewicz and D. Hreniak, Sci. Rep., 2017, 7, 41281 CrossRef CAS PubMed.
- F. Qin, H. Zhao, Y. Zheng, Z. Cheng, P. Wang, C. Zheng, Y. Yu, Z. Zhang and W. Cao, Opt. Lett., 2011, 36, 1806–1808 CrossRef PubMed.
- M. Stefanski, M. Lukaszewicz, D. Hreniak and W. Strek, J. Chem. Phys., 2017, 146, 104705 CrossRef CAS PubMed.
- S. Redmond, S. C. Rand, X. L. Ruan and M. Kaviany, J. Appl. Phys., 2004, 95, 4069–4077 CrossRef CAS.
- W. Xu, B. T. Chen, W. Yu, Y. S. Zhu, T. Liu, S. Xu, X. L. Min, X. Bai and H. W. Song, Dalton Trans., 2012, 41, 13525–13532 RSC.
- W. Strek, L. Marciniak, D. Hreniak and A. Lukowiak, J. Appl. Phys., 2012, 111, 024305 CrossRef.
- W. Strek, L. Marciniak, A. Bednarkiewicz, A. Lukowiak, R. Wiglusz and D. Hreniak, Opt. Express, 2011, 19, 14083–14092 CrossRef CAS PubMed.
- G. Bilir and O. Erguzel, Mater. Res. Express, 2016, 3, 106201 CrossRef.
- S. Balabhadra, M. L. Debasu, C. D. S. Brites, R. A. S. Ferreira and L. D. Carlos, J. Phys. Chem. C, 2017, 121, 13962–13968 CrossRef CAS.
- J. C. Martins, A. R. N. Bastos, R. A. S. Ferreira, X. Wang, G. Chen and L. D. Carlos, Adv. Photonics Res., 2021, 2, 2000169 CrossRef CAS.
- J. Mooney and P. Kambhampati, J. Phys. Chem. Lett., 2013, 4, 3316–3318 CrossRef CAS.
- J. Mooney and P. Kambhampati, J. Phys. Chem. Lett., 2014, 5, 3497–3497 CrossRef CAS PubMed.
- X. D. Wang, R. R. Valiev, T. Y. Ohulchanskyy, H. Agren, C. H. Yang and G. Y. Chen, Chem. Soc. Rev., 2017, 46, 4150–4167 RSC.
- S. A. Saleem, T. Sasikala, A. M. Babu, L. R. Moorthy, B. C. Jamalaiah and M. Jayasimhadri, Int. J. Appl. Glass Sci., 2011, 2, 215–221 CrossRef.
- M. Pollnau, D. R. Gamelin, S. R. Luthi, H. U. Gudel and M. P. Hehlen, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 3337–3346 CrossRef CAS.
- J. C. Wright, in Radiationless Processes in Molecules and Condensed Phases: in Molecules and Condensed Phases, ed. D. J. Diestler, F. K. Fong, K. F. Freed, R. Kopelman and J. C. Wright, Springer Berlin Heidelberg, Berlin, Heidelberg, 1976, vol. 15, pp. 239–295 Search PubMed.
- X. Qin, A. N. C. Neto, R. L. Longo, Y. M. Wu, O. L. Malta and X. G. Liu, J. Phys. Chem. Lett., 2021, 12, 1520–1541 CrossRef CAS PubMed.
- A. N. Carneiro Neto, R. T. Moura, J. A. A. Coelho, M. E. Silva-Junior, J. L. Costa, O. L. Malta and R. L. Longo, Chin. J. Lumin., 2022, 43, 1871–1891 Search PubMed.
- Y. Lei, H. Song, L. Yang, L. Yu, Z. Liu, G. Pan, X. Bai and L. Fan, J. Chem. Phys., 2005, 123, 174710–174715 CrossRef PubMed.
- A. M. Pires, O. A. Serra, S. Heer and H. U. Gudel, J. Appl. Phys., 2005, 98, 063529 CrossRef.
- K. Z. Zheng, D. S. Zhang, D. Zhao, N. Liu, F. Shi and W. P. Qin, Phys. Chem. Chem. Phys., 2010, 12, 7620–7625 RSC.
- G. Tian, Z. J. Gu, X. X. Liu, L. J. Zhou, W. Y. Yin, L. Yan, S. Jin, W. L. Ren, G. M. Xing, S. J. Li and Y. L. Zhao, J. Phys. Chem. C, 2011, 115, 23790–23796 CrossRef CAS.
- H. Y. Hao, H. Y. Lu, G. H. Ao, Y. L. Song, Y. X. Wang and X. R. Zhang, Dyes Pigm., 2018, 148, 298–305 CrossRef CAS.
- H. R. Tuxun, Z. F. Cai, M. Ji, B. B. Zhang, C. Y. Zhang, J. P. Li, X. D. Yu, Z. K. Fu, Z. L. Zhang and H. R. Zheng, Nanophotonics, 2022, 11, 979–986 CrossRef CAS.
- S. A. Wade, S. F. Collins and G. W. Baxter, J. Appl. Phys., 2003, 94, 4743 CrossRef CAS.
- C. D. S. Brites, S. Balabhadra and L. D. Carlos, Adv. Opt. Mater., 2019, 7, 1801239 CrossRef.
- S. K. Singh, K. Kumar and S. Rai, Appl. Phys. B: Lasers Opt., 2010, 100, 443–446 CrossRef CAS.
- Y. Tian, B. N. Tian, C. E. Cui, P. Huang, L. Wang and B. J. Chen, RSC Adv., 2015, 5, 14123–14128 RSC.
- W. Zheng, B. Y. Sun, Y. M. Li and R. Wang, ACS Appl. Nano Mater., 2021, 4, 3922–3931 CrossRef CAS.
- D. Li, B. A. Dong, X. Bai, Y. Wang and H. W. Song, J. Phys. Chem. C, 2010, 114, 8219–8226 CrossRef CAS.
- H. Guo, N. Dong, M. Yin, W. P. Zhang, L. R. Lou and S. D. Xia, J. Phys. Chem. B, 2004, 108, 19205–19209 CrossRef CAS.
- P. K. Yadaw, R. K. Padhi, V. Dubey, M. Rao and N. K. Swamy, Inorg. Chem. Commun., 2022, 143, 109736 CrossRef.
- T. Pang and W. H. Lu, Ceram. Int., 2017, 43, 1061–1065 CrossRef CAS.
- H. Cinkaya, G. Eryurek, G. Bilir, M. Erdem and B. Di Bartolo, J. Lumin., 2017, 181, 321–326 CrossRef CAS.
- M. Erdem, G. Eryurek and B. Di Bartolo, J. Alloys Compd., 2015, 639, 483–487 CrossRef CAS.
- G. Bilir and B. Di Bartolo, Opt. Mater., 2014, 36, 1357–1360 CrossRef CAS.
- M. Lukaszewicz, R. Tomala and R. Lisiecki, J. Mater. Chem. C, 2020, 8, 1072–1082 RSC.
- T. Liu, Y. P. Song, S. S. Wang, Y. J. Li, Z. Y. Yin, J. B. Qiu, Z. W. Yang and Z. G. Song, J. Alloys Compd., 2019, 779, 440–449 CrossRef CAS.
- H. Qin, D. Y. Wu, J. Sathian, X. Y. Xie, M. Ryan and F. Xie, Sci. Rep., 2018, 8, 12683 CrossRef PubMed.
- S. Singh, Kanika, G. Kedawat, J. H. Park, B. Ghorai, U. K. Ghorai, C. Upadhyay, B. A. Kaipparettu and B. K. Gupta, J. Photochem. Photobiol., 2021, 8, 100081 CrossRef.
- K. Z. Zheng, Z. Y. Liu, Y. Liu, W. Y. Song and W. P. Qin, J. Appl. Phys., 2013, 114, 183109 CrossRef.
- X. Q. Zhao, H. Suo, Z. Y. Zhang and C. F. Guo, Ceram. Int., 2018, 44, 2911–2918 CrossRef CAS.
- G. Bilir and G. Eryurek, Ceram. Int., 2016, 42, 6065–6071 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Structural characterization, energy gap determination, thermometric analysis, white-light emission, estimating the thermal conductivity, experimental procedure to temporal analysis. See DOI: https://doi.org/10.1039/d3nr01764h |
| This journal is © The Royal Society of Chemistry 2023 |