DOI:
10.1039/D2NR06409J
(Paper)
Nanoscale, 2023,
15, 10254-10263
Can magnetotransport properties provide insight into the functional groups in semiconducting MXenes?†
Received
16th November 2022
, Accepted 10th April 2023
First published on 14th April 2023
Abstract
Hall scattering factors of Sc2CF2, Sc2CO2 and Sc2C(OH)2 are calculated using Rode's iterative approach by solving the Boltzmann transport equation. This is carried out in conjunction with calculations based on density functional theory. The electrical transport in Sc2CF2, Sc2CO2 and Sc2C(OH)2 is modelled by accounting for both elastic (acoustic and piezoelectric) and inelastic (polar optical phonon) scattering. Polar optical phonon (POP) scattering is the most significant mechanism in these MXenes. We observe that there is a window of carrier concentration where the Hall factor acts dramatically; Sc2CF2 obtains an incredibly high value of 2.49 while Sc2CO2 achieves a very small value of approximately 0.5, and Sc2C(OH)2 achieves the so called ideal value of 1. We propose in this paper that such Hall factor behaviour has significant promise in the field of surface group identification in MXenes, an issue that has long baffled researchers.
1 Introduction
Following the discovery of graphene, two-dimensional (2D) materials are of great interest to researchers as they have a range of physical properties that make them suitable for a variety of applications in energy storage, catalysis, high performance electronic devices and so on.1–5 The reduced dimensionality of 2D materials promises to cater to the next generation of electronic technologies and applications. MXenes, a family of 2D materials consisting of early transition metal carbides, nitrides and carbonitrides are known to possess unique characteristics.6–11 They are formed by selective exfoliation of “A” from 3D layered MAX phases and sonication. MAX phases are precursors of MXene with space group P63/mmc and chemical composition Mn+1AXn where M is an early transition metal, A is a group IIIA or IVA element and X is C and/or N with n = 1–3. During the etching process, some functional groups (T) are left on the MXene surface so as to passivate the outer metal atom layer. From theoretical studies, it is known that bare MXenes (Mn+1Xn) are metallic and the electronic nature of functionalized MXenes (Mn+1XnTx) depends on the surface terminating species. Most of the functionalized MXenes retain the metallic nature of bare MXene and few MXenes like Ti2CO2, Zr2CO2, Hf2CO2, Sc2CF2, Sc2CO2 and Sc2C(OH)2 are reported to be semiconducting with an appreciable band gap.12 Sc2CO2 has an out-of-plane polarization Pz with magnitude, an order higher than the 1T phase of MoS2.13 These 2D scandium carbides are not yet experimentally synthesized but have excellent properties from theoretical investigation. There are studies in which scandium carbide MXenes are used as a heterostructure in combination with the same base material or other 2D materials to develop a nanodevice for use in photonics, electronics and optoelectronics.14,15 The semiconducting nature of scandium carbide MXenes makes them promising candidate materials for future electronic and optical devices.
Intrinsic carrier mobility is a good measure of electrical transport and graphene has extremely high carrier mobility among 2D materials.16 As graphene is gapless, it has a low on–off ratio.17 Though extensive efforts have been made to open a gap in graphene, it is apparently better to employ other 2D materials which have attributes like moderate band gap (ensures a high on–off ratio) and high intrinsic carrier mobility.18 Most of the studied 2D semiconductors in their monolayer form have very low carrier mobility (<100 cm2 V−1 s−1) at room temperature19–22 compared to bulk semiconductors like silicon and germanium. Therefore, it is essential to determine the factors that limit carrier transport in 2D semiconductors to design better electronic devices based on them. Carrier mobility is limited by the phonon interaction, which disturbs the potential experienced by electrons and its determination in principle involves the estimation of electron–phonon coupling in a rigorous manner, methods for which have been developed in recent years.23 In the present work, we treat acoustic phonons within the deformation potential approach as it has produced quite satisfactory results for many MXene systems.
Magnetotransport has been widely studied in bulk semiconductors like Si24–26 and GaAs27 and in 2D materials, graphene and WTe2 are reported to have large magnetoresistance (MR).28–31 We do not include spin–orbit coupling (SOC) in our ab initio calculations as it is more important for holes. Desai et al.32 demonstrated that to obtain an accurate isotropic conductivity tensor of silicon for hole carriers, the effect of SOC has to be considered. The mismatch in MR anisotropy obtained in calculations is due to the errors in the conductivity tensor determined without including SOC. Therefore, the key to accurate magnetotransport calculations for hole carriers is the inclusion of SOC and it has a minor effect on electron carriers. But, Si and Sc are different elements with p and d electrons respectively as valence electrons. It is also known that the strength of spin–orbit coupling depends on the fourth power of atomic number (Z4) and scandium is the transition metal with the smallest atomic number. To the best of our knowledge, none of the previous reports have ever reported a significant SOC effect in purely scandium based MXenes. Nevertheless, we have carried out band structure calculations including SOC and it is found that the band dispersion near the Fermi level (region of interest for transport calculations) and band gap are not affected.
Studies on magnetotransport of materials using first principles are very scarce. Macheda et al. investigated magnetotransport in diamond,33 and graphene,34 and our recent work on Ti2CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 are the few existing reports. Also, the transverse magnetoresistance of copper, bismuth and WP2 are determined by combining ab initio Fermi surfaces with Boltzmann transport theory by Zhang et al.36 Magnetotransport in semiconductors was used primarily to quantify carrier concentration, which facilitates the design and production of efficient electronic devices. We show that magnetotransport coefficients such as the Hall factor may be used as a guideline or a tool to determine the functional groups in semiconducting MXenes such as metal-carbides. The manuscript is structured as follows: in the subsequent part, we present the theoretical foundation for adopting Rode's iterative technique to compute electrical and magnetotransport. First-principles calculations are used to get all the parameters required for the transport calculations. Therefore, we briefly describe the structural details of the MXenes after outlining the details of our ab initio calculations. Following a brief description of these systems’ electronic structure and lattice dynamics, we go on to the results and discussion, and finally to conclusions.
35 are the few existing reports. Also, the transverse magnetoresistance of copper, bismuth and WP2 are determined by combining ab initio Fermi surfaces with Boltzmann transport theory by Zhang et al.36 Magnetotransport in semiconductors was used primarily to quantify carrier concentration, which facilitates the design and production of efficient electronic devices. We show that magnetotransport coefficients such as the Hall factor may be used as a guideline or a tool to determine the functional groups in semiconducting MXenes such as metal-carbides. The manuscript is structured as follows: in the subsequent part, we present the theoretical foundation for adopting Rode's iterative technique to compute electrical and magnetotransport. First-principles calculations are used to get all the parameters required for the transport calculations. Therefore, we briefly describe the structural details of the MXenes after outlining the details of our ab initio calculations. Following a brief description of these systems’ electronic structure and lattice dynamics, we go on to the results and discussion, and finally to conclusions.
2 Rode's iterative approach for the Boltzmann transport equation
The electrical and magnetotransport properties are calculated by the AMMCR code37,38 developed by us. When no magnetic field is present, considering a spatial homogeneous system in the steady state (under an electric field E), the following equation is solved to obtain the single electron distribution function f(r, k, t) given by,| | 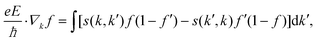 | (1) |
where s(k, k′) represents the transition rate of an electron from a state k to a state k′. At lower electric fields, the distribution function is given by39–41| | f(k) = f0[ε(k)] + g(k)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, θ, | (2) |
where f0[ε(k)] is the equilibrium distribution function given by 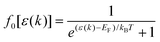 , EF is the Fermi-energy, g(k) is the perturbation to the distribution function due to the presence of the applied electric field, and cos
, EF is the Fermi-energy, g(k) is the perturbation to the distribution function due to the presence of the applied electric field, and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is the angle between the applied electric field and k. Here, we neglect higher order terms as mobility is calculated under low electric field conditions. It is required to calculate the perturbation in the distribution function g(k) for determining the low-field transport properties. Within the iterative formalism introduced by Rode, the perturbation to the distribution function g(k) is given by39–41
θ is the angle between the applied electric field and k. Here, we neglect higher order terms as mobility is calculated under low electric field conditions. It is required to calculate the perturbation in the distribution function g(k) for determining the low-field transport properties. Within the iterative formalism introduced by Rode, the perturbation to the distribution function g(k) is given by39–41| | 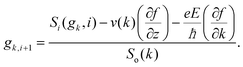 | (3) |
where Si represents the in-scattering rates due to the inelastic processes and So represents the sum of out-scattering rates. 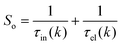 , where
, where 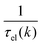 is the sum of the momentum relaxation rates of all elastic scattering processes and
is the sum of the momentum relaxation rates of all elastic scattering processes and 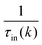 is the momentum relaxation rate due to the in-elastic processes.
is the momentum relaxation rate due to the in-elastic processes.
The expression for τel(k), Si and 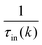 are given by the following equations
are given by the following equations
| | 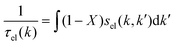 | (4) |
| | 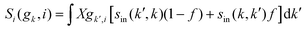 | (5) |
| | 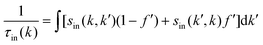 | (6) |
where
X is the cosine of the angle between the initial and the final wave vectors,
sin(
k,
k′) and
sel(
k,
k′) represents the transition rate of an electron from state
k to
k′ due to inelastic and elastic scattering mechanisms respectively. Since,
Si is a function of
g(
k), thus
eqn (3) is to be calculated iteratively.
41 We have used a similar procedure in our previous works, to determine the mobility of ZnSe
38 and CdS.
37 Drift mobility
μ is then calculated by the following expression
38| | 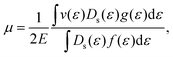 | (7) |
where
Ds(
ε) represents density of states. The carrier velocity is then calculated directly from the
ab initio band structure by using the form,
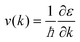
and the electrical conductivity can be calculated as
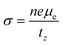
. Here,
n is the electron carrier concentration,
tz is the thickness of the MXene layers along the
z-direction.
When we consider the magnetic field as well, the distribution function in this case is given by:42
| | | f(k) = f0[ε(k)] + xg(k) + yh(k) | (8) |
where
h(
k) represents perturbation in distribution function due to the magnetic field, and
y is the direction cosine from B × E to
k, where
B is the applied magnetic field. Substituting
eqn (8) in
eqn (1), we get a pair of coupled equations that can be solved iteratively
42| | 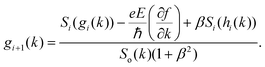 | (9) |
| | 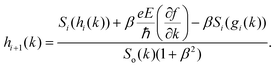 | (10) |
where
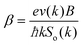
. The above expression shows that the perturbations to the distribution function due to the electric field (
g) and magnetic field (
h) are coupled to each other through factor
β and the scattering rates
Si. It should be highlighted that such a representation cannot be obtained using standard relaxation time approximation (RTA) and can only be seen using the current method. The components of the conductivity tensor in terms of perturbations are given by
| | 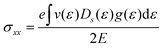 | (11) |
| | 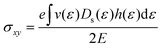 | (12) |
The Hall coefficient RH, Hall mobility μH and Hall factor r are respectively calculated by
| | 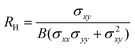 | (13) |
| | 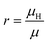 | (15) |
where
σxx(0) is the value of
σxx in the absence of the magnetic field. We have already discussed three scattering mechanisms: scattering due to acoustic phonons, piezoelectric scattering, and scattering due to polar optical phonons in Ref. 35 and how to determine the scattering rates are provided in detail.
In experiments, Hall measurements are carried out to estimate carrier concentration and drift mobility. A key quantity that characterizes these measurements is the Hall scattering factor, r, which is taken as the ratio of Hall mobility to drift mobility. In general, this factor is assumed to be around unity and this assumption is based on compound semiconductors with quasi-parabolic bands.34 In such cases, r dependence on temperature and scattering times is weak. Here, we calculate Hall factor, r as
| | 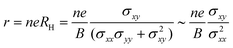 | (16) |
This equation can be rewritten as eqn (17) by replacing the conductivity tensor components σxx and σxy with their expressions including pertubations to the distribution function. The r dependence on temperature and scattering rates arises through these functions (g(ε) and h(ε)).
| | 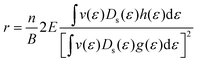 | (17) |
3 Computational details
We performed first principles calculations using density functional theory (DFT) implemented in the plane wave code, Vienna ab initio Simulation Package (VASP).43,44 The projector augmented wave (PAW) approach is employed for pseudopotentials.45,46 The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional is adopted for exchange–correlation interactions.47 The electron wavefunctions are expanded in plane waves with a cut off energy of 500 eV. The conjugate gradient algorithm is used for structural optimization. The atomic positions are fully relaxed until the residual force on each atom is less than 0.01 eV Å−1 and the energy convergence criterion is 10–6 eV. A vacuum of thickness 20 Å along the z-direction is employed to avoid interactions between the neighboring layers and Brillouin zone integrations are performed with Gamma-centered k-mesh of 18 × 18 × 1 for structure optimizations. The DFT-D2 method is used for van der Waals correction.48 The crystal structures are visualized using VESTA.49 Phonon spectra of Sc2CF2, Sc2CO2 and Sc2C(OH)2 are calculated using VASP in combination with Phonopy software.50 Here, we employ a supercell of size 4 × 4 × 1 and a 4 × 4 × 1 k-mesh to determine the dynamical matrix.
3.1 Structural model of the MXenes
The Sc2C monolayer is modelled from the Sc2AlC bulk phase. 1T and 2H phases of Sc2C are considered and the energetically more stable 1T phase is further used to study the effect of functionalization (F, O, OH). Depending on the position of functional groups on the bare MXene surface, there are four different configurations (I, II, III, and IV). For Sc2CF2, these configurations are given in Fig. S1† and their total energies are compared for each functional group. Among these geometries, configuration II of Sc2CF2 and Sc2C(OH)2 have the lowest total energy. O functionalization results in a structure (configuration IV) different from that of F and OH. It is also reflected in the bond lengths and bond angles of Sc2CO2, which are mentioned by Kumar et al.51 The optimized geometries for Sc2CF2, Sc2CO2 and Sc2C(OH)2 are presented in Fig. S1.† In the optimized structure of Sc2CO2 (Fig. S1(f)†), the oxygen atom on top lies in line with the scandium atom in the lower layer and the bottom oxygen atom is in line with carbon atom. For Sc2CF2 and Sc2C(OH)2, the functional group on top lies in line with the scandium atom in the lower layer and vice versa. The symmetry group of Sc2CF2 and Sc2C(OH)2 is P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (No. 164) whereas it is P3m1 (No. 156) for Sc2CO2. There is no inversion centre for Sc2CO2. The layer thickness of Sc2CF2, Sc2CO2 and Sc2C(OH)2 are 4.79, 3.85 and 6.91 Å, respectively, with Sc2CO2 exhibiting the smallest layer thickness.
m1 (No. 164) whereas it is P3m1 (No. 156) for Sc2CO2. There is no inversion centre for Sc2CO2. The layer thickness of Sc2CF2, Sc2CO2 and Sc2C(OH)2 are 4.79, 3.85 and 6.91 Å, respectively, with Sc2CO2 exhibiting the smallest layer thickness.
3.2 Electronic structure and lattice dynamics
The electronic band structure and density of states (DOS) of three MXenes Sc2CF2, Sc2CO2 and Sc2C(OH)2 are given in Fig. 1. They are semiconducting with indirect band gaps except for Sc2C(OH)2. Their band character also differs, which could be due to the distinct optimum structures for different functionalizations (from fat bands – not shown here). Sc2C(OH)2 has a direct band gap (Eg) of 0.34 eV with the valence band maximum (VBM) and conduction band minimum (CBM) at Γ. The CBM is dominated by O and H bands whereas Sc has more contribution towards the VBM. For Sc2CF2 and Sc2CO2, the Eg values are 0.97 and 1.83 eV respectively and CBM are formed by the Sc bands. Both of them have their VBM at Γ and CBM at M and K respectively. These results are in agreement with the reported ones.12,51,52 The phonon dispersion spectra of Sc2CF2, Sc2CO2 and Sc2C(OH)2 are also presented in Fig. 1. They do not have imaginary (negative) frequencies and hence these semiconducting MXenes are dynamically stable. For OH, there are high frequency optical branches above 100 THz. This feature is observed in other OH-functionalized MXenes and corresponds to the stretching modes of OH bonds.53,54 It can also be used to characterize the level of OH functionalization in MXenes which after chemical exfoliation have different functional groups on their surface.51
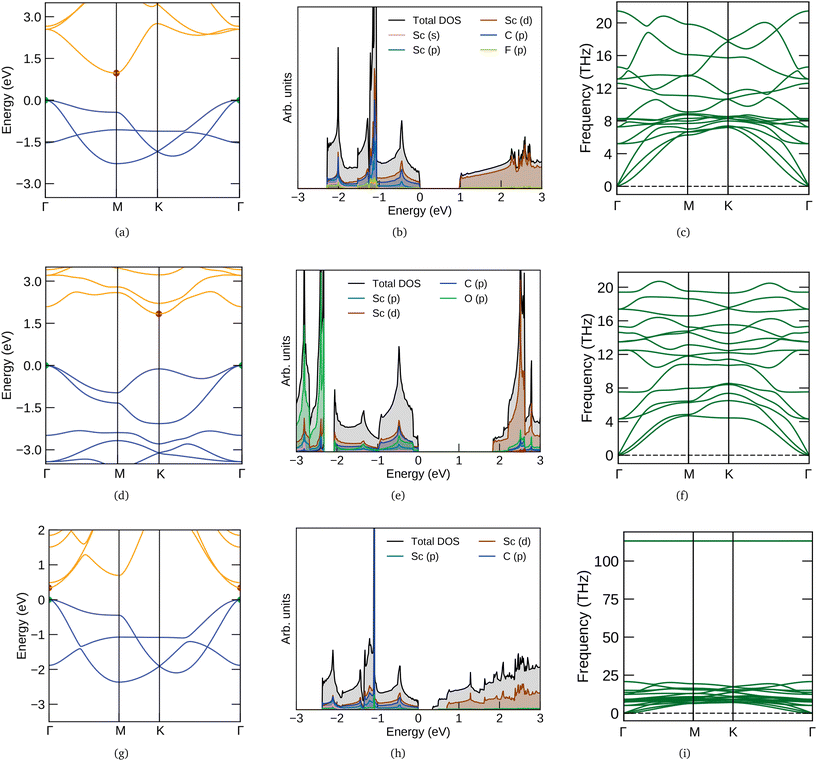 |
| | Fig. 1 Electronic band structures, density of states and phonon band structures of (a–c) Sc2CF2 (first row), (d–f) Sc2CO2 (second row) and (g–i) Sc2C(OH)2 (third row). The y (vertical) scale of DOS plots are multiplied by 2, 2 and 5 factors for F, O and OH functional groups respectively. In the electronic band structure, the VBM and CBM are denoted by green and red points respectively. | |
3.3
ab initio parameters needed for transport calculation
The ab initio parameters required to use the transport tool AMMCR37,38 are obtained from DFT calculations and these values are reported in Table 1. The piezoelectric and dielectric constants (both high and low frequency) are calculated using density functional perturbation theory (DFPT).55 The acoustic deformation potential constant of CBM for electrons and the elastic moduli under uniaxial strain are calculated along the out-of-plane (ZA), longitudinal (LA) and transverse (TA) directions using the method described by Xiong et al.56 For Sc2CF2, the calculation of acoustic deformation potentials and elastic moduli are given in the ESI.†
Table 1 Material parameters used for the MXenes
| Parameters |
Sc2CF2 |
Sc2CO2 |
Sc2C(OH)2 |
| PZ constant, e11 (C cm−1) |
4.79 × 10–17 |
42.35 × 10–17 |
55.28 × 10–17 |
|
Acoustic deformation potentials, D
A
(eV):
|
|
D
A,LA
|
2.17 |
5.13 |
0.83 |
|
D
A,TA
|
2.17 |
5.13 |
0.86 |
|
D
A,ZA
|
6.84 |
0.33 |
3.40 |
|
Elastic modulus, C
A
(N m
−1
)
|
|
C
A,LA
|
243.08 |
251.30 |
239.53 |
|
C
A,TA
|
243.08 |
251.30 |
239.53 |
|
C
A,ZA
|
174.26 |
115.77 |
355.62 |
|
Polar optical phonon frequency ω
pop
(THz)
|
|
ω
pop,LO
|
7.29 |
4.33 |
7.41 |
|
ω
pop,TO
|
7.29 |
4.33 |
7.41 |
|
ω
pop,ZO
|
12.60 |
7.54 |
13.67 |
| High frequency dielectric constant, κ∞ |
2.66 |
2.07 |
3.68 |
| Low frequency dielectric constant, κ0 |
7.43 |
3.33 |
9.19 |
4 Results and discussion
Let us discuss about electron transport first, before we go on to magnetotransport. Also, in order to fully understand magnetotransport in this material, these results must be comprehended. Fig. 2 shows the scattering rates due to both acoustic and optical phonons for Sc2CF2, Sc2CO2 and Sc2C(OH)2. The out-of-plane phonons also contribute towards electron transport and are denoted by ZA/ZO modes. We find that for the three scandium carbide MXenes considered here, polar optical phonon (POP) interaction is the most dominant scattering mechanism, followed by deformation potential scattering, and piezoelectric, which is the least. For Sc2CF2 and Sc2C(OH)2, it seen that the out-of-plane acoustic phonon called flexural phonon (ZA) has higher contribution when compared to the phonon scattering induced by longitudinal (LA) and transverse (TA) modes. It is the opposite for Sc2CO2 with ZA phonon scattering weaker than LA and TA phonons. The contribution of LA, TA and ZA phonon modes towards the scattering rate is shown in the ESI (Fig. S3†).
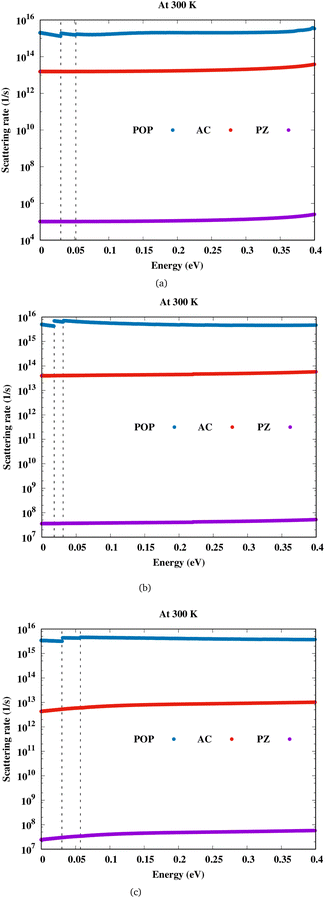 |
| | Fig. 2 Scattering rate versus energy for (a)Sc2CF2, (b)Sc2CO2 and (c)Sc2C(OH)2. | |
In these semiconductors, there is strong inelastic scattering as polar optical phonons play a major role. The black dashed lines in Fig. 2 correspond to the energy of LO/TO and ZO phonon modes. When the electron energy is smaller than optical phonon energy, the interactions are dominated by the absorption process. As energy increases, the jumps in the scattering rate represent the onset of the phonon emission process. In these MXenes, the two lowest optical branches (softer ones) are nonpolar modes/antiferroelectric, that is, the two Sc atoms (cations) have phonon dispersion eigen vectors pointing in opposite directions and so is the case of two T atoms (anions). Their mode effective charges calculated from the Born effective charge have values close to zero. The next two branches are polar optical modes with the cations and anions vibrating in the counter-phase. In the case of Sc2CF2, two Sc atoms vibrate in the same direction whereas the anions, C and F, in the other direction. Here, the mode effective charge has significant values. We have calculated the scattering rates with both set of frequencies and it is observed that optical phonon interactions are dominant. The mobility in these 2D materials are limited by POP (due to the reciprocal nature of the relation) and it is represented as a function of temperature and electron concentration using Matthiessen's rule
| | 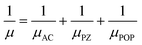 | (18) |
where
μ,
μAC,
μPZ, and
μPOP denotes the total mobility, acoustic, piezoelectric, and polar optical contributions, respectively.
Fig. 3 shows the variation of mobility as a function of temperature for Sc
2CF
2, Sc
2CO
2 and Sc
2C(OH)
2. For a particular electron concentration, the mobility decreases with increasing temperature. The mobility of Sc
2CF
2 decreases monotonously with increasing electron concentration up to 5 × 10
12 cm
−2 and the curves corresponding to different doping concentrations coincide at high temperatures (exceeding 500 K). Beyond this carrier concentration, the change in mobility with increasing electron concentration is irregular. Sc
2C(OH)
2 shows similar behaviour but for Sc
2CO
2, these limits are different.
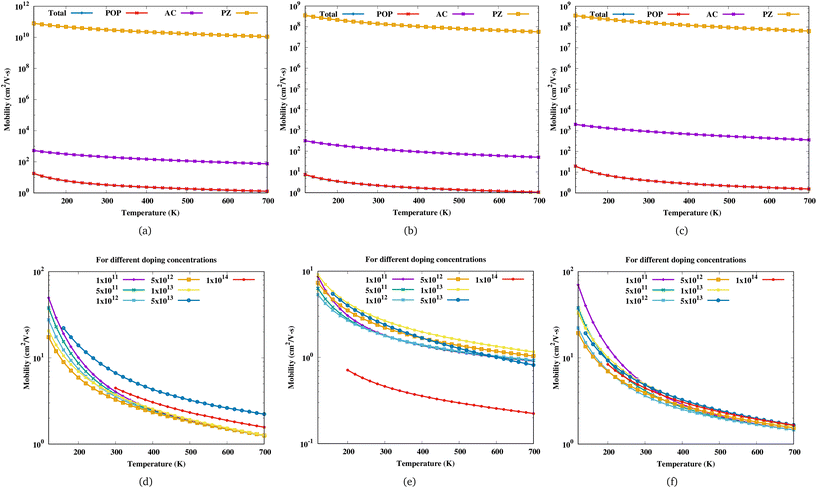 |
| | Fig. 3 Mobility of (a) Sc2CF2, (b) Sc2CO2 and (c) Sc2C(OH)2 as a function of temperature for an electron concentration of 5 × 1012 cm−2 with the contributions of POP, acoustic and PZ scattering. Mobility of (d) Sc2CF2, (e) Sc2CO2 and (f) Sc2C(OH)2 as a function of temperature for different electron concentrations in cm−2. | |
The variation of conductivity as a function of temperature at different carrier concentrations is given in Fig. S4.† The conductivity increases with the increase in electron concentration. At n = 1 × 1014 cm−2, there is a decrease in the conductivity of Sc2CO2. The conductivity value exceeds 1000 S cm−1 at high electron concentrations for Sc2CF2 and Sc2C(OH)2.
All magnetotransport calculations are performed at a small magnetic field of 0.4 T and the field is along the z-direction. With the change in the direction of the magnetic field, the Hall scattering factor can vary by a mass factor which is dependent on the material as shown in the case of hexagonal SiC.57 The change in Hall conductivity (σxx and σxy) of Sc2CF2, Sc2CO2 and Sc2C(OH)2 as a function of temperature at different electron concentrations is shown in Fig. 4. As the carrier concentration increases, the Hall conductivity increases and it has the largest value at the highest electron concentration considered. For Sc2CO2, the Hall conductivity decreases beyond an electron concentration of 5 × 1013 cm−2.
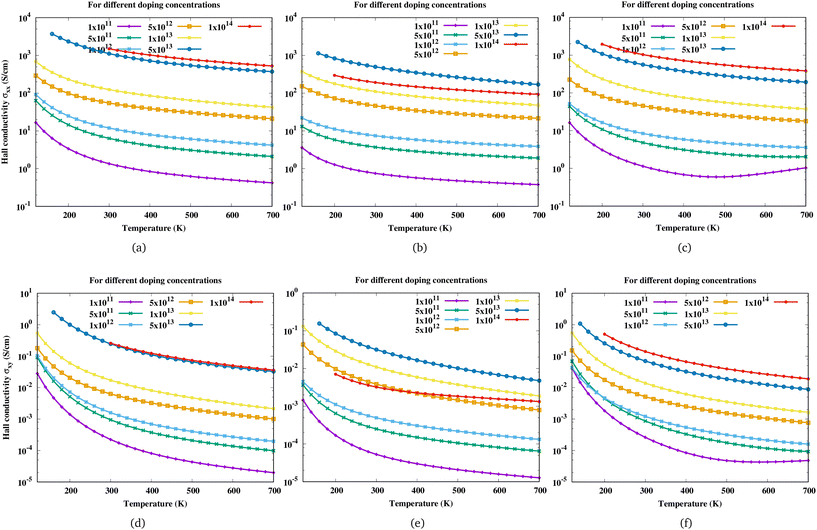 |
| | Fig. 4 Variation of Hall conductivity (σxx, σxy) of (a and d) Sc2CF2, (b and e) Sc2CO2, and (c and f) Sc2C(OH)2 with temperature at different electron concentrations. Here the first row corresponds to σxx and the second row to σxy. | |
In Fig. 5, we show the calculated Hall factor for all the three compounds, Sc2CF2, Sc2CO2 and Sc2C(OH)2 both as a function of temperature and electron concentration. It is important to note here that Hall factor formulated by us35 as shown in eqn (17) depends on both the perturbations g(ε) as well as h(ε). Such a method is quite distinct in comparison to the similar currently proposed method, for example, the one adopted by Macheda et al.,33 where the authors have calculated the Hall scattering factor in graphene in terms of the solution of the Boltzmann transport equation. However, they used relaxation time approximation (RTA) and the effect of the magnetic field on the distribution function were not considered in an explicit way as we have done. At a carrier concentration of 5 × 1012 cm−2 and magnetic field of 0.4 T along the z-direction, the difference in Hall factor obtained using RTA and Rode's iterative method (Δr = rRTA − rRode) is presented in the ESI (Fig. S5†). We see that, at low temperatures, the difference Δr is large and it reduces around room temperature. Beyond room temperature, Δr increases slightly for Sc2C(OH)2 whereas it further reduces for Sc2CO2.
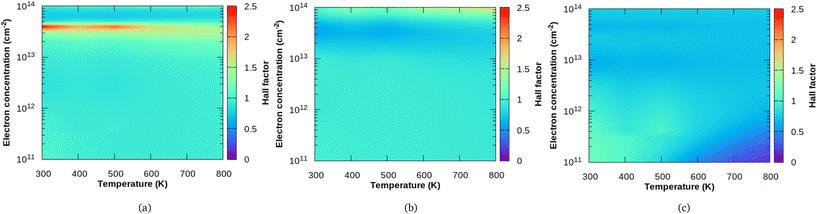 |
| | Fig. 5 Variation of the Hall factor in terms of temperature and concentration for (a) Sc2CF2, (b) Sc2CO2 and (c) Sc2C(OH)2. | |
For the three MXenes considered, the Hall scattering factor at different temperatures crossover with increasing carrier concentrations (which is more evident in xy plots in the ESI – Fig. S6†). The Hall factor varies over a large range with carrier concentration for Sc2CF2 when compared to Sc2CO2 and Sc2C(OH)2. At a carrier concentration of 4 × 1013 cm−2, Sc2CF2 has the highest value of r, which is close to 2.50. At low doping (carrier density), the Hall factor is around 1 for both Sc2CF2 and Sc2CO2. For the F functional group, it increases sharply with increasing electron concentration at lower temperatures. In the case of the O functional group, r values dip and at the highest electron concentration considered (1 × 1014 cm−2), it ranges from 0.9 to 1.6. For Sc2C(OH)2 at small doping and low temperature, r has a value of 1.17 and it drops to 0.76 with increasing temperature.
At low doping concentrations, we see that Hall factor of Sc2C(OH)2 is dependent on the temperature and decreases with increasing temperature, though the bands at the extrema have a quasi-parabolic nature. Also, the r value increases with temperature at high carrier concentrations for Sc2CO2. These are not in favour of the general assumption in Hall measurements where r is taken to be unity (based on the weak dependence of r on temperature and scattering mechanisms in bulk semiconductors with quasi-parabolic bands34 and with relaxation time approximation). But for Sc2CF2 and Sc2CO2, the Hall factor ranges around unity with no significant temperature dependence at low carrier concentrations.
For all three MXenes, we observe a unique behaviour in the carrier concentration region between 0.3 and 0.4 × 1014 cm−2. It is found that Sc2CF2 has the highest r value in this region and it diminishes with increasing temperature. Similarly for Sc2C(OH)2, there is a faint region of moderate r value which decreases with temperature in the specified carrier concentration range. The obtained r values are the lowest in that region for Sc2CO2, which increases slightly with temperature. This similarity in F- and OH-functionalized Sc2C could be attributed to the way in which they affect the electronic structure as they receive only one electron from the MXene surface whereas the O group obtains two electrons.
Such unique behaviour can further be understood in terms of eqn (17) and Table S3 of the ESI.† From eqn (17), it can be seen that the Hall factor depends on the ratio 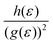 of the two distribution functions. It can be seen from Table S3† that in the region where the carrier concentration varies between 0.3 and 0.4 × 1014 cm−2, this ratio is largest at the Fermi energy
of the two distribution functions. It can be seen from Table S3† that in the region where the carrier concentration varies between 0.3 and 0.4 × 1014 cm−2, this ratio is largest at the Fermi energy 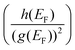 for Sc2CF2 followed by Sc2C(OH)2 and Sc2CO2. Since Fermi energy is the most relevant energy for the transport properties, the value of this ratio at this energy gives us a lot of insight. Such a behaviour tells us that the relative size of h(ε) in comparison to the square of g(ε) is the largest for Sc2CF2. This also demonstrates the necessity of splitting of the total distribution function into an electronic and a magnetic part.
for Sc2CF2 followed by Sc2C(OH)2 and Sc2CO2. Since Fermi energy is the most relevant energy for the transport properties, the value of this ratio at this energy gives us a lot of insight. Such a behaviour tells us that the relative size of h(ε) in comparison to the square of g(ε) is the largest for Sc2CF2. This also demonstrates the necessity of splitting of the total distribution function into an electronic and a magnetic part.
Furthermore, it can be seen that F- and OH-functionalized Sc2C shows weaker temperature dependence in comparison to the O-functionalized one. The signature of the Hall factor as a function of carrier concentration and temperature for the three considered scandium carbide MXenes is therefore different and unique, which makes it a promising tool to distinguish the samples with varying concentrations of these three surface functional groups. The theoretical determination of the Hall factor could be a first step towards the characterization of the level of different functional groups which are present simultaneously in the experimental samples by performing extensive transport calculations on MXenes with mixed surface functionalization.
5 Conclusions
We have investigated the electrical and magnetotransport properties of three semiconducting MXenes, Sc2CF2, Sc2CO2 and Sc2C(OH)2 using Rode's iterative method of solving the Boltzmann transport equation implemented in our AMMCR code. The input parameters are obtained from first principles calculations. We have included both elastic and inelastic scattering mechanisms in our determination of transport properties. It is the polar optical phonon interaction which contributes the most to the scattering rate and limits the electron mobility in these MXenes. The Hall scattering factor of these MXenes for a range of carrier concentration and temperature are determined. The Hall factor takes very distinct values with temperature at high doping concentrations for each of the scandium-carbide MXene considered, which can be used in functional group characterization in experiments.
Author contributions
SB conceived the idea. NAK performed all the calculations. The manuscript was written by SB and NAK. AKM, BM and SCL contributed to discussions.
Conflicts of interest
The authors declare that they have no conflict of interest.
Acknowledgements
AKM and BM gratefully acknowledge funding from the Indo-Korea Science and Technology Center (IKST), Bangalore.
References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D.-e. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- R. Mas-Balleste, C. Gomez-Navarro, J. Gomez-Herrero and F. Zamora, Nanoscale, 2011, 3, 20–30 RSC.
- D. Akinwande, C. J. Brennan, J. S. Bunch, P. Egberts, J. R. Felts, H. Gao, R. Huang, J.-S. Kim, T. Li, Y. Li, K. M. Liechti, N. Lu, H. S. Park, E. J. Reed, P. Wang, B. I. Yakobson, T. Zhang, Y.-W. Zhang, Y. Zhou and Y. Zhuo, Extreme Mech. Lett., 2017, 13, 42–77 CrossRef.
- K. S. Novoselov, D. Jiang, F. Schedin, T. Booth, V. Khotkevich, S. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451–10453 CrossRef CAS PubMed.
- A. C. Neto, F. Guinea, N. M. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109 CrossRef.
- M. W. Barsoum, Prog. Solid State Chem., 2000, 28, 201–281 CrossRef CAS.
- M. W. Barsoum and M. Radovic, Annu. Rev. Mater. Res., 2011, 41, 195–227 CrossRef CAS.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS PubMed.
- M. Naguib, O. Mashtalir, J. Carle, V. Presser, J. Lu, L. Hultman, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2012, 6, 1322–1331 CrossRef CAS PubMed.
- M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992–1005 CrossRef CAS PubMed.
- M. Ghidiu, M. Naguib, C. Shi, O. Mashtalir, L. Pan, B. Zhang, J. Yang, Y. Gogotsi, S. J. Billinge and M. W. Barsoum, Chem. Commun., 2014, 50, 9517–9520 RSC.
- M. Khazaei, M. Arai, T. Sasaki, C.-Y. Chung, N. S. Venkataramanan, M. Estili, Y. Sakka and Y. Kawazoe, Adv. Funct. Mater., 2013, 23, 2185–2192 CrossRef CAS.
- A. Chandrasekaran, A. Mishra and A. K. Singh, Nano Lett., 2017, 17, 3290–3296 CrossRef CAS PubMed.
- Y. Lee, Y. Hwang and Y.-C. Chung, ACS Appl. Mater. Interfaces, 2015, 7, 7163–7169 CrossRef CAS PubMed.
- G. Rehman, S. Ali Khan, R. Ali, I. Ahmad, L.-Y. Gan and B. Amin, J. Appl. Phys., 2019, 126, 143101 CrossRef.
- K. I. Bolotin, K. J. Sikes, Z. Jiang, M. Klima, G. Fudenberg, J. Hone, P. Kim and H. L. Stormer, Solid State Commun., 2008, 146, 351–355 CrossRef CAS.
- L. Liao, Y.-C. Lin, M. Bao, R. Cheng, J. Bai, Y. Liu, Y. Qu, K. L. Wang, Y. Huang and X. Duan, Nature, 2010, 467, 305–308 CrossRef CAS PubMed.
- J. Qiao, X. Kong, Z.-X. Hu, F. Yang and W. Ji, Nat. Commun., 2014, 5, 1–7 Search PubMed.
- W. Li, S. Poncé and F. Giustino, Nano Lett., 2019, 19, 1774–1781 CrossRef CAS PubMed.
- L. Cheng, C. Zhang and Y. Liu, J. Am. Chem. Soc., 2019, 141, 16296–16302 CrossRef CAS PubMed.
- T. Gunst, T. Markussen, K. Stokbro and M. Brandbyge, Phys. Rev. B, 2016, 93, 035414 CrossRef.
- L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 372–377 CrossRef CAS PubMed.
- J.-J. Zhou, J. Park, I.-T. Lu, I. Maliyov, X. Tong and M. Bernardi, Comput. Phys. Commun., 2021, 264, 107970 CrossRef CAS.
- P. Debye and T. Kohane, Phys. Rev., 1954, 94, 724 CrossRef CAS.
- I. Kirnas, P. Kurilo, P. Litovchenko, V. Lutsyak and V. Nitsovich, Phys. Status Solidi A, 1974, 23, K123–K127 CrossRef CAS.
- E. Putley and W. Mitchell, Proc. Phys. Soc., London, 1958, 72, 193 CrossRef CAS.
- G. Stillman, C. Wolfe and J. Dimmock, J. Phys. Chem. Solids, 1970, 31, 1199–1204 CrossRef CAS.
- V. Matveev, V. Levashov, O. Kononenko and V. Volkov, Scr. Mater., 2018, 147, 37–39 CrossRef CAS.
- K. Gopinadhan, Y. J. Shin, I. Yudhistira, J. Niu and H. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 195429 CrossRef.
- W. Wang, K. Gao, Z. Li, T. Lin, J. Li, C. Yu and Z. Feng, Appl. Phys. Lett., 2014, 105, 182102 CrossRef.
- M. N. Ali, J. Xiong, S. Flynn, J. Tao, Q. D. Gibson, L. M. Schoop, T. Liang, N. Haldolaarachchige, M. Hirschberger and N. P. Ong,
et al.
, Nature, 2014, 514, 205–208 CrossRef CAS PubMed.
- D. C. Desai, B. Zviazhynski, J.-J. Zhou and M. Bernardi, Phys. Rev. B, 2021, 103, L161103 CrossRef CAS.
- F. Macheda and N. Bonini, Phys. Rev. B, 2018, 98, 201201 CrossRef CAS.
- F. Macheda, S. Poncé, F. Giustino and N. Bonini, Nano Lett., 2020, 20, 8861–8865 CrossRef CAS PubMed.
- A. K. Mandia, N. A. Koshi, B. Muralidharan, S.-C. Lee and S. Bhattacharjee, J. Mater. Chem. C, 2022, 10, 9062–9072 RSC.
- S. Zhang, Q. Wu, Y. Liu and O. V. Yazyev, Phys. Rev. B, 2019, 99, 035142 CrossRef CAS.
- A. K. Mandia, B. Muralidharan, J.-H. Choi, S.-C. Lee and S. Bhattacharjee, Comput. Phys. Commun., 2021, 259, 107697 CrossRef CAS.
- A. K. Mandia, R. Patnaik, B. Muralidharan, S.-C. Lee and S. Bhattacharjee, J. Phys.: Condens. Matter, 2019, 31, 345901 CrossRef CAS PubMed.
- D. Rode, Phys. Rev. B: Solid State, 1970, 2, 1012 CrossRef.
- D. Rode, Phys. Rev. B: Solid State, 1970, 2, 4036 CrossRef.
-
D. Rode, Semiconductors and semimetals, Elsevier, 1975, vol. 10, pp. 1–89 Search PubMed.
- D. Rode, Phys. Status Solidi B, 1973, 55, 687–696 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- S. Kumar and U. Schwingenschlögl, Phys. Rev. B, 2016, 94, 035405 CrossRef.
- X.-H. Zha, K. Luo, Q. Li, Q. Huang, J. He, X. Wen and S. Du, EPL, 2015, 111, 26007 CrossRef.
- M. Khazaei, M. Arai, T. Sasaki, A. Ranjbar, Y. Liang and S. Yunoki, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 075411 CrossRef.
- T. Hu, J. Wang, H. Zhang, Z. Li, M. Hu and X. Wang, Phys. Chem. Chem. Phys., 2015, 17, 9997–10003 RSC.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- K. Xiong, P. Wang, G. Yang, Z. Liu, H. Zhang, S. Jin and X. Xu, Sci. Rep., 2017, 7, 1–8 CrossRef CAS PubMed.
- H. Iwata and K. M. Itoh, J. Appl. Phys., 2001, 89, 6228–6234 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Crystal structures of Sc2CTx; linear and parabolic fitting functions of Sc2CF2 under uniaxial strains; scattering rates due to acoustic phonons; conductivity as a function of temperature; difference in Hall scattering factors calculated using RTA and Rode's method; and Hall scattering factor and values of perturbation to distribution functions of Sc2CTx at Fermi energy. See DOI: https://doi.org/10.1039/d2nr06409j |
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  b,
Bhaskaran
Muralidharan
b,
Seung-Cheol
Lee
b,
Bhaskaran
Muralidharan
b,
Seung-Cheol
Lee
 *c and
Satadeep
Bhattacharjee
*c and
Satadeep
Bhattacharjee
 *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 are the few existing reports. Also, the transverse magnetoresistance of copper, bismuth and WP2 are determined by combining ab initio Fermi surfaces with Boltzmann transport theory by Zhang et al.36 Magnetotransport in semiconductors was used primarily to quantify carrier concentration, which facilitates the design and production of efficient electronic devices. We show that magnetotransport coefficients such as the Hall factor may be used as a guideline or a tool to determine the functional groups in semiconducting MXenes such as metal-carbides. The manuscript is structured as follows: in the subsequent part, we present the theoretical foundation for adopting Rode's iterative technique to compute electrical and magnetotransport. First-principles calculations are used to get all the parameters required for the transport calculations. Therefore, we briefly describe the structural details of the MXenes after outlining the details of our ab initio calculations. Following a brief description of these systems’ electronic structure and lattice dynamics, we go on to the results and discussion, and finally to conclusions.
35 are the few existing reports. Also, the transverse magnetoresistance of copper, bismuth and WP2 are determined by combining ab initio Fermi surfaces with Boltzmann transport theory by Zhang et al.36 Magnetotransport in semiconductors was used primarily to quantify carrier concentration, which facilitates the design and production of efficient electronic devices. We show that magnetotransport coefficients such as the Hall factor may be used as a guideline or a tool to determine the functional groups in semiconducting MXenes such as metal-carbides. The manuscript is structured as follows: in the subsequent part, we present the theoretical foundation for adopting Rode's iterative technique to compute electrical and magnetotransport. First-principles calculations are used to get all the parameters required for the transport calculations. Therefore, we briefly describe the structural details of the MXenes after outlining the details of our ab initio calculations. Following a brief description of these systems’ electronic structure and lattice dynamics, we go on to the results and discussion, and finally to conclusions.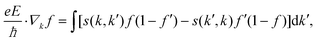
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,
θ,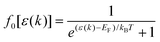 , EF is the Fermi-energy, g(k) is the perturbation to the distribution function due to the presence of the applied electric field, and cos
, EF is the Fermi-energy, g(k) is the perturbation to the distribution function due to the presence of the applied electric field, and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is the angle between the applied electric field and k. Here, we neglect higher order terms as mobility is calculated under low electric field conditions. It is required to calculate the perturbation in the distribution function g(k) for determining the low-field transport properties. Within the iterative formalism introduced by Rode, the perturbation to the distribution function g(k) is given by39–41
θ is the angle between the applied electric field and k. Here, we neglect higher order terms as mobility is calculated under low electric field conditions. It is required to calculate the perturbation in the distribution function g(k) for determining the low-field transport properties. Within the iterative formalism introduced by Rode, the perturbation to the distribution function g(k) is given by39–41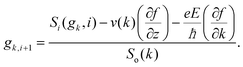
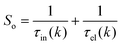 , where
, where 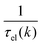 is the sum of the momentum relaxation rates of all elastic scattering processes and
is the sum of the momentum relaxation rates of all elastic scattering processes and 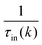 is the momentum relaxation rate due to the in-elastic processes.
is the momentum relaxation rate due to the in-elastic processes.
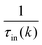 are given by the following equations
are given by the following equations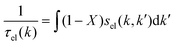
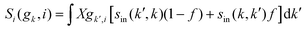
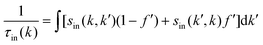
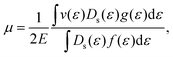
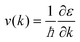 and the electrical conductivity can be calculated as
and the electrical conductivity can be calculated as 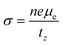 . Here, n is the electron carrier concentration, tz is the thickness of the MXene layers along the z-direction.
. Here, n is the electron carrier concentration, tz is the thickness of the MXene layers along the z-direction.
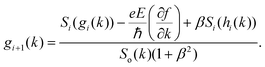
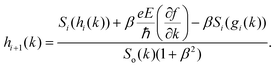
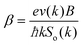 . The above expression shows that the perturbations to the distribution function due to the electric field (g) and magnetic field (h) are coupled to each other through factor β and the scattering rates Si. It should be highlighted that such a representation cannot be obtained using standard relaxation time approximation (RTA) and can only be seen using the current method. The components of the conductivity tensor in terms of perturbations are given by
. The above expression shows that the perturbations to the distribution function due to the electric field (g) and magnetic field (h) are coupled to each other through factor β and the scattering rates Si. It should be highlighted that such a representation cannot be obtained using standard relaxation time approximation (RTA) and can only be seen using the current method. The components of the conductivity tensor in terms of perturbations are given by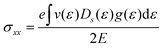
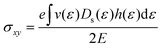
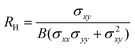
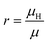
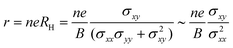
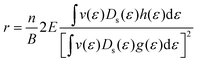
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (No. 164) whereas it is P3m1 (No. 156) for Sc2CO2. There is no inversion centre for Sc2CO2. The layer thickness of Sc2CF2, Sc2CO2 and Sc2C(OH)2 are 4.79, 3.85 and 6.91 Å, respectively, with Sc2CO2 exhibiting the smallest layer thickness.
m1 (No. 164) whereas it is P3m1 (No. 156) for Sc2CO2. There is no inversion centre for Sc2CO2. The layer thickness of Sc2CF2, Sc2CO2 and Sc2C(OH)2 are 4.79, 3.85 and 6.91 Å, respectively, with Sc2CO2 exhibiting the smallest layer thickness.
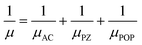

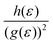 of the two distribution functions. It can be seen from Table S3† that in the region where the carrier concentration varies between 0.3 and 0.4 × 1014 cm−2, this ratio is largest at the Fermi energy
of the two distribution functions. It can be seen from Table S3† that in the region where the carrier concentration varies between 0.3 and 0.4 × 1014 cm−2, this ratio is largest at the Fermi energy 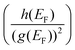 for Sc2CF2 followed by Sc2C(OH)2 and Sc2CO2. Since Fermi energy is the most relevant energy for the transport properties, the value of this ratio at this energy gives us a lot of insight. Such a behaviour tells us that the relative size of h(ε) in comparison to the square of g(ε) is the largest for Sc2CF2. This also demonstrates the necessity of splitting of the total distribution function into an electronic and a magnetic part.
for Sc2CF2 followed by Sc2C(OH)2 and Sc2CO2. Since Fermi energy is the most relevant energy for the transport properties, the value of this ratio at this energy gives us a lot of insight. Such a behaviour tells us that the relative size of h(ε) in comparison to the square of g(ε) is the largest for Sc2CF2. This also demonstrates the necessity of splitting of the total distribution function into an electronic and a magnetic part.



