Open Access Article
Open Access ArticleDNA-protamine condensates under low salt conditions: molecular dynamics simulation with a simple coarse-grained model focusing on electrostatic interactions†
Yun Hee
Jang
 *abc,
Eric
Raspaud
c and
Yves
Lansac
*abc,
Eric
Raspaud
c and
Yves
Lansac
 *abc
*abc
aGREMAN UMR 7347, Université de Tours, CNRS, INSA CVL, 37200 Tours, France. E-mail: lansac@univ-tours.fr
bDepartment of Energy Science and Engineering, DGIST, Daegu 42988, Korea. E-mail: yhjang@dgist.ac.kr
cLaboratoire de Physique des Solides, CNRS UMR 8502, Université Paris-Saclay, 91405 Orsay, France
First published on 17th August 2023
Abstract
Protamine, a small, strongly positively-charged protein, plays a key role in achieving chromatin condensation inside sperm cells and is also involved in the formulation of nanoparticles for gene therapy and packaging of mRNA-based vaccines against viral infection and cancer. The detailed mechanisms of such condensations are still poorly understood especially under low salt conditions where electrostatic interaction predominates. Our previous study, with a refined coarse-grained model in full consideration of the long-range electrostatic interactions, has demonstrated the crucial role of electrostatic interaction in protamine-controlled reversible DNA condensation. Therefore, we herein pay our attention only to the electrostatic interaction and devise a coarser-grained bead-spring model representing the right linear charge density on protamine and DNA chains but treating other short-range interactions as simply as possible, which would be suitable for real-scale simulations. Effective pair potential calculations and large-scale molecular dynamics simulations using this extremely simple model reproduce the phase behaviour of DNA in a wide range of protamine concentrations under low salt conditions, again revealing the importance of the electrostatic interaction in this process and providing a detailed nanoscale picture of bundle formation mediated by a charge disproportionation mechanism. Our simulations also show that protamine length alters DNA overcharging and in turn redissolution thresholds of DNA condensates, revealing the important role played by entropies and correlated fluctuations of condensing agents and thus offering an additional opportunity to design tailored nanoparticles for gene therapy. The control mechanism of DNA-protamine condensates will also provide a better microscopic picture of biomolecular condensates, i.e., membraneless organelles arising from liquid–liquid phase separation, that are emerging as key principles of intracellular organization. Such condensates controlled by post-translational modification of protamine, in particular phosphorylation, or by variations in protamine length from species to species may also be responsible for the chromatin–nucleoplasm patterning observed during spermatogenesis in several vertebrate and invertebrate species.
1. Introduction
Condensation of strongly-charged polymers or polyelectrolytes is an important biological process observed during DNA packaging,1,2 gene regulation,3–5 and cytoskeleton organization.6–8 It is now believed that, in diverse processes such as DNA repair, RNA metabolism, and signal transduction, cells use liquid–liquid phase separation or coacervation to create membraneless organelles, i.e., biomolecular condensates that selectively partition various proteins, DNA,9–11 and RNA.12,13DNA, one of the most studied polyelectrolytes, condense into various morphologies such as toroid, globule, and bundle as a function of their lengths and concentrations.14,15 Such an effective attraction between like-charged polyelectrolytes has been ascribed to a positional correlation between oppositely-charged condensing agents or molecular glues such as multivalent cations and arginine- or lysine-rich basic peptides and proteins, which condense along the polyelectrolyte chains.16–18 DNA aggregation occurs when a sufficient amount of condensing agents are present so that their short-range attraction to DNA mediated by correlated fluctuations of agents can compete with the long-range repulsion between DNA.19,20 Hence, an important parameter controlling DNA self-assembly is the charge ratio R+/− (=R+/R−) between the charge concentrations of cationic condensing agents (R+) and poly-anionic DNA (R−) added to the solution. It has been shown experimentally,20–22 in agreement with the Manning theory,23 that DNA condensation occurs when ∼90% of DNA charge is neutralized, but the exact onset R+/− for aggregation depends on the nature of condensing agent as well as the concentrations of DNA and monovalent salt. For instance, DNA condensation occurs with a large excess of small condensing agents (R+/− ≫ 1),20–22 while small R+/− even less than 1 is sufficient with strongly-charged (Z > 10) condensing agents such as arginine- or lysine-rich intrinsically-disordered basic protein domains.19,20
Protamine,24 a short, intrinsically-disordered, and arginine-rich strongly-positively-charged basic protein, condense DNA in sperm cells during spermatogenesis.25–28 In the early-to-middle stages of the spermatogenesis before completing the DNA condensation, some species exhibit patterns reminiscent of spinodal-decomposition-type phase separation.29–32 Such patterning is most likely a biomolecular condensation induced either by changes of interaction upon histone-to-protamine replacement or by post-translational modification of protamine such as a series of phosphorylation–dephosphorylation cycles occurring to organize protamine on DNA in human.33–35 Both mechanisms would effectively modulate the R+/− ratio.36 Protamine charge modulation directly related to the R+/− ratio may be sufficient to modify chromatin interactions and induce chromatin–nucleoplasm phase separations.34,35 Moreover, RNA droplets, which are made of RNA and short protamine-like arginine-rich peptides3 as another example of coacervates, can also be reversibly controlled in vitro by kinase and phosphatase enzymes modulating the R+/− ratio.37 Cells also actively control the number and size of RNA condensates by enriching or spatially-localizing regulatory enzymes to induce R+/−-shifting post-translational modification of condensing proteins.38 In addition, protamine, being a molecular glue for poly-anions including nucleic acids, is naturally a potential candidate for therapeutic gene delivery vehicle.39,40 Gene transfection and expression leading to a complex formation between DNA and cationic lipids are greatly improved by DNA pre-condensation with protamine41 or other poly-cations.42 Protamine is a potential packaging agent for anti-cancer or anti-virus mRNA vaccines43,44 whose immune-stimulating effects also depend strongly on the R+/− ratio between protamine and mRNA.45 Protamine has also been used to functionalize colloidal particles such as titanium oxide nanostructures46 and hallyosite nanotubes47 for biomolecular applications, and their R+/−-dependent self-assembly characteristics are similar to those found with DNA as well. It appears that the multivalent electrostatic interaction knobbed by R+/− in DNA-protamine condensation is indeed general and ubiquitous in various polyelectrolyte systems. Thus, the R+/− ratio is the first parameter to explore in our study on DNA-protamine condensates.
The R+/− dependence of DNA-protamine phase behaviours has been thoroughly studied by a combination of electrophoresis, light scattering, and cryoTEM experiments48–51 on a dilute solution of 146-base-pair (bp) short DNA in presence of 32-amino-acid (aa) salmon protamine (RRRR SSS R PV RRRRR P R VS RRRRRR GG RRRR),52 which is positively-charged up to +21|e| due to its 21 arginine (R) residues. The phase diagram was built over a wide range of R+/−, but it was only at moderate and high salt concentrations, including physiological salt concentrations where DNA precipitate in the whole range of R+/−. On the other hand, at salt concentrations lower than about 10 mM, the experiments were limited to a much narrower range of R+/−, around 0.33 < R+/− < 3.3, mostly because the complete precipitation of DNA occurs only near the isoelectric point, ∼0.8 < R+/− < ∼1. Further away from the isoelectric point, only small cylindrical nanoaggregates or bundles of the length of one DNA remain in suspension for months. These small bundles are negatively-charged and coexist with isolated DNA in excess of DNA (R+/− < 1), and positively-charged small bundles coexist with isolated protamine in excess of protamine (R+/− > 1). These finite-size rod-like bundles can be kinetically-arrested out-of-equilibrium states, which wait for rare near-parallel encounters53–55 and eventually coarsen into a divergent-size precipitate by charge disproportionation at any R+/−.56,57 They can also be a thermodynamic equilibrium state achieved when steric interaction between bulky condensing agents prevents a complete charge neutralization.58 A dilute solution of short semi-flexible polyelectrolytes experiencing only electrostatic interaction in a narrow range of Bjerrum lengths has been claimed to form finite-size bundles in a thermodynamic equilibrium as well.59,60 In all the cases, the origin of salt-dependent phase behaviours appear to be electrostatic interaction. Electrostatic repulsions between like-charged DNA may be well-screened at high and moderate salt concentrations and dominated by short-range dispersive attractions bringing all the DNA together, but the strong electrostatic repulsion between like-charged DNA unscreened at low salt concentrations would keep them away from each other and prevent formation of large bundles, explaining the experiments.
Then, what would happen if the experiments go even further away from the isoelectric point and explore a dilute low-salt DNA solution at R+/− much lower or higher than 1? Would the small bundles be still stable or would electrostatic repulsion prevent even the formation of small bundles? Since electrostatic repulsion between still-strongly-negatively-charged (when R+/− ≪ 1) or strongly-overcharged (when R+/− ≫ 1) DNA-protamine complexes is dominant in this regime, even small bundles may not be able to form. In this case, at which R+/− would the bundle start to form and to dissolve again? What R+/− would be the onsets for DNA aggregation and redissolution?
To answer these questions and to improve the nanoscale picture of the protamine-controlled DNA aggregation–redissolution cycle under very low salt conditions, we herein perform large-scale coarse-grained (CG) molecular dynamics (MD) simulations on salt-free dilute DNA solutions mixed with various concentrations of protamine at a wide range of R+/−. Staying far from physiological conditions, our studies may have little biological relevance but are still relevant for biomedical applications, e.g., gene therapies and RNA-based vaccines using protamine or low-molecular-weight protamine (LMWP) peptides as packaging and cell-penetrating agent for nucleic acids.40,61,62 In such applications, the particle size is tuned to treat specific organs or to activate specific immune responses by adjusting the nature of solutions of nucleic acids and condensing agents, e.g., to low concentrations (to avoid flocculation) and charge ratios R+/− above the isoelectric point (to target cell membranes). Most clinical applications and relevant research use small nanoparticles (<450 nm) to achieve good stability, efficient cell penetrating, and anticancer or antiviral immuno-stimulating properties,40,63–65 and thus nucleic acids and protamine (or LMWP peptides or any general poly-cations) are assembled in a low-ionic-strength solution or even in pure water to avoid flocculation induced by screened electrostatic repulsion.65–69
Assuming that the unscreened electrostatic interactions dominate short-range dispersive attractions at low-salt conditions, we pay a particular attention to fully considering the strong electrostatic interactions while treating other short-range interactions as simply as possible. It allows us to choose an extremely simple electrostatic-oriented CG model (see Section 2), which is useful for real-time-and-length-scale simulations. This simple CG model for DNA and protamine is taken from previous MD simulation studies on DNA mixed with small multivalent ions70–73 and our previous simulation study on DNA-protamine aggregation at a few values of R+/−, mostly at 0.5.48 The phase behaviours of the DNA-protamine mixtures studied herein at a much wider range of R+/− with this model are compared to those obtained previously in our another MD simulation with a more refined CG model,74 in order to validate our current model as well as our hypothesis on the predominance of electrostatic interactions under low-salt conditions (see Section 3.1).
We then explore the effect of protamine length on the formation and redissolution of DNA bundles (see Section 3.2). The length of protamine is another biologically and technologically important parameter to explore. While protamine are rather short oligopeptides characterized by the presence of several arginine tracks, their lengths vary from species to species and affect the mechanism and dynamics of nucleosome disassembly, nucleosome-to-protamine replacement, and DNA condensation during spermiogenesis,75,76 with possible consequence to male fertility. For instance, chicken protamine is twice longer than fish protamine and more efficient in disassembling nucleosomes in vitro.28 The protamine length is therefore another important knob available for species to control spermiogenesis and DNA condensation as well as the emergence and suppression of the chromatin–nucleoplasm patterns. Moreover, low-molecular-weight-protamine (LMWP) peptides,62 which can be quickly produced in mass quantity by direct enzymatic digestion of native protamine,66,77 not only exhibit enhanced cell-penetrating properties78,79 but also form small interfering RNA (siRNA) condensates with improved cell uptake as well as tumour localization and inhibition.67 Such LMWP gene carriers also display a lower level of immunogenicity than their parent protamine, reducing the risk of adverse reactions.80 Therefore, LMWP of different lengths and different arginine contents offer a supplementary means of controlling the condensate size and charge to achieve the best compromise between protection, cell membrane translocation, and intracellular dissociation. Better understanding of the relationship between the peptide length and the size, dynamics, and properties of these aggregates would help developing LMWP-peptide-formulated non-toxic gene-therapeutic nanoparticles with optimal cell-penetrating and delivery properties. We also expect that the knowledge accrued herein on the protamine-length dependence of DNA-protamine phase behaviours can be reciprocally applied to understand their DNA-length dependence.
2. Simulation details
2.1. Electrostatic-oriented simple CG models
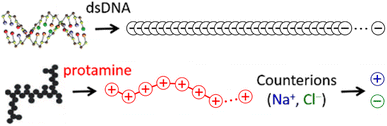
The 146-bp short double-stranded DNA (dsDNA) of ∼50 nm (≈145 × 0.34 nm when fully extended) and the 32-aa salmon protamine of ∼12 nm (≈31 × 0.38 nm when fully extended, assuming an average distance of 0.38 nm between consecutive amino acids) are modelled by single-chain beads and springs shown in Fig. 1, as done in previous studies.48,70–73 Counterions of DNA (Na+) and protamine (Cl−) added to ensure the electroneutrality of the system are represented by single beads. Focusing on the zero-salt or salt-free limit, simulations are performed without additional monovalent salt ions. Bonding interactions as well as steric and electrostatic contributions of non-bonding interactions are all taken into account between these beads, but in such a low salt regime where unscreened electrostatic interactions are dominant, we evaluate strong long-range electrostatic interactions as correctly as possible and treat other short-range interactions as simply as possible. Each bead is uniformly assigned a diameter σ of 0.4 nm,47,60–63 and the short-range steric contribution of non-bonding interaction is given by the repulsive Weeks–Chandler–Anderson potential with a cutoff rc of 21/6σ. As will be shown in Section S1, ESI,† the generic diameter of 0.4 nm leads to binding distances of ∼1 nm between two dsDNA at all R+/−, which are shorter than ∼3 nm obtained previously with a more refined model.74 However, the discrepancies are so uniform irrespective of R+/− that it is straightforward to interpret and correct them after simulation, e.g., during a back-mapping to more-refined models, and they hardly affect our conclusions on the phase behaviours. On the other hand, the binding energetics between two dsDNA, which is strongly dependent of R+/−, are well captured by this model. See Section S1, ESI† for more details.For the electrostatic contribution of non-bonding interaction, each bead belonging to DNA and Cl− is again uniformly assigned a negative unit charge (q = −|e|) and each bead belonging to protamine and Na+ carries a positive unit charge (q = +|e|). However, to represent the correct linear charge densities of dsDNA and protamine, i.e., −2|e| per 0.34 nm of dsDNA and +21|e| per ∼12 nm of protamine, the equilibrium bond lengths req between adjacent beads in dsDNA and protamine are chosen as 0.17 and 0.56 nm, respectively. The particle–particle particle-mesh method is used to efficiently deal with the long-range nature of their coulombic interactions. The water solvent is described implicitly as a continuum medium with a dielectric constant εr of 78. Although our MD simulations in the implicit solvent are unable to capture the correct diffusion properties of DNA and protamine, their relative diffusion coefficients are reproduced by our choice of masses, 14.35, 8.78, 1.00, and 1.53, for each bead of DNA, protamine, Na, and Cl, respectively. See Section S2, ESI† for details.
The bond stretching energy between two adjacent bonded beads i and j, which is a well-conserved part of bonding interaction, is again described by a standard harmonic potential
 | (1) |
The variable rij is the separation between the beads i and j, whose equilibrium value req is set to 1.7 Å for DNA and 5.6 Å for protamine. The stretching constant Kstretch is simply set to a standard value of 700 kcal mol−1 Å−2 both for DNA and protamine. For the angle bending energy, another part of bonding interaction, a harmonic potential
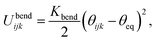 | (2) |
2.2. MD simulation with scaled-down CG models
Our CG models are employed in NVT (constant number, volume, and temperature) MD simulations performed at room temperature. A time step of 1 fs and the velocity-Verlet integrator are used as implemented in the Large-scale Atomic and Molecular Massively Parallel Simulator (LAMMPS) code.85,86 For computational efficiency, we first reduce the lengths of both DNA and protamine by a factor of three while keeping their experimental length ratio, ∼50 vs. ∼12 nm when fully extended. Thus, as shown in Fig. 1, a DNA rod is made of 100 beads 0.17 nm apart (≈17 nm; nDNA = 100) and a protamine chain is made of 7 beads 0.56 nm apart (≈4 nm; nPRO = 7). These scaled-down models reach steady states faster, owing to their fast diffusion (104 times faster than experiments; Section S2, ESI†). Reducing the DNA length is in fact an unavoidable choice for staying close to experimentally-investigated dilute-DNA regimes while still being able to handle their long-range electrostatic interactions in an affordable size of simulation box.2.3. Umbrella sampling
These scaled-down models are first used in umbrella sampling to compute the effective pairwise interaction potential between two DNA, whose results are shown in Section S1, ESI.† The reaction coordinate r is chosen as the separation between the geometrical centres of DNA (Fig. S1, Section S1, ESI†).87 For each simulation of 25 ns (5 ns equilibration and 20 ns averaging) at each window, r is restraint around a given value by a harmonic stretching potential applied between the two DNA. By both bending and torsion or only bending restraint potentials applied in addition, the two DNA are held parallel to each other or free to rotate within two parallel planes separated by r. Our simple and short CG model allows a 50-window simulation along a wide range of r (7–140 Å when restraint parallel and 7–60 Å when free to rotate). This can be twice wider than the range covered by our previous umbrella sampling with a more refined model (20–90 Å).74 The long-range electrostatic interaction is now properly evaluated close to its non-interacting limit where the two DNA are sufficiently far apart from each other. The same negligible levels of long-range repulsion reached around 140 Å when parallel and around 60 Å when free to rotate (Fig. S1, lower inset, Section S1, ESI†) justify our choice of different upper limits for the two umbrella samplings. The effective interaction (ΔF), the free energy difference between the free non-interacting DNA and bound DNA, as well as its error are constructed by combining simulations using the weighted histogram analysis method (WHAM).88,89 The procedure is repeated for a set of values in excess of DNA (R+/− = 0.5 and 0.8) or protamine (R+/− = 2) and at the isoelectric point (R+/− = 1).2.4. Unbiased MD simulation from a homogeneous mixture
To mimic the experimentally-investigated dilute solution of DNA fragments with a computationally-feasible-but-still-statistically-representative model, we build a semi-dilute solution whose DNA concentration (30 mM in phosphate) is 1000-fold higher than in experiments (30 μM). We randomly distribute 20 chains of the scaled-down 50-bp DNA models in a cubic periodic box of a side L of 48 nm (as a rough comparison, the DNA concentration in a human sperm cell is ∼150 mM, considering a 3 × 109-bp genome contained in a 5 μm-diameter sphere). The average distance between DNA in this box is about the same as the length of DNA, and thus this concentration corresponds to the upper limit of the dilute regime near the boundary to the semi-dilute regime. This DNA solution is mixed with various amounts of 7-bead protamine models to a wide range of R+/− (0.2, 0.5, 0.8, 1, 1.2, 2.4, 4, 8, and 12). Each system is submitted to a single 120 ns or 120 × 106-step unbiased MD simulation. However, at two critical R+/− values of 0.5 and 2.4, 20 independent simulations are performed to ensure the sufficient sampling of our simulations (see Section S4, ESI†).2.5. MD simulation from a pre-formed bundle
We also perform MD simulations on the reverse processes starting from a single bundle pre-formed at R+/− of 0.5, 0.8, and 2, whose results are shown in Section S5, ESI.† The hexagonal bundle composed of 19 DNA, i.e., 1, 6, and 12 at each shell, corresponds to a DNA concentration close to those used in the original forward simulations. Each simulation starts with 5 ns or 5 × 106 steps of equilibration, during which DNA are held fixed in a hexagonal lattice while protamine and counterions freely move and penetrate into the lattice, followed by 20 ns or 20 × 106 steps of production, during which DNA are also relaxed.2.6. MD simulation with long protamine
To investigate protamine-length dependence of bundle formation and redissolution, we triple the length of the 7-bead protamine model. The fully-flexible chain of 21 beads (≈12 nm with the same rPRO–PRO of 0.56 nm; nPRO = 21) with a total charge of +21|e| now mimics the overall length and charge of salmon protamine. We then reduce the number of protamine chains used in each simulation into one-third in order to keep the same R+/− as done with the scaled-down protamine model. We perform a single MD simulation of 100 ns at each R+/− of the same series, as well as 20 independent simulations run at two critical R+/− of 0.5 and 2.4 to ensure the sufficient sampling of our simulations (see Section S4, ESI†).2.7. MD analysis
DNA bundles forming during the MD simulations are identified and counted by an adapted friend-of-friend algorithm,90,91 which uses a linking length criterion of 6 Å between any pair of beads.74 An isolated DNA, either naked or decorated with protamine, is also counted as a bundle of size 1. The charge ratio of a bundle is calculated as the ratio between the total (qPRO) or net (qPRO*) positive charge of protamine and the total negative charge of DNA (qDNA) constituting the bundle, |qPRO/qDNA| counting only protamine for qPRO or |qPRO*/qDNA| also including Na+ and Cl− counterions in qPRO*. For a bundle of size NDNA containing NPRO protamine in it, |qPRO/qDNA| corresponds to (NPRO × nPRO)/(NDNA × nDNA). These bundle size, number, and charge ratio are averaged over the last 20 ns or 20 × 106 steps of each simulation at each R+/−.3. Results and discussion
3.1. MD from homogeneous mixture with short protamine
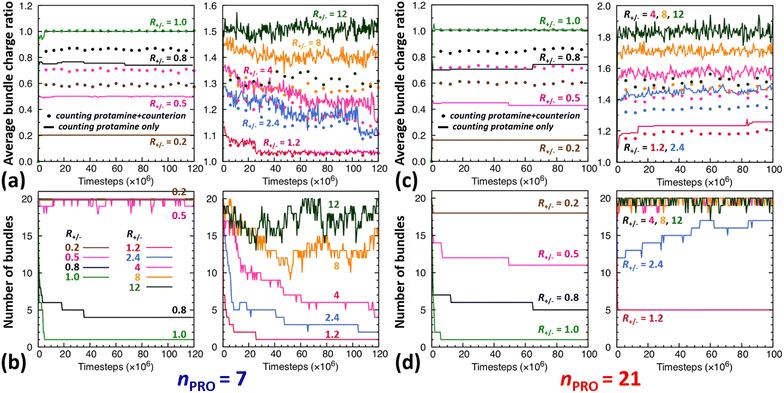
The time evolution of DNA bundles forming and redissolving during the unbiased MD simulation started from a homogeneous mixture at each R+/− is analysed in Fig. 2a and b. The number of bundles at each R+/− (Fig. 2b) all starts from 20 and then decreases quickly within 5 ns or 5 × 106-steps towards different numbers. The average bundle charge ratio changes even more quickly, almost instantaneously within 0.2 ns, and adjusts to different charge ratios from the very beginning of the simulation (near the y-intercepts of solid curves, Fig. 2a). Such drastic early changes imply that DNA aggregates form in two stages.In excess of DNA (R+/− = 0.2, 0.5, and 0.8), the average charge ratios of these DNA complexes (near the y axis, Fig. 2a) are about 0.2, 0.5, and 0.75 (solid curve, |qPRO/qDNA|) or 0.6, 0.7, and 0.9 (dotted curve, |qPRO*/qDNA|), respectively, and remain nearly constant over the entire 120 ns, leaving a large gap between the two curves. This indicates that essentially all the protamine added to the solution bind quickly to DNA (|qPRO/qDNA| = 0.2, 0.5, and 0.75 ≈ R+/−), replacing not all the Na+ counterions and leaving some on DNA (a gap between solid and dotted curves), but the DNA complexes are still negatively-charged (|qPRO*/qDNA| ≈ 0.6, 0.7, and 0.9 < 1).
At the isoelectric point (R+/− = 1) and in its immediate vicinity (R+/− = 1.2), these two types of average charge ratios are roughly the same (solid ≈ dotted, near the y axis, Fig. 2a), indicating that almost all the Na+ counterions are replaced by protamine. The DNA complexes are nearly neutral (|qPRO*/qDNA| ≈ 1). Some protamine start to remain in the solution at R+/− of 1.2 (|qPRO/qDNA| ≈ 1.15 < R+/−).
In larger excess of protamine (R+/− = 2.4–4), more protamine bind to DNA probably owing to their correlated fluctuations on DNA,16–18 but more protamine remain in the solution as well (|qPRO/qDNA| = 1.3–1.4 < R+/−; near the y axis, Fig. 2a). Since protamine itself is a strong polyelectrolyte whose Manning parameter ξ is ∼1.25 (= lB/b, where lB is the Bjerrum length at room temperature, ∼7 Å, and b is the inter-charge spacing, 5.6 Å), Cl− counterions adsorb on protamine bound to DNA (|qPRO/qDNA| > |qPRO*/qDNA|) (Fig. S4-3, ESI†), but the DNA complexes are still positively-charged (|qPRO*/qDNA| ≈ 1.2 > 1).
At even larger excess of protamine (R+/− = 8–12), more protamine and Cl− counterions bind to DNA and form strongly overcharged DNA complexes (|qPRO/qDNA| ≈ 1.5 > |qPRO*/qDNA| ≈ 1.3 > 1; Fig. 2a) but a majority of protamine stay in solution (|qPRO/qDNA| ≪ R+/−).
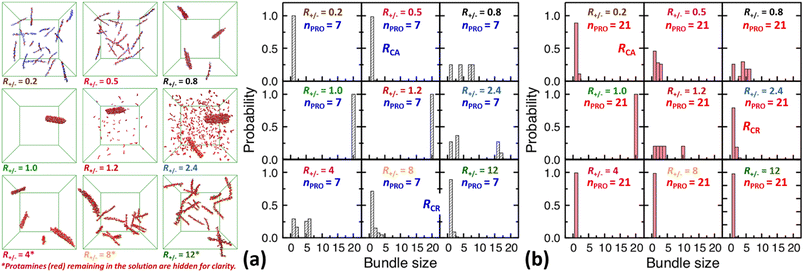 | ||
| Fig. 3 Final snapshots taken after 120 ns as well as DNA bundle size (NDNA = 1–20) distributions averaged over the last 20 ns of unbiased MD simulations started from homogeneous DNA solutions mixed with (a) 7-bead or (b) 21-bead protamine at R+/− of 0.2, 0.5, 0.8, 1, 1.2, 2.4, 4, 8, and 12. Na+ (blue) and Cl− (green) as well as some 7-bead protamine (red) remaining in the solution, i.e., not bound to DNA (grey), are hidden for clarity. The RCA and RCR denote the onset R+/− of DNA aggregation and redissolution, respectively, upon adding protamine to the solution. The average over 20 independent runs performed at R+/− of 0.5 and 2.4 are shown in Fig. S4-2, Section S4, ESI.† | ||
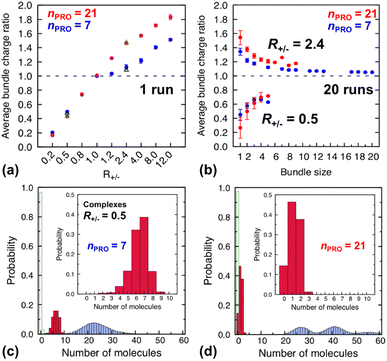 | ||
| Fig. 4 (Top) average charge ratios |qPRO/qDNA| of DNA bundles in a homogeneous mixture of DNA and 7-bead (blue) or 21-bead (red) protamine, which are shown as a function of (a) R+/− after averaging over the last 20 ns of a single simulation at each R+/− and (b) bundle size at R+/− of 0.5 (lower branch) and 2.4 (upper branch) after averaging over the last 20 ns of 20 independent simulations. Averages over 20 independent runs at R+/− = 0.5 and R+/− = 2.4 (Section S4, ESI†) are also shown as open black triangles (7-bead) and open green triangles (21-bead). (Bottom) distribution of each species, protamine (red box), Na+ (blue box) and Cl−(open green box), averaged over the last 20 ns of 20 independent runs for complexes formed at R+/− of 0.5 in presence of (c) 7-bead or (d) 21-bead protamine. Insets present an enlargement of the protamine distributions. | ||
In a large excess of DNA (R+/− = 0.2–0.5), the amount of protamine adsorbed to DNA is insufficient to overcome the strong repulsion acting between the highly-negatively-charged DNA complexes. This system, instead of entering the second stage, stays as a single-phase dispersion of 20 isolated DNA complexes at R+/− of 0.2 or 18–20 DNA bundles, i.e., 16–20 complexes and 1–2 short-lived pairs (or slightly less ∼16 bundles, i.e., ∼12 complexes and ∼4 pairs, when averaged over 20 independent runs, Fig. S4-1, Section S4, ESI†) at R+/− of 0.5. The short-lived pairs appearing at R+/− of 0.5 minimize the strong long-range repulsion between them by being perpendicular to each other near their tips, as discussed in Section S1, ESI.† These DNA pairs show a higher average charge ratio |qPRO/qDNA| than the complexes, which are slightly above and below R+/− of 0.5, respectively (0.58 ± 0.05 vs. 0.45 ± 0.08 when averaged over 20 independent runs; Fig. 4b, lower branch, blue, and Section S4, ESI†). This indeed demonstrates the theoretically-predicted charge disproportionation mechanism,57 which occurs when some complexes transfer some protamine to other complexes and bundles during transient encounters. Less-negatively-charged complexes approaching the charge ratio of 1 (charge neutrality) can attract each other, form bundles, and lead to a coexistence of more-charged complexes and less-charged bundles. However, the charge ratio around 0.5 is still too far from 1 and the repulsion between the complexes is too strong for any charge-disproportionation-induced assembly to occur. This is exactly the behaviour expected from the all-positive effective pairwise interaction curve at R+/− of 0.5, which has a very high free energy barrier and a shallow-and-still-positive free energy minimum (Fig. S1, magenta curve, Section S1, ESI†). A MD simulation started from a single bundle pre-formed at R+/− of 0.5 breaks the bundle immediately into a dispersion of isolated DNA complexes, pointing towards a probable thermodynamically stable state (Fig. S5, magenta curve, Section S5, ESI†).
On the other hand, when the DNA complexes are less negatively-charged at R+/− of 0.8, the system indeed proceeds to the second stage, locating the onset R+/− of DNA aggregation, RCA, somewhere between 0.5 and 0.8. Their average charge ratio |qPRO/qDNA| stays around 0.75 (Fig. 2a and 4a), but it is again lower on complexes (0.6) than on larger bundles (∼0.8) although the data are not shown here. Now that the charge ratios of less-charged complexes after charge disproportionation are closer to 1, they come closer to each other, align parallel to each other as seen in the umbrella sampling simulations performed without orientation restraints (Fig. S1, lower inset, red, Section S2, ESI†), and aggregate side by side to form four cylindrical bundles of size 1 to 6. Such a DNA aggregation mechanism induced by protamine reorganization between DNA is consistent with the effective short-range attraction originated from correlated positional fluctuation of adsorbed protamine (Fig. S1, black curve, Section S1, ESI†). Due to the dynamics slowed down upon coarsening, the nature of these small charged bundles is tricky to precisely assess between a thermodynamic equilibrium state and kinetically-trapped structures that eventually coalesce via charge disproportionation towards phase separation. However, since a MD simulation started from a single bundle pre-formed at R+/− of 0.8 also breaks the bundle into several small charged bundles within 1 ns (Fig. S5, black curve, Section S5, ESI†), these small bundles might rather correspond to a thermodynamic equilibrium state as well.
On the contrary, at the isoelectric point (R+/− = 1), a neutral single bundle forms extremely rapidly within 5 ns, as expected from the effective pairwise interaction curve with essentially no barrier and a very deep minimum (Fig. S1, green curve, Section S1, ESI†). In its immediate vicinity (R+/− = 1.2), the slightly-overcharged initial DNA complexes of charge ratio ∼1.15 forms an almost neutral single bundle with an average charge ratio of ∼1.03 quickly within 30 ns (Fig. 2a), releasing the redundant 10% of protamine to the solution as a result of charge-disproportionation-induced DNA aggregation. Such a neutral large bundle in solution most likely corresponds to a macroscopic phase separation or a two-phase coexistence of a DNA-rich phase (macroscopic DNA condensate or precipitate) and a DNA-poor phase (supernatant). This agrees with the experimental findings and the theoretical predictions.57,92–94
In larger excess of protamine (R+/− = 2.4–4), the initial overcharged DNA complexes of charge ratios 1.3–1.4 slowly assemble to 2–4 DNA bundles of size 1 to 17 (and larger bundles of size up to 20 with essentially no complex, when averaged on 20 independent runs at R+/− of 2.4, Fig. S4-1, Section S4, ESI†). Their average bundle charge ratios decrease down to 1.1–1.2 (Fig. 2a), and the decrease is more significant for larger bundles (∼1.1) than for complexes (∼1.4), as shown for R+/− of 2.4 from the average on the 20 independent runs (Fig. 4b, upper branch, blue, and Section S4, ESI†). This again indicates that the positively-overcharged complexes first approach each other in perpendicular orientations to minimize the electrostatic repulsion and finally form well-aligned bundles via charge disproportionation accompanied by protamine release into solution. The inner parts of the bundles remain neutral to ensure their stability, and the small net positive charges originate from the protamine present in excess on their surfaces.48 The entropy gain associated with the release of protamine and their Cl− counterions from the surface of the bundle into the solution as well as the correlated fluctuation of protamine in the bundle may drive the bundle aggregation. A depletion interaction induced by protamine remaining in solution may also contribute to the assembly.95,96 Again, as in the case of R+/− at 0.8, the dynamics slowed down upon coarsening hinders assessing the nature of these bundles between a thermodynamically stable state and kinetically-trapped structures that eventually coalesce. The effective interaction curves around these two R+/− values are indeed quite similar to each other (Fig. S1, blue and black curves, Section S1, ESI†). However, in the case of R+/− at 2.4, the latter type of nature, kinetic trap and eventual coalescence, is supported by a significant population of a single large bundle of size 20 newly observed in the extended sampling realized by 20 independent simulations at R+/− of 2.4 (Fig. S4-1, Section S4, ESI†) and by the persistence of a single large bundle pre-formed at R+/− of 2 during a 15 ns MD simulation (Fig. S5, Section S5, ESI†).
In even larger excess of protamine (R+/− = 8–12), the system stays mostly as highly-overcharged complexes (|qPRO/qDNA| = 1.4–1.5 and |qPRO*/qDNA| ≈ 1.3) due to strong repulsion between them, although some pairs and larger bundles with lower charge ratios (|qPRO/qDNA| = 1.3–1.4; |qPRO*/qDNA| ≈ 1.2) appear due probably to a limited amount of charge disproportionation. The homogeneous single phase of overcharged DNA complexes stabilized by long-range repulsion is the counterpart of the state stabilized in large excess of DNA (R+/− ≤ 0.5). Therefore, the onset R+/− for DNA redissolution or re-entrant condensation, RCR, where DNA re-enter into the solution due to strong overcharging, appears to be somewhere between 8 and 12. Such re-entrant behaviour in presence of protamine has been observed for long DNA chains under physiological salt conditions,97 short DNA fragments under low salt conditions,49–51 and other colloids46 and halloysite nanotubes.47 Such overcharging is known to be responsible for dissolution of other biomolecular condensates which are composed of RNA and arginine-rich intrinsically-disordered peptides and proteins as well.5,98,99
3.2. Protamine-length-dependent DNA assembly
On the other hand, after the three-fold increase of the protamine length, at R+/− of 0.5 we still observe ∼50% of small DNA bundles among a total of ∼11 bundles composed of ∼5 complexes, ∼3 pairs, and ∼3 trimers (or slightly more ∼60% of small bundles among ∼10.5 bundles composed of ∼4 complexes, ∼4 pairs, ∼2 trimers, and ∼0.5 tetramers, when averaged over 20 runs, Fig. S4-1, Section S4, ESI†), but at R+/− of 0.2 we observe only ∼10% of small bundles among a total of ∼18 bundles composed of ∼16 complexes and ∼2 pairs (Fig. 2d and 3b). The aggregation onset RCA is slightly lowered from right above 0.5 to right below 0.5, i.e., to the same level as found previously,74 with the longer 21-bead protamine. This is also consistent with a theoretical prediction57 and an experimental finding100 that longer poly-cations shift both RCA and RCR towards lower R+/−.
Indeed, the upper branches of Fig. 4a (R+/− > 1) and Fig. 4b (R+/− = 2.4) show that the red marks are positioned significantly farther from the blue marks, indicating that DNA complexes and bundles are significantly more overcharged with 21-bead protamine than with 7-bead protamine at the same R+/−. Stronger electrostatic repulsion between more overcharged DNA complexes and bundles with 21-bead protamine would redissolve DNA bundles at much lower R+/− than with 7-bead protamine. Indeed, the average charge ratios, 1.4–1.5, of DNA bundles formed with 7-bead protamine at R+/− of 8–12 are similar to charge ratio of 1.47 achieved with 21-bead protamine at a lower R+/− of 2.4, explaining the downward shift of redissolution onset RCR from 8–12 to ∼2.4 upon tripling the protamine length in excess of protamine.
On the other hand, in excess of DNA or in deficit of protamine (R+/− < 1), all the protamine available in the solution would eventually bind to DNA, regardless of their length. Indeed, the lower branches of Fig. 4a (R+/− ≤ 1) and Fig. 4b (R+/− = 0.5) show that essentially the same average charge ratios of DNA complexes and bundles, ∼0.75, ∼0.45, and ∼0.2, are produced at each R+/− by both protamine models (red ≈ blue) and they are essentially the same as the corresponding R+/− values. Hence, the influence of the protamine length on the DNA aggregation onset RCA would be minor in this regime, as observed here only by a slight decrease of R+/− value near 0.5.
Fig. 4c and d show the composition of complexes (NDNA = bundle size = 1) formed in excess of DNA at R+/− of 0.5 in presence respectively of short or long protamine. Comparing Fig. 4c and d, we notice that a significant quantity (∼14%, found in 50% of the independent runs, Section S4, ESI†) of complexes formed with 21-bead protamine are in fact naked DNA with no protamine adsorbed, while no naked DNA is found with 7-bead protamine. Na+ counterions are adsorbed on DNA regions depleted of protamine to reduce further the overall charge of the complexes. Interestingly, electrophoresis experiments performed on 146-bp DNA fragments in presence of salmon protamine in excess of DNA show also that negatively charged bundles coexist with isolated naked DNA.48 Condensation of DNA induced by protamine in last stage of spermiogenesis might also involve heterogeneous distribution of condensing agents exposing some naked DNA regions, in a way similar to nucleosome organization in somatic cell chromatin or by the bindings in patches of some proteins involved in bacterial chromatin.16,101
Thus, the protamine length dependence studied with our simple model not only resolves the discrepancy between our two CG models but also provides a molecular-level realization of the theoretical prediction on the effect of length-dependent entropy and correlated fluctuation of poly-cation57 as well as an additional insight that this length-dependent threshold shift is thus asymmetric, i.e., stronger for DNA redissolution in excess of protamine (R+/− > 1) than for DNA aggregation in excess of DNA (R+/− ≤ 1).
4. Conclusion
From a hypothesis that unscreened electrostatic interactions play a predominant role in protamine-controlled DNA condensation under low-salt conditions, we developed an extremely-simple electrostatic-oriented CG model which would be useful for real-time-and-length-scale simulations. This minimal bead-spring CG model represents the correct average linear charge densities on protamine and DNA chains for correct evaluation of long-range electrostatic interactions, while short-range bonding and steric interactions are described by generic terms taken from previous simulations without any sophisticated parameter-fitting procedure. MD simulations with this simple model reproduce semi-quantitatively the main low-salt-regime DNA phase behaviours observed by previous experiments and more-refined MD simulations, completing a microscopic picture of DNA aggregation and redissolution in a wide range of R+/−. Around the isoelectric point (R+/− ≈ 1), a single neutral DNA bundle forms extremely rapidly by a charge disproportionation mechanism, representing a two-phase coexistence between a DNA-rich phase and a supernatant. At a moderate excess of protamine (R+/− > 1), positively-charged DNA complexes coexist with less-positively-charged DNA bundles for a long period of time with occasional bundle aggregation. In a large excess of protamine (R+/− ≫ 1), a strong overcharging of DNA by protamine leads to a dispersion of strongly-positively-charged DNA complexes. In a large excess of DNA (R+/− ≪ 1), a similar situation of redissolution occurs with negatively-charged DNA complexes and naked DNA. The DNA precipitate coexisting with supernatant at the isoelectric point and the dispersion of strongly-charged DNA complexes at high or low R+/− are most likely both thermodynamic equilibrium phases. However, around the isoelectric point between these regimes, long-range electrostatic interactions slow down the dynamics of the small bundles coexisting in the semi-dilute DNA solution, preventing clear identification of this state between a finite-size equilibrium state and kinetically-arrested bundles. More work and longer simulations are needed to improve the sampling of such systems, and our simple CG model would be useful for this purpose. Indeed, when this model is employed for simulations with three-times-longer protamine and 20 independent simulations on each critical system to ensure sufficient sampling, the onsets of DNA aggregation and redissolution are both shifted towards lower R+/−, revealing an important role played by the length-dependent translational entropy and correlated fluctuation of condensing agents. Protamine length has a stronger effect on the redissolution onset than on the aggregation onset, and thus the range of R+/− inducing DNA condensation is narrower with longer protamine, agreeing even better with the low-salt-regime phase behaviour observed in the previous experiments and more-refined CGMD simulations, resolving discrepancy between our two CG models. We expect that our microscopic picture of liquid–liquid phase separation controlled by the charge, concentration, and length of condensing agents as a key organizational principle will help better understanding spermatogenesis in relation to the emerging concept of biomolecular condensates or membraneless organelles. The mechanism of the DNA-protamine bundle formation explored herein will help understanding other biomolecular condensates such as RNA droplets, which are critically controlled in cell and in vitro by RNA-to-protein ratio as another realization of coacervation. Such basic understandings will help designing various nano-complexes for gene therapy including mRNA vaccine carriers whose immune-stimulating effects strongly depend on the ratio between protamine and mRNA. The CG models developed and validated herein can be modified in a rather simple and straightforward manner to model other strong polyelectrolytes under low-salt conditions, mostly by assigning correct charge density along the chain to correctly capture the electrostatic interactions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research Foundation of Korea (2019R1A2C2003118 and 2021H1D3A2A01099453) and the computing resources were supported by KISTI (KSC-2022-CRE-0121).Notes and references
- P. Carrivain, A. Cournac, C. Lavelle, A. Lesne, J. Mozziconacci, F. Paillusson, L. Signon, J.-M. Victor and M. Barbi, Soft Matter, 2012, 8, 9285 RSC.
- B. A. Gibson, L. K. Doolittle, M. W. G. Schneider, L. E. Jensen, N. Gamarra, L. Henry, D. W. Gerlich, S. Redding and M. K. Rosen, Cell, 2019, 179, 470–484 CrossRef CAS PubMed.
- J. E. Henninger, O. Oksuz, K. Shrinivas, I. Sagi, G. LeRoy, M. M. Zheng, J. O. Andrews, A. V. Zamudio, C. Lazaris, N. M. Hannett, T. I. Lee, P. A. Sharp, I. I. Cissé, A. K. Chakraborty and R. A. Young, Cell, 2021, 184, 207–225 CrossRef CAS PubMed.
- G. Laflamme and K. Mekhail, Commun. Biol., 2020, 3, 773 CrossRef PubMed.
- A. N. Milin and A. A. Deniz, Biochemistry, 2018, 57, 2470–2477 CrossRef CAS PubMed.
- J. X. Tang and P. A. Janmey, J. Biol. Chem., 1996, 271, 8556–8563 CrossRef CAS PubMed.
- R. Bucki and P. A. Janmey, Curr. Opin. Colloid Interface Sci., 2016, 26, 84–89 CrossRef CAS.
- I. Borukhov, R. F. Bruinsma, W. M. Gelbart and A. J. Liu, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3673–3678 CrossRef CAS PubMed.
- B. R. Sabari, A. Dall'Agnese and R. A. Young, Trends Biochem. Sci., 2020, 45, 961–977 CrossRef CAS PubMed.
- M. Falk, Y. Feodorova, N. Naumova, M. Imakaev, B. R. Lajoie, H. Leonhardt, B. Joffe, J. Dekker and G. Fudenberg, Nature, 2019, 570, 395–399 CrossRef CAS PubMed.
- M. J. Rowley and V. G. Corces, Nat. Rev. Genet., 2018, 19, 789–800 CrossRef CAS PubMed.
- S. F. Banani, H. O. Lee, A. A. Hyman and M. K. Rosen, Nat. Rev. Mol. Cell Biol., 2017, 18, 285–298 CrossRef CAS PubMed.
- K. Rhine, V. Vidaurre and S. Myong, Annu. Rev. Biophys., 2020, 49, 247–265 CrossRef CAS PubMed.
- A. Leforestier and F. Livolant, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 9157–9162 CrossRef CAS PubMed.
- N. V. Hud and K. H. Downing, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 14925–14930 CrossRef CAS PubMed.
- V. B. Teif and K. Bohinc, Prog. Biophys. Mol. Biol., 2011, 105, 208–222 CrossRef CAS PubMed.
- A. Y. Grosberg, T. T. Nguyen and B. I. Shklovskii, Rev. Mod. Phys., 2002, 74, 329–345 CrossRef CAS.
- Y. Levin, Rep. Prog. Phys., 2002, 65, 1577–1632 CrossRef CAS.
- T. Akitaya, A. Seno, T. Nakai, N. Hazemoto, S. Murata and K. Yoshikawa, Biomacromolecules, 2007, 8, 273–278 CrossRef CAS PubMed.
- A. Estévez-Torres and D. Baigl, Soft Matter, 2011, 7, 6746–6756 RSC.
- E. Raspaud, M. Olvera de la Cruz, J. L. Sikorav and F. Livolant, Biophys. J., 1998, 74, 381–393 CrossRef CAS PubMed.
- Y. Burak, G. Ariel and D. Andelman, Biophys. J., 2003, 85, 2100–2110 CrossRef CAS PubMed.
- G. S. Manning, Q. Rev. Biophys., 1978, 11, 179–246 CrossRef CAS PubMed.
- J. D. Lewis, Y. Song, M. E. De Jong, S. M. Bagha and J. Ausió, Chromosoma, 2003, 111, 473–482 CrossRef PubMed.
- R. Balhorn, Genome Biol., 2007, 8, 227 CrossRef PubMed.
- R. E. Braun, Nat. Genet., 2001, 28, 10–12 CAS.
- L. R. Brewer, M. Corzett and R. Balhorn, Science, 1999, 286, 120–123 CrossRef CAS PubMed.
- R. Oliva and G. H. Dixon, Prog. Nucleic Acid Res. Mol. Biol., 1991, 40, 25–94 CAS.
- L. G. Harrison, H. E. Kasinsky, E. Ribes and M. Chiva, J. Exp. Zool., 2005, 303, 76–92 CrossRef PubMed.
- G. Martens, E. C. Humphrey, L. G. Harrison, B. Silva-Moreno, J. Ausió and H. E. Kasinsky, J. Cell. Biochem., 2009, 108, 1399–1409 CrossRef CAS PubMed.
- H. E. Kasinsky, J. M. Eirin-Lopez and J. Ausio, Protein Pept. Lett., 2011, 18, 755–771 CrossRef CAS PubMed.
- H. E. Kasinsky, S. Ellis, G. Martens and J. Ausió, Tissue Cell, 2014, 46, 415–432 CrossRef CAS PubMed.
- R. Balhorn, in A Clinician's Guide to Sperm DNA and Chromatin Damage, ed. A. Zini and A. Agarwal, Springer International Publishing, 2018, pp. 3–30 Search PubMed.
- G. R. Green, R. Balhorn, D. L. Poccia and N. B. Hecht, Mol. Reprod. Dev., 1994, 37, 255–264 CrossRef CAS PubMed.
- S. Papoutsopoulou, E. Nikolakaki, G. Chalepakis, V. Kruft, P. Chevaillier and T. Giannakouros, Nucleic Acids Res., 1999, 27, 2972–2980 CrossRef CAS PubMed.
- K. B. Chhetri, Y. H. Jang, Y. Lansac and P. K. Maiti, Biophys. J., 2022, 121, 4830–4839 CrossRef CAS PubMed.
- W. M. Aumiller Jr. and C. D. Keating, Nat. Chem., 2016, 8, 129–137 CrossRef PubMed.
- J. Söding, D. Zwicker, S. Sohrabi-Jahromi, M. Boehning and J. Kirschbaum, Trends Cell Biol., 2020, 20, 4–14 CrossRef PubMed.
- U. Lächelt and E. Wagner, Chem. Rev., 2015, 115, 11043–11078 CrossRef PubMed.
- I. Ruseska, K. Fresacher, C. Petschacher and A. Zimmer, Nanomaterials, 2021, 11, 1508 CrossRef CAS PubMed.
- F. L. Sorgi, S. Bhattacharya and L. Huang, Gene Ther., 1997, 4, 961–968 CrossRef CAS PubMed.
- V. Vijayanathan, T. Thomas and T. J. Thomas, Biochemistry, 2002, 41, 14085–14094 CrossRef CAS PubMed.
- Y. Wang, Z. Zhang, J. Luo, X. Han, Y. Wei and X. Wei, Mol. Cancer, 2021, 20, 33 CrossRef CAS PubMed.
- N. T. Jarzebska, S. Lauchli, C. Iselin, L. E. French, P. Johansen, E. Guenova, T. M. Kündig and S. Pascolo, Drug Deliv., 2020, 27, 1231–1235 CrossRef CAS PubMed.
- K.-J. Kallen, R. Heidenreich, M. Schnee, B. Petsch, T. Schlake, A. Thess, P. Baumhof, B. Scheel, S. D. Koch and M. Fotin-Mleczek, Hum. Vaccines Immunother., 2013, 9, 2263–2276 CrossRef CAS PubMed.
- P. Rouster, M. Pavlovic, E. Horváth, L. Forró, S. K. Dey and I. Szilagyi, Langmuir, 2017, 33, 9750–9758 CrossRef CAS PubMed.
- B. Katana, P. Rouster, G. Varga, S. Muráth, K. Glinel, A. M. Jonas and I. Szilagyi, ACS Appl. Bio Mater., 2020, 3, 522–530 CrossRef CAS PubMed.
- Y. Lansac, J. Degrouard, M. Renouard, A. C. Toma, F. Livolant and E. Raspaud, Sci. Rep., 2016, 6, 21995 CrossRef CAS PubMed.
- A. C. Toma, M. de Frutos, F. Livolant and E. Raspaud, Soft Matter, 2011, 7, 8847–8855 RSC.
- E. Raspaud, J. Pelta, M. de Frutos and F. Livolant, Phys. Rev. Lett., 2006, 97, 068103 CrossRef PubMed.
- S. Motta, P. Brocca, E. Del Favero, V. Rondelli, L. Cantù, A. Amici, D. Pozzi and G. Caracciolo, Appl. Phys. Lett., 2013, 102, 053703 CrossRef.
- P. Sautiere, G. Briand, M. Gusse and P. Chevaillier, Eur. J. Biochem., 1981, 119, 251–255 CrossRef CAS PubMed.
- B. Y. Ha and A. J. Liu, Phys. Rev. Lett., 1997, 79, 1289–1292 CrossRef CAS.
- B. Y. Ha and A. J. Liu, Phys. Rev. Lett., 1998, 81, 1011–1014 CrossRef CAS.
- B.-Y. Ha and A. J. Liu, Europhys. Lett., 1999, 46, 624–630 CrossRef CAS.
- A. M. Tom, R. Rajesh and S. Vemparala, J. Chem. Phys., 2016, 144, 034904 CrossRef PubMed.
- R. Zhang and B. I. Shklovskii, Phys. A, 2005, 352, 216–238 CrossRef CAS.
- M. L. Henle and P. A. Pincus, Phys. Rev. E, 2005, 71, 060801 CrossRef PubMed.
- M. Sayar and C. Holm, Europhys. Lett., 2007, 77, 16001 CrossRef.
- M. Sayar and C. Holm, Phys. Rev. E, 2010, 82, 031901 CrossRef PubMed.
- N. T. Jarzebska, M. Mellett, J. Frei, T. M. Kündig and S. Pascolo, Pharmaceutics, 2021, 13, 877 CrossRef CAS PubMed.
- H. He, J. Ye, E. Liu, Q. Liang, Q. Liu and V. C. Yang, J. Controlled Release, 2014, 193, 63–73 CrossRef CAS PubMed.
- C. Tros de Ilarduya, Y. Sun and N. Düzgüneş, Eur. J. Pharm. Sci., 2010, 40, 159–170 CrossRef CAS PubMed.
- F. Liu and L. Huang, J. Controlled Release, 2002, 78, 259–266 CrossRef CAS PubMed.
- L. Rettig, S. P. Haen, A. G. Bittermann, L. von Boehmer, A. Curioni, S. D. Krämer, A. Knuth and S. Pascolo, Blood, 2010, 115, 4533–4541 CrossRef CAS PubMed.
- Y.-J. Park, J. F. Liang, K. S. Ko, S. W. Kim and V. C. Yang, J. Gene Med., 2003, 5, 700–711 CrossRef CAS PubMed.
- Y.-S. Choi, J. Y. Lee, J. S. Suh, Y.-M. Kwon, S.-J. Lee, J.-K. Chung, D.-S. Lee, V. Yang, C.-P. Chung and Y.-J. Park, Biomaterials, 2010, 31, 1429–1443 CrossRef CAS PubMed.
- B. Scheel, S. Braedel, J. Probst, J.-P. Carralot, H. Wagner, H. Schild, G. Jung, H.-G. Rammensee and S. Pascolo, Eur. J. Immunol., 2004, 34, 537–547 CrossRef CAS PubMed.
- M. Tusup and S. Pascolo, in RNA Vaccines: Methods and Protocols, ed. T. Kramps and K. Elbers, Springer New York, New York, NY, 2017, pp. 155–163 Search PubMed.
- A. P. Lyubartsev and L. Nordenskiöld, J. Phys. Chem., 1995, 99, 10373–10382 CrossRef CAS.
- N. Grønbech-Jensen, R. J. Mashl, R. F. Bruinsma and W. M. Gelbart, Phys. Rev. Lett., 1997, 78, 2477–2480 CrossRef.
- M. J. Stevens, Biophys. J., 2001, 80, 130–139 CrossRef CAS PubMed.
- K.-C. Lee, I. Borukhov, W. M. Gelbart, A. J. Liu and M. J. Stevens, Phys. Rev. Lett., 2004, 93, 128101 CrossRef PubMed.
- A. Mukherjee, A. de Izarra, J. Degrouard, E. Olive, P. K. Maiti, Y. H. Jang and Y. Lansac, ACS Nano, 2021, 15, 13094–13104 CrossRef CAS PubMed.
- R. Oliva and C. Mezquita, Biochemistry, 1986, 25, 6508–6511 CrossRef CAS PubMed.
- R. Oliva, D. Bazett-Jones, C. Mezquita and G. H. Dixon, J. Biol. Chem., 1987, 262, 17016–17025 CrossRef CAS PubMed.
- R. Kharidia, K. A. Friedman and J. F. Liang, Biochemistry (Moscow), 2008, 73, 1162–1168 CrossRef CAS PubMed.
- C. Bechara and S. Sagan, FEBS Lett., 2013, 587, 1693–1702 CrossRef CAS PubMed.
- J. Hoyer and I. Neundorf, Acc. Chem. Res., 2012, 45, 1048–1056 CrossRef CAS PubMed.
- N. Kulesskaya, E. Mugantseva, R. Minkeviciene, N. Acosta, A. Rouhiainen, J. Kuja-Panula, M. Kislin, S. Piirainen, M. Paveliev and H. Rauvala, Front. Cell Dev. Biol., 2022, 10, 865275 CrossRef PubMed.
- P. J. Hagerman, Biopolymers, 1982, 20, 1503–1535 CrossRef PubMed.
- N. Korolev, D. Luo, A. P. Lyubartsev and L. Nordenskiöld, Polymers, 2014, 6, 1655–1675 CrossRef.
- A. Savelyev, Phys. Chem. Chem. Phys., 2012, 14, 2250–2254 RSC.
- S. Guilbaud, L. Salomé, N. Destainville, M. Manghi and C. Tardin, Phys. Rev. Lett., 2019, 122, 028102 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in 't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- J. P. Valleau, Chem. Phys., 1989, 129, 163–175 CrossRef CAS.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- M. Souaille and B. Roux, Comput. Phys. Commun., 2001, 135, 40–57 CrossRef CAS.
- N-Body Shop, University of Washington, https://faculty.washington.edu/trq/hpcc/tools/fof.html, accessed July 2, 2014.
- Y. C. Kwon, D. Nunley, J. P. Gardner, M. Balazinska, B. Howe and S. Loebman, in Scientific and Statistical Database Management, ed. M. Gertz and B. Ludäscher, Springer-Verlag, Berlin Heidelberg, 2010, pp. 132–150 Search PubMed.
- B. I. Shklovskii, Phys. Rev. E, 1999, 60, 5802–5811 CrossRef CAS PubMed.
- T. T. Nguyen, I. Rouzina and B. I. Shklovskii, J. Chem. Phys., 2000, 112, 2562–2568 CrossRef CAS.
- T. T. Nguyen and B. I. Shklovskii, J. Chem. Phys., 2001, 115, 7298–7308 CrossRef CAS.
- S. Asakura and F. Oosawa, J. Polym. Sci., 1958, 33, 183–192 CrossRef CAS.
- D. Marenduzzo, K. Finan and P. R. Cook, J. Cell Biol., 2006, 175, 681–686 CrossRef CAS PubMed.
- K. Besteman, K. van Eijk and S. G. Lemay, Nat. Phys., 2007, 3, 641–644 Search PubMed.
- P. R. Banerjee, A. N. Milin, M. M. Moosa, P. L. Onuchic and A. A. Deniz, Angew. Chem., Int. Ed., 2017, 56, 11354–11359 CrossRef CAS PubMed.
- I. Alshareedah, T. Kaur, J. Ngo, H. Seppala, L.-A. D. Kounatse, W. Wang, M. M. Moosa and P. R. Banerjee, J. Am. Chem. Soc., 2019, 141, 14593–14602 CrossRef CAS PubMed.
- F. Amaduzzi, F. Bomboi, A. Bonincontro, F. Bordi, S. Casciardi, L. Chronopoulou, M. Diociaiuti, F. Mura, C. Palocci and S. Sennato, Colloids Surf., B, 2014, 114, 1–10 CrossRef CAS PubMed.
- R. T. Dame, Mol. Microbiol., 2005, 56, 858–870 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2na00847e |
| This journal is © The Royal Society of Chemistry 2023 |