Integrating machine learning and digital microfluidics for screening experimental conditions†
Fatemeh
Ahmadi
 abc,
Mohammad
Simchi
abc,
Mohammad
Simchi
 d,
James M.
Perry
d,
James M.
Perry
 b,
Stephane
Frenette
b,
Habib
Benali
ab,
Jean-Paul
Soucy
b,
Stephane
Frenette
b,
Habib
Benali
ab,
Jean-Paul
Soucy
 be,
Gassan
Massarweh
e and
Steve C. C.
Shih
be,
Gassan
Massarweh
e and
Steve C. C.
Shih
 *abc
*abc
aDepartment of Electrical and Computer Engineering, Concordia University, 1455 de Maisonneuve Blvd. West, Montréal, Québec H3G 1M8, Canada. E-mail: steve.shih@concordia.ca; Tel: +1 (514) 848 2424 x7579
bPERFORM Centre, Concordia University, 7200 Sherbrooke Street West, Montréal, Québec H4B 1R6, Canada
cCentre for Applied Synthetic Biology, Concordia University, 7141 Sherbrooke Street West, Montréal, Québec H4B 1R6, Canada
dDepartment of Mechanical & Industrial Engineering, University of Toronto, 5 King's College Rd, Toronto, Ontario M5S 3G8, Canada
eMcConnell Brain Imaging Centre, Montreal Neurological Institute, McGill University, 3801 University Street, Montréal, Québec H3A 2B4, Canada
First published on 23rd November 2022
Abstract
Digital microfluidics (DMF) has the signatures of an ideal liquid handling platform – as shown through almost two decades of automated biological and chemical assays. However, in the current state of DMF, we are still limited by the number of parallel biological or chemical assays that can be performed on DMF. Here, we report a new approach that leverages design-of-experiment and numerical methodologies to accelerate experimental optimization on DMF. The integration of the one-factor-at-a-time (OFAT) experimental technique with machine learning algorithms provides a set of recommended optimal conditions without the need to perform a large set of experiments. We applied our approach towards optimizing the radiochemistry synthesis yield given the large number of variables that affect the yield. We believe that this work is the first to combine such techniques which can be readily applied to any other assays that contain many parameters and levels on DMF.
Introduction
Digital microfluidics (DMF) is a liquid-handling technique capable of automating complex biological1–5 and chemical assays.6–10 Droplets are placed on an array of electrodes that are deposited with a dielectric and coated with a hydrophobic layer. Users are able to create droplet actuation sequences11,12 such that droplets can move, dispense, merge, split, and mix13–16 simply through applying electrical potentials to an electrode. The advantages of automation have enabled DMF to be applied to multiple areas including rapid diagnostics,17–20 cell-based screening assays,4,21 and optimization of chemical synthesis parameters.7,22–25 These assays are well-suited to be implemented on digital microfluidic devices given the precise control of individual samples, allowing for multistep series of reactions and multiple conditions to be executed and analyzed on a device.While there are many types of biological and chemical assays that can be implemented on a DMF device, the number of experiments that can be performed in parallel is limited. The main reason for the limitation is the number of electrodes that can be accommodated on a single DMF device. The low electrode density only allows for tens of reactions to be performed in parallel. There are physical solutions to increase the electrode density (and to increase reactions in parallel): vertical addressing techniques,26–29 inkjet-printing techniques,30 and three dimensional stacking of substrates;31 however, there continues to be limits on the number of reactions or conditions that can be handled on the platform due to unreliable droplet movement, μL-volume requirements, and evaporation or biofouling challenges.
One method that optimizes screening conditions without physical implementation is the use of machine learning. Machine learning has the ability to predict the performance of your assay based on your input parameters that affect the assay and models the output response without costly fabrication and design iterations. Currently, the pairing of microfluidics and machine learning has been used for optimizing droplet generator designs,32 tumor cell classification,33 and image-based cell sorting techniques.34 Using these methods together, the authors were able to perform a set of experiments on the device and develop models to predict the output.35,36 Microfluidic-based optimization studies can also benefit from design-of-experiments (DoE) including full factorial37,38 and fractional factorial39,40 designs for an efficient screening of a multiparameter assay. These demonstrations, though few, represent the power of coupling microfluidics with either machine learning or DoE together.
Here, we report a new method for assay optimization on DMF, centered on the combination of digital microfluidics and design-of-experiments to optimize the output yield. We employed a method called OFAT (one-factor-at-a-time) to determine the significant parameters that affect the output. This method starts with automating the base experiment followed by ‘n’-parameter variable experiments. The variable experiments contain the base level parameters except that a change is made to the level (increasing or decreasing) for one of the parameters. Through statistical analysis, we determine the most significant factors by comparing the variable with the base case. Next, we obtain a database of output values to develop a model to predict the optimal output using OFAT and machine learning techniques. The new method was used to implement a seven-parameter optimization of fluorination labeling for [18F]FDG radiotracers. The resulting model provided an ideal and a practical optimized protocol, which reduced the synthesis time and improved the synthesis yield, relative to those from previous work.7,22,25 More importantly, these results establish the first report (to our knowledge) to combine digital microfluidics and machine learning algorithms enabling applications that require optimization of screening conditions. We propose that the new methods represent a useful development for users interested in using digital microfluidics for their biological and chemical screening applications.
Results and discussion
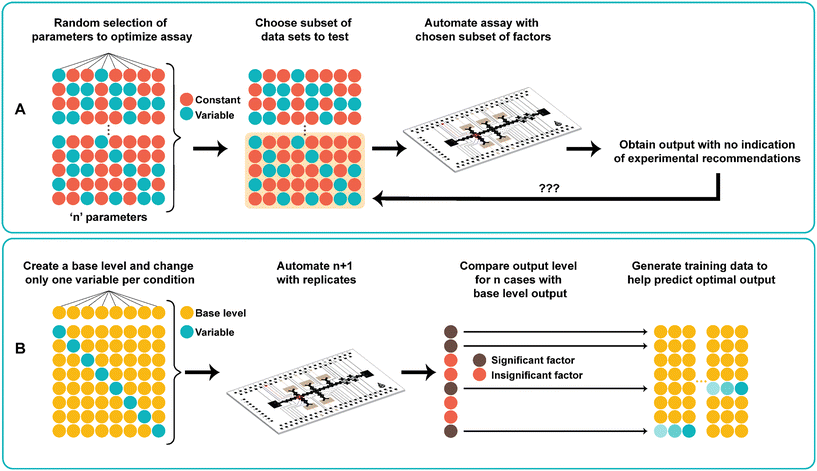
One-factor-at-a-time
In traditional digital microfluidic assays, several different parameters are tested to optimize assay conditions performed on DMF. These include titrating concentrations of all the combined reagents as well as adjusting reaction times and temperatures. As shown in Fig. 1A, the traditional approach to finding the optimal assay conditions uses a trial-and-error search process. The process starts by carefully choosing a set of conditions either without a priori knowledge or with values based on previously reported data. Given potentially vast numbers of possible parameter combinations, it is not practical to perform all experiments on the DMF device due to device limitations (e.g., electrode density) and tedium related to repeated device fabrication. Therefore, only a subset of the optimization landscape is tested, and a sample dataset is produced. However, this method does not help predict optimal assay parameters, nor identify any critical interactions between the parameters and the output.Fig. 1B shows the use of one-factor-at-a-time (OFAT), a systematic approach towards finding the optimal levels for ‘n’ parameters without requiring to perform a large set of experiments. The method starts with designing a base level for each parameter (values are either obtained from the literature or randomly generated). Next, for each parameter, we change the level of the parameter (increasing or decreasing the base value) while keeping the other parameters at the base level. Together with the base set, this creates n + 1 experiments to be automated on the DMF device. After obtaining the output from the variable case, we compare with the base level output to determine the impact (significant or non-significant) of each individual parameter on the assay. The use of OFAT provides several advantages compared to the traditional trial-and-error search process. First, it significantly reduces the number of experiments that need to be performed on the device. For example, a 33 full factorial experiment requires 27 experiments (and 108 with replicates41), but with OFAT, only 4 experiments (1 base case with 3 variable cases; 12 experiments with 3 biological replicates) are needed. Second, the parameters that affect the assay can be determined after performing OFAT. As such, this eliminates experiments with insignificant parameters, which saves time and costs in relation to device fabrication and assay preparation. Third, the method is compatible with any biological and chemical-based assay that requires many parameters and levels. Although we applied it to one type of assay (see below), the same method can be applied to the synthesis of other materials42,43 and to the metabolic production of pharmaceutical compounds44 that require optimization of multiple parameters and levels for optimal output production.
We evaluated the OFAT method by employing radiosynthesis of [18F]FDG7,22,25 on DMF using mannose triflate as the substrate and performed fluorination of [18F] to produce [18F]FDG (Fig. S1†). We used this assay to showcase our method given that there are seven parameters to be optimized (more than the typical assay performed on DMF) and there are data presented in the literature such that we can verify improvements in prediction accuracy and in the overall yield. In these assays, it started with delivering the [18F] via a syringe system to the reaction center on the device. Next, the [18F] was activated through evaporation at 120 °C, followed by dispensing droplets containing mannose triflate and mixing with the evaporated [18F] at 85 °C. Deprotection of the intermediate product was performed by hydrolysis with sodium hydroxide at room temperature producing [18F]FDG. We chose to produce [18F]FDG because this reaction has several different parameters, and we believe that the yield can be improved by using OFAT. Specifically, as shown by previous authors, the synthesis is affected by seven parameters.7,22,25 With each parameter broken intro 3 possible levels, we are required to automate 37 = 2187 reactions (without replicates) to obtain the full space of experiments – a nearly impossible task with the current DMF devices and fabrication methods. Using the OFAT approach, we can significantly reduce the number of experiments that are performed on the device and identify the significant parameters that affect the yield. The results comparing the traditional method with the OFAT method for optimizing synthesis are recorded in Fig. 2.
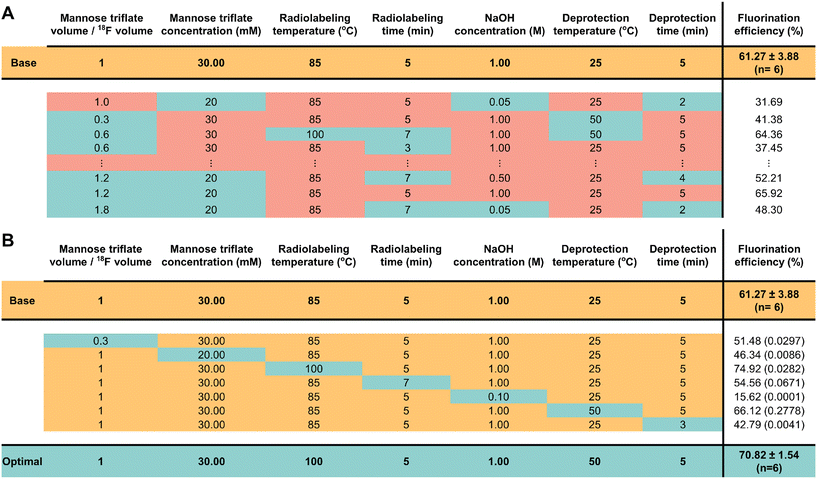 | ||
| Fig. 2 Comparison of the fluorination efficiency using traditional optimization vs. OFAT approaches. (A) The traditional approach changes the level of each parameter based on literature values. Each experiment (row) shows constant (red) and variable (blue) values. The constant values represent the parameter values kept at levels found from the literature and the variables represent the parameter values changing towards favorable conditions. For the full set of experiments performed, see Table S1.† (B) In OFAT, we use a base case (yellow) and create variable experiments by changing the level of only one variable (blue) while keeping all other levels at the base case. The optimal fluorination efficiency (blue) is obtained after 1 + 7 experiments. The t-values comparing the variable to the base case are shown in brackets beside the fluorination efficiency. | ||
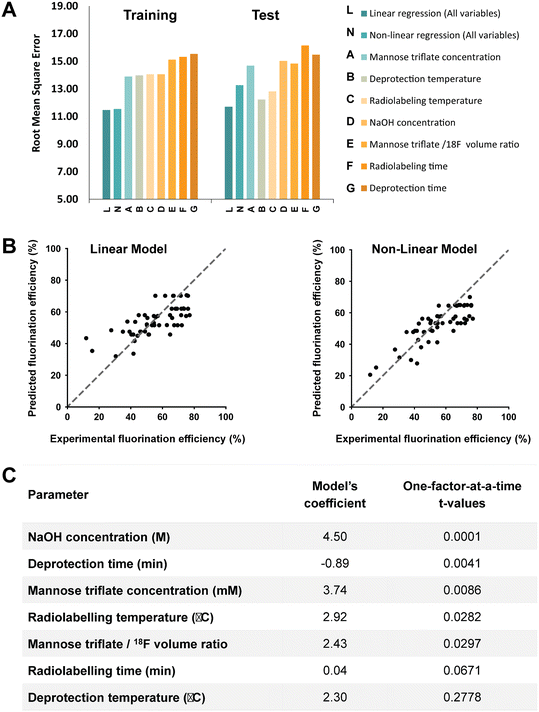
As shown in Fig. 2, the [18F]FDG fluorination efficiency results are shown for the different synthesis parameters for the traditional and OFAT methods. In the traditional approach, a base case was obtained by Keng et al.22 and Chen et al.25 and the parameters were changed via recommendation from previous work – lowering material concentrations, reducing synthesis time (higher temperatures, faster reaction), and optimizing the volume ratio between the carrier molecules and [18F]fluoride. For OFAT, eight experiments were created, starting from the same base case as the traditional approach, and we created seven variable experiments. Two key results were obtained from OFAT. First, we observed significant changes in the fluorination efficiency values for the variable output when compared to the base level output. A t-test revealed significant differences for parameters such as mannose triflate and NaOH concentration, radiolabeling temperature, and deprotection time (at 95% confidence level; P < 0.05) except for radiolabeling time and deprotection temperature. Second, OFAT resulted in a higher fluorination efficiency of 70.82 ± 1.54% compared to the traditional approach, which after ten experiments, (see Table S1† for the complete list of conditions), the best efficiency that we could obtain was 65.92%. The OFAT improvement is likely related to starting with a careful choice of a base level.7,22,25 Regardless, the data presented in Fig. 2 demonstrate that OFAT can help identify the significant parameters which can be useful for building a predictive model for the response as a function of the input variable (see below) and for converging towards maximizing the production of the output.
Constructing an output model with OFAT
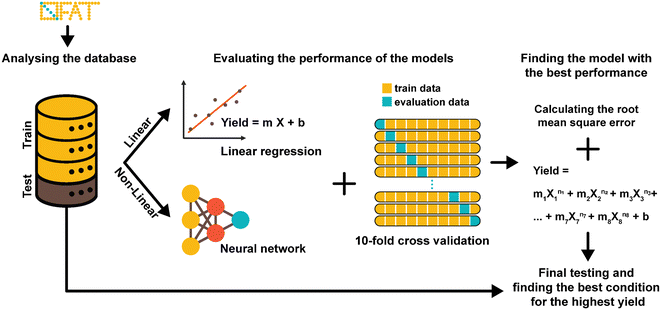
A key advantage of OFAT is that we can apply machine learning tools to produce a predictive model based on a small experimental dataset. A database of output values (obtained either from a standardized data depot45 or literature-based output values) can be used to generate a single input linear model (to determine the effects individual parameters have on the synthesis yield), a multiple input linear model (to determine interaction effects on the synthesis yield), or a non-linear model (to determine high order effects) (Fig. 3). Given that our radiosynthesis test case does not have standardized data from an online database, we used both experimentally derived and reported conditions22,25 to generate a database of 55 experiments with 80% of values used as the training set and 20% used as the test set (see Table S2† for the database). The initial experimental conditions were obtained from previous work and then were followed based on the recommendations from the literature and our own experience with the system. Toward the end of the optimization process, the experiments were more focused around the optimum points, and as a result, our database of values is distributed around the optimum point conditions. This approach could create an imbalance and can overfit the model and the model can be biased in favor of the majority datapoints.46,47 To circumvent this issue, which is common in many applications that do not have a large-set of values46,48 (e.g., disease diagnosis49), an oversampling algorithm was implemented to minimize the number of performed experiments. The algorithm replicates datapoints for conditions that have at least one “rare” (i.e., less frequent) tested condition (see Table S2† for ‘rare’ conditions) in the training dataset to improve the data distribution balance and to prevent model bias and overfitting towards the more frequent datapoints.49–51 Each training set was 10-fold cross-validated with one test case and each were fitted to the linear or the neural network derived (non-linear) models. These models were evaluated by calculating the root-mean square error (RMSE) and provided a method to validate OFAT (i.e., the significant parameters) and to generate a predictive model for the response as a function of the input parameters. In this work, the fluorination efficiency from the assays was used as the output response with seven input parameters.The RMSE values generated from the training data and test data for the linear and non-linear models are shown in Fig. 4A. A linear regression was fitted to the experimental output in the single input linear model (Fig. S2†), which resulted in a range of RMSE values between 13.89 ± 1.1 and 15.53 ± 1.3 for the training data. In addition, the single model was evaluated with the test data, and as expected, the model showed relatively higher errors than the training data. The single model also falls short on accurately predicting the fluorination efficiency (see Fig. S3†), which suggests that using a single parameter model approach is not the ideal case to predict the fluorination efficiency output. However, a multiple interaction model that considers all the variables for fluorination efficiency shows decreases in the RMSE for the training (11.47 ± 1.0) and test (11.71) datasets. In fact, using our model against a test dataset (i.e., unseen parameter conditions), the accuracy was higher compared to the best-performing single model (Fig. 4B). We also hypothesized that using a non-linear regression model (higher-order factors) would improve the accuracy; however, as shown, the non-linear model showed similar accuracy (RMSE for the training 11.54 ± 1.2 and test 13.26) compared to the single model, which is likely due to the limited number of experiments available in our database.52
From OFAT we identified significant factors via the t-test for base and variable cases. Using the multiple linear regression model, we verified the significant factors from OFAT by estimating the model's coefficients. As shown in Fig. 4C, we ordered the most significant factors by increasing t-values, with the most substantial effects determined from OFAT at the top. Generally, the highest coefficient from our multiple linear models matches with the significant factors determined by OFAT. For deprotection temperature, we calculated a relatively higher coefficient in contrast to what we expected from OFAT t-values. There are a number of potential causes for the difference: (1) a limited number of experiments and levels (25–50 °C) were studied with the parameter and (2) to train an accurate model requires a relatively large dataset (>1000s).32,53 However, we expect the accuracy to improve if more replicates or levels are automated. In these cases, we can still leverage the OFAT (only using the significant parameters) and machine learning approach that we developed here.
Improving radiosynthesis yield
Interestingly, OFAT and the model suggest that there are only five parameters that are significant to FDG incorporation. The parameters, NaOH concentration, mannose triflate concentration, radiolabeling temperature and mannose to [18F] volume ratio have significant positive coefficients; increasing these parameters results in higher FDG incorporation. Having a negative coefficient for deprotection time suggests that a shorter deprotection time coupled with higher concentrations, volume ratios, and radiolabeling temperature will increase the final FDG incorporation. However, increasing concentrations, volume ratios, and radiolabeling temperature will practically require longer deprotection time25 and therefore the increase will eventually plateau. In the completed model, constructed from only the significant parameters and coefficients (Fig. S4†), we used it to predict the optimal FDG incorporation value. We used the model to predict 100% fluorination efficiency and the maximum was achieved when we used an equal ratio of mannose/[18F] volume, 90 mM mannose triflate, 110 °C radiolabeling temperature, 5 minutes for radiolabeling time, 1.4 M NaOH, and 10 minutes at 50 °C for deprotection, (Fig. 5A). However, these conditions for radiosynthesis were nearly impossible to implement to completion on chip. For example, increasing the temperature from room to 100 °C causes several of the reagent droplets to decrease in droplet movement fidelity on the device (Fig. S5†). When droplets contained 1.4 M NaOH, the movement fidelity was poor (data not shown), which prevented the completion of the radiosynthesis process. Also, evaporation occurs faster at 110 °C for the concentrated mannose triflate, which makes droplet movement nearly impossible. Similar conditions were obtained for the 90 and 95% incorporation; however, experimental success was shown for the 85% model incorporation, which produced a similar fluorination efficiency value of 84.1%.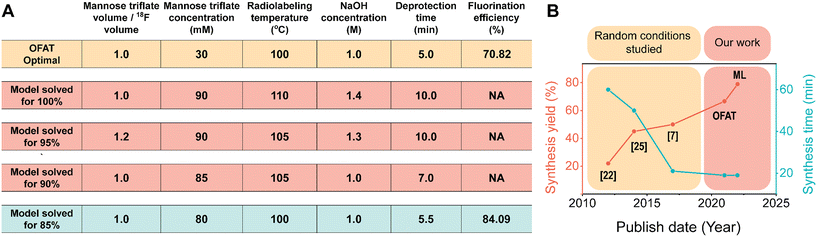 | ||
| Fig. 5 Optimal fluorination efficiency. (A) Comparing the fluorination efficiency for [18F]FDG radiosynthesis through OFAT and predictive modeling based on the significant parameters. Model conditions that were not practically possible to automate on our DMF device are highlighted in red. The optimal conditions obtained from OFAT (yellow) and the model (blue) are shown. (B) Graphical illustration comparing the total crude radiochemical yield achieved by OFAT assay optimization and comparing it with previous publications.7,22,25 The total crude radiochemical yield is determined by the product of the fluorination efficiency and the radioactivity recovery (94.1%; Table S3†). | ||
Surprisingly, the conditions derived at 85% were very similar to the OFAT optimal conditions (the only difference being the mannose triflate concentration 30 vs. 80 mM). This improvement is likely related to starting with a base case that is already close to the optimal conditions. A comparison of our method and previous work is presented in Fig. 5B. As shown, with the improved DMF design and the developed screening (OFAT) and optimization (ML) methods, the overall synthesis yield from OFAT resulted in an improved yield of 66.64% and a further increase to 79.13% with ML modeling. The overall synthesis time (∼ 19 ± 2 min; n = 6) also exhibited better performance compared to previous work. These improvements are critical, as increasing overall yield and reducing synthesis time provide the capability to supply more doses available for patients at the end of the synthesis.54
A final goal of the work was to demonstrate that our new method can be combined with other protocols and techniques to optimize the radiochemical yield. Optimization of the [18F]FDG yield efficiency is a continuous challenge due to the short half-life of [18F]. There have been multiple efforts towards developing automation systems,7,22,25,55 improving reagent delivery mechanisms,54–56 and integrating interfaces to couple with chromatography systems for purification57–59 to speed up the delivery of the tracer to the patient. We designed an on-chip purification scheme that purifies the sample immediately after synthesis. Discs with 2 or 6 mm diameter were created with alumina beads mixed with the PDMS elastomer prior to curing and directly placed on the DMF device (Fig. S6A†). After synthesis, the droplet with the incorporation of [18F]FDG was brought to the disc for incubation and moved around the adjacent electrodes to enhance the purification process of removing both the Kryptofix and unreacted [18F] and F−. After incubation, the droplet was actuated away from the disc and manually pipetted for downstream processing. Using this technique, we observed high purity (∼93.05 ± 2.46%) with 6 mm discs incubated for over 40 minutes (Fig. S6B†). All the final optimized results related to radioactive recovery, incorporation, and purity are shown in Table S3 in the ESI.† To our knowledge, this work is the first to integrate radiotracer synthesis with on-chip purification and to use OFAT optimization and ML modelling.
Experimental
Reagents, chemicals, and equipment
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 dpi transparent photomask (CAD/Art Services Inc., Bandon, OR), AZ1500 positive photoresist coated glass slides (Telic, Valencia, CA, USA), a CR-4 chromium etchant (OM Group, Cleveland, OH, USA), an AZ-300 T photoresist stripper (Integrated Micro Materials, Argyle, TX, USA), an MF321 developer (Kayaku Advanced Materials, Westborough, MA, USA), gamma-methacryloxypropyl trimethoxysilane (Silane A-174) and parylene C pellets (Specialty Coating Systems Inc., Indianapolis, IN, USA), Teflon™ AF 1600 (The Chemours Company, Wilmington, DE, USA), and indium tin oxide (ITO)-coated glass slides, RS = 15–25 Ω (cat no. CG-61IN-S207, Delta Technologies, Loveland, CO, USA) were used. Additional solvents and chemicals used for microfluidic chip fabrication, including acetone (cleanroom lab grade) and isopropanol (IPA, cleanroom lab grade), were purchased from Sigma-Aldrich (Oakville, ON, CA). The polylactic acid (PLA) material for 3D printing was purchased from Shop3D (Mississauga, ON, CA), and polydimethylsiloxane (PDMS) from Krayden Inc. (Westminster, CO, USA). DI water had a resistivity of 15 MΩ cm−1.
400 dpi transparent photomask (CAD/Art Services Inc., Bandon, OR), AZ1500 positive photoresist coated glass slides (Telic, Valencia, CA, USA), a CR-4 chromium etchant (OM Group, Cleveland, OH, USA), an AZ-300 T photoresist stripper (Integrated Micro Materials, Argyle, TX, USA), an MF321 developer (Kayaku Advanced Materials, Westborough, MA, USA), gamma-methacryloxypropyl trimethoxysilane (Silane A-174) and parylene C pellets (Specialty Coating Systems Inc., Indianapolis, IN, USA), Teflon™ AF 1600 (The Chemours Company, Wilmington, DE, USA), and indium tin oxide (ITO)-coated glass slides, RS = 15–25 Ω (cat no. CG-61IN-S207, Delta Technologies, Loveland, CO, USA) were used. Additional solvents and chemicals used for microfluidic chip fabrication, including acetone (cleanroom lab grade) and isopropanol (IPA, cleanroom lab grade), were purchased from Sigma-Aldrich (Oakville, ON, CA). The polylactic acid (PLA) material for 3D printing was purchased from Shop3D (Mississauga, ON, CA), and polydimethylsiloxane (PDMS) from Krayden Inc. (Westminster, CO, USA). DI water had a resistivity of 15 MΩ cm−1.
Device fabrication and operation
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) in a Pyrex dish for 15 min followed by a thorough rinse with 2-propanol and water, air drying, and baking on a hotplate at 80 °C.
1 v/v) in a Pyrex dish for 15 min followed by a thorough rinse with 2-propanol and water, air drying, and baking on a hotplate at 80 °C.
The devices were coated with 15 g of parylene-C (7 μm) as a dielectric layer in a SCS Labcoater 2 PDS 2010 (Specialty Coating Systems, Indianapolis, IN, USA) and then coated with Teflon™ AF 1600 (150 nm) in a Laurell spin coater (North Wales, PA, USA) set to 1500 rpm for 60 s with 300 rpm s−1 acceleration followed by 10 min baking at 165 °C. For the electrical ground plate, ITO-coated glass slides were cut into 1′′ × 3′′, coated with Teflon™ AF 1600 by spin coating, and then post-baked as described above. The ITO plate was then placed on top of the substrate separated with two pieces of double-sided tape (3M), resulting in an inter-plate gap of ∼140 μm.
For automated radiotracer synthesis, we used our automation system containing optocoupler switches, a thermoelectric device, and a reagent delivery system (see Fig. S7–S9† for temperature and reagent delivery control setups). Briefly, the thermoelectric device was controlled using an Arduino microcontroller (Arduino Uno, Italy) and a driver motor consisting of a two half-bridge driver chip and a low resistance N-channel MOSFET (Amazon, Mississauga, ON, Canada) following Perry et al.1,60 The reagent delivery system was built using a stepper motor that was also connected and controlled using an Arduino microcontroller.1 Droplet operation was controlled using our open-source software (see: https://bitbucket.org/shihmicrolab/f_ahmadi_2022) that was used to apply high-voltage potentials to a stack of optocoupler switches (the design of the stack was described elsewhere61).
To prepare for radiotracer synthesis on the device, a DMF device (only the bottom plate) was loaded onto a pogo-pin holder consisting of 104 pogopins with a spacing of 3 mm which will deliver 104 individual voltage inputs to the contact pads of the device to apply a sine wave 160 VRMS potential at 15 kHz between the top and bottom plates. The 14.8 × 14.8 mm2 thermoelectric device was directly placed below the bottom plate and will provide heating and cooling to 10 central electrodes on the device, which we set as the ‘reaction site’ (Fig. S1†). A syringe tube was fixed with tape on the pogo-pin holder and directed to the central electrode in the reaction site to deliver the radioisotope. After evaporation of [18F]fluoride (∼ 10 min), an ITO top plate was placed on top of the bottom substrate such that the edges of the ITO were aligned to the edges of the reservoir electrodes and were affixed by two pieces of double-sided tape. For purification experiments, discs were sandwiched between the top and bottom plates and aligned with a set of five electrodes, which we refer to as the ‘purification site’. When the bottom-plate was secured by the pogo pin holder and top-plate, reagent reservoirs were loaded by pipetting the reagents at the edge of the reservoir with the same applied voltage and frequency as above to draw the liquids into the reservoirs.
One factor at a time and predictive modeling
One-factor-at-a-time consisted of optimizing seven parameters (mannose triflate to [18F]fluoride volume ratio, mannose triflate concentration, sodium hydroxide concentration, radiolabeling temperature, deprotection temperature, radiolabeling time, deprotection time) that will potentially influence the FDG fluorination efficiency. The approach – also known as “OFAT” – started with base values for each parameter which was taken a priori from previous studies.22,25,62,63 Using base values, we performed the radiotracer synthesis on the chip (as described below) to determine the deprotected FDG fluorination efficiency. Ten pilot experiments (see Table S1†) were performed with the initial values to obtain an average objective value (i.e., the average deprotected fluorination efficiency value). Next, a series of seven radiosynthesis experiments were performed, and only one of the variables was changed to a new value with the remaining six variables set to the base values. The new fluorination efficiency values were compared to the objective and were designated an impact value (increase, decrease, or no impact) by calculating p-values of one-sample t-test (one-tailed), and p < 0.05 was considered as the cutoff for significance.To create a predictive model based on the “OFAT” experiments, we generated a database of 55 reactions. Each reaction set contained different levels for the significant parameters and the base level for the non-significant factors. We performed all reactions on the chip to determine the observed FDG fluorination efficiency value (see Table S2†). As shown, input parameters except for deprotection temperature and radiolabeling temperature have imbalanced distribution in the dataset. Data points outside the most frequent conditions are considered ‘rare’ data. For example, data points with NaOH concentration lower than 1M are considered a ‘rare’ condition since only one experiment was performed with this condition. The experimental data having at least one input parameter with rare frequency in the training dataset for our work were replicated to improve the data distribution balance (a method shown for other studies50,51 that only have few experimental datapoints). These collected experimental data points (experimental conditions and their resulting FDG fluorination efficiency) were used to fit a linear and a non-linear regression model to study the effect of the reaction parameters on the FDG incorporation.
The database was randomly divided into two sets: (1) a training set (80% of data) to generate the model and (2) a test set (20% of data) to evaluate the model's performance. Input data were standardized by subtracting the mean value and scaling to unit standard variation using eqn (1) below:
 | (1) |
The model was trained using a 10-fold cross validation technique,64 which partitions the training set into 10 different subsets and iteratively trains the model on 9 subsets while the remaining set was used as the validation set. The training goal was to minimize squared error between the measured fluorination efficiency and the predicted value. The model was tested with the independent, random test group. The mean absolute error and root mean squared error were calculated to measure the performance of the models.
Seven linear models were trained where only one parameter was used as the input. In comparison, a multiple linear regression model was trained with all seven variables as the input. The linear models followed eqn (2):
FDG fluorination efficiency = ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) · ·![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) + b + b | (2) |
The reported coefficients for the final linear models were obtained by using the whole database including training and test sets (55 data points presented in Table S2†). To prevent overfitting, the linear models were obtained using Ridge regression of the scikit-learn library.65 This method performed L2 regularization and the optimum regularization factor was found using the grid search cv algorithm from the scikit-learn library.65
A multi-layer feed-forward neural network was implemented using the Keras library (https://github.com/fchollet/keras66) for non-linear regression analysis. The artificial neural network consisted of an input layer of 7 neurons for the 7 experimental parameters and an output layer with a single node to represent the predicted FDG incorporation yield. A dense hidden layer of 4 neurons with a rectified linear unit (ReLU) activation function was used to add non-linearity to the regression model. Also, in the hidden layer, L2 regularization was used to prevent overfitting of the model to the training dataset.47 In L2 regularization, squared magnitude of the layer weights is added to the loss function as a penalty term. In this way, it forces the weights to be small to prevent overfitting.47 The regularization factor and the learning rate of the Adam optimizer were optimized using the grid search cv algorithm from the scikit-learn library.65 The optimized values were 0.5 and 1 for the regularization factor and learning rate, respectively. 10-fold cross-validation (scikit-learn library) was used to measure the model performance.65 The final model (trained with all the training data) was further tested with the separate test data. The performance of the models was reported in terms of the root mean squared error as shown above.
Conclusion
In summary, we report the first demonstration of “OFAT” on a DMF device with an application to reduce the number of experiments required for assay optimization. This new approach studies the effect of each influential parameter on the assay output and provides recommendation on how to systematically select a subset of multifactorial experiments and run on the device for assay optimization. We anticipate that this new method combined with a digital microfluidic platform can be broadly used by researchers seeking to greatly speed up any biological, chemical, pharmaceutical assay optimization.Author contributions
This research was designed by FA, HB, JPS, GM, and SCCS. All experiments and analyses were conducted by FA and SCCS. Machine learning algorithms, including OFAT and the predictive model, were developed and analyzed by MS and FA. JMP designed the setup of the automation hardware and software and helped FA with automation experiments. SF trained and helped FA with radiation safety and setup. All authors wrote, revised, and reviewed the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We would like to thank the radiochemistry team at the McConnell Brain Imaging Centre for granting us access to radiochemistry facilities and for providing us with the [18F]fluoride radioisotope and organic solvents. Specifically, we would like to thank Dr. Robert Hopewell, Dr. Dean Jolly, and Dr. Alexey Kostikov for radiosynthesis training and technical support at the McConnell Brain Imaging Centre. We also like to thank Nicholash Bedi and Ann-Fleur Lobbezoo for fruitful discussion regarding the modeling and purification work, respectively. We thank the Natural Sciences and Engineering Research Council (NSERC), the Fonds de Recherche Nature et technologies (FRQNT), and the Canadian Foundation of Innovation (CFI) for funding. FA thank the Concordia University Department of Electrical and Computer Engineering for FRS and FRQNT PBEEE for funding. SCCS thanks Concordia for a University Research Chair.References
- J. M. Perry, G. Soffer, R. Jain and S. C. C. Shih, Lab Chip, 2021, 21, 3730–3741 RSC.
- H. Sinha, A. B. V. Quach, P. Q. N. Vo and S. C. C. Shih, Lab Chip, 2018, 18, 2300–2312 RSC.
- L. M. Y. Leclerc, G. Soffer, D. H. Kwan and S. C. C. Shih, Biomicrofluidics, 2019, 13, 034106 CrossRef PubMed.
- M. C. Husser, P. Q. N. Vo, H. Sinha, F. Ahmadi and S. C. C. Shih, ACS Synth. Biol., 2018, 7, 933–944 CrossRef CAS PubMed.
- A. B. V. Quach, S. R. Little and S. C. C. Shih, Anal. Chem., 2022, 94, 4039–4047 CrossRef CAS PubMed.
- H. Wang, L. Chen and L. Sun, Front. Mech. Eng., 2017, 12, 510–525 CrossRef.
- J. Wang, P. H. Chao, S. Hanet and R. M. van Dam, Lab Chip, 2017, 17, 4342–4355 RSC.
- Z. Gu, M.-L. Wu, B.-Y. Yan, H.-F. Wang and C. Kong, ACS Omega, 2020, 5, 11196–11201 CrossRef CAS.
- S. C. Kim, I. C. Clark, P. Shahi and A. R. Abate, Anal. Chem., 2018, 90, 1273–1279 CrossRef CAS PubMed.
- B. Wu, S. von der Ecken, I. Swyer, C. Li, A. Jenne, F. Vincent, D. Schmidig, T. Kuehn, A. Beck, F. Busse, H. Stronks, R. Soong, A. R. Wheeler and A. Simpson, Angew. Chem., Int. Ed., 2019, 58, 15372–15376 CrossRef CAS PubMed.
- R. Fobel, C. Fobel and A. R. Wheeler, Appl. Phys. Lett., 2013, 102, 193513 CrossRef.
- P. Q. N. Vo, M. C. Husser, F. Ahmadi, H. Sinha and S. C. C. Shih, Lab Chip, 2017, 17, 3437–3446 RSC.
- M. J. Jebrail, M. S. Bartsch and K. D. Patel, Lab Chip, 2012, 12, 2452–2463 RSC.
- M. Abdelgawad and R. Wheeler Aaron, Adv. Mater., 2008, 21, 920–925 CrossRef.
- M. J. Jebrail and A. R. Wheeler, Curr. Opin. Chem. Biol., 2010, 14, 574–581 CrossRef CAS PubMed.
- D. Chatterjee, H. Shepherd and R. L. Garrell, Lab Chip, 2009, 9, 1219–1229 RSC.
- N. Grant, B. Geiss, S. Field, A. Demann and T. W. Chen, Micromachines, 2021, 12(9), 1065 CrossRef PubMed.
- H. Norian, R. M. Field, I. Kymissis and K. L. Shepard, Lab Chip, 2014, 14, 4076–4084 RSC.
- R. Sista, Z. Hua, P. Thwar, A. Sudarsan, V. Srinivasan, A. Eckhardt, M. Pollack and V. Pamula, Lab Chip, 2008, 8, 2091 RSC.
- R. S. Sista, R. Ng, M. Nuffer, M. Basmajian, J. Coyne, J. Elderbroom, D. Hull, K. Kay, M. Krishnamurthy, C. Roberts, D. Wu, A. D. Kennedy, R. Singh, V. Srinivasan and V. K. Pamula, Diagnostics, 2020, 10(1), 21 CrossRef CAS.
- B. B. Li, E. Y. Scott, M. D. Chamberlain, B. T. V. Duong, S. Zhang, S. J. Done and A. R. Wheeler, Sci. Adv., 2020, 6, eaba9589 CrossRef CAS.
- P. Y. Keng, S. Chen, H. Ding, S. Sadeghi, G. J. Shah, A. Dooraghi, M. E. Phelps, N. Satyamurthy, A. F. Chatziioannou, C. J. Kim and R. M. van Dam, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 690–695 CrossRef CAS.
- M. Torabinia, U. S. Dakarapu, P. Asgari, J. Jeon and H. Moon, Sens. Actuators, B, 2021, 330, 129252 CrossRef CAS.
- M. Torabinia, P. Asgari, U. S. Dakarapu, J. Jeon and H. Moon, Lab Chip, 2019, 19, 3054–3064 RSC.
- S. Chen, M. R. Javed, H. K. Kim, J. Lei, M. Lazari, G. J. Shah, R. M. van Dam, P. Y. Keng and C. J. Kim, Lab Chip, 2014, 14, 902–910 RSC.
- B. Hadwen, G. R. Broder, D. Morganti, A. Jacobs, C. Brown, J. R. Hector, Y. Kubota and H. Morgan, Lab Chip, 2012, 12, 3305–3313 RSC.
- Y. Xing, Y. Liu, R. Chen, Y. Li, C. Zhang, Y. Jiang, Y. Lu, B. Lin, P. Chen, R. Tian, X. Liu and X. Cheng, Lab Chip, 2021, 21, 1886–1896 RSC.
- S. Anderson, B. Hadwen and C. Brown, Lab Chip, 2021, 21, 962–975 RSC.
- S. von der Ecken, A. A. Sklavounos and A. R. Wheeler, Adv. Mater. Technol., 2021, 2101251 Search PubMed.
- C. Dixon, A. H. Ng, R. Fobel, M. B. Miltenburg and A. R. Wheeler, Lab Chip, 2016, 16, 4560–4568 RSC.
- B. F. Bender and R. L. Garrell, Micromachines, 2015, 6(11), 1655–1674 CrossRef.
- A. Lashkaripour, C. Rodriguez, N. Mehdipour, R. Mardian, D. McIntyre, L. Ortiz, J. Campbell and D. Densmore, Nat. Commun., 2021, 12, 25 CrossRef CAS.
- C. Wang, C. Wang, Y. Wu, J. Gao, Y. Han, Y. Chu, L. Qiang, J. Qiu, Y. Gao, Y. Wang, F. Song, Y. Wang, X. Shao, Y. Zhang and L. Han, Adv. Healthcare Mater., 2022, 2102800 CrossRef CAS PubMed.
- V. Anagnostidis, B. Sherlock, J. Metz, P. Mair, F. Hollfelder and F. Gielen, Lab Chip, 2020, 20, 889–900 RSC.
- D. McIntyre, A. Lashkaripour, P. Fordyce and D. Densmore, Lab Chip, 2022, 22(16), 2925–2937 RSC.
- S. Momtahen, F. Al-Obaidy and F. Mohammadi, IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), 2019, pp. 1–6 Search PubMed.
- D. M. Chadly, A. M. Oleksijew, K. S. Coots, J. J. Fernandez, S. Kobayashi, J. A. Kessler and A. J. Matsuoka, SLAS Technol., 2018, 24, 41–54 CrossRef.
- A. Avoundjian, M. Jalali-Heravi and F. A. Gomez, Anal. Bioanal. Chem., 2017, 409, 2697–2703 CrossRef CAS PubMed.
- C. R. F. Caneira, R. R. G. Soares, K. Nikolaidou, M. Nilsson, N. Madaboosi, V. Chu and J. P. Conde, IEEE 34th International Conference on Micro Electro Mechanical Systems (MEMS), 2021, pp. 575–578 Search PubMed.
- H. T. Nguyen, L. N. Dupont, E. A. Cuttaz, A. M. Jean, R. Trouillon and M. A. M. Gijs, Microelectron. Eng., 2018, 189, 33–38 CrossRef CAS.
- K. Choi, A. H. Ng, R. Fobel, D. A. Chang-Yen, L. E. Yarnell, E. L. Pearson, C. M. Oleksak, A. T. Fischer, R. P. Luoma, J. M. Robinson, J. Audet and A. R. Wheeler, Anal. Chem., 2013, 85, 9638–9646 CrossRef CAS PubMed.
- J. Ma, Y. Wang and J. Liu, Micromachines, 2017, 8(8), 255 CrossRef PubMed.
- M. B. Kulkarni and S. Goel, Nano Express, 2020, 1, 032004 CrossRef.
- M. E. Pyne, K. Kevvai, P. S. Grewal, L. Narcross, B. Choi, L. Bourgeois, J. E. Dueber and V. J. J. Martin, Nat. Commun., 2020, 11, 3337 CrossRef CAS PubMed.
- W. C. Morrell, G. W. Birkel, M. Forrer, T. Lopez, T. W. H. Backman, M. Dussault, C. J. Petzold, E. E. K. Baidoo, Z. Costello, D. Ando, J. Alonso-Gutierrez, K. W. George, A. Mukhopadhyay, I. Vaino, J. D. Keasling, P. D. Adams, N. J. Hillson and H. Garcia Martin, ACS Synth. Biol., 2017, 6, 2248–2259 CrossRef CAS PubMed.
- S. Kotsiantis, D. Kanellopoulos and P. Pintelas, GESTS International Transactions on Computer Science and Engineering, 2006, vol. 30, pp. 25–36 Search PubMed.
- X. Ying, J. Phys.: Conf. Ser., 2019, 1168, 022022 CrossRef.
- H. Han, W. Y. Wang and B. H. Mao, Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning, International conference on intelligent computing, 2005, pp. 878–887 Search PubMed.
- R. Mohammed, J. Rawashdeh and M. Abdullah, Machine learning with oversampling and undersampling techniques: overview study and experimental results, 11th international conference on information and communication systems (ICICS), 2020, pp. 243–248 Search PubMed.
- T. Zhu, Y. Lin, Y. Liu, W. Zhang and J. Zhang, Knowl.-Based Syst., 2019, 166, 140–155 CrossRef.
- M. Hayati, S. Mutmainah and S. Ghufran, Int. J. Artif. Intell., 2021, 4, 86 CrossRef.
- G. Cumming, F. Fidler and D. L. Vaux, J. Cell Biol., 2007, 177, 7–11 CrossRef CAS PubMed.
- T. Radivojević, Z. Costello, K. Workman and H. Garcia Martin, Nat. Commun., 2020, 11, 4879 CrossRef PubMed.
- A. M. Elizarov, R. M. van Dam, Y. S. Shin, H. C. Kolb, H. C. Padgett, D. Stout, J. Shu, J. Huang, A. Daridon and J. R. Heath, J. Nucl. Med., 2010, 51, 282–287 CrossRef CAS PubMed.
- C. C. Lee, G. Sui, A. Elizarov, C. J. Shu, Y. S. Shin, A. N. Dooley, J. Huang, A. Daridon, P. Wyatt, D. Stout, H. C. Kolb, O. N. Witte, N. Satyamurthy, J. R. Heath, M. E. Phelps, S. R. Quake and H. R. Tseng, Science, 2005, 310, 1793–1796 CrossRef CAS PubMed.
- H. Ding, S. Sadeghi, G. J. Shah, S. Chen, P. Y. Keng, C. J. Kim and R. M. van Dam, Lab Chip, 2012, 12, 3331–3340 RSC.
- S. Chen, A. A. Dooraghi, M. Lazari, R. M. V. Dam, A. F. Chatziioannou and C. C. Kim, IEEE 27th International Conference on Micro Electro Mechanical Systems (MEMS), 2014, pp. 284–287 Search PubMed.
- S. Chen, J. Lei, R. Van Dam, P.-Y. Keng and C.-J. Kim, Planar alumina purification of 18F-labeled radiotracer synthesis on EWOD chip for positron emission tomography (PET), 2012 Search PubMed.
- M. D. Tarn, G. Pascali, F. De Leonardis, P. Watts, P. A. Salvadori and N. Pamme, J. Chromatogr. A, 2013, 1280, 117–121 CrossRef CAS.
- E. Moazami, J. M. Perry, G. Soffer, M. C. Husser and S. C. C. Shih, Anal. Chem., 2019, 91, 5159–5168 CrossRef CAS.
- F. Ahmadi, K. Samlali, P. Q. N. Vo and S. C. C. Shih, Lab Chip, 2019, 19, 524–535 RSC.
- P. Y. Keng and R. M. van Dam, Mol. Imaging, 2015, 14, 13–14 CrossRef.
- J. Wang, P. H. Chao and R. M. van Dam, Lab Chip, 2019, 19, 2415–2424 RSC.
- R. Kohavi, A study of cross-validation and bootstrap for accuracy estimation and model selection, International Joint Conference on Artificial Intelligence (IJCAI), 1995, vol. 14, no. 2, pp. 1137–1145 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- F. Chollet, Keras, 2015, https://github.com/fchollet/keras Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2lc00764a |
| This journal is © The Royal Society of Chemistry 2023 |