High-precision double-spike Sn isotope analysis of geological materials by MC-ICP-MS†
Jia-Xin
She
 ab,
Weiqiang
Li
ab,
Weiqiang
Li
 *ab,
Shichao
An
ab and
Yuanfeng
Cai
a
*ab,
Shichao
An
ab and
Yuanfeng
Cai
a
aState Key Laboratory for Mineral Deposits Research, School of Earth Sciences and Engineering, Nanjing University, Nanjing, Jiangsu 210023, China. E-mail: liweiqiang@nju.edu.cn
bFrontiers Science Center for Critical Earth Material Cycling, Nanjing University, Nanjing, China
First published on 17th November 2022
Abstract
Stable Sn isotopes have the potential to constrain the behavior of Sn in various natural and anthropogenetic processes, however, studies on stable isotopes of Sn for terrestrial rock samples have been limited. Here, we present a high-precision Sn isotope analytical method of geological samples by the double spike technique. Samples were equilibrated with a 117Sn–122Sn double spike during dissolution, then Sn was purified from the rock matrix using TRU spec resin. The purified Sn solutions were analyzed on a Nu 1700 Sapphire MC-ICP-MS, and data reduction was performed using Newton–Raphson iteration. Effects of acid mismatch, concentration mismatch, and matrix elements were systematically tested to evaluate their impact on the accuracy and repeatability of the measurements. We show that the mismatch of acidity exerts negligible influences on the Sn isotope analysis. By contrast, the accuracy of Sn isotopic measurements could be compromised if the Sn concentration of the sample is below 40% of that of the standard. To ensure the accuracy of Sn isotope analysis, the concentration match between the sample and standard should be better than ±20%. When the measured solution has varying mass ratios of [X]/Sn (ng g−1/ng g−1) lower than 0.5 for Mg, Ca, Fe, Ti, U, Ni, Ag, As, Ru, and Mo, the measured Sn isotope composition was not affected. However, Cd in Sn samples could affect the accuracy of Sn isotope analysis by the 117Sn–122Sn double spike through the generation of 116CdH+ in plasma that interferes with 117Sn+. The Cd/Sn ratio needs to be below 0.01 to ensure analytical accuracy by the double spike method. The accuracy of this method was further verified by measuring the pure solution with both double spike and sample standard bracketing methods, as well as processing a synthetic solution through column chemistry. The Sn isotope compositions of geological samples measured using our method are reproducible and consistent with previous data from other laboratories. Additionally, Sn isotope data for geological reference materials BIR-1, RGM-1, and GSR-1 are reported for the first time. Based on repeated analyses of pure and geological reference materials, the long-term intermediate precision is better than ±0.069‰ on δ122/118Sn for a spiked solution of 100 μg g−1.
1. Introduction
Tin (Sn) plays an important role in various geological and cosmochemical processes due to its lithophile, moderately siderophile, chalcophile, and moderately incompatible geochemical properties.1–4 Tin is a major component of bronze and is important in archeological studies. Tin is a redox-sensitive element with mainly two oxidation states, Sn2+ and Sn4+, both of which play important roles in petrogenesis and ore-forming processes.5–11 Tin could complex with various ligands and exist in various geological materials2,12–18 and could be enriched during chemical weathering and the Earth differentiation processes to form granite-related Sn mineralization.19–22 Natural Sn abundance is 0.17 μg g−1 in the mantle and 1.7 μg g−1 in the crust,23,24 while it reaches a weight-percent level in Sn ores. Due to the “magic number” closed proton shell in its nucleus,25 Sn has ten stable isotopes with the largest mass variations in the periodic table.26–28Stable Sn isotopes are a powerful tool for studying the behavior of Sn in various processes,5,8,9,29–31 as well as tracking the provenance of Sn in various natural samples and archaeological artifacts,32–35 thus there has been a long interest in the Sn isotope variability of natural and artificial Sn-bearing samples. Early studies used thermal ionization mass spectrometry (TIMS) for Sn isotope measurements,36–38 however, the high ionization potential (7.3 eV) of Sn prevents efficient and stable ionization of Sn.1,25,36,37,39 As a result, the analytical precision was limited to a level of 0.12–0.17‰/amu for Sn isotopes by TIMS, hindering the studies of Sn isotope fractionation induced by magmatic and ore-forming processes.25,37,38 In the recent decade, the applications of multi-collector inductively coupled plasma mass spectrometry (MC-ICP-MS) made precise Sn isotope measurement possible.32,39,40 Different chemical purification procedures and mass spectrometric methods have been reported, and a boom of Sn isotope studies is ongoing.41–44
Presently, the majority of reported Sn isotopic data in the literature are from Sn-rich minerals such as cassiterite9,45–47 or Sn-bearing materials such as bronze.35,48,49 Knowledge of Sn isotope signatures of terrestrial rocks is still limited due to the scarcity of high-quality isotope data for igneous rocks, and there has been no community-recognized certified international Sn isotopic reference material. In this study, we developed a double-spike Sn isotope analytical method that can be applied to various geological materials, and we reported high-precision Sn concentrations and isotopic data for a wide range of geological reference materials.
2. Double spike design
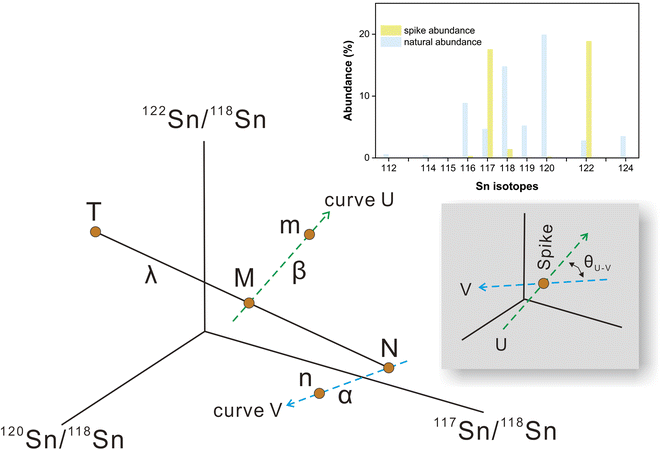
Sample standard bracketing method and element doping can be used for mass bias correction during Sn isotope analysis by MC-ICP-MS.50,51 However, Sn is volatile during sample dissolution, and vaporization loss of Sn could induce Sn isotope fractionation,47,52–54 compromising the accuracy of the Sn isotope analysis. Only the double spike method could rigorously correct the mass-dependent isotope fractionation processes that occur during sample processing, chromatographic purification, and mass spectrometry, given that the spike had been equilibrated with the sample prior to these processes.51 This method involves the measurement of isotope data for the mixture of the sample of interest with a well-calibrated double spike containing two enriched isotopes compared to natural abundance.36 Tin has more than four stable isotopes and is a suitable candidate for the application of the double spike technique for mass bias correction.The selection of the double spike combination is based on the following criteria: (1) the spike isotopes are not susceptible to potential interferences, (2) the spike combination fits the cup configuration and mass dispersion of the mass spectrometer, and (3) the spike combination is associated with minimum systematic errors in double-spike inversion. The low abundance isotopes of tin (112Sn, 114Sn, 115Sn) are susceptible to interferences of Cd and In, thus they are not considered.37,44 The isotopes of 116Sn, 119Sn, and 124Sn could also suffer from potential elemental and molecular interference from neighboring elements (Cd, Te, Mo, Ag) if they are not well-separated.41,43,44 Several spike assemblages, including 117Sn–122Sn and 117Sn–119Sn double spikes, had been used in previous studies.41,42,44117Sn–122Sn is preferred for the tolerance of a range of sample/spike ratios. Based on these considerations, we chose to use 117Sn–122Sn double spike with 117Sn–118Sn–120Sn–122Sn inversion and 118Sn as the denominator (Fig. 1), and simulations from the “double spike toolbox”55 show that this combination maintains minimal systematic errors over a spike/(spike + sample) ratio range of 0.2 to 0.65 (Fig. 2).
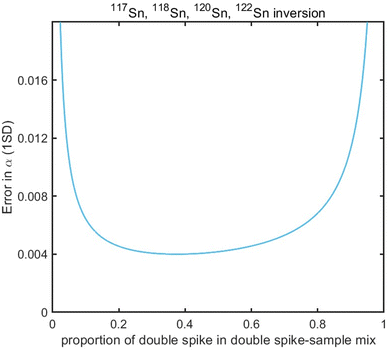 | ||
| Fig. 2 Theoretical error in α as a function of spike proportions in spike-sample mixtures with 117Sn–122Sn double spike using 117Sn–118Sn–120Sn–122Sn inversion. | ||
The Sn double spike was prepared as a mixture of two concentrated spike solutions. Two Sn metal ingots enriched in 117Sn and 122Sn respectively were purchased from Isoflex (https://www.isoflex.com). The spikes were carefully weighed and transferred to Teflon beakers for digestion with HCl. The double spike solution was prepared by mixing the two individual spikes properly to achieve a composition of approximately 53% 117Sn and 47% 122Sn. The double spike solution was stored in 1 M HCl at a concentration of 400 μg g−1 as a stock solution to be diluted for further isotope measurements.
The accuracy and repeatability of double spike data rely on the correct calibration of the spike compositions relative to the primary isotope standard. The double spike was calibrated by measuring a series spike-NIST 3161a mixture, with the spike proportion increasing gradually from pure standard to pure spike. The double spike composition is determined relative to the NIST 3161a standard following the approach of Klaver and Coath.56 A series of spike-standard mixtures, with the proportions of double spike varying from 0.2 to 0.8, were used to define the standard-spike mixing line and ensure the quality of the calibration. If the calibration is correct, the result for mixtures of different spike proportions should yield consistent close to zero results, which is illustrated in Fig. 3. For spike/(spike + sample) proportion within the range of 0.2 to 0.8, the accuracy of the double spike method is insensitive to the effect of the spike-to-sample ratio.
3. Experimental methods
3.1. Materials and reagents
All chemical treatments of samples were performed in an ISO Class 6 clean room with ISO Class 5 fume hoods at the State Key Laboratory for Mineral Deposits Research, Nanjing University. The semiconductor-grade acids (HCl, HNO3, HF) were purchased and used for all sample preparation and ion-exchange chromatography. Teflon beakers are soaked in 4.5 M nitric acid and then refluxed with concentrated HNO3–HF mixture and HCl at 130 °C for at least one day, then rinsed with ultrapure water (resistivity of 18.2 MΩ cm−1) before usage. Commercially available 100 μg g−1 multi-element stock solutions for column calibrations were supplied by Aladdin® (Lot #C2011). The single-element Sn standard solution used for quantitative analysis was purchased from Macklin® (Lot #C10053783, 1000 μg g−1). Since there have been no community-recognized international Sn isotopic reference materials, several 100 μg mL−1 pure Sn elemental standard solutions, including NIST 3161a (Lot #140917), SPEX (Lot #22-19SNY), and SnCl4 solutions, were used as in-house standards. Eight USGS and one Chinese geological reference materials, including basalts (BCR-2, BHVO-2, BIR-1), andesite (AGV-2), granites (GSP-2, JG-2, GSR-1), rhyolite (RGM-1), and marine sediment (NOD-A-1), were processed and analyzed to assess the accuracy and intermediate precision of our chemical and mass spectrometric procedures. These geological reference materials were selected to represent a wide spectrum of sample matrices.3.2. Sample preparation and digestion
Based on bulk rock concentration data, approximately 100 to 1000 mg of rock powders (containing 1–2 μg Sn) were digested in a tightly capped Teflon beaker with 8 mL 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of HNO3–HF on a hotplate at 130 °C. Before digestion, the sample was mixed with a 117Sn–122Sn double spike solution at an optimal spike-to-sample ratio of 39
1 mixture of HNO3–HF on a hotplate at 130 °C. Before digestion, the sample was mixed with a 117Sn–122Sn double spike solution at an optimal spike-to-sample ratio of 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 61. Initial digestion lasted for two days, during which the Sn dissolved from the rock powders was equilibrated with the double spike, then the solution was evaporated to dryness at 80 °C and re-dissolved in 6 mL aqua regia and dried. After that, the sample was dissolved in 8 mL concentrated HCl to reflux at 130 °C for two days to dissolve fluorides before drying again at 80 °C. About 100 μL HF was added to fix Sn before each evaporation step to prevent Sn loss by volatilization or hydrolysis. Afterwards, the sample was re-dissolved in 0.5 M HCl as required to be loaded on the column for Sn purification.
61. Initial digestion lasted for two days, during which the Sn dissolved from the rock powders was equilibrated with the double spike, then the solution was evaporated to dryness at 80 °C and re-dissolved in 6 mL aqua regia and dried. After that, the sample was dissolved in 8 mL concentrated HCl to reflux at 130 °C for two days to dissolve fluorides before drying again at 80 °C. About 100 μL HF was added to fix Sn before each evaporation step to prevent Sn loss by volatilization or hydrolysis. Afterwards, the sample was re-dissolved in 0.5 M HCl as required to be loaded on the column for Sn purification.
3.3. Column chemistry
The chemical separation of Sn used as the default method in this study was performed with 1.5 mL bed volume Eichrom TRU resin filled in Biorad plastic columns. The ion exchange chromatography method used in this study was similar to those reported by Creech et al.42 The resin was pre-cleaned sequentially with H2O, 0.5 M HCl, and 0.5 M HNO3 after resin loading and then conditioned with 0.5 M HCl (for details, see Table 1). After sample loading, the matrix elements were eluted with 0.5 M and 0.25 M HCl. Then Sn was recovered using an eluent of 12 mL 0.5 M HNO3. 100 μL of concentrated HF was added to the collection beaker to prevent Sn hydrolysis before the collection of Sn cut. Subsequently, the purified Sn fractions were dried down at 80 °C and were taken up again in 0.3 M HNO3 and 0.006 M HF.| Step | Eluant | Volume/mL |
|---|---|---|
| 1.5 mL TRU resin (100–150 mesh) | ||
| Cleaning | H2O | 5 |
| 0.5 M HCl | 5 | |
| H2O | 5 | |
| 0.5 M HNO3 | 5 | |
| H2O | 5 | |
| 0.5 M HNO3 | 5 | |
| H2O | 5 | |
| Conditioning | 0.5 M HCl | 4 |
| Loading | 0.5 M HCl | 2 |
| Matrix elution | 0.5 M HCl | 4 |
| 0.25 M HCl | 7 | |
| Sn collection (with 100 μL HF added first) | 0.5 M HNO3 | 12 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| 2 mL AG1-X8 resin (100–200 mesh) | ||
| Cleaning | H2O | 5 |
| 1 M HNO3 | 10 | |
| Conditioning | 1 M HCl | 10 |
| Loading | 1 M HCl | 10 |
| Matrix elution | 1 M HCl | 20 |
| 6 M HCl | 10 | |
| 1 M HNO3 | 2 | |
| Sn collection (with 100 μL HF added first) | 1 M HNO3 | 10 |
A two-stage column procedure with a second (additional) anionic chloride form AG1-X8 resin following Friebel et al.43 was also evaluated in this study. The elution steps for the second stage of chemistry are summarized in Table 1. After the first stage column treatment, the sample was loaded onto the second stage column with 10 mL 1 M HCl. Then the column was eluted with another 20 mL 1 M HCl, 10 mL 6 M HCl, and 2 mL 1 M HNO3.
3.4. Mass spectrometry
All double spike Sn isotope analysis was performed on a Nu 1700 Sapphire MC-ICP-MS at the State Key Laboratory for Mineral Deposits Research and Frontiers Science Center for Critical Earth Material Cycling, Nanjing University. The detailed instrument settings and operational parameters for data acquisition are summarized in Table 2. During Sn isotope analysis, Sb isotopes (123Sb, 123Sb) were measured for mass bias correction when applicable. The signals of 125Te and 111Cd were measured along with Sn isotopes to monitor the effects of isobaric interferences from Te and Cd on Sn isotopes (i.e., 124Te, 122Te, 120Te on 124Sn, 122Sn, and 120Sn, respectively; 116Cd on 116Sn) (Table S1†).| Parameter | Value | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RF power | 1300 W | |||||||||||
| Auxiliary gas flow rate | 1 L min−1 | |||||||||||
| Sample gas flow rate | 0.9 L min−1 | |||||||||||
| Plasma cooling gas flow rate | 13 L min−1 | |||||||||||
| Measurement mode | Static | |||||||||||
| Interface cones | Standard Ni cones | |||||||||||
| Acceleration voltage | ∼6000 V | |||||||||||
| Detector | Faraday cups | |||||||||||
| Amplifier | 10^11 Ω | |||||||||||
| Sample measurement time | 40 × 3 s integrations | |||||||||||
| Instrument resolution | 5258 | |||||||||||
| Nebulizer | MicroFlow PFA-100 μL min−1 | |||||||||||
| Sample introduction system | Aridus III | |||||||||||
| Aridus Ar sweep gas | 5.65 L min−1 | |||||||||||
| Solution concentration | 100 ng mL−1 | |||||||||||
| Cup configuration | H7 | H6 | H5 | H4 | H3 | H2 | H1 | Ax | L1 | L2 | L3 | L4 |
| 125Te | 124Sn | 123Sb | 122Sn | 121Sb | 120Sn | 119Sn | 118Sn | 117Sn | 116Sn | 115Sn | 111Cd | |
For double spike Sn isotope analysis, the concentration of all solutions was adjusted to 100 ng g−1 in a mixed acid of 0.3 M HNO3 and 0.006 M HF, except for acidity tests. The sample was introduced into the ICP via an Aridus III desolvator with a 100 μL min−1 PFA nebulizer. The data acquisition sequence consists of 40 seconds of sample uptake time and forty cycles of three seconds of signal integration on Faraday cups. The typical signal intensity for 120Sn was ∼12 V per μg g−1. Measurement of blanks was performed at the beginning of every session and corrected for both standards and samples. Between each isotope analysis, the sample introduction system was washed through uptaking 0.3 M HNO3 and 0.006 M HF solutions sequentially from three tubes, each for 40 seconds, to suppress the memory effect and bring the background to the pre-analysis level. The 120Sn background was measured to be lower than 9 mV after the three-step rinsing, which was >1000 times lower than the sample signal. Every sample was bracketed by a spiked NIST 3161a standard at the same concentration in an analytical session.
To validate the double spike method, several in-house standard Sn solutions were measured using elemental doping and sample-standard bracketing under wet plasma conditions. For this analysis, the 1 μg g−1 Sn solution was doped with 300 ng g−1 Sb and was introduced into ICP with a standard glass spray chamber via a 100 μL min−1 PFA nebulizer. The Faraday cup configuration was the same as the double spike method (Table 2). Data reduction of Sn isotope analysis for this method was similar to a previous study.52 All isotopic results are expressed as δ122/118Sn notation relative to the primary Sn isotopic reference solution NIST 3161a in this study, which is δ122/118Sn = [(122Sn/118Sn)sample/(122Sn/118Sn)3161a − 1] × 1000.
4. Results and discussion
4.1. Separation and isotope fractionation of Sn during ion exchange column chemistry
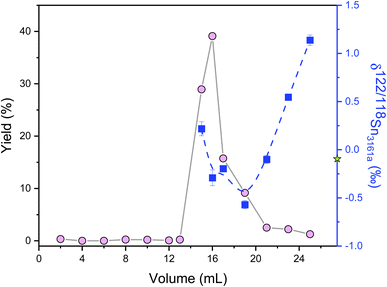
High-precision Sn isotope analysis, with or without a double spike, could be compromised by the isobaric and molecular interference of Te, Cd, In, and Mo41 (Table S1†), thus these elements need to be effectively separated from Sn during the column chemistry that is aimed at purifying Sn from the rock matrix. In the literature, different resins, including TBP, AG MP-1, and AG1-X8, had been used for the purification of Sn;25,30,41,43,44,57,58 more recently, several studies have utilized TRU resin for the Sn separation procedure.1,30,41–43,48,59The elution curves of different elements for the two different column procedures are shown in Fig. 4. For the TRU resin, the majority of matrix elements were eluted off the column completely with 0.5 M HCl, whereas In was released from the column during the elution of 0.25 M HCl. Then Sn was recovered by the elution of 0.5 M HNO3. Although a previous study stated that Bi, In, and Mo could not be separated well from Sn with TRU resin,44 our results show that the In/Sn ratio was lower than 0.007 and the [X]/[Sn] ratio of Bi, and Mo was lower than 0.001 after this stage of column chemistry for all igneous rocks. The yield of Sn by the treatment of TRU resin in this study was measured to be 99.8 ± 0.3% (2SD, N = 3). For comparison, AG1-X8 is an anion exchange resin that can separate Sn from a number of matrix elements, including Fe, Mg, Mo, In, and Cd.30,43,44 Various elements, including In and Pb, could be eluted off the column before the Sn cut, but the full separation of Sn, Cd, and Zn cannot be achieved. In this step, the recovery of Sn was 99.1 ± 2.5% (2SD, N = 2). The procedural blank from the dissolution and the two-stage column chemistry is lower than 5.6 ng, contributing to less than 0.3% of the analyzed samples.
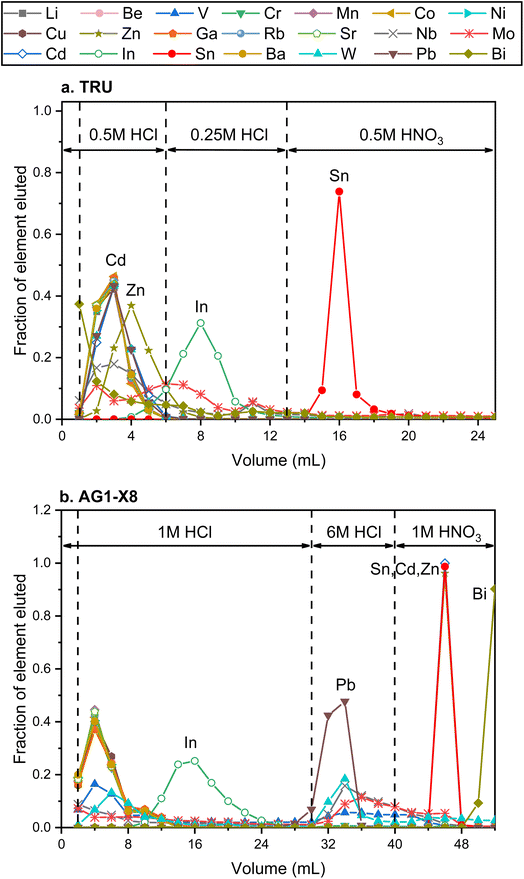 | ||
| Fig. 4 Elution curves of the Sn purification procedure using different reagents. (a) and (b) Represent the elution curves using TRU resin and AG1-X8 resin, respectively. | ||
Ion-exchange processes on chromatography columns are known to fractionate stable isotopes of Fe, Ga, Cu, Zn, Mo, and Ca.60–64 No Sn isotope fractionation was measured in previous studies involving TRU resin when the Sn recovery was above 94%.32,48,65 However, a significant Sn isotope offset after column chemistry was reported by Yamazaki et al.,66 which was thought to originate from the incomplete recovery or matrix effects. Therefore, it is important to assess the effect of incomplete recovery during ion-exchange column chemistry on Sn isotopes. This was done by double spike analysis of the different Sn fractions of the elution curve, as shown in Fig. 5. Remarkable Sn isotope fractionation occurred on the TRU ion-exchange column. The Sn (original δ122/118Sn3161a = −0.095 ± 0.030‰) that was firstly eluted off the TRU resin was isotopically heavier than the bulk Sn solution, implying that the resin held lighter Sn isotopes at the beginning. The light Sn isotopes were eluted off the column immediately after the peak of the elution curve (Fig. 5). Specifically, the majority of Sn (around 93%) cuts show a decreasing trend with δ122/118Sn3161a varying from 0.218 ± 0.073‰ to −0.570 ± 0.042‰, similar to Ca and Fe isotopes.60,61 However, the Sn eluted off the column as the tail of the elution curve became isotopically heavier again (Table S2†). The δ122/118Sn3161a for the remaining Sn (around 6%) cuts increased from −0.570 ± 0.042‰ to 1.138 ± 0.053‰. The origin of this phenomenon (v-shaped δ122/118Sn value for the Sn elution curve) is unclear but could be due to the transition of Sn species during the elution by HNO3. Based on the detailed elemental data from the elution curve, it is estimated that a 3% Sn loss (not collected) from the resin could cause an Sn isotope fractionation by 0.025‰ in δ122/118Sn, although we note that such an isotopic effect is corrected by the double spike method.
4.2. Double spike data inversion
Cadmium and Te are the main issues of concern during Sn isotope measurements as they form isobaric interferences on 116Sn, 122Sn, and 124Sn. We monitored 111Cd and 125Te to correct the effect of these elemental interferences before conducting double spike data inversion, following the convention of previous studies.44,67 During Sn isotope analysis for geological samples, however, we found that the measured 125Te intensities stayed constant at a level below 1.5 mV for all samples, and the signal for 111Cd was always lower than 0.7 mV. The results show no obvious difference with and without correction for the elemental interference of Te and Cd.The reduction of double-spike data can be achieved with a variety of methods, including Nest iteration,68,69 geometric method,70,71 and Newton–Raphson iteration approaches.51,55 All the data reduction of this study was performed using a double spike toolbox55 with a MATLAB@ code following the Newton–Raphson iteration approach. The inputs of the inversion include the measured intensities of all the isotopes for samples and the calibrated double-spike composition. To correct for potential deviations from the exponential law and shift of the gains for Faraday collectors during the measurements,42,44 a bracketing standard was used to normalize isotopic values after a double spike inversion of each sample.44,72–77 Therefore, all the data are reported as the deviation of δ122/118Sn of a sample relative to the average δ122/118Sn of two bracketing spiked NIST 3161a, similar to Wang et al.44 The geometrical method was also used for comparison using MATLAB@, and consistent results were found, for which the details are provided in the ESI A.†
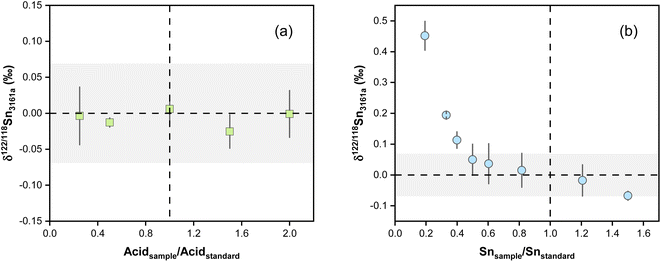
4.3. Effects of acidity and concentration mismatch
The effect of acid mismatch has been reported on K, Fe, and Ba isotope measurements by MC-ICP-MS using sample standard bracketing methods.78,79 The impact of the acid concentration mismatch between the samples and standards on the accuracy of Sn isotope analysis was evaluated by analyzing the NIST 3161a in various acid matrices. Spiked NIST 3161a solutions were diluted in HNO3–HF at various concentrations and analyzed against the NIST 3161a solution in 0.3 M HNO3 and 0.006 M HF. The results show no Sn isotopic deviation for the spiked NIST 3161a analyzed at different acid concentrations (Fig. 6a), indicating that Sn isotope measurements are insensitive to the different acid concentrations between bracketing standards and samples using our double spike method.Previous studies reported analytical inaccuracy when there was a mismatch in the concentration of the sample and standard during the double spike analysis of Cd and Se isotopes and sample-standard-bracketing analysis of K and Ba stable isotopes.80–83 The effect of intensity mismatch on Sn isotope analysis was evaluated by analyzing spiked NIST 3161a solutions of concentrations varying from 20 to 150 ng g−1 against the spiked NIST 3161a bracketing standard with a constant concentration of 100 ng g−1 Sn. Both the bracketing standards and samples were prepared from a 1 μg g−1 spiked NIST 3161a stock solution. The concentrations are calculated based on the total Sn intensities of all measured Sn isotopes. The measured δ122/118Sn values are plotted in Fig. 6b as a function of the ratio between the Sn concentration of the sample analyzed and the NIST 3161a standard. The results show that the measured δ122/118Sn3161a values decrease with increasing Sn concentrations following a curved relationship. When the Sn concentration of the sample is 20% of the standard (i.e., Isample/Istandard = 0.2), the inaccuracy in the measured δ122/118Sn3161a is up to 0.45‰. For sample/standard Sn concentration ratios lower than 0.4, we can observe an obvious offset of δ122/118Sn3161a relative to the bracketing standard (Fig. 6b). It is necessary to maintain a sample concentration of 80 to 120 ng g−1 to ensure accurate and precise results for the protocol in this study. We note that the effect of concentration mismatch is likely relevant to instrumental and double spike settings and may differ between different laboratories.
4.4. Matrix effects
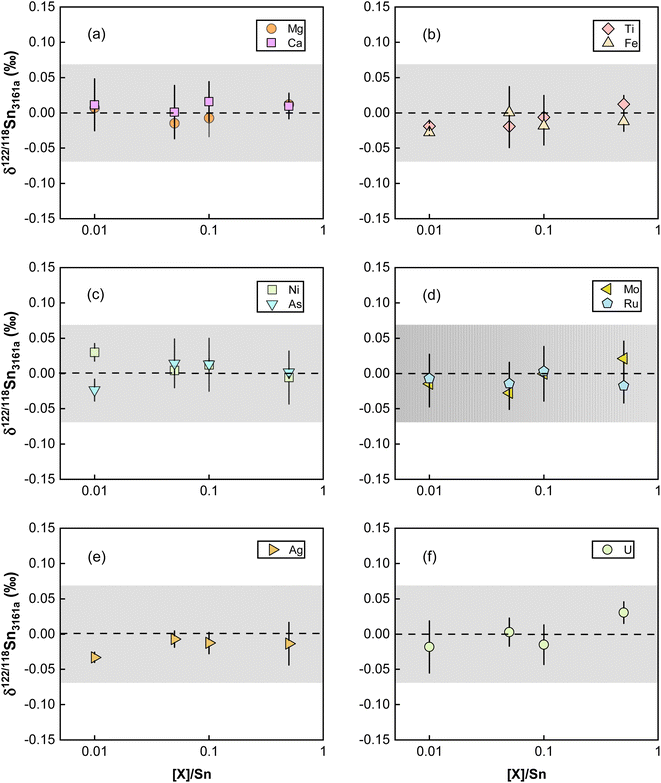
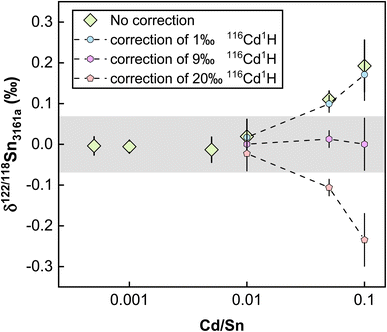
Elements other than the target element may affect the transport of the analyte in the ICP and the ion extraction in the interface, causing matrix effects.81,83 Abnormal isotopic results could also arise due to molecular and isobaric interferences caused by matrix elements.80 Although column chemistry was developed to purify the target elements from matrix elements, elements like Mg, Fe, and Ca are common and major elements in geological matrices. As also pointed out by previous studies, the existence of matrix elements such as U, Ag, Ru, Mo, and Cd in the Sn solution could lead to various interferences on Sn isotopes on MC-ICP-MS.41,84 The possible molecular, doubly charged, and isobaric interferences on Sn isotopes are summarized in Table S1.† To evaluate the matrix effects on Sn isotope measurements, we doped a series of matrix elements (Mg, Ca, Fe, Ti, Ni, As) to a spiked NIST 3161a Sn solution at the mass ratios of [X]/[Sn] (ng g−1/ng g−1) varying from 0.01 to 0.5. These matrix-doped Sn solutions were then measured against spiked pure NIST 3161a Sn. The results are shown in Fig. 7. We also doped U, Ag, Ru, Mo, and Cd into the spiked NIST 3161a Sn solution to quantitatively evaluate the effects of elements that might cause molecular and isobaric interferences. Our results demonstrate that the presence of U, Ag, Ru, and Mo below 50% of Sn causes a negligible effect on the accuracy of Sn isotope analysis with the double spike method; these results show that the double spike method is effective in correcting mass bias in the instrument even if the mass bias may vary due to the existence of matrix elements.However, we found that Cd/Sn > 0.01 (111Cd up to 68 mV for our setting) in sample solutions would cause obvious offset on the Sn isotope measurements (Fig. 8). Such a deviation did not originate from the isobaric interference of 116Cd on 116Sn, as the four isotopes for double spike inversion are 117Sn, 118Sn, 120Sn, and 122Sn. We speculate that the observed analytical inaccuracy was caused by the formation of cadmium hydride,85,86 specifically, the interference of 116Cd1H+ on 117Sn+. We performed the correction of 116Cd1H+ on 117Sn+ by assuming different production rates of cadmium hydride. The results are summarized in Fig. 8, which shows that when a production rate of 0.9% is assumed for cadmium hydride from cadmium ion, the influence of Cd can be corrected. We note that such a production rate of cadmium hydride could vary between different analytical sessions or experimental settings, thus, the safe protocol would be to ensure that Cd/Sn is lower than 0.01 for sample analysis.
4.5. Repeatability and intermediate precision
Different pure reference materials have been used in previous Sn isotope studies, including Johnson-Matthey Puratronic Sn,39 SPEX Sn standard solution in HNO3 (Lot #CL5-45SN,66,87 Lot #CL8-02SNY,88 Lot #CL6-83SNY43), SPEX Sn standard solution in HCl (Lot #14-84SN,66,87 Lot #20-168SNY,88 Lot #22-19SNY52), NIST 3161a (Lot #070330,41,43,44,47,66,87 Lot #140917 (ref. 52)), Sn_IPGP,42 and NCS Sn.41 The isotopic homogeneity of these reference solutions between different batch numbers has not been verified. In this study, three in-house standard solutions were repeatedly measured. The δ122/118Sn3161a compositions for our NIST 3161a, SPEX, and SnCl4 using the sample standard bracketing (SSB) method are consistent with our double spike (DS) method (Table 3) (Fig. 9). These values, measured on the Nu 1700 Sapphire MC-ICP-MS, are also consistent with those that were measured on a Neptune plus MC-ICP-MS as reported in our previous study,52 (Fig. 9). We obtained a long-term intermediate precision of better than ±0.041‰ based on these in-house reference solutions. We also measured the NIST 3161a from ETH with a different batch number (#070330) with SSB and DS methods, which was indistinguishable from our primary standard (Table 3).| δ 122/118Sn (‰) | Neptune SSBa | 2SD | Sapphire SSB | 2SD | N | Sapphire DS | 2SD | N | |
|---|---|---|---|---|---|---|---|---|---|
| a The data of Neptune SSB are from She et al.52 | |||||||||
| Without column chemistry | NIST 3161a (#140917) | −0.003 | 0.037 | 0.003 | 0.049 | 21 | 0.003 | 0.041 | 25 |
| SPEX (#22-19SNY) | 0.254 | 0.048 | 0.231 | 0.064 | 51 | 0.222 | 0.040 | 31 | |
| SnCl4 | 0.117 | 0.058 | 0.086 | 0.048 | 18 | 0.082 | 0.034 | 17 | |
| NIST 3161a (#070330) | 0.017 | 0.056 | 6 | −0.013 | 0.049 | 11 | |||
| With column chemistry | NIST 3161a (#140917) | −0.011 | 0.059 | 3 | 0.001 | 0.006 | 3 | ||
| NIST 3161a (#140917) | 0.005 | 0.027 | 3 | ||||||
| NIST 3161a (#140917) + matrix | 0.012 | 0.023 | 3 | ||||||
| Evaporated NIST 3161a (#140917) | 0.224 | 0.044 | 3 | ||||||
| SnCl4 | 0.141 | 0.085 | 3 | ||||||
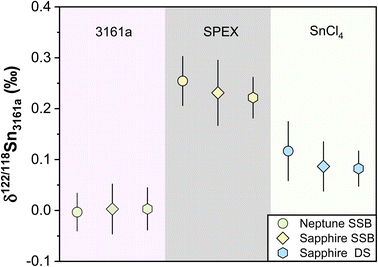 | ||
| Fig. 9 δ 122/118Sn3161a values of pure laboratory solutions of NIST 3161a, SPEX, and SnCl4 during the past half years. The data of Neptune SSB are from She et al.52 The Sapphire SSB and DS indicate the data measured with Nu Sapphire 1700 using both sample standard bracketing and double spike methods. All uncertainties on individual data points reflect the 2SD of the samples. | ||
To ensure that the chemical purification process does not introduce inaccuracy for Sn isotope measurements, we processed pure and synthetic spiked solutions with our column chemistry, and analyzed them as unknowns using SSB and DS methods. We processed two pure solutions of NIST 3161a and SnCl4 with column chemistry, confirming that no resolvable Sn isotope fractionation was induced by column chemistry (Table 3). In contrast, evaporation was found to induce Sn isotope fractionation of up to 0.22‰ for the non-spiked NIST 3161a solution (measured by the SSB method), which highlighted the necessity of application of double spike for Sn isotope analysis of geological samples. The pure spiked NIST 3161a solutions, as well as synthetic solutions of the spiked NIST 3161a doped with matrix elements equivalent to granite, were also processed. The measured δ122/118Sn3161a values of these solutions are identical to the original NIST 3161a (Table 3), validating the accuracy of chemical and mass spectrometry methods.
We also treated GSP-2 and BHVO-2 with the standard (default) one-stage TRU column procedure and the extended two-stage column (TRU + AG1-X8) procedure. The two-stage column treatment for GSP-2 and BHVO-2 yielded the δ122/118Sn3161a of 0.209 ± 0.011‰ and 0.346 ± 0.035‰, which are indistinguishable from their respective average compositions measured from the default one-stage TRU column procedure. This indicates that one TRU column chemistry is sufficient for processing the geological samples in our study. In addition, multiple total procedural replicates with independent digestion, column chemistry, and isotopic measurements were performed for geological reference materials to assess the intermediate precision of the analytical method. The Sn isotope compositions of reference materials are displayed in Table 4. The measured Sn isotope data of repeated measurements at different times, independent digestions, and different column chemistry over four months were consistent, attesting to the robustness of our double-spike Sn isotope analytical method. The repeated measurements of NOD-A-1 yield the largest 2SD error of ±0.040‰ among replicates of reference materials, which is within the largest error (±0.069‰) determined for the individual GSP-2. Therefore, we conservatively estimate that the intermediate precision in our method was better than ±0.069‰ on δ122/118Sn.
| Sample | GSP-2 | BCR-2 | AGV-2 | BHVO-2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Digestion date | Measurement date | Batch number | δ 122/118Sn | 2sd | Batch number | δ 122/118Sn | 2sd | Batch number | δ 122/118Sn | 2sd | Batch number | δ 122/118Sn | 2sd |
| 2022/5/27 | 2022/6/22 | 2507 | 0.213 | 0.033 | 1748 | 0.315 | 0.035 | 531 | 0.291 | 0.016 | 1743 | 0.357 | 0.031 |
| 0.226 | 0.012 | 0.291 | 0.022 | ||||||||||
| 608 | 0.226 | 0.012 | 362 | 0.331 | 0.011 | 227 | 0.299 | 0.043 | 3191 | 0.339 | 0.035 | ||
| 0.336 | 0.104 | ||||||||||||
| 2507 | 0.242 | 0.036 | 1748 | 0.316 | 0.042 | 531 | 0.28 | 0.01 | 1743 | 0.357 | 0.031 | ||
| 0.299 | 0.025 | ||||||||||||
| 0.33 | 0.035 | ||||||||||||
| 608 | 0.229 | 0.034 | 362 | 0.33 | 0.037 | 227 | 0.284 | 0.065 | 3191 | 0.349 | 0.064 | ||
| 0.227 | 0.035 | ||||||||||||
| 2022/6/1 | 2022/6/22 | 2507 | 0.217 | 0.069 | 1743 | 0.339 | 0.016 | ||||||
| 2022/6/20 | 2022/7/4 | 608 | 0.209 | 0.011 | 362 | 0.285 | 0.014 | 227 | 3191 | 0.346 | 0.035 | ||
| 608 | 0.199 | 0.023 | 362 | 0.312 | 0.039 | 227 | 0.305 | 0.038 | 3191 | 0.367 | 0.037 | ||
| 2022/7/7 | 2022/7/17 | 608 | 0.237 | 0.032 | |||||||||
| 2022/7/19 | 2022/8/17 | 608 | 0.209 | 0.053 | |||||||||
| 2022/8/15 | 2022/9/7 | 2507 | 0.246 | 0.05 | |||||||||
| Average | 0.223 | 0.312 | 0.292 | 0.349 | |||||||||
| 2sd | 0.029 | 0.035 | 0.021 | 0.021 | |||||||||
| N | 12 | 9 | 5 | 8 | |||||||||
| (Wang et al., 2022)41 | 0.24 ± 0.12 | 0.26 ± 0.06 | 0.38 ± 0.14 | ||||||||||
| (Wang et al., 20217)44 | 0.135 ± 0.030 | ||||||||||||
| (Creech et al., 20217)42 | 0.077 ± 0.022 | 0.301 ± 0.065 | 0.207 ± 0.120 | ||||||||||
| Sample | GSR-1 | JG-2 | NOD-A-1 | BIR-1 | RGM-1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Digestion date | Measurement date | δ 122/118Sn | 2sd | Batch number | δ 122/118Sn | 2sd | Batch number | δ 122/118Sn | 2sd | Batch number | δ 122/118Sn | 2sd | Batch number | δ 122/118Sn | 2sd |
| 2022/6/20 | 2022/7/4 | 0.215 | 0.031 | 6-174 | 0.514 | 0.018 | 12 | 0.343 | 0.008 | 859 | 0.351 | 0.036 | 53-13 | 0.206 | 0.04 |
| 0.251 | 0.039 | 6-174 | 0.5 | 0.047 | 12 | 0.315 | 0.02 | ||||||||
| 2022/7/7 | 2022/7/17 | 0.215 | 0.017 | 6-174 | 0.488 | 0.054 | 859 | 0.334 | 0.056 | 53-13 | 0.191 | 0.051 | |||
| 2022/7/19 | 2022/8/17 | 0.218 | 0.025 | ||||||||||||
| 2022/8/15 | 2022/9/7 | ||||||||||||||
| 2022/9/10 | 2022/9/24 | 0.248 | 0.036 | ||||||||||||
| Average | 0.229 | 0.501 | 0.329 | 0.343 | 0.199 | ||||||||||
| 2sd | 0.037 | 0.026 | 0.04 | 0.024 | 0.021 | ||||||||||
| N | 5 | 3 | 2 | 2 | 2 | ||||||||||
| (Wang et al., 2022)41 | 0.44 ± 0.10 | 0.28 ± 0.04 | |||||||||||||
4.6. Sn content and isotopic composition of geological reference materials
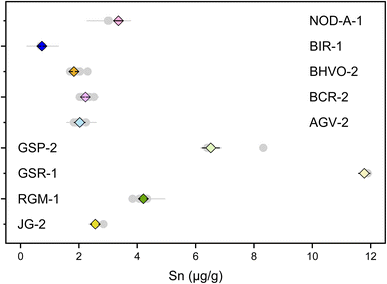
Previous studies have determined the Sn concentrations of geological reference materials with various methods, including isotope dilution (ID) ICP-MS, ID-TIMS, LA-ICP-MS, and standard addition ICP-QMS,41,89–92 however, the reported data are quite variable. The isotope dilution method is a powerful method to determine elemental concentration data precisely for geological materials. In this study, the double spike method could provide the most precise Sn concentration data because the analytical error would mainly arise from sample weighing and pipetting of spike solution. The Sn mass fractions of these geological reference materials are reported in Table S3.† The error for most of the Sn concentration data was within 0.05%, except for AGV-2 that has an error of 9%, which could be due to sample heterogeneity. The measured Sn contents are consistent with previous determinations for the reference materials analyzed in this study. Specifically, the Sn content measured for BHVO-2 (1.83 ± 0.05 μg g−1, N = 7) is in agreement with the literature data of 1.70 to 2.3 μg g−1.41,42,89,93,94 The Sn contents of other geological reference materials determined in this study (Fig. 10) are also in good agreement with the data from the literature.8,41,42,89–91,93To date, only three other laboratories have established the method for high-precision stable Sn isotope measurements on geological reference materials.41,42,44 However, there had been some inconsistency in the reported Sn isotope compositions for the geological reference materials, especially for BHVO-2.41 This could be due to Sn isotopic heterogeneity between different batches of reference materials or insufficient replicates.41 In this study, we used the different batches of BHVO-2 (#1743 and #3191), GSP-2 (#0527 and #0608), AGV-2 (#531 and #227), and BCR-2 (#1748 and #0362), performing independent digestion and measurements to test if there is any significant Sn isotope difference between different batches (aliquots) of geological reference materials (Table 4). The repeated digestions and measurements of BHVO-2 yielded a δ122/118Sn3161a of 0.349 ± 0.021‰ (N = 8), which is in agreement with the result of Wang et al. (2022),41 (δ122/118Sn3161a of 0.38 ± 0.14‰) but slightly higher than that of Wang et al. (2017),44 (Fig. 11). The δ122/118Sn3161a value for GSP-2, AGV-2, JG-2, and NOD-A-1 are 0.223 ± 0.029‰ (N = 12), 0.292 ± 0.021‰ (N = 5), 0.501 ± 0.026‰ (N = 3), and 0.329 ± 0.040‰ (N = 2), respectively, which are also consistent with the data of Wang et al. (2022).41 The BCR-2 has δ122/118Sn3161a of 0.312 ± 0.035‰ (N = 12). We found that the Sn isotope compositions of BCR-2 and AGV-2 from Creech et al.42 are in agreement with this study, whereas the δ122/118Sn3161a of GSP-2 is slightly lower in their result, assuming that BHVO-2 from both studies has an identical composition. The consistency of our replicate digestions and measurements for geological reference materials of different batches confirms the representativeness and reliability of our data. Furthermore, our results support the consistency of the Sn isotope composition of NIST 3161a with different batch numbers (#140917 versus #070330). We propose that future studies could report Sn isotope data with reference to NIST 3161a and Sn isotope data for the above USGS rock standards for data validation.
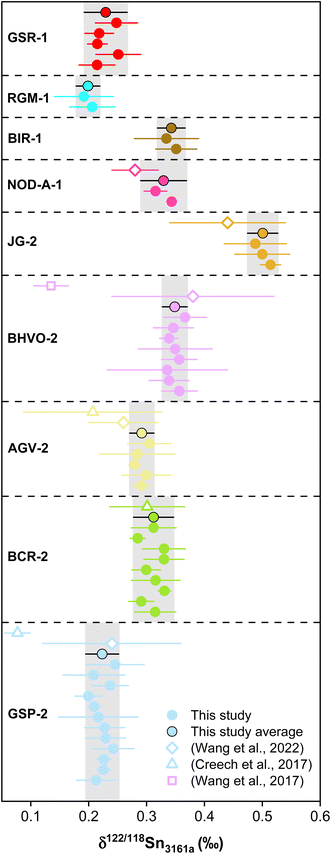 | ||
| Fig. 11 The δ122/118Sn3161a compositions of reference materials with various rock types and Sn mass fractions. The solid points are data from this study, while the open symbols represent the literature data (Creech et al., 2017;42 Wang et al., 2017;44 Wang et al., 2022).41 Errors in data reflect two standard deviations (2SD). | ||
In addition to the geological reference materials reported for Sn isotopes in previous studies, we also measured the Sn isotope composition of three new geological reference materials that had not been reported before. The rock standards of BIR-1, RGM-1, and GSR-1 yield the δ122/118Sn3161a values of 0.343 ± 0.024‰ (N = 2), 0.199 ± 0.021‰ (N = 2) and 0.229 ± 0.037‰ (N = 5). Overall, the results reveal large Sn isotope variations for the magmatic rocks, suggesting the potential of Sn isotopes for tracing magmatic-hydrothermal processes. Granite is the most abundant felsic intrusive rock on the upper continental crust. The δ122/118Sn3161a variation for the granitic reference materials is up to 0.278‰, which signifies the Sn isotopic heterogeneity for the upper continental crust.
5. Conclusion
This study reports a high-precision Sn isotope measurement method with 117Sn–122Sn double spike MC-ICP-MS. The factors affecting the accuracy and repeatability of Sn isotope measurements are systematically evaluated. The results show that matrix elements do not affect Sn isotope measurements with the mass ratios of [X]/Sn (ng g−1/ng g−1) lower than 0.5, except for Cd. Further tests demonstrate that the acid mismatch induces no resolvable Sn isotopic offset. At the same time, δ122/118Sn can be affected by the Sn concentration difference between the sample and bracketing standard, and a Sn concentration matching of better than ±20% is needed to ensure accurate and precise Sn isotopic measurements. Based on repeated measurements, the long-term intermediate precision of our method is better than ±0.069‰. We provide precise Sn contents and isotopic compositions for nine geological reference materials, reproducible and consistent with the previous study. Furthermore, the overall variation of reference materials is 0.30‰ in δ122/118Sn, indicating that Sn isotopes are fractionated significantly during various Earth's processes, including high-temperature magmatic processes.Author contributions
Jia-Xin She, data curation, formal analysis, visualization, writing—original draft; Weiqiang Li, supervision, conceptualization, funding acquisition, formal analysis, writing—review and editing; Shichao An, methodology, formal analysis; Yuanfeng Cai, supervision, resources, validation.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Ruiyu Yang and John Creech for discussions on double spike. SJX is supported by a grant from the China Scholarship Council (File No. 202006190253) and program B for the Outstanding PhD candidate of Nanjing University (File No. 202201B047). This study is supported by the Fundamental Research Funds for the Central Universities (14380165, 14380126, 14380141 to WL).References
- W. Yi, A. N. Halliday, D.-C. Lee and J. N. Christensen, Geochim. Cosmochim. Acta, 1995, 59, 5081–5090 CrossRef CAS.
- G. Witt-Eickschen, H. Palme, H. S. C. O'Neill and C. M. Allen, Geochim. Cosmochim. Acta, 2009, 73, 1755–1778 CrossRef CAS.
- C. A. Heinrich, Econ. Geol. Bull. Soc. Econ. Geol., 1990, 85, 457–481 CrossRef CAS.
- F.-Z. Teng, N. Dauphas, J. M. Watkins and De Gruyter, Non-Traditional Stable Isotopes: Retrospective and Prospective, Berlin, Boston, 2017, pp. 1–26 Search PubMed.
- N. Badullovich, F. Moynier, J. Creech, F. Z. Teng and P. A. Sossi, Geochem. Perspect. Lett., 2017, 5, 24–28 CrossRef.
- M. Roskosz, Q. Amet, C. Fitoussi, N. Dauphas, B. Bourdon, L. Tissandier, M. Y. Hu, A. Said, A. Alatas and E. E. Alp, Geochim. Cosmochim. Acta, 2020, 268, 42–55 CrossRef CAS.
- T. Wang, J.-X. She, K. Yin, K. Wang, Y. Zhang, X. Lu, X. Liu and W. Li, Geochim. Cosmochim. Acta, 2021, 300, 25–43 CrossRef CAS.
- X. Wang, Q. Amet, C. Fitoussi and B. Bourdon, Geochim. Cosmochim. Acta, 2018, 228, 320–335 CrossRef CAS.
- J. Yao, R. Mathur, W. Powell, B. Lehmann, F. Tornos, M. Wilson and J. Ruiz, Am. Mineral., 2018, 103, 1591–1598 CrossRef.
- I. M. Chou, R. Wang and J. Fang, Geochem. Perspect. Lett., 2021, 1–5, DOI:10.7185/geochemlet.2135.
- C. Schmidt, Geochim. Cosmochim. Acta, 2018, 220, 499–511 CrossRef CAS.
- D. Durce, S. Salah, L. Wang and N. Maes, Appl. Geochem., 2020, 123, 104775 CrossRef CAS.
- Y. Cheng, C. Spandler, A. Kemp, J. Mao, B. Rusk, Y. Hu and K. Blake, Am. Mineral., 2019, 104, 118–129 CrossRef.
- Q. Qu, G. Liu, R. Sun and Y. Kang, Environ. Geochem. Health, 2016, 38, 1–23 CrossRef CAS.
- R. C. Wang, L. Xie, J. Chen, A. Yu, L. Wang, J. Lu and J. Zhu, J. Asian Earth Sci., 2013, 74, 361–372 CrossRef.
- B. Lehmann, Lithos, 2021, 402–403 Search PubMed.
- K. J. Jackson and H. C. Helgeson, Geochim. Cosmochim. Acta, 1985, 49, 1–22 CrossRef CAS.
- V. J. Wall and J. R. Taylor, Econ. Geol., 1993, 88, 437–460 CrossRef.
- B. E. Kunz, C. J. Warren, F. E. Jenner, N. B. W. Harris and T. W. Argles, Geology, 2022, 50(11), 1219–1223 CrossRef CAS.
- P. Carr, M. D. Norman, V. C. Bennett and P. L. Blevin, Econ. Geol., 2020, 116, 147–167 CrossRef.
- M. Harlaux, K. Kouzmanov, S. Gialli, O. Laurent, A. Rielli, A. Dini, A. Chauvet, A. Menzies, M. Kalinaj and L. Fontboté, Econ. Geol., 2020, 115, 1665–1697 CrossRef.
- R. L. Romer and U. Kroner, Gondwana Res., 2016, 31, 60–95 CrossRef CAS.
- S. s. Sun and W. F. McDonough, Geol. Soc. Spec. Publ., 1989, 42, 313–345 CrossRef.
- R. L. Rudnick and S. Gao, in Treatise on Geochemistry, ed. H. D. Holland and K. K. Turekian, Pergamon, Oxford, 2003, pp. 1–64, DOI:10.1016/B0-08-043751-6/03016-4.
- N. J. McNaughton and K. J. R. Rosman, Geochim. Cosmochim. Acta, 1991, 55, 499–504 CrossRef CAS.
- R. D. Loss, K. J. R. Rosman and J. R. Delaeter, Geochim. Cosmochim. Acta, 1990, 54, 3525–3536 CrossRef CAS.
- D. D. Clayton, W. A. Fowler, T. E. Hull and B. A. Zimmerman, Ann. Phys., 1961, 12, 331–408 CAS.
- J. R. De Laeter and P. M. Jeffery, J. Geophys. Res., 1965, 70, 2895–2903 CrossRef CAS.
- J. B. Creech, F. Moynier and C. Koeberl, Chem. Geol., 2019, 528, 119279 CrossRef CAS.
- Q. Qu, G. Liu, M. Henry, D. Point, J. Chmeleff, R. Sun, J. E. Sonke and J. Chen, Appl. Geochem., 2020, 119, 104641 CrossRef CAS.
- X. Wang, C. Fitoussi, B. Bourdon, B. Fegley and S. Charnoz, Nat. Geosci., 2019, 12, 707–711 CrossRef CAS.
- M. Haustein, C. Gillis and E. Pernicka, Archaeometry, 2010, 52, 816–832 CrossRef CAS.
- E. Yamazaki, S. Nakai, Y. Sahoo, T. Yokoyama, H. Mifune, T. Saito, J. Chen, N. Takagi, N. Hokanishi and A. Yasuda, J. Archaeol. Sci., 2014, 52, 458–467 CrossRef CAS.
- D. Berger, G. Brügmann and E. J. A. Pernicka, Archaeol Anthropol Sci., 2019, 11, 293–319 CrossRef.
- A. Mason, W. Powell, H. A. Bankoff, R. Mathur, M. Price, A. Bulatović and V. Filipović, J. Archaeol. Sci., 2020, 122, 105181 CrossRef CAS.
- C. Devillers, T. Lecomte and R. Hagemann, Int. J. Mass Spectrom. Ion Phys., 1983, 50, 205–217 CrossRef CAS.
- K. J. R. Rosman and N. J. McNaughton, Int. J. Mass Spectrom. Ion Processes, 1987, 75, 91–98 CrossRef CAS.
- N. H. Gale, Archaeometry, 1997, 39, 71–82 CrossRef CAS.
- R. Clayton, P. Andersson, N. H. Gale, C. Gillis and M. J. Whitehouse, J. Anal. At. Spectrom., 2002, 17, 1248–1256 RSC.
- F. Moynier, T. Fujii and P. Telouk, Anal. Chim. Acta, 2009, 632, 234–239 CrossRef CAS.
- Z. Y. Wang, Z. Y. Luo, L. Zhang, J. J. Liu and J. Li, Geostand. Geoanal. Res., 2022, 46, 547–561 CrossRef CAS.
- J. B. Creech, F. Moynier and N. Badullovich, Chem. Geol., 2017, 457, 61–67 CrossRef CAS.
- M. Friebel, E. R. Toth, M. A. Fehr and M. Schönbächler, J. Anal. At. Spectrom., 2020, 35, 273–292 RSC.
- X. Wang, C. Fitoussi, B. Bourdon and Q. Amet, J. Anal. At. Spectrom., 2017, 32, 1009–1019 RSC.
- Z.-H. Zhou, J.-W. Mao, J.-Q. Zhao, X. Gao, S. Weyer, I. Horn, F. Holtz, P. A. Sossi and D.-C. Wang, Am. Mineral., 2022, 107, 2111–2127 CrossRef.
- P. Liu, J. Mao, B. Lehmann, S. Weyer, I. Horn, R. Mathur, F. Wang and Z. Zhou, Am. Mineral., 2021, 106, 1980–1986 CrossRef.
- R. Mathur, W. Powell, A. Mason, L. Godfrey, J. Yao and M. E. Baker, Geostand. Geoanal. Res., 2017, 41, 701–707 CrossRef CAS.
- E. Balliana, M. Aramendía, M. Resano, C. Barbante and F. J. A. Vanhaecke, Anal. Bioanal. Chem., 2013, 405, 2973–2986 CrossRef CAS PubMed.
- A. H. Mason, W. G. Powell, H. A. Bankoff, R. Mathur, A. Bulatović, V. Filipović and J. Ruiz, J. Archaeol. Sci., 2016, 69, 110–117 CrossRef CAS.
- C. N. Marechal, P. Telouk and F. Albarede, Chem. Geol., 1999, 156, 251–273 CrossRef CAS.
- F. Albarède and B. Beard, Rev. Mineral. Geochem., 2004, 55, 113–152 CrossRef.
- J.-X. She, T. Wang, H. Liang, M. N. Muhtar, W. Li and X. Liu, Geochim. Cosmochim. Acta, 2020, 269, 184–202 CrossRef CAS.
- D. Wang, R. Mathur, W. Powell, L. Godfrey and Y. Zheng, Geochim. Cosmochim. Acta, 2019, 250, 209–218 CrossRef CAS.
- D. Berger, E. Figueiredo, G. Bruegmann and E. Pernicka, J. Archaeol. Sci., 2018, 92, 73–86 CrossRef CAS.
- J. F. Rudge, B. C. Reynolds and B. Bourdon, Chem. Geol., 2009, 265, 420–431 CrossRef CAS.
- M. Klaver and C. D. Coath, Geostand. Geoanal. Res., 2018, 43, 5–22 CrossRef.
- B. Andris and J. Beňa, J. Radioanal. Nucl. Chem., 2016, 308, 781–788 CrossRef CAS.
- T. N. der Walt and P. P. Coetzee, Fresenius' J. Anal. Chem., 1996, 356, 425–429 CrossRef PubMed.
- E. P. Horwitz, R. Chiarizia, M. L. Dietz, H. Diamond and D. M. Nelson, Anal. Chim. Acta, 1993, 281, 361–372 CrossRef CAS.
- H. L. Zhu, Z. F. Zhang, G. Q. Wang, Y. F. Liu, F. Liu, X. Li and W. D. Sun, Geostand. Geoanal. Res., 2016, 40, 185–194 CrossRef CAS.
- A. D. Anbar, J. E. Roe, J. Barling and K. H. Nealson, Science, 2000, 288, 126–128 CrossRef CAS.
- L. A. Machlan and J. W. Gramlich, Anal. Chem., 1988, 60, 37–39 CrossRef CAS.
- C. Maréchal and F. Albarède, Geochim. Cosmochim. Acta, 2002, 66, 1499–1509 CrossRef.
- Y. Tachibana, Y. Yamazaki, M. Nomura and T. Suzuki, J. Radioanal. Nucl. Chem., 2015, 303, 1429–1434 CrossRef CAS.
- D. Nickel, M. Haustein, T. Lampke and E. Pernicka, Archaeometry, 2012, 54, 167–174 CrossRef CAS.
- E. Yamazaki, S. i. Nakai, T. Yokoyama, S. Ishihara and H. Tang, Geochem. J., 2013, 47, 21–35 CrossRef CAS.
- K. Shuai, W. Li and H. Hui, Anal. Chem., 2020, 92, 4820–4828 CrossRef CAS PubMed.
- X. Wang and T. M. Johnson, Anal. Chem., 2021, 93, 7449–7455 CrossRef CAS PubMed.
- T. M. Johnson, M. J. Herbel, T. D. Bullen and P. T. Zawislanski, Geochim. Cosmochim. Acta, 1999, 63, 2775–2783 CrossRef CAS.
- C. M. Johnson and B. L. Beard, Int. J. Mass Spectrom., 1999, 193, 87–99 CrossRef CAS.
- C. Siebert, T. F. Nägler and J. D. Kramers, Geochem., Geophys., Geosyst., 2001, 2, 2000GC000124 CrossRef.
- H.-G. Zhu, J.-M. Zhu, D. Tan, X. Lin, K. Lu and W. Yang, J. Anal. At. Spectrom., 2022, 37, 1063–1075 RSC.
- D. Tan, J.-M. Zhu, X. Wang, G. Han, Z. Lu and W. Xu, J. Anal. At. Spectrom., 2020, 35, 713–727 RSC.
- E. C. Inglis, J. B. Creech, Z. Deng and F. Moynier, Chem. Geol., 2018, 493, 544–552 CrossRef CAS.
- L.-L. Tian, Y.-Z. Gong, W. Wei, J.-T. Kang, H.-M. Yu and F. Huang, J. Anal. At. Spectrom., 2020, 35, 1566–1573 RSC.
- L.-L. Tian, Z. Zeng, X.-Y. Nan, H.-M. Yu and F. Huang, J. Anal. At. Spectrom., 2019, 34, 1459–1467 RSC.
- K. Moeller, R. Schoenberg, R.-B. Pedersen, D. Weiss and S. Dong, Geostand. Geoanal. Res., 2012, 36, 177–199 CrossRef CAS.
- F. Moynier, Y. Hu, K. Wang, Y. Zhao, Y. Gérard, Z. Deng, J. Moureau, W. Li, J. I. Simon and F.-Z. Teng, Chem. Geol., 2021, 571, 120144 CrossRef CAS.
- D. Malinovsky, A. Stenberg, I. Rodushkin, H. Andren, J. Ingri, B. Öhlander and D. C. Baxter, J. Anal. At. Spectrom., 2003, 18, 687–695 RSC.
- M. S. Liu, Q. Zhang, Y. Zhang, Z. Zhang, F. Huang and H. M. Yu, Geostand. Geoanal. Res., 2019, 44, 169–182 CrossRef.
- X. Nan, F. Wu, Z. Zhang, Z. Hou, F. Huang and H. Yu, J. Anal. At. Spectrom., 2015, 30, 2307–2315 RSC.
- M.-L. Pons, M.-A. Millet, G. N. Nowell, S. Misra and H. M. Williams, J. Anal. At. Spectrom., 2020, 35, 320–330 RSC.
- S. An, X. Luo and W. Li, Rapid Commun. Mass Spectrom., 2022, 36, e9289 CrossRef CAS PubMed.
- M. A. Fehr, M. Rehkämper and A. N. Halliday, Int. J. Mass Spectrom., 2004, 232, 83–94 CrossRef CAS.
- V. Yilmaz, L. Rose, Z. Arslan and M. D. Little, J. Anal. At. Spectrom., 2012, 27, 1895–1902 RSC.
- X. Liu, L. Chen, H. Peng, G. Wang, N. S. Belshaw, H. Zheng, S. Hu and Z. Zhu, Anal. Chim. Acta, 2022, 1215, 339980 CrossRef CAS PubMed.
- G. Bruegmann, D. Berger and E. Pernicka, Geostand. Geoanal. Res., 2017, 41, 437–448 CrossRef CAS.
- M. Schulze, M. Ziegerick, I. Horn, S. Weyer and C. Vogt, Spectrochim. Acta, Part B, 2017, 130, 26–34 CrossRef CAS.
- N. Braukmüller, F. Wombacher, A. Bragagni and C. Münker, Geostand. Geoanal. Res., 2020, 44, 733–752 CrossRef.
- A. J. B. Cotta and J. Enzweiler, Geostand. Geoanal. Res., 2013, 37, 35–50 CrossRef CAS.
- K. P. Jochum, U. Weis, B. Schwager, B. Stoll, S. A. Wilson, G. H. Haug, M. O. Andreae and J. Enzweiler, Geostand. Geoanal. Res., 2016, 40, 333–350 CrossRef CAS.
- Y. Lu, A. Makishima and E. Nakamura, Chem. Geol., 2007, 236, 13–26 CrossRef CAS.
- M. Kirchenbaur, A. Heuser, A. Bragagni and F. Wombacher, Geostand. Geoanal. Res., 2018, 42, 361–377 CrossRef CAS.
- D. Weis, B. Kieffer, C. Maerschalk, W. Pretorius and J. Barling, Geochem., Geophys., Geosyst., 2005, 6(2), 2004GC000852 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ja00339b |
| This journal is © The Royal Society of Chemistry 2023 |