Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A framework for understanding the bioconcentration of surfactants in fish†
Michael S.
McLachlan
 *a,
Andrea
Ebert
*a,
Andrea
Ebert
 b,
James M.
Armitage
c,
Jon A.
Arnot
b,
James M.
Armitage
c,
Jon A.
Arnot
 de and
Steven T. J.
Droge
de and
Steven T. J.
Droge
 f
f
aDepartment of Environmental Science, Stockholm University, 106 91 Stockholm, Sweden. E-mail: michael.mclachlan@aces.su.se
bDepartment of Analytical Environmental Chemistry, Helmholtz Centre for Environmental Research – UFZ, D-04318 Leipzig, Germany
cAES Armitage Environmental Sciences, Inc., Ottawa, Ontario K1L 8C3, Canada
dARC Arnot Research and Consulting Inc., Toronto, Ontario M4M 1W4, Canada
eDepartment of Physical and Environmental Sciences, University of Toronto Scarborough, Toronto, Ontario M1C 1A4, Canada
fWageningen Environmental Research, Team Environmental Risk Assessment, 6700 AA Wageningen, The Netherlands
First published on 23rd June 2023
Abstract
Surfactants are a class of chemicals released in large quantities to water, and therefore bioconcentration in fish is an important component of their safety assessment. Their structural diversity, which encompasses nonionic, anionic, cationic and zwitterionic molecules with a broad range of lipophilicity, makes their evaluation challenging. A strong influence of environmental pH adds a further layer of complexity to their bioconcentration assessment. Here we present a framework that penetrates this complexity. Using simple equations derived from current understanding of the relevant underlying processes, we plot the key bioconcentration parameters (uptake rate constant, elimination rate constant and bioconcentration factor) as a function of its membrane lipid/water distribution ratio and the neutral fraction of the chemical in water at pH 8.1 and at pH 6.1. On this chemical space plot, we indicate boundaries at which four resistance terms (perfusion with water, transcellular, paracellular, and perfusion with blood) limit transport of surfactants across the gills. We then show that the bioconcentration parameters predicted by this framework align well with in vivo measurements of anionic, cationic and nonionic surfactants in fish. In doing so, we demonstrate how the framework can be used to explore expected differences in bioconcentration behavior within a given sub-class of surfactants, to assess how pH will influence bioconcentration, to identify the underlying processes governing bioconcentration of a particular surfactant, and to discover knowledge gaps that require further research. This framework for amphiphilic chemicals may function as a template for improved understanding of the accumulation potential of other ionizable chemicals of environmental concern, such as pharmaceuticals or dyes.
Environmental significanceWe provide a framework to understand bioconcentration for surfactants. This process is a complex function of surfactant charge, pKa, membrane affinity and susceptibility to biotransformation, and it also depends on environmental pH. We introduce chemical space plots to clarify this complexity. Furthermore, we demonstrate how these plots can be used to discern how bioconcentration will change when the surfactant properties and environmental pH change, and to identify the underlying processes governing these changes. |
Introduction
Surfactants are used extensively in personal and home care products, for industrial and institutional cleaning, and in the food & beverage and textile industries. The structural diversity of surfactants is very large, including neutral, anionic, cationic and zwitterionic molecules. The common structural characteristics are a polar head group and one or more hydrophobic tails. The substances registered under the European REACH legislation include 4 anionic or cationic surfactants in the annual tonnage band 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–1
000–1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 16 in the tonnage band 10
000, 16 in the tonnage band 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–100
000–100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and 36 in the tonnage band 1000–10
000, and 36 in the tonnage band 1000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000,1,2 as well as a range of nonionic and zwitterionic surfactants (Tables S1 and S2†). A substantial fraction of surfactant production is incorporated into down-the-drain products, and thus large quantities of surfactants are released to municipal wastewater and can impact the aquatic environment. Consequently, sound assessment of the environmental risk is particularly important for this group of chemicals.
000,1,2 as well as a range of nonionic and zwitterionic surfactants (Tables S1 and S2†). A substantial fraction of surfactant production is incorporated into down-the-drain products, and thus large quantities of surfactants are released to municipal wastewater and can impact the aquatic environment. Consequently, sound assessment of the environmental risk is particularly important for this group of chemicals.
Bioaccumulation plays an important role in the environmental assessment of chemicals. The bioconcentration factor (BCF) in fish is a commonly used metric to assess bioaccumulation.3–6 The BCF of surfactants has been shown to be a complex function of substance properties and environmental conditions. The charge state of the molecule plays an important role, as charged molecules generally have a more difficult time than neutral molecules crossing membranes, which can influence their ability to be taken up by fish.7–9 This results in differences in the bioconcentration between nonionic, anionic and cationic surfactants. Within each of these groups the BCF can also vary widely, often increasing with the length of the hydrophobic tail.1,2,10 This has been related to the tendency of the surfactant to partition into tissue, which can reduce elimination via the gills and via biotransformation.10,11 Furthermore, the bioconcentration of some organic acids and bases, including cationic surfactants, has been shown to be pH-dependent, introducing another layer of complexity into the assessment of surfactant bioaccumulation.1,12–14
Assessing the bioconcentration of surfactants remains a challenge for regulators. A survey of REACH registration dossiers revealed that only 7 of 45 anionic surfactants and 7 of 34 cationic surfactants with tonnage >100 per year reported in vivo BCF information.1,2 There is thus a strong reliance on predictive tools to assess bioaccumulation, which is consistent with the 3R-principles for animal testing.15 Most currently available predictive tools were developed for neutral organic compounds and use KOW or DOW to describe partitioning behavior. However, these parameters have been shown to be inadequate for surfactants and can no longer be used to waive more detailed BCF assessment under REACH.16 The membrane lipid/water distribution ratio (DMLW) has shown promise as an alternative physical chemical property to describe partitioning of surfactants into tissue.11 This creates an opportunity to develop modified BCF modeling approaches that are suitable for surfactants. When it comes to evaluating predictive models, the pioneering work of Tolls provided high quality in vivo BCF data for nonionic surfactants and a few anionic surfactants,17–20 but until recently it was not possible to evaluate models of ionic surfactant bioconcentration in fish due to a paucity of measured BCF values. However, during the last 3 years measured BCF values have been published for a range of anionic and cationic surfactants,1,2 so it is now possible to evaluate new BCF modeling approaches tailored to surfactants.
In this work we endeavor to bring order to the complexity of surfactant bioconcentration by developing an interpretive framework that can be used to understand how BCF is influenced by chemical properties and pH. Grasping the opportunities outlined above, we build the framework around a model based on DMLW and evaluate it using the recently published in vivo BCF data for surfactants. After presenting the underlying theoretical concepts, we develop the framework with physiological, chemical property and empirical elements, presenting the results both as equations and graphs. We then compare the framework's estimates with existing measurements of surfactant bioconcentration, before closing with a discussion of the framework's potential and limitations.
Theory
One compartment model of bioconcentration
Bioconcentration can be measured under controlled laboratory conditions in which the fish are exposed to chemical in the water only.21 Bioconcentration is typically described with a one compartment model that considers the fish as a well-mixed box exchanging chemical with the water that it lives in. The defining equation is: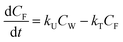 | (1) |
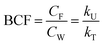 | (2) |
Dissociation
Surfactants are classified into nonionic and ionic surfactants, and ionic surfactants can be further broken down into anionic, cationic and zwitterionic surfactants. Many ionic surfactants dissociate in water, existing in both the neutral and ionic form. Anionic surfactants are typically relatively strong acids and almost entirely dissociated, while cationic surfactants are typically weak bases and can have a neutral fraction in the percent range at environmental pH. The degree of dissociation is defined by the acid dissociation constant, pKa, and by the pH of the water. While the fraction of the neutral form of an acid decreases with increasing pH, that of a base increases. The fraction neutral fneutral,W is defined as follows:24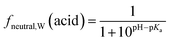 | (3a) |
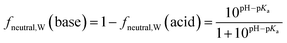 | (3b) |
These equations for monoprotic acids and bases can readily be extended to multiprotic molecules.25 Some cationic surfactants such as the quaternary ammonium compounds are permanently charged.
Partitioning
With a polar head group and a long non-polar chain, many ionic surfactants have a structure similar to the phospholipids that are a major component of biological membranes. Therefore, surfactants readily partition into membranes, making membranes a major storage compartment for surfactants in fish. Membrane lipid/water distribution ratios (DMLW) have been measured using a zwitterionic phospholipid experimental model for a large number of surfactants, and systematic relationships between surfactant structure and DMLW have been found (Droge et al., 2021A). For instance, adding 2 CH2 to the non-polar chain increases DMLW by a factor ∼13 across many surfactant groups. For an overview of fragment-based methods to estimate DMLW, see Droge et al.11Biological membranes also contain anionic phospholipids which enhance the sorption of cations by a factor of ∼20 compared to neutral phospholipids.26 Selecting a total phospholipid content of fish (fP-lipid,F) of 1.25%11 and an anionic phospholipid fraction of 17.5%26 results in the following equation for the fish/water distribution ratio DFW:
| DFW = 0.0125(0.825 + (0.175)(20))DMLW = 0.0541DMLW | (4) |
This approximation of DFW for ionic surfactants ignores the contribution of other tissues besides membranes to storage in fish. While it has been shown that the contribution of neutral lipids is negligible, binding to proteins could conceivably make a significant contribution but there are currently insufficient data to evaluate this.11 We note that eqn (4) will overestimate DFW for anionic surfactants, but it turns out that DFW does not influence the bioconcentration behavior of the anionic surfactants considered here due to significant biotransformation (see below). The framework will be less applicable to persistent anionic surfactants and compounds which are not stored primarily in lipids (e.g., some branched hydrocarbon surfactants, fluorinated surfactants).
For nonionic surfactants, as for other neutral organic molecules, lipids are the primary storage tissue in fish. The few available data suggest that DMLW overestimates the fish oil/water distribution ratio by a factor of ∼3.11 Assuming a fish lipid content of 5%, retaining the above assumption that 25% of total lipids is phospholipids and assuming that the remaining 75% is neutral lipids, we arrive at the following equation for DFW:
| DFW = 0.05(0.25DMLW + 0.75DMLW/3) = 0.025DMLW | (5) |
Mass transfer across gills
The gill transfer model builds on the work of Erickson et al.7 and Bittermann et al.27 Only passive mass transfer is considered. The unidirectional mass flow F (mol h−1) can be described as the product of the surface area of the gill over which mass transfer occurs Agill (m2) and the concentration of the diffusing entity C (mol m−3) divided by a mass transfer resistance R (h m−1):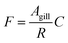 | (6) |
A mass transfer resistance is the reciprocal of a mass transfer coefficient. Mass transfer from the water across the gills to the circulatory system of the fish is constrained by a number of resistances (Fig. S1†): (a) delivery of the chemical with water into the gills; (b) diffusion through the laminar boundary layer of water at the outer gill surface; (c) transport across the gill epithelium; (d) diffusion through the laminar boundary layer on the inner side of the gill epithelium; (e) and removal with blood from the gill. The epithelial resistance can be divided into three resistances acting in parallel, the paracellular resistance, the transcellular resistance and the lateral resistance. Lateral transport has been found to be negligible for neutral compounds and assumed negligible for ionic compounds,27 and it is neglected here (see Text S1† for more details). The transcellular resistance can be broken down into three resistances acting in series: an apical membrane, the cytosolic fluid, and a basal membrane.27 Considering the case where the transcellular resistance is smaller than the paracellular resistance, we have four aqueous resistances acting in series (delivery of water to the gills, exterior boundary layer, cytosolic diffusion, and interior boundary layer). The size of these resistances depends on the same physical chemical property, the molecular diffusion coefficient, and hence the relative size of these resistances does not vary markedly between chemicals. Since the minimum resistance observed in some fish studies corresponds to the resistance for delivery of the water to the gills,28,29 we simplify the model by eliminating the other three aqueous resistances and combining the apical and basal membranes into one resistance. The resulting model has four resistances: perfusion with water, membrane, paracellular, and perfusion with blood, whereby the second and third act in parallel (Fig. S1†).
The water perfusion resistance for transfer from water to blood, RW,W→B (h−1 m), was approximated as the quotient of the specific surface area of the gill and the water flow rate through the gills QW,gill (m3 h−1):
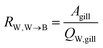 | (7) |
To model the membrane resistance for transfer from water to blood, RM,W→B (h−1 m), ideally the solubility diffusion model should be employed, which describes the permeation coefficient of a chemical in a membrane by the diffusion through and the partitioning into each layer of the membrane (see Text S2† for more details). However, to facilitate generalization we modeled the permeability as a function of DMLW, although DMLW is not the best measure of partitioning into those layers of the membrane that control diffusive transport. We used a modified empirical correlation to predict membrane permeability of the neutral form PM,n (m h−1) from DMLW (see Text S2†).
| PM,n = 0.189DMLW1.14 | (8) |
We assume that mass transport of ionized molecules is negligible, i.e. that only the neutral form of anionic and cationic surfactants diffuses through the membrane. This is a valid assumption for most compounds,30 although it may not be true for anionic surfactants with very low pKa values and permanently charged compounds (see Text S2†). This assumption results in the neutral fraction of the chemical in water fneutral,W being included in the membrane resistance:
| RM,W→B = (fneutral,W × 0.189DMLW1.14)−1 | (9) |
The paracellular resistance is modeled with a constant permeability Pparacell (m h−1) based on empirical observations (see Text S3†). Note that all types of surfactants including permanently charged compounds are assumed to undergo paracellular transport.
The blood perfusion resistance, RB,W→B (h−1 m), can be expressed in a similar manner as the water perfusion resistance, using the rate of blood perfusion of the gills QB,gill (m3 h−1). However, while the pH in fish blood is fixed (e.g., 8.1 in rainbow trout8), the pH in water can vary and hence ion-trapping effects can occur. The presence of a pH gradient between water and blood indicates that the resistance for paracellular transport of ions is much greater than the blood perfusion resistance. It follows that the blood perfusion resistance can only be the dominant resistance for neutral chemicals that take the transcellular route. In this case the ion-trapping effect can be accounted for by the ratio of fneutral,B and fneutral,W, which denotes that the freely dissolved concentration of the neutral form is driving equilibration between blood and water. Furthermore, there are membrane lipids and other sorbents in the blood that increase its capacity to transport the surfactants in both ionic and neutral form. This added capacity is accounted for by the product of DMLW and fM-lipid,B, the fraction of membrane lipid equivalents in the blood (kg L−1).
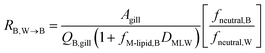 | (10) |
Combining the individual resistances in series and parallel as outlined above yields the following equation for the overall resistance for mass transfer across the gill water into fish's circulation RW→B:
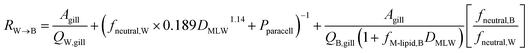 | (11) |
To estimate the uptake rate constant kU (L h−1 kg−1), the specific surface area of the gills Agill/M, where M is the mass of the fish (kg), is divided by RW→B, yielding:
 | (12) |
The rate constant for elimination across the gills k2 (h−1) can be estimated analogously to kU, whereby each of the resistances in eqn (11) is reformulated to describe transport in the other direction (fish to water) and the factor 1/DFW is added to convert CF into an equivalent freely dissolved concentration in blood.
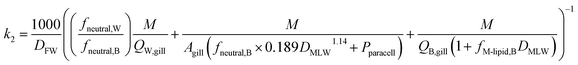 | (13) |
Biotransformation
In describing biotransformation, we assume that it occurs primarily in the liver. We start with the venous equilibrium liver model,31 which has been employed to conduct in vitro in vivo extrapolation of biotransformation in fish.32 It assumes the liver to be well-mixed and elimination kinetics to be first order. Furthermore, we assume that the biotransformation rate is proportional to the freely dissolved concentration of the chemical in blood. This model leads to the following equation for the rate constant for biotransformation in fish kB (for a complete derivation see the ESI in Ribbenstedt et al.2):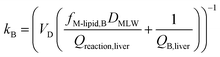 | (14) |
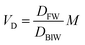 | (15) |
Framework
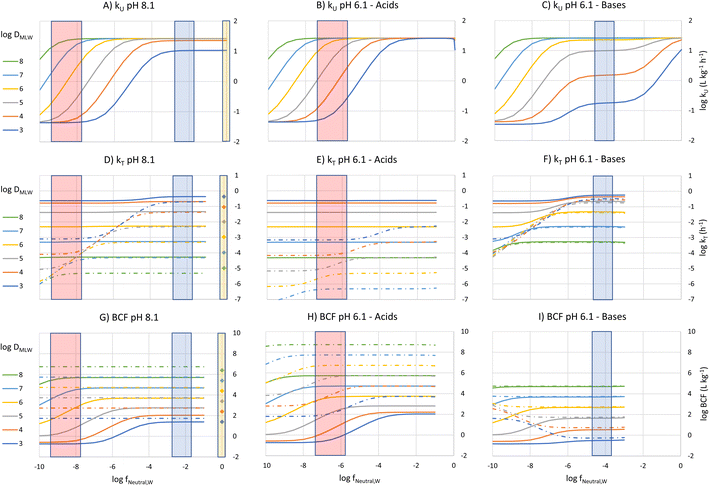
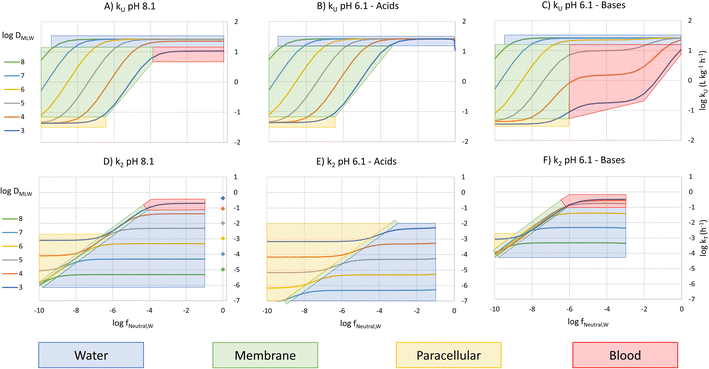
To construct an interpretive framework, we parameterize the above equations and explore how kU, kT and BCF vary as a function of key chemical and environmental variables. In parameterizing the theoretical equations, we use values representative for one common experimental fish, a 10 g juvenile rainbow trout. Most of the available in vivo data on bioconcentration of surfactants are for juvenile rainbow trout in this size range. The framework is illustrated in two figures: Fig. 1 plots kU, kT and BCF, both with and without biotransformation, in a two-dimensional chemical space of fneutral,Wversus DMLW, and marks the location of common anionic and cationic surfactants in the chemical space; Fig. 2 shows kU and k2 in the same chemical space and marks which transport resistance dominates.Uptake
For kU (L kg−1 h−1), constant parameter values were assigned for M, QW,gill, Agill, Pparacell, QB,gill, and fM-lipid,B (see Text S3†), resulting in the equation: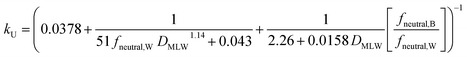 | (16) |
k U is dependent on 3 chemical and environmental variables: DMLW, fneutral,W and fneutral,B, whereby the DMLW is a property of the chemical only while fneutral,W and fneutral,B are properties of both the chemical (through pKa) and the environment (through pH of the water at the gill surface, which depends on the properties of the water body, and the pH in blood, which is physiologically regulated), e.g., fneutral,W is 0.0001 for an acidic surfactant with a pKa of 1 in water with a pH of 5, and 0.001 for a cationic surfactant with a pKa of 10 in water with a pH of 7 (eqn (3a) and (3b)).
To visualize the relationship between these properties and kU, kU was plotted as a function of fneutral,W for different values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW, assuming that fneutral,B = fneutral,W (Fig. 1A). Given that the pH of rainbow trout blood is 8.1,8 this means that the pH of the water at the gill surface is also 8.1. Note that the pH in the gills can be considerably lower than the pH in bulk water due to the local pH reduction arising from the exhalation of CO2. Even in well-buffered water with alkalinity of 4 mmol L−1, a pH of 8.1 at the exit of the gill channels corresponds to a pH of 9 in the bulk water. Hence, fneutral,B = fneutral,W corresponds to a relatively alkaline pH scenario, but this scenario helps facilitate communication of the interaction of the various parameters on key processes and the BCF.
DMLW, assuming that fneutral,B = fneutral,W (Fig. 1A). Given that the pH of rainbow trout blood is 8.1,8 this means that the pH of the water at the gill surface is also 8.1. Note that the pH in the gills can be considerably lower than the pH in bulk water due to the local pH reduction arising from the exhalation of CO2. Even in well-buffered water with alkalinity of 4 mmol L−1, a pH of 8.1 at the exit of the gill channels corresponds to a pH of 9 in the bulk water. Hence, fneutral,B = fneutral,W corresponds to a relatively alkaline pH scenario, but this scenario helps facilitate communication of the interaction of the various parameters on key processes and the BCF.
Fig. 1A shows 3 plateaus of kU (i.e., where kU is independent of fneutral,W). Referring to eqn (16), the first and last terms are independent of fneutral,W as is the middle term when the paracellular resistance dominates. Inspection of Fig. 2A shows that the upper plateau corresponds to water resistance. The water resistance determines kU for fneutral,W > 0.0001 for all compounds with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW > 4. The middle plateau, which is seen in the same fneutral,W range when log
DMLW > 4. The middle plateau, which is seen in the same fneutral,W range when log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW = 3, corresponds to blood resistance limitation. As DMLW drops, the sorption of the compound to blood solids drops, reducing the capacity of the blood to transport the compound out of the gills, and thereby increasing the blood resistance. The lower plateau represents limitation by paracellular transport. This occurs for all compounds when fneutral,W is sufficiently low. In the region between the upper two plateaus and the lower plateau, kU is constrained by the membrane resistance, which increases linearly as a function of fneutral,W and thus results in a linear inverse relationship between kU and fneutral,W.
DMLW = 3, corresponds to blood resistance limitation. As DMLW drops, the sorption of the compound to blood solids drops, reducing the capacity of the blood to transport the compound out of the gills, and thereby increasing the blood resistance. The lower plateau represents limitation by paracellular transport. This occurs for all compounds when fneutral,W is sufficiently low. In the region between the upper two plateaus and the lower plateau, kU is constrained by the membrane resistance, which increases linearly as a function of fneutral,W and thus results in a linear inverse relationship between kU and fneutral,W.
The fneutral,W range of common anionic, cationic and nonionic surfactants is shown in Fig. 1A. Anionic surfactants like sulfates and sulfonates have very small pKa values, and as a result fneutral,W is small. Consequently, the membrane resistance generally limits uptake so that kU is small and linearly dependent on DMLW (red-shaded region in Fig. 1A). Common cationic surfactants like primary, secondary and tertiary amines have higher fneutral,W values of about 0.01 which is due to them having pKa values much closer to the pH (8.1). The framework predicts that these chemicals will have the same kU (water perfusion resistance is dominant) irrespective of both pKa and DMLW except for those with low DMLW (<10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, blood perfusion resistance is dominant, blue-shaded region). The same behavior is predicted for non-ionic surfactants (fneutral,W = 1, yellow-shaded region). On the other hand, for permanently charged cationic surfactants like quaternary ammonium compounds (fneutral,W = 0), kU is predicted to be very low (lower plateau in Fig. 1A, paracellular resistance dominant).
000, blood perfusion resistance is dominant, blue-shaded region). The same behavior is predicted for non-ionic surfactants (fneutral,W = 1, yellow-shaded region). On the other hand, for permanently charged cationic surfactants like quaternary ammonium compounds (fneutral,W = 0), kU is predicted to be very low (lower plateau in Fig. 1A, paracellular resistance dominant).
A similar behavior is observed for acids at a gill water pH of 6.1 (i.e., fneutral,B/fneutral,W = 0.01, Fig. 1B, note that there is a negligible effect of CO2 exhalation on pH at the gills at pH 6.1). The only major change in the relationship between kU, fneutral,W and DMLW is that there is no longer a lower maximum kU value when log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW = 3 (red-shaded region, compare Fig. 1B and A). With the lower fneutral,B/fneutral,W, the blood perfusion resistance is 100 times smaller at a given DMLW and thus the blood perfusion resistance does not become limiting in the DMLW range shown (Fig. 2B). The other change is that the relevant fneutral,W range for the anionic surfactants on the figure shifts to the right. This results in kU being higher at pH 6.1 than at pH 8.1 by as much as 2
DMLW = 3 (red-shaded region, compare Fig. 1B and A). With the lower fneutral,B/fneutral,W, the blood perfusion resistance is 100 times smaller at a given DMLW and thus the blood perfusion resistance does not become limiting in the DMLW range shown (Fig. 2B). The other change is that the relevant fneutral,W range for the anionic surfactants on the figure shifts to the right. This results in kU being higher at pH 6.1 than at pH 8.1 by as much as 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units, depending on whether or not a resistance other than the membrane resistance was limiting uptake.
log units, depending on whether or not a resistance other than the membrane resistance was limiting uptake.
For bases at pH 6.1 (i.e., fneutral,B/fneutral,W = 100) the relationships are more complex (Fig. 1C and 2C). While the left-hand part of the figure is unchanged, a broader range of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW values (3–5) now shows a pronounced intermediate plateau where the blood perfusion resistance becomes limiting. This is because of the linear effect of fneutral,B/fneutral,W on the blood perfusion resistance (eqn (16)). Furthermore, the relevant fneutral,B/fneutral,W range for the cationic surfactants shifts two log units to the left. As a result, the kU values of the cationic surfactants with log
DMLW values (3–5) now shows a pronounced intermediate plateau where the blood perfusion resistance becomes limiting. This is because of the linear effect of fneutral,B/fneutral,W on the blood perfusion resistance (eqn (16)). Furthermore, the relevant fneutral,B/fneutral,W range for the cationic surfactants shifts two log units to the left. As a result, the kU values of the cationic surfactants with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW < 6 are as much as 100 times lower at a gill water pH of 6.1 versus 8.1.
DMLW < 6 are as much as 100 times lower at a gill water pH of 6.1 versus 8.1.
Elimination
Two different elimination pathways are considered in the framework: (a) passive elimination across the gills (k2); (b) biotransformation (kB). The equation for k2 (eqn (13)) was parameterized analogously to the equation for kU, yielding: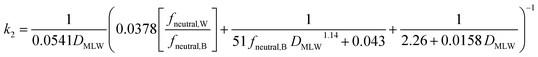 | (17) |
The fneutral,W dependence of k2 mirrors that of kU, with no dependence at high values of fneutral,W (because the water resistance constrains elimination) and at low values of fneutral,W (paracellular resistance constrains) while there is a linear dependence at intermediate values (membrane resistance constrains, see Fig. 1D, dotted lines, Fig. 2D). The DMLW dependence of k2 is more complex than for kU because of the influence of DMLW on the fish/water distribution ratio DFW. This leads to a linear dependence at high and low fneutral,W (when the water or paracellular resistances limit transport) and almost no dependence at intermediate fneutral,W (when the membrane resistance limits transport).
There is a stronger pH-dependence of the relationship between fneutral,W, DMLW and k2 than for kU (Fig. 2E and F compared to 2D versusFig. 2B and C compared to 2A). This arises because of the sensitivity of the water resistance to pH; when the water resistance dominates, k2 is lower at pH 6.1 for acids and higher for bases (Fig. 2E and F compared to 2D). For elimination, the water resistance describes the capacity of the water to carry away chemical that has migrated from the blood across the epithelium. Thus, for elimination the water flow rate through the gills must be corrected for the difference in carrying capacity of the water compared to the blood (eqn (17), this is analogous to the correction of the blood flow for the blood resistance during uptake, eqn (12)). Furthermore, for bases the blood resistance becomes constraining at low log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW, which eliminates the DMLW dependence of k2 (Fig. 2F).
DMLW, which eliminates the DMLW dependence of k2 (Fig. 2F).
The rate constant for biotransformation kB (h−1) was estimated using an empirical parameterization of eqn (14) derived from in vivo measurements of the elimination rate constants of eight sulfonated anionic surfactants, augmented by in vitro estimates for two further structures.2
| kB = (0.000204DMLW + 4.07)−1 | (18) |
Examining this equation, at low values of DMLWkB is constant (see also Fig. 1 in ref. 2). This reflects the situation in which perfusion of the liver limits kB (the equation reduces to kB = 1/4.07 ≈ 0.25). At values of DMLW ≫ 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, kB is inversely proportional to DMLW. In this case the rate of reaction is limiting kB, and kB decreases with increasing DMLW due to increasing sequestration of the chemical into solids in the blood (i.e., less chemical is available for reaction). Note that the empirically based parameterization from Ribbenstedt et al.2 assumes that Qreaction,liver, the clearance rate in the liver, and VD, the volume of distribution, are constant. This assumption is unlikely to be valid for all surfactants, and the applicability domain of eqn (18) may even be limited to the linear sulfonated anionic surfactants studied in that work. No information is available on the influence of fneutral,B on the rate of biotransformation, and thus in eqn (18)kB is independent of fneutral,B.
000, kB is inversely proportional to DMLW. In this case the rate of reaction is limiting kB, and kB decreases with increasing DMLW due to increasing sequestration of the chemical into solids in the blood (i.e., less chemical is available for reaction). Note that the empirically based parameterization from Ribbenstedt et al.2 assumes that Qreaction,liver, the clearance rate in the liver, and VD, the volume of distribution, are constant. This assumption is unlikely to be valid for all surfactants, and the applicability domain of eqn (18) may even be limited to the linear sulfonated anionic surfactants studied in that work. No information is available on the influence of fneutral,B on the rate of biotransformation, and thus in eqn (18)kB is independent of fneutral,B.
The overall elimination rate constant kT, determined from the sum of k2 and kB, is largely independent of fneutral,W (Fig. 1D–F). Comparing the solid and broken lines gives insight into the relative importance of biotransformation when the clearance rate in the liver and volume of distribution are assumed constant. Looking specifically at the surfactant classes, for the high pH scenario biotransformation is approximately 10 times more important than gill transfer for cationic surfactants, while for anionic surfactants this difference is up to up to 4 orders of magnitude. For high DMLW anionic surfactants the difference is larger at pH 6.1 as a result of the smaller values of k2. Since k2 is small compared to kB for the anionic surfactants considered here across the environmental pH range, DFW has no influence on either kT or BCF. For cationic surfactants, on the other hand, elimination is generally dominated by gill transfer at pH 6.1 as a result of the larger k2 values. This indicates that for cationic surfactants the relative importance of biotransformation may be pH-dependent.
BCF
The BCF was calculated from kU, k2 and kB according to eqn (2) and plotted against fneutral,W for different values of DMLW (see Fig. 1G). Excluding biotransformation, BCF is constant for a given DMLW at a level that at pH 8.1 represents the fish/water equilibrium distribution ratio (dotted lines). Recall that a pH of 8.1 at the gill surface corresponds to a pH of ∼9 in bulk water with an alkalinity of 4 mmol L−1. Including biotransformation lowers the BCF in a manner that mirrors its influence on kT. Looking at the surfactant groups, BCF for the cationic surfactants is independent of fneutral,W (pKa) and approximately linearly proportional to DMLW. In contrast, for the anionic surfactants the BCF is sensitive to fneutral,W (pKa) through much of the DMLW range. If we set a log BCF of 3 (BCF = 1000 L kg−1) as a level of concern, cationic surfactants with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW > 5.2 would be of concern, whereby for anionic surfactants only more strongly sorbing molecules would do so (log
DMLW > 5.2 would be of concern, whereby for anionic surfactants only more strongly sorbing molecules would do so (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW > 6.0–6.7).
DMLW > 6.0–6.7).
At a gill water pH of 6.1 the relationships between BCF, fneutral,W, and DMLW are very similar to those at pH 8.1 for acids (Fig. 1G and H, solid lines). The major difference is that fneutral,W for the anionic surfactants is now 2 orders of magnitude higher, and as a result the BCF is markedly higher for all anionic surfactants due to the ion-trapping effect, except for some with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW > 7. This pH influence on the BCF of anionic surfactants is coupled to the inverse relationship between fneutral,W and the membrane resistance. At pH 6.1 anionic surfactants with a log
DMLW > 7. This pH influence on the BCF of anionic surfactants is coupled to the inverse relationship between fneutral,W and the membrane resistance. At pH 6.1 anionic surfactants with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW > 5.3 could exceed the BCF concern level.
DMLW > 5.3 could exceed the BCF concern level.
For cationic surfactants at a pH of 6.1, BCF continues to be independent of fneutral,W, but the BCF values have fallen by 1–2 orders of magnitude (Fig. 1I). BCF is linearly proportional to DMLW and is now approximately equal to the ion-trapping corrected DFW. Several factors contribute to this change in behavior: the blood resistance has become dominant for a larger range of DMLW, ion-trapping has become an important determinant of equilibrium concentration in the fish, and gill elimination has become the dominant elimination mechanism. Like the anionic surfactants, BCF of the cationic surfactants is strongly dependent on pH, but with the opposite trend. At pH 6.1 only cationic surfactants with DMLW > 6.2 are above the BCF concern threshold.
The predicted BCF of nonionic surfactants, neglecting biotransformation, are shown on the right-hand side of Fig. 1G. The BCF is linearly proportional to DMLW. The BCFs for the nonionic surfactants are very similar to the BCFs for the ionic surfactant where biotransformation is negligible (compare dotted lines and symbols of the same color). A nonionic surfactant with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW > 4.3 and negligible biotransformation is predicted to exceed a BCF concern level of 1000 L kg−1.
DMLW > 4.3 and negligible biotransformation is predicted to exceed a BCF concern level of 1000 L kg−1.
Influence of pH
It is also informative to switch our perspective from the influence of chemical properties on bioaccumulation to the influence of environmental conditions. Bulk water pH is the major environmental variable of interest because it influences the fraction of the neutral form of ionic surfactants. pH varies widely in surface water. For instance, the pH range of 3075 European water bodies was found to vary between 4.0 and 10.1, with 95% of the sites between 7.0 and 8.5. There were more lakes than rivers with acidic water, but <1% of the sites had a pH below 6.0.34 In a survey of Dutch surface water bodies which also included many small ditches, 96% of the sites had a pH between 7.0 and 9.5.35To calculate the bioconcentration variables as a function of bulk water pH, the framework was coupled with a model to estimate pH in water along the gill channel.1 The average neutral fraction along the gill channel was used to calculate the membrane resistance, while the neutral fraction at the exit of the gill channel was used to calculate the water and blood resistances. Assuming a temperature of 10 °C and an alkalinity of 1 mmol L−1, kU, kT and BCF were estimated for two chemicals: (i) a base with pKa = 10 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW = 5; (b) an acid with pKa = −1 and log
DMLW = 5; (b) an acid with pKa = −1 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW = 5. kT and BCF were calculated both with biotransformation (eqn (18)) and without.
DMLW = 5. kT and BCF were calculated both with biotransformation (eqn (18)) and without.
Fig. 3 shows that at low pH log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kU is linearly proportional to pH before the curve flattens off at higher pH. For the base the blood resistance dominates at low pH, but as pH increases the difference in the transport capacity between blood and water decreases and around a pH of 6.5 the water resistance becomes rate limiting. For the acid, the membrane resistance dominates at all pHs and the decrease in kU with increasing pH is caused by the decreasing neutral fraction in water. The flattening off at high pH is due to the pH in the gill channel being lower than the pH in the water. We note that the relationship between gill channel pH and water pH-depends on the alkalinity of the water; if the alkalinity would be higher, then the kUvs. pH curve would flatten off at higher pH.
kU is linearly proportional to pH before the curve flattens off at higher pH. For the base the blood resistance dominates at low pH, but as pH increases the difference in the transport capacity between blood and water decreases and around a pH of 6.5 the water resistance becomes rate limiting. For the acid, the membrane resistance dominates at all pHs and the decrease in kU with increasing pH is caused by the decreasing neutral fraction in water. The flattening off at high pH is due to the pH in the gill channel being lower than the pH in the water. We note that the relationship between gill channel pH and water pH-depends on the alkalinity of the water; if the alkalinity would be higher, then the kUvs. pH curve would flatten off at higher pH.
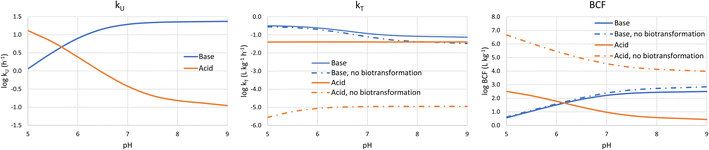 | ||
Fig. 3 Dependence of kU, kT and BCF on bulk water pH for a base with a base with pKa = 10 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW = 5 (blue lines), and an acid with pKa = −1 and log DMLW = 5 (blue lines), and an acid with pKa = −1 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW = 5 (red lines). DMLW = 5 (red lines). | ||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kT is largely independent of pH. Although it might seem intuitive that transport out of the fish would not be impacted by pH in water, the water resistance is pH-dependent. The water resistance is also rate limiting for the base at pH > 6.5, but the pH-dependence of k2 is dampened by the fact that gill channel pH is largely independent of bulk water pH at high pH (see above).
kT is largely independent of pH. Although it might seem intuitive that transport out of the fish would not be impacted by pH in water, the water resistance is pH-dependent. The water resistance is also rate limiting for the base at pH > 6.5, but the pH-dependence of k2 is dampened by the fact that gill channel pH is largely independent of bulk water pH at high pH (see above).
The pH-dependence of BCF largely follows the pH-dependence of kU. At low pH log BCF is proportional to pH for the base and inversely proportional for the acid. At high pH (>7.5) BCF is largely independent of pH, whereby this pH threshold is influenced by the alkalinity of the water. Due to the weak pH-dependence of k2, the pH-dependence of BCF is similar regardless of whether the primary elimination mechanism is respiration or biotransformation.
Comparison of the framework with observations
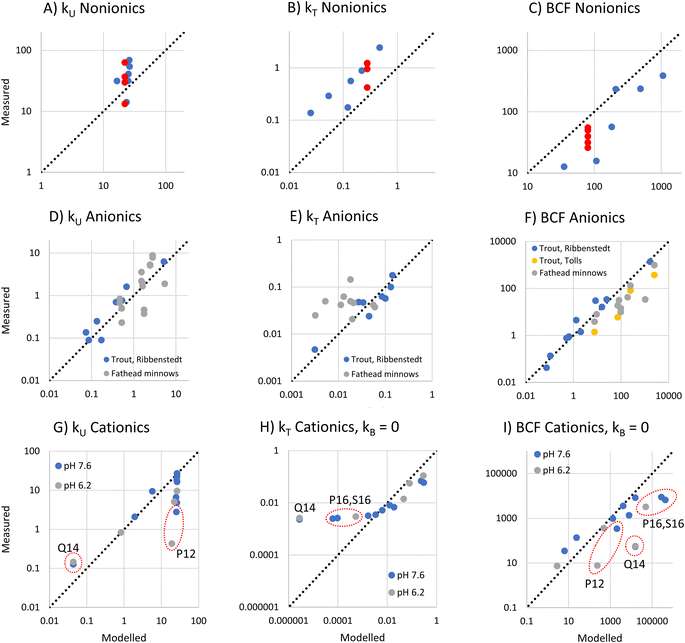
To evaluate the utility of the framework, we compared framework predicted values of kU, kT, and BCF with observations from BCF experiments that provide data for several surfactants within a surfactant group.Nonionic surfactants
For nonionic surfactants, we used data for 7 alcohol ethoxylates obtained from 5 separate experiments, and DMLW values as measured or extrapolated.36 One of the surfactants was studied in all the experiments, while the other 6 were studied in just one experiment.18The modeled and measured kU values were close the to line of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 agreement. The framework predicts little variation in kU while the observations show some variation (Fig. 4A). However, the variation between 4 values for the same surfactant (red dots in Fig. 4A–C) obtained from different experiments was similar to the variation between the 7 different experiments, which suggests that some of the observed variation was due to inter-study variability.
1 agreement. The framework predicts little variation in kU while the observations show some variation (Fig. 4A). However, the variation between 4 values for the same surfactant (red dots in Fig. 4A–C) obtained from different experiments was similar to the variation between the 7 different experiments, which suggests that some of the observed variation was due to inter-study variability.
The framework predicts that kT is dominated by biotransformation, which is also the conclusion drawn from the in vivo studies.17 The modeled and measured kT values were highly correlated (r2 = 0.84), indicating that the framework correctly captures the influence of the major variables determining kT (Fig. 4B). This suggests that the framework assumption that the liver clearance rate (Qreaction,liver) is constant applies within this group of alcohol ethoxylates. However, the model systematically underestimates kT. One possible explanation is that Qreaction,liver is higher for the nonionic surfactants than for the sulfur-based anionic surfactants that were used to parameterize the model. This could most likely be a consequence of the different dominant biotransformation processes in fish liver: central fission for alcohol ethoxylates17,37versus ω-/β-oxidation for anionic LAS.19
For BCF the framework predicts that there is a linear relationship with DMLW. The modeled and measured BCF are highly correlated, indicating that this simple model captures most of the influence of chemical properties on BCF. However, the modeled values have a positive bias (Fig. 4C). This is a direct consequence of the underestimation of kT.
Anionic surfactants
To assess anionic surfactants, we used experimental data from one study of 10 sulfur-based surfactants and two studies of multiple LAS isomers.2,17,20 Obtaining reliable estimates of the pKa for these surfactants is challenging. For instance, we determined values for alkyl sulfonate using 3 predictive tools (ACD Labs M1, ChemAxon and COSMOtherm) that ranged over almost 4 units (1.84, −0.59, and −2.0, respectively). In light of this large uncertainty, we assumed that the pKa of all sulfur-based surfactants was the same and estimated this pKa from kU data for 8 sulfur-based surfactants in rainbow trout2 using inverse modeling of eqn (12). We obtained a value of −0.6 which lies within the range of the estimation methods. Using this, we modeled kU, kT and BCF for the same rainbow trout dataset as well as for further data for LAS isomers in rainbow trout and fathead minnows.For the very low values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fneutral,W (−7.5 to −7.8 under the conditions in the experiments) and the range of log
fneutral,W (−7.5 to −7.8 under the conditions in the experiments) and the range of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW (3.0–6.2) covered by this dataset, the framework predicts that kU is proportional to the product of fneutral,W and DMLW (Fig. 1A, eqn (16)). The modeled kU data show good agreement with the measurements (Fig. 4D). The fact that the model describes most of the variability in the observations indicates that fneutral,W × DMLW is indeed the major variable determining kU for these data, i.e., the membrane resistance to uptake of the neutral form determines uptake. It also indicates that it was reasonable to assume that pKa was the same for all of the surfactants. Although the Ribbenstedt data are expected to group around the line of 1
DMLW (3.0–6.2) covered by this dataset, the framework predicts that kU is proportional to the product of fneutral,W and DMLW (Fig. 1A, eqn (16)). The modeled kU data show good agreement with the measurements (Fig. 4D). The fact that the model describes most of the variability in the observations indicates that fneutral,W × DMLW is indeed the major variable determining kU for these data, i.e., the membrane resistance to uptake of the neutral form determines uptake. It also indicates that it was reasonable to assume that pKa was the same for all of the surfactants. Although the Ribbenstedt data are expected to group around the line of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 agreement because they were used to estimate pKa, the fathead minnow data were independent. That they also group around the line of 1
1 agreement because they were used to estimate pKa, the fathead minnow data were independent. That they also group around the line of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 agreement provides further confirmation of the usefulness of the framework.
1 agreement provides further confirmation of the usefulness of the framework.
For kT, the modeled data agree well with Ribbenstedt's observations for sulfur-based surfactants in rainbow trout (Fig. 4E). This is expected given that the biotransformation model in the framework was derived from these observations. Some of the fathead minnow data also agree well with the observations, but a good number are under-predicted by as much as a factor of 10. kT varies little among the LAS isomers, even though DMLW varies over almost two orders of magnitudes. This suggests that the framework assumption that Qreaction,liver is constant may not apply to the LAS; more strongly sorbing LAS isomers may have a more rapid liver clearance rate.
Finally, there is generally good agreement between modeled and measured BCF, except for some of the LAS isomers in fathead minnows (Fig. 4F). These findings can be explained by the results for kU and kT discussed above.
Deprotonating cationic surfactants
To assess deprotonating cationic surfactants, data from a recent study of 9 alkyl amines in juvenile rainbow trout were used.1 For 4 of these substances, measurements were made at two bulk water pHs, 7.6 and 6.2, which corresponded to pHs of 7.1 and 6.2 in the gill channel. The kinetic parameters for these experiments were recalculated from the experimental observations using a Bayesian model as described in Ribbenstedt et al.2 in order to obtain more reliable uncertainty estimates of kU, kT and BCF. The recalculated parameters are presented in Table S3† and the model fits are illustrated in Fig. S2.†The framework predicts that at high gill water pH kU is constant in the range of the amines (−3.5 < log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fneutral,W < −2.9) except at very low log
fneutral,W < −2.9) except at very low log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW, while at low pH the reduction in kU at low log
DMLW, while at low pH the reduction in kU at low log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW increases (Fig. 1A and C). The reduction in kU at low DMLW is caused by a higher perfusion resistance tied to a lower carrying capacity of the blood for the chemical. Comparing the model with the observations, kU was modeled well in some cases (Fig. 4G). In particular, the framework captured kU correctly for the highest log
DMLW increases (Fig. 1A and C). The reduction in kU at low DMLW is caused by a higher perfusion resistance tied to a lower carrying capacity of the blood for the chemical. Comparing the model with the observations, kU was modeled well in some cases (Fig. 4G). In particular, the framework captured kU correctly for the highest log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW compounds as well as for the lowest, the tertiary amines T9 and T10. It also captured the influence of pH on T10. However, lower kU values were also measured for compounds with intermediate log
DMLW compounds as well as for the lowest, the tertiary amines T9 and T10. It also captured the influence of pH on T10. However, lower kU values were also measured for compounds with intermediate log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW values (P12, S12 and P13) and a pronounced pH-dependence was observed in one case (P12), none of which was predicted by the framework. This suggests that we do not yet fully understand the influence of cationic surfactant properties on the blood perfusion resistance.
DMLW values (P12, S12 and P13) and a pronounced pH-dependence was observed in one case (P12), none of which was predicted by the framework. This suggests that we do not yet fully understand the influence of cationic surfactant properties on the blood perfusion resistance.
For kT, the framework predicts a maximum value of 1 h−1 at low log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW with progressively lower kT as log
DMLW with progressively lower kT as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW increases, an effect which is stronger at high gill water pH. The modeled biotransformation contributes to kT for high log
DMLW increases, an effect which is stronger at high gill water pH. The modeled biotransformation contributes to kT for high log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW compounds at pH 8.1, but not at pH 6.1 (Fig. 1C and F). Comparison with the observations showed that kT of all but the highest log
DMLW compounds at pH 8.1, but not at pH 6.1 (Fig. 1C and F). Comparison with the observations showed that kT of all but the highest log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMLW amines was overpredicted by the framework (see Fig. S3†). This could in part be due to the parameterization of biotransformation, which was based on observations for anionic surfactants. To explore the effect of the uncertain parameterization of biotransformation, we recalculated kT and BCF assuming kB = 0. Good agreement between modeled and measured kT was then obtained for most chemicals (Fig. 4H). P16 and S16 were exceptions, with the measured kT markedly exceeding the modeled kT. Biotransformation is one possible explanation, but this would require a 30–70 times more rapid liver clearance rate (Qreaction,liver) than the value embedded in eqn (18). This is difficult to reconcile with the fact that including eqn (18) results in an overestimation of kT for the other deprotonating cationic surfactants. Another possible explanation is that the one compartment fish model does not apply to P16 and S16. A study of the tissue distribution of cationic surfactants in rainbow trout after exposure via water for 7 days found that a much larger fraction of P16 and S16 was stored in the gills (58% and 53%, respectively, of total body residues) compared to the other cationic surfactants in Fig. 4H.38 This could be a result of slow distribution of P16 and S16 from the gills to other fish tissues, which would violate the assumption of rapid distribution inherent in the one compartment model.
DMLW amines was overpredicted by the framework (see Fig. S3†). This could in part be due to the parameterization of biotransformation, which was based on observations for anionic surfactants. To explore the effect of the uncertain parameterization of biotransformation, we recalculated kT and BCF assuming kB = 0. Good agreement between modeled and measured kT was then obtained for most chemicals (Fig. 4H). P16 and S16 were exceptions, with the measured kT markedly exceeding the modeled kT. Biotransformation is one possible explanation, but this would require a 30–70 times more rapid liver clearance rate (Qreaction,liver) than the value embedded in eqn (18). This is difficult to reconcile with the fact that including eqn (18) results in an overestimation of kT for the other deprotonating cationic surfactants. Another possible explanation is that the one compartment fish model does not apply to P16 and S16. A study of the tissue distribution of cationic surfactants in rainbow trout after exposure via water for 7 days found that a much larger fraction of P16 and S16 was stored in the gills (58% and 53%, respectively, of total body residues) compared to the other cationic surfactants in Fig. 4H.38 This could be a result of slow distribution of P16 and S16 from the gills to other fish tissues, which would violate the assumption of rapid distribution inherent in the one compartment model.
The modeled and measured BCFs agreed well for many of the deprotonating cationic surfactants (see Fig. 4I). The discrepancies reflect the deviations in modeled kU and kT discussed above, whereby in some cases the errors cancel each other out. The tendency to overpredict BCF for the longest chained compounds, P16 and S16, particularly needs to be addressed, given that long-chained (high DMLW) protonating cationic surfactants are the compounds for which both predicted and measured in vivo BCF exceed regulatory thresholds.
Permanently charged cationic surfactants
Comprehensive experimental data were found for one permanently charged quaternary ammonium compound, N,N,N-trimethyl-1-tetradecylammonium (Q14), in juvenile rainbow trout. The framework predicts that the paracellular resistance controls mass transfer across the gills. The modeled kU value was a factor 2.4–2.8 less than the measured kU (Fig. 4G). However, the framework correctly predicts kU to be independent of pH. When biotransformation is assumed to be negligible (as for the deprotonating cationic surfactants), kT is underpredicted by a factor 1000 (Fig. 4H), whereas when biotransformation is modeled according to eqn (18), modeled kT exceeds measured kT by a factor 8 (Fig. S3†). This suggests that biotransformation could dominate the elimination of Q14. However, experiments with rainbow trout liver S9 fractions have shown no biotransformation of Q14.39 Another explanation is that the well mixed assumption of the model does not apply to Q14. The tissue distribution experiment found quantifiable levels of Q14 in only gills and external mucus after seven days of exposure, with traces in blood.38 If the chemical is only found in a small portion of the fish, approximating DFW as the product of DMLW and the membrane lipid content of the fish will give a gross overestimation DFW, which will result in an underestimation of kT. Regarding BCF, the measurements indicate that it is very low (Table S3†), but it is not predicted well by the framework due to the uncertainty in kU and kT (Fig. 4I).Potential and limitations of the framework
Potential
The framework provides a graphical visualization of how physical chemical properties and pH affect bioconcentration properties of surfactants. This facilitates understanding of the complex interactions of the main variables governing bioconcentration. The described behavior can also be easily traced back to the underlying equations and process descriptions. The comparison with observations showed that the framework describes the bioconcentration properties of surfactants in fish in a manner that is generally consistent with the existing literature.One interesting use of the graphical visualization is to explore the pH-dependence of BCF or bioconcentration kinetics. Comparing the panels horizontally in Fig. 1 indicates whether the relationship between fneutral,W, DMLW and the parameter of interest changes with gill water pH. The second feature for assessing pH influence is the vertical bar (used for cationic and anionic surfactant groups in Fig. 1), which is used as a slider that moves across the figures as pH changes, tracking the influence of pH on fneutral,W for the compound of interest.
Another useful feature of the framework is that it can be used to highlight the major processes controlling bioconcentration. For a given surfactant and pH, it identifies the major resistance governing uptake, and it is even possible to make some general statements. For instance, the water resistance or the blood resistance is generally dominant for non-ionic and cationic surfactants, while for anionic surfactants the blood resistance can generally be neglected, but the membrane resistance or the paracellular resistance can play a major role. Furthermore, the framework gives an indication of the expected relative importance of respiration versus biotransformation for elimination. These features allow appropriate prioritization of the gathering of further information to reduce uncertainty in the bioconcentration assessment. This was illustrated for several surfactant classes in the comparison of the framework with observations.
There may be potential to apply the framework to a broader domain of ionizable chemicals of environmental concern, such as (veterinary) pharmaceuticals and industrial processing chemicals (e.g., dyes in textile industry, disinfectants, etc.). This would require critical exploration of the framework boundaries, refinement of the underlying equations, and further evaluation against empirical observations.
Limitations
In constructing the framework, we have consciously simplified process descriptions to facilitate graphical presentation and communication. For example, there are more sophisticated models of membrane transport, as discussed in Text S1.† As such, the framework is not expected to capture all the variability caused by chemical properties and environmental conditions. It does not provide precise estimates of bioconcentration parameters, but rather rough estimates. Furthermore, caution is advised in applying it to chemicals or environmental conditions that are very different than those for which it has been evaluated.One area where the framework is inadequate was identified above, namely the influence of the chemical properties of cationic surfactants on the blood perfusion resistance. Measurement of partitioning of cationic surfactants between water and blood or blood components could provide further insight.
We have assumed that only the neutral form of the anionic and cationic surfactants can cross the gills via the transcellular pathway. This assumption has significant consequences. In particular, the BCF of the anionic surfactants is predicted to be inversely proportional to pH. This prediction is dependent on the pKa, which is highly uncertain for the anionic surfactants and had to be estimated from the observations. Due to this uncertainty, the pH-dependence of the BCF of anionic surfactants should be tested experimentally.
Related to this, Tolls et al. reported a small influence of water hardness on kU for the anionic surfactant LAS.20 Their explanation was that hardness influences the ability of anions to be transferred from water to the membrane surface. We have not included this effect in the framework, partly because the reported effect was relatively small and limited to low hardness and to isomers of LAS with low DMLW (and thus low BCF), and partly because we assume that the anions do not cross the membrane. However, further research on this question would be useful.
Biotransformation is clearly an important process for the nonionic and anionic surfactants considered here. A major limitation of the framework is that it does not describe how molecular properties influence Qreaction,liver (clearance rate in the liver) or VD (volume of distribution). By assuming that these parameters are constant, the framework cannot provide accurate estimates of kT and BCF for many surfactants. However, it does provide an indication of the relative importance of biotransformation for surfactants with different properties and at different pHs. To obtain more accurate estimates, in vitro measurement of biotransformation coupled with in vitro–in vivo extrapolation (IVIVE) models have proven to be useful2,40 and quantitative structure–activity relationships (QSARs) for predicting kB from chemical structure have been validated41–43 and are publicly available (https://www.eas-e-suite.com).
The framework does not describe the bioconcentration behavior of long-chained alkyl amines and quaternary ammonium compounds as well as for the other ionic surfactants. Within the fish, these chemicals are strongly concentrated in gill tissue; Q14 was almost entirely sequestered into surface tissues (gills and external mucous) of rainbow trout, and these tissues accounted for 60% of the P16 and S16 residues.38 This suggests that the conceptual model underlying the framework, namely uptake of the surfactant across the gills and subsequent distribution throughout the fish, does not apply to these substances. More research on this compound group is needed to understand the kinetics of their distribution in the fish and their long-term uptake and elimination behavior. Prioritization of longer chained cationic surfactants is warranted as they possess BCFs that approach or exceed regulatory thresholds for B categorization (i.e., BCFs > 1000–2000 L kg−1).
We have not evaluated the applicability of the framework to zwitterionic surfactants. Many zwitterionic surfactants have a quaternary ammonium group and a strongly dissociating acid group, which means that at environmental pH they will have a double charge but be overall electrically neutral. In the context provided by the framework, it is unclear to what extent they should be treated like permanently charged surfactants with the paracellular resistance dominating transport across the gills, and to what extent they should be treated like neutral molecules capable of taking the transcellular pathway. We found no bioconcentration data for zwitterionic surfactants that could be used to resolve this question. Looking forward, it could be particularly useful to measure the uptake rate constants of a homologous series of zwitterionic surfactants covering a range of DMLW, as this could provide insight into the relative importance of transcellular and paracellular transport. For the case that transcellular transport is important, the pH dependence would also need to be explored.
Additional research needs also include: (i) high quality measured bioaccumulation factors (BAFs) and the development of models for environmentally relevant BAFs that incorporate other significant exposure pathways in addition to gill respiration; (ii) improved quantification of the sorption of surfactants to material in the water in order to estimate the dissolved (bioavailable) fractions. Cationic surfactants in particular are susceptible to sorption to negatively charged sites on minerals and natural organic matter,44 and the framework would benefit from inclusion of this process.
Finally, the framework has been developed and evaluated using data for mostly linear hydrocarbon surfactants. More research is required to assess its applicability to other kinds of surfactants (e.g., strongly branched structures, fluorinated surfactants).
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Felix Günther for recalculating the kinetic parameters for the cationic surfactants. The majority of empirical data leveraged to develop this framework were generated for the CEFIC-LRI ECO37 project (D-BASS, https://cefic-lri.org/projects/eco37-d-bass-developing-a-bioaccumulation-assessment-strategy-for-surfactants/).References
- A. Kierkegaard, M. Sundbom, B. Yuan, J. M. Armitage, J. A. Arnot, S. T. J. Droge and M. S. McLachlan, Bioconcentration of several series of cationic surfactants in rainbow trout, Environ. Sci. Technol., 2021, 55, 8888–8897 CrossRef CAS PubMed.
- A. Ribbenstedt, J. M. Armitage, F. Günther, J. A. Arnot, S. T. J. Droge and M. S. McLachlan, In vivo bioconcentration of 10 anionic surfactants in rainbow trout explained by in vitro data on partitioning and S9 clearance, Environ. Sci. Technol., 2022, 56, 6305–6314 CrossRef CAS PubMed.
- A. V. Weisbrod, K. B. Woodburn, A. A. Koelmans, T. F. Parkerton, A. E. McElroy and K. Borgå, Evaluation of bioaccumulation using in vivo laboratory and field studies, Integr. Environ. Assess. Manage., 2009, 5, 598–623 CrossRef CAS PubMed.
- Government of Canada, Persistence and Bioaccumulation Regulations, SOR/2000-107, https://laws-lois.justice.gc.ca/eng/regulations/sor-2000-107/page-1.html Search PubMed.
- ECHA, Guidance on Information Requirements and Chemical Safety Assessment Chapter R.11: PBT/vPvB assessment, ver. 3.0, 2017, https://echa.europa.eu/documents/10162/13632/information_requirements_r11_en.pdf/a8cce23f-a65a-46d2-ac68-92fee1f9e54f Search PubMed.
- Stockholm Convention on Persistent Organic Pollutants (POPs), http://chm.pops.int/TheConvention/Overview/TextoftheConvention/tabid/2232/Default.aspx.
- R. J. Erickson, J. M. McKim, G. J. Lien, A. D. Hoffman and S. L. Batterman, Uptake and elimination of ionizable organic chemicals at fish gills: I. Model formulation, parameterization, and behavior, Environ. Toxicol. Chem., 2006, 25, 1512–1521 CrossRef CAS PubMed.
- R. J. Erickson, J. M. McKim, G. J. Lien, A. D. Hoffman and S. L. Batterman, Uptake and elimination of ionizable organic chemicals at fish gills: II. Observed and predicted effects of pH, alkalinity, and chemical properties, Environ. Toxicol. Chem., 2006, 25, 1522–1532 CrossRef CAS PubMed.
- J. M. Armitage, J. A. Arnot, F. Wania and D. Mackay, Development and evaluation of a mechanistic bioconcentration model for ionogenic organic chemicals in fish, Environ. Toxicol. Chem., 2013, 32, 115–128 CrossRef CAS PubMed.
- J. Tolls, M. Haller, I. de Graaf, M. A. T. C. Thijssen and D. T. H. M. Sijm, Bioconcentration of LAS: experimental determination and extrapolation to environmental mixtures, Environ. Sci. Technol., 1997, 31, 3426–3431 CrossRef CAS.
- S. T. J. Droge, P. Scherpenisse, J. A. Arnot, J. M. Armitage, M. S. McLachlan, J. Nichols, P. von der Ohe, M. Bonnell and G. Hodges, Screening the baseline fish bioconcentration potential of various types of surfactants using phospholipid binding data, Environ. Sci.: Process. Impacts, 2021, 23, 1930–1948 CAS.
- Z. Nakamura, H. Yamamoto, J. Sekizawa, T. Kondo, N. Hirai and N. Tatarazako, The effects of pH on fluoxetine in Japanese medaka (Oryzias latipes): Acute toxicity in fish larvae and bioaccumulation in juvenile fish, Chemosphere, 2008, 70, 865–873 CrossRef PubMed.
- C. Rendal, K. O. Kusk and S. Trapp, Optimal choice of pH for toxicity and bioaccumulation studies of ionizing organic chemicals, Environ. Toxicol. Chem., 2011, 30, 2395–2406 CrossRef CAS PubMed.
- J. W. Nichols, B. Du, J. P. Berninger, K. A. Connors, C. K. Chambliss, R. J. Erickson, A. D. Hoffman and B. W. Brooks, Observed and modeled effects of pH on bioconcentration of diphenhydramine, a weakly basic pharmaceutical, in fathead minnows, Environ. Toxicol. Chem., 2015, 34, 1425–1435 CrossRef CAS PubMed.
- W. M. S. Russell and R. L. Burch, The Principles of Humane Experimental Technique, Methuen, London, 1959 Search PubMed.
- European Union, Commission Regulation (EU) 2021/979 of 17 June 2021 Amending Annexes VII to XI to Regulation (EC) No 1907/2006 Search PubMed.
- J. Tolls and D. T. H. M. Sijm, Bioconcentration and biotransformation of the nonionic surfactant octaethylene glycol monotridecyl ether 14C-C13EO8, Environ. Toxicol. Chem., 1999, 18, 2689–2695 CrossRef CAS.
- J. Tolls, M. Haller, W. Seinen and D. T. H. M. Sijm, Experimental determination of bioconcentration of the nonionic surfactant alcohol ethoxylate, Environ. Toxicol. Chem., 2000, 19, 646–653 CrossRef CAS.
- J. Tolls, M. P. Lehmann and D. T. H. M. Sijm, Quantification of in vivo biotransformation of the anionic surfactant C12-2-linear alkylbenzene sulfonate in fathead minnows, Environ. Toxicol. Chem., 2000, 19, 2394–2400 CrossRef CAS.
- J. Tolls, M. Haller, E. Labee, M. Verweij and D. T. H. M. Sijm, LAS bioconcentration: tissue distribution and effect of hardness – implications for processes, Environ. Sci. Technol., 2000, 34, 304–310 CrossRef CAS.
- Organization for Economic Co-operation and Development, OECD Guidelines for Testing Chemicals, Test No. 305, Bioaccumulation in Fish: Aqueous and Dietary Exposure, Paris, 2012 Search PubMed.
- A. Spacie and J. L. Hamelink, Alternative models for describing the bioconcentration of organics in fish, Environ. Toxicol. Chem., 1982, 1, 309–320 CrossRef CAS.
- M. C. Barber, A review and comparison of models for predicting dynamic chemical bioconcentration in fish, Environ. Toxicol. Chem., 2003, 22, 1963–1992 CrossRef CAS PubMed.
- R. P. Schwarzenbach, P. M. Gschwend and D. M. Imboden, Environmental Organic Chemistry, John Wiley & Sons, Hoboken, 2017 Search PubMed.
- B. I. Escher, R. Abagyan, M. Embry, N. Klüver, A. D. Redman, C. Zarfl and T. F. Parkerton, Recommendations for improving methods and models for aquatic hazard assessment of ionizable organic chemicals, Environ. Toxicol. Chem., 2020, 39, 269–286 CrossRef CAS PubMed.
- W. Schmitt, General approach for the calculation of tissue to plasma partition coefficients, Toxicol. In Vitro, 2008, 22, 457–467 CrossRef CAS PubMed.
- K. Bittermann, L. Linden and K.-U. Goss, Screening tools for the bioconcentration potential of monovalent organic ions in fish, Environ. Sci.: Process. Impacts, 2018, 20, 845–853 CAS.
- W. Larisch, T. N. Brown and K.-U. Goss, A toxicokinetic model for fish including multiphase sorption features, Environ. Toxicol. Chem., 2017, 36, 1538–1546 CrossRef CAS PubMed.
- J. McKim, P. Schmieder and G. Veith, Absorption dynamics of organic chemical transport across trout gills as related to octanol-water partition coefficient, Toxicol. Appl. Pharm., 1985, 77, 1–10 CrossRef CAS PubMed.
- A. Ebert, C. Hannesschlaeger, K.-U. Goss and P. Pohl, Passive permeability of planar lipid bilayers to organic anions, Biophys. J., 2018, 115, 1931–1941 CrossRef CAS PubMed.
- M. Rowland, L. Z. Benet and G. G. Graham, Clearance concepts in pharmacokinetics, J. Pharmacokinet. Pharmacodyn., 1973, 1, 123–136 CrossRef CAS PubMed.
- J. W. Nichols, I. R. Schultz and P. N. Fitzsimmons, In vitro-in vivo extrapolation of quantitative hepatic biotransformation data for fish. I. A review of methods, and strategies for incorporating intrinsic clearance estimates into chemical kinetic models, Aquat. Toxicol., 2006, 78, 74–90 CrossRef CAS PubMed.
- J. W. Nichols, D. B. Huggett, J. A. Arnot, P. N. Fitzsimmons and C. E. Cowan-Ellsberry, Toward improved models for predicting bioconcentration of well-metabolized compounds by rainbow trout using measured rates of in vitro intrinsic clearance, Environ. Toxicol. Chem., 2013, 32, 1611–1622 CAS.
- M. Bundschuh, A. Weyers, M. Ebeling, D. Elsaesser and R. Schulz, Narrow pH range of surface water bodies receiving pesticide input in Europe, Bull. Environ. Contam. Toxicol., 2016, 96, 3–8 CrossRef CAS PubMed.
- J. J. T. I. Boesten, P. I. Adriaanse, M. M. S. ter Horst, A. Tiktak and A. M. A. van der Linden, Guidance Proposal for Using Available DegT50 Values for Estimation of Degradation Rates of Plant Protection Products in Dutch Surface Water and Sediment (WOt-werkdocument 284), Wettelijke Onderzoekstaken Natuur & Milieu, Wageningen, 2014, p. 42, https://www.wageningenur.nl/en/Publication-details.htm?publicationId=publication-way-343534383938 Search PubMed.
- M. T. Müller, A. J. Zehnder and B. I. Escher, Liposome-water and octanol-water partitioning of alcohol ethoxylates, Environ. Toxicol. Chem., 1999, 18, 2191–2198 Search PubMed.
- C. S. Newsome, D. Howes, S. J. Marshall and R. A. Van Egmond, Fate of some anionic and alcohol ethoxylate surfactants in Carassius auratus, Tenside, Surfactants, Deterg., 1995, 32, 498–503 CrossRef CAS.
- A. Kierkegaard, C. Chen, J. M. Armitage, J. A. Arnot, S. Droge and M. S. McLachlan, Tissue distribution of several series of cationic surfactants in rainbow trout (Oncorhynchus mykiss) following exposure via water, Environ. Sci. Technol., 2020, 54, 4190–4199 CrossRef CAS PubMed.
- S. T. J. Droge, J. M. Armitage, J. A. Arnot, P. N. Fitzsimmons and J. W. Nichols, Biotransformation potential of cationic surfactants in fish assessed with rainbow trout liver S9 fractions, Environ. Toxicol. Chem., 2021, 40, 3123–3136 CrossRef CAS PubMed.
- S. Krause and K.-U. Goss, In vitro – in vivo extrapolation of hepatic metabolism for different scenarios – a toolbox, Chem. Res. Toxicol., 2018, 31, 1195–1202 Search PubMed.
- J. A. Arnot, W. Meylan, J. Tunkel, P. H. Howard, D. Mackay, M. Bonnell and R. S. Boethling, A quantitative structure-activity relationship for predicting metabolic biotransformation rates for organic chemicals in fish, Environ. Toxicol. Chem., 2009, 28, 1168–1177 CrossRef CAS PubMed.
- T. N. Brown, J. A. Arnot and F. Wania, Iterative fragment selection: a group contribution approach to predicting fish biotransformation half-lives, Environ. Sci. Technol., 2012, 46, 8253–8260 CrossRef CAS PubMed.
- E. Papa, L. van der Wal, J. A. Arnot and P. Gramatica, Metabolic biotransformation half-lives in fish: QSAR modelling and consensus analysis, Sci. Total Environ., 2014, 470–471, 1040–1046 CrossRef CAS PubMed.
- M. J. Sánchez-Martín, M. C. Dorado, C. del Hoyo and M. S. Rodríguez-Cruz, Influence of clay mineral structure and surfactant nature on the adsorption capacity of surfactants by clays, J. Hazard. Mater., 2008, 150, 115–123 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Text providing details of the model formulation and framework parameterization; figures illustrating the gill resistance model, remodeled BCF kinetics for cationic surfactants, and comparison of modeled and measured kT for cationic surfactants; tables of nonionic and zwitterionic surfactants with tonnage >100 per y in the EU, and parameter values of remodeled BCF kinetic for cationic surfactants (PDF); spreadsheet demonstrating the framework calculation (XLS). See DOI: https://doi.org/10.1039/d3em00070b |
| This journal is © The Royal Society of Chemistry 2023 |