The impact of non-adiabatic effects on reaction dynamics: a study based on the adiabatic and non-adiabatic potential energy surfaces of CaH2+
Received
26th May 2023
, Accepted 9th August 2023
First published on 12th August 2023
Abstract
The two-state non-adiabatic potential energy matrices of the CaH2+ system are calculated via a diabatization approach by using a neural network model. Subsequently, the adiabatic and non-adiabatic potential energy surfaces (PESs) are constructed based on these non-adiabatic potential energy matrices. Furthermore, based on the adiabatic and non-adiabatic PESs, the Ca+(4s2S) + H2(X1Σ+g) → H(2S) + CaH+(X1Σ+) reaction is studied using the time-dependent wave packet method. Comparative analysis of the experimental and theoretical integral reaction cross-sections (ICSs) indicates that the maximum deviation between the results obtained from the adiabatic PES and the corresponding experimental value is 12.7 bohr2; in contrast, the maximum discrepancy between the theoretical result derived from the non-adiabatic PES and the experimental value is merely 0.42 bohr2. The potential well along the reaction path acts as a ‘filter’, selectively guiding intermediates with longer lifetimes in the potential well back to the reactant channel. This phenomenon indicates that the non-adiabatic effects significantly influence the reaction dynamics of the CaH2+ system.
1. Introduction
With the increasing prominence and growing depth of research on elementary reactions, the investigation of reaction dynamics has progressively become diverse. Over the past few decades, chemical reactions occurring on adiabatic potential energy surfaces (PESs) have become the research hotspot. With the advancement in non-adiabatic theory and enhancement of computational capabilities, researchers are now capable of constructing non-adiabatic PESs with remarkable accuracy. Consequently, research on non-adiabatic dynamics has also experienced significant advancement in recent decades.1–14 In most elementary reaction dynamics calculations, it is imperative to consider non-adiabatic effects for obtaining meaningful results. However, some theoretical calculations of reaction dynamics by using solely adiabatic PESs can still produce sound theoretical outcomes that align well with the experimental results.15,16 This suggests that the influence of non-adiabatic effects on reaction dynamics varies across different systems. For comprehensive analysis of the impact of non-adiabatic effects on chemical reactions where both reactants and products exist on the same adiabatic PES, it is essential to investigate the reaction dynamics of the same chemical reaction on both adiabatic and non-adiabatic PESs. Notably, the characteristics of PESs differ among various reactions; therefore, the extent to which non-adiabatic effects influence different reactions also differs.
Due to the very long-range asymptotic region between hydrogen-like ions and H2 molecules, the reaction between an alkaline-earth metal atom and a H2 molecule constitutes an ideal candidate for researching atom–diatom collisions under cold and ultra-cold conditions.17–29 Non-adiabatic transitions often occur in an elementary reaction process; therefore, if non-adiabatic effects are not considered in theoretical calculations, the obtained theoretical results may significantly differ from the experimental results. For instance, in experiments, the integral cross-section (ICS) of the Li + HCl → LiH + Cl reaction is 27 Å2 at a collision energy of 2.7 kcal mol−1.30 However, the theoretical results obtained using two different adiabatic PESs correspond to approximately 4 Å2, which is much smaller than the experimental one.31,32 The ICS of the Ca+ + H2 → CaH+ + H reaction obtained in the experiment is about 0.15 Å2 at a collision energy of 4.5 eV.25 Recently, an ICS of the Ca+ + H2 → CaH+ + H reaction calculated from a quantum dynamics work based on an adiabatic PES is 3.3 Å2, which is 22 times larger than the experimental result.33 The main objective of this study is to investigate whether the significant difference in the ICS between the adiabatic PES calculation and the experimental result can be attributed to the presence of non-adiabatic effects. For this purpose, both the adiabatic and non-adiabatic PESs of the CaH2+ system are constructed. The state-to-state dynamics of the Ca+(4s2S) + H2(X1Σ+g) → H(2S) + CaH+(X1Σ+) reaction is calculated based on the non-adiabatic PES. At the same time, for comparing the non-adiabatic effects, the quantum dynamics of the same reaction on the adiabatic PES are also calculated. For the convenience of discussion, the reactions involved in this article are designated as follows:
| | | Ca+(4s2S) + H2(X1Σ+g) → H(2S) + CaH+(X1Σ+), | (R1a) |
| | | Ca+(4s2S) + H2(X1Σ+g) → H(2S) + CaH+(X1Σ+), | (R1b) |
| | | Ca+(4s2S) + H2(X1Σ+g) → Ca+(4s2S) + H2(X1Σ+g), | (R2) |
| | | Ca+(4s2S) + H2(X1Σ+g) → Ca+(3d2D) + H2(X1Σ+g), | (R3) |
where the
(R1a) reaction takes place on the adiabatic PES and (R1b), (R2), and (R3) reactions take place on the non-adiabatic PES.
This paper is organized as follows: Section II provides the construction details of the PES and the diabatization scheme, and introduces the characteristics of the PES in detail. Section III presents the dynamics results in detail and provides an in-depth analysis of the dynamics results. Section IV presents the conclusions.
2. Potential energy surfaces
2.1
Ab initio calculations
In ab initio calculations, in order to consider the relativistic effects of the inner electrons in Ca+ ions, the aug-cc-pwCVTZ basis set is selected for Ca+ ions, while the aug-cc-pVTZ basis set is utilized for H atoms. In the ab initio calculations, the multi-reference configuration interaction method is used to treat the dynamic correlation,34 while the state-averaged complete active space self-consistent field (SA-CASSCF) method is used to treat the static correlation.35 In the SA-CASSCF calculations, five electronic states (12A′, 22A′, 14A′, 12A′′, and 22A′′) with equal weight and three valence electrons are considered. A total of 17 orbitals are included in the CASSCF calculations; 9 (7a′ + 2a′′) of them are double-occupied and the remaining 8 (5a′ + 3a′′) are active orbitals. In order to compensate for the impact of higher-order correlation, the final ab initio energy is included with Davidson correction.
Finally, 19265 points are calculated to construct the PES. All ab initio calculations in this study are carried out by using the MOLPRO package.36
2.2 Diabatization scheme & PES fitting
Many non-adiabatic theories have been developed so far. The main objective of these theories is to find the adiabatic–diabatic transformation matrix. The energy under the adiabatic representation can be converted to the non-adiabatic representation through the transformation matrix. Considering the case of a two-state system as an example, the specific transformation formula is as follows:| | 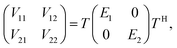 | (1) |
where T denotes the adiabtic–diabatic transformation matrix:| | 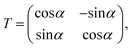 | (2) |
where α is the mixing angle. Obviously, the mixing angle is the key point of the diabatization scheme. Many different methods are available to calculate the mixing angle; some methods are based on non-adiabatic coupling matrix elements, some methods are based on adiabatic eigenfunction coefficients, and the remaining methods are based on molecular properties.37
In this study, the neural network (NN) method is adopted to construct non-adiabatic PESs. To the best of our knowledge, it is the one which has been widely used in the construction of adiabatic PESs. However, the NN method has been rarely applied to the construction of non-adiabatic PESs. This may be attributed to the fact that it is a very complex process to obtain the potential matrix elements. This study provides a brief introduction about the application of the NN method in the construction of non-adiabatic PESs, and a more detailed introduction can be found in the relevant literature reports.38–41 The artificial NN generally consists of three parts, namely the input layer, the hidden layer and the output layer. To consider the exchange symmetry of identical atoms, the fundamental invariants (FIs) method is used in the calculations. The FIs are generated by using the following functions:
| | 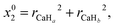 | (4) |
where
x0i = (
i = 1–3) is the input signals of the input layer. The hidden layer contains a large number of neurons with adjustable parameters (weight and bias), which is initially randomly generated. In this study, there are two hidden layers in the NN model and 30 neurons are included in each hidden layer. The NN functions can be expressed as follows:
| | 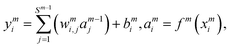 | (6) |
where
wmi,j is the connection weight between the
jth neuron of the (
m − 1)th layer and the
ith neuron of the
mth layer,
bmi is the bias of the
ith neuron of the
mth layer, and
ymi and
ami are the input and output of the
ith neuron of the
mth layer, respectively. The transfer function
f(
x) is a hyperbolic tangent function.
| | 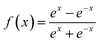 | (7) |
In the construction of an adiabatic PES, there is only one output term (
Efit), while in the construction of two-states non-adiabatic PESs, there are three output terms, namely potential matrix elements
V11,
V22 and
V12. Then, the fitted energies are obtained by using the following formulas:
| | 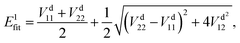 | (8) |
| | 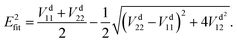 | (9) |
The NN parameters are optimized by minimizing the following performance index
| | 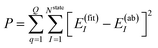 | (10) |
where
Q is the number of geometries and
E(ab)I denotes the
ab initio energies.
For the two-state case, it is considered that Vd12 = Vd21. In addition, there is an additional constraint for the coupling term Vd12, that is, the line integral of the derivative coupling along a closed loop around a conical intersection should yield a value of π:41
| | 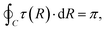 | (11) |
When the integral path tends to be infinitely small, the integral path
C becomes a very small circle. At this time,
eqn (11) can be changed into the following form:
| | 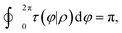 | (12) |
where
ρ is the radius of the small circle and
φ denotes the polar angle. The derivative coupling can be expressed as follows:
41| | 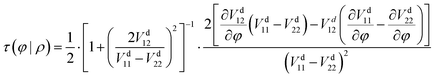 | (13) |
To guarantee the appropriate behavior of the coupling term
Vd12 near the
C2v configurations, a multiplicative factor, cos(
θ), is adopted in this study, which can also guarantee that the off-diagonal terms are anti-symmetry for
θ in [0, 2π]. The refined functional form for these three terms is written as follows:
| | Vd12 = NN3(FI)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (16) |
where NN
i(FI) are NN functions of FIs, and
θ is the Jacobi angle.
2.3 Topological characteristics of the potential energy surface
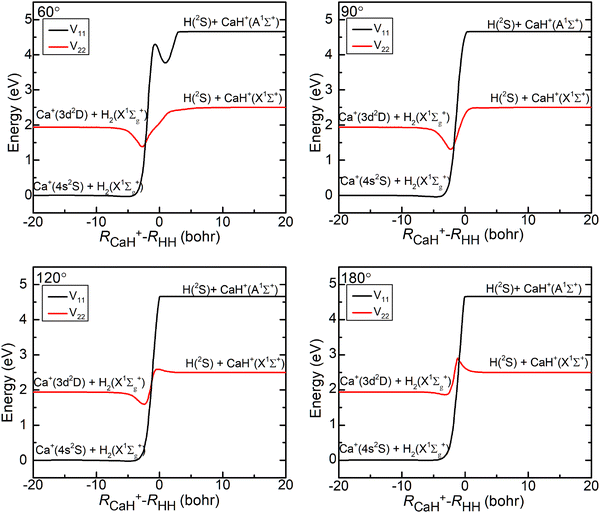
The three-dimensional contour maps of the V11 and V22 surfaces are presented in Fig. 1 at Ca–H–H angles of 60°, 90°, 120°, and 180°, respectively. The zero-point of the potential energy is set at the dissociation limit of the three atoms. The valleys at the left and right ends of the V11 surface correspond to Ca+(4s2S) + H2(X1Σ+g) and H (2S) + CaH (A1Σ+), respectively. The valleys at the left and right ends of the V22 surface correspond to Ca+(3d2D) + H2(X1Σ+g) and H(2S) + CaH+(X1Σ+), respectively. It is evident from the figure that the studied reaction initiates at the left end of the V11 surface, undergoes a transition in the interaction region to the V22 surface, and finally yields the product at the right end of the V22 surface. Additionally, it can be observed that the seam of the two PESs shifts with the change in the Ca–H–H angle. In order to analyze the reaction process more precisely, the minimum energy paths (MEPs) corresponding to the PESs shown in Fig. 1 are illustrated in Fig. 2.
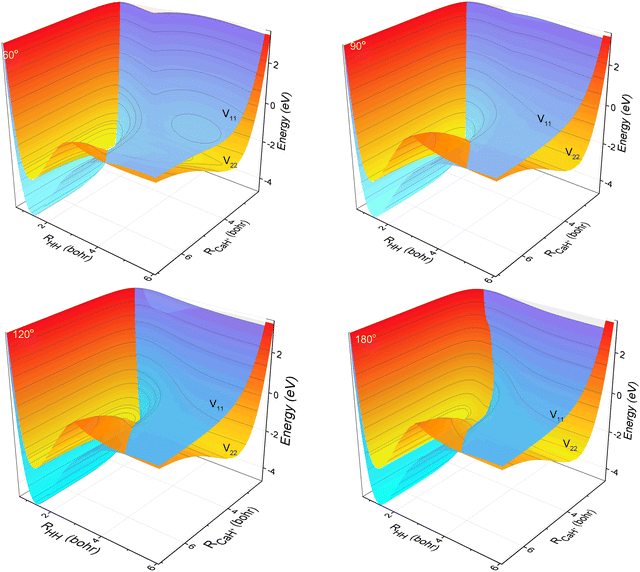 |
| | Fig. 1 3D PESs of the non-adiabatic states V11d and V22d for Ca–H–H with bond angles of 60.0°, 90.0°, 120.0° and 180.0°. | |
 |
| | Fig. 2 Minimum energy paths of V11d and V22d for the Ca–H–H angle fixed at 60.0°, 90.0°, 120.0° and 180.0°. | |
In Fig. 2, the black curves represent the MEPs on the V11 surface, and the red curves represent the MEPs on the V22 surface. The potential energy difference between the reactant Ca+ (4s2S) + H2 (X1Σ+g) channel and the product H(2S) + CaH(X1Σ+) channel is about 2.5 eV, which decreases to about 2.32 eV when considering the zero-point energy of the ground state H2 molecule and the ground state CaH+(X1Σ+) molecule. After further examination of the four subplots in Fig. 2, it is evident that the position of the crossover point between the two MEPs is subject to change with variations in the Ca–H–H angle. At an angle of 60°, the crossover point is situated at the bottom of the potential well on the V22 surface. However, as the Ca–H–H angle increases, the potential well on the V22 surface progressively becomes shallower, and the crossover point gradually shifts toward the top of the potential barrier on the V22 surface.
The aforementioned diagrams illustrate that the reaction studied herein takes place on the ground state adiabatic PES 12A′ of the CaH2+ system. Fig. 3a shows the adiabatic PES for the motion of a Ca+ ion around a H2 molecule when the bond length of the HH molecule is 7.32 bohr. Fig. 3b shows the adiabatic PES for the motion of the H ion around a CaH+ molecule when the bond length of the CaH+ molecule is 5.06 bohr. The coordinate origins of Fig. 3a and b are set at the center of the H2 molecule and the center of the CaH molecule, respectively. The minimum potential energy shown in Fig. 3a is located in the middle region of the hydrogen molecule, indicating that the Ca+ ion tends to approach the H2 molecule along a direction perpendicular to the HH bond. Fig. 3b exhibits the presence of potential wells around both the Ca+ ion and the H atom. However, it is evident that the potential well around the hydrogen atom is deeper than that around the Ca+ ion, and the farther away it is from the Ca+ ion, the lower the potential energy.
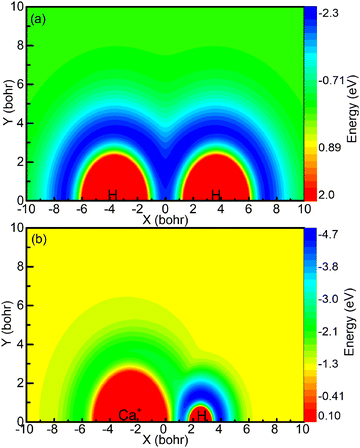 |
| | Fig. 3 (a) Contour plot for a Ca+ ion moving around a HH molecule fixed at RHH = 7.32 bohr and lying along the x-axis. (b) Color plot for a H atom moving around a CaH+ molecule ion fixed at RCaH = 5.06 bohr. The dissociation limit of the CaH2+ molecule ion is set as the zero point of potential energy. | |
3. Reaction dynamics
3.1 Dynamical calculations
The time-dependent wave packet (TDWP) method employed in this study was developed by Zhang et al. and improved by Sun et al.42,43 The TDWP method has been proven to be a reliable and efficient method for theoretical calculations of elementary reaction dynamics. Herein, the main focus is on the dynamics, while a detailed introduction of the TDWP method can be found in previous relevant literature reports.42,43 In the TDWP method, the body-fixed Jacobi coordinate is employed to represent the wave functions. The coordinates for the reactant A + BC are represented by R, r, and θ, where R is the length from A to the BC center of mass, r is the BC bond length, and θ represents the angle between R and r. In this study, the propagation of the wave packets is performed in the coordinates of the reactant. A dividing surface is set in the product region, and detailed dynamics information can be obtained by calculating the scattering wave functions that reach the dividing surface. To prevent the wave packets reaching the grid boundary along R and r, the absorption potentials are placed at the end of each channel. The dynamics calculations of the title reaction are performed based on adiabatic and diabatic PESs, respectively. In addition, a number of convergence tests have been carried out on both adiabatic and non-adiabatic PESs. Table 1 lists the converged parameters obtained from the TDWP calculations based on the adiabatic PES, while Table 2 summarizes the converged parameters based on the non-adiabatic PES. In Tables 1 and 2, the NtotR, Ntotr and j represent the total grid points in R, r, and θ degrees of freedom, respectively. NintR and Nintr represent the grid points in the interaction region along the R and r direction, respectively. R0 and ΔR denote the position and width of the initial wave packet, respectively. E0 represents the energy at the center of the wave packet. The absorbing potential is an exponential function which can be expressed as follows:| | 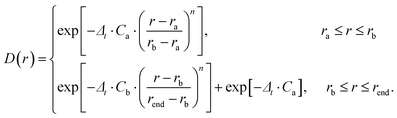 | (17) |
In the present calculations, the maximum total angular momentum is 99, which is large enough to ensure convergence of the calculations in the range with a collision energy of less than 4.5 eV.
Table 1 Numerical parameters used in the adiabatic dynamics calculations
| Grid/basis range and size |
R ∈ [0.01 a.u., 18.0 a.u.], NtotR = 255, NintR = 199 |
|
r ∈ [0.01 a.u., 18.0 a.u.], Ntotr = 255, Nintr = 79 |
|
j
min = 0 ∼ jmax = 120 |
| Initial wavepacket |
R
0 = 12.0 a.u, ΔR = 0. 2 a.u., E0 = 3.6 eV |
| Absorbing potential in R coordinate |
n = 2 CRa = 0.12 CRb = 0.07 Ra = 14.0 Rb = 17.0 |
| Absorbing potential in r coordinate |
n = 2 Cra = 0.1 Crb = 0.2 ra = 14.0 rb = 17.0 |
| Total propagation time |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 a.u. 000 a.u. |
| Time step |
Δ
t
= 10 a.u. |
Table 2 Numerical parameters used in the non-adiabatic dynamics calculations
| Grid/basis range and size |
R ∈ [0.01 a.u., 18.0 a.u.], NtotR = 255, NintR = 145 |
|
r ∈ [0.01 a.u., 18.0 a.u.], Ntotr = 179, Nintr = 79 |
|
j
min= 0 ∼ jmax = 120 |
| Initial wavepacket |
R
0 = 12.0 a.u, ΔR = 0. 22 a.u., E0 = 3.5 eV |
| Absorption functions in R coordinate |
n = 2 CRa = 0.1 CRb = 0.07 Ra = 14.0 Rb = 17.0 |
| Absorption functions in r coordinate |
n = 2 CRa = 0.1 CRb = 0.2 Ra = 14.9 Rb = 17.9 |
| Total propagation time |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 a.u. 000 a.u. |
| Time step |
10 a.u. |
3.2 Dynamics results
The reaction probabilities for the (R1a) and (R1b) reactions are depicted in Fig. 4a and b, respectively. The observed reaction probability threshold aligns with the previous MEPs result, and the probability gradually increases as the collision energy rises. Upon comparing the reaction probabilities at different total angular momenta, it becomes evident that both (R1a) and (R1b) reactions exhibit higher thresholds with increasing total angular momentum. This trend is attributed to the growing centrifugal potential as the total angular momentum increases, which leads to the increase in the minimum energy required to initiate the chemical reaction. Additionally, it is notable that the reaction probabilities of the (R1a) reaction are significantly greater than those of the (R1b) reaction.
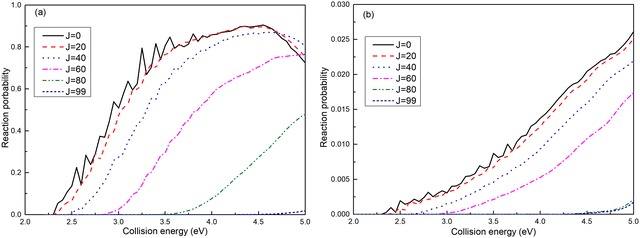 |
| | Fig. 4 Reaction probabilities of the Ca+(4s2S) + H2(X1Σ+g) → H(2S) + CaH+(X1Σ+) reaction calculated from adiabatic PES (a) and non-adiabatic PES (b). | |
To assess the distribution of the wave packet among different channels on the non-adiabatic PES, Fig. 5 illustrates the reaction probabilities for (R1b), (R2), and (R3) reactions at a total angular momentum of J = 0. From Fig. 5, it is evident that the probability of the wave packet returning to the reactant channel (R2) significantly outweighs the probabilities of those entering the excited state channel of the Ca+ ion (R3) and the product channels ((R1b)). Furthermore, the probability of the wave packet entering the product channel slightly surpasses that of entering the excited state channel of the Ca+ ion. Based on the MEPs shown in Fig. 2 and the reaction probabilities presented in Fig. 5, herein, a plausible reaction mechanism is proposed; i.e., the wave packet enters the interaction region through the reactant channel, and undergoes non-adiabatic transitions at the intersection of the two PESs, and then transitions from the ground state to the first excited state. However, since the intersection is just in the potential well of the excited PES, the wave packet transitioning to the first excited state is trapped in the potential well. Owing to the confinement of the potential well, most wave packets oscillate within the potential well and eventually return to the reactant channel, with only a small fraction entering the product channel. The potential well in the excited state functions as a ‘filter’, selectively guiding wave packets with longer lifetimes in the potential well back to the ground state PES, thereby yielding a significantly higher probability of returning to the reactant channel.
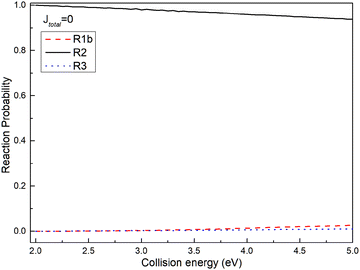 |
| | Fig. 5 Reaction probabilities of (R1b), (R2) and (R3) reactions at total angular momentum J = 0. | |
The ICSs for the (R1a) and (R1b) reactions are illustrated in Fig. 6, alongside the experimental results reported by Georgiadis et al.25 Apparently, the ICS of the (R1b) reaction exhibits a significantly better agreement with the experimental data compared to the ICS of the (R1a) reaction. This indicates that the results obtained based on non-adiabatic PES are more in line with the actual situation. However, it can also be observed that the deviation between the ICS of the (R1b) reaction and the experimental value increases gradually with the increase of the collision energy. In our calculations, the H2 molecule is in its rovibrational ground state, while in the experiment, the rotational energy of the H2 molecule is about 0.024 eV, which may account for the difference between the ICS of the (R1b) reaction and the experimental results. Within the collision energy range below 4.6 eV, the ICS of the (R1a) reaction increases rapidly as a function of collision energy. However, when the collision energy exceeds 4.6 eV, the ICS of the (R1a) reaction gradually diminishes with a further increase in collision energy. This phenomenon can be attributed to the increasing proportion of wave packets entering the dissociation channel as the collision energy exceeds 4.6 eV, resulting in a decline in ICS. Simultaneously, the ICS of the (R1b) reaction continues to increase with the collision energy, even after exceeding 4.6 eV. When the collision energy is greater than the dissociation energy of the product molecule, the reaction can still yield the H(2S) + CaH+(X1Σ+) product, indicating that a portion of the collision energy has been converted into the relative translational energy between the H atom and CaH+ molecule, while the remaining energy is converted into the internal energy of the CaH+ molecule, which is below its dissociation energy.
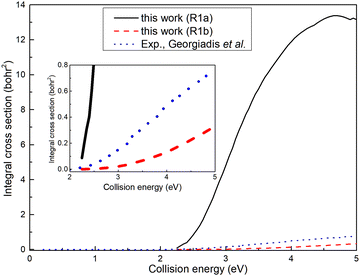 |
| | Fig. 6 Total ICSs of the Ca+(4s2S) + H2(X1Σ+g) → H(2S) + CaH+(X1Σ+) reaction calculated from the adiabatic PES and non-adiabatic PES compared with experimental values. | |
Based on the analysis of Fig. 6, it is evident that the conversion of collision energy into internal energy of the product molecules is more efficient in the (R1a) reaction compared to that in the (R1b) reaction. In order to gain a better understanding of these distinct reaction mechanisms based on the two types of PESs, vibrational state-resolved ICSs are further computed. The vibrational state-resolved ICS obtained from the adiabatic and non-adiabatic PESs are depicted in Fig. 7a and b, respectively. From Fig. 7a, it is observed that the vibrational state with the highest population increases as the collision energy increases. In contrast, Fig. 7b reveals that within the collision energy range below 4.0 eV, the vibrational state with the highest population remains v′ = 0. However, as the collision energy continues to increase, it shifts to v′ = 1. The result presented in Fig. 7b indicates that collision energy cannot be effectively converted into the vibrational energy of the CaH+ molecule on non-adiabatic PES. Based solely on the results shown in Fig. 7, it is not clear how energy is distributed during the process, and more detailed information on the product molecules is needed.
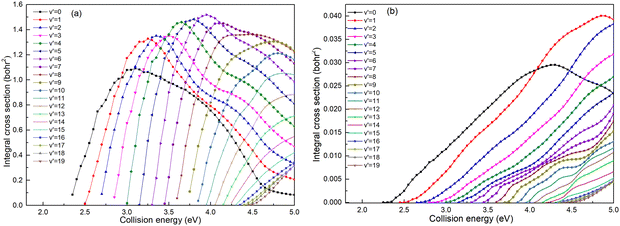 |
| | Fig. 7 Vibrational state-resolved ICSs of the Ca+(4s2S) + H2(X1Σ+g) → H(2S) + CaH+(X1Σ+) reaction calculated based on the adiabatic PES (a) and non-adiabatic PES (b). | |
The rovibrational state-resolved ICSs are presented in Fig. 8. The results calculated at collision energies of 3.6 and 4.5 eV are shown in the upper and lower panels, respectively. The left and right panels depict the results of (R1a) and (R1b) reactions, respectively. The rovibrational state-resolved ICSs of the (R1a) reaction exhibit a peak corresponding to a lower rotational quantum number compared to the (R1b) reaction at the same collision energy. These results indicate that in the non-adiabatic reaction, the collision energy is predominantly converted into the rotational energy of the CaH+ molecules during the conversion from the intermediate to the product. By combining the findings from Fig. 7 and 8, it can be inferred that the (R1b) reaction yields product molecules with higher relative translational energy compared to the (R1a) reaction.
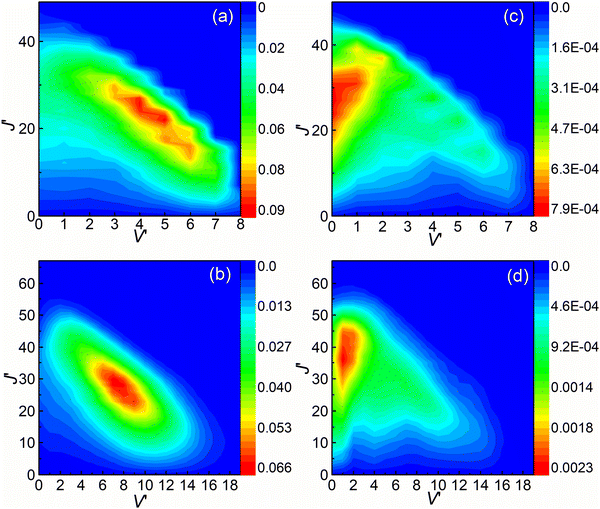 |
| | Fig. 8 Rovibrational state resolved ICSs of the (R1a) (left panels) and (R1b) (right panels) reaction at the collision energies of 3.6 and 4.5 eV. | |
The analysis of the reaction mechanism relies on the indispensable information provided by the differential cross-section (DCS). Fig. 9 exhibits the DCSs at collision energies of 3.6 and 4.5 eV. Similar to the previous figure, the left panels (Fig. 9a and b) display the results for the (R1a) reaction, while the right panels (Fig. 9c and d) depict the results for the (R1b) reaction. The CaH+ molecules generated on the adiabatic PES exhibit a pronounced forward scattering trend, whereas the value for backward and sideways scattering can be almost ignored. The CaH+ molecules generated on the non-adiabatic PES also exhibit significant forward scattering, but the sideways and backward scattering distributions are different from the previous case and cannot be ignored. By comparing the reaction paths of the (R1a) and (R1b) reactions, it becomes apparent that the (R1a) reaction lacks a potential well along its reaction path. Furthermore, due to the substantial difference in mass between the Ca+ ion and the H2 molecule, the velocity direction of the CaH+ molecule is primarily determined by the velocity of the Ca+ ion, resulting in evident forward scattering in the (R1a) reaction. Generally, the longer the life of intermediate products in the potential well, the more likely the scattering direction of product molecules exhibits significant isotropy. However, there is a potential well on the reaction path of the (R1b) reaction, which is just in the intersection area of two non-adiabatic PESs. This potential well acts as a 'filter' for the intermediate products, guiding long-lived intermediates back into the reactant molecular channel while short-lived intermediates swiftly escape the potential well and transform into products. The DCS on the non-adiabatic PES for the (R1b) reaction exhibits a prominent forward scattering peak, along with noticeable values for backward and forward scattering, indicating the presence of two distinct reaction mechanisms within the (R1b) reaction.
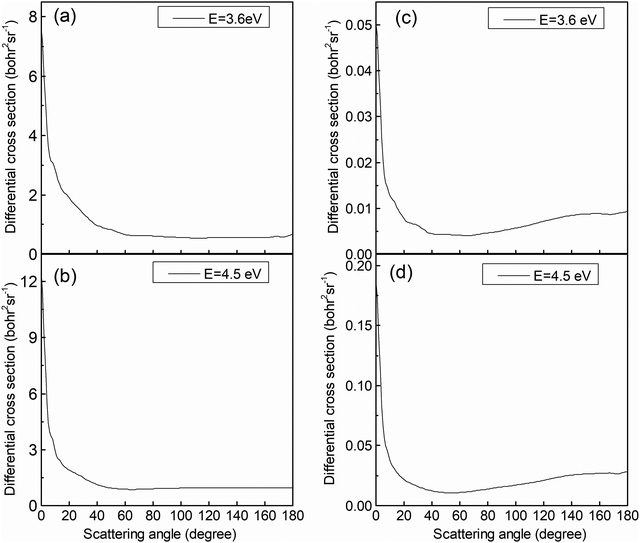 |
| | Fig. 9 DCSs of the (R1a) (left panels) and (R1b) (right panels) reaction at the collision energies of 3.6 and 4.5 eV. | |
To verify our hypothesis, the vibrational state-resolved DCS for a collision energy of 4.5 eV is presented in Fig. 10. Fig. 10a and b depict the results calculated from (R1a) and (R1b) reactions, respectively. In Fig. 10a, it is evident that the peak of forward scattering is centered around v′ = 8. Fig. 10b reveals a striking similarity in the forward scattering distribution to that observed in Fig. 10a. Additionally, Fig. 10b demonstrates that for both backward and sideways scattering, the CaH+ molecules primarily concentrate around the vibrational level v′ = 2. Moreover, the distribution of backward and sideways scattering is broader compared to that of forward scattering. Consequently, this accounts for the vibrational state-resolved ICS peak being at v′ = 2 instead of v′ = 8 at a collision energy of 4.5 eV for the (R1b) reaction, as depicted in Fig. 8.
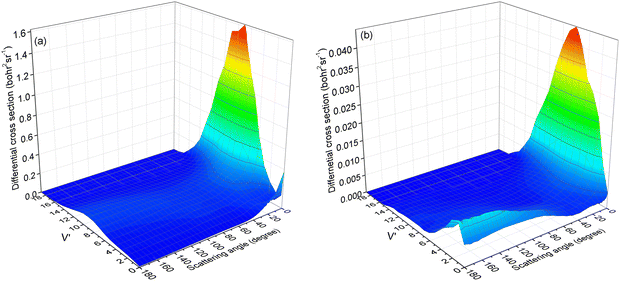 |
| | Fig. 10 Vibrational state-resolved DCSs of the (R1a) (left panel) and (R1b) (right panel) reaction at a collision energy of 4.5 eV. | |
The forward scattering distribution in the (R1a) reaction closely resembles that of the forward scattering in the (R1b) reaction, suggesting consistency in the reaction mechanisms of the (R1a) reaction and the reaction responsible for generating forward scattering molecules in the (R1b) reaction. The main difference in the vibrational energy level distribution arises from the sideways and backward scattering of CaH+ molecules. In the (R1b) reaction, the CaH+ molecules that scatter backward and sideways possess lower vibrational energy levels. This observation indirectly implies that the majority of the collision energy is converted into relative translational energy between the H atom and CaH+ molecule. One possible reaction process is that the intermediate product composed of H atoms and CaH+ molecules contains a large rotational energy before escaping the potential well. With the separation of the H atom and CaH+ molecule, this rotational energy is transformed into relative translational energy between the H atom and CaH+ molecule. From the contour plot presented in Fig. 3b, it is evident that when the H atom rotates around the CaH+ molecule, it tends to depart from the CaH+ molecule along the path with smaller changes in the potential energy gradient, i.e., away from the CaH+ molecule at the end of the Ca+ ion. Consequently, this reaction mechanism contributes to the prevalence of sideways or backward scattering in the CaH+ molecules.
4. Conclusion
We investigate the state-to-state dynamics of the Ca+(4s2S) + H2(X1Σ+g) → H(2S) + CaH+(X1Σ+) reaction on both adiabatic and non-adiabatic PESs that we constructed. The calculations reveal that the reaction probability and the obtained ICS on the adiabatic PES are significantly higher compared to those on the non-adiabatic PES. These results indicate that non-adiabatic effects have a profound influence on the Ca+(4s2S) + H2(X1Σ+g) → H(2S) + CaH+(X1Σ+) reaction. This influence arises due to the intersection seam of the non-adiabatic PES being precisely located within the potential well of the excited-state adiabatic PES. Consequently, intermediate products with longer lifetimes within the well show a high probability of returning to the reactant channel, resulting in substantial differences in reaction probability and ICS between the reactions occurring on the adiabatic and non-adiabatic PESs. Furthermore, we have conducted calculations for the vibrational and vibrational-rotational state-resolved ICSs of the reaction on both the adiabatic and non-adiabatic PESs. The results of the vibrational state-resolved ICSs show that the collision energy can be more effectively converted into the internal energy of the molecule in the reaction on the adiabatic PES. On the other hand, the results of the vibrational-rotational state-resolved ICS reveal that the intermediates in the reaction on the non-adiabatic PES tend to distribute the collision energy to the rotational degree of freedom of the product molecule. Based on the results of the DCS and vibrational state-resolved DCS, two different reaction mechanisms are identified in the reaction on the non-adiabatic PES. One mechanism is dominated by the Ca+ ion, which inserts into the H2 molecule bond to form an intermediate product. In this collision mechanism, the collision energy can be effectively converted into the vibrational energy of the product molecule. However, most of these intermediate products exhibit longer lifetimes in the potential well and only a small fraction of them can smoothly transform into the product molecule. The CaH+ molecule generated by this mechanism shows almost the same velocity direction as the incident Ca+ ion, which leads to a significant forward scattering in the DCS. The other mechanism involves the Ca+ ion capturing an H atom at one end of the H2 molecule to form a CaH+ molecule. Moreover, the other H atom does not immediately separate from the CaH+ molecule but rotates around it and eventually separates from the Ca atom at the other end of the molecule. This mechanism effectively converts the collision energy into a relative translational energy between the H atom and the CaH+ molecule, and the CaH+ molecules generated by this mechanism exhibit significant sideways and backward scattering.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (grant no. 12274191)
References
- P. Halvick and D. G. Truhlar, J. Chem. Phys., 1992, 96, 2895–2909 CrossRef CAS.
- C. Maierle, G. C. Schatz, M. S. Gordon, P. McCabe and J. Connor, J. Chem. Soc., Faraday Trans., 1997, 93, 709–720 RSC.
- S. Gray, C. Petrongolo, K. Drukker and G. Schatz, J. Phys. Chem. A, 1999, 103, 9448–9459 CrossRef CAS.
- S. A. Nizkorodov, W. W. Harper, W. B. Chapman, B. W. Blackmon and D. J. Nesbitt, J. Chem. Phys., 1999, 111, 8404–8416 CrossRef CAS.
- M. Hack and D. Truhlar, J. Phys. Chem. A, 2000, 104, 7917–7926 CrossRef CAS.
- S. Mahapatra, H. Köppel, L. Cederbaum, P. Stampfuss and W. Wenzel, Chem. Phys., 2000, 259, 211–226 CrossRef CAS.
- G. C. Schatz, B. Fisher, W. Grande, K. Kumayama and L. A. Pederson, J. Phys. Chem. A, 2001, 105, 2515–2521 CrossRef CAS.
- C. R. Evenhuis, X. Lin, D. H. Zhang, D. Yarkony and M. A. Collins, J. Chem. Phys., 2005, 123, 134110 CrossRef PubMed.
- R. F. Lu, T. S. Chu and K. L. Han, J. Phys. Chem. A, 2005, 109, 6683–6688 CrossRef CAS PubMed.
- T. S. Chu, K. L. Han and G. C. Schatz, J. Phys. Chem. A, 2007, 111, 8286–8290 CrossRef CAS PubMed.
- S. Y. Lin, H. Guo, B. Jiang, S. Zhou and D. Xie, J. Phys. Chem. A, 2010, 114, 9655–9661 CrossRef CAS PubMed.
- Z. Sun, S. Y. Lin and Y. Zheng, J. Chem. Phys., 2011, 135, 234301 CrossRef PubMed.
- P. Y. Zhang and K. L. Han, J. Phys. Chem. A, 2013, 117, 8512–8518 CrossRef CAS PubMed.
- H. Guo and D. R. Yarkony, Phys. Chem. Chem. Phys., 2016, 18, 26335–26352 RSC.
- T. Yang, J. Chen, L. Huang, T. Wang, C. Xiao, Z. Sun, D. Dai, X. Yang and D. H. Zhang, Science, 2015, 347, 60–63 CrossRef CAS PubMed.
- Z. Sun and D. H. Zhang, Int. J. Quantum Chem., 2015, 115, 689–699 CrossRef CAS.
- H. S. Lee, Y. S. Lee and G. H. Jeung, J. Phys. Chem. A, 1999, 103, 11080–11088 CrossRef CAS.
- T. J. Martínez, Chem. Phys. Lett., 1997, 272, 139–147 CrossRef.
- M. Ben-Nun, T. Martinez and R. Levine, J. Phys. Chem. A, 1997, 101, 7522–7529 CrossRef CAS.
- S. Bililign, P. Kleiber, W. Kearney and K. Sando, J. Chem. Phys., 1992, 96, 218–229 CrossRef CAS.
- L. H. Fan, J. J. Chen, Y. Y. Lin and W. T. Luh, J. Phys. Chem. A, 1999, 103, 1300–1305 CrossRef CAS.
- B. Roth, P. Blythe, H. Wenz, H. Daerr and S. Schiller, Phys. Rev. A, 2006, 73, 042712 CrossRef.
- P. F. Staanum, K. Højbjerre, R. Wester and M. Drewsen, Phys. Rev. Lett., 2008, 100, 243003 CrossRef PubMed.
- M. Satta, M. Marquéz-Mijares, E. Yurtsever, S. Bovino and F. A. Gianturco, Int. J. Mass Spectrom., 2013, 351, 47–55 CrossRef CAS.
- R. Georgiadis and P. Armentrout, J. Phys. Chem., 1988, 92, 7060–7067 CrossRef CAS.
- A. K. Hansen, M. A. Sørensen, P. F. Staanum and M. Drewsen, Angew. Chem., Int. Ed., 2012, 32, 7960–7962 CrossRef PubMed.
- C. W. Chou, C. Kurz, D. B. Hume, P. N. Plessow, D. R. Leibrandt and D. Leibfried, Nature, 2017, 545, 203–207 CrossRef CAS PubMed.
- K. Mølhave and M. Drewsen, Phys. Rev. A, 2000, 62, 011401 CrossRef.
- N. Kimura, K. Okada, T. Takayanagi, M. Wada, S. Ohtani and H. A. Schuessler, Phys. Rev. A, 2011, 83, 033422 CrossRef.
- C. Becker, P. Casavecchia and P. Tiedemann, J. Chem. Phys., 1980, 73, 2833 CrossRef CAS.
- D. He, J. Yuan, H. Li and M. Chen, J. Chem. Phys., 2016, 145, 234312 CrossRef PubMed.
- R. S. Tan, H. C. Zhai, W. Yan, F. Gao and S. Y. Lin, J. Chem. Phys., 2017, 146, 164305 CrossRef PubMed.
- Z. Yang, H. Chen, Y. Mao and M. Chen, Phys. Chem. Chem. Phys., 2022, 24, 19209–19217 RSC.
- H. J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- A. J. Dobbyn and P. J. Knowles, Mol. Phys., 1997, 91, 1107–1124 CAS.
- D. M. Williams, A. Viel and W. Eisfeld, J. Chem. Phys., 2019, 151, 164118 CrossRef PubMed.
- D. M. Williams and W. Eisfeld, J. Phys. Chem. A, 2020, 124, 7608–7621 CrossRef CAS PubMed.
- C. Xie, C. L. Malbon, D. R. Yarkony and H. Guo, J. Chem. Phys., 2017, 147, 044109 CrossRef PubMed.
- C. Xie, X. Zhu, D. R. Yarkony and H. Guo, J. Chem. Phys., 2018, 149, 144107 CrossRef PubMed.
- Z. Sun, H. Guo and D. H. Zhang, J. Chem. Phys., 2010, 132, 084112 CrossRef PubMed.
- Z. Sun, X. Lin, S. Y. Lee and D. H. Zhang, J. Phys. Chem. A, 2009, 113, 4145–4154 CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a,
Wentao
Li
*a,
Wentao
Li
 b,
Quanjiang
Li
a,
Shenghui
Chen
a,
Li
Wang
b,
Quanjiang
Li
a,
Shenghui
Chen
a,
Li
Wang
 a,
Yanli
Liu
a,
Yanli
Liu
 a and
Meishan
Wang
*a
a and
Meishan
Wang
*a
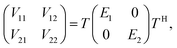
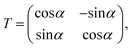
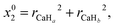
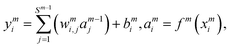
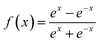
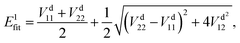
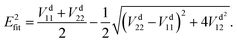
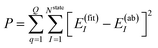
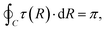
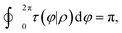
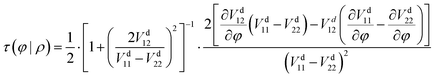
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ

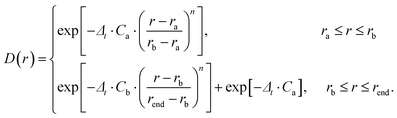
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 a.u.
000 a.u.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 a.u.
000 a.u.







