Phase transition model of FA cation ordering in FAPbX3 (X = Br, I) hybrid perovskites
Mantas
Šimėnas
 *a,
Sergejus
Balčiūnas
a,
Mirosław
Mączka
*a,
Sergejus
Balčiūnas
a,
Mirosław
Mączka
 b and
Jūras
Banys
a
b and
Jūras
Banys
a
aFaculty of Physics, Vilnius University, Sauletekio 3, LT-10257 Vilnius, Lithuania. E-mail: antas.simenas@ff.vu.lt
bInstitute of Low Temperature and Structure Research, Polish Academy of Sciences, Okólna 2, PL-50-422 Wroclaw, Poland
First published on 25th February 2022
Abstract
A proper understanding of structural phase transitions and cation dynamics in hybrid lead halide perovskites is important for further enhancement of the photovoltaic properties of these materials. Here, we propose a model describing the FA cation ordering in FAPbX3 (X = Br, I) hybrid perovskites. Our model is based on the available structural information of these compounds and involves short-range framework-mediated interactions between the FA cations. We solve the model using Monte Carlo simulations, which allows us to reproduce the cubic-tetragonal phase transition and the FA cation arrangement. We show that a spontaneous electric polarization does not appear during this transition, which is supported by the thermally stimulated depolarization current experiments. We also extend our model to describe the FA cation ordering and frustration in the mixed FA1−xCsxPbX3 system, which reveals a frustrated dipole behavior at low temperature.
1 Introduction
Hybrid perovskites attract extraordinary attention from the scientific community due to their potential applications as efficient and solution-processable photovoltaic materials.1,2 The power conversion efficiency of solar cells based on methylammonium (MA, CH3NH3+) and formamidinium (FA, HC(NH2)2+) lead halides experienced a drastic boost in the last decade and currently exceeds 25%.3–8 An interplay between several key physical factors such as large absorption coefficient,9 optimal bandgap,10 long carrier diffusion length,11,12 low exciton binding energy,13 and defect tolerance14 is responsible for the high performance of these materials. These properties can be affected by the molecular cation dynamics and structural phase transitions occurring in these materials.10,15–19Currently, the best performing perovskite solar cells are based on FAPbI3,7,8 which exhibits broad absorption and higher thermal stability compared to MAPbI3.20 Despite extensive use of FAPbX3 (X = Br, I) in solar cell fabrication, a detailed understanding of the structural phase transitions and cation dynamics in these compounds is still under intense investigation.19,21–30 FAPbI3 typically crystallizes into the photoinactive yellow hexagonal phase (δ), which can be converted to a metastable black cubic phase (α) by thermal annealing.25,31–33 Upon cooling from the cubic phase, FAPbI3 exhibits a phase transition at 285 K to a tetragonal phase (β), and another phase transition appears below 140 K (γ-phase).25,34 The exact symmetry and degree of cation disorder of the latter phase still remains questionable.12,23,25,34,35
The bromide analogue crystallizes into the cubic perovskite phase, and the phase transition sequence is similar to the black phase of FAPbI3. It exhibits two phase transitions at 266 K and 153 K, which correspond to the cubic → tetragonal → orthorhombic symmetry lowering.19,27,30,36,37 In addition, this compound also shows three crystallographically unresolvable transitions at 182, 162, and 118 K that involve subtle changes of the FA cation dynamics.19,38
The FA cation dynamics and ordering in FAPbX3 were also investigated using theoretical methods such as density functional theory (DFT)21,23,39–41 and molecular dynamics (MD).21,25,41,42 The DFT calculations provide the atomistic picture of the ordering, but are constrained to small system sizes and poor ability to probe entropic effects such as phase transitions. The effects of temperature can be captured using MD, but such simulations may also suffer from the pronounced finite-size effects, especially if the ab initio MD is employed.
Another method to study phase transition and ordering phenomena is Monte Carlo (MC) simulations of effective model Hamiltonians. This technique is capable of simulating many-particle systems and temperature effects, but usually the atomistic picture must be simplified to a coarse-grained model. Lahnsteiner et al. demonstrated that with a proper choice of a model Hamiltonian, such an approach is comparable with the machine-learning force field predictions.43 The effective model Hamiltonians were used to successfully reproduce the phase transitions and related phenomena in MAPbX344–47 and other48–50 hybrid perovskites. However, such an approach for the simulation of more complicated FAPbX3 perovskites is still absent.
In this work, we propose a model describing the FA cation ordering in FAPbX3 (X = Br, I). We construct our model based on the available structural data of these compounds and solve it using the MC simulations. Our simulations reproduce the cubic (α)-tetragonal (β) phase transition and the FA cation arrangement in both structural phases. We supplement our simulations by the thermally stimulated depolarization current experiments, which reveal the absence of the spontaneous electric polarization in FAPbBr3 and FAPbI3. We also extend our model to simulate mixed cation systems revealing cation frustration and dipolar glass signatures in FA1−xCsxPbX3.
2 Model and simulation details
The construction of a microscopic model describing the FA cation ordering in FAPbX3 requires a detailed analysis of the available structural data. We base our model on the structure of FAPbBr3 in the cubic and tetragonal phases determined by Franz et al. using neutron powder diffraction and synchrotron X-ray diffraction techniques.27 We also assume that FAPbI3 has a very similar FA cation arrangement in both phases as revealed by several other studies.12,21,25,26The FA cation arrangement in the cubic and tetragonal phases of FAPbBr3 is presented in Fig. 1. According to the experimental data, in the cubic phase, the FA cation is dynamically disordered between 48 states (Fig. 1a), while the disorder is decreased to 4-fold in the tetragonal phase (Fig. 1b–d). The FA cations in this phase form a checkerboard arrangement in the ab-plane, where each cation is surrounded by four others having approximately perpendicular orientation (Fig. 1b and c). To accommodate such a cation arrangement, the lead bromide cuboids are elongated along the longer cation axis forming a pattern of alternating rhombuses, as shown in Fig. 1c. The same framework deformation is translated along the c-axis forming rhombic channels such that in each channel the FA cations lie within the same plane (see Fig. 1b and d).
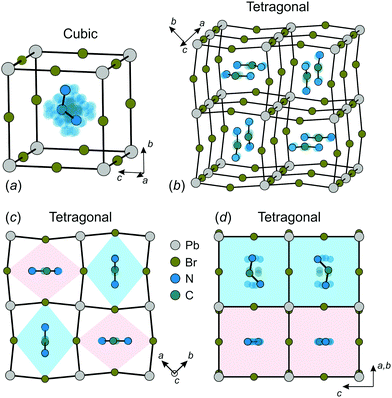 | ||
| Fig. 1 Structure of FAPbBr3 in the (a) cubic and (b–d) tetragonal phases. There are 48 and 4 equivalent orientations (indicated by transparent atoms) of FA cation in the cubic and tetragonal phase, respectively. Color coding in (d) corresponds to the colors of the rhombic channels in (c). Structural data taken from ref. 27. | ||
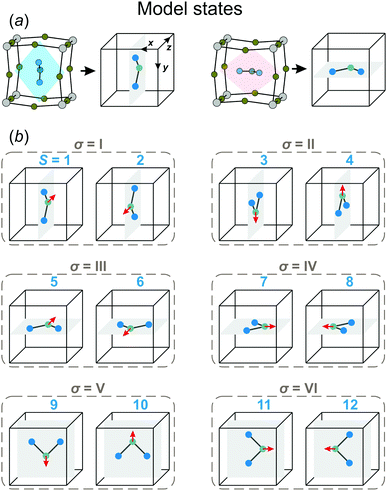
In our model, we map the experimental structure on a simple cubic lattice (xyz-coordinate frame), where each lattice point corresponds to a single FA cation (see Fig. 2a). For simplicity, we assume that the C2 symmetry axis (electric dipole moment) of the cation is perpendicular to the cube side and points into its center. As a result, our model consists of twelve FA cation states (orientations) denoted as S = 1,⋯,12 (see Fig. 2b). Each state can be defined by the direction of the electric dipole moment and the plane, in which the cation is situated. For example, state S = 1 has the dipole moment pointing along the +z direction, while the cation itself is in the yz-plane (see Fig. 2a for a reference frame). Our simplification results in a 4× and 2× lower degree of a cation disorder in the cubic (48 vs. 12) and tetragonal (4 vs. 2) phases, respectively, compared to the experimental data.27 We also form pairs of the S states that are in the same plane, but have the opposite dipole moment resulting in six paired states, which we denote by the Roman numerals: σ = I,⋯,VI (see Fig. 2b). Note that the direction of the electric dipole moment is undefined in the σ-representation.
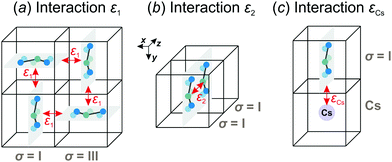
We consider interactions only between the nearest neighbor cation states and do not explicitly take into account the lead halide framework, though its deformation induced by the FA cations acts as a medium for transfer of the interactions. We consider two short-range interactions with energies ε1 and ε2 between the cations. The interaction ε1 occurs between the cations that lie in the orthogonal planes and have parallel C2 symmetry axes (Fig. 3a). This interaction occurs due to the quadrupolar moment of the FA cations38 and is effectively responsible for the experimentally observed checkerboard cation order and framework deformation in the ab-plane. An example of this interaction is presented in Fig. 3a, where it involves σ = I (S = 1,2) and III (S = 5,6) states in the xy-plane of our reference system (I↔xyIII; here, the subscript denotes the plane in which the interaction occurs). By symmetry, this interaction also occurs between other σ-states: II↔xzV and IV↔yzVI.
The Hamiltonian describing interaction ε1 can be expressed as48,49
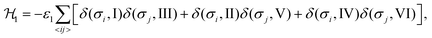 | (1) |
The interaction ε2 describes the FA cation ordering along the c-axis and thus it is responsible for the formation of the ordered channels and coupling of the ab-planes into a three-dimensional structure (Fig. 1b). In our model, it occurs between the same σ-states that lie in the same plane and have parallel symmetry axes as, for example, indicated in Fig. 2b for two σ = I (S = 1,2) states along the z-axis (I↔zI). Equivalent interactions between other σ-states can be obtained from symmetry: II↔yII, III↔zIII, IV↔xIV, V↔yV, VI↔xVI. The magnitude of this interaction is obtained by fine tuning of the phase transition temperature of our model to the experimental data (see results and discussion).
The Hamiltonian describing this interaction can be expressed as
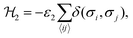 | (2) |
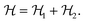 | (3) |
The ground state of this Hamiltonian consists of the planes having a checkerboard cation arrangement (interaction ε1) and coupled via the ε2 interaction. Such cation order in the planes and along the channels resembles the classical antiferromagnetic and ferromagnetic two-state Potts (Ising) models,51 respectively, although a precise mapping seems not feasible.
We also extend our model to study the mixed FA/Cs perovskites by including an effective interaction εCs between the FA states and smaller Cs+ cations. This interaction occurs when the nitrogen atom (negative charge density) of the FA cation is pointing to the Cs+ ion as indicated in Fig. 3c. The identical interaction was also recently used to propose the FA cation frustration in the FA1−xCsxPbBr3 system.38
Note that some previous studies of hybrid perovskites and related compounds also included the dipolar interactions between the molecular cations.39,44,46–48,52,53 For example, we demonstrated that this interaction is essential to obtain a complete phase transition sequence in MAPbX3 perovskites.46 In this work, for simplicity, we ignore the dipolar interactions, as the electric dipole moment of the FA cation (0.21 D) is small compared to other molecular cations such as MA (2.29 D).10
We used the single-flip Metropolis MC algorithm54 to solve our model Hamiltonian. All calculations started from a randomly generated lattice configuration, and the algorithm was implemented by randomly choosing a cation in the lattice and calculating its initial interaction energy Ei using the full Hamiltonian of our system. Then the chosen state was randomly changed to one of the remaining states, and the final energy Ef was evaluated. The cation state was changed with a probability min(1, e−ΔE/kBT), where ΔE = Ef − Ei is the energy difference, T is the temperature, and kB denotes the Boltzmann constant. Afterwards, a new lattice site was randomly selected, and the Metropolis procedure was repeated. The simulations were performed on a simple cubic lattice with the implemented periodic boundary conditions. The lattice size was L × L × L, where L = 10–20 (in terms of the lattice constant). At each temperature, we discarded the initial 5 × 105 MC steps and then used up to 106 steps for the calculation of the thermodynamic averages.
To study the phase transition properties of our model, we calculated the heat capacity at constant volume using the following equation:54
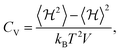 | (4) |
![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) = (Px, Py, Pz) by averaging the total electric dipole moment of the cation system:
= (Px, Py, Pz) by averaging the total electric dipole moment of the cation system: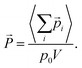 | (5) |
Here, 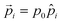 denotes a dipole moment of a cation state at lattice site i. We assume that all states have the same magnitude p0, but the direction
denotes a dipole moment of a cation state at lattice site i. We assume that all states have the same magnitude p0, but the direction ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) may differ as indicated in Fig. 2b.
may differ as indicated in Fig. 2b.
3 Sample preparation and experimental details
Single crystals of FAPbBr3 were grown using antisolvent vapor-assisted crystallization. In the typical synthesis, 2 mmol of formamidinium acetate (99%, Sigma-Aldrich) was added to a mixture containing 2 mmol of PbBr2 (98%, Sigma-Aldrich), 10 mmol of hydrobromic acid (48 wt% in H2O, Sigma-Aldrich) and 5 mL of acetonitrile (Sigma-Aldrich). Then dimethyl sulfoxide (DMSO, Sigma-Aldrich) was added to the prepared solution under stirring until complete dissolution of the orange precipitate (∼1 mL). The clear solution was transferred into a glass vial, and this vial was placed in a second larger glass vial containing methyl acetate. The lid of the outer vial was thoroughly sealed, but the lid of the inner vial was loosened to allow diffusion of the methyl acetate into the precursor solution. Orange crystals were harvested after 5 days and dried at room temperature.Single crystals of FAPbI3 (yellow δ-phase) were grown in a similar way as recently proposed by Fateev et al. for crystallization of MAPbI3 and a number of two-dimensional iodides.55 In our synthesis, a mixture of propylene carbonate (PC, 99.7%, Sigma-Aldrich) and HI (57 wt% in H2O, stabilized with H3PO2, Sigma-Aldrich) was added to 4 mmol of formamidinium acetate and 4 mmol of PbI2 under stirring until complete dissolution of the solids (∼6 mL). The PC:HI volume ratio was 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The clear solution was transferred into a glass vial with the lid slightly loosened. Then the vial was kept at 40 °C for 2 days, and the grown yellow needle-like crystals were separated from the liquid and dried at room temperature.
1. The clear solution was transferred into a glass vial with the lid slightly loosened. Then the vial was kept at 40 °C for 2 days, and the grown yellow needle-like crystals were separated from the liquid and dried at room temperature.
We used these samples with the applied silver paste electrodes to perform the thermally stimulated depolarization current measurements. A single crystal of FAPbBr3 (thickness 0.99 mm, electrode area 8.46 mm2) was used for these experiments, while, due to a small size of the crystals, we had to press FAPbI3 into a pellet (thickness 2.00 mm, electrode area 50.26 mm2) using 0.1 GPa axial pressure. Afterwards, the FAPbI3 pellet was heated to 420 K to ensure conversion to the black phase, which was monitored using dielectric spectroscopy.33 The FAPbBr3 and FAPbI3 samples were cooled down to 125 K with the applied electric field of 2 and 0.25 kV cm−1, respectively. After cooling, the poling voltage was removed and a 10 kΩ resistor was used to short the samples. The current was measured using a Keithley 6514 electrometer during heating at a rate of 3 K min−1. The depolarization current was separated from the measured data by subtracting the exponential increase of current with increasing temperature.
4 Results and discussion
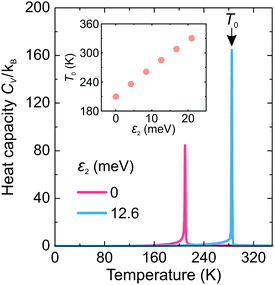
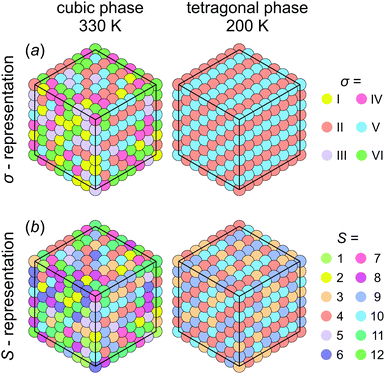
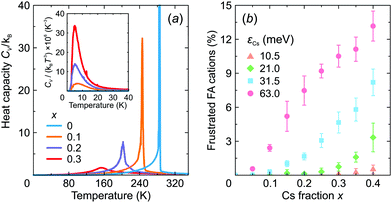
First, we investigated the phase transition behavior of our model by calculating the temperature dependence of the heat capacity CV of our model (see Fig. 4). For ε1 = 21 meV and ε2 = 0, the phase transition anomaly of CV occurs at T0 = 210 K, which is lower than the cubic-tetragonal phase transition temperature of 280 K of FAPbI3.23,25,26 In addition, as expected from the ground state analysis, for ε2 = 0, the low temperature phase corresponds to the uncoupled two-dimensional layers having a checkerboard cation order. The layers become coupled for ε2 >0, and the phase transition temperature shows a linear increase with increasing ε2 (see inset in Fig. 4). The experimental value of 280 K is reached for ε2 = 12.6 meV. For FAPbBr3, the value of this parameter is 8.4 meV due to a slightly smaller phase transition temperature of about 260 K.30,36,37 For the subsequent simulations, we fixed ε2 to 12.6 meV.Fig. 5 shows snapshots of the cation arrangement in the disordered (330 K) and ordered (200 K) phases of our model. In the σ-representation (Fig. 5a), the cations are disordered in the cubic phase, while in the tetragonal phase the expected long-range order of the coupled planes is observed. In the S-representation (Fig. 5b), the ordering is not complete, as the degeneracy related to the paired S-states creates a two-fold disorder (cations with opposite dipole moments) in close agreement with recent studies23–25,27,30 (also see Fig. 1b and d).
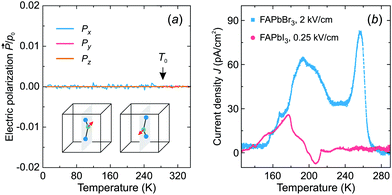
Fig. 6a shows the simulated temperature dependence of the total electric polarization of the FA cations revealing no spontaneous polarization in the tetragonal phase. In the cubic phase, the polarization averages out due to the thermal fluctuations between the cation states, while its absence in the tetragonal phase results from the degeneracy of the cation states with opposite dipole moments (see inset in Fig. 6a).
To support our simulations, we performed thermally stimulated depolarization current experiments of FAPbBr3 and FAPbI3 samples. The FAPbI3 sample was first converted from the hexagonal δ-phase to the cubic α-phase by heating of the sample (see sample preparation and experimental details). The obtained experimental results for both compounds are presented in Fig. 6b revealing broad weak anomalies of the current density compared to ferroelectric or pyroelectric materials.56,57 By integrating the current density, we obtained a negligible spontaneous electric polarization of less than about 0.15 μC cm−2. We tentatively assign the observed anomalies to the release of charged defects and ferroelastic domains.19 Our results are in agreement with the electric polarization loop measurements, which revealed no ferroelectric response in these compounds.58
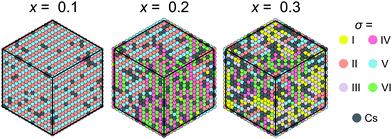
Our model can also be easily modified to simulate mixed cation hybrid perovskites. Here, we study the FA1−xCsxPbX3 system, where the effective interaction εCs between the FA and Cs+ cations is defined in Fig. 3c. We observed that introduction of Cs+ in our model causes the formation of the FA domain structures in the ordered phase for x >0.1 and εCs = 31.5 meV as revealed in Fig. 7. For x ≳ 0.3, the ordered phase has a multidomain character, although the FA cation order is still preserved in the medium range. We did not consider very high values of x, as the solubility limit of Cs in FAPbBr3 is about 40%.38 Note that a similar disruption of the long-range cation order by charged defects was also simulated in the MAPbX3 system.47
We also calculated the temperature dependence of the heat capacity of FA1−xCsxPbX3 to investigate how mixing affects the structural phase transition. The obtained CV curves are presented in Fig. 8a revealing a significant broadening of the phase transition anomaly with an increasing level of mixing in agreement with recent experimental studies of this26 and related30,53,59 systems. As shown by our simulations, the broadening occurs due to the disruption of the long-range FA cation order.
We also observed that introduction of Cs+ causes frustration of the neighboring FA cations in the low temperature phase. Here, we define frustration, when at least two σ-states of a given FA cation have the same interaction energy. The obtained fraction of the frustrated FA cations as a function of x is presented in Fig. 8b revealing a gradual increase of frustration up to 13% with increasing mixing at the highest value of εCs = 63 meV considered in this work. Note that Mozur et al. invoked FA cation frustration to explain the disappearance of the crystallographically unresolvable phase transitions in FAPbBr3 upon mixing with Cs+ cations.38
The frustration phenomenon is also tightly related to the formation of a dipolar (orientational) glass phase,60,61 signatures of which were recently observed in mixed hybrid perovskites.30,53,59 Typically, such a phase reveals itself as a peak in the CV/T3vs. T representation.60 Our simulations indeed show such an anomaly for x > 0 indicating the onset of the dipolar glass formation (see inset in Fig. 8a), which we also relate to the formation of the multidomain structure for higher values of x.
Finally, we address the shortcomings of our model, which arise from the simplifications we had to introduce to make the MC simulations feasible. Our model has twelve available cation orientations, while in the real materials this number is higher as is evident from the 48-fold disorder of the cations in the cubic phase of FAPbBr3.27 Such a coarse-graining is sufficient to reproduce the essential elements of the long-range cation order as was also demonstrated for MAPbX3 perovskites,43,46 but fine details of the cation arrangement (e.g. crystallographically unresolvable phase transitions in FAPbBr319,38) are obscured. Additional states may also affect the temperature of the phase transition, which is also related to the magnitude of the interaction energies. We also do not explicitly take into account the deformation of the lead halide framework, and thus our model cannot be used to study the related phenomena such as lattice polarizability invoked by the lone-pair electrons and associated off-centering of the lead cations.62 Lastly, in our simulations of the mixed FA/Cs system, we ignore interactions between Cs+ cations, which results in a decrease of the transition temperature upon mixing in contrast to the experimental observations.26,38 This discrepancy can be overcome by taking into account interactions between the Cs+ ions or effectively tuning the interactions between the FA cations.
5 Summary and conclusions
In this study, guided by the available structural data, we constructed and numerically solved the phase transition model describing the FA cation ordering in FAPbX3 (X = Br, I) hybrid perovskites. Our model involves twelve FA cation states (orientations), which interact via short-range strain-mediated interactions. It correctly described the cubic (α)–tetragonal (β) phase transition and cation arrangement in both structural phases of these compounds. Our simulations revealed no net macroscopic electric polarization in the tetragonal phase, which was supported by the thermally stimulated depolarization current experiments of FAPbI3 and FAPbBr3.We also extended our model by including the effective interactions between the FA and Cs+ cations, which allowed us to probe the mixed FA1−xCsxPbX3 system. We observed that a substantial fraction of cesium-neighboring FA cations may become frustrated upon mixing resulting in the multidomain structure and signatures of the dipolar glass phase.
Our model is easily modifiable and thus it can be used to study more intricate aspects of the FA cation ordering in these and related compounds including mixed perovskites. It can also serve as a basis for the construction of the tetragonal-orthorhombic phase transition model of FAPbX3 once the reliable structural data is available. The model can also be extended to probe other important phenomena such as cation frustration in non-mixed FAPbX3 compounds, which could help to further understand the relationship between the FA cations and peculiar properties of these hybrid perovskites.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been funded by the Research Council of Lithuania (LMTLT) (agreement No. S-MIP-19-4). The authors thank Dr Anna Gągor for useful discussion about the diffraction data.References
- H. J. Snaith, J. Phys. Chem. Lett., 2013, 4, 3623–3630 CrossRef CAS.
- M. Grätzel, Nat. Mater., 2014, 13, 838–842 CrossRef PubMed.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- M. Liu, M. B. Johnston and H. J. Snaith, Nature, 2013, 501, 395–398 CrossRef CAS PubMed.
- N.-G. Park, J. Phys. Chem. Lett., 2013, 4, 2423–2429 CrossRef CAS.
- Z. Li, T. R. Klein, D. H. Kim, M. Yang, J. J. Berry, M. F. A. M. van Hest and K. Zhu, Nat. Rev. Mater., 2018, 3, 18017 CrossRef CAS.
- J. Jeong, M. Kim, J. Seo, H. Lu, P. Ahlawat, A. Mishra, Y. Yang, M. A. Hope, F. T. Eickemeyer, M. Kim, Y. J. Yoon, I. W. Choi, B. P. Darwich, S. J. Choi, Y. Jo, J. H. Lee, B. Walker, S. M. Zakeeruddin, L. Emsley, U. Rothlisberger, A. Hagfeldt, D. S. Kim, M. Grätzel and J. Y. Kim, Nature, 2021, 592, 381–385 CrossRef CAS PubMed.
- J. J. Yoo, G. Seo, M. R. Chua, T. G. Park, Y. Lu, F. Rotermund, Y.-K. Kim, C. S. Moon, N. J. Jeon, J.-P. Correa-Baena, V. Bulović, S. S. Shin, M. G. Bawendi and J. Seo, Nature, 2021, 590, 587–593 CrossRef CAS PubMed.
- J. S. Manser, J. A. Christians and P. V. Kamat, Chem. Rev., 2016, 116, 12956–13008 CrossRef CAS PubMed.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. van Schilfgaarde and A. Walsh, Nano Lett., 2014, 14, 2584–2590 CrossRef CAS PubMed.
- S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Science, 2013, 341–344 CrossRef CAS PubMed.
- T. Chen, W.-L. Chen, B. J. Foley, J. Lee, J. P. C. Ruff, J. Y. P. Ko, C. M. Brown, L. W. Harriger, D. Zhang, C. Park, M. Yoon, Y.-M. Chang, J. J. Choi and S.-H. Lee, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7519–7524 CrossRef CAS PubMed.
- A. Miyata, A. Mitioglu, P. Plochocka, O. Portugall, J. T.-W. Wang, S. D. Stranks, H. J. Snaith and R. J. Nicholas, Nat. Phys., 2015, 11, 582 Search PubMed.
- J. M. Ball and A. Petrozza, Nat. Energy, 2016, 1, 16149 Search PubMed.
- J. M. Frost and A. Walsh, Acc. Chem. Res., 2016, 49, 528–535 CrossRef CAS PubMed.
- D. A. Egger, A. M. Rappe and L. Kronik, Acc. Chem. Res., 2016, 49, 573–581 CrossRef CAS PubMed.
- I. Anusca, S. Balčiūnas, P. Gemeiner, S. Svirskas, M. Sanlialp, G. Lackner, C. Fettkenhauer, J. Belovickis, V. Samulionis, M. Ivanov, B. Dkhil, J. Banys, V. V. Shvartsman and D. C. Lupascu, Adv. Energy Mater., 2017, 7, 1700600 CrossRef.
- L. M. Herz, J. Phys. Chem. Lett., 2018, 9, 6853–6863 CrossRef CAS PubMed.
- E. M. Mozur, J. C. Trowbridge, A. E. Maughan, M. J. Gorman, C. M. Brown, T. R. Prisk and J. R. Neilson, ACS Mater. Lett., 2019, 1, 260–264 CrossRef CAS.
- G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 982–988 RSC.
- M. T. Weller, O. J. Weber, P. F. Henry, A. M. Di Pumpo and T. C. Hansen, Chem. Commun., 2015, 51, 4180–4183 RSC.
- D. H. Fabini, T. Hogan, H. A. Evans, C. C. Stoumpos, M. G. Kanatzidis and R. Seshadri, J. Phys. Chem. Lett., 2016, 7, 376–381 CrossRef CAS PubMed.
- D. H. Fabini, T. A. Siaw, C. C. Stoumpos, G. Laurita, D. Olds, K. Page, J. G. Hu, M. G. Kanatzidis, S. Han and R. Seshadri, J. Am. Chem. Soc., 2017, 139, 16875–16884 CrossRef CAS PubMed.
- S. Sun, Z. Deng, Y. Wu, F. Wei, F. Halis Isikgor, F. Brivio, M. W. Gaultois, J. Ouyang, P. D. Bristowe, A. K. Cheetham and G. Kieslich, Chem. Commun., 2017, 53, 7537–7540 RSC.
- O. J. Weber, D. Ghosh, S. Gaines, P. F. Henry, A. B. Walker, M. S. Islam and M. T. Weller, Chem. Mater., 2018, 30, 3768–3778 CrossRef CAS.
- S. Kawachi, M. Atsumi, N. Saito, N. Ohashi, Y. Murakami and J.-I. Yamaura, J. Phys. Chem. Lett., 2019, 10, 6967–6972 CrossRef CAS PubMed.
- A. Franz, D. M. Többens, F. Lehmann, M. Kärgell and S. Schorr, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76, 267–274 CrossRef CAS PubMed.
- V. K. Sharma, R. Mukhopadhyay, A. Mohanty, M. Tyagi, J. P. Embs and D. D. Sarma, J. Phys. Chem. Lett., 2020, 11, 9669–9679 CrossRef CAS PubMed.
- C. Abia, C. A. Lopez, M. C. Alvarez-Galvan, L. Canadillas-Delgado, M. T. Fernandez-Diaz and J. A. Alonso, J. Mater. Chem. C, 2021, 9, 17003–17011 RSC.
- M. Šimėnas, S. Balciunas, S. Svirskas, M. Kinka, M. Ptak, V. Kalendra, A. Gagor, D. Szewczyk, A. Sieradzki, R. Grigalaitis, A. Walsh, M. Maczka and J. Banys, Chem. Mater., 2021, 33, 5926–5934 CrossRef.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS PubMed.
- T. Chen, B. J. Foley, C. Park, C. M. Brown, L. W. Harriger, J. Lee, J. Ruff, M. Yoon, J. J. Choi and S.-H. Lee, Sci. Adv., 2016, 2, e1601650 CrossRef PubMed.
- F. Cordero, F. Craciun, F. Trequattrini, A. Generosi, B. Paci, A. M. Paoletti and G. Pennesi, J. Phys. Chem. Lett., 2019, 10, 2463–2469 CrossRef CAS PubMed.
- A. Francisco-López, B. Charles, M. I. Alonso, M. Garriga, M. Campoy-Quiles, M. T. Weller and A. R. Goñi, J. Phys. Chem. C, 2020, 124, 3448–3458 CrossRef.
- D. H. Fabini, C. C. Stoumpos, G. Laurita, A. Kaltzoglou, A. G. Kontos, P. Falaras, M. G. Kanatzidis and R. Seshadri, Angew. Chem., Int. Ed., 2016, 55, 15392–15396 CrossRef CAS PubMed.
- E. C. Schueller, G. Laurita, D. H. Fabini, C. C. Stoumpos, M. G. Kanatzidis and R. Seshadri, Inorg. Chem., 2018, 57, 695–701 CrossRef CAS PubMed.
- M. Keshavarz, M. Ottesen, S. Wiedmann, M. Wharmby, R. Küchler, H. Yuan, E. Debroye, J. A. Steele, J. Martens, N. E. Hussey, M. Bremholm, M. B. J. Roeffaers and J. Hofkens, Adv. Mater., 2019, 31, 1900521 CrossRef PubMed.
- E. M. Mozur, M. A. Hope, J. C. Trowbridge, D. M. Halat, L. L. Daemen, A. E. Maughan, T. R. Prisk, C. P. Grey and J. R. Neilson, Chem. Mater., 2020, 32, 6266–6277 CrossRef CAS.
- C. Motta, F. El-Mellouhi and S. Sanvito, Phys. Rev. B, 2016, 93, 235412 CrossRef.
- W. Sukmas, U. Pinsook, P. Tsuppayakorn-aek, T. Pakornchote, A. Sukserm and T. Bovornratanaraks, J. Phys. Chem. C, 2019, 123, 16508–16515 CrossRef CAS.
- K. Druzbicki, R. Laven, J. Armstrong, L. Malavasi, F. Fernandez-Alonso and M. Karlsson, J. Phys. Chem. Lett., 2021, 12, 3503–3508 CrossRef CAS PubMed.
- M. A. Carignano, Y. Saeed, S. A. Aravindh, I. S. Roqan, J. Even and C. Katan, Phys. Chem. Chem. Phys., 2016, 18, 27109–27118 RSC.
- J. Lahnsteiner, R. Jinnouchi and M. Bokdam, Phys. Rev. B, 2019, 100, 094106 CrossRef CAS.
- A. M. A. Leguy, J. M. Frost, A. P. McMahon, V. G. Sakai, W. Kochelmann, C. Law, X. Li, F. Foglia, A. Walsh, B. C. O'Regan, J. Nelson, J. T. Cabral and P. R. F. Barnes, Nat. Commun., 2015, 6, 7124 CrossRef PubMed.
- L. Z. Tan, F. Zheng and A. M. Rappe, ACS Energy Lett., 2017, 2, 937–942 CrossRef CAS.
- M. Šimėnas, S. Balčiūnas, M. Maczka, J. Banys and E. E. Tornau, J. Phys. Chem. Lett., 2017, 8, 4906–4911 CrossRef PubMed.
- M. Šimėnas, J. Banys and E. E. Tornau, J. Mater. Chem. C, 2018, 6, 1487–1494 RSC.
- M. Šimėnas, S. Balčiūnas, M. Maczka, J. Banys and E. E. Tornau, Phys. Chem. Chem. Phys., 2016, 18, 18528–18535 RSC.
- M. Šimėnas, A. Ibenskas, A. Stroppa, A. Gągor, M. Mączka, J. Banys and E. E. Tornau, J. Phys. Chem. C, 2019, 123, 19912–19919 CrossRef.
- C. Coates, H. Gray, J. Bulled, H. Boström, A. Simonov and A. Goodwin, Philos. Trans. R. Soc., A, 2018, 377, 20180219 CrossRef PubMed.
- F. Y. Wu, Rev. Mod. Phys., 1982, 54, 235–268 CrossRef.
- J. M. Frost, K. T. Butler and A. Walsh, APL Mater., 2014, 2, 081506 CrossRef.
- M. Šimėnas, S. Balciunas, J. N. Wilson, S. Svirskas, M. Kinka, A. Garbaras, V. Kalendra, A. Gagor, D. Szewczyk, A. Sieradzki, M. Maczka, V. Samulionis, A. Walsh, R. Grigalaitis and J. Banys, Nat. Commun., 2020, 11, 5103 CrossRef PubMed.
- D. P. Landau and K. Binder, A Guide to Monte Carlo Simulations in Statistical Physics, Cambridge University Press, 3rd edn, 2009 Search PubMed.
- S. A. Fateev, A. A. Petrov, A. A. Ordinartsev, A. Y. Grishko, E. A. Goodilin and A. B. Tarasov, Chem. Mater., 2020, 32, 9805–9812 CrossRef CAS.
- M. E. Lines and A. M. Glass, Principles and Applications of Ferroelectrics and Related Materials, Oxford University Press, 2001 Search PubMed.
- G.-C. Xu, X.-M. Ma, L. Zhang, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2010, 132, 9588–9590 CrossRef CAS PubMed.
- S. Govinda, B. P. Kore, D. Swain, A. Hossain, C. De, T. N. Guru Row and D. D. Sarma, J. Phys. Chem. C, 2018, 122, 13758–13766 CrossRef CAS.
- E. M. Mozur, A. E. Maughan, Y. Cheng, A. Huq, N. Jalarvo, L. L. Daemen and J. R. Neilson, Chem. Mater., 2017, 29, 10168–10177 CrossRef CAS.
- U. Höchli, K. Knorr and A. Loidl, Adv. Phys., 1990, 39, 405–615 CrossRef.
- W. Kleemann, Phys. Status Solidi B, 2014, 251, 1993–2002 CrossRef CAS.
- D. H. Fabini, R. Seshadri and M. G. Kanatzidis, MRS Bull., 2020, 45, 467–477 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |