Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Not the sum of their parts: understanding multi-donor interactions in symmetric and asymmetric TADF emitters†
Andrew
Danos‡
 *a,
Dalius
Gudeika‡
*a,
Dalius
Gudeika‡
 b,
Nadzeya A.
Kukhta‡
b,
Nadzeya A.
Kukhta‡
 cd,
Ramunas
Lygaitis
b,
Marco
Colella
a,
Heather F.
Higginbotham
a,
Aisha N.
Bismillah
c,
Paul R.
McGonigal
cd,
Ramunas
Lygaitis
b,
Marco
Colella
a,
Heather F.
Higginbotham
a,
Aisha N.
Bismillah
c,
Paul R.
McGonigal
 c,
Juozas Vidas
Grazulevicius
c,
Juozas Vidas
Grazulevicius
 b and
Andrew P.
Monkman
b and
Andrew P.
Monkman
 a
a
aDepartment of Physics, Durham University, South Road, Durham, DH1 3LE, UK. E-mail: andrew.danos@durham.ac.uk
bDepartment of Polymer Chemistry and Technology, Kaunas University of Technology, Kaunas 51423, Lithuania
cDepartment of Chemistry, Durham University, South Road, Durham, DH1 3LE, UK
dMaterials Science and Engineering Department, University of Washington, Seattle, Washington 98195, USA
First published on 18th November 2021
Abstract
A pair of thermally activated delayed fluorescence (TADF) emitters with symmetric and asymmetric D–A–D structure are investigated. Despite displaying near-identical photoluminescence spectrum and quantum yields, the symmetric material possesses significantly better delayed fluorescence characteristics and OLED performance. Building on a previous study of analogous D–A materials we are able to explain these differences in terms of different strengths of electronic interactions between the two donor units. This interaction lowers the energy of the TADF-active triplet state in the asymmetric molecule, increasing its singlet–triplet energy gap and leading to worse performance. This result therefore demonstrates a new strategy to selectively control the triplet states of TADF molecules, in contrast to established control of singlet states using host environment. These results also show that multi-donor TADF emitters cannot be understood simply as the sum of their isolated parts; these parts have different electronic interactions depending on their relative positions, even when there is no scope for steric interaction.
Introduction
Due to tremendous research efforts in recent years, purely organic thermally activated delayed fluorescence (TADF) materials have proven their potential for optoelectronic applications.1 Not only have TADF materials found utilization in highly efficient organic light emitting diodes (OLEDs),2–4 but their emissive and triplet-management properties have also enabled cross-disciplinary applications in fluorescence sensing and imaging,5 optical temperature sensing,6 and catalysis.6 The widely acknowledged success of TADF emitters is primarily due to their near optimal quantum efficiency in electroluminescent devices; 100% values can be achieved7 in comparison to the 25% limit for conventional fluorescence emitters. Additional benefits include their largely reduced cost, lowered toxicity, and potential ability to achieve deep blue emission – each of which are intractable challenges for pre-existing rare- or heavy-metal containing organometallic phosphorescent emitters.8 These merits have brought TADF emitters to the forefront of materials science, and intense research directed towards deeper understanding of the underlying mechanism and development of novel compounds continues presently.The TADF mechanism is based on a second-order spin–vibronic coupling between a charge transfer triplet state (3CT) and a local excited triplet (3LE) to mediate the up-conversion reverse intersystem crossing (rISC) of the coupled 3LE/3CT triplet(s) to the emissive charge transfer singlet (1CT) state.9,10 In turn, achieving fast rISC directly depends on the minimization of the singlet–triplet energy gap (ΔEST) – an essential, but not sufficient condition for the observation of TADF. Much work has been carried out to discover chemical motifs that minimize the ΔEST gap, and correspondingly maximize rISC.11–16 As a result of this multidisciplinary work, generic design rules for successful TADF emitters have emerged.17 Primarily, bridging of sterically hindered electron donor (D) and acceptor (A) groups in a twisted D–A architecture commonly results in weakly overlapping highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO). Consequently, such materials frequently possess charge transfer (CT) states with low electron exchange energy.18–20 In recent years through-space (exciplex-like) D–A interactions and non-overlapping single-molecule multi-resonant electronic structures have also been shown to deliver unexpected and outstanding TADF performance.21–26
The choice of specific D and A chromophores and any structural modulation of the dihedral angle between them is often the foremost tool for tuning of the CT character, emission energy, and reduction of ΔEST towards engineering efficient rISC and TADF. However, additional undesirable effects such as red-shifting and broadening of the emission as well as severe reduction of the oscillator strength27 can also occur somewhat unpredictably. In attempts to realize narrow TADF emission of a target colour and high efficiency, several investigations into more subtle aspects of molecular design have been reported. Recently, binding the D and/or A chromophores through various linking topologies (ortho-, meta-, para-) was shown to be an effective strategy for fine-tuning the energy levels and couplings of the moieties.13,26,28–33 For instance, in our previous work we have attributed the differences in the performance of isomeric TADF emitters to various resonance and inductive effects around the acceptor unit's aromatic π-system.29 This work showed that control over the dihedral angle alone is insufficient for fast rISC and efficient TADF, and that chemically identical donors can induce different TADF properties purely based on the position in which they are installed. Despite different conjugation strengths at the meta- and para-positions (expected to lead to varying extents of molecular planarization) the dimethylacridine (DMAC) donor was also found to have the same dihedral angle at either position. This surprising result was explained in terms of the DMAC donor self-regulating its steric environment with the C–H bonds at the 1- and 8-positions. This final conclusion stands in contrast to other more compact donors such as carbazole,34,35 with dihedral angles that are more susceptible to external influences. This property also makes DMAC an ideal donor for comparing more subtle aspects of molecular design, with the influence of dihedral angle variation largely controlled.
Another popular strategy in TADF material design involves introduction of additional donors, resulting in D–A–D or D–A–D′ molecular architectures. A plethora of multicolour TADF emitters have been developed using this approach.36–44 Even a number of white emitters with D–A–D′ structure have been reported,45–47 although it remains unclear how to correlate the properties of the D–A–D′ materials from those of the individual D–A and D′–A analogues.48 An early advance in the D–A–D approach was made by Adachi et al., who introduced multiple donors with mutual steric interactions. For instance, 4CzIPN is a high-performance green TADF emitter based on the multi-donor approach which has received sustained research attention.49–51 While originally it was believed that introduction of multiple donors ensured fixed dihedral angles between the D and A, the cumulative electronic effect of the donors was more recently attributed to the sum of the donating fragments52 in a ‘bottom up’ investigation. Similar recent reports into multi-carbazole systems have also attempted to explain findings in terms of influences of individual donor units53,54 on the larger electronic system.
This multi-donor approach has also inspired a number of subsequent works.55–57 For instance, Oh et al. focused on acceptor substitution pattern in a series of isomeric multi-donor TADF emitters, comprising carbazole and 2,4-diphenyl-1,3,5-triazine as the donor and acceptor, respectively.56,58 Their thorough theoretical and experimental approach allowed them to unravel the complexity of the steric interactions between the donors. From the photophysical analysis, the authors concluded that 2-/3- and 2-/6-substitutions of the donors feature decreased energy gaps and shortened delayed fluorescence lifetimes by means of large dihedral angle of the donors. Such a dihedral effect allowed for a degree of control over the energy gap and a rISC rate, resulting in OLEDs with correlated efficiencies and roll-offs. While significant attention in this work was dedicated to the investigation of the steric effects (which dominate dihedral angles for carbazole donors34,35), many questions regarding the electronic communication in multi-donor TADF emitters remained unanswered.
Building on the previous findings of our group29,56 and aiming to better understand the connection between analogous D–A and D–A–D molecules, we investigate two isomeric D–A–D TADF emitters comprised of a benzonitrile acceptor and acridine donors attached at the 2,5- or 2,6-positions of the acceptor. Comparison to previously reported D–A materials (facilitated by the self-regulating dihedral angle of DMAC59) allows us to compare these systems with minimal additional complexity introduced by the second D unit. Using a combination of experimental and theoretical methods, we demonstrate that electronic interaction between the donating moieties – modulated by the relative position of each – alters the 3LE energy and thus also ΔEST and TADF performance. We therefore demonstrate a viable strategy of selectively controlling the LE triplet energy in TADF multi-donor emitters, without altering the CT singlet energy. This provides a counterpart to the commonly-employed host tuning strategy that minimise ΔEST by external action on the polarity-sensitive CT singlet state.3,60 Furthermore, this work establishes that multi-donor TADF emitters cannot be understood simply as the sum of the donating fragments, or as perturbations of analogous D–A materials. Instead, emergent inter-donor interactions must be taken into account, which immediately disqualify such bottom-up approaches.
Results
Synthesis and characterisation
The two isomers (o,m)ACA (2,5-bis(9,9-dimethyl-9,10-dihydroacridin-10-yl)benzonitrile) and (o,o)ACA (2,6-bis(9,9-dimethyl-9,10-dihydroacridin-10-yl)benzonitrile) were synthesized by the procedures shown in Scheme 1, with full details in the ESI.† Earlier investigations of OLEDs using (o,m)ACA as a non-doped emissive layer have been previously reported.44 The target compounds were prepared in yields of 58–61% through a Pd-catalyzed Buchwald–Hartwig cross-coupling reaction between 9,10-dihydro-9,9-dimethylacridine and 2,5-dichlorobenzonitrile or 2,6-dichlorobenzonitrile. | ||
| Scheme 1 Synthesis of (o,m)ACA and (o,o)ACA (left), and structures of previously investigated D–A materials29 (right). | ||
Additional thermal, electrochemical, and crystallographic properties of the two molecules are also included in the ESI,† demonstrating their near-identical physical properties – including equal electron affinity and ionisation potentials.
Photophysical properties
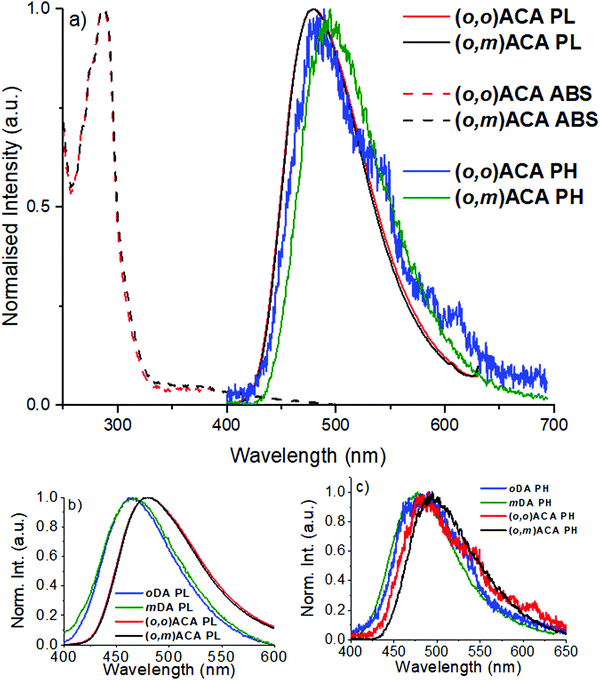
In anticipation of their applications in OLEDs and guided by optimised doping concentrations reported for similar DMAC containing TADF materials,13,61 the optical properties of (o,m)ACA and (o,o)ACA were investigated primarily in 25% v/v co-doped evaporated films using bis[2-(diphenylphosphino)phenyl]ether oxide (DPEPO) as host. Fig. 1a shows the UV-vis absorption, photoluminescence (PL), and time-resolved low temperature phosphorescence spectra (PH) of the films. Also shown are comparisons of the PL (Fig. 1b) and PH spectra (Fig. 1c) with those of oDA and mDA (10% w/w drop cast films in DPEPO), the single D and A analogues.The similarities in optical properties between (o,m)ACA and (o,o)ACA are striking, with UV-vis and PL spectra nearly identical (Fig. 1a). This trend is also preserved in a range of different solvents (Fig. S9 and S10, ESI†). oDA and mDA also have very similar singlet energies to each other in DPEPO (taken from PL onset wavelength), although with mDA marginally higher in energy than oDA and with broader PL band. This trend is consistent with what was previously reported for these D–A materials in polymer host zeonex, and arises from differences in electron–hole separation in the CT excited state62 as well as differences in acceptor strength at different locations around the central benzonitrile ring.29 Key photophysical properties are presented in Table 1, with the similarities in singlet energy and PLQY strongly indicating that both (o,m)ACA and (o,o)ACA emit through the same CT state, formed by the donor unit ortho- to the acceptor unit. Conversely, the meta- donor unit in (o,m)ACA is expected to form a higher-energy CT state (as it does in mDA compared to oDA), and thus must have limited influence on the singlet state properties in (o,m)ACA – evidenced by its identical PL spectrum to (o,o)ACA, which does not possess this structural feature.
| S1a (eV) | T1b (eV) | ΔESTc (meV) | PLQYd | PF lifetimee (ns) | DF lifetimee (μs) | k f (× 106 s−1) | k ISC (× 107 s−1) | k rISC (× 106 s−1) | |
|---|---|---|---|---|---|---|---|---|---|
| a From steady-state PL onset. b From PH onset (>50 ms delay, 80 K). c S1–T1. d Measured in integrating sphere under nitrogen, 310 nm excitation. e From exponential fitting of PF or DF decay regions. f Rates of fluorescence (kf), ISC (kISC), and rISC (krISC) from kinetic fitting of PF and DF region.63 | |||||||||
| (o,m)ACA | 2.89 | 2.81 | 80 | 70 | 62 ± 12 | 17 | 3.6 | 1.5 | 0.6 |
| (o,o)ACA | 2.88 | 2.86 | 20 | 75 | 80 ± 20 | 8.7 | 4.3 | 2.7 | 1.8 |
Both (o,m)ACA and (o,o)ACA have significantly lower singlet state energies than the D–A materials, despite both lacking the tBu donor substituents that make it more strongly electron donating.61 We note that due to this structural difference the energies of the D–A and D–A–D materials should not be compared directly – only the trends within each pair. Although the absence of the tBu groups would typically lead to weaker CT strength and blue-shifted emission, the opposite observation here hints at cooperative effects between the two donors yielding a stronger overall CT state than each D can generate alone. Similar effects are likely responsible for the different emission colours of 4CzIPN/2CzIPN, 4CzPN/2CzPN (both pairs green/blue49,52 with additional/fewer Cz units), and other multi-carbazole systems.56 However, this comparison is complicated by the potential for steric interactions between neighbouring carbazoles.34 Such steric interactions can be disregarded for the well-spaced and intrinsically perpendicular DMAC donors in the present materials though, giving clearer insight into the purely electronic effects associated with different substituent positions.
In terms of triplet energies the materials show more noticeable differences. The triplet energy of mDA (2.95 eV, from PH onset wavelength) is higher than that of oDA (2.91 eV), which was previously explained in terms of different D–A coupling strengths and conjugation at different positions relative to the A, arising from the effects of electronic resonance structures. The triplet energy of (o,m)ACA (2.81 eV) is surprisingly significantly lower than that of (o,o)ACA (2.86 eV). In both materials the common oDA sub-unit appears to control the lowest energy triplet state, but it is not readily apparent why (o,m)ACA has a significantly lower triplet energy (50 meV) than (o,o)ACA. Indeed, the only structural difference is the presence of the mDA sub-unit in (o,m)ACA, which has a higher intrinsic triplet energy. Combined with near-identical singlet energies, this lower triplet energy therefore also leads (o,m)ACA to have a significantly larger ΔEST gap. Although it is not immediately clear how this intrinsically higher triplet energy structural subunit could lead (o,m)ACA to have a lower overall triplet energy, the consequences of this difference are immediately evident in subsequent measurements.
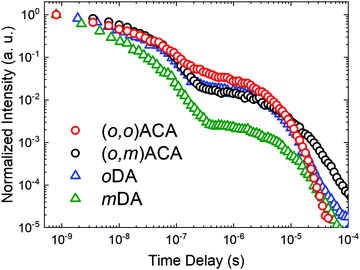
The emission decay kinetics of (o,m)ACA and (o,o)ACA are presented in Fig. 2, alongside those of mDA and oDA. Similar to what was previously observed with the D–A materials, the individual time-resolved spectra that make up the (o,o)ACA and (o,m)ACA decays (Fig. S6 and S7, ESI†) stayed roughly constant throughout the prompt fluorescence time regime (PF, 1–100 ns), later undergoing a slight spectral redshift through the delayed fluorescence (DF, 100 ns onward). This behaviour is typical of TADF materials with C–N linkages, arising from structural relaxation and/or dispersion of rISC rates associated with a distribution of molecular geometries and CT energies.
Overall the decay kinetics of (o,o)ACA and (o,m)ACA are much more alike than those of mDA and oDA. In particular the similar PF decay lifetimes (Table 1) strongly suggest that the emission emerges from the same CT state in both materials (i.e. that formed between the acceptor and an ortho-donor). In contrast the PF lifetimes are considerably different in mDA and oDA, reflecting the different CT states which give rise to these emission regimes in those two materials.
In the DF regime the delayed emission is significantly stronger and more rapid for oDA than for mDA, previously explained due to the different donor–acceptor electronic couplings at the different positions around the benzonitrile ring. While the DF emission is both weaker and slower in (o,m)ACA than in (o,o)ACA, the differences between the D–A–D materials are much less pronounced than for the D–A materials. Nonetheless, this inferior DF performance in (o,o)ACA presumably results from smaller relative rates of ISC (controlling DF intensity) and smaller rates of rISC (controlling DF decay rate) extracted by kinetic fitting of the decays.63 In (o,m)ACA and (o,o)ACA the established differences in ΔEST are able to explain these differences, as both processes rely on near-isoenergetic electronic states to make the otherwise spin-forbidden rISC process proceed at appreciable rates.
OLED performance
The electroluminescence performances of (o,o)ACA and (o,m)ACA were investigated in a previously optimised13,61,64–66 device architecture consisting of ITO|NPB (40 nm)|TSBPA (10 nm)|emitter:DPEPO x vol% (30 nm)|DPEPO (10 nm)|TPBi (40 nm)|LiF (1 nm)|Al (100 nm). The concentration of emitter in the emissive layer was optimised at 20% for (o,o)ACA, with this concentration then also used for (o,m)ACA. The key electroluminescence properties of the devices are presented in Fig. 3, and in Table 2. This device architecture relies on DPEPO for electron transport through the emissive layer, with the DMAC-containing emitter providing hole transport. Consequently, (o,o)ACA devices using hole-transporting mCP as the emissive layer host (with no material capable of providing electron transport) displayed slightly blue-shifted emission spectra but much lower efficiencies (typically <10% EQEmax, Fig. S8, ESI†). This is despite the triplet energies of the mCP (∼2.97 eV)67 and (o,o)ACA (2.86 eV) appearing compatible from photophysical measurements.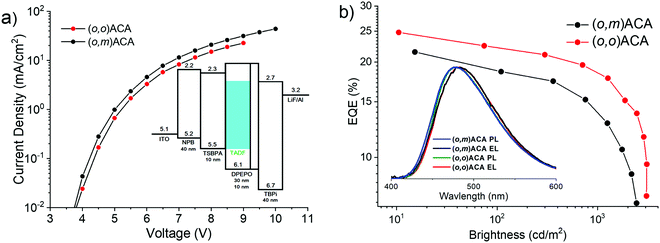 | ||
| Fig. 3 OLED performance of D–A–D materials: (a) I–V curves with device stack inset. (b) EQE curves with EL and PL spectra inset. | ||
| Turn on voltage (V) | EQEmax (%@cd m−2) | EQE100 (%@cd m−2) | EQE1000 (%@cd m−2) | EQEMax![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Brt (%@cd m−2) Brt (%@cd m−2) |
CIE (x, y) | |
|---|---|---|---|---|---|---|
| (o,m)ACA | 4.0 | 21.4@15 | 18.6@109 | 12.8@1250 | 5.6@2511 | 0.18, 0.33 |
| (o,o)ACA | 4.0 | 24.8@10 | 22.5@74 | 17.8@1266 | 9.5@3090 | 0.18, 0.33 |
The near-identical electroluminescence colour (and CIE coordinates) of the (o,o)ACA and (o,m)ACA devices are in line with their near-identical film PL spectra. The near identical I–V curves also indicate near identical charge transport properties as well. We note that the emission colour is not as deep-blue as similar materials reported by Noda et al.,68 confirming that the analogous diphenylacridine D unit is a weaker electron donor than DMAC. The maximum external quantum efficiencies (EQEmax) of the two emitters are both in line with their similar PLQYs and different rISC rates, which govern OLED performance in the low-driving regime where rISC competes favourably with other quenching mechanism.
At higher driving voltages the performance of the (o,m)ACA device suffers considerably, as the same quenching processes that rISC competes with at low driving conditions scale strongly with current and exciton density. Normalised EQE curves are presented in Fig. S8 (ESI†) to facilitate comparison of this efficiency roll-off behaviour. Accordingly, the maximum brightness that the (o,m)ACA device can achieve is also lower. All of this behaviour is consistent with its lower rate of rISC, leaving it unable to harvest triplet states fast enough to avoid multi-exciton or charge-exciton quenching and degradation processes at larger driving currents. While the (o,o)ACA device also suffers quenching at higher driving, it is able to resist these processes more effectively due to its faster rISC rate.
The device performance is therefore entirely in line with expectations built upon the preceding optical results. We note that alongside the following physical insights arising from comparison of (o,m)ACA and (o,o)ACA, these results also establish both materials as objectively high-performance cyan TADF emitters. Such emitters with good TADF but less-than-ideal emission colour are currently enjoying expanded utility as sensitisers for deep-blue hyperfluorescence OLEDs.53,65,69–73
Discussion and DFT calculations
As previously stated, all of the optoelectronic results in the previous section flow logically from the observation of similar singlet but different triplet energies for (o,m)ACA and (o,o)ACA. From a materials design perspective, the interesting question is why the triplet energies are so different, despite their similar chemical subunits and identical singlet energies. This question is especially difficult to answer as it goes against the trend established in the simpler oDA and mDA materials. This outcome means that the underlying cause must somehow be an emergent property arising from the presence of both donors and their resulting interactions – interactions absent in the D–A materials. If this were not the case, (i.e. if these materials behaved simply as the sum of their D–A analogues/fragments) we would expect the triplet energies to either be identical, or to follow the same trend as seen for the D–A materials with the mDA fragment leading to higher overall triplet energy in (o,m)ACA – in conflict with observation.To better understand this behaviour we turn to DFT calculations. Calculations were performed with the Gaussian 09 package74 using isolated molecules optimized at the rBMK/6-31G(d) level in gas phase. The spectroscopic properties of the molecules and their excited states were calculated by means of time-dependent DFT (TD-DFT)75 also employing the 6-31G(d) basis set. The BMK functional was chosen as it has shown to be adequately reliable for the description of the low energy excited states in D–A CT compounds (including oDA and mDA), both by us29,61,76–78 and by others including in benchmarking studies.79–81
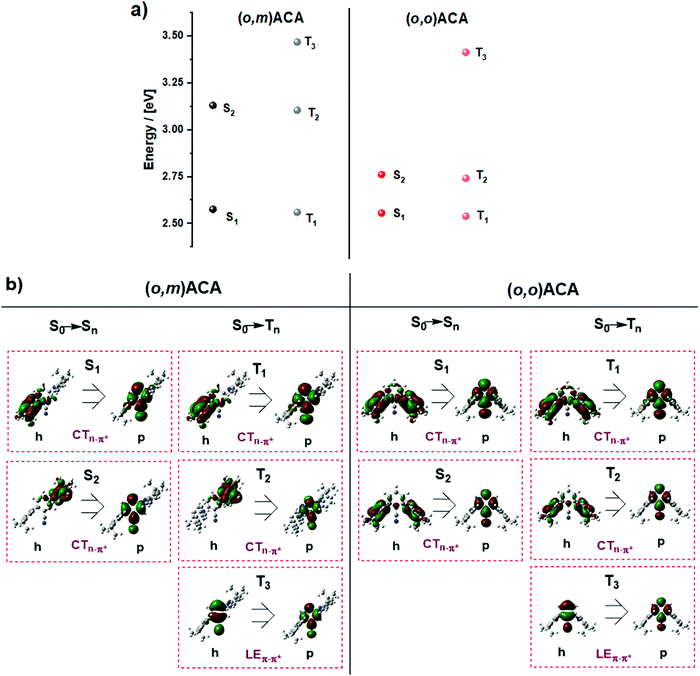
Fig. 4 shows the NTOs and energies calculated for relevant triplet and singlet states in (o,m)ACA and (o,o)ACA. By inspecting the singlet NTOs in (o,m)ACA we first note that the CT singlet associated with the ortho-donor (S1) is lower in energy than that associated with the meta-donor CT state (S2). This is in agreement with expectations and the trends established for oDA and mDA, while the similarities between the donor/acceptor-centred NTOs here and donor/acceptor-centred HOMO/LUMO distributions previously reported for oDA and mDA confirm that these are predominantly CT transitions. In (o,o)ACA the S1 and S2 states are much closer in energy, and each involves both of the ortho-donor units. We suggest that these represent symmetric (S1) and antisymmetric (S2) combinations of otherwise degenerate CT states associated with either the left or right donor individually, and that the involvement of both donor units may contribute to the slightly faster kf and higher PLQY observed for (o,o)ACA. This is analogous to the formation of symmetric (bonding) and antisymmetric (antibonding) molecular orbitals from combinations of degenerate atomic orbitals (Fig. 5a). For the first two triplet states of CT nature similar trends are observed.
The first calculated triplet state of LE nature is T3, centred on the A unit in both materials and with nearly identical NTOs. This LE triplet state is the one relevant to vibronic coupling and rISC, and corresponds to the same triplet state identified by phosphorescence measurements in the previous sections (labelled in that section as T1, with CT triplet states frequently non-emissive). To discount the alternative assignment (i.e., PH from CT states), we note that although the PH spectra are not structured, this alone is not enough to assign CT character to the PH state. Ultimately in the discussions below we present a mechanism that can cause the LE triplet sates to be significantly different in energy while leaving CT singlet states unaffected – as is observed experimentally. In contrast, we are not aware of any mechanism that could explain different CT triplet states in (o,m)ACA and (o,o)ACA while leaving CT singlet states unaffected.
Interestingly, the calculated T3 energies of (o,m)ACA and (o,o)ACA are in the opposite order as found experimentally, with about the same difference in triplet energies in both cases (∼50 meV). In the following discussion we propose a mechanism that explains the observed triplet energy ordering and why this is not reflected in calculations. We note that the reason for the experimental (o,m)ACA triplet energy being lower than (o,o)ACA cannot be due to the combination of individual couplings of the A to the two D units. If this were the case we would expect the two materials to either have identical lowest triplet energies (from coupling between the A and the ortho-D in each material), or for (o,m)ACA to have a higher triplet energy than (o,o)ACA (due to coupling between A and meta-D, which is intrinsically higher in energy as in mDA). Any such state-mixing between LE and CT states is also unlikely to be a contributing factor, due to the forbidden nature of mixing these states with different orbital symmetries.82,83
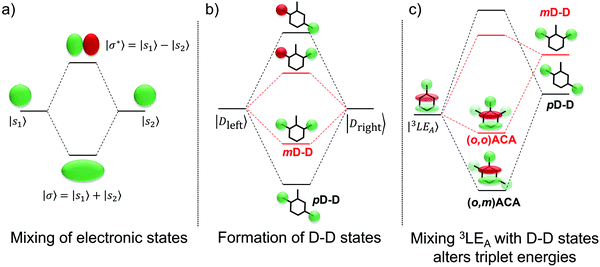
Instead we propose that the LE T3 states in both (o,m)ACA and (o,o)ACA interact with higher-lying LE states delocalised across both donor units (D–D states). A representative state diagram is presented in Fig. 5b, showing how these unoccupied electronic states would form. A similar explanation was recently employed to explain the performances of a series of differently connected multicarbazole TADF materials, although that study invoked the active participation of delocalised multi-D or multi-A states in the formation of CT states. The conclusions of that work are also complicated by the potential for additional steric interactions between the carbazole donors.53 These factors are avoided here by the use of well-spaced donors, and the ability of DMAC to manage its own steric environment.29
The proposed D–D states are (to first approximation) formed by linear combinations of the individual donor LE states (Fig. 5b), and so one of these D–D states (the symmetric combination) is expected to be the lowest-energy LE singlet state in each molecular system. This expectation is supported by the absorption spectra of the two materials, discussed in more detail below and presented in Fig. S9 (ESI†), which show the first major absorption band at a wavelength consistent with DMAC.84 These D–D states (in either singlet or triplet multiplicity) are therefore also some of the closest LE states in energy to the (o,m)ACA and (o,o)ACA LE T3 state, and so are likely candidates for explaining why their energies differ. These D–D states are also unoccupied, which explains why the DFT calculations are unable to accurately predict the order of (o,m)ACA and (o,o)ACA T3 energies compared to experiment. Accurately accounting for such interactions with unoccupied states would instead require more advanced multireference or complete active space ab initio methods, which are impractical for molecules of this size.
Applying molecular orbital theory in the symmetric and asymmetric D–A–D systems, we can infer several properties of the D–D states and how they would differ. Due to different conjugation strengths across the linker unit for (o,m)ACA (pD–D state) than for (o,o)ACA (mD–D state), we would expect the pD–D state to be lower in energy and have larger electron density on the central bridge region (Fig. 5b). This would subsequently lead to a larger orbital overlap between the pD–D state and the 3LE state associated with the A unit (3LEA) in (o,m)ACA as compared to mD–D in (o,o)ACA. The resulting state mixing between D–D and 3LEA states lowers the observed phosphorescence energies in both materials compared to calculations, which cannot account for interactions with unoccupied orbitals. Due to increased orbital overlap the state mixing with the 3LEA is more extensive for pD–D than for mD–D, leading to a yet lower triplet energy in (o,m)ACA and the observed ordering of experimental phosphorescence energies (Fig. 5c). While other higher-energy LE states would also be influenced by interactions with the D–D states, none of these higher LE states are measured or expected to influence the TADF properties. Due to differences in the shapes of their excited state wavefunctions leading to zero overlap integral, the CT states are not expected to interact with the D–D states, and so are totally unaffected both in calculations and experiment (identical PL spectra and S1 energies).
Supporting these expected properties of the D–D states, similar trends in excited state energy in other para- or meta-linked bichromophores are commonly reported,67,85,86 for example the higher triplet energy of mCBP (2.8 eV) compared to para-linked CBP (2.6 eV). Donor interactions of a similar nature over para-linkages may also be responsible for lower energy emission in recently reported multi-resonance materials using para-bichromophore designs,26 or when decorated with additional carbazoles.33 This explanation is also entirely consistent with the effects of donor position on excited-state energies previously reported for oDA and mDA29 and by others in analogous systems.32
The lower triplet energy in (o,m)ACA is therefore identified as an emergent property of the pair of donors. This lowering of triplet energy is irrelevant to the analogous oDA or mDA materials, and is impossible to predict by considering these fragments in isolation. These results therefore demonstrate that a ‘bottom-up’ approach to understanding TADF materials – recently espoused for 4CzIPN52 – is simply untenable as it cannot account for these kinds of emergent higher-order effects. We also suggest that much of the complex photophysics of 4CzIPN is more likely attributable to the presence of persistent dimer species.34,50,51
Although based on well-established principles of molecular orbital theory, much of the previous explanation is speculative. Nonetheless some evidence for the existence of the proposed D–D states can be found in the experimental absorption spectra (Fig. S9, ESI†). In DPEPO films and a range of solvents we consistently observe a redshift in the main absorbance band (peak at ∼275 nm, attributed to DMAC) in (o,m)ACA compared to (o,o)ACA. We suggest that this redshift is due to the presence of a weak underlying band associated with excitation of the pD–D singlet state. In (o,o)ACA the mD–D state is expected to exist at higher energies, and therefore remains subsumed by the main donor DMAC absorption band. These D–D states then go on to influence the relevant LE triplet energy in each material. Furthermore, the absorbance spectra also show the same weak direct CT absorption bands in both (o,o)ACA and (o,m)ACA at ∼375 nm. In each material this band corresponds to two closely spaced (unresolved) CT state absorptions, consistent with the DFT calculations and prior understanding of the oDA or mDA materials. In both cases this indicates that formation of the CT state involves only a single donor, and is unimpacted by the presence of the other (consistent with both materials sharing the same PL spectrum).
Because (o,m)ACA and (o,o)ACA introduce minimum additional complexity compared to oDA or mDA, there are few other explanations aside from D–D interactions that can potentially explain the trends seen here. While an intuitively satisfying example of basic physical chemistry principles in action, these results also demonstrate a new method of control in TADF materials. In contrast to external host-tuning of CT singlet states to minimise ΔEST,3 multi-donor interactions may in future be used as a tool to selectively tune triplet states. These results also firmly demonstrate that ‘bottom-up’ approaches to understanding TADF materials are overly simplistic, and that understanding the properties of D–A–D materials purely in terms of their D–A subunits may not be a generally achievable goal.
Conclusion
Two D–A–D TADF materials were compared with analogous D–A compounds. Despite displaying near-identical singlet energies and PLQYs, the triplet energies – and subsequent TADF performances – were markedly different and showed opposite trends to the D–A materials. We suggest that molecular orbital interactions with higher energy multi-donor LE states are responsible for these unexpected changes in triplet energy, with interaction strength modulated by the linkage patterns of the two donor subunits. The identification of these emergent multi-donor effects – not complicated here by any additional impacts of steric environment changes – demonstrates that bottom-up approaches to understanding TADF behaviour are unlikely to succeed. This includes the previously coveted ability of extrapolating D–A–D properties from those of smaller D–A fragments. These multi-donor effects nonetheless demonstrate a new approach for selectively tuning molecular triplet states, which may work in tandem with more well-established host-tuning of excited singlet states.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Dmitry S. Yufit of the Durham crystallography service for XRD measurements and technical support.The Authors also thank the European Union's Horizon 2020 Research and Innovation Programme for funding under Grant agreements No. 641725 (PHEBE), 674990 (EXCILIGHT), 732013 (HYPEROLED), and 812872 (TADFlife). ANB acknowledges an EPSRC Doctoral Training Grant.
References
- K. Wang, C.-J. Zheng, W. Liu, K. Liang, Y.-Z. Shi, S.-L. Tao, C.-S. Lee, X.-M. Ou and X.-H. Zhang, Adv. Mater., 2017, 29, 1701476 CrossRef PubMed.
- J. Chen, T. Yu, E. Ubba, Z. Xie, Z. Yang, Y. Zhang, S. Liu, J. Xu, M. P. Aldred and Z. Chi, Adv. Opt. Mater., 2019, 7, 1801593 CrossRef.
- P. L. Dos Santos, J. S. Ward, M. R. Bryce and A. P. Monkman, J. Phys. Chem. Lett., 2016, 7, 3341–3346 CrossRef CAS PubMed.
- T.-T. Bui, F. Goubard, M. Ibrahim-Ouali, D. Gigmes and F. Dumur, Beilstein J. Org. Chem., 2018, 14, 282–308 CrossRef CAS PubMed.
- F. Ni, N. Li, L. Zhan and C. Yang, Adv. Opt. Mater., 2020, 8, 1902187 CrossRef CAS.
- A. Steinegger, I. Klimant and S. M. Borisov, Adv. Opt. Mater., 2017, 5, 1700372 CrossRef.
- F. B. Dias, K. N. Bourdakos, V. Jankus, K. C. Moss, K. T. Kamtekar, V. Bhalla, J. Santos, M. R. Bryce and A. P. Monkman, Adv. Mater., 2013, 25, 3707–3714 CrossRef CAS PubMed.
- Z. Yang, Z. Mao, C. Xu, X. Chen, J. Zhao, Z. Yang, Y. Zhang, W. Wu, S. Jiao, Y. Liu, M. P. Aldred and Z. Chi, Chem. Sci., 2019, 10, 8129–8134 RSC.
- J. Gibson, A. P. Monkman and T. J. Penfold, ChemPhysChem, 2016, 17, 2956–2961 CrossRef CAS.
- F. B. Dias, T. J. Penfold and A. P. Monkman, Methods Appl. Fluoresc., 2017, 5, 012001 CrossRef.
- T. Cardeynaels, S. Paredis, A. Danos, D. Vanderzande, A. P. Monkman, B. Champagne and W. Maes, Dyes Pigm., 2021, 186, 109022 CrossRef CAS.
- T. Cardeynaels, S. Paredis, A. Danos, A. Harrison, J. Deckers, S. Brebels, L. Lutsen, D. Vanderzande, A. P. Monkman and B. Champagne, et al. , Dyes Pigm., 2021, 190, 109301 CrossRef CAS.
- P. Stachelek, J. S. Ward, P. L. Dos Santos, A. Danos, M. Colella, N. Haase, S. J. Raynes, A. S. Batsanov, M. R. Bryce and A. P. Monkman, ACS Appl. Mater. Interfaces, 2019, 11, 27125–27133 CrossRef CAS.
- I. E. Serdiuk, C. H. Ryoo, K. Kozakiewicz, M. Mońka, B. Liberek and S. Y. Park, J. Mater. Chem. C, 2020, 8, 6052–6062 RSC.
- A. Shang, T. Lu, H. Liu, C. Du, F. Liu, D. Jiang, J. Min, H. Zhang and P. Lu, J. Mater. Chem. C, 2021, 9, 7392–7399 RSC.
- H. L. Lee, K. H. Lee, J. Y. Lee and H. J. Lee, J. Mater. Chem. C, 2021, 9, 7328–7335 RSC.
- Y. Im, M. Kim, Y. J. Cho, J.-A. Seo, K. S. Yook and J. Y. Lee, Chem. Mater., 2017, 29, 1946–1963 CrossRef CAS.
- Y. Pan, W. Li, S. Zhang, L. Yao, C. Gu, H. Xu, B. Yang and Y. Ma, Adv. Opt. Mater., 2014, 2, 510–515 CrossRef CAS.
- Y. H. Lee, S. Park, J. Oh, S.-J. Woo, A. Kumar, J.-J. Kim, J. Jung, S. Yoo and M. H. Lee, Adv. Opt. Mater., 2018, 1800385 CrossRef.
- D. De Sa Pereira, D. R. Lee, N. A. Kukhta, K. H. Lee, C. L. Kim, A. S. Batsanov, J. Y. Lee and A. P. Monkman, J. Mater. Chem. C, 2019, 7, 10481–10490 RSC.
- M. Colella, A. Danos and A. P. Monkman, J. Phys. Chem. Lett., 2019, 10, 793–798 CrossRef CAS PubMed.
- S. Kumar, L. G. Franca, K. Stavrou, E. Crovini, D. B. Cordes, A. M. Z. Slawin, A. P. Monkman and E. Zysman-Colman, J. Phys. Chem. Lett., 2021, 12, 2820–2830 CrossRef CAS PubMed.
- Y. Wada, H. Nakagawa, S. Matsumoto, Y. Wakisaka and H. Kaji, Nat. Photonics, 2020, 14, 643–649 CrossRef CAS.
- Y. Kondo, K. Yoshiura, S. Kitera, H. Nishi, S. Oda, H. Gotoh, Y. Sasada, M. Yanai and T. Hatakeyama, Nat. Photonics, 2019, 13, 678–682 CrossRef CAS.
- X. Tang, L. S. Cui, H. C. Li, A. J. Gillett, F. Auras, Y. K. Qu, C. Zhong, S. T. E. Jones, Z. Q. Jiang, R. H. Friend and L. S. Liao, Nat. Mater., 2020, 19, 1332–1338 CrossRef CAS PubMed.
- J. Wei, C. Zhang, D. Zhang, Y. Zhang, Z. Liu, Z. Li, G. Yu and L. Duan, Angew. Chem., Int. Ed., 2021, 60, 12269–12273 CrossRef CAS.
- Y. Wada, K. Shizu and H. Kaji, J. Phys. Chem. A, 2021, 125, 4534–4539 CrossRef CAS PubMed.
- R. Huang, J. Avó, T. Northey, E. Chaning-Pearce, P. L. dos Santos, J. S. Ward, P. Data, M. K. Etherington, M. A. Fox and T. J. Penfold, et al. , J. Mater. Chem. C, 2017, 5, 6269–6280 RSC.
- N. A. Kukhta, H. F. Higginbotham, T. Matulaitis, A. Danos, A. N. Bismillah, N. Haase, M. K. Etherington, D. S. Yufit, P. R. McGonigal and J. V. Gražulevičius, et al. , J. Mater. Chem. C, 2019, 7, 9184–9194 RSC.
- T. Matulaitis, P. Imbrasas, N. A. Kukhta, P. Baronas, T. Bučiunas, D. Banevičius, K. Kazlauskas, J. V. Gražulevičius and S. Juršėnas, J. Phys. Chem. C, 2017, 121, 23618–23625 CrossRef CAS.
- F. M. Xie, J. X. Zhou, Y. Q. Li and J. X. Tang, J. Mater. Chem. C, 2020, 8, 9476–9494 RSC.
- T. Sudyoadsuk, S. Petdee, C. Kaiyasuan, C. Chaiwai, P. Wongkaew, S. Namuangruk, P. Chasing and V. Promarak, J. Mater. Chem. C, 2021, 9, 6251–6256 RSC.
- Y. Xu, C. Li, Z. Li, Q. Wang, X. Cai, J. Wei and Y. Wang, Angew. Chem., Int. Ed., 2020, 59, 17442–17446 CrossRef CAS.
- L. Salah, M. K. Etherington, A. Shuaib, A. Danos, A. A. Nazeer, B. Ghazal, A. Prlj, A. T. Turley, A. Mallick and P. R. McGonigal, et al. , J. Mater. Chem. C, 2021, 9, 189–198 RSC.
- L. S. Cui, H. Nomura, Y. Geng, J. U. Kim, H. Nakanotani and C. Adachi, Angew. Chem., Int. Ed., 2017, 56, 1571–1575 CrossRef CAS.
- J. Lee, K. Shizu, H. Tanaka, H. Nomura, T. Yasuda and C. Adachi, J. Mater. Chem. C, 2013, 1, 4599–4604 RSC.
- B. Huang, Q. Qi, W. Jiang, J. Tang, Y. Liu, W. Fan, Z. Yin, F. Shi, X. Ban, H. Xu and Y. Sun, Dyes Pigm., 2014, 111, 135–144 CrossRef CAS.
- B. Li, Z. Li, F. Guo, J. Song, X. Jiang, Y. Wang, S. Gao, J. Wang, X. Pang, L. Zhao and Y. Zhang, ACS Appl. Mater. Interfaces, 2020, 12, 14233–14243 CrossRef CAS.
- K. Kawasumi, T. Wu, T. Zhu, H. S. Chae, T. Van Voorhis, M. A. Baldo and T. M. Swager, J. Am. Chem. Soc., 2015, 137, 11908–11911 CrossRef CAS.
- K. Shizu, H. Tanaka, M. Uejima, T. Sato, K. Tanaka, H. Kaji and C. Adachi, J. Phys. Chem. C, 2015, 119, 1291–1297 CrossRef CAS.
- S. Xu, T. Liu, Y. Mu, Y.-F. Wang, Z. Chi, C.-C. Lo, S. Liu, Y. Zhang, A. Lien and J. Xu, Angew. Chem., Int. Ed., 2015, 54, 874–878 CrossRef CAS.
- Y. Chen, J. Guo, X. Wu, D. Jia and F. Tong, Dyes Pigm., 2018, 148, 180–188 CrossRef CAS.
- Z. Xie, C. Chen, S. Xu, J. Li, Y. Zhang, S. Liu, J. Xu and Z. Chi, Angew. Chem., Int. Ed., 2015, 54, 7181–7184 CrossRef CAS.
- D. Gudeika, O. Bezvikonnyi, D. Volyniuk and J. V. Grazulevicius, Dyes Pigm., 2020, 172, 107789 CrossRef CAS.
- H. L. Lee, H. J. Jang and J. Y. Lee, J. Mater. Chem. C, 2020, 8, 10302–10308 RSC.
- M. Aydemir, S. Xu, C. Chen, M. R. Bryce, Z. Chi and A. P. Monkman, J. Phys. Chem. C, 2017, 121, 17764–17772 CrossRef CAS.
- N. A. Kukhta and M. R. Bryce, Mater. Horiz., 2021, 8, 33–55 RSC.
- G. Haykir, M. Aydemir, A. Danos, S. Gumus, G. Hizal, A. P. Monkman and F. Turksoy, Dyes Pigm., 2021, 194, 109579 CrossRef CAS.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef CAS PubMed.
- E. Cho, M. Hong, V. Coropceanu and J. L. Brédas, Adv. Opt. Mater., 2021, 2002135 CrossRef CAS.
- M. K. Etherington, N. A. Kukhta, H. F. Higginbotham, A. Danos, A. N. Bismillah, D. R. Graves, P. R. McGonigal, N. Haase, A. Morherr and A. S. Batsanov, et al. , J. Phys. Chem. C, 2019, 123, 11109–11117 CrossRef CAS PubMed.
- H. Noda, X. K. Chen, H. Nakanotani, T. Hosokai, M. Miyajima, N. Notsuka, Y. Kashima, J. L. Brédas and C. Adachi, Nat. Mater., 2019, 18, 1084–1090 CrossRef CAS.
- D. Zhang, X. Song, A. J. Gillett, B. H. Drummond, S. T. E. Jones, G. Li, H. He, M. Cai, D. Credgington and L. Duan, Adv. Mater., 2020, 32, 1908355 CrossRef CAS.
- H. Noda, H. Nakanotani and C. Adachi, Sci. Adv., 2018, 4, eaao6910 CrossRef PubMed.
- U. Balijapalli, M. Tanaka, M. Auffray, C. Y. Chan, Y. T. Lee, Y. Tsuchiya, H. Nakanotani and C. Adachi, ACS Appl. Mater. Interfaces, 2020, 12, 9498–9506 CrossRef CAS.
- C. S. Oh, D. D. S. Pereira, S. H. Han, H. J. Park, H. F. Higginbotham, A. P. Monkman and J. Y. Lee, ACS Appl. Mater. Interfaces, 2018, 10, 35420–35429 CrossRef CAS.
- N. R. Paisley, C. M. Tonge and Z. M. Hudson, Front. Chem., 2020, 8, 229 CrossRef CAS PubMed.
- C. S. Oh, H. L. Lee, S. H. Han and J. Y. Lee, Chem. – Eur. J., 2019, 25, 642–648 CrossRef CAS.
- R. Ansari, W. Shao, S.-J. Yoon, J. Kim and J. Kieffer, ACS Appl. Mater. Interfaces, 2021, 13, 28529–28537 CrossRef CAS PubMed.
- K. Stavrou, L. G. Franca and A. P. Monkman, ACS Appl. Electron. Mater., 2020, 2, 2868–2881 CrossRef CAS.
- R. Huang, N. A. Kukhta, J. S. Ward, A. Danos, A. S. Batsanov, M. R. Bryce and F. B. Dias, J. Mater. Chem. C, 2019, 7, 13224–13234 RSC.
- M. Colella, A. Danos and A. P. Monkman, J. Phys. Chem. Lett., 2019, 10, 793–798 CrossRef CAS.
- N. Haase, A. Danos, C. Pflumm, A. Morherr, P. Stachelek, A. Mekic, W. Brütting and A. P. Monkman, J. Phys. Chem. C, 2018, 122, 29173–29179 CrossRef CAS.
- J. S. Ward, A. Danos, P. Stachelek, M. A. Fox, A. S. Batsanov, A. P. Monkman and M. R. Bryce, Mater. Chem. Front., 2020, 4, 3602–3615 RSC.
- K. Stavrou, A. Danos, T. Hama, T. Hatakeyama and A. Monkman, ACS Appl. Mater. Interfaces, 2021, 13, 8643–8655 CrossRef CAS PubMed.
- E. Aksoy, A. Danos, C. Varlikli and A. P. Monkman, Dyes Pigm., 2020, 183, 108707 CrossRef CAS.
- M. Colella, A. Danos and A. P. Monkman, J. Phys. Chem. C, 2019, 123, 17318–17324 CrossRef CAS.
- H. Noda, R. Kabe and C. Adachi, Chem. Lett., 2016, 45, 1463–1466 CrossRef CAS.
- C. Y. Chan, M. Tanaka, Y. T. Lee, Y. W. Wong, H. Nakanotani, T. Hatakeyama and C. Adachi, Nat. Photonics, 2021, 15, 203–207 CrossRef CAS.
- S. O. Jeon, K. H. Lee, J. S. Kim, S. G. Ihn, Y. S. Chung, J. W. Kim, H. Lee, S. Kim, H. Choi and J. Y. Lee, Nat. Photonics, 2021, 15, 208–215 CrossRef CAS.
- S. H. Han, J. H. Jeong, J. W. Yoo and J. Y. Lee, J. Mater. Chem. C, 2019, 7, 3082–3089 RSC.
- N. Haase, A. Danos, C. Pflumm, P. Stachelek, W. Brütting and A. P. Monkman, Mater. Horiz., 2021, 8, 1805 RSC.
- T. B. Nguyen, H. Nakanotani, T. Hatakeyama and C. Adachi, Adv. Mater., 2020, 32, 1906614 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- K. S. Thanthiriwatte and S. R. Gwaltney, J. Phys. Chem. A, 2006, 110, 2434–2439 CrossRef CAS.
- N. A. Kukhta, D. A. da Silva Filho, D. Volyniuk, J. V. Grazulevicius and G. Sini, Chem. Mater., 2017, 29, 1695–1707 CrossRef CAS.
- N. A. Kukhta, A. S. Batsanov, M. R. Bryce and A. P. Monkman, J. Phys. Chem. C, 2018, 122, 28564–28575 CrossRef CAS.
- N. A. Kukhta, R. Huang, A. S. Batsanov, M. R. Bryce and F. B. Dias, J. Phys. Chem. C, 2019, 123, 26536–26546 CrossRef CAS.
- J. Fan, Y. Zhang, Y. Zhou, L. Lin and C.-K. Wang, J. Phys. Chem. C, 2018, 122, 2358–2366 CrossRef CAS.
- S. Feng, K. Wen, Y. Si, X. Guo and J. Zhang, J. Comput. Chem., 2018, 39, 2601–2606 CrossRef CAS PubMed.
- A. D. Boese and J. M. L. Martin, J. Chem. Phys., 2004, 121, 3405–3416 CrossRef CAS.
- D. De Sa Pereira, C. Menelaou, A. Danos, C. Marian and A. P. Monkman, J. Phys. Chem. Lett., 2019, 10, 3205–3211 CrossRef CAS.
- M. K. Etherington, J. Gibson, H. F. Higginbotham, T. J. Penfold and A. P. Monkman, Nat. Commun., 2016, 7, 1–7 Search PubMed.
- M. Hempe, N. A. Kukhta, A. Danos, M. A. Fox, A. S. Batsanov, A. P. Monkman and M. R. Bryce, Chem. Mater., 2021, 33, 3066–3080 CrossRef CAS PubMed.
- S. A. Bagnich, S. Athanasopoulos, A. Rudnick, P. Schroegel, I. Bauer, N. C. Greenham, P. Strohriegl and A. Köhler, J. Phys. Chem. C, 2015, 119, 2380–2387 CrossRef CAS.
- I. A. Wright, A. Danos, S. Montanaro, A. S. Batsanov, A. P. Monkman and M. R. Bryce, Chem. – Eur. J., 2021, 27, 6545–6556 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2088958–2088960. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1tc04171a |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |