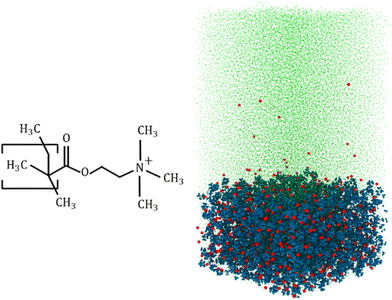
Machine learning enabled quantification of the hydrogen bonds inside the polyelectrolyte brush layer probed using all-atom molecular dynamics simulations†
Turash Haque
Pial
and
Siddhartha
Das
 *
*
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA. E-mail: sidd@umd.edu
First published on 18th November 2022
Abstract
The configuration of densely grafted charged polyelectrolyte (PE) brushes is strongly dictated by the properties and behavior of the counterions that screen the PE brush charges and the solvent molecules (typically water) that solvate the brush molecules and these screening counterions. Only recently, efforts have been made to study the PE brushes atomistically, thereby shedding light on the properties of brush-supported ions and water molecules. However, even for such efforts, there are limitations associated with using a generic definition to estimate certain properties of water and ions inside the brush layer. For example, water–water hydrogen bonds (HBs) will behave differently for locations outside and inside the brush layer, given the fact that the densely closely grafted PE brush molecules create a soft nanoconfinement where the water connectivity becomes highly disrupted: therefore, using the same definition to quantify the HBs inside and outside the brush layer will be unwise. In this paper, we address this limitation by employing an unsupervised machine learning (ML) approach to predict the water–water hydrogen bonding inside a cationic PE brush layer modeled using all-atom molecular dynamics (MD) simulations. The ML method, which relies on a clustering approach and uses the equilibrium coordinates of the water molecules (obtained from the all-atom MD simulations) as the input, is capable of identifying the structural modification of water–water HBs (revealed through appropriate clustering of the data) inside the PE brush layer induced soft nanoconfinement. Such capabilities would not have been possible by using a generic definition of the HBs. Our calculations lead to four key findings: (1) the clusters formed inside and outside the brush layer are structurally similar; (2) the margin of the cluster is shorter inside the PE brush layer confirming the possible disruption of the HBs inside the PE brush layer; (3) the average “hydrogen–acceptor-oxygen–donor-oxygen” angle that defines the HB is reduced for the HBs formed inside the brush layer; (4) the use of the generic definition (definition usable for characterizing the HBs in brush-free bulk) leads to an overprediction of the number of HBs formed inside the PE brush layer.
Introduction
Polyelectrolyte (PE) brushes, which refer to charged PE chains densely grafted to a surface, have received wide attention1–8 owing to their extensive applications in a variety of disciplines including fabrication of ionic diodes,9 ion and biosensors,10,11 and current rectifiers,12 energy conversion,13–15 targeted drug delivery,16 water harvesting,17 oil treatment,18 and many more. For all these applications, the responsiveness of the PE molecules to the environmental stimuli (e.g., pH and ion concentration of the aqueous medium) becomes critical. While there has been significant experimental,19–23 theoretical,24–30 and simulation31–34 studies focused on probing such responsiveness and behavior of the PE molecules as functions of the water and ion properties, a pinpointed atomistic understanding of the behavior of the brush supported water molecules and ions has remained very limited. Only recently, there have been efforts to study the PE brushes and the brush supported ions and water molecules using all-atom molecular dynamics (MD) simulations:35–40 the utility of such an approach is that they provide unprecedented fundamental understanding about the atomistic structure, properties, and behaviors of brush-supported ions and water molecules, which in turn can be leveraged for a variety of potential applications (such as coion-driven electroosmotic transport41 and simultaneous energy harvesting and flow augmentation42 in PE brush functionalized nanochannels).Among the parameters of interests that get revealed by the all-atom MD simulations, one of the most important one is the water–water hydrogen bonds (HBs) formed by the water molecules within the PE brush layer.37 In the brush-free bulk (i.e., outside the brush layer), water shows connectivity with nearby water molecules forming HBs; on the other hand, closely grafted PE brush molecules create a soft nanoconfinement where the water connectivity becomes highly disrupted thereby affecting the HBs inside the PE brush layer. In a previous study,37 we showed that there occurred a significant decrease in the water–water and water–PE hydrogen bond strengths with an increase in the degree of PE brush-induced confinement (quantified by the grafting density of the brushes). In that study,37 we employed a generic definition of the HB when analyzing water–water HBs inside the brush layer. A similar definition was also used for quantifying the PE–water HBs. In this generic definition, a cutoff value for the oxygen–oxygen distance as well as the angle formed by oxygens and hydrogens is used to describe a HB. These values are examined thoroughly and highly calibrated, although mainly for bulk water. Inside a highly charged confined system (inside a densely grafted polyelectrolyte or PE brush layer, for example), on the other hand, it is possible that water network is disrupted by the charged atoms, as we showed in our previous study.37 Other studies have shown that HBs might demonstrate different structural behaviors when formed under different settings (e.g., in presence or in absence of confinements, with variation in species participating in such HB formation, etc.), and in the process, cover a large range of structural properties and energy values.43–45 As water structure and water density might change inside the brush layer, a definition of the HB, which is used for the water molecules present in the bulk water (i.e., outside the highly charged confined system), might not be representative of the actual local environment. Therefore, it is not always prudent to use a generic definition (known for water) for quantifying the HBs without considering the scenario where such bonds have formed. On the other hand, a method to analyze and quantify HB that is specific to a particular system (e.g., HBs formed inside the PE brush layer) will not only ensure a more robust quantification (including the number density, angle associated with the HB, etc.) of the HBs formed inside the soft nanoconfinement, but will also unearth several finer features of the HBs that would have been missed if one would have used the existing generic definition of characterizing the HBs. A machine learning (ML) algorithm can help in this case. A cluster-based algorithm, for example, can analyze the atomic coordinates (of the atoms of the water molecules present inside the densely grafted layer of the charged PE brushes) and provide us useful information about the distribution of bonds associated with these coordinates. From these clusters, we can identify hydrogen bonds and as a result we can also check how the structural definition of hydrogen bond is changing inside a highly charged confined environment (namely the densely grafted layer of the charged PE brushes).
In this paper, we first obtain an all-atom MD simulation-based description of the structure of a cationic PE brush and the brush-supported ions and water molecules. Using this all-atom MD simulation enabled information of the equilibrated atomic coordinates of the water molecules inside the cationic brush, we employ an unsupervised machine-learning (ML) based approach for obtaining an agnostic definition of HB structure46 inside the PE brush layer. The approach relies on identifying the structural modification of water–water HBs inside the PE brush layer and in the process quantifies the disruption of the number density of the HBs inside the brush-enforced soft nanoconfinement. Our machine learning model is based on the model of Gasparotto and Ceriotti,46 which identifies atomic patterns automatically from molecular trajectories, thereby providing an algorithmic definition of a bond (here a HB) based solely on structural information. There have been several studies in the broad domain of application of ML in soft matter systems, where unsupervised learning has been employed to discover previously unknown recurring structural patterns or motifs in different macromolecular systems.47–49 The specific method of Gasparotto and Ceriotti provides clusters of possible short ranges of recurring patterns: HBs can be distinguished from other clusters by analyzing the corresponding inter-atomic distances. As this method relies solely on the available atomic coordinates, possible modification of the HB structure inside the PE brush layer can be analyzed using this method. Using these clusters, we can provide the structural definition of a HB inside the brush layer. Our calculations, enable us to obtain the following key results. First, we find a qualitative similarity in the cluster formation inside the brush layer and in the bulk (outside the brush layer). Second, the analysis of the HB cluster (or the cluster that can be considered to represent HBs) shows that the margin (in terms of the parameters used to define the cluster) of the cluster is shorter inside the PE brush layer. This result indicates the possible disruption of the HBs inside the soft nanoconfinement imposed by the grafted PE brush layer. Third, the average “hydrogen – acceptor-oxygen – donor-oxygen” angle that defines the HB is reduced for the HBs formed inside the brush layer (as compared to the HBs formed in the brush-free bulk). Fourth and final, our approach enables us to define a more rigorous set of conditions that should be used in defining the HBs that are formed inside the specific cationic PE brush layer simulated here: use of these set of conditions in defining the HBs show that we invariably overpredict the number water–water HBs formed inside the brush layer in case we use a generic definition (used to define the HBs in the brush-free bulk) to characterize the HBs inside the brush layer.
Methods
Molecular dynamics simulation
Our all-atom MD simulations considered 36 fully charged (positively charged) poly(2-methacryloyloxy)-ethyl-trimethylammonium (PMETAC) chains grafted in a 6 × 6 (x × y) array (Fig. 1 shows the PMETAC molecule and the simulation snapshot). Cl− counterions are used to neutralize the polyelectrolyte (PE) segmental charge in a solvent consisting of explicitly-modeled SPC/E water molecules.50 Continuous Lennard Jones (LJ, 12–6) and reflective walls (the LJ σ or the LJ distance parameter is 3 Å, with a cutoff of 3.36 Å) are placed at the bottom and the top of the simulation box, respectively. This prevented the mobile counterions and the water molecules from leaving the simulation system. Because of the LJ parameter and associated cutoff, the wall does not allow any atom up to a distance 3.36 Å from the wall. Chains are grafted by fixing the end carbon above the bottom reflective wall. The distance between the wall and the grafted carbon is 3.36 Å. The size of the equilibrated simulation system is x × y × z = 9.4 × 9.4 × 19 nm3 (the z distance is the wall-to-wall distance). Also, the bulk water region considered for analysis is around 5 nm above the PE layer. The bulk water resides within the box. We have checked the water density along the simulation box system. The water density is smaller within the PE brush layer since a significant amount of water is replaced by the PE atoms (please see Fig. S2 in the ESI†). The particle trajectories were calculated using the Velocity–Verlet algorithm with a time step of 2 fs. Non-bonded interactions were modelled as the sum of a shifted-truncated 12–6 Lennard Jones potential (ULJ) maintaining the cut-off of 13 Å. PPPM (particle–particle particle–mesh) algorithm was used to calculate the long-range coulombic interactions.51 The bonds and angles of water molecules were conserved using the SHAKE algorithm.52 Periodic boundary conditions were applied in x and y directions, while the fixed boundary condition was incorporated in z direction. Simulations were performed in LAMMPS (version 21st July, 2020).53 OVITO was used to visualize the simulation system.54 We have used OPLS-AA force field55 to model the interaction parameters for the PMETAC chains. The Lennard Jones (LJ) parameters for the Cl− counterions were taken from the work of Joung and Cheathan.56 Geometric mixing rules were used for calculating the LJ interactions between the different atom types. For mobile-ion-water interactions, we used the Lorentz–Berthelot mixing rules to be consistent with Joung et al.56 These parameters are very accurate for monovalent ions in an aqueous system. For example, ion parameters are calibrated to obtain proper hydration free energy of the solvated ions, as well as proper ion–oxygen distance. The LJ parameters are also calibrated for different water models, and we are using the calibrated value for SPC/E water model.56 The different forcefield parameters have been summarized in the ESI.†After creating the initial configuration, the system was first simulated in the NPzT ensemble (the subscript Z means that only the system height was allowed to change) to obtain the correct simulation box height at a temperature of 300 K and a pressure of 1 atmosphere by applying the Nosé–Hoover thermostat and the Nosé–Hoover barostat,57,58 with relaxation times of 0.1 ps and 1 ps for temperature and pressure, respectively. Subsequently, the system was equilibrated in the NVT ensemble to obtain the correct equilibrium configuration of the system by using the Langevin thermostat.59 We performed simulation until the brush height reached a plateau. After equilibration, we performed the production run for 12 ns.
Agnostic description of hydrogen bond
We have used unsupervised machine learning approach to identify hydrogen bonds (HBs) inside the brush layer as well as in the bulk (i.e., outside the brush layer). This machine learning approach, which follows the method proposed by Gasparotto and Ceriotti,46 has been briefly described below.The basis of the machine learning approach is that we consider structural features to identify the formation of HBs. A HB involves three atoms: one hydrogen atom (“H” atom), one donor oxygen atom (“O” atom), and one acceptor oxygen atom (“O′” atom). The distances between these three atoms can be checked to identify the formation of a HB.
Following Gasparotto and Ceriotti, we create a training data set χ = {xi}, where {xi} is a three-dimensional vector such that each element of {xi} can be expressed as  ,
, 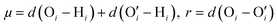 . Here v is the proton transfer coordinate, μ is the symmetric stretch coordinate, and r is the acceptor–donor coordinate. These three parameters describe the configuration of a triplet of atoms (namely, the H, O, and O′ atoms, see above) that might lead to the formation of a HB. r indicates the distance between O and O′ atoms; v and μ specify the position of H. These coordinates have been schematically shown in Fig. 2. This data set χ will be used to obtain the corresponding probability distribution: we employ the kernel density estimation (KDE) to obtain an estimate of this probability distribution.
. Here v is the proton transfer coordinate, μ is the symmetric stretch coordinate, and r is the acceptor–donor coordinate. These three parameters describe the configuration of a triplet of atoms (namely, the H, O, and O′ atoms, see above) that might lead to the formation of a HB. r indicates the distance between O and O′ atoms; v and μ specify the position of H. These coordinates have been schematically shown in Fig. 2. This data set χ will be used to obtain the corresponding probability distribution: we employ the kernel density estimation (KDE) to obtain an estimate of this probability distribution.
To select a sparser set of data points (for computational efficiency) that will be used to calculate the KDE, we select subset of the data samples Y ⊆ χ using minmax criteria. Obviously, one can write Y = {yi}. Subsequently, the KDE on each grid point (of the data set Y) can be expressed as:
 | (1) |
In eqn (1), K is a Gaussian kernel expressed as: where a Gaussian kernel is used as
 | (2) |
Also, in eqn (1)N is the total number of distance tuples, wj is a weight function, and σj is an adaptive kernel width. We follow the procedure of Gasparotto and Ceriotti46 to obtain wj and σj. Also, in eqn (2), D is the dimensionality of the problem (for our case D = 3).
After calculating KDE, we proceed to identify different clusters. Quick shift60 algorithm is used to separate different clusters. With the knowledge of the set of data points yi and the probability P(yi) [obtained using eqn (1)] associated with that data point, the quick shift algorithm constructs a tree where each data point serves as a node, while the data point with highest probability value serves as the root. Each data point is connected to the nearest point with a higher probability density; in other words, yi is connected to yj such that
 | (3) |
This search for data point with higher probability density is stopped by introducing a cut-off length λ. If no data point with higher probability is found within λ from the current data point, the quick shift stops moving and an enclosed cluster is found. It is to be noted that the quick shift is not particularly influenced by this cut-off, so it automatically selected at around ∼5σj where σj is the kernel grid point width (see eqn (1)). By this procedure we automatically get clusters associated with the atomic arrangements of H, O, and O′ atoms. From these clusters we can define the hydrogen bonds to be associated with the clusters with the shortest (v, μ, r) tuples as this will give strongest non-bonded interactions.
Results and discussions
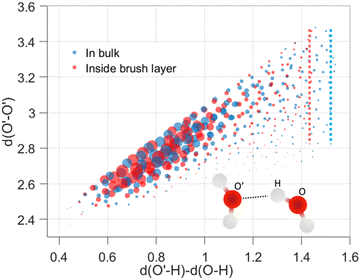
We analyzed the structural modification of HBs inside the cationic PE brush layer, as compared to the HBs in the bulk (outside the brush layer), by using the machine learning approach described above. For this purpose, we consider the positions of H and O atoms of the water molecules from two slabs (one inside the brush layer and another in the PE free bulk) of height 30 Å. We use a cutoff of μ, r ≤ 4 Å to exclude non-hydrogen bonded interactions. Fig. 2 shows the distribution of (v, μ, r) tuples in the bulk (outside the brush layer) and inside the brush layer. One observes a symmetry along v = 0 since a given O atom behaves as a “donor” in one HB and an “acceptor” in another HB. The probability density values are colored according to the partition in clusters. Several clusters indicate that there are more than one recurring configurations, possibly happening in the second solvation shell. Generally, in aqueous solution, water mediated HBs are considered to have been formed when the oxygen–oxygen distance is less than 3.5 Å and the H–O′–O angle is less than 30°.61,62 In Fig. 2, among the different clusters, the blue cluster (for v > 0) and the green cluster (for v < 0) are the representation of the HBs. Water connectivity is severely disrupted inside the PE brush layer (or the confinement effect imposed by the densely grafted PE brushes) since the PE atoms take up a significant amount of space and introduce additional interactions between PE atoms and water atoms. Despite such possible disruption, qualitatively similar clusters are observed for water both in the bulk as well as inside the brush layer. Other than the HBs, four different clusters (two for v > 0 and two for v < 0) are also partitioned inside the brush layer. This shows that long-ranged recurring patterns continue to remain distinguishable even after the water connectivity is disrupted by the presence of the PE chains. This method can be important for analyzing effects (such as ion–ion correlation, ion condensation, and bridging interactions), which significantly influence the morphology and properties of the PE chains.We next look into the hydrogen bond clusters (blue and green clusters in Fig. 2) more closely in Fig. 3. As SHAKE algorithm is used to keep the H–O distance fixed (∼1 Å),  is always ∼2 Å less than
is always ∼2 Å less than  . So, a 2D scatter plot of (μ, r) corresponds one-to-one to the 3D plot of (v, μ, r) In Fig. 3, we plot the two hydrogen bond cluster in (μ, r) space: one cluster represented [in 2D (μ, r) space] the HBs formed by the water molecules inside the PE brush layer, while the other cluster represented [in 2D (μ, r) space] the HBs formed by the water molecules in the bulk (outside the PE brush layer). We can see the qualitative similarity between these two clusters; both the clusters peaked around v = 0.75 Å and r = 2.7 Å and smeared out at high v values. Interestingly, we can observe the margin of the cluster is shorter inside the PE brush layer. These points after the margin are now clustered with the next cluster. These findings confirm that the HB clusters are getting compacted inside the brush layer. Water molecules form extensive HB network in the bulk water. But the water molecules cannot form these extensive networks inside the brush layer due to the presence of the polyelectrolytes. Our results indicate that this disruption can influence the putative HBs with large v. As large v indicates that the acceptor O is very far from the doner H, the spatial disruption caused by the presence of the PE chain can cause the HBs to break or get disrupted. As a result, we are not seeing HBs in this region. As a result, we are not seeing HB in this region This result shows the importance of agnostic definition of structural motifs in different situations and the manner in which a generic definition of a quantity (here HBs) can be modified inside a nanoconfinement (here, this nanoconfinement is the densely grafted PE brush layer enforced nanoconfinement).
. So, a 2D scatter plot of (μ, r) corresponds one-to-one to the 3D plot of (v, μ, r) In Fig. 3, we plot the two hydrogen bond cluster in (μ, r) space: one cluster represented [in 2D (μ, r) space] the HBs formed by the water molecules inside the PE brush layer, while the other cluster represented [in 2D (μ, r) space] the HBs formed by the water molecules in the bulk (outside the PE brush layer). We can see the qualitative similarity between these two clusters; both the clusters peaked around v = 0.75 Å and r = 2.7 Å and smeared out at high v values. Interestingly, we can observe the margin of the cluster is shorter inside the PE brush layer. These points after the margin are now clustered with the next cluster. These findings confirm that the HB clusters are getting compacted inside the brush layer. Water molecules form extensive HB network in the bulk water. But the water molecules cannot form these extensive networks inside the brush layer due to the presence of the polyelectrolytes. Our results indicate that this disruption can influence the putative HBs with large v. As large v indicates that the acceptor O is very far from the doner H, the spatial disruption caused by the presence of the PE chain can cause the HBs to break or get disrupted. As a result, we are not seeing HBs in this region. As a result, we are not seeing HB in this region This result shows the importance of agnostic definition of structural motifs in different situations and the manner in which a generic definition of a quantity (here HBs) can be modified inside a nanoconfinement (here, this nanoconfinement is the densely grafted PE brush layer enforced nanoconfinement).
We next check the manner in which the hydrogen bond angle is modified inside the PE brush layer. We use the (v, r) margins from Fig. 3 as the cutoff of the HB search. We manually analyzed the simulation snapshots using v and r and count this angle (charactering the HB formation). It can be observed that there is a significant modification of the angle distribution (H – acceptor-O – donor-O angle or H–O′–O angle) inside the brush layer. For the HBs distribution inside the brush layer, there is a slight shift of the distribution peak towards the smaller values of the H–O′–O angle: this indicates that the HBs inside the brush layer become more linear. From this HB distribution plot, we also observe the possibility of the number of HBs with larger H–O′–O angle reducing inside the brush layer. This kind of variation in hydrogen bond angles have been previously observed in different ice phases as well as in HBs formed by different molecules;63–65 here we are witnessing this with water being a strong confinement imposed by the presence of the densely grafted PE brushes. Generally, an angle criterion of H–O′–Oangle being less than 30° is used in the structural definition of water mediated hydrogen bond formation. In Fig. 4, we calculate that for the HBs in the brush-free bulk, 90% of the HBs correspond to the H–O′–O angles that are smaller than 30°. However, for the HBs inside the PE brushes, as the H–O′–O angle distribution (corresponding to which HBs are formed) is shifted towards the smaller angle (see above), 90% of the HBs will correspond to a much lower value of the H–O′–O angle: indeed, our calculations using Fig. 4 establish this cut-off angle as 24° for the case of the HBs inside the PE brush layer.
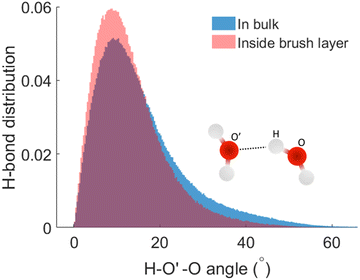 | ||
| Fig. 4 Normalized distribution of the HBs as functions of the H–O′–O (H–acceptor-O–donor-O) angles inside the PE brush layer and the brush-free bulk. | ||
Finally, we calculate the total number of HBs per water molecules inside the brush layer. We consider two conditions or definitions (see below) used to identify the formation of the HBs and compare their impact on the total number of HBs inside the PE brush layer. The first condition/definition is the generally accepted definition for the HB formation in the bulk water: oxygen–oxygen distance is less than 3.5 Å and the H–O′–O angle is less than 30°. In second definition, we modify the condition on the H–O′–O angle that is associated with the HB formation inside the PE brush layer: as per Fig. 4, we identify this condition on the H–O′–O angle to be less than 30°. Table 1 provides the number of HBs computed by these two separate definitions at different locations within the PE brush layer. This second definition leads to a much smaller number of HBs inside the brush layer. This result, therefore, shows that if we use the definition of HB in a bulk water for calculating the HBs inside a densely grafted (affording significant nanoconfinement) PE brush layer, we would overcount the number of HBs.
| Distance from grafted carbon | 5.4 Å | 15.7 Å | 26.0 Å | 36.3 Å |
|---|---|---|---|---|
| Using generally accepted definition | 2.50 | 2.51 | 2.53 | 2.57 |
| Using modified definition | 2.29 | 2.37 | 2.39 | 2.42 |
Conclusions
ML based approach has been used to account for the specific scenario, associated with the soft nanoconfinement effect experienced by the water molecules present inside the densely grafted cationic PE brush layer, probed using all-atom MD simulations, while calculating the water–water HBs inside the PE brush layer. The ML method is based on a clustering approach: the result is multiple groups of clusters and the HBs are represented only by certain specific clusters. While the overall clustering data is similar to for the water molecules inside and outside the PE brush layer, through these data, we are able to identify several differences between the water–water HBs formed inside and outside the PE brush layer. First, we are able to identify that the margin of the cluster gets shortened within the PE brush layer: this can be attributed to the possible disruption of the HBs inside the PE brush layer. Second the H–O′–O angle that characterizes the HBs gets reduced for the case of the water–water HBs formed inside the PE brush layer: this can be interpreted as the HBs inside the brush layer becoming more linear. Third, we establish if the HBs that are formed inside the specific cationic PE brush layer simulated here are characterized by the generic definition of the HBs (used to define the HBs in the bulk water outside the brush layer), we overpredict the number water–water HBs formed inside the brush layer. Overall, we anticipate that our paper will motivate new research problems aimed at re-evaluating the properties of ions and water molecules inside a PE brush layer using a more system-specific definition/characterization motivated by different ML approaches.Author contributions
S. D. conceived the problem. T. H. P. ran the simulations, analyzed the data. T. H. P. and S. D. wrote the paper. All authors commented on the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Department of Energy Office of Science grant DE-SC0017741. The authors also gratefully acknowledge the Deepthought2 High-Performance Computing cluster at the University of Maryland for providing necessary computational resources.References
- P. Pincus, Macromolecules, 1991, 24, 2912 CrossRef CAS.
- M. Ballauff and O. Borisov, Curr. Opin. Colloid Interface Sci., 2006, 11, 316 CrossRef CAS.
- M. Ballauff, Prog. Polym. Sci., 2007, 32, 1135 CrossRef CAS.
- M. Geoghegan, Soft Matter, 2022, 18, 2500 RSC.
- Y. Mir, P. Auroy and L. Auvray, Phys. Rev. Lett., 1995, 75, 2863 CrossRef CAS PubMed.
- E. B. Zhulina and M. Rubinstein, Macromolecules, 2014, 47, 5825 CrossRef CAS PubMed.
- T. Kreer, Soft Matter, 2016, 12, 3479 RSC.
- S. Das, M. Banik, G. Chen, S. Sinha and R. Mukherjee, Soft Matter, 2015, 11, 8550 RSC.
- M. Ali, P. Ramirez, S. Mafe, R. Neumann and W. Ensinger, ACS Nano, 2009, 3, 603 CrossRef CAS PubMed.
- M. Ali, B. Yameen, R. Neumann, W. Ensinger, W. Knoll and O. Azzaroni, J. Am. Chem. Soc., 2008, 130, 16351 CrossRef CAS PubMed.
- S. Umehara, M. Karhanek, R. W. Davis and N. Pourmand, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 4611 CrossRef CAS PubMed.
- M. Ali, B. Yameen, J. Cervera, P. Ramirez, R. Neumann, W. Ensinger, W. Knoll and O. Azzaroni, J. Am. Chem. Soc., 2010, 132, 8338 CrossRef CAS PubMed.
- S. Chanda, S. Sinha and S. Das, Soft Matter, 2014, 10, 7558 RSC.
- G. Chen, H. S. Sachar and S. Das, Soft Matter, 2018, 14, 5246 RSC.
- H. S. Sachar, V. S. Sivasankar and S. Das, Soft Matter, 2019, 15, 5973 RSC.
- S. Mura, J. Nicolas and P. Couvreur, Nat. Mater., 2013, 12, 991 CrossRef CAS PubMed.
- G. Liu, M. Cai, X. Wang, F. Zhou and W. Liu, ACS Appl. Mater. Interfaces, 2014, 6, 11625 CrossRef CAS PubMed.
- L. Yang, K. Shen, J. Xu, M. Ren and F. Cao, J. Appl. Polym. Sci., 2022, 139, e52709 CAS.
- J. Xu, N. E. Jackson, X. Xu, B. K. Brettmann, M. Ruths, J. J. de Pablo and M. Tirrell, Sci. Adv., 2017, 3, eaao1497 CrossRef PubMed.
- J. D. Willott, B. A. Humphreys, G. B. Webber, E. J. Wanless and W. M. de Vos, Langmuir, 2019, 35, 2709 CrossRef CAS PubMed.
- J. Yu, J. Mao, G. Yuan, S. Satija, Z. Jiang, W. Chen and M. Tirrell, Macromolecules, 2016, 49, 5609 CrossRef CAS.
- J. Yu, N. E. Jackson, X. Xu, Y. Morgenstern, Y. Kaufman, M. Ruths, J. J. de Pablo and M. Tirrell1, Science, 2018, 360, 1434 CrossRef CAS PubMed.
- R. Farina, N. Laugel, P. Pincus and M. Tirrell, Soft Matter, 2013, 9, 10458 RSC.
- S. Misra, S. Varanas and P. P. Varanasi, Macromolecules, 1989, 22, 4173 CrossRef CAS.
- E. B. Zhulina and O. V. Borisov, J. Chem. Phys., 1997, 107, 5952 CrossRef CAS.
- I. O. Lebedeva, E. B. Zhulina and O. V. Borisov, J. Chem. Phys., 2017, 146, 214901 CrossRef PubMed.
- E. B. Zhulina and O. V. Borisov, Langmuir, 2011, 27, 10615 CrossRef CAS PubMed.
- O. V. Borisov and E. B. Zhulina, J. Chem. Phys., 2018, 149, 184904 CrossRef PubMed.
- H. S. Sachar, V. S. Sivasankara and S. Das, Soft Matter, 2019, 15, 559 RSC.
- S. A. Etha, V. S. Sivasankar, H. Singh Sachar and S. Das, Phys. Chem. Chem. Phys., 2020, 22, 13536 RSC.
- S.-Z. He, H. Merlitz, L. Chen, J.-U. Sommer and C.-X. Wu, Macromolecules, 2010, 43, 7845 CrossRef CAS.
- H. Merlitz, C. Li, C. Wu and J.-U. Sommer, Soft Matter, 2015, 11, 5688 RSC.
- N. E. Jackson, B. K. Brettmann, V. Vishwanath, M. Tirrel and J. J. de Pablo, ACS Macro Lett., 2017, 6, 155 CrossRef CAS PubMed.
- P. R. Desai, S. Sinha and S. Das, Phys. Rev. E, 2018, 97, 032503 CrossRef CAS PubMed.
- H. S. Sachar, T. H. Pial, P. R. Desai, S. A. Etha, Y. Wang, P. W. Chung and S. Das, Matter, 2020, 2, 1509 CrossRef.
- H. S. Sachar, T. H. Pial, B. S. Chava and S. Das, Soft Matter, 2020, 16, 7808 RSC.
- H. S. Sachar, B. S. Chava, T. H. Pial and S. Das, Macromolecules, 2021, 54, 2011 CrossRef CAS.
- T. H. Pial, H. S. Sachar and S. Das, Macromolecules, 2021, 54(9), 4154–4163 CrossRef CAS.
- H. S. Sachar, B. S. Chava, T. H. Pial and S. Das, Macromolecules, 2021, 54, 6342 CrossRef CAS.
- T. H. Pial, M. Prajapati, B. S. Chava, H. S. Sachar and S. Das, Macromolecules, 2022, 55, 2413 CrossRef CAS.
- T. H. Pial, H. S. Sachar, P. R. Desai and S. Das, ACS Nano, 2021, 15, 6507 CrossRef CAS PubMed.
- H. S. Sachar, T. H. Pial, V. S. Sivasankar and S. Das, ACS Nano, 2021, 15, 17337 CrossRef CAS PubMed.
- M. Jabłoński and M. Solà, J. Phys. Chem. A, 2010, 114, 10253 CrossRef PubMed.
- K. Wendler, J. Thar, S. Zahn and B. Kirchner, J. Phys. Chem. A, 2010, 114, 9529 CrossRef CAS PubMed.
- J. Grdadolnik, F. Merzel and F. Avbel, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 323 CrossRef.
- P. Gasparotto and M. Ceriotti, J. Chem. Phys., 2014, 141, 174110 CrossRef PubMed.
- A. L. Ferguson, J. Phys.: Condens. Matter, 2018, 30, 043002 CrossRef PubMed.
- N. E. Jackson, M. A. Webb and J. J. de Pablo, Curr. Opin. Chem. Eng., 2019, 23, 106 CrossRef.
- I.-B. Magdău and T. F. Miller, Macromolecules, 2021, 54, 3377 CrossRef.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269 CrossRef CAS.
- R. W. Hockney and J. W. Eastwood, Computer Simulations Using Particles, McGraw-Hill International Book Co; New York, 1981 Search PubMed.
- J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1 CrossRef CAS.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225 CrossRef CAS.
- I. S. Joung and T. E. Cheatham III, J. Phys. Chem. B, 2008, 112, 9020 CrossRef CAS PubMed.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511 CrossRef.
- T. Schneider and E. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 17, 1302 CrossRef.
- A. Vedaldi and S. Soatto, Computer Vision-ECCV 2008, Springer, 2008, pp. 705–718 Search PubMed.
- S. Han, Sci. Rep., 2018, 8, 9347 CrossRef PubMed.
- A. Luzar and D. Chandler, Nature, 1996, 379, 55 CrossRef CAS.
- R. Zangi and A. E. Mark, J. Chem. Phys., 2004, 120, 7123 CrossRef CAS PubMed.
- W.-H. Zhao, J. Bai, L.-F. Yuan, J. Yanga and X. C. Zeng, Chem. Sci., 2014, 5, 1757 RSC.
- I. Jukić, M. Požar, B. Lovrinčević and A. Perera, Phys. Chem. Chem. Phys., 2021, 23, 19537 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00997h |
| This journal is © The Royal Society of Chemistry 2022 |