Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stretchable reflective coating for soft optical waveguides and sensors†
Simone
Lantean‡
 *a,
Matteo
Lo Preti‡
*a,
Matteo
Lo Preti‡
 ab and
Lucia
Beccai
ab and
Lucia
Beccai
 *a
*a
aSoft BioRobotics Perception, Istituto Italiano di Tecnologia (IIT), Genova, Italy. E-mail: simone.lantean@iit.it
bThe BioRobotics Institute, Scuola Superiore Sant’Anna, Pontedera, Italy
First published on 20th September 2022
Abstract
Soft robots must embody mechanosensing capabilities to merge with and act in the environment. Stretchable waveguides are making a mark in soft mechanical sensing since they are built from pristine elastomers. Therefore, they are insensitive to electromagnetic fields and weakly affect the deformations of the robot. However, issues in light-shielding, signal decoupling, and core-cladding interfaces are still open challenges. In this work, titanium oxide particles (TiO2) are dispersed in silicone elastomers to develop a soft optical shield coating. Results show that the added particles do not harden the matrix and reduce light transmission. Almost full NIR shielding is achieved by adding 1.0 vol% of TiO2 in 150 μm thick films. These properties make the proposed shielding coating an excellent candidate for soft mechanosensing. An open-access tool is developed to design soft optical devices by programming light transmittance at desired wavelengths by tuning, both, TiO2 concentration and film thickness. Finally, two proof-of-concepts are demonstrated, a soft waveguide and a soft strain sensor, by integrating the developed material to shield a transparent PDMS resin and a semi-transparent Ecoflex00-10 matrix, respectively. The soft waveguide can stretch up to 40% with very low optical loss, while the optical strain sensor can detect strain up to 90%. In both cases, bending, folding, and indentation of the devices have a significantly low impact on light transmission. These results can pave the way to design new optical transmission devices and sensors that exploit light reflection and that allow for discriminating different types of mechanical stimuli in soft robots.
Introduction
Mechanosensing is fundamental in robotic systems as it allows adaptation and reaction to unexpected situations. On one hand, sensing external mechanical cues (e.g., pressure, directional forces, vibration, etc.) allows exploring the outer world and manipulating unknown objects. On the other hand, robots need to reconstruct their own movements to be controlled.1 This is critical in soft robots as they need to discriminate various mechanical stimuli. The sensors must be highly compliant not to physically burden the robot body due to the application of thick and stiff artificial skins on its surface. Also, in the case of distributed sensing, high wiring volumes should be avoided by developing ad hoc transduction principles.In this vision, stretchable waveguide sensors are gaining increased attention because of some peculiar aspects,2,3 among which are their insensitivity to electromagnetic fields and intrinsic safety. Moreover, the optically clear soft matrix is in direct contact with the environment, protecting the electronic components underneath.4 This hugely increases the robustness and lifespan of these kinds of sensors. Yet, there is still a need to avoid signal dispersion and losses from the transduction medium effectively and to decouple possible sources of light variations.
In general, optical waveguides are composed of two elements: (i) a high refractive index optical medium (the core) and (ii) a low refractive index material (cladding) surrounding the core. This design allows light to be confined within the core by internal light reflection and avoiding optical loss upon bending of the waveguide.
When using this design in soft robotics, the applied materials, besides optical properties, must fulfill specific mechanical requirements. Indeed, the material must be highly deformable and stretchable, i.e., low elastic modulus and high elongation at break, to enhance the compliance of the final device.5
Conventional optical transducers and waveguides (i.e., fibers) are made of silica glass. They are rigid, stiff, and fragile, thus, not suitable for developing soft sensors, or for being integrated in soft actuators or soft robot bodies in general. In the past, much effort was put into replacing traditional glass-based optical fibers with polymeric materials such as polymethylmethacrylate6 (PMMA), cyclic olefin copolymers,7 and hydrogels.8 However, the reduced compliance and stretchability of these materials limited their application in more demanding applications. Recently, silicones and polyurethane elastomers have emerged as good candidates for soft optical devices as they combine low elastic moduli (in general lower than 5 MPa) and a high elongation at break (>300%), with low optical absorbance in the visible (VIS) and near infra-red (NIR) range.3 In the literature, several examples of soft and stretchable optical devices working in the NIR range can be found based on the conventional core-cladding, or only core, designs.9,10
In the last decade, there has been increasing research effort to develop soft waveguides, i.e., deformable light conductors. Martincek et al. developed a new fabrication method to produce stretchable light fibers made of polydimethylsiloxane (PDMS) elastomers with enhanced control in their length and diameter, without a cladding material.11 Massinne and coauthors fabricated silicone-based waveguides by coupling different silicone elastomers as core and cladding materials (Nusil LS-6941 and Dow Corning Sylgard 184, respectively). The optical waveguides were able to withstand stretching up to 30% with relatively low optical loss, and they were tolerant to bending up to curvature radii larger than 7 mm.12 Guo et al. recently developed stretchable PDMS-based waveguides, where the refractive index between the core and the cladding was tuned by modifying the ratio between the resin and the cross-linkers. Embedding thermal-sensitive upconversion nanoparticles in the core, the authors developed a temperature-sensitive optical fiber stretchable up to 80%.13
In parallel, new designs of stretchable optical sensors were introduced. Harnett et al. used polyurethanes and silicones, as core and cladding, respectively, in optical fibers capable of detecting strains up to 100%;14 conversely, Zhao et al. used silicone for the core and polyurethane for the cladding in a tactile sensor demonstrated in a prosthetic hand.15 Similar stretchable optical fibers based on silicone gels were doped with thermochromic pigments to develop haptic sensors sensitive to thermal variations.16 H. Bai et al. decoupled bending, stretching and localized pressure in stretchable fibers by embedding a discrete color-block pattern. The variations of light intensity and chromaticity were read simultaneously by coupling two polyurethane cores and a silicone cladding.17 Moreover, Leber et al. showed an optical sensor capable of measuring strain up to 300% by fabricating fibers with a polystyrene core and a fluorinated polymer cladding.18 Also, J. Guo and coauthors developed a 1 cm-long optical strain sensor by adding dyes in a PDMS fiber. The fabricated sensors could detect strains up to 100% and be tolerant to bending at curvature radii larger than 6 cm.19 Recently, Heiden et al. 3D printed biodegradable stretchable waveguides based on a gelatin-based hydrogel.20
Despite the excellent results in terms of stretchability of the components, several issues must still be addressed both for waveguides used as connecting optical components and as strain sensors. Indeed, their reliability from the mechanical point of view, but also for the optical signal transmission and sensing output, is strongly limited by the aspects described in the following:
(i) Debonding at the core and cladding interface. The combination of two elastomers having a different chemical nature, e.g., polyurethane-silicone and polystyrene-fluorinated polymers, is not trivial as their interfacing may lead to unpredicted optical effects and early rupture of the component. Debonding at the interface may occur upon repeated high stretching loads and several mechanical deformations,18 generating defects and voids and thus altering light transmission within the core material.
(ii) Environmental light-shielding. As the developed devices are commonly not shielded, environmental light, as well as objects made of materials with a different refractive index, may interfere with light transmission in the optical devices.
(iii) Concurrent mechanical stimuli. Soft optical sensors are very sensitive to stretching, compression, bending, and twisting, and all such mechanical stimuli contribute to the variation of the optical signal. Hence, the sensors must be designed to detect only the desired stimulus.
(iv) Safety and hazardous risks. Mechanical sensors are often produced starting from castable polyurethanes containing isocyanates, which are harmful to human health. Thus, safety protocols are applied during the fabrication process, potentially limiting their large-scale production.
In this work, all the above aspects are addressed by using silicone-based matrices only, thus avoiding safety issues. A coating layer capable of shielding the external light is developed, allowing selectivity and improving the adhesion between the core and the cladding materials. Moreover, the reflective coating is used to build a soft strain sensor that is not affected by bending, folding, and indentation.
A good strategy to avoid debonding at the interface between the core and the cladding would be to apply the same elastomeric matrix for both parts of the waveguide. However, using the same material prevents internal reflection and light guiding since the refractive indices between the core and cladding cannot have large variations. Our strategy involves developing a new highly reflecting and deformable coating with the two-fold function of the cladding and shielding materials in optical waveguides. This is achieved by adding highly reflective particles in elastomeric materials and by exploiting the internal reflection mechanism to guide light within the optical device.
Several compounds can be added to organic matrices to develop reflective coating. This was deeply investigated to produce cool coatings and protections in, e.g., buildings and solar cells.21–23 A similar approach can be applied to develop efficient soft devices since the optical properties of the fillers are, in principle, independent of the host matrices. In the past, different materials were added to polymeric matrices to enhance the reflective power of the coatings, such as metal particles (Al, Ag, and Cu),21 metal oxide particles (TiO2, ZnO, CeO2, and Y2O3),23–28 and organic pigments.22
Among these, TiO2 particles are the perfect candidate to produce reflective coatings as this filler exhibits superior optical properties. Also, the particles are commercially available. Thus, no complex synthesis method is required. In particular, rutile is the most thermodynamically stable phase, it exhibits the highest reflectivity to near-infrared (NIR) radiation,29 and its optical properties are not influenced by either temperature or moisture.23
In this work, two different optical devices are proposed, i.e., a waveguide and a strain sensor. PDMS is chosen for the waveguide fabrication as it is thermally stable and isotropic and has nominally zero absorbance in the NIR range.11 On the other hand, another silicon-based elastomer, Ecoflex00-10, is used as the core material for the strain sensor as it is not fully transparent in the NIR range, and its light absorption can be exploited to evaluate the strain of the material. Micrometric TiO2 particles (5 μm) are added to PDMS or Ecoflex10 to develop a highly reflective shielding coating for both the waveguide and the strain sensor. By tuning the composite film thickness and the concentration of TiO2 particles, composite coatings that are able to shield and reflect light without stiffening the material are fabricated. Then, an open-access platform is developed, which determines the TiO2 concentration and the film thickness needed for a specific light transmittance at a known wavelength, for developing new optical soft devices. Finally, as proof-of-concepts, a PDMS-based waveguide and an Ecoflex-based strain sensor are built by using composite films as coatings, proving their superior performance in terms of selectivity and light-shielding.
Methodology
Sample preparation
Titanium oxide and rutile particles (TiO2, <10 μm) were purchased from Sigma Aldrich and dispersed in a commercial polydimethylsiloxane resin (Sylgard 184, Dow Corning) in different volume concentrations: 0.10, 0.25, 0.50, and 1.00 vol% with respect to the prepolymer content. The cross-linker was added at the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio to all the prepared formulations. For PDMS-based waveguides, the cross-linker was added at the 20
1 ratio to all the prepared formulations. For PDMS-based waveguides, the cross-linker was added at the 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio to enhance the deformation of the device.
1 ratio to enhance the deformation of the device.
For the optical sensors, the TiO2 particles were added at 1.00 vol% to a mixture 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of Ecoflex-0010 part A and Ecoflex-0010 part B (Smooth-on).
1 of Ecoflex-0010 part A and Ecoflex-0010 part B (Smooth-on).
The prepared formulations were mixed for 30 seconds in a planetary centrifugal mixer (Thinky ARE-250) and defoamed for 30 seconds to improve the particle dispersion and homogenize the formulations. After, the formulations were carefully degassed in a vacuum chamber for about 10 minutes to eliminate air bubbles in the resin. Once cast, the formulations were again placed in a vacuum chamber for 10 minutes. Curing was performed in an oven (Vacutherm, Thermo Scientific) at 60 °C and lasted 6 hours for PDMS and 2 hours for Ecoflex-based samples.
All the molds used in this work were fabricated via a Fused Filament Fabrication (FFF) 3D printer (Ultimaker S3) by extruding acrylonitrile butadiene styrene (ABS) filaments.
The photoemitters (PEs) used in the devices (infrared LEDs, VSMY1850) have a peak of emission at 850 nm, matched to the peak of reception of the photoreceivers (PRs) (silicon NPN epitaxial planar detectors, VEMT2023SLX01).
Characterization
Optical images were taken using a HIROX KH-8700 digital optical microscope at different magnifications.Fourier-transform Infrared spectroscopy (FTIR) in ttenuated total reflection (ATR) mode was performed by (Shimadzu, Miracle 10) monitoring the peak centered at 2160 cm−1 corresponding to the reacting Si–H groups of the polymeric matrix. All the spectra were normalized to the univariant peak of C–H groups placed at 789 cm−1.
Ultra-violet-visible-near infrared (UV-Vis-NIR) spectrometry was performed by LAMBDA 650 (PerkinElmer), measuring the transmitted light percentage (%T) in the 1100–300 nm range.
Reflectance was measured using a Varian Cary 5000 spectrophotometer equipped with an integrating sphere (Diffuse Reflectance Accessory, Agilent).
The mechanical tensile tests on the composite materials were performed with a ProLine (ZwickRoell) equipped with a 10 N load cell. The samples were cast in a dog bone shape (cross section of 4 × 3 mm, length of 30 mm), preloaded at 0.1 N, and tested with a strain rate of 2 mm s−1.
The soft optical devices were characterized using ad hoc tensile test apparatus. The samples were arranged in the setup undergoing an aluminum clamping mechanism. A tensile force was applied by a micrometric servo-controlled translation stage (M-414.1DG, Physik Instrumente, Karlsruhe, Germany) and measured through a uniaxial load cell (Burster 8431 with USB interface 9206, Burster gmbh & co kg, Gernsbach, Germany). The response of the photoreceiver was captured using a DAQ system (USB-6218, National Instruments, Austin, TX, USA). The protocol for the acquisition consisted of: (i) manual adjustment of the distance between the clamps,; (ii) positioning of the sample, (iii) setting the sample in tension, and (iv) selecting the test parameters (e.g., number of cycles, displacement, speed). Each test was performed for 5 cycles up to a displacement of 100% and a speed of 0.5 mm s−1.
Indentation tests were carried out using a second experimental setup. The sample was fixed using a bi-adhesive tape to a Lab Jack (Newport 271, MKS Instruments, Inc.), which was positioned under a force platform. The latter consisted of one orthogonal manual micrometric translation stage (M-105.10, Physik Instrumente, Karlsruhe, Germany) coupled with a micrometric servo-controlled translation stage (M-111.1DG, Physik Instrumente, Karlsruhe, Germany) (for a precision vertical positioning). A Delrin probe was mechanically interfaced to the previous translation stage and to a triaxial load cell (ATI Nano 17, ATI Industrial Automation, Inc., Apex, NC, USA). The probe exerted a vertical force on the sample beneath it. The response of the photoreceiver is captured using a DAQ system (USB-6218, National Instruments, Austin, TX, USA). Each acquisition starts by bringing the stage to the highest vertical position, while the hardware peripherals are initialized. The vertical position is controlled via software, such that each acquisition starts at the same probe–sample distance. The tests were performed for 5 cycles and 30% of indentation depth.
Results and discussion
Formulation characterization
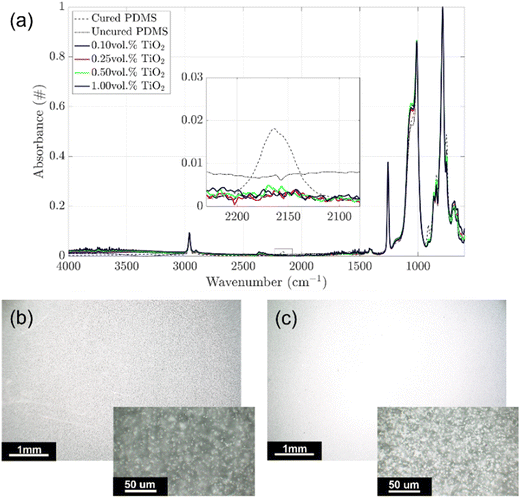
Four different concentrations of TiO2 particles in PDMS were tested: 0.1, 0.25, 0.5, and 1 vol%. Adding inorganic and more dense fillers (PDMS = 0.98 g cm−3 and TiO2 = 3.5 g cm−3) may lead to the aggregation and sedimentation of the particles causing instability and deterioration of the final properties of the material. The stability of the PDMS–TiO2 formulations was evaluated on the system at the highest TiO2 concentration (1 vol%, PDMS_1TiO2) as it is more likely to undergo precipitation and sedimentation. The tested formulation remained stable for more than 6 hours, which is comparable to the curing time of the PDMS (Fig. S1, ESI†). Hence, the investigated system is suitable for conventional casting manufacturing methods.The effect of TiO2 particles on the polymerization process of the hosting silicone matrix was investigated. Fourier-transform Infrared (FT-IR) spectroscopy in the attenuated total reflection (ATR) method was used to analyze the infrared spectra of uncured PDMS and cured samples at increasing TiO2 concentrations. Sylgard 184 cures via a platinum-catalyzed hydrosilation reaction between the vinyl groups in the prepolymer and the silane groups (SiH4) contained in the curing agent. Therefore, the polymerization of the elastomer was monitored following the variation of the peak placed at 2160 cm−1, which is ascribable to the stretching vibration of SI–H groups of the curing agent.30–32 All the spectra were normalized with respect to the peak placed at 789 cm−1, corresponding to the bending of C–H groups, which are not involved in the polymerization of silicones. The peak related to Si–H groups completely flattened for all the cured samples regardless of the particle concentration (Fig. 1a), demonstrating full curing of the composite materials. This proved that TiO2 particles do not alter the thermal curing of the PDMS matrix, since the full conversion of the reacting groups was achieved for all the tested samples.
The lowest and the highest TiO2-loaded formulations (PDMS_0.25TiO2 and PDMS_1TiO2 samples, respectively) were coated on a microscope slide with 150 μm thickness and characterized by optical microscopy to evaluate the dispersion of the fillers in the hosting matrix. The images taken at low magnification (Fig. 1b and c) are of difficult interpretation due to a strong reflection of the microscope light. However, this is a qualitative indication of the reflective properties of the composite films. Images at higher magnification (insets in Fig. 1) showed that TiO2 particles are well dispersed in the host matrix, indicating that the optical and mechanical properties of the designed coatings were likely to be homogenous.
Optical properties
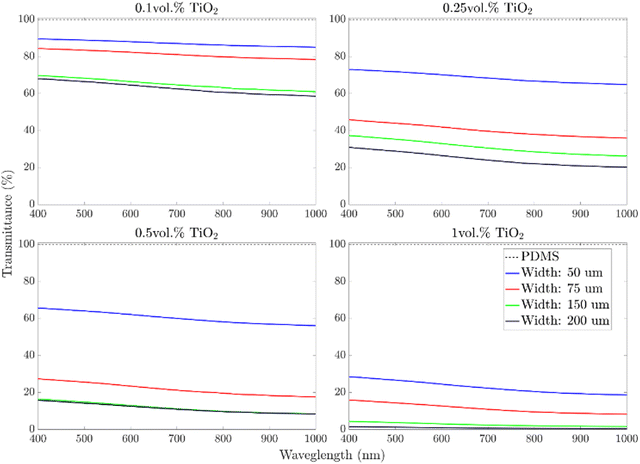
Ultra-violet-visible-near infrared (UV-Vis-NIR) spectroscopy was used to investigate the optical properties and the shielding capability of the silicone–titania-based samples. Four samples at increasing TiO2 concentrations (0.1, 0.25, 0.5, and 1 vol%) were coated on a microscope slide with different film thicknesses (50, 75, 150, and 200 μm) and cured in an oven (60 °C, 6 h). Pristine PDMS samples were tested and used as a reference. This characterization can only evaluate a decrease in light intensity (or light transmittance) through the samples. However, since TiO2 particles are found to be completely reflective,33 light signal losses must be ascribed to reflecting and scattering phenomena rather than light absorption.33The pure PDMS samples showed 100% light transmittance (zero loss) in the light range from 300 to 1100 nm regardless of the film thickness, proving the well-known transparency in the visible and NIR spectrum of this material (grey dashed line in Fig. 2).34–36 When TiO2 particles were added, an overall decrease in light transmittance (%T) was observed. The amount of the optical loss depends on the amount of TiO2 particles and the film thickness. For instance, the %T values of PDMS_1.0TiO2 are generally 3 folds lower than those measured for the PDMS_0.1TiO2 sample (30% vs. 90% in the case of 50 μm thick films). On the other hand, the impact of film thickness seems lower than the concentration of TiO2 particles, and its influence is lower in the thicker samples (150 μm and 200 μm samples). In general, the lowest values of %T were obtained in the NIR region of the spectrum (800–1100 nm). In particular, almost full NIR shielding (0%T) was achieved for 150 μm- and 200 μm-thick PDMS_1.0TiO2 samples.
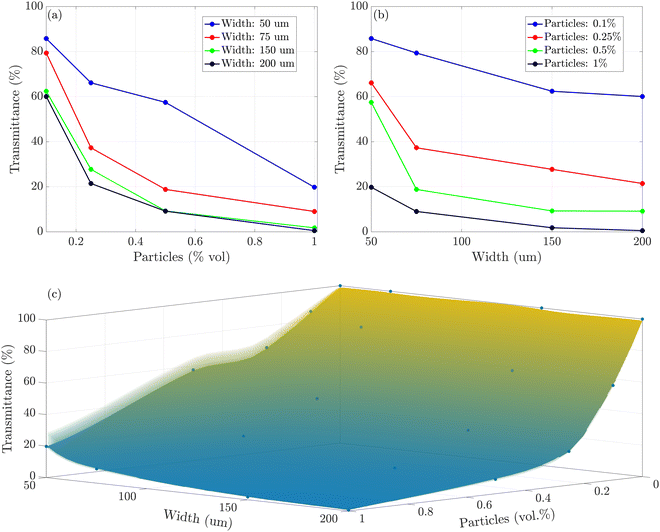
The NIR photoemitters used in the fabrication of the optical devices have an emission spectrum centered at 850 nm of the electromagnetic spectrum. Therefore, the effect of TiO2 particles concentration and film thickness at this wavelength was evaluated. Fig. 3a shows that for the same layer thickness, the transmittance decreased with the TiO2 load following a decaying exponential law. Moreover, any significant difference was observed between 150 μm- and 200 μm-thick samples, suggesting the existence of a threshold above which the effect of film thickness is negligible. Fig. 3b underlines the role of the film thickness, and after a fast decay in light transmittance occurring up to 75 μm, the curves flattened, reaching a pseudo-plateau at 150 μm. The effect of the particles’ concentration and the film thickness can be combined in order to produce a 3D diagram that describes the variation in light transmittance by varying these two parameters (Fig. 3c).
Based on our experimental data and results, we relied on the universal approximation theorem37,38 to determine the required vol% of TiO2 particles to be dispersed in a PDMS matrix to obtain desired transmittance in a layer with a chosen width at a desired wavelength. The resulting graphical user interface is available at the following link (https://www.mathworks.com/matlabcentral/fileexchange/114280-tio2-particle-concentration), and it can be a helpful tool in designing new optical devices by material selection. All the technical details are reported in the ESI.†
To further validate the TiO2-composite films as reflecting shielding materials, the reflectance of 1 mm thick PDMS_0.1TiO2 and PDMS_1.0TiO2 samples was measured (Fig. S2, ESI†). Focusing on the wavelength of the emission spectrum of the optical component (850 nm), the reflectance increased from 70% for the sample with 0.1 vol% of particles to 87% for the sample with the highest load of fillers (i.e. 1 vol%). These results confirm the possibility of applying PDMS–TiO2 composite materials as NIR shielding and reflective coatings for optical applications. It is important to mention that the results achieved in terms of light-shielding are only ascribable to the addition of TiO2 particles. Therefore, similar results can be achieved by loading TiO2 particles to different polymeric matrices widening the range of application of the proposed approach.
Mechanical properties
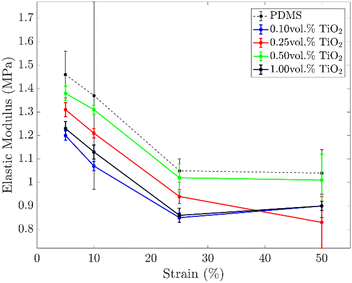
In general, the addition of inorganic particles within a polymeric matrix leads to a stiffening of the final composite material. This limits the deformability of active soft structures and devices and is one of the bottlenecks in developing soft transducers. The stiffening often leads to an increase of the elastic modulus and a decrease in the elongation at break. Both these aspects must be avoided in the fabrication of waveguides and strain sensors, as they limit the compliance of the devices. Indeed, stiffer devices deform under higher forces and have a lower stretching range, i.e. the device undergoes rupture at lower elongations.The mechanical properties of the composite coating were investigated with the aid of uniaxial tensile tests (Fig. S3, ESI†). In Fig. 4, the trends of the elastic moduli at different strains for different concentrations of TiO2 particles are shown. Unlike the expected, all the samples loaded with TiO2 particles showed lower elastic moduli than the pristine PDMS samples. In particular, the samples with the highest concentration of particles (and best shielding properties) have an elastic modulus ∼20% lower than net PDMS (1.23 vs. 1.46 MPa@5% strain, and 1.13 vs. 1.37 MPa@10% strain). However, a clear trend between the concentration of particles and the elastic moduli of the resulting composite materials is not observed.
 | ||
| Fig. 4 Elastic module versus strain percentage of dog bone PDMS-based specimens at increasing TiO2 particle concentrations. Data are acquired by uniaxial testing. | ||
The silicone matrix's reduction of the elastic moduli by adding TiO2 particles (in rutile and anatase phases) is already reported in the literature.33,39–41 However, an exhaustive explanation of this trend still does not exist. As no large aggregates were observed by optical microscopy (Fig. 1), the reduction of the elastic moduli cannot be ascribed to defects produced by the addition of TiO2 particles. Most likely, the effect of TiO2 particles is the result of two competing mechanisms: the softening effect of TiO2 particles due to interference with the cross-linking process of the elastomeric matrix (majoritarian effect) and the hardening effect due to the high intrinsic modulus of TiO2 particles (minority effect).39 However, ATR analysis witnessed that TiO2 particles did not alter the polymerization yield of the silicone matrix, but the full conversion of the Si–H groups was always achieved (see Fig. 1a). Thus, most probably the softening effect is due to a reduction of the cross-linking density of the polymeric network caused by the presence of the inorganic fillers.
The mechanical tests demonstrate that the addition of TiO2 in PDMS does not stiffen the material but results in a softer composite material. Therefore, PDMS–TiO2 composites are good candidates for soft optical devices as they guarantee superior light-shielding properties without affecting the compliance of the waveguides or strain sensors.
Proof-of-concepts: transparent waveguide and strain sensor
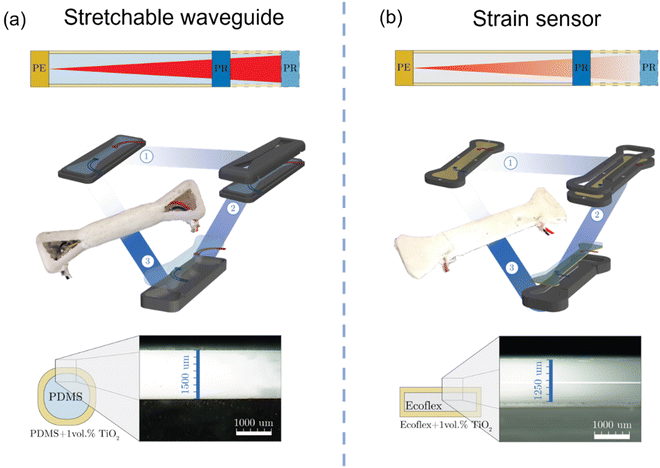
As proof-of-concepts, a transparent waveguide and a strain sensor were fabricated via a multi-step casting procedure. Regarding the reflective cladding material, UV-Vis-NIR spectroscopy proved that PDMS_1.0TiO2 200 μm-thick films were already effective in reflecting light in the NIR range. However, to facilitate the casting procedures and improve the tolerance to failure, the thickness was increased up to 1.25 mm. The increase of the cladding thickness is not expected to strongly harden the device as the composite material is softer than the pristine silicone (core material).The transparent PDMS waveguides were fabricated using a circular and rectangular cross-section and coated/uncoated. In principle, both shapes could be used in the future as optical connectors in soft robotics, and the aim was to evaluate the effect of the shape and the reflecting TiO2 material on the performance of the devices. To improve the deformability of the objects, PDMS 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was used as the core material. The strain sensor was designed using a rectangular cross-section, as this shape could in the future allow for the development of extended artificial skins.
1 was used as the core material. The strain sensor was designed using a rectangular cross-section, as this shape could in the future allow for the development of extended artificial skins.
Starting from the circular waveguide (Fig. 5a), the fabrication process consisted of the following steps: (i) half of the core of the waveguide was poured into a mold, and after curing, the photoemitter and the photoreceiver were glued on the top with Sil-Poxy 30 mm apart; (ii) the top part of the core mold was placed on top of the first one, and PDMS was poured to finally obtain the whole core of the waveguide; (iii) in order to coat the core with the TiO2 composite, a third mold was used. The coating mold had a rounded cavity in the central body to allow uniform coating on the bottom portion of the waveguide leading to a coating layer of 1.25 mm thickness. After the curing of the first layer, the waveguide was flipped, and the coating process was repeated for the remaining part. Finally, a uniform coating layer of about 1400 μm thickness was obtained at the central rounded section of the waveguide.
In the case of the rectangular strain sensor (Fig. 5b), the fabrication process consisted of the following: (i) the Ecoflex_1.0TiO2 coating was poured into a mold to fabricate the bottom coating and cured. Afterwards, the photoemitter and the photodetector were glued with Sil-Poxy on the bottom layer 20 mm apart; (ii) the core mold was secured on top of the previous one, and pristine Ecoflex-0010 resin was poured to obtain the core of the waveguide; (iii) after curing, the bottom layer and the core were demolded and placed into a third mold to fabricate the coating. The coating mold was 1.25 mm larger in all directions to allow the infiltration of Ecoflex_1.0TiO2 as the lateral and top coating layer. Optical microscopy images showed a uniform coating of 1250 μm thickness. A rectangular PDMS-based waveguide was also produced using the optical components 30 mm apart for comparison with the circular one. A sketch reporting the dimension of the fabricated devices is reported in Fig. S4 (ESI†).
| T = I1/I0 = e−Kλl | (1) |
| kλ = 0, T = I1/I0 = e(0·l) = 1 → I1 = I0 | (2) |
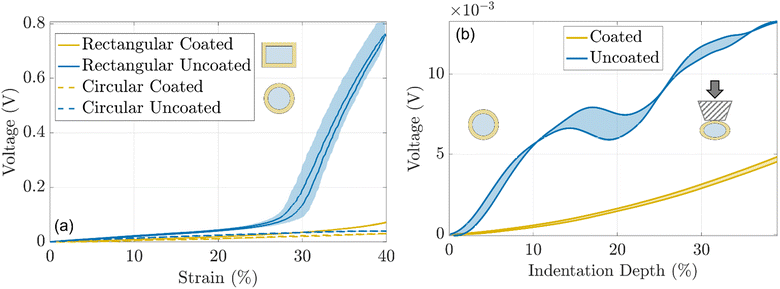
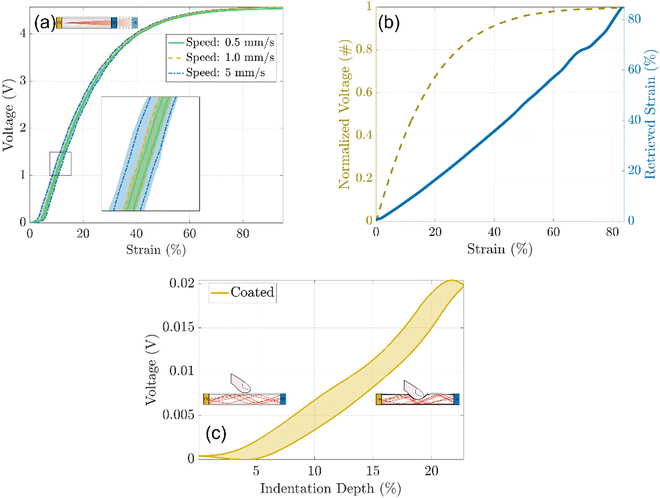
Fig. 6a shows the voltage variation of the photoreceiver when circular and rectangular, coated, and uncoated waveguides were stretched (5 cycles, 1 mm s−1 strain rate). The voltage read by the photoreceiver ranged from 0 V (full light) to 4.8 V (no light). The uncoated rectangular waveguide showed the poorest performance in guiding light as around 25% of strain an abrupt increase in the voltage was observed probably due to border effects. The corresponding rectangular coated waveguide showed improved performance. Yet, an increase in the optical loss was still detected at around 32% of strain. The circular waveguides had the lowest optical losses with very low variation in the optical signal up to 40% of strain. In both cases, the coated devices displayed superior performance proving the efficacy of the reflecting coatings. As rectangular waveguides showed the poorest performance upon stretching, the next characterizations were performed only on the circular ones.
The behavior of coated and uncoated circular waveguides upon indentation was investigated using ad hoc testing apparatus (5 cycles, 0.5 mm s−1). The coated waveguide showed 3 fold lower optical losses compared to the uncoated one, for up to 40% of indentation depth (Fig. 6b). This result can be explained considering that for the uncoated waveguide, the indenter comes in contact with the core of the device and optical loss occurs due to frustrated total internal reflection (fTIR). For the waveguide with a reflective coating, the optical wave is internally reflected within the core with no significant loss since the indenter does not come in contact with the core material. Video S1 (ESI†) shows the performances of the uncoated and coated circular waveguides for arbitrary indentation profiles.
Moreover, the effectiveness of the TiO2 coating for shielding environmental light was evaluated. The two waveguides were placed first in a black box and later under conventional laboratory conditions to measure the optical signal variance due to the presence of external light. The optical signal of the uncoated waveguide increased by about 22% witnessing that environmental light influenced the readout of the photoreceiver. Instead, the rise of the optical signal in the coated waveguide was only 0.6%, proving that the TiO2 layer effectively shields the environmental light.
Finally, the two circular waveguides were qualitatively tested to evaluate their response by repeated manual deformation. Video S1 (ESI†) shows the different performances of coated and uncoated waveguides when they were indented, bent, and folded. The coated waveguide showed superior tolerance to indentation and bending showing an overall optical loss five times lower than the corresponding uncoated waveguide. This demonstrated the effectiveness of the TiO2 coating in limiting the optical loss for different mechanical interactions by promoting internal light reflection.
| Retrieved strain (%) = −14.69 × ln(1 − Vnorm) | (3) |
With this transformation, the characteristic curve showed a linear trend between 0 and 90% of the strain with sensitivity equal to 1/14.96 = 0.068, and an average resolution close to 1% which corresponds approximately to 100 μm.
As for the waveguides, the response of the optical strain sensor was evaluated upon indentation, bending, or folding (Video S2, ESI†). Owing to the reflective coating used as a cladding material, the optical sensor was slightly affected by the induced mechanical stresses. When the strain sensor was indented, the optical loss was two orders of magnitude lower than similar deformations at elongation (Fig. 7c). This proved the selectivity to a specific mechanical stimulus, as the developed optical sensor was mainly sensitive to stretching, while no important variations in the optical output were detected for compression or bending.
Finally, as the stretchable sensor is composed of a highly compliant material (Ecoflex-0010) it is expected to not physically burden the soft robot but easily follow its deformations.
The application of the reflective coating based on TiO2 particles allowed to reflect internally the light when the device was bent or indented without any significant optical loss. As the reflective properties of the coating are only ascribable to the presence of titania particles, in principle, our approach can be easily implemented in other elastomeric matrices improving the performances of other soft optical devices.
Conclusions
In this work, a straightforward and inexpensive method to develop highly reflective coatings is proposed, for developing soft optical components (like waveguides also used as sensors), by adding TiO2 particles in elastomeric matrices. Controlling the filler load and film thickness, the shielding abilities of the composite films are predicted for every wavelength belonging to the visible and near infra-red region of the electromagnetic spectrum. Moreover, the addition of the ceramic particles does not lead to stiffening of the material but rather to softening, making the developed coatings good candidates as cladding materials in stretchable waveguides and optical sensors. As a proof of concept, a PDMS-based waveguide and an Ecoflex-based optical sensor coated with the shielding coatings are demonstrated. They both show superior resistance to external mechanical stimuli such as bending, folding, and indentation, thanks to the internal reflection of light within the devices.The possibility to produce stretchable optical sensors in a compliant material such as Ecoflex0010 is promising for soft robotics, since innovative sensorized skins could be developed in the near future without constraining the deformations of a soft robot. Finally, it is remarkable that as the reflective properties of the coatings are only linked to the presence of TiO2 particles, it is possible to develop different elastomeric reflective composites, which can pave the way for new designs of optical sensors exploiting light reflection rather than their absorption.
Author contributions
S. L., M. L. P., and L. B. conceptualized research. S. L. and M. L. P. designed methodology, performed experiments, and analysed the data. S. L., M. L. and L. B. discussed the results and wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the European Union's Horizon 2020 Program under Grant 863212 PROBOSCIS. The authors would like to acknowledge Gabriele La Rosa for the characterization performed by spectrophotometry with integrating sphere.Notes and references
- L. Beccai, C. Lucarotti, M. Totaro and M. Taghavi, Soft Robotics Mechanosensing, ed. C. Laschi, J. Rossiter, F. Iida, M. Cianchetti and L. Margheri, Springer International Publishing, Cham, 2017, pp. 11–21 Search PubMed.
- J. Guo, C. Yang, Q. Dai and L. Kong, Sensors, 2019, 19, 3771 CrossRef CAS.
- H. Wang, M. Totaro and L. Beccai, Adv. Sci., 2018, 5, 1800541 CrossRef.
- M. Lo Preti, M. Totaro, E. Falotico and L. Beccai, Electronic Skin: Sensors and Systems, River Publishers, 2020, pp. 73–100 Search PubMed.
- D. Chen and Q. Pei, Chem. Rev., 2017, 117, 11239–11268 CrossRef CAS PubMed.
- H. Y. Tam, C.-F. J. Pun, G. Zhou, X. Cheng and M. L. V. Tse, Opt. Fiber Technol., 2010, 16, 357–366 CrossRef CAS.
- I. P. Johnson, W. Yuan, A. Stefani, K. Nielsen, H. K. Rasmussen, L. Khan, D. J. Webb, K. Kalli and O. Bang, Electron. Lett., 2011, 47, 271–272 CrossRef CAS.
- M. Umar, K. Min and S. Kim, APL Photonics, 2019, 4, 120901 CrossRef CAS.
- Z. Liu, Z. F. Zhang, H.-Y. Tam and X. Tao, Photonics, Multidisciplinary Digital Publishing Institute, 2019, vol. 6, p. 48 Search PubMed.
- C. Wu, X. Liu and Y. Ying, ACS Sens., 2021, 6, 1446–1460 CrossRef CAS PubMed.
- I. Martincek, D. Pudis and M. Chalupova, IEEE Photonics Technol. Lett., 2014, 26, 1446–1449 Search PubMed.
- J. Missinne, S. Kalathimekkad, B. Van Hoe, E. Bosman, J. Vanfleteren and G. Van Steenberge, Opt. Express, 2014, 22, 4168–4179 CrossRef CAS PubMed.
- J. Guo, B. Zhou, C. Yang, Q. Dai and L. Kong, Adv. Funct. Mater., 2019, 29, 1902898 CrossRef.
- C. K. Harnett, H. Zhao and R. F. Shepherd, Adv. Mater. Technol., 2017, 2, 1700087 CrossRef.
- H. Zhao, K. O’Brien, S. Li and R. F. Shephered, Sci. Robot., 2016, 1, eaai7529 CrossRef PubMed.
- J. A. Barreiros, A. Xu, S. Pugach, N. Iyengar, G. Troxell, A. Cornwell, S. Hong, B. Selman and R. F. Shephered, Sci. Robot., 2022, 7, eabi6745 CrossRef PubMed.
- H. Bai, S. Li, J. Barreiros, T. Y. Tu, C. R. Pollock and R. F. Shephered, Science, 2020, 370, 848–852 CrossRef CAS PubMed.
- A. Leber, B. Cholst, J. Sandt, N. Vogel and M. Kolle, Adv. Funct. Mater., 2019, 29, 1802629 CrossRef.
- J. Guo, M. Niu and C. Yang, Optica, 2017, 4, 1285–1288 CrossRef.
- A. Heiden, D. Preninger, L. Lehner, M. Baumgarten, M. Drack, E. Woritzka, D. Schiller, R. Gerstmayr, F. Hartmann and M. Kaltenbrunner, Sci. Robot., 2022, 7, eabk2119 CrossRef CAS PubMed.
- V. Fang, J. V. Kennedy, J. Futter and J. Manning, GNS Science Report, 2013 Search PubMed.
- I. Roppolo, N. Shahzad, A. Sacco, E. Tresso and M. Sangermano, Prog. Org. Coat., 2014, 77, 458–462 CrossRef CAS.
- P. Jeevanandam, R. S. Mulukutla, M. Phillips, S. Chaudhuri, L. E. Erickson and K. J. Klabunde, J. Phys. Chem. C, 2007, 111, 1912–1918 CrossRef CAS.
- J. Zhang, C. Zhu, J. Lv, W. Zhang and J. Feng, ACS Appl. Mater. Interfaces, 2018, 10, 40219–40227 CrossRef CAS PubMed.
- S. Soumya, A. P. Mohamed, L. Paul, K. Mohan and S. Ananthakumar, Sol. Energy Mater. Sol. Cells, 2014, 125, 102–112 CrossRef CAS.
- B. Xiang, X. Yin and J. Zhang, Compos. Sci. Technol., 2017, 145, 149–156 CrossRef CAS.
- L. Yuan, X. Weng, M. Zhou, Q. Zhang and L. Deng, Nanoscale Res. Lett., 2017, 12, 597 CrossRef PubMed.
- F. H. Alkallas, K. M. Elshokrofy and S. A. Mansour, Nanomater. Nanotechnol., 2019, 9, 1–7 Search PubMed.
- H. Tang, H. Berger, P. E. Schmid and F. Lévy, Solid State Commun., 1994, 92, 267–271 CrossRef CAS.
- G. Riccucci, L. Pezzana, S. Lantean, A. Tori, S. Spriano and M. Sangermano, Appl. Sci., 2021, 11, 5663 CrossRef CAS.
- E. C. Murphy, J. H. Dumont, C. H. Park, G. Kestell, K.-S. Lee and A. Labouriau, J. Appl. Polym. Sci., 2020, 137, 48530 CrossRef CAS.
- J. González-Rivera, R. Iglio, G. Barillaro, C. Duce and M. R. Tinè, Polymer, 2018, 10, 616 Search PubMed.
- G. Ouyang, K. Wang and X. Y. Chen, J. Micromech. Microeng., 2012, 22, 74002 CrossRef.
- C. Markos, K. Vlachos and G. Kakarantzas, Opt. Mater. Express, 2012, 2, 929–941 CrossRef CAS.
- D. K. Cai, A. Neyer, R. Kuckuk and H. M. Heise, Opt. Mater., 2008, 30, 1157–1161 CrossRef CAS.
- F. Schneider, J. Draheim, R. Kamberger and U. Wallrabe, Sens. Actuators, A, 2009, 151, 95–99 CrossRef CAS.
- K. Hornik, M. Stinchcombe and H. White, Neural Networks, 1989, 2, 359–366 CrossRef.
- K. Hornik, Neural Networks, 1991, 4, 251–257 CrossRef.
- D. T. Vaimakis-Tsogkas, D. G. Bekas, T. Giannakopoulou, N. Todorova, A. S. Paipetis and N.-M. Barkoula, Mater. Chem. Phys., 2019, 223, 366–373 CrossRef CAS.
- M. Razzaghi Kashani, S. Javadi and N. Gharavi, Smart Mater. Struct., 2010, 19, 35019 CrossRef.
- F. Carpi and D. D. Rossi, IEEE Trans. Dielectr. Electr. Insul., 2005, 12, 835–843 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00869f |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |