Bond strength regime dictates stress relaxation behavior

Abstract

Reconfigurable polymer networks are gaining interest for their potential applications as self-healing, recyclable, and stimuli-responsive smart materials. Relating the bond strength of dynamic interactions to material properties including stress relaxation time and modulus is crucial for smart material design. In this work, in situ crosslinked transition metal–terpyridine reconfigurable networks were utilized to modulate the characteristic network stress relaxation time, τ_R. The use of stress relaxation experiments rather than oscillatory frequency sweeps allowed for the measurement of network bond dynamics across a wider dynamic range than has been previously reported. The stress relaxation time was shown to be tunable by metal center, counterion, and crosslink density. Remarkably, the network crosslinked with covalent-like ruthenium chloride–terpyridine interaction, while having a longer τ_R, was qualitatively similar to the other metal–ligand networks. Furthermore, the relaxation time was independent of crosslink density in strongly bonded networks, allowing for independent tunability of modulus and τ_R. In contrast, increasing crosslink density reduced τ_R in networks crosslinked with weaker interactions.

---

Introduction

Reconfigurable polymer networks are interconnected by transient bonds that can break and reform in response to stimuli. These transient bonds can be composed of either dynamic covalent bonds such as those found in esters^1–3 and disulfides^4,5 or supramolecular bonds such as hydrogen-bonding,^6,7 π–π stacking,^8,9 ionic,¹⁰ and transition metal–ligand.^11,12 The bond-breaking and reforming ability of these interactions make them great candidates for self-healing, reconfigurable, and stress dissipating materials. The self-healing and stress relaxation responses are controlled by the bond-exchange time that is generally related to the bond strength. Elucidating the relationship between the bond exchange and stress relaxation behavior is critical for smart reconfigurable polymer network design.

Transition metal–ligand based networks are of great interest due to simple tunability of the bond strength. Specifically, terpyridine–metal interactions are an excellent choice since they provide a wide range of binding constants thus allowing for the control of network relaxation behavior with respect to bond exchange time.^13–18 The binding strength can be further tuned by the choice of solvent and counterion. Where ruthenium–terpyridine interactions are considered to be covalent-like,¹² binding equilibrium constants, K, of manganese–terpyridine interactions differ by nine orders of magnitude depending on solvent choice.¹⁸ More recently, a variety of polymer backbones with terpyridine functionalization either at the side-chain^12,19,20 or the end-group^18,21,22 have been studied to understand relaxation behavior, making the transition metal–terpyridine systems an excellent model system to study reconfigurable networks.

Terpyridine–metal networks are commonly characterized using oscillatory shear frequency sweeps to elucidate the network bond dynamics. The inverse of the crossover frequency where the storage and loss moduli are equal provides the characteristic network stress relaxation time, τ_R. However, characterization of long timescale relaxations has been limited the absence of a crossover frequency in the typical rheometer-accessible range for many systems.^18,23–25 For example, the cobalt–terpyridine interaction, did not show a crossover frequency despite its relatively weak binding strength.¹⁸

Herein, we report the first example of in situ crosslinked metal–ligand networks that allows for stoichiometric metal : ligand ratio, homogenous mixing before polymerization, and efficiency in changing network parameters such as molecular weight and crosslink density. To the best of our knowledge, for the first time we utilize indentation tests for stress relaxation experiments to study stress relaxation time of reconfigurable metal–ligand networks. Stress relaxation experiments enabled measurements of τ_R even for ruthenium–terpyridine networks, which fall well outside of the accessible range for conventional frequency sweeps. Changing the metal ion (Mn-, Zn-, Co-, Ni-, Fe-, Ru-) and counterion (Cl⁻, CH₃COO⁻) species varied τ_R in a consistent manner with reported bond exchange times.^13,14,18 For most systems, τ_R was found to be independent of crosslink density. By extending Rubinstein, Leibler, and coworkers’ telechelic theory on sticker concentration, the independence of τ_R on crosslink density was explained for systems with strong binding strength.²⁶ This model was further tested to predict that zinc acetate–terpyridine networks, with an even weaker bond strength, should exist in the so-called “intermediate bond strength regime”. This means that stress relaxation time should decrease with increasing crosslink density, which was confirmed experimentally herein. These findings also show a unique property of in situ crosslinked reconfigurable networks where stress relaxation time can be kept constant while increasing modulus by increasing crosslink density.

Results

Synthetic design

Metal–ligand networks are commonly made by post-addition of a metal salt into a polymer solution.^{12,18–20,22,27,28} This post-addition of metal salts often leads to intramolecular crosslinking, inhomogeneous network formation, and long waiting times for network equilibration. This method may also lead to a fraction of open ligands in the system at stoichiometric ratios.^20,24 To address this challenge, we designed an in situ crosslinking platform in which the terpyridine ligands are saturated with metal centers and reactants are well-mixed at the beginning of polymerization reactions. Instead of adding the metal salt into the polymer solution, a crosslinker that consists of two terpyridines complexed with a metal center and polymerizable norbornene end groups was designed (Fig. 1). This crosslinker was copolymerized with norbornene via ring-opening metathesis polymerization (ROMP) in chloroform:methanol mixture. ROMP was chosen as it was shown to have high functional group tolerance and can successfully polymerize cationic monomers in short reaction times.^29–31 Grubbs’ second generation catalyst (G2) was used due to higher stability; however, G2 can lead to a broader molecular weight distribution and in situ crosslinking prevents molecular weight characterization.³² This system allows for tunability of the network crosslink density by simply changing the crosslinker to monomer ratio. Additionally, it ensures that all ligands are saturated with metal centers before polymerization (Fig. 1). All metal–ligand dynamic networks were characterized as synthesized without further swelling or drying.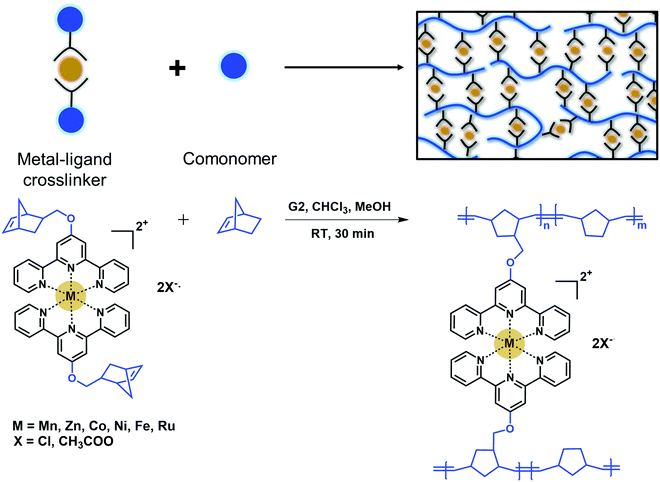

Fig. 1 Schematic representation and the synthesis of dynamic metal–ligand networks via in situ crosslinking.

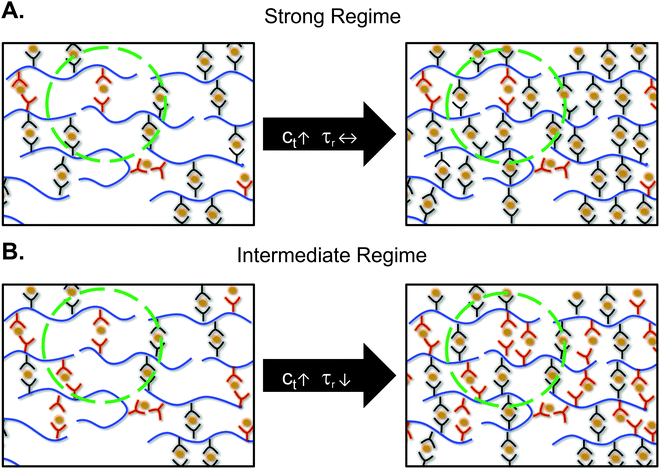
The mechanical properties and stress relaxation behavior of metal–ligand networks can be tuned by changing the metal center, solvent, counterion, polymer volume fraction, and crosslink density. In order to relate the bond lifetime to experimental measurements, a theory of bond lifetime renormalization was developed.^26,33,34 This renormalization results from the fact that a sticker has to bind to the same partner many times before finding another open sticker to experience a macroscopic relaxation. Therefore, the experimentally measured stress-relaxation times are prolonged compared to the bond lifetimes.^7,26 Rubinstein, Leibler, and coworkers’ work established bond strength regimes depending on the number of open stickers in the pervaded volume. In the intermediate regime there are many open stickers in the pervaded volume for an open sticker to recombine with a new partner. In contrast, in the high bond strength regime, the open stickers are far apart and cannot find each other.²⁶ These bond strength regimes are defined as:

k_BT ln N < ε < 2k_BT ln N (Intermediate regime)

2k_BT ln N < ε (Strong regime)

where k_B is the Boltzmann constant, T is temperature, N is the number of monomers between stickers and ε is the bond energy. This theory also suggests that the macroscopic relaxation will be dictated by crosslink density only when the interaction strength is in the intermediate regime.

Transition metals are well-documented as interacting strongly with terpyridine.^{13–18,35,36} We designed our systems to span both the intermediate and strong regimes based on reported interaction strengths.¹³ Networks were synthesized with various metal salts and varying crosslink densities of 2.5, 5, and 10 mol%. The nomenclature for networks is the metal salt used in bold where the superscript denotes the crosslink density. For example, ^2.5%FeCl₂ denotes a network with 2.5 mol% bis(norbornene terpyridine) iron chloride crosslinks with respect to the total monomer amount. Notations without superscripts refer to the networks with 10 mol% crosslinks. The total monomer-to-initiator ratio was kept constant at 150 for all crosslink densities, whereas molecular weight between crosslinks, i.e., monomer-to-crosslinker ratio, was varied. The τ_R is predicted to be independent of the crosslink density for strongly bonded networks; namely, RuCl₂, FeCl₂, NiCl₂, CoCl₂, ZnCl₂, and CoAc₂ based on interaction strength values reported in literature. In contrast, the weaker binding ZnAc₂ and MnAc₂ networks are predicted to have intermediate regime behavior, allowing crosslink density-dependent τ_Rs in these networks.

Effect of metal centers

We performed stress relaxation experiments via flat-punch indentation tests that have been utilized to characterize soft networks and tissues in the literature.^37–39 Stress relaxation curves were collected via flat-punch indentation at predefined force values. A poly(ethylene glycol) thiol–ene network was also included in the study as a covalent control. All metal–ligand dynamic networks were characterized as is without further swelling or drying. Additional characterization by oscillatory shear frequency sweeps expectedly showed no crossover frequency in RuCl₂ and FeCl₂ networks, further supporting utilization of stress relaxation experiments as a better choice to study reconfigurable networks (Fig. S1, ESI†).

The complete stress relaxation curves for RuCl₂, NiCl₂, and ZnCl₂ are shown in Fig. 2A, where the indenter radius is 0.36 mm and loading force is ∼10 mN. Metal–ligand networks were grouped into three distinct timescales, where MnCl₂ and ZnCl₂ were significantly faster while the RuCl₂ network was the slowest. CoCl₂, FeCl₂, and NiCl₂ showed similar intermediate stress relaxation time. Hence, only one network from each set (RuCl₂, NiCl₂, ZnCl₂) was shown in the main figure for clarity, whereas the inset shows early stress-relaxation (0–50 s) for all networks including the covalent control. Complete stress-relaxation curves for all networks can be found in Fig. S2 and S3 (ESI†). The stress relaxation followed the order of RuCl₂ > FeCl₂ > NiCl₂ > CoCl₂> ZnCl₂ > MnCl₂. This trend is well-explained by metal–terpyridine bond exchange data and complex stability.^9,31 Overall, stress relaxation experiments were sensitive to differences in networks crosslinked with various metal centers.

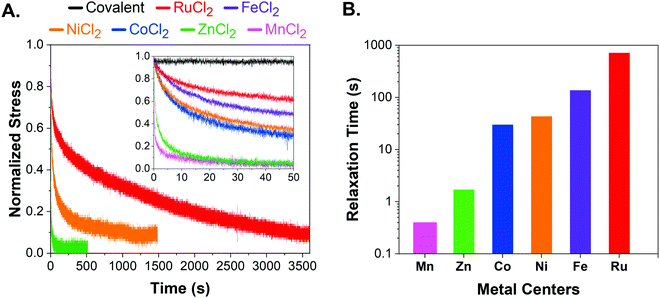Fig. 2 (A) Stress-relaxation curves of RuCl₂ (red), FeCl₂ (purple), NiCl₂ (orange), CoCl₂ (blue), ZnCl₂ (green), MnCl₂ (pink), and covalent network (black). Only RuCl₂, NiCl₂, and ZnCl₂ are shown in the main graph for clarity. The inset shows the short time stress-relaxation behavior (0–50 s) for all chloride networks. The stress was normalized by the maximum value in that dataset. The data was shifted to reach maximum force at zero seconds. The complete curves for each system can be found in Fig. S2 (ESI†). (B) Stress-relaxation times of RuCl₂ (red), FeCl₂ (purple), NiCl₂ (orange), CoCl₂ (blue), ZnCl₂ (green), MnCl₂ (pink) were calculated utilizing the 1/e method.

The stress relaxation time was calculated according to the 1/e method where 63% stress decay gives τ_R for a network system that follows single exponential decay. (Fig. 2B).⁴⁰ Although it was proposed that a more complex relaxation process might be involved,⁴¹ many metal–ligand networks have been shown to follow Arrhenius and single exponential decay behavior.^{18,23,28,42,43} Therefore, utilizing 1/e method and single exponential decay remains the most common method to analyze relaxation in metal–ligand networks. Furthermore, it allows for uniform treatment of all studied networks and provides comparable relaxation timescales.

Expectedly, the high binding strength of the ruthenium–terpyridine bond led to the slowest relaxation among metal–ligand networks. Although it is accepted that the ruthenium–terpyridine bond is as strong as a covalent bond, there are no rheological studies that provide a characteristic relaxation time due to its high complex stability.^12,35 To our knowledge, the only study that included ruthenium–terpyridine is a qualitative study of terpyridine–metal complexes utilizing MALDI-TOF by Meier et al.³¹ Despite the strong ruthenium–terpyridine interaction, the RuCl₂ network exhibited up to 95% stress relaxation over an hour, which is significantly different than the covalent network. For the first time, stress-relaxation tests show the dynamic nature of ruthenium–terpyridine interactions when compared to a covalent network.

Poroelasticity and ion clustering were studied as possible contributors for stress-relaxation behavior in reconfigurable networks. Poroelastic relaxation was tested by changing indenter radius as discussed in earlier studies (Fig. S5 and S6, ESI†).^38,44,45 Wide angle X-ray scattering (WAXS) was performed to probe ion clustering, where diffractograms did not show any ion clustering (Fig. S7, ESI†). Analyzing these results concluded that neither poroelasticity nor ion clustering had a significant role in stress relaxation. Additionally, quenching the Grubbs’ second generation catalyst with ethyl vinyl ether was shown to have none to very little effect on stress relaxation curves (Fig. S8, ESI†).

Effect of counterion

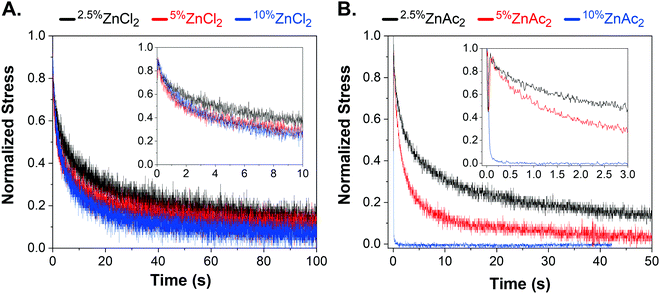
The species of counterion is known to affect the bond lifetime of metal–ligand interactions by changes in nucleophilicity and solubility.^28,46 In order to access intermediate bond strength regimes and obtain faster relaxation times, acetate counterions for Co-, Zn-, and Mn-networks were studied. Both CoAc₂ and ZnAc₂ networks showed faster stress relaxation compared to their chloride counterparts (Fig. S9A and B, ESI†). Interestingly, the MnAc₂ sample was a viscous liquid that could not store elastic strain energy in indentation tests. These results agree with decreased relaxation time from chloride to acetate in Co-, Zn-, and Mn-networks. This increase in bond exchange can be attributed to better solvation of acetate anions in organic solvents, i.e. methanol–chloroform mixture and higher ability of acetate ions to act as a ligand.²⁸

Effect of crosslink density

Networks with 2.5 and 5 mol% crosslink densities were prepared by changing monomer to crosslink ratio while keeping the degree of polymerization the same. The change in crosslink density did not affect the stress-relaxation time for networks in the strong regime, namely RuCl₂ and CoCl₂ (Fig. S10, ESI†). Even ZnCl₂, one of the fastest networks in the chloride counterion series, was almost insensitive to changes in crosslink density, indicating that the zinc chloride–terpyridine interaction belongs to the strong binding regime (Fig. 3A). Furthermore, the loading moduli of CoCl₂, ZnCl₂, and MnCl₂ increased with increasing crosslink density, while their stress relaxation times remained the same (Table S2, ESI†). For example, increasing the crosslink density from 2.5 to 10 mol% for MnCl₂ network, increased the elastic modulus from 7 to 32 kPa. Our synthetic platform provides a method to modulate the effective elastic modulus of a network independent of its stress relaxation time. In contrast, the fastest relaxing network ZnAc₂ exhibited crosslink density-dependent τ_R. The network with highest crosslink density, ^10%ZnAc₂, was the fastest relaxing network followed by ^5%ZnAc₂ and ^2.5%ZnAc₂ (Fig. 3B).

Fig. 3 (A) Stress-relaxation curves of ^2.5%ZnCl₂ (black), ^5%ZnCl₂ (red), and ^10%ZnCl₂ (blue) that correspond to networks crosslinked with 2.5, 5, and 10 mol% bis(norbornene terpyridine) zinc chloride, respectively. Inset shows the early relaxation curves between 0–10 seconds for ^2.5%ZnCl₂, ^5%ZnCl₂, and ^10%ZnCl₂. (B) Stress-relaxation curves of ^2.5%ZnAc₂ (black), ^5%ZnAc₂ (red), ^10%ZnAc₂ (blue) that correspond to networks crosslinked with 2.5, 5, and 10 mol% bis(norbornene terpyridine) zinc acetate, respectively. Inset shows the early relaxation behavior between 0–3 seconds for ^2.5%ZnAc₂, ^5%ZnAc₂, and ^10%ZnAc₂. Stress relaxation data was collected by flat-punch indentation with an indenter radius of 0.36 mm and a preset load of ∼10 mN. The data was shifted to reach maximum force at zero seconds. The stress was normalized by the maximum value in that dataset.

Discussion

Bond strength regimes

Rubinstein, Leibler, and coworkers developed a theory stating the crosslink density affected the macroscopic network relaxation only in the intermediate bond strength regime.²⁶ This theory agrees well with our observations: increasing crosslink density led to a faster stress relaxation time only for the fastest network in this study, ZnAc₂. The strong and intermediate regimes are defined by the probability of finding an open ligand in the exploration volume of a ligand. In the intermediate regime, there are multiple open ligands present in the volume for a ligand to successfully partner exchange, whereas in the strong regime on average there is less than one open ligand present (Fig. 4). The bond strength regimes for our networks have been calculated by defining N as the number of monomers between crosslinkers, N_c. The distance between two crosslinkers was calculated to be ∼5 nm at 10 mol% crosslinks (Section S7 and Fig. S11, ESI†). As an example, the root mean squared distance between two open stickers, Δr_open, was calculated as 103 nm for CoCl₂ using the equilibrium constant of cobalt–terpyridine interaction in water (Section S8 and Table S1, ESI†).¹³ZnAc₂ was shown to be weaker than ZnCl₂ and even the equilibrium constant of zinc–terpyridine interaction was inaccessible.¹³ Therefore, we treated the lowest measurable K (10⁶ M⁻¹) as the upper limit for zinc acetate–terpyridine interaction, giving the upper limit of Δr_open as 24 nm. In other words, the closest distance between two open ligands in the CoCl₂ network is at least four times higher than that of the ZnAc₂ network.

Fig. 4 Schematic representations of metal–ligand networks with bond strengths in the (A) strong and (B) intermediate regime at different crosslink densities (c_t). Red ligands denote open stickers in the system, whereas black ligands represent closed stickers. The dashed circle shows the pervaded volume of one open sticker. Counterions are not shown for clarity. In the strong regime, only one open sticker is present in the pervaded volume regardless of crosslink density. In the intermediate regime, increasing the crosslinker density leads to multiple open stickers in the pervaded volume, raising the probability to find another open sticker to exchange. As a result, higher crosslink densities lead to faster relaxation only in the intermediate regime.

In the strong regime, most of the ligands stay closed for long periods of time. The time that stickers stay bonded dominates the stress relaxation time, rather than the time spent searching for an open sticker. Therefore, τ_R stays independent of crosslink density, and the bond lifetime dictates the relaxation time. In contrast, in the intermediate regime, the bond lifetime is much faster making searching for another sticker the rate limiting step. In this case, as the number of crosslinks increases, the probability of finding an open ligand should increase. As a result, increasing the number of crosslinks resulted in faster relaxation only for ZnAc₂.

Of note, Tibbitt and coworkers utilized boronic ester-based dynamic covalent networks to link molecular parameters to the viscoelastic properties. The stress-relaxation time was modulated by pH-dependent changes in activation energy; however, 4-fold increase in sticker concentration demonstrated no change in the τ_R of these networks while increasing the plateau modulus from 3 kPa to 26 kPa (Fig. S12, ESI†).¹ Considering the network parameters and strength of boronic esters, their system is expected to be in the strong bond strength regime, and thus demonstrating crosslink density-independent τ_R behavior (Section S8, ESI†).⁴⁷ This observation further demonstrates the applicability of bond strength regime theory on various reconfigurable networks.

Conclusion

There are two main findings from this work. First, the use of stress relaxation tests allows for the τ_R of ruthenium chloride–terpyridine networks to be measured for the first time. This finding confirms that while ruthenium–terpyridine was argued to be as strong as a covalent bond, and is the strongest metal–ligand system in this study, it is still dynamic and behaves qualitatively the same as any other studied metal center. Second, Rubinstein, Leibler, and coworkers’ model for telechelic, reconfigurable networks was extended to these side-chain linked systems below entanglement concentration capturing the two bond strength regimes. The strong bond strength regime allows for the crosslink density- and number of monomers between crosslinks (N_c)-independent τ_R. Given this, it is possible to design reconfigurable networks with the same stress relaxation times, but various moduli and presumably other properties such as gel fracture energy.⁴⁸ These findings inform reconfigurable network design by elucidating the relation between molecular parameters and material properties.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors acknowledge funding support from the Office of Naval Research (ONR grant number N00014-17-1-2056). The authors would like to thank Mrs. Heather S. C. Hamilton and Dr. Huyen Vu for their assistance in preparing the manuscript. The authors would also like to thank Dr. Michael T. Kwasny for his guidance in the synthesis of reconfigurable networks.

References

1. B. Marco-Dufort, R. Iten and M. W. Tibbitt, J. Am. Chem. Soc., 2020, 142, 15371–15385.
2. J.-C. Lai, J.-F. Mei, X.-Y. Jia, C.-H. Li, X.-Z. You and Z. Bao, Adv. Mater., 2016, 28, 8277–8282.
3. W. A. Ogden and Z. Guan, J. Am. Chem. Soc., 2018, 140, 6217–6220.
4. B. D. Fairbanks, S. P. Singh, C. N. Bowman and K. S. Anseth, Macromolecules, 2011, 44, 2444–2450.
5. Y. Amamoto, H. Otsuka, A. Takahara and K. Matyjaszewski, Adv. Mater., 2012, 24, 3975–3980.
6. P. Cordier, F. Tournilhac, C. Soulié-Ziakovic and L. Leibler, Nature, 2008, 451, 977–980.
7. B. J. Gold, C. H. Hövelmann, N. Lühmann, N. K. Székely, W. Pyckhout-Hintzen, A. Wischnewski and D. Richter, ACS Macro Lett., 2017, 6, 73–77.
8. H. Shao and J. R. Parquette, Chem. Commun., 2010, 46, 4285.
9. S. Burattini, B. W. Greenland, D. H. Merino, W. Weng, J. Seppala, H. M. Colquhoun, W. Hayes, M. E. Mackay, I. W. Hamley and S. J. Rowan, J. Am. Chem. Soc., 2010, 132, 12051–12058.
10. C. F. J. Faul and M. Antonietti, Adv. Mater., 2003, 15, 673–683.
11. K. J. Calzia and G. N. Tew, Macromolecules, 2002, 35, 6090–6093.
12. S. Bode, L. Zedler, F. H. Schacher, B. Dietzek, M. Schmitt, J. Popp, M. D. Hager and U. S. Schubert, Adv. Mater., 2013, 25, 1634–1638.
13. R. H. Holyer, C. D. Hubbard, S. F. A. Kettle and R. G. Wilkins, Inorg. Chem., 1965, 224, 622–625.
14. R. Hogg and R. G. Wilkins, J. Chem. Soc., 1962, 2, 341–350.
15. K.-Y. Kim and G. H. Nancollas, J. Phys. Chem., 1977, 81, 948–952.
16. U. S. Schubert, C. Eschbaumer and Q. An, J. Inclusion Phenom. Macrocyclic Chem., 1999, 35, 35–43.
17. I. M. Henderson and R. C. Hayward, J. Mater. Chem., 2012, 22, 21366–21369.
18. T. Rossow and S. Seiffert, Polym. Chem., 2014, 5, 3018–3029.
19. T. Rossow, S. Hackelbusch, P. Van Assenbergh and S. Seiffert, Polym. Chem., 2013, 4, 2515–2527.
20. J. Brassinne, F. D. Jochum, C. A. Fustin and J. F. Gohy, Int. J. Mol. Sci., 2015, 16, 990–1007.
21. S. Hackelbusch, T. Rossow, P. van Assenbergh and S. Seiffert, Macromolecules, 2013, 46, 6273–6286.
22. F. Zhuge, J. Brassinne, C. A. Fustin, E. Van Ruymbeke and J. F. Gohy, Macromolecules, 2017, 50, 5165–5175.
23. T. Rossow, A. Habicht and S. Seiffert, Macromolecules, 2014, 47, 6473–6482.
24. J. Brassinne, A. Cadix, J. Wilson and E. van Ruymbeke, J. Rheol., 2017, 61, 1123–1134.
25. Y. Wang, Y. Gu, E. G. Keeler, J. V. Park, R. G. Griffin and J. A. Johnson, Angew. Chem., Int. Ed., 2017, 56, 188–192.
26. E. B. Stukalin, L. H. Cai, N. A. Kumar, L. Leibler and M. Rubinstein, Macromolecules, 2013, 46, 7525–7541.
27. D. E. Fullenkamp, L. He, D. G. Barrett, W. R. Burghardt and P. B. Messersmith, Macromolecules, 2013, 46, 1167–1174.
28. S. Bode, M. Enke, R. K. Bose, F. H. Schacher, S. J. Garcia, S. Van Der Zwaag, M. D. Hager and U. S. Schubert, J. Mater. Chem., 2015, 22145–22153.
29. T. J. Clark, N. J. Robertson, H. A. K. Iv, E. B. Lobkovsky, P. F. Mutolo, H. D. Abruña and G. W. Coates, J. Am. Chem. Soc., 2009, 131, 12888–12889.
30. Y. Zha, M. L. Disabb-Miller, Z. D. Johnson, M. A. Hickner and G. N. Tew, J. Am. Chem. Soc., 2012, 4493–4496.
31. L. Zhu, T. J. Zimudzi, N. Li, J. Pan, B. Lina and M. A. Hickner, Polym. Chem., 2016, 7, 2464–2475.
32. C. Slugovc, Macromol. Rapid Commun., 2004, 25, 1283–1297.
33. A. N. Semenov and M. Rubinstein, Macromolecules, 1998, 31, 1373–1385.
34. A. N. Semenov and M. Rubinstein, Macromolecules, 2002, 35, 4821–4837.
35. H. Hofmeier and U. S. Schubert, Chem. Soc. Rev., 2004, 33, 373–399.
36. I. M. Henderson and R. C. Hayward, Polym. Chem., 2012, 3, 1221–1230.
37. X. Wang, J. A. Schoen and M. E. Rentschler, J. Mech. Behav. Biomed. Mater., 2013, 20, 126–136.
38. Z. I. Kalcioglu, R. Mahmoodian, Y. Hu, Z. Suo and K. J. Van Vliet, Soft Matter, 2012, 8, 3393–3398.
39. R. M. Delaine-Smith, S. Burney, F. R. Balkwill and M. M. Knight, J. Mech. Behav. Biomed. Mater., 2016, 60, 401–415.
40. L. E. Porath and C. M. Evans, Macromolecules, 2021, 54, 4782–4791.
41. S. Tang, A. Habicht, S. Li, S. Seiffert and B. D. Olsen, Macromolecules, 2016, 49, 5599–5608.
42. F. Zhuge, L. G. D. Hawke, C.-A. Fustin, J.-F. Gohy and E. van Ruymbeke, J. Rheol., 2017, 61, 1245–1262.
43. J. P. Collin, I. M. Dixon, J. P. Sauvage, J. A. G. Williams, F. Barigelletti and L. Flamigni, J. Am. Chem. Soc., 1999, 121, 5009–5016.
44. Y. Hu, X. Zhao, J. J. Vlassak and Z. Suo, Appl. Phys. Lett., 2010, 96, 121904.
45. D. G. T. Strange, T. L. Fletcher, K. Tonsomboon, H. Brawn, X. Zhao and M. L. Oyen, Appl. Phys. Lett., 2013, 102, 031913.
46. J. Pignanelli, Z. Qian, X. Gu, M. J. Ahamed and S. Rondeau-Gagne, New J. Chem., 2020, 8977–8985.
47. B. Kang and J. A. Kalow, ACS Macro Lett., 2022, 11, 394–401.
48. C. W. Barney, Z. Ye, I. Sacligil, K. R. McLeod, H. Zhang, G. N. Tew, R. A. Riggleman and A. J. Crosby, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, 1–6.

---

Footnotes

† Electronic supplementary information (ESI) available: Materials, instrumentation, monomer and metal-ligand network synthesis, synthetic schemes, ¹H NMR, WAXS, further stress relaxation data, calculations and application of the theory discussed to other systems. See DOI: https://doi.org/10.1039/d2sm00499b

‡ Present address: Materials Research Laboratory, Department of Mechanical Engineering, and Department of Chemical Engineering, University of California, Santa Barbara, CA 93106, USA.

---