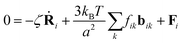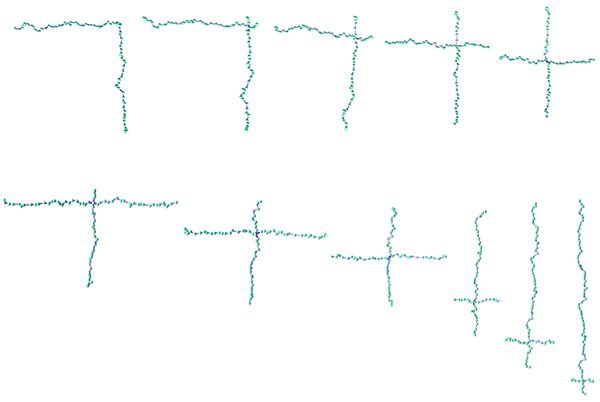Brownian simulations for tetra-gel-type phantom networks composed of prepolymers with bidisperse arm length†
Yuichi
Masubuchi
 *a,
Ryohei
Yamazaki
b,
Yuya
Doi
*a,
Ryohei
Yamazaki
b,
Yuya
Doi
 a,
Takashi
Uneyama
a,
Naoyuki
Sakumichi
a,
Takashi
Uneyama
a,
Naoyuki
Sakumichi
 c and
Takamasa
Sakai
c and
Takamasa
Sakai
 c
c
aDepartment of Materials Physics, Nagoya University, Nagoya 4648603, Japan. E-mail: mas@mp.pse.nagoya-u.ac.jp; Tel: +81-527892551
bDepartment of Engineering Physics, Nagoya University, Nagoya 4648603, Japan
cDepartment of Bioengineering, The University of Tokyo, Tokyo 1138654, Japan
First published on 27th May 2022
Abstract
We studied the effect of arm length contrast of prepolymers on the mechanical properties of tetra-branched networks via Brownian dynamics simulations. We employed a bead-spring model without the excluded volume interactions, and we did not consider the solvent explicitly. Each examined 4-arm star branch prepolymer has uneven arm lengths to attain two-against-two (2a2) or one-against-three (1a3) configurations. The arm length contrast was varied from 38–2 to 20–20 for 2a2, and from 5–25 to 65–5 for 1a3, with the fixed total bead number of 81, including the single bead located at the branch point for prepolymers. We distributed 400 molecules in the simulation box with periodic boundary conditions, and the bead number density was fixed at 4. We created polymer networks by cross-end-coupling of equilibrated tetra-branched prepolymers. To mimic the experiments of tetra gels, we discriminated the molecules into two types and allowed the reaction only between different types of molecules at their end beads. The final conversion ratio was more than 99%, at which unreacted dangling ends are negligible. We found that the fraction of double linkage, in which two of the four arms connect a pair of branch points, increases from 3% to 15% by increasing the arm length contrast. We stretched the resultant tetra-type networks to obtain the ratio of mechanically effective strands. We found that the ratio is 96% for the monodisperse system, decreasing to 90% for high arm length contrast. We introduced bond scission according to the bond stretching to observe the network fracture under sufficiently slow elongation. The fracture behavior was not correlated with the fraction of double linkage because the scission occurs at single linkages.
1. Introduction
Tetra gels are known as a class of defect-free polymer networks.1,2 Wallace et al.3 first synthesized a tetra-branched gel created from mixtures of tetra-N-succinimidyl poly(ethylene glycol) (tetra-NHS-PEG) and tetra-thiol-derivatized PEG (tetra-TD-PEG) for biomedical use. Sakai et al.4 employed tetra-amine-derivatized PEG (tetra-AD-PEG) instead of tetra-TD-PEG and defined tetra gels as polymer gels formed from two tetra-branched prepolymers with mutually reactive functional groups. They examined the mechanical properties and the network structure of a series of tetra gels. They found that tetra gels have a uniform network with a negligible number of defects to exhibit superior mechanical toughness. Here, the defects mean entanglements, loops, unreacted dangling ends, and polydispersity in the strand length. Due to the binary nature, given that the gelation time is appropriately tuned, there is no primary loop formation in tetra gels and a limited number of unreacted ends.5–8 Besides, one can control the uniformity of the strand length and entanglement formation by the molecular weight of prepolymers.9,10 The network uniformity is a distinguishable feature of tetra gels from the other network polymers, and the studies based on the uniformity have been made both toward fundamental and application directions.11–15An interesting approach is to utilize tetra gels as reference materials for studying the effects of defects. Sakai et al.16 have conducted such an attempt using tetra gels made of prepolymers with the arm length contrast. They mixed a monodisperse tetra-NHS-PEG (arm molecular weight of 5 k) with bidisperse tetra-AD-PEGs (arm molecular weights of 1.3 k and 5 k). The mixtures realize a contrast in the strand molecular weights of 6.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 at the maximum. They have summarized that the examined arm length contrast does not significantly affect the toughness of resultant gels. We note that if further contrast is introduced, the inhomogeneous stretching of strands probably depresses the toughness, as suggested by earlier studies for end-linked17,18 and randomly cross-linked19 poly (dimethylsiloxane) (PDMS) elastomers.
10 at the maximum. They have summarized that the examined arm length contrast does not significantly affect the toughness of resultant gels. We note that if further contrast is introduced, the inhomogeneous stretching of strands probably depresses the toughness, as suggested by earlier studies for end-linked17,18 and randomly cross-linked19 poly (dimethylsiloxane) (PDMS) elastomers.
Although most studies have reported that the inclusion of defects suppresses the mechanical properties of polymer networks, a few studies imply that some inhomogeneity may improve the toughness. For instance, Lin and Zhao20 have theoretically proposed that the fracture energy of polymer networks increases with increasing number of double linkages (i.e., cyclic loops in their terminology). Here, the double linkage expresses connectivity between a pair of network nodes that share two strands. They calculated the fracture energy from the required work to elongate the strand up to its scission, assuming that double linkages are located on the crack path. The obtained fracture energy linearly increases with increasing the fraction of double linkages. Although the crack path may not propagate by selectively cutting double linkages, this direction is worth investigating. For instance, let us consider an asymmetric tetra-branched polymer having long and short arms as a prepolymer. In this case, the fraction of double linkages in the resultant gel increases with increasing the ratio between the molecular weights of long and short arms, as expected from the conformational distribution function.21 (We do not consider the primal loop formation, in which two arms of a single polymer connect because the primal loop is forbidden in the reaction.) Based on the theory, the toughness of such networks may be better than that of the network made of symmetric prepolymers. One may argue that this thought contradicts the results by Sakai et al.16 mentioned above. However, their range of molecular weight contrast is rather limited, and they only examined the mixtures of symmetric prepolymers.
Molecular simulations would be useful for the problem. There have been several simulation studies for tetra-gel-type networks. Lange et al.22 have investigated the fraction of double and higher-order linkages with respect to the prepolymer concentration via a bond-fluctuation Monte Carlo method to report that the results are qualitatively consistent with NMR measurements. Lin et al.23 have performed a similar analysis based on kinetic graph theory in addition to the Monte Carlo simulations. Nishi et al.24 have calculated the elastic modulus of a series of tetra-gel-type networks with various connectivity ratios between the network nodes. Sugimura et al.25 have extended the method to discuss the fracture. Wang and Escobedo26 have constructed coarse-grained models of defect-free tetra-gel networks to exhibit stress–strain relations. Furuya and Koga27 performed bead-spring simulations to see the number of effective strands in the tetra-gel-type networks. Apart from the simulations for tetra-gel-type networks, very recently, Arora et al.28 have conducted simulations for polymer networks made of linear prepolymers and tetra-functional cross-linkers. They reported that the toughness decreases with increasing number of primary loops. Nevertheless, these earlier studies did not discuss the effect of double linkages on mechanical properties.
In this study, we performed Brownian dynamics simulations of tetra-gel-type networks formed from prepolymers, for which the arm molecular weight is bidisperse. From such prepolymers, networks were created via Brownian simulations of gelation. The introduced bidispersity of the arm molecular weights does not affect the gelation kinetics and the conversion ratio. In contrast, the number of double linkages increases with increasing arm length contrast. The resultant networks were uniaxially stretched, and the number of mechanically effective strands was estimated from the elastic modulus. We also examined the fracture behavior by introducing bond scission according to the bond stretching to discuss the toughness. The results imply that the inclusion of double linkages does not improve the mechanical properties. Details are shown below.
2. Model and simulations
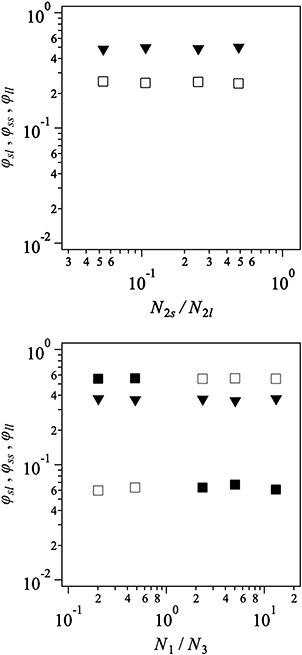
We consider 4-arm star prepolymers represented by bead-spring chains. All the chains are phantom since we neglect the effects of excluded volume interactions, including entanglements. No solvent is considered explicitly. The bead position {Ri} obeys the standard Langevin equation of motion written asIn RHS, the first term is the drag force, the second term is the contribution of connected springs, and the third term is the thermal random force. ζ is the friction coefficient, a is the average bond length, and bik ≡ Ri − Rk is the bond vector between the connected beads. fik is the spring factor for finite chain extensibility. We had fik = 1 for the simulations with Gaussian springs, whereas 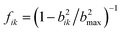 with bmax = 3 for the case with the finite extensibility. We have confirmed that this choice of bmax avoids thermal degradation for the examined networks. Fi is the Gaussian random force, which obeys 〈Fi〉 = 0 and 〈Fi (t)Fj (t′)〉 = 2kBTδijδ (t − t′)I/ζ, where I is the unit tensor. We chose units of length, energy, and time as a, kBT and τ = ζ a2/kBT, and quantities reported hereafter are normalized. For the numerical integration, a second-order scheme29 was employed.
with bmax = 3 for the case with the finite extensibility. We have confirmed that this choice of bmax avoids thermal degradation for the examined networks. Fi is the Gaussian random force, which obeys 〈Fi〉 = 0 and 〈Fi (t)Fj (t′)〉 = 2kBTδijδ (t − t′)I/ζ, where I is the unit tensor. We chose units of length, energy, and time as a, kBT and τ = ζ a2/kBT, and quantities reported hereafter are normalized. For the numerical integration, a second-order scheme29 was employed.
We examined several star prepolymers, as shown in Table 1 and Fig. 1. The arm molecular weights were bidispersed in two-against-two (2a2) and one-against-three (1a3) manners. The total molecular weight of polymers was fixed at 81, including one bead at the branch point and the other 80 beads on the stemming arms. We mimicked the formation of tetra gels by considering two types of molecules (A and B) that react only with the other type of molecules. The prepolymer configurations were common for A and B prepolymers. For comparison, a network created by random linking of a single long chain (for which the molecular weight is 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400) across periodic boundary conditions was also provided and subjected to mechanical tests. The number of cross-links in this case was common with the tetra systems, and the distribution of the strand length between crosslinks is given in the ESI.†
400) across periodic boundary conditions was also provided and subjected to mechanical tests. The number of cross-links in this case was common with the tetra systems, and the distribution of the strand length between crosslinks is given in the ESI.†
| Code | N l | M l | N s | M s |
|---|---|---|---|---|
| a Number of beads for the long arm. b Number of long arms stemming from the branch point. c Number of beads for the short arm. d Number of short arms stemming from the branch point. e Created via random linking of a single long chain. | ||||
| 2a2-3802 | 38 | 2 | 2 | 2 |
| 2a2-3604 | 36 | 2 | 4 | 2 |
| 2a2-3208 | 32 | 2 | 8 | 2 |
| 2a2-2713 | 27 | 2 | 13 | 2 |
| s2020 | 20 | 4 | — | — |
| 1a3-0525 | 25 | 3 | 5 | 1 |
| 1a3-1123 | 23 | 3 | 11 | 1 |
| 1a3-3515 | 35 | 1 | 15 | 3 |
| 1a3-5010 | 50 | 1 | 10 | 3 |
| 1a3-6505 | 65 | 1 | 5 | 3 |
| Rnde | — | — | — | — |
The polymers were dispersed in a simulation box, for which periodic boundary conditions were employed. The number of molecules was 200, both for A and B polymers to attain equimolar conditions. The bead number density was fixed at 4. This density is sufficiently higher than the overlapping concentration30 of prepolymers (C* ∼0.8), and we did not observe any structural inhomogeneity even after the gelation. Fig. 2 shows a typical snapshot of an s2020 system. Note that all the chains are phantom, and bead overlapping is allowed. For sols, equilibration was attained with fik = 1 and the numerical integration time step size Δt = 0.1. The equilibration time was chosen at 104, which is sufficiently longer than the Rouse relaxation time of prepolymers (<300).
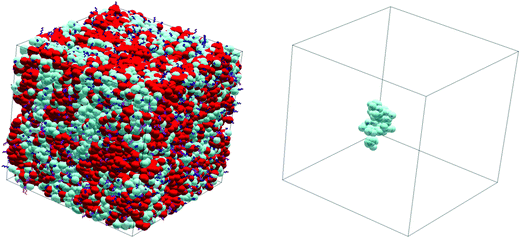 | ||
| Fig. 2 Snapshot of an equilibrated sol for the s2020 system and one of the involved 800 molecules. Red and blue beads represent the segments on type-A and B prepolymers, respectively. | ||
After equilibration of sols, we performed gelation simulations with fik = 1 and Δt = 0.1. We had a reaction site at the end of each arm stemming from the branch point. This reaction site was connected to another one when the two reaction sites came close within a predetermined reaction distance with a certain reaction probability and only when the two sites considered were on different types of molecules. We chose the reaction distance at unity and the cumulative probability at 0.1, respectively. The gelation was performed until the conversion ratio became more than 99% as shown later.
The mechanical properties of created networks were examined as follows. To see the elastic modulus, we uniaxially stretched the network with fik = 1 and Δt = 0.1. The stretching rate was ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 2 × 10−5, which is sufficiently lower than the relaxation rate of the single strand. We also performed stretch simulations considering bond scission to discuss the toughness of networks. In this case, we employed the non-linear spring with finite extensibility to avoid bond scission due to thermal fluctuations. (One may argue that such a thermal degradation does not occur if the critical bond length of scission is set at a large value. However, in such a case, we have to apply an impractical magnitude of stretching to achieve the scission.) The length of each bond was monitored, and the bond was broken when |bij| > 0.9bmax (with bmax = 3 as mentioned above). The result of the fracture simulation strongly depends on the stretching rate, as shown in the ESI,† because of large-scale structural relaxations following every single bond scission. We empirically chose the stretching rate to be
= 2 × 10−5, which is sufficiently lower than the relaxation rate of the single strand. We also performed stretch simulations considering bond scission to discuss the toughness of networks. In this case, we employed the non-linear spring with finite extensibility to avoid bond scission due to thermal fluctuations. (One may argue that such a thermal degradation does not occur if the critical bond length of scission is set at a large value. However, in such a case, we have to apply an impractical magnitude of stretching to achieve the scission.) The length of each bond was monitored, and the bond was broken when |bij| > 0.9bmax (with bmax = 3 as mentioned above). The result of the fracture simulation strongly depends on the stretching rate, as shown in the ESI,† because of large-scale structural relaxations following every single bond scission. We empirically chose the stretching rate to be ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 2 × 10−5, below which the result is practically insensitive to the stretching rate. Δt for the breakage simulations was chosen at 0.002 according to the tests reported in the ESI.†
= 2 × 10−5, below which the result is practically insensitive to the stretching rate. Δt for the breakage simulations was chosen at 0.002 according to the tests reported in the ESI.†
3. Results and discussion
3.1 Gelation kinetics and network structures
Fig. 3 shows the time development of the arm number fractions for different connectivity for 2a2-3802 and s2020. φa is the fraction of unreacted arms. Because all the arms are unreacted at t = 0, φa decays from unity. In the long-time region, φa exhibits a power-law decay with the exponent of −1. This behavior is consistent with the mean-field theory.31,32 In most experimental studies, the exponent is larger than −1 due to the retardation induced by several reasons, including entanglement between polymers.33,34 We do not consider such effects for simplicity. In the resultant network at t = 105, the conversion rate is more than 99%. The entire behavior of φa is not sensitive to all the examined prepolymers regardless of the arm length contrast. This result is rational in the late stage because the molecular weight is common, and the diffusion constant of the prepolymers is identical. φs and φd are the fractions of reacted arms forming the single and double linkages. Here, a single linkage means that two network nodes are connected only by a single network strand. As mentioned above, a double linkage is referred to as a cyclic loop or a secondary loop in earlier studies.30φd is apparently larger for the case with the arm length contrast 2a2-3802 (black broken curve) than that for the symmetric arm length s2020 (red broken curve). Due to this difference, the number of single links (solid curves) depends on the arm length contrast, though it is not visible in the log plot. We do not discuss triple and quad linkages27 because the fraction is quite small.Fig. 4 shows φa, φs, and φd in the resultant network plotted against the arm length contrast. Hereafter, N2s/N2l is the bead number ratio of the short arms to the long arms for 2a2 systems, and N1/N3 is that of the minor arms to the major arms for 1a3 systems. As seen in Fig. 4, most of the strands form single linkages, and the arm fraction involved in such strands, φs, is close to unity for all the examined cases (see filled circle). The fraction of unreacted arms, φa, is independent of the arm length contrast and is less than 0.4% (cross). In contrast, the arm fraction in double linkages φd (unfilled circle) depends on the arm length contrast. Both panels exhibit that the double link formation is enhanced when the contrast becomes large.
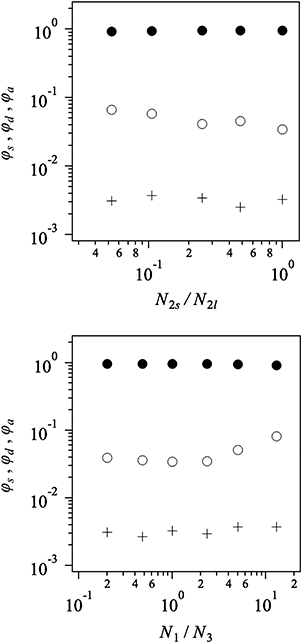 | ||
| Fig. 4 Arm fractions in dangling ends φa (cross), single linkages φs (filled circle), and double linkages φd (unfilled circle) in the resultant networks for 2a2 and 1a3 systems. | ||
For the symmetric case (N2s/N2l = N1/N3 = 1), Lange et al.22 have reported φd as a function of the prepolymer concentration C normalized by the overlapping concentration C*. According to their Monte Carlo simulations, the value of φd at our concentration (C/C* ∼5) is ca. 0.05. This value is close to but slightly larger than our result (φd = 0.04). The discrepancy is probably due to the excluded volume effect neglected in our simulations and the difference in the employed models for the reaction kinetics. The other simulations23,27 suggest similar values of φd, though a direct comparison is difficult.
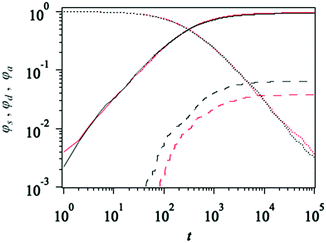
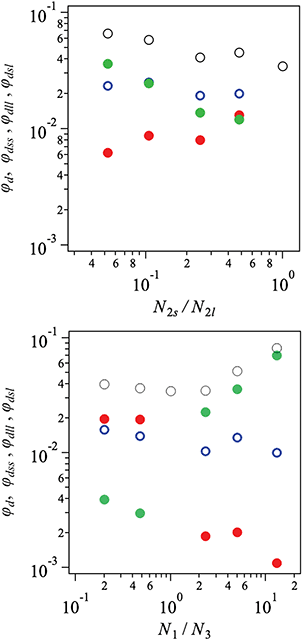
Fig. 5 shows the number fraction of strands formed by two short arms φss, long arms φll, and long and short arms φsl. For 2a2 systems (left panel), φsl ∼1/2 (triangle) and φss–φll ∼1/4 (square). For 1a3 systems (right panel), φll and φss are 1/16 or 9/16 (filled and unfilled square), depending on which arm is dominant. φsl ∼6/16 (triangle). These results are consistent with the expected values from the number ratio between short and long arms. The effect of the unreacted portion is negligible.
Fig. 6 shows the fractions of double linkages formed by two short arms φdss, two long arms φdll, and a pair of short and long arms φdsl. φd (= φdss + φdll + φdsl) is also plotted for comparison. Note that φd cannot be decomposed for the symmetric case (N2s/N2l = N1/N3 = 1). For 2a2 systems (left panel), φdss (green filled circle) is dominant when N2s/N2l is small. With increasing N2s/N2l, φdss decreases and becomes smaller than φdsl (blue unfilled circle). In contrast, φdll (red filled circle) increases with increasing N2s/N2l. For 1a3 systems (right panel), due to the asymmetry of the arm number, φdll is much larger than φdss when N1/N3 < 1. In contrast, double linkages for N1/N3 > 1 are formed mainly by the short–short connection, and φdll becomes negligible. φdsl is not that sensitive to the arm length contrast for both cases.
3.2 Elastic modulus of Gaussian networks
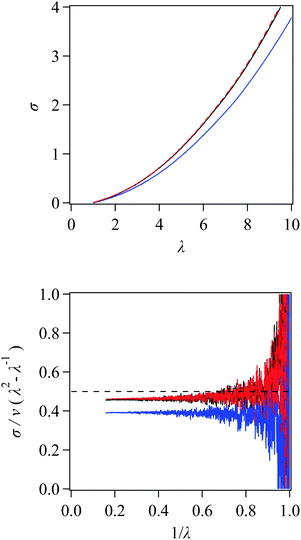
To evaluate the fraction of effective strands that contribute to the mechanical response, we stretched the networks with fik = 1. Fig. 7 shows the stress–stretch (σ − λ) relation and the Mooney plot. In the latter, we normalize the stress by υ (λ2 − λ−1) (where υ is the strand number density calculated from the number of prepolymers) and plot it against λ−1 to see if the (σ − λ) relation follows the neo-Hookean prediction. As seen for the large λ region (i.e., the small λ−1 region), the normalized stress exhibits a horizontal line consistent with the neo-Hookean behavior. We note that the stress fluctuations are large in the small λ region even though the presented results are ensemble-averaged for eight different networks, and the fluctuations are not visible in the top panel.Nevertheless, assuming the neo-Hookean behavior, we can determine the elastic modulus G = σ/υ (λ2 − λ−1) by averaging the value in the range λ−1 ≤ 0.5, where the λ-independent behavior is clearly seen in Fig. 7. The value of G is slightly smaller than the theoretical value of 0.5 for the defect-free network.35,36 As discussed earlier,22,24,27 this reduction of G is due to defects that do not sustain the stress. (Note that the strand number density υ introduced above is calculated from the number of dispersed prepolymers, and inactive strands and double linkages are not excluded.) As we see that the modulus of the symmetric case (s2020, red curve) and that of a 2a2 system (2a2-3802, black curve) are similar, the fraction of defects is not drastically affected by the arm length contrast. Meanwhile, the randomly connected network (Rnd, blue curve) exhibits a modulus significantly smaller than the tetra-gel-type networks.
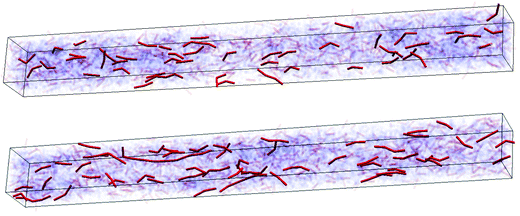
Fig. 8 top panel shows the spatial distribution of stretched segments for a s2020 network at the applied stretching of 5. This snapshot exhibits no clear force chain formation,37 implying that the stress is not localized. Although not shown, the distribution for the other tetra systems is similar even for the systems formed by highly asymmetric prepolymers. In contrast, in the bottom panel for Rnd, there exist some long, colored chains that indicate stress localization along the dominant force chains. This result is consistent with the modulus shown in Fig. 7.
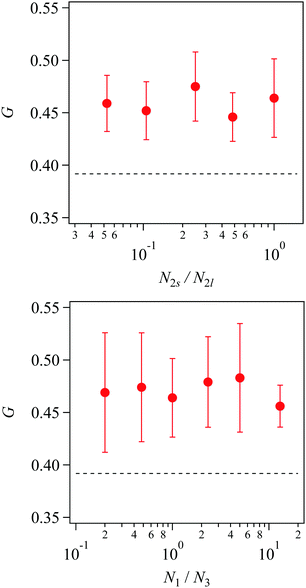
Fig. 9 shows the modulus G as a function of the arm length contrast for 2a2 and 1a3 systems. As the difference is within the error-bar, the modulus is essentially insensitive to the arm length contrast. Since the modulus is more than 0.45, 90% of the strands carry the stress for the examined tetra-gel-type networks. Meanwhile, the modulus is ca. 0.38 for Rnd, indicating that the fraction of effective strands is less than 80%. Since Rnd systems were created from single chains, there are neither isolated clusters nor dangling ends. As such, the small modulus reflects inhomogeneity due to the widely dispersed strand length. In this respect, modulus of tetra-branched networks would become lower if further contrast is introduced for the strand length.
3.3 Fracture
Fig. 10 shows stress–stretch relations for 2a2 systems with bond scission. (The results for 1a3 systems are available in the ESI.†) The stress σ increases up to a certain maximum σmax, and it decays following the peak. The stretching at the peak λp is located around 16 for s2020. This λp is consistent with the maximum stretch λmax for a single network strand containing 40 bonds with the maximum bond stretch of 3 (λmax = 3 × 40/√40 ~ 19). The curves for 8 independent simulation runs are rather similar to each other for s2020, whereas the curves become diverse for the networks with asymmetrical strand lengths. For instance, the curves are largely scattered for the random networks (Rnd) to exhibit similar σmax and different mitigation behaviors. This variation of λp implies that the bond scission happens at network strands with various segment numbers. Indeed, for the tetra-gel-type networks with asymmetrical strand lengths, we see a few bundles of curves that reflect the strand length subjected to the scission. Takahashi et al.19 have shown that for PDMS gels the elongation at break is significantly reduced when they introduced the strand length distribution. Our result is in harmony with this report, though a direct comparison is difficult since our polydispersity index is only 2 for Rnd, whereas it was ca. 600 for their study.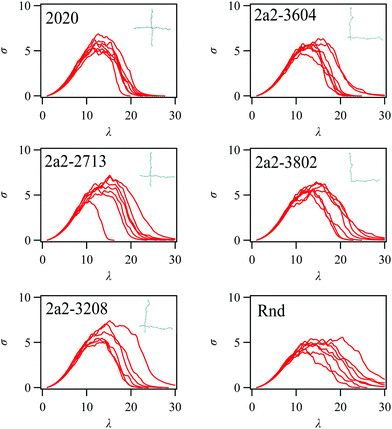 | ||
| Fig. 10 Stress–stretch curves for 2a2 systems. The results from 8 independent simulation runs are shown. The results for the random network (Rnd) are also shown for comparison. The results for 1a3 systems are available in the ESI.† | ||
We note that the simulated stress–strain curves are different from typical experimental data. Namely, in most of mechanical experiments, the stress immediately drops to zero when the specimen is broken, and the stress exhibits a sharp-edged peak. In contrast, the simulated stress mitigates with a certain duration after a dull peak. This discrepancy is due to structural relaxations induced by every single bond scission. The structural relaxation takes place with a long relaxation time, when the fragmented dangling domains become large. If we choose a stretch rate smaller than the slowest relaxation rate of the entire system, it should be smaller than ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 3 × 10−8 as we have 32
= 3 × 10−8 as we have 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 Rouse beads in total. Such a stretching rate is significantly smaller than the employed rate chosen at
800 Rouse beads in total. Such a stretching rate is significantly smaller than the employed rate chosen at ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 2 × 10−5, being hardly achieved with practical computation costs. One may argue that this problem can be solved if the network structure is immediately relaxed at each bond scission according to the energy minimization.25,38 For example, Lei et al.38 have reported such a calculation, in which obtained stress–strain relations are close to those in typical experiments. However, they neglect thermal fluctuations at the network nodes, and thus, the model construction is rather macroscopic. Arora et al.28 have very recently reported another simulation scheme to discuss the effect of primary loops on the mechanical properties of the network. Although they cleverly implemented the relaxation process during the network fracture in their numerical scheme, their stress–strain curves are similar to ours exhibiting dull peaks. As such, to the best of our knowledge, no impeccable simulation scheme for the targeted problem is available at present. Nevertheless, we have confirmed that the result does not strongly depend on the stretching rate below the employed value as shown in the ESI,† and we note that the presented results include the effect of structural relaxations.
= 2 × 10−5, being hardly achieved with practical computation costs. One may argue that this problem can be solved if the network structure is immediately relaxed at each bond scission according to the energy minimization.25,38 For example, Lei et al.38 have reported such a calculation, in which obtained stress–strain relations are close to those in typical experiments. However, they neglect thermal fluctuations at the network nodes, and thus, the model construction is rather macroscopic. Arora et al.28 have very recently reported another simulation scheme to discuss the effect of primary loops on the mechanical properties of the network. Although they cleverly implemented the relaxation process during the network fracture in their numerical scheme, their stress–strain curves are similar to ours exhibiting dull peaks. As such, to the best of our knowledge, no impeccable simulation scheme for the targeted problem is available at present. Nevertheless, we have confirmed that the result does not strongly depend on the stretching rate below the employed value as shown in the ESI,† and we note that the presented results include the effect of structural relaxations.
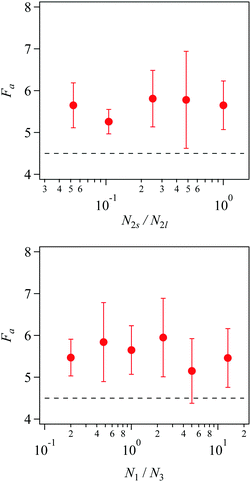
We evaluated the toughness from the obtained stress–strain curves by numerically integrating the curve to obtain the required work for fracture. (Note that the curves in Fig. 10 exhibit true stress versus stretch, and the work for fracture was calculated from the relation between true stress versus true strain.) Fig. 8 shows the apparent fracture energy Fa, which is the required work for the network fracture calculated from the stress–strain curve. Note that we refer to Fa as the apparent energy because the stress–stretch curve includes the contribution of structural relaxation as mentioned above. The examined tetra-gel-type networks exhibit higher Fa values than the random network (shown by broken horizontal line) being essentially independent of the arm length contrast of prepolymers. This result is in harmony with the experiment by Sakai et al.16
One may argue that our result is different from earlier studies for end linked PDMS gels, for which the toughness is significantly dependent on the bimodality of the network strand.18,39–42 The discrepancy is highly likely due to the difference in the short strand fraction. The strategy proposed by Mark39 for the improvement of mechanical properties is the inclusion of a small number of long strands in a network mainly composed of short prepolymers. For example, in the case of Llorente et al.,40 the fraction of short strand is 90% for the network that exhibits superior mechanical properties. Our examined cases for the 2a2 networks are opposite; long strands are the majority. For the 1a3 systems, the network strands are trimodal (see Fig. 5). Nevertheless, the volume fraction of the shortest strand is not the largest. The strand length contrast is also different from each other. For the study by Llorente et al.,40 the molecular weights of prepolymers are 660 and 220 g mol−1 for the short chains and 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 g mol−1 for the long chain. The ratios of the short strand lengths to that of the long chain are 0.035 and 0.012, respectively. These ratios are smaller than our smallest ratio 4/76 = 0.053 realized for 2a2-3802.
500 g mol−1 for the long chain. The ratios of the short strand lengths to that of the long chain are 0.035 and 0.012, respectively. These ratios are smaller than our smallest ratio 4/76 = 0.053 realized for 2a2-3802.
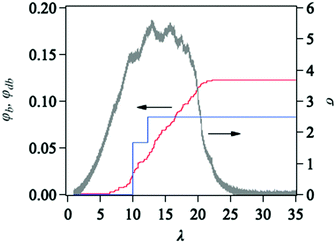
Fig. 4 and 11 demonstrate that the inclusion of double linkages does not improve the toughness of tetra-gel-type networks. We rationalize this result by exhibiting the scission rate of linkages. Fig. 12 shows a typical example of the fraction of broken strands during the stretch for one of the 1a3-6505 networks. The stress and the broken fraction of double linkages are also shown for comparison. The network does not sustain stress after the broken strand fraction reaches ca. φb ∼0.13. Meanwhile, for this specific case, we observe the scission of double linkages up to φdb = 0.08. Note that φdb is the ratio of broken double linkages to all the embedded double linkages. Because the number of double linkages is not large as shown in Fig. 4, the evolution of φdb is discrete.
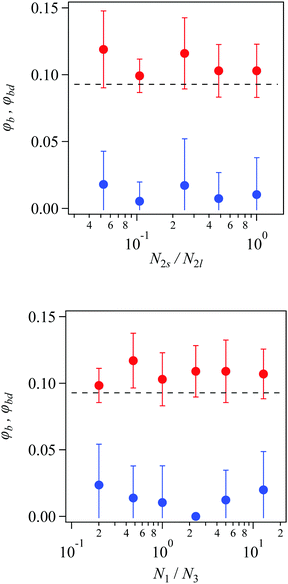
Fig. 13 shows the broken strand fraction φb and φdb observed at the final broken networks. For all the examined tetra-gel-type networks, φb is ca.0.12, irrespective of the arm length contrast. This value is larger than that for Rnd, originating the toughness shown in Fig. 8. Concerning double linkages, the broken fraction φdb is less than 1/4 of φb for the examined cases. This result demonstrates that double linkages are relatively tougher than single linkages. In this respect, our results are in harmony with the theory by Lin and Zhao.20 However, double linkages survive, and they do not contribute to the toughness of the network, since the fracture propagates mainly through single linkages. Consequently, the inclusion of double linkages does not improve the mechanical properties of the examined tetra-gel-type networks.
4. Conclusions
To discuss the effect of the arm length distribution of prepolymers for tetra-gel-type networks, we performed Brownian simulations for a series of tetra prepolymer mixtures with various bidispersed prepolymer arm lengths, without dealing with the solvent explicitly. Since we did not consider the excluded volume effect, the gelation kinetics followed the mean-field theory, and the conversion ratio was more than 99% for all the examined cases. For the resultant networks, the number of ineffective strands involved in dangling portions and isolated clusters was estimated from the elastic modulus. The obtained modulus indicated that more than 90% of the strands contributed to the stress, irrespective of the arm length contrast of prepolymers. Besides, we observed the formation of double linkages, and their number increased with increasing arm molecular weight contrast. To the resultant networks, we applied large stretching to observe the network fracture by introducing bond scission. From the observed stress–stretch curves, we calculated the apparent work for fracture to discuss the toughness of networks. The obtained fracture energy does not depend on the arm length contrast of prepolymers. This insensitivity of toughness to the strand length distribution is in harmony with the earlier experimental study.16 The result also implies that the toughness is not sensitive to the inclusion of double linkages, contrary to the recent theoretical prediction.20 This inconsistency is indeed due to the toughness of double linkages, which are rarely broken in comparison to single linkages. As such, to be fair, we note that double linkages may improve network toughness as theoretically suggested, if the fraction of double linkages becomes higher than the examined range, and/or double linkages are installed by different strategies from the present work.Concerning the employed model and the simulation scheme, the present results include some effects of network relaxation during the fracture. Besides, we did not consider non-bonded interactions and solvent molecules, which may change the results via the effects of entanglement and network swelling. For a quantitative comparison to a specific experiment, a coarse-grained model systematically constructed as proposed earlier26 is necessary. Studies toward such directions are ongoing and the results will be reported elsewhere.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This study was supported in part by JST-CREST (JPMJCR1992) and JSPS KAKENHI Grant Number 22H01189.References
- M. Shibayama, X. Li and T. Sakai, Colloid Polym. Sci., 2019, 297, 1–12 CrossRef CAS.
- T. Sakai, Nihon Reoroji Gakkaishi, 2019, 47, 183–195 CrossRef CAS.
- D. G. Wallace, G. M. Cruise, W. M. Rhee, J. A. Schroeder, J. J. Prior, J. Ju, M. Maroney, J. Duronio, M. H. Ngo, T. Estridge and G. C. Coker, J. Biomed. Mater. Res., 2001, 58, 545–555 CrossRef CAS PubMed.
- T. Sakai, T. Matsunaga, Y. Yamamoto, C. Ito, R. Yoshida, S. Suzuki, N. Sasaki, M. Shibayama and U. Chung, Macromolecules, 2008, 41, 5379–5384 CrossRef CAS.
- K. Nishi, K. Fujii, Y. Katsumoto, T. Sakai and M. Shibayama, Macromolecules, 2014, 47, 3274–3281 CrossRef CAS.
- K. Hashimoto, K. Fujii, K. Nishi, T. Sakai and M. Shibayama, Macromolecules, 2016, 49, 344–352 CrossRef CAS.
- Y. Yoshikawa, N. Sakumichi, U. Chung and T. Sakai, Soft Matter, 2019, 15, 5017–5025 RSC.
- T. Katashima, H. Sakurai, U. Chung and T. Sakai, Nihon Reoroji Gakkaishi, 2019, 47, 61–66 CrossRef CAS.
- Y. Yoshikawa, N. Sakumichi, U. Chung and T. Sakai, Phys. Rev. X, 2021, 11, 11045 CAS.
- N. Sakumichi, Y. Yoshikawa and T. Sakai, Polym. J., 2021, 53, 1293–1303 CrossRef CAS.
- D. E. Apostolides, C. S. Patrickios, T. Sakai, M. Guerre, G. Lopez, B. Améduri, V. Ladmiral, M. Simon, M. Gradzielski, D. Clemens, C. Krumm, J. C. Tiller, B. Ernould and J. F. Gohy, Macromolecules, 2018, 51, 2476–2488 CrossRef CAS.
- T. Fujiyabu, N. Sakumichi, T. Katashima, C. Liu, K. Mayumi, U. Chung and T. Sakai, Sci. Adv., 2022, 8, 1–10 Search PubMed.
- S. Okata, K. Hoshina, K. Hanada, H. Kamata, A. Fujisawa, Y. Yoshikawa and T. Sakai, Ann. Vasc. Surg., 2022, 1–7 Search PubMed.
- Y. Miura, Y. Tsuji, R. Cho, A. Fujisawa, M. Fujisawa, H. Kamata, Y. Yoshikawa, N. Yamamichi, T. Sakai and K. Koike, Sci. Rep., 2021, 11, 1–7 CrossRef PubMed.
- K. Hayashi, F. Okamoto, S. Hoshi, T. Katashima, D. C. Zujur, X. Li, M. Shibayama, E. P. Gilbert, U. Chung, S. Ohba, T. Oshika and T. Sakai, Nat. Biomed. Eng., 2017, 1, 1–7 CrossRef.
- T. Sakai, Y. Akagi, S. Kondo and U. Chung, Soft Matter, 2014, 10, 6658–6665 RSC.
- A. L. Andrady, M. A. Llorente and J. E. Mark, J. Chem. Phys., 1980, 72, 2282–2290 CrossRef CAS.
- Z. Zhang and J. E. Mark, J. Polym. Sci., Polym. Phys. Ed., 1982, 20, 473–480 CrossRef CAS.
- H. Takahashi, Y. Ishimuro and H. Watanabe, Polym. J., 2008, 40, 465–474 CrossRef CAS.
- S. Lin and X. Zhao, Phys. Rev. E, 2020, 102, 52503 CrossRef CAS PubMed.
- P. G. de Gennes, Scaling concepts in polymer physics, Cornell University Press; Ithaca, 1979 Search PubMed.
- F. Lange, K. Schwenke, M. Kurakazu, Y. Akagi, U. Chung, M. Lang, J. U. Sommer, T. Sakai and K. Saalwächter, Macromolecules, 2011, 44, 9666–9674 CrossRef CAS.
- T. S. Lin, R. Wang, J. A. Johnson and B. D. Olsen, Macromolecules, 2018, 51, 1224–1231 CrossRef CAS.
- K. Nishi, H. Noguchi, T. Sakai and M. Shibayama, J. Chem. Phys., 2015, 143, 184905 CrossRef PubMed.
- A. Sugimura, M. Asai, T. Matsunaga, Y. Akagi, T. Sakai, H. Noguchi and M. Shibayama, Polym. J., 2013, 45, 300–306 CrossRef CAS.
- E. Wang and F. Escobedo, Macromol. Theory Simul., 2017, 26, 1–12 Search PubMed.
- T. Furuya and T. Koga, Polymer, 2020, 189, 122195 CrossRef CAS.
- A. Arora, T. S. Lin and B. D. Olsen, Macromolecules, 2022, 55, 4–14 CrossRef CAS.
- R. L. Honeycutt, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 600–603 CrossRef CAS PubMed.
- T. Sakai, Physics of Polymer Gels, Wiley, 2020 Search PubMed.
- D. Toussaint and F. Wilczek, J. Chem. Phys., 1983, 78, 2642–2647 CrossRef CAS.
- K. Kang and S. Redner, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 435–447 CrossRef CAS PubMed.
- D. S. Achilias, Macromol. Theory Simul., 2007, 16, 319–347 CrossRef CAS.
- Y. Masubuchi and T. Uneyama, Soft Matter, 2019, 15, 5109–5115 RSC.
- P. J. Flory, Proc. R. Soc. London, Ser. A, 1976, 351, 351–380 CAS.
- R. Everaers, New J. Phys., 1999, 1, 12.1–12.54 CrossRef.
- R. Everaers, K. Kremer and G. S. Grest, Macromol. Symp., 1995, 93, 53–67 CrossRef CAS.
- J. Lei, Z. Li, S. Xu and Z. Liu, J. Mech. Phys. Solids, 2021, 156, 104599 CrossRef CAS.
- J. E. Mark, Rubber Chem. Technol., 1999, 72, 465 CrossRef CAS.
- M. A. Llorente, A. L. Andrady and J. E. Mark, J. Polym. Sci., Polym. Phys. Ed., 1981, 19, 621–630 CrossRef CAS.
- J. E. Mark and M. Y. Tang, J. Polym. Sci., Part A-2: Polym. Phys., 1984, 22, 1849–1855 CrossRef CAS.
- J. E. Mark, J. Phys. Chem. B, 2003, 107, 903–913 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d2sm00488g |
| This journal is © The Royal Society of Chemistry 2022 |