3D printed linear soft multi-mode actuators expanding robotic applications†
Ryan
Drury
a,
Vitor
Sencadas
 abc and
Gursel
Alici
abc and
Gursel
Alici
 *ab
*ab
aSchool of Mechanical, Materials, Mechatronic and Biomedical Engineering and Applied Mechatronics and Bimedical Engineering Research (AMBER) Group, University of Wollongong, Wollongong, NSW 2522, Australia. E-mail: gursel@uow.edu.au
bARC - Center of Excellence for Electromaterials Science, University of Wollongong, 2522 NSW, Australia
cDepartment of Materials and Ceramic Engineering, CICECO - Aveiro Institute of Materials, University of Aveiro, 3810-193 Aveiro, Portugal
First published on 14th February 2022
Abstract
Soft pneumatic actuators can produce a range of motions and deliver a high force-to-mass ratio whilst offering intrinsic compliance. Presently, the majority of soft pneumatic actuators are used to create bending motions, with very few able to produce significant linear movements. Fewer can actively produce strains in multiple directions. The purpose of this study is to produce and characterize a novel 3D printed actuator which is capable of both extension and contraction under differential pressures. A new elastomeric resin was synthesized to be used on digital light projection (DLP) 3D printers. The presented pneumatic device, a linear soft multi-mode actuator (LSOMMA), is demonstrably scalable and provides a stable response over its lifetime of >10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles. The LSOMMA operates at low pressures, achieving full contraction and expansion at gauge pressures of −25 kPa and 75 kPa, respectively, corresponding to actuator strains of up to −50% and 37%. All actuators presented in this study had a rise time of less than 250 ms. The applications of these multi-mode actuators were demonstrated by developing a pipe-crawling robot capable of traversing horizontal, vertical, and bent sections of a pipe, and a ground locomotion robot capable of moving up to 652 mm min−1 and turn at 361° min−1. An untethered locomotion robot which could navigate multiple surface materials was assembled to demonstrate the potential of the developed technologies for autonomous robotic applications.
000 cycles. The LSOMMA operates at low pressures, achieving full contraction and expansion at gauge pressures of −25 kPa and 75 kPa, respectively, corresponding to actuator strains of up to −50% and 37%. All actuators presented in this study had a rise time of less than 250 ms. The applications of these multi-mode actuators were demonstrated by developing a pipe-crawling robot capable of traversing horizontal, vertical, and bent sections of a pipe, and a ground locomotion robot capable of moving up to 652 mm min−1 and turn at 361° min−1. An untethered locomotion robot which could navigate multiple surface materials was assembled to demonstrate the potential of the developed technologies for autonomous robotic applications.
1 Introduction
The field of soft robotic actuators has seen a surge of interest and developments in recent years, owing to shifting workplace and task priorities.1,2 Traditional ‘hard’ robotic systems are unable to intrinsically provide the necessary compliance, safety, or task flexibility without the addition of complex sensory mechanisms and control schemes.3,4 Compliance in moving systems is necessary for safe working conditions involving soft materials.3,5–7 A growing alternative to the integration of safety measures to established devices is the production of intrinsically soft devices, exploiting the compliant nature of polymers as both structural components and actuation methods.7–10 Soft pneumatic devices are among the most favorable new technologies, featuring of high power-to-weight ratios, rapid response times, and a versatile range of construction geometries.7,8,11The earliest forms of soft pneumatic actuators, pneumatic artificial muscles (PAMs), create small contractile strains under high pressures, but have been superseded due to their highly non-linear dynamics, poor contraction ratios, and non-back-drivability.3,12,13 Newer soft pneumatic actuator designs mostly focus on soft bending motions, which can produce high degrees of freedom and large structural deformation achievable in a single actuator, especially useful in grasping tasks involving irregular shaped objects.2,5,14 The most common topology of these type of actuators utilizes a number of discrete chambers in series combined with a flexible and non-extensible strip along one side to generate a desirable bending motion. These actuators are known by a number of different names, such as pneumatic networks (PneuNets), PneuFlex actuators, or fluidic elastomer actuators (FEAs).2,7,9,15 Most often these actuators are manufactured by the moulding or soft lithography of a silicone elastomer, such as polydimethylsiloxane (PDMS).2,4,15,16 Researchers are often challenged when using PDMS due to its low strain at break and moulding techniques limiting it to relatively simple shapes.4,16,17
Soft linear pneumatic actuators are highly desirable as they function similarly to biological muscle, and make suitable replacements for heavy and rigid pistons or rack and pinion mechanisms.7,18 Linearly operating soft pneumatic actuators, however, are rare in the literature and often require very high pressures to produce useful strokes.1,8,18–20 The linear soft vacuum actuator (LSOVA) requires a vacuum of 96% to produce linear contractions.8 These actuators are scalable, have a predictable linear relationship between applied pressure and blocked force such that they are tailorable for numerous human–machine interfaces and soft robotic applications. These actuators are 3D printed using fused deposition modelling (FDM) from the commercially available thermoplastic NinjaFlex. Many soft linear pneumatic actuators share the inability to function under both positive and vacuum pressures.1,8,18,21–24 This shortcoming means that the operating potential of the LSOVA is halved and prevents the use of such actuators from applications where active forces in two directions are desired, or else require a more complex antagonistic design.
3D printing is a category of additive manufacturing processes in which components are created by the progressive fusion of base materials.17 One of the largest advantages of 3D printing is its innate ability to produce a singular part consisting of intricate shapes and hollows, avoiding the difficult and lengthy processes of molding multiple parts and their assembly.10,25–27 Of the many additive manufacturing processes, the digital light projection (DLP) method of stereolithography (SLA) has significant potential for producing sophisticated elastomeric parts.10,28,29 DLP involves the selective curing of a liquid photosensitive resin using a light source to progressively produce a part, one layer at a time, resulting in airtight complex geometric shapes.17,27 As DLP bonds an entire layer at once to the preceding under-cured layer, the result is a continuous network of polymer chains, a major advantage over FDM.17,30,31 The biggest limitation to the creation of soft actuators using DLP is the lack of suitable materials currently on the market. Two of the most flexible commercial DLP resins fail at elongations well below 200% and behave more like a polyamide material rather than an elastomer.27,32,33 Despite researchers long being aware of this distinct lack of suitable materials, there has been limited progress to address this need, thus novel materials are often synthesized by researchers in order to explore the vast potential.10,17,27,28,31,34,35
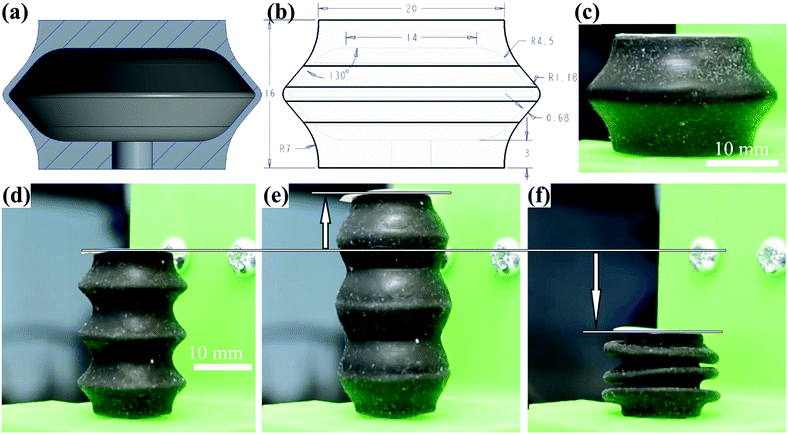
A new soft elastomeric resin, designated ElastAMBER, was created for the purpose of DLP printing soft, flexible parts.31 It exhibits high elastic strains, low stiffness, and low hysteresis compared to other 3D printable materials.31 ElastAMBER was used to produce Linear Soft Multi-Mode Actuators (LSOMMAs), which could provide significant contractile and extensile forces under negative and positive pressures, respectively. The main feature of the LSOMMA is to produce bidirectional actuation in the same design (Fig. 1), widening their application prospects. This is a significant advantage over most other soft actuators, as the dual operating mode allows for both push and pull actions. Additionally, operations requiring the rapid switching of actuators between states, the application of the opposite pressure type can provide faster responses than passive material restoration. Significantly, the magnitude of differential pressure required to deform the actuator is greatly reduced. This allows for the use of smaller and cheaper pneumatic pumps, which in addition to making it more available for use, smaller autonomous devices can be created for small-scale applications.
2 Experimental
2.1 Materials and methods
The elastomeric resin, ElastAMBER, which was used in the DLP printing fabrication of the actuators was synthesized from a commercial off-the-shelf oligomer, two types of reactive diluent monomers, a photoinitiator, and a pigment.31 The ratio between the oligomer and monomers was selected after iterative evaluations, providing a good compromise of low viscosity, high elasticity, and low hysteresis. The synthesis was robust and can produce materials with an increase in any one of these properties by adjusting the ratio. Further information can be found in the ESI.† The ElastAMBER formulation used in this work was shown to have an average maximum strain at break of 302%, an elastic modulus of 0.58 MPa at 100% strain, and a viscosity of 1000 MPa s at 40 °C.31A Titan 2 HR DLP 3D printer was used in the manufacture of the polymer materials. This machine was modified to improve performance and printability. To improve printability and efficiency, the projector's stock optical filter was replaced with one which permitted the transmission of UV light above 360 nm. Additionally, temperature-controlled heating elements were added to the vat to maintain the resin at an elevated temperature of 60 °C throughout the printing process. The printer was scaled to provide theoretical pixel resolution of 37.5 µm px−1 (XY resolution), and a Z-axis step size of 50 µm was selected.
To produce the specimens, the resin was preheated to 60 °C, shaken vigorously to re-homogenize the mixture, and placed in a vacuum oven to remove air bubbles which formed in the resin during shaking. The resin was then poured into the vat with the heating elements switched on. Once the temperature had stabilized the printing process was initiated. After printing, the build platform and attached polymeric structures were placed in a 60 °C oven overnight to lightly anneal the polymer and reduce the internal stresses. The parts were then detached from the print platform and any support structures trimmed. The exterior surfaces and interior chambers were then repeatedly flushed with isopropyl alcohol and wiped with a microfiber cloth to remove remaining resin residue. Lastly, the actuators were subjected to post-curing by submerging in water and being placed inside a UV oven set to 60 °C for 30 minutes of UV exposure, rotated once at the halfway mark.
The testing environment which facilitated the characterization experiments was MATLAB Simulink (r2018b, MathWorks Inc.) via a PCI-6221 (National Instruments) data acquisition device, through which data was recorded and processed. Two pressure regulator devices were used to control the flow of air through the actuators, one for vacuum pressure (ITV0090-3BL, SMC) and another for positive pressure (VPPM-6L-L-1, Festo). Both regulators provided internal pressure feedback via analogue output voltages. In experiments where both positive and negative pressures were delivered to the actuators, a solenoid valve (VUVS-L20-P53U, Festo) was used to switch the pneumatic connections. The positive pressure regulator was fed a constant 3 MPa of air pressure from a wall outlet, while a diaphragm motor-pump (1410-304-VD, Gardner Denver) constantly evacuated a negative pressure vessel, which improved response times and lessened transient effects. Additional loss factors include the lengths of pneumatic tubing, valve losses, and energy absorbed through material deformation. The laser displacement sensor (optoNCDT 1420, Micro-Epsilon) utilized had an analogue output with a theoretical step size of approximately 0.15 mm per step. This may be observed on the data curves after noise filtering has taken place but was considered as negligible and acceptable. The force sensors used for the expansion and contraction force measurements were the FX29 (TE Connectivity) and the FG-5005 (Lutron), respectively.
3 Results
Experimental tests were performed to gauge the pressure limits of the LSOMMAs. The vacuum pressure required for complete contraction of the actuators was discovered to be approximately −25 kPa. Vacuum pressures up to −70 kPa (the limit of the motor-pump) were tolerated without issue. When testing for the maximum operable positive pressure, some actuators tolerated pressures up to 100 kPa without damage, although at pressures above 80 kPa, the inflation became irregular and the actuators began ballooning. While the LSOMMAs can perform under higher pressures, this study focused on a maximum of 75 kPa differential pressure for general expansion tests. The initial, fully expanded, and fully contracted positions of a 3C 14 mm LSOMMA can be viewed in Fig. 1(d), (e), and (f) respectively.3.1 Scalability
Three actuator configurations were chosen to be studied. The first, a single chamber LSOMMA with 20 mm base diameter, was selected so that direct comparisons of performance could be made between this study and the vacuum linear actuators reported by Tawk et al.8 In order to assess scalability, the first actuator was scaled down by 70% to create the second actuator. This allowed a comparison between size and performance and provided insights into the effect of wall thickness. The third actuator was created with three separate pneumatic chambers and was scaled down similarly to the second actuator type. The additional chambers allow for a greater actuation deformation whilst maintaining its minimal cross-sectional area. These actuators are referred to as 1C 20 mm, 1C 14 mm, and 3C 14 mm, respectively. Actuator performance was measured using a step input of pressure as well as a ramp input to provide insight into the transient and hysteresis effects of the viscoelastic material on the operating metrics. The step input performance and critical geometric properties of the LSOMMAs are summarized in Table 1.| Actuator | L 0 (mm) | D f (mm) | t w (mm) | m (g) | ΔP (kPa) | δ (mm) | ε (%) | F b (N) | T r (ms) | ω b (rad s−1) | L t (cycles) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| L 0: original length, Df: face diameter (mm), tw: model wall thickness (mm), m: unit mass (g), ΔP: actuation differential pressure, δ: linear displacement (mm), ε: actuator strain (%), Fb: blocked force (N), Tr: rise time (ms), ωb: estimated 3 dB bandwidth (rad s−1), Lt: expansion cycles before failure (cycles). | |||||||||||
| 1C 20 mm | 16.0 | 20.0 | 0.68 | 2.74 | 75 | 5.09 | 31.8 | 19.4 | 252 | 18.1 | 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 132 132 |
| −25 | −7.59 | −47.4 | −5.46 | 145 | 11.9 | >50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|||||
| 1C 14 mm | 11.2 | 14.0 | 0.48 | 0.92 | 75 | 3.60 | 32.1 | 9.10 | 91 | 38.1 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 911 911 |
| −25 | −5.19 | −46.3 | −3.06 | 57 | 26.8 | — | |||||
| 3C 14 mm | 29.4 | 14.0 | 0.48 | 2.04 | 75 | 10.3 | 37.1 | 12.3 | 200 | 17.7 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 353 353 |
| −25 | −14.6 | −49.7 | −3.14 | 127 | 11.0 | — | |||||
3.2 Step response
The linear displacements of the actuators under a variety of step pressure inputs were recorded over time (Fig. 2). Upon vacuum pressurization, the LSOMMAs rapidly contracted in length, and restored to their initial positions when the vacuum was released back to atmospheric pressure. Similarly, positive pressurization resulted in a swift elongation in the axial direction. The rise times were shorter than the fall times due to the passive nature of the latter. The viscoelastic strain relaxation of the ElastAMBER material caused the final sections of the dynamic motions in both directions to be prolonged, which is especially evident in the 10% to 0% sections of the return stroke. Compared to the smaller units, the 1C 20 mm units were more significantly affected by the interior walls sticking together on vacuum tests, with a greater wall contact area to be separated on the return stroke, prolonging the fall times. Additionally, the actuators with more chambers showed a slightly higher strain response, likely a result of having a greater proportion of unit length in the active region. Some displacement overshoot can be observed at lower positive pressures. This is attributed to the regulator settings causing pressure overshoot to affect faster response times.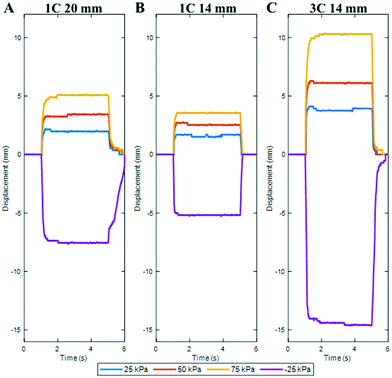 | ||
| Fig. 2 Displacement responses to step inputs. (A) 1C 20 mm step responses. (B) 1C 14 mm step responses. (C). 3C 14 mm step responses. | ||
The complete range of motion for the 3C 14 mm LSOMMA from fully contracted to fully extended is 24.9 mm (Movie S1, ESI†). If multi-mode operations are not required, the LSOMMA could easily be configured to start at one end of motion by pre-loading it, which would provide enhanced stroke functionality. The actuator, if initially held at −25 kPa (Fig. 1(f)), having a height of 14.8 mm, produces an elongation of 168% when pumped to 75 kPa (Fig. 1(e)). Similarly, the magnitude of contraction can be improved by beginning the motion from an extended state. This adds to the versatility of the LSOMMA by expanding its stroke range while maintaining the ability to both push and pull. Compared to other soft linear vacuum actuators, the LSOMMA produces a greater contraction ratio under a quarter the actuation pressure.18,36 Additionally, the slowest actuator observed had a rise time three times faster than reported by Yang et al.18
3.3 Hysteresis
Hysteresis is the loss of mechanical energy in a system through heat, measured by applying a dynamic closed cycle to the material. The viscoelastic nature of the ElastAMBER material was previously estimated through stress-relaxation analysis, showing a total stress relaxation of 3.5%.31 The hysteresis curves for the actuators were obtained by applying a pressure ramp to the actuator of 1 kPa s−1 from zero to max then back down to zero, plotting displacement with respect to internal pressure (Fig. 3). The area between the loading and unloading curves is an indicator of how much loss there is in the system. The curves also show where the critical pressure regions lie for the actuator, that is, the pressure range across which most of the deformation occurs. The displacement response of the LSOMMAs, like most other soft pneumatic devices, are non-linear. However, the displacement responses under positive pressures show higher linearity than the contractions under the vacuum, as seen in the hysteresis plots. Originally, the actuator was designed only to buckle under a certain vacuum pressure range to produce the linear displacement, which appears as a non-uniform relation between pressure and displacement. The buckling phenomenon does not occur under positive pressure, thus the relation is more uniform. The displacement hysteresis between the output strokes and the return strokes for positive pressures is essentially zero, with the difference arising from the sensitivity step of the displacement sensor.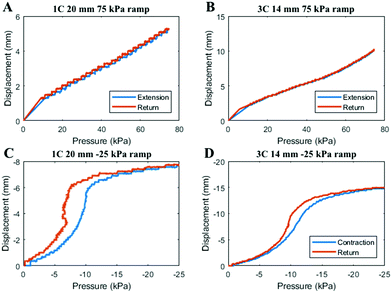 | ||
| Fig. 3 Hysteresis curves of ramped pressure cycles in LSOMMAs. (A) 1C 20 mm 75 kPa. (B) 3C 14 mm 75 kPa. (C) 1C 20 mm −25 kPa. (D) 3C 14 mm −25 kPa. | ||
The larger hysteresis magnitudes in the vacuum tests are due to the interior annular surfaces of the contracted actuator remaining stuck together while pressure is being released. In particular, the ‘S’ shaped discontinuity in the return stroke (Fig. 3) occurred when the last stuck section peeled off, and the actuator jumped upright. This peeling phenomenon, observable in Supplementary Movie S2 (ESI†), can be reduced by a minimum operating vacuum pressure of greater than or equal to −20 kPa, as was the case in the evaluation of the robotic devices. The adhesion between the surfaces is dependent not only upon the applied pressure and load, but also the polymer and surface properties. The UV post-curing of the outside of the LSOMMAs removed most of the tackiness, but the interior surfaces were unable to be processed in the same manner. A method or device which could be inserted inside the LSOMMAs to UV post-cure the insides would certainly reduce this self-adhesion. Alternatively, a low viscosity lubricant could be used to coat the internal surfaces, or the wall geometry could be altered to reduce its effects.
3.4 Blocked force
The ends of the unpressurised actuators were constrained such that the force was passed through a force gauge at one end while the other was fixed. For the expansive force tests, a conical frustum was placed between the unrestrained surface of the actuator and the restrained load cell. To perform the measurement of contraction forces, a hook was bonded to the free surface of the actuator, which was then linked to the end of another load cell, then the screw lift was used to remove the slack from the system.The actuators were pressurized under step inputs while the blocked force outputs were recorded. It was observed that the force was roughly proportional to the area of the actuator. The assertion made by Tawk et al.8 that blocked force is independent of the length was also supported by our findings. Despite not testing the LSOMMAs at such extreme pressures of 95.7% vacuum, we may assume the blocked forces created at those pressures would be lower than those of the LSOVAs. This is because stiffer materials do not stretch as much and can transfer greater forces.36 As noted previously, the stretchable material used in the presented actuators would absorb some of the energy supplied to the system to be used as deformation, which creates internal stresses opposing those of applied blocked forces. The pulling force of ∼5.5 N generated by the 1C 20 mm LSOMMAs closely matched that of the shear-VAM, ∼5.7 N, presented by Yang et al. which was made of a material of similar Young's modulus.36 This is in accordance with the force–pressure–area relationship, as our actuator was roughly four times the area but operated at a quarter of the relative pressure.36
3.5 Pressure stability
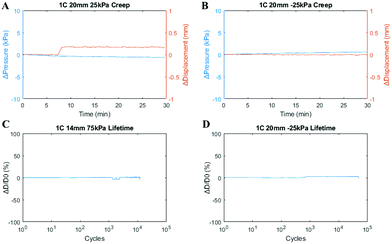
By maintaining the pressure input and measuring the change in the displacement of the actuator over time, one may ascertain if an actuator suffers from any substantial creep. As regulators would systematically adjust for pressure decays in a closed system, a pneumatic syringe was used in place of the regulators to provide system pressure, allowing for accurate measuring of the potential pressure decay. The 1C 20 mm actuators had ±25 kPa pressurization which was maintained for a duration of 30 minutes, showing minimal pressure decay and a displacement fluctuation attributable to one step of the laser displacement sensor analogue output (Fig. 4(A) and (B)). In the highest recorded case, the pressure drop was 0.8 kPa (or 3.2% of the step input pressure) and is most likely a result of air escaping through the pneumatic fittings.3.6 Lifetime
An estimate of the cycle durability of the soft material LSOMMA was determined by recording the number of cycles completed before actuator failure. As positive pressure creates more stress and is more likely to result in tearing or rupturing during expansion, it was used to determine the actuator lifetime, over the much gentler vacuum contractions.37 The test was conducted at a pressure of 75 kPa, a frequency of 1 Hz, and a duty cycle of 50%. The 1C 20 mm LSOMMA showed a lifetime of over 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, while the thinner walled actuators both lasted over 10
000 cycles, while the thinner walled actuators both lasted over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles before failure (Fig. 4(C)). The most common location of failure was just above the outer supports, where the unsupported overhang is at a maximum during printing. This defect, which took the shape of a shallow notch across a small arc, is due to the imperfect fusion of the thin-walled layers at high overhang angles. The other area where ruptures were likely to occur was along the widest circumference of the LSOMMA, where the cross-section's radius of curvature is highest. Finite element analysis simulations confirm this to be the location of maximum stress under positive pressures. A 1C 20 mm LSOMMA was also evaluated for its lifetime under cyclic vacuum pressures of −20 kPa, surviving over 50
000 cycles before failure (Fig. 4(C)). The most common location of failure was just above the outer supports, where the unsupported overhang is at a maximum during printing. This defect, which took the shape of a shallow notch across a small arc, is due to the imperfect fusion of the thin-walled layers at high overhang angles. The other area where ruptures were likely to occur was along the widest circumference of the LSOMMA, where the cross-section's radius of curvature is highest. Finite element analysis simulations confirm this to be the location of maximum stress under positive pressures. A 1C 20 mm LSOMMA was also evaluated for its lifetime under cyclic vacuum pressures of −20 kPa, surviving over 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles without rupturing or significant change in stroke (Fig. 4(D)). A soft pneumatic actuator which was created using one of the few commercially available flexible DLP resins had an average failure lifetime of just 9 cycles, though one sample was able to survive 50 cycles.35 Similarly, a FDM printed PneuNet device averaged 606 cycles at 250 kPa.38
000 cycles without rupturing or significant change in stroke (Fig. 4(D)). A soft pneumatic actuator which was created using one of the few commercially available flexible DLP resins had an average failure lifetime of just 9 cycles, though one sample was able to survive 50 cycles.35 Similarly, a FDM printed PneuNet device averaged 606 cycles at 250 kPa.38
3.7 Pipe crawler robot
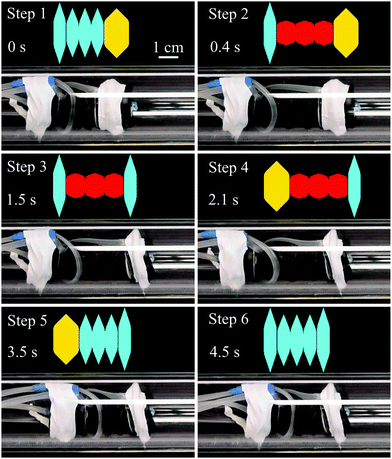
Robots which can traverse small pipes can be used for maintenance and inspections. We constructed a pipe crawling robot which could travel both horizontal and vertical pipes of 30 mm diameter (Fig. 5). The crawling robot was created using a central 3C 14 mm LSOMMA and two 1C 20 mm LSOMMAs attached at either end. The middle LSOMMA provided the bulk of the motion, whereas the front and rear LSOMMAs expanded outwards to grip the pipe wall while under vacuum pressure. These two actuators had their outer surfaces wrapped in PTFE tape to reduce the sliding friction against the pipe. The robot, with a total length of 61.5 mm, travels at horizontal and vertical velocities of 78.8 mm min−1 and 73.2 mm min−1 (Movie S3, ESI†), respectively, using only a vacuum pressure source. When applying a sequence of both vacuum and gauge pressures to the central actuator, the horizontal and vertical speeds increased to 124.5 mm min−1 (Movie S4, ESI†) and 145.9 mm min−1 (Movie S5, ESI†), respectively, clearly demonstrating the benefits of utilizing actuators capable of multi-mode operations. In terms of speed with respect to the robot's body length (BL), these equate to 2.02 BL min−1 and 2.37 BL min−1, respectively. The pipe crawler can be made to reverse its direction simply by altering the inflation sequence. We further demonstrated its pipe crawling abilities having it journey through a 32 mm diameter pipe with a 90° bend from horizontal to vertical orientation (Movie S6, ESI†).This robot is a clear improvement over a similar sized LSOVA-based pipe crawling robot, showing a 25% increase in vertical climbing speed under vacuum pressure alone, and a 150% increase when operating using multiple modes.8 This soft robot also compares favorably to another recently published crawling robot, which requires 8 individual actuators operating at vacuum pressures of −70 kPa to achieve movement.19 This considerably larger robot (∼235 mm long) could move along pipes with diameters of around 120 mm at horizontal and vertical speeds of 2.04 BL min−1 and 1.35 BL min−1, respectively.3.8 Ground locomotion robot
The pipe crawling robot design was adapted into a general crawling robot to evaluate its locomotion abilities (Fig. 6). Two 3C 14 mm LSOMMAs were placed in parallel, with structures attached between the ends for support. Feet were added to the front and rear ends of the LSOMMAs to improve traction with the surface. Small flaps of ElastAMBER rubber were attached to the plastic feet, allowing asymmetric slide-stick movements to alternate between the anchor points. The tethered locomotion robot weighed 14 g and had dimensions of 50 mm in length, 40 mm in width, and 25 mm in height. Utilizing only a vacuum pressure source of −20 kPa, the robot travelled linearly at a velocity of 469 mm min−1 (9.38 BL min−1) (Movie S7, ESI†) and turned at a rate of 172° min−1. Upon applying positive pressures of 50 kPa in sequence with the vacuum pressures to the robot, these speeds increased to 652 mm min−1 (13.0 BL min−1) (Movie S8, ESI†) walking, and 361° min−1 (Movie S9, ESI†) turning on the rubber mat surface. These substantial increases are due in part to the increased stroke length of contraction–extension movements compared to the contraction–rest cycle. Also contributing to the faster speeds are the strokes being actively driven in both directions, as opposed to the vacuum only version undergoing only active contractions with passive returns. A soft crawling robot capable of linear and rotational movements was presented by Jiao et al.19 The robot, comprised of 7 individual actuators operating under vacuum pressures of −70 kPa which were directed by 5 solenoid valves, had a length of 255 mm, and weighed 312 g. When moving along a rubber mat, it averaged a linear speed of 4.27 BL min−1 and had a maximum turning speed of 25.7° s−1 a single direction, as its asymmetric design operated slower when rotating in the other direction. However, their robot is 5 times longer, 22 times heavier, requires 5 more actuators, and used a far greater vacuum pressure to operate when compared to the design presented here. Our work also compares favorably to a slightly larger soft robot which achieved tethered locomotion using a bellows-like actuator and soft bistable valve.39 This robot, powered by an air pressure supply of 17 kPa, could move linearly at a rate of 84 mm min−1. Compared to other soft robots which also utilize two-anchor crawling mechanisms, our design performs far above the average.40It is possible to create untethered robots that crawl autonomously using LSOMMA by using mini pneumatic solenoids and pumps. The electrical components and control system are described in the Supplementary Information section. This was mounted to the rear of the locomotion robot and the rear foot was relocated to beneath the enclosure. The performance of the untethered locomotion robot was distinctly lower than that of the tethered locomotion robot for two reasons. Firstly, the micro air pump was rated far lower in terms of vacuum pressure and flow rate compared to the tethered robot's pump. Second was the dramatic increase in mass because of the payload of mounted control components. The untethered locomotion robot weighed 95 g and had dimensions of 87 mm in length, 43 mm in width, and 36 mm in height (Fig. 6 (c)). The untethered version operated under vacuum pressures only, as the inclusion of the components required to achieve positive pressure motion would severely increase the system's complexity, weight, and volume. When activated, the robot travelled linearly at a velocity of 423 mm min−1 (4.86 BL min−1) (Movie S10, ESI†) and could turn at a rate of 74.4° min−1 (Movie S11, ESI†). It was able to traverse various surfaces such as a wooden desk, rubber foam mat, and office carpet (Movie S12, ESI†).
This robot is contrasted to other similarly sized untethered soft pneumatic crawling robots and summarized in Table 2. Our robot had the second fastest speed relative to body length, outperformed due to the first place robot being built taller than it was long and was restricted to smooth level surfaces.37 In terms of turning speed, it outperformed all other robots of a similar size, bested only by a robot with a mass over twenty times greater. Additionally, its operation uses the lowest vacuum pressure and the second lowest pressure magnitude overall, while having the second lowest mass.
| Crawling robots | P (kPa) | m (g) | L (mm) | v (BL min−1) | ω (° min−1) |
|---|---|---|---|---|---|
| P: operating pressure, gauge (kPa), m: mass of untethered robot (g), L: length of untethered robot in direction of travel (mm), v: linear velocity proportional to body length (BL min−1), ω: angular velocity (° min−1). | |||||
| This work | −20 | 95 | 87 | 4.86 | 74.4 |
| Duggan et al.41 | 16 | 200 | 210 | 0.08 | 8 |
| Rafsanjani et al.20 | 16 | 65 | 275 | 1.43 | — |
| Yang et al.37 | −35 | N/A | 50 | 6.28 | — |
| Waynelovich et al.42 | 90 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
N/A | 0.056 | 103.9 |
| Tolley et al.43 | 138 | 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
650 | 0.462 | 11.7 |
4 Conclusions
In this article, we have presented an advancement in soft pneumatic actuator technologies by utilizing a new elastomeric resin31 to DLP 3D print actuators capable of multiple mode operations. Soft pneumatic actuators with the ability to actively produce strains in multiple directions are rarely found in literature, despite the obvious benefits of actively producing both pushing and pulling forces using a single actuator. We have demonstrated that these soft actuators have low pressure requirements for operation, achieving meaningful strains at pressures far below many other pneumatic devices.15,19,23,37,42,43 By using a DLP printer to manufacture the actuators, their walls formed fully three-dimensional elastomeric chains, creating completely airtight chambers which could survive tens of thousands of cycles without creep before failure.Through the construction and analysis of two mobile robots, we showed the applicability of LSOMMAs in the field of soft robotics and emphasized the benefits of multi-modal operations. A peristaltic crawler was able to rapidly move vertically, around bends, and adapt to changes in pipe diameter. Ground-based crawling robots was also assembled to how LSOMMAs can be used for unconstrained locomotion, including the ability to turn. Importantly, the lower operating pressures of LSOMMAs permit the use of smaller and lighter pumps and other control components, allowing possibilities for the creation of mobile devices. An untethered version of the ground locomotion robot was able to traverse multiple surface materials, including difficult ones like carpet. Importantly, both the tethered and untethered versions performed significantly better in many categories in comparison to many of the other soft robots of similar natures in the literature. There is considerable room for optimizing the geometry of LSOMMAs in terms performance under both pressures. The wall thickness of soft pneumatic actuators, which is a crucial factor in the force characteristics and peak stresses, was not directly assessed in this work. The integration of a mini camera and more robust control system would help guide the untethered robots autonomously in multiple environments for operations such as exploration, inspection and monitoring, and search and rescue.
Author contributions
Conceptualization; R. D., V. S., and G. A.; data curation, R. D.; formal analysis, R. D. and G. A.; funding acquisition, G. A.; investigation, R. D.; methodology, R. D. and V. S.; project administration, V. S. and G. A.; resources, R. D., V. S., and G. A.; software, R. D.; supervision, V. S. and G. A.; validation, R. D.; visualization, R. D. and V. S.; writing – original draft, R. D.; writing – review & editing, R. D., V. S., and G. A.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Rahim Mutlu for his contributions and support to the doctoral study of the first author during his time at the University of Wollongong. This research was supported by the Australian Government Research Training Program Award, and internal funds available to the AMBER group.Notes and references
- L. Hines, K. Petersen, G. Z. Lum and M. Sitti, Adv. Mater., 2016, 1 Search PubMed.
- J. Hughes, U. Culha, F. Giardina, F. Guenther, A. Rosendo and F. Iida, Front. Robot. AI, 2016, 3, 1 Search PubMed.
- A. Hošovský, J. Piteľ, K. Židek, M. Tóthová, J. Sárosi and L. Cveticanin, Mech. Mach. Theory, 2016, 103, 98–116 CrossRef.
- F. Ilievski, A. D. Mazzeo, R. F. Shepherd, X. Chen and G. M. Whitesides, Angew. Chem., Int. Ed., 2011, 50, 1890–1895 CrossRef CAS PubMed.
- A. De Greef, P. Lambert and A. Delchambre, Precis. Eng., 2009, 33, 311–321 CrossRef.
- J. H. Low, H. A. Marcelo and C. H. Yeow, New York, 2015.
- P. Polygerinos, N. Correll, S. A. Morin, B. Mosadegh, C. D. Onal, K. Petersen, M. Cianchetti, M. T. Tolley and R. F. Shepherd, Adv. Eng. Mater., 2017, 19, 1 CrossRef CAS.
- C. Tawk, G. Spinks, M. in het Panhuis and G. Alici, IEEE ASME Trans. Mechatron., 2019, 1–11 Search PubMed.
- D. Rus and M. T. Tolley, Nature, 2015, 521, 467–475 CrossRef CAS PubMed.
- E. Sachyani Keneth, A. Kamyshny, M. Totaro, L. Beccai and S. Magdassi, Adv. Mater., 2021, 33, 2003387 CrossRef CAS PubMed.
- J. E. Huber, N. A. Fleck and M. F. Ashby, Proc. R. Soc. London, Ser. A, 1997, 453, 2185–2205 CrossRef.
- D. Buchler, H. Ott and J. Peters, Proceedings - IEEE International Conference on Robotics and Automation, 2016.
- D. X. Ba, T. Q. Dinh and K. K. Ahn, IEEE ASME Trans. Mechatron., 2016, 21, 1835–1845 Search PubMed.
- S. Kim, C. Laschi and B. Trimmer, Trends Biotechnol., 2013, 31, 287–294 CrossRef CAS PubMed.
- R. Deimel and O. Brock, Proceedings - IEEE International Conference on Robotics and Automation, Karlsruhe, 2013.
- S. Park, K. Mondal, R. M. Treadway, V. Kumar, S. Ma, J. D. Holbery and M. D. Dickey, ACS Appl. Mater. Interfaces, 2018, 10, 11261–11268 CrossRef CAS PubMed.
- R. L. Truby and J. A. Lewis, Nature, 2016, 540, 371–378 CrossRef CAS PubMed.
- D. Yang, M. S. Verma, J.-H. So, B. Mosadegh, C. Keplinger, B. Lee, F. Khashai, E. Lossner, Z. Suo and G. M. Whitesides, Adv. Mater. Technol., 2016, 1, 1 Search PubMed.
- Z. Jiao, C. Ji, J. Zou, H. Yang and M. Pan, Adv. Mater. Technol., 2019, 4, 1 Search PubMed.
- A. Rafsanjani, Y. Zhang, B. Liu, S. M. Rubinstein and K. Bertoldi, Sci. Robot., 2018, 3, eaar7555 CrossRef PubMed.
- E. W. Hawkes, D. L. Christensen and A. M. Okamura, Proceedings - IEEE International Conference on Robotics and Automation, 2016.
- G. Andrikopoulos, G. Nikolakopoulos and S. Manesis, 2011 19th Mediterranean Conference on Control and Automation, MED 2011, Corfu, 2011.
- K. Han, N. H. Kim and D. Shin, Soft Robot., 2018, 5, 554–566 CrossRef PubMed.
- A. J. Veale, I. A. Anderson and S. Q. Xie, Proc. SPIE-Int. Soc. Opt. Eng., 2015.
- K. Kowsari, B. Zhang, S. Panjwani, Z. Chen, H. Hingorani, S. Akbari, N. X. Fang and Q. Ge, Addit. Manuf., 2018, 24, 627–638 CAS.
- C. J. Thrasher, J. J. Schwartz and A. J. Boydston, ACS Appl. Mater. Interfaces, 2017, 9, 39708–39716 CrossRef CAS PubMed.
- D. K. Patel, A. H. Sakhaei, M. Layani, B. Zhang, Q. Ge and S. Magdassi, Adv. Mater., 2017, 1 Search PubMed.
- H. Hingorani, Y. F. Zhang, B. Zhang, A. Serjouei and Q. Ge, Int. J. Smart Nano Mater., 2019, 10, 225–236 CrossRef.
- J. W. Stansbury and M. J. Idacavage, Dent. Mater., 2016, 32, 54–64 CrossRef CAS PubMed.
- H. N. Chia and B. M. Wu, J. Biol. Eng., 2015, 9, 1 CrossRef CAS PubMed.
- R. Drury, V. Sencadas and G. Alici, J. Appl. Polym. Sci., 2022, e52123 CrossRef.
- Formlabs, Flexible FLFLGR02 Material Properties, 2016.
- Spot-A Materials, Spot-E Technical Data Sheet, 2017.
- K. Suzomori, A. Koga and R. Haneda, Proceedings IEEE Micro Electro Mechanical Systems An Investigation of Micro Structures, Sensors, Actuators, Machines and Robotic Systems, 1994, 136–141 Search PubMed.
- B. N. Peele, T. J. Wallin, H. Zhao and R. F. Shepherd, Bioinspiration Biomimetics, 2015, 10, 1 Search PubMed.
- D. Yang, M. S. Verma, E. Lossner, D. Stothers and G. M. Whitesides, Adv. Mater. Technol., 2017, 2, 6323 Search PubMed.
- D. Yang, B. Mosadegh, A. Ainla, B. Lee, F. Khashai, Z. Suo, K. Bertoldi and G. M. Whitesides, Adv. Mater., 2015, 27, 6323–6327 CrossRef CAS PubMed.
- H. K. Yap, H. Y. Ng and C. H. Yeow, Soft Robot., 2016, 3, 144–158 CrossRef.
- P. Rothemund, A. Ainla, L. Belding, D. J. Preston, S. Kurihara, Z. Suo and G. M. Whitesides, Sci. Robot., 2018, 3, eaar7986 CrossRef PubMed.
- M. Calisti, G. Picardi and C. Laschi, J. R. Soc., Interface, 2017, 14, 1 CrossRef PubMed.
- T. Duggan, L. Horowitz, A. Ulug, E. Baker and K. Petersen, RoboSoft 2019 - 2019 IEEE International Conference on Soft Robotics, 2019.
- J. Waynelovich, T. Frey, A. Baljon and P. Salamon, Soft Robot., 2016, 3, 64–70 CrossRef.
- M. T. Tolley, R. F. Shepherd, B. Mosadegh, K. C. Galloway, M. Wehner, M. Karpelson, R. J. Wood and G. M. Whitesides, Soft Robot., 2014, 1, 213–223 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d2sm00050d |
| This journal is © The Royal Society of Chemistry 2022 |