Open Access Article
Open Access ArticleMachine learning potential era of zeolite simulation
Sicong
Ma
 a and
Zhi-Pan
Liu
a and
Zhi-Pan
Liu
 *abc
*abc
aKey Laboratory of Synthetic and Self-Assembly Chemistry for Organic Functional Molecules, Shanghai Institute of Organic Chemistry, Chinese Academy of Sciences, Shanghai 200032, China
bShanghai Key Laboratory of Molecular Catalysis and Innovative Materials, Key Laboratory of Computational Physical Science, Department of Chemistry, Fudan University, Shanghai 200433, China. E-mail: zpliu@fudan.edu.cn
cShanghai Qi Zhi Institution, Shanghai 200030, China
First published on 12th April 2022
Abstract
Zeolites, owing to their great variety and complexity in structure and wide applications in chemistry, have long been the hot topic in chemical research. This perspective first presents a short retrospect of theoretical investigations on zeolites using the tools from classical force fields to quantum mechanics calculations and to the latest machine learning (ML) potential simulations. ML potentials as the next-generation technique for atomic simulation open new avenues to simulate and interpret zeolite systems and thus hold great promise for finally predicting the structure–functionality relation of zeolites. Recent advances using ML potentials are then summarized from two main aspects: the origin of zeolite stability and the mechanism of zeolite-related catalytic reactions. We also discussed the possible scenarios of ML potential application aiming to provide instantaneous and easy access of zeolite properties. These advanced applications could now be accomplished by combining cloud-computing-based techniques with ML potential-based atomic simulations. The future development of ML potentials for zeolites in the respects of improving the calculation accuracy, expanding the application scope and constructing the zeolite-related datasets is finally outlooked.
1. Introduction
Zeolites are a class of crystalline microporous materials with wide applications in chemical industries, particularly as catalysts for converting petrochemicals.1–7 The unique functionalities of zeolites can be largely attributed to their different channels, cages and acidic sites in the framework packed by corner-sharing [TO4] tetrahedral units (T: Si, Al, P, etc.). Interestingly, although millions of likely zeolite structures have been constructed in theory using the [TO4] corner-sharing rule,8–11 only ∼250 distinct zeolite frameworks have been successfully synthesized in the past century according to the International Zeolite Association of Structure Commission (IZC-SC) database.12 The large gap in the numbers between hypothetical and synthetic zeolites evokes persistent efforts in synthesizing and characterizing new zeolites,13–15 which, in turn, demands deep understanding of the thermodynamics and kinetics of zeolites.Owing to the great variety and complexity in structure, the atomic simulations based on quantum mechanics (QM), although being available in the 1960s, have not been widely applied to zeolite systems until the 1990s. Instead, the classical force field has long been the standard in simulating zeolites, such as to describe the interactions between zeolite skeletons and structure-directing agents (SDAs),16,17 to understand the zeolite acidity and to capture the molecular diffusions in zeolite channels.18 The force field has two obvious advantages in describing the potential energy surface (PES) of materials. First, the force field calculation has a much faster computational speed compared to QM calculations and is thus particularly useful for modelling zeolite crystals that are often large in periodicity. Second, the force field calculation can capture van de Waals interaction with a low cost, which is critical to describe weak interactions in zeolite frameworks, e.g. during molecule diffusion. To date, many force fields were developed for (alumino)silicate zeolites to describe the interactions between different [TO4] tetrahedra, e.g. the Sanders–Leslie–Catlow19 and Gabrieli20 interatomic potential optimized for (alumino)silicate zeolites. They generally have the following formula in eqn (1) and (2), in which the total energy is split into bonded terms for covalently bonded atoms and non-bonded terms,20–22 and the parameters in each term can be fitted from QM calculations or from experimental data.
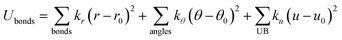 | (1) |
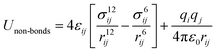 | (2) |
However, the parameter fitting becomes frustrated in dealing with systems with many elements as often encountered in zeolite applications (e.g. P, Na, K and other heteroatoms). In addition, the high accuracy is also difficult to achieve by classical force fields in describing complex chemical environments, for example, those with varied Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratios. Another well-known deficiency of classic force fields is the incapability to describe chemical reactions (with chemical bond making and breaking) due to the rigid bonding-oriented formula. This disallows the application of force fields in studying catalytic processes in zeolites and the zeolite formation process.
Al ratios. Another well-known deficiency of classic force fields is the incapability to describe chemical reactions (with chemical bond making and breaking) due to the rigid bonding-oriented formula. This disallows the application of force fields in studying catalytic processes in zeolites and the zeolite formation process.
The advent of density functional theory (DFT) calculations in 1990s has reshaped largely the field, which becomes an essential complement to experiment in the discovery and understanding of the fundamental properties of zeolites;23,24 especially, DFT calculations are now widely used to describe the zeolite-related catalytic reactions.14,25,26 Nevertheless, the computational costs of DFT remain to be a major bottleneck for long time simulation, particularly for systems with more than 100 atoms, leading to the difficulty in predicting in general zeolite thermodynamics and kinetics properties.
In the past decade, with the rapid development of artificial intelligence methods, the machine learning (ML) technique has been utilized to provide both accurate and efficient description of the PES of materials.27–29 The ML potential can be considered as an advanced version of classic force fields, which contains significantly more fitting parameters without the explicit correspondence between the physical interaction term and the fitting functional form. At present, there are many different ML potentials developed to date using different ML techniques, such as neural network (NN) potentials,30–36 Gaussian approximation potentials37–39 and moment tensor potentials.40 The key for generating ML potentials is mapping the atomic coordinates into structure descriptors and then establishing the linkage between structure descriptors and the total energy.
There are two possible ways to establish the linkage, namely the many-body expansion in eqn (3) and the atomic energy summation in eqn (4).
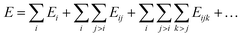 | (3) |
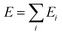 | (4) |
Inherited from the classical force field method, the many-body expansion method splits the total energy as the interaction terms of one-, two- and three-body terms (Ei, Eij and Eijk, where i, j, and k are the indices of atoms in eqn (3)), but the functional form in each term, although still being a function of atomic coordinates, does not have explicit physical meanings. This method is generally limited to small molecular systems due to the exponential explosion for the number of many-body terms (four-body and above) in complex material systems.
On the other hand, the atomic energy summation method that splits the total energy as the summation of individual atomic energy (eqn (4)) proposed in the high-dimensional NN scheme by Behler and Parrinello32,33,41,42 is linear scaling with respect to the number of atoms and thus has a great advantage for complex material systems. In this method, the many-body interaction is encapsulated into each atomic energy that can be correlated with the local chemical environment of each atom, which can be numerically represented by a series of structural descriptors. The atomic energy Ei can thus be fitted using an element-distinguished NN with the structural descriptor as the input layer.
For mapping the atomic coordinates into structure descriptors, many local geometry representations are developed, e.g. Gaussian-type symmetry functions, power-type structure descriptors (PTSD), bispectrum and smooth overlap of atomic positions, etc.43 These structure descriptors are designed to be invariant with respect to the permutation, translation and rotation of atomic coordinates. As an example, PTSD is one of the most sophisticate local geometry representations, in which the power functions and the triangular/spherical functions are utilized to describe the radial and the angular part in two-body and three-body terms, respectively, as shown in eqn (5)–(8)).44
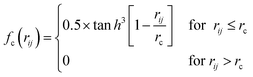 | (5) |
| Rn(rij) = rnij·fc(rij) | (6) |
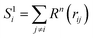 | (7) |
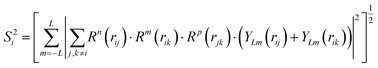 | (8) |
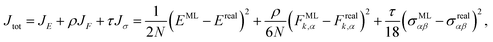 | (9) |
It is important to bear in mind that due to the large number of parameters and the lack of physical meaning for the functional form, the predictability of the ML potential is very sensitive to the training dataset. In other words, the accuracy of the ML potential is not guaranteed for systems that are drastically different from the systems used in the training dataset. Therefore, a self-learning procedure is highly recommended until the accuracy of PES is satisfactory for the target system. A good practice in our group is to first establish a global NN (G-NN) by learning unbiasedly the global PES of different systems (bulk, surface, and cluster) at varied chemical compositions using the stochastic surface walking (SSW) global optimization method, the so-called SSW-NN method.45 The G-NN potential can be refined later for the target system by a new self-learning procedure. Using the SSW-NN method, e.g. after ∼100 self-learning cycles, a robust and accurate G-NN potential can be obtained together with a compact training set containing a variety of structures. The accuracy for the G-NN is typically 1–10 meV per atom for root mean square errors (RMSE) of energy and 0.1–0.2 eV Å−1 for RMSE of force. Interested readers on ML potential should refer to previous reviews.45,46
With the advent of the ML potential, the atomic simulation of zeolites has been accelerated. To date, several G-NN potentials (e.g. Si–Al–P–O–H and Si–Al–P–O–H–Na) were reported to describe (alumino)silicate and silicoaluminophosphate (SAPO) zeolites under different pH conditions.47,48 This perspective serves to highlight the recent contributions of ML potentials in solving zeolite-related problems, e.g. zeolite formation and zeolite–molecule interactions, and discuss the next move for zeolite property prediction assisted by ML potential simulations.
2 Current status of ML potential applications in zeolites
2.1 Zeolite formation
Since the most stable structure of SiO2 is the densely packed quartz phase, the presence of channels and cages in zeolites triggers the quest for the origin of zeolite stability started from 1970s when the theoretical simulation of zeolites began. Some interesting questions remain open in the field, such as how many are there the stable or reasonable zeolite structure? Can a proposed zeolite structure be synthesized in experiment?Indeed, various theoretical methods have been developed to quickly predict zeolite structures, including symmetry-constrained geometric linkage of [TO4] subunits, tiling theory, genetic algorithms coupled with bonding rules and lattice energy minimization programs based on various force fields (the first level in Fig. 1a). However, such predicted zeolite structures are more than millions, at least 4 orders of magnitude more than the number of synthesized zeolite frameworks. To further narrow down the promising candidates, many criteria were proposed by learning the features of existing zeolites. For example, Li et al. suggested a number of empirical rules on the zeolite structure, including the T–O distances, O–T–O angles, T–O–T angles, etc., which successfully reduce the zeolite candidates.49 Based on the force field calculation, Bushuev et al.50 proposed an empirical criterion to assess the thermodynamic feasibility: the upper energetic limit of ∼0.17 eV per SiO2 formula units (f. u.) (ΔE is the relative energy to quartz phase).
 | ||
| Fig. 1 Roadmap of theoretical investigations on zeolite stability and formation mechanism. (a) A broad classification of theoretical research on zeolites in the past 30 years. (b) Global PES contour plot of Al6P6O24 minima. The x axis is the framework density (FD), and the y axis is the total energy of minima with respect to global minimum (quartz phase). Reproduced from ref. 51 with permission from The Royal Society of Chemistry, copyright 2020. (c) Quantitative evaluation of phase competition for zeolite interaction with various SDA. Each element of the binding matrix is defined as the molecule-framework binding energy at the most favourable loading, normalized by the number of framework atoms or SDA molecules (materials and methods). Along the organic SDA column, the binding energies are ranked to determine how directive a molecule is toward a zeolite. Along the zeolite row, the phase competition is quantified for a given SDA. Reproduced from ref. 16 with permission from AAAS, copyright 2021. (d) An atomic view for the zeolite formation in solution. Pink, gold, purple, red and white balls represent the Al, Si, Na, O and H atoms, respectively. | ||
Recently, we utilized a Si–Al–P–O–H five-element global NN (G-NN) potential to explore aluminophosphate (AlPO) global PES. The global AlPO PES maps out a variety of low energy structures, ranging from two-dimensional (2D) layered structures to caged and three-dimensional densely packed structures as illustrated in Fig. 1b.51 From the global PES, we provided a physically meaningful explanation of upper energy limit of zeolite formation, being the formation energy of the 2D layered framework, the one with the infinitely large cage size. The caged structures have energies higher than that of the quartz but lower than that of the layered structure. 0.17 eV per AlPO4 f. u. or 0.18 eV per SiO2 f. u. above quartz phase is identified as the upper energy limit, being consistent with the empirical value suggested by Bushuev et al.50 With this criterion, only ∼14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 (∼4.5% of all structures) hypothetical zeolite structures from the DEEM PCOD database52 satisfy the energy criterion, suggesting still a huge number of likely zeolites that may be potentially synthesized.
900 (∼4.5% of all structures) hypothetical zeolite structures from the DEEM PCOD database52 satisfy the energy criterion, suggesting still a huge number of likely zeolites that may be potentially synthesized.
Since a large number of zeolite candidates survived from the screening using energy and structure criteria, it becomes apparent that zeolite synthesis, particularly influenced by the synthetic conditions, could be more important for determining whether a desirable zeolite can be synthesized. However, the zeolite synthesis involves complex chemical transformation, for example, from silicate/aluminate condensation in solution, to nucleation and to the crystal growth.
A number of groups53–62 studied the silicate/aluminate condensation and nucleation starting from the reaction between Si(OH)4 and Si(OH)3O− monomers, where the anion attacks the neutral species to form an intermediate structure containing a 5-fold coordinated Si center. The initial dimerization reaction appears fast since the reaction barrier is as low as 0.36 eV from DFT calculations, but the continuous polymerization is sensitive to the solution conditions. For example, an Al–Si dimer condenses further either with the Al(OH)4Na monomers to form the Al–Si–Al trimer or with another Al–Si dimer to form the Al–Si–Al–Si tetramer.63 These early studies generally utilize DFT calculations that can treat chemical reactions properly, but due to the low speed even the formation of the simplest secondary structural units of zeolites, such as the double-six-ring (d6r) and sod cages, cannot be reached in DFT simulation.
Once the formation of simple secondary structural units finishes, they are expected to wrap around SDAs for the further polymerization to yield a zeolite skeleton. The direct atomic simulation at this stage needs a long-time scale in order to capture the assembly of the zeolite 3D framework, which is still out of reach for current theoretical methods. Alternatively, the thermodynamics analyses can be utilized to evaluate the role of SDA. From the chemical intuition, It is widely believed that the most effective SDAs observed in experiment should have the highest binding energy with the target zeolite skeleton (ΔEzeo-SDAs, second level in Fig. 1a).64 Therefore, by starting from a fixed zeolite skeleton, various SDAs can be added into zeolite cages and channels and the obtained overall stability between different candidates can be utilized to identify the optimal SDAs. Following this idea, many docking algorithms are therefore developed to screen out the optimal SDAs with the highest ΔEzeo-SDAs, e.g. Zebeddee,65 ZEOMICS66 and Zeo++.67 Recently, Deem and co-workers68 developed a ML potential to predict the ΔEzeo-SDAs for Beta zeolite. Zeolite Beta has been synthesized through the use of a number of SDAs, but no pure Beta A zeolite was reported. Through de novo materials design runs, a total of 3062 promising SDAs were identified, and there are 469 SDAs with verified stabilization energies below −17 kJ (mol−1 Si), comparable to or even better than currently used SDAs for zeolite Beta synthesis.
Beyond the approach in minimizing ΔEzeo-SDAs, Schwalbe-Koda et al.16 proposed a phase competition mechanism; that is, an optimal SDA must exhibit both strong binding affinity toward the desired zeolite and weak binding affinity toward all other frameworks. By computing the binding energy for each SDA-zeolite pair, they obtained a binding matrix with ∼112![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 entries (Fig. 1c). The phase selectivity was then quantified by sorting the binding matrix using two metrics: the directivity of an SDA (D), how close a molecule is to the best SDA for a given zeolite framework, and the competitivity of a framework (C), how close a zeolite is to the best host for the given SDA. The method can rationalize the framework competition under the same SDA. They proposed tris-(dimethylamino)-(methyl)-phosphonium with the favourable volume and phase competition metrics as a new candidate for the synthesis of SSZ-39 zeolite. Following this recipe, SSZ-39 zeolite can indeed be prepared in experiment using this SDA.
400 entries (Fig. 1c). The phase selectivity was then quantified by sorting the binding matrix using two metrics: the directivity of an SDA (D), how close a molecule is to the best SDA for a given zeolite framework, and the competitivity of a framework (C), how close a zeolite is to the best host for the given SDA. The method can rationalize the framework competition under the same SDA. They proposed tris-(dimethylamino)-(methyl)-phosphonium with the favourable volume and phase competition metrics as a new candidate for the synthesis of SSZ-39 zeolite. Following this recipe, SSZ-39 zeolite can indeed be prepared in experiment using this SDA.
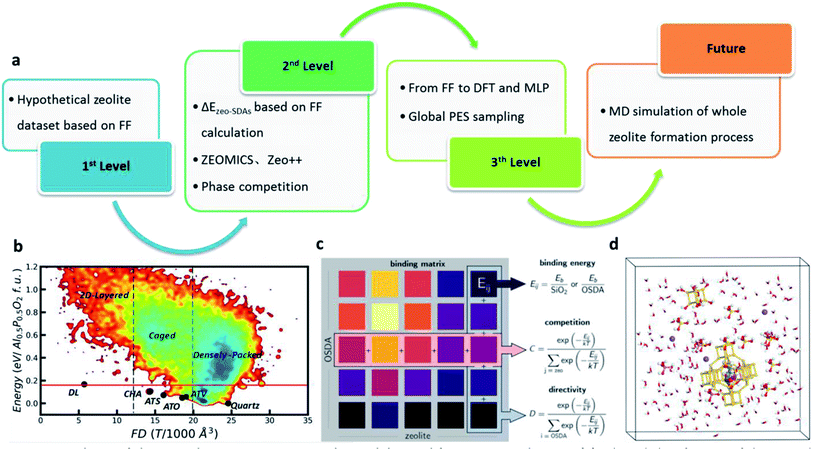
By combining the ML potential with the enhanced stochastic surface walking (SSW) PES exploration methods, we achieved the automatic formation of zeolite structures by global PES exploration for the SixAlyPzO2Hy−z system in the presence of SDAs which are simplified by a rigid ball (the third level in Fig. 1a).51 The increase of SDA size (rs) rapidly decreases the framework density value, as illustrated in Fig. 2a. Too large or too small rs fails to identify the zeolite, leading to either two-dimensional layered or three-dimensional densely packed structures. The zeolite only turns out to be the global minimum under the suitable rs being applied, i.e. in between 3.5 and 5.5 Å. The four known zeolites, i.e. ATV-, ATO-, ATS- and CHA-type, do emerge as the global minimum at rs = 3.5, 4, 4.5 and 5–5.5 Å, respectively. Indeed, in experiment these zeolites are synthesized using selected-size molecular SDAs: for example, the synthesis of ATO- and ATS-type AlPO utilizes tripropylamine and dipropylamine, respectively (9.2 and 8 Å diameter, plus 3 Å for distances between H in SDAs and O in the zeolite skeleton in Fig. 2b).69
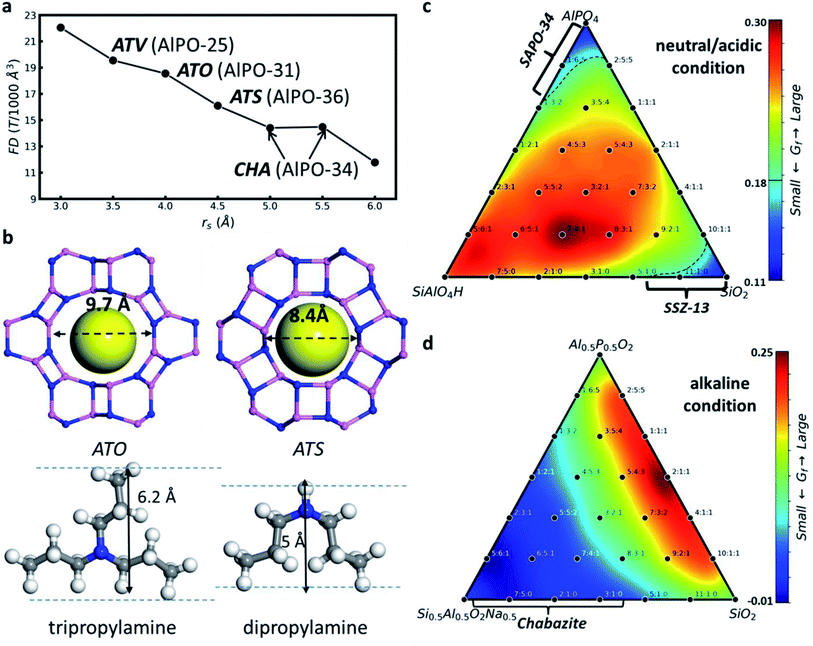 | ||
Fig. 2 Global PES exploration using the enhanced SSW method based on the G-NN potential. (a) The variation of the AlPO global minimum identified from global PES search in the presence of a rigid body at different rigid body size (rs) values. (b) The structures of SDAs and zeolites. Yellow spheres indicate the rigid ball. (c and d) Gibbs formation free energy (Gf) contour plot in the ternary phase diagram for each Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al : P composition with a CHA type skeleton under (c) neutral/acid and (d) alkaline conditions. Reproduced from ref. 51 with permission from Royal Society of Chemistry, copyright 2020. Al : P composition with a CHA type skeleton under (c) neutral/acid and (d) alkaline conditions. Reproduced from ref. 51 with permission from Royal Society of Chemistry, copyright 2020. | ||
In addition, we have analyzed the influence of pH and other synthetic conditions on zeolite synthesis. We constructed the thermodynamic ternary phase diagrams based on Gibbs formation free energy (Gf) with CHA-type SiO2, AlPO and SiAlO4H/SiAlO4Na as the vertexes, where H and Na as the counter ions represent the neutral/acid and alkaline pH environments, respectively. The minima appear nearby two vertexes, Al0.5P0.5O2 and SiO2 under the neutral/acid pH environments (Fig. 2c), but appear nearby the left-bottom corner (Si0.5Al0.5O2Na0.5) under the alkaline pH environments (Fig. 2d). It supports directly the observed pH effect on zeolite synthesis; namely, most aluminosilicate zeolites avoid the acidic condition but phosphate-containing zeolite forms in weak acidic or near neutral conditions.70,71
To date, the atomic simulation of a complete zeolite formation process is still not feasible, although ML potential simulations are the most plausible one compared with other methods (future in Fig. 1a). We expect the next decade would witness ML atomic simulation to explore the condensation and nucleation mechanism of zeolites that naturally involve many atoms, e.g. the formation of d6r and sod cages, and the assembly of these small cages to different zeolites in the presence of SDAs (Fig. 1d).
2.2 Zeolite-related catalytic reactions
The rich microstructure in zeolites has made them excellent microreactors for many important catalytic processes, ranging from zeolite-framework catalysis, e.g. the methanol-to-olefin (MTO) and methanol-to-gasoline (MTG) conversion catalysed by the solid Brønsted acid, to doped metal catalysis, e.g. the methane activation catalysed by Fe-doped zeolite,72 and to encapsulated metal cluster catalysis, e.g. propane dehydrogenation for PtSn alloy in zeolites.73–75 By tuning the acid strength, the porous structure and the doped/encapsulated metals, the product selectivity can be further optimized, leading to versatile catalytic performance of zeolites.76–78In tradition, the simulation of chemical reactions is governed by QM calculations, which is the only tool capable of computing accurately the reaction transition state and thus the reaction kinetics. However, the QM-based calculation faces great difficulties in exploring likely catalytic reactions in zeolites that occur at high temperatures (>600 K) with many high energy intermediates (radicals). In MTO reaction, for example, a number of products including ethylene, propylene, ethane and propane are present together with many different methylated radical intermediates. Given numerous possible reaction routes and the large size of zeolite systems, even DFT-based reaction pathway search and long-time MD simulations are practically infeasible with the current computing facilities.
Recent progress in ML-based reaction pathway search holds great promise for better understanding zeolite catalysis in future. As reported by Kang et al.,79 they resolved the whole reaction network of glucose pyrolysis based on the C–H–O–N G-NN potential and identified the lowest reaction channels. In total, 6407 elementary reactions are screened out from more than 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 reaction pairs in glucose pyrolysis and the most possible reaction pathway is finally identified. For the zeolite-related catalytic reactions, it is essential to further take into account the zeolite framework, particularly those related to the Brønsted acidic sites. Once such a G-NN potential is available, the same reaction pathway sampling could act as the workhorse to automatically resolve the product distribution in zeolite catalysis.
000 reaction pairs in glucose pyrolysis and the most possible reaction pathway is finally identified. For the zeolite-related catalytic reactions, it is essential to further take into account the zeolite framework, particularly those related to the Brønsted acidic sites. Once such a G-NN potential is available, the same reaction pathway sampling could act as the workhorse to automatically resolve the product distribution in zeolite catalysis.
Another important application of ML potentials is to resolve the free energy profile considering the large entropy contribution for the high temperatures in zeolites. This could significantly speed up the free energy computation traditionally carried out by ab-initio MD simulations (AIMD). Recently, Bučko et al.80,81 introduced a theoretical approach that effectively couples different level QM calculations with the ML potential to make free energy calculations more affordable. Based on this method, the free energy calculations at high temperatures with multiple levels of DFT approximations with (RPA, PBE-D2, PBE-MBD, and vdW-DF2-B86R) or without (PBE and HSE06) dispersion corrections can be completed at a low cost. They showed that the carbonylation reaction of methoxy groups (CO + CH3-Zeo → CH3CO+ + Zeo−) in the side pockets (SP) of mordenite zeolite is preferred compared to that in the main channels (MC, Fig. 3), and after the consideration of the explicit dispersion interaction the preference is even larger.81
 | ||
| Fig. 3 Free energy profile for the methanol carbonylation reaction in MOR side pockets (SP) and main channels (MC) computed using DFT at the PBE-D2 level. Reproduced from ref. 81 with permission from Elsevier, copyright 2021. | ||
In addition to the ML potential applications in exploring reaction pathways, ML potentials for this high speed in computation can also be utilized to determine the metal cluster status in zeolite catalysts. Recently, with ML potential-based MD simulation, we explored structure evolutions of the SiO2 MFI zeolite encapsulated PtSnOx catalyst during the catalyst preparation procedure.82 The functionalities of the two stages (high-temperature calcination and H2 reduction) in catalyst preparation are clarified, namely, the oxidative clustering and the reductive transformation, which form separated Sn4O4 and PtSn alloy clusters in MFI. With the presence of the zeolite skeleton, these confined clusters have high thermal stability at the intersection voids of the MFI zeolite because of the formation of “mortise-and-tenon joinery” (Fig. 4a), and a phenomenon named “channel-oriented anisotropy” that the Sn element in PtSn clusters generally exposes towards the straight and sinusoidal channels is observed owing to the different interactions between Pt/Sn and O in the zeolite. Therefore, the zeolite skeleton not only confines the size of the cluster, but also determines the preferential exposure of elements, i.e. Sn in this case, towards the open channels.
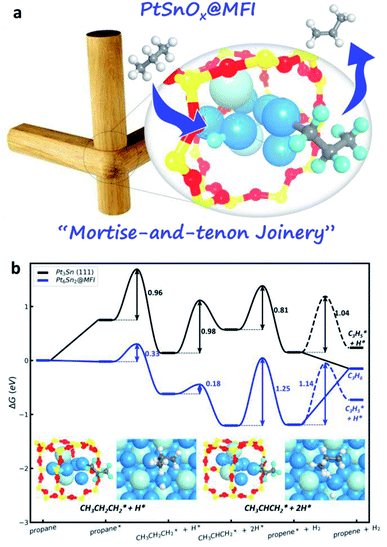 | ||
| Fig. 4 Zeolite-confined subnanometric PtSn for catalytic propane dehydrogenation. (a) The sketch map of mortise-and-tenon joinery for subnanometric PtSn within MFI zeolite. (b) Gibbs free energy profiles for PDH reaction on Pt6Sn2@MFI and Pt3Sn (111) surfaces at 773 K and 1 bar propane pressure (see ref. 82). | ||
The channel-oriented anisotropy affects strongly the catalytic performance since only the atoms towards the open channels are accessible by incoming molecules (Fig. 4a). For the propane dehydrogenation (PDH) reaction, only the PtSn alloys with the Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sn ratio lager than 1
Sn ratio lager than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 can potentially act as the catalyst. Owing to the presence of the low coordinated Pt atom, the subnanometric PtSn alloy clusters can significantly enhance the adsorption of all reaction intermediates, leading to a three orders magnitude improvement of PDH catalytic activity relative to the conventional bulk Pt3Sn metal (Fig. 4b).82 With this knowledge on reactions, we also predicted that the IMF, ITH, ITR, MEL, NES, SFG, TER and WEN, whose structure patterns contain both the larger intersection regions and cross-linked channels, may also be good zeolite candidates for encapsulating the subnanometric metal clusters.
1 can potentially act as the catalyst. Owing to the presence of the low coordinated Pt atom, the subnanometric PtSn alloy clusters can significantly enhance the adsorption of all reaction intermediates, leading to a three orders magnitude improvement of PDH catalytic activity relative to the conventional bulk Pt3Sn metal (Fig. 4b).82 With this knowledge on reactions, we also predicted that the IMF, ITH, ITR, MEL, NES, SFG, TER and WEN, whose structure patterns contain both the larger intersection regions and cross-linked channels, may also be good zeolite candidates for encapsulating the subnanometric metal clusters.
3. Advanced zeolite applications using ML potentials
As overviewed in the previous section, the ML potential owing to its great advantages in describing complex material PES is becoming an important tool for understanding zeolite chemistry. However, the future applications of ML potentials should not be limited to the large-scale atomic simulation in the manner of case-by-case studies, but could be extended broadly to all users in chemistry with fast and easy access. In the following, we show that such end-to-end applications of ML potentials can indeed be facilitated by web-based computer techniques.3.1 Zeolite stability evaluation
Given a proposed zeolite structure, it is desirable to quickly evaluate its thermodynamics stability, which is now affordable with the advent of the ML potential. To date, two G-NN potentials, i.e. Si–Al–P–O–H and Si–Al–P–O–Na–H potentials, are available in the LASP project,47 and thus a wide range of different types of zeolites (SiO2, SAPO and Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al) can be evaluated with very low computational cost.
Al) can be evaluated with very low computational cost.
For this purpose, we developed an online interface for energy calculation based on the G-NN potential as illustrated in Fig. 5a, see the website https://www.lasphub.com/#/lasp/calculation. It provides the cloud-computing ability for users who only need to prepare a structure file (e.g. in cif format). The computation is based on the back-end LASP software47 calculation that can automatically select the correct G-NN potential in the LASP G-NN potential library. The whole calculation takes typically a few seconds and the online interface will return the total energy of the input structure. Obviously, these calculations are not limited to zeolites, but can be applied to any materials that the current G-NN potentials are able to handle.
For zeolites, as shown in Fig. 5b, we have analyzed all existing zeolite frameworks which show that 245 out of 252 zeolites have the total energy below 0.18 eV per SiO2 f.u. and the remaining 7 zeolites with the energy above 0.18 eV per SiO2 f.u. generally contain hetero-atoms, such as GaGeO for JST-type zeolite, not belonging to typical zeolites with Si–Al–P–O–H elements. Therefore, the 0.18 value can be utilized as a convenient measure to judge whether a proposed zeolite framework is likely to be synthesized or not. More works are currently carried out to include more elements in the G-NN potential, e.g. to handle the hetero-atoms and the organic molecules.
3.2 Prediction of zeolite morphology and exposed surfaces
Zeolite morphology is known to play important roles in the catalytic performance. For example, strong Lewis acid sites can easily be formed on the (010) orientation of ZSM-5 zeolite (MFI-type), whereas they are unlikely to occur at the (101) surface.83 Since the morphology of the material is largely determined by the surface energies, it is thus in principle possible to explore the equilibrium morphology using Wulff construction by computing the surface energies of zeolites.84 For the Si–O covalent bonding nature in the zeolite framework, the exposed surfaces of the zeolite should be terminated by silanol groups and the likely H-bonding network may contribute to the surface stability. The computational cost for exploring the likely surface configurations of different zeolites is thus too demanding for DFT calculations. The experimental progress is largely governed by trial-and-error practice.85Using the Si–Al–P–O–H G-NN potential, we have explored the low Miller index surfaces for all as-synthesized ∼250 zeolites with SiO2 composition. The surface energies are then utilized for constructing the Wulff morphology of the zeolite, as shown in the website https://www.lasphub.com/zeolite. This online database provides the simulated Wulff morphology plot, surface energy, Wulff area ratio and corresponding surface structure which are then compared with the experimental results, if available.86 The website provides the easy display of the morphology via cloud database-based data search.
In Fig. 6a, we show that for known zeolites the theoretically predicted morphology agrees well with the observation from experimentally synthesized zeolites, suggesting the general validity of thermodynamics in controlling the large size zeolite particles. For example, the AST-type zeolite has a bulk crystal of F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m symmetry and the morphology is predicted to be a truncated octahedron with the exposed surfaces being (001), (111) and (011). The experimentally synthesized material has a truncated octahedron structure, identical to theoretical prediction.87 Perhaps more importantly, the zeolite morphology database can be used to search for zeolites with the desired morphology. For example, five zeolites (AFS, CAS, ITR, MWW and SBN) are predicted to prefer the two-dimensional layered morphology, desirable for reducing the mass transfer resistance (Fig. 6b).88 It is worth noting that the NH3 adsorption energy is calculated by the G-NN-based static calculation with the harmonic thermodynamic correction. To take the anharmonic entropy effects into consideration at different temperatures, the G-NN-based MD simulation can be performed to obtain the more accurate NH3 adsorption energies.
3m symmetry and the morphology is predicted to be a truncated octahedron with the exposed surfaces being (001), (111) and (011). The experimentally synthesized material has a truncated octahedron structure, identical to theoretical prediction.87 Perhaps more importantly, the zeolite morphology database can be used to search for zeolites with the desired morphology. For example, five zeolites (AFS, CAS, ITR, MWW and SBN) are predicted to prefer the two-dimensional layered morphology, desirable for reducing the mass transfer resistance (Fig. 6b).88 It is worth noting that the NH3 adsorption energy is calculated by the G-NN-based static calculation with the harmonic thermodynamic correction. To take the anharmonic entropy effects into consideration at different temperatures, the G-NN-based MD simulation can be performed to obtain the more accurate NH3 adsorption energies.
3.3 Zeolite acidity prediction
ML potentials can also be utilized for the fast prediction of the zeolite Brønsted acidity, an important catalytic property of zeolites. The acidic density and strength of zeolites are experimentally measured by the adsorption of basic probe molecules (such as pyridine or ammonia) on the solid acid site in the zeolite framework.89–91 The acid density is related to the accessible acid site concentration and its strength is determined by the pKa of hydroxyl groups. These can be monitored by spectroscopy (e.g. nuclear magnetic resonance92) or by molecular desorption using the temperature-programmed desorption (TPD).93,94 While theoretical simulation may be utilized to compute the strength of Brønsted acids85,89 following the same procedure as an experiment (e.g. by evaluating ammonia adsorption energy), the huge configuration space for the possible acid sites and consequently the base adsorption structures prohibit a systematic and facile prediction of the acid strength for all likely zeolite structures. In practice, the large heterogeneity of acid sites in different locations of zeolites together with the variable Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al : P composition is the major obstacle to predict the relevant acid site from theory. The theoretical studies reported to date tend to focus on a particular zeolite with small periodicity and fixed Si
Al : P composition is the major obstacle to predict the relevant acid site from theory. The theoretical studies reported to date tend to focus on a particular zeolite with small periodicity and fixed Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al : P ratio for the purpose of explaining experimental results. For example, Mozgawa et al.94 simulated the NH3-TPD spectrum by calculating the NH3 adsorption energy at different acid sites on Cu-SSZ-13 zeolite based on DFT calculations. They manage to assign each desorption peak to the corresponding Brønsted acid sites.
Al : P ratio for the purpose of explaining experimental results. For example, Mozgawa et al.94 simulated the NH3-TPD spectrum by calculating the NH3 adsorption energy at different acid sites on Cu-SSZ-13 zeolite based on DFT calculations. They manage to assign each desorption peak to the corresponding Brønsted acid sites.
By developing a Si–Al–P–O–N–H six-element G-NN potential, we have managed to evaluate the NH3 adsorption energy on different Brønsted acid sites for all as-synthesized ∼250 zeolites with three common compositions (SAPO, Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al > 39 and Si
Al > 39 and Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al < 5). As a result, an online zeolite acidity database characterized by NH3 desorption temperature is now available from the website https://www.lasphub.com/zeolite, which provides easy access for a range of acid properties, including the simulated NH3-TPD plot, the skeleton stabilization energy, NH3 adsorption energy, desorption temperature and the corresponding atomic structure for the acid site structure. In these calculations, the free energy of NH3 adsorption is evaluated approximately by correcting the zero-point-energy with harmonic approximation and the entropy contribution of the gas phase molecule, as commonly practiced for heterogeneous catalysis calculations.95 For more accurate free energy calculation, the ML potential-based long-time MD simulation is required, which can account for the configuration and vibrational entropy beyond the harmonic approximation at finite temperatures.
Al < 5). As a result, an online zeolite acidity database characterized by NH3 desorption temperature is now available from the website https://www.lasphub.com/zeolite, which provides easy access for a range of acid properties, including the simulated NH3-TPD plot, the skeleton stabilization energy, NH3 adsorption energy, desorption temperature and the corresponding atomic structure for the acid site structure. In these calculations, the free energy of NH3 adsorption is evaluated approximately by correcting the zero-point-energy with harmonic approximation and the entropy contribution of the gas phase molecule, as commonly practiced for heterogeneous catalysis calculations.95 For more accurate free energy calculation, the ML potential-based long-time MD simulation is required, which can account for the configuration and vibrational entropy beyond the harmonic approximation at finite temperatures.
An example for the zeolite acidity results from the online query of SAPO-34 zeolite is shown in Fig. 7a and b; two major desorption peaks around 450–550 and 600–750 K are observed in the experimental and theoretically simulated NH3-TPD spectrum.96,97 The acid sites as characterized by a particular NH3-TPD temperature can be assigned readily and visualized in the zeolite acidity database (Fig. 7c). For example, the desorption peaks at 590 and 730 K correspond to the Brønsted acid sites originating from the oxygen atom linking the two d6r cages and the oxygen atom linking the two six-membered rings in one d6r cage, respectively (Fig. 7d). The establishment of the zeolite acidity database allows for a computer-aided design of Brønsted acids for zeolites.
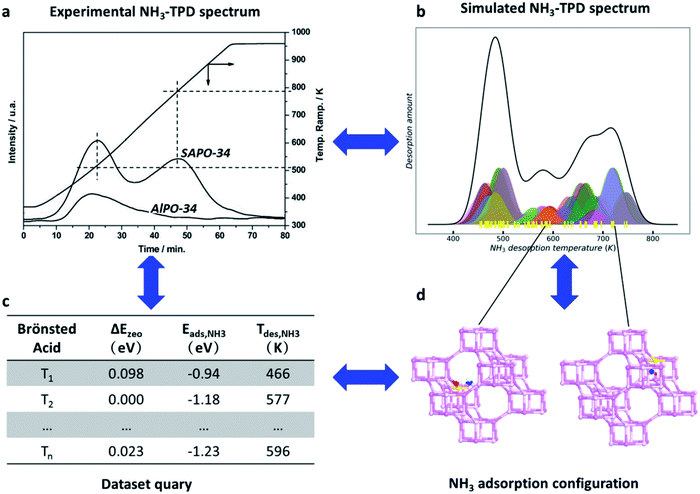 | ||
| Fig. 7 Online search of the Brønsted acid site structure and strength based on the simulated NH3-TPD spectrum. (a) The experimental NH3-TPD spectrum of SAPO-34 zeolite. Reproduced from ref. 96 with permission from American Chemical Society, copyright 2008. (b) The simulated NH3-TPD spectrum of SAPO-34 zeolite. (c) The zeolite acidity database including the skeleton stabilization energy (ΔEzeo), NH3 adsorption energy (Eads) and the NH3 desorption temperature (Tdes) for the different Brønsted acid sites. (d) The adsorption configurations of NH3 on different Brønsted acid sites. All data are now available at the website https://www.lasphub.com/zeolite. | ||
Based on the zeolite acidity database, we can easily screen out the zeolites with very strong Brønsted acid sites. At Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al > 39 with the most stable skeleton as the structure, by choosing the desorption temperature larger than 850 K (strong Brønsted acid site), we found that 24 zeolites hit the target. Among them, 11 zeolites (ATT, BIK, EON, GOO, JBW, MAZ, MON, MOR, SZR, THO and WEN) were already synthesized in the form of aluminosilicate with high Si
Al > 39 with the most stable skeleton as the structure, by choosing the desorption temperature larger than 850 K (strong Brønsted acid site), we found that 24 zeolites hit the target. Among them, 11 zeolites (ATT, BIK, EON, GOO, JBW, MAZ, MON, MOR, SZR, THO and WEN) were already synthesized in the form of aluminosilicate with high Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio (Si
Al ratio (Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al > 5) where 4 of them (BIK,98 MAZ,99 MOR93 and SZR100) have indeed been reported to have strong Brønsted acid sites.
Al > 5) where 4 of them (BIK,98 MAZ,99 MOR93 and SZR100) have indeed been reported to have strong Brønsted acid sites.
4. Outlook
This perspective overviews the present status of atomic simulations for zeolites, and presents a few showcases for the advanced ML potential applications in zeolite systems. Due to the characteristics of zeolites, i.e. containing many elements (commonly five elements Si–Al–P–O–H) with variable compositions, having rich microstructures and generally large periodicity, it has long been a big challenge to predict the structure and properties of zeolites. The ML potential as the recently developed theoretical method aims to describe the PES of complex material systems both accurately and economically and is thus expected to provide breakthrough contributions in the field of zeolite research.The accuracy in describing PES, without question, is the leading concern for ML potentials, particularly for such complex material systems as zeolites, where both the strong covalent bonding in the zeolite framework and the weak bonding between molecules and the zeolite wall are present. Because the accuracy of the ML potential is a complex issue, related to both the completeness of the training dataset and the architecture of ML potentials, it is still too early to comment on how far ML potentials can be utilized for complex material systems and also for the topics related to zeolites. It is, nevertheless, well established that the more fitting parameters the ML potential has, the more accurate the ML potential could be in fitting the training dataset but the slower the calculation would be. The accuracy and the speed are a pair of paradoxes that needs to be in balance in practice. In particular, in achieving the fast speed of ML potential calculations, the structure descriptors for an atom in ML potentials are generally limited to a short-to-medium range, e.g. a 5–8 Å circle around the atom, which inevitably causes the accuracy sacrifice in long-range interactions.
The G-NN potential developed by our group learns the global PES dataset and thus represents a type of ML potential with desirable transferability and good predictability to complex materials. The basic architecture of the G-NN is the atom-wise NN (one NN producing one atomic energy), and a multiple-net architecture has been developed in order to further improve the accuracy and increase the ability to describe multiple element systems. In this new architecture, each element can be represented by multiple NNs with the total energy being the sum of all NN energies, as shown in Fig. 8.48 In contrast to the basic architecture where the atomic energy of an atom is only contributed by a NN describing the whole local environment of the atom, the multiple-net architecture can let the atomic energy of this atom be constituted by several partial energies from multiple NNs, each net representing a different local environment. This provides a simple way to train and add extra elements upon an original G-NN potential without losing the accuracy. For example, a Si–Al–P–O–C–H–N 7-element potential can be upgraded upon the Si–Al–P–O–C–H 6-element potential using the double-net scheme by amending the dataset for those related to NH3 adsorption in zeolites, which has been utilized to predict the acid strength of zeolites as introduced in Section 3.3.
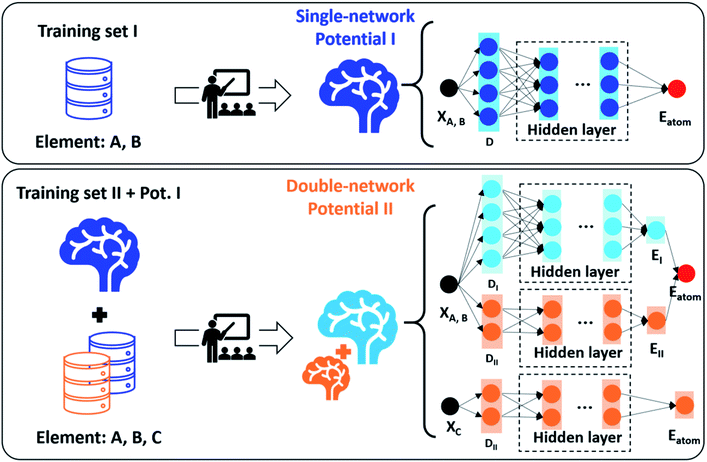 | ||
| Fig. 8 A schematic illustration of the double-network framework. X represents the Cartesian coordinates of each atom. Eatom represents the atomic energy of each atom. D represents the structural descriptor. Reproduced from ref. 48 with permission from AIP Publishing, copyright 2021, licensed under a Creative Commons Attribution (CC BY) license. | ||
Another promising way to improve the accuracy could be the incorporation of the many-body expansion in eqn (3), which can be introduced to explicitly describe the long-range interaction. The long-range interaction is often small in contribution but plays key roles in kinetics. Considering that the current NN potential can already provide good descriptions for local interactions that are dominant in energy, the implementation of the many-body expansion could act as the appendix function to introduce explicit two-body and three-body interaction terms. The idea has recently been implemented in the G-NN architecture released in the latest version of LASP code. Alternatively, the electrostatic part of long-range interaction was recently suggested to be included as the Coulomb energy based on the atomic charge either from first principles data or fitted from self-consistent charge equilibration schemes.101 In addition, the van der Waals (vdW) interaction should also be considered appropriately, either being included in the total energy of the training dataset (e.g. using the BEEF-vdW functional102) or being trained separately as an additional term.103
Apart from the accuracy concerns in ML potentials, it is now perhaps more urgent to generate as many as possible ML potentials for different applications in zeolites. From our experience, while it is extremely difficult to go beyond ten elements in the current ML potentials, the generation of ML potentials with up to 7 elements to describe the PES of zeolite-related applications is now realizable with the help of supercomputing facilities. For example, not limited to catalysts, zeolites have also been used as the membrane material for separating gases (CO2, CH4, etc.)104 and recently as a solid electrolyte for solid-state lithium ion batteries.105 These applications ask for detailed knowledge on the diffusion and migration of gas molecules and alkali metal cations in zeolites. The construction of ML potentials for these systems and creation of the user-friendly online database would certainly be beneficial for researchers in the field to accelerate the material design.
While the large-scale atomic simulations, e.g. beyond five thousand atoms, are highly desirable for elucidating the mechanism of zeolite growth, they were however seldom performed within the current ML potential framework. This is to a large extent because the speed of the current ML potential is not fast enough and it is still difficult to carry out such large-scale simulations to a long-time scale (e.g. 1 ms). The computational cost of ML potentials comes mainly from two parts, the calculation of many structural descriptors and the evaluation of the ML model, the former of which cannot be readily expedited even with the latest GPU hardware. The less-computational-demanding ML potential is certainly a key research direction in the future, which may involve the modification of the ML architecture34 and the development of new structure descriptors, e.g. being more efficient in parallel computation.106 The commercial packages that combine the power of the CPU and GPU, such as TensorFlow, Caffe, and MXNet, should also enlighten the development of more efficient ML potentials, particularly on constructing new ML models and solving numerically the ML model.
Finally, we may add comments on that the concomitant efforts in collecting and generating data are absolutely important in the ML era. In the zeolite field there are already good databases on structures, e.g. IZA-SC zeolite structure dataset12 with all as-synthesized zeolite structure parameter information; Yu AlPO structure dataset107 with over 200 AlPO structures from the literature; DEEM hypothetical zeolite topology structure dataset52 with millions of hypothetical zeolite structures; LASP zeolite database on Wulff morphology dataset86 and acidity;97 Sholl 2D zeolitic slab dataset84 with 650![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 2D zeolitic slabs and ∼150
000 2D zeolitic slabs and ∼150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 slab termination pairs; Gomez-Bombarelli SDAs-zeolite dataset108 with SDA-zeolite pair structures and related interaction energy. The data exchange and method sharing between research groups need to be easier and transparent. It may not be surprising that more application-orientated zeolite databases, e.g. those related to particular catalytic reactions, appear in the future that prove their value in the ML-based material design. Overall, for the great structure diversity of zeolites and their vast applications, there is ample room to develop new ML methods and apply these new technologies for expediting the fundamental research and applications of zeolites.
000 slab termination pairs; Gomez-Bombarelli SDAs-zeolite dataset108 with SDA-zeolite pair structures and related interaction energy. The data exchange and method sharing between research groups need to be easier and transparent. It may not be surprising that more application-orientated zeolite databases, e.g. those related to particular catalytic reactions, appear in the future that prove their value in the ML-based material design. Overall, for the great structure diversity of zeolites and their vast applications, there is ample room to develop new ML methods and apply these new technologies for expediting the fundamental research and applications of zeolites.
Data availability
All reported data in this paper can be found in the related references and the website of https://www.lasphub.com/zeolite.Author contributions
Z.-P. Liu conceived the project and contributed to the design of the writing logic. S. Ma summarize the references, wrote the draft and established the website. All the authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key Research and Development Program of China (2018YFA0208600), National Science Foundation of China (12188101, 22033003, 91945301, 91745201) and the Tencent Foundation for XPLORER PRIZE.Notes and references
- K. Na, C. Jo, J. Kim, K. Cho, J. Jung, Y. Seo, R. J. Messinger, B. F. Chmelka and R. Ryoo, Science, 2011, 333, 328–332 CrossRef CAS.
- J. Y. Li, J. H. Yu, W. F. Yan, Y. H. Xu, W. G. Xu, S. L. Qiu and R. R. Xu, Chem. Mater., 1999, 11, 2600–2606 CrossRef CAS.
- J. H. Yu, J. Y. Li, K. X. Wang, R. R. Xu, K. Sugiyama and O. Terasaki, Chem. Mater., 2000, 12, 3783–3787 CrossRef CAS.
- J. Yu and R. Xu, Acc. Chem. Res., 2010, 43, 1195–1204 CrossRef CAS PubMed.
- Y. Jin, Q. Sun, G. Qi, C. Yang, J. Xu, F. Chen, X. Meng, F. Deng and F.-S. Xiao, Angew. Chem., Int. Ed., 2013, 52, 9172–9175 CrossRef CAS PubMed.
- S. S. Arora, D. L. S. N. Ieskens, A. Malek and A. Bhan, Nat. Catal., 2018, 1, 666–672 CrossRef CAS.
- I. Yarulina, K. De Wispelaere, S. Bailleul, J. Goetze, M. Radersma, E. Abou-Hamad, I. Vollmer, M. Goesten, B. Mezari, E. J. M. Hensen, J. S. Martinez-Espin, M. Morten, S. Mitchell, J. Perez-Ramirez, U. Olsbye, B. M. Weckhuysen, V. Van Speybroeck, F. Kapteijn and J. Gascon, Nat. Chem., 2018, 10, 897 CrossRef CAS PubMed.
- M. Treacy, I. Rivin, E. Balkovsky, K. Randall and M. Foster, Microporous Mesoporous Mater., 2004, 74, 121–132 CrossRef CAS.
- S. M. Woodley and R. Catlow, Nat. Mater., 2008, 7, 937–946 CrossRef CAS.
- R. Pophale, P. A. Cheeseman and M. W. Deem, Phys. Chem. Chem. Phys., 2011, 13, 12407–12412 RSC.
- M. Moliner, Y. Roman-Leshkov and A. Corma, Acc. Chem. Res., 2019, 52, 2971–2980 CrossRef CAS PubMed.
- IZA-SC bank, https://www.iza-structure.org/databases.
- P. Del Campo, C. Martinez and A. Corma, Chem. Soc. Rev., 2021, 50, 8511–8595 RSC.
- B. M. Weckhuysen and J. Yu, Chem. Soc. Rev., 2015, 44, 7022–7024 RSC.
- M. Shamzhy, M. Opanasenko, P. Concepcion and A. Martinez, Chem. Soc. Rev., 2019, 48, 1095–1149 RSC.
- D. Schwalbe-Koda, S. Kwon, C. Paris, E. Bello-Jurado, Z. Jensen, E. Olivetti, T. Willhammar, A. Corma, Y. Román-Leshkov, M. Moliner and R. Gómez-Bombarelli, Science, 2021, 374, 308–315 CrossRef CAS PubMed.
- J. E. Schmidt, M. W. Deem and M. E. Davis, Angew. Chem., Int. Ed., 2014, 53, 8372–8374 CrossRef CAS PubMed.
- A. Ghysels, S. L. C. Moors, K. Hemelsoet, K. De Wispelaere, M. Waroquier, G. Sastre and V. Van Speybroeck, J. Phys. Chem. C, 2015, 119, 23721–23734 CrossRef CAS.
- M. J. Sanders, M. Leslie and C. R. A. Catlow, J. Chem. Soc., Chem. Commun., 1984, 1271–1273 RSC.
- A. Gabrieli, M. Sant, P. Demontis and G. B. Suffritti, J. Phys. Chem. C, 2013, 117, 503–509 CrossRef CAS.
- J. B. Nicholas, A. J. Hopfinger, F. R. Trouw and L. E. Iton, J. Am. Chem. Soc., 1991, 113, 4792–4800 CrossRef CAS.
- A. M. Thomas, S. Nag, D. K. Yadav, S. Uniyal, S. Uma and Y. Subramanian, Microporous Mesoporous Mater., 2020, 300, 110119 CrossRef CAS.
- Z. P. Liu, P. Hu and A. Alavi, J. Am. Chem. Soc., 2002, 124, 14770–14779 CrossRef CAS PubMed.
- Z. P. Liu and P. Hu, J. Am. Chem. Soc., 2003, 125, 1958–1967 CrossRef CAS PubMed.
- E. T. C. Vogt and B. M. Weckhuysen, Chem. Soc. Rev., 2015, 44, 7342–7370 RSC.
- V. Van Speybroeck, K. De Wispelaere, J. Van der Mynsbrugge, M. Vandichel, K. Hemelsoet and M. Waroquier, Chem. Soc. Rev., 2014, 43, 7326–7357 RSC.
- T. W. Ko, J. A. Finkler, S. Goedecker and J. Behler, Acc. Chem. Res., 2021, 54, 808–817 CrossRef CAS PubMed.
- P. O. Dral, J. Phys. Chem. Lett., 2020, 11, 2336–2347 CrossRef CAS.
- M. Kulichenko, J. S. Smith, B. Nebgen, Y. W. Li, N. Fedik, A. I. Boldyrev, N. Lubbers, K. Barros and S. Tretiak, J. Phys. Chem. Lett., 2021, 12, 6227–6243 CrossRef CAS.
- J. B. Witkoskie and D. J. Doren, J. Chem. Theory Comput., 2005, 1, 14–23 CrossRef CAS PubMed.
- T. B. Blank, S. D. Brown, A. W. Calhoun and D. J. Doren, J. Chem. Phys., 1995, 103, 4129–4137 CrossRef CAS.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed.
- J. Behler, Chem. Rev., 2021, 121, 10037–10072 CrossRef CAS PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- N. Lubbers, J. S. Smith and K. Barros, J. Chem. Phys., 2018, 148, 241715 CrossRef PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- A. P. Bartók and G. Csányi, Int. J. Quantum Chem., 2015, 115, 1051–1057 CrossRef.
- J. Y. Xu, X. M. Cao and P. Hu, J. Chem. Theory Comput., 2021, 17, 4465–4476 CrossRef CAS PubMed.
- A. V. Shapeev, Multiscale Model. Simul., 2016, 14, 1153–1173 CrossRef.
- J. Behler, J. Phys.: Condens. Matter, 2014, 26, 183001–1830024 CrossRef CAS PubMed.
- J. Behler, Angew. Chem., Int. Ed., 2017, 56, 12828–12840 CrossRef CAS PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B, 2013, 87, 184115 CrossRef.
- S.-D. Huang, C. Shang, P.-L. Kang and Z.-P. Liu, Chem. Sci., 2018, 9, 8644–8655 RSC.
- S. Ma, C. Shang and Z.-P. Liu, J. Chem. Phys., 2019, 151, 050901 CrossRef.
- P. L. Kang, C. Shang and Z. P. Liu, Acc. Chem. Res., 2020, 53, 2119–2129 CrossRef CAS PubMed.
- S. D. Huang, C. Shang, P. L. Kang, X. J. Zhang and Z. P. Liu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, e1415 CAS.
- P. L. Kang, C. Shang and Z. P. Liu, Chin. J. Chem. Phys., 2021, 34, 583–590 CrossRef CAS.
- Y. Li, J. Yu and R. Xu, Angew. Chem., Int. Ed., 2013, 52, 1673–1677 CrossRef CAS PubMed.
- Y. G. Bushuev and G. Sastre, J. Phys. Chem. C, 2010, 114, 19157–19168 CrossRef CAS.
- S. Ma, C. Shang, C.-M. Wang and Z.-P. Liu, Chem. Sci., 2020, 11, 10113–10118 RSC.
- DEEM hypothetical zeolite database, https://www.hypotheticalzeolites.net.
- G. J. McIntosh, Phys. Chem. Chem. Phys., 2013, 15, 17496–17509 RSC.
- H. Henschel, A. M. Schneider and M. H. Prosenc, Chem. Mater., 2010, 22, 5105–5111 CrossRef CAS.
- T. T. Trinh, A. P. J. Jansen, R. A. van Santen and E. J. Meijer, Phys. Chem. Chem. Phys., 2009, 11, 5092–5099 RSC.
- T. T. Trinh, A. P. J. Jansen, R. A. van Santen, J. VandeVondele and E. J. Meijer, ChemPhysChem, 2009, 10, 1775–1782 CrossRef CAS PubMed.
- X. Q. Zhang, T. T. Trinh, R. A. van Santen and A. P. J. Jansen, J. Am. Chem. Soc., 2011, 133, 6613–6625 CrossRef CAS PubMed.
- X. L. Cheng, D. R. Chen and Y. J. Liu, ChemPhysChem, 2012, 13, 2392–2404 CrossRef CAS PubMed.
- X. Q. Zhang, T. T. Trinh, R. A. van Santen and A. P. J. Jansen, J. Phys. Chem. C, 2011, 115, 9561–9567 CrossRef CAS.
- T. T. Trinh, K. Q. Tran, X. Q. Zhang, R. A. van Santen and E. J. Meijer, Phys. Chem. Chem. Phys., 2015, 17, 21810–21818 RSC.
- X. Liu, C. Liu, Z. Feng and C. G. Meng, ACS Omega, 2021, 6, 22811–22819 CrossRef CAS PubMed.
- N. L. Mai, H. Do, N. H. Hoang, A. H. Nguyen, K. Q. Tran, E. J. Meijer and T. T. Trinh, J. Phys. Chem. B, 2020, 124, 10210–10218 CrossRef CAS PubMed.
- C. S. Yang, J. M. Mora-Fonz and C. R. A. Catlow, J. Phys. Chem. C, 2012, 116, 22121–22128 CrossRef CAS.
- V. Van Speybroeck, K. Hemelsoet, L. Joos, M. Waroquier, R. G. Bell and C. R. A. Catlow, Chem. Soc. Rev., 2015, 44, 7044–7111 RSC.
- D. W. Lewis, D. J. Willock, C. R. A. Catlow, J. M. Thomas and G. J. Hutchings, Nature, 1996, 382, 604–606 CrossRef CAS.
- E. L. First, C. E. Gounaris, J. Wei and C. A. Floudas, Phys. Chem. Chem. Phys., 2011, 13, 17339–17358 RSC.
- T. F. Willems, C. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- F. Daeyaert, F. D. Ye and M. W. Deem, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 3413–3418 CrossRef CAS PubMed.
- J. M. Bennett and R. M. Kirchner, Zeolites, 1992, 12, 338–342 CrossRef CAS.
- R. Xu, W. Pang, J. Yu, Q. Huo and J. Chen, Chemistry of Zeolites and Related porous Materials: Synthesis and Structure, Wiley Online Books, 2007, p. 17 Search PubMed.
- M. Moliner, F. Rey and A. Corma, Angew. Chem., Int. Ed., 2013, 52, 13880–13889 CrossRef CAS PubMed.
- X. G. Guo, G. Z. Fang, G. Li, H. Ma, H. J. Fan, L. Yu, C. Ma, X. Wu, D. H. Deng, M. M. Wei, D. L. Tan, R. Si, S. Zhang, J. Q. Li, L. T. Sun, Z. C. Tang, X. L. Pan and X. H. Bao, Science, 2014, 344, 616–619 CrossRef CAS PubMed.
- L. C. Liu and A. Corma, Nat. Catal., 2021, 4, 453–456 CrossRef CAS.
- L. C. Liu, M. Lopez-Haro, C. W. Lopes, S. Rojas-Buzo, P. Concepcion, R. Manzorro, L. Simonelli, A. Sattler, P. Serna, J. J. Calvino and A. Corma, Nat. Catal., 2020, 3, 628–638 CrossRef CAS.
- H. Wang, L. Wang and F. S. Xiao, ACS Cent. Sci., 2020, 6, 1685–1697 CrossRef CAS PubMed.
- A. Corma, Chem. Rev., 1995, 95, 559–614 CrossRef CAS.
- A. Bhan and E. Iglesia, Acc. Chem. Res., 2008, 41, 559–567 CrossRef CAS PubMed.
- U. Olsbye, S. Svelle, K. P. Lillerud, Z. H. Wei, Y. Y. Chen, J. F. Li, J. G. Wang and W. B. Fan, Chem. Soc. Rev., 2015, 44, 7155–7176 RSC.
- P. L. Kang, C. Shang and Z. P. Liu, J. Am. Chem. Soc., 2019, 141, 20525–20536 CrossRef CAS PubMed.
- T. Bucko, M. Gesvandtnerova and D. Rocca, J. Chem. Theory Comput., 2020, 16, 6049–6060 CrossRef CAS PubMed.
- M. Gešvandtnerová, D. Rocca and T. Bučko, J. Catal., 2021, 396, 166–178 CrossRef.
- S. Ma and Z.-P. Liu, Nat. Commun., 2022 Search PubMed , accepted.
- L. Treps, A. Gomez, T. de Bruin and C. Chizallet, ACS Catal., 2020, 10, 3297–3312 CrossRef CAS.
- O. Knio, A. J. Medford, S. Nair and D. S. Sholl, Chem. Mater., 2019, 31, 353–364 CrossRef CAS.
- C. Chizallet, ACS Catal., 2020, 10, 5579–5601 CrossRef CAS.
- Liu zeolite thermodynamic wulff morphology dataset, https://www.lasphub.com/zeolite/.
- S. I. Zones, S. J. Hwang, S. Elomari, I. Ogino, M. E. Davis and A. W. Burton, C. R. Chim., 2005, 8, 267–282 CrossRef CAS.
- E. Schulman, W. Wu and D. X. Liu, Materials, 2020, 13, 1822 CrossRef CAS PubMed.
- M. Boronat and A. Corma, ACS Catal., 2019, 9, 1539–1548 CrossRef CAS PubMed.
- C. Liu, I. Tranca, R. A. van Santen, E. J. M. Hensen and E. A. Pidko, J. Phys. Chem. C, 2017, 121, 23520–23530 CrossRef CAS PubMed.
- K. Gora-Marek and I. Melian-Cabrera, Microporous Mesoporous Mater., 2021, 310, 110638 CrossRef CAS.
- D. H. Brouwer, R. J. Darton, R. E. Morris and M. H. Levitt, J. Am. Chem. Soc., 2005, 127, 10365–10370 CrossRef CAS PubMed.
- F. Lonyi and J. Valyon, Microporous Mesoporous Mater., 2001, 47, 293–301 CrossRef CAS.
- B. Mozgawa, F. Zasada, M. Fedyna, K. Góra-Marek, E. Tabor, K. Mlekodaj, J. Dědeček, Z. Zhao, P. Pietrzyk and Z. Sojka, Chem.–Eur. J., 2021, 27, 17159 CrossRef CAS PubMed.
- J. K. Nørskov, F. Studt, F. Abild-Pedersen and T. Bligaard, Fundamental concepts in heterogeneous catalysis, John Wiley & Sons, 2014 Search PubMed.
- G. V. A. Martins, G. Berlier, C. Bisio, S. Coluccia, H. O. Pastore and L. Marchese, J. Phys. Chem. C, 2008, 112, 7193–7200 CrossRef CAS.
- Liu zeolite acidity dataset, https://www.lasphub.com/zeolite/.
- E. G. Derouane, J. C. Vedrine, R. R. Pinto, P. M. Borges, L. Costa, M. A. N. D. A. Lemos, F. Lemos and F. R. Ribeiro, Catal. Rev.: Sci. Eng., 2013, 55, 454–515 CrossRef CAS.
- P. Rejmak, J. Datka and E. Broclawik, Int. J. Quantum Chem., 2019, 119, e25873 CrossRef.
- Z. Xiong, E. Zhan, M. Li and W. Shen, Chem. Commun., 2020, 56, 3401–3404 RSC.
- T. W. Ko, J. A. Finkler, S. Goedecker and J. Behler, Nat. Commun., 2021, 12, 398 CrossRef CAS PubMed.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B, 2012, 85, 235149 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- N. Kosinov, J. Gascon, F. Kapteijn and E. J. M. Hensen, J. Membr. Sci., 2016, 499, 65–79 CrossRef CAS.
- X. W. Chi, M. L. Li, J. C. Di, P. Bai, L. N. Song, X. X. Wang, F. Li, S. Liang, J. J. Xu and J. H. Yu, Nature, 2021, 592, 551–557 CrossRef CAS PubMed.
- C. Shang, S. D. Huang and Z. P. Liu, J. Comput. Chem., 2019, 40, 1091–1096 CrossRef CAS PubMed.
- Yu AlPO structure dataset, https://zeobank.jlu.edu.cn/.
- Gomez-Bombarelli SDAs-zeolite dataset, https://zeodb.mit.edu/.
| This journal is © The Royal Society of Chemistry 2022 |