Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Measurement of gas-phase OH radical oxidation and film thickness of organic films at the air–water interface using material extracted from urban, remote and wood smoke aerosol†
Rosalie H.
Shepherd
ab,
Martin D.
King
 *b,
Adrian R.
Rennie
*b,
Adrian R.
Rennie
 c,
Andrew D.
Ward
c,
Andrew D.
Ward
 a,
Markus M.
Frey
a,
Markus M.
Frey
 d,
Neil
Brough‡
d,
Neil
Brough‡
 d,
Joshua
Eveson
d,
Sabino
Del Vento
d,
Adam
Milsom
d,
Joshua
Eveson
d,
Sabino
Del Vento
d,
Adam
Milsom
 f,
Christian
Pfrang
f,
Christian
Pfrang
 f,
Maximilian W. A.
Skoda
f,
Maximilian W. A.
Skoda
 e and
Rebecca J. L.
Welbourn
e and
Rebecca J. L.
Welbourn
 e
e
aCentral Laser Facility, Research Complex at Harwell, STFC Rutherford Appleton Laboratory, Oxford, OX11 0FA, UK
bDepartment of Earth Sciences, Royal Holloway, University of London, Egham, Surrey, TW20 0EX, UK. E-mail: m.king@rhul.ac.uk
cDepartment of Chemistry – Ångström Laboratory, Uppsala University, 75121 Uppsala, Sweden
dBritish Antarctic Survey, Natural Environment Research Council, High Cross, Madingley Road, Cambridge, CB3 0ET, UK
eISIS Pulsed Neutron and Muon Source, Rutherford Appleton Laboratory, Oxford, OX11 0QX, UK
fSchool of Geography, Earth and Environmental Sciences, The University of Birmingham, Birmingham, B15 2TT, UK
First published on 12th April 2022
Abstract
The presence of an organic film on a cloud droplet or aqueous aerosol particle has the potential to alter the chemical, optical and physical properties of the droplet or particle. In the study presented, water insoluble organic materials extracted from urban, remote (Antarctica) and wood burning atmospheric aerosol were found to have stable, compressible, films at the air–water interface that were typically ∼6–18 Å thick. These films are reactive towards gas-phase OH radicals and decay exponentially, with bimolecular rate constants for reaction with gas-phase OH radicals of typically 0.08–1.5 × 10−10 cm3 molecule−1 s−1. These bimolecular rate constants equate to initial OH radical uptake coefficients estimated to be ∼0.6–1 except woodsmoke (∼0.05). The film thickness and the neutron scattering length density of the extracted atmosphere aerosol material (from urban, remote and wood burning) were measured by neutron reflection as they were exposed to OH radicals. For the first time neutron reflection has been demonstrated as an excellent technique for studying the thin films formed at air–water interfaces from materials extracted from atmospheric aerosol samples. Additionally, the kinetics of gas-phase OH radicals with a proxy compound, the lipid 1,2-distearoyl-sn-glycero-3-phosphocholine (DSPC) was studied displaying significantly different behaviour, thus demonstrating it is not a good proxy for atmospheric materials that may form films at the air–water interface. The atmospheric lifetimes, with respect to OH radical oxidation, of the insoluble organic materials extracted from atmospheric aerosol at the air–water interface were a few hours. Relative to a possible physical atmospheric lifetime of 4 days, the oxidation of these films is important and needs inclusion in atmospheric models. The optical properties of these films were previously reported [Shepherd et al., Atmos. Chem. Phys., 2018, 18, 5235–5252] and there is a significant change in top of the atmosphere albedo for these thin films on core–shell atmospheric aerosol using the film thickness data and confirmation of stable film formation at the air–water interface presented here.
Environmental significanceOrganic films on cloud droplets or aqueous aerosol particles may alter the chemical, optical and physical properties of the droplets or particles. Measurement of the (I) film thickness formed by typical atmospheric materials is critical for calculation of light scattering by core–shell aerosol and (II) oxidation lifetime of the film by OH radicals is important for an assessment of atmospheric persistence. Organic film material extracted from atmospheric aerosol is shown to form stable compressible films at the air-water interface that are ∼6–18 Å thick and reactive towards atmospheric oxidation by OH radicals with chemical lifetimes competitive with comparable to aerosol residence times. Film material extracted from urban, Antarctic and wood-burning was shown be different to a model lipid compound. |
1 Introduction
Atmospheric aerosols have a crucial role in global climate1,2 they contribute directly to global climate by either warming or cooling the planet by absorption or scattering incoming solar radiation, and indirectly affect global climate via cloud condensation effects.1,3 However, current knowledge of atmospheric aerosols is far from complete.4,5Aqueous aerosol and cloud droplets are susceptible to organic film formation at the air–water interface.6–11 The presence of such a film may change the chemical and physical properties through (a) reducing the rate of evaporation,12–15 (b) inhibiting the transport of chemicals from the gas to the liquid phase,6 (c) reducing the scavenging of the droplet or aerosol by larger cloud and ice particles,3,16 (d) altering the cloud condensation nuclei activation potential,17,18 (e) changing the optical properties of the droplet or aerosol7 and (f) altering the reactive uptake ability.19 An organic film at the air–water interface is susceptible to oxidation owing to atmospheric chemistry,20–23 a consequence of which is film ageing.24,25 For the purpose of atmospheric modelling the aerosol could be considered to behave as either an uncoated aerosol or a coated aerosol if the oxidation lifetime of the chemical film is less than a few seconds or greater than ∼10 days,26 respectively. However, an oxidation lifetime between the extremes would require oxidation of the film to be considered in atmospheric aerosol modelling; therefore understanding the chemical oxidation lifetime of the organic film is paramount. Previously it has been shown that it is critical to use good proxies for real material extracted from the atmosphere for such studies.25
Despite vast developments in our knowledge of atmospheric aerosol, current understanding of the physical and chemical characteristics is still limited.27,28 The present study broadens knowledge of organic films on atmospheric aerosols by directly investigating the oxidation with gas-phase OH radicals of films from urban atmospheric aerosol sourced at Royal Holloway, University of London, remote atmospheric aerosol sourced from Antarctica and wood smoke aerosol. Alongside the remote atmospheric aerosol, organic extracts from Antarctic seawater were also collected. The sea-surface micro-layer and sub-surface layer contain many natural and anthropogenic organic materials21,22,29–33 that will enter the atmosphere through bubbles bursting when waves break or from surface wind generating aerosol droplets.7,34–36 The four samples may be interpreted as being from polluted urban, biomass burning, remote marine atmospheric aerosols and seawater. The refractive indices of these samples have previously been studied and reported.37
Thin films present at air–water interfaces have been studied by a variety of techniques including X-ray and neutron studies24,38–42 and laser studies.43–47 In the present work, neutron reflectivity was used to study oxidation of thin films extracted from atmospheric samples at the air–water interface. Oxidation chemistry of proxy-organic films have been studied previously, examples include oleic acid,24,38,48,49 pinonic acid,50 anthracene,51 lipids52–54 and methyl oleate.24 The use of OH radicals as the atmospheric oxidant has additionally featured in a number of studies.55,56 The present study extends previous work that used proxies by investigating the oxidation kinetics of material extracted from the atmosphere as a thin film at the air–water interface. Once the film is spread at the air–water interface, the thickness of the film and neutron scattering length density were determined by measurement of the neutron reflectivity: the scattering length density of a material is dependent on its elemental composition and density, as will be explained in Section 2.2. In addition, the reaction kinetics for the films when oxidized by gas-phase OH radicals was determined. The oxidation reaction was followed through continuous collection of neutron reflectivity profiles that allowed the neutron scattering length density per unit area of the interfacial layer to be followed with time. A bimolecular rate constant for the oxidation reaction was determined and a kinetic model57 was fitted to the data and used to estimate the chemical lifetime of the film with respect to OH radical oxidation in the atmosphere. OH radicals are a very reactive, lower atmosphere, oxidants present during the daytime,58,59 and at a lower mixing ratio at night. OH radicals react with both saturated and unsaturated organic material.60 Lipids are commonly used as proxies for films on atmospheric aerosols.45,61–65 Hence, through comparing the reaction kinetics of DSPC with atmospheric aerosol extract under the same conditions, the validity of using lipids as proxy aerosols could be probed. The reaction between the deuterated lipid 1,2-distearoyl-sn-glycero-3-phosphocholine (DSPC) and gas-phase OH radicals was also studied to determine whether DSPC could be used as a kinetic proxy compound for organic films extracted from atmospheric matter and as a model reaction substrate as the materials collected from the atmosphere are limited.
2 Experimental
The air–water interface was formed in a shallow polytetrafluoroethylene (PTFE) trough enclosed in a Tedlar bag; the bag was sealed to allow the development of the appropriate gaseous oxidising environment above the film. Film thickness and neutron scattering length density of the atmospheric aerosol film and how the film alters upon oxidation with gas-phase OH radicals was studied with neutron reflection techniques.382.1 Sample collection and extraction of atmospheric aerosol
Urban, remote and wood smoke atmospheric aerosol extracts as well as remote seawater samples were collected. Urban aerosol was collected ∼15 m above the ground on the campus of Royal Holloway, University of London; urban aerosol was continuously collected for over a year in ∼30 day periods. The aerosols collected from the sampling point represent aerosols likely to be found in polluted air from London. Additionally, owing to the proximity to three major motorways M25, M40 and M4 (approximately 2–7 km away) and the large international airport Heathrow (approximately 10 km away), the samples were categorised as urban. Remote aerosol and seawater samples were collected from coastal Antarctica; two Antarctica aerosol filter samples were collected at the Halley Clean Air Sector Laboratory operated by the British Antarctic Survey during the 2015 and 2016 southern hemisphere summers.66 For each sample, atmospheric aerosol was continuously sampled for approximately 60 days. A sample of Antarctic seawater was collected on a sea ice cruise ship in the Weddell Sea (Antarctica) during the southern summer of 2014. Wood smoke aerosol was collected from the chimney of a domestic wood burner; the fire was kept burning for six hours with seasoned wood (Wild Cherry), aerosol being collected continuously. For all samples, analytical blanks were collected to account for any filter contamination. To ensure there was an accurate representation of all possible contamination, the analytical blanks travelled to the sample sites under identical conditions to the filters used for aerosol collections.To collect the urban atmospheric aerosol, air was pulled through short sections (10 cm × 1/4′′ OD) of clean stainless-steel pipelines into a filter holder using an air pump at a flow of 30 L min−1 at local ambient temperature and pressure and caught on pre-combusted 47 mm quartz filters (SKC) encased within perfluoroalkoxy (PFA) Savillex filter holders. To collect remote atmospheric aerosol extracts ambient air was sampled from a half metre length of quarter inch OD perfluoroalkoxy tubing onto a filter holder using a Staplex low volume air sampler (Model VM-4) at a flow rate of 20 L min−1 at local ambient temperature and pressure. A more robust filter holder was required to collect wood smoke aerosol. These samples were collected on the same type of filters, but housed in aluminium and steel filter holders machined at Royal Holloway, University of London that had the same internal dimensions as the Savillex commercial filter holder. All instrumentation used in sample collection was cleaned with ultrapure water (>18 MΩ cm) and chloroform (Sigma-Aldrich, 0.5–1% ethanol as stabilizer) multiple times and were assembled and dissembled in a clean glove bag. After collection, sample plus filter were stored in the dark at −18 °C in clean glass Petri dishes until extraction.
To prepare the samples for use in the neutron reflection experiments, each filter was cut in half in a glove bag to avoid contamination. One half was for extraction, the other half was stored in the dark at −18 °C. The filter half was placed in a sealed glass conical flask with 10 mL of chloroform and 10 mL of water and very gently sonicated for five minutes and then filtered through a pre-combusted quartz filter (SKC) to remove the original filter paper. The chloroform fraction contained any organic material from the aerosol which could form an insoluble film at the air–water interface.67 The chloroform was separated from the water and subsequently evaporated under nitrogen leaving behind the organic atmospheric aerosol extract as a wax or oily residue, depending on the aerosol source. To the residue, 2 mL of chloroform was added. The sample was stored in amber glass bottles at −18 °C in the dark until use on the beam line. More detailed information on the extraction process can be found elsewhere.37
For the Antarctic seawater sample: approximately, 1 L of remote seawater was pumped from a water depth of ∼10 m using the ship's continuous water sampling. The water was collected in a prepared PTFE travel jar, which was subsequently sealed and frozen at −18 °C until analysis in the UK. Detritus was separated from the seawater samples by first filtering the water into a clean glass beaker. The water sample was subsequently shaken and extracted with chloroform in the method applied for atmospheric aerosol. To the resultant residue, again 2 mL of chloroform was added and the sample stored in amber glass bottles at −18 °C in the dark until use on the beam line. All glassware was cleaned with ultra-pure water and chloroform before use and all sample preparation was conducted in a clean environment and or glove bags. DSPC was purchased from Avanti Polar Lipids.
2.2 Neutron reflection
Using the neutron reflectometer INTER at ISIS Pulsed Neutron and Muon Source, Rutherford Appleton Laboratory, Oxfordshire,68 specular neutron reflectivity as a function of momentum transfer of thermal neutrons was collected to give neutron reflectivity profiles. Specular reflectivity is the ratio of intensity of the reflected neutron beam to that of the incident neutron beam onto the sample, whilst neutron momentum, Q, is defined as:39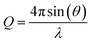 | (1) |
In the present study, the film thickness and neutron scattering length density of the atmospheric aerosol extract films were determined.38 The neutron scattering length density, ρ, is defined as:39
| ρ = ∑nibi | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8.1 volume ratio of water and deuterium oxide forms a solution with an effective neutron scattering length density of zero. The solution is called air-contrast-matched-water and was used as the sub-phase for all experiments.
8.1 volume ratio of water and deuterium oxide forms a solution with an effective neutron scattering length density of zero. The solution is called air-contrast-matched-water and was used as the sub-phase for all experiments.
The experimentally determined neutron reflectivity profiles were simulated using an optical formalism69 to determine values of the film thickness, δ, and neutron scattering length density, ρ. These parameters are related to the surface coverage, Γ, by the relationship:
| Γb = δρ | (3) |
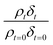 is followed as a function of time, as in previous studies.38,42 Abelès formalism as implemented in the software Motofit,70 was used to calculate reflectivity versus momentum transfer. The films of atmospheric aerosol extract at the air–water interface were simulated as a single layer lying between two layers of infinite thickness. The regions of infinite thickness represent the aqueous sub-phase below the film, and the air above the film, and the neutron scattering length density of both of these was held at zero. In addition, the roughness of each layer was held at 3 Å and the background around 5 to 6 × 10−6.
is followed as a function of time, as in previous studies.38,42 Abelès formalism as implemented in the software Motofit,70 was used to calculate reflectivity versus momentum transfer. The films of atmospheric aerosol extract at the air–water interface were simulated as a single layer lying between two layers of infinite thickness. The regions of infinite thickness represent the aqueous sub-phase below the film, and the air above the film, and the neutron scattering length density of both of these was held at zero. In addition, the roughness of each layer was held at 3 Å and the background around 5 to 6 × 10−6.
Neutron reflectivity model profiles, neutron reflectivity versus momentum transfer, such as will be displayed later in Fig. 1, were calculated by varying the values of the scattering length density, ρ, and the thickness of the film, δ, at the air–water interface until an excellent fit to the experimental neutron reflectivity profile was achieved, across the range of the momentum transfer measured. The surface coverage of material at the air–water interface, Γ, cannot be directly calculated from the product ρδ because the identity of the material at the interface and thus the value of b is unknown. Thus, for following the kinetics of the material at the air–water interface, the quantity ρδ is followed. Although the quantity ρδ contains the film thickness, δ, it should be considered as the scattering length per unit area of the film at the air–water interface and may only be crudely viewed as a metric for the amount of materials at the interface, weighted by the neutron scattering ‘potential’. Note the quantity ρδ may only be considered in this manner as the scattering length densities of the bulk materials above and below (air and water) have effectively zero scattering length density. Values of the scattering length density, ρ, and thickness, δ, were determined as a function of the time for the neutron reflectivity profiles for structural analysis of the film, but the quantity ρδ was followed kinetically.
For the lipid, DSPC, a more ordered structure was simulated as a two layer system: one layer at the water interface representing the phosphocholine head groups of the lipid, and a second layer at the air interface representing the tail (hydrocarbon chains) of the lipid with different neutron scattering length densities and film thicknesses.71 It was also possible to simulate the neutron reflectivity profiles as a one layer system at the air–water interface, especially during the reaction with OH radical.
2.3 Experimental procedure
To record the neutron reflectivity profile of the films, two PTFE troughs were used. The first was a Nima Langmuir trough with an approximate volume of 350 cm3 and PTFE barriers with a surface pressure sensor. The second trough was custom made to facilitate the production of an atmosphere of OH radicals above the trough and consists of a PTFE trough enclosed in a Tedlar gas bag with a UV photolysis lamp. The setup had two thin aluminium windows through which the neutron beam passed. The volume of the trough was approximately 90 cm3; a small trough was used due to limited sample. Each trough was cleaned with chloroform and then filled with air-contrast-matched water to create an air–water interface. The first trough had a surface area of ∼270 cm2 and the second trough a surface area of ∼168 cm2.Between 100 and 400 μL of atmospheric aerosol extract dissolved in chloroform was added to the air–water interface using a Hamilton syringe. The amount of material added was typically a few microliters less than that which would produce visible lens formation at the air–water interface as determined by off-line experiment. After preparing the film, the thickness and neutron scattering length density of the film were determined from measurements prior to the OH radical oxidation.
UV lamps were required to create gas-phase OH radicals. The UV lamps were fluorescent germicidal lamps with an output wavelength peaking at 254 nm. The lamps were suspended 9 cm above the trough and provided an even irradiation. The Langmuir trough and lamps were enclosed within a Tedlar bag to create a sealed environment. Gas-phase OH radicals were generated by the photolysis of gas-phase ozone in the presence of water vapour.58 An atmosphere of ozone and water vapour was generated by bubbling oxygen through air-contrast-matched-water at a flow rate of 1 L min−1. The flow was then directed through an ozonizer (Ultra-Violet Products Ltd) that generated ozone by photolysis of oxygen with a mercury pen-ray lamp. Subsequently, the flow passed into the Tedlar bag that had an approximate volume of 25 L with a gaseous mixing time of ∼25 minutes, 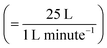 assuming mixing in the Tedlar bag was efficient. To ensure the relative humidity of the experiment environment was maintained, a water reservoir with an approximate volume of 50 mL was included within the Tedlar bag. Measurements of the neutron reflectivity of the filter sample blanks were made for each film at the air–water interface. Two experimental blanks (controls) were also performed: one experimental control for each sample was measured with the film exposed to just ozone (in the absence of UV radiation). The second experimental control was a measurement with only oxygen conducted with the ozoniser switched off, but the UV lights remaining on. However, oxygen is likely to photolyse in the presence of UV light forming ozone and then OH radicals (by photolysis of ozone in the presence of water vapour) and hence some alteration in the film may be expected in this latter case.
assuming mixing in the Tedlar bag was efficient. To ensure the relative humidity of the experiment environment was maintained, a water reservoir with an approximate volume of 50 mL was included within the Tedlar bag. Measurements of the neutron reflectivity of the filter sample blanks were made for each film at the air–water interface. Two experimental blanks (controls) were also performed: one experimental control for each sample was measured with the film exposed to just ozone (in the absence of UV radiation). The second experimental control was a measurement with only oxygen conducted with the ozoniser switched off, but the UV lights remaining on. However, oxygen is likely to photolyse in the presence of UV light forming ozone and then OH radicals (by photolysis of ozone in the presence of water vapour) and hence some alteration in the film may be expected in this latter case.
2.4 Estimation of OH radical concentration
To accurately estimate the concentration of the OH radicals produced requires knowledge of the concentrations of water vapour and ozone and the photolysis rate coefficient for the photolysis of ozone. The concentration of ozone in the tedlar bag was 0.85 ppm as measured by UV-VIS spectrometry of the ozoniser output in a 10 cm path length glass cell sampled just before entering the tedlar bag. The photolysis rate coefficient of ozone, J(O(1D)), for the reaction,| O3 + hν → O(1D) + O2 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 73). The value of the rate constant used for the photolysis of molecular oxygen was the value for ozone, scaled by the product of the absorption cross-sections and the quantum yields. To estimate the concentration of gas-phase OH radicals in the Tedlar bag, kinetic modelling was based on a series of first-order differential equations using a Runge–Kutta algorithm.74,75 Atkinson et al.76 provide data for the basic HOx and Ox reactions occurring in the photolysis of ozone in the presence of water vapour in their reactions 1 to 30. A first-order coefficient of wall loss with regard to OH radicals was added to these reaction using the method outlined by Dilbeck and Finlayson-Pitts.54 The wall loss was calculated to be 2 s−1, assuming the Tedlar bag maintained a volume of 25 L and surface area of 0.612 m2 in the experimental setup and the reaction probability, γ, for OH radicals on Tedlar was similar to halocarbon wax (γ = 6 × 10−4).77 Overall, the concentration of OH radicals present in the Tedlar bag was estimated to be 7 × 106 molecule per cm3. A sensitivity analysis of the kinetic model demonstrated that it was approximately equally sensitive to the concentrations of water vapour and ozone, the values of the photolysis rate coefficient and the wall loss coefficient. Thus the major uncertainty in the determination of the hydroxyl radical concentration is the wall-loss rate coefficient for OH radicals on the walls of the Tedlar bag.
73). The value of the rate constant used for the photolysis of molecular oxygen was the value for ozone, scaled by the product of the absorption cross-sections and the quantum yields. To estimate the concentration of gas-phase OH radicals in the Tedlar bag, kinetic modelling was based on a series of first-order differential equations using a Runge–Kutta algorithm.74,75 Atkinson et al.76 provide data for the basic HOx and Ox reactions occurring in the photolysis of ozone in the presence of water vapour in their reactions 1 to 30. A first-order coefficient of wall loss with regard to OH radicals was added to these reaction using the method outlined by Dilbeck and Finlayson-Pitts.54 The wall loss was calculated to be 2 s−1, assuming the Tedlar bag maintained a volume of 25 L and surface area of 0.612 m2 in the experimental setup and the reaction probability, γ, for OH radicals on Tedlar was similar to halocarbon wax (γ = 6 × 10−4).77 Overall, the concentration of OH radicals present in the Tedlar bag was estimated to be 7 × 106 molecule per cm3. A sensitivity analysis of the kinetic model demonstrated that it was approximately equally sensitive to the concentrations of water vapour and ozone, the values of the photolysis rate coefficient and the wall loss coefficient. Thus the major uncertainty in the determination of the hydroxyl radical concentration is the wall-loss rate coefficient for OH radicals on the walls of the Tedlar bag.
2.5 Calculation of a bimolecular rate constants and atmospheric aerosol extract lifetime
To estimate the lifetime of the atmospheric aerosol extracts in the atmosphere upon exposure to gas-phase OH radicals, the bimolecular rate constant, k5, was calculated for the following reaction:| OH + organic film → products | (5) |
The surface coverage of the aerosol extracts at the air–water interface is related to time by
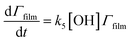 | (6) |
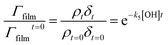 | (7) |
A graph of versus time can then be plotted, and subsequently fitted to an exponential decay of the form e−k5[OH]t to yield the bimolecular rate constant, k5. The atmospheric lifetime, τ, of the film was calculated by extracting the film half-life from the output of the KM-SUB kinetic model57 described in Section 2.7. Atmospheric concentrations of OH radicals have been reported to range between 2 to 4 × 106 molecule per cm3 for a clean environment,78 and 4 to 6 × 106 molecule per cm3 for a polluted environment.79 In the present study, a concentration of 1 × 106 molecule per cm3 has been used to estimate the atmospheric lifetime, τ.
2.6 Estimation of an initial uptake coefficient
Smith et al.,65 Hanson,80 Worsnop et al.81 have demonstrated that it is possible to estimate a value for the uptake coefficient for a gas-phase reagent with a surface by studying the changes in concentration of the surface species. Using their formalism it is possible to estimate the initial uptake coefficient, that is the probability that the OH radical undergoing a gas-kinetic collision with a surface is actually taken up at the surface.65,80,81 To estimate a value for a uptake of OH radicals, γ, on a very thin organic film at the air–water interface, using the conductance analogy80,81 and the assumption of case 2 in ref. 65 that all reactive uptake is dominated by reaction at the interface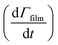 normalised to the gas-surface collision rate
normalised to the gas-surface collision rate 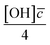 .
. | (8) |
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) is mean molecular speed of a hydroxyl radical, in the gas-phase. The calculation of the uptake coefficient in eqn (8) assumes the value of k5 is solely for reaction with OH radical. Also, the values, and their uncertainties, determined for the OH uptake coefficient do not consider the gas-phase diffusion of the OH radical and should be used accordingly.
is mean molecular speed of a hydroxyl radical, in the gas-phase. The calculation of the uptake coefficient in eqn (8) assumes the value of k5 is solely for reaction with OH radical. Also, the values, and their uncertainties, determined for the OH uptake coefficient do not consider the gas-phase diffusion of the OH radical and should be used accordingly.
2.7 Kinetic modelling of the film-OH radical reaction
The kinetic model of aerosol surface and bulk chemistry (KM-SUB) was applied to the kinetic decays presented here.57 The model resolves surface adsorption and desorption of OH radical and considers the surface reaction between the film and adsorbed OH radicals. The insoluble film was modelled as a monolayer consisting of one species due to the lack of chemical information associated with these real atmospheric samples. For an estimate of the initial film surface coverage, the inverse square of the modelled film thickness was used, assuming the modelled film thickness is the average length of a film molecule. The resulting film surface concentrations are similar to those obtained for monolayers of fatty acids (∼10−18 to 10−17 molecule per m2). The reaction scheme used in the model is that presented in eqn (5). The model was optimised to the experimental data using a global optimisation algorithm (differential evolution)82 employed by Milsom et al.83 and is similar to the Monte Carlo Genetic Algorithm (MCGA) approach of Berkemeier et al.84 Only the surface reaction coefficient (ksurf) was varied with other parameters held constant to physically meaningful values (the molecular diameter of OH radical was 0.3 nm, the surface desorption lifetime of OH was 1 × 10−7 s, the mean thermal velocity of OH radical is 6.1 × 104 cm s−1, a temperature of 298 K, and a surface accommodation coefficient of 1). It is possible to model with an Eley–Rideal or Langmuir–Hinshelwood mechanism. However, the selected desorption lifetime of OH assumes the Langmuir–Hinshelwood surface reaction mechanism, for which there is experimental and modelling evidence.56,85,86 The constraint was necessary as the desorption lifetime and the value of ksurf are reasonably correlated.85 Additionally, Markov Chain Monte Carlo (MCMC) sampling of the parameter space was carried out in order to quantify the uncertainty in the fitted model parameter.87,88 A description of the model, its optimisation and the MCMC sampling procedure is presented in the ESI.†3 Results and discussion
Material extracted from atmospheric aerosol and seawater successfully formed films at the air–water interface, and the thickness and neutron scattering length density of the films were determined by neutron reflection measurements. The oxidation of the films by gas-phase OH radicals was followed by continuously measuring neutron reflectivity for known time periods.3.1 Atmospheric aerosol films
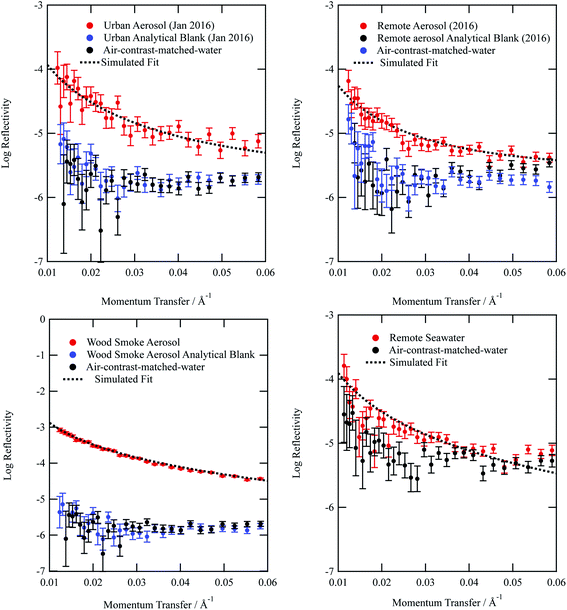
Typical neutron reflectivity profiles (neutron reflectivity vs. momentum transfer) for the thin films at an air–water interface are shown in Fig. 1. The neutron reflection results for the atmospheric aerosol extracts are distinguishable from the sub-phase and it can be inferred that films at the air–water interface were successfully formed. The technique of neutron reflectometry at air–water interfaces typically records significantly more reflective neutron reflectivity profiles, by at least an order of magnitude, as the sample would normally be synthesised as a deuterated isotopologue, which provides greater contrast. Measurement of environmental samples extracted from the atmosphere represent a significant achievement in neutron reflectometry techniques. Included in Fig. 1 is the neutron reflectivity profile obtained for the remote seawater extract. The film thickness and neutron scattering length density values obtained for the organic content of remote seawater (and displayed in Table 1) are slightly larger than values obtained for remote aerosol extracts. The source for remote aerosol is likely to be marine organic material,89 however material extracted from the atmosphere has been exposed to oxidants and hence remote aerosol may differ slightly in composition to Antarctic seawater organic content. Kieber et al.90 demonstrated the potential for dissolved oceanic organic content to photochemically oxidize once in the atmosphere.| Aerosol extract | Film thickness δ/Å | Scattering length density ρ/10−6 Å | Bimolecular rate constant k5/cm3molecule−1 s−1 | Uptake coefficient | Atmospheric half-life τ/hours | k surf/cm2 s−1 |
|---|---|---|---|---|---|---|
| a The refractive index of this sample is reported37 as urban spring. b The refractive index of this sample is reported37 as urban winter. c The refractive index of this sample is reported37 as remote. d The refractive index, Ångström coefficient and mass density of this sample is reported37 as Woodsmoke extract B. | ||||||
| Urbana (May 2015) | 6.1 ± 0.4 | 0.83 ± 0.06 | — | — | — | — |
| Urbana (May 2015) | 3.6 ± 0.2 | 0.68 ± 0.05 | (1.3 ± 0.11) × 10−10 | ∼0.86 | ∼2.5 | (5.0 ± 2.8) × 10−5 |
| Urbanb (January 2016) | 10.2 ± 0.3 | 0.89 ± 0.05 | (1.5 ± 0.05) × 10−10 | ∼0.99 | ∼2.5 | (2.3 ± 1.5) × 10−7 |
| Remote (Antarctic)c (Summer 2015) | 9.0 ± 0.8 | 0.62 ± 0.05 | — | — | — | — |
| Remote (Antarctic)c (Summer 2015) | 7.6 ± 0.3 | 0.67 ± 0.05 | (1.4 ± 0.14) × 10−10 | ∼0.93 | ∼1.7 | (5.0 ± 2.0) × 10−7 |
| Remote (Antarctic) (Summer 2016) | 10.5 ± 0.4 | 0.67 ± 0.05 | (9.3 ± 1.3) × 10−11 | ∼0.62 | ∼5.2 | (9.3 ± 3.2) × 10−8 |
| Wood smoked | 18.6 ± 0.5 | 1.72 ± 0.05 | (8.1 ± 4.5) × 10−12 | ∼0.054 | ∼2.2 | (6.2 ± 0.3) × 10−8 |
| Remote seawater (Summer 2015) | 11.3 ± 0.4 | 0.79 ± 0.06 | — | — | — | — |
From Fig. 1a–d, it can be observed that the analytical blanks for each sample are indistinguishable from the neutron reflectivity profile of the sub-phase air-contrast-matched-water, thereby showing that the analytical blanks do not form films at the air–water interface. The lack of signal demonstrates the success of collecting atmospheric aerosol by the method described in the study. The use of pre-combusted quartz filters and scrupulous clean working conditions contributed to the lack of contamination in all samples.
The neutron scattering length density determined by fitting models to the neutron reflectivity profile for urban and remote aerosol films lies below 1 × 10−6 Å−2, whilst the wood smoke films had a higher neutron scattering length density of nearly 1.7 × 10−6 Å−2. The neutron scattering length density may be crudely used to indicate the possible composition of the films through comparing the experimentally obtained value for a film of the atmospheric aerosol extracts to those for various pure compounds, as depicted in Fig. 2. Classes of chemicals tend to fall into certain ranges, for example − 0.5 × 10−6 Å−2 for saturated alkanes, 1 × 10−6 Å−2 for aromatic groups and (1.5–2) × 10−6 Å−2 for polysaccharides. Compounds chosen for the comparison directly relate to the aerosols studied in the work presented here: levoglucosan is a common tracer species of biomass burning aerosol,91 whilst methyl oleate, oleic acid and linoleic acid are common compounds used as aerosol-proxies.24,38,61,64,92,93 It is necessary to consider that the neutron scattering length density obtained experimentally for atmospheric aerosol extracts is (a) probably a mixture of compounds with a range of individual neutron scattering length densities and (b) slightly different to the values listed in Fig. 2 owing to the sample not packing the same way at the air–water interface as in the pure compound. Fig. 2 demonstrates that the atmospheric aerosol films have scattering length densities greater than fatty acids, and indicates that the content of urban and remote aerosol might be similar in composition to organic compounds containing a small amount of oxygen, phosphorous or nitrogen atoms. The composition of wood smoke might be similar to polymers such as cellulose or levoglucosan (a common pyrolysis product of cellulose).
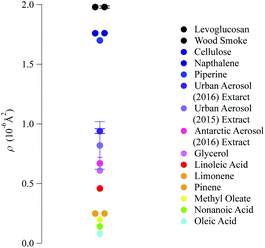 | ||
| Fig. 2 Comparison of the neutron scattering length density for the films formed with material extracted from the aerosol filters and the scattering length density of some common pure compounds. The neutron scattering length density of pure compounds are calculated from tabulated scattering lengths94 and estimated mass densities. | ||
Simulating the neutron reflectivity profiles to reproduce the experimental neutron reflectivity profiles allowed the film thickness to be determined; aerosol extracts sourced from urban and remote locations had film thicknesses that did not exceed 11 Å, however the wood smoke extract formed a much thicker film of approximately 19 Å. In the absence of other data sources, the thickness determined in the study could be used in atmospheric modelling of core–shell aerosols.
The values of the neutron scattering length density and film thickness displayed in Table 1 were obtained by comparing a simulated neutron reflectivity to an experimentally obtained neutron reflectivity profile. Applying a χ2 test provided a means of demonstrating the level of confidence provided by the fitting procedure,
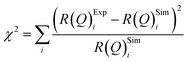 | (9) |
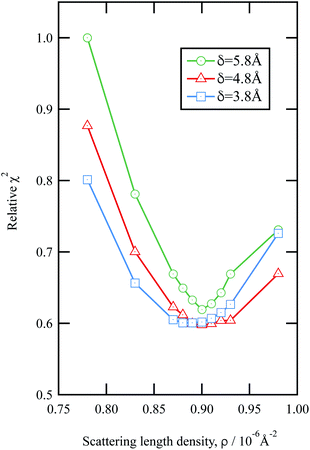 | ||
| Fig. 3 An example of the uncertainties in the fitting of scattering length density and film thickness of the material extracted from an urban RHUL January sample at the air–water interface to a neutron reflection profile similar to that in Fig. 1. Note less sample was added to the interface than in Fig. 1. The goodness of fit, χ2 (eqn (9)) is plotted as a function of the scattering length density and thickness of the film. The values of χ2 have been normalised to the largest value of χ2 plotted in the figure. | ||
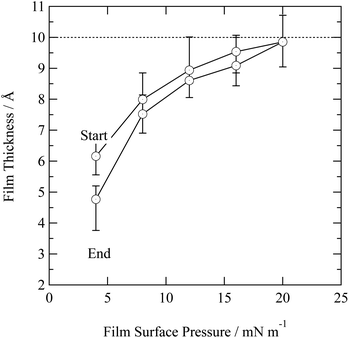
In nature a hydrometeor coated in a thin film may experience a compression or relaxation of surface pressure as the hydrometeor size changes in response to local relative humidity of the atmosphere. The organic films were further studied by changing the surface pressure of the air–water interface. Closing and opening the barriers of the Langmuir trough compressed and expanded the film at the air–water interface. Fig. 4 depicts the compression and expansion of an atmospheric aerosol extract film and the data is shown as a function of surface pressure rather than area per molecule because the sample was composed of an unknown complex mixture of chemicals and therefore the number of molecules at the interface could not be determined. At each new surface pressure, a neutron reflectivity profile was collected and the film thickness determined by the method described in the Section 2.2. Owing to limited sample, the experiment was conducted on just one material: urban aerosol. An increase in surface pressure caused an increase in surface thickness as the molecules rearranged at the air–water interface to reduce the area they occupied. Expansion of the barriers caused surface pressure and surface thickness to reduce. The film thickness was lower than the thickness measured prior to the compression and expansion of the film, indicating that material may have been lost from the interface, altered or taking a long time to re-equilibrate. The material may be tending towards a limit of ∼10 Å.
Neutron reflection techniques for study at the air–water interface tend to use deuterated surfactants to generate a strong contrast with air and air-contrasted matched water. The work presented here demonstrates the technique can be used to study non-deuterated natural samples collected from the atmosphere with reflectivity much closer to the experimental background. It would be difficult to accurately determine with confidence if oxidation of the atmospheric films produces a product film. A product film from the deuterated DSPC may be determined if produced in sufficient yield. Thus, the assumption for the kinetics that there is no product film (for the atmospheric samples) appears plausible for the work presented here, but other techniques may be needed to demonstrate unequivocally if there is a product film or not.
3.2 Kinetics of atmospheric aerosol oxidation
Oxidation kinetics of proxy aerosol samples have been well studied,95 commonly using ozone,24,38,96 OH radicals55,64,97–100 photosensitization53,101–103 or nitrate radicals104–107 as the oxidants. In the study presented here, films of aerosol extract formed at the air–water interface were oxidized through exposure to gas-phase OH radicals. The alteration in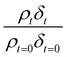 as a function of time is shown in Fig. 5–7. The resultant decay of the relative quantity of
as a function of time is shown in Fig. 5–7. The resultant decay of the relative quantity of 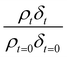 as a function of time suggests the interface was changing to look more like water, and may indicate that either the surface material is becoming more hydrated or material is being lost from the interface. The error in
as a function of time suggests the interface was changing to look more like water, and may indicate that either the surface material is becoming more hydrated or material is being lost from the interface. The error in 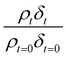 was estimated by calculating the propagation of error108 and fitting simulated neutron reflection profiles to experimental neutron reflection profiles.
was estimated by calculating the propagation of error108 and fitting simulated neutron reflection profiles to experimental neutron reflection profiles.
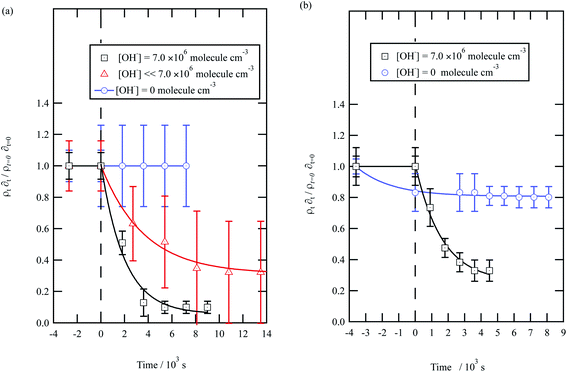 | ||
| Fig. 5 Decay kinetics for the oxidation of a film of material extracted from urban aerosol collected during (a) May 2015 and (b) January 2016 at the air–water interface. The plot is the relative change in neutron scattering length per unit area (i.e. amount of material at the interface) versus time. The vertical dashed line represents the time when the UV lamp was switched on to generate gas-phase OH radicals. The film was exposed to just ozone (blue circles), just oxygen and UV lamp (red triangles) and ozone and UV lamp (black squares). The film is shown to be resistant to oxidation by ozone relative to OH radicals – no significant decay with the blue squares. The film reacts readily with gas-phase OH radicals as demonstrated by the decay of the black squares. The film also decays readily in the presence of oxygen and the UV lamp as the UV lamp generates ozone and subsequently OH radicals. Exponential decays are (eqn (7)) are solid lines. The error bars are the propagation of uncertainties from those of the neutron scattering length and film thickness. | ||
The decay profiles could be fitted to exponential curves described by eqn (7). Fig. 5 depicts the decay for the two urban aerosol extracts, the rate constants for the two urban aerosol extracts (extracted during the months of May and January) are the same within error, suggesting that the reactivity of the aerosol material sourced from the urban site with OH radicals may not be seasonally dependent, although further study is needed. The decay rate of  for the remote aerosol extract collected in 2015 and 2016 are shown in Fig. 6 and overlap within error suggesting the same rate constants for reaction 5 may be used to describe the reaction of OH radicals with both Antarctic atmospheric aerosols for multiple years. Fig. 5(a) and 6(a) both show a much slower decay of the films when the films are exposed to oxygen, rather than ozone with the UV lamps, owing to a lower ozone concentration present under these conditions, produced by molecular oxygen photolysis, reducing the concentration of OH radicals, and thus slowing the rate of reaction. Importantly, the decrease in decay illustrates the film is not decaying solely from UV photolysis. Neither the urban nor the remote aerosol extracts demonstrated a reaction with ozone.
for the remote aerosol extract collected in 2015 and 2016 are shown in Fig. 6 and overlap within error suggesting the same rate constants for reaction 5 may be used to describe the reaction of OH radicals with both Antarctic atmospheric aerosols for multiple years. Fig. 5(a) and 6(a) both show a much slower decay of the films when the films are exposed to oxygen, rather than ozone with the UV lamps, owing to a lower ozone concentration present under these conditions, produced by molecular oxygen photolysis, reducing the concentration of OH radicals, and thus slowing the rate of reaction. Importantly, the decrease in decay illustrates the film is not decaying solely from UV photolysis. Neither the urban nor the remote aerosol extracts demonstrated a reaction with ozone.
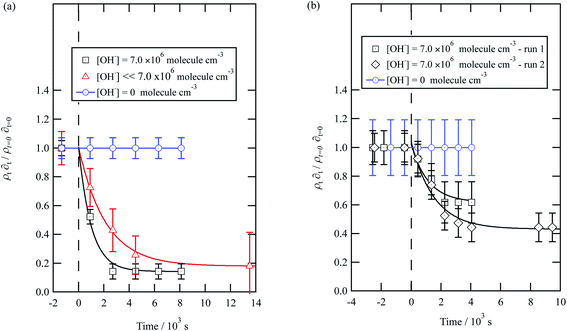 | ||
| Fig. 6 Decay kinetics for the oxidation of a film of material extracted from remote aerosol collected during (a) 2015 and (b) 2016 at the air–water interface. The plot is the relative change in neutron scattering length per unit area (i.e. amount of material at the interface) versus time. The horizontal dashed line represents the time when the UV lamp may have been switched on to generate gas-phase OH radicals. The film was exposed to just ozone (blue circles), just oxygen and UV lamp (red triangles) and ozone and UV lamp (black squares). The film is shown to be resistant to oxidation by ozone relative to OH radicals – no significant decay with the blue squares. The film reacts readily with gas-phase OH radicals as demonstrated by the decay of the black squares. The film also decays readily in the presence of oxygen and the UV lamp as the UV lamp generates ozone and subsequently OH radicals. Exponential decays are fitted (eqn (7)) are fitted to decays as solid lines. The error bars are the propagation of uncertainties of the determination of the value of neutron scattering length and film thickness. | ||
Water insoluble wood smoke aerosol extracts have a decay similar to the urban and remote aerosol extract (Fig. 7), demonstrating a similar reactivity towards the OH radical. In contrast to all the other samples, the wood smoke aerosol extract decays when exposed to ozone only. The extract was collected directly from the smoke plume and therefore had not been atmospherically processed and may contain unsaturated material.25 Gonçalves et al.109 and Zhou et al.110 have investigated the oxidation kinetics of natural sea-surface material when exposed to gas-phase ozone, and observed a decrease in coverage. The decrease in coverage was attributed to unsaturated compounds present in the layer reacting with the ozone and products leaving the air–water interface. Water insoluble surface-active extracts sourced from urban and remote locations did not react with ozone. For approximately 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 seconds the neutron scattering length density per unit area of the material did not change, demonstrating the stability of the urban and remote aerosol extracts at the air–water interface. The extracts may not have decayed with ozone either because they originally contain a small mass ratio of unsaturated organic compounds to saturated material or because the unsaturated content of the extract had been removed by atmospheric processing before collection. The latter suggestion is usually applied to extracts sourced from urban locations.25 Results obtained from the study demonstrate a need for research that focuses on the ageing of saturated aerosol films; a number of studies have focused on the oxidation of films at the air–water interface,24,38 however the studies predominantly concentrated on the oxidation kinetics of films containing unsaturated functional groups.
000 seconds the neutron scattering length density per unit area of the material did not change, demonstrating the stability of the urban and remote aerosol extracts at the air–water interface. The extracts may not have decayed with ozone either because they originally contain a small mass ratio of unsaturated organic compounds to saturated material or because the unsaturated content of the extract had been removed by atmospheric processing before collection. The latter suggestion is usually applied to extracts sourced from urban locations.25 Results obtained from the study demonstrate a need for research that focuses on the ageing of saturated aerosol films; a number of studies have focused on the oxidation of films at the air–water interface,24,38 however the studies predominantly concentrated on the oxidation kinetics of films containing unsaturated functional groups.
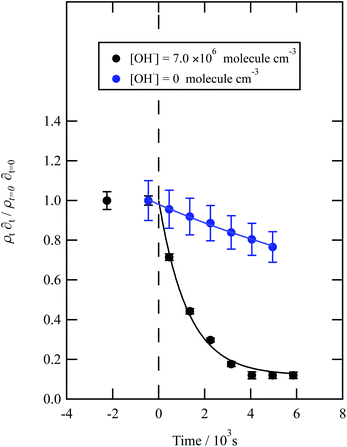 | ||
| Fig. 7 Decay kinetics for the oxidation of a film of material extracted from wood smoke at the air–water interface. The plot is the relative change in neutron scattering length per unit area (i.e. amount of material at the interface) versus time. The vertical dashed line represents the time when the UV lamp was switched on to generate gas-phase OH radicals. The film was exposed to just ozone (blue circles), and hydroxyl radicals – ozone and UV lamp (black squares). The film is not resistant to oxidation by ozone relative to OH radicals – with a slight decay with the blue squares. The film reacts readily with gas-phase OH radicals as demonstrated by the decay of the black squares. Exponential decays (eqn (7) are fitted to decays as solid lines. The error bars are the propagation of uncertainties of the determination of the value of neutron scattering length and film thickness. | ||
The bimolecular rate constant, k5, reported in Table 1, for reaction 5 is attributed to reaction with the OH radical. The value of this rate constant could be considered an upper limit as reactions with ozone (woodsmoke samples only) and direct photolysis by the lamps may require consideration. The reaction between ozone and woodsmoke results in a pseudo-first-order rate constant of ∼1.5 s−1 relative to a considerably larger value of ∼21 s−1 in the presence of gas-phase ozone and the photolysis lamps. Thus, the contribution of the reactions of ozone with woodsmoke films is considered not important. The decay of organic material at the air–water interface in the presence of molecular oxygen, water vapour and the photolysis lamps has been attributed to a reaction with gas-phase OH radical at a smaller, unknown, concentration when gas-phase ozone is present. The photolysis lamps produce a small concentration of gas-phase ozone from the photolysis of molecular oxygen. The decay in the organic materials at the air–water interface may also be attributed to direct photolysis and unfortunately direct photolysis was not tested in the presence of an oxygen-free atmosphere as oxygen impurities remained. Thus, the values of the bimolecular rate constant, k5, reported in Table 1 are considered to be owing to reaction with OH radicals, but may also be considered as upper limits to a cautious reader.
3.3 Comparison of uptake coefficient with literature
The uptake of OH radicals on several different surfaces has been previously measured and presented in Table 3. It is useful to compare the uptake coefficients estimated from the work presented here with measurements on other organic surfaces. As can be seen by from Table 3 the uptake coefficients in this work are broadly comparable to those in the literature with the exception of fresh woodsmoke.3.4 Kinetic modelling of the film-OH radical reaction
Kinetic modelling of the experimental data obtained from these samples returned a similar trend in ksurf to the trend observed in bimolecular rate constants, k5, (Table 1). Values of ksurf obtained from this modelling are consistent with kinetic multi-layer model fits to data from particles of biomass burning markers. In particular, the optimised values of ksurf for the wood smoke film ((6.2 ± 0.3) × 10−8 cm2 s−1) is in agreement with the range reported by Arangio et al. (∼10−12 to 10−6 cm2 s−1) for levoglucosan particles.111 Note that the value of the atmospheric half life is calculated from the model output does not necessarily follow the trend in the value of ksurf owing to the different initial surface coverages used for each film estimated from their thicknesses (Table 1). The model was particularly sensitive to the value of ksurf. It was assumed that the value of αs,0 = 1. By definition, αs,0 has to be larger than the uptake coefficient (see Table 1).112 It is possible to use both the quantities αs,0 and ksurf as fitting parameters. Optimising the model with αs,0 and ksurf as varying parameters returned values of αs,0 ∼ 1 and ksurf within the uncertainty quoted in Table 1. Therefore, there is confidence that reactive uptake is dominated by the surface reaction, justifying the use of eqn (8) to calculate the uptake coefficient and the use of ksurf as the fitting parameter.3.5 Oxidation kinetics of a proxy atmospheric aerosol
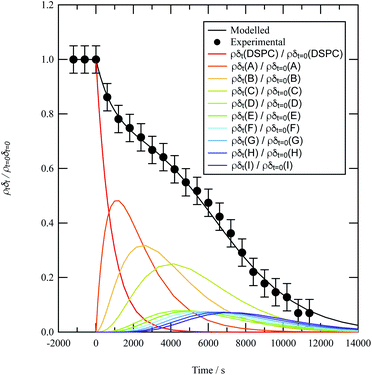
A film of DSPC, a phosphocholine lipid with saturated hydrocarbon tails, was formed at the air–water interface and oxidised by gas-phase OH radicals as a test proxy aerosol material. The effect of the OH radicals on both the head and tail region of the lipid DSPC as a test proxy aerosol material.could be estimated from the neutron data individually, however to understand the decay process undergone by DSPC films the value of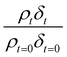 of the head and tail layer regions were combined by adding weighted values. An example of this decay as a function of time is shown in Fig. 8. Three different films of DSPC at the air–water interface were exposed to gas-phase OH radicals, and all showed similar decay profiles. The thin films of DSPC at the air–water interface displayed a decay that was characteristic of a step-wise degradation mechanism when exposed to gas-phase OH radicals,113 whereas the atmospheric-aerosol extracts demonstrated an exponential decay. A simulated fit for the decay of
of the head and tail layer regions were combined by adding weighted values. An example of this decay as a function of time is shown in Fig. 8. Three different films of DSPC at the air–water interface were exposed to gas-phase OH radicals, and all showed similar decay profiles. The thin films of DSPC at the air–water interface displayed a decay that was characteristic of a step-wise degradation mechanism when exposed to gas-phase OH radicals,113 whereas the atmospheric-aerosol extracts demonstrated an exponential decay. A simulated fit for the decay of 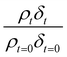 versus time was found by using a kinetic model based on a differential equation solved by a Runge–Kutta algorithm. The product of neutron scattering length density and film thickness of the DSPC film at the air–water interface taken as a weighted sum of the products A to J. The algorithm used a weighting in each step (A to J in eqn (10)) of the reaction to ensure an accurate fit between the experimental and simulated data. The first product was weighted as 0.75, and each further product as 0.05 less, representing a loss of 5 percent of the molecules at the interface for each subsequent attack by the OH radicals until the film was no longer surface active. The degradation mechanism could be modelled accurately using ten overlapping kinetic steps, with the product of the first nine steps remaining at the air–water interface. The kinetic steps are:
versus time was found by using a kinetic model based on a differential equation solved by a Runge–Kutta algorithm. The product of neutron scattering length density and film thickness of the DSPC film at the air–water interface taken as a weighted sum of the products A to J. The algorithm used a weighting in each step (A to J in eqn (10)) of the reaction to ensure an accurate fit between the experimental and simulated data. The first product was weighted as 0.75, and each further product as 0.05 less, representing a loss of 5 percent of the molecules at the interface for each subsequent attack by the OH radicals until the film was no longer surface active. The degradation mechanism could be modelled accurately using ten overlapping kinetic steps, with the product of the first nine steps remaining at the air–water interface. The kinetic steps are: | (10) |
| Rate constant/10−10 cm3 molecule−1 s−1 | |||
|---|---|---|---|
| Film I | Film II | Film III | |
| k 1 | 1.7 ± 0.43 | 1.0 ± 0.40 | 1.6 ± 0.49 |
| k 2 | 0.93 ± 0.21 | 1.0 ± 0.40 | 1.6 ± 0.49 |
| k 3 | 0.93 ± 0.21 | 1.0 ± 0.40 | 1.6 ± 0.49 |
| k 4 | 0.93 ± 0.21 | 2.1 ± 0.42 | 1.6 ± 0.49 |
| k 5 | 2.9 ± 0.70 | 2.1 ± 0.42 | 1.6 ± 0.49 |
| k 6 | 2.9 ± 0.70 | 2.1 ± 0.42 | 1.4 ± 0.57 |
| k 7 | 2.9 ± 0.26 | 2.9 ± 0.57 | 1.4 ± 0.57 |
| k 8 | 2.9 ± 0.26 | 2.9 ± 0.57 | 1.4 ± 0.57 |
| k 9 | 2.9 ± 0.26 | 2.9 ± 0.57 | 1.4 ± 0.57 |
| k 10 | 2.9 ± 0.26 | 2.9 ± 0.57 | 1.4 ± 0.57 |
| Aerosol composition | Technique | Uptake coefficient | Reference |
|---|---|---|---|
| Aerosol extract – urban | Neutron reflection | γ = (0.86–0.99) | This work |
| Aerosol extract – Antarctic | γ = (0.62–0.93) | This work | |
| Aerosol extract – wood smoke | γ = ∼0.054 | This work | |
| Bis(2-ethylhexyl) sebacate | Aerosol flow tube | γ = (1.3 ± 0.4) | 117 |
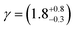
|
118 | ||
| Hexacosane | Smog chamber | γ = (1.04 ± 0.21) | 119 |
| Squalane | Aerosol flow tube | γ = (0.3 ± 0.07) | 120 |
| γ = (0.49 ± 0.04) | 86 | ||
| Stirred flow reactor | γ = (0.51 ± 0.10) | 121 | |
| Squalene | Flow tube | γ = (2.34 ± 0.07) | 122 |
| Palmitic acid | Flow reactor | γ = (0.8–1) | |
| Flow tube | γ = (0.14–1) | 99 | |
| Oxidised resorcinol (Brown carbon proxy) | Chamber | γ ∼ 1 | 123 |
| β-D-Glucopyranoside | Flow reactor | γ = (0.92–1.9) | 124 |
| Aqueous 2-methylglutaric acid | Aerosol flow tube | γ = (1.9–2.6) | 125 |
| Citric acid | Chamber | γ = (1.61 ± 0.16)–(1.35 ± 0.14) | 126 |
| Oleic acid | Chamber | γ = (1.72 ± 0.08) | 64 |
| Linoleic acid | Flow reactor | γ = (3.75 ± 0.18) | 122 |
| Linolenic acid | Flow reactor | γ = (5.73 ± 0.14) | 64 |
| Paraffin wax | Flow tube | γ = 0.34 | 77 |
| Packed flow tube | γ = 0.03–1 | 127 | |
| γ > 0.2 | 128 | ||
| Octadecyltrichlorosilane | Flow reactor | γ > 0.2 | 128 |
| Methyl terminated monolayer | Flow tube | γ = 0.29 | 77 |
| Vinyl terminated monolayer | Flow tube | γ = 0.60 | 77 |
| Stearic-palmitic acid | Flow tube | γ = 0.34 | 77 |
| Erythritol | Flow reactor | γ = 0.77 ± 0.10 | 129 |
| Levoglucosan | Flow reactor | γ = 0.91 ± 0.08 | 129 |
| Flow tube | γ = (0.12–1) | 99 | |
| Tartaric acid | Flow reactor | γ = (0.40 ± 0.13) | 130 |
| Citric acid | Flow reactor | γ = (0.37 ± 0.08) | 130 |
| Glutaric acid | Packed flow reactor | γ = (0.03–1) | 127 |
| 1,2,3,4-Butanetetra-carboxylic acid | Flow reactor | γ = (0.51 ± 0.19) | 130 |
A series of checks were carried out to ensure that the weighting and number of steps in the degradation mechanism represented the method of decay for DSPC thin films at the air–water interface. First, the weighting of each kinetic step was adjusted and the change in quality of fit quantitatively determined. For the first three kinetic steps, the weighting contribution could be varied by 5 percent whilst maintaining a reasonable fit, whereas for the following kinetic steps a variation of 15 percent in the weighting of the contribution maintained an adequate fit. The result from analysing the weight contribution demonstrates the importance of the first few kinetic steps in determining an accurate fit to the decay. Additionally, the number of kinetic steps was determined iteratively by altering the number of steps, manually adjusting the rate constants to allow a reasonable fit and then determining the quality of the fit with a χ2 test,
 | (11) |
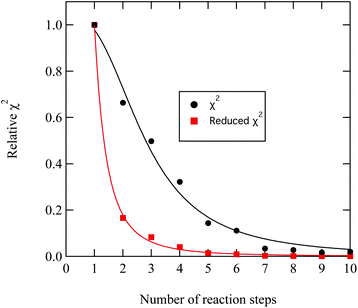 | ||
| Fig. 9 Demonstration of the improvement in the quality of fit between experimental and modelled DSPC reaction profiles similar to that shown in Fig. 8 by increasing the number of reaction steps in eqn. (11)). The values of χ2 have been normalised to the largest value of χ2 plotted in the figure. | ||
3.6 Atmospheric implications
Neutron reflectivity profiles of the aerosol films at the air–water interface allowed an estimate of the film thickness and confirmed that the materials formed stable thin films at the air–water interface. Use of a film thickness from this work in light scattering calculations will aid the accurate modelling of aerosol scenarios in the atmosphere. Shepherd et al.37 presented calculations in the change in top of atmosphere albedo for core–organic shell aerosol with increasing thickness of films based on measurement of the optical properties of the same film samples as are described here. Thus with the data of Shepherd et al.37 it has been demonstrated that materials found in atmospheric aerosol can form stable thin films at the air–water interface of approximately 10 Å with known optical properties. The work described here also allows an estimation of the persistence of these thin films. The oxidation kinetics of the atmospheric film when exposed to OH radicals demonstrated an exponential decay. The atmospheric lifetime, τ, of each film was estimated from the half-life of the kinetic model outputs at a representative atmospheric OH concentration (1 × 106 molecule per cm3) and presented in Table 1.Studies using proxy aerosol material have found the lifetime to vary from minutes24 to hours38,40,115,116 and even to days;63 the range in aerosol lifetime is likely caused by the phase and composition of the aerosol.63 An aerosol film lifetime as determined in the study is similar to literature values, and hence would be relevant for short term or long-term atmospheric studies.
Lifetimes calculated from the optimised kinetic models described in Section 2.7 range from minutes to hours to days depending on the atmospheric concentration of OH radical used, Fig. 10. These models were run with a range of atmospherically relevant OH radical concentrations (104 to 108 molecule per cm3) using the mean value of ksurf from the MCMC sampling procedure for each separate film type in Table 1. The film half-life was calculated for each model run over OH radical concentration range from 104 to 108 molecule per cm3, the half-life for all films ranges from minutes (∼10 minutes at ∼2 × 107 molecule per cm3) to a day (∼1 day at 1.5 × 105 molecule per cm3). Extension to even lower OH radical concentrations, (<1 × 105 molecule per cm3), show a half-life increase up to ∼7−10 days. This large range of film half-lives with respect to the OH radical highlights the potential for real organic films to persist over an atmospherically relevant timescale and for the need of oxidation kinetics to be included in atmospheric modelling of core-organic shell aerosol.
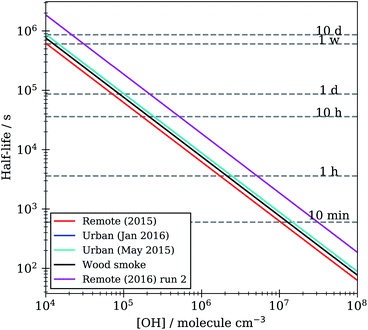 | ||
| Fig. 10 Film half-life versus atmospheric OH radical concentration for KM-SUB models optimised to organic film kinetic decay data in Table 1. | ||
4 Conclusions
Insoluble material extracted from atmospheric aerosol forms films at the air–water interface, from which the neutron scattering length density and thickness of the film can be resolved, demonstrating that neutron reflectivity is a useful technique for the study of aerosol extract films at the air–water interface. Urban and remote water insoluble surface active material extracted from aerosol formed films at the air–water interface with a neutron scattering length density value between 0.6 to 0.8 × 10−6 Å−2 and a film thickness between 3 and 11 Å, whilst wood smoke aerosol films were thicker (approximately 18 Å) and had higher neutron scattering length density (1.7 × 10−6 Å−2). Neutron reflectivity measurement allowed the thickness of interfacial films to be determined and it permitted observation of the decay of the organic film when subjected to oxidizing conditions. The gas-phase oxidation demonstrated an exponential decay and not a step-wise degradation mechanism for all the aerosol films. The bimolecular rate constant obtained from the decay ranged from 5.2 to 10.0 × 10−11 cm3 molecule−1 s−1. The lifetime of the atmospheric aerosol extracts is on the timescale of hours, and is comparable in terms of aerosol residence times in the atmosphere. It is therefore essential that the presence of a film and its change with time is considered in atmospheric modelling studies. The potential atmospheric aerosol proxy DSPC demonstrated different kinetics to samples extracted from the atmosphere, and thus should not be used as a proxy in future atmospheric experiments.Author contributions
The experiments were conceived by MDK, performed by RS, ARR, MDK, ADW, MS, and RW and analysed by RS, ARR, MDK, MS and RW. The aerosol samples were collected and extracted by MMF, NB, JE, SD and MDK. Kinetic modelling of the results was performed by MDK and RS for DSPC and AM and CP for the KM-SUB modelling.Data availability
Data is available at the following https://doi.org/10.5286/ISIS.E.61784247, https://doi.org/10.5286/ISIS.E.67767756, https://doi.org/10.5286/ISIS.E.81474355 and https://doi.org/10.5286/ISIS.E.79107195.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to thank STFC ISIS for awarding the beam time grants RB1510455, RB1520410 and RB1610119. RHS would like to thank STFC for funding the student grant ST/L504279/1. MDK would like to thank NERC for grant NE/T00732X/1.Notes and references
- IPCC, Climate Change 2013: the Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013, p. 1535 Search PubMed.
- O. B. Toon and J. B. Pollack, Am. Sci., 1980, 68, 268–278 CAS.
- M. Andreae and D. Rosenfeld, Earth-Sci. Rev., 2008, 89, 13–41 CrossRef.
- J. B. Burkholder, J. P. D. Abbatt, I. Barnes, J. M. Roberts, M. L. Melamed, M. Ammann, A. K. Bertram, C. D. Cappa, A. G. Carlton, L. J. Carpenter, J. N. Crowley, Y. Dubowski, C. George, D. E. Heard, H. Herrmann, F. N. Keutsch, J. H. Kroll, V. F. McNeill, N. L. Ng, S. A. Nizkorodov, J. J. Orlando, C. J. Percival, B. Picquet-Varrault, Y. Rudich, P. W. Seakins, J. D. Surratt, H. Tanimoto, J. A. Thornton, Z. Tong, G. S. Tyndall, A. Wahner, C. J. Weschler, K. R. Wilson and P. J. Ziemann, Environ. Sci. Technol., 2017, 51, 2519–2528 CrossRef CAS PubMed.
- T. Stocker, D. Qin, G.-K. Plattner, L. Alexander, S. Allen, N. Bindoff, F.-M. Bréon, J. Church, U. Cubasch, S. Emori, P. Forster, P. Friedlingstein, N. Gillett, J. Gregory, D. Hartmann, E. Jansen, B. Kirtman, R. Knutti, K. Krishna Kumar, P. Lemke, J. Marotzke, V. Masson-Delmotte, G. Meehl, I. Mokhov, S. Piao, V. Ramaswamy, D. Randall, M. Rhein, M. Rojas, C. Sabine, D. Shindell, L. Talley, D. Vaughan and S.-P. Xie, in Technical Summary, ed. T. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex and P. Midgley, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013, book section TS, pp. 33–115 Search PubMed.
- D. J. Donaldson, J. Phys. Chem. A, 1999, 103, 62–70 CrossRef CAS.
- D. J. Donaldson and V. Vaida, Chem. Rev., 2006, 106, 1445–1461 CrossRef CAS PubMed.
- G. B. Ellison, A. F. Tuck and V. Vaida, J. Geophys. Res. Atmos., 1999, 104, 11633–11641 CrossRef CAS.
- R. B. Husar and W. R. Shu, J. Appl. Meteorol., 1975, 14, 1558–1565 CrossRef CAS.
- V. McNeill, N. Sareen and A. Schwier, in Surface-Active Organics in Atmospheric Aerosols., ed. V. McNeill and P. Ariya, Springer, Berlin, Heidelberg, 2013, vol. 339 Search PubMed.
- H. Tervahattu, K. Hartonen, V.-M. Kerminen, K. Kupiainen, P. Aarnio, T. Koskentalo, A. F. Tuck and V. Vaida, J. Geophys. Res. Atmos., 2002, 107, AAC-1 Search PubMed.
- J. F. Davies, R. E. H. Miles, A. E. Haddrell and J. P. Reid, Proc. Natl. Acad. Sci. U.S.A., 2013, 110, 8807–8812 CrossRef CAS PubMed.
- T. Eliason, S. Aloisio, D. Donaldson, D. Cziczo and V. Vaida, Atmos. Environ., 2003, 37, 2207–2219 CrossRef CAS.
- T. Kaiser, G. Roll and G. Schweiger, Appl. Opt., 1996, 35, 5918–5924 CrossRef CAS PubMed.
- G. McFiggans, P. Artaxo, U. Baltensperger, H. Coe, M. C. Facchini, G. Feingold, S. Fuzzi, M. Gysel, A. Laaksonen, U. Lohmann, T. F. Mentel, D. M. Murphy, C. D. O'Dowd, J. R. Snider and E. Weingartner, Atmos. Chem. Phys., 2006, 6, 2593–2649 CrossRef CAS.
- G. Feingold and P. Y. Chuang, J. Atmos. Sci., 2002, 59, 2006–2018 CrossRef.
- C. N. Cruz and S. N. Pandis, J. Geophys. Res. Atmos., 1998, 103, 13111–13123 CrossRef CAS.
- C. R. Ruehl and K. R. Wilson, J. Phys. Chem. A, 2014, 118, 3952–3966 CrossRef CAS PubMed.
- S. Enami, M. R. Hoffmann and A. J. Colussi, J. Phys. Chem. A, 2010, 114, 5817–5822 CrossRef CAS PubMed.
- F. Bernard, R. Ciuraru, A. Boréave and C. George, Environ. Sci. Technol., 2016, 50, 8678–8686 CrossRef CAS PubMed.
- R. Ciuraru, L. Fine, M. van Pinxteren, B. D'Anna, H. Herrmann and C. George, Sci. Rep., 2015, 5, 12741 CrossRef CAS PubMed.
- R. Ciuraru, L. Fine, M. v. Pinxteren, B. D'Anna, H. Herrmann and C. George, Environ. Sci. Technol., 2015, 49, 13199–13205 CrossRef CAS PubMed.
- S. Rossignol, L. Tinel, A. Bianco, M. Passananti, M. Brigante, D. J. Donaldson and C. George, Science, 2016, 353, 699–702 CrossRef CAS PubMed.
- C. Pfrang, F. Sebastiani, C. O. M. Lucas, M. D. King, I. D. Hoare, D. Chang and R. A. Campbell, Phys. Chem. Chem. Phys., 2014, 16, 13220–13228 RSC.
- S. H. Jones, M. D. King, A. D. Ward, A. R. Rennie, A. C. Jones and T. Arnold, Atmos. Environ., 2017, 161, 274–287 CrossRef CAS.
- S. Pandis, A. S. Wexler and J. H. Seinfeld, J. Phys. Chem., 1995, 99, 9646 CrossRef CAS.
- S. Fuzzi, M. O. Andreae, B. J. Huebert, M. Kulmala, T. C. Bond, M. Boy, S. J. Doherty, A. Guenther, M. Kanakidou, K. Kawamura, V.-M. Kerminen, U. Lohmann, L. M. Russell and U. Poschl, Atmos. Chem. Phys., 2006, 6, 2017–2038 CrossRef CAS.
- K. A. Prather, C. D. Hatch and V. H. Grassian, Annu. Rev. Anal. Chem., 2008, 1, 485–514 CrossRef CAS PubMed.
- A. Cincinelli, A. Stortini, M. Perugini, L. Checchini and L. Lepri, Mar. Chem., 2001, 76, 77–98 CrossRef CAS.
- A. Cincinelli, A. M. Stortini, L. Checchini, T. Martellini, M. D. Bubba and L. Lepri, J. Environ. Monit., 2005, 7, 1305–1312 RSC.
- H. Fu, R. Ciuraru, Y. Dupart, M. Passananti, L. Tinel, S. Rossignol, S. Perrier, D. J. Donaldson, J. Chen and C. George, J. Am. Chem. Soc., 2015, 137, 8348–8351 CrossRef CAS PubMed.
- J. Knulst and A. Södergren, Chemosphere, 1994, 29, 1339–1347 CrossRef CAS.
- J. C. Knulst, D. Rosenberger, B. Thompson and J. Paatero, Langmuir, 2003, 19, 10194–10199 CrossRef CAS.
- D. C. Blanchard, Science, 1964, 146, 396–397 CrossRef CAS PubMed.
- R. E. Cochran, O. Laskina, T. Jayarathne, A. Laskin, J. Laskin, P. Lin, C. Sultana, C. Lee, K. A. Moore, C. D. Cappa, T. H. Bertram, K. A. Prather, V. H. Grassian and E. A. Stone, Environ. Sci. Technol., 2016, 50, 2477–2486 CrossRef CAS PubMed.
- K. E. Gustafson and R. M. Dickhut, Environ. Sci. Technol., 1997, 31, 140–147 CrossRef CAS.
- R. H. Shepherd, M. D. King, A. A. Marks, N. Brough and A. D. Ward, Atmos. Chem. Phys., 2018, 18, 5235–5252 CrossRef CAS.
- M. D. King, A. R. Rennie, K. C. Thompson, F. N. Fisher, C. C. Dong, R. K. Thomas, C. Pfrang and A. V. Hughes, Phys. Chem. Chem. Phys., 2009, 11, 7699–7707 RSC.
- J. Lu, R. Thomas and J. Penfold, Adv. Colloid Interface Sci., 2000, 84, 143–304 CrossRef CAS PubMed.
- K. C. Thompson, A. R. Rennie, M. D. King, S. J. O. Hardman, C. O. M. Lucas, C. Pfrang, B. R. Hughes and A. V. Hughes, Langmuir, 2010, 26, 17295–17303 CrossRef CAS PubMed.
- A. Milsom, A. M. Squires, B. Woden, N. J. Terrill, A. D. Ward and C. Pfrang, Faraday Discuss., 2021, 226, 364–381 RSC.
- M. D. King, S. H. Jones, C. O. M. Lucas, K. C. Thompson, A. R. Rennie, A. D. Ward, A. A. Marks, F. N. Fisher, C. Pfrang, A. V. Hughes and R. A. Campbell, Phys. Chem. Chem. Phys., 2020, 22, 28032–28044 RSC.
- L. Tinel, S. Rossignol, A. Bianco, M. Passananti, S. Perrier, X. Wang, M. Brigante, D. J. Donaldson and C. George, Environ. Sci. Technol., 2016, 50, 11041–11048 CrossRef CAS PubMed.
- L. F. Voss, C. M. Hadad and H. C. Allen, J. Phys. Chem. B, 2006, 110, 19487–19490 CrossRef CAS PubMed.
- L. F. Voss, M. F. Bazerbashi, C. P. Beekman, C. M. Hadad and H. C. Allen, J. Geophys. Res. Atmos., 2007, 112, D06209 Search PubMed.
- S. H. Jones, M. D. King and A. D. Ward, Chem. Commun., 2015, 51, 4914–4917 RSC.
- M. D. King, A. R. Rennie, C. Pfrang, A. V. Hughes and K. C. Thompson, Atmos. Environ., 2010, 44, 1822–1825 CrossRef CAS.
- B. J. Dennis-Smither, R. E. H. Miles and J. P. Reid, J. Geophys. Res. Atmos., 2012, 117, D20204 CrossRef.
- E. Gonzalez-Labrada, R. Schmidt and C. E. DeWolf, Phys. Chem. Chem. Phys., 2007, 9, 5814–5821 RSC.
- S. Enami and Y. Sakamoto, J. Phys. Chem. A, 2016, 120, 3578–3587 CrossRef CAS PubMed.
- B. T. Mmereki and D. J. Donaldson, J. Phys. Chem. A, 2003, 107, 11038–11042 CrossRef CAS.
- K. C. Thompson, S. H. Jones, A. R. Rennie, M. D. King, A. D. Ward, B. R. Hughes, C. O. M. Lucas, R. A. Campbell and A. V. Hughes, Langmuir, 2013, 29, 4594–4602 CrossRef CAS PubMed.
- C. George, M. Brüggemann, N. Hayeck, L. Tinel and D. Donaldson, in Interfacial Photochemistry, 2018, pp. 435–457 Search PubMed.
- C. W. Dilbeck and B. J. Finlayson-Pitts, Phys. Chem. Chem. Phys., 2013, 15, 9833–9844 RSC.
- C. D. Cappa, D. L. Che, S. H. Kessler, J. H. Kroll and K. R. Wilson, J. Geophys. Res. Atmos., 2011, 116, D15204 CrossRef.
- S. Enami, M. R. Hoffmann and A. J. Colussi, J. Phys. Chem. A, 2014, 118, 4130–4137 CrossRef CAS PubMed.
- M. Shiraiwa, C. Pfrang and U. Pöschl, Atmos. Chem. Phys., 2010, 10, 3673–3691 CrossRef CAS.
- B. J. Finlayson-Pitts and J. N. Pitts, Science, 1997, 276, 1045–1051 CrossRef CAS PubMed.
- R. G. Prinn, J. Huang, R. F. Weiss, D. M. Cunnold, P. J. Fraser, P. G. Simmonds, A. McCulloch, C. Harth, P. Salameh, S. O'Doherty, R. H. J. Wang, L. Porter and B. R. Miller, Science, 2001, 292, 1882–1888 CrossRef CAS PubMed.
- K. R. Kolesar, G. Buffaloe, K. R. Wilson and C. D. Cappa, Environ. Sci. Technol., 2014, 48, 3196–3202 CrossRef CAS PubMed.
- E. R. Garland, E. P. Rosen, L. I. Clarke and T. Baer, Phys. Chem. Chem. Phys., 2008, 10, 3156–3161 RSC.
- K. Jain, A. Siddam, A. Marathi, U. Roy, J. Falck and M. Balazy, Free Radic. Biol. Med., 2008, 45, 269–283 CrossRef CAS PubMed.
- J. W. Morris, P. Davidovits, J. T. Jayne, J. L. Jimenez, Q. Shi, C. E. Kolb, D. R. Worsnop, W. S. Barney and G. Cass, Geophys. Res. Lett., 2002, 29, 71 Search PubMed.
- T. Nah, S. H. Kessler, K. E. Daumit, J. H. Kroll, S. R. Leone and K. R. Wilson, Phys. Chem. Chem. Phys., 2013, 15, 18649–18663 RSC.
- G. D. Smith, E. Woods, C. L. DeForest, T. Baer and R. E. Miller, J. Phys. Chem. A, 2002, 106, 8085–8095 CrossRef CAS.
- A. E. Jones, E. W. Wolff, R. A. Salmon, S. J.-B. Bauguitte, H. K. Roscoe, P. S. Anderson, D. Ames, K. C. Clemitshaw, Z. L. Fleming, W. J. Bloss, D. E. Heard, J. D. Lee, K. A. Read, P. Hamer, D. E. Shallcross, A. V. Jackson, S. L. Walker, A. C. Lewis, G. P. Mills, J. M. C. Plane, A. Saiz-Lopez, W. T. Sturges and D. R. Worton, Atmos. Chem. Phys., 2008, 8, 3789–3803 CrossRef CAS.
- F. MacIntyre, Sci. Am., 1974, 230, 62–77 CrossRef CAS.
- J. Webster, S. Holt and R. Dalgliesh, Phys. B Condens. Matter, 2006, 385–386, 1164–1166 CrossRef CAS.
- F. Abelès, J. Phys. Radium, 1950, 11, 310–314 CrossRef.
- A. Nelson, J. Appl. Crystallogr., 2006, 39, 273–276 CrossRef CAS.
- A. P. Dabkowska, J. P. Talbot, L. Cavalcanti, J. R. P. Webster, A. Nelson, D. J. Barlow, G. Fragneto and M. J. Lawrence, Soft Matter, 2013, 9, 7095–7105 RSC.
- A. R. Webb, A. F. Bais, M. Blumthaler, G.-P. Gobbi, A. Kylling, R. Schmitt, S. Thiel, F. Barnaba, T. Danielsen, W. Junkermann, A. Kazantzidis, P. Kelly, R. Kift, G. L. Liberti, M. Misslbeck, B. Schallhart, J. Schreder and C. Topaloglou, J. Atmos. Ocean. Technol., 2002, 19, 1049–1062 CrossRef.
- W. Haynes, CRC Handbook of Chemistry and Physics, 95th edn, CRC, 2016 Search PubMed.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes: the Art of Scientific Computing, Cambridge University Press, New York, NY, USA, 3rd edn, 2007 Search PubMed.
- A. Sandu and R. Sander, Atmos. Chem. Phys., 2006, 6, 187–195 CrossRef CAS.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Atmos. Chem. Phys., 2004, 4, 1461–1738 CrossRef CAS.
- A. K. Bertram, A. V. Ivanov, M. Hunter, L. T. Molina and M. J. Molina, J. Phys. Chem. A, 2001, 105, 9415–9421 CrossRef CAS.
- G. J. Frost, M. Trainer, R. L. Mauldin, F. L. Eisele, A. S. H. Prevot, S. J. Flocke, S. Madronich, G. Kok, R. D. Schillawski, D. Baumgardner and J. Bradshaw, J. Geophys. Res. Atmos., 1999, 104, 16041–16052 CrossRef CAS.
- L. A. George, T. M. Hard and R. J. O'Brien, J. Geophys. Res. Atmos., 1999, 104, 11643–11655 CrossRef CAS.
- D. R. Hanson, J. Phys. Chem. B, 1997, 101, 4998–5001 CrossRef CAS.
- D. R. Worsnop, J. W. Morris, Q. Shi, P. Davidovits and C. E. Kolb, Geophys. Res. Lett., 2002, 29, 57 CrossRef.
- R. Storn and K. Price, J. Global Optim., 1997, 11, 341–359 CrossRef.
- A. Milsom, A. M. Squires, A. D. Ward and C. Pfrang, Atmos. Chem. Phys. Discuss., 2021, 2021, 1–21 Search PubMed.
- T. Berkemeier, M. Ammann, U. K. Krieger, T. Peter, P. Spichtinger, U. Pöschl, M. Shiraiwa and A. J. Huisman, Atmos. Chem. Phys., 2017, 17, 8021–8029 CrossRef CAS.
- A. M. Arangio, J. H. Slade, T. Berkemeier, U. Pöschl, D. A. Knopf and M. Shiraiwa, J. Phys. Chem. A, 2015, 119, 4533–4544 CrossRef CAS PubMed.
- P. A. J. Bagot, C. Waring, M. L. Costen and K. G. McKendrick, J. Phys. Chem. C, 2008, 112, 10868–10877 CrossRef CAS.
- D. Foreman-Mackey, D. W. Hogg, D. Lang and J. Goodman, Publ. Astron. Soc. Pac., 2013, 125, 306–312 CrossRef.
- D. W. Hogg and D. Foreman-Mackey, Astrophys. J. Suppl., 2018, 236, 11 CrossRef.
- M. Legrand, F. Ducroz, D. Wagenbach, R. Mulvaney and J. Hall, J. Geophys. Res. Atmos., 1998, 103, 11043–11056 CrossRef CAS.
- D. J. Kieber, W. C. Keene, A. A. Frossard, M. S. Long, J. R. Maben, L. M. Russell, J. D. Kinsey, I. M. B. Tyssebotn, P. K. Quinn and T. S. Bates, Geophys. Res. Lett., 2016, 43, 2765–2772 CrossRef CAS.
- G. Engling, C. M. Carrico, S. M. Kreidenweis, J. L. Collett, D. E. Day, W. C. Malm, E. Lincoln, W. M. Hao, Y. Iinuma and H. Herrmann, Atmos. Environ., 2006, 40, 299–311 CrossRef.
- M. D. King, K. C. Thompson, A. D. Ward, C. Pfrang and B. R. Hughes, Faraday Discuss., 2008, 137, 173–192 RSC.
- M. D. King, K. C. Thompson and A. D. Ward, J. Am. Chem. Soc., 2004, 126, 16710–16711 CrossRef CAS PubMed.
- V. F. Sears, Neutron News, 1992, 3(3), 26–37 CrossRef.
- R. C. Chapleski, Y. Zhang, D. Troya and J. R. Morris, Chem. Soc. Rev., 2016, 45, 3731–3746 RSC.
- C. Pfrang, M. Shiraiwa and U. Pöschl, Atmos. Chem. Phys., 2010, 10, 4537–4557 CrossRef CAS.
- I. George, R.-W. Chang, V. Danov, A. Vlasenko and J. Abbatt, Atmos. Environ., 2009, 43, 5038–5045 CrossRef CAS.
- C. R. Ruehl, T. Nah, G. Isaacman, D. R. Worton, A. W. H. Chan, K. R. Kolesar, C. D. Cappa, A. H. Goldstein and K. R. Wilson, J. Phys. Chem. A, 2013, 117, 3990–4000 CrossRef CAS PubMed.
- J. H. Slade and D. A. Knopf, Phys. Chem. Chem. Phys., 2013, 15, 5898–5915 RSC.
- A. Vlasenko, I. J. George and J. P. D. Abbatt, J. Phys. Chem. A, 2008, 112, 1552–1560 CrossRef CAS PubMed.
- P. Alpert, R. Ciuraru, S. Rossignol, M. Passananti, L. Tinel, S. Perrier, Y. Dupart, S. Steimer, M. Ammann, D. Donaldson and C. George, Sci. Rep., 2017, 7, 12693 CrossRef PubMed.
- R. Chiu, L. Tinel, L. Gonzalez, R. Ciuraru, F. Bernard, C. George and R. Volkamer, Geophys. Res. Lett., 2016, 44, 1079–1087 CrossRef.
- N. Hayeck, I. Musa, S. Perrier and C. George, ACS Earth Space Chem., 2020, 4(8), 1247–1253 CrossRef CAS.
- D. A. Knopf, S. M. Forrester and J. H. Slade, Phys. Chem. Chem. Phys., 2011, 13, 21050–21062 RSC.
- L. Lee, P. Wooldridge, T. Nah, K. Wilson and R. Cohen, Phys. Chem. Chem. Phys., 2013, 15, 882–892 RSC.
- T. Moise, R. K. Talukdar, G. J. Frost, R. W. Fox and Y. Rudich, J. Geophys. Res. Atmos., 2002, 107, AAC-6 CrossRef.
- Y. Zhang, R. C. Chapleski, J. W. Lu, T. H. Rockhold, D. Troya and J. R. Morris, Phys. Chem. Chem. Phys., 2014, 16, 16659–16670 RSC.
- P. Bevington and D. Robinson, Data Reduction and Error Analysis for the Physical Sciences, McGraw-Hill, 2003 Search PubMed.
- C. Gonçalves, C. Alves, A. P. Fernandes, C. Monteiro, L. Tarelho, M. Evtyugina and C. Pio, Atmos. Environ., 2011, 45, 4533–4545 CrossRef.
- S. Zhou, L. Gonzalez, A. Leithead, Z. Finewax, R. Thalman, A. Vlasenko, S. Vagle, L. A. Miller, S.-M. Li, S. Bureekul, H. Furutani, M. Uematsu, R. Volkamer and J. Abbatt, Atmos. Chem. Phys., 2014, 14, 1371–1384 CrossRef.
- A. M. Arangio, J. H. Slade, T. Berkemeier, U. Pöschl, D. A. Knopf and M. Shiraiwa, J. Phys. Chem. A, 2015, 119, 4533–4544 CrossRef CAS PubMed.
- U. Pöschl, Y. Rudich and M. Ammann, Atmos. Chem. Phys., 2007, 7, 5989–6023 CrossRef.
- S. Enami, M. R. Hoffmann and A. J. Colussi, J. Phys. Chem. Lett., 2015, 6, 527–534 CrossRef CAS PubMed.
- K. J. Laidler, Chemical Kinetics, 3rd edn, Pearson, 1987 Search PubMed.
- D. J. Donaldson and K. T. Valsaraj, Environ. Sci. Technol., 2010, 44, 865–873 CrossRef CAS PubMed.
- J. Gilman, T. Eliason, A. Fast and V. Vaida, J. Colloid Interface Sci., 2004, 280, 234–243 CrossRef CAS PubMed.
- I. J. George, A. Vlasenko, J. G. Slowik, K. Broekhuizen and J. P. D. Abbatt, Atmos. Chem. Phys., 2007, 7, 4187–4201 CrossRef CAS.
- J. D. Hearn and G. D. Smith, Geophys. Res. Lett., 2006, 33 CrossRef CAS.
- A. T. Lambe, J. Zhang, A. M. Sage and N. M. Donahue, Environ. Sci. Technol., 2007, 41, 2357–2363 CrossRef CAS PubMed.
- J. D. Smith, J. H. Kroll, C. D. Cappa, D. L. Che, C. L. Liu, M. Ahmed, S. R. Leone, D. R. Worsnop and K. R. Wilson, Atmos. Chem. Phys., 2009, 9, 3209–3222 CrossRef CAS.
- D. L. Che, J. D. Smith, S. R. Leone, M. Ahmed and K. R. Wilson, Phys. Chem. Chem. Phys., 2009, 11, 7885–7895 RSC.
- T. Nah, S. H. Kessler, K. E. Daumit, J. H. Kroll, S. R. Leone and K. R. Wilson, J. Phys. Chem. A, 2014, 118, 4106–4119 CrossRef CAS PubMed.
- E. G. Schnitzler and J. P. D. Abbatt, Atmos. Chem. Phys., 2018, 18, 14539–14553 CrossRef CAS.
- H. Fan, M. R. Tinsley and F. Goulay, J. Phys. Chem. A, 2015, 119, 11182–11190 CrossRef CAS PubMed.
- M. M. Chim, C. Y. Chow, J. F. Davies and M. N. Chan, J. Phys. Chem. A, 2017, 121, 1666–1674 CrossRef CAS PubMed.
- M. M. Chim, C. Y. Lim, J. H. Kroll and M. N. Chan, ACS Earth Space Chem., 2018, 2, 1323–1329 CrossRef CAS.
- J.-H. Park, A. V. Ivanov and M. J. Molina, J. Phys. Chem. A, 2008, 112, 6968–6977 CrossRef CAS PubMed.
- M. J. Molina, A. V. Ivanov, S. Trakhtenberg and L. T. Molina, Geophys. Res. Lett., 2004, 31 CrossRef CAS.
- S. H. Kessler, J. D. Smith, D. L. Che, D. R. Worsnop, K. R. Wilson and J. H. Kroll, Environ. Sci. Technol., 2010, 44, 7005–7010 CrossRef CAS PubMed.
- S. H. Kessler, T. Nah, K. E. Daumit, J. D. Smith, S. R. Leone, C. E. Kolb, D. R. Worsnop, K. R. Wilson and J. H. Kroll, J. Phys. Chem. A, 2012, 116, 6358–6365 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d2ea00013j |
| ‡ Present address: National Institute of Water and Atmospheric Research, Wellington, New Zealand. |
| This journal is © The Royal Society of Chemistry 2022 |