Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nonadiabatic excited-state dynamics of ReCl(CO)3(bpy) in two different solvents†
Adam
Šrut
 ab,
Sebastian
Mai
ab,
Sebastian
Mai
 c,
Igor V.
Sazanovich
c,
Igor V.
Sazanovich
 d,
Jan
Heyda
d,
Jan
Heyda
 *ab,
Antonín
Vlček
ae,
Leticia
González
*ab,
Antonín
Vlček
ae,
Leticia
González
 *c and
Stanislav
Záliš
*c and
Stanislav
Záliš
 *a
*a
aJ. Heyrovský Institute of Physical Chemistry, Academy of Sciences of the Czech Republic, 182 23 Prague, Czech Republic. E-mail: stanislav.zalis@jh-inst.cas.cz; Tel: +420 26605 3268
bDepartment of Physical Chemistry, University of Chemistry and Technology, Prague, 166 28 Prague, Czech Republic. E-mail: jan.heyda@vscht.cz; Tel: +420 22044 4297
cInstitute of Theoretical Chemistry, Faculty of Chemistry, University of Vienna, Währinger Straße 17, 1090 Vienna, Austria. E-mail: leticia.gonzalez@univie.ac.at; Tel: +43 1 4277 52750
dCentral Laser Facility, Research Complex at Harwell, STFC, Rutherford Appleton Laboratory, Harwell Oxford, Didcot, Oxfordshire OX11 0QX, UK
eDepartment of Chemistry, Queen Mary University of London, London, E1 4NS, UK
First published on 24th October 2022
Abstract
We present a study of excited-states relaxation of the complex ReCl(CO)3(bpy) (bpy = 2,2-bipyridine) using a nonadiabatic TD-DFT dynamics on spin-mixed potential energy surfaces in explicit acetonitrile (ACN) and dimethylsulfoxide (DMSO) solutions up to 800 fs. ReCl(CO)3(bpy) belongs to a group of important photosensitizers which show ultrafast biexponential subpicosecond fluorescence decay kinetics. The choice of solvents was motivated by the different excited-state relaxation dynamics observed in subpicosecond time-resolved IR (TRIR) experiments. Simulations of intersystem crossing (ISC) showed the development of spin-mixed states in both solvents. Transformation of time-dependent populations of spin-mixed states enabled to monitor the temporal evolution of individual singlet and triplet states, fitting of bi-exponential decay kinetics, and simulating the time-resolved fluorescence spectra that show only minor differences between the two solvents. Analysis of structural relaxation and solvent reorganization employing time-resolved proximal distribution functions pointed to the factors influencing the fluorescence decay time constants. Nonadiabatic dynamics simulations of time-evolution of electronic, molecular, and solvent structures emerge as a powerful technique to interpret time-resolved spectroscopic data and ultrafast photochemical reactivity.
1 Introduction
Spin-change (intersystem crossing, ISC) dynamics is an important issue in designing photoactive transition–metal complexes. For example, ultrafast and efficient ISC is highly desirable in the case of luminophores for OLEDs or sensors, whose operation requires strong long-lived phosphorescence from the lowest triplet state, which is the case of polypyridine and phenyl-pyridine IrIII complexes. On the other hand, it is a mixed blessing for light-energy harvesting, where efficient ISC wastes a significant portion of absorbed light energy but produces long-lived triplet states capable of storing a part of the excitation energy through slower follow-up electron transfer processes and charge separation. Photophysics and photochemistry of heavy-metal d6 systems is traditionally explained assuming optical excitation of metal-to-ligand charge transfer (MLCT) or ππ intraligand (IL) singlet excited states, from which the lowest triplet state is populated on a subpicosecond timescale with a (near) unity efficiency. Despite their very short lifetime, initially populated 1MLCT states of d6 complexes have been detected by fluorescence upconversion1–3 and their very fast decay kinetics were customarily attributed to ISC. For example, fluorescence lifetimes were determined for complexes of RuII (<30 fs),4,5 OsII (∼100 fs),6 and IrIII (50–110 fs).7 It is also of relevance that UV-excited high-lying 1IL excited states of IrIII (2-phenyl-pyridine)3 decay with a 70 fs lifetime to the lowest 3MLCT state, proceeding through a cascade of steps faster than 10 fs.8Rhenium(I) tricarbonyl-polypyridine complexes, which comprise another important group of photosensitizers,9,10 show ultrafast biexponential fluorescence decay11–13 followed by long-lived (ns–μs) phosphorescence. This is the case of the photooxidant fac-[Re(im)(CO)3 (phen)]+ (im = imidazole, phen = 1,10-phenanthroline) whose fluorescence decays with lifetimes of 144 and 1500 fs (in N,N-dimethylformamide) that were originally attributed to a direct ISC from optically populated 1MLCT to the lowest 3MLCT state and to a parallel slower ISC through an intermediate 3IL (phen-localized ππ intraligand) state, respectively.13 This picture has recently been challenged by a theoretical study14 that simulated ultrafast excited-state dynamics of this complex employing the surface-hopping methodology15 where the electronic wavefunction was allowed to spread over different electronic states whose nonadiabatic and spin–orbit couplings were taken into account. Solvent water molecules were included explicitly. A set of optically excited low-lying singlet states was found to undergo a ∼8 fs electronic-driven ISC to a 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 mixture of triplet and singlet states that further evolved in a nuclear-driven ∼420 fs “retarded” ISC, during which the overall triplet-to-singlet ratio increased only slightly to ca. 80
30 mixture of triplet and singlet states that further evolved in a nuclear-driven ∼420 fs “retarded” ISC, during which the overall triplet-to-singlet ratio increased only slightly to ca. 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 at 250 fs, while the triplet population was redistributed among various states. The population distribution at 250 fs expressed in terms of spin-free states showed significant contributions from three lowest-lying triplets and the lowest singlet, plus minor contributions from higher states. This computational result can be attributed either to a mixture of molecules in different electronic states or to a strong mixing of singlet and triplet states in the final electronic wavefunction through spin–orbit coupling. A preliminary observation of two excited-state features in IR spectra of analogous complexes measured at 1 ps after excitation13 supports the former interpretation. This theoretical work has very important implications for our understanding of the rich photochemistry and photophysics of ReI carbonyl–diimine complexes and their use as photosensitizers and photocatalysts. It has showed that the conventional assignment of ultrafast fluorescence decay kinetics to ISC has to be revisited. A good match between experimental13 and simulated14 time-resolved fluorescence spectra suggests that femtosecond fluorescence decay kinetics has to be interpreted beyond the singlet population decay, considering the overall excited-state and structural dynamics. The intriguing possibility that a mixture of molecules in different excited states persists into the picosecond time range implies that follow-up relaxation and photochemistry can proceed through different channels.
20 at 250 fs, while the triplet population was redistributed among various states. The population distribution at 250 fs expressed in terms of spin-free states showed significant contributions from three lowest-lying triplets and the lowest singlet, plus minor contributions from higher states. This computational result can be attributed either to a mixture of molecules in different electronic states or to a strong mixing of singlet and triplet states in the final electronic wavefunction through spin–orbit coupling. A preliminary observation of two excited-state features in IR spectra of analogous complexes measured at 1 ps after excitation13 supports the former interpretation. This theoretical work has very important implications for our understanding of the rich photochemistry and photophysics of ReI carbonyl–diimine complexes and their use as photosensitizers and photocatalysts. It has showed that the conventional assignment of ultrafast fluorescence decay kinetics to ISC has to be revisited. A good match between experimental13 and simulated14 time-resolved fluorescence spectra suggests that femtosecond fluorescence decay kinetics has to be interpreted beyond the singlet population decay, considering the overall excited-state and structural dynamics. The intriguing possibility that a mixture of molecules in different excited states persists into the picosecond time range implies that follow-up relaxation and photochemistry can proceed through different channels.
In this work, we have focused on the prototypical member of the ReI tricarbonyl-polypyridine family, the fac-ReCl(CO)3(bpy) complex, Rebpy, that is well known for its 40 ns-lived phosphorescence,9,10 photoredox chemistry, and as a photo- and electro-catalyst of CO2 reduction.16 Its low-lying singlet and triplet excited states have an MLCT character but, unlike [Re(im)(CO)3(phen)]+, with a Cl→bpy LL'CT contribution.9,11,17–20 Similarly to [Re(im)(CO)3(phen)]+, Rebpy fluorescence decays biexponentially with 85 and 340 fs lifetimes in acetonitrile (ACN).11–13 It is of interest that the fluorescence decay kinetics slows down upon changing the axial ligand X in ReX(CO)3(bpy) from Cl (85, 340 fs) to Br (128, 470 fs) and I (152, 1180 fs), that is opposite than expected based on increasing spin–orbit coupling.11 This observation has led to the proposal that the ISC dynamics is governed by the Re–X stretching vibration11 and stimulated much theoretical work,21,22 including spin–orbit17,23–25 and vibronic26,27 coupling calculations, as well as wavepacket propagation.24,25 Photophysics and photochemistry of Rebpy is also affected by the solvent. Fluorescence decay slows down on going from ACN (85, 340 fs) to N,N-dimethylformamide (97, 1090 fs)11–13 and relaxation dynamics is solvent-dependent in the 1–20 ps range.28–33 Importantly, excited-state solvation dynamics was found to determine the efficiency of Rebpy photoreduction by triethanolamine, which is the first step of photocatalytic CO2 reduction.34
Excited-state dynamics that gives rise to observed biphasic subpicosecond fluorescence decay kinetics, time-dependent distribution of populated low-lying excited states, as well as the role of structural and solvation changes at early times after excitation are some of the photophysical questions we address in this study employing full-dimensional surface-hopping simulations. Predictions emerging from these calculations aid interpreting the fluorescence decay as well as ultrafast spectral changes and time-dependent band-shapes observed in time-resolved IR absorption (TRIR) and femtosecond stimulated Raman scattering (FSRS) spectra. The choice of solvents (Fig. S1, ESI†), ACN and dimethylsulfoxide (DMSO), was motivated by good solubility of Rebpy in both solvents and distinctly different excited-state relaxation dynamics observed in our new TRIR experiments. Simulations were carried out up to 800 fs, in order to access times relevant to ultrafast excited-state reactions, such as intramolecular electron transfer.35–38 Indeed, the present theoretical work has important implications for our mechanistic understanding of photoinduced electron transfer. It is argued that (sub)picosecond photochemical processes of Re(I) tricarbonyl-diimine complexes may occur from a manifold of excited states spread in energy, instead of being limited to the lowest triplet state only.
2 Methods
Classical simulations were performed with the Amber 14 software39 at a constant pressure 1 bar and temperature 300 K maintained by weak-coupling thermostat and barostat, with a coupling time of 1 ps.40 A 1 fs time step and 3D-periodic boundary conditions were employed. Rebpy intramolecular geometry corresponding to the ground-state energetic minimum in vacuum was fixed during classical simulations. Nonbonding interactions were determined from a generalized Amber force-field (GAFF) and partial charges were taken from a Mulliken population analysis. Solvent molecules were parametrized by the recommended protocol,41,42i.e., GAFF was used for bonded and nonbonded interactions, and partial charges were determined via restricted electrostatic potential fitting procedure (RESP). Resulting charges for ACN and DMSO are depicted in Fig. S1, ESI.†Adiabatic QM/MM MD simulations were carried out using Amber 14 software39 interfaced with TERAChem simulation package43,44 employing electrostatic embedding and without periodic boundary conditions. A 1 fs time step was employed and a weak-coupling thermostat was applied.40 Only Rebpy was treated quantum mechanically at a DFT level of theory: PBE0, 6-31g* basis for non-metallic atoms, LANL2DZ basis for Re with effective core potential45 and D3 dispersion correction.46,47 Solvent was described at a MM level with the same parameterization as in classical simulations. The choice of the simulation setup and the QM level were based on our previous work on electron transfer processes.17,48,49 PBE0 functional was chosen because the previous static TD-DFT (Time-Dependent Density Functional Theory) calculations with electrostatic solvent correction at optimized structures of Rebpy interpreted well its UVvis spectra.17 Because of the extensive re-equilibration at QM/MM level of theory, the accuracy of the force field (GAFF) should not affect the results obtained.
Non-adiabatic QM/MM MD simulations were performed in a fewest-switches surface hopping51 fashion employing the SHARC package52 interfaced with ORCA and Tinker.53 QM/MM MD calculations employed the PBE0 functional, ZORA relativistic Hamiltonian,54 ZORA-def2-SVP55 basis set for non-metallic atoms, SARC-ZORA-TZVP56 basis set for Re, D3 dispersion correction46,47 and SARC/J auxiliary basis set.57 The system was propagated at a constant energy (i.e., in a microcanonical ensemble) with a 0.5 fs time step. In the non-adiabatic framework, the energy based decoherence58 was used, non-adiabatic coupling vectors were replaced by wavefunction overlaps59 and the time step for the three-step wavefunction propagator60 of 0.005 fs was used. Surface hopping was performed on diagonal (spin-mixed) surfaces. This methodology was tested and successfully applied in recent studies of an analogous rhenium complex [Re(im)(CO)3(phen)]+.14 Sampling of the initial conditions at different temperatures can lead to population of different excited states or to different ISC pathways.61 Therefore the temperature effect was taken into account (see Section S.1.2, ESI†).
Preparation of initial conditions is schematically described in Fig. 1. A cubic box with dimensions 40 × 40 × 40 Å containing Rebpy and 550 DMSO molecules was created. The simulation box was then equilibrated at a constant temperature (300 K) and pressure (1 bar) employing 3D-periodic boundary conditions, geometry of Rebpy was frozen during this step. The equilibration step was followed by several long QM/MM simulations (of total length 550 ps) starting from different points of the MM/MD equilibration run at a constant temperature and without periodic boundary conditions. 500 snapshots with temporal spacing of 1 ps were extracted from the generated trajectories and served as initial conditions. Vertical excitations considering 20 singlet and 20 triplet states were performed for each initial condition in order to determine the initial active state.14 Out of these, 100 initial conditions were selected and simulated in non-adiabatic dynamics. Non-adiabatic trajectories were simulated for up to 800 fs. 8 trajectories started in the S1 state, 92 in S2.
The simulation set in ACN was prepared in a similar manner. A cubic box with dimensions 40 × 40 × 40 Å containing Rebpy and 950 ACN molecules was created. The simulation box was then equilibrated at a constant temperature (300 K) and pressure (1 bar) employing 3D-periodic boundary conditions, with the Rebpy geometry frozen during this step. The equilibration run was elongated to a nanosecond time scale. Next, 500 uncorrelated snapshots were generated for further prolongation as QM/MM trajectories at a constant temperature and without periodic boundaries up to 2 ps. For each of resulting 500 initial conditions vertical excitations with 20 singlet and 20 triplet states were computed and the initial active state determined. In this case, 97 non-adiabatic trajectories were simulated for up to 770 fs, from which 4 started in S1 and 93 in S2.
3 Results and discussion
Non-adiabatic TD-DFT molecular dynamics simulations of electronically excited Rebpy were carried out in two different solvents (ACN, DMSO) on spin-mixed potential energy surfaces,60 as implemented in the SHARC package (Section S.1 in ESI†).52 The electronic ground state is labeled as GS, excited singlet states as S1, S2, S3,…, Sn and excited triplet states as T1, T2, T3,…, Tn. The choice of the initial active state for non-adiabatic dynamics was based on analysis of Rebpy electronic absorption spectrum (Fig. 2) calculated from a large number of initial conditions (uncorrelated positions and velocities). Excitations were simulated with an infinitely narrow pulse, hence only transition between states with the same multiplicity as the ground state, i.e., singlets, are relevant at time zero. After vertical excitation to the singlet manifold at time zero, 97 non-adiabatic trajectories (4 starting in S1 and 93 in S2) were simulated for 770 fs in ACN and 100 non-adiabatic trajectories (8 starting in S1 and 92 in S2) were simulated for 800 fs in DMSO.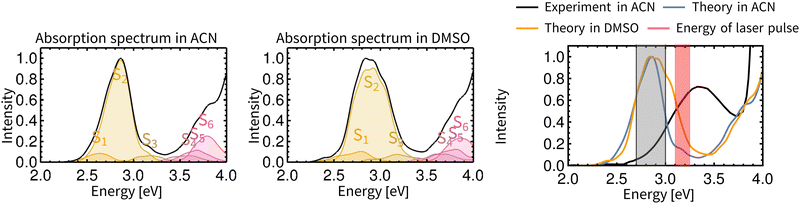 | ||
| Fig. 2 TD-DFT calculated electronic absorption spectra of Rebpy in ACN (left) and DMSO (middle). The final spectrum is represented by a solid black line, contributions of the six lowest-lying singlet states are given in colour. The rightmost panel compares simulated and experimental spectra in ACN. The red window depicts the laser-pulse energies used in most photophysical experiments.11,13,50 The gray shaded area shows the energy window used for excitation in this work. Details of absorption spectrum calculation are provided in Section S.1.2, ESI.† | ||
Fig. 2 compares calculated and experimental electronic spectra of Rebpy in the UV-Vis region. The computed spectrum in ACN reproduces the shape of the experimental spectrum, with the lowest-energy feature red-shifted with respect to the experiment.
In agreement with previously published results,11–13,62–64 the two lowest singlet and triplet states have Re(CO)3→bpy MLCT character with ca 20% Cl→bpy LLCT admixture (Fig. S3, ESI†). The solvation environment affects the character of the electronic wavefunction only slightly. It is supposed that the S2 state will be preferably populated by excitation in the visible region, and then undergoes ISC to lower energy states T2 and T1. The rightmost plot in Fig. 2 depicts the experimentally used laser pulse energies (3.1–3.25 eV).11,13,50 In order to populate experimentally relevant active states, the energy window for excitations (2.7–3.0 eV) was used in the calculations. This ensures that sufficient number of initial conditions for non-adiabatic trajectories will be produced. Characters and densities of states at time zero are discussed in detail in the Section S.2 in ESI.†
3.1 Intersystem crossing
Fig. 3 presents the temporal evolution of four predominantly populated spin-mixed states for simulations in both solvents (left), together with their compositions (right). In both solvents, the MLCT and LLCT characters of the lowest singlet and triplet individual spin-free states are preserved during the whole simulation time (full plots are showed in Section S.4 in ESI†).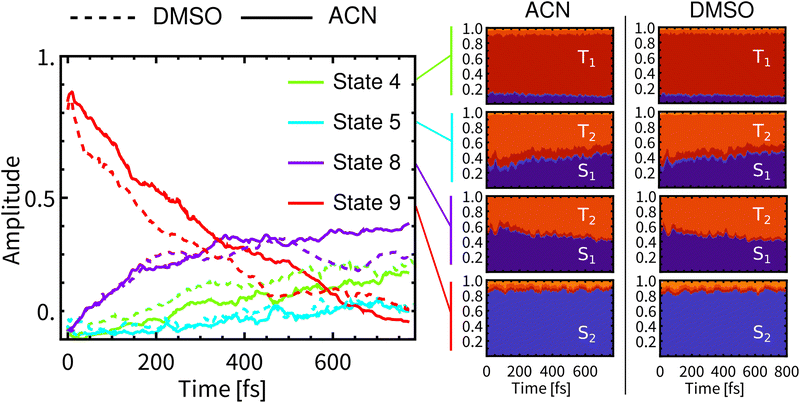 | ||
| Fig. 3 Left: Development of populations of spin-mixed states (left panel) in DMSO (dashed) and ACN (full). Only four most populated states are plotted (State 1 is the ground state). Right: Composition of spin-mixed states in a spin-free basis. The spin-free representation was obtained via ensemble averaged columns of transformation matrix U defined in ref. 60. The evolution of all spin-mixed states is presented in Fig. S15, ESI.† Compositions of the lowest 20 spin-mixed states are represented in Fig. S16 and S17, ESI.† | ||
At the beginning of simulations, the wavefunction is described predominantly by State 9 (red line). This state is bright and contributes significantly to the fluorescence. During the simulation in ACN, the contribution of State 9 diminishes continuously and monotonically to ca 10% at 800 fs. After laser-pulse excitation in ACN the population of State 8 (purple) rapidly increases in the first 350 fs, followed by a slow gradual increase, reaching ca 40% at 770 fs. In contrast, the populations of States 8 and 9 in DMSO are non-monotonous. State 8 reaches a maximum at about 500 fs and then decreases to ca 30% at 800 fs. This is reflected also in non-monotonous behavior of State 9. The contribution of State 4 (green line) grows continuously to ca 30% in both solvents. At around 500 fs, the differences in contributions of spin-mixed states between the two solvents becomes apparent. The most prominent changes concern States 9 and 8. At long times the ensemble of molecules can be still described by spin-mixed states, which most likely evolve toward an equilibrium that could persist on the ps timescale. Such behavior can explain the observed formation of an additional band in time-resolved infrared spectra (Section 3.6).
The average composition of spin-mixed states varies only slightly during simulations in both solvents (Fig. 3-right). State 9 remains predominantly composed of S2 and thus will have a significant contribution to the fluorescence. Luminescence from State 8 is expected to be weak since S1 exhibits only a small transition dipole moment to the ground electronic state,17 moreover the contribution of S1 decreases over the simulation time, being compensated by a rising contribution of T2. Experimentally observed long-lived phosphorescence on ps timescales11 can be assigned to States 8 and 4, since their populations persist to longer times and they have a significant contribution of S1. State 4 is mainly composed of T1 and, along with States 2 and 3 (also mostly T1), it will be the final state after the ISC. However, these states will become predominant at much longer times than the total simulation time.
As the above analysis may have lost some information on the composition of spin-mixed states by ensemble averaging, we have analysed individual spin–orbit coupling matrix elements (SOCMEs) and inspected the temporal evolution of their distribution (Fig. 4). As a common trend for both solvents we found a minor increase of S1–T2 and S2–T1 couplings, and a more significant decrease of S1–T1 and S2–T2 couplings. The observed decrease of S1–T1 and S2–T2 SOCME in ACN is faster than their counterparts in DMSO, which may lead to a decreasing rate of the ISC (slow component τslow).
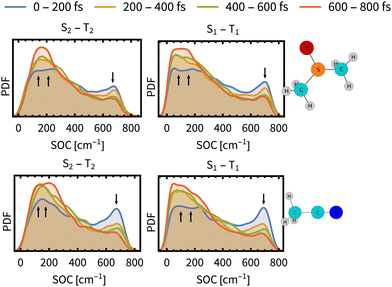 | ||
| Fig. 4 Time evolution of the distribution of spin–orbit coupling energies between the most prominent states S1–T1 and S2–T2 (PDF denotes the probability density function). The distributions are determined over the ensemble of simulated trajectories. Arrows indicates decrease or increase during the simulation time. SO couplings between other states and energy gaps between spin-free states are presented in Section S9, ESI.† | ||
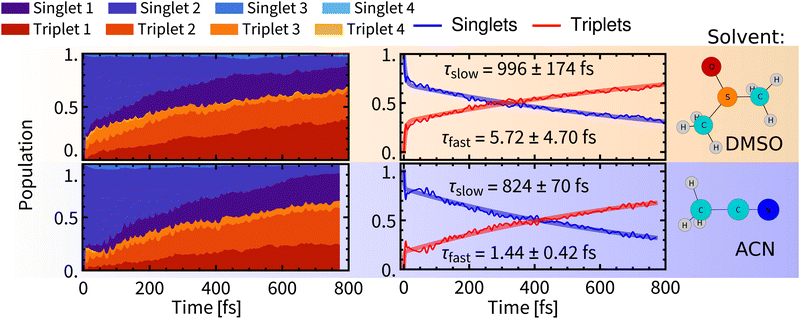 | ||
| Fig. 5 Left: Temporal evolution of singlet and triplet spin-free states. Right: Temporal evolution of total singlet and total triplet populations fitted with bi-exponential kinetics. Errors were estimated by bootstrapping.65 Details of the fitting procedures can be found in Section S6, ESI.† | ||
After relaxation of the molecular spin–orbit wavepacket, a minor decrease of the triplet population in 10–100 fs was observed in ACN and is mirrored by an increase of the singlet population. As would be expected after the formation of the quantum wavepacket at time zero, due to the interaction with the environment, the wavefunction of the system will eventually collapse into one electronic state. Apparently, the spin–orbit electronic state with the major contribution to the wavefunction is dominated by singlet states, hence the increase of singlet population. This effect is, however, quickly superimposed by non-adiabatic effects, that lead to increasing population of triplet states.
Biexponential global fits of time-dependent total singlet and triplet populations provided time constants τslow of approx. 1000 fs and 800 fs in DMSO and ACN, respectively. The time constant τslow is attributable to the intramolecular vibrational redistribution (IVR) with frequent non-adiabatic effects that drive further the singlet-to-triplet conversion and population redistribution within the singlet and triplet manifolds (Fig. 5, left). It follows that a non-negligible singlet population persists on longer simulation times, which is attributed to reaching an equilibrium between spin-mixed electronic states but also to a minor admixture of singlet states to final electronic states through the spin–orbit interaction. The “slow” ISC component is slightly slower in DMSO (∼1000 fs) than in ACN (∼800 fs). The evolution of the ensemble-averaged excited-state characters is virtually identical in both solvents, with only minor differences in the first 100 fs (Section S.4 and Fig. S5 in ESI†).
A comparison of Rebpy (τfast 1–6 fs, 20%; τslow 800–1000 fs) with [Re(CO)3 (im)(phen)]+ (τfast = 8 fs, 70%; τslow = 420 fs, ref. 14) indicates large effects of the coordination sphere composition and excited-state character on ISC kinetics and yields. Namely, the majority of singlet states in [Re(CO)3(im)(phen)]+ is converted during the fast wavepacket relaxation, in contrast with Rebpy where most of ISC appears to be IVR-driven, occurring in the “slow” kinetics component. In both cases, the “slow” kinetics converts only units of percent of the singlet population per 100 fs (Fig. 5). This difference can be attributed to the lack of low frequency Re–Cl vibration in the imidazole complex and different excited-state characters as the bright state of [Re(CO)3(im)(phen)]+ lacks the L→L′ CT contribution and MLCT amounts to ca 70%.
3.2 Luminescence decay
Experimental time-resolved luminescence spectra (Fig. 6-right) obtained upon 80 fs, 400 nm excitation exhibited a very broad band peaking at about 530 nm that has rapidly decayed in intensity and shifted to the red, eventually converting into a long-lived weak phosphorescence signal at ≈610 nm. The initial decay kinetics is biexponential. The time constants τ1 = 85 fs and τ2 = 340 fs were determined in ACN and attributed to the direct ISC from the optically prepared 1MLCT S2 state to T1 and to an indirect process via an intermediate triplet state, respectively.11,12 To understand the apparent contradiction with the simulated ISC dynamics, we have simulated also the time-resolved luminescence spectra, assuming that the emission intensity is proportional to the product of total singlet population and the transition moment that was calculated explicitly at each time delay. Calculated radiative transitions were broadened in time by a 100 fs full width at half maximum (fwhm) Gaussian to mimic the experimental response function and also in the energy domain by a 0.5 eV fwhm Gaussian to obtain continuous spectral bands (Section S5, ESI†). Simulated luminescence spectra and decay kinetics show a good match with the experiment (Fig. 6 and 7). Fitting parameters τ1 = 72 fs and τ2 = 343 fs of our simulation results are in an excellent agreement with the global kinetics fit of experimentally measured time-resolved fluorescence spectra in ACN.11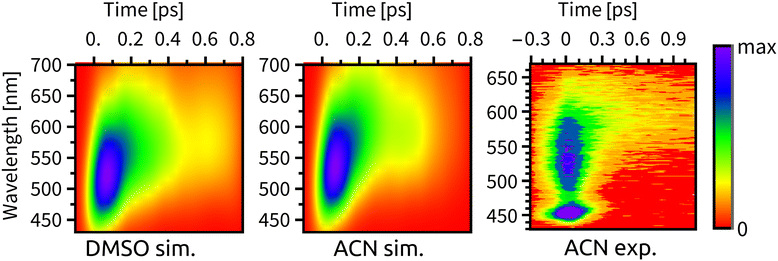 | ||
| Fig. 6 Time-resolved fluorescence spectra, from left to right: simulated spectrum in DMSO, simulated spectrum in ACN, experimental spectrum in ACN from ref. 11. We note that the peak at ∼450 nm in the experimental spectrum is the ACN Raman line. | ||
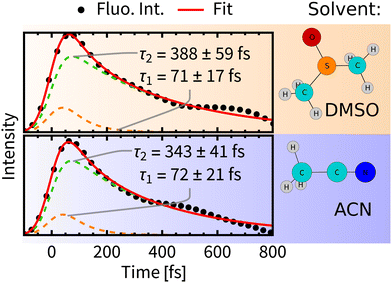 | ||
| Fig. 7 Decay of total fluorescence intensity convoluted with the instrumental response function (dots) fitted with bi-exponential decay (red line). Errors were estimated by bootstrapping.65 For details of the fitting procedures see Section S6, ESI.† | ||
A comparison of luminiscence decay kinetics in the two solvents reveals that the time constants τ1 are similar, i.e., about 70 fs, being consistent with the experimental finding that τ1 depends only slightly on the quality of the solvent.12 On the other hand, τ2 possesses some solvent-specificity with a slightly faster luminescence decay in ACN, τ2 = 343 fs than in DMSO, τ2 = 388 fs.
Importantly, the luminescence decay lifetimes τ1 and τ2 are substantially different from the τfast and τslow lifetimes of the singlet-population decay (Fig. 5). This indicates that fluorescence decay cannot be solely driven by the ISC and that ultrafast time-evolution of luminescence spectra does not originate solely from changing populations of emitting states. A changing value of the transition moment and, presumably, population redistribution within the singlet-state manifold in the course of the IVR and structural relaxation appear to be important factors in the present case. Changing interactions with the solvent environment will influence the luminescence as well.
Comparable rates of the ISC in both solvents and faster decay of the luminescence decay component (τ2) in ACN along with a good agreement with experimental data give rise to an important question: what quantity is actually affected by a presence of explicit solvent molecules? Due to the similar dielectric constants of both solvents an electrostatic approach (e.g., PCM) cannot provide any variation of spectroscopic properties. The faster luminescence decay may originate from direct interactions of Rebpy with explicit solvent molecules. In the next sections we will examine which quantities could be affected by such specific solvation.
3.3 Structural relaxation dynamics
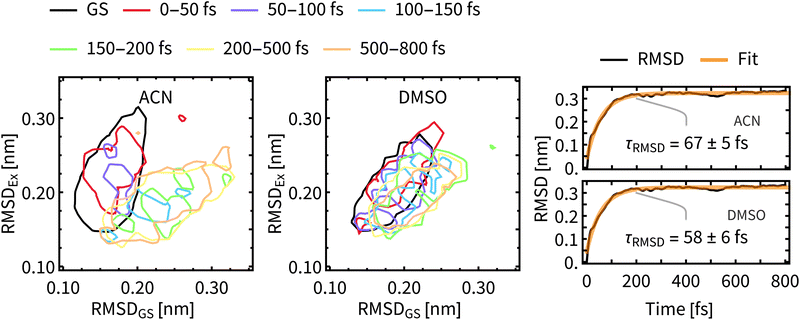
As a measure of structural changes of Rebpy during the ISC we used the time evolution of the root-mean-square deviation (RMSD) from the geometry at time zero. Results shown in the right panel of Fig. 8 represent the ensemble average over all trajectories, allowing to follow a net evolution (deviation) of Rebpy geometry. The temporal evolution of RMSD follows exponential kinetics, but the interpretation of fitted time constant is not straightforward. On physical grounds, we may interpret τRMSD as a rate of motion in the space of geometries. That is a rate of motion from the ground-state region to the region of excited states. In order to get a better insight into this geometric relaxation, time evolution of geometry ensembles was monitored by means of cluster analysis (Fig. 8-left). To that end, two references, the average geometry of the main GS cluster (about 70% of all frames) and the average geometry of the near-equilibrium excited-state cluster (i.e., simulation time window 650–800 fs, about 70% of frames) were defined. Next, for different time windows, geometries of Rebpy in the main cluster (about 70% of all frames) were characterized by their distance (measured as RMSD) to these two references.Results from the clustering analysis (Fig. 8-left) offer an intuitive interpretation of the geometric relaxation. In the electronic GS, Rebpy geometries exhibit a narrow distribution with a low mean value in the RMSDGS domain (black curve), i.e., they are close to the average GS geometry. In the first 100 fs (red and purple curves) the distribution of Rebpy geometries evolves towards the diagonal which results in a broad distribution of RMSD with respect to both GS and near-equilibrium excited state. In time windows 100–150 fs and 150–200 fs (blue and green curves) the distribution gets bellow the diagonal, i.e., RMSDEx decreases and narrows, while RMSDGS grows and broadens.
Only minor changes in distribution are observed beyond 200 fs, meaning that Rebpy geometries are fluctuating around the new equilibrium. The actual transition from the average GS geometry to that of a near-equilibrated excited state is described by alignment of bpy and equatorial CO ligands into a single plane (see Fig. S9, ESI†). In both solvents the geometric relaxation is significant only in the first 200 fs, distributions of geometries in ACN are, however, much broader than in DMSO. This indicates a more compact and stiffer Rebpy geometry ensemble in DMSO. Also, geometric relaxation is faster in DMSO since the distance from the GS region to the near-equilibrium excited state region is on average shorter than in ACN.
The time constants for geometric relaxation τRMSD(ACN) = 67 fs and τRMSD(DMSO) = 58 fs are close to the time constants calculated for luminescence decay τ1(ACN) = 72 fs and τ1(DMSO) = 71 fs. We propose a close connection between τRMSD and τ1, the luminescence decay at short times is driven by bleaching of the oscillator strengths due to the structural relaxation of Rebpy. The closer connection between structural relaxation and luminescence decay kinetics is established in Fig. 9 where a strong anti-correlation is observed on simulation times 10–200 fs.
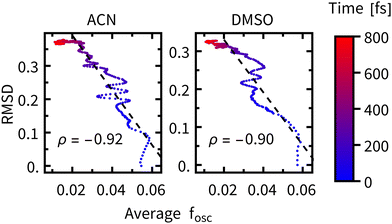 | ||
| Fig. 9 RMSD plotted against the average oscillator strength at different times after excitation (color-coded), ρ represents the correlation coefficient over the 0–200 fs interval (black dashed line). | ||
The faster luminescence decay component τ1 thus appears to be driven by geometric relaxation of Rebpy. It is, however, not possible to completely disentangle the contribution of ISC to the time constant τ1, because of its non-negligible impact on the oscillator strengths. In another words, the active electronic state determines the Rebpy geometries (and specific solvation), but also the actual Rebpy geometry (and specific solvation) steps in the selection of the active electronic state. Another implication of these findings is that at short times (<200 fs) the overall change of total luminescence is not directly proportional to the population of any electronic state, which limits applicability of time-resolved fluorescence spectroscopy in determining kinetics of ultrafast photochemical and photophysical processes.11–13
3.4 Solvent relaxation dynamics
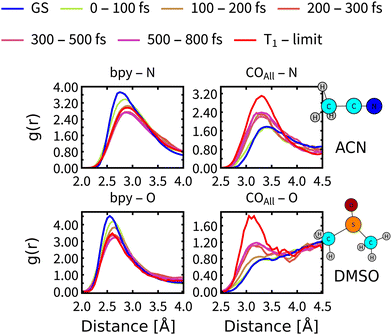
On simulation times above 200 fs, the structural relaxation of Rebpy is no longer an important process whereas relaxation of the solvent environment persists. Solvent dependence of the calculated (Fig. 6) as well as experimental11–13 time constant τ2 (Fig. 7) could be explained by different relaxation of solvation shells around Rebpy. As a measure of solvent relaxation, we employed the proximal radial distribution function66,67 (pRDF, described in Section S8, ESI†), which allowed us to monitor solvation in the vicinity of each ligand within Rebpy.In Fig. 10, we present non-equilibrium solvent distribution during non-adiabatic dynamics with temporal resolution of either 100 or 200 fs. Equilibrium distributions in the ground electronic state (GS) and in the lowest triplet state (denoted as T1 – limit) are serving as references to estimate the solvent relaxation kinetics.
The solvation shell around a bipyridine ligand experiences a decrease of the density of negatively charged solvent atoms (O, N) after excitation, which can be explained by decreasing charge on the bipyridine ligand due to an Re(CO)3→bpy MLCT character of the populated excited states. On the other hand, the solvation shell in the vicinity of carbonyl ligand experiences increasing density of negatively charged solvent atoms caused by electron-density transfer from carbonyls (becoming more positively charged) to bipyridine.
pRDFs describe relaxation as an increase (enrichment) or decrease (depletion) of the local density of negatively charged atoms in the first solvation shell, which cannot be viewed as a complete solvent reorganization. We can make a use of an experimental study by Horng et al.,68 based on measuring a solvent response to a sudden change of electrical field and determined the fastest components of the experimental dielectric relaxation response as 89 fs for ACN and 214 fs for DMSO, thus predicting faster relaxation of ACN by a factor of 2.4. We note, that experimental measurements of Rebpy in polar solvents and our theoretical approach resembles a principal similarities with above mentioned study. Quantitative agreement is, however, not expected, since in the ref. 68 the solvent relaxation was studied around a planar molecule (Coumarin 153) while the Rebpy complex has a 3-dimensional structure.
Comparison of the pRDF evolution from the GS distribution towards the T1 – limit stresses much faster relaxation of ACN than DMSO molecules. It takes less than 200 fs for ACN molecules to approach the new equilibrium distribution around bpy, whereas DMSO molecules need almost 300 fs. Situation around carbonyl ligands is qualitatively different, relaxation of DMSO is again slower by approximately 100 fs but system is approaching a different equilibrium distribution than that of the T1 state (see right panels of Fig. 10). This is a clear indication that the relaxation of the solvent environment is also not a single-step process and will differ for each site of Rebpy. The limit distribution corresponding to the T1 state will be reached at times well beyond the total simulation time.
In summary, after approximately 200 fs three relaxation processes are persisting: (i) the ISC driven by substantial nonadiabatic effects occurring during the whole simulation times. This process has a similar rate in both ACN and DMSO solvents. (ii) Relaxation of the solvation shell, whose rate is different for each solvent. (iii) Decay of the total luminescence that was on a shorter time scale driven by geometric relaxation and independent of the solvation environment as was described in the previous section and experimental studies.12 At longer times it is the relaxation of the solvent environment what drives the rate of the luminescence decay. Another major cause of decaying luminescence is the ISC which, however, cannot alone explain the different behaviour in ACN and DMSO since the ISC rates are comparable in both solvents.
3.5 Coherent vibrational motions
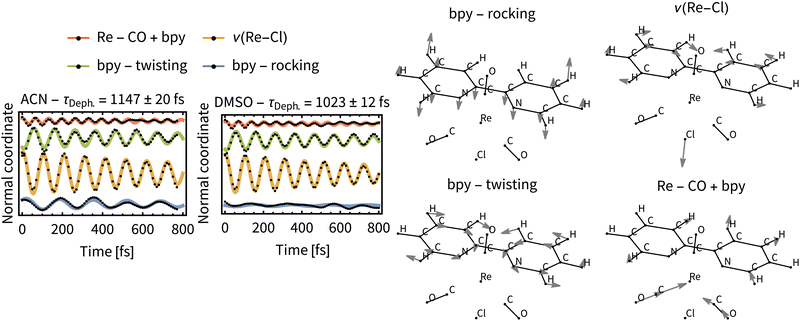
Excitation of a molecule with the δ-pulse (or generally with a femtosecond laser pulse) will in many cases form a vibrational wavepacket.69–71 Although surface hopping dynamics do not allow for existence of discrete vibrational levels, a coherent motion of atomic nuclei in the ensemble of trajectories is allowed and resembles the motion of a vibrational wavepacket.71 Such classical coherent motion is initiated at time zero by excitation from the ground electronic state to the excited state and dephased over time by intra- and intermolecular perturbations.71 In our case, intramolecular perturbations are represented by changes of electronic states and intermolecular perturbations by the solvent motion.In order to find coherent motions, the simulated non-adiabatic trajectories were transformed from Cartesian to normal coordinates and averaged. Visual inspection then uncovered significant oscillations of the average values for four normal modes, indicating their coherent motion in the ensemble of trajectories. Global fitting with damped sine functions then determined the dephasing time constant τDeph. for each solvent. The function for global fitting of oscillating average values of normal coordinates Qi has the form:
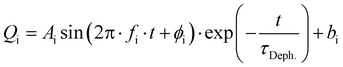 | (1) |
Most significant oscillations were identified for four normal modes, which are depicted in Fig. 11. All of them are in the low frequency range (200–500 cm−1) and dephase with τDeph. of ca 1 ps in both solvents. This indicates a long-lived vibrational wavepacket that could persist into the ps time scale. The observed behavior can be nowadays measured by ultrafast time-resolved spectroscopies in real time,72 for example employing femtosecond time-resolved X-ray solution scattering (sensitive to metal–ligand bond distances).73 Recently, it has been shown that these large amplitude motions are observable in the liquid phase.74
We can assume that intramolecular perturbations are similar for the two solvents, since the ISC rates are comparable. Intermolecular perturbations are, however, different because of different solvation rates of ACN and DMSO. The similarity of the dephasing time constants for ACN (τDeph.= 1147 fs) and DMSO (τDeph.= 1023 fs) indicates that intramolecular perturbations (i.e., changes of the electronic states) dominate the dephasing of the vibrational wavepacket. Moreover, the time constants for the “slow” ISC component, τslow, which are a direct measure for the intramolecular perturbations, are close to the τDeph..
3.6 Nonadiabatic dynamics effects in time-resolved vibrational spectroscopy
Some of the predictions of our nonadiabatic dynamics simulations have important implications for interpreting experimentally measured time-resolved spectroscopic data and ultrafast photochemical reactivity. Whereas the sub-10 fs ISC is experimentally largely elusive, the IVR- and solvation-driven “slow” ISC, and the simultaneous presence of molecules in different electronically excited states persisting into times longer than 800 fs (Fig. 3 and 5) can be tested experimentally. Time-resolved vibrational spectroscopy is especially suitable since time-resolved IR absorption (TRIR) and femtosecond stimulated Raman scattering (FSRS) provide complementary insights into Rebpy excited-state dynamics by monitoring C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O stretching vibrations, ν(C
O stretching vibrations, ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O), of the Re(CO)3 fragment and bpy-ligand vibrations, respectively. Our previous FSRS study75 of Rebpy in ACN and ACN-d3 have shown an evolving excited-state feature with 4–5 apparent maxima in the 1475–1600 cm−1 range, which coalesce into two bands at about 200 fs. Its total intensity grows with time constants of 380 fs and 21 ps. Finally, it evolves into two distinct bands at 1500 and 1546 cm−1 due to interring ν(C–C) and aromatic ν(CC)/(CN) vibrations of the relaxed excited state, respectively (Fig. S18, ESI†). In view of the present simulations, the initial band-shape changes likely reflect the changing molecular geometry (Fig. 5) and the 380 fs rise component is attributable to IVR/intramolecular restructuring and can be qualitatively related to the “slow” ISC process.
O), of the Re(CO)3 fragment and bpy-ligand vibrations, respectively. Our previous FSRS study75 of Rebpy in ACN and ACN-d3 have shown an evolving excited-state feature with 4–5 apparent maxima in the 1475–1600 cm−1 range, which coalesce into two bands at about 200 fs. Its total intensity grows with time constants of 380 fs and 21 ps. Finally, it evolves into two distinct bands at 1500 and 1546 cm−1 due to interring ν(C–C) and aromatic ν(CC)/(CN) vibrations of the relaxed excited state, respectively (Fig. S18, ESI†). In view of the present simulations, the initial band-shape changes likely reflect the changing molecular geometry (Fig. 5) and the 380 fs rise component is attributable to IVR/intramolecular restructuring and can be qualitatively related to the “slow” ISC process.
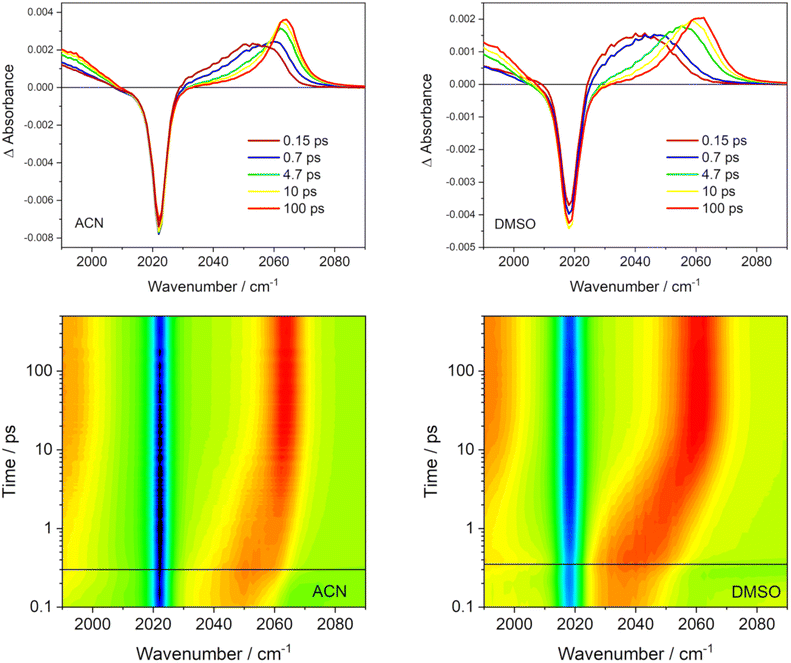
IR spectra of Re(I) tricarbonyl-polypyridine complexes show strong ν(C≡O) bands that shift to higher wavenumbers upon MLCT excitation, owing to diminishing Re → CO π back-donation.76–80 The behavior of the highest ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O) band due to the in-phase totally symmetrical stretching vibration of the three C
O) band due to the in-phase totally symmetrical stretching vibration of the three C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O ligands (labeled A′(1))76 is especially informative (Fig. 12). The excited-state A′(1) band emerges concomitantly with laser-pulse excitation as a broad unresolved asymmetric feature that envelops several close-lying IR bands. It rapidly (fs–ps) shifts to higher wavenumbers and narrows, gradually acquiring a shape of an asymmetric band that can be fitted by two Gaussian peaks – one coinciding with the spectral band maximum and a minor peak that accounts for the low-wavenumber tail. The most dramatic band-shape changes occur within the first 4 ps after excitation. The composed character of the excited-state A′(1) spectral feature accords with the population of several different electronic excited states over the ensemble of excited Rebpy molecules. It appears the that simultaneous population of two (or more) different excited states persists at least up to 5–10 ps or even longer. The shape of the excited-state A′(1) ν(C
O ligands (labeled A′(1))76 is especially informative (Fig. 12). The excited-state A′(1) band emerges concomitantly with laser-pulse excitation as a broad unresolved asymmetric feature that envelops several close-lying IR bands. It rapidly (fs–ps) shifts to higher wavenumbers and narrows, gradually acquiring a shape of an asymmetric band that can be fitted by two Gaussian peaks – one coinciding with the spectral band maximum and a minor peak that accounts for the low-wavenumber tail. The most dramatic band-shape changes occur within the first 4 ps after excitation. The composed character of the excited-state A′(1) spectral feature accords with the population of several different electronic excited states over the ensemble of excited Rebpy molecules. It appears the that simultaneous population of two (or more) different excited states persists at least up to 5–10 ps or even longer. The shape of the excited-state A′(1) ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O) band remains asymmetric in spectra measured at long time delays, for example 100 ps (Fig. 12) but the low-wavenumber shoulder is weak. It appears that higher electronic excited state(s) remain populated to a small extent even at these long times. In addition, two combination bands of bpy vibrations likely contribute to the weak shoulder as well, but their combined calculated intensity (2.5% of the A′(1) intensity) is rather small.81 It should be noted that the time-evolving composed band-shape of the excited-state A′(1) feature have been observed for many neutral and cationic Re(I) tricarbonyl polypyridine complexes with a predominantly 3MLCT lowest excited state in different media.13,29,31,82,83 Simultaneous population of several electronic excited states persistent at least on a ps timescale thus appears to be a general feature of this class of complexes, in agreement with nonadiabatic dynamics simulations of Rebpy as well as [Re(im)(CO)3 (phen)]+.14
O) band remains asymmetric in spectra measured at long time delays, for example 100 ps (Fig. 12) but the low-wavenumber shoulder is weak. It appears that higher electronic excited state(s) remain populated to a small extent even at these long times. In addition, two combination bands of bpy vibrations likely contribute to the weak shoulder as well, but their combined calculated intensity (2.5% of the A′(1) intensity) is rather small.81 It should be noted that the time-evolving composed band-shape of the excited-state A′(1) feature have been observed for many neutral and cationic Re(I) tricarbonyl polypyridine complexes with a predominantly 3MLCT lowest excited state in different media.13,29,31,82,83 Simultaneous population of several electronic excited states persistent at least on a ps timescale thus appears to be a general feature of this class of complexes, in agreement with nonadiabatic dynamics simulations of Rebpy as well as [Re(im)(CO)3 (phen)]+.14
TRIR spectra also show an interesting solvent-dependence (Fig. 12). The band shapes of 150 fs and 650–700 fs spectra agree with a broader distribution of populated excited-states in ACN than in DMSO (Fig. 5 shows higher T2 and S1 populations in ACN, at the expense of T1). In ACN, the time-wavenumber map shows a large “instantaneous” shift of the A′(1) band to higher wavenumbers upon excitation (a difference between the blue and red signals close to t = 0) followed by a small dynamic shift. In contrast, the “instantaneous” shift in DMSO is small but followed by a large dynamic shift taking place within the first 10 ps. This different behavior can be related to larger initial structural changes calculated in ACN (hence large “instantaneous” spectral shift) than in DMSO (Fig. 8). Apparently, most of the excitation-induced structural changes in DMSO involve slower solvation changes and adjusting solute–solvent interactions. Later-time solvation dynamics and TRIR temporal evolution are currently under investigation in our labs, using results of nonadiabatic dynamics as a convenient starting point.
4 Conclusions
Nonadiabatic excited-state dynamics simulations of Rebpy suggest that subpicosecond excited-state dynamics of Rebpy can be understood in terms of temporal evolution of four spin-mixed excited states that lasts longer than our simulation length of 800 fs. At this time, the lowest excited state is populated only by about 25% in both ACN and DMSO. Population of higher excited states depends slightly on the solvent (Fig. 3). A similar picture emerges in the spin-free representation that describes the excited-state evolution mostly in terms of two singlet and three triplet excited states whose population evolves and redistributes in hundreds of femtoseconds, probably well into the ps time range (Fig. 5). ISC (defined as a conversion of total singlet to total triplet population) occurs in two phases: “fast” (<10 fs) ISC driven by spin–orbit wavepacket relaxation14 and a “slow” ISC that occurs with about 800 fs (ACN) and 1000 fs (DMSO) time constants, driven by IVR, structural, and solvational changes. This ISC mechanism is qualitatively similar to that proposed14 for [Re(im)(CO)3(phen)]+ but with two important quantitative differences: the “fast” ISC in Rebpy is much less efficient (20% vs. 70%) and the “slow” ISC component is considerably slower (ca. 1000 vs. 420 fs). Intramolecular structural changes after excitation were calculated to occur mostly within the first 200 fs after excitation while solvation dynamics remain important at longer timescales. DMSO appears to restrict the extent of the initial intramolecular restructuring. Additionally, coherent oscillations of several normal coordinates were uncovered to occur during the “slow” ISC phase. In the computational framework used, they represent a classical analogue of temporal evolution of a vibrational wavepacket.Nonadiabatic simulations have important experimental implications. They match time-resolved fluorescence spectra and decay kinetics measured in ACN11–13 but change the interpretation: femtosecond Rebpy fluorescence decay kinetics is not solely attributable to decaying population of fluorescent excited state(s) as the oscillator strength diminishes in the course of intramolecular structural changes and relaxation of the solvent environment. Populations and oscillator-strength effects are interrelated and hard to disentangle. (Detailed measurements of emission-wavelength dependence of the decay kinetics could provide some insight.) Changes of oscillator strength in the course of excited-state relaxation likely is a general effect that can extend to pico- and nanosecond time domains in slow-relaxing complex media such as ionic liquids or proteins.82–84 Results of our nonadiabatic simulations also qualitatively match femtosecond evolution of Raman features observed in Rebpy FSRS spectra,75 that are now attributable to the initial restructuring during the “slow” ISC phase.
The theoretical prediction that several different excited states are populated simultaneously in the excited ensemble on femtosecond and early picosecond timescales is supported by the shape of the highest ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O) band in TRIR spectra that envelops at least two Gaussian peaks. This result has to be considered when interpreting ultrafast photoinduced electron transfer (ET) reactions of Re(I) tricarbonyl polypyridine complexes, either in solvent cages as in photocatalyzed CO2 reduction34 or in donor–acceptor assemblies. ET could occur from several different electronic excited states (Fig. 3, 5 and Fig. S15, ESI†) whose energies (and, hence, ET driving forces) span a broad range and change with time (Fig. S14, ESI†). This would lead to complicated ET kinetics. Indeed, photooxidation of tryptophan in azurin mutants by a covalently attached [Re(im)(CO)3(4,7-Me2-phen)]+ sensitizer shows multiexponential kinetics attributable to several parallel ET and relaxation steps.35–37,77,85 We expect similar behavior for currently investigated Rebpy-based covalent donor–acceptor systems and photocatalysts. A simultaneous presence of molecules in different excited states persisting on a picosecond timescale after excitation could, in principle, lead to a non-Kasha photochemistry where the predominant photochemical pathway bypasses the lowest excited state. It remains to be shown how general this effect is beyond the rhenium-carbonyl-polypyridine family.
O) band in TRIR spectra that envelops at least two Gaussian peaks. This result has to be considered when interpreting ultrafast photoinduced electron transfer (ET) reactions of Re(I) tricarbonyl polypyridine complexes, either in solvent cages as in photocatalyzed CO2 reduction34 or in donor–acceptor assemblies. ET could occur from several different electronic excited states (Fig. 3, 5 and Fig. S15, ESI†) whose energies (and, hence, ET driving forces) span a broad range and change with time (Fig. S14, ESI†). This would lead to complicated ET kinetics. Indeed, photooxidation of tryptophan in azurin mutants by a covalently attached [Re(im)(CO)3(4,7-Me2-phen)]+ sensitizer shows multiexponential kinetics attributable to several parallel ET and relaxation steps.35–37,77,85 We expect similar behavior for currently investigated Rebpy-based covalent donor–acceptor systems and photocatalysts. A simultaneous presence of molecules in different excited states persisting on a picosecond timescale after excitation could, in principle, lead to a non-Kasha photochemistry where the predominant photochemical pathway bypasses the lowest excited state. It remains to be shown how general this effect is beyond the rhenium-carbonyl-polypyridine family.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Czech Science Foundation (GAČR) Grant No. 21-05180S and STFC and EPSRC grant no. EP/R029687/1e. This work was supported by the Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID:90140), Project OPEN-17-38. The supercomputer time was supported by Vienna Scientific Cluster (VSC). LG and SM thank the University of Vienna for continuous support and the OeAD, program WTZ (Project FR 03/2019). AS thanks to Vítek Svoboda for an inspiring discussion and Merck'sche Gesellschaft für Kunst und Wissenschaft for financial support. JH, SZ and AV thank to Milan Ončák for discussions and early attempts to investigate these interesting systems. Open access funding financed by the project “Rozvoj kapacit UFCH JH, v.v.i. pro výzkum a vývoj II (CZ.02.2.69/0.0/0.0/18_054/0014591)”.Notes and references
- O. Bräm, F. Messina, A. M. El-Zohry, A. Cannizzo and M. Chergui, Chem. Phys., 2012, 393, 51–57 CrossRef.
- M. Chergui, Dalton Trans., 2012, 41, 13022–13029 RSC.
- M. Chergui, Acc. Chem. Res., 2015, 48, 801–808 CrossRef CAS PubMed.
- O. Bräm, A. Cannizzo and M. Chergui, Phys. Chem. Chem. Phys., 2012, 14, 7934–7937 RSC.
- A. Cannizzo, F. Van Mourik, W. Gawelda, G. Zgrablic, C. Bressler and M. Chergui, Angew. Chem., Int. Ed., 2006, 45, 3174–3176 CrossRef CAS PubMed.
- O. Bräm, F. Messina, E. Baranoff, A. Cannizzo, M. K. Nazeeruddin and M. Chergui, J. Phys. Chem. C, 2013, 117, 15958–15966 CrossRef.
- E. Pomarico, M. Silatani, F. Messina, O. Braem, A. Cannizzo, E. Barranoff, J. H. Klein, C. Lambert and M. Chergui, J. Phys. Chem. C, 2016, 120, 16459–16469 CrossRef CAS.
- F. Messina, E. Pomarico, M. Silatani, E. Baranoff and M. Chergui, J. Phys. Chem. Lett., 2015, 6, 4475–4480 CrossRef CAS PubMed.
- A. Vlček, Top. Organomet. Chem., 2010, 29, 73–114 CrossRef.
- A. Kumar, S. S. Sun and A. J. Lees, in Topics in Organometallic Chemistry, ed. A. Lees, Springer-Verlag Berlin, Heidelberger Platz 3, D-14197 Berlin, Germany, 2010, vol. 29, pp. 37–71 Search PubMed.
- A. Cannizzo, A. M. Blanco-Rodríguez, A. E. Nahhas, J. Šebera, S. Záliš, A. Vlček and M. Chergui, J. Am. Chem. Soc., 2008, 130, 8967–8974 CrossRef CAS PubMed.
- A. E. Nahhas, A. Cannizzo, F. V. Mourik, A. M. Blanco-Rodríguez, S. Záliš, A. Vlček and M. Chergui, J. Phys. Chem. A, 2010, 114, 6361–6369 CrossRef PubMed.
- A. El Nahhas, C. Consani, A. M. Blanco-Rodríguez, K. M. Lancaster, O. Braem, A. Cannizzo, M. Towrie, I. P. Clark, S. Záliš, M. Chergui and A. Vlček, Inorg. Chem., 2011, 50, 2932–2943 CrossRef CAS PubMed.
- S. Mai and L. González, Chem. Sci., 2019, 10, 10405–10411 RSC.
- J. P. Zobel and L. González, JACS Au, 2021, 1, 1116–1140 CrossRef CAS PubMed.
- H. Takeda and O. Ishitani, Coord. Chem. Rev., 2010, 254, 346–354 CrossRef CAS.
- R. Heydová, E. Gindensperger, R. Romano, J. Sýkora, A. Vlček, S. Záliš and C. Daniel, J. Phys. Chem. A, 2012, 116, 11319–11329 CrossRef PubMed.
- A. M. B. Rodríguez, A. Gabrielsson, M. Motevalli, P. Matousek, M. Towrie, J. Sebera, S. Záliš and A. Vlček, J. Phys. Chem. A, 2005, 109, 5016–5025 CrossRef PubMed.
- A. El Nahhas, R. M. Van Der Veen, T. J. Penfold, V. T. Pham, F. A. Lima, R. Abela, A. M. Blanco-Rodriguez, S. Záliš, A. Vlček, I. Tavernelli, U. Rothlisberger, C. J. Milne and M. Chergui, J. Phys. Chem. A, 2013, 117, 361–369 CrossRef CAS PubMed.
- S. Záliš, C. J. Milne, A. El Nahhas, A. M. Blanco-Rodríguez, R. M. Van Der Veen and A. Vlček, Inorg. Chem., 2013, 52, 5775–5785 CrossRef PubMed.
- J. Eng, C. Gourlaouen, E. Gindensperger and C. Daniel, Acc. Chem. Res., 2015, 48, 809–817 CrossRef CAS PubMed.
- C. Daniel, Phys. Chem. Chem. Phys., 2021, 23, 43–58 RSC.
- S. Mai, H. Gattuso, M. Fumanal, A. Muñoz-Losa, A. Monari, C. Daniel and L. González, Phys. Chem. Chem. Phys., 2017, 19, 27240–27250 RSC.
- M. Fumanal, E. Gindensperger and C. Daniel, J. Chem. Theory Comput., 2017, 13, 1293–1306 CrossRef CAS PubMed.
- C. Gourlaouen, J. Eng, M. Otsuka, E. Gindensperger and C. Daniel, J. Chem. Theory Comput., 2015, 11, 99–110 CrossRef CAS PubMed.
- Y. Harabuchi, J. Eng, E. Gindensperger, T. Taketsugu, S. Maeda and C. Daniel, J. Chem. Theory Comput., 2016, 12, 2335–2345 CrossRef CAS PubMed.
- M. Fumanal, F. Plasser, S. Mai, C. Daniel and E. Gindensperger, J. Chem. Phys., 2018, 148, 124119 CrossRef PubMed.
- J. B. Asbury, Y. Wang and T. Lian, Bull. Chem. Soc. Jpn., 2002, 75, 973–983 CrossRef CAS.
- D. J. Liard, M. Busby, P. Matousek, M. Towrie and A. Vlček, J. Phys. Chem. A, 2004, 108, 2363–2369 CrossRef CAS.
- V. A. Lenchenkov, C. She and T. Lian, J. Phys. Chem. B, 2004, 108, 16194–16200 CrossRef CAS.
- A. M. Blanco-Rodríguez, M. Towrie, J. P. Collin, S. Záliš and A. Vlček, Dalton Trans., 2009, 3941–3949 RSC.
- L. M. Kiefer, J. T. King and K. J. Kubarych, Acc. Chem. Res., 2015, 48, 1123–1130 CrossRef CAS PubMed.
- L. M. Kiefer and K. J. Kubarych, J. Phys. Chem. A, 2015, 119, 959–965 CrossRef CAS PubMed.
- L. M. Kiefer and K. J. Kubarych, Chem. Sci., 2018, 9, 1527–1533 RSC.
- C. Shih, A. K. Museth, M. Abrahamsson, A. M. Blanco-Rodriguez, A. J. Di Bilio, J. Sudhamsu, B. R. Crane, K. L. Ronayne, M. Towrie, A. Vlček, J. H. Richards, J. R. Winkler and H. B. Gray, Science, 2008, 320, 1760–1762 CrossRef CAS PubMed.
- K. Takematsu, H. Williamson, A. M. Blanco-Rodríguez, L. Sokolová, P. Nikolovski, J. T. Kaiser, M. Towrie, I. P. Clark, A. Vlček, J. R. Winkler and H. B. Gray, J. Am. Chem. Soc., 2013, 135, 15515–15525 CrossRef CAS PubMed.
- K. Takematsu, H. R. Williamson, P. Nikolovski, J. T. Kaiser, Y. Sheng, P. Pospíšil, M. Towrie, J. Heyda, D. Hollas, S. Záliš, H. B. Gray, A. Vlček and J. R. Winkler, ACS Cent. Sci., 2019, 5, 192–200 CrossRef CAS PubMed.
- E. D. Olmon, P. A. Sontz, A. M. Blanco-Rodríguez, M. Towrie, I. P. Clark, A. Vlček and J. K. Barton, J. Am. Chem. Soc., 2011, 133, 13718–13730 CrossRef CAS PubMed.
- D. A. Case, K. Belfon, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz, R. Harris, S. Izadi, S. A. Izmailov, K. Kasavajhala, A. Kovalenko, R. Krasny, D. M. York and P. A. Kollman, AMBER 2020, 2020 Search PubMed.
- H. J. Berendsen, J. P. Postma, W. F. Van Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS PubMed.
- A. V. Titov, I. S. Ufimtsev, N. Luehr and T. J. Martinez, J. Chem. Theory Comput., 2013, 9, 213–221 CrossRef CAS PubMed.
- C. Song, L. P. Wang and T. J. Martínez, J. Chem. Theory Comput., 2016, 12, 92–106 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Záliš, J. Heyda, F. Šebesta, J. R. Winkler, H. B. Gray and A. Vlček, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2024627118 CrossRef PubMed.
- R. Baková, M. Chergui, C. Daniel, A. Vlček Jr. and S. Záliš, Coord. Chem. Rev., 2011, 255, 975–989 CrossRef.
- A. M. Blanco-Rodríguez, H. Kvapilová, J. Sýkora, M. Towrie, C. Nervi, G. Volpi, S. Záliš and A. Vlček, J. Am. Chem. Soc., 2014, 136, 5963–5973 CrossRef PubMed.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- S. Mai, M. Richter, M. Heindl, M. F. S. J. Menger, A. Atkins, M. Ruckenbauer, F. Plasser, L. M. Ibele, S. Kropf, M. Oppel, P. Marquetand and L. González, SHARC2.1: Surface Hopping Including Arbitrary Couplings’ Program Package for Non-Adiabatic Dynamics, sharc-md.org, 2019, https://sharc-md.org Search PubMed.
- J. A. Rackers, Z. Wang, C. Lu, M. L. Laury, L. Lagardère, M. J. Schnieders, J. P. Piquemal, P. Ren and J. W. Ponder, J. Chem. Theory Comput., 2018, 14, 5273–5289 CrossRef CAS PubMed.
- C. Van Wüllen, J. Chem. Phys., 1998, 109, 392–399 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. Bühl, C. Reimann, D. A. Pantazis, T. Bredow and F. Neese, J. Chem. Theory Comput., 2008, 4, 1449–1459 CrossRef PubMed.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2011, 7, 677–684 CrossRef CAS.
- G. Granucci, M. Persico and A. Zoccante, J. Chem. Phys., 2010, 133, 134111 CrossRef PubMed.
- F. Plasser, M. Ruckenbauer, S. Mai, M. Oppel, P. Marquetand and L. González, J. Chem. Theory Comput., 2016, 12, 1207–1219 CrossRef CAS PubMed.
- S. Mai, P. Marquetand and L. González, Int. J. Quantum Chem., 2015, 115, 1215–1231 CrossRef CAS.
- J. P. Zobel, J. J. Nogueira and L. González, Phys. Chem. Chem. Phys., 2019, 21, 13906–13915 RSC.
- S. Mai and L. González, Angew. Chem., Int. Ed., 2020, 59, 16832–16846 CrossRef CAS PubMed.
- A. Vlček and S. Záliš, Coord. Chem. Rev., 2007, 251, 258–287 CrossRef.
- K. Kalyanasundaram, J. Chem. Soc., Faraday Trans. 2, 1986, 82, 2401–2415 RSC.
- SHARC2.1: Manual, https://sharc-md.org/?page_id=50#tth_sEc8.4.
- B. Lin and B. M. Pettitt, J. Chem. Phys., 2011, 134, 2011–2013 Search PubMed.
- P. K. Mehrotra and D. L. Beveridge, J. Am. Chem. Soc., 1980, 102, 4287–4294 CrossRef CAS.
- M. L. Horng, J. A. Gardecki, A. Papazyan and M. Maroncelli, J. Phys. Chem., 1995, 99, 17311–17337 CrossRef CAS.
- D. Brinks, F. D. Stefani, F. Kulzer, R. Hildner, T. H. Taminiau, Y. Avlasevich, K. Müllen and N. F. Van Hulst, Nature, 2010, 465, 905–908 CrossRef CAS PubMed.
- E. R. Hosler and S. R. Leone, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 1–7 Search PubMed.
- A. H. Zewail, J. Phys. Chem. A, 2000, 104, 5660–5694 CrossRef CAS.
- M. Rebholz, T. Ding, V. Despré, L. Aufleger, M. Hartmann, K. Meyer, V. Stooß, A. Magunia, D. Wachs, P. Birk, Y. Mi, G. D. Borisova, C. D. C. Castanheira, P. Rupprecht, G. Schmid, K. Schnorr, C. D. Schröter, R. Moshammer, Z. H. Loh, A. R. Attar, S. R. Leone, T. Gaumnitz, H. J. Wörner, S. Roling, M. Butz, H. Zacharias, S. Düsterer, R. Treusch, G. Brenner, J. Vester, A. I. Kuleff, C. Ott and T. Pfeifer, Phys. Rev. X, 2021, 11, 31001 CAS.
- K. J. Gaffney, Chem. Sci., 2021, 12, 8010–8025 RSC.
- C. Wang, M. D. J. Waters, P. Zhang, J. Suchan, V. Svoboda, T. T. Luu, C. Perry, Z. Yin, P. Slavíček and H. J. Wörner, Nat. Chem., 2022, 14(10), 1126–1132 CrossRef CAS PubMed.
- M. Pižl, A. Picchiotti, M. Rebarz, N. Lenngren, L. Yingliang, S. Záliš, M. Kloz and A. Vlček, J. Phys. Chem. A, 2020, 124, 1253–1265 CrossRef PubMed.
- A. Vlček, in Topics in Organometallic Chemistry, ed. A. J. Lees, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, vol. 29, pp. 73–114 Search PubMed.
- A. Vlček, H. Kvapilová, M. Towrie and S. Záliš, Acc. Chem. Res., 2015, 48, 868–876 CrossRef PubMed.
- D. M. Dattelbaum, K. M. Omberg, J. R. Schoonover, R. L. Martin and T. J. Meyer, Inorg. Chem., 2002, 41, 6071–6079 CrossRef CAS PubMed.
- D. M. Dattelbaum, K. M. Omberg, P. J. Hay, N. L. Gebhart, R. L. Martin, J. R. Schoonover and T. J. Meyer, J. Phys. Chem. A, 2004, 108, 3527–3536 CrossRef CAS.
- M. W. George, F. P. Johnson, J. R. Westwell, P. M. Hodges and J. J. Turner, J. Chem. Soc., Dalton Trans., 1993, 2977–2979 RSC.
- H. Kvapilová, A. Vlček, V. Barone, M. Biczysko and S. Záliš, J. Phys. Chem. A, 2015, 119, 10137–10146 CrossRef PubMed.
- A. M. Blanco-Rodríguez, K. L. Ronayne, S. Záliš, J. Sýkora, M. Hof and A. Vlček, J. Phys. Chem. A, 2008, 112, 3506–3514 CrossRef PubMed.
- A. M. Blanco-Rodríguez, M. Busby, K. Ronayne, M. Towrie, C. Gradinaru, J. Sudhamsu, J. Sýkora, M. Hof, S. Záliš, A. J. Di Bilio, B. R. Crane, H. B. Gray and A. Vlček, J. Am. Chem. Soc., 2009, 131, 11788–11800 CrossRef PubMed.
- P. Pospíšil, J. Sýkora, K. Takematsu, M. Hof, H. B. Gray and A. Vlček, J. Phys. Chem. B, 2020, 124, 788–797 CrossRef PubMed.
- A. M. Blanco-Rodríguez, A. J. Di Bilio, C. Shih, A. K. Museth, I. P. Clark, M. Towrie, A. Cannizzo, J. Sudhamsu, B. R. Crane, J. Sýkora, J. R. Winkler, H. B. Gray, S. Záliš and A. Vlček, Chem. – Eur. J., 2011, 17, 5350–5361 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details, wavefunction characters of excited states, frozen nuclei dynamics, character of the electronic wavefunction, time-resolved fluorescence spectra, fitting procedures of: kinetic model for intersystem crossing dynamics, fluorescence decay, and vibrational ground state recovery, average geometries of the ground and excited states in the two solvents, derivation of the proximal radial distribution function, detailed analysis of spin–orbit couplings, temporal evolution of compositions of spin-mixed states, and time-resolved spectroscopy (PDF). See DOI: https://doi.org/10.1039/d2cp02981b |
| This journal is © the Owner Societies 2022 |