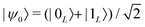Open Access Article
Open Access ArticleQuantum error correction with molecular spin qudits
Mario
Chizzini
 ab,
Luca
Crippa
ab,
Luca
Crippa
 ac,
Luca
Zaccardi
ac,
Luca
Zaccardi
 ad,
Emilio
Macaluso
ad,
Emilio
Macaluso
 abd,
Stefano
Carretta
abd,
Stefano
Carretta
 abd,
Alessandro
Chiesa
abd,
Alessandro
Chiesa
 abd and
Paolo
Santini
abd and
Paolo
Santini
 *abd
*abd
aDipartimento di Scienze Matematiche, Università di Parma, Fisiche e Informatiche, I-43124 Parma, Italy. E-mail: paolo.santini@unipr.it
bINFN-Sezione di Milano-Bicocca, gruppo collegato di Parma, I-43124 Parma, Italy
cIBM Italia s.p.a., Circonvallazione Idroscalo, I-20090 Segrate, Italy
dUdR Parma, INSTM, I-43124 Parma, Italy
First published on 14th July 2022
Abstract
Thanks to the large number of levels which can be coherently manipulated, molecular spin systems constitute a very promising platform for quantum computing. Indeed, they can embed quantum error correction within single molecular objects, thus greatly simplifying its actual realization in the short term. We consider a recent proposal, which exploits a spin qudit to encode the protected unit, and is tailored to fight pure dephasing. Here we compare the implementation of this code on different molecules, in which the qudit is provided by either an electronic or a nuclear spin (S, I > 1), coupled to a spin-1/2 electronic ancilla for error detection. By thorough numerical simulations we show that a significant gain in the effective phase memory time can be achieved. This is further enhanced by exploiting pulse-shaping techniques to reduce the leakage and/or the impact of decoherence during correction. Moreover, we simulate the implementation of single-qubit operations on the encoded states.
1 Introduction
Open-shell molecular spin systems, either Molecular Nanomagnets (MNM)1–13 or genuinely organic compounds,14–17 are very promising units of a future quantum computing architecture. A prominent feature which makes MNMs more attractive than many other established platforms18–26 (based on encoding and manipulating information on two level units called qubits) is represented by their intrinsic multi-level structure.27 Indeed, these many low-energy and highly coherent levels,5,28–30 easily accessible by electro-magnetic pulses,31–33 can be exploited to encode information and design algorithms based on a multi-level (qudit) logic.34–41In particular, MNMs can embed quantum-error correction (QEC) within a single molecular object, as opposed to standard implementations, where logical units are encoded into a large collection of qubits.42,43 Note that, due to the intrinsic fragility of quantum system, the achievement of quantum error correction represents a crucial milestone towards the realization of a scalable quantum-computing architecture, able to outclass classical computers in the solution of a wide variety of problems. However, the great overhead of qubits and operations required to protect information via QEC makes the resulting register still intractable, even for the most advanced realizations. The complementary point of view offered by multi-level molecular spin systems would significantly facilitate the actual realization of error-protected quantum computing units.13
To achieve this goal, we have recently proposed a scheme which allows one to suppress the most important source of noise in molecular spin systems, represented by pure dephasing.44–46 The proposal relies on the use of a spin S > 1 as the elementary logical unit of our quantum computer. Its 2S + 1 energy levels, exceeding the number of two required to encode the logical states 0 and 1, provide the additional degrees of freedom needed to encode a protected state, such that errors can be identified and corrected. This detection is accomplished with the help of a spin 1/2 ancilla, which allows one to flag each error without corrupting the encoded logical state.
We present here an analysis of the performance of this code on different molecular platforms, based on realistic parameters. Although the implementation of a molecular quantum computer equipped with QEC is still a long-term goal, here we would like to trace a route towards the first proof-of-principle demonstrations of this scheme, focusing in particular on the chemical requirements and on pulse sequence design. The examined platforms consist of either an electronic or a nuclear spin qudit, coupled to an electronic spin 1/2 ancilla by exchange or hyperfine interactions. We perform numerical simulations including the full sequence of pulses that implement the code. We show how to improve its performance with the help of proper pulse-shaping techniques, such as the derivative removal by adiabatic gate (DRAG).47,48 We show that this technique is particularly useful to reduce the duration of the sequence (and hence the effect of decoherence) without inducing a relevant leakage to unwanted transitions. By combining these results, a significant enhancement in the effective phase memory time of the spin qudit can be achieved, compared to an 1/2 isolated spin.
Finally, we illustrate how to implement single-qubit rotations on the encoded states protected by QEC.
2 Methods
In what follows, we consider two different molecular spin systems. The first is an electronic spin dimer (referred to as (e) from now on), whose spin Hamiltonian is given by| He = μBB0(gzSz + gAzsAz) + DSz2 + S·J·sA. | (1) |
The second system (called (n) hereafter) consists of a single magnetic ion, typically a transition metal, containing an electronic spin sA = 1/2, coupled by hyperfine interaction to a magnetic nucleus I > 1. It is described by the following spin Hamiltonian:
| Hn = B0(gNμNIz + gAzμBsAz) + QIz2 + I·A·sA, | (2) |
In both cases, we work in a weak coupling regime, in which the eigenstates of Hamiltonians (1,2) are practically factorized and can thus be labelled with the quantum numbers |M, m〉, i.e. the eigenvalues of Sz (Iz) and sAz. This condition is automatically guaranteed for (n) by using easily available magnetic fields B0 ≥ 0.1 T, such that gAzμBB0 ≫ Ax,y. As far as (e) is concerned, we require Jx,y to be significantly smaller than the difference between excitation energies of the qudit M → M + 1, and of the qubit, i.e., |Jx,y| ≪ |(gz − gAz)μBB0 + D(2M + 1)|. This condition can also be fulfilled, by proper choice of the spin system and of the external field (see below).
As we explain in detail below, in both the electronic and nuclear systems, the spin 1/2 unit acts as an ancilla, exploited for detecting errors, while the S, I > 1 multi-level spin encodes the protected unit. All transitions between the eigenstates of He(Hn) are theoretically addressable, thanks to the zero-field splitting (quadrupole) and interaction terms, which make all of them spectrally distinguishable. In practice, individually addressing each transition might be experimentally challenging, and we discuss below how proper choice of the pulse shape might help.
These transitions are driven by time-dependent magnetic fields b1(t) parallel to x, which couple to the system via the Hamiltonian
| H1e = μBb1(t)(gAxsAx + gxSx), | (3) |
| H1n = b1(t)(μBgAxsAx + μNgNIx) | (4) |
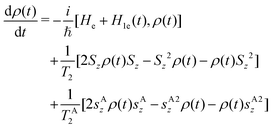 | (5) |
3 Results
3.1 Quantum-error correction with molecular spin qudits
Quantum systems are inherently fragile, because their interaction with the external environment tends to induce relaxation towards thermal equilibrium and to destroy quantum superpositions. However, to implement quantum computing algorithms and/or to store information in quantum memories, the state of the quantum register must be kept in superpositions of the Hamiltonian eigenstates for rather long times. Such states are particularly vulnerable. Hence, a strategy to overcome decoherence is mandatory to realize a reliable quantum computer. Quantum error correction provides a clear route towards this goal.To give an intuitive picture of the working principles of a QEC code, we consider the elementary unit of a quantum computer, i.e. a qubit. This consists of a two-level quantum system, such as a spin 1/2, which can encode the two binary logical states |0〉 and |1〉. If we prepare the qubit in a generic superposition α|0〉 + β|1〉, the effect of unwanted errors is to corrupt the logical state, by changing the relative population of the two states and/or by inducing a decay of their coherence. In both cases, the information initially encoded into the complex coefficients α and β is deformed and cannot be recovered. This is because any error acts into the two-dimensional space which is already completely used to encode the logical state.
To make errors detectable, we need to extend the available space with the addition of some extra-levels. Intuitively, if errors bring the encoded superposition state rigidly into these extra levels (without altering α and β), then these errors can be detected and properly corrected. To achieve this, one needs to.
(1) identify the errors (or at least the leading ones) affecting the investigated system.
(2) Properly encode the logical states into code words |0L〉 and |1L〉, represented by superpositions of the Hamiltonian eigenstates. In particular, errors must have a symmetric effect on |0L〉 and |1L〉, bringing them rigidly outside from the computational space.
(3) Design a strategy to detect and correct errors without corrupting α and β.
The formalization of these concepts is given by Knill–Laflamnme conditions:49 given a set of error operators {Ek}, logical states |0L〉 and |1L〉 enable error detection and correction if and only if the following identities hold:
| 〈0L|E†kEj|1L〉 = 0 |
| 〈0L|E†kEj|0L〉 = 〈1L|E†kEj|1L〉. | (6) |
We now consider the application of these concepts to the concrete case under investigation: a spin S molecular system, as first proposed in ref. 44. At low temperature, the leading error is given by pure dephasing, originating from the interaction between the central spin and the surrounding nuclear spin bath.45 To pinpoint the error operators Ek, we consider the effect of pure dephasing on the time evolution of the density matrix. This is expressed by the Lindblad equation (second line of eqn (6): ![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = 1/T2(2SzρSz − Sz2ρ − ρSz2). The solution of this equation at time t can be expanded in series,
= 1/T2(2SzρSz − Sz2ρ − ρSz2). The solution of this equation at time t can be expanded in series, 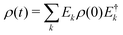 , with error operators
, with error operators
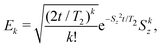 | (7) |
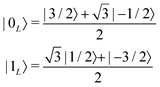 | (8) |
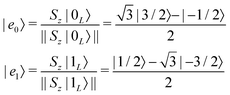 | (9) |
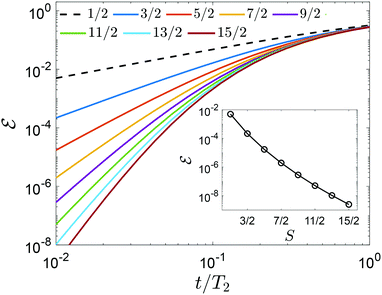
By increasing the number of levels in the system, higher powers of Sz can also be corrected, thus in principle improving the capacity of the code.44 This is shown in Fig. 1, where we report the error ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) = 1 − 〈ψ(0)|ρ(t)|ψ(0)〉 after a memory time t, for a system initialized in
= 1 − 〈ψ(0)|ρ(t)|ψ(0)〉 after a memory time t, for a system initialized in 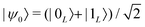 . At fixed t/T2 (inset), we note that
. At fixed t/T2 (inset), we note that ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) decreases by increasing the number of levels in qudit levels, i.e. the spin S. In general, 2(n + 1) levels (half for each logical state) are needed to distinguish (and hence possibly correct) n different errors. Otherwise, different errors overlap and correction becomes impossible.
decreases by increasing the number of levels in qudit levels, i.e. the spin S. In general, 2(n + 1) levels (half for each logical state) are needed to distinguish (and hence possibly correct) n different errors. Otherwise, different errors overlap and correction becomes impossible.
We remark, however, that the actual corrective capability of the code is limited by the finite duration of the pulses needed to physically implement the correction. Indeed, during this step the system (which is not protected) accumulates errors arising from (i) leakage (i.e. unwanted transitions to neighboring levels, different from the addressed ones) and (ii) decoherence. Hence, a trade-off must be found between the gain obtained from QEC and the cost of actually implementing it, both increasing with the number of available levels.44
Having this in mind, we focus here on spin 3/2 qudit systems, which already ensure the possibility to correct the leading (first order) dephasing error (associated to Sz operator), while still limiting the complexity of the manipulations. This, together with the proper choice of the system (see next section), makes the proposal closer to possible experimental demonstrations.
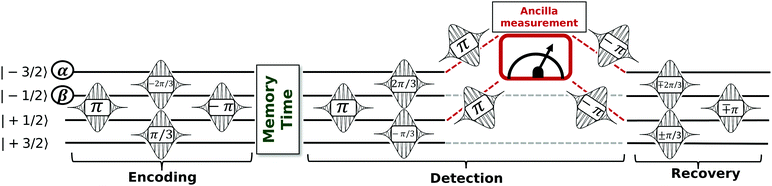
Hereafter, we describe step by step the sequence of resonant pulses (see Fig. 2) that can be used to (i) encode the logical states (ii) detect the whether an Sz error has occurred or not and (iii) recover the initial state. Horizontal lines represent the eigenstates of the qudit Hamiltonian, labelled by the expectation value of Sz(Iz). At the beginning of the sequence we prepare the ancilla in the |↓〉 state and we store logic qubit information in the first two top levels |−3/2〉 and |−1/2〉. The first step consists of four pulses (two of which in parallel) and implements the transformation |−3/2〉 → |0L〉 and |−1/2〉 → |1L〉, which encode the wavefunction into the protected logical state. We then let the system evolve freely during the memory time (only subject to decoherence). The next sequence of pulses is used to detect possible errors. We first decode information by mapping each of the four states {|0L〉,|1L〉, |e0〉,|e1〉} to a different |M〉 state. This brings the correct superposition to α|−3/2〉 + β|1/2〉 and the wrong one to α|−1/2〉 + β|3/2〉. Thanks to the qudit-ancilla interaction, the excitation energy of the ancilla depends on the state of the qudit. We exploit this feature to conditionally excite the ancilla via two parallel π pulses corresponding to the qudit in states |−3/2〉 and |1/2〉. The corrupted and uncorrupted qudit states can now be easily distinguished by measuring the ancilla. Based on the measurement result, we then reconstruct the protected quantum information with the final sequence of three recovery pulses (with top/bottom sign of rotation angle depending if the ancilla was found to be |↑〉/|↓〉).
In the following we study the performance of the code on different, realistic systems and different forms of the driving field b1(t). Simulations are performed by numerically integrating eqn (5), with the system always subject to decoherence, even during the implementation of the pulses. Our aim is to find system-specific optimal working points to limit leakage and decoherence during the implementation of the whole error-correction procedure. Reducing the former requires long (frequency-selective) pulses, while to limit the latter one needs short pulses. Hence, a proper trade-off must be identified.
3.2 Physical implementations
In order to guide future synthetic efforts towards the first proof-of-principle experiments, the QEC scheme described above is applied to realistic model systems. We recall that the curves reported in Fig. 1 represent the ideal performance of the QEC code, as if correction pulses were (i) instantaneous, (ii) perfectly monochromatic and (iii) with the ancilla completely factorized from the qudit state.These three conditions are not entirely satisfied in a real implementation and lead to different errors that are accounted for by our simulations:
(1) the finite duration of the pulses translates into decoherence occurring also during the QEC procedure, when the state is not encoded and hence the correction provided by the code is not active.
(2) The unavoidable presence of frequency components slightly different from the leading one induces leakage to levels others than those addressed by each pulse.
(3) The mixing between qudit and ancilla wavefunctions is induced by transverse components of the coupling (Jx,y) and yields a measurement error during the detection step of Fig. 2. This means there is a finite probability of finding ancilla |↓〉 even when no error had occurred and vice versa.
All of these imperfections yield a plateau in the final error ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) at short t/T2, appearing in both Fig. 3b and 4b, at odds with Fig. 1. For large t/T2, the performance of the code approaches the ideal situation. We now discuss the effect of these different imperfections in the two test-cases under investigation, whose parameters are listed in Table 1.
at short t/T2, appearing in both Fig. 3b and 4b, at odds with Fig. 1. For large t/T2, the performance of the code approaches the ideal situation. We now discuss the effect of these different imperfections in the two test-cases under investigation, whose parameters are listed in Table 1.
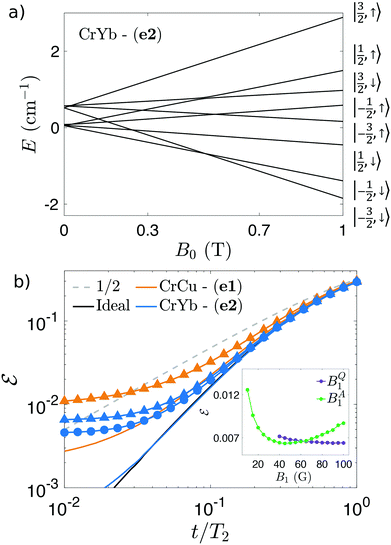 | ||
| Fig. 3 (a) Energy levels as function of the static field B0 for the (e2) system,50 with the practically factorized states labelled by Sz and sAZ expectation values. (b) Comparison between (e1) and (e2) implementations of the QEC scheme. The grey dashed line represents the error for an uncorrected s = 1/2 spin subject to decoherence. The continuous black line is the ideal performance of QEC scheme on a S = 3/2 qudit. Solid orange (blue) line are measurement errors for (e1) ((e2)) using BQ1 = 100 G and BA1 = 45 G at B0 = 1 T. Corresponding symbols are simulations including also decoherence and leakage errors. For (e2) dimer we show results using two possible values of TA2: 1 μs (triangles) and 3 μs (circles). Inset: Total error as a function of the amplitude of the Gaussian driving field for qudit (violet) and ancilla (green) excitations on (e2), for fixed t/T2 = 0.035, T2 = 50 μs and TA2 = 3 μs. | ||
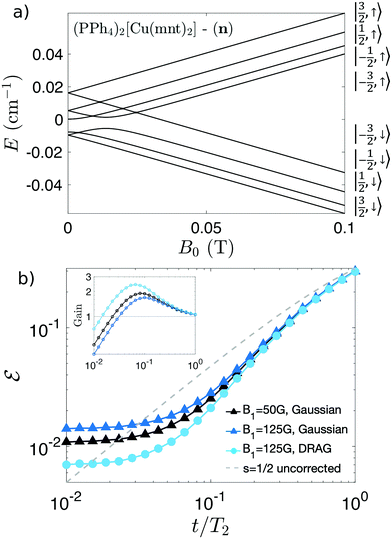 | ||
| Fig. 4 (a) Energy levels of (PPh4)2[Cu(mnt)2] n, consisting of a Cu2+ ion (electronic spin sA = 1/2), coupled to the nuclear I = 3/2 spin by hyperfine interaction (as reported in ref. 28), as function of the external field B0. The composition of the eigenstates is indicated on the right. (b) Symbols: error after implementation of the QEC scheme with T2 = 0.5 ms, B0 = 0.1 T, TA2 = 68 μs (as reported in ref. 28), BA1 = 30G, with different forms of the driving fields BQ1: Gaussian (triangles) and DRAG (circles). Dashed grey line: error for an uncorrected s = 1/2 spin due to decoherence. Inset: Corresponding gain, i.e. ratio between errors on an uncorrected qubit and on a protected system. | ||
| g | D/Q (cm−1) | (Jx, Jy, Jz)/(Ax, Ay, Az) (cm−1) | (gAx, gAy, gAz) | T 2 (μs) | T A2 (μs) | |
|---|---|---|---|---|---|---|
| CrCu (e1) | 1.98 | −0.24 | (1.7, 1.7, −3.3) × 10−2 | (2.1, 2.1, 2.3) | 50 | 5 |
| CrYb (e2) | (2.9, 2.9, 4.2) | 50 | 1–3 | |||
| (PPh4)2 [Cu(mnt)2] (n) | 1.48 | 1.7 × 10−3 | (0.4, 0.4, 1.7) × 10−2 | (2.0, 2.0, 2.1) | 102–103 | 68 |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) , is reported in panel (b), as a function of the memory time.
, is reported in panel (b), as a function of the memory time.
The measurement error arising from imperfect factorization deserves a preliminary discussion. To highlight its importance and disentangle it from other errors, we report by solid coloured lines the final error obtained with ideal pulses, but measurement operators resulting from diagonalization of the system Hamiltonian, thus including small qudit-ancilla entanglement. At fixed B0 = 1 T, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) is significantly larger for (e1), due the smaller gAz − gz, and sets a lower limit to the accuracy of the whole procedure. In the case of (e2), factorization is much higher (see blue solid curve in Fig. 3) and the final error can be neglected, compared to leakage and decoherence. Clearly, a similar situation could be achieved for (e1) by increasing B0.
is significantly larger for (e1), due the smaller gAz − gz, and sets a lower limit to the accuracy of the whole procedure. In the case of (e2), factorization is much higher (see blue solid curve in Fig. 3) and the final error can be neglected, compared to leakage and decoherence. Clearly, a similar situation could be achieved for (e1) by increasing B0.
We now turn our attention to errors due to leakage and decoherence. In the simulations reported in this section, we use Gaussian shaped pulses, b1(t) = B1e−(t−t0)2/2τ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt, choosing ω for each pulse to be in resonance with the pair of energy levels coupled by the corresponding transition indicated in Fig. 2. We find that leakage is practically irrelevant when addressing qudit transitions. Indeed, thanks to the large difference between energy gaps ensured by D, we can safely employ B1 up to 100 G without significantly transfer population to unwanted states. This is demonstrated in the inset of Fig. 3b, where we show
ωt, choosing ω for each pulse to be in resonance with the pair of energy levels coupled by the corresponding transition indicated in Fig. 2. We find that leakage is practically irrelevant when addressing qudit transitions. Indeed, thanks to the large difference between energy gaps ensured by D, we can safely employ B1 up to 100 G without significantly transfer population to unwanted states. This is demonstrated in the inset of Fig. 3b, where we show ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) at fixed t/T2, as a function of BQ1 (the amplitude of the driving field used for qudit transitions). We note that
at fixed t/T2, as a function of BQ1 (the amplitude of the driving field used for qudit transitions). We note that ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) is monotonically decreasing with BQ1. This means that by shortening the pulses we gain further and further and hence that the total error is limited by decoherence. We thus fix BQ1 = 100 G, as provided state-of-the-art pulse electron-paramagnetic resonance technology.52 Conversely, excitations of the ancilla (depending on the qudit state) are resolved by Jz and hence the corresponding transitions are closer in energy. Hence, a smaller amplitude of the oscillating field (BA1) must be chosen, in order to reduce leakage. This optimal value is set by the position of the minimum of
is monotonically decreasing with BQ1. This means that by shortening the pulses we gain further and further and hence that the total error is limited by decoherence. We thus fix BQ1 = 100 G, as provided state-of-the-art pulse electron-paramagnetic resonance technology.52 Conversely, excitations of the ancilla (depending on the qudit state) are resolved by Jz and hence the corresponding transitions are closer in energy. Hence, a smaller amplitude of the oscillating field (BA1) must be chosen, in order to reduce leakage. This optimal value is set by the position of the minimum of ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) as a function of BA1 (∼45 G), reported again in the inset of Fig. 3b. For BA1 smaller than the optimal working point pulses are frequency selective but rather long, and hence decoherence dominates. Above the minimum, pulses are shorter but broader in frequency, and hence leakage becomes more important.
as a function of BA1 (∼45 G), reported again in the inset of Fig. 3b. For BA1 smaller than the optimal working point pulses are frequency selective but rather long, and hence decoherence dominates. Above the minimum, pulses are shorter but broader in frequency, and hence leakage becomes more important.
The resulting simulations, using the optimal values of BQ1 and BA1, are shown by symbols in Fig. 3b, with T2 = 50 μs. This is a rather optimistic value, but within the range of attainable coherence times for transition metal complexes with properly engineered ligand cage.
The performance of (e1) dimer (orange triangles) is mainly limited by the measurement error discussed above, which is negligible for (e2) (blue symbols). As far as TA2 is concerned, we can safely assume a value significantly smaller than T2, because the ancilla is only excited during the error-detection step, while it is kept in its ground state for most of the time. Nevertheless, we find TA2 relevant to determine the final performance of the code. We used 5 μs for (e1) and 1 μs for (e2), as found in ref. 51. By increasing TA2 from 1 to 3 μs (blue circles), the total error is further reduced (see blue triangles vs. circles), reaching values below 5 × 10−3 at short times.
In the simulations reported below, we use B0 = 0.1 T, in order to exploit the small mixing between electronic and nuclear spin wave function to speed-up nuclear manipulations. Indeed, this optimal value of B0 allows us to both keep the eigenstates factorized, while enhancing by ∼50 the matrix element of nuclear transitions.55,56
Thanks to the large difference between electronic and nuclear excitation energies, factorization here is not an issue, having a maximum states mixing of 10−3. We can therefore focus on errors due to decoherence and leakage. As far as the nuclear coherence time T2 is concerned, we do not have experimental data at hand. However, a reasonable estimate can be done by comparison with similar systems, consisting of hyperfine-coupled electronic and nuclear spins. At the rather low fields considered here, decoherence of the central qudit is induced by the coupling with the surrounding magnetic nuclei, primarily mediated by the electronic spin component of the system state. Hence, the nuclear T2 is directly related to the electronic one and is found to be at least ten times larger in recent studies on Yb(trensal) and vanadyl tetraphenylporphyrinate.12,55 The latter consists of a spin 1/2 electronic spin coupled to a I = 7/2 nucleus, with hyperfine interaction very similar to (PPh4)2[Cu(mnt)2] and hence represents an optimal benchmark. Here, given the remarkably long value measured for TA2 at 5 K (68 μs), it is reasonable to first assume, for the associated nuclear qudit, T2 = 0.5 ms. In addition, we set BQ1 = 50 G and BA1 = 30 G. The resulting final error is shown in Fig. 4 by black triangles, while the inset reports the corresponding gain, i.e. the ratio between the error on a not-protected qubit (dashed line) and that on the protected qudit. The maximum gain reaches values close to 2. To improve it, one could try to increase B1. Larger values of the driving field amplitude would reduce the duration of the sequence (and hence the impact of decoherence), at the price of increasing leakage to neighboring levels. This harmful effect is dominant for BQ1 = 125 G, as evidenced by the increase of from black and blue triangles in Fig. 4b. Hence, faster sequences require proper pulse-shaping techniques, as illustrated in the next section.
3.3 Pulse engineering to improve the performance of the code: DRAG
We investigate here pulse-shaping techniques to speed up pulses as much as possible while still keeping leakage under control. This will reduce the effect of decoherence during the implementation of QEC, when the system is not protected.The goal is particularly challenging when the difference between the gaps is similar to the spectral width of the pulse.
Several techniques exist to minimize leakage while using rather short pulses, such as Sideband Modulation (WhaWha: anharmonicity with average Hamiltonian)57,58 and the SWIPHT (speeding up wave forms by inducing phases to harmful transitions).59,60 Here we focus on the derivative removal by adiabatic gate (DRAG), which allows us to get high-fidelity two-level rotations with significant gate speedups.48,61,62 The main idea behind DRAG is that a second control pulse that is the time derivative of the first creates a spectral hole. Then, by adjusting the time-derivative pulse, the spectral hole can be moved close to the unwanted transition, thereby minimizing leakage to a third level, as shown in the inset of Fig. 5. More specifically, the driving field assumes the form:
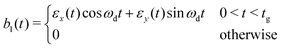 | (10) |
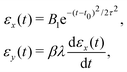 | (11) |
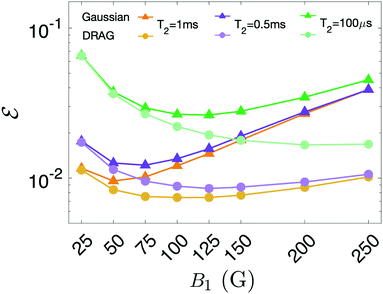 | ||
| Fig. 5 Effect of DRAG on the error after QEC on system (n) as a function of B1, for different values of T2. Computations are performed on a t/T2 near to the maximum gain, as reported in Fig. 4 inset. Dark (light) lines refer to Gaussian (DRAG) pulses, while different colours represent different values of T2. The advantage of DRAG is maximum at intermediate B1 for long T2 and moves to larger B1 by decreasing T2. | ||
In its simplest implementation, DRAG method works well when a unique transition disturbs the selected one. Hence, we have applied this technique only to qudit transitions (BQ1) of the (n) system, to distinguish transitions |3/2〉 ↔ |1/2〉 and |−1/2〉 ↔ |−3/2〉 from |1/2〉 ↔ |−1/2〉. In the case of excitations of the ancilla, we usually have two gaps close to the selected transitions.
The advantage of DRAG is clear when we use fast pulses and we consider a system with similar energy gaps. Indeed, in this regime the difference between the gaps is comparable to the width of the pulse and hence the leakage becomes an issue.
We compare in Fig. 5 the performance of the code by using simple Gaussian or DRAG pulses, as a function of B1 and for different values of T2, computed near the t/T2 maximum gain, as reported in Fig. 4 inset. To clearly highlight the effect of proper pulse-shaping, we investigate regimes even employing magnetic field amplitudes larger than those available in current experimental apparatus (close to 120 G for pulse nuclear magnetic resonance experiments63). The aim is to guide future technological developments in this direction.
Results are shown in Fig. 5, with dark (light) curves referred to Gaussian (DRAG) pulses and different colours indicating different values of T2. In all the examined cases, the use of Gaussian driving pulses leads to a minimum in ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) at intermediate B1. Below this minimum value, pulse length is the limiting factor and hence decoherence is the leading error. For larger B1 (i.e. shorter pulses), above the minimum, the final accuracy is substantially limited by leakage, due to the fact that pulses become less monochromatic. By increasing T2, the effect of decoherence is reduced and hence the minimum moves to lower values of B1. In the infinite T2 limit,
at intermediate B1. Below this minimum value, pulse length is the limiting factor and hence decoherence is the leading error. For larger B1 (i.e. shorter pulses), above the minimum, the final accuracy is substantially limited by leakage, due to the fact that pulses become less monochromatic. By increasing T2, the effect of decoherence is reduced and hence the minimum moves to lower values of B1. In the infinite T2 limit, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) becomes monotonically increasing with B1. The reduction of leakage by application of the DRAG method is clearly evidenced by the reduction of the slope of
becomes monotonically increasing with B1. The reduction of leakage by application of the DRAG method is clearly evidenced by the reduction of the slope of ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) above the minimum. For T2 = 100 μs the minimum is above 250 G, and its position is (again) lowered by increasing T2. However, compared to the case of Gaussian pulses, the increase of
above the minimum. For T2 = 100 μs the minimum is above 250 G, and its position is (again) lowered by increasing T2. However, compared to the case of Gaussian pulses, the increase of ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) with B1 remains much weaker. Hence, application of the DRAG technique significantly improves the overall performance of the QEC code.
with B1 remains much weaker. Hence, application of the DRAG technique significantly improves the overall performance of the QEC code.
3.4 Single-qubit gates on encoded states
Here we present a scheme to implement single-qubit gates on encoded states, such as Rz(ϑ) and Ry(ϑ) rotations of an arbitrary angle ϑ. By combining them, a generic single-qubit operation can be obtained. For instance, the Hadamard gate (involved in many quantum algorithms) results from Rz(π)Ry(π/2).Our aim is to design a strategy which exploits transitions between energy levels while keeping the states encoded as much as possible. Reducing the amount of time the system is un-encoded helps to limit the effect of decoherence while the system is not protected.
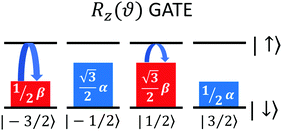
The effect of a Rz(ϑ) gate consists in adding a relative phase between |0L〉 and |1L〉, i.e. implementing the transformation
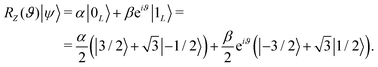 | (12) |
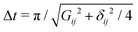 adds a phase
adds a phase 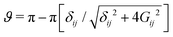 to the system wave function, with Gij the matrix element of the transition.64 By employing only excitations of the ancilla, this scheme allows us to implement the Rz(ϑ) gate without ever decoding quantum information stored in the qudit, which therefore remains protected from dephasing (Fig. 6).
to the system wave function, with Gij the matrix element of the transition.64 By employing only excitations of the ancilla, this scheme allows us to implement the Rz(ϑ) gate without ever decoding quantum information stored in the qudit, which therefore remains protected from dephasing (Fig. 6).
R x,y(ϑ) rotations are more tricky. Indeed, they necessarily involve population transfer between energy levels (such as ±3/2) which are not directly connected by H1e,n. Hence, the implementation of logical Rx,y(ϑ) gates on a spin S qudit requires a decomposition into several pulses, which in turn implies to leave the protected code-space for some time. To limit this time as much as possible, one could for instance exploit excitations of the ancilla to manipulate in parallel ±3/2 and ±1/2 components of the qudit state.
4 Discussion and conclusions
To sum up, we have shown the performance of two realistic molecular spin qudits as protected logical units for quantum computation, embedding quantum error correction against pure dephasing, the leading error in this class of systems.We have investigated by extensive numerical simulations the improvement in the final error after implementation of a targeted quantum error correction procedure, compared to an uncorrected qubit. Our study has focused on two different implementations, based on an existing nuclear spin 3/2 qudit, coupled to an electronic ancilla by hyperfine interaction, and on a hypothetical (but realistic) electronic spin dimer, where a S = 3/2 qudit encodes quantum information, while an effective spin 1/2 plays the role of ancilla. The latter is used to detect errors without corrupting quantum information stored into the qudit degrees of freedom. We deeply investigate different sources of error which limit the performance of the code and we identify the proper range of couplings and coherence times allowing us to achieve a good protection. In addition, we study the dependence of our results on the form of the driving field, we find system-specific optimal working points and we apply pulse-shaping techniques to reduce the length of the pulses, while keeping leakage under control. In both the electronic and the nuclear case, we reach residual errors significantly lower than 10−2. We note, in turn, that optimal quantum control methods could be applied to further reduce leakage to neighboring levels and pulse length, as recently shown in ref. 65. Finally, multi-spin molecules with small total spin but a large connectivity between energy levels could be used,66,67 thus potentially speeding-up manipulations.
Being based on realistic choices of the experimental parameters, our results indicate a clear route to guide the synthesis of molecules for future proof-of-concepts experiments.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has received funding from the European Unions Horizon 2020 research and innovation programme (FET-OPEN project FATMOLS) under grant agreement no. 862893.Notes and references
- A. Chiesa, G. F. S. Whitehead, S. Carretta, L. Carthy, G. A. Timco, S. J. Teat, G. Amoretti, E. Pavarini, R. E. P. Winpenny and P. Santini, Sci. Rep., 2014, 4, 7423 CrossRef CAS PubMed.
- D. Aguilà, D. Barrios, V. Velasco, O. Roubeau, A. Repollés, P. Alonso, J. Sesé, S. Teat, F. Luis and G. Aromí, J. Am. Chem. Soc., 2014, 136, 14215 CrossRef PubMed.
- A. Ardavan, A. M. Bowen, A. Fernandez, A. J. Fielding, D. Kaminski, F. Moro, C. A. Muryn, M. D. Wise, A. Ruggi, E. J. L. McInnes, K. Severin, G. A. Timco, C. R. Timmel, F. Tuna, G. F. S. Whitehead and R. E. P. Winpenny, npj Quantum Inf., 2015, 1, 15012 CrossRef.
- J. Ferrando-Soria, E. Moreno-Pineda, A. Chiesa, A. Fernandez, S. A. Magee, S. Carretta, P. Santini, I. Vitorica-Yrezabal, F. Tuna, E. J. L. McInness and R. E. P. Winpenny, Nat. Commun., 2016, 7, 11377 CrossRef CAS PubMed.
- M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154–2157 CrossRef CAS PubMed.
- M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 11234–11244 CrossRef CAS PubMed.
- E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501–513 RSC.
- E. Macaluso, M. Rubín, D. Aguilà, A. Chiesa, J. I. M. L. A. Barrios, P. J. Alonso, O. Roubeau, F. Luis, G. Aromí and S. Carretta, Chem. Sci., 2020, 11, 10337 RSC.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301 CrossRef PubMed.
- M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339 CrossRef CAS PubMed.
- C. Bonizzoni, A. Ghirri, F. Santanni, M. Atzori, L. Sorace, R. Sessoli and M. Affronte, npj Quantum Inf., 2020, 6, 68 CrossRef.
- S. J. Lockyer, A. Chiesa, G. A. Timco, E. J. L. McInnes, T. S. Bennett, I. J. Vitorica-Yrezebal, S. Carretta and R. E. P. Winpenny, Chem. Sci., 2021, 12, 9104 RSC.
- S. Carretta, D. Zueco, A. Chiesa, A. Gómez-León and F. Luis, Appl. Phys. Lett., 2021, 118, 240501 CrossRef CAS.
- S. Nakazawa, S. Nishida, T. Ise, T. Yoshino, N. Mori, R. D. Rahimi, K. Sato, Y. Morita, K. Toyota, D. Shiomi, M. Kitagawa, H. Hara, P. Carl, P. Höfer and T. Takui, Angew. Chem., Int. Ed., 2012, 51, 9860–9864 CrossRef CAS PubMed.
- S. Yamamoto, S. Nakazawa, K. Sugisaki, K. Sato, K. Toyota, D. Shiomi and T. Takui, Phys. Chem. Chem. Phys., 2015, 17, 2742–2749 RSC.
- B. K. Rugg, M. D. Krzyaniak, B. T. Phelan, M. A. Ratner, R. M. Young and M. R. Wasielewski, Nat. Chem., 2019, 11, 981–986 CrossRef CAS PubMed.
- M. D. E. Wasielewski, M. R. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith, T. Goodson, M. L. Kirk, J. P. McCusker, J. K. Ogilvie, D. A. Shultz, S. Stoll and K. B. Whaley, Nat. Rev. Chem., 2020, 4, 490–504 CrossRef CAS.
- C. D. Bruzewicz, J. Chiaverini, R. McConnell and J. M. Sage, Appl. Phys. Lett., 2019, 6, 021314 Search PubMed.
- F. Tacchino, A. Chiesa, S. Carretta and D. Gerace, Adv. Quantum Technol., 2019, 3, 1900052 CrossRef.
- I. Pogorelov, T. Feldker, C. D. Marciniak, L. Postler, G. Jacob, O. Krieglsteiner, V. Podlesnic, M. Meth, V. Negnevitsky, M. Stadler, B. Höfer, C. Wächter, K. Lakhmanskiy, R. Blatt, P. Schindler and T. Monz, PRX Quantum, 2021, 2, 020343 CrossRef.
- A. Chiesa, F. Tacchino, M. Grossi, P. Santini, I. Tavernelli, D. Gerace and S. Carretta, Nat. Phys., 2019, 15, 455 Search PubMed.
- F. Arute, et al. , Nature, 2019, 574, 505 CrossRef CAS PubMed.
- F. Arute, et al. , Science, 2020, 369, 1084 CrossRef CAS PubMed.
- P. Jurcevic, A. Javadi-Abhari, L. S. Bishop, I. Lauer, D. F. Bogorin, M. Brink, L. Capelluto, O. Günlük, T. Itoko, N. Kanazawa, A. Kandala, G. A. Keefe, K. Krsulich, W. Landers, E. P. Lewandowski, D. T. McClure, G. Nannicini, A. Narasgond, H. M. Nayfeh, E. Pritchett, M. B. Rothwell, S. Srinivasan, N. Sundaresan, C. Wang, K. X. Wei, C. J. Wood, J.-B. Yau, E. J. Zhang, O. E. Dial, J. M. Chow and J. M. Gambetta, Quantum Sci. Technol., 2021, 6, 025020 CrossRef.
- A. Blais, A. L. Grimsmo, S. M. Girvin and A. Wallraff, Rev. Mod. Phys., 2021, 93, 025005 CrossRef CAS.
- A. Chatterjee, P. Stevenson, S. De Franceschi, A. Morello, N. P. de Leon and F. Kuemmeth, Nat. Rev. Phys., 2021, 3, 157–177 CrossRef.
- Y.-S. Ding, Y.-F. Deng and Y.-Z. Zheng, Magnetochemistry, 2016, 2, 40 CrossRef.
- K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2014, 5, 5304 CrossRef CAS PubMed.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488 CrossRef CAS PubMed.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348 CrossRef CAS PubMed.
- M. Fataftah, J. M. Zadrozny, S. C. Coste, M. J. Graham, D. M. Rogers and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 1344 CrossRef CAS PubMed.
- M. K. Wojnar, D. W. Laorenza, R. D. Schaller and D. E. Freedman, J. Am. Chem. Soc., 2020, 142, 14826–14830 CrossRef CAS PubMed.
- J. Zadrozny and D. E. Freedman, Inorg. Chem., 2015, 54, 12027–12031 CrossRef CAS PubMed.
- Y. Wang, Z. Hu, B. C. Sanders and S. Kais, Front. Phys., 2020, 8, 479 Search PubMed.
- C. Cafaro, F. Maiolini and S. Mancini, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 86, 022308 CrossRef.
- F. Tacchino, A. Chiesa, R. Sessoli, I. Tavernelli and S. Carretta, J. Mater. Chem. C, 2021, 9, 10266 RSC.
- C. Godfrin, A. Ferhat, R. Ballou, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Phys. Rev. Lett., 2017, 119, 187702 CrossRef CAS PubMed.
- B. Mischuck and K. Mølmer, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 87, 022341 CrossRef.
- E. O. Kiktenko, A. K. Fedorov, O. V. Man'ko and V. I. Man'ko, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 91, 042312 CrossRef.
- P. Imany, J. A. Jaramillo-Villegas, M. S. Alshaykh, J. M. Lukens, O. D. Odele, A. J. Moore, D. E. Leaird, M. Qi and A. M. Weiner, npj Quantum Inf., 2019, 5, 59 CrossRef.
- E. Kiktenko, A. Fedorov, A. Strakhov and V. Man'ko, Phys. Lett. A, 2015, 379, 1409 CrossRef CAS.
- S. J. Devitt, W. J. Munro and K. Nemoto, Rep. Progr. Phys., 2013, 76, 076001 CrossRef PubMed.
- B. M. Terhal, Rev. Mod. Phys., 2015, 87, 307 CrossRef.
- A. Chiesa, E. Macaluso, F. Petiziol, S. Wimberger, P. Santini and S. Carretta, J. Phys. Chem. Lett., 2020, 11, 8610 CrossRef CAS PubMed.
- F. Petiziol, A. Chiesa, S. Wimberger, P. Santini and S. Carretta, npj Quantum Inf., 2021, 7, 133 CrossRef.
- A. Chiesa, F. Petiziol, E. Macaluso, S. Wimberger, P. Santini and S. Carretta, AIP Adv., 2021, 11, 025134 CrossRef CAS.
- M. Werninghaus, D. J. Egger, F. Roy, S. Machnes, F. K. Wilhelm and S. Filipp, npj Quantum Inf., 2021, 7, 14 CrossRef.
- J. M. Gambetta, F. Motzoi, S. T. Merkel and F. K. Wilhelm, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 012308 CrossRef.
- E. Knill and R. Laflamme, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 55, 900–911 CrossRef CAS.
- T. Sanada, T. Suzuki, T. Yoshida and S. Kaizaki, Inorg. Chem., 1998, 37, 4712 CrossRef CAS PubMed.
- K. S. Pedersen, A.-M. Ariciu, S. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, J. Am. Chem. Soc., 2016, 138, 5801–5804 CrossRef CAS PubMed.
- P. A. S. Cruickshank, D. R. Bolton, D. A. Robertson, R. I. Hunter, R. J. Wylde and G. M. Smith, Rev. Sci. Instrum., 2009, 80, 103102 CrossRef PubMed.
- M. Fujii, F. Wakai, H. Abe and A. Hirai, J. Phys. Soc. Jpn., 1981, 50, 1109 CrossRef CAS.
- C. Mazzoli, G. Allodi, G. Guidi, R. De Renzi and P. Ghigna, J. Magn. Magn. Mater., 2004, 272, 106 CrossRef.
- R. Hussain, G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. Pedersen, R. D. Renzi, S. Piligkos and S. Carretta, J. Am. Chem. Soc., 2018, 140, 9814 CrossRef CAS PubMed.
- S. Chicco, A. Chiesa, G. Allodi, E. Garlatti, M. Atzori, L. Sorace, R. De Renzi, R. Sessoli and S. Carretta, Chem. Sci., 2021, 12, 12046 RSC.
- R. Schutjens, F. A. Dagga, D. J. Egger and F. K. Wilhelm, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 052330 CrossRef.
- L. S. Theis, F. Motzoi and F. K. Wilhelm, Phys. Rev. A, 2016, 93, 012324 CrossRef.
- S. P. Premaratne, J.-H. Yeh, F. C. Wellstood and B. S. Palmer, Phys. Rev. A, 2019, 99, 012317 CrossRef CAS.
- S. E. Economou and E. Barnes, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 161405 CrossRef.
- F. Motzoi, J. M. Gambetta, P. Rebentrost and F. K. Wilhelm, Phys. Rev. Lett., 2009, 103, 110501 CrossRef CAS PubMed.
- A. De, Quantum Inf. Process., 2019, 18, 165 CrossRef.
- K. J. Sanders, A. J. Pell, S. Wegner, C. P. Grey and G. Pintacuda, Chem. Phys. Lett., 2018, 697, 29 CrossRef CAS.
- A. Chiesa, P. Santini and D. A. Gerace, Sci. Rep., 2015, 5, 16036 CrossRef PubMed.
- A. Castro, A. G. Carrizo, D. Zueco and F. Luis, https://arxiv.org/abs/2111.15313.
- L. M. Baker, et al. , Chem. – Eur. J., 2016, 22, 1779–1788 CrossRef PubMed.
- R. J. Woolfson, G. A. Timco, A. Chiesa, I. J. Vitorica-Yrezabal, F. Tuna, T. Guidi, E. Pavarini, P. Santini, S. Carretta and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2016, 55, 8856–8859 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2022 |