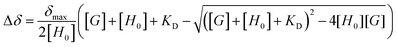Unveiling the role of pyrylium frameworks on π-stacking interactions: a combined ab initio and experimental study

Abstract

A multidisciplinary study is presented to shed light on how pyrylium frameworks, as π–hole donors, establish π–π interactions. The combination of CSD analysis, computational modelling (ab intitio, DFT and MD simulations) and experimental NMR spectroscopy data provides essential information on the key parameters that characterize these intereactions, opening new avenues for further applications of this versatile heterocycle.

---

Reyes Núñez-Franco

Reyes Núñez-Franco received her degree in chemistry from University of Seville (2017), where her BSc final project focused on the synthesis of pyrylium complexes as templates for non-covalent interactions. She then moved to the Universitat Autònoma de Barcelona to earn a master's degree in Bioinformatics. Since 2019, she has been a PhD student at CIC bioGUNE (Bilbao) where she applies computational methodologies to study relevant biological processes.

Gonzalo Jiménez-Osés

Gonzalo Jiménez-Osés received his PhD from Universidad de La Rioja, Spain, before moving to Universidad de Zaragoza-CSIC, Spain, to work on metal catalysis and then to UCLA, United States, to work with Ken Houk as a postdoctoral researcher in computational chemistry. He has been the leader of the Computational Chemistry group at CIC bioGUNE since 2019 and an Ikerbasque Research Associate since 2020. His research is highly collaborative and cross-disciplinary—using state-of-the art multiscale simulation methods to predict and understand complex chemical and biological processes, with special focus on glycobiology, bioconjugation and enzyme design.

Jesús Jiménez-Barbero

Jesús Jiménez-Barbero received his PhD in Chemistry (1987) at Madrid. After postdoctoral stays at Zurich, Mill Hill, and Pittsburgh, he returned to Madrid (CSIC). In 2002, he was promoted to CSIC Research Professor and was appointed Ikerbasque Research Professor and Scientific Director of CIC bioGUNE (Bilbao) in 2014. His scientific interest is focused on molecular recognition and chemical glycobiology, employing a multidisciplinary approach that combines synthesis, biochemistry, molecular biology, biophysics, molecular modelling, and NMR.

Francisca Cabrera-Escribano

Francisca Cabrera-Escribano obtained her PhD in Organic Chemistry from the University of Seville (US), working on the chemistry of aminoglycoside antibiotics. After receiving her doctorate, she trained as a postdoctoral fellow at the Institut de Chimie des Substances Naturelles (CNRS) in Gif sur Yvette (France), where she worked on fluorinated carbohydrates. She has more than twenty years of experience in the study of carbohydrates of biological (pharmacological) and technological interest. Currently, she has a research group that focuses on the development of new derivatives of chitosan as biomaterials for biomedical applications. Since 2013, she has been a member of the Board of the European Chitin Society.

Antonio Franconetti

Antonio Franconetti received his PhD in Chemistry (2016) from the Universidad de Sevilla (Spain), working on the preparation of new chitosan derivatives for multidisciplinary applications. After a postdoctoral appointment at Barcelona, he joined the group of Antonio Frontera at UIB working on non-covalent interactions from a computational perspective. In 2019, he moved to CIC bioGUNE (Bilbao) as a Juan de la Cierva postdoctoral researcher. Since 2020, he has been the president of the Young Chemists division of the Royal Spanish Society of Chemistry (RSEQ). His research interests are focused on supramolecular chemistry, carbohydrates, and modelling.

---

Introduction

Pyrylium heterocycle (Fig. 1) is an aromatic cation discovered more than a century ago.¹ However, this six-membered ring remained underestimated for years, thus inducing the idea that the golden age of this ancient salt had already passed. Recent breakthroughs, however, have established a successful present far from single green shoots.

Fig. 1 (a) Structure of unsubstituted pyrylium cation and (b) structure of synthesized 2,4-di-(4-methylphenyl)-4-(4-fluorophenyl) tetrafluoroborate (1).

The different chemical and physical properties of pyrylium-based scaffolds have been exploited in multiple fields. For instance, pyrylium compounds with extended conjugation have recently been applied as fluorophores, since they display photostability, good quantum yields and low cytotoxicity in targeting mitochondria organelles.² From a chemical perspective, the electrophilic C2/C6 positions allow modification of the polysaccharide chitosan, introducing a fluorescent function on its backbone.³ Similarly, the C–N activation of alkylamines⁴ and the activation of low nucleophilic aminoheterocycles also take advantage of this reactivity.⁵ In addition, the excellent photoredox behaviour of pyrylium derivatives⁶ has provided an alternative metal-free photocatalyst for ring-opening metathesis polymerization (ROMP) reactions.⁷

Pioneering work by Schlüter and co-workers reported the X-ray structure of a new 2D polymeric material based on a [2+2]-cycloaddition between two styrylpyrylium structures.⁸ The crystal-to-crystal synthesis for obtaining this covalent stacked material sparked a new hot topic in material science because the pyrylium core can be easily transformed, thus increasing its applicability.⁹ The stability between its layers is presumably underpinned by van der Waals interactions,¹⁰ thus it has also been referred to as a cation-π-controlled crystal.¹¹

Besides this evidence, a feature of pyrylium derivatives not to be overlooked is their accompanying anions which have been proposed to establish anion–π interactions with their cationic partners.¹²

Nowadays, non-covalent interactions are widely understood to be driving entities in supramolecular chemistry, particularly in molecular recognition processes. At first glance, each molecule or scaffold has interactive properties and spontaneously organizes itself with complementarity. The ways in which these molecules interact differ in their directionality, strength or cooperative effects. For this reason, this field has been rapidly developed and the current knowledge has tremendously expanded in the last decades. Beyond hydrogen and halogen bonds or π–π stacking, a plethora of new noncovalent interactions covering σ– and π–hole families,¹³ such as tetrel,¹⁴ chalcogen,¹⁵ coinage¹⁶ or spodium bonds,¹⁷ have blossomed.

In general, crystallographic structures are the reference sources for obtaining valuable information about these intermolecular interactions. In these densely packed environments, molecules are highly ordered, displaying multiple contacts at distances shorter than ∑R_vdw (±0.2 Å) and strong cooperativity effects.¹⁸ The combination of solid-state structural analyses and theoretical calculations affords a precise characterization of the energetic and geometric features of the relevant interactions. However, another situation arises in solution, where non-covalent interactions are often weaker and highly dynamic. In addition, the surrounding solvent molecules may significantly tune the pre-organization of the acceptor and donor moieties, thus modulating their final intermolecular association. The current standard methodology to experimentally study these interactions with high accuracy is based on molecular balances and has been applied to understand cation-π interactions involving pyridinium systems.¹⁹

To the best of our knowledge, experimental and/or computational studies of intermolecular interactions involving pyrylium frameworks as main players are scarce. The precise type of interaction should have molecular consequences (strength, directionality and cooperativity) and supramolecular features (reactivity and 2D interlayer distance).

To address these shortcomings, herein we report a computer-aided study to support the growing interest in pyrylium⋯arene interactions. Different X-ray structures were retrieved from the Cambridge Structural Database (CSD) and analyzed. Additionally, a systematic ab initio study was carried out to dissect the influence of substituents and fully characterize this interaction. Finally, data in solution (NMR) were recorded for a synthetic pyrylium tetrafluoroborate to provide a full picture of the molecular recognition event.

Results and discussion

CSD analysis

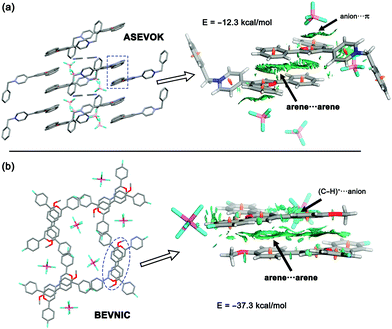
The solid-state architectures of pyrylium compounds account for their ability to self-assemble into near-planar π-stacked helical motifs.²⁰ In most cases, these complexes participate in a four-ring antiparallel dimerization pattern displaying centroid-to-centroid distances in the range of 3.44 to 4.16 Å. In addition, analysis of the crystallographic structures also revealed that the anions are placed inside the formed channels or pores. In this context, two feasible arrangements for anions have been previously described: (a) anion–π contacts and (b) (C–H)⁺⋯anion.¹² To obtain a more meaningful interpretation, an NCIplot index analysis²¹ was carried out for refcodes ASEVOK (Fig. 2a) and BEVNIC (Fig. 2b) to qualitatively characterize the weak and strong contacts between the pyrylium layers. These two structures cover the aforementioned possibilities of the anion locations (ASEVOK and BEVNIC for anion–π and (C–H)⁺⋯anion, respectively).

Fig. 2 X-ray architectures and NCIplots of (a) refcode ASEVOK and (b) refcode BEVNIC. For NCI plot, the gradient cut-off is s = 0.35 a.u. and the colour scale is −0.04 < ρ < 0.04 a.u. BSSE-corrected energies at PBE0-D3/def2-TZVP are also given. Colour coding for atoms is carbon in grey, oxygen in red, nitrogen in dark blue, fluorine in light blue and boron in pink.

Although the cation–π interaction has been invoked as one of the intermolecular motifs stabilizing these channels, according to the sign(λ₂)ρ value, the NCIplots computed for these X-ray structures suggest a weak van der Waals interaction (green colour) as expected for arene⋯arene contact. In addition, NCIplots also highlight the intermolecular CH/π contacts between other substituents. The attractive nature of the combined interactions was confirmed by their large interaction energies (ΔE_int = −12.3 and −37.3 kcal mol⁻¹ for ASEVOK and BEVNIC, respectively).

Theoretical study

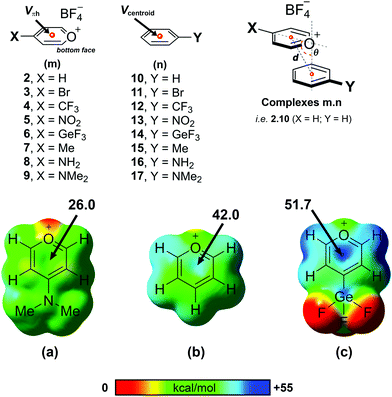
From a computational perspective, it should be noted that the pyrylium cation has an unusual behaviour. In the presence of its anion, the pyrylium shows two different faces. The first one is involved in anion recognition¹² and is essentially locked for participating in another intermolecular contact, whereas the second one is available to establish additional interactions. Molecular electrostatic potential (MEP) surfaces of the pyrylium cation (Pyry⁺) and pyrylium tetrafluoroborate (Pyry-BF₄, 2) shed light on this behaviour. The positive region of electrostatic potential (V_πh, Fig. 3) perpendicular to the molecular plane is defined as a π–hole.²² The MEP value corresponding to this π–hole for the Pyry⁺ cation was +128.0 kcal mol⁻¹, while complex 2 shows a decrease in π–hole intensity (V_s,πh +42.0 kcal mol⁻¹, Fig. 3b). However, the ability of its bottom face to act as an excellent π–hole donor was retained better than that of hexafluorobenzene (HFB, V_πh = +19.1 kcal mol⁻¹).

Fig. 3 Pyrylium models (2–9), aromatic derivatives (10–17) and complexes (m.n) used in this work. MEP surfaces plotted on the 0.001 a.u. molecular surface for pyrylium tetrafluoroborates 9 (a), 2 (b), and 6 (c). The locations of π–holes are indicated and their intensity (V_πh) values are given in kcal mol⁻¹.

The influence of different substituents with electron-donating and electron-withdrawing properties on the geometry and energetic features of BF₄–Pyry⋯π contacts was computationally analysed. For this purpose, we selected para-substituted pyrylium molecules as π–hole donors and mono-substituted aromatic rings as “electron-rich” molecules using a high-level ab initio MP2(fc)/def2-TZVP method. Despite four stable geometries being feasible (I–IV, Fig. S1, ESI†), the whole study was carried out only on geometry I (antiparallel-displaced structure) as it is the most similar to those found in the CSD.

As a first step, we carried out a MEP study at the π–hole in complexes 2–9 (Table 1 and Fig. 3). The substituent attached to the pyrylium core (X) has a significant influence on the V_πh, following the trend NMe₂ < NH₂ < Me < H < Br < CF₃ < NO₂ < GeF₃ ≪ Pyry⁺. As expected, electron-withdrawing substituents increased the intensity of V_πh up to 9.7 kcal mol⁻¹ whereas electron-donating substituents decreased it by 16.0 kcal mol⁻¹ (see Table S1 for comparison with Pyry⁺, ESI†). The opposite behaviour is observed for the V_centroid values in complexes 10–17. This suggests that the pyrylium core acts as an electron-deficient aromatic ring (similar to 2,4,6-trifluoro-s-triazine, V_πh +42.5 kcal mol⁻¹).

Table 1 MEP values (kcal mol⁻¹) for compounds 2–17 at the MP2(fc)/def2-TZVP level of theory and Hammet's σ_p parameters of the substituents

Compound	V πh	Compound	V centroid	σ p
2, X = H	+42.0	10, Y = H	−16.8	0.00
3, X = Br	+43.5	11, Y = Br	−9.7	0.23
4, X = CF3	+49.3	12, Y = CF3	−5.8	0.54
5, X = NO2	+50.6	13, Y = NO2	−1.4	0.78
6, X = GeF3	+51.7	14, Y = GeF3	−0.8	0.97
7, X = Me	+38.6	15, Y = Me	−18.3	−0.17
8, X = NH2	+30.4	16, Y = NH2	−21.3	−0.66
9, X = NMe2	+26.0	17, Y = NMe2	−22.0	−0.83

---

Ab initio calculations show that the BSSE-corrected interaction energies (E_BSSE) for complexes 2.10–9.17 (Table S2, ESI†) are moderately strong, ranging from −9.4 to −3.2 kcal mol⁻¹. The most stable complexes contained electron-withdrawing groups attached to the pyrylium moiety. For instance, complex 6.17 (X = GeF₃; Y = NMe₂) is the most stable dimer and 8.14 (X = NH₂; Y = GeF₃) is the weakest one.

The electrostatic nature of such intermolecular interactions was further analysed using Hammett parameters σ_p, which reflect the inductive/mesomeric effects of para-substituents. Thus, by plotting the individual Hammett constants (σ_p)²³vs. the calculated interaction energies E_BSSE for each interacting pair, the electronic fingerprint of the pyrylium⋯arene interaction was obtained (Fig. 4a). To account for the combined influence of both para-substituted moieties on E_BSSE (Fig. 4b), the mixed σ_p(XY) parameter²⁴ [σ_p(XY) = −1.45 × σ_p(X) + 2.41 × σ_p(Y)] was defined using coefficients obtained from multiple linear regression (see ESI†). A negative sign of β_x (−1.45) indicates an inverse correlation between the electron-donating properties of the para-substituents in the pyrylium fragment and the interaction energy, while a positive sign of β_y (2.41) shows a direct correlation. The fact that the absolute value of β_y outweighs β_x in these complexes points toward a larger influence of arene substitution on the strength of the interaction energy.

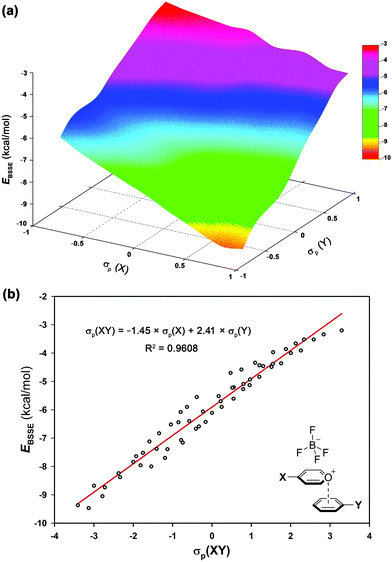Fig. 4 (a) Electronic fingerprint of π-stacking interaction involving pyrylium frameworks and (b) Hammett's plot based on mixed σ_p(XY) of complexes 2.10–9.17.

An assessment in which pyrylium templates were linked to arenes was carried out and compared with related cation–π and π–π interactions. Three descriptors (E_BSSE, d and θ, Fig. 3) were selected to characterize three systems: (a) Pyry⁺⋯π, (b) complex 2.10 (X = Y = H) and (c) benzene dimer (Fig. S2, ESI†). The most stable system proved to be Pyry⁺⋯π (ca. −11.1 kcal mol⁻¹), a model for cation–π interaction. On the other hand, complex 2.10 is more stable than the benzene dimer (ΔΔE_BSSE = 2.4 kcal mol⁻¹). The trend Pyry⁺ > 2.10 > benzene also suggests an excellent π–hole donor instead of a canonical cation. In agreement with this trend, the centroid-to-centroid distance in complex 2.10 is slightly larger (Δd = 0.07 Å) than that in Pyry⁺⋯π but equally short compared to the benzene dimer (Δd = −0.07 Å). However, both 2.10 and Pyry⁺ complexes have the same angle between the two aromatic rings (tilt angle, θ = 102.0°) whereas the angle is closer to 90° for benzene⋯benzene stacking. An energy decomposition analysis (LMO-EDA, Fig. S3, ESI†) was also applied to separate the interaction energy into individual contributions. The quantitative analysis was mainly focused on electrostatic (E_elec) and dispersion (E_disp) terms. As expected, a dominant role of the dispersion term was obtained for the benzene⋯benzene dimer. In addition, the smallest electrostatic component was also obtained in this system. The opposite situation was found for Pyry⁺⋯π, which is clearly dominated by E_elec. On the other hand, complex 2.10 displayed intermediate behaviour with similar E_elec and E_disp terms.

Instead of the ordered environment found in X-ray architectures, the association between molecules in solution becomes more tangled because of solvation. Upon binding, solvent molecules are released to the bulk, often followed by an energetic penalty and an entropic benefit whose net consequences to the association free energy are difficult to predict.²⁵ Hence, particularly when charged species are involved, the net stabilization might be smaller than the values calculated in the gas phase. In addition, the main driving forces toward binding (electrostatic and dispersion) might be altered in solution. In some cases, dispersion and electrostatic interactions are attenuated but still significant.²⁶

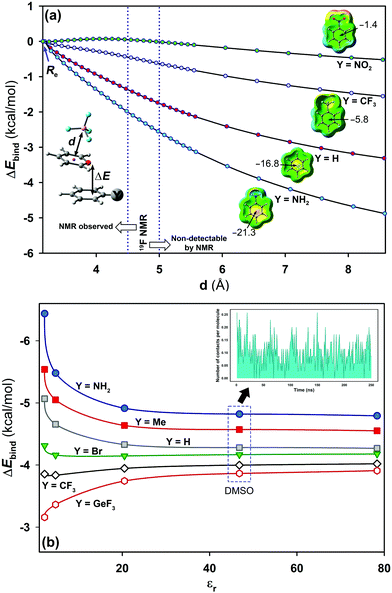
As a jumping-off point, MD simulations (250 ns) were carried out to test the behaviour of pyrylium tetrafluoroborate 1 in DMSO, which is known to better solvate cations than anions. Theoretical distances from the centroid of all pyrylium rings to the centroid of all tetrafluoroborates were calculated. It was found that the most frequent distance between the pyrylium centroids and the nearest BF₄ anion is 9.9 ± 0.2 Å (Fig. S4, ESI†). MD simulations revealed that the closest pyrylium centroid⋯ BF₄ contact is, on average, 4.7 ± 1.2 Å. This distance is still within the boundary for subsequent NMR detection based on NOE experiments (up to 5 Å), but the calculated ratio of these ionic pairs (shorter than 5 Å) is only around 3% (Fig. 5b, inset). These geometrical findings should modify the role of the pyrylium⋯BF₄ interaction. For this reason, interaction energies were adapted (Fig. 5a). At large distances, these systems should evolve towards cation-π interaction. In this situation, electron-donating substituents stabilize (in the gas phase) the system (ΔE_4.5Å = −2.1 kcal mol⁻¹, complex 2.16), while the interaction energy slightly dropped with electron-withdrawing ones (ΔE_4.5Å = +0.05 kcal mol⁻¹, complex 2.13).

Fig. 5 (a) Evolution towards cation-π interactions for complexes 2.10 (Y = H), 2.12 (Y = CF₃), 2.13 (Y = NO₂) and 2.16 (Y = NH₂) calculated from R_e (ca. 3.15 Å) to 8.57 Å; (b) solvent effect on interaction energies for compounds 2.10–2.16. Solvents considered in turn: 1,4-dioxane (ε_r = 2.2), CHCl₃ (ε_r = 4.7), acetone (ε_r = 20.5), DMSO (ε_r = 46.8) and H₂O (ε_r = 78.4). In the inset, the number of contacts per molecule throughout a MD simulation (250 ns) is shown. Contacts are measured using a threshold distance of 5 Å.

Solvent effects were included in the PCM continuum solvation model for complexes 2.10–2.16 (Fig. 5b). The results showed a dependency of the interaction energy on the dielectric constant (ε_r).²⁷ At large dielectric constant values (ε_r > 20.5, acetone), the electrostatic component vanishes and dispersion forces dominate in solution. A representative situation is found with complex 2.14 (X = H; Y = GeF₃). In the gas phase, this compound exhibits weak strength which is slightly increased with polar solvents. The opposite effect was observed for complex 2.16 (X = H; Y = NH₂). For this complex, the interaction energy suffers a significant penalty at large dielectric values (ca. 1.5 kcal mol⁻¹).

Experimental study

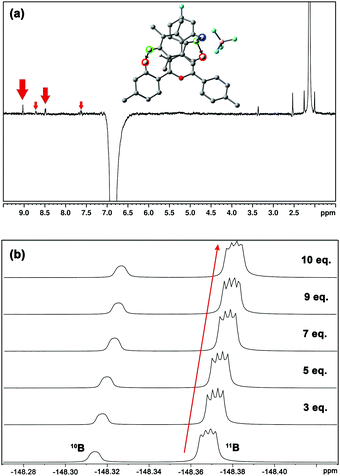
The experimental behaviour of these systems was analysed using DMSO (ε_r = 46.8) and acetone (ε_r = 20.5) as aprotic solvents. We prepared compound 1 (Fig. 1b) to study the interactions in solution. This compound displays a moderate V_πh (+23.2 kcal mol⁻¹), is stable enough in solution (attached phenyl rings at C-2 and C-4 positions) and bears NMR observable atoms (¹H and ¹⁹F). We then prepared the symmetric pyrylium tetrafluoroborate molecule by following a previous synthetic methodology.^12a,c Briefly, the Lewis acid BF₃·Et₂O catalyses the reaction between methyl acetophenone and 4-fluorobenzaldehyde, affording the desired compound (1) in a 29% yield. One of the most important features of this kind of compound is the singular chemical shift of the aromatic H3/H5 protons at 9.03 ppm (DMSO-d₆).

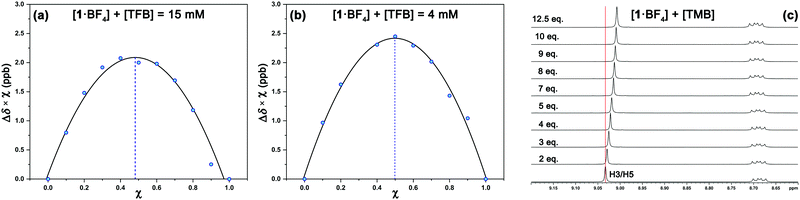
¹H NMR experiments were employed to monitor the chemical shift perturbation of this signal upon binding with tetramethylbenzene (TMB) and tetrafluorobenzene (TFB). First, we applied the continuous variation method, commonly referred to as a Job's plot, to determine the stoichiometry of 1·BF₄⋯arene complexes (Fig. 6). Despite this method's limitations, especially for 1 : 2 host–guest stoichiometries,²⁸ it is suitable for our outcomes since we obtained a 1 : 1 equilibrium between the complexes studied at two sets of concentrations and solvents ([1·BF₄] + [Arene] = 4 mM and 15 mM, for deuterated acetone and DMSO, respectively).

Fig. 6 Representative Job's plots for the interaction of compound 1 and TFB at (a) 15 mM in DMSO-d₆ and (b) 4 mM in acetone-d₆; (c) ¹H NMR titration spectra (500 MHz) of 1·BF₄ (20 mM) with TMB in DMSO-d₆. Key H3/H5 protons are labeled.

The increasing number of equivalents of TMB provokes a slight upfield shift (Δδ = 27 ppb, Fig. 6c) of the signal assigned to the H3/H5 protons. This effect agrees with the observed shielding of protons in spatial proximity to an aromatic ring.^29,30 Theoretical calculations provide a meaningful interpretation (Fig. S5, ESI†). Starting from different initial geometries, the calculated minimum of the PES corresponds to π–π stacking with the BF₄ anion displaying the aforementioned (C–H)⁺⋯anion contact, a binding mode commonly found in the CSD. This geometry (Fig. 7a, inset), with near-planar C2 and C6 phenyl rings, is in agreement with the intermolecular contacts between TMB and pyrylium protons (mainly H3/H5 and H2/H6a) obtained by selective 1D NOESY experiments (Fig. 7a). The calculated binding constant for this association, K_a, was estimated to be 2.91 ± 0.55 M⁻¹. The calculated ΔG for this π⋯π association (−0.63 kcal mol⁻¹) is in agreement with the ΔΔG obtained from DFT calculations (−0.70 kcal mol⁻¹; see ESI,† for more details).

Fig. 7 (a) Selective 1D ¹H NOESY experiment. Protons of TMB were employed for selective excitation (green-labelled in the inset). Protons involved in the interaction are shown. Arrows qualitatively reflect the intensity of NOE. (b) Titration experiments monitoring the BF₄ anion by ¹⁹F NMR.

Finally, monitoring the chemical shift of the BF₄⁻ anion by ¹⁹F-NMR,³¹ we observed an analogous variation in chemical shift for the fluorine-coupled ¹⁰B and ¹¹B isotope signals (Fig. 7b). The theoretical distance of anion⋯TMB in the ternary complex anion-Pyry-π was too large (d = 7.02 Å) to be detected by NMR. Therefore, the observed variations in ¹⁹F chemical shifts also support the proposed structure.

Conclusions

This systematic study highlights the ability of pyrylium frameworks to act as excellent π–hole donors to establish π–π stacking interactions. The pyrylium tetrafluoroborates behave as exacerbated arenes instead of canonical cations. In fact, an excellent correlation between interaction energies and mixed Hammett constants σ_p(XY) was found. In addition, our computational modelling in solution points to the possibility of switching their aromatic (dispersive) or cationic (electrostatic) character depending on dielectric constant (ε_r) values.

The experimental NMR-based results allowed us to propose feasible π–π stacking geometries similar to those found in the crystallographic structures. The additional stabilization of this geometry was also estimated and correlates with those obtained from DFT calculations. Moreover, ¹⁹F NMR data suggest a straightforward arene⋯anion contact through the (C–H)⁺⋯anion arrangement.

Given that this study covers all environments where the applicability of pyrylium complexes is currently significant, the obtained results suggest a bright future for this versatile heterocycle in supramolecular chemistry.

Experimental

Synthesis of 2,4-di-(4-methylphenyl)-4-(4-fluorophenyl)pyrylium tetrafluoroborate (1)

To a solution of 4-fluorobenzaldehyde (432 μL, 4.03 mmol) and 4-methylacetophenone (1.62 mL, 12.09 mmol), BF₃·Et₂O (1.49 mL, 12.09 mmol) was added. The reaction mixture was heated at 80 °C. Monitoring of the reaction (TLC, 4 : 1 Hexane : AcOEt) showed that the reaction was completed after 16 h. The solvent was evaporated and the product was then recrystallized from acetone to obtain compound 1 (523 mg, 29%) as an orange solid (see ESI,† for characterization data).

Binding stoichiometries and NMR titration experiments

The determination of stoichiometry for the interaction of compound 1 with methylated (TMB) and fluorinated (TFB) benzene analogues was carried out using Job's method.³² The aggregation propensity of compound 1 was overcome by changing the concentration of NMR samples. For Job's plot analysis, the concentrations [1·BF₄] + [Arene] were 15 mM (for DMSO-d₆) and 4 mM (for acetone-d₆). Keeping the concentration constant, the molar fraction χ of each component in the mixture was varied from 0 to 1, with increments of 0.1 for each prepared sample. In all cases, the molar fraction χ = 1 was assigned to the solution containing just the host (compound 1).

NMR titrations were carried out in DMSO-d₆ at 300 K. Increasing amounts (ranging from 1–12.5 equivalents) of the appropriate benzene analogue were prepared in different NMR tubes containing a constant concentration [1·BF₄] of 20 mM. The titration isotherms were fitted to a 1 : 1 binding model (Fig. S6, ESI†) using Thordarson's equation³³ as follows.

As Δδ represents the chemical shift difference at each titration point (Δδ = δ − δ_H), δ_max is the difference between the chemical shift of the saturated complex and the chemical shift when only the host is present. [G] is the guest concentration and [H₀] the free host concentration.

Spectra were acquired on a Bruker Avance 500 MHz spectrometer equipped with a 5 mm BBFO broadband probe head incorporating a z-gradient coil. Acetone-d₆ or DMSO-d₆ containing 0.1% TMS was used as the solvent. Spectra were acquired using a high-power 901 pulse of 14.8 ms and a recycle delay of 5 s. The ¹⁹F chemical shifts were referenced indirectly to CCl₃F (Ξ = 94.094011).³⁴

Theoretical methods

Ab initio and DFT calculations. The geometries of complexes used in this study were fully optimized at the MP2(fc)³⁵/def2-TZVP³⁶ level employing the Gaussian 16 package.³⁷ The optimization of complexes 18–81 was carried out by imposing the C_s symmetry point group. The interaction energies, ΔE, were calculated at the same level of theory as the energy difference between the optimized ternary systems and the sum of the optimized pyrylium tetrafluoroborates (Py⁺BF₄⁻) and the different aromatic monomers (ΔE = E_syst − E_PyBF4 − E_Ar). In all cases, these energies take into account the correction for the basis set superposition error (BSSE) by applying the Boys-Bernardi counterpoise technique.³⁸ Most complexes (within 2.10–9.17 geometries) displayed small imaginary frequencies from −4 to −20 cm⁻¹. These frequencies were not taken into consideration since the final goal of this study is to understand the feasible raw geometries of stacking interactions in ternary systems involving pyrylium tetrafluoroborates. The effect of anion⋯π interaction on pyrylium⋯arene contacts was roughly estimated by scanning the F₄B⋯centroid distance of the pyrylium rings (rigid scan) at the MP2/def2-TZVP level. Molecular electrostatic potential (MEP) surfaces were computed at the same level using the 0.001 a.u. isosurface. Diverse contributions (electrostatic, exchange, repulsion, polarization, and dispersion) to the interaction energies were calculated through the localized molecular orbital energy decomposition analysis³⁹ as implemented in Gamess.⁴⁰

The geometries and energies of larger systems, for example, the interactions of compound 1 with different benzene analogues or crystallographic structures, were obtained at the PBE0⁴¹-D3⁴²/def2-TZVP level of theory. The minimal nature of interactions involving this compound was confirmed by frequency analysis calculations. For these compounds, NCIplot isosurfaces⁴³ were computed using cubefiles (high quality grid) generated from the Multiwfn v. 3.8 program.⁴⁴ The color scheme for studying weak non-covalent interactions depends on the value of the reduced density gradient. In general, the colour codes are red (repulsive, ρ⁺_cut), and blue (attractive, ρ⁻_cut), while yellow-green surfaces indicate weak repulsive and weak attractive interactions, respectively.

Molecular dynamic (MD) simulations. The QM-optimized geometry for the pyrylium salt was used as starting coordinates for simulations. These simulations were carried out with the AMBER 20 package⁴⁵ implemented with general Amber force fields (GAFF2).⁴⁶ Pyrylium parameters were generated by the antechamber module of AMBER, using the GAFF2 force field and tetrafluoroborate parameters were also generated (see ESI†). Initial structures were set at the centre of a cubic DMSO⁴⁷ box with a buffering distance between solute and box of 10 Å. For each system, we followed a two-stage geometry optimization approach: the first stage minimizes only the positions of solvent molecules and ions and the second stage is an unrestrained minimization of all the atoms in the simulation cell. The system was then heated by incrementing the temperature from 0 to 100 K under a constant pressure of 1 atm and periodic boundary conditions and then from 100 to 300 K under the same conditions. Harmonic restraints of 10 kcal mol⁻¹ were applied to the solute under the Andersen temperature coupling scheme.^48,49 The time step was kept at 1 fs during the heating stages, allowing potential inhomogeneities to self-adjust. DMSO molecules were treated with the SHAKE algorithm⁵⁰ so that the angle between the hydrogen atoms was kept fixed through the simulations. Long-range electrostatic effects were modelled using the particle mesh Ewald method.⁵¹ An 8 Å cut-off was applied to Lennard-Jones interactions. Each system was equilibrated for 2 ns with a 2 fs time step at a constant volume and temperature of 300 K. The produced trajectory was then run for additional 250 ns.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Agencia Estatal de Investigación (Spain) for financial support (projects RTI2018-094751-B-C21, RTI2018-099592-B-C22 and CTQ2016-78703) and Severo Ochoa Excellence Accreditation SEV-2016-0644. A. F. acknowledge the Spanish Ministerio de Ciencia e Innovación (Spain) for a Juan de la Cierva contract (IJC2019-042061-I).

Notes and references

1. Y. Li, H. Wang and X. Li, Chem. Sci., 2020, 11, 12249.
2. X. Chen, L. Yan, Y. Liu, Y. Yang and J. You, Chem. Commun., 2020, 56, 15080.
3. A. Franconetti, L. Contreras-Bernal, R. Prado-Gotor and F. Cabrera-Escribano, RSC Adv., 2015, 5, 74274.
4. C. H. Basch, J. Liao, J. Xu, J. J. Piane and M. P. Watson, J. Am. Chem. Soc., 2017, 139, 5313.
5. (a) Y. Ma, Y. Pang, S. Chabbra, E. J. Reijerse, A. Schnegg, J. Niski, M. Leutzsch and J. Cornella, Chem. – Eur. J., 2020, 26, 3738; (b) D. Moser, Y. Duan, F. Wang, Y. Ma, M. J. O’Neill and J. Cornella, Angew. Chem., Int. Ed., 2018, 57, 11035.
6. M. A. Miranda and H. Garcia, Chem. Rev., 1994, 94, 1063.
7. P. Lu, V. K. Kensy, R. L. Tritt, D. T. Seidenkranz and A. J. Boydston, Acc. Chem. Res., 2020, 53, 2325.
8. R. Z. Lange, G. Hofer, T. Weber and A. D. Schlüter, J. Am. Chem. Soc., 2017, 139, 2053.
9. R. Z. Lange, K. Synnatschke, H. Qi, N. Huber, G. Hofer, B. Liang, C. Huck, A. Pucci, U. Kaiser, C. Backes and A. D. Schlüter, Angew. Chem., Int. Ed., 2020, 132, 5732.
10. F. Hu, W. Hao, D. Mücke, Q. Pan, Z. Li, H. Qi and Y. Zhao, J. Am. Chem. Soc., 2021, 143, 5636.
11. S. Yamada, Coord. Chem. Rev., 2020, 415, 213301.
12. (a) A. Franconetti, R. Núñez-Franco, G. de Gonzalo, J. Iglesias-Sigüenza, E. Álvarez and F. Cabrera-Escribano, ChemPhysChem, 2018, 19, 327; (b) D. Quiñonero, Molecules, 2015, 20, 11632; (c) A. Franconetti, L. Contreras-Bernal, S. Jatunov, M. Gómez-Guillén, M. Angulo, R. Prado-Gotor and F. Cabrera-Escribano, Phys. Chem. Chem. Phys., 2014, 16, 18442.
13. (a) J. S. Murray, P. Lane, T. Clark, K. E. Riley and P. Politzer, J. Mol. Model., 2012, 18, 541–548; (b) P. Politzer, J. S. Murray and P. Lane, Int. J. Quantum Chem., 2007, 107, 3046–3052; (c) T. Clark, M. Henneman, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296.
14. (a) A. Franconetti and A. Frontera, Chem. – Eur. J., 2019, 25, 6007; (b) A. Bauzá, S. K. Seth and A. Frontera, Coord. Chem. Rev., 2019, 384, 107; (c) A. Frontera and A. Bauzá, Chem. – Eur. J., 2018, 24, 16582; (d) A. Bauzá, T. J. Mooibroek and A. Frontera, Chem. Rec., 2016, 16, 473; (e) A. Bauzá, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2013, 52, 12317; (f) J. S. Murray, P. Lane and P. Politzer, J. Mol. Model., 2009, 15, 723–729.
15. (a) A. Bauzá and A. Frontera, ChemPhysChem, 2020, 21, 26; (b) A. Franconetti, D. Quiñonero, A. Frontera and G. Resnati, Phys. Chem. Chem. Phys., 2019, 21, 11313; (c) R. Shukla and D. Chopra, Phys. Chem. Chem. Phys., 2016, 18, 13820; (d) S. P. Thomas, K. Satheeshkumar, G. Mugesh and T. N. Guru Row, Chem. – Eur. J., 2015, 21, 6793; (e) J. S. Murray, P. Lane and P. Politzer, Int. J. Quantum Chem., 2008, 108, 2770; (f) J. S. Murray, P. Lane, T. Clark and P. Politzer, J. Mol. Model., 2007, 13, 1033–1038.
16. (a) M. N. Piña, A. Frontera and A. Bauzá, J. Phys. Chem. Lett., 2020, 11, 8259; (b) J. H. Stenlid, A. J. Johansson and T. Brinck, Phys. Chem. Chem. Phys., 2018, 20, 2676; (c) A. Frontera and A. Bauzá, Chem. – Eur. J., 2018, 24, 7228; (d) J. H. Stenlid and T. Brinck, J. Am. Chem. Soc., 2017, 139, 11012.
17. (a) R. M. Gomila, A. Bauzá, T. J. Mooibroek and A. Frontera, CrystEngComm, 2021, 23, 3084; (b) A. Buzá, I. Alkorta, J. Elguero, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2020, 59, 17482; (c) I. Alkorta, J. Elguero and A. Frontera, Crystals, 2020, 10, 180.
18. M. K. Corpinot and D.-K. Bučar, Cryst. Growth Des., 2018, 18, 6404.
19. (a) S. Yamada, N. Yamamoto and E. Takamori, J. Org. Chem., 2016, 81, 11819; (b) S. Yamada, N. Yamamoto and E. Takamori, Org. Lett., 2015, 17, 4862.
20. R. A. Wiscons, M. Zeller and J. C. Rowsell, Cryst. Growth Des., 2016, 16, 2201.
21. (a) F. Pecatti, J. Chem. Inf. Model., 2020, 60, 6; (b) J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625.
22. (a) A. Bauzá, A. Frontera and T. J. Mooibroek, Chem. – Eur. J., 2019, 25, 13436; (b) A. Franconetti, A. Frontera and T. J. Mooibroek, CrystEngComm, 2019, 21, 5410; (c) A. Bauzá, T. J. Mooibroek and A. Frontera, Chem. Commun., 2015, 51, 149.
23. C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165.
24. A. Franconetti and A. Frontera, Dalton Trans., 2019, 48, 11208.
25. (a) F. Würthner, J. Org. Chem., 2021 DOI:10.1021/acs.joc.1c00625; (b) M. D. Driver, M. J. Williamson, J. L. Cook and C. A. Hunter, Chem. Sci., 2020, 11, 4456.
26. (a) L. Montalvillo-Jiménez, A. G. Santana, F. Corzana, G. Jiménez-Osés, J. Jiménez-Barbero, A. M. Gómez and J. L. Asensio, J. Am. Chem. Soc., 2019, 141, 13372; (b) L. Yang, J. B. Brazier, T. A. Hubbard, D. M. Rogers and S. L. Cockrift, Angew. Chem., Int. Ed., 2016, 55, 912; (c) E. Jiménez-Moreno, A. M. Gómez, A. Bastida, F. Corzana, G. Jiménez-Oses, J. Jiménez-Barbero and J. L. Asensio, Angew. Chem., Int. Ed., 2015, 54, 4344; (d) E. Jiménez-Moreno, G. Jiménez-Osés, A. M. Gómez, A. G. Santana, F. Corzana, A. Bastida, J. Jiménez-Barbero and J. L. Asensio, Chem. Sci., 2015, 6, 6076.
27. Y. Liu, A. Sengupta, K. Raghavachari and A. H. Flood, Chem, 2017, 3, 411.
28. D. B. Hibbert and P. Thordarson, Chem. Commun., 2016, 52, 12792.
29. (a) G. Platzer, M. Mayer, A. Beier, S. Brüschweiler, J. E. Fuchs, H. Engelhardt, L. Geist, G. Bader, J. Schörghuber, R. Lichtenecker, B. Wolkerstorfer, D. Kessler, D. B. McConnell and R. Konrat, Angew. Chem., Int. Ed., 2020, 132, 14971; (b) A. Gimeno, S. Delgado, P. Valverde, S. Bertuzzi, M. A. Berbís, J. Echavarren, A. Lacetera, S. Martín-Santamaría, A. Surolia, F. J. Cañada, J. Jiménez-Barbero and A. Ardá, Angew. Chem., Int. Ed., 2019, 58, 7268.
30. The references provided at ref. 28 are examples on CH/π interactions on inside a protein binding pocked. However, they are suitable to understand the behaviour of acidic protons participating in non-covalent contacts.
31. (a) J. D. Martínez, A. I. Manzano, E. Calviño, A. de Diego, B. Rodriguez de Francisco, C. Romanò, S. Oscarson, O. Millet, H.-J. Gabius, J. Jiménez-Barbero and F. J. Cañada, J. Org. Chem., 2020, 85, 16072; (b) J. D. Martínez, A. S. Infantino, P. Valverde, T. Diercks, S. Delgado, N.-C. Reichardt, A. Ardá, F. J. Cañada, S. Oscarson and J. Jiménez-Barbero, Pharmaceuticals, 2020, 13, 179.
32. (a) J. S. Renny, L. L. Tomasevich, E. H. Tallmadge and D. B. Collum, Angew. Chem., Int. Ed., 2013, 52, 11998; (b) K. Hirose, J. Inclusion Phenom. Macrocyclic Chem., 2001, 39, 193; (c) P. Job, Ann. Chim., 1928, 9, 113.
33. P. Thordarson, Chem. Soc. Rev., 2011, 40, 1305.
34. (a) R. K. Harris, E. D. Becker, S. M. Cabral de Menezes, R. Goodfellow, P. Granger, R. E. Hoffman and K. W. Zilm, Pure Appl. Chem., 2008, 80, 59; (b) R. K. Harris, E. D. Becker, S. M. Cabral de Menezes, R. Goodfellow and P. Granger, Pure Appl. Chem., 2001, 73, 1795.
35. M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 275.
36. (a) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297; (b) F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057.
37. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
38. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
39. P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102.
40. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery Jr, J. Comput. Chem., 1993, 14, 1347.
41. (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865; (b) J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982.
42. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
43. (a) J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625; (b) E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498.
44. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580.
45. D. A. Case, K. Belfon, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, III, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz, R. Harris, S. Izadi, S. A. Izmailov, K. Kasavajhala, A. Kovalenko, R. Krasny, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, V. Man, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, A. Onufriev, F. Pan, S. Pantano, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, L. Wilson, R. M. Wolf, X. Wu, Y. Xiong, Y. Xue, D. M. York and P. A. Kollman, 2020, AMBER 2020, University of California, San Francisco.
46. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157.
47. T. Fox and P. A. Kollman, J. Phys. Chem. B, 1998, 102, 8070.
48. H. C. Andersen, J. Chem. Phys., 1980, 72, 2384.
49. T. A. Andrea, W. C. Swope and H. C. Andersen, J. Chem. Phys., 1983, 79, 4576.
50. S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952.
51. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089.

---

Footnote

† Electronic supplementary information (ESI) available: Additional figures and tables, experimental data and Cartesian coordinates. See DOI: 10.1039/d1cp02622d

---