Optical and magnetic characterization of one-dimensional Cu(II)-based perovskite: a high UV–Vis–NIR absorber†
Wiem
Jabeur
a,
Rawia
Msalmi
a,
Marcus
Korb
b,
Mariia
Holub
 c,
Edoardo
Mosconi
d,
Erik
Čižmár
c,
Edoardo
Mosconi
d,
Erik
Čižmár
 c,
Anowar
Tozri
e,
Numa A.
Althubiti
*e and
Houcine
Naïli
c,
Anowar
Tozri
e,
Numa A.
Althubiti
*e and
Houcine
Naïli
 *a
*a
aLaboratory Physico Chemistry of the Solid State, Department of Chemistry, Faculty of Sciences of Sfax, Sfax University, Tunisia. E-mail: houcine_naili@yahoo.com
bThe University of Western Australia, Faculty of Sciences, School of Molecular Sciences, 35 Stirling Highway, Crawley, Perth, Western Australia 6009, Australia
cP.J. Šafárik University in Košice, Faculty of Sciences, Institute of Physics, Park Angelinum 9, SK-041 54 Košice, Slovakia
dComputational Laboratory for Hybrid/Organic Photovoltaics (CLHYO), Istituto CNR di Scienze e Tecnologie Chimiche “Giulio Natta” (CNR-SCITEC), Via Elce di Sotto 8, 06123 Perugia, Italy
ePhysics Department, College of Science, Jouf University, Sakaka 2014, Saudi Arabia. E-mail: naalthubiti@ju.edu.sa
First published on 17th November 2021
Abstract
A one dimensional copper(II)-based perovskite, (C5H8N3)[CuCl3], was successfully synthesized. XR-diffraction demonstrates that the mineral framework of this perovskite is formed by infinite needle-like chains [CuCl3]−∝, where each Cu2+ ion, with its [4+2] coordination sphere, adopts a nearly tetragonal symmetry. The simultaneous TGA/DSC analyses demonstrate the stability of the material at ambient temperature and up to 130 °C. The convergence of the optical experimental results and the theoretical DFT calculations of the electronic structure demonstrates the semiconducting character of the synthesized compound with an experimental direct band gap energy of 2.21 eV. The optical analysis shows that a cooperative Jahn–Teller effect is manifested around the copper ions. Both ligand to metal charge transfer (LMCT) transitions and crystal field transitions (d–d) make the material suitable for green solar cell applications. The magnetic properties of (C5H8N3)[CuCl3] can be described by a model of S = 1/2 antiferromagnetic dimers with exchange interaction J/kB = −122.7 K.
Introduction
Since 2009, three dimensional (3D) lead halide perovskites that are derived from the parent structure ABX3 (with A = CH3NH3 or HC(NH2)2; B = Pb and X = Br, Cl, or I) have attracted significant attention in the photovoltaic (PV) solar cell (SC) community1,2 In particular, CH3NH3PbI3 and CH3NH3PbBr3 result in high performance in SCs due to their simplicity of deposition and semiconducting properties with high electron–photon conversion efficiency (EPCE) reaching 3.8% for CH3NH3PbI3.1 Unfortunately, the application of Pb-based perovskites in SCs suffers from the limitation of their commercialization because of the use of the environmentally, as well as health, hazardous lead.3 In addition, lead halide perovskites are thermally unstable and have shown high degradation under real-world conditions; they must be protected from oxygen and moisture.4,5 Nowadays, the increasing exigency in the environmentally friendly energy conversion devices has led to the advancement of lead-free perovskite SCs. Theoretical studies on the electronic properties of Pb-based perovskites have shown that their electronic structure and the existence of the dormant 6s orbitals are accountable for the PV performance. So, an effective strategy to achieve non-hazardous SC devices is the substitution of the Pb ions by other cations that comprise the dormant s orbitals, such as Ge2+, Sn2+, Bi3+, and Cu2+.6–9 Despite their promising EPCE of 13%,8 comparable to Pb-based SCs, the Sn-based devices exhibit instability because of their oxidation and ambient hydrolysis.10 Due to their smaller atomic radius than that of Pb, the application of transition metals to substitute Pb led towards the stabilization of two-dimensional hybrid perovskites (RNH3)2MX4.11,12 This reduction of the dimensionality from 3D to 2D generates major changes in the optical, magnetic and dielectric properties due to the multi-quantum electronic structure of 2D perovskites.13 A typical two dimensional perovskite exhibits a value of excitonic binding energy up to 300 meV and its large band gaps make it suitable for light emitting devices.14 In the last years, Cu-based low dimensional perovskites have been extensively studied due to their high piezoelectric as well as ferro/antiferromagnetic responses.15–17 Recently, Cu-based 2D perovskites have demonstrated their performance as alternative to Pb-based absorbers in SCs. In 2016, D. Cortecchia et al. studied the optoelectronic properties of a series of MA2CuClxBr4−x layered perovskites, which are characterized with gap energies ranging 2.8 and 3.1 eV, and proved their performance for green SC applications with a low power conversion efficiency (PCE) reaching only 0.017% with MA2CuCl4.9 This very low efficiency was related to the low absorption coefficient in the visible region, and authors revealed that the integration of aromatic organic cations with transition metals in the low dimensional perovskites will improve their PV performance compared to MA2CuClxBr4−x. This prediction is proved by the reported C6H4NH2CuBr2I which exhibits a PCE of 0.5%.18 In a report by Cui et al. a PV device based on (p-F-C6H5C2H4NH3)2CuBr4 perovskite, with band gap energy of 1.74 eV, revealed a PCE of 0.51%.19 Moreover, low-dimensional Cu-based metal halides have recently attracted great attention due to their excellent good stability under ambient conditions.20–22 The two-dimensional layered (C6H5CH2NH3)2CuBr4 perovskite, investigated for SC application with a PCE of 2.0%, is humidity-stable, heat-stable, and ultraviolet (UV) light-stable.23 Recently, K. Ahmad and S. M. Mobin have employed high water-stable (Cu)-based perovskites (C6H4NH2CuBr2I and C6H4NH2CuCl2I) as light absorbers for the development of Pb-free PSCs.24 Most two dimensional Cu-based perovskites showed a green emission band around 500 nm. A. Elseman et al. developed (CH3NH3)2CuX4-based perovskite SCs and indicated that (CH3NH3)2CuCl4 presents photoluminescent properties.25 Then, R. Valiente and F. Rodriguez have commented this work and demonstrated that this material does not show any photoluminescence under UV-excitation and that this is extended to all others copper(II) based 2D perovskites previously studied.26 In fact, the d–d transitions improve visible light absorption and enhance PCE.9,26 Hence, the use of Cu(II) blocks the photoluminescence mechanism, thanks to the d–d electronic transitions within the Cu2+ cation. Recently, a 1D Cu-based perovskite (C5H14N2)[CuCl4], characterized with an energy gap of 2.56 eV, has been developed by our group as a light absorber material for SC applications.27 In the present work, a novel low dimensional lead free perovskite, (C5H8N3)[CuCl3], is synthesized for green SC applications.Experimental section
Materials
Given the importance of obtaining high quality crystals, all the employed chemicals and reagents were received from commercial sources (Sigma-Aldrich). CuCl2·2H2O (99.999%) and C5H7N3 (97%) were used without further purification. Hydrochloric acid (HCl) and distilled water were introduced into this synthesis.Synthesis
(C5H8N3)[CuCl3] was prepared via slow evaporation technique at room temperature. 0.2 mg of 2-Amino-4-methylpyrimidine was dissolved in 5 ml of distilled water; hydrochloric acid (HCl) (pH ≈ 2.5) was added drop by drop to the solution and stirred with 5 ml of solution containing 0.17 mg of CuCl2·2H2O until the solution became clear. The mixture was stirred for 30 minutes using a magnetic stirrer and slowly evaporated at room temperature. Green single crystals, with suitable dimensions for crystallographic study, were collected after a few days. The microscope image in Fig. 1(a) shows the morphology of the crystals.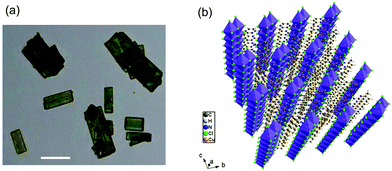 | ||
| Fig. 1 (a) Microscopy image of the microcrystals (scale bar, 25 μm) and (b) perspective view of the structure of (C5H8N3)[CuCl3]. | ||
Instruments
The FT-IR spectrum was obtained using a PerkinElmer 1600FT spectrometer with frequency in the range of 500 and 4000 cm−1 by producing on a pressed pellet of the powdered sample dispersed in KBr at room temperature. The UV–Vis–NIR diffuse reflectance spectrum was recorded at room temperature using a Varian Carry 5000 spectrophotometer. TGA–DSC measurements (10.416 mg sample) were performed using a Mettler Toledo TGA/DSC1 1100 system with a UMX1 balance, in a hermetically sealed capsule under thermal recording conditions at a heating rate of 10 K min−1 between 40 °C and 800 °C, and an argon flow of 20 ml min−1. The magnetic properties were measured using a Quantum Design MPM3 magnetometer on a nascent polycrystalline sample held in a gelatin capsule. The diamagnetic contribution of the capsule, core diamagnetism estimated using Pascal's constants, and typical temperature-independent paramagnetism were subtracted from the measured data.X-ray diffraction analysis
Data of (C5H8N3)[CuCl3] were collected using an Oxford Gemini S diffractometer with Mo Kα radiation (λ = 0.71073 Å) at 125 K. The molecular structure was solved by direct methods using SHELXS-1328 and refined by full-matrix least-squares procedures on F2 using SHELXL-13.29 A summary of the important crystallographic data, data collection and refinement details is presented in Table S1 (ESI†). Two main domains were present in the used crystal and hence, two-component twin integration was carried out resulting in a BASF of 0.5967. All non-hydrogen atoms were refined anisotropically. Hydrogen atoms were placed in calculated positions and constrained to ride on their parent atoms with Uiso(H) = 1.2 Ueq(C) and a X–H distance of 0.93 Å for aromatic (X = C, N), Uiso(H) = 1.5 Ueq(C) and a C–H distance of 0.96 Å for methyl, and Uiso(H) = 1.2 Ueq(C) and a N–H distance of 0.86 Å for the NH2–H atoms. The latter was treated as a terminal CH2 group in order to reduce the number of parameters in the non-centrosymmetric space group.Computational details
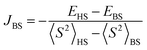 from single-point approach (using the X-ray determined structure), with a spin Hamiltonian in the form Ĥ = −2JBSŜ1Ŝ2. Relativistic effects were taken into account by using the zeroth-order regular approximation (ZORA)37,38 together with the corresponding segmented all-electron relativistic contracted (SARC) version of the triple-ζ basis set Def2-TZVP39,40 for all atoms. All calculations utilized the RI approximation, and the chain-of-spheres (RIJCOSX) approximation to exact exchange41 with appropriate decontracted auxiliary basis sets SARC/J and Def2-TZVP/C.42,43 Integration grid DefGrid2 and tight SCF convergence criteria were used.
from single-point approach (using the X-ray determined structure), with a spin Hamiltonian in the form Ĥ = −2JBSŜ1Ŝ2. Relativistic effects were taken into account by using the zeroth-order regular approximation (ZORA)37,38 together with the corresponding segmented all-electron relativistic contracted (SARC) version of the triple-ζ basis set Def2-TZVP39,40 for all atoms. All calculations utilized the RI approximation, and the chain-of-spheres (RIJCOSX) approximation to exact exchange41 with appropriate decontracted auxiliary basis sets SARC/J and Def2-TZVP/C.42,43 Integration grid DefGrid2 and tight SCF convergence criteria were used.
Results
Description of the crystal structure
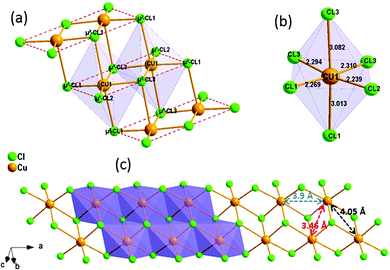
(C5H8N3)[CuCl3] crystallizes in the centrosymmetric space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) of the triclinic system with Z = 2. All the measurement conditions and crystallographic parameters are collated in Table S1 (ESI†). The asymmetric unit consists of one CuCl3 inorganic fragment and one organic cation [C5H8N3]+. The molecular crystal visualization, in Fig. 1(b), shows that the structure is formed with infinite polymeric inorganic fragments extended along the [100] direction. These inorganic chains are separated by the organic protonated molecules. As described in Fig. 2(a), the inorganic part of this structure is formed with parallel slipped stacks of an edge-shared bis(square planar) cluster [Cu2Cl6]. Therein, the copper ions interact with the Cl1 atom of the above and the Cl3 atom of the below-positioned layers. Hence, the copper(II) coordination is transformed from the square planar to the [4+2] coordination sphere where the Cu2+ ions adopt a nearly tetragonal symmetry. The Cu2+ anion is surrounded by one terminal chlorine μ1–Cl2, two doubly bridging μ2–Cl1 and three triply bridging μ3–Cl3 (see Fig. 2(a and b)). The four equatorial Cu–Cl bonds have the values 2.269(2), 2.239(2), 2.294(2) and 2.310(2) Å while the two axial distances are 3.013 and 3.082 Å. The distortion index (Δ) of the [CuCl6]2− octahedron was calculated using eqn (1) and found to be 2.06 × 10−2, being too close to that of (C5H14N2)[CuCl4], which indicates that the hexa-chlorocuperate(II) octahedra are highly distorted and that the Jahn Teller effect is arising around the copper ions.
of the triclinic system with Z = 2. All the measurement conditions and crystallographic parameters are collated in Table S1 (ESI†). The asymmetric unit consists of one CuCl3 inorganic fragment and one organic cation [C5H8N3]+. The molecular crystal visualization, in Fig. 1(b), shows that the structure is formed with infinite polymeric inorganic fragments extended along the [100] direction. These inorganic chains are separated by the organic protonated molecules. As described in Fig. 2(a), the inorganic part of this structure is formed with parallel slipped stacks of an edge-shared bis(square planar) cluster [Cu2Cl6]. Therein, the copper ions interact with the Cl1 atom of the above and the Cl3 atom of the below-positioned layers. Hence, the copper(II) coordination is transformed from the square planar to the [4+2] coordination sphere where the Cu2+ ions adopt a nearly tetragonal symmetry. The Cu2+ anion is surrounded by one terminal chlorine μ1–Cl2, two doubly bridging μ2–Cl1 and three triply bridging μ3–Cl3 (see Fig. 2(a and b)). The four equatorial Cu–Cl bonds have the values 2.269(2), 2.239(2), 2.294(2) and 2.310(2) Å while the two axial distances are 3.013 and 3.082 Å. The distortion index (Δ) of the [CuCl6]2− octahedron was calculated using eqn (1) and found to be 2.06 × 10−2, being too close to that of (C5H14N2)[CuCl4], which indicates that the hexa-chlorocuperate(II) octahedra are highly distorted and that the Jahn Teller effect is arising around the copper ions.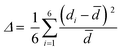 | (1) |
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) is the average value of the Cu–Cl distances and di are the six Cu–Cl distances.
is the average value of the Cu–Cl distances and di are the six Cu–Cl distances.
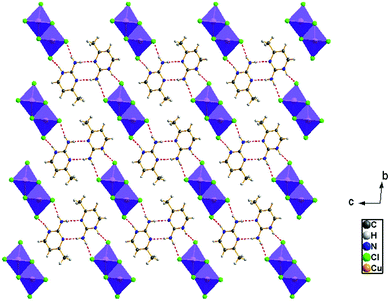
The view of the inorganic part in Fig. 2(c) shows that the mineral polymeric fragment is formed by two infinite strings along the a-axis. Each string is formed with two opposed edges shared CuCl6 octahedra. These strings are condensed together through three μ3–Cl ions in a way that each octahedron shares four edges with four neighboring octahedra to form an infinite needle-like chain [CuCl3]−∝. The shortest intra-chain Cu–Cu distance is 3.460 (2) Å, while the two other contacts are about 3.9 and 4.05 Å. The geometric data of the inorganic fragment are tabulated in Table S2 (ESI†). 2-Amino-4-methylpyrimidinium is observed in its N1-protonated form. The C–C and C–N bond lengths do not allow for a distinction between single and double bond and range within 1.325(11) and 1.397(12) Å. These values are similar to reported structures, e.g. [C5H8N3]2ClSbCl4·H2O and C5H8N3H2PO4.44,45 The short distance of 1.299(11) Å for the C1–N3 bond confirms the sp2 hybridization of the exocyclic N3 nitrogen atom. The reduced basicity of the N3 nitrogen might favor the protonation at N1, similar to the compounds reported in the literature.46–49 Within the organic network, two pyrimidinium ions interact with each other via hydrogen bonds between N3–H3NA and N3 with a H3NA⋯N3 distance of 2.16 Å. The organic cations are linked to the inorganic polymeric fragments via the H⋯Cl bonds to lead to a linear hydrogen bond network extending along [–211] (Fig. 3). The geometric parameters of the hydrogen bonds are collated in Table S3 (ESI†). The (C5H8N3)[CuCl3] structure is considered as a 1D copper(II)-based perovskite.
Infrared spectroscopy
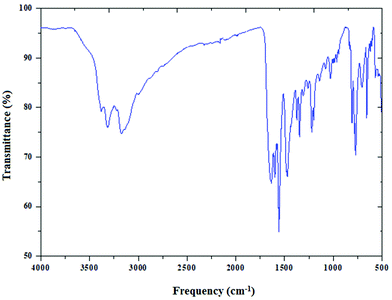
The infrared spectrum of (C5H8N3)[CuCl3] is based on the comparison with those of similar compounds reported in the literature, that contain the (C5H8N3)+ cation.44Fig. 4 reports the presence of different bands cited below.Two important bands at 3310 and 3400 cm−1 are attributed to the NH+ vibrations due to the protonation of the amine. The moderately intense bands appearing at 3175 and 3092 cm−1 correspond to the νC–H stretching vibration of the 2-amino-4-methyl pyrimidine group. In addition, the band corresponding to the δas of (CH3) is found at 3002 cm−1. The asymmetric (νas) and the symmetric (νs) stretching vibrations of the NH2 group appear at 1563 cm−1 and 1640 cm−1, respectively. The vibration of the double bond (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) appears as two lines at 1450 and 1600 cm−1. The peak at 1463 cm−1 is assigned to νC–H. Also the two peaks around 1343 cm−1 and 1222 cm−1 are attributed to the C–N stretching vibration. Besides, the Off-plane deformation is displayed at 770 cm−1. Eventually, the peak centered at 682 cm−1 is relative to the stirring of NH2.
C) appears as two lines at 1450 and 1600 cm−1. The peak at 1463 cm−1 is assigned to νC–H. Also the two peaks around 1343 cm−1 and 1222 cm−1 are attributed to the C–N stretching vibration. Besides, the Off-plane deformation is displayed at 770 cm−1. Eventually, the peak centered at 682 cm−1 is relative to the stirring of NH2.
Thermal analysis
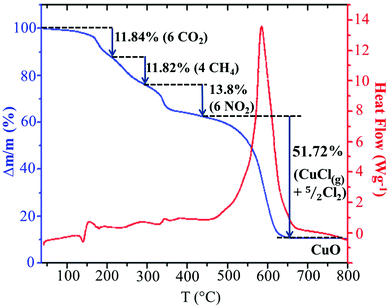
In order to analyze the thermal stability of the synthesized compound, simultaneous TGA–DSC measurements were carried out (Fig. 5). To simplify the description of the degradation mechanism, we have chosen to discuss the decomposition of a cluster, (C5H8N3)2[Cu2Cl6], containing two organic cations and an inorganic Cu2Cl6 dimer. The Fig. 5 shows that the total degradation of the title compound occurs in two stages. The first one is observed between 150 and 449 °C and corresponds to the departure of two organic cations. The second stage of weight loss observed between 450 and 650 results from the decomposition of the mineral moieties. As we can see in the TGA curve, the decomposition of the organic moieties occurs in three steps. As the degradation analysis is performed under O2 atmosphere, they can be attributed to the oxidation of organic matter and the gaseous products that arise during thermal decomposition. The obtained theoretical values suggest the departure of the carbon atoms in two different steps. The first step can be assigned to the oxidation of three carbons from the ring with the elimination of CO2 with mass loss of 11.84% (theor. 12.86%). The weight loss of 11.82% corresponds to the departure of the two remaining carbon atoms as CH4 gas (theor. 11.46%). The nitrogen atoms are probably oxidized into NO2 gas with weight loss of 13.8% (theor. 15%). During the second stage of the degradation, the inorganic fragment Cu2Cl6 is probably transformed into 2CuCl2 after the departure of one Cl2. As observed in the decomposition mechanism of CuCl2 solid under inert atmosphere,50 the CuCl2(s) decompose into CuCl(s) at 455.5 °C with the departure of 1/2 Cl2 and the obtained CuCl(s) melt at the same temperature. Then, a part of the CuCl(liq) evaporate at 488.5 °C. The comparison of this mechanism with the experimental results suggests that the decomposition of the inorganic network is done according to the same mechanism up to the evaporation of a part of CuCl(l). As the analysis is done under O2 atmosphere, 10.76% of the final decomposition product is the corresponding metal oxide CuO (theor. 11.3%) obtained after the oxidation of the remaining CuCl(l) and the elimination of 1/2 Cl2. Hence, the second decomposition stage accompanied by a weight loss of 51.72% is associated with the departure of CuCl(g) and 5/2 Cl2 gases (theor. 49.34%). This decomposition process is accompanied by a large endothermic peak on the DSC curve at about 586 °C.Optical properties
| F(R) = (1 − R)2/2R | (2) |
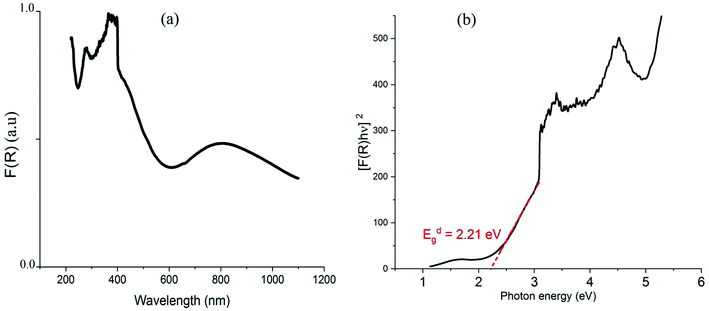
Using the Tauc plot, the direct fundamental band gap, which corresponds to electron excitation from the valence band to the conduction band, was determined from the following relation:54
| [FKM(R) × hν] = A0(hν – Eg)n |
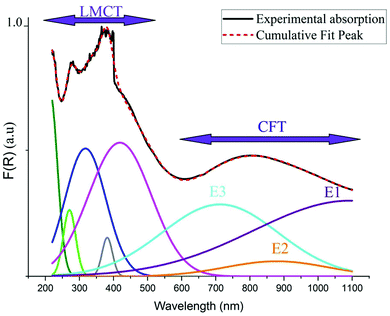
As indicated in previously reported Cu-based materials,9,55,56 the most energetic band corresponds to ligand to metal charge transfers (LMCT) from the p-orbitals of the Cl− anions to the d-orbitals of the Cu2+ cations. The Gaussian fitting of the OA spectrum, plotted in Fig. 7, shows that the material exhibits five LMCT transitions. The lowest energetic band observed at 803 nm results from the crystal field transitions (CFT) within the Cu(II) ions.57 The shift of these transitions to low energy regions confirms the housing of the copper anions within octahedral elongated sites with a tetragonal symmetry D4h.56 This local deformation is the result of the high Jahn Teller effect around the d(Cu)-orbitals. Fig. 7 shows that this broad-band overlaps three d–d transition bands E1, E2 and E3 from the a1g, b2g and eg orbitals to the highest energetic level b1g, respectively.9,56 These bands are very intense, when compared to those of the one-dimensional (C5H14N2)[CuCl4],27 so that they overlap with the LMCT bands which make the material an excellent UV–Vis–NIR absorber and suitable for use in SC photovoltaic devices. With reference to (C5H14N2)[CuCl4], we list in Table 1 the assignments of the peaks observed below 550 nm to their corresponding LMCT transitions.
| Assignment | Observed transition in (C5H8N3)[CuCl3] | Transition in (C5H14N2)[CuCl4] |
|---|---|---|
| a 2u (π + σ) → b1g (x2–y2) | 448 | 418 |
| e u (π + σ) → b1g (x2–y2) | 406 | 381 |
| b 2u (π) → b1g (x2–y2) | 349 | 317 |
| e u (π + σ) → b1g (x2–y2) | 288 | 270 |
| e u (σ + π) → b1g (x2–y2) | 249 | — |
| a 2u (σ + π) → b1g (x2–y2) | — | 213 |
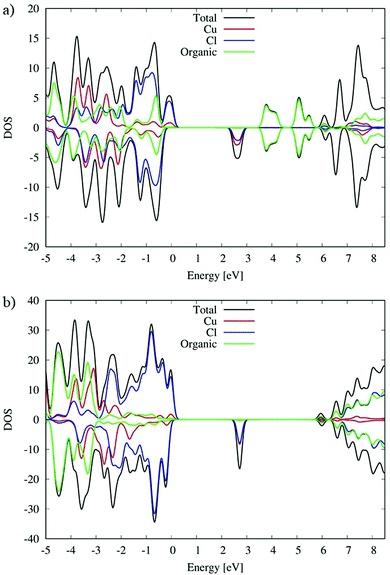
As we can see from the DOSs in Fig. 8, the calculated HOMOα–LUMOβ band gap of (C5H8N3)[CuCl3] is 2.5 eV and it is 0.2 eV lower than the previous simulated band gap of (C5H14N2)[CuCl4] (2.7 eV).27 Both calculated values slightly overestimate the experimental measurements (2.21 and 2.56 eV,27 respectively) but calculation accurately reproduces the relative difference.
The VB and CB nature of the two different species are similar, and in particular, the main contribution to the VB is associated with the Cl species mixed with a Cu contribution while the first unoccupied band is mainly associated with Cu with a lower Cl contribution.
However, the contribution of the organic molecules is different. For the (C5H14N2)[CuCl4] species the organic molecules in green, see Fig. 8(b), show the intense signal of their HOMOα 3 eV below the VB edge and the signal of their LUMOβ 6 eV above the VB edge of the systems. This is expected due to the aliphatic nature of the organic cation. Moving to the (C5H8N3)[CuCl3] species, the conjugated character of the organic molecules induces a different alignment between the inorganic and organic material partial density of states (PDOS) contributions. In particular, in that case (Fig. 8(a)) the organic contribution to the VB in green is close to the edges lying only 0.5 eV below. A similar situation is retrieved for the CB, where the organic contribution is 1.1 eV above the CB edge. This role of the organic cation implies a higher electronic coupling between the organic and inorganic frameworks of (C5H8N3)[CuCl3] with respect to (C5H14N2)[CuCl4] that could in principle increase the electronic transport, charge transfer and charge hopping upon photo-excitation, as already proposed in our previous papers.58
Magnetic properties
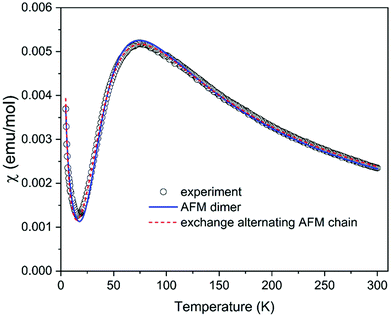
The magnetic properties of (C5H8N3)[CuCl3] are governed by the magneto-structural correlations within polymeric chains formed by [Cu2Cl6] units along the a-axis, separated by the 2-amino-4-methylpyrimidinium cations, and this structural motive resembles a frustrated spin ladder. The six chlorine atoms in the structure octahedrally coordinate each Cu2+ ion. The Jahn–Teller effect leads to the elongation of the octahedron, as shown in Fig. 2(b). In this case, the single unpaired electron resides in the dx2–y2 orbital with its lobes oriented in the equatorial plane of the elongated bipyramid. This configuration leads to an effective overlap of the dx2–y2 orbitals between the two closest Cu2+ ions with 3.46 Å separation shown in Fig. 2, and a strong exchange interaction is expected between them (dimers forming ladder rungs). On the other hand, the interaction between these copper dimers is expected to be weak along the a-axis. The exchange interactions can also be evaluated using the results of Hatfield and Hodgson et al.,59 who studied a series of bichloride bridged Cu2+ dimers. The ratio of the bridging Cu–Cl–Cu angle and the longer Cu–Cl distance Φ/R correlate structural features with the expected exchange interactions. Indeed, the parameter Φ/R = 42.18 Å−1 corresponding to a strong antiferromagnetic (AFM) exchange interaction of about −144 K is found for a Cu2+ pair on the rungs. For a pair of Cu2+ ions along the legs of the ladder (separated by a distance of 3.9 Å), the parameter Φ/R = 31.4 Å−1 and negligible exchange interaction are expected. Two possible values of Φ/R, 31.3 Å−1 and 29.7 Å−1, can be estimated for a pair of Cu2+ ions separated by the distance of 4.5 Å (Fig. 2(c)) suggesting the presence of a negligible or a weak AFM interaction of about −10 K.In addition, we have performed a simple BS DFT calculation using the ORCA package with the B3LYP exchange–correlation functional to estimate possible exchange interactions. A fragment of the ladder structure was selected; non-magnetic Zn2+ ions replaced all Cu2+ ions except for two selected Cu2+ ions in the center of the fragment representing a pair for the BS DFT calculation. For the rung exchange interaction a fragment of 3 rungs and for the leg and frustrating exchange interaction a fragment of 4 rungs were selected as shown in Fig. S2 (ESI†). The results are summarized together with magneto-structural correlations in Table 2. The results clearly indicate strong AFM dimers on the rungs of the ladder structure. At the same time, other interactions seem to be negligible, spanning the range of small AFM or ferromagnetic (FM) values.
The analysis of magneto-structural correlation and BS DFT calculations thus indicates that (C5H8N3)[CuCl3] can be described as a system of weakly interacting S = 1/2 AFM dimers or an exchange alternating S = 1/2 AFM chain (or, in other terms, dimerized AFM chain). The temperature dependence of the susceptibility measured in the temperature range of 4.2–300 K shown in Fig. 9 is characterized by a maximum at T = 76 K compatible with the proposed AFM models. A Curie-like tail at the lowest temperatures most probably originates from intrinsic impurities often observed in dimerized AFM systems as a signature of the fragmentation. The experimental data were first analyzed using a simple model of S = 1/2 AFM dimers described by the well-known Bleaney–Bowers formula,60 including a Curie contribution in the form χ = (1 − 2ρ)χdimer + ρχCurie, where ρ represents the concentration of paramagnetic spins. The spin dimer model is described by the Hamiltonian in the form Ĥdimer = −JŜ1Ŝ2. The fit yielded the exchange interaction within dimer J/kB = −122.7 K, g-factor g = 2.11, and ρ = 0.04 in a good agreement with the values suggested from magneto-structural correlations. To fit the susceptibility using high-temperature series expansion (HTSE) formulas for an AFM spin ladder61,62 or exchange alternating AFM chain63 might be tricky for the present data, since HTSE works well only at temperatures kBT/J > 0.25. Since the model of exchange alternating AFM chain is more appropriate here, as suggested from the previous discussion, we tried to use the HTSE formula proposed by Hatfield,63 including Curie contribution in the form χ = (1–2ρ)χalterchain + ρχCurie. The fit yields J/kB = −125.2 K, alternation parameter α = 0.265, g = 2.18, and ρ = 0.043 with the curve almost indistinguishable from the spin dimer model. The alternation parameter may be overestimated in this case due to the lower accuracy of the model at low temperatures. Our attempt to fit the spin ladder model with Jrung = J and Jleg resulting from the studies of Gu et al.64 and Landee65 (valid for Jleg/Jrung < 0.1) indeed yields negligible Jleg = 0 with Jrung/kB = −122.7 K, g = 2.11, and ρ = 0.04 identical to the simple S = 1/2 AFM dimer model. In summary, despite the ladder-like arrangement of the Cu2+ ions, the magnetic properties of (C5H8N3)[CuCl3] are best described by the model of S = 1/2 AFM dimers with J/kB = −122.7 K.
Conclusion
In summary, a 1D lead-free hybrid perovskite based on copper (C5H8N3)[CuCl3] was successfully fabricated. Optical characterization studies show that, due to the Jahn Teller effect, the CFT improve the absorption behaviors of the material in the visible region. The theoretical DFT calculation of the electronic structure demonstrates that the use of a conjugated cation enhances the electronic transport, the charge transfer and charge hopping upon photo-excitation. The good agreement between the experimental and the theoretical results reveals the semiconducting properties of the material with a fundamental energy gap of 2.21 eV. Therefore, thanks to the intense LMCT transitions and CFT, in the presence of aromatic organic rings, this new material can be suitable for green SCs application as a good UV–Vis–NIR absorber. The magnetic properties of the investigated material are described by the model of S = 1/2 AFM dimers with J/kB = −122.7 K.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this work through the project number “375213500”. The authors would like to extend their sincere appreciation to the central laboratory at Jouf University for supporting this study. E. Č. and M. H. were supported by the Scientific Grant Agency of Ministry of Education, Science, Research and Sport of the Slovak Republic under contract No. VEGA 1/0426/19 and Slovak Research and Development Agency under contract No. APVV SK-BY-RD-19-0008 and APVV-18-0197..Notes and references
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 6050–6051 CrossRef CAS PubMed.
- T. M. Koh, K. Fu, Y. Fang, S. Chen, T. C. Sum, N. Mathews, S. G. Mhaisalkar, P. P. Boix and T. Baikie, J. Phys. Chem. C, 2014, 118, 16458–16462 CrossRef CAS.
- A. Babayigit, A. Ethirajan, M. Muller and B. Conings, Nat. Mater., 2016, 15, 247–251 CrossRef CAS PubMed.
- B. Conings, J. Drijkoningen, N. Gauquelin, A. Babayigit, J. D’Haen, L. D’Olieslaeger, A. Ethirajan, J. Verbeeck, J. Manca, E. Mosconi, F. De Angelis and H. G. Boyen, Adv. Energy Mater., 2015, 5, 1–8 Search PubMed.
- T. Leijtens, G. E. Eperon, N. K. Noel, S. N. Habisreutinger, A. Petrozza and H. J. Snaith, Adv. Energy Mater., 2015, 5, 1–23 Search PubMed.
- C. C. Stoumpos, L. Frazer, D. J. Clark, Y. S. Kim, S. H. Rhim, A. J. Freeman, J. B. Ketterson, J. I. Jang and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 6804–6819 CrossRef CAS PubMed.
- B. W. Park, B. Philippe, X. Zhang, H. Rensmo, G. Boschloo and E. M. J. Johansson, Adv. Mater., 2015, 27, 6806–6813 CrossRef CAS PubMed.
- K. Nishimura, M. A. Kamarudin, D. Hirotani, K. Hamada, Q. Shen, S. Iikubo, T. Minemoto, K. Yoshino and S. Hayase, Nano Energy, 2020, 74, 104858 CrossRef CAS.
- D. Cortecchia, H. A. Dewi, J. Yin, A. Bruno, S. Chen, T. Baikie, P. P. Boix and M. Gra, Inorg. Chem., 2016, 55, 1044–1052 CrossRef CAS PubMed.
- L. Lanzetta, T. Webb, N. Zibouche, X. Liang, D. Ding, G. Min, R. J. E. Westbrook, B. Gaggio, T. J. Macdonald, M. S. Islam and S. A. Haque, Nat. Commun., 2021, 12, 2853 CrossRef CAS PubMed.
- C. Li, X. Lu, W. Ding, L. Feng, Y. Gao and Z. Guo, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 702–707 CrossRef CAS PubMed.
- C. Li, K. C. K. Soh and P. Wu, J. Alloys Compd., 2004, 372, 40–48 CrossRef CAS.
- J. Yin, H. Li, D. Cortecchia, C. Soci and J. L. Brédas, ACS Energy Lett., 2017, 2, 417–423 CrossRef CAS.
- A. Yangui, S. Pillet, E. E. Bendeif, A. Lusson, S. Triki, Y. Abid and K. Boukheddaden, ACS Photonics, 2018, 5, 1599–1611 CrossRef CAS.
- S. Huang, G. Tang, H. Huang, X. Gang Wu, P. Zhou, L. Zou, L. Xie, J. Deng, X. Wang, H. Zhong and J. Hong, Sci. Bull., 2018, 63, 1254–1259 CrossRef CAS.
- M. E. Kamminga, M. Azhar, J. Zeisner, A. M. C. Maan, B. Büchner, V. Kataev, J. Baas, G. R. Blake, M. Mostovoy and T. T. M. Palstra, Phys. Rev. Mater., 2018, 2, 1–7 Search PubMed.
- M. Abid Derbel, M. M. Turnbull, H. Naïli and W. Rekik, Polyhedron, 2020, 175, 114220 CrossRef CAS.
- X. Li, X. Zhong, Y. Hu, B. Li, Y. Sheng, Y. Zhang, C. Weng, M. Feng, H. Han and J. Wang, J. Phys. Chem. Lett., 2017, 8, 1804–1809 CrossRef CAS PubMed.
- X. P. Cui, K. J. Jiang, J. H. Huang, Q. Q. Zhang, M. J. Su, L. M. Yang, Y. L. Song and X. Q. Zhou, Synth. Met., 2015, 209, 247–250 CrossRef CAS.
- L. Xie, B. Chen, F. Zhang, Z. Zhao, X. Wang, L. Shi, Y. Liu, L. Huang, R. Liu, B. Zou and Y. Wang, Photonics Res., 2020, 8, 768 CrossRef CAS.
- F. Zhang, Z. Zhao, B. Chen, H. Zheng, L. Huang, Y. Liu, Y. Wang and A. L. Rogach, Adv. Opt. Mater., 2020, 8, 1901723 CrossRef CAS.
- Z. Guo, J. Li, R. Pan, J. Cheng, R. Chen and T. He, Nanoscale, 2020, 12, 15560–15576 RSC.
- X. Li, B. Li, J. Chang, B. Ding, S. Zheng, Y. Wu, J. Yang, G. Yang, X. Zhong and J. Wang, ACS Appl. Energy Mater., 2018, 1, 2709–2716 CrossRef CAS.
- K. Ahmad and S. M. Mobin, Energy Technol., 2020, 8, 1901185 CrossRef CAS.
- A. M. Elseman, A. E. Shalan, S. Sajid, M. M. Rashad, A. M. Hassan and M. Li, ACS Appl. Mater. Interfaces, 2018, 10, 11699–11707 CrossRef CAS PubMed.
- R. Valiente and F. Rodriguez, ACS Appl. Mater. Interfaces, 2020, 12, 37807–37810 CrossRef CAS PubMed.
- M. Bourwina, R. Msalmi, S. Walha, M. M. Turnbull, T. Roisnel, F. Costantino, E. Mosconi and H. Naïli, J. Mater. Chem. C, 2021, 9, 5970–5976 RSC.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, A46, 467–473 CrossRef CAS.
- G. Sheldrick, SHELX-97 Programs Cryst. Struct. Anal., University of Göttingen, Göttingen, Germany, 1997 Search PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- H. Nagao, M. Nishino, Y. Shigeta, T. Soda, Y. Kitagawa, T. Onishi, Y. Yoshioka and K. Yamaguchi, Coord. Chem. Rev., 2000, 198, 265–295 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS.
- K. Yamaguchi, Y. Takahara and T. Fueno, in Applied Quantum Chemistry, Springer, Netherlands, Dordrecht, 1986, pp. 155–184 Search PubMed.
- C. Van Wüllen, J. Chem. Phys., 1998, 109, 392–399 CrossRef.
- E. Van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- D. A. Pantazis, X. Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597 Search PubMed.
- Z. Aloui, M. Essid, S. Abid, M. Rzaigui and C. Ben Nasr, Monatsh. Chem., 2015, 146, 1465–1471 CrossRef CAS.
- S. P. Thomas and J. Sunkari, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2013, 69(Pt 4), o529, DOI:10.1107/S160053681300648X.
- N. Hfidhi, N. Krayem, J. Erwann, T. Bataille and H. Naïli, J. Inorg. Organomet. Polym. Mater., 2021, 31, 1549–1564 CrossRef CAS.
- N. Mhadhbi, S. Saïd, S. Elleuch, T. Lis and H. Naïli, J. Mol. Struct., 2016, 1105, 16–24 CrossRef CAS.
- P. Panneerselvam, P. T. Muthiah and S. Francis, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, 60, o747–o749 CrossRef CAS.
- J. N. Low, D. Cannon, A. Quesada, A. Marchal, M. Melguizo, M. Nogueras, A. Sánchez and C. Glidewell, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2001, 57, 604–607 CrossRef CAS PubMed.
- S. Zhou, S. Shen, D. Zhao, Z. Zhang and S. Yan, J. Therm. Anal. Calorim., 2017, 129, 1445–1452 CrossRef CAS.
- E. Frank and A. Settle, 1997.
- C. Aydn, M. S. Abd El-Sadek, K. Zheng, I. S. Yahia and F. Yakuphanoglu, Opt. Laser Technol., 2013, 48, 447–452 CrossRef.
- C. C. B. Philips-Invernizzi and D. Dupont, Opt. Eng., 2001, 40, 1082 CrossRef.
- M. Duvenhage, M. Ntwaeaborwa, H. G. Visser, P. J. Swarts, J. C. Swarts and H. C. Swart, Opt. Mater., 2015, 42, 193–198 CrossRef CAS.
- M. Bochalya, P. K. Kanaujia, G. V. Prakash and S. Kumar, J. Solid State Chem., 2019, 273, 219–225 CrossRef CAS.
- R. Valiente and F. Rodriguez, J. Phys. Chem. Solids, 1996, 57, 571–587 CrossRef CAS.
- P. K. Olshin, O. S. Myasnikova, M. V. Kashina, A. O. Gorbunov, N. A. Bogachev, V. O. Kompanets, S. V. Chekalin, S. A. Pulkin, V. A. Kochemirovsky, M. Yu and A. S. Mereshchenko, Chem. Phys., 2018, 503, 14–19 CrossRef CAS.
- N. Marchal, E. Mosconi, G. García-Espejo, T. M. Almutairi, C. Quarti, D. Beljonne and F. De Angelis, J. Phys. Chem. Lett., 2021, 12, 2528–2535 CrossRef CAS PubMed.
- W. E. Marsh, K. C. Patel, W. E. Hatfield and D. J. Hodgson, Inorg. Chem., 1983, 22, 511–515 CrossRef CAS.
- B. Bleaney and K. D. Bowers, Proc. R. Soc. London, Ser. A, 1952, 214, 451–465 CAS.
- Z. Weihong and R. R. P. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 8052–8055 CrossRef CAS.
- D. C. Johnston, M. Troyer, S. Miyahara, D. Lidsky, K. Ueda, M. Azuma, Z. Hiroi, M. Takano, M. Isobe, Y. Ueda, M. A. Korotin, V. I. Anisimov, A. V. Mahajan and L. L. Miller, 2000.
- J. W. Hall, W. E. Marsh, R. R. Weller and W. E. Hatfield, Inorg. Chem., 2002, 20, 1033–1037 CrossRef.
- Q. Gu, D.-K. Yu and J.-L. Shen, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 3009 CrossRef CAS.
- C. P. Landee, M. M. Turnbull, C. Galeriu, J. Giantsidis and F. M. Woodward, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 4 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1897590. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1tc04336f |
| This journal is © The Royal Society of Chemistry 2021 |