Open Access Article
Open Access ArticleFrom radical to triradical thin film processes: the Blatter radical derivatives†
Arrigo
Calzolari
 a,
Andrzej
Rajca
a,
Andrzej
Rajca
 b and
Maria Benedetta
Casu
b and
Maria Benedetta
Casu
 *c
*c
aCNR-NANO Istituto Nanoscienze, Centro S3, I-41125 Modena, Italy
bDepartment of Chemistry, University of Nebraska, Lincoln, USA
cInstitute of Physical and Theoretical Chemistry, University of Tübingen, Auf der Morgenstelle 18, 72076 Tübingen, Germany. E-mail: benedetta.casu@uni-tuebingen.de
First published on 13th May 2021
Abstract
We demonstrate the possibility to evaporate Blatter radical derivatives in a controlled environment obtaining thin films that preserve the (poly)radical magnetic character. However, their thermal evaporation is challenging. We analyse the evaporation process and the thin film formation using thermodynamic concepts and describe the material properties also using first principles calculations. The presence of more than one radical site makes the radical more reactive, narrowing the windows left for evaporation, thus, favouring the assembly of molecules and island formation rather than two-dimensional growth.
Introduction
Understanding thin film processes in materials is a central issue to develop new devices and technologies. Not only have thin films different properties than bulk, but their use also led to device miniaturization. Thin films of inorganic and organic materials have been investigated since decades, with a great attention for surfaces and interfaces, the latter being of uppermost importance in designing a device.1 In this landscape, thin films of organic magnetic materials have recently been in focus for their promising applications in magnetism and quantum technologies.2–4 Their properties are usually due to the presence of a magnetic element and organic ligands. Open-shell purely organic materials, i.e., molecular radicals, can carry a magnetic moment and, thus, magnetic properties, too. Their thin film processes have been unknown for a long time, also because it was commonly thought that they would be too reactive to survive evaporation.5 Thermal evaporation is a preparation method that is required in specific technological fields because of the possibility to exactly control the preparation conditions and the cleanness of the environment that is an important prerequisite, for example, in developing quantum devices.We have successfully addressed the deposition of purely organic radicals, by using organic molecular beam deposition (OMDB)6 and we have introduced the use of soft X-ray based techniques to investigate their surfaces and interfaces, in combination with atomic force microscopy and ab initio simulations.7 Our approach supports the use of a range of spectroscopies and microscopies, much larger than the ones traditionally used to characterize organic radicals.
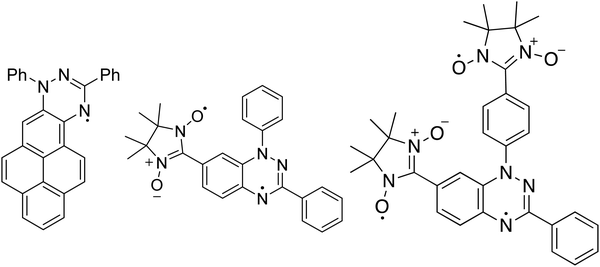
The Blatter radical8 is a stable radical that revealed to be a very promising material for applications in various fields.9–14 In this work, we review and compare our results focusing on three derivatives of the Blatter radical, from a mono- to a di- and a tri-radical, analysing the effect that the number of radicals implies for evaporation of the molecules, thin film preparation and thin film formation. We support our results also with ab initio calculations. The Blatter monoradical is fused to a pyrene in the Blatter-pyr15 (Fig. 1) while the diradical and the triradical are obtained fusing the latter radical to a nitronyl nitroxide (NN) radical moiety (NN-Blatter,16Fig. 1) and to two nitronyl nitroxide radicals (diNN-Blatter,17Fig. 1), respectively. The nitronyl nitroxide radical was selected because it is relatively stable, and it has a large negative spin density at the C2 position (i.e., the carbon atom between the two nitrogen atoms). This negative spin density is important for obtaining high-spin ground state (with a significant energy gap) when connected to the Blatter radical with positive spin density at the connecting carbon.18 In terms of film forming properties, we have demonstrated in our previous work that the NN and the Blatter monoradical are thermally stable and they can be evaporated without degradation, forming also ultra-high vacuum (UHV) and air stable films.7 Thus, they are promising building block for polyradical thin films grown by controlled evaporation.
Methods
Experimental section
Thin films were prepared in situ under UHV conditions by OMBD using a Knudsen cell. Native SiO2/n-Si(111) wafers are used as the substrate for all thin films. The wafers were cleaned in an ultrasonic bath by immersion in ethanol and acetone for one hour each and annealed at around 500 K for several hours. Cleanness was checked by X-ray photoelectron spectroscopy (XPS). Nominal film thicknesses were calculated using XPS from the attenuation of the substrate signal. The substrate was kept at room temperature during deposition. The UHV system had a dedicated OMDB chamber connected to an analysis chamber (2 × 10−10 mbar base pressure) equipped with a monochromatic Al Kα source (SPECS Focus 500) and a SPECS Phoibos 150 MCD hemispherical electron analyzer. Survey spectra were measured at 50 eV pass energy and highly resolved core level spectra at 20 eV pass energy, both calibrated to the Si 2p signal at 99.8 eV. To hinder/minimize potential radiation damage, only freshly prepared films were measured, and radiation exposure was limited. Atomic force microscopy was measured ex situ and under ambient conditions with a Digital Instruments Nanoscope III Multimode microscope using tapping mode. Note that while the XPS information on the decay of the substrate signal is obtained in situ without breaking the vacuum, the AFM images are obtained after air exposure.Calculation details
Calculations were performed using the density functional theory (DFT) based code implemented in the Quantum Espresso package.19 Ultra-soft pseudopotentials with a cut-off energy of 30 Ry were employed for the description of the ionic potentials. The Perdew, Burke and Ernzerhof (PBE)20 parameterisation of the generalised gradient approximation (GGA) was used to describe the exchange correlation functional for geometry optimization; van der Waals corrections were included within the semiempirical method proposed by S. Grimme (DFT-D2).21 The electronic structure was described by using B3LYP hybrid-functional without further atomic relaxation on the optimized PBE structures. Spin degree of freedom was treated within the local spin-density approximation. A (2 × 2 × 2) Monkhorst–Pack sampling scheme was used for Brillouin zone integration of bulk systems; centre-zone Γ-point was used in the case of single molecules. All structures were fully relaxed until forces on all atoms become lower than 0.03 eV Å−1. The N 1s core level spectra were calculated in the pseudopotential framework using the final state theory.22Results and discussion
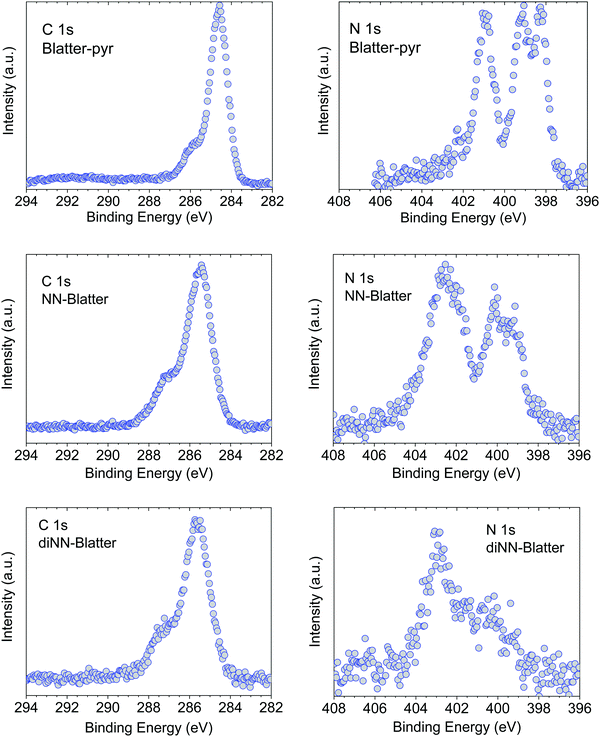
Soft X-ray techniques are powerful fingerprint techniques that can describe in detail the electronic structure of materials. XPS provides information on the occupied states, it is element-sensitive, and extremely sensitive to the chemical environment of each specific element of the system under investigation.23,24 Looking at the chemical composition of the three molecules (Fig. 1), we observe that the important core levels are those linked to excitations from the carbon and the nitrogen atoms. Specifically, the N 1s core level curves own the information on the unpaired electron(s) that gives rise to the magnetic moment. We compare them for the three systems in Fig. 2. The three molecules have carbon atoms with similar chemical environment, although different stoichiometric ratio. This is reflected from the C 1s spectroscopic line that has a similar shape in all three cases, characterised by two features, with a different intensity ratio between them. The main feature at lower binding energy is due to photoelectrons emitted from carbon atoms bound to other carbon atoms and hydrogen atoms, and the feature at higher binding energy is due to photoelectrons emitted from carbon atoms bound to nitrogen atoms. The addition of the NN groups push the main line to the higher binding energy range, because of the stronger electronegativity of the nitrogen and oxygen atoms and a less efficient screening of the core-hole due to a limited delocalization in the NN group with respect to the Blatter radical (see also the ab initio calculations below).The N 1s core level curves are complicated by the numerous different chemical environments, in the Blatter radical the three nitrogen atoms have three different environments that can be identified by the presence of the three features in the N 1s spectroscopic line (Fig. 2, upper panel). Their presence is clearly evidenced also in the NN-Blatter N 1s core level spectrum. The nitronyl nitroxide contributes a further feature at higher binding energy (Fig. 2, middle panel, at around 402 eV) that becomes more evident in intensity in the diNN-Blatter N 1s spectrum (Fig. 2, lower panel) because of stoichiometric reasons, since this molecule carries two nitronyl nitroxide moieties.
We have previously demonstrated that these spectral features correspond in all three cases to the evaporation and deposition of intact molecules.15–17 We use a specific protocol to assess the intactness.25 We consider (1) the stoichiometric information from the XPS spectra, (2) the comparison between films and powder XPS spectra (the powder does not undergo evaporation) looking at the shape and the components of the single spectroscopic lines using a best-fit procedure26 that we have also previously correlated with electron spin resonant (ESR) spectroscopic investigations;10,15,27,28 (3) the comparison between the experimental and the theoretical curves obtained by DFT calculations.25 When the films are stable enough under air, they are also investigated by using ESR spectroscopy.
Evaporation becomes more and more difficult with increasing the number of radical sites in the investigated molecules. This agrees with the generally accepted rule of thumb that states that the more unpaired electrons in a molecule, the worse its thermal stability is. Before our work, this rule led to the hypothesis that polyradicals could not be evaporated because they would decompose during sublimation.5 In all experiments the substrates are SiO2/Si(111) wafers, kept at room temperature during deposition, thus, differences in substrate and its treatment do not play a role in the comparison. The onset of the thermogravimetric analysis (TGA) decreases from the Blatter-pyr to the NN-Blatter and the diNN-Blatter from 523 K to 433/439 K, shrinking the size of the temperature window available for the evaporation that must be higher than the energy of formation of the bulk.25 This allows sublimating the molecules from the powder and targeting the substrate with a molecular beam using a Knudsen cell. Film formation onto a substrate is a phenomenon that is against the thermodynamic equilibrium between adsorption and desorption.29 Working in non-equilibrium conditions establishes a no-net growth on the surface. This is achieved in OMBD working in supersaturation, Δμ.29,30 As a first approximation, supersaturation depends on the substrate temperature, on the deposition rate, the heat of sublimation, the molecular weight, and the entropy of sublimation.30,31 It describes the thermodynamics of the film formation. To sustain layer growth rather than three dimensional (3D) aggregations that is always possible, it is necessary to reach higher values of supersaturation. To grow a layer, it is necessary to overcome a critical value of supersaturation that equals the difference between the energy per molecule of the molecule–adjacent molecular layer interaction, ψmol, and the energy per molecule of the molecule–substrate interaction, ψmol–sub: Δμcri = ψmol − ψmol–sub.30
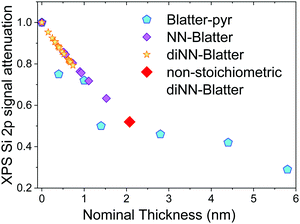
We performed annealing experiments on the various thin films that identified that the temperature of complete film desorption is higher for the Blatter-pyr thin films (see ESI,† too).15,16 This indicates that the molecule–substrate interaction strength in the case of Blatter-pyr, ψmol–sub(Blatter-pyr), is higher than ψmol–sub(NN-Blatter) and ψmol–sub(diNN-Blatter), i.e., the analogous strengths for the diradical and the triradical, respectively. Additionally, NN-Blatter and diNN-Blatter show strong antiferromagnetic interactions between the molecules in the bulk. Specifically, the intrachain antiferromagnetic coupling in NN-Blatter is by far the strongest among all studied 1D S = 1 chains of organic radicals.16 Therefore, we can infer that Blatter-pyr has the smallest value of Δμcri among the three molecules. This, along with the fact that its TGA onset is the highest (see Table 1), allows for a larger 2D growth window and higher nucleation density for Blatter-pyr thin films, keeping the same substrate temperature. In fact, Blatter-pyr thin films growth following the Stranski–Krastanov growth mode (layer + island) while NN-Blatter and diNN-Blatter thin films follow the Volmer–Weber growth mode, as it is clearly indicated by the decay in situ of the signal substrate during evaporation (Fig. 3). We note here that the sticking coefficient under the same preparation conditions is very low for NN-Blatter and diNN-Blatter, evidencing that the probability of desorption from the surface is very high. Considering the substrate time exposure, at stable evaporation rate, the thickness of the obtained films and their corresponding AFM images (Fig. 4) we have noticed that there is a certain delay before nucleation occurs, suggesting a deadtime before reaching the necessary supersaturation for film formation. This indicates that at the initial stage of the growth process, the number of molecules impinging and sticking on the substrate is at the thermal equilibrium with the number of molecules leaving the substrate because of desorption. To overcome the thermal equilibrium, reaching supersaturation conditions, a certain “time delay” is necessary before to observe a net growth. We also observe that island nucleation on defective sites is favoured, as the defects act as a potential sink (Fig. 4c). This leaves most of the surface exposed (Fig. 4b and c), in agreement with the decrease of the XPS substrate signal during evaporation that shows a very slow decay (Fig. 3).16,25 Furthermore, the temperature range necessary to evaporate the intact diradical and triradical leads to enhanced island formation and it hinders the growth of films nominally thicker than 2 nm (the nominal thickness is the thickness of the equivalent film assuming an ideal layer growth mode). Growing thicker films needs higher evaporation temperatures that damage the radical moiety (Fig. 3, and Fig. S1 in the ESI†). Lower temperature of the substrate during evaporation would increase the sticking probability, however, we expect that this might affect the structure of the films and consequently their electronic and magnetic character.32–35
| Blatter-pyr | NN-Blatter | diNN-Blatter | |
|---|---|---|---|
| Formula | C29H18N3 | C26H25N5O2 | C33H36N7O4 |
| Formula weight (g mol−1) | 408.46 | 481.97 | 594.69 |
| Density (Mg m−3) | 1.397 | 1.363 | 1.303 |
| Spin | 1/2 | 1 | 3/2 |
| TGA onset (K) | 523 | 433 | 439 |
| Evaporation temperature (K) | 418 | 363–373 | 373–383 |
| T (TGAonset-Tevaporation) (K) | 105 | 60–70 | 56–66 |
| E for (calc) (eV mol−1) | −1.8 | −0.9 | −2.4 |
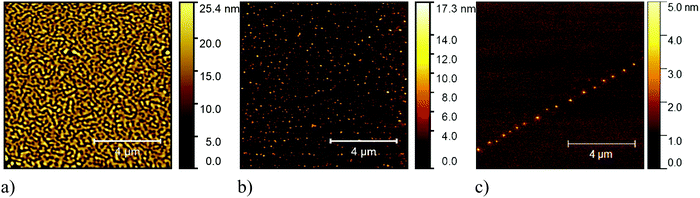 | ||
| Fig. 4 Typical 10 μm × 10 μm AFM (a) image of a Blatter-pyr thin film, (b) of a NN-Blatter thin film, and (c) of a diNN-Blatter thin film. | ||
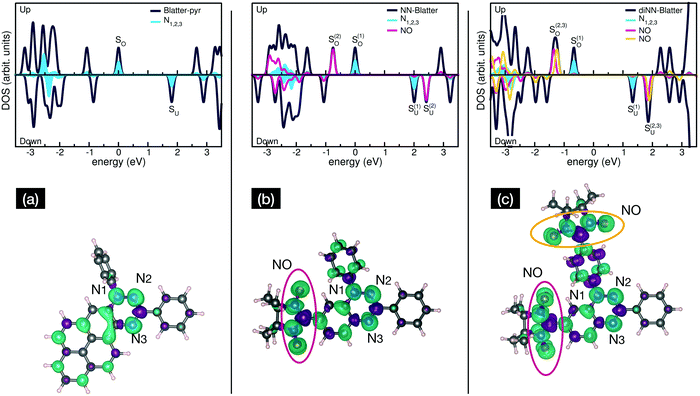
Electronic and magnetic properties of the three Blatter derivatives are described by first principles calculations. The electronic structure for the single radicals is summarized in Fig. 5. The three molecules have an increasing number of spin-unpaired electrons, which runs from 1 to 3 moving from the mono- to the triradical. For each molecule, the ground state configuration corresponds to the maximum of the total spin, which is S = 1/2, S = 1, and S = 3/2 for Blatter-pyr, NN-Blatter and diNN-Blatter, respectively. This gives rise to the appearance of an increasing number of single occupied (unoccupied) molecular orbital SOMO (SUMO), labelled SO and SU in Fig. 5. In all cases, the highest SOMO and lowest SUMO correspond to the Blatter core, common to the three radicals and mostly localized on the nitrogen atoms, with a partial contribution from the entire aromatic ring. In the NN systems another SO–SU pair of states appears for each nitronyl nitroxide unit fused to the Blatter core. The latter molecular orbitals are strongly localized on the NO bonds of the NN units (Fig. 5). The evolution of the magnetic properties of the radicals is visually summarized by the charge spin-density plots (ρup–ρdown) included in the bottom panel of Fig. 5. The simulated N 1s core level shift (CLS) spectra are shown in Fig. 6.
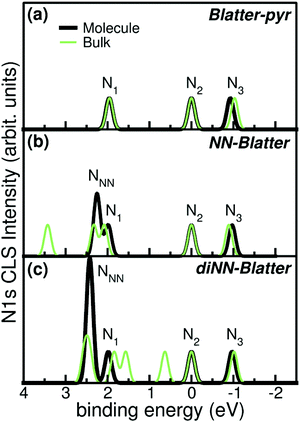 | ||
| Fig. 6 Simulated N 1s CLS spectra for (a) Blatter-pyr, (b) NN-Blatter, and (c) diNN-Blatter in both single molecule (thick black) and bulk (thin green) configuration. Labels refers to Fig. 5. | ||
The molecular arrangement in the crystalline bulk and/or thin films strictly depends on the steric arrangement of the lateral functional groups (e.g., phenyls, methyl) which decorate the radicals. The resulting crystals (monoclinic symmetry) are densely packed and energetically very stable. The calculated formation energies of the bulk with respect to the isolated constituents vary from −0.9 to −2.4 eV mol−1 in the case of NN-Blatter and diNN-Blatter, respectively (see Table 1). Despite the specific differences, due to the details of the molecular structure, the high stability of the solid-state systems stems from the π–π coupling of stacked Blatter cores along with a direct Coulomb interaction between the NN units. The intermolecular coupling results in the appearance of an energy dispersion (of the order of 100 meV) in the band structure of the molecular crystals.35 The effect of the local bonding as well as of the intramolecular interaction is evident from the calculated N 1s CLS spectra shown in Fig. 6. The simulation approach provides only the relative shift between the core level binding energies of inequivalent atoms, while their absolute value is not defined. Here, we fix as zero reference energy the contribution of the N2 atom (Fig. 5) of the Blatter core. The comparison between the molecular radicals (black lines) indicates the persistence of the spectral features associated to the Blatter nitrogen atoms (N1, N2, and N3), and the higher energy contribution of the N atoms of the NN groups (NNN), in excellent agreement with the experimental results discussed above. The NNN peaks are mostly affected by the intermolecular interaction that splits the degeneracy of the single molecule in multicomponents which correspond to the increase of the broadening of the experimental N-band, as the number of NN group is increased.
The intermolecular coupling affects also the long-range magnetic order in the solid state: even though each radical locally maintain its intrinsic spin order n↑ (intramolecular parallel ordering with n = 1, 2, 3 for mono-, di- and tri-radicals), globally in the solid state the molecules exhibit and alternating antiferromagnetic (AF) molecular spin alignment (n↑–n↓–n↑–n↓). The ferromagnetic (FM) alignment (n↑–n↑–n↑–n↑) is energetically slightly unfavoured with respect to the AF case by ΔE < 10 meV mol−1; while the non-magnetic phase is not a metastable solution for any of the Blatter-derivative crystals.
Conclusions
The Blatter radical and its derivatives are very promising molecules for applications, from electronics to quantum technologies.9,10 Some of the applications require the molecules be attached to a surface in a controlled environment by using evaporation. We have demonstrated that it is possible to successfully evaporate Blatter radical derivatives with up to three radical sites. The conditions are stringent and the space of the required parameters for a successful evaporation is very limited. This implies that, if working with the substrate at room temperature, the molecules aggregate in islands rather than form closed films. Decreasing the substrate temperature might help to enhance 2D growth, however, the structural properties of the films might change causing effects that are mostly unknown. Conversely, this method might revel useful in case of applications foreseeing the attachment of a single monolayer to a surface.Author contributions
A. C. performed the calculations. A. R. designed and synthetized the radicals. M. B. C. took part in the measurements, conceived, and supervised the project; interpreted the data and wrote the manuscript together with A. C. All authors contributed to the discussion and commented on the manuscript.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
We thank all the current and former Casu and Rajca co-workers who contributed to the research on the thin films of Blatter radicals and whose names appear in the references, and in particular Tobias Junghoefer, Francesca Ciccullo, Nolan M. Gallagher, Shuyang Zhang, Chan Shu, Elke Nadler, Drs Suchada Rajca and Hui Zhang. Our special thanks go to Dr Maren Pink who helped us to characterize structurally the Blatter radicals. We would like to thank Helmholtz-Zentrum Berlin (HZB) for providing beamtime at BESSY II (Berlin, Germany) that allowed us to assess the structural properties of the thin films, Erika Giangrisostomi and Ruslan Ovsyannikov for their support at the beamline. The authors also thank Prof. T. Chassé for the access to the photoelectron spectroscopy lab at the University of Tübingen. Financial support from the German Research Foundation (DFG) under the contract CA852/11-1 is gratefully acknowledged. We thank the National Science Foundation (NSF), Chemistry Division, for support of this research under Grants CHE-1665256 and CHE-1955349 (A.R.).References
- H. Kroemer, Surf. Sci., 1983, 132, 543–576 Search PubMed.
- J. Lehmann, A. Gaita-Arino, E. Coronado and D. Loss, J. Mater. Chem., 2009, 19, 1672–1677 Search PubMed.
- M. R. Wasielewski, M. D. E. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith, T. Goodson, M. L. Kirk, J. K. McCusker, J. P. Ogilvie, D. A. Shultz, S. Stoll and K. B. Whaley, Nat. Rev. Chem., 2020, 4, 490–504 Search PubMed.
- E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104 Search PubMed.
- Z. Huang, Y. Zhang, Y. He, H. Song, C. Yin and K. Wu, Chem. Soc. Rev., 2017, 46, 1955–1976 Search PubMed.
- S. R. Forrest, Chem. Rev., 1997, 97, 1793–1896 Search PubMed.
- M. B. Casu, Acc. Chem. Res., 2018, 51, 753–760 Search PubMed.
- H. M. Blatter and H. Lukaszewski, Tetrahedron Lett., 1968, 9, 2701–2705 Search PubMed.
- Y. Ji, L. Long and Y. Zheng, Mater. Chem. Front., 2020, 4, 3433–3443 Search PubMed.
- F. Ciccullo, A. Calzolari, K. Bader, P. Neugebauer, N. M. Gallagher, A. Rajca, J. van Slageren and M. B. Casu, ACS Appl. Mater. Interfaces, 2019, 11, 1571–1578 Search PubMed.
- Y. Zhang, Y. Zheng, H. Zhou, M.-S. Miao, F. Wudl and T.-Q. Nguyen, Adv. Mater., 2015, 27, 7412–7419 Search PubMed.
- X. Hu, H. Chen, L. Zhao, M. Miao and Y. Zheng, Chem. Mater., 2019, 31, 10256–10262 Search PubMed.
- X. Hu, H. Chen, L. Zhao, M. Miao, J. Han, J. Wang, J. Guo, Y. Hu and Y. Zheng, Chem. Commun., 2019, 55, 7812–7815 Search PubMed.
- X. Hu, H. Chen, G. Xue and Y. Zheng, J. Mater. Chem. C, 2020, 8, 10749–10754 Search PubMed.
- F. Ciccullo, N. M. Gallagher, O. Geladari, T. Chasse, A. Rajca and M. B. Casu, ACS Appl. Mater. Interfaces, 2016, 8, 1805–1812 Search PubMed.
- N. Gallagher, H. Zhang, T. Junghoefer, E. Giangrisostomi, R. Ovsyannikov, M. Pink, S. Rajca, M. B. Casu and A. Rajca, J. Am. Chem. Soc., 2019, 141, 4764–4774 Search PubMed.
- C. Shu, M. Pink, T. Junghoefer, E. Nadler, S. Rajca, M. B. Casu and A. Rajca, J. Am. Chem. Soc., 2021, 143, 5508–5518 Search PubMed.
- N. M. Gallagher, J. J. Bauer, M. Pink, S. Rajca and A. Rajca, J. Am. Chem. Soc., 2016, 138, 9377–9380 Search PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 Search PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 Search PubMed.
- E. Pehlke and M. Scheffler, Phys. Rev. Lett., 1993, 71, 2338–2341 Search PubMed.
- K. Siegbahn, C. Nordling, A. Fahlman, R. Nordberg, K. Hamrin, J. Hedman, G. Johansson, T. Bergmark, S.-E. Karlsson, I. Lindgren and B. Lindberg, ESCA, Atomic, Molecular and Solid State Structure Studied by Means of Electron Spectroscopy, Almqvist and Wiksells, Uppsala, 1967 Search PubMed.
- K. M. Siegbahn, Nobel Lecture: Electron Spectroscopy for Atoms, Molecules and Condensed Matter, http://www.nobelprize.org/nobel_prizes/physics/laureates/1981/siegbahn-lecture.html, (accessed 09 June 2020, 2020).
- T. Junghoefer, N. M. Gallagher, K. Kolanji, E. Giangrisostomi, R. Ovsyannikov, T. Chassé, M. Baumgarten, A. Rajca, A. Calzolari and M. B. Casu, Chem. Mater., 2021, 33, 2019–2028 Search PubMed.
- T. Junghoefer, E. M. Nowik-Boltyk, J. A. de Sousa, E. Giangrisostomi, R. Ovsyannikov, T. Chassé, J. Veciana, M. Mas-Torrent, C. Rovira, N. Crivillers and M. B. Casu, Chem. Sci., 2020, 11, 9162–9172 Search PubMed.
- S.-A. Savu, I. Biswas, L. Sorace, M. Mannini, D. Rovai, A. Caneschi, T. Chassé and M. B. Casu, Chem. – Eur. J., 2013, 19, 3445–3450 Search PubMed.
- R. Kakavandi, S.-A. Savu, A. Caneschi and M. B. Casu, J. Phys. Chem. C, 2013, 117, 26675–26679 Search PubMed.
- J. A. Venables, Introduction to Surface and Thin Film Processes, Cambridge University Press, Cambridge, 2000 Search PubMed.
- S. Verlaak, S. Steudel, P. Heremans, D. Janssen and M. S. Deleuze, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 195409 Search PubMed.
- M. Ohring, Materials Science of Thin Films, Academic Press, San Diego, 2002 Search PubMed.
- S. Duhm, G. Heimel, I. Salzmann, H. Glowatzki, R. L. Johnson, A. Vollmer, J. P. Rabe and N. Koch, Nat. Mater., 2008, 7, 326–332 Search PubMed.
- B. Klett, C. Cocchi, L. Pithan, S. Kowarik and C. Draxl, Phys. Chem. Chem. Phys., 2016, 18, 14603–14609 Search PubMed.
- P. Poulopoulos and K. Baberschke, J. Phys.: Condens. Matter, 1999, 11, 9495–9515 Search PubMed.
- T. Junghoefer, I. Baev, M. Glaser, F. Ciccullo, E. Giangristomi, R. Ovsyannikov, F. Kielgast, M. Nissen, J. Schwarz, N. M. Gallagher, A. Rajca, M. Martins, A. Calzolari and M. B. Casu, 2021, arXiv:1911.02082 [cond-mat.mtrl-sci].
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc01541a |
| This journal is © The Royal Society of Chemistry 2021 |