Open Access Article
Open Access ArticleFast reversible isomerization of merocyanine as a tool to quantify stress history in elastomers†
Yinjun
Chen‡
 a,
C. Joshua
Yeh§
a,
C. Joshua
Yeh§
 a,
Qiang
Guo
b,
Yuan
Qi
b,
Rong
Long
a,
Qiang
Guo
b,
Yuan
Qi
b,
Rong
Long
 b and
Costantino
Creton
b and
Costantino
Creton
 *a
*a
aLaboratory of Soft Matter Science and Engineering, ESPCI Paris, PSL University, CNRS, Sorbonne Université, 75005 Paris, France. E-mail: costantino.creton@espci.psl.eu
bDepartment of Mechanical Engineering, University of Colorado Boulder, Boulder, CO, 80309 USA
First published on 17th December 2020
Abstract
A mechanochemistry based approach is proposed to detect and map stress history during dynamic processes. Spiropyran (SP), a force sensitive molecular probe, was incorporated as a crosslinker into multiple network elastomers (MNE). When these mechanochromic MNEs are loaded, SP undergoes a well-known force-activated reaction to merocyanine (MC) changing its absorption in the visible range (visible blue color). This SP to MC transition is not reversible within the time frame of the experiment and the color change reports the concentration of activated molecules. During subsequent loading–unloading cycles the MC undergoes a fast and reversible isomerization resulting in a slight shift of absorption spectrum and results in a second color change (blue to purple color corresponding to the loading–unloading cycles). Quantification of the color changes by using chromaticity shows that the exact color observed upon unloading is characteristic not only of the current stress (reported by the shift in color due to MC isomerization), but of the maximum stress that the material has seen during the loading cycle (reported by the shift in color due to the change in MC concentration). We show that these two color changes can be separated unambiguously and we use them to map the stress history in the loading and unloading process occurring as a crack opens up and propagates, breaking the material. Color maps on fractured samples are compared with finite element simulations and the agreement is excellent.
Introduction
Although soft and elastic materials are found in many industrial applications, predicting their strength from their molecular structure remains difficult in particular because there are few tools to characterize damage and fracture at the molecular scale. Hence materials design relies still on empirical methods. In particular the extent of damage of an elastomer is currently modeled with fully phenomenological methods and no feedback can be given to materials designers to make the materials structure more damage resistant. Such a feedback can only be given if physically based models are developed and such models require experimental data to be calibrated.One of the major recent advances to characterize the mechanical properties of polymeric materials at the molecular level has been the development of force-sensitive mechanophore molecules that exhibit mechanically activated optical responses, such as light emission (luminescence),1 color changes2 and fluorescence3 in response to the application of a mechanical force to a specific chemical bond. When these molecules are incorporated in the polymer network in a load-bearing position, they can be activated and respond locally to the application of a stress on a macroscopic sample, making it therefore possible to spatially map the optical activation. These responses have mainly been used to qualitatively investigate the mechanical properties of materials,4 the interactions between different interfaces,5 the damage zone around a crack tip,6 and the tailoring of physical properties.7 Only a few studies8 focused on the actual quantification of the mechanically activated optical signals, which is needed to understand how stresses and strains are distributed to molecules and to develop physically based constitutive models.
One of the reasons is that mechanophore molecules are currently not commercially available and need to be incorporated into the materials with a suitable synthetic method, which is specific for each new material. Furthermore the technique competes with the versatile digital image correlation (DIC)9 and particle tracking10 techniques, that are able to quantitatively detect the strain field with high accuracy in many situations11 without any chemical labeling of the material.
Although mechanophores still provide less quantitative information than DIC for the time being, they allow direct optical visualization of the spatially resolved level of activation. Recently, Xia et al.12 incorporated mechanochromic spiropyran based (SP) molecules as crosslinkers into Sylgard 184 (an elastomer containing nanofillers) and demonstrated their usefulness for mapping strains in fast impact experiments. A color change due to the activation of SP into merocyanine (MC) was observed during the deformation of the materials and the distribution of color change was qualitatively consistent with the prediction of Von Mises strain fields by finite element analysis suggesting that activation is caused by an average level of strain. Park et al.13 also incorporated SP into a nanocomposite with pores and silica nanoparticles and observed color changes with increasing strain. With their particular material they observed enhanced activation even at moderate stress, a useful property for responsive electronic skin elastomers. However, the complex structure of the materials makes it difficult to directly connect molecular activation and strains.
If strain fields can be mapped by DIC, detecting stress is much more difficult and this is where mechanophores can have an edge. If DIC is used, a constitutive model is needed to calculate the stress field from the strain field. For soft polymer networks, many constitutive models have been proposed and are used such as the neo-Hookean model, the Mooney–Rivlin model,14 Ogden's model,15 Gent's model.16 Although these models fit the data well in uniaxial extension, they are often not validated by direct experimental evidence in other geometries involving multiaxial loading. In addition, when strain-hardening materials are deformed to large strains such as near fracture points, the displacement measurement obtained from DIC and particle tracking becomes inaccurate and result in large uncertainties in the stresses predicted by the assumed constitutive modeling.
Motivated by this fact, in a previous work17 we quantified the color changes of multiple network elastomers (MNEs) containing SP undergoing uniaxial tension. We demonstrated that the color of the sample was directly proportional to the concentration of activated SP in the material. By constructing a calibration curve between color change and nominal stress during loading, the stress field around a crack tip prior to propagation was quantitatively mapped and the results were validated with finite element simulations. This quantification work was however limited to mapping the stress evolution during loading by the force-activated transition between SP and merocyanine (MC). As we argued in our previous work the observed color change is due to an increase in concentration of MC as the macroscopic load on the sample increases. Yet the force-induced SP → MC transition is not reversible within the time scale of the experiment so that the concentration of MC in the sample is only dependent on the maximum stress seen by the sample and does not change if the load is removed. Yet it would be very helpful to map stresses in dynamic experiments where materials can be locally loaded, damaged and then unloaded such as in the case of the propagation of a crack. For this situation DIC does not give a unique answer for the stress (because of near crack tip damage during loading).
Craig et al.2d incorporated SP as a crosslinker in a PDMS elastomer and observed a change in color from transparent (before force-activation) to blue (upon loading) to purple (upon full unloading). From the molecular point of view, the instantaneous and fully reversible color change during unloading and reloading was attributed to the isomerization of MC as shown in Fig. 1a. Namely, there are no less than two isomers of MC corresponding to the loading and unloading,18 respectively. In other words the MC concentration does not change upon unloading and reloading but the relative proportion of the two isomers has a force dependent equilibrium with a very low activation energy.
Weng et al.19 also used this color change to demonstrate unloading around the crack tip during the propagation of a crack in polyurethane illustrating that the two-color change is sensitive to the change in stress in the materials. However, their approach was not quantitative.
The purpose and novelty of this paper is to extend the quantitative color analysis approach of Chen et al.17 to two additional mechanical situations involving the application of a decreasing load:
(1) The optical quantitative mapping of the maximum stress seen by the material point near the fracture plane measured post-mortem.
(2) The optical quantitative mapping in a time-resolved way of the propagation of a crack including in the regions unloaded by the propagation of the crack.
Both measurements are essential to calibrate and improve analytical and computational mechanical models to predict crack propagation in particular when the material is extensively damaged before failing.
To do that, we incorporate SP-based crosslinkers in ethyl acrylate-based multiple network elastomers6b,20 (MNE) following a previously developed synthetic procedure. Unlike PU, the MNEs exhibit no measurable viscoelasticity in uniaxial deformation and are sufficiently tough to activate a detectable amount of SP into MC upon loading. Hence, MNE are good model systems. After proper calibration, a direct measure of the change in local color (due to the isomerization of MC) with a simple RGB camera will be carried out on a propagating crack and on fracture surfaces. The experimental results will then be compared with finite element simulations to check the validity of this novel quantitative and time-resolved approach.
Results
Synthesis of mechanochromic multiple network elastomers and characterization of their mechanical properties
As previously reported,6b,20,21 MNEs consist of a more highly crosslinked first network (the filler network) interpenetrated with one or more less crosslinked network(s) (the matrix networks), synthesized by sequences of monomer swelling and free radical polymerization. The filler network was prepared by UV photopolymerizing a mixture of ethyl acrylate (EA) monomers, spiropyran (SP) and 1,4-butanediol diacrylate (BDA) crosslinkers, and 2-hydroxy-2-methylpropiophenone (HMP) initiator. Since the crosslinking and entanglement structure of the filler network controls the stiffness and extensibility of the MNEs6b,20,21 we prepared networks with two crosslinking concentrations of 0.5 mol% and 0.2 mol% relative to EA monomers at a constant SP concentration. The composition used to prepare the much less crosslinked matrix networks was made of EA, 0.01 mol% BDA and 0.01 mol% HMP relative to EA monomers (see Section S1 of the ESI† for details of the synthesis). In the following, each sample is named Ax-y(z), where A, x, y, z denote the monomer, crosslinker concentration, SP concentration, and isotropic prestretch from swelling of the filler network. The detailed information on materials properties is shown in Table 1. All the data are measured in uniaxial extension at a stretch rate of 0.05 s−1.| Polymer name | λ 0 | E (MPa) | σ m (MPa) | (λb) |
|---|---|---|---|---|
| a λ 0: pre-stretch of filler network, E: Young's modulus, σm: nominal stress at break, λb: stretch at break. | ||||
| EA0.2-0.05(1) | 1 | 0.62 | 0.86 | 4.1 |
| EA0.2-0.05(1.70) | 1.70 | 0.90 | 10 | 4.2 |
| EA0.2-0.05(2.61) | 2.61 | 1.24 | 11.3 | 3.1 |
| EA0.5-0.05(1) | 1 | 0.85 | 1.1 | 2.1 |
| EA0.5-0.05(1.56) | 1.56 | 1.16 | 4.6 | 2.5 |
| EA0.5-0.05(2.23) | 2.23 | 1.88 | 15.7 | 2.7 |
While a significant improvement in stiffness and fracture toughness was observed for both families of materials consistent with results reported in previous work6b,20,21 (Fig. S1† and Table 1), the more highly prestretched elastomers (EA0.5-0.05(2.23) and EA0.2-0.05(2.61)) with the highest Young's modulus and failure stress were selected for our experiments to maximize SP activation before fracture.
Mechanical response-color change in cyclic loading
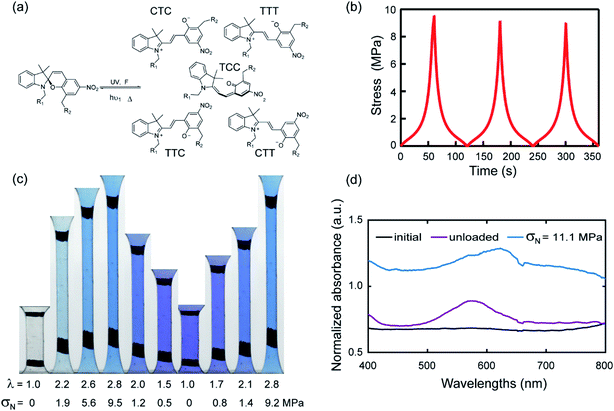
To illustrate the reversible mechanochromic properties of the materials, the EA0.2-0.05(2.61) material was subjected to loading–unloading cycles in uniaxial extension and example results are summarized in Fig. 1. Stress–time data is shown in Fig. 1b for three cycles of loading–unloading. Fig. 1c shows images of the same sample for one and a half cycle to λ = 2.8. The initially transparent (colorless) sample becomes blue during loading because of the force-activated conversion of SP into MC (an irreversible reaction within the time frame of the experiment) and purple during unloading, qualitatively consistent with previous studies on other materials.2d,19 The second (and fast reversible within the time frame of the experiment) color change can be attributed to the coexistence of different isomers of merocyanine (MC) as shown in Fig. 1a.2eTo characterize more precisely the two-color changes, a UV-vis absorption spectrum was obtained for the EA0.2-0.5(2.61) samples during cyclic loading tests. In Fig. 1d, the absorption spectrum of the loaded sample (blue curve) presents a broad peak between the wavelength of 600 and 650 nm during loading. When the sample was fully unloaded, the absorption peak shifted to 580 nm (purple line). According to Wohl et al.,22 different stable isomers have different characteristic absorption peaks in the visible light region and thus result in different colors. The conversion from one absorption peak to another during loading and unloading validates the probable shift between two main isomers of MC reverting into each other during the cyclic loading test. Based on the computational work of Craig et al.,2e the SP derivative used in this work mainly transforms into five isomers as shown in Fig. 1a. Since these isomers are sensitive to stress and are able to transform into each other reversibly over the time scale of the loading/unloading experiment, once the SP is activated into MC, the materials reversibly and instantaneously shift between different colors in response to the change in stress as shown in Fig. 1c. EA0.2-0.05(2.61) samples gradually shift from blue color into purple with decreasing applied stress. This suggests that the exact color may be directly related to the level of stress in the material, giving us therefore in principle the ability to quantify the stress during the unloading process.
Although the exact nature of the main isomers presents during loading and unloading cannot be ascertained, this does not matter for the quantification of stress as long as the respective stability of the isomers is sensitive to the stress level in the same way.
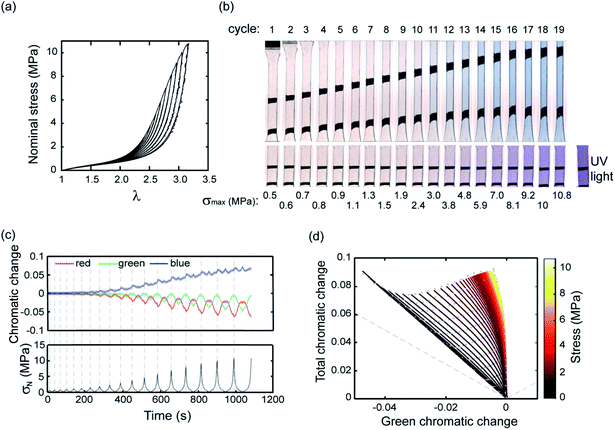
Construction of the 3D color-stress map and quantification
After presenting this example we now proceed to a systematic quantification to establish a calibration map. Fig. 2a shows stress–stretch data for a step cyclic loading performed on EA0.2-0.05(2.61) samples at increasing values of λmax. Note that the EA0.2-0.05(2.61) samples exhibit an excellent reversible elasticity up to an extension of λ ∼ 1.7 and loading at different strain rates had little effect on the results, indicating that viscoelasticity can be ignored. When σN reaches 3 MPa in the third cycle, a mechanical hysteresis becomes observable, which suggests an initiation of damage (random bond scission) occurring in the materials. The hysteresis for each cycle and the total hysteresis were calculated as shown in Fig. S3.† Due to the weak C–O bond in SP, SP is activated (on average) prior to the onset of damage as shown in Fig. 2b and in Fig. S3† since an obvious color change is visible in the third cycle before mechanical hysteresis is detected. More SP are then activated with increasing maximum stretch resulting in the progressive increase in chromaticity in step cycle loading tests not only for the loaded sample but also for the unloaded samples (λ = 1) where the shade of purple becomes more intense as λmax increases.To quantify these changes in color, an RGB analysis based on color chromaticity was carried out for the step cyclic loading. Chromaticity relates to the intensity of specific color channels, i.e. red, green and blue. Sratio, is defined as the ratio of the intensity of a color channel in eqn (1):
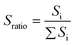 | (1) |
To improve the sensitivity of chromatic changes to stress and the detection limit, a total chromatic change was defined. The total chromatic change, ΔTratio, was calculated based on the Euclidean norm:
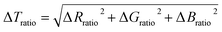 | (2) |
The total and green chromatic changes were selected as parameters to visually separate the loading and unloading by associating the loading and unloading along the y and x axes of Fig. 2d, respectively. However, in principle, any two chromatic descriptors can be selected to fully describe the color state (see Section S2 of the ESI† for more details). A 3D color-stress map can be plotted, where coordinates on the color plane are assigned a nominal stress value. Color coded to stress lines as a function of green and total chromatic change are shown in Fig. 2d. The right edge of the map shows the stress curve during the loading of a virgin sample where SP changes into MC. The left part of the map corresponds to relaxation and reloading. Note that the color change during reloading retraces the unloading curves, indicating the reversibility between blue and purple. This result is consistent with the observation that the unloading and reloading curves in the stress-extension response overlap in Fig. 2a. This color-stress calibration map can then be used to measure the magnitude of the stress for each pixel in the sample region of an image during both the loading and unloading process. Since the concentration of MC in the sample (all isomers included) is only dependent on the maximum stress that the sample has seen, this information can be deduced from the chromatic change coordinates.
We will now examine how this mechanochemical approach can be used to investigate a fully macroscopic solid mechanics problem: the propagation of a crack in a sample from an initial notch. As the crack propagates the material points that were initially loaded in front of the crack tip, become progressively unloaded. This information that is currently impossible to obtain experimentally by any other method, is important to estimate the real energy release rate and the stress history of the sample.
Quantification of stress during the propagation of a crack
Fig. 3 shows a single edge notched rectangular sample (SEN) of EA0.2-0.05(2.61) being stretched monotonously at a constant stretch rate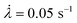 . When the stretch exceeds a critical value, the crack catastrophically propagates and the sample fails. The calibration map can be used to map a scalar representation of the principal components of the stress around the crack tip during crack propagation.17 A color camera (capturing at a rate of 30 frames per second) records the evolution of the color change around a crack tip during the test. Because of the fast crack velocity, only two frames were captured during the propagation process. As shown in Fig. 3a, color around the crack tip gradually changes into a deep blue from frames I to IV before the propagation of the crack starts. During the fast propagation, one of the frames was captured as shown in Fig. 3a (frame VI). Although frames taken during propagation are slightly blurry, regions of deep blue and purple are clearly visible and the color distribution on both sides of the crack tip are approximately symmetrical. As discussed above, the purple regions suggest a shift in the distribution between the isomeric MC populations due to unloading. A detailed color analysis was performed on each frame in order to create a pixel by pixel stress map of the loaded and unloaded regions. Note that the large difference in crack opening between frame V and frame VI with only a small change in λ is due to the fact that the stretch is measured far from the tip. An actual video of the propagation is shown in ESI Movie S1† and similar images are available for the EA0.5-0.05(2.23) samples in Section S3 of the ESI.†
. When the stretch exceeds a critical value, the crack catastrophically propagates and the sample fails. The calibration map can be used to map a scalar representation of the principal components of the stress around the crack tip during crack propagation.17 A color camera (capturing at a rate of 30 frames per second) records the evolution of the color change around a crack tip during the test. Because of the fast crack velocity, only two frames were captured during the propagation process. As shown in Fig. 3a, color around the crack tip gradually changes into a deep blue from frames I to IV before the propagation of the crack starts. During the fast propagation, one of the frames was captured as shown in Fig. 3a (frame VI). Although frames taken during propagation are slightly blurry, regions of deep blue and purple are clearly visible and the color distribution on both sides of the crack tip are approximately symmetrical. As discussed above, the purple regions suggest a shift in the distribution between the isomeric MC populations due to unloading. A detailed color analysis was performed on each frame in order to create a pixel by pixel stress map of the loaded and unloaded regions. Note that the large difference in crack opening between frame V and frame VI with only a small change in λ is due to the fact that the stretch is measured far from the tip. An actual video of the propagation is shown in ESI Movie S1† and similar images are available for the EA0.5-0.05(2.23) samples in Section S3 of the ESI.†
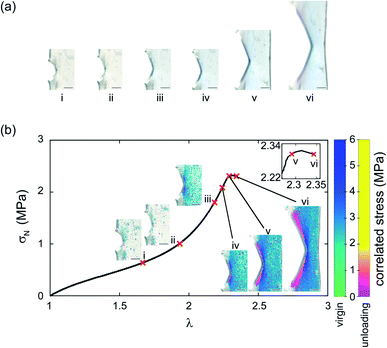 | ||
| Fig. 3 (a) Image of EA0.2-0.05(2.61) during crack propagation; (b) stress map of the image in (a). The scale bar in the images represents 0.5 mm. | ||
The calibration color-stress map of Fig. 2d can then be used to detect the spatial position of the unloaded regions of the sample, the 2D maps of the values of the local stress σloc during the loading of the SEN sample and the propagation of the crack are shown in Fig. 3b for different macroscopic values of tensile stretch and nominal stress. Around the peak macroscopic stress two regions in the shape of wedges where the material is unloaded are clearly visible (images V and VI). The unloaded regions start from the areas that exhibit the maximum stress concentration around the crack tip before crack propagation, gradually extending to areas further away from the crack as shown in Fig. 3b. This is the first time that the stress relaxation in the dynamic process of crack propagation is observed and quantified. In unloaded areas, the magnitude of the relaxation of stress increases with distance away from the crack tip (right to left) as shown in frame VI in Fig. 3b. The stress in the unloaded areas almost relaxes to 0. Note that crack propagation, starts to occur before the peak stress when most of the material is still under load. This is also an interesting result with potential practical relevance since it is notoriously difficult to identify exactly when the crack starts to propagate. By default the peak average stress (measured with the load cell far from the sample) is often used to determine Γc but our results show that this may not be true and that the crack may propagate before.
Post mortem analysis of the loading history
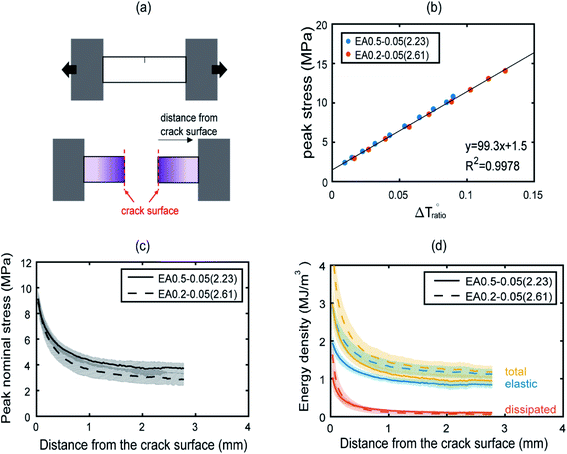
Although with our current standard camera we could not follow in detail the evolution of the stress map during the fast propagation, the samples could also be imaged post-mortem to determine in the fully unloaded state, the concentration of MC in the sample (reflecting the maximum stress seen by the sample) as a function of position from the fracture surface. This information is very useful to compare experimental results to FE modeling of crack growth.From the chromatic change after failure, the maximum stress of each pixel can be extracted from the calibration color-stress map and hence the relationship between the distance away from the fracture plane and the maximum stress seen by that pixel, an information that can in principle be compared to modeling of crack propagation for multiple network elastomers. To validate the usefulness of this method, post mortem analysis was performed for EA0.2-0.05(2.61) and EA0.5-0.05(2.23), two materials made from different filler networks that exhibit a different strain stiffening behavior.
A schematic of the geometry of the sample is shown in Fig. 4a. The presence of a strong purple color near the fracture surface is observed, indicating a high level of SP activation (see also Fig. S20†). The intensity of the purple color decreases progressively with increasing distance away from the fracture surface.
Fig. 4b plots the peak stresses that the sample has seen in the uniaxial cyclic test as a function of the corresponding total chromatic change, once the sample is back in the relaxed zero stress state for EA0.2-0.05(2.61). The same procedure was applied for the stiffer materials of EA0.5-0.05(2.23) and as expected17 the experimental points for the EA0.5-0.05(2.23) fall on the same straight line as those of the EA0.2-0.05(2.61) as shown in Fig. 4b, validating the feasibility to deduce maximum load from chromatic change after materials failure. The maximum stress distribution as a function of distance away from the edge is shown in Fig. 4c for both materials. EA0.2-0.05(2.61) shows a slightly lower peak nominal stresses at the same distance from the crack face compared to EA0.5-0.05(2.23). This is qualitatively consistent with the softer nature of the EA0.2-0.05(2.61) due to the lower crosslinker concentration in the filler network (see Fig. S3†).
Once the maximum stress information is extracted it is also possible to approximately separate the dissipated energy (through bond scission) from the released elastic energy. The dissipated energy density was calculated by integrating the hysteretic area in the cyclic stress–strain curves shown in Fig. 2a and S3a.† This allowed the construction of a calibration curve between the dissipated energy and the peak stress, which can then be used to create an averaged dissipated energy profile perpendicular to the crack edge, as shown in Fig. 4d. A detailed procedure of the analysis can be found in the ESI.† In Fig. 4d, the total and elastic energy densities for the softer EA0.2-0.05(2.61) materials both exhibited higher values than for the stiffer EA0.5-0.05(2.23) material reflecting the reduction in crosslinker concentration in the filler network and the larger extensibility of the filler network. For regions close to the edge, the dissipated energy density for the soft material is larger than for the stiff material, which is consistent with the idea that a larger dissipated energy region leads to a higher fracture toughness.
Simulation of crack propagation
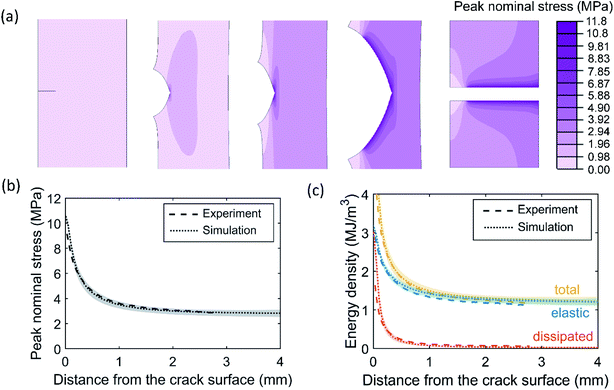
The measured stress history can provide critical inputs for developing fracture models capable of simulating crack propagation in soft elastomers. To demonstrate this point, we built a FE model for the SEN sample of EA0.2-0.05(2.61) (see Fig. S21†). A constitutive model was developed to capture the nonlinear, hysteretic stress–strain relation in this material by fitting the cyclic uniaxial tension data in Fig. 2a (see Fig. S22a†). Moreover, we implemented a cohesive zone model to describe the fracture process at the crack tip, which required two key parameters: intrinsic fracture energy Γ0 and cohesive strength σc_max (Fig. S21†). It is a challenging task to calibrate these two parameters for soft elastomers due to the lack of sufficient understanding on the crack tip fracture process. We leveraged the post-mortem analysis, specifically the peak nominal stress distribution in Fig. 4c, to determine the cohesive parameters. First, σc_max was set to be 11.3 MPa according to the nominal stress at break under macroscopic tension for EA0.2-0.05(2.61) (see Table 1), which is close to the maximum peak nominal stress observed in Fig. 4c. Second, Γ0 was determined by fitting the peak nominal stress distribution (see Fig. S23†) and was found to be 4.6 kJ m−2.Using the calibrated FE model, we were able to simulate the crack propagation in EA0.2-0.05(2.61) (see Fig. 5a). After complete crack propagation, the contour of peak nominal stress exhibited a decay as one moved away from the crack surface, except around the original crack surface where material points did not experience as large loading as those around the newly created crack surface. Quantitative comparisons between the simulation results and the post-mortem analysis were made in Fig. 5b and c for the peak nominal stress and energy densities, showing excellent agreement. We also found that the stress maps plotted using the simulation results (Fig. S24†) resembled those measured by the mechanophore (Fig. 3c). The agreement between FE simulation and experimental data further supported the utility and validity of the stress history measurement using mechanophores.
Conclusion
We have conclusively demonstrated the potential of incorporating spiropyran mechanophore molecules in a soft polymer network to measure stress history. As previously reported the transformation of SP into MC by mechanical force can be used to quantify stresses during loading but we exploit here the reversible change of MC from an isomeric form (stable under load) to another isomeric form (stable in the unloaded state). This fast and reversible change is accompanied by a change in light absorption and hence to a change in color. By constructing a 3D color-stress map of the change in chromaticity from loading and unloading uniaxial tensile tests, we can attribute a unique color hue not only to the actual stress seen by the sample but also to the stress history (i.e. the maximum stress seen by the sample during the cycle). Since the color analysis can be done with a simple RGB camera, we used the stress color map to investigate the spatial stress distribution in the dynamic process of crack propagation analyzing the propagation of a crack and showing that even in a highly elastic material such as our MNE, the crack starts moving before the peak stress.We further explored the possibility to obtain the maximum stress seen by each material point by performing a color analysis after failure due to crack propagation. From this chromaticity information we obtained the map of the maximum stress seen by each pixel near the crack and validated the measurement by finite element simulations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge helpful discussions with Prof. Rint Sijbesma, Prof. Hugh R. Brown, Dr Artem Kovalenko and Dr Huan Zhang. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program under grant agreement AdG No 695351. Yinjun Chen has benefitted from a scholarship from the Chinese Scholarship Council. Rong Long acknowledge support from a U.S. National Science Foundation CAREER AWARD (NSF CMMI-1752449). All data needed to evaluate the conclusions in the paper are present in the paper and/or the ESI.† Additional data available from authors upon request.References
- (a) Y. Chen and R. P. Sijbesma, Macromolecules, 2014, 47, 3797–3805 CrossRef CAS; (b) Y. Chen, A. J. Spiering, S. Karthikeyan, G. W. Peters, E. W. Meijer and R. P. Sijbesma, Nat. Chem., 2012, 4, 559–562 CrossRef CAS PubMed; (c) J. M. Clough, C. Creton, S. L. Craig and R. P. Sijbesma, Adv. Funct. Mater., 2016, 26, 9063–9074 CrossRef CAS.
- (a) B. A. Beiermann, S. L. B. Kramer, P. A. May, J. S. Moore, S. R. White and N. R. Sottos, Adv. Funct. Mater., 2014, 24, 1529–1537 CrossRef CAS; (b) D. A. Davis, A. Hamilton, J. Yang, L. D. Cremar, D. Van Gough, S. L. Potisek, M. T. Ong, P. V. Braun, T. J. Martinez, S. R. White, J. S. Moore and N. R. Sottos, Nature, 2009, 459, 68–72 CrossRef CAS PubMed; (c) G. R. Gossweiler, C. L. Brown, G. B. Hewage, E. Sapiro-Gheiler, W. J. Trautman, G. W. Welshofer and S. L. Craig, ACS Appl. Mater. Interfaces, 2015, 7, 22431–22435 CrossRef CAS PubMed; (d) G. R. Gossweiler, G. B. Hewage, G. Soriano, Q. Wang, G. W. Welshofer, X. Zhao and S. L. Craig, ACS Macro Lett., 2014, 3, 216–219 CrossRef CAS; (e) G. R. Gossweiler, T. B. Kouznetsova and S. L. Craig, J. Am. Chem. Soc., 2015, 137, 6148–6151 CrossRef CAS PubMed; (f) K. Imato, T. Kanehara, T. Ohishi, M. Nishihara, H. Yajima, M. Ito, A. Takahara and H. Otsuka, ACS Macro Lett., 2015, 4, 1307–1311 CrossRef CAS; (g) M. Li, Q. Zhang and S. Zhu, Polymer, 2016, 99, 521–528 CrossRef CAS; (h) G. O'Bryan, B. M. Wong and J. R. McElhanon, ACS Appl. Mater. Interfaces, 2010, 2, 1594–1600 CrossRef PubMed; (i) H. Oka, K. Imato, T. Sato, T. Ohishi, R. Goseki and H. Otsuka, ACS Macro Lett., 2016, 5, 1124–1127 CrossRef CAS; (j) M. J. Robb, T. A. Kim, A. J. Halmes, S. R. White, N. R. Sottos and J. S. Moore, J. Am. Chem. Soc., 2016, 138, 12328–12331 CrossRef CAS PubMed; (k) Q. Wang, G. R. Gossweiler, S. L. Craig and X. Zhao, Nat. Commun., 2014, 5, 4899 CrossRef PubMed; (l) T. Wang, N. Zhang, J. Dai, Z. Li, W. Bai and R. Bai, ACS Appl. Mater. Interfaces, 2017, 9, 11874–11881 CrossRef CAS PubMed; (m) Z. Wang, Z. Ma, Y. Wang, Z. Xu, Y. Luo, Y. Wei and X. Jia, Adv. Mater., 2015, 27, 6469–6474 CrossRef CAS PubMed.
- (a) R. Gostl and R. P. Sijbesma, Chem. Sci., 2016, 7, 370–375 RSC; (b) H. Li, R. Göstl, M. Delgove, J. Sweeck, Q. Zhang, R. P. Sijbesma and J. P. A. Heuts, ACS Macro Lett., 2016, 5, 995–998 CrossRef CAS; (c) T. Wang, N. Zhang, K. Zhang, J. Dai, W. Bai and R. Bai, Chem. Commun., 2016, 52, 9679–9682 RSC.
- (a) Y. Chen, H. Zhang, X. Fang, Y. Lin, Y. Xu and W. Weng, ACS Macro Lett., 2014, 3, 141–145 CrossRef CAS; (b) X. Fang, H. Zhang, Y. Chen, Y. Lin, Y. Xu and W. Weng, Macromolecules, 2013, 46, 6566–6574 CrossRef CAS; (c) G. Hong, H. Zhang, Y. Lin, Y. Chen, Y. Xu, W. Weng and H. Xia, Macromolecules, 2013, 46, 8649–8656 CrossRef CAS; (d) S. Jiang, L. Zhang, T. Xie, Y. Lin, H. Zhang, Y. Xu, W. Weng and L. Dai, ACS Macro Lett., 2013, 2, 705–709 CrossRef CAS.
- (a) J. Li, T. Shiraki, B. Hu, R. A. Wright, B. Zhao and J. S. Moore, J. Am. Chem. Soc., 2014, 136, 15925–15928 CrossRef CAS PubMed; (b) J. Sung, M. J. Robb, S. R. White, J. S. Moore and N. R. Sottos, J. Am. Chem. Soc., 2018, 140, 5000–5003 CrossRef CAS PubMed.
- (a) E. Ducrot, Y. Chen, M. Bulters, R. P. Sijbesma and C. Creton, Science, 2014, 344, 186–189 CrossRef CAS PubMed; (b) P. Millereau, E. Ducrot, J. M. Clough, M. E. Wiseman, H. R. Brown, R. P. Sijbesma and C. Creton, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9110–9115 CrossRef CAS PubMed.
- Z. Chen, J. A. M. Mercer, X. Zhu, J. A. H. Romaniuk, R. Pfattner, L. Cegelski, T. J. Martinez, N. Z. Burns and Y. Xia, Science, 2017, 357, 475–479 CrossRef CAS PubMed.
- J. Slootman, V. Waltz, C. J. Yeh, C. Baumann, R. Göstl, J. Comtet and C. Creton, Soft Condensed Matter, 2020 Search PubMed.
- S. Mzabi, D. Berghezan, S. Roux, F. Hild and C. Creton, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 1518–1524 CrossRef CAS.
- Y. Qi, Z. Zou, J. Xiao and R. Long, J. Mech. Phys. Solids, 2019, 125, 326–346 CrossRef CAS.
- (a) G. Besnard, F. Hild and S. Roux, Exp. Mech., 2006, 46, 789–803 CrossRef; (b) F. Hild, A. Bouterf and S. Roux, Int. J. Fract., 2015, 191, 77–105 CrossRef.
- Z. Xia, V. D. Alphonse, D. B. Trigg, T. P. Harrigan, J. M. Paulson, Q. T. Luong, E. P. Lloyd, M. H. Barbee and S. L. Craig, Molecules, 2019, 24, 524 CrossRef PubMed.
- J. Park, Y. Lee, M. H. Barbee, S. Cho, S. Cho, R. Shanker, J. Kim, J. Myoung, M. P. Kim, C. Baig, S. L. Craig and H. Ko, Adv. Mater., 2019, 31, e1808148 CrossRef PubMed.
- (a) R. S. Rivlin, Philos. Trans. R. Soc., A, 1948, 241, 379–397 CrossRef; (b) A. P. S. Selvadurai, J. Mech. Phys. Solids, 2006, 54, 1093–1119 CrossRef.
- (a) R. W. Ogden, Proc. R. Soc. London, Ser. A, 1972, 326, 565–584 CrossRef CAS; (b) R. W. Ogden and D. G. Roxburgh, Proc. R. Soc. London, Ser. A, 1999, 455, 2861–2877 CrossRef.
- A. N. GENT, Rubber Chem. Technol., 1996, 69, 59–61 CrossRef CAS.
- Y. Chen, C. J. Yeh, Y. Qi, R. Long and C. Creton, Sci. Adv., 2020, 6, eaaz5093 CrossRef CAS PubMed.
- (a) J. Hobley and V. Malatesta, Phys. Chem. Chem. Phys., 2000, 2, 57–59 RSC; (b) O. Kovalenko, Y. Lopatkin, P. Kondratenko and D. Belous, Eur. Phys. J. D, 2018, 72, 20 CrossRef.
- H. Zhang, Y. Chen, Y. Lin, X. Fang, Y. Xu, Y. Ruan and W. Weng, Macromolecules, 2014, 47, 6783–6790 CrossRef CAS.
- E. Ducrot and C. Creton, Adv. Funct. Mater., 2016, 26, 2482–2492 CrossRef CAS.
- W. Qiu, P. A. Gurr and G. G. Qiao, Macromolecules, 2020, 53, 4090–4098 CrossRef CAS.
- C. J. Wohl and D. Kuciauskas, J. Phys. Chem. B, 2005, 109, 22186–22191 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc06157c |
| ‡ Current address: Department of Chemical Engineering & Chemistry and Institute for Complex Molecular Systems, Eindhoven University of Technology, 5600 MB Eindhoven, Netherlands |
| § Current address: 3M research center, St-Paul, MN, USA. |
| This journal is © The Royal Society of Chemistry 2021 |