Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Consistent inclusion of continuum solvation in energy decomposition analysis: theory and application to molecular CO2 reduction catalysts†
Yuezhi
Mao‡§
 *a,
Matthias
Loipersberger‡
*a,
Matthias
Loipersberger‡
 a,
Kareesa J.
Kron
a,
Kareesa J.
Kron
 b,
Jeffrey S.
Derrick
b,
Jeffrey S.
Derrick
 a,
Christopher J.
Chang
a,
Christopher J.
Chang
 acd,
Shaama Mallikarjun
Sharada
acd,
Shaama Mallikarjun
Sharada
 be and
Martin
Head-Gordon
be and
Martin
Head-Gordon
 *ac
*ac
aDepartment of Chemistry, University of California at Berkeley, Berkeley, CA 94720, USA. E-mail: yuezhi.mao@berkeley.edu; mhg@cchem.berkeley.edu
bMork Family Department of Chemical Engineering and Material Science, University of Southern California, Los Angeles, CA 90089, USA
cChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
dDepartment of Molecular and Cell Biology, University of California Berkeley, Berkeley, CA 94720, USA
eDepartment of Chemistry, University of Southern California, Los Angeles, CA 90089, USA
First published on 27th November 2020
Abstract
To facilitate computational investigation of intermolecular interactions in the solution phase, we report the development of ALMO-EDA(solv), a scheme that allows the application of continuum solvent models within the framework of energy decomposition analysis (EDA) based on absolutely localized molecular orbitals (ALMOs). In this scheme, all the quantum mechanical states involved in the variational EDA procedure are computed with the presence of solvent environment so that solvation effects are incorporated in the evaluation of all its energy components. After validation on several model complexes, we employ ALMO-EDA(solv) to investigate substituent effects on two classes of complexes that are related to molecular CO2 reduction catalysis. For [FeTPP(CO2-κC)]2− (TPP = tetraphenylporphyrin), we reveal that two ortho substituents which yield most favorable CO2 binding, –N(CH3)3+ (TMA) and –OH, stabilize the complex via through-structure and through-space mechanisms, respectively. The coulombic interaction between the positively charged TMA group and activated CO2 is found to be largely attenuated by the polar solvent. Furthermore, we also provide computational support for the design strategy of utilizing bulky, flexible ligands to stabilize activated CO2via long-range Coulomb interactions, which creates biomimetic solvent-inaccessible “pockets” in that electrostatics is unscreened. For the reactant and product complexes associated with the electron transfer from the p-terphenyl radical anion to CO2, we demonstrate that the double terminal substitution of p-terphenyl by electron-withdrawing groups considerably strengthens the binding in the product state while moderately weakens that in the reactant state, which are both dominated by the substituent tuning of the electrostatics component. These applications illustrate that this new extension of ALMO-EDA provides a valuable means to unravel the nature of intermolecular interactions and quantify their impacts on chemical reactivity in solution.
1 Introduction
Intermolecular interactions play an essential role in modern chemical research. Most chemical processes take place in solution, making it desirable to develop computational chemistry tools to model and analyze intermolecular interactions with solvent effects taken into account. The inclusion of solvent brings new challenges to the existing methods as solvation is able to modulate intermolecular interactions in a variety of ways. For interactions involving ionic species, the solvent helps stabilize the charged moieties while screening the long-range electrostatic interactions as a dielectric medium. Even for a neutral solute species, its electronic structure and related properties, such as multipole moments, may be altered by polar solvents, which in turn affects its interaction with other solute molecules. Such effects can impose profound influences on relative stability of intermolecular complexes as well as thermodynamics and kinetics of chemical reactions in solution.1,2Implicit solvent models, which typically treat the solvent environment as a dielectric continuum and ignore its molecular-level resolution, remain widely used in modern quantum chemistry calculations to incorporate solvation effects.3–5 These methods are also known as self-consistent reaction field (SCRF) models, since the implicit solvent perturbs the quantum mechanical (QM) Hamiltonian via an external field, and the field itself depends on the QM electron density. Many variants of SCRF models that differ significantly in their formulation and complexity have been developed, including methods based on apparent surface charges (ASC),6–16 generalized Born models,17–19 and models based on direct solution of inhomogeneous Poisson–Boltzmann equations.20–24 The popular conductor-like (C-PCM)8–10 and integral-equation-formalism (IEF-PCM)11,12 polarizable continuum models are outstanding examples among the ASC models.
Energy decomposition analysis (EDA)25–29 is a powerful tool that facilitates one's understanding of intermolecular interactions by quantifying the relative importance of various physically motivated components, such as permanent electrostatics, polarization, dispersion, etc. While there are many perturbative or variational EDA schemes available, these developments have been focusing on intermolecular interactions in vacuum. To extend the utility of EDA approaches to intermolecular interactions under solvent environment, it is natural to integrate existing EDA schemes with implicit solvent models, considering the wide usage of the latter for describing solute–solvent interactions with minimal computational cost. The simplest approach to achieve that is to include the solvent contribution to interaction energy as an a posteriori correction to the gas-phase EDA result. This approach was adopted, for instance, in the EDA scheme implemented in the ONETEP30 linear-scaling density functional theory (DFT) program.31,32 While such an approach is applicable to most EDA schemes, it is not entirely satisfactory as it is unable to describe the solvation effect on each individual energy component.
In a pioneering effort to consistently incorporate solvent effect in an EDA procedure, Cammi et al.33 modified the Kituara–Morokuma (KM)-EDA34,35 by adding the SCRF potential of the full dimer complex to the Fock matrix that was used to generate the energy components in this EDA scheme. Similar approaches were later proposed by Contador et al.36 to study hydrogen-bonded complexes in solution, where the KM-EDA was applied to decompose interaction energies evaluated within “dimeric” cavities, and also by Gora et al.37 where the intermolecular interaction (free) energy was separated into electrostatics, exchange-repulsion, delocalization, and reaction field (solvation) contributions. Fedorov and Kitaura extended their pair-interaction (PI)-EDA scheme38 to treat intermolecular interactions in solution by combining the fragment molecular orbital (FMO) method39 with PCM models,40 in which they characterized two types of solvent effects: (i) screening of electrostatics and (ii) desolvation upon the formation of complex.
The EDA-PCM scheme developed by Su et al.,41 which was based upon the localized molecular orbital (LMO)-EDA scheme,42 is more closely related to the present work. It accounts for the solvation environment in two stages: (i) the isolated fragment orbitals (LMOs) are optimized with continuum solvent, and are then used to construct the intermediate states that are required for the evaluation of the electrostatics, exchange, repulsion, and polarization terms; (ii) a “desolvation” term, which describes the change in solute–solvent interaction energies associated with the destruction of monomer SCRFs and the formation of the full complex SCRF, is introduced in addition to the original LMO-EDA scheme. In the more recent generalized Kohn–Sham (GKS)-EDA,43,44 this same approach is used to incorporate the solvent contribution to the interaction free energy. While this is a rather sophisticated approach that integrates implicit solvation with a modern DFT-based EDA, the solvent reaction field is constructed only for the initial (isolated fragment) and final (full complex) states. Since it is not re-optimized for the intermediates, the solvent effect on each individual term is still not explicitly characterized.
In this paper, we integrate SCRF implicit solvent models with energy decomposition analysis of DFT calculations based on absolutely localized molecular orbitals (ALMO-EDA), whose gas-phase version was previously developed by some of us.29,45–47 For brevity, we denote this new extension of the ALMO-EDA for studying non-covalent interactions in solution as “ALMO-EDA(solv)” throughout this paper. The second-generation ALMO-EDA method46,47 partitions the total interaction energy (ΔEINT) into contributions from permanent electrostatics (ELEC), Pauli repulsion (PAULI), dispersion (DISP), polarization (POL), and charge transfer (CT):
| ΔEINT = ΔEELEC + ΔEPAULI + ΔEDISP + ΔEPOL + ΔECT | (1) |
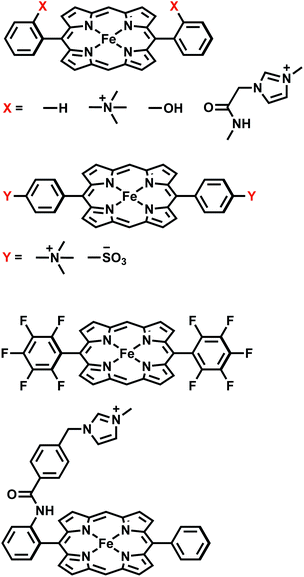
We then utilize the ALMO-EDA(solv) scheme to investigate the role of intermolecular interactions in two distinct examples of catalyzed CO2 reduction reactions: one is assisted by the [Fe(II)TPP]0 catalyst (TPP = tetraphenylporphyrin) or its derivatives,51 which facilitates the 2e−/2H+ reduction of CO2 to CO with fast turnover rates and high product selectivity at a low overpotential52 by acting as an “electron mediator” between the electrode and CO2 in solution and stabilizing intermediates such as adducts of activated CO2; the other involves a single-electron transfer from a photoactivated and then reduced oligo(p-phenylenes) photocatalyst (OPP) to CO2.53 The catalysts investigated in this work for these two CO2 reduction processes are summarized in Fig. 1 and 2, respectively. Electronic structure calculations and EDA can help provide vital insights into catalytic pathways by identifying key intermediates and characterizing substrate–catalyst interactions, allowing one to understand the origin of activity or selectivity as well as the cause of any intrinsic limitation of a catalyst.54–57 Many CO2 reduction catalysts operate in aprotic polar solvents,51–53,58 aqueous solutions,59 or water/organic solvent mixtures.60,61 In such cases, it is essential to incorporate solvation effects in electronic structure calculations for one to obtain meaningful and reliable energetic results, especially for adducts of activated CO2 (CO2˙−) whose interactions with other species would be vastly different in the gas and solution phases.
2 Theory
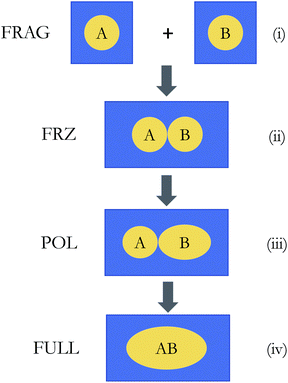
The overall procedure of ALMO-EDA(solv) is illustrated in Fig. 3, which, like the gas-phase second-generation ALMO-EDA (eqn (1)), separates the total interaction into five terms:| ΔE(s)INT = ΔE(s)ELEC + ΔE(s)PAULI + ΔE(s)DISP + ΔE(s)POL + ΔE(s)CT | (2) |
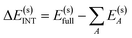 | (3) |
| = ΔE(s)FRZ + ΔE(s)POL + ΔE(s)CT | (4) |
The frozen interaction energy (ΔE(s)FRZ) describes the energy change upon the formation of a solvated complex from several individually solvated, non-interacting fragments without relaxing their orbitals. It corresponds to the energy change from (i) to (ii) in Fig. 1:
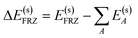 | (5) |
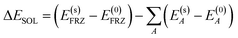 | (6) |
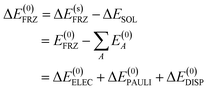 | (7) |
The overall decomposition of the frozen interaction energy, including solvation, is thus given by
| ΔE(s)FRZ = ΔESOL + ΔE(0)ELEC + ΔE(0)PAULI + ΔE(0)DISP | (8) |
For most generic implicit solvent models, the solute–solvent interaction comprises both electrostatic and non-electrostatic components. While the description of the electrostatic component plays a pivotal role in the formulation of a solvent model, the non-electrostatic solute–solvent interaction is typically described by empirical, highly parameterized functions (e.g. the cavity-dispersion-solvent structure (CDS) term in the SMD model14) and sometimes even ignored. Upon the formation of a complex, the solute–solvent electrostatic interaction may be drastically changed due to the Coulomb interaction between induced charges on different fragment cavities as well as modifications to the shape of molecular cavities. The overall effect of the change in solute–solvent electrostatic interaction, as we observe in practice, is often screening the electrostatic interaction between each fragment's “internal” charge distribution (ΔE(0)ELEC). The change in the non-electrostatic component of the solute–solvent interaction energy is usually of lesser importance compared to the electrostatic component, and in most cases it supplies a destabilizing effect due to the reduction of total surface area of molecular cavities upon the formation of a complex. Bearing these considerations in mind, we separate ΔESOL into electrostatic (ΔEelSOL) and non-electrostatic (ΔEnon-elSOL) components: the former is combined with ΔE(0)ELEC, giving rise to a solvent-corrected electrostatic term that is denoted as ΔE(s)ELEC, and the latter is combined with ΔE(0)PAULI because of their common short-ranged nature. The decomposition of the frozen term in ALMO-EDA(solv) (eqn (8)) can thus be rewritten as
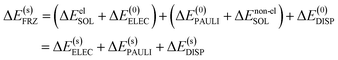 | (9) |
One should note that in eqn (9) we have assumed that ΔE(s)DISP ≈ ΔE(0)DISP, that is, the dispersion interaction between fragments is unaffected by the presence of solvent except that the fragment wavefunctions are optimized with solvent. This assumption is plausible when the two interacting moieties are in close contact, especially when they reside in the same molecular cavity, but may become less justified when the two moieties are well-separated and reside in two non-overlapping cavities, since dispersion interaction, which can be viewed as interactions between fluctuating dipoles, may also be screened by the dielectric medium.63 This many-body dispersion effect64 seems non-trivial to include in a continuum solvent model, so we stick with this assumption for now and decompose the frozen interaction energy based on eqn (9) in the rest of this paper.
The polarization energy (ΔE(s)POL) in ALMO-EDA(solv) is defined as the energy difference between the polarized intermediate state and the solvated frozen complex, which corresponds to the energy change from stage (ii) to (iii) in Fig. 3:
| ΔE(s)POL = E(s)POL − E(s)FRZ | (10) |
Finally, we perform a standard, unconstrained SCF calculation within the solvent environment, and the energy lowering relative to the POL state (from (iii) to (iv) in Fig. 3) is defined as the charge-transfer (CT) energy:
| ΔE(s)CT = E(s)full − E(s)POL | (11) |
In summary, the energy decomposition given by the ALMO-EDA(solv) scheme is formally identical to its gas-phase counterpart. The explicit change in solute–solvent interaction energy upon the formation of complex is reflected in ΔESOL, which can be further partitioned into electrostatic and non-electrostatic components that serve as corrections to the internal ELEC and PAULI terms, respectively. The POL and CT contributions to the interaction are calculated with all involved intermediate states properly solvated, and hence the solvent effect on these terms will also be taken into account.
3 Computational details
We implemented the ALMO-EDA(solv) scheme in a locally modified Q-Chem 5.2 software package,67 which serves as an extension of the original routines for the second-generation ALMO-EDA for DFT calculations.46,47 While this scheme, in principle, should be compatible with most of the available SCRF models, in this work we demonstrate it with two widely used approaches: the conductor-like PCM (C-PCM)8–10 and the SMD model.14 The non-electrostatic effects of the solvent were ignored in our calculations using C-PCM, whereas the solvation free energy (ΔGS) produced by SMD comprises both electrostatic and non-electrostatic contributions, which correspond to the “electronic-nuclear-polarization” (ENP) and the “cavity-dispersion-solvent structure” (CDS) terms, respectively:14| ΔGS = ΔGENP + ΔGCDS |
Both C-PCM and IEF-PCM require solving for discretized point charges on the surface of a molecular cavity. In our calculations using C-PCM, the molecular cavities were constructed using the union of a series of atom-centered spheres whose radii are determined using each atom's van der Waals radius from the Universal Force Field68 scaled by a factor of 1.2. The boundary between solute and solvent constructed thereof is known as the solvent accessible surface (SAS). The calculations using SMD construct the molecular cavities in a similar manner but use its own set of atomic radii.69 To ensure the smoothness of potential energy surfaces (PESs) associated with molecular complexes, the switching/Gaussian method developed by Lange and Herbert15,16 was employed in both C-PCM and SMD calculations, in which the atomic spheres are discretized using Lebedev grids rather than more traditional tessellation schemes (e.g. the GEPOL algorithm70). In this work, 302 Lebedev points were used for all atoms in our calculations using C-PCM or SMD.
Unless otherwise specified, the second-generation ALMO-EDA calculations are performed with the ωB97X-V functional,71 which was shown to be one of the best-performing functionals for non-covalent interactions via extensive benchmarks72–74 and gave excellent results in our previous studies involving systems such as ion–water complexes.62,75,76 The DFT calculations employ a (99, 590) grid (99 radial shells with 590 Lebedev points on each) for the integration of the exchange–correlation (XC) functional and the SG-1 grid77 for the VV10 non-local correlation functional78 in ωB97X-V. The decomposition of the frozen interaction energy in ALMO-EDA calculations follows the “quasiclassical” scheme48,62 exclusively in this work, as we have noted in Section 2. For the separation between POL and CT, the more sophisticated fragment electrical response function (FERF) method50 featuring a well-defined basis set limit was used for the small model systems (Sections 4.1 and 4.2), while the original ALMO scheme based on partition of the AOs45,49 was used for the applications in Sections 4.3 and 4.4 with more moderate basis sets (def2-TZVPP and def2-TZVPD,79,80 respectively) given the substantial sizes of these systems.
4 Results
4.1 The sodium-chloride model complex
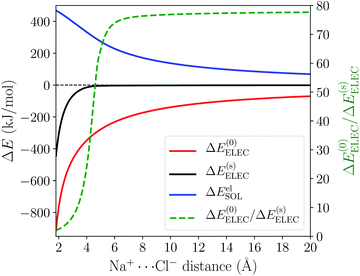
To validate the treatment of solvent effects in ALMO-EDA(solv), we first investigate a Na+⋯Cl− model complex where the two ions are separated by 20 Å and immersed in solvent with varying dielectric constant described by C-PCM. At the asymptotic limit, the strength of the electrostatic interaction between Na+ and Cl− in a dielectric medium is 1/ε of that in vacuum according to Coulomb's law, where ε is the (relative) dielectric constant of the medium. This relation is reproduced by ALMO-EDA(solv) as demonstrated in Table 1. The ΔE(0)ELEC term reflects the strength of the Coulomb interaction in vacuum, while ΔEelSOL is the correction from solute–solvent electrostatic interaction, which is an unfavorable term as its net effect is to damp the attractive Coulomb interaction between Na+ and Cl−. The sum of these two terms obtained in EDA calculations gives the effective (screened) electrostatic interaction in solution, ΔE(s)ELEC, whose relative strength against ΔE(0)ELEC shows excellent agreement with the dielectric constants (ε) specified as an initial parameter in these calculations. This agreement can also be reproduced with the widely used IEF-PCM approach (see Table S1 in the ESI†), confirming that the treatment of solvent-screened permanent electrostatics in our EDA shows correct asymptotic behavior.| ε | ΔE(0)ELEC | ΔEelSOL | ΔE(s)ELEC | ΔE(0)ELEC/ΔE(s)ELEC |
|---|---|---|---|---|
| 1 | −69.47 | 0.00 | −69.47 | 1.0 |
| 10 | −69.47 | 62.52 | −6.95 | 10.0 |
| 20 | −69.47 | 65.99 | −3.48 | 20.0 |
| 40 | −69.47 | 67.73 | −1.74 | 40.0 |
| 80 | −69.47 | 68.60 | −0.87 | 79.9 |
The distance dependence of the three electrostatics-related terms in Table 1 is shown in Fig. 4, where H2O (ε = 78.2) described by C-PCM is employed as the implicit solvent. At long range, the attraction between Na+ and Cl− is subjected to strong solvent screening, which renders the effective electrostatic interaction in solution minimal (e.g. at 5 Å ΔE(s)ELEC is only −4.3 kJ mol−1). Furthermore, the ΔE(0)ELEC/ΔE(s)ELEC ratio stays close to the asymptotic limit (78.2) in this range, albeit with more pronounced deviation when moving closer. In contrast, at shorter distances (<5 Å) this ratio decreases rapidly indicating less effective screening of the attractive electrostatics. At the minimum-energy distance (2.5 Å), ΔE(s)ELEC gains appreciable magnitude (−140 kJ mol−1) and the value of ΔE(0)ELEC/ΔE(s)ELEC lowers to 4.1. Further examining the distance dependence of ΔEelSOL reveals an inflection point at 3.35 Å, i.e., the curve starts to flatten when moving to shorter distances.
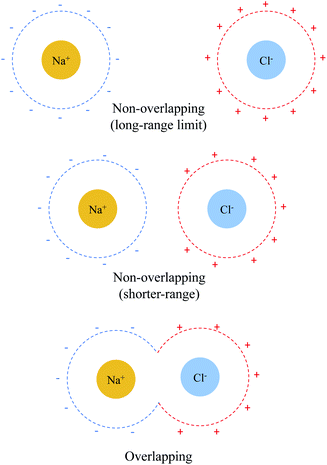
The sharp contrast between the short- and long-range behavior of these terms can be rationalized schematically with Fig. 5. In the long-range limit (upper panel), the cavities for Na+ and Cl− are well-separated and the surface charges are mainly induced by their respective nuclei and electrons, yielding strong solvent screening of the long-range electrostatics. With the decrease in inter-fragment distance, even before the cavities start to overlap, the surface charges on each cavity will be influenced by both solutes (Na+ and Cl−) simultaneously, which then largely cancel each other in the inter-fragment region (see mid-panel of Fig. 5). This would result in weakened screening and potentially explains the modest increase in the deviation from the long-range limit for ΔE(0)ELEC/ΔE(s)ELEC. Finally, when the two cavities start to overlap and merge with each other (for this system it occurs at 4.8 Å with our computational setup for PCM), as shown in the lower panel of Fig. 5, the dielectric solvent between the two fragments is “squeezed out” and the screening becomes even more incomplete. In addition, the inter-penetration of QM electron densities in the overlapping regime enhances the internal electrostatic attraction between Na+ and Cl−, which further contributes to the decrease in the value of ΔE(0)ELEC/ΔE(s)ELEC since this short-ranged effect is subjected to almost no solvent screening. These effects, all together, result in only partial screening of the attractive internal electrostatics as well as the inflection point in the magnitude of ΔEelSOL at short Na+⋯Cl− distances.
4.2 Potential energy curves for ion–water interactions
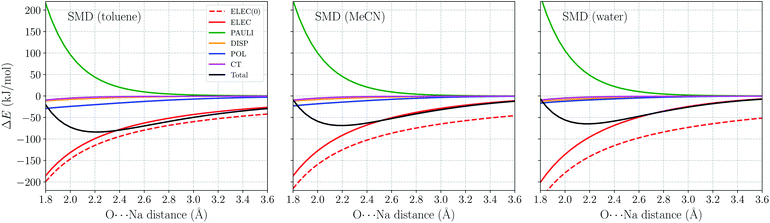
As a further validation of ALMO-EDA(solv), we employ it to investigate the distance dependence of ion–water interactions (H2O⋯Na+ and H2O⋯Cl−) in three different solvents: toluene (ε = 2.37), acetonitrile (ε = 37.5), and water (ε = 78.3). The gas-phase ALMO-EDA results for these systems are available in ref. 62. The long-range electrostatics in these systems can be depicted as charge-dipole interactions (R−2), and in the short range polarization also contributes significantly to binding (especially in the H2O⋯Na+ case). These strong interactions, however, will be diminished in solution due to solvent screening.Fig. 6 shows the ωB97X-V/def2-TZVPPD total interaction energy and its components for the H2O⋯Na+ complex vs. rO–Na in the range of 1.8–3.6 Å. Permanent electrostatics makes the largest contribution to binding at this full range despite solvent screening. Comparing the results for different solvents, one remarkable feature is that the internal electrostatic interaction, ELEC(0), becomes more favorable with the increase in solvent dielectric constant (from left to right in Fig. 6). This is because the dipole moment of an isolated H2O molecule increases when placed in a more polar solvent environment. Nonetheless, since more polar solvent also screens more strongly, the total electrostatic interaction (ELEC) shows similar strength in both solvents around equilibrium (∼2.2 Å). The strength of long-range electrostatics and the total interaction energy, on the other hand, is governed by solvent screening, as evidenced by the smaller magnitude of ELEC at 3.6 Å in water vs. toluene in Fig. 6.
Another energy component that is strongly impacted by solvent effects is polarization (POL). According to ref. 62, the gas-phase polarization energy for H2O⋯Na+ at 2.2 Å is around −25 kJ mol−1, while this value reduces to around −9 kJ mol−1 in SMD water. Similar to long-range electrostatics, POL becomes less diminished when the solvent is less polar. The other three energy components, PAULI, DISP, and CT show much smaller variance with the change of solvent. They are apparently less affected by the solvent properties, at least within the present ALMO-EDA(solv) model.
Within the SMD model, the solvent contribution to binding can be further partitioned into electrostatic and non-electrostatic contributions. The distance dependence of these two terms as well as that of the overall ΔESOL is shown in Fig. S1 in the ESI.† The non-electrostatic (CDS) term has minimal significance compared to the electrostatic contribution and vanishes in the long range when the cavities of two fragments are fully separated. It is noteworthy that the non-electronic contribution to binding does not have a definite sign: among the three solvents here, ΔEnon-elSOL is exclusively positive for toluene while negative for acetonitrile and water. This is presumably a consequence of the CDS term in SMD aiming to account in aggregate for non-electrostatic solvation effects to better reproduce experimental solvation free energies.
The solvent electrostatic contribution (ΔEelSOL), on the other hand, is repulsive over the full range (1.8–8.0 Å) for all three solvents. As in the Na+ ⋯Cl− case (Fig. 4(a)), this contribution first increases rapidly with the shortening of intermolecular distance, which damps the increasingly attractive internal electrostatic interaction. ΔEelSOL is more repulsive in solvents with larger dielectric constants, indicating their stronger screening capability. Moving into the overlapping regime, the solvent electrostatic term flattens first and then reaches a maximum when the O⋯Na+ distance is slightly below 3 Å, i.e., the magnitude of ΔEelSOL starts to decrease when the intermolecular distance is further shortened. This maximum in the solvent electrostatic contribution was also revealed by Su et al. with their LMO-EDA-PCM scheme for the water dimer.41 We attribute this behavior to the merging of fragment cavities upon the formation of complex, which leads to diminished screening of the internal electrostatic interaction (vide supra).
In the ESI† we also show the analogues of Fig. 6 and S1† for the H2O⋯Cl− complex (Fig. S2 and S3†). The ELEC and POL terms obtained from ALMO-EDA(solv) with different solvents (Fig. S2†) show similar trends as in the H2O⋯Na+ case except that the relative strength of solvent screening (indicated by their dielectric constants) has a more substantial impact on the electrostatic interaction and total interaction energy around the equilibrium distance, rendering the intermolecular binding notably stronger in the least polar solvent (toluene). In addition, the location of the maximum in the solvent electrostatic contribution (ΔEelSOL) varies from solvent to solvent: it appears at a notably longer O⋯Cl distance in H2O than in the other two solvents. This distinction between solvents is more pronounced than in the H2O⋯Na+ case where the maxima in ΔEelSOL with different solvents appear at similar distances.
4.3 Substituent effects on the stability of [FeTPP(CO2˙−)] complexes: through-space vs. through-structure mechanisms
There is tremendous research interest in homogeneous electrochemical reduction of CO2,81–83 because CO2 conversion to carbon-based fuels could underpin a future carbon-neutral economy. The initial step is activating CO2, whose one-electron reduction potential is quite unfavorable (−1.90 V vs. NHE) by comparison with the reduction potential to convert CO2 to more reduced products such as the 2e− reduction to CO (−0.53 V vs. NHE). The first function of a catalyst is thus to stabilize the activated CO2 as it drives the first reduction, and thereby reduce the thermodynamic overpotential. Molecular catalysts are of great interest for this purpose, in addition to enhancing turnover rates, and suppressing competitive side reactions such as the hydrogen evolution reaction (HER). Among available transition metal based catalysts, iron complexes have received particular attention because of the earth abundance of Fe and their low toxicity. To date, several iron catalysts with different ligand frameworks have been developed for the reduction of CO2.57,60,84–86 The most prominent family is [Fe(II)TPP]0 (TPP = tetraphenylporphyrin)87,88 and its derivatives.51,89–92 Mechanistic studies indicate that stabilizing the activated CO2 adduct intermediate can substantially improve the performance of the catalyst.51,58,93 An “electronic scaling relationship” (so-called because it reflects electronic substituent effects) between overpotential and turnover frequency (TOF) was previously established by stepwise fluorination of the phenyl groups in the TPP ligand framework.90 The four derivatives FeTPP, FeF5TPP, FeF10TPP and FeF20TPP (full fluorination of zero, one, two, and four phenyl rings, respectively) show a linear correlation between a favorable decrease in overpotential and an unfavorable decrease in TOF. This effect stems from stronger inductive effects that accompany the addition of –F substituents, which was referred to as a “through-structure” electronic effect.90A subsequent experimental study51 further demonstrated that charged substituents can break electronic scaling relationships. Introducing a positively charged trimethylammonio (TMA, –NMe3+) group to either the ortho or para position of each phenyl group yields tetra-trimethylanilinium–porphyrin complexes (Fe-o-TMA or Fe-p-TMA). Unlike the fluorinated complexes, Fe-o-TMA exhibits high TOFs at low overpotentials. In contrast, introducing the negatively charged sulfonate (–SO3−) group to the para positions to yield Fe-p-SUL results in lower TOF at a higher overpotential relative to FeTPP and Fe-o/p-TMA. Based on these results, the authors hypothesized that in these cases the strength of CO2 binding is not only controlled by the through-structure inductive effect of the electron-withdrawing groups but more importantly modulated by the long-range (through-space) electrostatic interactions between these charged substituents and the negatively charged CO2˙− moiety. This suggested mechanism could explain why Fe-o-TMA catalyzes CO2 reduction at such high TOFs.51 Further evidence for the importance of stabilizing the activated CO2 adduct is provided by the ortho hydroxyl substituted TPP complex, tetrakis-(2′,6′-dihydroxyphenyl)-porphyrin (CAT).89 This derivative is also a more active catalyst than unsubstituted FeTPP, where the stabilization of activated CO2 may also result from favorable (through-space) interactions between the hydroxyl groups and negatively charged CO2˙−.
Here we employed the ALMO-EDA(solv) approach to gain insights into the stabilization mechanisms of activated CO2 in the [FeTPP(CO2-κC)]2− adducts arising from the reaction of CO2 with the doubly reduced FeTPP ([FeTPP]2−, which is formally Fe(0)) complex (see Fig. 7 for a simplified reaction scheme). The solvent MeCN was described by C-PCM with the dielectric constant set to 35.88.94 The electronic ground state of the complex is a (broken-symmetry) triplet in an η1-κC binding mode, whose spin density contours (Fig. 8) reveal a significant amount of excess spin in the ligand framework as well as on the CO2 moiety indicating reduction of both the CO2 and the non-innocent TPP ligand. These reduced moieties are both antiferromagnetically coupled to the metal center as previously discussed in ref. 58. Therefore, this complex can be best represented as [Fe(II)(TPP˙3−)(CO2˙−-κC)]2−. For brevity, in the following discussion we omit the “κC” notation that specifies the binding mode of CO2 to the metal center.
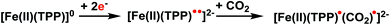 | ||
| Fig. 7 Simplified steps in the catalytic pathway of FeTPP leading to the activated CO2 intermediate. | ||
 | ||
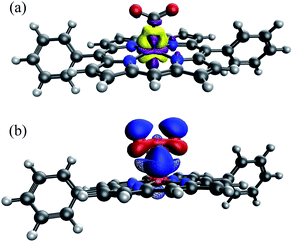
| Fig. 8 Spin density of the doubly reduced CO2 adduct [FeTPP(CO2-κC)]2− (green: excess α spin; gold: excess β spin). | ||
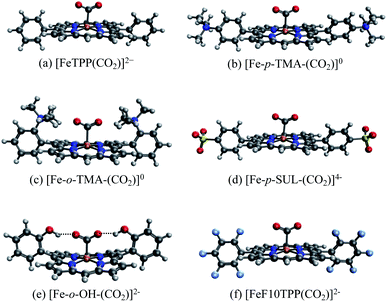
We illustrate the effects of different substituents by comparing the EDA results of complexes with varying substitutions (–H, –NMe3+, –SO3−, –OH) on the phenyl rings. To reduce the computational expense, we truncated these systems by removing two of the four phenyl groups based on the fact that the CO2 moiety is positioned in such a way that only two substituent groups can strongly interact with it (see Fig. 9). In total, we compare six different CO2 adducts with varying net charges due to the distinction in substituents: (a) unsubstituted ([FeTPP(CO2)]2−), (b) para –NMe3+ substituted ([Fe-p-TMA-(CO2)]0), (c) ortho –NMe3+ substituted ([Fe-o-TMA-(CO2)]0), (d) para –SO3− substituted ([Fe-p-SUL-(CO2)]4−), (e) ortho –OH substituted ([Fe-o-OH-(CO2)]2−), and (f) perfluorinated ([FeF10TPP(CO2)]2−). The geometries of these complexes are shown in Fig. 9.
The results of the EDA calculations depend on the choice of reference states of both fragments, i.e., the electronic states they are in when they are infinitely separated. In this example two fragmentation schemes are plausible: (i) the “natural” fragmentation that corresponds to reactants in the catalytic cycle, where a neutral CO2 (S = 0) molecule is bound to a doubly reduced iron complex (S = 1); (ii) fragmentation based on the charge population of the final product complex, giving a singly reduced metal complex (S = 3/2) and a singly reduced (activated) CO2 radical anion (CO2˙−, S = 1/2). Our results show that the former fragmentation scheme is unsuitable here due to the drastic geometry distortion energy (>200 kJ mol−1) that is associated with the bending of a neutral CO2 molecule, which would lead to EDA results that are dominated by this geometry distortion term and are thus less insightful (see Table S2 in the ESI†). In contrast, the geometry distortion term associated with the CO2˙− moiety in the latter fragmentation scheme is minimal (less than 1 kJ mol−1). Therefore, we selected the second fragmentation scheme in the following discussion, which corresponds to the binding of CO2˙− with singly reduced FeTPP and its substituted derivatives.
Our choice yields (up to) two charged fragments where the net charge on the FeTPP moiety depends on the substituents. A comparison across all these compounds without considering the solvent effect would lead to unreasonably large variations in total interaction energy due to the large variation in gas-phase electrostatic interaction (see Table S5†). Hence, we employ the new ALMO-EDA(solv) approach to better capture these interactions in solution. The EDA results for unsubstituted [FeTPP(CO2)]2− are shown in Table S4 in the ESI.† This complex is subjected to strong Pauli repulsion (634 kJ mol−1), which arises from the repulsion between the iron d-electrons and CO2˙− whose excess spin density is mainly located on the carbon atom (see Fig. S4†). The strongly favorable electrostatic interaction (−363 kJ mol−1) makes the largest contribution to binding, and is comprised of (i) a moderate gas-phase ELEC term (ΔE(0)ELEC = −94 kJ mol−1) and (ii) a substantially favorable contribution from solute–solvent interaction (ΔESOL = −269 kJ mol−1). The former can be rationalized by the attractive short-range Coulomb interaction between the CO2˙− moiety and the partially positive-charged iron center, and the latter reflects the solvent screening of the repulsive coulombic interaction between CO2˙− and the reduced π system of the TPP ligand. Despite the appreciable electrostatic contribution, the net frozen interaction is still strongly repulsive (+205 kJ mol−1), and thus both POL (−135 kJ mol−1) and CT (−123 kJ mol−1) are essential to the stabilization of CO2˙−. The electron density difference between the frozen and polarized states reveals that the occupation of iron's d-orbitals changes due to interaction with CO2˙−. This is mainly to alleviate Pauli repulsion, via depopulating the 3dz2 orbital (see Fig. 11(a)). The analysis of complementary occupied-virtual pairs (COVPs)95 further demonstrates that the charge transfer in [FeTPP(CO2)]2− is dominated by the donation from the odd-electron orbital of CO2˙− into the vacant 3dz2 orbital of Fe, where CO2˙− acts as a σ-donor as illustrated in Fig. 11(b)).
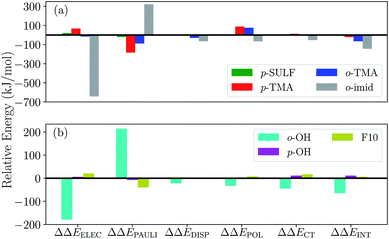
To gauge the effect of the charged substituents (ortho- and para-TMA and para-sulfonate), we compare the total interaction energies and EDA components of these adducts against the results for the unsubstituted [FeTPP(CO2-κC)]2−. The results are shown in Fig. 10(a). While para substitution with sulfonate groups alters the total charge of the CO2 adduct from −2 to −4, its effect on the total interaction strength is small. The largest changes in the EDA components occur in the ELEC and PAULI terms: the former becomes slightly less favorable due to the more negatively charged TPP ligand, while the latter is diminished (becoming less unfavorable) by a similar amount, which is possibly related to the weak electron-withdrawing inductive effect of the sulfonate group and the slightly lengthened Fe–C distance in [Fe-p-SUL-(CO2)]4− (see Table S3†). Besides the changes in ELEC and PAULI that largely cancel each other, the effects of p-sulfonate on other energy components (DISP, POL, and CT) are negligible.
The p-TMA group changes the total charge of the CO2 adduct from −2 to 0 and strengthens the total interaction by 21 kJ mol−1 relative to the unsubstituted FeTPP. Interestingly, the electrostatic interaction is made more repulsive by the p-TMA substitution relative to the unsubstituted adduct (by 67 kJ mol−1), despite the presence of positively charged TMA groups that can favorably interact with CO2˙−. Indeed, if one performs EDA in the gas phase, the ELEC term in [Fe-p-TMA-(CO2)]0 is stabilized by ∼250 kJ mol−1 relative to unsubstituted [FeTPP(CO2)]2−. However, the electrostatic attraction between the p-TMA groups and CO2˙− is screened to a large extent in the solvation environment due to the long distance between them (r(N⋯O) > 8 Å for N in TMA and O in CO2). Complemented by other secondary effects of the strongly electron-withdrawing TMA groups, the ELEC component in fact destabilizes [Fe-p-TMA-(CO2)]0 relative to the unsubstituted adduct.
Surprisingly, the largest change among EDA components appears to be the reduction in Pauli repulsion (−183 kJ mol−1). This reduction cannot be solely explained by the change in the Fe–C distance since its value is almost identical in [Fe-p-SUL-(CO2)]4− and [Fe-p-TMA-(CO2)]0 (see Table S4†). We attribute it to the decrease in electron density at the iron center, which originates from the weaker coordination of the TPP ligand due to the strong electron-withdrawing inductive effect of the TMA groups and the rigidity of the porphyrin framework that inhibits the further shortening of the Fe–N distances. The polarization term is less favorable in [Fe-p-TMA-(CO2)]0 than that in the unsubstituted adduct, which, however, is a less substantial effect compared to the reduction in Pauli repulsion, and the relative changes in dispersion and charge transfer are of even less significance. Therefore, according to the results of ALMO-EDA(solv), the enhanced CO2 stabilization resulting from the p-TMA substitution almost entirely arises from the reduction of Pauli repulsion stemming from the strong inductive effect of the TMA group, which is via a through-structure rather than through-space mechanism.
Moving the charged TMA groups closer to the CO2˙− moiety in [Fe-o-TMA-(CO2)]0 yields more significant relative stabilization than p-TMA substitution (65 kJ mol−1 relative to the unsubstituted adduct). Surprisingly, the contribution from electrostatic interaction to this relative stabilization is only 16 kJ mol−1, which serves as only the third largest contributor. As the distance between CO2˙− and TMA is still long in [Fe-o-TMA-(CO2)]0 (r(N⋯O) = 3.8 Å for N in TMA and O in CO2), the favorable electrostatic interaction remains strongly screened by the (implicit) solvent. As in the p-TMA case, the strong inductive effect of the TMA groups reduces Pauli repulsion by 89 kJ mol−1, making the largest contribution to the enhanced stabilization. Note that the reduction in the Pauli term here is not as pronounced as that in the p-TMA case, which might result from the steric effect of the bulky methyl groups that are in close contact with CO2˙−. In addition, the Fe–C distance is slightly shorter in the o-TMA complex (r(Fe–C) = 2.06 Å (o-TMA) vs. 2.10 Å (p-TMA)), which implies a stronger baseline Pauli repulsion. The close contact between methyl groups and CO2˙− also results in the strengthened dispersion interaction in the o-TMA adduct, which is 30 kJ mol−1 more favorable than that in the unsubstituted case and serves as the second largest contributor to the relative stabilization. Combining these factors together, in [Fe-o-TMA-(CO2)]0 we see stabilization of activated CO2via both through-space (enhanced dispersion and attractive electrostatics) and through-structure (reduction in Pauli repulsion due to the strong inductive effect of TMA) mechanisms, and our EDA results reveal the more significant role of the latter. The co-existence of these two mechanisms leads to larger stabilization of the o-TMA substituted adduct.
We next apply our EDA analysis to investigate the stabilization of activated CO2 within two adducts whose total charge remains unchanged (−2) upon substitution: the ortho hydroxyl substituted adduct [Fe-o-OH-(CO2)]2− and the F10 derivative. The results are shown in Fig. 10(b). The o-OH substitution stabilizes the CO2 adduct by 64 kJ mol−1, and the EDA results reveal a significantly strengthened electrostatic interaction and moderately increased DISP, POL, and CT components relative to the unsubstituted TPP adduct. Collectively these attractive terms outweigh the increase in Pauli repulsion. A pattern like this is typical of EDA results for hydrogen bonds,45,46,96 which in this case are formed between –OH groups at the ortho positions of phenyl and the oxygen atoms in CO2˙− (see Fig. 9(c)) thanks to the short distance between them (r(H⋯O) = 1.79 Å for H in o-OH and O in CO2). When one moves the hydroxyl group to the para position (p-OH), no such hydrogen bonds can be formed and consequently there is no notable difference in any of the energy components relative to the unsubstituted adduct. This stark contrast between the results for the o-OH and p-OH substituted derivatives suggests that the –OH group at the ortho position stabilizes CO2˙− almost exclusively via a through-space mechanism (hydrogen bonding). We note that the stabilization of activated CO2 through hydrogen bonds can be further enhanced by precisely tuning the position of H-donor, which was achieved by Nichols et al. by introducing amide pendants at the ortho position of the meso phenyl groups.97 In contrast to [Fe-o-OH-(CO2)]2−, the F10 derivative with only through-structure electron-withdrawing inductive effect does not lead to enhanced stabilization of CO2 since the reduction in Pauli repulsion is far less pronounced than that in [Fe-p-TMA-(CO2)]0 or [Fe-o-TMA-(CO2)]0, which is then almost fully compensated by the diminished ELEC and CT contributions.
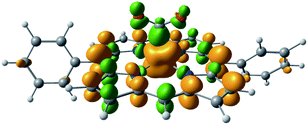
The EDA results for the TMA-substituted derivatives suggest that the strategy to stabilize activated CO2 through long-range electrostatic attraction may not be fully effective in solution due to solvent screening. However, making use of the steric effects of the substituents, one may be able to create a solvent-free “pocket” in which electrostatic interaction is almost unscreened. It was reported by Khadhraoui et al. that the introduction of four bulky, methylimidazolium-containing groups at the ortho positions of the phenyl groups in FeTPP elevates its electrocatalytic activity.98 Due to the substantial size of the substituent, we optimized the structure of the CO2 adduct of this FeTPP derivative with only one methylimidazolium-containing “arm” included (reducing the negative charge from −2 to −1), which is denoted as [Fe-o-imid-(CO2)]−. The optimized structure of this adduct is depicted in Fig. 12(a). Differing from [Fe-o-TMA-(CO2)]0, the charged moiety (imidazolium ring) is far away from the central metal, excluding the possibility of any electron-withdrawing inductive effect from this positively charged substituent. A remarkable feature of the optimized structure is that this “long-arm” substituent folds over the activated CO2 and thereby creating a small pocket that is inaccessible by solvent. The geometry also demonstrates that the activated CO2 is stabilized by both the hydrogen bonding from the amide group and the electrostatic attraction from the positively charged methylimidazolium moiety: the H⋯O distance in this hydrogen bond is 1.98 Å, and the distance between the mid-point of two N atoms in the imidazolium ring and the closest O atom in CO2 is 4.55 Å.
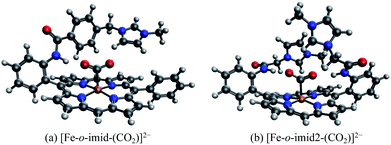 | ||
| Fig. 12 Optimized geometries for (a) [Fe-o-imid-(CO2)]−, which carries one methylimidazolium-containing group that was reported in ref. 98, and (b) [Fe-o-imid2-(CO2)]2−, which carries two modified methylimidazolium-containing groups. | ||
Our results show that [Fe-o-imid-(CO2)]− stabilizes CO2 more strongly by −49.2 kJ mol−1 relative to the unsubstituted FeTPP (see Table S4 in the ESI†), similar to the o-OH and o-TMA cases. However, it should be noted that here we only included one substituent group (“arm”) whereas the other derivatives are doubly substituted in our calculations. Therefore, once the two methylimidazolium-containing “arms” are both included, one can expect that this complex can stabilize activated CO2 more than the o-OH and o-TMA derivatives. The ALMO-EDA(solv) results (Table S4†) show that the dominant contributor to stabilization is electrostatic interaction (−85.9 kJ mol−1), which stems from both the N–H⋯O hydrogen bond and the positively charged methylimidazolium. The key difference from the p-TMA substituent is that this bulky ligand effectively “squeezes out” solvent from the space in between the activated CO2 and the positively charged moiety, rendering the attractive electrostatics nearly unscreened. Furthermore, as in the o-OH case, the strength of dispersion, polarization, and charge transfer is also enhanced by the introduction of this methylimidazolium-containing substituent, which, together with the gain in attractive electrostatics, contribute to this more stabilized CO2 adduct.
In order to further optimize this interaction motif, we removed the phenyl group in the methylimidazolium-containing “arm”, which moves the methylimidazolium moiety closer to the CO2 moiety. The optimized structure for this adduct (denoted as [Fe-o-imid2-(CO2)]0 since the second substituent is added for a better comparison with the results of other derivatives) is shown in Fig. 12(b), in which the distance between the mid-point of two N atoms in the imidazolium ring and the closest O atom in CO2 reduces to 3.74 Å. The stabilization energy relative to the unsubstituted adduct is −143.5 kJ mol−1, which is significantly larger than that of the second most stabilized o-TMA and o-OH derivatives (see Fig. 10(a)). The relative stabilization arising from the electrostatic attraction is by far the strongest among the adducts that we investigated (−642.0 kJ mol−1), and we estimate that −140 kJ mol−1 out of that stems from the two hydrogen bonds (see the “NH-ref” results in Table S4†) and the rest (about −500 kJ mol−1) from the imidazolium rings. These results indicate the importance of taking solvent effects into account if one wants to harness through-space Coulomb interaction in solution and pursue the promise of bulky, flexible substituents that can form a solvent-free “active” pocket mimicking that in enzymes to facilitate much stronger electrostatic interaction with CO2.
It is important to point out that we focused here on the concept of strengthening the binding of activated CO2 in adducts as that was presumed to accelerate catalysis. However, the substituents may also affect other intermediates in a catalytic cycle. This is illustrated by the ortho hydroxyl substituted TPP complex, CAT, where the hydroxyl group stabilizes the activated CO2 and also leads to a fast intramolecular protonation pathway.58 Ultimately, detailed mechanistic studies are necessary to fully unravel the influence of each substituent on the catalytic activity.
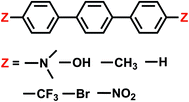
4.4 Electron transfer from terphenyl˙− to CO2: substituent effects on the intermolecular binding of reactant and product complexes
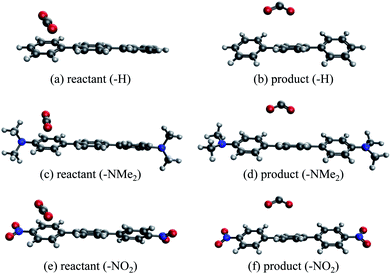
An alternative to transition metal based catalysts for CO2 reduction is organic (photo)redox catalysts, which can be more environment-friendly, economical, and are likewise highly tunable with substituents.99 These catalysts access their electronic excited states through UV-Vis absorption and are subsequently quenched, yielding a reactive radical species that serves as the electron donor to CO2.99,100 A prominent class of examples are oligo(p-phenylenes) (OPPs), which, for instance, are able to catalyze hydrocarboxylation from CO2.53 The introduction of different substituents alters the absorption wavelength but also impacts the rate of electron transfer. Some of us recently101 investigated the substituent effects on the calculated rate of electron transfer (ET) reaction from an OPP radical anion to molecular CO2 using double terminal-substituted p-terphenyl as examples. We have shown that electron-donating groups (EDGs) facilitate this reaction in general by increasing the free energy driving force (ΔG in Marcus theory102) since they elevate the LUMO level of OPP. Besides the reductive potential of OPP/OPP˙−, the difference in the association energies of the reactant (OPP˙−⋯CO2) and product (OPP⋯CO2˙−) complexes in solution, ΔΔEINT = ΔEINT(Rr) − ΔEINT(Rp), also contributes to the free energy driving force (Rr and Rp denote optimized structures for the reactant and product states, respectively). Here we employ ALMO-EDA(solv) to investigate the substituent effects on the association energies of the reactant and product complexes in CH2Cl2 (ε = 8.93) described by the SMD model, which will afford us deeper insight into how these chemical modifications affect the reactivity of OPPs as photoredox catalysts.The geometries of the reactant and product complexes are directly taken from our previous work,101 which were optimized on their respective diabatic PESs constructed from constrained DFT (CDFT)103,104 calculations at the B3LYP-D3(BJ)/6-311G(d,p)105–107 level of theory with C-PCM. As illustrative examples, in Fig. 13 we show the optimized structures of the reactant and product complexes between CO2 (or CO2˙−) and p-terphenyl˙− (or neutral p-terphenyl) substituted with dimethylamino (–NMe2) and nitro (–NO2) groups. Compared to the reactant complexes where CO2 is linear and mainly interacting with one of the terminal phenyl groups, in the product state the CO2 moiety is bent and moves closer to the middle ring of p-terphenyl. By contrast with the adducts with FeTPP where CO2˙− is ligated to Fe through the κC mode (see Section 4.3), here in the product state the two oxygen atoms of CO2˙− are in closer contact with the p-terphenyl moiety, an orientation that is favored by these dispersion-dominated anion-π interactions (vide infra).
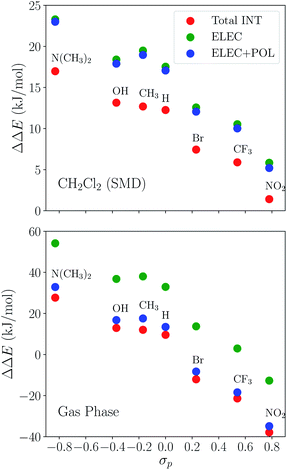
The substituent effect on the difference between interaction energies in the reactant and product states (ΔΔEINT) in CH2Cl2 solution is exhibited in the upper panel of Fig. 14 with three electron-donating (–NMe2, –OH, –CH3) and three electron-withdrawing (–Br, –CF3, –NO2) groups. The strength of the electronic effects of these substituent groups can be characterized using their Hammett parameters108 (σp): more negative (positive) σp indicates stronger electron-donating (withdrawing) ability. It is shown that the difference in interaction energies decreases monotonically with increases in σp, i.e., strong electron-withdrawing groups (EWGs) such as –NO2 facilitate the stabilization of the product complex relative to the reactant. Relative to the unsubstituted species, the differential product stabilization by the strongest EWG, –NO2, is over 10 kJ mol−1. ALMO-EDA(solv) reveals that this prominent substituent effect is dominated by electrostatics despite the presence of solvent (see Table S6 in ESI† for the full EDA results). As shown in the left panel of Fig. 14, ΔΔEELEC reproduces the trend in ΔΔEINT with only one marginal exception (–CH3).
To demonstrate the effect of solvent on the trend in ΔΔEINTversus σp, we also performed ALMO-EDA calculations for the same set of complexes in vacuum (see Table S7 in ESI† for the complete results). The results for the total interaction energy and the ELEC component are shown in the lower panel of Fig. 14. While the same trend in ΔΔEINT (monotonically decrease with increasing σp) is reproduced without solvent, the magnitude of ΔΔEINT with different substituent groups exhibits a much wider range, which, once again, mainly results from the larger variation in ΔΔEELEC in vacuum. In contrast to the solution phase where the polarization component exhibits only minimal effects on ΔΔEINT, in the gas phase, POL stabilizes the product complex by ∼20 kJ mol−1 relative to the reactant for these complexes. The contrast between the upper and lower panels of Fig. 14 demonstrates the attenuation of substituent effects on the differential interaction energies due to solvent screening.
In our previous study101 where the ALMO-EDA calculations were performed in vacuum at the B3LYP-D3(BJ)/6-311G(d,p) level of theory, we identified CT as another main contributor to the stabilization of the product complexes relative to the reactant ones and also to the trend in substituent effects. This contradicts the gas-phase ALMO-EDA results obtained here with ωB97X-V/def2-TZVPD, according to which CT only makes a minimal contribution to each complex's ΔΔEINT (see the comparison between Tables S7 and S8 in the ESI†). We ascribe this discrepancy to the more substantial delocalization error109,110 associated with the B3LYP functional than that of ωB97X-V, which, as shown in Table S10 in the ESI,† has a more pronounced effect in the gas phase. We refer the reader to Section S3 in the ESI† for a detailed discussion.
We then turn to the full ALMO-EDA(solv) results for the reactant and product complexes to gain further insights into the substituent effects on ΔΔEINT revealed in Fig. 14. The reactant complexes (Fig. 15(a)) are mainly bound by electrostatic and dispersion interactions, which, taken together, overcome the Pauli repulsion between p-terphenyl˙− (or its substituted derivatives) and the neutral CO2 moiety. Moderate substituent effects are exhibited among the reactant complexes, where the EDGs yield more attractive total interactions in general (e.g. the NMe2-substituted complex is more favorable than NO2-substituted by ∼3 kJ mol−1). This trend, as revealed by the EDA results, mainly stems from the enhancement in electrostatic interaction with stronger electron-donating substituents. The same trend is also exhibited in the strength of POL and CT across different substituents, despite the relatively small magnitude of these two components. The product complexes, on the other hand, are not as strongly bound as in their respective reactant state, and they are mainly stabilized by dispersion interaction according to our EDA results (Fig. 15(b)). The magnitude of the total interaction is strongly impacted by the substituent group on the p-terphenyl moiety: with EDGs (–NMe2, –OH, and –CH3), the intermolecular binding between terphenyl and CO2˙− is of only minimal strength (less favorable than −1 kJ mol−1), while with EWGs (–Br, –CF3, and –NO2) the interaction becomes increasingly more favorable with the increase in substituent's electron-withdrawing ability (σp). Note that the resulting interaction energy for the NMe2-substituted product complex is net repulsive (+1.96 kJ mol−1), which most likely arises from the distinct levels of theory that were used in our previous CDFT geometry optimizations101 and the ALMO-EDA(solv) calculations in the present paper. Similar to the reactant complexes, the substituent effects on the total interaction strength in the product state is also dominated by the ELEC component, where the EWGs are shown to strengthen the binding by reducing the electrostatic repulsion between CO2˙− and the π electrons on the p-terphenyl moiety.
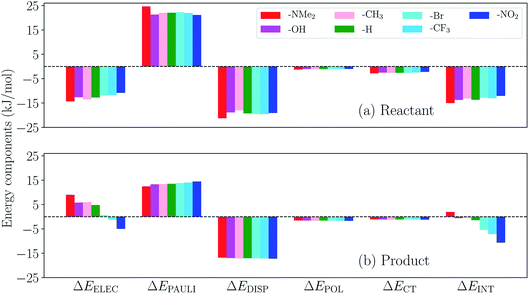 | ||
| Fig. 15 ALMO-EDA(solv) results (in kJ mol−1) for the (a) reactant and (b) product complexes between p-terphenyl and CO2 (one of these two species carries −1 charge) with different substituent groups. | ||
To summarize, the substituent effects on the intermolecular binding strength of the reactant and product p-terphenyl⋯CO2 radical anion complexes exhibit opposite trends, where EWGs diminish and enhance the interaction in the reactant and product states, respectively. While dispersion contributes significantly to binding in both states, the substituent effects are mainly controlled by the electrostatic component in both states despite the presence of solvent environment. These two opposite trends, combined together, lead to the trend shown in Fig. 14 where EWGs yield more strongly bound product complexes relative to the reactant ones. Interestingly, the trend in ΔΔEINT with respect to varying σp is opposite to that in the total free energy change (ΔG) upon the electron transfer (ET), where EDGs yield more favorable driving forces.101 This implies that although EWGs assist in stabilizing the product complexes, they are unable to reverse the trend in the free energy driving force dominated by the gap between the monomer energies before and after ET. In Table S11 in the ESI,† we show the comparison between ΔΔEINT and the energy associated with the reactant-to-product electronic transitions at the monomer level (denoted as ΔEPREP) for this series of complexes.
5 Conclusions
In this work, we have developed the ALMO-EDA(solv) scheme to incorporate solvation effects described by dielectric continuum models into the second-generation ALMO-EDA based on DFT calculations.46 This method possesses the following main features:(1) The implicit solvent environment is included in the construction of all states across the EDA procedure. Hence all energy differences (ΔEFRZ, ΔEPOL, and ΔECT) are always computed between two consecutive states that are both properly solvated.
(2) A new term, ΔESOL, is introduced to describe the direct change in solute–solvent interaction energy upon the formation of the frozen complex. In most generic cases, it comprises both electrostatic and non-electrostatic components, which can further be combined into the ELEC and PAULI components of the (internal) frozen interaction energy.
ALMO-EDA(solv) consistently incorporates continuum solvent effects, which permits study of solvation effects on each energy component in a systematic, physically motivated manner. To validate our EDA scheme, we first investigated the electrostatics-related terms using a solvated Na+⋯Cl− model complex. Our EDA reproduces the correct bulk limit for long-range electrostatics in solvent. We also rationalized diminished screening in the short range. We next analyzed the distance dependence of the energy components produced by ALMO-EDA(solv) for the H2O⋯Na+ and H2O⋯Cl− complexes and demonstrated how solvents with varying dielectric constants affect the net strength of permanent electrostatics and polarization in these systems. The results further confirmed that ALMO-EDA(solv) yields physically sensible results for the energy components of these simple interactions in the solution phase and correctly reflects the trend in the relative strength of solvent effect.
We then employed ALMO-EDA(solv) to investigate more complex chemical systems related to catalysis of CO2 reduction reactions. We first considered CO2 complexes with doubly reduced FeTPP (TPP = tetraphenylporphyrin) and its substituted derivatives.51,90 We found that the most strongly bound o-TMA-substituted complex is not mainly stabilized via through-space electrostatic attraction as was presumed (since the solvation environment screens this interaction significantly). Instead, it mainly benefits from reduced Pauli repulsion compared to the unsubstituted [FeTPP(CO2-κC)]2− complex. This originates from the substantial electron-withdrawing inductive effect of the positively charged trimethylammonio groups that reduces electron density around the Fe center and give rise to a more Lewis acidic metal center. This stabilization is thus via a through-structure mechanism. Another strongly bound complex with o-OH substitution, in contrast, is mainly stabilized via hydrogen bonding between the o-OH groups and the negatively charged CO2 moiety, which is exclusively a through-space effect. Our study thus provides new insights into how substituent effects influence the ability of FeTPP to stabilize activated CO2. Inspired by the EDA results and the ligand reported in ref. 98, we designed a bulky, floppy substituent group that contains a positively charged methylimidazolium moiety. When introduced to the ortho positions of the phenyl groups in FeTPP, they can create a solvent-inaccessible “pocket” in that stabilization of activated CO2via long-range Coulomb interaction can be achieved due to the removal of solvent screening effects.
Second, we investigated complexes associated with the electron transfer reaction from p-terphenyl˙− (and its double terminal-substituted derivatives) to CO2. We demonstrated that differences between the interaction energies in the reactant and product states (ΔΔEINT) are considerably modulated by the substituents, where electron-withdrawing groups were shown to stabilize the product complexes while moderately destabilizing the ones in the reactant state. Our EDA results further revealed that although dispersion plays an important role in the formation of both reactant and product complexes, the substituent tuning of ΔΔEINT is almost entirely achieved through modulating the electrostatic component (ΔEELEC) especially that in the product state. This example shows how ALMO-EDA(solv) assists in elucidating the nature of intermolecular interactions and mechanisms of chemical processes in the solution phase.
Finally, we shall note some of the limitations of the present ALMO-EDA(solv) scheme. First, as we have noted in Section 2, currently available DFT-based EDA schemes including our approach are most likely unable to fully describe the many-body solvent effect on dispersion interactions. Second, the current ALMO-EDA(solv) scheme is limited to the decomposition of single-point (vertical) interaction energies, and it is certainly desirable to further extend its capability to enable analysis of molecular property shifts in solution based upon our previously developed adiabatic ALMO-EDA scheme.111 This would require the development of nuclear gradients for the FRZ and POL intermediate states in the presence of implicit solvent. Besides these limitations from the perspective of EDA, one should also bear in mind that there are many other molecular approaches to describe solvent effects in modern theoretical chemistry that are more sophisticated than the relatively simple dielectric continuum model. It is an interesting challenge to make an EDA scheme compatible with those more advanced solvation models. These limitations, on the other hand, provide a wide range of future opportunities to further extend the treatment of solvation effects in ALMO-EDA calculations.
Conflicts of interest
The authors declare the following competing financial interest(s): M. H.-G. is a part-owner of Q-Chem Inc.Acknowledgements
Y. M., M. L., and M. H.-G. acknowledge support from the U.S. National Science Foundation through Grant No. CHE-1955643, and additional support from CALSOLV. K. J. K. acknowledges USC's Graduate Fellowship (2018–19) and the Mork Fellowship (2019–20). S. M. S. acknowledges support from USC's startup funds. J. S. D and C. J. C. were supported by the Director, Office of Science, Office of Basic Energy Sciences, and the Division of Chemical Sciences, Geosciences, and Bioscience of the U.S. Department of Energy at Lawrence Berkeley National Laboratory (Grant No. DE-AC02-05CH11231 to C. J. C.). C. J. C. is a CIFAR Fellow. Y. M. thanks Dr Xiaotian Qi for inspiring this development, Prof. John M. Herbert and Dr Zhi-Qiang You for the help on solvation models in Q-Chem, and Prof. Yihan Shao for fruitful discussions.Notes and references
- G. T. de Jong and F. M. Bickelhaupt, J. Chem. Theory Comput., 2007, 3, 514–529 CrossRef CAS.
- J. J. Varghese and S. H. Mushrif, React. Chem. Eng., 2019, 4, 165–206 RSC.
- J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027–2094 CrossRef CAS.
- C. J. Cramer and D. G. Truhlar, Chem. Rev., 1999, 99, 2161–2200 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS.
- A. Klamt and G. Schürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 1993, 799–805 RSC.
- A. Klamt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 699–709 CAS.
- T. N. Truong and E. V. Stefanovich, Chem. Phys. Lett., 1995, 240, 253–260 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS.
- E. Cances, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef CAS.
- B. Mennucci, E. Cances and J. Tomasi, J. Phys. Chem. B, 1997, 101, 10506–10517 CrossRef CAS.
- D. M. Chipman, J. Chem. Phys., 2000, 112, 5558–5565 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- A. W. Lange and J. M. Herbert, J. Phys. Chem. Lett., 2010, 1, 556–561 CrossRef CAS.
- A. W. Lange and J. M. Herbert, J. Chem. Phys., 2010, 133, 244111 CrossRef.
- A. V. Marenich, R. M. Olson, C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2007, 3, 2011–2033 CrossRef CAS.
- C. J. Cramer and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 760–768 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2013, 9, 609–620 CrossRef CAS.
- J.-L. Fattebert and F. Gygi, J. Comput. Chem., 2002, 23, 662–666 CrossRef CAS.
- J.-L. Fattebert and F. Gygi, Int. J. Quantum Chem., 2003, 93, 139–147 CrossRef CAS.
- D. A. Scherlis, J.-L. Fattebert, F. Gygi, M. Cococcioni and N. Marzari, J. Chem. Phys., 2006, 124, 074103 CrossRef.
- J. Dziedzic, H. H. Helal, C.-K. Skylaris, A. A. Mostofi and M. C. Payne, Europhys. Lett., 2011, 95, 43001 CrossRef.
- C. J. Stein, J. M. Herbert and M. Head-Gordon, J. Chem. Phys., 2019, 151, 224111 CrossRef.
- M. J. Phipps, T. Fox, C. S. Tautermann and C.-K. Skylaris, Chem. Soc. Rev., 2015, 44, 3177–3211 RSC.
- E. Pastorczak and C. Corminboeuf, J. Chem. Phys., 2017, 146, 120901 CrossRef.
- L. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1345 Search PubMed.
- G. Bistoni, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1442 CAS.
- Y. Mao, M. Loipersberger, P. R. Horn, A. Das, O. Demerdash, D. S. Levine, S. P. Veccham, T. Head-Gordon and M. Head-Gordon, submitted.
- J. C. Prentice, J. Aarons, J. C. Womack, A. E. Allen, L. Andrinopoulos, L. Anton, R. A. Bell, A. Bhandari, G. A. Bramley and R. J. Charlton, et al., J. Chem. Phys., 2020, 152, 174111 CrossRef CAS.
- M. J. Phipps, T. Fox, C. S. Tautermann and C.-K. Skylaris, J. Chem. Theory Comput., 2016, 12, 3135–3148 CrossRef CAS.
- M. Phipps, T. Fox, C. Tautermann and C.-K. Skylaris, J. Chem. Theory Comput., 2017, 13, 1837–1850 CrossRef CAS.
- R. Cammi, F. O. del Valle and J. Tomasi, Chem. Phys., 1988, 122, 63–74 CrossRef CAS.
- K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–340 CrossRef CAS.
- K. Morokuma, Acc. Chem. Res., 1977, 10, 294–300 CrossRef CAS.
- J. Contador, M. Aguilar, M. Sánchez and F. O. del Valle, J. Mol. Struct.: THEOCHEM, 1994, 314, 229–239 CrossRef.
- R. W. Gora, W. Bartkowiak, S. Roszak and J. Leszczynski, J. Chem. Phys., 2004, 120, 2802–2813 CrossRef CAS.
- D. G. Fedorov and K. Kitaura, J. Comput. Chem., 2007, 28, 222–237 CrossRef CAS.
- D. G. Fedorov and K. Kitaura, J. Phys. Chem. A, 2007, 111, 6904–6914 CrossRef CAS.
- D. G. Fedorov and K. Kitaura, J. Phys. Chem. A, 2012, 116, 704–719 CrossRef CAS.
- P. Su, H. Liu and W. Wu, J. Chem. Phys., 2012, 137, 034111 CrossRef.
- P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102 CrossRef.
- P. Su, Z. Jiang, Z. Chen and W. Wu, J. Phys. Chem. A, 2014, 118, 2531–2542 CrossRef CAS.
- P. Su, Z. Tang and W. Wu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, e1460 Search PubMed.
- R. Z. Khaliullin, E. A. Cobar, R. C. Lochan, A. T. Bell and M. Head-Gordon, J. Phys. Chem. A, 2007, 111, 8753–8765 CrossRef CAS.
- P. R. Horn, Y. Mao and M. Head-Gordon, Phys. Chem. Chem. Phys., 2016, 18, 23067–23079 RSC.
- Y. Mao, D. S. Levine, M. Loipersberger, P. R. Horn and M. Head-Gordon, Phys. Chem. Chem. Phys., 2020, 22, 12867–12885 RSC.
- P. R. Horn, Y. Mao and M. Head-Gordon, J. Chem. Phys., 2016, 144, 114107 CrossRef.
- R. Z. Khaliullin, M. Head-Gordon and A. T. Bell, J. Chem. Phys., 2006, 124, 204105 CrossRef.
- P. R. Horn and M. Head-Gordon, J. Chem. Phys., 2015, 143, 114111 CrossRef.
- I. Azcarate, C. Costentin, M. Robert and J.-M. Savéant, J. Am. Chem. Soc., 2016, 138, 16639–16644 CrossRef CAS.
- R. Francke, B. Schille and M. Roemelt, Chem. Rev., 2018, 118, 4631–4701 CrossRef CAS.
- H. Seo, M. H. Katcher and T. F. Jamison, Nat. Chem., 2017, 9, 453–456 CrossRef CAS.
- J. Song, E. L. Klein, F. Neese and S. Ye, Inorg. Chem., 2014, 53, 7500–7507 CrossRef CAS.
- J. A. Keith, K. A. Grice, C. P. Kubiak and E. A. Carter, J. Am. Chem. Soc., 2013, 135, 15823–15829 CrossRef CAS.
- C. Riplinger, M. D. Sampson, A. M. Ritzmann, C. P. Kubiak and E. A. Carter, J. Am. Chem. Soc., 2014, 136, 16285–16298 CrossRef CAS.
- M. Loipersberger, D. Z. Zee, J. A. Panetier, C. J. Chang, J. R. Long and M. Head-Gordon, Inorg. Chem., 2020, 59, 8146–8160 CrossRef CAS.
- C. Costentin, G. Passard, M. Robert and J.-M. Savéant, J. Am. Chem. Soc., 2014, 136, 11821–11829 CrossRef CAS.
- C. Costentin, M. Robert, J.-M. Savéant and A. Tatin, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 6882–6886 CrossRef CAS.
- D. Z. Zee, T. Chantarojsiri, J. R. Long and C. J. Chang, Acc. Chem. Res., 2015, 48, 2027–2036 CrossRef CAS.
- D. Z. Zee, M. Nippe, A. E. King, C. J. Chang and J. R. Long, Inorg. Chem., 2020, 59, 5206–5217 CrossRef CAS.
- Y. Mao, O. Demerdash, M. Head-Gordon and T. Head-Gordon, J. Chem. Theory Comput., 2016, 12, 5422–5437 CrossRef CAS.
- L. Yang, C. Adam, G. S. Nichol and S. L. Cockroft, Nat. Chem., 2013, 5, 1006–1010 CrossRef CAS.
- A. Tkatchenko, R. A. DiStasio Jr, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef.
- H. Stoll, G. Wagenblast and H. Preuß, Theor. Chem. Acc., 1980, 57, 169–178 Search PubMed.
- E. Gianinetti, M. Raimondi and E. Tornaghi, Int. J. Quantum Chem., 1996, 60, 157–166 CrossRef CAS.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O’Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- A. K. Rappé, C. J. Casewit, K. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef.
- M. Mantina, R. Valero, C. J. Cramer and D. G. Truhlar, Atomic radii of the elements, CRC Press, London, 2013, vol. 94 Search PubMed.
- J.-L. Pascual-ahuir, E. Silla and I. Tunon, J. Comput. Chem., 1994, 15, 1127–1138 CrossRef CAS.
- N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924 RSC.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS.
- L. A. Burns, J. C. Faver, Z. Zheng, M. S. Marshall, D. G. Smith, K. Vanommeslaeghe, A. D. MacKerell Jr, K. M. Merz Jr and C. D. Sherrill, J. Chem. Phys., 2017, 147, 161727 CrossRef.
- L. Goerigk, A. Hansen, C. A. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- Y. Mao, Y. Shao, J. Dziedzic, C.-K. Skylaris, T. Head-Gordon and M. Head-Gordon, J. Chem. Theory Comput., 2017, 13, 1963–1979 CrossRef CAS.
- Y. Mao, Q. Ge, P. R. Horn and M. Head-Gordon, J. Chem. Theory Comput., 2018, 14, 2401–2417 CrossRef CAS.
- P. M. Gill, B. G. Johnson and J. A. Pople, Chem. Phys. Lett., 1993, 209, 506–512 CrossRef CAS.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef.
- A. M. Appel, J. E. Bercaw, A. B. Bocarsly, H. Dobbek, D. L. DuBois, M. Dupuis, J. G. Ferry, E. Fujita, R. Hille, P. J. A. Kenis, C. A. Kerfeld, R. H. Morris, C. H. F. Peden, A. R. Portis, S. W. Ragsdale, T. B. Rauchfuss, J. N. H. Reek, L. C. Seefeldt, R. K. Thauer and G. L. Waldrop, Chem. Rev., 2013, 113, 6621–6658 CrossRef CAS.
- R. Francke, B. Schille and M. Roemelt, Chem. Rev., 2018, 118, 4631–4701 CrossRef CAS.
- K. Elouarzaki, V. Kannan, V. Jose, H. S. Sabharwal and J. M. Lee, Adv. Energy Mater., 2019, 9, 1900090 CrossRef.
- L. Chen, Z. Guo, X.-G. Wei, C. Gallenkamp, J. Bonin, E. Anxolabéhère-Mallart, K.-C. Lau, T.-C. Lau and M. Robert, J. Am. Chem. Soc., 2015, 137, 10918–10921 CrossRef CAS.
- H. Takeda, C. Cometto, O. Ishitani and M. Robert, ACS Catal., 2017, 7, 70–88 CrossRef CAS.
- J. Derrick, M. Loipersberger, R. Chatterjee, D. Iovan, P. T. Smith, K. Chakarawet, J. Yano, J. R. Long, M. Head-Gordon and C. Chang, J. Am. Chem. Soc., 2020 DOI:10.1021/jacs.0c10664.
- M. Hammouche, D. Lexa, J. Savéant and M. Momenteau, J. Electroanal. Chem., 1988, 249, 347–351 CrossRef CAS.
- I. Bhugun, D. Lexa and J.-M. Savéant, J. Am. Chem. Soc., 1996, 118, 1769–1776 CrossRef CAS.
- C. Costentin, S. Drouet, M. Robert and J.-M. Savéant, Science, 2012, 338, 90–94 CrossRef CAS.
- I. Azcarate, C. Costentin, M. Robert and J.-M. Savéant, J. Phys. Chem. C, 2016, 120, 28951–28960 CrossRef CAS.
- R. B. Ambre, Q. Daniel, T. Fan, H. Chen, B. Zhang, L. Wang, M. S. Ahlquist, L. Duan and L. Sun, Chem. Commun., 2016, 52, 14478–14481 RSC.
- Y. Okabe, S. K. Lee, M. Kondo and S. Masaoka, J. Biol. Inorg. Chem., 2017, 22, 713–725 CrossRef CAS.
- J.-M. Savéant, Chem. Rev., 2008, 108, 2348–2378 CrossRef.
- L. G. Gagliardi, C. B. Castells, C. Rafols, M. Rosés and E. Bosch, J. Chem. Eng. Data, 2007, 52, 1103–1107 CrossRef CAS.
- R. Z. Khaliullin, A. T. Bell and M. Head-Gordon, J. Chem. Phys., 2008, 128, 184112 CrossRef.
- Y. Mao and M. Head-Gordon, J. Phys. Chem. Lett., 2019, 10, 3899–3905 CrossRef CAS.
- E. M. Nichols, J. S. Derrick, S. K. Nistanaki, P. T. Smith and C. J. Chang, Chem. Sci., 2018, 9, 2952–2960 RSC.
- A. Khadhraoui, P. Gotico, B. Boitrel, W. Leibl, Z. Halime and A. Aukauloo, Chem. Commun., 2018, 54, 11630–11633 RSC.
- N. A. Romero and D. A. Nicewicz, Chem. Rev., 2016, 116, 10075–10166 CrossRef CAS.
- M. H. Shaw, J. Twilton and D. W. MacMillan, J. Org. Chem., 2016, 81, 6898–6926 CrossRef CAS.
- K. J. Kron, S. J. Gomez, Y. Mao, R. J. Cave and S. Mallikarjun Sharada, J. Phys. Chem. A, 2020, 124, 5359–5368 CrossRef CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599 CrossRef CAS.
- Q. Wu and T. Van Voorhis, Phys. Rev. A, 2005, 72, 024502 CrossRef.
- Q. Wu and T. Van Voorhis, J. Phys. Chem. A, 2006, 110, 9212–9218 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96–103 CrossRef CAS.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Science, 2008, 321, 792–794 CrossRef CAS.
- D. Hait and M. Head-Gordon, J. Phys. Chem. Lett., 2018, 9, 6280–6288 CrossRef CAS.
- Y. Mao, P. R. Horn and M. Head-Gordon, Phys. Chem. Chem. Phys., 2017, 19, 5944–5958 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: additional results and structures of the investigated complexes. See DOI: 10.1039/d0sc05327a |
| ‡ These two authors contributed equally. |
| § Present address: Department of Chemistry, Stanford University, Stanford, CA 94305, USA. |
| This journal is © The Royal Society of Chemistry 2021 |