Open Access Article
Open Access ArticleHolmium(III) molecular nanomagnets for optical thermometry exploring the luminescence re-absorption effect†
Junhao
Wang
 a,
Jakub J.
Zakrzewski
a,
Jakub J.
Zakrzewski
 b,
Mikolaj
Zychowicz
b,
Mikolaj
Zychowicz
 bc,
Veacheslav
Vieru
bc,
Veacheslav
Vieru
 cd,
Liviu F.
Chibotaru
cd,
Liviu F.
Chibotaru
 c,
Koji
Nakabayashi
c,
Koji
Nakabayashi
 a,
Szymon
Chorazy
a,
Szymon
Chorazy
 *b and
Shin-ichi
Ohkoshi
*b and
Shin-ichi
Ohkoshi
 *a
*a
aDepartment of Chemistry, School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan. E-mail: ohkoshi@chem.s.u-tokyo.ac.jp
bFaculty of Chemistry, Jagiellonian University, Gronostajowa 2, 30-387 Kraków, Poland. E-mail: chorazy@chemia.uj.edu.pl
cTheory of Nanomaterials Group, Katholieke Universiteit Leuven, Celestijnenlaan 200F, 3001 Leuven, Belgium
dMaastricht Science Programme, Faculty of Science and Engineering, Maastricht University, Paul-Henri Spaaklaan 1, 6229 EN Maastricht, The Netherlands
First published on 30th October 2020
Abstract
Coordination complexes of lanthanide(3+) ions can combine Single-Molecule Magnetism (SMM) with thermally modulated luminescence applicable in optical thermometry. We report an innovative approach towards high performance SMM-based optical thermometers which explores tunable anisotropy and the luminescence re-absorption effect of HoIII complexes. Our concept is shown in dinuclear cyanido-bridged molecules, {[HoIII(4-pyridone)4(H2O)2][MIII(CN)6]}·nH2O (M = Co, 1; Rh, 2; Ir, 3) and their magnetically diluted analogues, {[HoIIIxYIII1–x(4-pyridone)4(H2O)2][MIII(CN)6]}·nH2O (M = Co, x = 0.11, 1@Y; Rh, x = 0.12, 2@Y; Ir, x = 0.10, 3@Y). They are built of pentagonal bipyramidal HoIII complexes revealing the zero-dc-field SMM effect. Experimental studies and the ab initio calculations indicate an Orbach magnetic relaxation with energy barriers varying from 89.8 to 86.7 and 78.7 cm−1 K for 1, 2, and 3, respectively. 1–3 also differ in the strength of quantum tunnelling of magnetization which is suppressed by hyperfine interactions, and, further, by the magnetic dilution. The YIII-based dilution governs the optical properties as 1–3 exhibit poor emission due to the dominant re-absorption from HoIII while 1@Y–3@Y show room-temperature blue emission of 4-pyridone. Within ligand emission bands, the sharp re-absorption lines of the HoIII electronic transitions were observed. Their strong thermal variation was used in achieving highly sensitive ratiometric optical thermometers whose good performance ranges, lying between 25 and 205 K, are adjustable by using hexacyanidometallates. This work shows that HoIII complexes are great prerequisites for advanced opto-magnetic systems linking slow magnetic relaxation with unique optical thermometry exploiting a luminescence re-absorption phenomenon.
Introduction
Broad scientific interest is currently devoted to advanced opto-magnetic materials combining magnetic properties, including ferromagnetism or spin transitions, with optical functionalities such as photo-induced phase transitions or luminescence.1–8 Among modern magnetic materials, Single-Molecule Magnets (SMMs) stand at the research forefront as they reveal a slow magnetic relaxation effect resulting in the hysteresis loop of a molecular origin.9,10 It opens applications in high-density information storage,11,12 spintronics,13 and quantum computing.14 In the pursuit towards novel opto-magnetic systems, lanthanide(III) SMMs are of primary interest due to the designable conjunction of magnetic anisotropy and luminescence related to their f–f electronic transitions.15,16 They exhibit the highest anisotropic energy barriers producing the magnetic bistability even at 80 K,17,18 and form a unique class of luminescent SMMs showing magneto–optical correlations,19–27 and the perspective for magnetic switching of emission.28Recently, a research pathway consisting of the application of lanthanide SMMs in the construction of luminescent molecular thermometers emerged.29–34 Optical thermometry utilizing thermally activated luminescence of f-block metal ions was broadly investigated in the last decade35–39 as it opens the avenue to contactless temperature sensors for electronic devices,40 medical diagnostics,41 or chemical reactors.42 The molecular approach is particularly attractive due to the sensing ability at the nanoscale.40–43 When combining this property with the SMM effect, multifunctional magnetic luminescent thermometers are accessible.29–34 They can realize a multitasking concept,33,44 and they are promising building blocks for smart electromagnetic SMM-based devices with a self-monitored temperature.29
Achieving optical thermometers using lanthanide SMMs demands the simultaneous design of magnetic anisotropy and thermally modulated emission. This challenging task was realized by applying intrinsic properties of DyIII or YbIII complexes.29–34 The DyIII centres reveal very strong magnetic anisotropy,45 but their yellow luminescence is relatively weak, hampering the utility for optical thermometry.46,47 Interest was also devoted to YbIII due to its efficiently modulated NIR emission.48–50 However, its magnetic relaxation has to be induced by a direct-current (dc) magnetic field due to the strong quantum tunnelling of magnetization (QTM).51,52 These indicated a large difficulty in controlling of lanthanide anisotropy along with T-activated luminescence.
In this context, we propose the application of Ho3+ ions for high-performance SMM-based optical thermometers. The HoIII centres are rarely used for SMMs but they can reveal the zero-dc-field slow magnetic relaxation in the axial distribution of charged ligands with the support of hyperfine interactions that suppress the QTM.53–64 The classical luminescence from the HoIII f–f electronic transitions is weak,65,66 and an alternative up-conversion luminescence requires the presence of other 4f metal ions.67 In contrast, Ho3+ ions exhibit an efficient luminescent re-absorption effect due to the numerous absorption peaks in the visible range.68,69 Due to the presence of hot bands and variable thermal dependence of electronic transitions, the HoIII absorption peaks can be strongly T-dependent,70,71 which is a tool for optical thermometry.72,73 Using the re-absorption effect, these absorption peaks may be easily detected on the emission pattern of the attached luminophore.68,69 Following these perspectives, we decided to examine the idea of a HoIII-SMM-based optical thermometer. We focused on lanthanide(III)–hexacyanidometallate(III) systems as cyanido transition metal complexes are efficient in inducing of both strong lanthanide magnetic anisotropy and tunable emission properties.74–79 We selected the 4-pyridone ligands which exhibit pronounced blue emission and ensure substantial magnetic anisotropy of DyIII.79 Thus, we combined 4-pyridone with HoIII and hexacyanidometallates of CoIII, RhIII, and IrIII, used to amend the properties of attached 4f-metal ions. We report structural, magnetic, and optical properties of the series of dinuclear molecules, {[HoIII(4-pyridone)4(H2O)2][MIII(CN)6]}·nH2O (M = Co, 1; Rh, 2; Ir, 3) and their magnetically diluted analogues, {[HoxY1–x(4-pyridone)4(H2O)2][M(CN)6]}·nH2O (M = Co, x = 0.11, 1@Y; Rh, x = 0.12, 2@Y; Ir, x = 0.10, 3@Y), showing the SMM effect and optical thermometry related to the HoIII re-absorption effect within the 4-pyridone emission, with both effects modulated by [MIII(CN)6]3– ions.
Results and discussion
Structural studies
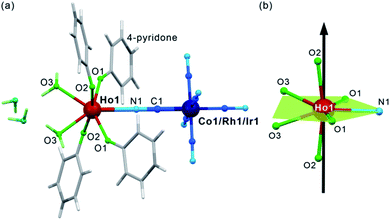
After mixing of the hot aqueous solution containing Ho3+ ions and 4-pyridone with the cold aqueous solution of [MIII(CN)6]3– (M = Co, Rh, and Ir) ions, yellowish block crystals of 1–3 were formed (see Experimental details in the ESI,†). After preliminary characterization through IR spectroscopy, TGA, and elemental analyses (Fig. S1–S2, Table S1†), the crystal structures of 1–3 were determined by using a single-crystal X-ray diffraction (SC-XRD) method (Table S2†). The structural analysis revealed that 1–3 are isostructural and consist of dinuclear {HoIII[MIII(CN)6]} molecules crystallizing together with water of crystallization in the orthorhombic Cmcm space group (Fig. 1a, S3, and S4, and Table S3†). Each molecule is built of octahedral [MIII(CN)6]3– ions bridged by a single cyanido ligand (C1–N1) to the HoIII centre coordinating also four O-atoms of the 4-pyridone ligands and two O-atoms of water molecules. The resulting seven-coordinated HoIII complexes resemble a four-blade propeller shape due to the specific alignment of 4-pyridone ligands within the ac plane (Fig. S4†) but, taking into account only atoms coordinated to HoIII, its coordination geometry can be described as a distorted pentagonal bipyramid of the pseudo-D5h symmetry (Fig. 1b, Table S4†). The axial positions are occupied by the O2 atoms of 4-pyridone ligands, and the O2–Ho1–O2 direction approximately corresponds to the easy magnetic axis of the complex (see below). The deviation from the strict D5h symmetry is represented by the imperfect axiality depicted by the O2–Ho1–O2 angles of 167.4°, 169.7°, and 168.4° for 1, 2, and 3, respectively, as well as by the non-ideal positions of O1, O3 and N1 atoms within the equatorial plane of the bipyramid (Fig. 1b and Table S3†). The cyanido-bridged molecules in 1–3 are stabilized in the respective supramolecular frameworks by the π–π stacking between aromatic groups of 4-pyridone ligands as well as the hydrogen bonding network involving terminal cyanides and water molecules. It makes the crystalline samples of 1–3 stable in air as proven by the powder X-ray diffraction (P-XRD) method confirming also the validity of the structural model for the bulk samples and their phase purity (Fig. S5†). For the studies of magnetic and optical properties, the YIII-diluted samples of 1, 2, and 3, named 1@Y, 2@Y, 3@Y, respectively, were prepared and characterized (see Experimental details). They are isostructural with 1–3 as shown by the P-XRD patterns (Fig. S5†), thus, they consist of the identical {HoIII[MIII(CN)6]} molecules dispersed in small amounts, 11%, 12%, and 10% for 1@Y, 2@Y, and 3@Y, respectively, within the supramolecular matrix composed of the analogous {YIII[MIII(CN)6]} units. We also prepared bimetallic YIII–CoIII analogue (4), and the whole series of trimetallic {HoxY1–x[CoIII(CN)6]} (x = 0.03, 0.05, 0.08, 0.16, 0.22, 0.33; 1@Y-HoxY1–xCo) molecules, also isostructural to 1–3 (Fig. S6†).Magnetic properties
Due to the presence of HoIII complexes of the pseudo-D5h geometry, which is a promising tool for the SMM effect,61,63 magnetic properties of 1–3, including direct-current (dc) and alternate-current (ac) magnetic measurements were investigated (Fig. 2, S7–S10, and Table 1). The room-temperature χMT values are 13.8, 13.7, and 13.7 cm3 mol−1 K, for 1, 2, and 3, respectively, which are close to the theoretical limit of 14.1 cm3 mol−1 K for a free Ho3+ ion. The temperature dependences of the χMT for 1–3 reveal the monotonous decrease of the signal on cooling to ca. 12 cm3 mol−1 K at T = 2 K which is due to the gradual depopulation of the mJ states within the ground 5I8 multiplet (Fig. S7†). No drastic changes in the χMT(T) plots was observed indicating a lack of significant magnetic coupling as expected for HoIII centres separated by diamagnetic 4-pyridone ligands and [MIII(CN)6]3– ions. Field dependences of magnetization at T = 2 K also show a featureless increase with increasing field to 5.0 μB at 50 kOe, which lies in the range typical for uncoupled HoIII centres (Fig. S7,† the insets).53–64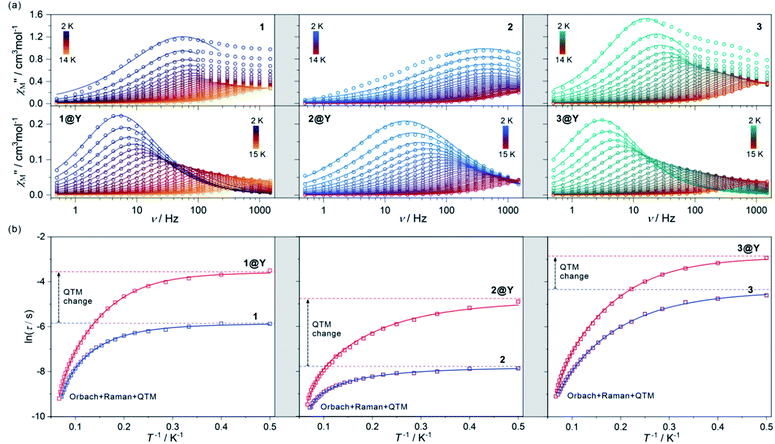 | ||
| Fig. 2 The alternate-current (ac) magnetic characteristics of 1 (left), 2 (centre), and 3 (right), and their respective magnetically diluted samples, 1@Y (left), 2@Y (centre), and 3@Y (right): the frequency dependences of the out-of-phase magnetic susceptibility, χ′′M(ν), at Hac = 3 Oe and Hdc = 0 Oe in the indicated temperature ranges with the fittings according to the generalized Debye model (a), the temperature dependences of the resulting relaxation times, shown in the form of ln(τ) = f(T−1), fitted using the combined contributions from Orbach, Raman and QTM processes (b) (see Table 1 for the best-fit parameters). The empty circle (a) and square (b) points represent the experimental data while the solid lines represent the respective fits. In (b), the additional dashed lines represent the fitted contributions from the QTM effect. The fitting of zero-dc-field magnetic data was performed for 1–3 while the simultaneous fitting of magnetic relaxation times both for zero and optimal dc fields was performed for 1@Y–3@Y (see Fig. S11–S20, Table S5† and text for details). | ||
| Fitting type | Parameter | 1 | 1@Y | 2 | 2@Y | 3 | 3@Y |
|---|---|---|---|---|---|---|---|
| Overall fitting with Orbach, Raman and QTM relaxation processes | ΔE in cm−1 | 89.8 cm−1 | 86.7 cm−1 | 78.7 cm−1 | |||
| [ΔE/kB in K] (fixed) | [129.2 K] | [124.8 K] | [113.2 K] | ||||
| τ 0/s | 3.3(4) × 10−8 | 6.0(6) × 10−8 | 4.0(6) × 10−8 | 5.5(6) × 10−8 | 4.8(2) × 10−6 | 2.3(3) × 10−7 | |
| C Raman/s−1 K−n | 1.9(3) | 0.12(2) | 64(13) | 6.6(8) | 2.2(2) | 0.20(2) | |
| n | 3.04(8) | 3.95(5) | 1.90(8) | 2.57(5) | 3.09(3) | 3.77(4) | |
| τ QTM/s | 0.00289(7) | 0.0286(9) | 0.00042(13) | 0.0086(6) | 0.0130(4) | 0.058(3) | |
| Limited fitting according to the Arrhenius law | ΔE in cm−1 | 40(2) cm−1 | 87(3) cm−1 | 25(4) cm−1 | 78(4) cm−1 | 31.3(9) cm−1 | 73.0(14) cm−1 |
| [ΔE/kB in K] | [57(3) K] | [125(4) K] | [36(6) K] | [113(6) K] | [45.1(13) K] | [105(2) K] | |
| τ 0/s | 1.8(4) × 10−6 | 2.4(7) × 10−8 | 5(2) × 10−6 | 4.2(2) × 10−8 | 4.9(4) × 10−6 | 1.0(2) × 10−7 | |
The ac magnetic characteristics gathered with an oscillating ac field of 3 Oe indicate the presence of zero-dc-field slow magnetic relaxation in 1–3 (Fig. 2, and S8–S10†). In the frequency range of 0.5–1500 Hz, the non-negligible ac signal was found from 2 K to 17 K (Fig. S8–S10†), however, the χ′M(ν) and χ′′M(ν) dependences could be analysed using a generalized Debye model for the T-range of 2–14 K (Fig. 2a). The model employing a single relaxation process was used, however, the frequency ranges were limited as the visible tails in the χ′′M(ν) plots were observed. This can be ascribed to the disturbing influence of dipolar interactions between neighbouring HoIII centres insufficiently isolated within the structures of 1–3.76,80 To prove this, the magnetically diluted analogues, 1@Y–3@Y were also examined (Fig. 2a, and S11–S20, Table S5†). They exhibit zero-dc-field slow magnetic relaxation in the only slightly extended T-range of 2–18 K (2–15 K for the fitted ac curves) in comparison to 1–3 but with the symmetrical shapes of the χ′′M(ν) maxima typical for single relaxation. Moreover, the positions of χ′′M maxima for 1–3 are almost invariant on temperature below 6 K suggesting the strong QTM effect.75 In 1@Y–3@Y, they are more dependent on the frequency and shifted toward its lower range below 100 Hz. This indicates that the magnetic dilution leads to at least partial suppression of the QTM which should be related to the cancelling of remaining magnetic interactions between HoIII centres. All these findings were quantified by analysing temperature dependences of the extracted relaxation times in 1–3 and 1@Y–3@Y (Fig. 2b, and S8–S13†). The ln(τ) versus T−1 plots for all phases strongly deviate from linearity expected for the Arrhenius-type dependence of an Orbach relaxation. Nevertheless, the higher temperature regimes were employed in fitting to the Arrhenius law (Fig. S8–S13†) which results in the effective energy barriers, ΔE lying in the range of 25–40 cm−1 (Table 1). These values increase upon magnetic dilution to the range of 73–87 cm−1. However, even for 1@Y–3@Y, the ln(τ) versus T−1 dependences still deviate from linearity suggesting the presence of the QTM and other relaxation processes such as the Raman relaxation in all investigated compounds. Therefore, the reliable discussion on the SMM effect in 1–3 and 1@Y–3@Y needs the fitting of the whole ln(τ) versus T−1 curves taking into account three accessible magnetic relaxation processes. It was performed using eqn (1):
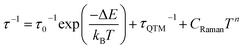 | (1) |
The best-fit parameters representing the ac magnetic data confirm the presence of three different relaxation processes (Orbach, Raman, and QTM) in 1–3 and 1@Y–3@Y. The best-fit curves with the visualized contribution from the QTM are presented in Fig. 2b while an insight into all relaxation pathways is shown in Fig. S8–S13, S15, S17, and S19–S20.† The obtained parameters prove the SMM character of 1–3 and show that the highest single-ion anisotropy represented by the highest energy barrier of an Orbach process of 89.8 cm−1 (129.2 K) is observed in 1, the slightly smaller ΔE of 86.7 cm−1 (124.8 K) in 2, and a much smaller value of 78.7 cm−1 (113.2 K) in 3. However, the strength of the QTM adopts a different trend as the slowest related relaxation time, τQTM is observed in 3, much faster in 1, and the strongest QTM in 2. The Raman relaxation also differs within 1–3. 1 and 3 show very similar contributions from this relaxation which is depicted by nearly identical, ca. T−3 dependence of the related relaxation time, τRaman, while 2 exhibits the weaker thermal variation of τRaman, close to T−2. It indicates the important role of a diamagnetic metal ion in the modification of Raman relaxation of attached paramagnetic HoIII centres which can be ascribed to the modulated phonon modes scheme going from Ho–Co (1) and Ho–Ir (3) to Ho–Rh (2) crystal lattices.81,82 In this regard, the critical role can be played partially by the distinguishable energies of numerous available vibrational states (Fig. S1†) as well as by the water content which is slightly different for the RhIII analogue (see Experimental details). The results for 1@Y–3@Y indicate that the magnetic dilution affects both the QTM and Raman relaxation pathways. The magnetic dilution leads to the stronger temperature dependence of the Raman relaxation time as depicted by the increase of the power “n” from 3.04, 1.90, and 3.09, to 3.95, 2.57, and 3.77, for 1@Y, 2@Y, and 3@Y, respectively. This can be explained by the modification of a phonon mode scheme upon the replacement of paramagnetic and heavier HoIII centres with diamagnetic and much lighter YIII centres. As the magnetic dilution is similar within the whole series of 1@Y–3@Y, the resulting changes in the Raman relaxation process were also found to be analogous. The magnetic dilution leads also to the partial suppression of the QTM as depicted by the significant slowdown of the τQTM which is in line with the shift of the χ′′M(ν) maxima to lower frequencies (Fig. 2a). The most efficient weakening of the QTM is observed in 2, while smaller QTM changes are ascribed to 1 and 3 (Fig. 2b). The final τQTM value is the highest (5.8 ms) in 3@Y which means that the slowest magnetic relaxation is achievable for HoIII–IrIII molecules.
To rationalize the differences in the experimental SMM characteristics in 1–3, the ab initio calculations of the HoIII crystal-field effect were performed (Fig. 3, and S21–S23, Tables S6–S10†). The calculations were of a CASSCF/RASSI/SINGLE_ANISO type executed within an OpenMolcas package using the experimental geometries of {Ho[M(CN)6]} molecules from the SC-XRD analysis (Fig. S21, details in the ESI†).83 In the first approach, the dinuclear molecules of 1–3 were used for the calculations. For each case, three basis sets (small, S model; large, L model; and very large, V model) differing in the applied basis function qualities for the selected parts of calculated structural fragments were employed (Table S6†). All of them reveal the whole energy splitting of the ground 5I8 multiplet of ca. 300 cm−1 in 1–3 (Tables S7–S9†). As Ho3+ is a non-Kramers ion, it is necessary to separately consider each of the 16 mJ levels of the ground multiplet as the degeneracy of 8 possible mJ doublets is not ensured.53–64 However, in all applied basis sets, the pairs of the lowest lying mJ levels of 1–3 are close in energy, and well-separated from other states lying at least 70 cm−1 higher. These ground states are of a predominant |±8〉 character (ca. 97%) with the high value of the gz component (>19.5) of their pseudo-g-tensors, as expected for the HoIII SMMs of the pseudo-D5h symmetry,61 but there are the non-negligible admixtures of others states, mainly ca. 2% of |±5〉. It results in the non-zero energy difference between the two lowest lying states (Tables S7–S9†). This tunneling gap (Δtun) directly affects the QTM strength, and should completely vanish in the QTM-free SMMs. The Δtun values in 1–3 are relatively high, lying in the range of 0.16–0.34 cm−1, which should lead to the fast QTM rather cancelling the zero-dc-field SMM effect.53–64 This is in contrast to the experimental observation of slow magnetic relaxation in 1–3 under Hdc = 0 (Fig. 2); thus, we re-considered the performed ab initio calculations. Firstly, we found that the increase of the size of the basis sets from the S to L models leads to the decrease in the Δtun values, e.g. from 0.26 to 0.18 cm−1 in 1 (Tables S7–S8†). However, the change in the very large basis sets did not follow this trend as the V model slightly overestimates the whole energy splitting (Table S9†). Thus, we expanded the calculated structural fragments by taking into account crystallization water (W models, Fig. S21†), and we repeated the ab initio calculations for all basis sets. The resulting S–W, L–W and V–W models gave the further decrease of the Δtun values to 0.12, 0.19, and 0.09 for 1, 2, and 3, respectively, for the L–W models (Table S8†). This indicates a crucial role of the second coordination sphere for the HoIII crystal-field effect in 1–3. For 3, in the L–W model showing the lowest Δtun, we also performed the calculations with the enlarged active space using a RASSCF scheme but the Δtun value remained similar (Table S10†). Due to the lowest Δtun values, we used the results of the L–W models for further discussion. They well reproduce the experiment (Fig. S7†), both the χMT(T) and M(H) plots, however, the similar magnetic curves were simulated with the other models (Fig. S22†).
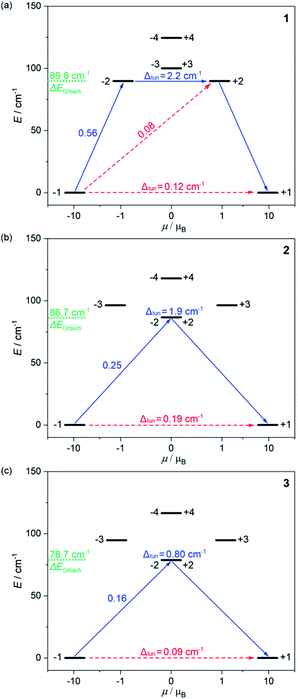 | ||
| Fig. 3 The energy splitting of the ground 5I8 multiplet of HoIII in 1 (a), 2 (b), and 3 (c) obtained from the ab initio calculations. Only the lowest energy part was presented. The resulting energy barriers of the Orbach relaxation were shown in green colour. The numbers above each arrow represent the corresponding matrix element of the transversal magnetic moment while the Δtun shows the tunnelling gap of the indicated doublets. Red arrows indicate the less possible whereas blue arrows show the most probable relaxation pathway. The scheme is obtained for the L–W models (Table S8†). | ||
The energy splitting scheme of the ground 5I8 multiplet of HoIII in 1–3 for the lowest energy region is shown in Fig. 3. The smallest tunnelling gap, Δtun is observed in 3, the slightly higher in 1, and the highest in 2, which is in good agreement with the acceleration of the QTM relaxation time, τQTM in the trend of 3, 1, and 2 (Table 1). As the magnetically diluted 1@Y–3@Y better represent the intrinsic QTM of HoIII complexes, we investigated the related values of τQTM−1 in the function of the square of the Δtun (Fig. S23†). A linear dependence suggests that the experimental QTM changes in 1–3 are exclusively due to the variable Δtun related to the composition of the ground states (Table S8†). While the Δtun values between the lowest lying pairs of mJ levels are small, the analogous tunnelling gaps for higher lying sublevels are much higher, at least 0.8 cm−1 for the whole series of 1–3. This proves that an Orbach relaxation occurs through the first excited mJ states (blue arrows in Fig. 3). Thus, the average energy positions of these mJ states represent the energy barriers of an Orbach process, ΔE. The ab initio studies reveal the highest ΔE of 89.8 cm−1 in 1, a lower of 86.7 cm−1 in 2, and the lowest of 78.7 cm−1 in 3. The validity of this trend was proved using the ΔE values in the successful fitting of the T-dependences of relaxation times (see above).
The results of ab initio calculations well rationalize the observed differences in the SMM effects of 1–3. However, the obtained Δtun values between the ground mJ sublevels remain at the level of 0.09–0.19 cm−1 for the optimal L–W models (Fig. 3).53–64 Moreover, we investigated the ac magnetism for the series of variously diluted {HoxY1–x[CoIII(CN)6]} (x = 0.03, 0.05, 0.08, 0.16, 0.22, and 0.33; 1@Y-HoxY1–xCo) systems. We found a strong correlation between the relaxation time and the amount of HoIII centres which can be assigned to the gradual weakening of the QTM effect (Fig. S24†). In particular, the above-mentioned 1@Y (x = 0.11) was shown to contain the remaining QTM effect as 1@Y-Ho0.03Y0.97Co reveals a nearly two times slower relaxation time. This indicates that ideally isolated HoIII complexes of 1–3 exhibit an almost fully quenched QTM effect which is not perfectly reflected in the results of ab initio studies. It may be related to the non-ideal crystallographic data, e.g. the imperfect findings of the hydrogen positions.83 However, the final explanation of the observed zero-dc-field SMM effects in 1–3 is related to the additional energy splitting occurring by taking into account the hyperfine interactions of magnetic moment of electrons with the nuclear spin of HoIII (I = 7/2 for 165Ho isotope of 100% abundance).53,61,84–87 We performed the field-dependent ac magnetic studies for 1@Y–3@Y revealing the characteristic oscillations of relaxation times under the increasing dc field which is the sign of hyperfine interaction (Fig. S25–S28†).61 Then, using the crystal field parameters from the ab initio calculations, we determined the energy splitting due to the hyperfine interactions (Tables S11–S15, details in the ESI†). The hyperfine parameter, Ahf of 0.025 cm−1 was optimized by comparison with the field-variable ac magnetic data on the basis of the Zeeman effect and the avoided level crossing rule (Fig. S28†). As a result, instead of one ground quasi-doublet, we obtained 8 ground hyperfine Kramer doublets, and all appeared to be very axial with the very small values of transversal gx and gy components (<0.0045) in the whole series of 1–3 (Table S15†). This indicates the efficient suppression of the QTM effect in all compounds. However, the residual non-zero transversal components of the g-tensors remain, which stays in line with the observation of a non-negligible QTM relaxation rate even for the magnetically diluted samples of 1@Y–3@Y under the optimal dc field (Fig. S14–S19†). As a result, a magnetic hysteresis loop is not detectable even at the lowest accessible temperature of 1.8 K which is typical among the reported HoIII SMMs.53–64 In 1–3, this effect can be ascribed to the insufficiently pure mJ = ±8 ground state which is related to the non-ideal D5h geometry of HoIII complexes (Fig. 1). All differences within 1–3, including the strength of the residual QTM and in the energy barriers found the rational reflection in the energy splitting modified by the hyperfine interactions (see discussion in the ESI†).
The distinguishable SMM features of 1–3 can be ascribed to the subtle structural variation (Table S3†). The HoIII complexes reveal a pentagonal bipyramidal geometry, thus, the important role in the magnitude of energy splitting, determining the ΔE, can be played by the distances from Ho1 to the axial O2 atoms of 4-pyridone bearing a partial negative charge (Fig. 2b). They are similar in 1–3 but the increasing trend in the Ho1–O2 bond lengths of 2.231, 2.233, and 2.235 Å for 1, 2, and 3, corresponds well to the decreasing ΔE from 1 to 3. The negative charge is also ascribed to the O1 atoms lying in the equatorial plane. Their distances to Ho1 also follow the increasing trend of 2.272, 2.276, and 2.278 Å for 1, 2, and 3, respectively. Moreover, their positions within the plane, represented by the O2–Ho1–O1 angles, are more deviated from the 90° in 1 (2.72°) and 2 (2.69°) than in 3 (2.37°). All these differences contribute to the stronger crystal field in 1–2. In contrast, the distance between Ho1 and the N1 atom of cyanido bridge is shorter in 2 (2.434 Å) than in 1 (2.460 Å) and 3 (2.452 Å). The shorter distance of the cyanido ligand to Ho1 in the Ho–Rh species can lead to the stronger mixing of the mJ levels giving the stronger QTM. Moreover, the average distance between Ho1 and equatorial atoms is longer in 1 and 3 (2.356 Å) than in 2 (2.346 Å) which may delimit their disturbing role in the stabilization of the |±8〉 ground state in 1 and 3 producing the lower QTM rate. These findings prove a non-innocent role of [MIII(CN)6]3– ions in modulating the HoIII SMM effect.
Optical thermometry
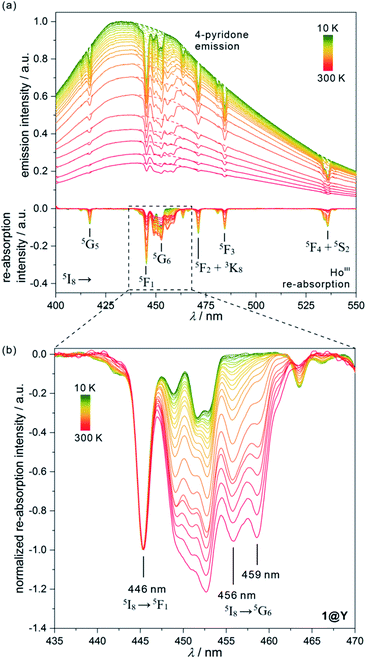
Due to the presence of multiple emissive components of HoIII, 4-pyridone, and [MIII(CN)6]3– ions,65,78,88 optical properties of 1–3 and their YIII-diluted analogues, including 1@Y–3@Y, were investigated (Fig. 4, 5, S29–S33, and Tables 3, S16–S17†). Solid-state UV-vis-NIR absorption spectra (Fig. S29†) indicate that 1–3 exhibit a strong UV absorption band at 270 nm accompanied with weaker sharp peaks in the visible region (Fig. S29†). The UV absorption can be mainly assigned to the spin-allowed π–π* electronic transitions of 4-pyridone. In 1 and 2, the d–d 1A1g → 1T2g transitions of [MIII(CN)6]3– ions also contribute to the UV absorption when another 1A1g → 1T1g transition results in the weaker band at ca. 310 nm, well distinguished only in 1.79 In 3, the 4-pyridone transitions completely dominate as the absorption of the [IrIII(CN)6]3– ion is shifted below 250 nm.88 In contrast, the weak absorption peaks covering the whole visible range can be exclusively assigned to f–f electronic transitions of HoIII centres occurring thanks to their ladder-type electronic structure (Table S16†).89 Following the strong UV and weak visible light absorption, the possible photoluminescence of 1–3 was examined. We checked various excitation wavelengths from the UV range but no distinct emission signal was observed. Only under the UV excitation around 370 nm, corresponding to the typical excitation of 4-pyridone phosphorescence of the π–π* origin,79 weak ligand-based emission was detected (Fig. S30†). This can be assigned to the strong luminescence quenching, including the re-absorption effect related to HoIII complexes, present in large numbers in 1–3. This is supported by the presence of a series of negative re-absorption peaks occurring within the broad emission band. Moreover, we detected strong room-temperature blue emission originating from 4-pyridone for 4, containing exclusively {YIII[CoIII(CN)6]} molecules (Fig. S30†). Therefore, two trimetallic derivatives with the variable Ho![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y ratio, 1@Y (1@Y-Ho0.11Y0.97Co) and 1@Y-Ho0.33Y0.67 Co, were examined, and distinct ligand emission with a series of negative HoIII-based re-absorption peaks was observed. The overall emission is weakened while the relative intensity of the negative peaks increases with the increasing amount of HoIII. We found that 1@Y exhibits a good equilibrium giving the significant ligand emission and easily detectable sharp re-absorption peaks. Therefore, for this compound and for their Rh- and Ir-based analogues, 2@Y and 3@Y, we performed detailed luminescence studies (Fig. 4 and S31–S33†).
Y ratio, 1@Y (1@Y-Ho0.11Y0.97Co) and 1@Y-Ho0.33Y0.67 Co, were examined, and distinct ligand emission with a series of negative HoIII-based re-absorption peaks was observed. The overall emission is weakened while the relative intensity of the negative peaks increases with the increasing amount of HoIII. We found that 1@Y exhibits a good equilibrium giving the significant ligand emission and easily detectable sharp re-absorption peaks. Therefore, for this compound and for their Rh- and Ir-based analogues, 2@Y and 3@Y, we performed detailed luminescence studies (Fig. 4 and S31–S33†).
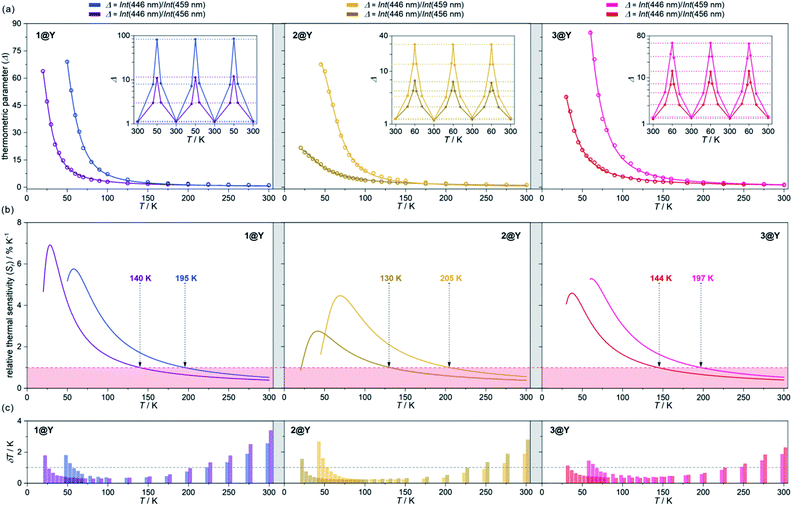 | ||
| Fig. 5 Luminescent thermometric characteristics of 1@Y (left), 2@Y (centre), and 3@Y (right) using two selected ratiometric parameters, Δ, obtained from the temperature-dependent emission spectra (Fig. 4 and S31–S33†): the experimental temperature dependences of Δ (empty circles) together with the fitted calibration curves (eqn (2), solid lines) and the repeatability of thermometric behaviour within three cooling–heating cycles in the insets (a), the temperature dependences of relative thermal sensitivity, Sr calculated from calibration curves (solid lines) with the indicated regime below 1% K−1 (coloured area) and the indicated temperature below which Sr exceeds 1% K−1 (b), and the temperature uncertainties, δT at each measurement point with the indicated limit of δT < 1 K (dashed line) (c). | ||
All YIII-diluted compounds, regardless of UV excitation, 1@Y–3@Y reveal similar ligand-based emission at 300 K, and no other emission peaks, possibly originating from [MIII(CN)6]3– electronic states,88 were detected. However, the emission maxima slightly vary from 420 nm in 3@Y, 435 nm in 1@Y, to 445 nm in 2@Y (Fig. S31–S33†). Taking 1@Y as an example, we found that, under the optimal 370 nm excitation, a series of HoIII-re-absorption-based negative peaks are observed within the 4-pyridone emission pattern (Fig. 4a). By comparison with the interpreted UV-vis absorption spectra (Table S16†), these peaks were assigned to the HoIII f–f electronic transitions from the ground 5I8 multiplet to various excited states. Upon cooling of 1@Y to 10 K, a gradual increase of overall emission intensity was detected; however, the re-absorption effect also intensified as visible in the deeper negative peaks. More importantly, we observed distinguishable changes in the strength of re-absorption peaks at different wavelengths which is a prerequisite for optical thermometry. To quantify this effect, the re-absorption peaks were extracted from the featureless ligand emission bands used as a background (Fig. 4a). The strongest re-absorption effect accompanied by the most significant thermally induced changes was detected in the 435–470 nm range related to the combined contributions from the 5I8 → 5F1 and 5I8 → 5G6 electronic transitions. We analysed this region by applying the intensity normalization to the distinct peak at 446 nm of the 5I8 → 5F1 transition (Fig. 4b). As a result, we detected a strong temperature dependence of the neighbouring re-absorption peaks whose relative intensity decreases upon cooling. Primarily, this can be explained by their different origin, that is the assignment to the 5I8 → 5G6 transition, which is expected to show distinguishable thermal variation.70,71 Considering all accessible peaks from this pattern, we found the strongest thermal changes for peaks at 456 and 459 nm. They almost disappear at low temperatures suggesting that they can be connected with the hot bands from one of the excited mJ levels of the ground 5I8 multiplet (Fig. 3). Thus, their strong T-dependence in relation to the peak at 446 nm is a combined result of the appearance of hot bands and variable thermal dependences of different electronic transitions. The analogous T-dependences of luminescence spectra and the extracted re-absorption effect were found for 2@Y and 3@Y, thus, they were analysed in an identical manner (Fig. S31–S33†).
To perform a precise characterization of the thermometric effect and discuss the differences along the series of 1@Y–3@Y, two different thermometric parameters (Δ) were defined as the ratios between the intensities of transitions located at 446 nm and two selected bands at 456 and 459 nm (Fig. 4b). These thermometric parameters strongly depend on temperature, particularly in the 25–200 K range (Fig. 5a). They correspond to the thermal variation of absorption peaks which can be mainly assigned to the role of thermally activated vibrational motions governing the intensity of the f–f electronic transitions.70,71,90,91 Within this model, applying for T-dependent absorption spectra of HoIII-based systems,70,71 the Δ values of 1@Y–3@Y can be presented using eqn (2):
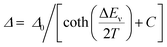 | (2) |
The current arbitrary conditions for good optical thermometers are defined as the temperature regions for which Sr > 1% K−1 along with δT < 1 K, and these boundaries were depicted in Fig. 5b and c. It is clearly seen that reliable optical thermometric behaviour was achieved in 1@Y–3@Y for the broad ranges from ca. 20 K up to 200 K. In all compounds, this region is adjusted by the selection of the re-absorption peak. The 459 nm band is more appropriate for the temperatures above 60 K but works up to even 200 K whereas the 459 nm line serves reliably from very low temperatures of 20 K but only to the limits of ca. 140 K. The operating ranges of optical thermometers are also modulated by the selection of cyanido complexes within the series of 1@Y–3@Y (Table 2). The broadest range, covering 150 K, accompanied by the highest temperature of good performance thermometry of 205 K, was achieved in 2@Y for the Δ parameter involving the 459 nm peak. This is due to the flattened calibration curve with the relatively small changes but extended within the large T-region (Fig. 5a). However, this leads to the lower values of Sr for 2@Y as depicted by the comparison of maximal thermal sensitivities within the series (Table 2). The highest Sr of 6.9% K−1 is accessible for 1@Y which is the impressive value among the optical thermometers.35–39 Slightly lower maximal Sr limits are observed in 3@Y while 2@Y exhibits significantly lower thermal sensitivities, never exceeding 4.5% K−1. All these findings indicate a non-negligible role of hexacyanidometallates in controlling of the optical thermometer performance. This is an indirect influence as the applied thermometric effect utilizes the intrinsic absorption property of HoIII and phosphorescence of the organic ligand. Moreover, the procedure for extracting the re-absorption effect (Fig. 4) made the resulting optical thermometer basically independent of the overall emission intensity which is significantly amended by the cyanido complexes exhibiting the electronic states at the variable parts of the visible range.88 However, the thermally tunable absorption properties of HoIII centres can be also affected by the cyanido complexes due to the role of their rich vibrational states such as cyanido stretching vibrations appearing in the 2100–2200 cm−1 region of the IR spectrum (Fig. S1†). The energies of these states decrease in the trend of 2 > 3 > 1,88 corresponding well to the observed improvement of the maximal thermal sensitivity (Table 2). It can be suggested that one of the vibrational modes contributing to the thermal variation of the HoIII electronic states belong to the coordinated cyanido ligand, and their energy, depending on the transition metal, plays a non-innocent role. This is in line with the recent findings on the critical role of cyanido stretching vibrations in the [M(CN)x]-dependent tuning of optical properties of f-block metal complexes.88,93 In addition to the above characterization of optical thermometry, we have also performed three thermal heating–cooling cycling experiments checking the thermometric parameters at three different temperatures (Fig. 5a). It demonstrates the perfect repeatability (>97%) of the thermometric behaviour in the whole series of 1@Y–3@Y.
| Compound | Thermometric parameter, Δ | Good thermometric performance range | Maximal Sr value (at temperature, T) |
|---|---|---|---|
| 1@Y | Int(446 nm)/Int(456 nm) | 25–140 K (115 K range) | 6.9% K −1 (T = 28 K) |
| Int(446 nm)/Int(459 nm) | 60–195 K(135 K) | 5.8% K−1 (T = 58 K) | |
| 2@Y | Int(446 nm)/Int(456 nm) | 25–130 K (105 K) | 2.7% K−1 (T = 42 K) |
| Int(446 nm)/Int(459 nm) | 55–205 K (150 K) | 4.5% K−1 (T = 69 K) | |
| 3@Y | Int(446 nm)/Int(456 nm) | 35–144 K (109 K) | 4.6% K−1 (T = 37 K) |
| Int(446 nm)/Int(459 nm) | 70–197 K (127 K) | 5.3% K−1 (T = 61 K) |
The representative region of 435–470 nm of the luminescence re-absorption spectra of 1@Y–3@Y (Fig. 4 and S31–S33†), which shows the most effective thermometric effect, can be also used for magneto–optical correlations. This part of the spectrum contains the complex pattern related mainly to the 5I8 → 5G6 electronic transitions, only partially overlapped with the bands assignable to the 5I8 → 5F1 transition. The analysis of the low-temperature (10 K) spectrum in this range provides the information regarding only the energy splitting of the excited 5G6 multiplet while the higher-temperature patterns become the complex sum of electronic transitions from various states of the ground 5I8 multiplet not only to the lowest state of the 5G6 multiplet but also to the higher-lying ones (Fig. S34†). This hampers a straightforward optical estimation of the anisotropic energy barrier (ΔE) of Orbach relaxation which is illustrated by the energy difference between the two lowest quasi-doublets of the ground multiplet (Fig. 3).19–27 However, the comparison of the low- (10 K) and high-temperature (300 K) re-absorption patterns agrees well with the calculated energy splitting of the ground multiplet determined from the ab initio calculations, including both the energy positions of the maxima related to the groups of closely lying excited states as well as the overall energy of the crystal field splitting for the ground multiplet, slightly exceeding 300 cm−1 (Fig. S34, and detailed discussion in the ESI†). Therefore, the luminescence re-absorption spectra support the results of ab initio calculations (Fig. 3, and Table S8†), thus supporting also the interpretation of magnetic relaxation effects in 1–3.
Conclusions
We report a series of dinuclear cyanido-bridged molecules, {[HoIII(4-pyridone)4(H2O)2][MIII(CN)6]} (M = Co, Rh, and Ir) together with their magnetically YIII-diluted analogues exhibiting a Single-Molecule Magnet (SMM) character thanks to the combined contributions from the pentagonal bipyramidal geometry, the axial charge distribution, and the supporting role of the hyperfine interactions. They realize a novel concept of SMM-based optical thermometers exploring a temperature-dependent luminescence re-absorption effect of HoIII centres detectable within the emission of organic ligands. We prove that the application of HoIII complexes is a promising tool for achieving both the slow magnetic relaxation effect and the highly sensitive optical thermometry. Our approach is different from the reported strategies towards magnetic optical thermometers as we explore the re-absorption effect of HoIII and commonly observed ligand-based emission. It opens a convenient route to generate the optical thermometric effect by the incorporation of HoIII centres into diverse emissive organic or inorganic matrices. This idea can be also developed in the smart SMM-based opto-magnetic devices built of HoIII magnetic molecules deposited onto the emissive surfaces. Therefore, we show a promising avenue to combine the SMM property with optical thermometry without the necessity to control luminescence quenching effects within the lanthanide complex. Moreover, we achieved high thermal sensitivity, reaching up to 6.9% K−1 at the lowest temperatures below 40 K which is the working range of SMMs, thus, such molecular systems are good candidates for SMM-based devices with self-monitoring of temperature. Our approach takes advantage of the supporting hexacyanidometallates of transition metals which were able to modulate the SMM features and the optical thermometric performance. The best-performance SMM, in the context of the most efficient suppression of the QTM, was obtained using heavy [IrIII(CN)6]3– ions, which have never before been applied for the construction of molecular nanomagnets. Their utility in the further improvement of HoIII-based SMMs will be now investigated along with testing of diverse emissive ligands and coordination skeletons cooperating with HoIII centres in the generation of multifunctional opto-magnetic materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financed by the National Science Centre of Poland within the OPUS-15 project, Grant no. 2018/29/B/ST5/00337, and by the Japanese Society for the Promotion of Sciences (JSPS) within the Grant-in-Aid for JSPS fellows (grant no. 19J22088) and the Grant-in-Aid for Scientific Research on Innovative Area Soft Crystals (area no. 2903, 17H06367). M. Z. acknowledges the research grant under the “Diamond Grant” program (DI2018 017948) of the Polish Ministry of Science and Higher Education. The present research was also supported in part by a JSPS Grant-in-Aid for Specially Promoted Research Grant No. 15H05697, Grant-in-Aid for Scientific Research(A) Grant No. 20H00369, KAKENHI Grant No. 19K05366, and IM-LED LIA (CNRS). We acknowledge the Cryogenic Research Centre, The Univ. of Tokyo, the Centre for Nano Lithography & Analysis, The Univ. of Tokyo supported by MEXT, and Quantum Leap Flagship Program (Q-LEAP) by MEXT.Notes and references
- J. Ferrando-Soria, H. Khajavi, P. Serra-Crespo, J. Gascon, F. Kapteijn, M. Julve, F. Lloret, J. Pasan, C. Ruiz-Perez, Y. Journaux and E. Pardo, Adv. Mater., 2012, 24, 5625–5629 CrossRef CAS.
- C. R. Gros, M. K. Peprah, B. D. Hosterman, T. V. Brinzari, P. A. Quintero, M. Sendova, M. W. Meisel and D. R. Talham, J. Am. Chem. Soc., 2014, 136, 9846–9849 CrossRef CAS.
- S. Ohkoshi, S. Takano, K. Imoto, M. Yoshikiyo, A. Namai and H. Tokoro, Nat. Photonics, 2014, 8, 65–71 CrossRef CAS.
- S. Chorazy, K. Nakabayashi, S. Ohkoshi and B. Sieklucka, Chem. Mater., 2014, 26, 4072–4075 CrossRef CAS.
- M. Estrader, J. S. Uber, L. A. Barrios, J. Garcia, P. Lloyd-Williams, O. Roubeau, S. J. Teat and G. Aromi, Angew. Chem., Int. Ed., 2017, 56, 15622–15627 CrossRef CAS.
- A. C. Felts, A. Slimani, J. M. Cain, M. J. Andrus, A. R. Ahir, K. A. Abboud, M. W. Meisel, K. Boukheddaden and D. R. Talham, J. Am. Chem. Soc., 2018, 140, 5814–5824 CrossRef CAS.
- C. Lochenie, K. Schötz, F. Panzer, H. Kurz, B. Maier, F. Puchtler, S. Agarwal, A. Köhler and B. Weber, J. Am. Chem. Soc., 2018, 140, 700–709 CrossRef CAS.
- B. Benaicha, J. Van Do, A. Yangui, N. Pittala, A. Lusson, M. Sy, G. Bouchez, H. Fourati, C. J. Gomez-Garcia, S. Triki and K. Boukheddaden, Chem. Sci., 2019, 10, 6791–6798 RSC.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS.
- J. M. Zazdrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577–581 CrossRef.
- M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, E. Sciancelepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194–197 CrossRef CAS.
- M. Mannini, F. Bertani, C. Tudisco, L. Malavolti, L. Poggini, K. Misztal, D. Menozzi, A. Motta, E. Otero, P. Ohresser, P. Sainctavit, G. G. Condorelli, E. Dalcanale and R. Sessoli, Nat. Commun., 2014, 5, 4582 CrossRef CAS.
- A. Candini, S. Klyatskaya, M. Ruben, W. Wernsdorfer and M. Affronte, Nano Lett., 2011, 11, 2634–2639 CrossRef CAS.
- S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138 CrossRef CAS.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- J.-H. Jia, Q.-W. Li, Y.-C. Chen, J.-L. Liu and M.-L. Tong, Coord. Chem. Rev., 2019, 378, 365–381 CrossRef CAS.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS.
- F. Pointillart, B. Le Guennic, S. Golhen, O. Cador, O. Maury and L. Ouahab, Chem. Commun., 2013, 49, 615–617 RSC.
- Q.-W. Li, J.-L. Liu, J.-H. Jia, Y.-C. Chen, J. Liu, L.-F. Wang and M.-L. Tong, Chem. Commun., 2015, 51, 10291–10294 RSC.
- K. Soussi, J. Jung, F. Pointillart, B. Le Guennic, B. Lefeuvre, S. Golhen, O. Cador, Y. Guyot, O. Maury and L. Ouahab, Inorg. Chem. Front., 2015, 2, 1105–1117 RSC.
- F. Pointillart, B. Le Guennic, O. Cador, O. Maury and L. Ouahab, Acc. Chem. Res., 2015, 48, 2834–2842 CrossRef CAS.
- E. L. Gavey, M. Al Hareri, J. Regier, L. D. Carlos, R. A. S. Ferreira, F. S. Razavi, J. M. Rawson and M. Pilkington, J. Mater. Chem. C, 2015, 3, 7738–7747 RSC.
- S. Chorazy, M. Rams, K. Nakabayashi, B. Sieklucka and S. Ohkoshi, Chem.–Eur. J., 2016, 22, 7371–7375 CrossRef CAS.
- Y.-C. Chen, J.-L. Liu, Y. Lan, Z.-Q. Zhong, A. Mansikkamäki, L. Ungur, Q.-W. Li, J.-H. Jia, L. F. Chibotaru, J.-B. Han, W. Wernsdorfer, X.-M. Chen and M.-L. Tong, Chem.–Eur. J., 2017, 23, 5708–5715 CrossRef CAS.
- M. A. Sorensen, U. B. Hansen, M. Perfetti, K. S. Pedersen, E. Bartolome, G. S. Simeoni, H. Mutka, S. Rols, M. Jeong, I. Zivkovic, M. Retuerto, A. Arauzo, J. Bartolome, S. Pilgkos, H. Weihe, L. H. Doerrer, J. van Slageren, H. M. Ronnow, K. Lefmann and J. Bendix, Nat. Commun., 2018, 9, 1292 CrossRef.
- J. J. Zakrzewski, S. Chorazy, K. Nakabayashi, S. Ohkoshi and B. Sieklucka, Chem.–Eur. J., 2019, 25, 11820–11825 CrossRef CAS.
- Y. Bi, C. Chen, Y.-F. Zhao, Y.-Q. Zhang, S.-D. Jiang, B.-W. Wang, J.-B. Han, J.-L. Sun, Z.-Q. Bian, Z.-M. Wang and S. Gao, Chem. Sci., 2016, 7, 5020–5031 RSC.
- D. Errulat, R. Marin, D. A. Galico, K. L. M. Harriman, A. Pialat, B. Gabidullin, F. Iikawa, O. D. D. Couto Jr, J. O. Moilanen, E. Hemmer, F. A. Sigoli and M. Murugesu, ACS Cent. Sci., 2019, 5, 1187–1198 CrossRef CAS.
- K. Kumar, D. Abe, K. Komori-Orisaku, O. Stefanczyk, K. Nakabayashi, J. R. Shakirova, S. P. Tunik and S. Ohkoshi, RSC Adv., 2019, 9, 23444–23449 RSC.
- G. Brunet, R. Marin, M.-J. Monk, U. Resch-Genger, D. A. Galico, F. A. Sigoli, E. A. Suturina, E. Hemmer and M. Murugesu, Chem. Sci., 2019, 10, 6799–6808 RSC.
- D. A. Galico, R. Marin, G. Brunet, D. Errulat, E. Hemmer, F. A. Sigoli, J. O. Moilanen and M. Murugesu, Chem.–Eur. J., 2019, 25, 14625–14637 CrossRef CAS.
- J. Wang, J. J. Zakrzewski, M. Heczko, M. Zychowicz, K. Nakagawa, K. Nakabayashi, B. Sieklucka, S. Chorazy and S. Ohkoshi, J. Am. Chem. Soc., 2020, 142, 3970–3979 CrossRef CAS.
- M. Fondo, J. Corredoira-Vazquez, A. M. Garcia-Deibe, J. Sanmartin-Matalobos, M. Amoza, A. M. P. Botas, R. A. S. Ferreira, L. D. Carlos and E. Colacio, Inorg. Chem. Front., 2020, 7, 3019–3029 RSC.
- J. Rocha, C. D. S. Brites and L. D. Carlos, Chem.–Eur. J., 2016, 22, 14782–14795 CrossRef CAS.
- Y. Hasegawa and Y. Kitagawa, J. Mater. Chem. C, 2019, 7, 7494–7511 RSC.
- M. Hatanaka, Y. Hirai, Y. Kitagawa, T. Nakanishi, Y. Hasegawa and K. Morokuma, Chem. Sci., 2017, 8, 423–429 RSC.
- D.-F. Lu, Z.-F. Hong, J. Xie, X.-J. Kong, L.-S. Long and L.-S. Zheng, Inorg. Chem., 2017, 56, 12186–12192 CrossRef CAS.
- G. Bao, K.-L. Wong, D. Jin and P. A. Tanner, Light: Sci. Appl., 2018, 7, 96 CrossRef.
- C. D. S. Brites, M. C. Fuertes, P. C. Angelome, E. D. Martinez, P. P. Lima, G. J. A. A. Soler-Illia and L. D. Carlos, Nano Lett., 2017, 17, 4746–4752 CrossRef CAS.
- X. Zhu, J. Li, X. Qiu, W. Feng and F. Li, Nat. Commun., 2018, 9, 2176 CrossRef.
- R. G. Geitenbeek, A.-E. Nieuwelink, T. S. Jacobs, B. B. V. Salzmann, J. Goetze, A. Meijerink and B. M. Weckhuysen, ACS Catal., 2018, 8, 2397–2401 CrossRef CAS.
- C. D. S. Brites, S. Balabhadra and L. D. Carlos, Adv. Opt. Mater., 2018, 18012139 Search PubMed.
- M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154–2157 CrossRef CAS.
- J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441–5450 CrossRef CAS.
- G. Zucchi, O. Maury, P. Thuery, F. Gumy, J.-C. G. Bünzli and M. Ephritikhine, Chem.–Eur. J., 2009, 15, 9686–9696 CrossRef CAS.
- T. Xia, Y. Cui, Y. Yang and G. Qian, J. Mater. Chem. C, 2017, 6, 5044–5047 RSC.
- I. Hernandez, Y.-X. Zheng, M. Motevalli, R. H. C. Tan, W. P. Gillin and P. B. Wyatt, Chem. Commun., 2013, 49, 1933–1935 RSC.
- S. Chorazy, M. Rams, J. Wang, B. Sieklucka and S. Ohkoshi, Dalton Trans., 2017, 47, 13668–13672 RSC.
- L. Marciniak and A. Bednarkiewicz, Sens. Actuators, B, 2017, 243, 388–393 CrossRef CAS.
- K. S. Pedersen, J. Dreiser, H. Weihe, R. Sibille, H. V. Johannesen, M. A. Sorensen, B. E. Nielsen, M. Sigrist, H. Mutka, S. Rols, J. Bendix and S. Piligkos, Inorg. Chem., 2015, 54, 7600–7606 CrossRef CAS.
- T.-Q. Liu, P.-F. Yan, F. Luan, Y.-X. Li, J.-W. Sun, C. Chen, F. Yang, H. Chen, X.-Y. Ziu and G. M. Li, Inorg. Chem., 2015, 54, 221–228 CrossRef CAS.
- N. Ishikawa, M. Sugita and W. Wernsdorfer, J. Am. Chem. Soc., 2005, 127, 3650–3651 CrossRef CAS.
- M. A. AlDamen, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Arino, C. Marti-Gastaldo, F. Luis and O. Montero, Inorg. Chem., 2009, 48, 3467–3479 CrossRef CAS.
- R. J. Blagg, F. Tuna, E. J. L. McInnes and R. E. P. Winpenny, Chem. Commun., 2011, 47, 10587–10589 RSC.
- S. Ghosh, S. Datta, L. Friend, S. Cardona-Serra, A. Gaita-Arino, E. Coronado and S. Hill, Dalton Trans., 2012, 41, 13697–13704 RSC.
- S. Cardono-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Arino, A. Camon, M. Evangelisti, F. Luis, M. Martinez-Perez and J. Sese, J. Am. Chem. Soc., 2012, 134, 14982–14990 CrossRef.
- J. Dreiser, R. Westerström, Y. Zhang, A. A. Popov, L. Dunsch, K. Krämer, S.-X. Liu, S. Decurtins and T. Greber, Chem.–Eur. J., 2014, 20, 13536–13540 CrossRef CAS.
- M. Viciano-Chumillas, F. Koprowiak, I. Mutikainen, W. Wernsdorfer, T. Mallah and H. Bolvin, Phys. Rev. B, 2017, 96(8), 214427 CrossRef.
- F. Pointillart, O. Cador, B. Le Guennic and L. Ouahab, Coord. Chem. Rev., 2017, 346, 150–175 CrossRef CAS.
- Y.-C. Chen, J.-L. Liu, W. Wernsdorfer, D. Liu, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, Angew. Chem., Int. Ed., 2017, 56, 4996–5000 CrossRef CAS.
- T. P. Latendresse, V. Vieru, A. Upadhyay, N. S. Bhuvanesh, L. F. Chibotaru and M. Nippe, Chem. Sci., 2020, 11, 3936–3951 RSC.
- Y. Ma, Y.-Q. Zhai, Y.-S. Ding, T. Han and Y.-Z. Zheng, Chem. Commun., 2020, 56, 3979–3982 RSC.
- S.-M. Chen, Y.-Q. Zhang, J. Xiong, B.-W. Wang and S. Gao, Inorg. Chem., 2020, 59, 5835–5844 CrossRef CAS.
- E. G. Moore, G. Szigethy, J. Xu, L.-O. Pälsson, A. Beeby and K. M. Raymond, Angew. Chem., Int. Ed., 2008, 47, 9500–9503 CrossRef CAS.
- S. Chorazy, M. Arczynski, K. Nakabayashi, B. Sieklucka and S. Ohkoshi, Inorg. Chem., 2015, 54, 4724–4736 CrossRef CAS.
- M. K. Muhata, T. Koppe, K. Kumar, H. Hofsäss and U. Vetter, Sci. Rep., 2020, 10, 8775 CrossRef.
- J.-C. Rybak, L. V. Meyer, J. Wagenhöfer, G. Sextl and K. Müller-Buschbaum, Inorg. Chem., 2012, 51, 13204–13213 CrossRef CAS.
- T. Ribbeck, S. H. Zottnick, C. Kerpen, J. Landmann, N. V. Ignat’ev, K. Müller-Buschbaum and M. Finze, Inorg. Chem., 2017, 56, 2278–2286 CrossRef CAS.
- S. Gutzov, S. Berendts, M. Lerch, C. Geffert, A. Börger and K. D. Becker, Phys. Chem. Chem. Phys., 2009, 11, 636–640 RSC.
- V. Petrov, N. Danchova and S. Gutzov, Spectrochim. Acta, Part A, 2020, 227, 117527 CrossRef CAS.
- T. Shiraki, A. Dawn, Y. Tsuchiya and S. Shinkai, J. Am. Chem. Soc., 2010, 132, 13929–13935 CrossRef.
- C. D. S. Brites, P. P. Lima, N. J. O. Silva, A. Millan, V. S. Amaral, F. Palacio and L. D. Carlos, Nanoscale, 2012, 4, 4799–4829 RSC.
- K. Kumar, S. Chorazy, K. Nakabayashi, H. Sato, B. Sieklucka and S. Ohkoshi, J. Mater. Chem. C, 2018, 6, 8372–8384 RSC.
- Y. Xin, J. Wang, M. Zychowicz, J. J. Zakrzewski, K. Nakabayashi, B. Sieklucka, S. Chorazy and S. Ohkoshi, J. Am. Chem. Soc., 2019, 141, 18211–18220 CrossRef CAS.
- S. Chorazy, J. J. Zakrzewski, M. Reczyński, K. Nakabayashi, S. Ohkoshi and B. Sieklucka, J. Mater. Chem. C, 2019, 7, 4164–4172 RSC.
- Y. Liu, Y.-C. Chen, J. Liu, W.-B. Chen, G.-Z. Huang, S.-G. Wu, J. Wang, J.-L. Liu and M.-L. Tong, Inorg. Chem., 2020, 59, 687–694 CrossRef CAS.
- S. Chorazy, J. Wang and S. Ohkoshi, Chem. Commun., 2016, 52, 10795–10798 RSC.
- J. Wang, S. Chorazy, K. Nakabayashi, B. Sieklucka and S. Ohkoshi, J. Mater. Chem. C, 2018, 6, 473–481 RSC.
- F. Habib, P.-H. Lin, J. Long, I. Korobkov, W. Wernsdorfer and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 8830–8833 CrossRef CAS.
- L. Spree, C. Schlesier, A. Kostanyan, R. Westerström, T. Greber, B. Büchner, S. M. Avdashenko and A. A. Popov, Chem.–Eur. J., 2020, 26, 2436–2449 CrossRef CAS.
- L. Anh Ho and L. F. Chibotaru, Phys. Rev. B, 2018, 97, 024427 CrossRef.
- L. Ungur and L. F. Chibotaru, Chem.–Eur. J., 2017, 23, 3708–3718 CrossRef CAS.
- W. Wernsdorfer, A. Caneschi, R. Sessoli, D. Gatteschi, A. Cornia, V. Villar and C. Paulsen, Phys. Rev. Lett., 2000, 84, 2965–2968 CrossRef CAS.
- D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268–297 CrossRef CAS.
- F. Troiani, A. Ghirri, M. Affronte, S. Carretta, P. Santini, G. Amoretti, S. Piligkos, G. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2005, 94(4), 207208 CrossRef CAS.
- N. Ishikawa, M. Sugita and W. Wernsdorfer, Angew. Chem., Int. Ed., 2005, 44, 2931–2935 CrossRef CAS.
- S. Chorazy, J. J. Zakrzewski, M. Reczyński and B. Sieklucka, Chem. Commun., 2019, 55, 3057–3060 RSC.
- J. B. Gruber, G. W. Burdick, U. V. Valiev, K. L. Nash, S. A. Rakhimov and D. K. Sardar, J. Appl. Phys., 2009, 106, 113110 CrossRef.
- S. Gutzov, A. Börger and K. D. Becker, Phys. Chem. Chem. Phys., 2007, 9, 491–496 RSC.
- B. Di Bartolo, Optical Interactions in Solids, Wiley, 1968, pp. 20–35 Search PubMed.
- M. Back, E. Trave, J. Ueda and S. Tanabe, Chem. Mater., 2016, 28, 8347–8356 CrossRef CAS.
- J. J. Zakrzewski, B. Sieklucka and S. Chorazy, Inorg. Chem., 2020, 59, 1393–1404 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details. IR spectra. TGA curves. Detailed structure parameters. Additional structural views. Results of continuous shape measure analysis. P-XRD patterns. Direct-current (dc) magnetic properties. Complete alternate-current (ac) magnetic characteristics. Details of ab initio calculations. Detailed discussion on the impact of hyperfine interactions on the electronic structure of HoIII complexes. Solid-state UV-vis-NIR absorption spectra. Complete results of temperature-variable photoluminescent studies. CCDC 1983881–1983883. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc04871b |
| This journal is © The Royal Society of Chemistry 2021 |