Open Access Article
Open Access ArticleTerahertz chiral sensing and magneto-optical enhancement for ferromagnetic nanofluids in the chiral metasurface
Fei
Fan
 ab,
Changzhi
Zhong
a,
Ziyang
Zhang
a,
Shanshan
Li
a and
Shengjiang
Chang
*ab
ab,
Changzhi
Zhong
a,
Ziyang
Zhang
a,
Shanshan
Li
a and
Shengjiang
Chang
*ab
aInstitute of Modern Optics, Nankai University, Tianjin Key Laboratory of Micro-scale Optical Information Science and Technology, Tianjin 300350, China. E-mail: sjchang@nankai.edu.cn
bTianjin Key Laboratory of Optoelectronic Sensor and Sensing Network Technology, Tianjin 300350, China
First published on 5th July 2021
Abstract
The highly sensitive detection and magnetic field sensing of magnetic nanomaterials have received extensive attention, and its weak magneto-optical effect in the terahertz (THz) band limits its application. In this study, we investigated a chiral metasurface sensor filled with ferromagnetic nanofluids. Based on its artificial chiral resonance, the nanoparticle concentration and magneto-optical chiral response of the ferromagnetic nanofluids have both been detected using the THz time-domain polarization spectroscopy. The results show that the detection sensitivity of the concentration of the magnetic nanoparticles can reach 5.5 GHz %−1 by chiral sensing, needing only a trace amount of the nanofluid. More importantly, in this hybrid device, the magneto-optical chiral response of the ferromagnetic nanoparticles can be greatly enhanced by the chiral metasurface, which results in higher sensitivity to the external magnetic field. The Verdet constant of the ferromagnetic nanofluid in the metasurface is 15 times stronger than that without the chiral microstructure. This THz chiral sensing for nanoparticles and the chirality enhancement mechanism will promote a new sensing method and chiral manipulation device, especially for the highly sensitive magneto-optical device in the THz band.
1. Introduction
In recent years, terahertz (THz) technology and its applications have made great progress in many fields.1–4 For further development of the THz application system, there is high demand for efficient devices for sensing and manipulating THz waves in their amplitude, phase, and polarization.5–8 The unique magnetic anisotropy, nonreciprocity, and magnetic tunability of magneto-optical materials make them play an irreplaceable role in the isolator, magneto-optical polarization convertor, modulator, and magnetic field sensor.9–14 However, research studies on the magnetic properties of THz waves seriously lag, so it is necessary to fill the “terahertz gap” by not only electrical but also magnetic means.In recent years, magneto-optical effects of some gyromagnetic ferrite and gyroelectric semiconductor materials in the terahertz band have been reported,15–22 such as YIG, InSb, and graphene. For example, Crassee et al. observed the Faraday rotation angle up to 0.1 rad for a single graphene layer when B = 7 T and T = 3 K in the THz regime.19 Graphene exhibits significant THz Faraday rotation and circular dichroism in an external magnetic field, but needs to be operated at low temperature or an extremely high biased magnetic field.19–22 Other gyroelectric semiconductors, e.g., InSb and HgTe,17,18 also need to work at low temperatures to show their THz magneto-optical effect. The ferrite-like YIG and ferromagnetic nanofluid can work at room temperature, but their magnetic resonance is located in the microwave band, so their THz magneto-optical activity is very weak. For example, Li et al. reported that the Faraday rotation angle of 10 layers of 105 μm thick La:YIG single-crystal films is only 15° under 150 mT magnetic field.23
Ferromagnetic nanofluid is a colloidal suspension composed of magnetic nanoparticles in a carrier liquid, which has a significant advantage due to its liquid form and weak magnetic field requirement, especially in liquid-filled photonic devices.24,25 Shalaby et al. demonstrated that the magnetic nanofluid has a weak Faraday rotation in the THz regime, but is not adequate for a THz Faraday isolator.26,27 Therefore, the limitation for developing a THz magneto-optical device is mainly the lack of materials with strong magneto-optical activity and low loss in the THz regime. Under the limitations of the material thickness, magneto-optical coefficient, and external magnetic field, one of the ways to obtain a stronger THz magneto-optical activity response is to combine the artificial microstructure with magneto-optical nano materials.28
Artificial electromagnetic microstructures, such as photonic crystals, metamaterials and metasurfaces, and plasmonics, have been extensively investigated to manipulate THz waves.29–32 When the mirror and rotational symmetry of these microstructures are broken in geometry, a chiral microstructure has a strong artificial optical chirality response at the proper wavelength,33–37 which is similar to the medium composed of chiral molecules. The difference in the propagation speed and absorption of the left circularly polarized (LCP) and right circularly polarized (RCP) light makes the polarization rotation (i.e., optical activity, OA) and circular dichroism (CD), respectively. In recent years, the chiral metasurfaces have been reported to manipulate artificial OA, CD, and polarization conversion. Decker et al.38 proposed a stacked and twisted split-ring resonator arranged in a C4 symmetric lattice. The eigenmodes are truly chiral and exhibit huge optical activity with a polarization rotation angle of 30°. Li et al.39 proposed a graphene active chiral metasurface for dynamic THz wavefront modulation. If the chiral metasurface can obtain a narrow-band and high-Q artificial chiral response, the detection of the optical chiral parameters can be used for the sensing, especially for chirality sensing of the samples in the surrounding environment.40–43 In this case, the localized enhancement of the chiral field in the chiral metasurface may bring more information, higher sensitivity, and a new physical perspective. However, there have been few reports on the chiral sensing and enhancement of metasurfaces in the THz band.
In this paper, we prepared a double-layer chiral metasurface sensor and filled the interval layer of the metasurface with ferromagnetic nanofluids. Based on its artificial chiral resonance, the concentration of the magnetic nanoparticles and the magneto-optical chiral response in ferromagnetic nanofluids have been detected by THz time-domain polarization spectroscopy (THz-TDPS). The results show that the detection sensitivity of the concentration of the magnetic nanoparticles in volume percentage can reach 5.5 GHz %−1 by the chiral sensing of the metasurface, only using a trace amount of the nanofluid. More importantly, in this hybrid device, the magneto-optical chiral response of ferromagnetic nanoparticles can be greatly enhanced by the localized chiral field of the chiral metasurface, which results in a stronger magneto-optical activity and higher sensitivity to the external magnetic field. The Verdet constant of the ferromagnetic nanofluid in the metasurface is 15 times stronger than that of the ferromagnetic nanofluid without the chiral microstructure.
3. Results and discussion
3.1 THz optical property of the ferromagnetic nanofluid
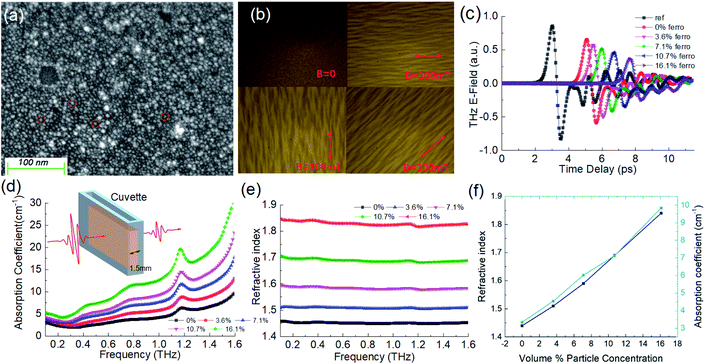
The ferromagnetic nanofluid used in our work is Fe3O4 nanoparticles dispersed in the iso-paraffinic light hydrocarbon oil (C25H43NO3), which are prepared by EMG 900 Series Ferrofluids from Ferrotec Corporation (Japan). The average diameter of the nanoparticles is less than 10 nm, and the volume fraction of the nanoparticles can be proportioned from 0 to 16.1%. The SEM photograph of the dry nanoparticles is shown (Fig. 1(a)), and we randomly labeled four nanoparticles with red circles. These magnetic nanoparticles were dispersed in the oil, which are uniformly distributed in the nanofluid without the magnetization as shown in the first photograph of Fig. 1(b). After being magnetized by a weak biased magnetic field of 100 mT, the particles were triggered to form the magnetic cluster chains along the direction of the biased magnetic field, as shown in Fig. 1(b). We also find that these magnetic cluster chain structures will disappear soon after the magnetic field is removed.We used a THz-TDPS system to measure the THz optical properties of the ferromagnetic nanofluids without a biased magnetic field. The detailed experimental setup, measurement method, and data processing method can be found in Section 3. The time-domain signal of the blank cuvette without a sample is used as the reference, and the time-domain signal of the carrier liquid without nanoparticles (0%) and the four nanofluid samples with different nanoparticle concentrations (3.6–16.1%) are shown in Fig. 1(c). The nanofluid is filled in a 1.5 mm gap quartz cuvette, as shown in Fig. 1(d). In Fig. 1(c), the delay time of the sample signals compared to the reference is proportional to the average refractive index of the nanofluid. Moreover, the attenuation in the amplitude of the sample compared to the reference is proportional to the average absorption of the nanofluid in the THz regime. Therefore, with the increase of the nanoparticle concentration, the refractive index and absorption of the ferrofluid rise in the THz regime. Fig. 1(d) shows that the absorption coefficients of all the samples are lower than 5 cm−1 at 0.2 THz and increase with the frequencies, which indicates that these nanofluids have a low absorption for THz waves. Fig. 1(e) shows that these nanofluids have no dispersion in the THz band, and their refractive index can be increased from 1.45 to 1.85 in proportion to the nanoparticle concentration, as shown in Fig. 1(f). Therefore, a wide range of refractive indices can be obtained by controlling the nanoparticle concentration.
The above results are obtained in a very thick cuvette with a 1.5 mm gap. A large number of nanofluid samples are consumed to obtain enough significant phase delay to accurately measure the refractive index of the sample, thus obtaining the concentration of the ferromagnetic nanoparticles. Therefore, we use a chiral metasurface sensor to sensitively detect the concentration of the nanofluids with trace amounts.
3.2 THz chiral sensing for ferromagnetic nanofluids
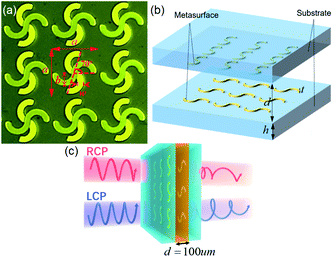
To achieve optical chirality, the mirror symmetry and rotational symmetry of the transmission system must be broken. Our proposed chiral metasurface consists of two layers of metallic subwavelength structures and the nanofluid layer of the only d = 100 μm thickness filled in the middle layer, as shown in Fig. 2(a) and (b). The metallic metasurface structures are fabricated by conventional photolithography and lift-off. The substrate is the JGS1 glass with h = 500 μm thickness, and the metallic structure with a thickness of t = 200 nm is periodically attached to the surface. For each layer, it is composed of a square two-dimensional array with a period of a = 100 μm. Each unit metallic structure is composed of two half rings, which are inversely symmetric with the center to form an “S”-like structure. The outer radius of the ring is b = 25 μm, and the width of the metal strip is w = 10 μm. The unit structure “S” between the upper and lower metallic layers has a 70° rotation along the z-axis. In this case, the mirror symmetry and rotational symmetry of this device are broken for the transmissive light, so this metasurface can exhibit strong intrinsic optical chirality, leading to the strong capabilities of polarization conversion and chiral selectivity for THz waves. Therefore, the anisotropic interaction between the chiral sample and THz wave is enhanced, and the sensitivity in chirality sensing can be improved.In the following discussion, we focus on the THz polarization response of the metasurface and ferromagnetic nanofluid samples excited by a pair of conjugated chiral light fields, that is the LCP and RCP waves, as shown in Fig. 2(c). The optical chiral response of the interaction between the sample and the metasurface to THz waves is characterized by two chirality parameters, CD and OA spectra. The CD reflects the intensity difference between LCP and RCP, and the OA indicates the phase difference between LCP and RCP. The OA also reflects the rotation angle of the polarization direction. The details of the formula of these parameters can be found in Section 3.
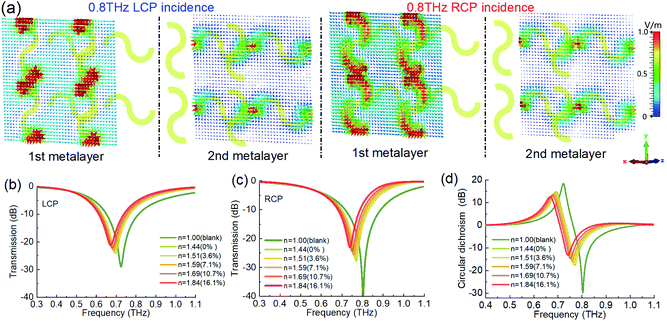
The numerical simulations are modeled by the finite-difference time-domain (FDTD) method in the commercial software FDTD SOLUTION from Ansys Lumerical Enterprise. The refractive index of the glass substrate is set as 1.98, which is measured by experiment. A pair of periodic boundary conditions are set for a unit cell structure. In the middle layer, the different refractive indexes are used to represent the different concentrations of ferromagnetic nanofluid. The absorption loss and magneto-optical effect caused by remanence from the ferromagnetic nanofluid are ignored in this simulation. Fig. 3(a) shows the electric field vector distribution on the upper and lower metallic structures of the metasurface when the LCP and RCP waves are incident with it at 0.8 THz, respectively. On the upper surface, there is mainly the strong dipole resonance at the metal slit, and the local resonance field of the RCP is stronger than the LCP at 0.8 THz. On the lower surface, the LCP generates a counter-clockwise rotating field along the S-shaped metal strip, while the RCP excites a clockwise rotating field. These results show that this chiral metasurface not only generates a localized resonance, but also excites an enhanced chiral field. We also simulate the LCP and RCP transmittance spectra, and CD spectra of the chiral metasurface filled with different concentrations of nanofluids, as shown in Fig. 3(b)–(d), which will be analyzed with the experimental results in the following discussion.
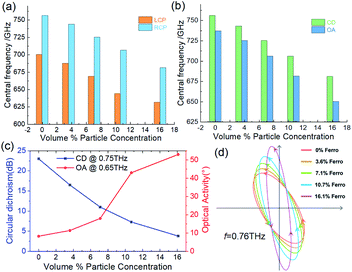
Next, we use the THz-TDPS system to measure and reconstruct the THz chiral spectra of the metasurface filled with ferromagnetic nanofluids, as shown in Fig. 4. The detailed experimental method and data processing can be found in Section 3. Fig. 4(a) and (b) show the transmission spectra of the LCP and RCP waves through the metasurface, respectively. For the blank metasurface without filling nanofluid, the resonance is located at 0.7 THz for the LCP and 0.78 THz for the RCP. This difference shows the artificial circular dichroism of the metasurface. When the nanofluids are filled in the metasurface, with the increase of concentration, the resonance spectra of both LCP and RCP shift to a lower frequency. These experimental results are in good agreement with the simulation results in Fig. 3(b) and (c), indicating that the shift of resonance spectra of the LCP and RCP is mainly caused by the refractive index change of the intermediate layer of the metasurface. The central resonant frequency, as a function of nanoparticle concentration, shows that there is a good linear relationship between the particle concentration and the resonant peak position, which is also shown in Fig. 5(a). For the LCP, the resonant frequency changes from 0.7 THz to 0.627 THz when the concentration changes from 0 to 16.1%. For the RCP, the resonant frequency moves from 0.76 THz to 0.687 THz. According to the change of unit concentration, the sensitivity is 4.5 GHz %−1 for both LCP and RCP, but the quality factor (i.e., Q value) of RCP sensing is higher than that of LCP because the resonance intensity of RCP is about 10 dB higher than that of LCP. We consider that the refractive index corresponds to the nanoparticle concentration. The sensitivity of the device is 182.5 GHz RIU−1.
Fig. 4(c) and (d) show the optical chirality, i.e., CD and OA spectra, respectively, through the metasurface. Their spectral lines also redshift with the concentrations. For the CD spectra, the CD value increases with the frequency, and a positive peak is obtained near 0.7 THz. This peak value jumps to a negative peak and finally decreases to 0. The simulation results in Fig. 3(d) are consistent with the experimental results in Fig. 4(c). If the frequency shift of the CD peak is selected as the sensing parameter, the sensing sensitivity can reach 4.9 GHz %−1, as shown in Fig. 5(b). For the OA spectra, as shown in Fig. 4(d), the OA value reaches its peak at the frequency of drastic change in the CD spectrum, and its sensing sensitivity can reach 5.5 GHz %−1 (that is equivalent to 223 GHz RIU−1), which is higher than other parameters. Therefore, we can detect the concentration of the ferromagnetic nanoparticles in the liquid accurately by measuring the change of the optical chiral parameters (i.e., CD and OA) through the chiral metasurface filled with a very small amount of nanofluid.
For a specific frequency, the polarization state of the output wave will change regularly with the nanoparticle concentration because the optical chiral parameter changes with the concentration. Fig. 5(c) shows that the CD and OA values vary monotonously with the concentration of nanoparticles at two specific frequencies, 0.75 THz and 0.65 THz, respectively, which can be also used as new physical parameters for chiral sensing. Fig. 5(d) displays intuitively the polarization ellipsoid of the chiral metasurface with different ferromagnetic nanofluids when the y-LP wave at 0.76 THz is incident. In this case, the CD reflects the ellipticity of the ellipse, and the larger the value of CD is, the closer the ellipse is to a circle. The OA reflects the angle of rotation of the major axis of the ellipse relative to the y-axis. Moreover, as a device for THz chiral manipulation, filling ferromagnetic nanofluid with different concentrations can also flexibly shift the frequency band of strong optical chirality and manipulate the polarization state of the THz waves.
3.3 Enhancement of the THz magneto-optical activity in chiral metasurface
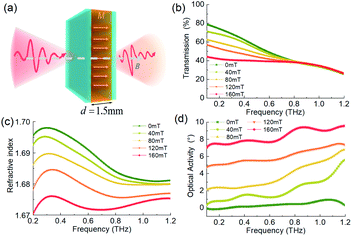
Next, we focus on the THz magneto-optical effect of the ferromagnetic nanofluids by applying a longitudinal bias magnetic field as the Faraday configuration, as illustrated in Fig. 6(a). First, we filled the ferromagnetic nanofluid of 10.7% concentration into the cuvette of the 1.5 mm-gap, and use the THz-TDPS system to measure the THz transmission, phase, and polarization properties through the sample under different biased magnetic fields from 0 to 160 mT. Here, a y-LP wave illuminates the sample and the second THz polarizer is rotated to 0° to detect the output y-LP component. The transmittance spectra are measured, as shown in Fig. 6(b), and the phase spectra are obtained, so that the refractive index can be derived from the phase spectra, as shown in Fig. 6(c). The transmittance of the low-frequency signal below 0.8 THz decreases with the increase of the magnetic field, while the high-frequency signal remains nearly unchanged. The refractive index also drops with the increase of the magnetic field, and this change is significant at the lower frequency, while the varying range of higher frequency is small. Compared with the refractive index change caused by the nanoparticle concentration discussed above, the magnetically induced refractive index change of ferromagnetic fluid is very weak.Then, we rotated the second THz polarizer to ±45° to detect the complete polarization state of the output light. It is still an LP light, but it shows a weak Faraday magneto-optical rotation effect with rotating to a small polarization angle, which is shown in the OA spectra in Fig. 6(d). The Faraday rotation angle increases linearly with the increase of the biased magnetic field, and the dispersion is small in the THz band. These characteristics are consistent with the magneto-optical property of the gyromagnetic material in the THz band. Considering the thickness of 1.5 mm, the Faraday rotation angle is only 8° at 160 mT, so the THz Faraday effect of the ferromagnetic nanofluid is very weak, and its Verdet constant is only 33° mm−1 T−1.
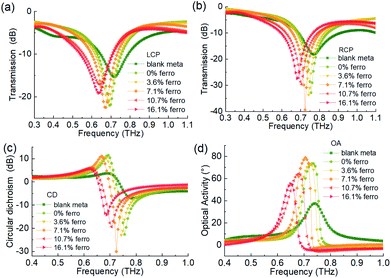
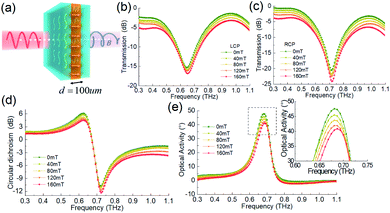
Finally, we investigated the magnetic response of the chiral metasurface filled with ferromagnetic nanofluid in its double-layer interval, as illustrated in Fig. 7(a). We measured the transmission spectra of LCP and RCP under different biased magnetic fields. Different from the frequency shift of the chiral spectral resonance peak caused by the change of refractive index shown in Fig. 4, the change of the chiral spectral resonance intensity is caused by the biased magnetic field in Fig. 7(b) and (c). Considering the difference of amplitude and phase of the conjugated chiral light, the variation of the CD and OA spectra with the magnetic field is shown in Fig. 7(d) and (e), respectively. The THz optical chirality mainly originated from the chiral metasurface structure, but there is also a contribution by the ferromagnetic nanofluids. The peak of the polarization rotation angle at 0.65 THz shown in Fig. 7(e) changes from 48° to 40° when the magnetic field is tuned from 0 to 160 mT. This change of 8° in the OA spectrum under different external magnetic fields is due to the THz magneto-optical effect of the ferromagnetic nanofluids. Although it is also changed to 8°, compared to the ferromagnetic nanofluids in the 1.5 mm cuvette, the thickness of the nanofluid layer in the chiral metasurface is only 100 μm.
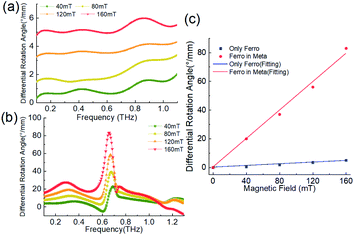
To better compare the Faraday rotation effect of the two cases above, we calculate the differential polarization rotation angle (DRA) spectrum per millimeter thickness of ferromagnetic nanofluid in Fig. 8. We subtract the OA spectrum of B = 40–160 mT from the OA value of B = 0 T to get each DRA spectrum, which eliminates the contribution of the artificial OA effect of the metasurface structure itself. Then, we divide it by the thickness of the nanofluid layer of the sample to get the results of Fig. 8(a) and (b), which eliminates the contribution of different thickness accumulation. By contrast, we can see that the ferromagnetic nanofluids in the chiral metasurface have higher magneto-optical activity, especially in the frequency band where the artificial optical chirality of the metasurface varies strongly. As shown in Fig. 8(b), when the biased magnetic field reaches 160 mT, the DRA at the peak value exceeds 80° mm−1 at 0.65 THz in the metasurface, while the value in Fig. 8(a) is only 5.3° mm−1 in the cuvette. Since the optical activity of the artificial metasurface itself has been deducted, the magneto-optical activity has been significantly improved in the frequency band where the artificial optical activity is the strongest, which indicates that the chiral metasurface structure enlarges the THz magneto-optical effect of the ferromagnetic nanofluids, and its artificial THz chiral field and local field resonance enhance the chiral interaction between THz wave and magnetic medium. Fig. 8(c) shows the relationship between the DRA value and the biased magnetic field of two samples at 0.65 THz, which are fitted as the straight line and its slope is the Verdet constant. The Verdet constant of the ferromagnetic nanofluid in the metasurface is as high as 500° mm−1 T−1, which is 15 times stronger than the ferromagnetic nanofluid without the enhancement by the chiral microstructure. Because of its good linearity and sensitivity, this result can also be used as a magnetic field sensor, of which the sensitivity is just 500° mm−1 T−1.
4. Experimental methods
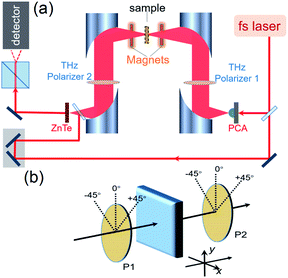
The THz optical properties were measured by a THz-TDPS system, as shown in Fig. 9(a). All experiments were carried out at room temperature. A photoconductive antenna was used to generate the THz pulses, which is excited by a Ti:sapphire laser with 75 fs duration at 800 nm. The polarization direction of the incident THz wave is along the y-axis. After that, the first THz metallic wire polarizer (P1) was placed in front of the sample to rotate the polarization direction of the incident wave to 0° and ±45°. We measured the time-domain signals of the samples, of which the reference signal Er(t) and the sample signal Es(t) are obtained. After Fourier transforms, their amplitudes Er(ω), Es(ω) and phases δr(ω), δs(ω) of the samples and reference in the frequency domain are obtained, correspondingly. The transmission amplitude is A(ω) = Es(ω)/Er(ω), and the phase shift between the sample and the reference is Δδ(ω) = δs(ω) − δr(ω).Furthermore, the effective refractive index n(ω) and absorption coefficient α(ω) can be calculated as follows:
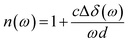 | (1) |
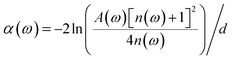 | (2) |
As shown in Fig. 9(b), when the P1 is rotated to ±45°, a pair of orthogonal LP waves are generated, which is equivalent to a pair of orthogonal circularly polarized waves, so the complex transmission coefficients of RCP and LCP, i.e., tRCP and tLCP, respectively, can be expressed as follows:
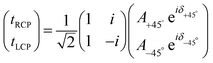 | (3) |
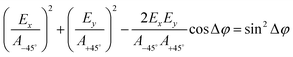 | (4) |
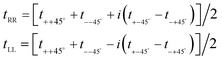 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(TRCP/TLCP) and the OA spectrum OA = δRCP − δLCP.46–48 Thus, the results in Fig. 4 and 7 can be obtained.
log(TRCP/TLCP) and the OA spectrum OA = δRCP − δLCP.46–48 Thus, the results in Fig. 4 and 7 can be obtained.
5. Conclusions
In summary, we investigated a chiral metasurface sensor filled with ferromagnetic nanofluids. By using the chiral sensing based on the artificial CD and OA spectra of the chiral metasurface, the nanoparticle concentration can be detected with a very small amount of nanofluid. Its sensing sensitivity can reach up to 5.5 GHz %−1 (223 GHz RIU−1). Conversely, as a device for THz chiral manipulation, filling ferromagnetic nanofluid with different concentrations can also flexibly control the strong optical chirality of this metasurface and manipulate the output polarization state of the THz waves. In addition, this work shows that the ferrofluid based on liquid metal or magnetic medium will play an important role in the development of soft electronic and photonic devices, which brings more flexible morphological plasticity and functional diversity to devices.49,50More importantly, the chiral metasurface structure enlarges the THz magneto-optical effect of ferromagnetic nanofluids, and its artificial THz chiral field and local field resonance enhance the chiral interaction between the THz wave and magnetic medium, which results in higher sensitivity to the external magnetic field. The Verdet constant of the ferromagnetic nanofluid in the metasurface is 15 times stronger than that without the chiral microstructure. This THz chiral sensing for nanoparticles and the chirality enhancement mechanism will promote a new sensing method and chiral manipulation device, especially for the highly sensitive magneto-optical device in the THz band.
Author contributions
Fei Fan: conceptualization, investigation, methodology, resource, writing – the original draft, writing – review & editing. Changzhi Zhong: investigation, validation, data curation. Ziyang Zhang: methodology. Shanshan Li: scanning electron microscope operation. Shengjiang Chang: supervision, project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the National Natural Science Foundation of China (61971242, 61831012); National Key Research and Development Program of China (2017YFA0701000); Natural Science Foundation of Tianjin City (19JCYBJC16600).References
- D. M. Mittleman, Opt. Express, 2018, 26, 9417–9431 CrossRef CAS PubMed
.
- X. C. Zhang, A. Shkurinov and Y. Zhang, Nat. Photonics, 2017, 11, 16–18 CrossRef CAS
.
- Y. Yang, Y. Yamagami, X. Yu, P. Pitchappa, J. Webber, B. Zhang, M. Fujita, T. Nagatsuma and R. Singh, Nat. Photonics, 2020, 14, 446–451 CrossRef CAS
.
- J. Chen, K. Nitta, X. Zhao, T. Mizuno, T. Minamikawa, F. Hindle, Z. Zheng and T. Yasui, Adv. Photonics, 2020, 2, 036004 CAS
.
- J. Li, Y. Zhang, J. Li, X. Yan, L. Liang, Z. Zhang, J. Huang, J. Li, Y. Yang and J. Yao, Nanoscale, 2019, 11, 5746–5753 RSC
.
- Y. Ji, F. Fan, S. Xu, J. Yu and S. Chang, Nanoscale, 2019, 11, 4933–4941 RSC
.
- Y. Ji, F. Fan, X. Zhang, J. Cheng and S. Chang, J. Lightwave Technol., 2020, 38, 4030–4036 CAS
.
- D. Kong, X. Wu, B. Wang, T. Nie, M. Xiao, C. Pandey, Y. Gao, L. Wen, W. Zhao, C. Ruan, J. Miao, Y. Li and L. Wang, Adv. Opt. Mater., 2019, 7, 1900487 CrossRef CAS
.
- W. Zhang, P. Maldonado, Z. Jin, T. Seifert, J. Arabski, G. Schmerber, E. Beaurepaire, M. Bonn, T. Kampfrath, P. Oppeneer and D. Turchinovich, Nat. Commun., 2020, 11, 4247 CrossRef CAS PubMed
.
- S. Lin, S. Silva, J. Zhou and D. Talbayev, Adv. Opt. Mater., 2018, 6, 1800572 CrossRef
.
- F. Fan, C. Xiong, J. Cheng and S. Chang, Opt. Lett., 2018, 43, 687–690 CrossRef CAS PubMed
.
- T. Tang, J. Li, L. Luo, P. Sun and J. Yao, Adv. Opt. Mater., 2018, 6, 1701212 CrossRef
.
- T. Tang, J. Li, M. Zhu, L. Luo, J. Yao, N. Li and P. Zhang, Carbon, 2018, 135, 29–34 CrossRef CAS
.
- D. Bulgarevich, Y. Akamine, M. Talara, V. Mag-usara, H. Kitahara, H. Kato, M. Shiihara, M. Tani and M. Watanabe, Sci. Rep., 2020, 10, 1158 CrossRef CAS PubMed
.
- M. Shalaby, M. Peccianti, Y. Ozturk and R. Morandotti, Nat. Commun., 2013, 4, 1558 CrossRef PubMed
.
- K. Amelin, Y. Alexanian, U. Nagel, T. Rõõm, J. Robert, J. Debray, V. Simonet, C. Decorse, Z. Wang, R. Ballou, E. Constable and S. Brion, Phys. Rev. B, 2020, 102, 134428 CrossRef CAS
.
- Q. Mu, F. Fan, S. Chen, S. Xu, C. Xiong, X. Zhang, X. Wang and S. Chang, Photonics Res., 2019, 7, 325–331 CrossRef CAS
.
- H. Zhao, X. Chen, C. Ouyang, H. Wang, D. Kong, P. Yang, B. Zhang, C. Wang, G. Wei, T. Nie, W. Zhao, J. Miao, Y. Li, L. Wang and X. Wu, Adv. Photonics, 2020, 2, 066003 CAS
.
- I. Crassee, J. Levallois, A. Walter, M. Ostler, A. Bostwick, E. Rotenberg, T. Seyller, D. Marel and A. Kuzmenko, Nat. Phys., 2011, 7, 48–51 Search PubMed
.
- M. Tamagnone, C. Moldovan, J. Poumirol, A. Kuzmenko, A. Ionescu, J. Mosig and J. Perruisseau-Carrier, Nat. Commun., 2016, 7, 11216 Search PubMed
.
- J. Poumirol, P. Liu, T. Slipchenko, A. Nikitin, L. Martin-Moreno, J. Faist and A. Kuzmenko, Nat. Commun., 2017, 8, 14626 Search PubMed
.
- I. Nedoliuk, S. Hu, A. Geim and A. Kuzmenko, Nat. Nanotechnol., 2019, 14, 756–761 CrossRef CAS PubMed
.
- Y. Li, T. Li, Q. Wen, F. Fan, Q. Yang and S. Chang, Opt. Express, 2020, 28, 21062–21071 CrossRef CAS PubMed
.
- S. Mitu, D. Dey, K. Ahmed, B. Paul, Y. Luo, R. Zakaria and V. Dhasarathan, J. Magn. Magn. Mater., 2020, 494, 165831 CrossRef CAS
.
- X. Liu, L. Xiong, X. Yu, S. He, B. Zhang and J. Shen, J. Phys. D: Appl. Phys., 2018, 51, 105003 CrossRef
.
- M. Shalaby, M. Peccianti, Y. Ozturk, M. Clerici, I. Al-Naib, L. Razzari, T. Ozaki, A. Mazhorova, M. Skorobogatiy and R. Morandotti, Appl. Phys. Lett., 2012, 100, 241107 CrossRef
.
- M. Shalaby, M. Peccianti, Y. Ozturk, I. Al-Naib, C. Hauri and R. Morandotti, Appl. Phys. Lett., 2014, 105, 151108 CrossRef
.
- F. Fan, S. Chen and S. Chang, IEEE J. Sel. Top. Quantum Electron., 2017, 23, 8500111 Search PubMed
.
- W. Withayachumnankul, M. Fujita and T. Nagatsuma, Adv. Opt. Mater., 2018, 6, 1800401 CrossRef
.
- M. Qiu, M. Jia, S. Ma, S. Sun, Q. He and L. Zhou, Phys. Rev. Appl., 2018, 9, 054050 CrossRef
.
- L. Cong, Y. Srivastava, H. Zhang, X. Zhang, J. Han and R. Singh, Light: Sci. Appl., 2018, 7, 1–9 CAS
.
- Q. Yang, X. Chen, Q. Xu, C. Tian, Y. Xu, L. Cong, X. Zhang, Y. Li, C. Zhang, X. Zhang, J. Han and W. Zhang, Photonics Res., 2018, 6, 1056–1061 CrossRef CAS
.
- K. Justyna, T. Michael, S. Michael, D. Manuel, B. Klaus, S. Volker, V. Georg, L. Stefan and W. Martin, Science, 2009, 325, 1513–1515 CrossRef PubMed
.
- H. Mario, S. Martin, X. Duan, G. Harald and N. Liu, Sci. Adv., 2017, 3, e1602735 CrossRef PubMed
.
- Y. Chen, X. Yang and J. Gao, Light: Sci. Appl., 2018, 7, 1–10 CrossRef PubMed
.
- Q. Ana, C. Grégory, M. Myriam, B. Jean and K. Eugenia, J. Am. Chem. Soc., 2017, 136, 4788–4793 Search PubMed
.
- K. Ventsislav, J. Jeremy, S. Concita and V. Thierry, Adv. Mater., 2013, 25, 2517–2534 CrossRef PubMed
.
- M. Decker, R. Zhao, C. Soukoulis, S. Linden and M. Wegener, Opt. Lett., 2010, 35, 1593–1595 CrossRef CAS PubMed
.
- J. Li, J. Li, Y. Yang, J. Li, Y. Zhang, L. Wu, Z. Zhang, M. Yang, C. Zheng, J. Li, J. Huang, F. Li, T. Tang, H. Dai and J. Yao, Carbon, 2020, 163, 34–42 CrossRef CAS
.
- Y. Chen, C. Zhao, Y. Zhang and C. Qiu, Nano Lett., 2020, 20, 8696–8703 CrossRef CAS PubMed
.
- Y. Lee, R. Kim, S. Im, M. Balamurugan and K. Nam, Nanoscale, 2020, 12, 58–66 RSC
.
- S. Yoo and Q. Park, Nanophotonics, 2019, 8, 249–261 Search PubMed
.
- E. Mohammadi, K. Tsakmakidis, A. Askarpour, P. Dehkhoda, A. Tavakoli and H. Altug, ACS Photonics, 2018, 5, 2669–2675 CrossRef CAS
.
- J. Zhou, D. Roy Chowdhury, R. Zhao, A. Azad, H. Chen, C. Soukoulis, A. Taylor and J. O'Hara, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 035448 CrossRef
.
- M. Cole, W. Chen, M. Liu, S. Kruk, W. Padilla, I. Shadrivov and D. Powell, Phys. Rev. Appl., 2017, 8, 014019 CrossRef
.
- R. Zhao, L. Zhang, J. Zhou, T. Koschny and C. Soukoulis, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 83, 63–75 Search PubMed
.
- Y. Cui, L. Kang, S. Lan, S. Rodrigues and W. Cai, Nano Lett., 2014, 14, 1021–1025 CrossRef CAS PubMed
.
- L. Cong, N. Xu, W. Zhang and R. Singh, Adv. Opt. Mater., 2015, 3, 1176–1183 CrossRef CAS
.
- S. Merhebi, M. Mayyas, R. Abbasi, M. Christoe, J. Han, J. Tang, M. Rahim, J. Yang, T. Tan, D. Chu, J. Zhang, S. Li, C. Wang, K. Kalantar-Zadeh and F. Allioux, ACS Appl. Mater. Interfaces, 2020, 12, 20119–20128 CrossRef CAS PubMed
.
- I. Castro, A. Chrimes, A. Zavabeti, K. Berean, B. Carey, J. Zhuang, Y. Du, S. Dou, K. Suzuki, R. Shanks, R. Nixon-Luke, G. Bryant, K. Khoshmanesh, K. Kalantar-zadeh and T. Daeneke, Nano Lett., 2017, 17, 7831–7838 CrossRef PubMed
.
| This journal is © The Royal Society of Chemistry 2021 |