Evaluation of ultrasmall coinage metal M₁₃(dppe)₆ M = Cu, Ag, and Au clusters. Bonding, structural and optical properties from relativistic DFT calculations

Abstract

Ultrasmall ligand-protected clusters are prototypical species for evaluating the variation at the bottom of the nanoscale range. Here we explored the ultrasmall gold–phosphine M₁₃(dppe)₆ cluster, as a prototypical framework to gain insights into the fundamental similarities and differences between Au, Ag, and Cu, in the 1–3 nm size range, via relativistic DFT calculations. Different charge states involving 8- and 10-cluster electron (ce) species with a 1S²1P⁶ and 1S²1P⁶1D² configuration, leading to structural modification in the Au species between Au₁₃(dppm)₆⁵⁺ and Au₁₃(dppm)₆³⁺, respectively. Furthermore, this structural distortion of the M₁₃ core is found to occur to a lower degree for the calculated Ag and Cu counterparts. Interestingly, optical properties exhibit similar main patterns along with the series, inducing a blue-shift for silver and copper, in comparison to the gold parent cluster. For 10-ce species, the main features of 8-ce are retained with the appearance of several weak transitions in the range. The ligand–core interaction is enhanced for gold counterparts and decreased for lighter counterparts resulting in the Au > Cu > Ag trend for the interaction stabilization. Hence, the Ag and Cu counterparts of the Au₁₃(dppm)₆ cluster appear as useful alternatives, which can be further explored towards different cluster alternatives for building blocks for nanostructured materials.

---

Peter L. Rodríguez-Kessler

Peter L. Rodríguez-Kessler was born in San Luis Potosí, México. He obtained his degree in Physics in 2006 at the Autonomous University of San Luis Potosí, UASLP. In 2015 he earned a PhD in Nanoscience and Nanotechnology in the Institute for Scientific and Technological Research of San Luis Potosi, IPICYT, involving the exploration of the structure and reactivity properties of platinum-based materials, extended to other relevant systems based on silver and copper. In 2016 he initiated a postdoctoral position in the Center for Research and Advanced Studies of the National Polytechnic Institute CINVESTAV campus Mérida at the Gabriel Merino group. He joined the Muñoz-Castro group under a second postdoctoral position investigating the first-principles properties of bare gas-phase and ligand-protected clusters.

Macarena Rojas-Poblete

Macarena Rojas-Poblete received her PhD in Molecular Physical-Chemistry (2017) at the Universidad Andrés Bello, Chile, under the direction of Ramiro Arratia-Pérez in synthesis and properties of a hexarhenium (III) cluster and Relativistic Computational Chemistry of these species. She is currently a postdoctoral fellow in the Muñoz-Castro group at the Universidad Autónoma de Chile, undergoing her research work on the exploratory synthesis and optical properties of molecular clusters and terpyridines. In addition, she has other research interests, mainly host–guest interactions in supramolecular chemistry and its scope.

Alvaro Muñoz-Castro

Alvaro Muñoz-Castro received his PhD degree in Molecular Physical-Chemistry (2010) at Universidad Andres Bello, Chile, under the direction of Ramiro Arratia-Pérez in relativistic computational chemistry of inorganic species. Currently, he is a fulltime professor at Universidad Autónoma de Chile, since 2014. His research interests range from molecular clusters and superatoms, endohedral metallofullerenes, host–guest species, and carbon nanostructures, involving the understanding of magnetic response, optical, luminescent, electron-delocalization, and structural properties. He is part of the international advisory editorial board from ChemPhysChem. His achievements have been recorded to date in more than 220 publications and three book chapters, and four supervised PhD theses, being part of strong national and international networks.

---

Introduction

Atomically precise gold clusters have attracted increased interest due to their unique properties relative to the bulk material,^1–9 enabling further elucidation of the nonscalable properties of ultrasmall nanoparticles.^10–12 In the last few decades, several synthetic breakthroughs^13–24 led the characterization of ligand passivated clusters in the 1–3 nm range with both structural and electronic features ascribed to the nature of the metallic core,^25–30 usually rationalized via the divide-and-protect approach.^31,32

Among the different stabilizing groups, thiolates and phosphine ligands are widespread in the literature,^{25–28,33,34} ensuring strong gold–gold and gold–ligand bonds in stable structures against degradation.^35–42 Au₂₅(SR)₁₈⁻ (R = ligand) is one of the most noticeable ligand-protected gold clusters, composed of an atom-centered icosahedral core surrounded by six staple units, Au₂(SR)₃,^35,43–45 featuring eight cluster electrons (8-ce)^25,46 in a 1S²1P⁶ electronic configuration. This fact accounts for its particular stability⁴⁷ in analogy to closed-shell atoms, which are coined as superatoms with the central Au₁₃⁵⁺ core⁴⁸ as a recursive motif in small and ultrasmall nanoparticles.⁴⁹ It is noteworthy that Au₂₅(SR)₁₈⁻ possesses a silver isoelectronic and isostructural analog, Ag₂₅(SR)₁₈⁻,^50,51 suggesting that the Au₁₃⁵⁺ core features can also be observed in other lighter coinage metals³¹ such as Ag₁₃⁵⁺,^50,52 and Cu₁₃⁵⁺.⁵³

Recently, ultrasmall Au₁₃(dppm)₆ has been the focus of renewed interest since its early structural characterization in 1981,¹³ depicting a fully phosphine-protected Au₁₃ core. Independently, Sun and Zhu groups showed full characterization of UV/vis and cyclic-voltammetry patterns and synthetic advantages, denoting the stability of such a cluster in several charge states, with structural rearrangements between the +5 and +3 charge states.^54,55 The electronic structure of Au₁₃(dppm)₆⁵⁺ is based on a closed-shell 1S²1P⁶ configuration, similarly to Au₂₅(SR)₁₈⁻, providing a 1D character of low-lying unoccupied levels, with a variable structure in Au₁₃(dppm)₆³⁺ denoting a distorted 10-ce Au₁₃ core in a 1S²1P⁶1D² configuration.

Such species provide useful templates to further evaluate the bonding and electronic characteristics, denoting the role of the ligand–shell in the stabilization and the relation between the core–structure and optical properties. Herein, we set to evaluate the plausible formation of lighter coinage-metal group counterparts to gain more insights into the century-old concern of fundamental similarities and differences between Au, Ag, and Cu, in terms of the structure and related properties, involving different charge states. In this contribution, we provide information on the overall ligand–core interaction, and optical and structural properties, for the ultrasmall M₁₃(dppm)₆ series, by using relativistic DFT methods, as a prototypical case of ligand-protected clusters.

Computational details

Computations were carried out at the relative density functional level of theory⁵⁶ by using the ADF code,⁵⁷ incorporating scalar corrections via the ZORA Hamiltonian.⁵⁸ The triple-ξ Slater basis set, plus two polarization functions (STO-TZ2P) for valence electrons, were employed within the generalized gradient approximation (GGA) according to the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional.^59,60 Dispersion corrections to DFT were taken into account via the pairwise Grimme3 approach.^61,62 The use of the PBE-GGA functional provides accurate results for both the structure and optical properties of gold nanoclusters with minimal ligand simplifications,^44,63–67 at an affordable computational cost, as denoted by Muniz-Miranda and coworkers.⁶⁸ Optical properties were simulated by using the Van Leeuwen and Baerends functional (LB94),⁶⁹ denoting a good performance in the study of excitation in ligand-protected clusters.^70–74 Solvation effects were taken into account via a continuum solvation scheme given by the ‘COnductor-like Screening Model’ (COSMO) module from ADF, to describe the screening effects from solvation by using dichloromethane.⁷⁵

The frozen core approximation was applied to the [1s²–4f¹⁴] shells for Au, [1s²] for C, and [2s²] for P, leaving the remaining electrons to be treated variationally. Geometry optimizations were performed without any symmetry restraint via the analytical energy gradient method implemented by Versluis and Ziegler.⁷⁶ An energy convergence criterion of 10⁻⁴ Hartree, gradient convergence criteria of 10⁻³ Hartree Å⁻¹, and radial convergence criteria of 10⁻² Å were employed for the evaluation of the relaxed structures.

Results and discussion

The characterized fully phosphine-protected Au₁₃ core in its +5 charge state,⁵⁵ exhibits a distorted atom-centered icosahedron passivated with six dppm units (Fig. 1), as the structure features two groups of distances found for the central atom and icosahedral cage (Au_cent–Au_ico) length of 2.702 and 2.925 Å, respectively. Similarly, two groups of Au_ico–P distances are obtained of 2.282 and 2.346 Å, respectively, owing to a slight icosahedron ↔ cuboctahedron distortion with an elongation of certain distances (Table S1, ESI†). In its +3 charge state counterpart, the distortion of the icosahedron is increased⁵⁴ leading to several Au_cent–Au_ico distances (Tables S1 and S2, ESI†) in roughly six groups, which average to 2.819 Å, slightly shorter than 2.832 Å obtained for [Au₁₃(dppm)₆]⁵⁺, denoting a decrease of the cage radius upon addition of two electrons.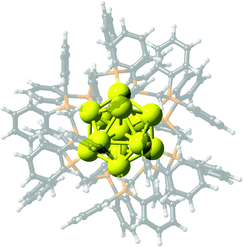

Fig. 1 Schematic structures for M₁₃(dppm)₆ clusters. Color code: Au, Ag, Cu, yellow; C: black; P: orange; H: white.

The calculated Au_cent–Au_ico distances for [Au₁₃(dppm)₆]⁵⁺ (1), are averaged in two groups of 2.817 and 2.921 Å, respectively, leading to an average of 2.869 Å (Table 1), in good agreement to experimental values (2.832 Å), as also obtained for Au_ico–P separations (2.327 and 2.341 Å). For the +3 charge state (2), similar values to experimental data are obtained, with an averaged Au_cent–Au_ico bond distance of 2.321 Å (experimental 2.314 Å).⁵⁴

Table 1 Averaged geometrical parameters in angstroms (Å), and HOMO–LUMO gap values in eV, for q = +5 and +3 species of [M₁₃(dppm)₆]^q. In addition, continuous-shape-measure data for the M₁₃ core is given

M	Mcent–Mico	CShM	Mico–P	H–L gap
a Experimental data from ref. 55 (q = +5) and ref. 54 (q = +3).
q = +5
Au	2.869	0.315	2.334	1.431
Au (Exp.)^a	2.832	0.568	2.314
Ag	2.881	0.178	2.502	1.375
Cu	2.537	0.144	2.312	1.440
q = +3
Au	2.872	17.472	2.321	1.502
Au (Exp.)^a	2.819	17.352	2.314
Ag	2.889	0.217	2.503	0.183
Cu	2.483	0.058	2.279	0.323

---

In order to account for structural deviations from an ideal atom-centered icosahedron (I_h), we evaluated the continuous-shape-measure (CShM) developed by the group of Alvarez and coworkers.^77–79 The resulting CShM values are close to zero for structures fully coincident with the reference icosahedron and increasing values accounting for the distortion degree. For the X-ray structure of [Au₁₃(dppm)₆]⁵⁺ (1), the Au₁₃ core exhibits a CShM value of 0.568 (Calculated, 0.315), denoting the distortion of the cage given by the different groups of Au_cent–Au_ico distances (vide intra). Moreover, for [Au₁₃(dppm)₆]³⁺ (2), the CShM value increases consequently to 17.352 (calc. 17.472) owing to the different types of Au_cent–Au_ico distances.

The comparison between a perfect icosahedral structure, obtained by constraining equal Au_ico–Au_ico distances previous to relax the protecting ligand shell, and the fully optimized structure for [Au₁₃(dppm)₆]⁵⁺ (1), reveals a small energy difference of 6.0 kcal mol⁻¹, in agreement with the small deviation accounted by the CShM value. In contrast, the larger distortion observed for [Au₁₃(dppm)₆]³⁺ (2) leads to a larger energy difference of 171.5 kcal mol⁻¹ in comparison with the relaxed and perfect icosahedral Au₁₃ core structure, denoting the preference for a high distortion of the core in the latter charge state.

The electronic structure for [Au₁₃(dppm)₆]⁵⁺ (1) is evaluated in terms of the superatom approach,^{25,46,80–82} denoting an 8 cluster electron (ce) count for the Au₁₃⁵⁺ core, fulfilling a 1S²1P⁶ configuration (Fig. 2).^25,46 The 1P shell remains the highest occupied molecular orbital (HOMO), in an almost three-fold degenerate level, whereas the low-lying unoccupied MO is a split of the 1D shell into three- and two-fold levels (Fig. 2), leading to a sizable HOMO–LUMO gap of 1.534 eV, in the range of the determined by electrochemical and UV-vis data (1.66 and 1.68 eV, respectively).⁵⁵ Interestingly, for 2, the extra two-electrons reside at the 1D_z² level, which in turn leads to a high stabilization of this shell. Now the HOMO–LUMO gap amounts to 1.502 eV, suggesting that the observed structural distortion of the Au₁₃³⁺ core enables a sizable HOMO–LUMO gap in a 10-ce 1S²1P⁶1D²_z2 configuration. Isosurfaces for relevant shells are given at the ESI† (Fig. S1).

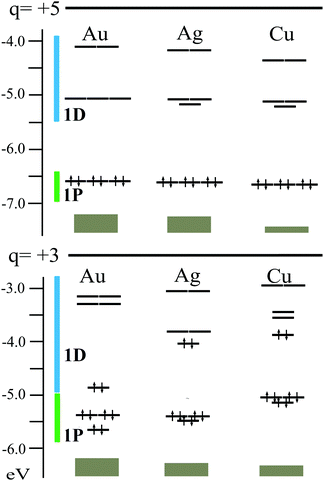Fig. 2 Electronic structure for M₁₃(dppm)₆ at +5 and +3 charge states. M = Au, Ag, and Cu 1P and 1D superatomic shells are denoted by green and blue.

Furthermore, driven by the full characterization of Ag₂₅(SR)₁₈⁻ with a central Ag₁₃⁵⁺ core,^50,51 and similarities between Au₁₃⁵⁺ and Cu₁₃⁵⁺ cores,³¹ here we evaluate the hypothetical Ag and Cu counterparts of [Au₁₃(dppm)₆]⁵⁺. Interestingly, similar electronic features are found with calculated HOMO–LUMO gaps of 1.375 and 1.440 eV, for Ag and Cu species, respectively, denoting 1P and 1D based frontier orbitals. The relaxed structures show similar averaged M_cent–M_ico distances for Ag (2.881 Å) and the Au parent (2.869 Å), with contraction to 2.537 Å for Cu species, denoting deviations from a perfect icosahedron core as given by the CShM values of 0.178 and 0.144, respectively, where values >0.1 are considered as distorted icosahedral cores.³⁴ Moreover, this small distortion from the icosahedron led to a decreased energy difference between an ideal I_h-M₁₃ core situation and the fully relaxed structures, of 6.1 for Ag (6.1 kcal mol⁻¹) and for Cu (4.0 kcal mol⁻¹) counterparts, which are similar to the observed for [Au₁₃(dppm)₆]⁵⁺ (1) (6.0 kcal mol⁻¹).

However, the +3 charge state exhibits larger differences along with the series where the 10-ce 1S²1P⁶1D²_z2 configuration exhibits a decreased HOMO–LUMO gap of 0.183 and 0.323 eV for Ag and Cu, respectively (Fig. 2). The relaxed structures for [Ag₁₃(dppm)₆]³⁺ and [Cu₁₃(dppm)₆]³⁺, are slightly distorted from a perfect icosahedron with CShM values of 0.217 and 0.058, respectively, in comparison to the Au parent (CShM = 17.472). Such a result denotes that the capabilities of coinage metal clusters to enable a structural rearrangement to maximize the HOMO–LUMO gap in 10-ce clusters, are different along with the triad, which is mostly enabled in gold species, whereas lighter silver and copper counterparts suggest lower structural flexibility upon 8- to 10-ce shift. Thus, such results suggest gold clusters to be more prone to reaccommodate structurally rather than Ag and Cu counterparts, resulting in a small HOMO–LUMO gap for the latter hypothetical species suggesting a lower kinetic and chemical stability. Hence, for 10-ce counterparts Ag and Cu clusters are less favored than the parent gold system, in contrast to 8-ce species which are expected to have a similar in magnitude HOMO–LUMO gap along the coinage metal group.

In order to gain more insights into the favorable stabilization given by the protecting layer of dppm ligands, the M₁₃⁵⁺-dppm interaction energy is evaluated (ΔE_int, Table 2). A more favorable situation is obtained for the Au case, amounting to −1168.2 kcal mol⁻¹, which decreases to −856.9 kcal mol⁻¹ for Ag, and −1038.0 kcal mol⁻¹ for Cu. Thus, the favorable bonding situation evolves along with the triad according to Au > Cu > Ag, as depicted for PPh₃ and other ligands.⁸³ In addition, for [Au₁₃(dppm)₆]³⁺ (2), the ΔE_int amounts to −787.8 kcal mol⁻¹ as a result of the two-extra electrons in the Au₁₃ core denoting a sizable decrease in the core–ligand stabilization, which is similarly found for Ag and Cu, to −507.7 and −628.3 kcal mol⁻¹, respectively. The preference for electronegative ligands for silver protected clusters observed in the literature over electroneutral ligands,³⁴ account for the calculated less favorable core–ligand interaction along with the series, suggesting that electronegative ligands provide stronger interaction. However, the core–ligand interaction energy (ΔE_int) for silver counterpart suggest a decreased but still sizable interaction, which in addition to the sizable HOMO–LUMO gap, provides the basis for further conceivable characterization.

Table 2 Energy decomposition analysis for the core–ligand interaction. Values in kcal mol⁻¹, at different charge states, +5 and +3, respectively

Charge +5	Au		Ag		Cu
ΔEPauli	1917.6		876.8		878.2
ΔEelstat	−1722.1	55.8%	−901.6	52.0%	−917.9	47.9%
ΔEorb	−1254.3	40.6%	−745.5	43.0%	−902.1	47.1%
ΔEdisp	−109.4	3.5%	−86.6	5.0%	−96.2	5.0%
ΔEint	−1168.2		−856.9		−1038.0

---

Charge +3	Au		Ag		Cu
ΔEPauli	2178.7		1037.3		1097.3
ΔEelstat	−1854.3	62.5%	−914.5	59.2%	−985.3	57.1%
ΔEorb	−990.0	33.4%	−546.1	35.3%	−636.4	36.9%
ΔEdisp	−122.2	4.1%	−84.4	5.5%	−103.8	6.0%
ΔEint	−787.8		−507.7		−628.3

---

Moreover, the nature of the core–ligand interaction is accounted by the energy decomposition analysis (EDA) within the Morokuma–Ziegler scheme,^84–86 dissecting the ΔE_int quantity into different chemically meaningful terms, as^85,87,88

ΔE_int = ΔE_Pauli + ΔE_elstat + ΔE_orb + ΔE_disp

In this framework, the stabilizing ΔE_elstat and ΔE_orb terms are related to the electrostatic and covalent character of the interaction, respectively.⁸⁸ The ΔE_Pauli term is given by the repulsive four-electron two-orbital interactions between occupied orbitals of the different fragments. In addition, the pairwise correction of Grimme62 (DFT-D3) accounts for London dispersion interactions (ΔE_disp) of stabilizing character. To overcome the basis set superposition error (BSSE) in the fragment interaction analysis of ΔE_orb, the counterpoise method was employed.

For [Au₁₃(dppm)₆]⁵⁺ (1), the interaction is given by a 55.8% of electrostatic character (ΔE_elstat), and 40.6% from covalent contributions (ΔE_orb), and a small addition from ΔE_disp. Thus, the core–ligand interaction is of the main electrostatic character with a sizable bonding contribution. Upon addition of two electrons, in the 10-ce [Au₁₃(dppm)₆]³⁺ (2) species, the interaction is similarly of electrostatic character, denoting a sizable decrease in the bonding contribution (ΔE_orb) from −1254.3 in 1 to −990.0 kcal mol⁻¹ in 2, and an increase in the Pauli repulsion term, owing to the shorter Au_ico–P distance required to maximize the bonding stabilization in the latter.

For silver and copper counterparts, the nature of the core–ligand interaction is similar in nature to gold species, which denotes a decrease in the contributing terms. Interestingly, by comparing Ag and Cu species, the different energetic terms remain similar, with the exception of the covalent character, which increases sizably for Cu counterparts, resulting in the Au > Cu > Ag trend for the interaction stabilization.

Moreover, the covalent character (ΔE_orb) can be further decomposed through the Natural Orbitals for Chemical Valence^89–91 extension of EDA (EDA-NOCV).⁹¹ As a result, the identification of different individual orbital contributions given by their deformation densities accounts for individual charge-transfer channels between the core and the ligand layer.^92,93 The obtained results exhibit a σ-donation from the phosphine ligands towards the core, as the main source of the bonding interaction in the Au₁₃(dppm)₆ formation (Fig. S2, ESI†).

The cyclic voltammetry (CV) results for [Au₁₃(dppm)₆]⁵⁺ (1),⁵⁵ exhibit reversible redox couples for both first oxidation (+5 → +6) and reduction (+5 → +4). In addition, a redox couple above the solvent window (>−2.20 V vs. Ag/Ag⁺) is expected from calculations, suggesting the plausible formation of [Au₁₃(dppm)₆]³⁺ (2) by electrochemical methods. The calculations for the different charge states observed from CV experiments of 1, and by the +3 state in 2, allows us to evaluate the evolution from +3 to +6 species. The structures for [Au₁₃(dppm)₆]^q from q = +3 to +6 (Table S1, ESI†), suggest similar averaged Au_cent–Au_ico distances, accounting for a similar Au₁₃ radius along with the redox processes. For silver, the averaged Ag_cent–Ag_ico tend to decrease slightly from 2.889 to 2.872 Å, suggesting a small compression of the Ag₁₃ cage, which contrasts with that found for the copper case, where averaged Cu_cent–Cu_ico distance increases from 2.483 to 2.634 Å. Such results suggest a variation of the M₁₃ radii along with different charge states, depicted as a decrease in Ag, a lesser variation for Au, and in contrast, increasing for Cu species, according to the electron count from 10- to 7-ce. In comparison, for Au₂₅(PET)₁₈ species with charge states from −1 to +1, denoting 8- to 5-ce, the averaged Au_cent–Au_ico distances taken from X-ray structures,^35,94 show an increase as 2.774 < 2.783 < 2.808 Å (Table S3, ESI†), denoting that the ligand shell environment is relevant in a further relaxation of the core upon different charge states.

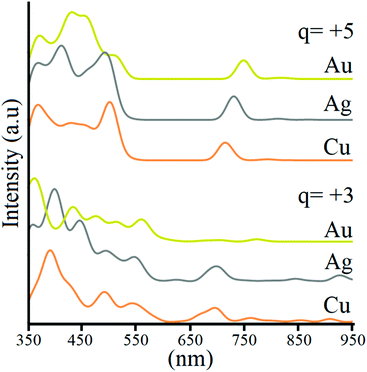
Lastly, optical properties were evaluated to account for the possible variation of the optical transition in the coinage metal triad. For [Au₁₃(dppm)₆]⁵⁺ (1),⁵⁵ the optical spectrum is dominated by an absorption band at 440 nm, and weak transitions between 500 and 750 nm, which are ascribed to the main 1P → 1D transition via time-dependent DFT calculations, which are located mainly at the Au₁₃⁵⁺ core (ESI†). Our calculations are in agreement with the previous analysis for Au₁₃, with the absorption maxima at 437 nm involving a wide 1P → Ligand, and 5d-Au block → 1D character manifold, denoting lower energy transitions between 1P-HOMO and 1D-LUMO as a small peak at 747 nm, and very weak lower energy transitions (Fig. 3). At 515 nm, a small shoulder is found, contributed by 71% of 1P → 1D, and 29% from Ligand → 1D transitions. Interestingly, for Ag and Cu counterparts, the same features of the absorption spectrum remain with a slight hypsochromic (blue-) shift of all the signals, with a small peak located at 728 and 713 nm, for Ag and Cu, respectively, showing an increase in the intensity of the Ligand → 1D shoulder, now located at 490 and 499 nm, respectively. The main transition is shifted to 409 and 366 nm, for Ag and Cu, denoting a similar pattern expected for the UV/vis spectrum, with a blue-shift of main peaks. At the +3 charge state, the spectrum retains the features shown for the +5 species, with the addition of several lower energy transitions of weak intensity owing to the appearance of 1D²_dz2 → 1D⁰ excitations, allowed by structural distortions within the M₁₃ core. Hence the main features of the UV-vis spectrum are preserved with the addition of weak lower energy peaks for the 10-ce clusters.

Fig. 3 Simulated optical absorption spectrum for [M₁₃(dppm)₆] (M = Au, Ag, and Cu) species at +5 and +3 charge states. Absorption spectra data were interpolated by applying a Gaussian broadening with a full width of 0.03 eV.

Conclusions

The ultrasmall Au₁₃(dppm)₆ cluster was studied in its +5 and +3 charge states, denoting structural, bonding, and optical property variations, ascribed to the respective 8- and 10-cluster electron counts. For Au₁₃(dppm)₆⁵⁺, the Au₁₃ core deviates from the ideal icosahedral structure, which is increased upon the addition of two electrons at Au₁₃(dppm)₆³⁺, but retaining a similar averaged Au_core–Au_ico bond distance, accounting for the core radius. For Ag and Cu, the distortion from a perfect icosahedron is to a lesser extent, resulting in a reduced HOMO–LUMO gap for 10-ce (+3 charge state) species, in contrast to the sizable gap in 8-ce. Interestingly, the more significant distortion in Au₁₃(dppm)₆³⁺ enables a further stabilization of the 1D_z² shell, retaining a sizable HOMO–LUMO gap, despite the intermediate electron count. Thus, Cu₁₃(dppm)₆³⁺ and Ag₁₃(dppm)₆³⁺ species are expected to be less stable owing to the decreased HOMO–LUMO gap.

Ligand–core interactions are larger for gold, followed by Cu, and lastly, Ag species, in agreement with the Au > Cu > Ag bonding energy trend observed for other ligands in monometallic complexes. From 8- to 10-ce, the ligand–core bonding decreases, owing to the two extra electrons in the M₁₃ core, for all the species.

Optical properties reveal common features with a small blue-shift of the relevant peaks for lighter coinage metals, which are retained between 8- and 10-ce species, where the latter includes weak low-energy transition owing to 1D_z² → 1D transitions slightly allowed by the deviations from a perfect icosahedron core. Hence, lighter coinage metal counterparts of the parent Au₁₃(dppm)₆ appear as feasible targets for further exploratory synthesis efforts, resulting in similar properties towards alternative ligand-protected clusters as building blocks for nanostructured materials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by FONDECYT/ANID 1180683. Support from FONDECYT/ANID postdoctoral fellowship grants was involved in the current work. M. R-P. acknowledges Fondecyt postdoctorado 3190335. P. L. R.-K. acknowledges Fondecyt postdoctorado 3190329.

References

1. C. N. R. Rao, A. Müller and A. K. Cheetham, The Chemistry of Nanomaterials, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, FRG, 2004.
2. Y. Sun, Shape-Controlled Synthesis of Gold and Silver Nanoparticles, Science, 2002, 298, 2176–2179.
3. Y. Yin and D. Talapin, The chemistry of functional nanomaterials, Chem. Soc. Rev., 2013, 42, 2484.
4. R. Jin, C. Zeng, M. Zhou and Y. Chen, Atomically Precise Colloidal Metal Nanoclusters and Nanoparticles: Fundamentals and Opportunities, Chem. Rev., 2016, 116, 10346–10413.
5. W. Kurashige, Y. Niihori, S. Sharma and Y. Negishi, Precise synthesis, functionalization and application of thiolate-protected gold clusters, Coord. Chem. Rev., 2016, 320–321, 238–250.
6. A. Fernando, K. L. D. M. Weerawardene, N. V. Karimova and C. M. Aikens, Quantum Mechanical Studies of Large Metal, Metal Oxide, and Metal Chalcogenide Nanoparticles and Clusters, Chem. Rev., 2015, 115, 6112–6216.
7. T. Stoll, E. Sgrò, J. W. Jarrett, J. Réhault, A. Oriana, L. Sala, F. Branchi, G. Cerullo and K. L. Knappenberger, Superatom State-Resolved Dynamics of the Au₂₅(SC₈H₉)¹⁸⁻ Cluster from Two-Dimensional Electronic Spectroscopy, J. Am. Chem. Soc., 2016, 138, 1788–1791.
8. R. Costi, A. E. Saunders and U. Banin, Colloidal Hybrid Nanostructures: A New Type of Functional Materials, Angew. Chem., Int. Ed., 2010, 49, 4878–4897.
9. I. Chakraborty and T. Pradeep, Atomically Precise Clusters of Noble Metals: Emerging Link between Atoms and Nanoparticles, Chem. Rev., 2017, 117, 8208–8271.
10. X. Jiang, B. Du, Y. Huang and J. Zheng, Ultrasmall noble metal nanoparticles: breakthroughs and biomedical implications, Nano Today, 2018, 21, 106–125.
11. B. H. Kim, M. J. Hackett, J. Park and T. Hyeon, Synthesis, Characterization, and Application of Ultrasmall Nanoparticles, Chem. Mater., 2014, 26, 59–71.
12. K. Zarschler, L. Rocks, N. Licciardello, L. Boselli, E. Polo, K. P. Garcia, L. De Cola, H. Stephan and K. A. Dawson, Ultrasmall inorganic nanoparticles: state-of-the-art and perspectives for biomedical applications, Nanomed. Nanotechnol., Biol. Med., 2016, 12, 1663–1701.
13. J. W. A. van der Velden, F. A. Vollenbroek, J. J. Bour, P. T. Beurskens, J. M. M. Smits and W. P. Bosnian, Gold clusters containing bidentate phosphine ligands. Preparation and X-Ray structure investigation of [Au₅(dppmH)₃(dppm)](NO₃)₂ and [Au₁₃(dppmH)₆](NO₃)_n, Recl. des Trav. Chim. des Pays-Bas, 1981, 100, 148–152.
14. B. K. Teo and H. Zhang, Cluster of clusters. Structure of a new cluster [(p-Tol₃P)₁₀Au₁₃Ag₁₂Cl₇](SbF₆)₂ containing a nearly staggered-eclipsed-staggered metal configuration and five doubly-bridging ligands, Inorg. Chem., 1991, 30, 3115–3116.
15. C. E. Briant, B. R. C. Theobald, J. W. White, L. K. Bell, D. M. P. Mingos and A. J. Welch, Synthesis and X-ray structural characterization of the centred icosahedral gold cluster compound [Au₁₃(PMe₂Ph)₁₀Cl₂](PF₆)₃; the realization of a theoretical prediction, J. Chem. Soc., Chem. Commun., 1981, 201–202.
16. A. Ghosh, O. F. Mohammed and O. M. Bakr, Atomic-Level Doping of Metal Clusters, Acc. Chem. Res., 2018, 51, 3094–3103.
17. Z. Lei, J. Li, Z. Nan, Z. Jiang and Q. Wang, Cluster From Cluster: A Quantitative Approach to Magic Gold Nanoclusters [Au₂₅(SR)₁₈]⁻, Angew. Chem., Int. Ed., 2021, 60, 14415–14419.
18. W. Wang and R. W. Murray, Reaction of Triphenylphosphine with Phenylethanethiolate-Protected Au₃₈ Nanoparticles, Langmuir, 2005, 21, 7015–7022.
19. L. C. McKenzie, T. O. Zaikova and J. E. Hutchison, Structurally Similar Triphenylphosphine-Stabilized Undecagolds, Au₁₁(PPh₃)₇Cl₃ and [Au₁₁(PPh₃)₈Cl₂]Cl, Exhibit Distinct Ligand Exchange Pathways with Glutathione, J. Am. Chem. Soc., 2014, 136, 13426–13435.
20. D. M. P. Mingos, H. R. Powell and T. L. Stolberg, Synthesis and structural characterization of the tetrahedral cluster [Au₄(PPh₃)₄(μ₂-SnCl₃)₂], Trans. Met. Chem., 1992, 17, 334–337.
21. Y.-Z. Li, R. Ganguly, K. Y. Hong, Y. Li, M. E. Tessensohn, R. Webster and W. K. Leong, Stibine-protected Au₁₃ nanoclusters: syntheses, properties and facile conversion to GSH-protected Au₂₅ nanocluster, Chem. Sci., 2018, 9, 8723–8730.
22. H. Ube, Q. Zhang and M. Shionoya, A Carbon-Centered Hexagold(I) Cluster Supported by N-Heterocyclic Carbene Ligands, Organometallics, 2018, 37, 2007–2009.
23. M. R. Narouz, S. Takano, P. A. Lummis, T. I. Levchenko, A. Nazemi, S. Kaappa, S. Malola, G. Yousefalizadeh, L. A. Calhoun, K. G. Stamplecoskie, H. Häkkinen, T. Tsukuda and C. M. Crudden, Robust, Highly Luminescent Au₁₃ Superatoms Protected by N-Heterocyclic Carbenes, J. Am. Chem. Soc., 2019, 141, 14997–15002.
24. H. Shen, S. Xiang, Z. Xu, C. Liu, X. Li, C. Sun, S. Lin, B. K. Teo and N. Zheng, Superatomic Au₁₃ clusters ligated by different N-heterocyclic carbenes and their ligand-dependent catalysis, photoluminescence, and proton sensitivity, Nano Res., 2020, 13, 1908–1911.
25. M. Walter, J. Akola, O. Lopez-Acevedo, P. D. Jadzinsky, G. Calero, C. J. Ackerson, R. L. Whetten, H. Grönbeck and H. Häkkinen, A unified view of ligand-protected gold clusters as superatom complexes, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9157–9162.
26. A. W. Castleman and S. N. Khanna, Clusters, Superatoms, and Building Blocks of New Materials, J. Phys. Chem. C, 2009, 113, 2664–2675.
27. P. D. Jadzinsky, G. Calero, C. J. Ackerson, D. A. Bushnell and R. D. Kornberg, Structure of a Thiol Monolayer-Protected Gold Nanoparticle at 1.1 Å Resolution, Science, 2007, 318, 430–433.
28. S. A. Claridge, A. W. Castleman, S. N. Khanna, C. B. Murray, A. Sen and P. S. Weiss, Cluster-assembled materials, ACS Nano, 2009, 3, 244–255.
29. T. Bürgi, Properties of the gold-sulphur interface: from self-assembled monolayers to clusters, Nanoscale, 2015, 7, 15553–15567.
30. T. Fehlner, J.-F. Halet and J.-Y. Saillard, Molecular Clusters. A Bridge to Solid State Chemistry, Cambridge Univ. Press. Cambridge, UK, 2007.
31. F. Gam, D. Paez-Hernandez, R. Arratia-Perez, C. W. W. Liu, S. Kahlal, J.-Y. J.-Y. Saillard and A. Muñoz-Castro, Coinage Metal Superatomic Cores: Insights into Their Intrinsic Stability and Optical Properties from Relativistic DFT Calculations, Chem. – Eur. J., 2017, 23, 11330–11337.
32. T. Tsukuda and H. Häkkinen, Protected Metal Clusters: From Fundamentals to Applications, Elsevier, 2015.
33. M. I. Bruce, J.-F. Halet, B. Le Guennic, B. W. Skelton, A. N. Sobolev, C. J. Sumby and A. H. White, Structural systematics of some trinuclear alkynyl and diynyl Group 11 complexes containing dppm [dppm = CH₂(PPh₂)₂], Coord. Chem. Rev., 2018, 375, 2–12.
34. S. Takano and T. Tsukuda, Chemically Modified Gold/Silver Superatoms as Artificial Elements at Nanoscale: Design Principles and Synthesis Challenges, J. Am. Chem. Soc., 2021, 143, 1683–1698.
35. M. W. Heaven, A. Dass, P. S. White, K. M. Holt and R. W. Murray, Crystal structure of the gold nanoparticle [N(C₈H₁₇)₄][Au₂₅(SCH₂CH₂Ph)₁₈], J. Am. Chem. Soc., 2008, 130, 3754–3755.
36. O. Toikkanen, V. Ruiz, G. Rönnholm, N. Kalkkinen, P. Liljeroth and B. M. Quinn, Synthesis and Stability of Monolayer-Protected Au₃₈ Clusters, J. Am. Chem. Soc., 2008, 130, 11049–11055.
37. H. Qian, C. Liu and R. Jin, Controlled growth of molecularly pure Au₂₅(SR)₁₈ and Au₃₈(SR)₂₄ nanoclusters from the same polydispersed crude product, Sci. China: Chem., 2012, 55, 2359–2365.
38. P. Maity, S. Xie, M. Yamauchi and T. Tsukuda, Stabilized gold clusters: from isolation toward controlled synthesis, Nanoscale, 2012, 4, 4027–4037.
39. H. Häkkinen, The gold–sulfur interface at the nanoscale, Nat. Chem., 2012, 4, 443–455.
40. G. Schmid, The relevance of shape and size of Au₅₅ clusters, Chem. Soc. Rev., 2008, 37, 1909.
41. L. Srisombat, A. C. Jamison and T. R. Lee, Stability: a key issue for self-assembled monolayers on gold as thin-film coatings and nanoparticle protectants, Colloids Surf., A, 2011, 390, 1–19.
42. R. Juarez-Mosqueda, S. Malola and H. Häkkinen, Stability, electronic structure, and optical properties of protected gold-doped silver Ag_29−xAu_x (x = 0–5) nanoclusters, Phys. Chem. Chem. Phys., 2017, 19, 13868–13874.
43. X. Kang, H. Chong and M. Zhu, Au₂₅(SR)₁₈: the captain of the great nanocluster ship, Nanoscale, 2018, 10, 10758–10834.
44. J. Akola, M. Walter, R. L. Whetten, H. Häkkinen and H. Grönbeck, On the structure of thiolate-protected Au₂₅, J. Am. Chem. Soc., 2008, 130, 3756–3757.
45. T. Dainese, S. Antonello, J. A. Gascón, F. Pan, N. V. Perera, M. Ruzzi, A. Venzo, A. Zoleo, K. Rissanen and F. Maran, Au₂₅(SEt)₁₈, a Nearly Naked Thiolate-Protected Au₂₅ Cluster: Structural Analysis by Single Crystal X-ray Crystallography and Electron Nuclear Double Resonance, ACS Nano, 2014, 8, 3904–3912.
46. H. Häkkinen, Atomic and electronic structure of gold clusters: understanding flakes, cages and superatoms from simple concepts, Chem. Soc. Rev., 2008, 37, 1847–1859.
47. D. Jiang and S. Dai, From Superatomic Au₂₅(SR)₁₈⁻ to Superatomic M@Au₂₄ (SR)₁₈^q Core–Shell Clusters, Inorg. Chem., 2009, 48, 2720–2722.
48. F. K. Sheong, J.-X. Zhang and Z. Lin, An [Au₁₃]⁵⁺ Approach to the Study of Gold Nanoclusters, Inorg. Chem., 2016, 55, 11348–11353.
49. S. Jin, S. Wang and M. Zhu, Insight into the Geometric and Electronic Structures of Gold/Silver Superatomic Clusters Based on Icosahedron M₁₃ Units and Their Alloys, Chem. – Asian J., 2019, 14, 3222–3231.
50. C. P. Joshi, M. S. Bootharaju, M. J. Alhilaly and O. M. Bakr, [Ag₂₅(SR)₁₈]⁻: The “Golden” Silver Nanoparticle, J. Am. Chem. Soc., 2015, 137, 11578–11581.
51. H. Hirai, S. Ito, S. Takano, K. Koyasu and T. Tsukuda, Ligand-protected gold/silver superatoms: current status and emerging trends, Chem. Sci., 2020, 11, 12233–12248.
52. L. G. AbdulHalim, M. S. Bootharaju, Q. Tang, S. Del Gobbo, R. G. AbdulHalim, M. Eddaoudi, D. Jiang and O. M. Bakr, Ag₂₉(BDT)₁₂(TPP)₄: A Tetravalent Nanocluster, J. Am. Chem. Soc., 2015, 137, 11970–11975.
53. A. Baghdasaryan and T. Bürgi, Copper nanoclusters: designed synthesis, structural diversity, and multiplatform applications, Nanoscale, 2021, 13, 6283–6340.
54. S. Jin, W. Du, S. Wang, X. Kang, M. Chen, D. Hu, S. Chen, X. Zou, G. Sun and M. Zhu, Thiol-Induced Synthesis of Phosphine-Protected Gold Nanoclusters with Atomic Precision and Controlling the Structure by Ligand/Metal Engineering, Inorg. Chem., 2017, 56, 11151–11159.
55. S.-S. Zhang, L. Feng, R. D. Senanayake, C. M. Aikens, X.-P. Wang, Q.-Q. Zhao, C.-H. Tung and D. Sun, Diphosphine-protected ultrasmall gold nanoclusters: opened icosahedral Au₁₃ and heart-shaped Au₈ clusters, Chem. Sci., 2018, 9, 1251–1258.
56. K. G. Dyall and K. Fægri, Introduction to Relativistic Quantum Chemistry, Oxford University Press, New York, 2007.
57. Amsterdam Density Functional (ADF), 2019Code, Vrije Universiteit: Amsterdam, The Netherlands. Available at: http://www.scm.com.
58. E. van Lenthe, E.-J. J. Baerends and J. G. Snijders, Relativistic total energy using regular approximations, J. Chem. Phys., 1994, 101, 9783.
59. J. P. Perdew, K. Burke and Y. Wang, Generalized gradient approximation for the exchange-correlation hole of a many-electron system, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539.
60. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1997, 78, 1396.
61. S. Ehrlich, J. Moellmann and S. Grimme, Dispersion-Corrected Density Functional Theory for Aromatic Interactions in Complex Systems, Acc. Chem. Res., 2013, 46, 916–926.
62. S. Grimme, Density functional theory with London dispersion corrections, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228.
63. O. Lopez-Acevedo, J. Akola, R. L. Whetten, H. Grönbeck and H. Häkkinen, Structure and Bonding in the Ubiquitous Icosahedral Metallic Gold Cluster Au₁₄₄(SR)₆₀, J. Phys. Chem. C, 2009, 113, 5035–5038.
64. D. Jiang, The expanding universe of thiolated gold nanoclusters and beyond, Nanoscale, 2013, 5, 7149–7160.
65. J. Akola, K. A. Kacprzak, O. Lopez-Acevedo, M. Walter, H. Grönbeck and H. Häkkinen, Thiolate-Protected Au₂₅ Superatoms as Building Blocks: Dimers and Crystals, J. Phys. Chem. C, 2010, 114, 15986–15994.
66. D. Jiang, M. Kühn, Q. Tang and F. Weigend, Superatomic Orbitals under Spin-Orbit Coupling, J. Phys. Chem. Lett., 2014, 5, 3286–3289.
67. M. Zhou, Z. Lei, Q. Guo, Q.-M. Wang and A. Xia, Solvent Dependent Excited State Behaviors of Luminescent Gold(I)–Silver(I) Cluster with Hypercoordinated Carbon, J. Phys. Chem. C, 2015, 119, 14980–14988.
68. F. Muniz-Miranda, M. C. Menziani and A. Pedone, Assessment of Exchange-Correlation Functionals in Reproducing the Structure and Optical Gap of Organic-Protected Gold Nanoclusters, J. Phys. Chem. C, 2014, 118, 7532–7544.
69. R. van Leeuwen and E. J. Baerends, Exchange-correlation potential with correct asymptotic behavior, Phys. Rev. A, 1994, 49, 2421–2431.
70. C. M. Aikens, Effects of Core Distances, Solvent, Ligand, and Level of Theory on the TDDFT Optical Absorption Spectrum of the Thiolate-Protected Au₂₅ Nanoparticle, J. Phys. Chem. A, 2009, 113, 10811–10817.
71. E. B. Guidez and C. M. Aikens, Quantum mechanical origin of the plasmon: from molecular systems to nanoparticles, Nanoscale, 2014, 6, 11512–11527.
72. N. Durante, A. Fortunelli, M. Broyer and M. Stener, Optical Properties of Au Nanoclusters from TD-DFT Calculations, J. Phys. Chem. C, 2011, 115, 6277–6282.
73. G.-T. Bae and C. M. Aikens, Time-Dependent Density Functional Theory Studies of Optical Properties of Au Nanoparticles: Octahedra, Truncated Octahedra, and Icosahedra, J. Phys. Chem. C, 2015, 119, 23127–23137.
74. P. Ai, M. Mauro, A. A. Danopoulos, A. Muñoz-Castro and P. Braunstein, Dual Emission of a Cyclic Hexanuclear Gold(I) Complex. Interplay between Au₃ and Au₂ Ligand-Supported Luminophores, J. Phys. Chem. C, 2019, 123, 915–921.
75. A. Klamt and V. Jonas, Treatment of the outlying charge in continuum solvation models, J. Chem. Phys., 1996, 105, 9972.
76. L. Versluis and T. Ziegler, The determination of molecular structures by density functional theory. The evaluation of analytical energy gradients by numerical integration, J. Chem. Phys., 1988, 88, 322–328.
77. A. Ruiz-Martínez, D. Casanova and S. Alvarez, Polyhedral Structures with an Odd Number of Vertices: Nine-Coordinate Metal Compounds, Chem. – Eur. J., 2008, 14, 1291–1303.
78. S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Shape maps and polyhedral interconversion paths in transition metal chemistry, Coord. Chem. Rev., 2005, 249, 1693–1708.
79. J. Cirera, E. Ruiz and S. Alvarez, Continuous Shape Measures as a Stereochemical Tool in Organometallic Chemistry, Organometallics, 2005, 24, 1556–1562.
80. S. Khanna and P. Jena, Assembling crystals from clusters, Phys. Rev. Lett., 1992, 69, 1664–1667.
81. J. U. Reveles, S. N. Khanna, P. J. Roach and A. W. Castleman, Multiple valence superatoms, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 18405–18410.
82. A. Muñoz-Castro, sp³-hybridization in superatomic clusters. Analogues to simple molecules involving the Au₆ core, Chem. Sci., 2014, 5, 4749–4754.
83. A. Muñoz-Castro, D. MacLeod Carey and R. Arratia-Perez, Relativistic effects on dative carbon-coinage metal bond. Evaluation of NHC-MCl (M = Cu, Ag, Au) from relativistic DFT, Polyhedron, 2021, 197, 115020.
84. K. Morokuma, Molecular Orbital Studies of Hydrogen Bonds. III. C=O⋯H–O Hydrogen Bond in H₂CO⋯H₂O and H₂CO⋯2H₂O, J. Chem. Phys., 1971, 55, 1236–1244.
85. G. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders, T. Ziegler, G. T. E. Velde, C. F. Guerra and S. J. A. Gisbergen, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967.
86. T. Ziegler and A. Rauk, On the calculation of bonding energies by the Hartree Fock Slater method, Theor. Chim. Acta, 1977, 46, 1–10.
87. M. von Hopffgarten and G. Frenking, Energy decomposition analysis, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43–62.
88. G. Frenking, M. Bickelhaupt and F. Matthias Bickelhaupt, The Chemical Bond, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2014, pp. 121–157.
89. R. F. Nalewajski, J. Mrozek and A. Michalak, Two-electron valence indices from the Kohn-Sham orbitals, Int. J. Quantum Chem., 1997, 61, 589–601.
90. A. Michalak, R. L. DeKock and T. Ziegler, Bond multiplicity in transition-metal complexes: applications of two-electron valence indices, J. Phys. Chem. A, 2008, 112, 7256–7263.
91. in The Chemical Bond: Fundamental Aspects of Chemical Bonding, ed. G. Frenking and S. Shaik, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2014.
92. A. Michalak, M. Mitoraj and T. Ziegler, Bond orbitals from chemical valence theory, J. Phys. Chem. A, 2008, 112, 1933–1939.
93. M. P. Mitoraj, A. Michalak and T. Ziegler, A combined charge and energy decomposition scheme for bond analysis, J. Chem. Theory Comput., 2009, 5, 962–975.
94. M. A. Tofanelli, K. Salorinne, T. W. Ni, S. Malola, B. Newell, B. Phillips, H. Häkkinen and C. J. Ackerson, Jahn-Teller effects in Au₂₅(SR)₁₈, Chem. Sci., 2016, 7, 1882–1890.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02451e

---