Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Material properties particularly suited to be measured with helium scattering: selected examples from 2D materials, van der Waals heterostructures, glassy materials, catalytic substrates, topological insulators and superconducting radio frequency materials
Bodil
Holst
 *a,
Gil
Alexandrowicz
*a,
Gil
Alexandrowicz
 b,
Nadav
Avidor
b,
Nadav
Avidor
 c,
Giorgio
Benedek
c,
Giorgio
Benedek
 de,
Gianangelo
Bracco
f,
Wolfgang E.
Ernst
de,
Gianangelo
Bracco
f,
Wolfgang E.
Ernst
 g,
Daniel
Farías
g,
Daniel
Farías
 h,
Andrew P.
Jardine
c,
Kim
Lefmann
h,
Andrew P.
Jardine
c,
Kim
Lefmann
 i,
Joseph R.
Manson
i,
Joseph R.
Manson
 ej,
Roberto
Marquardt
ej,
Roberto
Marquardt
 k,
Salvador Miret
Artés
k,
Salvador Miret
Artés
 le,
Steven J.
Sibener
le,
Steven J.
Sibener
 m,
Justin W.
Wells
m,
Justin W.
Wells
 no,
Anton
Tamtögl
no,
Anton
Tamtögl
 g and
William
Allison
c
g and
William
Allison
c
aDepartment of Physics and Technology, University of Bergen, Allegaten 55, 5007 Bergen, Norway. E-mail: bodil.holst@uib.no
bDepartment of Chemistry, College of Science, Swansea University, Swansea, SA2 8PP, UK
cDepartment of Physics, Cavendish Laboratory, University of Cambridge, J. J. Thompson Avenue, Cambridge CB3 0HE, UK
dDipartimento di Scienza dei Materiali, Universitá di Milano-Bicocca, Via R. Cozzi 55, 20125 Milano, Italy
eDonostia International Physics Center (DIPC), Paseo Manuel de Lardizabal 4, 20018 Donostia/San Sebastián, Spain
fCNR-IMEM, Department of Physics, University of Genova, V. Dodecanesco 33, 16146 Genova, Italy
gInstitute of Experimental Physics, Graz University of Technology, 8010 Graz, Austria
hDepartamento de FÍsica de la Materia Condensada, Instituto Nicolás Cabrera and Condensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, 28049 Madrid, Spain
iNanoscience Center, Niels Bohr Institute, University of Copenhagen, 2100 Copenhagen, Denmark
jDepartment of Physics and Astronomy, Clemson University, Clemson, South Carolina 29634, USA
kLaboratoire de Chimie Quantique de l’Institut de Chimie, UMR 7177 CNRS/UdS Université de Strasbourg, 1, rue Blaise Pascal, 67008 Strasbourg, France
lInstituto de Física Fundamental, Consejo Superior de Investigaciones Científicas, Serrano 123, 28006 Madrid, Spain
mJames Franck Institute and Department of Chemistry, University of Chicago, Chicago, Illinois 60637, USA
nCenter for Quantum Spintronics, Department of Physics, Norwegian University of Science and Technology, 7491, Trondheim, Norway
oDepartment of Physics, University of Oslo, Sem Sælands vei 24, 7491, Oslo, Norway
First published on 1st February 2021
Abstract
Helium Atom Scattering (HAS) and Helium Spin-Echo scattering (HeSE), together helium scattering, are well established, but non-commercial surface science techniques. They are characterised by the beam inertness and very low beam energy (<0.1 eV) which allows essentially all materials and adsorbates, including fragile and/or insulating materials and light adsorbates such as hydrogen to be investigated on the atomic scale. At present there only exist an estimated less than 15 helium and helium spin-echo scattering instruments in total, spread across the world. This means that up till now the techniques have not been readily available for a broad scientific community. Efforts are ongoing to change this by establishing a central helium scattering facility, possibly in connection with a neutron or synchrotron facility. In this context it is important to clarify what information can be obtained from helium scattering that cannot be obtained with other surface science techniques. Here we present a non-exclusive overview of a range of material properties particularly suited to be measured with helium scattering: (i) high precision, direct measurements of bending rigidity and substrate coupling strength of a range of 2D materials and van der Waals heterostructures as a function of temperature, (ii) direct measurements of the electron–phonon coupling constant λ exclusively in the low energy range (<0.1 eV, tuneable) for 2D materials and van der Waals heterostructures (iii) direct measurements of the surface boson peak in glassy materials, (iv) aspects of polymer chain surface dynamics under nano-confinement (v) certain aspects of nanoscale surface topography, (vi) central properties of surface dynamics and surface diffusion of adsorbates (HeSE) and (vii) two specific science case examples – topological insulators and superconducting radio frequency materials, illustrating how combined HAS and HeSE are necessary to understand the properties of quantum materials. The paper finishes with (viii) examples of molecular surface scattering experiments and other atom surface scattering experiments which can be performed using HAS and HeSE instruments.
1 Introduction
New materials require adequate tools in order to characterise and understand their fundamental properties. No single technique provides all the answers. It is usually necessary to use several different probes in combination. Each technique exploits the unique features of the interaction between the probe and the material under investigation. A key feature of all the methods in use today is the ability to provide information with high spatial resolution since the design of new materials rests on characterisation on the atomic scale. Furthermore, the enormous developments in 2D materials, van der Waals (vdW) heterostructures and nano-structured surfaces in general, have enhanced the need for surface/few atomic layers sensitive techniques.Many probes are available to characterise materials and they offer a rich palette of opportunity because their properties and their interaction with the material differ so profoundly. In general the best quantitative information on the smallest length scale with ordered structures is obtained from scattering experiments, while microscopy is preferred on longer length scales and with heterogeneous structures. In this paper we concentrate exclusively on scattering experiments done using beam-probes: photons, electrons, ions, neutrons, and neutral molecules or atoms. Scattering experiments separate into experiments probing “static” structure, such as diffraction and experiments probing dynamical processes such as diffusion or vibrations (i.e., phonons). The energy of the scattering particles together with the nature of the interaction potential define the information that can be obtained from an experiment. Major (interrelated) parameters of a scattering probe are (i) wavelength, (ii) time-resolution, (iii) energy and (iv) penetration depth. The wavelength determines the spatial resolution. The time-resolution is of central importance to the study of dynamical processes (i.e., phonons and diffusion). It is usually limited by beam intensity and detector response, or by the range of energy-transfer that is accessible. The energy determines both the wavelength and thus the spatial resolution, as well as the excitations that can be observed and also the damage that individual quanta can create through inelastic scattering. It also has some influence on the penetration depth. Furthermore the energy spread of the incident beam limits the time-resolution. This limitation can be overcome by the spin-echo principle, see Section 3.6. The final parameter, the penetration depth, is particularly important for the investigation of surfaces and “few atomic layers” materials. If the scattered signal contains a too large contribution from the bulk the information from the surface/first few atomic layers may be entirely swamped. The penetration depth is determined by the interaction potential between the scattering probe and the sample in combination with the probe energy: electrons, X-rays and neutrons all scatter off the electronic cloud of the atomic cores and atomic nuclei in the sample, and always have a certain penetration into the bulk. Specific methods have been developed to enhance the surface sensitivity of the techniques: low energy electron diffraction,1 grazing incidence wide angle X-ray scattering,2 grazing incidence small-angle X-ray scattering3 and grazing incidence small-angle neutron scattering,4 but a certain penetration always remains for these probes.
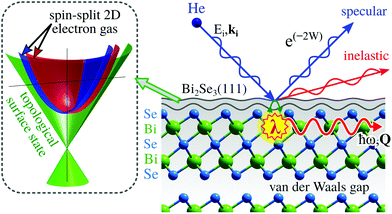
The only scattering probes that do not penetrate at all into the bulk are neutral molecular and atomic beams including neutral helium, created by supersonic expansion. Unlike electrons, X-rays and neutrons which all interact with the core electronic cloud and atomic nuclei in the sample, as described above, the neutral molecules and atoms scatter off the outermost electron density distribution at the sample surface. This is illustrated for helium in Fig. 1. The surface sensitivity arises from a combination of low energies and the Pauli exclusion principle, which gives an interaction dominated by the valence electrons of the sample. The classical turning point for helium is a few Ångstroms above the surface.5 A key feature of the He-electron collision is its softness: the energy of a 0.1 nm wavelength helium atom is only 20 meV, see Section 2, so no sample damage is induced. Helium scattering can probe essentially all materials and adsorbates, including fragile and/or insulating materials and light adsorbates such as hydrogen. The technique has been presented as the surface analogy to neutron scattering from bulk materials. As we shall see it is still possible to probe some properties related to the first few atomic layers.
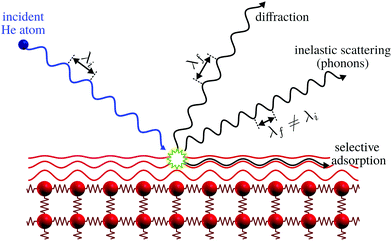 | ||
| Fig. 1 Graphical representation of the different processes for the scattering of He atoms on a crystal surface. Note how the helium atom scatters off the electron density distribution, indicated as red lines, without any penetration into the bulk. Selective adsorption refers to the trapping of a helium atom in the helium surface interaction potential, see ref. 9 for further discussion. Here λi and λf denote the wavelength of the incident and scattered helium atoms, respectively. Inelastic scattering leads to a wavelength change. | ||
Despite a significant body of literature, including both hard and soft surfaces and metal, semiconductor and insulating materials, helium atom scattering (HAS) and helium spin-echo (HeSE) cannot be described as mainstream techniques, due to the fact that they are not readily accessible for the broad scientific community at present. The purpose of this paper is to describe, through a series of examples, the unique benefits offered by helium scattering with an emphasis on encouraging and extending its range of application. For overviews of work on HAS and HeSE see ref. 6–8 and the very recent book by Benedek and Toennies dedicated to surface phonon dispersion measurements.9 This book also serves as an excellent introduction to the topic of helium atom scattering. See also the classical work on Atomic and Molecular Beam Methods edited by Scoles, in particular the chapter by Miller on free jet sources.10
2 The experimental setup
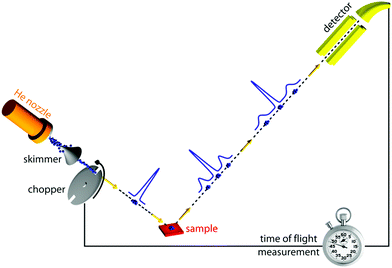
Of all scattering techniques, helium scattering arguably uses the simplest source: a helium pressure bottle. The first helium scattering experiment was performed by Otto Stern and co-workers in 1930.11 The observation of diffraction peaks from LiF and NaCl not only confirmed the de Broglie matter wave hypothesis for atoms but also provided the basis for a new material characterisation technique. However, the low pressure, effusive source used in the initial experiments with a broad velocity distribution and low intensity was not ideal for scattering experiments. A breakthrough came in 1951 when Kanrowitz and Grey proposed to use gas at high pressure.12 In these novel sources, the pressure is so high that the atoms collide in the exit aperture of the source (the nozzle) as the beam expands into vacuum. The centre part of the beam is selected by a so called skimmer and the resulting supersonic beam has a source pressure dependent velocity distribution narrower than the equilibrium Maxwell distribution of the gas in the source. The velocity of the beam can be changed by cooling or heating the nozzle. A liquid nitrogen cooled beam has a wavelength around 0.1 nm corresponding to a velocity of around 1000 m s−1 and an energy of around 20 meV.10 The energy is usually kept at less than 0.1 eV to stay in the quantum mechanical scattering regime, see Section 3.8.3. The energy resolution, as determined by the velocity spread of the beam, varies with pressure and temperature, but is typically around 0.3 meV for a liquid nitrogen cooled beam.13,14 Essentially, two different types of experiments can be performed in HAS: Elastic and inelastic scattering. The different scattering processes are illustrated in Fig. 1.Fig. 2 shows a diagram of a standard HAS instrument. See Section 3.6 for a description of the HeSE extension. Elastic scattering measures the angular dependence of helium atoms that scatter without energy loss or gain. Elastic scattering experiments can be used to obtain information about the surface topography (corrugation) of crystalline surfaces and amorphous surfaces that are corrugated on the nanoscale. For crystalline materials the lattice parameter and corrugation amplitude can be extracted from the diffracted intensities whereby the term corrugation amplitude refers to the electronic charge corrugation at the surfaces. For amorphous surfaces, the characteristic distance can be determined by the radius of the amorphous (vitreous) ring. For further discussion of the measurement of nanoscale surface topography using HAS, see Section 3.5.
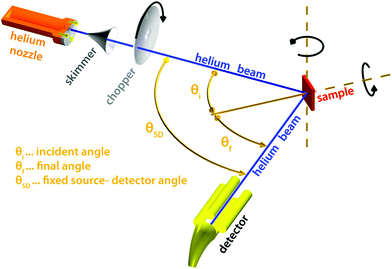 | ||
| Fig. 2 Diagram of a HAS instrument. Shown here in a fixed source-detector angle configuration. The beam is produced by supersonic expansion of He gas through a nozzle, with the central part of the expansion selected by a skimmer. For energy resolved experiments the beam is pulsed using a chopper and the arrival time of the pulse measured (time-of-flight – TOF), see Fig. 3. Typical dimensions are around 1.5–2 m for each beam arm. | ||
Inelastic helium scattering is illustrated in Fig. 3. Here the energy loss or gain through the surface scattering process is measured using time-of-flight (TOF). By varying the incident angle of the beam (and hence the in-plane wavevector component K), phonon dispersion curves can be measured. An example for graphene on Cu(111) can be found in Fig. 4. Moreover, low energy vibrations of adsorbed molecules such as frustrated translational and rotational modes can be measured below the energy range that is accessible with optical methods.15 In general the phonon energy that can be probed in a scattering experiment is determined by the energy of the incident probe. HAS, with its incident energy of less than 0.1 eV is the only technique that can probe surface phonons exclusively in the low energy regime. The upper limit probed can be tuned down by cooling of the nozzle as discussed above. The very low energy of the helium beam (4 orders of magnitude less than an electron at a similar wavelength) combined with the inertness also makes helium very attractive for probing insulating, fragile structures as well as 2D materials or materials where the interaction within a few atomic layers are of particular interest, such as van der Waals heterostructures and topological insulators.
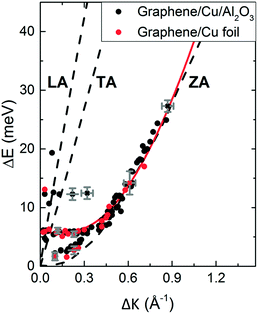 | ||
Fig. 4 Experimentally derived surface phonons for Gr/Cu(111)/Al2O3 (black dots) and Gr on Cu(111) foil (red dots) measured along the 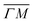 direction shown with DFT calculations for free standing Gr (dashed curves).25 The red curve is a fit to the experimental data using eqn (2) with ΔE = ħωcoupledZA(ΔK). In the abscissa ΔK is the change in parallel wave vector of the helium atoms, and ΔE the change of energy of the helium atoms which is the energy exchange (loss or gain) with the surface corresponding to phonon excitation or annihilation. See also Fig. 3. Reproduced with permission from ref. 24 ©(2015) Elsevier. direction shown with DFT calculations for free standing Gr (dashed curves).25 The red curve is a fit to the experimental data using eqn (2) with ΔE = ħωcoupledZA(ΔK). In the abscissa ΔK is the change in parallel wave vector of the helium atoms, and ΔE the change of energy of the helium atoms which is the energy exchange (loss or gain) with the surface corresponding to phonon excitation or annihilation. See also Fig. 3. Reproduced with permission from ref. 24 ©(2015) Elsevier. | ||
3 Selected material properties particularly suited to be measured with helium scattering
We now approach to a series of examples of studies of material properties, where the use of HAS is instrumental.3.1 Bending rigidity and substrate coupling strength of 2D materials
In this section we show how HAS is the most versatile method for measuring the bending rigidity of 2D materials and the only method which can potentially measure the temperature dependence of bending rigidity for a range of 2D materials, something which to the best of our knowledge has not been done so far. Furthermore we show that HAS is a very unique method for precise measurements of the substrate coupling strength for 2D materials.The mechanical properties of 2D materials are crucial for a number of applications, from biological membranes to flexible electronics. To design flexible electronic components that do not fracture when bent, it is important to know how flexible the different material layers are, relative to each other. This is expressed by the bending rigidity, κ, a measure of material resistance to deformation. It is particularly important to know how the bending rigidity varies with temperature, κ(T), to design flexible electronics components with a big enough temperature working range for specific applications, typically −40 °C to 85 °C for commercial electronics.16
In classical mechanics κ can be derived for an amorphous membrane structure of thickness h using Young's modulus Y and Poisson's ratio σ as17
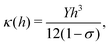 | (1) |
In 2013 Amorim and Guinea presented an analytical expression for extracting the bending rigidity for a free-standing thin membrane (i.e., graphene, Gr), from a phonon dispersion curve for the perpendicular acoustic (ZA) phonon mode, obtained from a membrane weakly bound to a substrate:22
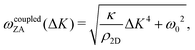 | (2) |
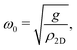 | (3) |
In 2015 Al Taleb et al. applied eqn (2) as a new method for measuring the bending rigidity of 2D materials by means of HAS.24 Since He beams used in HAS are typically 1–5 mm in diameter, the method provides information over a large sample area.
We illustrate the way in which both the bond strength and the bending rigidity are determined with HAS for the case of Gr/Cu(111).24Fig. 4 shows the acoustic phonon dispersion curves measured with HAS along the 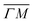 direction for two different Gr/Cu(111) samples. Phonon dispersion curves for free standing Gr calculated from first principles25 are also shown as dashed lines.
direction for two different Gr/Cu(111) samples. Phonon dispersion curves for free standing Gr calculated from first principles25 are also shown as dashed lines.
The ZA phonon mode is clearly visible. This is the mode that corresponds to the dispersion curve in eqn (2). The transverse acoustic (TA) mode is forbidden for planar scattering in the 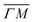 direction, whereas the low cross section for excitation of the longitudinal acoustic (LA) mode makes its detection quite difficult. First principles phonon calculations of a Gr/Cu interface predict a few meV shift of the ZA mode near the
direction, whereas the low cross section for excitation of the longitudinal acoustic (LA) mode makes its detection quite difficult. First principles phonon calculations of a Gr/Cu interface predict a few meV shift of the ZA mode near the 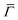 point,26 which is a direct measure of the Gr–Cu coupling strength according to eqn (3). A similar shift (of a different energy) was recently predicted for graphene on another weakly bound substrate SiC.27 This shift is clearly seen at ħω0 ∼ 6 meV in Fig. 4. An overtone of this mode is also observed at ħω ∼ 12 meV. An unshifted dispersion curve is also present, which resembles the ZA mode of free-standing Gr. This is very likely due to the Rayleigh wave of the Cu(111) substrate, since at this wavevector the penetration depth of He atoms is large enough to sample it.28 Fitting the ZA mode using eqn (2), it is possible to determine both g and κ. The best-fit (red curve in Fig. 4) leads to g = (5.7 ± 0.4) × 1019 N m−3 and κ = (1.30 ± 0.15) eV. The derived g is 2–3 times smaller than that reported for Gr/SiO2 interfaces, which is very reasonable.29 The derived κ value is consistent with DFT calculations that predict values of κ in the range 1.20–1.61 eV.30
point,26 which is a direct measure of the Gr–Cu coupling strength according to eqn (3). A similar shift (of a different energy) was recently predicted for graphene on another weakly bound substrate SiC.27 This shift is clearly seen at ħω0 ∼ 6 meV in Fig. 4. An overtone of this mode is also observed at ħω ∼ 12 meV. An unshifted dispersion curve is also present, which resembles the ZA mode of free-standing Gr. This is very likely due to the Rayleigh wave of the Cu(111) substrate, since at this wavevector the penetration depth of He atoms is large enough to sample it.28 Fitting the ZA mode using eqn (2), it is possible to determine both g and κ. The best-fit (red curve in Fig. 4) leads to g = (5.7 ± 0.4) × 1019 N m−3 and κ = (1.30 ± 0.15) eV. The derived g is 2–3 times smaller than that reported for Gr/SiO2 interfaces, which is very reasonable.29 The derived κ value is consistent with DFT calculations that predict values of κ in the range 1.20–1.61 eV.30
HAS was recently used to obtain also the bending rigidity and coupling strength of a 2D silica bilayer weakly bound on Ru.31 Furthermore the bending rigidity and coupling strength of graphene on sapphire32 have been measured. The latter experiment illustrates how the defect density affects the bending rigidity of the graphene.
The fact that measurements done on a 2D material weakly bound to a substrate can be used to extract the value of κ for the free-standing 2D material, is a big experimental advantage which should make it possible to measure κ(T) for the free-standing material simply by varying the temperature of the substrate. So far no such temperature dependent measurements have been published. As mentioned at the beginning of this section it is particularly important to know how the bending rigidity changes with temperature to design flexible electronics components with a big enough temperature working range for specific applications. The theoretical values for the temperature dependence of the bending rigidity of various 2D materials are heavily contested in the literature. For graphene, several publications claim it will decrease with temperature whereas others predict that it will increase, see for example.33,34 For bilayer graphene, there are also conflicting results suggesting both increase and decrease with temperature and deviations of more than two orders of magnitude as summarised in ref. 19, see also ref. 35.
Another important point is to understand the behaviour of κ as a function of material thickness. How thick does a 2D material have to be to behave classically and follow eqn (1) The answer is likely to differ for different material classes. First experiments on bilayer silica (SiO2) mentioned above31 suggest that it already behaves classically, which is not the case for bilayer graphene.
Finally it should be mentioned that phonon dispersion curves are extremely sensitive to interatomic forces of adsorbed layers, including the interaction between adlayer and substrate atoms also for non-weakly bound systems. A range of HAS measurements of graphene on metal surfaces provide a good example of how small changes in the substrate coupling strength modify the corresponding phonon dispersion curves.36 Softening of optical modes and signatures of the substrate’s Rayleigh wave are observed for strong graphene–substrate interactions,37 while acoustic phonon modes resemble those of free-standing graphene for weakly interacting systems.32 Moreover, phonon dispersion curves provide an excellent scenario to test the performance of current state-of-the-art calculations.
3.2 The electron–phonon coupling constant λ in the low energy range
In this section we show how HAS is idealy suited to measure the electron–phonon e–ph coupling constant λ (also known as the mass correction factor of superconductivity) exclusively in the low energy range (<0.1 eV, tuneable) for 2D materials and van der Waals heterostructures. The energy range can be tuned to a desired maximum by changing the energy and/or the incident angle of the helium beam. As will be explained in more detail below, measurements of λ in the low energy range are of particular importance for understanding superconductivity in 2D materials.The e–ph coupling constant λ came into importance in 1957 when Bardeen, Cooper and Schrieffer developed the first comprehensive theory of superconductivity.38 They gave what is now known as a crude expression for the superconducting transition temperature in terms of λ, which was later developed into a more accurate expression by McMillan.39 In bulk materials λ plays a role in all phenomena in which phonons interact with electrons. For bulk materials λ can be determined from heat capacity measurements, the linewidths of spectral lines emitted from bulk samples, heat transfer between electrons and phonons under non-equilibrium conditions, laser pump–probe measurements and many other experiments.40 Since the early HAS measurements by Toennies and coworkers on metal surfaces,41,42 e–ph interaction was shown to have remarkable effects, unveiled by the discovery of a soft longitudinal resonance, now recognized as an ubiquitous feature of all metal surfaces. This discovery led to a radical change in the theory of inelastic HAS from a conducting surface: from the two-body collision model to the e–ph interaction model described below.
In recent years several 2D materials have been shown to be superconducting. A particularly prominent example being Jarillo-Herrero and co-workers’ magic-angle graphene demonstration in 2018 that two graphene sheets placed on top of each other on hexagonal boron nitride and twisted 1.1° relative to each other display superconductivity.43
In 2019 it was shown that trilayer graphene (ABC type) on hexagonal boron nitride also shows signs of superconductivity.44 Another class of 2D materials that displays superconductivity is the transition metal chalcogenides: among others, monolayer MoS2,45 monolayer and bilayer WS246,47 and monolayer NbSe2.48 However, the nature of superconductivity in several of these new 2D superconductors, in particular, the relative contributions from e–ph coupling and electron correlation are not at all understood. For example, there is an intense debate about the value of λ for magic-angle graphene. Some simulations indicate electron correlation is dominant and hence λ should be small (≪1),43,49 whereas other studies suggest that the e–ph coupling is dominant for the superconductivity and λ could be as large as 1.050–53 or even as large as 1.5.54 Further, if the e–ph coupling is dominant, it is not clear if it is the higher or lower energy phonons that mediate the superconductivity. This lack of understanding of λ makes it difficult to decide on the best experimental path for designing new 2D materials that display superconductivity at higher temperatures.
One problem has been that, while there are several ways to measure λ for bulk materials as discussed above, up to very recently there was no straightforward method for measuring λ directly for the low energy phonon regime.203
Up until now the experimental method usually applied to measure λ in 2D materials has been angular resolved photoelectron spectroscopy (ARPES). ARPES measures the momentum distribution of electrons ejected from a solid exposed to UV light/soft X-rays (typically the energy of the incident beam is around 20 eV; note, this is around 1000 times bigger than the energy of the atoms in a helium scattering beam). The ejected electrons reflect the electronic excitations in the material and thus allow the electronic structure to be probed. λ can be measured as so-called “kinks” in the valence bands. ARPES is a very powerful technique, but the measurements of λ tend to be biased towards the higher energy optical phonon modes. In the cases where the momentum transfer is small (and dispersive), i.e., when the relevant phonon mode(s) is the low energy part of the acoustic mode(s) ARPES may struggle: The contribution from the lower energy phonons (in the acoustic phonon regime) cannot be extracted without extensive calculations that are not always feasible (this is discussed in more details in Section 3.2.2). λ values for higher energy phonons have been successfully extracted using ARPES for example for graphene (σ-band)55 and MoS2.56 For graphene, the σ-band is too far away from the Fermi level to have any influence on superconductivity. For MoS2 the values found for λ were too low to contribute to superconductivity.
A further challenge with ARPES for 2D material examination is that there are some cases where the substrate bands mask the 2D material bands. Furthermore the interaction between a 2D material and the supporting substrate modifies the outermost electron density distribution of the 2D material, which will particularly affect the low energy e–ph coupling23 (see also the final paragraph of Section 3.1). This illustrates how complex the superconducting challenge is: for 2D materials, λ is not necessarily a material constant but may depend on the interaction with the substrate underneath. This is supported by a paper on superconductivity in MoS2 published in 2020, where the superconductivity appears to be “induced” by the Pb substrate45 and another paper from the same year, which shows that the superconducting properties of magic-angle graphene improve significantly, when the magic-angle graphene is placed on a monolayer of WSe2 instead of boron nitride.57 Furthermore, a recent theoretical paper shows that for monolayer graphene, the main phonon mode involved in e–ph coupling in the π-band for moderate doping is one of the lower energy acoustic modes.58 It appears that an informed design of new 2D materials, with the ultimate aim of achieving room temperature superconductivity, will require systematic measurements of λ in the low energy phonon regime for a broad range of 2D material systems.
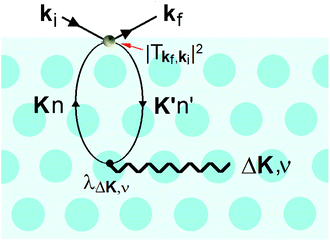
It is also at the repulsive part of the potential where the He atoms sense the vibrations of the surface, i.e., the phonons. Since the 1980s it has been known that HAS is uniquely sensitive to measuring phonon modes in the surface region, such as the Rayleigh mode or modes due to adsorbate layers. However, the He atoms do not directly sense the vibrational motions of the atomic cores, instead they measure the phonons of the electron density that are induced by the cores. In other words, inelastic He atom scattering excites phonon modes in the cores via the e–ph interaction. This is shown schematically in Fig. 5.
This process was theoretically quantified in 2011 where it was shown that the He atom scattering intensity associated with excitation of a surface phonon, having parallel momentum ħΔK and mode number ν, is directly proportional to its corresponding mode component of the e–ph coupling constant λΔK,ν.28,60 The e–ph coupling constant λ is given by the average over the mode components, 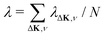 where N is the total number of modes.61 The He atom scattering inelastic intensity IΔK,ν for a specific phonon mode is given by28
where N is the total number of modes.61 The He atom scattering inelastic intensity IΔK,ν for a specific phonon mode is given by28
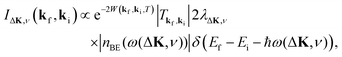 | (4) |
The Debye–Waller factor multiplies all quantum mechanical intensities, which includes diffraction peaks, single-phonon peaks, diffuse elastic intensity due to defects and adsorbates, etc. It describes the attenuation of all quantum features due to the phonons that are excited in the collision. Its argument 2W(kf,ki,T) is proportional to the mean square phonon displacement, hence for temperatures larger than the zero point motion region it is approximately proportional to the temperature T. Since 2W(kf,ki,T) depends on an average over all phonon modes, it is intuitively reasonable to expect that it could also be expressed as a function of the e–ph constant since λ is also an average over all modes. Recently, it has been demonstrated that the Debye–Waller exponent is proportional to λ and for the special case of the specular diffraction peak it can be written simply as62
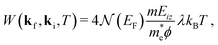 | (5) |
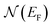 is the electron density of states at the Fermi surface, m is the He atomic mass,
is the electron density of states at the Fermi surface, m is the He atomic mass, 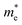 is the effective electron mass, Eiz is the incident He atom energy due to motion normal to the surface, ϕ is the work function, and kB is the Boltzmann constant. Eqn (5) shows that the temperature dependence of the Debye–Waller exponent, which is easily measured, can be used to extract values of λ. For simple metals, the effective mass
is the effective electron mass, Eiz is the incident He atom energy due to motion normal to the surface, ϕ is the work function, and kB is the Boltzmann constant. Eqn (5) shows that the temperature dependence of the Debye–Waller exponent, which is easily measured, can be used to extract values of λ. For simple metals, the effective mass 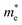 is known and a reasonable approximation to the density of states is that of a free electron gas
is known and a reasonable approximation to the density of states is that of a free electron gas 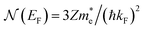 where ħkF is the Fermi momentum and Z is the valence number. Using eqn (5) with the free electron gas density of states, Table 1 shows, in the next-to-last column, the values of λ = λHAS that are obtained from all simple metals for which the temperature dependence of the Debye–Waller factor has been measured. The values obtained from HAS are remarkably similar to values of λ from other sources shown in the last column, which are almost all measured for the bulk metal crystals.62 HAS measurements have recently been used to obtain values for λ in the low energy range also for degenerate semiconductors (PtTe2, PdTe2)63,64 and a transition metal chalagonide MoS2,65 see also the specific science case on topological materials. Section 3.7.1.
where ħkF is the Fermi momentum and Z is the valence number. Using eqn (5) with the free electron gas density of states, Table 1 shows, in the next-to-last column, the values of λ = λHAS that are obtained from all simple metals for which the temperature dependence of the Debye–Waller factor has been measured. The values obtained from HAS are remarkably similar to values of λ from other sources shown in the last column, which are almost all measured for the bulk metal crystals.62 HAS measurements have recently been used to obtain values for λ in the low energy range also for degenerate semiconductors (PtTe2, PdTe2)63,64 and a transition metal chalagonide MoS2,65 see also the specific science case on topological materials. Section 3.7.1.
| Surface |
Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I (T)/ΔT [10−3 K −1] I (T)/ΔT [10−3 K −1] |
k iz 2 [Å−2] | ϕ [eV] | k F [Å−1] | Z | λ HAS | λ (bulk and other sources) |
|---|---|---|---|---|---|---|---|
| Cu(111) | 4.2 θi = 56.9° | 30.36 | 4.94 | 0.25 | 1 | 0.083 | 0.093 |
| 0.13 | |||||||
| 0.15 | |||||||
| Cu(110) | 1.7 θi = 67° | 6.20 | 4.48 | 0.25 | 1 | 0.148 | 0.17 |
| 0.23 | |||||||
| Cu(001) | 6.61 θi = 19° | 108.2 | 4.59 | ∼0.6 | 1 | 0.195 | 0.15 ± 0.03 |
| 0.13 | |||||||
| Ni(111) | 1.25 | 14.7 | 5.15 | 1.49 | 10 | 0.19 | 0.21–0.24 |
| 0.167 | |||||||
| W(001)1 × 1 | 4.1 | 26.3 | 4.32 | 1.19 | 6 | 0.31 | 0.28 |
| Pb(111) | 5.0 | 5.65 | 4.25 | 0.65 | 4 | 0.769 | 0.95 |
| 0.7–0.9 | |||||||
| Ag(111) (1,0) peak | 3.4 | 16.82 | 4.74 | 0.22 | 1 | 0.082 | 0.059 |
| 0.12 | |||||||
| 0.13 ± 0.04 | |||||||
| K(110) | 8.07 | 16.29 | 2.30 | 0.27 | 1 | 0.16 | 0.13 ± 0.03 |
| 0.11 | |||||||
| Cs(110) | 17.8 | 26.9 | 2.1 | 0.26 | 1 | 0.18 | 0.15 ± 0.03 |
| 0.16 | |||||||
| Sb(111) | 5.6 | 22.8 | 4.56 | 0.80 | 5 | 0.28 | 0.27 |
| Bi(111) | 11.5 | 16.79 | 4.23 | 0.72 | 5 | 0.57 | 0.60 |
| 0.45 |
3.3 The surface boson peak
In this section we show how HAS is the only method which can be used to directly measure the boson peak on a surface for glassy materials. This implies that HAS is also the only method that can be used to measure directly the boson peak on 2D materials. The boson peak as a 2D phenomenon has been predicted,68 and recently observed in a model system of a highly jammed two-dimensional granular material,69 but not yet experimentally measured in a 2D material.The Debye model predicts that the vibrational density of states (VDOS) for a material is proportional to the frequency squared in the low energy range. However in many materials the spectrum departs from this law and thus, when the VDOS is normalized by the frequency squared, a peak (or rather a hump) occurs, i.e., an excess in the phonon density of states with a corresponding excess in heat capacity. This peak/hump is known as the boson peak. It has been observed in the bulk of numerous materials using optical,70 neutron71 and thermal72 techniques. The boson peak has long been considered a feature of disordered materials such as glassy materials, where it is typically observed at energies in the THz range (1 THz ≈ 4 meV), but recently it has also been observed in single crystals.73 A theoretical explanation for this was provided last year.74 Recent result on polymer glasses show that the boson peak frequency is proportional to 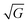 , where G is the macroscopic shear modulus.72
, where G is the macroscopic shear modulus.72
Given the importance of the heat capacity for a big range of material applications, it is clearly very important to understand and potentially tailor the magnitude and/or position of the boson peak also for surfaces and 2D materials. As mentioned above theoretical predictions suggest that the boson peak should be present in 2D materials,68 however, none of the standard methods used to measure boson peaks can be applied to surfaces and 2D materials because they penetrate too far into the materials. The only, method that can be used to probe the boson peak on surfaces in the THz (meV) range, relevant for glassy materials, is the strictly surface sensitive HAS.
A few years back the first and so far only measurements of the boson peak on a surface were performed using HAS on vitreous silica, where it was found at an energy of around 1 THz (4 meV). As mentioned above the boson peak is typically observed at energies in the THz (meV) range, exactly the energy range that can be probed by HAS. The first publication showed that the surface boson peak was in the predicted energy range.75 In a second publications it could be shown that the surface boson peak on vitreous silica displays a strong temperature dependence, blueshifting with increasing temperature,76 see also ref. 77 and 78.
3.4 Polymer chain surface dynamics under nano-confinement
In this section we argue that HAS is a useful complimentary method for investigating dynamical properties of polymer thin films. Polymers represent a very important class of glassy materials, they are usually “soft” and insulating, which means that they can be challenging to investigate with other techniques, in particular with regards to the surface properties. HAS has proven a very useful probe for studying the vibrational dynamics of polymer surfaces, revealing how the surface dynamics change due to nano-confinement as film thickness approaches the radii of gyration of the polymer chains,79–81 and how surface vibrational dynamics change when going from the amorphous to the crystalline phase.82 HAS measurements provide a precise window into polymer surface dynamics, complementing other spectroscopic or X-ray scattering methods while revealing a clear picture of surface dynamics isolated from the bulk signatures.823.5 Nanoscale surface topography
In this section we show how HAS in some cases can provide important information about surface topography, that cannot be obtained with other techniques.As discussed in Sections 1 and 3.2.1, HAS is unique in that the atoms scatter off the outmost electron density distribution of the surface. For this reason a close-packed crystalline metal surface, with its de-localized outer valence band, appears flat with negligible diffraction peaks in a HAS experiment.6 For more corrugated periodic structures including adsorbate structures, the HAS diffraction peaks can provide very accurate information about the characteristic lateral repeat distance. The information can be extracted using the standard reciprocal lattice formalism. In cases where the diffraction pattern can potentially be explained by contributions from domains, a combination with a direct imaging technique is necessary to determine the surface structure. One of the largest surface reconstructions ever observed on a bulk substrate, a 5.55 ± 0.07 nm reconstruction on annealed α-quartz was recently identified in a combined HAS and atomic force microscopy study.83 HAS can also be used to extract information about the vertical step-height by looking at the conditions for positive and negative interference effects in the perpendicular k-vector. This can also be used to monitor thin film growth modes.8,84–86 and real time relaxation effects by monitoring changes in the Helium signal after the deposition has been completed,87 see also specific science case Section 3.7.2. As mentioned in Section 1 HAS is particularly sensitive to light adsorbates, including hydrogen, which has been used in a large number of fundamental structure and dynamic studies, see for example ref. 9, 15 and 88. In principle HAS can also provide very precise information of the surface topography for periodic structures. The surface corrugation is reflected in the relative intensities of the HAS diffraction peaks (the form factor). However, because inelastic scattering also plays a role, knowledge about the interaction potential between the helium atom and the surface is required to extract the surface corrugation. This can be obtained as a model issued mainly from first principle calculations (or ab initio calculations) or some simple interaction and geometrical models with fitting parameters. The best and more convenient dynamical theory is the close-coupling formalism which is exact when the numerical convergence is reached. In this formalism, the different diffraction channels are coupled among them and the number of channels depend strongly on the surface corrugation. Single and multi-phonon events need to be calculated in order to obtain the attenuated diffraction intensities.89 This method has been used, among others, to determine the surface corrugation on semi-metals.90 Recently, an extension of this theory which takes into account the e–ph coupling has also been proposed.91 It should also be noted that the position, shape and width of selective adsorption resonances, see Fig. 1, provides a powerful route for an experimental determination of the attractive part of the atom–surface interaction potential92 (see also Section 3.6.2). An article describing in detail the methods for obtaining atom–surface interaction potentials from HAS experiments can be found as part of this special issue.92
It is appropriate to compare the capabilities of HAS to the standard tools for measuring nanoscale topography: Scanning Tunnelling Microscopy (STM) and Atomic Force Microscopy (AFM). Firstly it should be noted that both of these techniques are obviously more versatile than HAS because they provide real space images and thus do not require the investigated samples to contain periodic features.
STM probes a combination of the surface topography and the local density of states (LDOS). Which LDOS are sampled depends on the bias voltage.93 In many cases this is a big strength of STM because this flexibility in bias voltage can provide additional, important information, but in some cases it can be valuable to distinguish the contribution from the surface topography, a couple of examples are provided in Sections 3.5.1 and 3.5.2 below. It should also be noted that STM requires the substrate to be conducting.
AFM probes the interaction potential between a tip and the surface. It is a very powerful technique which works regardless of the substrate conductivity. Topographic information can be obtained with any type of AFM imaging mode, but atomic resolution generally needs the use of dynamic AFM.94 In particular non-contact AFM has succeeded in atomic resolution imaging,95 however, as in STM, the contrast may be convoluted with other effects. For example it has been demonstrated that the type of atoms that form the tip apex decide the contrast, which has lead to, e.g., hydrogen adsorbed on an oxide being imaged inversely as holes in the surface.96
3.6 HeSE: a unique tool for studying surface dynamics
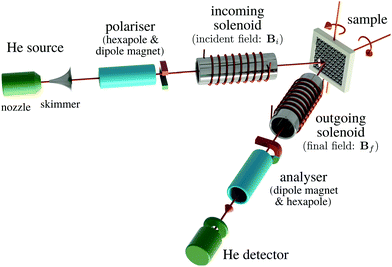
Helium spin-echo (HeSE) is a recent variation on the HAS technique109,110 which adds manipulation of the helium wavepackets using the nuclear spin of 3He atoms, to enable dynamical measurements to be obtained in a completely different way. Essentially, each helium wavepacket is split into two spin-components, which are separated by a time, tSE, using a magnetic field, before they scatter in turn from the surface being studied. The two scattered components are then recombined, and by averaging over the beam a surface correlation measurement is obtained as a function of the time, tSE, see Fig. 6.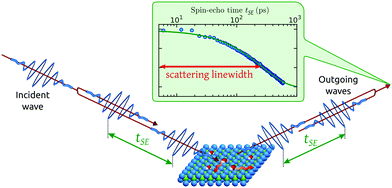 | ||
| Fig. 6 Two wavepackets scatter from the surface with a time difference tSE, allowing the motion of molecules on the surface to be interrogated through the loss in correlation, measured through the polarisation of the beam. The top inset shows a typical measurement with the linewidth caused by a small Doppler broadening upon scattering from moving adsorbates and thus corresponding to the timescale of the molecular movement.111 Since the process is based on self-interference of each 3He atom, the polarisation loss depends only on the change in energy and not the beam energy itself.109 | ||
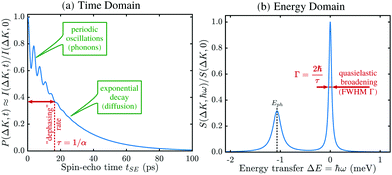
A schematic of the experimental setup can be found in Fig. 7. Measurements typically have the general form shown in Fig. 8, where phonons and other vibrations show up as oscillations and aperiodic changes, such as diffusion, show up as an overall decay.
The result is a very powerful surface-correlation measurement in reciprocal space. The technique is sensitive between timescales of less than a picosecond and nanoseconds, and on lengthscales between Ångstroms and many tens of nanometres. A very wide range of important physical processes occur within this measurement window (a more detailed comparison of experimental techniques is given in ref. 110) and in particular there are simply no other techniques that can probe equilibrium processes at surfaces in this regime. The nearest comparable technique – neutron spin-echo – is only weakly surface sensitive, so is limited to certain very specific systems.112 HeSE has therefore become the tool of choice for studying many surface processes and has already revealed a range of unique and otherwise unavailable physical insights. Moreover, due to the low energy of the probing particle beam delicate adsorbates such as water can be studied without disruption of the motion113 or dissociation of the molecule (see also Section 3.5.3).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 106 people world wide. It has the potential to dramatically reduce energy consumption in chemical industry and the production of greenhouse gases, thus having an important impact on sustainability and the huge socio-economic benefits that such changes will bring.
106 people world wide. It has the potential to dramatically reduce energy consumption in chemical industry and the production of greenhouse gases, thus having an important impact on sustainability and the huge socio-economic benefits that such changes will bring.
While significant progress has been made in recent decades to understand heterogeneous catalysis, many elementary steps remain unresolved. Very important steps include the diffusion of the chemically reacting adsorbates on the catalytic substrate, in order to find the reaction site,130 followed by reorientation of molecules for reaction, as well as the nature of the forces between species that control these steps when multiple adsorbates are present. The challenge has been that only within the last decade has a technique been available which can measure these steps with the required picosecond time resolution: HeSE.
Experiments on the diffusion of adsorbates on catalytic substrates using HeSE, as described earlier and in,110,131 have opened the possibility to assess adsorbate mobility with high spatial resolution in all directions of the substrate, as well as molecular reorientation.116 These experiments allow us to gather information on the topography of the catalytic surfaces, the interactions with the substrate atoms, and the motion of the adsorbed particles that participate in the catalytic reaction. For example, the discovery of the uncorrelated motion of CO molecules on Pt(111), where strong pairwise interactions were previously thought to dominate,121 is a particularly clear example of the need for such data.
However, only a small number of relevant substrates have been investigated with HeSE so far and these measurements often raise important questions about the fundamental behavior of adsorbates. For instance, the barrier to diffusion of CO on a copper surface is predicted to be three times higher along the 〈110〉 direction than along the 〈100〉,132 whereas, from ref. 131, the spin echo experiments seem to indicate that the barriers should be similar. Understanding the interplay between adsorbate interaction potentials and adsorbate-substrate energy exchange is likely to be fundamental to resolving such questions.
From a more recent work, the need for further HeSE measurements also becomes obvious. Recent first principle calculations133 have, for the very first time, shown that quantum effects are important even above room temperature. The theory developed in that work allowed the calculation of diffusion rates α for H and H2 on Pd(111), see Fig. 9, yielding significant differences. These results are in quantitative agreement with similar experimental results from diffusion on Pt(111), but can themselves only be verified with new HeSE data.
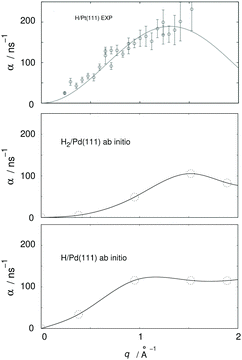 | ||
| Fig. 9 Ab initio results for H2 and H/Pd111 (adapted from ref. 134, lowest and middle panel) and comparison with experimental HeSE data for H/Pt(111) (adapted from ref. 119, upper panel); q is the momentum transferred to the adsorbate in the HeSE measurements. The upper panel shows experimental results at 0.1 monolayer coverage. The middle panel shows results from periodic cell calculations at 0.22 monolayer coverage including interactions between the hydrogen atoms located in one cell. The lower panel shows results at 0.11 monolayer coverage. | ||
Together, the combination of further HeSE experiments on relevant surfaces, combined with further theoretical developments, will enable us to discover and unravel the fundamental steps in catalytic processes. The result will provide crucial knowledge that can facilitate the intelligent design of new catalysts.
3.7 Specific science cases for combined HAS/HeSE investigations
In this section we present two important classes of materials where HAS and HeSE are instrumental in understanding their properties.Topological insulators (TIs) fall under the term of quantum materials whose electronic properties are determined by many interacting degrees of freedom like lattice vibrations, electron orbital and spin strictly connected by the laws of quantum mechanics. TIs belong to the class of Dirac materials where the unifying framework is an electronic surface state with a linear energy-momentum relationship, a so-called Dirac cone (left inset in Fig. 10).136 In typical Dirac materials such as graphene and TIs, low-energy fermionic excitations behave as massless Dirac particles. Moreover, TIs such as Bi2Se3 or Bi2Te3 exhibit an insulating gap in the bulk while the surface is electrically conducting137 and the electronic surface state exhibits no spin degeneracy due to the large spin–orbit splitting (see, e.g., ref. 138 and 139). Implications include surface dominated electronic transport and spin-polarised charge transport with intrinsically reduced backscattering.138 In other words, spin-dependent surface currents should experience no resistance. Such materials hold great promises for future use in quantum technology, such as quantum information transfer and storage.
Three-dimensional TIs, are commonly composed of layered hexagonal structures that are bound by weak vdW forces (see Fig. 10). Aside from the interest in spintronic devices based on TIs, surface dominated transport is a major route towards applications, for instance in quantum sensing by employing electronic changes upon adsorption140–142 for the realisation of miniature sensors capable of monitoring single atoms or molecules. The electronic properties of TIs have been shown to be tunable by adsorption of atomic or molecular species that can serve as n- or p-type doping agents.140,141
However, at finite temperatures, the ideal zero-Kelvin behaviour of TIs is perturbed by e–ph coupling and energy dissipation into the bulk thus giving rise to energy losses.143–145 Already at this point, it is clear that information about e–ph coupling and collective charge excitations at surfaces, thin film quantum wells and nano-structures are of paramount importance for the understanding and application of-relevant properties of topological materials. Hence we need experimental techniques that help to gain a deeper fundamental understanding of (a) the electronic structure and electronic transport, (b) the phonon dispersion and the e–ph coupling constant λ (see Section 3.2.1), as well as (c) the effect of adsorption on property modification of topological materials.
ARPES addresses the electronic band structure as discussed in Section 3.2.1, while STM, AFM, and electron microscopy provide a real space analysis of the surface structure. HAS, on the other hand, is based on the interaction of an atomic matter wave with a periodic crystal surface where the lattice constants and the wavelength are of the same order of magnitude. Compared to electron or X-ray diffraction, atoms of the same wavelength deliver much less energy to the surface and due to the scattering mechanism, do not penetrate into the sample, but get scattered purely by the electronic charge distribution at the sample surface as discussed in the introduction. Moreover, HAS has the advantage that TI samples are not exposed to any intense ultraviolet illumination which has been reported to trigger energetic shifts of the electronic bands.146
Having said this, the relation to microscopy and microanalysis differs from the mentioned classical real space analysis by rather yielding results in a reciprocal space picture.9,147 In this way, periodicity is measured at highest precision, see also Section 3.5, which allows for example an exact determination of surface phase transitions. Hofmann et al.148 recently showed a transition to a dimerisation-like reconstruction in the one-dimensional atomic chains on the Bi(114) surface at low temperatures. While STM images give a nice spatial picture and the idea of a Peierls-like distortion, complementary HAS measurements clearly show a change of the periodicity in the appearance of additional diffraction peaks at low temperature, halfway between the peaks for the “normal” phase.
Due to the heavy elements in typical TIs such as Bi2Se3, the energies of (acoustic) surface lattice vibrations are typically in the low meV energy region and thus measurements of the surface phonon dispersion require high energy resolution as well as surface sensitive probes. HAS provides also access to the e–ph coupling strength at surfaces9,149 (see Section 3.2.1), a quantity that determines energy losses in surface electronic transport. While scattering from defects and other lattice imperfections can possibly be controlled by the quality and a careful growth of crystals and films, phonons will be excited in even the most perfect crystals. Consequently, e–ph coupling should be the dominant scattering mechanism for surface electronic states at finite temperatures. TIs such as Bi2Te3 are also classic thermoelectric materials150,151 with a large Seebeck coefficient and, as such, they have been used in thermoelectric refrigeration for a long time. Since the thermoelectric performance is closely related to the phonon dispersion and details of their electronic structure, information on the phonon dispersion and the e–ph coupling is essential to fully understand their thermoelectric properties.151–153
Hence, HAS provides a sensitive probe to determine the surface phonon dispersion and energy dissipation processes in terms of the e–ph coupling constant, λ, on the surfaces of these materials. The obtained experimental data of various TIs92,145,154–159 promise to evolve a more general picture about the surface dynamics and the atom–surface interaction of these peculiar surfaces. The e–ph coupling, as determined for several topological insulators belonging to the class of bismuth chalcogenides, suggests a dominant contribution of the surface quantum well states over the Dirac electrons in terms of λ.145 Investigations of the archetypal TI which is Bi2Te3(111)155 show a prominent surface acoustic mode that may have important implications in layered and nanoscale devices. Moreover, thanks to the high resolution experimental data, it was shown in comparison with ab initio calculations that the inclusion of vdW interactions is necessary for an exact theoretical description of application-relevant issues like the thermal conductivity of layered structures in general.155
The influence of e–ph coupling also shows up by softening phonon modes at specific values of momentum transfer, a phenomenon known as a Kohn anomaly.144,160,161 Whether Kohn anomalies at a phonon momentum that connects opposite sides of a topological Dirac cone are possible, is still an open question as it would require a phonon-induced transition involving a spin–flip.144,160,162,163 The latter may become possible by creating or annihilating a phonon which carries an angular momentum of 1 quantum number. While Kohn anomalies have been reported in the lower part of the phonon spectrum of TIs,155,160,162 recent studies have shown that the major contribution to e–ph coupling in these materials comes from polar optical modes.145,155,158 The ability of HAS to determine the surface averaged e–ph coupling constant λ, directly from the thermal attenuation of HAS spectra (see Section 3.2), has the advantage that a wide range of experimental conditions can be used for the evaluation compared to the limited range where e–ph effects are visible in ARPES.145 Furthermore λ can be measured exclusively for the low energy range as discussed in Section 3.2.
Since HAS or HeSE excite phonons via phonon-induced surface charge density oscillations, another consequence is that these probes may in principle excite also low-energy collective electronic excitations like surface phasons,147 surface acoustic plasmons in the THz and sub THz domains,9,158 charge density waves147,148 as well as electron–hole excitations.9,147 The observation of collective electronic excitations such as phasons and surface acoustic plasmons in interesting 2D conducting materials like topological insulators and graphene,147,164 makes HAS a tool for the investigation of THz plasmonics, with great relevance for sensors and other nano-technologies.
Furthermore, HAS can detect subsurface phonons as deep as the range of e–ph interaction, allowing investigations of the phonon dispersion curves and their e–ph interaction not only at surfaces but also in ultra-thin films.28,149,165 The possibility of observing the dispersion and knowing the e–ph coupling of waves localised at the interface of supported ultra-thin films,86 subsurface layers166 or optical branches in Bi2Te3 and Bi2Se3155 opens the prospect of developing an interface or sub-surface phononics, thus avoiding contamination problems which would affect surface acoustic wave devices in the THz domain.
Finally, as described in Section 3.6, HeSE is capable of delivering detailed information on the whole energy landscape for adsorbate-surface systems by observing the way that an adsorbate moves around in the potential at the surface, resolving diffusion processes on timescales from ns to sub-ps,117 which is beyond the scope of other techniques. This information is particularly valuable for possible sensing applications of TIs as well as for the assembly of molecular qubits167,168 on technologically relevant surfaces. For example, in a study of the diffusion of water on the TI Bi2Te3(111),113 the mechanisms underlying the molecular motion of water are specified and by comparison with first-principle calculations, aspects of its adsorption geometry are identified, as well as the energy landscape for the motion. A qualitative assessment of the rates of energy transfer between water molecules and the TI on which they move is made. The latter is discussed in terms of the nanoscale-friction affecting the motion, where a TI is particularly interesting since certain friction mechanisms are disallowed by the topological character of the substrate.
3.8 Applying helium scattering instruments for molecular-surface scattering and other atom-surface scattering experiments
In this section we discuss molecular surface scattering experiments and atom surface scattering experiments which can be carried out using a HAS apparatus. Essentially all that is required is to change the gas bottle, modify the detector settings and possibly, for scattering in the classical regime, heat the nozzle.To complete our understanding of the molecule–surface properties of materials, it is important to study directly the collision of the gas phase molecule with the surface. Unlike helium, when a molecule hits a surface, it has a certain probability to react upon impact. These interactions lie at the heart of surface based chemistry and valuable information about the molecule–surface chemistry can be extracted by monitoring the fraction of the molecular beam which sticks to the surface,171 as well as by studying the angular distribution, time-of-flight and quantum-state populations of the beam which continues towards the detector.170
A different scenario is direct quantum scattering of the molecules. In this case a diffraction pattern can be measured providing information about the structure of the surface, the dynamics of the collision and the molecule–surface potentials.172 These diffraction experiments are directly analogous to helium scattering and can be performed with the same type of apparatus. Small molecule scattering can be used to extract precise information on molecule–surface interaction potentials by measuring elastic diffraction, rotationally inelastic, and bound state selective adsorption resonant scattering. Experiments with H2, D2, and HD (including rotationally state-selected beams of para-H2 and ortho-D2), when combined with quantum scattering calculations, can lead to an accurate determination of molecule–surface physisorption potentials including spatially anisotropic terms.173–176
Another illustrative example is a diffraction study of hydrogen from a platinum surface, where an experimental molecular diffraction pattern was compared with state-of-the-art potentials to scrutinize the highly useful Born–Oppenheimer approximation in hydrogen–metal interactions.177 Molecular diffraction experiments were also performed on various isotopes of hydrogen as well as other light molecules like methane.178–180 A review of molecular hydrogen scattering experiments from metal surfaces can be found here.181
Similar to an atom, the collision of a molecule with a surface is sensitive to both the long and short range interaction potential. Unlike an atom, the rotational motion of molecules changes the interaction with the surface and needs to be taken into account in order to understand molecule–surface collisions. Significant efforts are being made to include the effect of molecular rotations in theoretical studies and obtain reliable multi-dimensional interaction potential surfaces. To support these efforts is it vital to measure experimentally the effect molecular rotations have on molecule–surface collisions. One way of studying this is by measuring inelastic rotational scattering events, where the excitation and de-excitation of rotational energy quanta can be seen as distinct diffraction peaks,179,180 measured by photo-exciting the scattered beam,182 or assesed by comparing the scattering of ortho–para spin isomers.183
Unlike the rotational quantum state, J, the rotational orientation of a molecule, characterised by the rotational projection quantum number, mJ, has been generally inaccessible to experiments. The few studies which have been performed were mainly restricted to photo-excited and paramagnetic molecules where sophisticated experimental techniques have been developed.184,185
Recently, a new type of magnetic manipulation experiment has been developed, where a modified helium-spin-echo apparatus is used to control and measure the rotational orientation of a ground state molecule.186 Two types of magnetic manipulations underlie this technique. One involves using a magnetic hexapole lens to focus certain quantum populations and defocus others,187,188 and the second involves passing the beam through a homogenous electromagnet where coherent control of the molecular quantum states is achieved and the rotational projection quantum state of the molecules which reach the surface can be both altered and determined.186 A unique aspect of these rotationally controlled molecular scattering experiments is that unlike regular diffraction measurements they can be used to determine the full scattering matrix empirically, i.e., measure all the quantum state-to-state probabilities and phase changes which characterise the gas-surface collision. A first measurement of a scattering matrix was demonstrated recently for hydrogen molecules scattering from an LiF surface.189 The results of this study demonstrated that this simple salt surface acts as both a rotational orientation polarizer and a rotational orientation analyser for hydrogen molecules, and the extracted scattering matrix elements provide what is arguably the most sensitive experimental bench mark for further development of theoretical molecule–surface interaction potentials.
In spite of the fact that the spectra do not exhibit the detailed features seen in the quantum regime a significant amount of information about the surface can be extracted through analysis of experimental data using classical mechanics. These include, among others, determination of the root mean square surface corrugation amplitude,200 isotope sensitivity in the surface composition201 and surface segregation in alloy mixtures of liquid metals.202
4 Conclusion and outlook
In this paper we show how the helium scattering, through its unique combination of low energy, charge neutrality, inertness and strict surface sensitivity can complement other scattering techniques such as photons (X-rays), electrons, ions and neutrons. We present selected examples of material properties uniquely suited to be measured using either helium atom scattering (HAS) or helium spin-echo scattering (HeSE). We also present examples of molecular surface scattering experiments and atom–surface scattering experiments in the classical regime, which can be performed using HAS and HeSE instruments. We emphasize that the examples of material properties provided in this paper are by no means a complete list, furthermore several topics such as seeded beams or neutral helium microscopy have been left out due to space limitations. We also do not discuss instrumental development, which of course is ongoing.The overarching purpose of this paper is to show that helium scattering is a great and unique technique with a very large amount of interesting and important experiments waiting to be done. However, if these experiments are to be carried out, helium scattering must be made readily available to the materials research community. This can be realised by creating a helium scattering facility, co-located and co-administrated with a synchrotron or neutron facility (or both). This would have the additional great advantage of enabling the use of two complimentary scattering techniques in parallel on the same sample.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This paper is a collected effort with broad participation from the materials characterisation community. This is reflected in the author list, which includes experts from both experimental and theoretical helium atom scattering and helium spin-echo scattering as well as experts from the synchrotron, ARPES and neutron scattering communities. We are grateful for careful readings and discussions with other members of the scattering and scanning probe communities. Particular thanks goes to Robert Feidenhansl, Liv Hornkær and Jeppe V. Lauritsen. Finally we acknowledge the contributions made by many people to the development and refinement of the methods discussed here. Among these we note, in particular, the work of J. Peter Toennies and his co-workers over an extended period of time. Their joint contribution forms the technical and scientific foundation on which recent developments have been built.References
-
M. A. van Hove, W. H. Weinberg and C.-M. Chan, Low-Energy Electron Diffraction, Springer Series in Surface Science, 1986 Search PubMed
.
- J. Perlich, J. Rubeck, S. Botta, R. Gehrke, S. V. Roth, M. A. Ruderer, S. M. Prams, M. Rawolle, Q. Zohng, V. Körstens and P. Müller-Buschbaum, Rev. Sci. Instrum., 2010, 2010, 105105 CrossRef
.
-
G. Santoro and S. Yu, Grazing Incidence Small Angle X-Ray Scattering as a Tool for In-Situ Time-Resolves Studies, in X-ray Scattering, ed. A. E. Ares, IntechOpen, 2017, p. 2 Search PubMed
.
- P. Müller-Buschbaum, Polym. J., 2013, 45, 34 CrossRef
.
- A. R. Alderwick, A. P. Jardine, W. Allison and J. Ellis, Surf. Sci., 2018, 678, 65 CrossRef CAS
.
-
B. Holst and G. Bracco, in Surface Science Techniques, ed. G. Bracco and B. Holst, Springer Verlag, Berlin, 2013, ch. 12 Search PubMed
.
-
A. Jardin, in Surface Science Techniques, ed. G. Bracco and B. Holst, Springer Verlag, Berlin, 2013, ch. 13 Search PubMed
.
- D. Farias and K.-H. Rieder, Rep. Prog. Phys., 1998, 61, 1575 CrossRef CAS
.
-
G. Benedek and J. P. Toennies, Atomic Scale Dynamics at Surfaces: Theory and Experimental Studies with Helium Atom Scattering, Springer Verlag, Berlin, 2018 Search PubMed
.
-
D. R. Miller, in Atomic and molecular beam methods, ed. G. Scoles, Oxford University Press, New York, 1988, vol. I, p. 14 Search PubMed
.
- I. Estermann and O. Stern, Z. Phys., 1930, 88, 95 CrossRef
.
- A. Kantrowitz and J. Grey, Rev. Sci. Instrum., 1951, 22, 328 CrossRef CAS
.
- L. Pedemonte and G. Bracco, J. Chem. Phys., 2003, 119, 1433 CrossRef CAS
.
- S. D. Eder, A. Salvador Palau, T. Kaltenbacher, G. Bracco and B. Holst, Rev. Sci. Instrum., 2018, 89, 113301 CrossRef CAS
.
- A. P. Graham, Surf. Sci. Rep., 2003, 49, 115 CrossRef CAS
.
- A. Gumyusenge, D. T. Tran, X. Luo, G. M. Pitch, Y. Zhao, K. Jenkins, T. J. Dunn, A. L. Ayzner, B. M. Savoie and J. Mei, Science, 2018, 362, 1131 CrossRef CAS
.
-
L. D. Landau, L. P. Pitaevskii, A. M. Kosevich and E. M. Lifshitz, Theory of Elasticity, Butterworth-Heinemann, 2012 Search PubMed
.
- D. Akinwande, C. J. Brennan, J. Scott Bunch, P. Egberts, J. R. Felts, H. Gao, R. Huang, J. Kim, T. Li, Y. Li, K. M. Liechti, N. Lu, H. S. Park, E. J. Reed, P. Wang, B. I. Yakobson, T. Zhang, Y.-W. Zhang, Y. Zhou and Y. Zhu, Extreme Mech. Lett., 2017, 13, 42–77 CrossRef
.
- N. Lindahl, D. Midtvedt, J. Svensson, O. A. Nerushev, N. Lindvall, A. Isacsson and E. E. B. Campbell, Nano Lett., 2012, 12, 2531–3526 CrossRef
.
- G. Casillas, U. Santiago, H. Barron, D. Alducin, A. Ponce and M. Jose-Yacaman, J. Phys. Chem. C, 2014, 119, 710 CrossRef
.
- G. Nicklow, N. Wakabayashi and H. G. Smith, Phys. Rev. B: Solid State, 1972, 5, 4951 CrossRef
.
- B. Amorim and F. Guinea, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 115418 CrossRef
.
- G. Benedek, J. R. Manson and S. Miret-Artés, Phys. Chem. Chem. Phys., 2020 10.1039/D0CP04729E
.
- A. Al Taleb, H. K. Yu, G. Anemone, D. Farías and A. M. Wodtke, Carbon, 2015, 95, 731 CrossRef CAS
.
- J. A. Yan, W. Y. Ruan and M. Y. Chou, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125401 CrossRef
.
- L. Chen, Z. Huang and S. Kumar, Appl. Phys. Lett., 2013, 103, 115418 Search PubMed
.
- B. Hellsing, T. Frederiksen, F. Mazzola, T. Balasubramanian and J. W. Wells, Phys. Rev. B, 2018, 98, 205428 CrossRef CAS
.
- I. Sklyadneva, G. Benedek, E. V. Chulkov, P. M. Echenique, R. Heid, K.-P. Bohnen and J. P. Toennies, Phys. Rev. Lett., 2011, 107, 095502 CrossRef
.
- B. N. J. Persson and H. Ueba, Europhys. Lett., 2010, 91, 56001 CrossRef
.
- Y. Wei, B. Wang, J. Wu, R. Yang and M. L. Dunn, Nano Lett., 2013, 13, 26 CrossRef CAS
.
- C. Büchner, S. D. Eder, T. Nesse, P. Kuhness, P. Schlexer, G. Pacchioni, J. R. Manson, M. Heyde, B. Holst and H.-J. Freund, Phys. Rev. Lett., 2018, 120, 2261010 CrossRef
.
- G. Anemone, E. Climent-Pascual, H. K. Yu, A. Al Taleb, F. Jiménez-Villacorta, C. Prieto, A. M. Wodtke, A. De Andrés and D. Farías, RSC Adv., 2016, 25, 21235 RSC
.
- P. Liu and Y. W. Zhang, Appl. Phys. Lett., 2009, 94, 231912 CrossRef
.
- Y. Lijun, AIP Adv., 2018, 8, 075104 CrossRef
.
- D. B. Zhang, E. Akatyeva and T. Dumitrica, Phys. Rev. Lett., 2011, 106, 255503 CrossRef
.
- A. Al Taleb and D. Farías, J. Phys.: Condens. Matter, 2016, 28, 103005 CrossRef
.
- A. Politano, B. Borca, M. Minniti, J. J. Hinarejos, A. L. Vázquez de Parga, D. Farías and R. Miranda, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 035450 CrossRef
.
- J. Barden, L. N. Cooper and J. R. Schrieffer, Phys. Rev., 1957, 108, 1175 CrossRef
.
- W. L. McMillan, Phys. Rev., 1968, 167, 331 CrossRef CAS
.
-
G. Grimvall, The Electron-Phonon Interaction in Metals, North-Holland, New York, 1981 Search PubMed
.
- R. B. Doak, U. Harten and J. P. Toennies, Phys. Rev. Lett., 1983, 51, 578 CrossRef CAS
.
- U. Harten, J. P. Toennies and C. Wöll, Faraday Discuss. Chem. Soc., 1985, 80, 137 RSC
.
- Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken, J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, E. Kaxiras, R. C. Ashoori and P. Jarillo-Herrero, Nature, 2018, 556, 80 CrossRef CAS
.
- G. Chen, A. L. Sharpe, P. Gallagher, I. Rosen, E. J. Fox, L. Jiang, B. Lyu, L. Hongyuan, K. Watanabe, T. Taniguchi, J. Jung, Z. Shi, D. Goldhaber-Gordon, Y. Zhang and Y. Wang, Nature, 2019, 572, 215 CrossRef CAS
.
- D. J. Trainer, B. Wang, F. Bobba, N. Samuelson, X. Xi, J. Zasdzinski, J. Nieminen, A. Bansil and M. Iavarone, ACS Nano, 2020, 14, 2718 CrossRef CAS
.
- O. Zheliuk, J. Lu, J. Yang and J. Ye, Phys. Status Solidi, 2017, 11, 1700245 CrossRef
.
- O. Zheliuk, J. M. Lu, Q. H. Chen, A. A. El Yumin, S. Golightly and J. T. Ye, Nat. Nanotechnol., 2019, 14, 1123 CrossRef CAS
.
- H. Wang, X. Huang, J. Lin, J. Cui, Y. Chen, C. Zhu and F. Liu, Nat. Commun., 2017, 8, 394 CrossRef
.
- R. Bistritzer and A. H. MacDonald, Proc. Natl. Acad. Sci. U. S. A., 2018, 108, 12233 CrossRef
.
- U. Mogera and G. U. Kulkarni, Carbon, 2020, 156, 470 CrossRef CAS
.
- C. C. Liu, L. D. Zhang, W. Q. Chen and F. Yang, Phys. Rev. Lett., 2018, 121, 217001 CrossRef CAS
.
- M. Yankowitz, S. Chen, H. Polshyn, Y. Zhang, K. Watanabe, T. Taniguchi, D. Graf, A. F. Young and C. R. Dean, Science, 2019, 363, 1059 CrossRef CAS
.
- F. Wu, A. H. MacDonald and I. Martin, Phys. Rev. Lett., 2018, 121, 217001 CrossRef
.
- Y. W. Choi and H. J. Choi, Phys. Rev. B, 2018, 98, 241412 CrossRef CAS
.
- F. Mazolla, T. Fredriksen, T. Balasubramanian, P. Hofmann, P. Hellsing and J. W. Wells, Phys. Rev. B, 2017, 95, 075430 CrossRef
.
- S. K. Mahatha, A. Ngankeu, N. F. Hinsche, I. Mertig, K. Guilloy, P. L. Matzen, M. Bianchi, C. E. Sanders, J. A. Miwa, H. Bana, E. Travaglia, L. Paolo, L. Bignardi, D. Lizzit, R. Larciprete, A. Baraldi, S. Lizzit and P. Hofmann, Surf. Sci., 2019, 681, 64 CrossRef CAS
.
- H. S. Arora, R. Polski, Y. Zhang, A. Thomson, Y. Choi, H. Kim, Z. Lin, I. Z. Wilson, X. Xu and J. H. Chu, Nature, 2020, 583, 379–384 CrossRef CAS
.
- E. Thingstad, A. Kamra, J. W. Wells and A. Sudbø, Phys. Rev. B, 2020, 101, 214513 CrossRef CAS
.
- N. Esbjerg and J. K. N. Nørskov, Phys. Rev. Lett., 1980, 45, 807 CrossRef CAS
.
- G. Benedek, M. Bernasconi, K.-P. Bohnen, D. Campi, E. V. Chulkov, I. Y. Sklyadneva and J. P. Toennies, Phys. Chem. Chem. Phys., 2014, 16, 7159 RSC
.
- P. B. Allen, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 6, 2577 CrossRef CAS
.
- J. R. Manson, G. Benedek and S. Salvador Miret-Artés, J. Phys. Chem. Lett., 2016, 7, 1016 CrossRef CAS
.
- G. Anemone, M. Garnica, M. Zappia, P. Casado Aguilar, A. Al Taleb, C.-N. Kuo, C. S. Lue, A. Politiano, G. Benedek, A. L. Vazquez de Parga, R. Miranda and D. Farias, 2D Mater., 2020, 7, 025007 CrossRef CAS
.
- G. Anemone, M. Garnica, M. Zappia, P. Casado Aguilar, A. Al Taleb, C.-N. Kuo, C. S. Lue, A. Politiano, A. L. Vazquez de Parga, G. Benedek, R. Miranda and D. Farias, npj 2D Mater. Appl., 2020 DOI:10.1038/s41699-021-00204-5
.
- G. Anemone, A. Al Taleb, G. Benedek, A. Castellanos-Gomez and D. Farias, J. Phys. Chem. C, 2019, 123, 3698 CrossRef
.
- S. Lisi, X. Lu, T. Benschop, T. A. de Johng, P. Stepanov, J. R. Duran and F. Margot, 2020, arXiv, arXiv:2002.02289.
- J. E. Gayone, C. Kirkegaard, J. W. Wells, S. V. Hoffmann, Z. Li and P. Hofmann, Appl. Phys. A: Mater. Sci. Process., 2005, 80, 943–949 CrossRef CAS
.
- D. A. Conyuh, Y. M. Beltukov and D. A. Parshin, J. Phys.: Conf. Ser., 2017, 929, 012031 CrossRef
.
- L. Zhang, J. Zheng, Y. Wang, L. Zhang, Z. Jin, L. Hong, Y. Wang and J. Zhang, Nat. Commun., 2017, 8, 67 CrossRef
.
- J. Schroeder, M. Lee, S. K. Saha and P. D. Persans, J. Non-Cryst. Solids, 1997, 222, 342 CrossRef CAS
.
- U. Buchenau, Condens. Matter Phys., 2019, 22, 43601 CrossRef CAS
.
- N. Tomoshige, H. Mizuno, T. Mori, K. Kim and N. Matubayasi, Sci. Rep., 2019, 9, 19514 CrossRef CAS
.
- A. Chumakov, G. Monaco, A. Fontana, A. Bosak, R. P. Hermann, D. Bessas, B. Wehinger, W. A. Crichton, M. Krisch, R. Rüffer, G. Baldi, G. Carini Jr., G. Carini, G. Dæangelo, E. Gilioli, G. Tripodo, M. Zanatta, B. Winkler, V. Milman, K. Refson, M. T. Dove, N. Dubrovinskaia, L. Dubrovinsky, R. Keding and Y. Z. Yue, Phys. Rev. Lett., 2014, 112, 025502 CrossRef CAS
.
- M. Baggioli and A. Zaccone, Phys. Rev. Lett., 2019, 122, 145501 CrossRef CAS
.
- W. Steurer, A. Apfolter, M. Koch, W. E. Ernst, B. Holst, E. Søndergård and J. R. Manson, Phys. Rev. Lett., 2007, 99, 035503 CrossRef CAS
.
- W. Steurer, A. Apfolter, M. Koch, W. E. Ernst, E. Søndergård, J. R. Manson and B. Holst, Phys. Rev. Lett., 2008, 100, 135504 CrossRef CAS
.
- W. Steurer, A. Apfolter, M. Koch, W. E. Ernst, E. Søndergård, J. R. Manson and B. Holst, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 045427 CrossRef
.
- W. Steurer, A. Apfolter, M. Koch, W. E. Ernst, E. Søndergård, J. R. Manson and B. Holst, J. Phys.: Condens. Matter, 2008, 20, 224003 CrossRef
.
- M. A. Freedman, A. W. Rosenbaum and S. J. Sibener, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 113410 CrossRef
.
- M. A. Freedman, J. S. Becker, A. W. Rosenbaum and S. J. Sibener, J. Chem. Phys., 2008, 129, 044906 CrossRef
.
- M. A. Freedman, J. S. Becker and S. J. Sibener, J. Phys. Chem. B, 2008, 112, 16090 CrossRef CAS
.
- J. S. Becker, R. D. Brown, D. R. Killelea, H. Yuan and S. J. Sibener, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 977 CrossRef CAS
.
- S. D. Eder, K. Fladischer, S. R. Yeandel, A. Lelarge, S. C. Parker, E. Søndergård and B. Holst, Sci. Rep., 2015, 5, 14545 CrossRef CAS
.
- J. Braun, J. P. Toennies and C. Wöll, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 117075 CrossRef
.
- E. M. McIntosh, J. Ellis, A. P. Jardine, P. Licence, R. G. Jones and W. Allison, Chem. Sci., 2014, 5, 667 RSC
.
- A. Tamtögl, E. Bahn, J. Zhu, P. Fouquet, J. Ellis and W. Allison, J. Phys. Chem. C, 2015, 119, 25983 CrossRef
.
- B. Holst, M. Nohlen, K. Wandelt and W. Allision, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 10195 CrossRef
.
- C. Wöll, J. Phys.: Condens. Matter, 2004, 16, 2981 CrossRef
.
- A. S. Sanz and S. Salvador Miret-Artés, Phys. Rep., 2007, 451, 37 CrossRef
.
- P. Kraus, A. Tamtögl, M. Mayrhofer-Reinhartshuber, F. Apolloner, C. Gösweiner, S. Miret-Artés and W. E. Ernst, J. Phys. Chem. C, 2015, 119, 17235 CrossRef CAS
.
- G. Benedek, J. R. Manson and S. Salvador Miret-Artés, Surf. Sci. Rep., 2021 Search PubMed
, unpublished.
- A. Tamtögl, A. Ruckhofer, D. Campi, W. Allison and W. E. Ernst, Phys. Chem. Chem. Phys., 2020 10.1039/D0CP05388K
.
-
L. J. Whitman, Digital Encyclopedia of Applied Physics, Wiley, 2003, p. 361 Search PubMed
.
- A. Extance, Nature, 2018, 555, 545 CrossRef CAS
.
- J. V. Lauritsen, M. C. R. Jensen, K. Venkataramani, B. Hinnemann, S. Helveg, B. S. Clausen and F. Besenbacher, Phys. Rev. Lett., 2009, 103, 076103 CrossRef CAS
.
- G. H. Enevoldsen, A. S. Foster, M. C. Christensen, J. V. Lauritsen and F. Besenbacher, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 205415 CrossRef
.
- C. Büchner and M. Heyde, Prog. Surf. Sci., 2017, 92, 341 CrossRef
.
- D. Martoccia, P. R. Willmott, T. Brugger, M. Björck, S. Günther, C. M. Schlepütz, A. Cervellino, S. A. Pauli, B. D. Patterson, S. Marchini, J. Wintterlin, W. Moritz and T. Greber, Phys. Rev. Lett., 2008, 101, 126102 CrossRef CAS
.
- A. L. Vázquez de Parga, F. Calleja, B. Borca, M. C. G. Passeggi, J. J. Hinarejos, F. Guinea and R. Miranda, Phys. Rev. Lett., 2008, 100, 056807 CrossRef
.
- B. Borca, S. Barja, M. Garnica, M. Minniti, A. Politano, J. M. Rodriguez-García, J. J. Hinarejos, D. Farías, A. L. V. D. Parga and R. Miranda, New J. Phys., 2010, 12, 093018 CrossRef
.
- A. L. V. de Parga, F. Calleja, B. Borca, M. C. G. Passeggi, J. J. Hinarejos, F. Guinea and R. Miranda, Phys. Rev. Lett., 2008, 101, 099704 CrossRef
.
- D. Stradi, S. Barja, C. Diaz, M. Garnica, B. Borca, J. J. Hinarejos, D. Sanchez-Portal, M. Alcami, A. Arnau, A. L. Vazques de Parga, R. Miranda and F. Martin, Phys. Rev. Lett., 2011, 106, 186102 CrossRef CAS
.
- N. Avidor and W. Allison, J. Phys. Chem. Lett., 2016, 7, 4520 CrossRef CAS
.
- C. Lin, G. Corem, O. Godsi, G. Alexandrowicz, G. R. Darling and A. Hodgson, J. Am. Chem. Soc., 2018, 140, 15804 CrossRef CAS
.
- G. Corem, P. Kole, J. Zhu, T. Kravchuk, J. R. Manson and G. Alexandrowicz, J. Phys. Chem. C, 2013, 117, 23657 CrossRef CAS
.
- E. Bahn, A. Tamtögl, J. Ellis, W. Allison and P. Fouquet, Carbon, 2017, 114, 504 CrossRef CAS
.
- O. Björneholm, M. H. Hansen, A. Hodgson, L.-M. Liu, D. T. Limmer, A. Michaelides, P. Pedevilla, J. Rossmeisl, H. Shen, G. Tocci, E. Tyrode, M.-M. Walz, J. Werner and H. Bluhm, Chem. Rev., 2016, 116, 7698 CrossRef
.
- N. Avidor, H. Hedgeland, G. Held, A. P. Jardine, W. Allision, J. Ellis, T. Kravchuck and G. Alexandrowicz, J. Phys. Chem. A, 2011, 115, 7205 CrossRef CAS
.
- A. Jardine, H. Hedgeland, G. Alexandrowicz, W. Allison and J. Ellis, Prog. Surf. Sci., 2009, 84, 323 CrossRef CAS
.
- A. P. Jardine, G. Alexandrowicz, H. Hedgeland, W. Allison and J. Ellis, Phys. Chem. Chem. Phys., 2009, 11, 3355 RSC
.
- A. Tamtögl, Nachr. Chem., 2020, 68, 65 CrossRef
.
- P. Fouquet, H. Hedgeland, A. P. Jardine, G. Alexandrowicz, W. Allison and J. Ellis, Physica B, 2006, 385-386, 269 CrossRef CAS
.
- A. Tamtögl, M. Sacchi, N. Avidor, I. Calvo-Almazán, P. S. M. Townsend, M. Bremholm, P. Hofmann, J. Ellis and W. Allison, Nat. Commun., 2020, 11, 278 CrossRef
.
- B. A. J. Lechner, P. R. Kole, H. Hedgeland, A. P. Jardine, W. Allison, B. J. Hinch and J. Ellis, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 121405 CrossRef
.
- H. Hedgeland, P. Fouquet, A. P. Jardine, G. Alexandrowicz, W. Allison and J. Ellis, Nat. Phys., 2009, 5, 561 Search PubMed
.
- B. A. J. Lechner, M. Sacchi, A. P. Jardine, H. Hedgeland, W. Allison, J. Ellis, S. J. Jenkins, P. C. Dastoor and B. J. Hinch, J. Phys. Chem. Lett., 2013, 4, 1953 Search PubMed
.
- P. Rotter, B. A. J. Lechner, A. Morherr, D. M. Chisnall, D. J. Ward, A. P. Jardine, J. Ellis, W. Allison, B. Eckhardt and G. Witte, Nat. Mater., 2016, 15, 397 CrossRef CAS
.
- S. Paterson, W. Allison, H. Hedgeland, J. Ellis and A. P. Jardine, Phys. Rev. Lett., 2011, 106, 256101 CrossRef CAS
.
- A. P. Jardine, E. Y. M. Lee, D. J. Ward, G. Alexandrowicz, H. Hedgeland, W. Allison, J. Ellis and E. Pollak, Phys. Rev. Lett., 2010, 105, 136101 CrossRef CAS
.
- M. Sacchi, P. Singh, D. M. Chisnall, D. J. Ward, A. P. Jardine, W. Allison, J. Ellis and H. Hedgeland, Faraday Discuss., 2017, 204, 471 RSC
.
- G. Alexandrowicz, P. Kole, E. Lee, H. Hedgeland, R. Ferrando, A. P. Jardine, W. Allison and J. Ellis, J. Am. Chem. Soc., 2008, 130, 6789 CrossRef CAS
.
- S. P. Rittmeyer, D. J. Ward, P. Gütlein, J. Ellis, W. Allison and K. Reuter, Phys. Rev. Lett., 2016, 117, 196001 CrossRef
.
- S. P. Rittmeyer, V. J. Bukas and K. Reuter, Adv. Phys., 2018, 3, 1381574 Search PubMed
.
- B. A. J. Lechner, A. S. de Wijn, H. Hedgeland, A. P. Jardine, B. J. Hinch, W. Allison and J. Ellis, J. Chem. Phys., 2013, 138, 194710 CrossRef CAS
.
- H. Hedgeland, M. Sacchi, P. Singh, A. J. McIntosh, A. P. Jardine, G. Alexandrowicz, D. J. Ward, S. J. Jenkins, W. Allison and J. Ellis, J. Phys. Chem. Lett., 2016, 7, 4819 CrossRef CAS
.
- G. Alexandrowicz and A. P. Jardine, J. Phys.: Condens. Matter, 2007, 19, 305001 CrossRef
.
- P. R. Kole, A. P. Jardine, H. Hedgeland and G. Alexandrowicz, J. Phys.: Condens. Matter, 2010, 22, 304018 CrossRef CAS
.
- A. Jones, A. Tamtögl, I. Calvo-Almazán and A. Hansen, Sci. Rep., 2016, 6, 27776 CrossRef
.
- C. Adams, Top. Catal., 2019, 52, 1219 Search PubMed
.
- G. Ertl, Angew. Chem., Int. Ed. Engl., 1990, 29, 1219 CrossRef
.
- G. Alexandrowicz, A. P. Jardine, P. Fouquet, S. Dworski, W. Allison and J. Ellis, Phys. Rev. Lett., 2004, 93, 156103 CrossRef CAS
.
- R. Marquardt, F. Cuvelier, R. A. Olsen, E. J. Baerends, J. C. Tremblay and P. Saalfrank, J. Chem. Phys., 2010, 132, 074108 CrossRef
.
- T. Firmino, R. Marquardt, F. Gatti and W. Dong, J. Phys. Chem. Lett., 2014, 5, 4270 CrossRef CAS
.
-
T. Firmino, R. Marquardt, F. Gatti, D. Zanuttini and W. Dong, Full Quantum Calculations of the Diffusion Rate of Adsorbates, inFronties in Quantum Methods and Application in Chemistry and Physics: Selected and Edited PRoceedings of QSCP-XVIII, ed. M. A. C. Nascimento, Springer Verlag, Berlin, 2015, p. 177 Search PubMed
.
- G. Grüner, Rev. Mod. Phys., 1988, 60, 1129 CrossRef
.
- T. Wehling, A. Black-Schaffer and A. Balatsky, Adv. Phys., 2014, 63, 1 CrossRef CAS
.
- L. Barreto, L. Kühnemund, F. Edler, C. Tegenkamp, J. Mi, M. Bremholm, B. B. Iversen, C. Frydendahl, M. Bianchi and P. Hofmann, Nano Lett., 2014, 14, 3755 CrossRef CAS
.
- J. Moore, Nat. Phys., 2009, 5, 378 Search PubMed
.
- X.-L. Qi and S.-C. Zhang, Rev. Mod. Phys., 2011, 83, 1057 CrossRef CAS
.
- D. Hsieh, Y. Xia, D. Qian, L. Wray, J. H. Dil, F. Meier, J. Osterwalder, L. Patthey, J. G. Checkelsky, N. P. Ong, A. V. Fedorov, H. Lin, A. Bansil, D. Grauer, Y. S. Hor, R. J. Cava and M. Z. Hasan, Nature, 2009, 460, 1101 CrossRef CAS
.
- M. Caputo, M. Panighel, S. Lisi, L. Khalil, G. D. Santo, E. Papalazarou, A. Hruban, M. Konczykowski, L. Krusin-Elbaum, Z. S. Aliev, M. B. Babanly, M. M. Otrokov, A. Politano, E. V. Chulkov, A. Arnau, V. Marinova, P. K. Das, J. Fujii, I. Vobornik, L. Perfetti, A. Mugarza, A. Goldoni and M. Marsi, Nano Lett., 2016, 16, 3409 CrossRef CAS
.
- L. M. Schoop, F. Pielnhofer and B. V. Lotsch, Chem. Mater., 2018, 30, 3155 CrossRef CAS
.
- Z.-H. Pan, A. V. Fedorov, D. Gardner, Y. S. Lee, S. Chu and T. Valla, Phys. Rev. Lett., 2012, 108, 187001 CrossRef
.
- X. Zhu, L. Santos, C. Howard, R. Sankar, F. C. Chou, C. Chamon and M. El-Batanouny, Phys. Rev. Lett., 2012, 108, 185501 CrossRef
.
- G. Benedek, S. Miret-Artés, J. R. Manson, A. Ruckhofer, W. E. Ernst and A. Tamtögl, J. Phys. Chem. Lett., 2020, 11, 1927 CrossRef CAS
.
- E. Frantzeskakis, S. V. Ramankutty, N. de Jong, Y. K. Huang, Y. Pan, A. Tytarenko, M. Radovic, N. C. Plumb, M. Shi, A. Varykhalov, A. de Visser, E. van Heumen and M. S. Golden, Phys. Rev. X, 2017, 7, 041041 Search PubMed
.
- A. Tamtögl, P. Kraus, M. Mayrhofer-Reinhartshuber, G. Benedek, M. Bernasconi, D. Dragoni, D. Campi and W. E. Ernst, npj Quantum Mater., 2019, 4, 28 CrossRef
.
- P. Hofmann, M. M. Ugeda, A. Tamtögl, A. Ruckhofer, W. E. Ernst, G. Benedek, A. J. Martínez-Galera, A. Stróżecka, J. M. Gómez-Rodríguez, E. Rienks, M. F. Jensen, J. I. Pascual and J. W. Wells, Phys. Rev. B, 2019, 99, 035438 CrossRef CAS
.
- G. Benedek, J. R. Manson and S. Miret-Artés, Adv. Mater., 2020, 32, 2002072 CrossRef CAS
.
- Y. V. Ivanov, A. T. Burkov and D. A. Pshenay-Severin, Phys. Status Solidi B, 2018, 255, 1800020 CrossRef
.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105 CrossRef CAS
.
- A. J. Minnich, M. S. Dresselhaus, Z. F. Ren and G. Chen, Energy Environ. Sci., 2009, 2, 466 RSC
.
- J. Liang, L. Cheng, J. Zhang, H. Liu and Z. Zhang, Nanoscale, 2016, 8, 8855 RSC
.
- A. Tamtögl, P. Kraus, N. Avidor, M. Bremholm, E. M. J. Hedegaard, B. B. Iversen, M. Bianchi, P. Hofmann, J. Ellis, W. Allison, G. Benedek and W. E. Ernst, Phys. Rev. B, 2017, 95, 195401 CrossRef
.
- A. Tamtögl, D. Campi, M. Bremholm, E. M. J. Hedegaard, B. B. Iversen, M. Bianchi, P. Hofmann, N. Marzari, G. Benedek, J. Ellis and W. Allison, Nanoscale, 2018, 10, 14627 RSC
.
- A. Tamtögl, M. Pusterhofer, M. Bremholm, E. M. Hedegaard, B. B. Iversen, P. Hofmann, J. Ellis, W. Allison, S. Miret-Artés and W. E. Ernst, Surf. Sci., 2018, 678, 25–31 CrossRef
.
- A. Ruckhofer, A. Tamtögl, M. Pusterhofer, M. Bremholm and W. E. Ernst, J. Phys. Chem. C, 2019, 123, 17829–17841 CrossRef CAS
.
- A. Ruckhofer, D. Campi, M. Bremholm, P. Hofmann, G. Benedek, M. Bernasconi, W. E. Ernst and A. Tamtögl, Phys. Rev. Res., 2020, 2, 023186 CrossRef CAS
.
- A. Ruckhofer, S. Halbritter, H. E. Lund, A. J. Holt, M. Bianchi, M. Bremholm, G. Benedek, P. Hofmann, W. E. Ernst and A. Tamtögl, Phys. Chem. Chem. Phys., 2020 10.1039/D0CP04738D
.
- X. Zhu, L. Santos, R. Sankar, S. Chikara, C. Howard, F. C. Chou, C. Chamon and M. El-Batanouny, Phys. Rev. Lett., 2011, 107, 186102 CrossRef
.
- S. Kalish, C. Chamon, M. El-Batanouny, L. H. Santos, R. Sankar and F. C. Chou, Phys. Rev. Lett., 2019, 122, 116101 CrossRef CAS
.
- C. Howard, M. El-Batanouny, R. Sankar and F. C. Chou, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 035402 CrossRef
.
- C. Howard and M. El-Batanouny, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 075425 CrossRef
.
- D. Maccariello, D. Campi, A. A. Taleb, G. Benedek, D. Farías, M. Bernasconi and R. Miranda, Carbon, 2015, 93, 1 CrossRef CAS
.
- P. Kraus, A. Tamtögl, M. Mayrhofer-Reinhartshuber, G. Benedek and W. E. Ernst, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 245433 CrossRef
.
- A. Tamtögl, P. Kraus, M. Mayrhofer-Reinhartshuber, D. Campi, M. Bernasconi, G. Benedek and W. E. Ernst, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035410 CrossRef
.
- M. Warner, S. Din, I. S. Tupitsyn, G. W. Morley, A. M. Stoneham, J. A. Gardener, Z. Wu, A. J. Fisher, S. Heutz, C. W. M. Kay and G. Aeppli, Nature, 2013, 503, 504 CrossRef CAS
.
- M. J. Graham, J. M. Zadrozny, M. S. Fataftah and D. E. Freedman, Chem. Mater., 2017, 29, 1885 CrossRef CAS
.
- A. A. McMillan, J. D. Graham, S. A. Willson, R. G. Garber, C. J. Thompson and S. J. Sibener, Supercond. Sci. Technol., 2020, 33, 105012 CrossRef
.
- A. Kleyn, Chem. Soc. Rev., 2003, 32, 87 RSC
.
- R. van Lent, S. V. Auras, K. Cao, A. J. Walsh, M. A. Gleeson and L. B. Juurlink, Science, 2019, 363, 155 CrossRef CAS
.
- D. Faras and R. Miranda, Prog. Surf. Sci., 2011, 86, 222 CrossRef
.
- K. B. Whaley, J. C. Light, J. P. Cowin and S. J. Sibener, Chem. Phys. Lett., 1982, 89, 89 CrossRef CAS
.
- C. F. Yu, K. B. Whaley, C. S. Hogg and S. J. Sibener, Phys. Rev. Lett., 1983, 51, 2210 CrossRef CAS
.
- C. F. Yu, K. B. Whaley, C. S. Hogg and S. J. Sibener, J. Chem. Phys., 1985, 83, 4217 CrossRef CAS
.
- K. B. Whaley, C. F. Yu, C. S. Hogg, J. C. Light and S. J. Sibener, J. Chem. Phys., 1985, 83, 4235 CrossRef CAS
.
- P. Nieto, E. Pijper, D. Barredo, G. Laurent, R. A. Olsen, E.-J. Baerends, G.-J. Kroes and D. Faras, Science, 2006, 312, 86 CrossRef CAS
.
- J. P. Cowin, C.-F. Yu, S. J. Sibener and L. Wharton, J. Chem. Phys., 1983, 79, 3537 CrossRef CAS
.
- Y. Ekinci and J. P. Toennies, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 205430 CrossRef
.
- A. Al Taleb, G. Anemone, L. Zhou, H. Guo and D. Faras, J. Phys. Chem. Lett., 2019, 10, 1574 CrossRef CAS
.
- D. Farías, H. F. Busnengo and F. Martín, J. Phys.: Condens. Matter, 2007, 19, 305003 CrossRef
.
- G. O. Sitz, A. C. Kummel and R. N. Zare, J. Chem. Phys., 1987, 87, 3247 CrossRef CAS
.
- M. Bertino, A. Glebov, J. Toennies, F. Traeger, E. Pijper, G. Kroes and R. Mowrey, Phys. Rev. Lett., 1998, 81, 5608 CrossRef CAS
.
- A. Hodgson, Prog. Surf. Sci., 2000, 63, 1 CrossRef CAS
.
- L. Vattuone, L. Savio, F. Pirani, D. Cappelletti, M. Okada and M. Rocca, Prog. Surf. Sci., 2010, 85, 92 CrossRef CAS
.
- O. Godsi, G. Corem, Y. Alkoby, J. T. Cantin, R. V. Krems, M. F. Somers, J. Meyer, G.-J. Kroes, T. Maniv and G. Alexandrowicz, Nat. Commun., 2017, 8, 1 CrossRef
.
- T. Kravchuk, M. Reznikov, P. Tichonov, N. Avidor, Y. Meir, A. Bekkerman and G. Alexandrowicz, Science, 2011, 331, 319 CrossRef CAS
.
- C. Krüger, E. Lisitsin-Baranovsky, O. Ofer, P.-A. Turgeon, J. Vermette, P. Ayotte and G. Alexandrowicz, J. Chem. Phys., 2018, 149, 164201 CrossRef
.
- Y. Alkoby, H. Chadwick, O. Godsi, H. Labiad, M. Bergin, J. T. Cantin, I. Litvin, T. Maniv and G. Alexandrowicz, Nat. Commun., 2020, 11, 1 Search PubMed
.
- K. J. Nihill, J. D. Graham and S. J. Sibener, Phys. Rev. Lett., 2017, 119, 176001 CrossRef
.
- T. Ruf, R. W. Henn, M. Asen-Palmer, E. Gmelin, M. Cardona, H.-J. Pohl, G. G. Devyatych and P. G. Sennikov, Solid State Commun., 2000, 115, 243 CrossRef CAS
.
- J.-Y. Li, C.-T. Huang, L. P. Rokhinson and J. C. Sturm, Appl. Phys. Lett., 2013, 103, 162105 CrossRef
.
- J. A. Barker and D. J. Auerbach, Faraday Discuss., 1985, 80, 277 RSC
.
- W. W. Hayes and J. R. Manson, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 113408 CrossRef
.
- J. R. Manson, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 6924 CrossRef
.
- B. Gumhalter, Phys. Rep., 1985, 351, 1 CrossRef
.
- S. Miret-Artés and E. Pollak, Surf. Sci. Rep., 2012, 67, 161 CrossRef
.
- W. W. Hayes and J. R. Manson, Adv. Quantum Chem., 2019, 80, 319 CrossRef CAS
.
- M. F. Bertino, J. R. Manson and W. Silvestri, J. Chem. Phys., 1998, 108, 10239 CrossRef CAS
.
- W. W. Hayes and J. R. Manson, Phys. Rev. Lett., 2012, 109, 063203 CrossRef CAS
.
- A. Muis and J. R. Manson, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 2205 CrossRef CAS
.
- J. Dai and J. R. Manson, J. Chem. Phys., 2003, 119, 9842 CrossRef CAS
.
- G. Benedek, J. R. Manson, S. Miret-Artés, A. Ruckhofer, W. E. Ernst, A. Tamtögl and J. P. Toennies, Condens. Matter, 2020, 5, 79 CrossRef CAS
.
| This journal is © the Owner Societies 2021 |